Towards unconstrained compartment modeling in white matter using diffusion-relaxation MRI with tensor-valued diffusion encoding

Abstract

Purpose:

To optimize diffusion-relaxation MRI with tensor-valued diffusion encoding for precise estimation of compartment-specific fractions, diffusivities and T₂ values with a two-compartment model of white matter, and to explore the approach in vivo.

Methods:

Sampling protocols featuring different b-values (b), b-tensor shapes (b_Δ), and echo times (TE) were optimized using Cramér-Rao lower bounds (CRLB). Whole-brain data were acquired in children, adults, and elderly with white matter lesions. Compartment fractions, diffusivities and T₂ values were estimated in a model featuring two microstructural compartments represented by a ‘stick’ and a ‘zeppelin’.

Results:

Precise parameter estimates were enabled by sampling protocols featuring seven or more ‘shells’ with unique b/b_Δ/TE-combinations. Acquisition times were approximately 15 minutes. In white matter of adults, the ‘stick’ compartment had a fraction of approximately 0.5 and, compared with the ‘zeppelin’ compartment, featured lower isotropic diffusivities (0.6 vs. 1.3 μm²/ms) but higher T₂ values (85 vs. 65 ms). Children featured lower ‘stick’ fractions (0.4). White matter lesions exhibited high ‘zeppelin’ isotropic diffusivities (1.7 μm²/ms) and T₂ values (150 ms).

Conclusions:

Diffusion-relaxation MRI with tensor-valued diffusion encoding expands the set of microstructure parameters that can be precisely estimated and therefore increases their specificity to biological quantities.

1 |. INTRODUCTION

Diffusion MRI (dMRI) has gained widespread use due to its sensitivity to brain tissue microstructure (1). Methods such as diffusion tensor imaging (DTI) (2) and diffusion kurtosis imaging (DKI) (3) detect microstructural alterations in diseases such as multiple sclerosis (4), white matter lesions (5, 6), gliomas (7) and parkinsonian disorders (8) as well as in normal processes such as learning (9, 10) and maturation (11–13). Although sensitive, DTI and DKI parameters do not report on specific quantities of the tissue microstructure (14, 15). Recent research has therefore aimed to develop methods with specificity to microstructural quantities such as the axonal density.

One approach to estimate microstructural quantities from dMRI data is to use a forward model that parameterizes the signal in terms of such quantities and fit the model to acquired data (1). Such models tend to represent tissue by ‘compartments’ with specific signal contributions weighted by fractions (16–28). In white matter, water diffusion in the intra- and extra-axonal spaces are typically modelled by ‘stick’ and ‘zeppelin’ diffusion tensors, respectively. Correlations have been found between parameters of such models and microstructural quantities from histology. For example, the ‘stick’ fraction (the fraction of the ‘stick’ compartment) has been correlated with the axonal volume fraction (29) and the radial diffusivity of the ‘zeppelin’ compartment has been correlated with the myelin volume fraction (30).

While a complete description of the tissue microstructure requires many parameters, dMRI normally supports the estimation of just a few (31–33). Trying to estimate many microstructural parameters from dMRI data leads to problems with degeneracy and low precision, which has been addressed by the introduction of various model constraints. For example, compartment diffusivities may be fixed to specific values or assumed to follow given relations (16, 23, 27). Although such constraints increase precision, they introduce another problem: the estimated parameters represent microstructural quantities truthfully only when the constraints are valid. For example, interpreting the ‘stick’ fraction as a volume fraction without estimating compartment-specific T₂ relaxation values is valid only if these values are equal. If they are different, as in white matter lesions, the results can be strongly misleading (28).

To estimate microstructural quantities across a wide range of conditions, model constraints should be replaced with independent information. Here we explore two approaches for acquiring such information. The first is tensor-valued diffusion encoding, which adds information by acquiring data with multiple shapes of the b-tensor (34–36). Such data can be used to estimate all parameters in the relatively unconstrained ‘standard model’ (37, 38). The second is diffusion-relaxation experiments, which adds information by acquiring diffusion data for multiple echo times (TE) (39–42). Such data can be used to estimate compartment-specific T₂ values in brain tissue (28, 40). These approaches have previously been used separately but not in combination.

In this work, we investigate how to best combine tensor-valued diffusion encoding and diffusion-relaxation experiments for maximal information encoding. For this purpose, we defined sampling protocols in terms of ‘shells’ with different b-values (b), shapes of the b-tensor (b_Δ) and echo times (TE). A minimally constrained two-compartment model was used to optimize protocols for minimal parameter variance based on Cramér-Rao lower bounds (CRLB) (43, 44). The importance of each independent acquisition dimension was assessed, and the performance of different sampling protocols was evaluated. The clinical feasibility of the approach was tested by using the principles learned from the optimization to design an in vivo protocol and acquire data in children, adults, and elderly with white matter lesions.

2 |. THEORY

2.1 |. A general diffusion-relaxation compartment model

We start by considering the class of models (18, 19, 29, 33, 40, 45–47) that describe the dMRI signal as an ‘isotropic convolution’ ($⊛$) (48) on the unit sphere between an axisymmetric microstructure kernel K and an orientation distribution function (ODF) P, according to

$$S\left(\mathbf{u}\right)=\left(K⊛P\right)\left(\mathbf{u}\right)={\int }_{\left|\mathbf{n}\right|=1}^{}K\left(\mathbf{u}·\mathbf{n}\right)P\left(\mathbf{n}\right)\mathrm{d}\mathbf{n},$$ Eq. 1

where u is the symmetry axis of the diffusion encoding and n is the symmetry axis of the kernel.

To define a general compartment model of diffusion and T₂ relaxation, we consider kernels on the form

$$K\left(\mathbf{u}·\mathbf{n}\right)=S_0{\sum }_{\mathrm{j}=1}^{\mathrm{J}}{f}_{\mathrm{j}}\exp \left(-\mathbf{B}\left(\mathbf{u}\right):{\mathbf{D}}_{\mathrm{j}}\left(\mathbf{n}\right)\right)\exp \left(-\frac{\mathrm{T}\mathrm{E}}{{\mathrm{T}}_{2;\mathrm{j}}}\right).$$ Eq. 2

The experiment is described by the axisymmetric diffusion-encoding tensor (b-tensor) B with symmetry axis u (35, 36) and the echo time TE. Each compartment is described by an axisymmetric diffusion tensor D_j and a T₂ value T_2;j, and is weighted by a fraction f_j (Σf_j = 1). Assuming that the model captures the diffusion and T₂ relaxation properties of all relevant compartments, the fractions theoretically represent the proton density- and T₁-weighted volume fractions of those compartments.

As in Eriksson (49), we parameterize D in terms of its isotropic diffusivity D_I and anisotropy D_Δ, which relate to the axial (D_||) and radial (D_⊥) diffusivities according to D_I = (D_|| + 2D_⊥)/3 and D_Δ = (D_|| – D_⊥)/(D_|| + 2D_⊥). The double inner product B:D is given by

$$\mathbf{B}\left(\mathbf{u}\right):\mathbf{D}\left(\mathbf{n}\right)={bD}_{\mathrm{I}}{(1+2b}_{\Delta }{D}_{\Delta }{\mathrm{L}}_2\left(\mathbf{u}·\mathbf{n}\right)),$$ Eq. 3

where b is the conventional b-value (50), b_Δ is the shape of the b-tensor, which ranges from –0.5 (planar tensor encoding; PTE) through zero (spherical tensor encoding; STE) to unity (linear tensor encoding; LTE), and L₂ is the second Legendre polynomial (49).

We simplify the convolution in Eq. 1 by expanding K and P in the spherical harmonic basis, according to

$$S\left(\mathbf{u}\right)=\left(K⊛P\right)\left(\mathbf{u}\right)=\sum _l\sum _m{k}_{l0}{p}_{lm}{Y}_{lm}\left(\mathbf{u}\right)\sqrt{\frac{4\mathrm{\pi }}{2l+1}},$$ Eq. 4

for order l = 0, 2, …, and degree m = –l, –l + 1, …, l. With u = (sinθ cosφ, sinθ sinφ, cosθ), the spherical harmonic basis functions are given by

$$Y_{lm}\left(\mathrm{\theta },\mathrm{\phi }\right)=\sqrt{\frac{2l+1}{4\mathrm{\pi }}\frac{\left(l-m\right)!}{\left(l+m\right)!}}{\mathrm{L}}_l^m\left(\cos \mathrm{\theta }\right)\exp im\mathrm{\phi },$$ Eq. 5

where ${\mathrm{L}}_l^m$ are the associated Legendre polynomials (m = 0 yields the regular Legendre polynomials) (48, 51). The coefficients for K (k_l0) and P (p_lm) are obtained by inner products, according to

$$c_{lm}=⟨C|Y_{lm}⟩={\int }_0^{2\mathrm{\pi }}{\int }_0^{\mathrm{\pi }}C{\overline{Y}}_{lm}\sin \left(\mathrm{\theta }\right)\mathrm{d}\mathrm{\theta }\mathrm{d}\mathrm{\phi }$$ Eq. 6

where the overbar denotes complex conjugation. Eq. 4 uses the axial symmetry of K. First, K(θ,φ) = K(θ), wherefore k_lm = 0 for m ≠ 0. Second, K(–θ) = K(θ), wherefore k_l0 ≠ 0 only for even l (odd-order harmonics are antisymmetric). Eqs. 2–6 yield k_l0 (referred to as k_l), according to

$$k_l=S_0{\sum }_{\mathrm{j}=1}^{\mathrm{J}}{f}_{\mathrm{j}}\exp \left(-b{D}_{\mathrm{I};\mathrm{j}}\left(1-b_{\Delta }{D}_{\Delta ;\mathrm{j}}\right)\right)\sqrt{4\mathrm{\pi }\left(2l+1\right)}{\mathrm{I}}_{l\mathrm{j}}\exp \left(-\frac{\mathrm{T}\mathrm{E}}{{\mathrm{T}}_{2;\mathrm{j}}}\right)$$ Eq. 7

where

$${\mathrm{I}}_{l\mathrm{j}}={\int }_0^1{e}^{{-\mathrm{\alpha }}_{\mathrm{j}}{\mathrm{x}}^2}{·\mathrm{L}}_l\left(\mathrm{x}\right)\mathrm{d}\mathrm{x}$$ Eq. 8

and

$${\alpha }_{\mathrm{j}}=3{bD}_{\mathrm{I};\mathrm{j}}{b}_{\Delta }{D}_{\Delta ;\mathrm{j}}.$$ Eq. 9

For the first two harmonic orders, the integral evaluates to

$${\mathrm{I}}_{0\mathrm{j}}=\sqrt{\frac{\pi }{4{\alpha }_{\mathrm{j}}}}\mathrm{erf}\left(\sqrt{{\alpha }_{\mathrm{j}}}\right)$$ Eq. 10

and

$${\mathrm{I}}_{2\mathrm{j}}=\frac{1}{2}\left[{\mathrm{I}}_{0\mathrm{j}}\left(\frac{3}{2{\alpha }_{\mathrm{j}}}-1\right)-\frac{3}{2{\alpha }_{\mathrm{j}}}{e}^{-{\alpha }_{\mathrm{j}}}\right].$$ Eq. 11

Note that fitting the l = 0 term in Eq. 4 to the signal’s zeroth order coefficient 〈S|Y₀₀〉 is equivalent to the ‘powder-averaging’ approach (52–54), and that jointly fitting the l = 2 terms to the second order coefficients 〈S|Y_2m〉 (after transformation to rotational invariants) yields the ‘RotInv’ approach (33, 40, 46).

2.2 |. Two-compartment diffusion-relaxation model

We define a two-compartment diffusion-relaxation model by limiting the kernel (Eq. 2) to feature a ‘stick’ compartment (S) with D_Δ;S = 1 (D_⊥;S = 0) and a ‘zeppelin’ compartment (Z). The ‘stick’ property of zero radial diffusivity (16) is expected for diffusion within cylindrical structures having a radius smaller than the resolution limit (55) and has been experimentally indicated in white matter (53, 56, 57). Using Eqs. 4–11 with the harmonic expansion truncated at l^max = 2, and p₀₀ = Y₀₀ = 1/$\sqrt{4\pi }$ for ODF normalization, yields the full signal equation

$$S\left(\mathbf{e},\mathbf{ }\mathbf{m}\right)=S_0\left[f_{\mathrm{S}}\exp \left(-b{D}_{\mathrm{I};\mathrm{S}}\left(1-b_{\Delta }\right)\right)({\mathrm{I}}_{0;\mathrm{S}}+4\mathrm{\pi }{\mathrm{I}}_{2;\mathrm{S}}\sum _m{p}_{2m}{Y}_{2m}\left(\mathrm{\theta },\mathrm{\phi }\right))\exp \left(-\frac{\mathrm{T}\mathrm{E}}{{\mathrm{T}}_{2;\mathrm{S}}}\right)+{(1-f}_{\mathrm{S}}\left)\exp \left(-b{D}_{\mathrm{I};\mathrm{Z}}\left(1-b_{\Delta }{D}_{\Delta ;\mathrm{Z}}\right)\right)\right({\mathrm{I}}_{0;\mathrm{Z}}+4\mathrm{\pi }{\mathrm{I}}_{2;\mathrm{Z}}\sum _m{p}_{2m}{Y}_{2m}\left(\mathrm{\theta },\mathrm{\phi }\right))\exp \left(-\frac{\mathrm{T}\mathrm{E}}{{\mathrm{T}}_{2;\mathrm{Z}}}\right)\right]$$ Eq. 12

where m ∈ {–2, –1, 0, 1, 2}. It is a function of five scalar experiment-related parameters,

$$\mathbf{e}=[b,b_{\mathrm{\Delta }},\text{θ},\mathrm{\phi },\text{TE}],$$ Eq. 13

where θ and φ are the colatitude and longitude of the b-tensor symmetry axis, and twelve scalar model parameters,

$$\mathbf{m}=[S_0,f_{\text{s}},D_{\text{I:S}},D_{\text{I:Z}},D_{\text{Δ:Z}},{\text{T}}_{\text{2:S}},{\text{T}}_{\text{2:Z}},p_{20},\text{Re}(p_{21}),\text{Im}(p_{21}),\text{Re}(p_{22})\text{Im}(p_{22})],$$ Eq. 14

where f_S is the ‘stick’ fraction, D_I;S and D_I;Z are the isotropic diffusivities of the ‘stick’ and ‘zeppelin’, D_Δ;Z is the ‘zeppelin’ shape, T_2;S and T_2;Z are the T₂ values of the ‘stick’ and ‘zeppelin’, respectively. The requirement of a real ODF enforces conjugate symmetry, according to p_2-m = (–1)^m${\overline{p}}_{2m}$, leaving five real numbers describing it. As in Novikov (33), we use the rotational invariant Euclidean norm of the p_2m coefficients to derive an ‘orientation coherence’ parameter, according to

$$p_l=\sqrt{\sum _m{\left|p_{lm}\right|}^2}/\sqrt{\frac{2l+1}{4\mathrm{\pi }}}$$ Eq. 15

The normalization ensures p_l ∈ [0 1]. Since p_l is rotational invariant and increases with ODF anisotropy, p_l = p_l^max when P’ = δ(θ = 0)/(4π), where δ is the delta function. With P’ plugged into Eq. 6, Eq. 15 yields p_l^max = 4π${\int }_0^{\frac{\mathrm{\pi }}{2}}\left(\text{θ}=0\right)/\left(4\pi \right){ Y}_{l0}\mathrm{d}\text{θ}$, since Y_lm(θ = 0) = 0 for m = 0. Using Eq. 5 and L_l(1) = 1 yields p_l^max = $\sqrt{(2l+1)/4}$. Here, the parameter of interest is p₂.

2.3 |. Parameter relations commonly used to constrain the two-compartment diffusion-relaxation model

Models adapted for conventional multi-shell dMRI acquired with a single TE tend to address degeneracy issues by constraining parameters to follow given relations. What we refer to as the ‘density assumption’ is a relation implicitly enforced when referring to compartment fractions as volume fractions without accounting for T₂ relaxation (28). It assumes equal T₂ values across compartments, here according to

$${\text{T}}_{2;\text{s}}={\text{T}}_{2;\text{Z}}.$$ Eq. 16

With a shared compartment T₂ value and data acquired for a single TE, the T₂ dependence is factored into S₀. Another set of relations, here referred to as ‘proportional diffusivities’, link axial diffusivities between compartments as

$$D_{\Vert :\text{S}}=c\cdot D_{\Vert :Z}$$ Eq. 17

This has been used to enforce equal axial diffusivities (c = 1) (16, 23, 25) or equal isotropic diffusivities (c = 3) (27, 58). Yet another relation is the ‘tortuosity relation’, which connects the shape of the ‘zeppelin’ compartment to the ‘stick’ fraction (21, 23, 25, 59, 60), according to

$$D_{\Delta ;\text{Z}}=f_{\text{S}}/\left(3-2f_{\text{S}}\right)$$ Eq. 18

In this work, we extend this expression to incorporate myelin. We first note that Eq. 18 was derived for diffusion around parallel cylinders where simulations showed that (61)

$$D_{\Delta ;\text{Z}}=\left(1-v_{\text{E}}\right)/\left(1+2v_{\text{E}}\right),$$ Eq. 19

where v_E is the extra-axonal volume fraction. While Eq. 18 assumes v_E = 1 – f_S, a more plausible relation includes myelin, according to v_E = 1 – v_A – v_M, where v_A and v_M are the volume fractions of axons and myelin, respectively. These are related via the g-ratio, according to g² = v_A / (v_A + v_M) (62, 63). By adjusting for MR-invisible myelin, we can relate f_S to v_A, according to f_S = v_A / (1 – v_M), to obtain

$$D_{\Delta ;\mathrm{Z}}=\frac{f_{\mathrm{S}}}{f_{\mathrm{S}}\left(1-g^2\right)+g^2}/(3-2\frac{f_{\mathrm{S}}}{f_{\mathrm{S}}\left(1-g^2\right)+g^2})$$ Eq. 20

This relation could be used to update Eq. 18, which assumes g = 1 (no myelin), with g-ratio values obtained through independent means. Alternatively, it could be used to fit g using estimates of D_Δ;Z and f_S from the two-compartment diffusion relaxation model. However, note that this assignment is valid if and only if the compartment model is also accurate.

Finally, if the ODF is assumed to be axisymmetric, the Watson distribution is a less complex alternative to the truncated spherical harmonic expansion used here (64). It is described by mean orientation unit vector μ and concentration parameter κ with values from zero (spherical ODF) to infinity (delta function ODF). The OD parameter of Zhang (23) remaps κ to represent orientation dispersion from zero (OD = 0; κ = ∞) to complete (OD = 1; κ = 0), according to

$$\mathrm{O}\mathrm{D}=\frac{2}{\mathrm{\pi }}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left(\frac{1}{\mathrm{\kappa }}\right)$$ Eq. 21

2.4 |. Cramér-Rao lower bounds

Cramér-Rao lower bounds (CRLB) express the lower bound of the noise-induced variance in unbiased estimators (43, 44) and have been used previously to quantify the impact of the sampling protocol on the variance in model parameter estimates (59, 60, 65, 66). The CRLB are obtained as the diagonal elements of the inverse of the Fisher information matrix (F). For an experiment described by N samples e_n, assuming Gaussian noise with standard deviation σ_noise, F has the elements

$$F_{ij}={\sigma }_{\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}^{-2}\sum _{\mathrm{n}=1}^{\mathrm{N}}\frac{\partial S_{\mathrm{n}}}{\partial m_{\mathrm{i}}}\frac{\partial S_{\mathrm{n}}}{\partial m_{\mathrm{j}}}\left({\mathbf{e}}_{\mathrm{n}},\mathbf{m}\right),$$ Eq. 22

where ∂S_n/∂m_i and ∂S_n/∂m_j are partial derivatives of the signal model for measurement n with respect to model parameters m_i and m_j ∈ m (59). Here, we defined F using S, e and m from Eqs. 12, 13 and 14, respectively.

3 |. METHODS

The procedures described in this section were performed using MATLAB (R2015b, MathWorks, Natick, MA, USA) and in-house code, available at https://github.com/belampinen/lampinen_mrm_2019.

3.1 |. Protocol optimization

We optimized sampling protocols by minimizing an objective function based on the model parameters’ CRLB (from Eq. 22) converted into an optimization metric referred to as the ‘weighted parameter variance’ (V_W), defined as

$${\mathrm{V}}_{\mathrm{W}}=\frac{1}{3}\sum _{\mathrm{X}=\left\{\mathrm{A},\mathrm{B},\mathrm{C}\right\}}{({\mathbf{w}}^{\mathbf{T}}\mathbf{v}}_{\mathrm{C};\mathrm{X}})f_{\text{Tacq}},$$ Eq. 23

where w is a vector of weights, v_C = [CRLB₁, …, CRLB₁₂], and the average is across the prior sets in Table 1, which were intended to represent white matter (A), deep gray matter (B), and white matter lesions (C). Furthermore, f_Tacq is an ‘efficiency factor’ that makes V_W invariant to the actual acquisition time (T^acq). The weights were defined to ignore S₀ and the ODF parameters, using w = 0 for these, and to bring the remaining kernel parameters to comparable scales, using w^–1 values of 0.05 for f_S, 0.1 μm²/ms for D_I;S and D_I;Z, 0.1 for D_Δ;Z and 10 ms for T_2;S and T_2;Z. The efficiency factor was defined as f_Tacq = T^acq/T^acq;ref with T^acq;ref = 30 minutes and T^acq = (τ_fat + TE_max + τ_EPI /2) n_sliceN, using the time for the fat saturation pulse (τ_fat = 5 ms), the maximal TE, the EPI readout time (τ_EPI = 45 ms), the number of slices (n_slice = 40) and the protocol’s number of measurements (N). The final objective function was given by

$$\text{OF}={\text{V}}_{\text{W}}{\text{ϕ}}_{\text{SNR}}{\text{ϕ}}_{\text{grad}}$$ Eq. 24

Table 1 –

Model parameter prior sets and bounds

Prior sets	fS	DI;S	DI;Z	DΔ;Z	T2;S	T2;Z	ODb
A	0.45	0.6	1.3	0.57	80	60	0.20
B	0.15	0.3	0.9	0.40	75	55	0.45
C	0.40	0.6	1.7	0.40	80	150	0.35
Bounds	fS	DI;S	DI;Z	DΔ;Z	T2;S	T2;Z
Minimum	0	0.07a	0.2a	–0.46a	30	30
Maximum	1	1.33a	4.0a	0.86a	300	1000

Diffusivities are in μm²/ms and T₂ values are in ms.

^aFrom enforcing D_||;S, D_||;Z and D_⊥;Z ∈ [0.2 4.0] μm²/ms.

^bThe parameters describing spherical harmonic coefficients, p₂₀, Re(p₂₁), Im(p₂₁), Re(p₂₂), Im(p₂₁), are, for simplicity, represented by the corresponding OD from the Watson distribution (Eq. 21) assuming a main direction of [0 0 1].

To account for scanner limitations, the penalty factors ϕ_SNR and ϕ_grad approximate step functions by (linearly) increasing rapidly from unity under certain conditions (see GitHub link for details). The first factor penalized SNR < 2, where the Gaussian noise assumption in Eq. 22 is particularly biased (67). The SNR was estimated based on data from Szczepankiewicz (68) assuming an approximate voxel T₂ of 80 ms. The second factor penalized gradient amplitudes g > g_max (default 80 mT/m).

As in our previous work (66), we minimized Eq. 24 using the stochastic Self Organizing Migrating Algorithm (SOMA) (69). SOMA was repeated six times per optimization after which the best protocol was chosen. The optimization task was to specify b, b_Δ and TE for each of a predetermined number of shells as well as the number of b-tensor symmetry axis orientations (n_dir) across which to repeat these parameters. The allowed parameter values were b ∈ [0, 0.1, …, 10] ms/μm², b_Δ ∈ [–0.50, –0.45, …, 1], TE ∈ [50, 60, …, 300] ms, and n_dir ∈ [6, 10, 15, 30, 45]. The directional set [θ_i, φ_i] corresponding to each n_dir was selected from platonic solids (36) for simplicity and optimization performance. The lower bound of TE = 50 ms should guarantee that myelin water contributes to the non-diffusion weighted signal by less than 2%, assuming an approximate volume fraction of 0.15 with a T₂ value of 15 ms in white matter (70, 71). To obtain a protocol suitable for clinical conditions, referred to as the ‘in vivo protocol’, we manually adapted a CRLB-optimized protocol to repeat a set of DTI and DKI-compatible shells using LTE (b_Δ = 1) for different TE.

3.2 |. Model fitting

Fitting was performed with least-squares minimization using MATLAB and the multidimensional dMRI toolbox (72). Minimization used the lsqcurvefit function with default settings and parameter bounds from Table 1. The diffusivity bounds were enforced through penalties ensuring axial and radial diffusivities between 0.2 and 4 μm²/ms. A lower bound above zero is the ‘zeppelin’ compartment’s main characteristic and avoids representing water at the ‘dot-compartment’ limit of zero isotropic diffusivity (73–76), which is presumably negligible in healthy white matter (57, 76, 77). For T₂ values, the lower bound avoids representing water presumably fully attenuated at our echo times (e.g. myelin water), and the upper bounds were considered safe assumptions for water within ‘stick-like’ structures and in tissue without major contamination with cerebrospinal fluid (CSF), respectively. Fitting was performed twice with initial guesses randomly selected from uniform distributions within the parameter bounds, after which the best fitting solution was kept. The probability of finding the global solution using two initial guesses was estimated to approximately 99.96% using in vivo data.

3.3 |. Optimization evaluation (simulations)

To assess the impact on parameter precision of the different acquisition dimensions, we optimized protocols under restrictions on b, b_Δ and TE, one at a time, as well as on the number of unique combinations of these properties (shells). To assess the effect of the maximal gradient amplitude, the optimizations under b and TE restrictions were performed for g_max values of 200 mT/m and infinity in addition to 80 mT/m.

To illustrate the ability to determine the ‘stick’ fraction using different protocols, we used the normalized residual variance (NRV) (28). For a given protocol, a signal was synthesized for each prior set in Table 1 using Eq. 12, after which Eq. 12 was fitted with f_S fixed to different values between zero and one. The NRV then yields a goodness-of-fit metric for each fixed f_S, according to

$$\mathrm{N}\mathrm{R}\mathrm{V}=\frac{1}{\mathrm{I}}\sum _{\mathrm{i}=1}^{\mathrm{I}}{\mathrm{\sigma }}_{\mathrm{R};\mathrm{i}}^2{/\mathrm{\sigma }}_{\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}^2= \frac{1}{\mathrm{I}}\sum _{\mathrm{i}=1}^{\mathrm{I}}\sum _{\mathrm{n}=1}^{\mathrm{N}}{{\left[\right(S}_{\mathrm{n}}-{\stackrel{-}{S}}_{\mathrm{n}})}^2 / (\mathrm{N}-\mathrm{M})] {/\mathrm{\sigma }}_{\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}^2$$ Eq. 25

where the average is across I = 10 realizations of Gaussian noise with standard deviation σ_noise, S_n is the noised signal, S_n-overbar is the fitted signal, N is the protocol’s number of measurements and M is the number of free model parameters (M = 11, after fixing f_S). Plotting the NRV against the fixed f_S illustrates how precisely this parameter can be determined with a given protocol, which is challenging using a model with free compartment T₂ values and diffusivities (28).

To explore the precision of parameter estimates under challenging model priors, we fitted Eq. 12 to signals synthesized with the in vivo protocol (Table 2, protocol II) assuming four different sets of priors for the two-compartment model, modified so that the ODF was represented by a Watson distribution rather than the truncated spherical harmonics. The three first sets of priors mimicked set A in Table 1, but with gradually increasing orientation dispersion achieved by setting OD (Eq. 21) to 0.05, 0.5, and 1. The fourth set mimicked the full orientation dispersion set but with equal compartment isotropic diffusivities (0.95 μm²/ms) and T₂ values (70 ms). The simulations were performed for 200 realizations of noise from the Rice distribution to obtain distributions of estimated parameter values.

Table 2 –

Sampling protocols: an optimized protocol (I), the in vivo protocol (II), an optimized LTE-only protocol (III) and a protocol from Lampinen (28) (IV), featuring multiple TE only for low b-values.

Protocol	Shell #	b [ms/μm2]	bΔ	TE [ms]	ndir
I	1	0	1	50	10
	2	0	1	90	10
	3	0.7	0.1	75	30
	4	1.9	1	70	30
	5	0	1	140	10
	6	1.2	0.1	140	6
	7	1.8	1	140	15
	8	2.1	1	140	45
	9	6.2	1	80	45
	10	3.6	0.15	105	45
II	1,2,3a	0.1,1.0,2.0	1	63	6,15,45
	4,5,6,7b	0.1,1.0,2.0,5.0	1	85	6,6,15,45
	8,9,10c	0.1,1.0,2.0	1	130	30,6,30
	11,12,13d	0.1,2.0,2.5	0.6	85	6,15,45
III	1,2	0,0.4	1	50	6,45
	3	0.9	1	60	15
	4	2.7	1	70	45
	5	8.9	1	85	45
	6	10	1	90	30
	7,8,9,10	0,2.1,2.1,2.2	1	100	6,30,10,10
IV	1,2,3,4,5	0.1,0.5,1.0,1.5,2.0	1	106	6,6,10,16,30
	6,7,8,9,10	0.1,0.5,1.0,1.5,2.0	0	106	6,6,10,16,30
	11,12	0,0.5	1	50	1,6
	13,14	0,0.5	1	85	1,6
	15,16	0,0.5	1	120	1,6
	17,18	0,0.5	1	155	1,6

The gradient waveforms used for the in vivo protocol (II) had a pause duration of 12.4 ms and durations before (δ₁) and after (δ₂) refocusing given by

^aδ₁ = 16.5 ms, δ₂ = 16.5 ms

^bδ₁ = 27.5 ms, δ₂ = 27.5 ms

^cδ₁ = 50.0 ms, δ₂ = 50.0 ms

^dδ₁ = 30.0 ms, δ₂ = 27.5 ms

All simulations used the same SNR estimations as described for the optimization. In the NRV simulations, acquisition time differences were accounted for according to SNR’ = SNR · (T^acq;ref/T^acq)^1/2, with T^acq;ref = 30 minutes.

3.4 |. In vivo acquisition and processing

To study white and deep gray matter of the normal adult and maturing brain, we included five adult volunteers (age 31 ± 5 years; male/female = 3/2) and five children from a reading intervention study (age 6 ± 1 years; male/female = 4/1). To study age-related white matter lesions, we included data from five elderly subjects that were controls in a Parkinson’s disease study (age 76 ± 3 years; male/female = 2/3), some of which contributed data to a previous study (28). The experiments were approved by the regional ethical review board in Lund and all subjects gave informed consent.

dMRI data were acquired on a MAGNETOM Prisma 3T system (Siemens Healthcare, Erlangen, Germany), using a prototype diffusion-weighted spin-echo sequence (68). Encoding gradient waveforms were optimized to maximize the b-value for a given TE (78) and to remove concomitant field gradient effects (79). The diffusion-encoding directions were translated into gradient waveform rotations as specified in Szczepankiewicz (80). For the adults and the children, protocol II in Table 2 was used, featuring LTE, prolate (PrTE) b-tensors and multiple TE. The sampling order was volume-interleaved to distribute energy consumption and heating evenly over time (81) and to reduce potential bias from system drift (82). Total acquisition time was 15 minutes for a 2.5 mm isotropic resolution, matrix size = 88×88, 40 slices, multiband factor 2 (83), parallel imaging factor 2 (GRAPPA), partial Fourier factor 0.75, bandwidth = 1775 Hz/pixel, and ‘strong’ fat saturation. TR was 3.4 s, except for one subject with SMS (3.7 s) and another subject without SMS (6.4 s). For the elderly subjects, protocol IV in Table 2 was used, featuring LTE, STE and multiple TE for a single set of low b-values and directions, see Lampinen (28). All data were corrected for eddy-currents and subject motion using ElastiX (84) with extrapolated target volumes (85). To obtain parameter maps, Eq. 12 was fitted voxel-by-voxel to data smoothed using a Gaussian kernel with a standard deviation of 0.45 times the voxel dimensions.

3.5 |. In vivo data evaluation

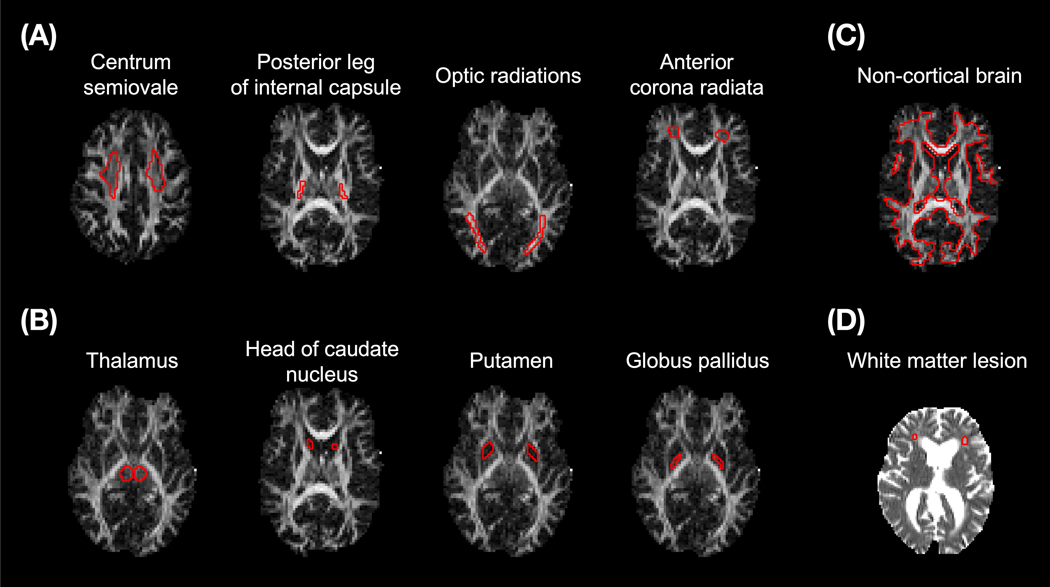
To assess parameter values from fitted maps, values were extracted from regions of interests (ROIs; Figure 1). For the adults and the children, ROIs were defined in white matter (Figure 1A), deep gray matter (Figure 1B), and the whole brain excluding the cortex and the ventricles to avoid CSF contamination (Figure 1C). For the elderly subjects, the anterior corona radiata featuring a white matter lesion was defined (Figure 1D).

Figure 1 –

Regions of interest (ROIs) are shown in red for one adult volunteer (A–C) on top of an FA map and for one elderly subject (D) on top of an MD map. The ROIs were defined on maps obtained from a DTI analysis of data from shell 1 and 2 of the in vivo protocol (II in Table 2). Non-cortical brain tissue (C) was defined by manually including deep gray matter and the brainstem within a white matter mask generated by thresholding the μFA parameter from a QTI analysis (36).

To explore whether our data supported popular or novel model constraints, we assessed different parameter relations using data obtained with our comparatively rich sampling protocol. First, we compared the predictions of some commonly enforced relations (Eqs. 16–18) with our (ROI-averaged) estimates. Second, we investigated the impact on estimated parameters from enforcing these relations by fitting the corresponding simplified models (using c = 1 in Eq. 17) to our data and comparing the results to those obtained when fitting the full model (Eq. 12). For each model, parameter values were obtained from all subjects by fitting to the ROI-averaged signals within white matter (Figure 1A and 1D), and parameter maps were obtained from one subject through voxel-by-voxel fitting within one slice of non-cortical brain (Figure 1C). For these maps, data were smoothed using a Gaussian kernel with a standard deviation of 0.75 times the voxel dimensions. Third, we tested whether enforcing these relations resulted in a significantly worse fit. Model selection maps were obtained for the non-cortical brain slice by thresholding an F-statistic at a 5% confidence level. F was calculated as the quotient between (SSR₁ – SSR₂)/(M₂ – M₁) and SSR₂/(N – M₂), using the sum of squared residuals (SSR) and the number of fitted parameters (M) of the simplified (1) and the full model (2) and the number of measurements N. The SSR values were obtained by fitting to unsmoothed data and, for each voxel, averaging across a 3×3 neighborhood. Fourth, we explored alternative parameter relations, including the tortuosity relation based on different g-ratios (Eq. 20).

4 |. RESULTS

4.1 |. Sampling protocols and parameter precision

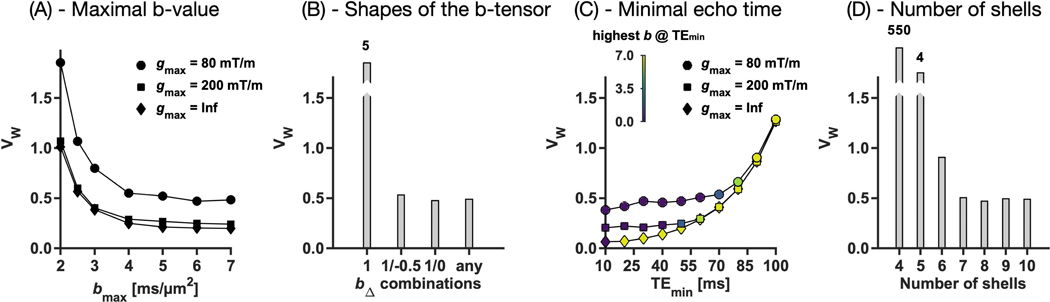
Figure 2 illustrates the impact on precision of the acquisition dimensions represented by b-value (b; A), b-tensor shape (b_Δ; B) and echo time (TE; C), as well as of the number of shells (b/b_Δ/TE-combinations; D). The x-axes show protocols optimized under different restrictions, and the y-axes show parameter variance by the CRLB-derived V_W parameter (Eq. 23). Numerical simulations confirmed that the CRLB accurately quantified the parameter variance (Supporting Information Figure S1).

Figure 2 –

The impact of the acquisition dimensions on parameter precision. Plots show the weighted parameter variance (V_W; Eq. 23; lower is better) for sampling protocols optimized under different restrictions indicated on the x-axis: maximal b-value (b_max) in panel A, shapes of the b-tensor (b_Δ) in panel B, minimal echo times (TE_min ) in panel C, and number of shells in panel D. The impact on precision from b_max and TE_min was independent on the maximal gradient amplitude (g_max; indicated by shape), although stronger gradients increased precision by allowing shorter TE.

Increasing b_max improved precision up until approximately 4 ms/μm² (Figure 2A). Acquiring data using at least two b-tensor shapes dramatically improved precision (Figure 2B). For example, using both b_Δ = 1 and b_Δ = –½ reduced V_W to a tenth compared with using only b_Δ = 1. No particular shape combinations were favored, however. Decreasing TE_min improved precision, but primarily when this was achievable for high b-values (Figure 2C). As a consequence, returns diminished below approximately 60–70 ms for g_max = 80 mT/m. Protocols with at least seven shells had the best precision and adding shells beyond the seventh had marginal impact (Figure 2D). Access to higher maximal gradient amplitudes improved precision by enabling shorter TE (Figure 2A/C). Increasing g_max from 80 to 200 mT/m reduced V_W by approximately 50%.

Table 2 shows four protocols: an optimized protocol with 10 shells (I), the in vivo protocol (II), an optimized LTE-only protocol (III), and a protocol used in Lampinen (28) (IV). Protocol I is representative of optimized protocols in general. In particular, it features both low and high b-values using short TE (shells 1–4) as well as long TE (shells 5–8), an ‘ultra-high’ b-value (shell 9) and a high b-value for a non-LTE b-tensor shape (b_Δ ≠ 1; shell 10). Protocol II was designed for in vivo use and also exhibited these features but was adapted to enable separate DTI and DKI analyses. Protocol III was restricted to only use LTE and featured a very high maximal b-value and comparatively short TE. Protocol IV from Lampinen (28) had a different design and acquired a range of b-values using two b-tensor shapes (b_Δ = 0 and 1) for a single TE and low b-values for multiple TE.

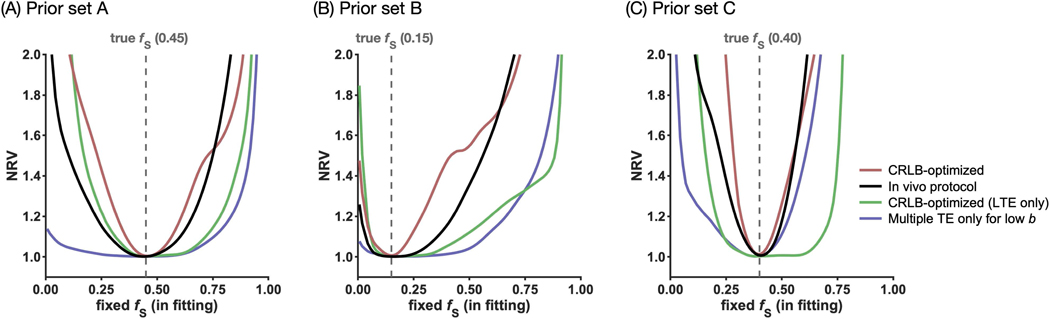
Figure 3 illustrates the ability to determine the ‘stick’ fraction using the protocols in Table 2 under the priors in Table 1. The NRV curves (Eq. 25) indicate parameter precision by the width of the minima around the true f_S. For the optimized protocol (I) and the in vivo protocol (II), the minima were narrow, indicating high precision. For the LTE-only protocol (III) and the protocol acquiring multiple TE only for low b-values (IV), however, the curve minima were wide and flat, indicating multiple equivalent solutions and poor precision. The exception was a narrower minimum for protocol IV under large compartmental differences in isotropic diffusivities (Figure 3C), as expected from Lampinen (28).

Figure 3 –

Illustration of the ability to determine the ‘stick’ fraction (f_S). The plot shows the NRV (normalized residual variance, Eq. 25) versus the value to which f_S was fixed while fitting the other model parameters, for the protocols in Table 2 under the priors in Table 1. The width of the curve around the ground truth (dashed vertical line) indicates precision by the range of f_S that yield similar goodness-of-fit values. The minima were narrow (high precision) for the CRLB-optimized protocol (I) and the in vivo protocol (II), but wide (poor precision) for the LTE-only protocol (III) and the protocol with multiple TE only for low b-values (IV). However, protocol IV achieved better precision where compartmental difference in isotropic diffusivities were large (C). CRLB-optimized protocols can be susceptible to local minima (B), although the in vivo protocol appeared robust.

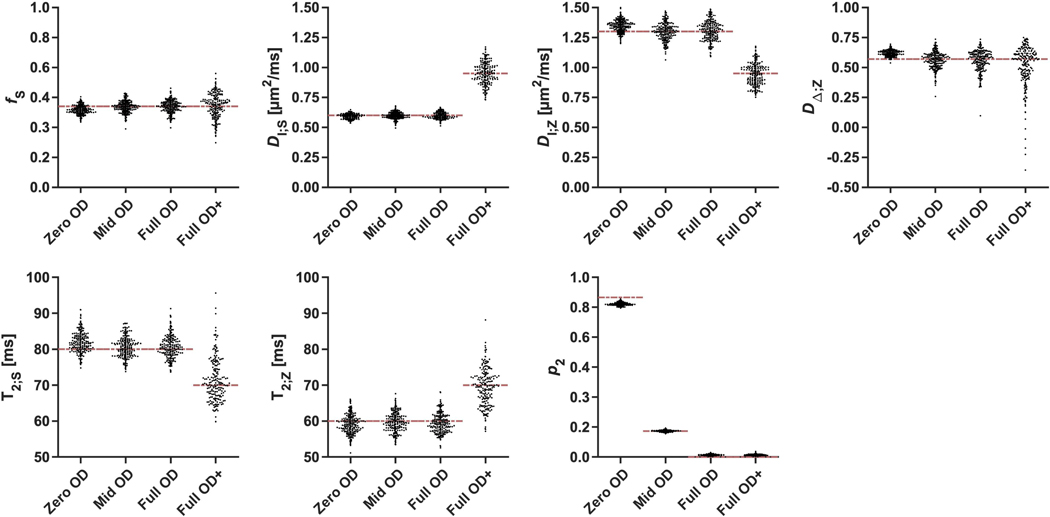
Figure 4 illustrates parameter precision using the in vivo protocol (Table 2, protocol II) under challenging model priors, showing distributions of parameter estimates from simulations. Precision was highest under no orientation dispersion (‘Zero OD’), decreased only slightly for a more realistic scenario (‘Mid OD’) and was largely retained even under full orientation dispersion (‘Full OD’). Removing both the directional information and compartmental differences in isotropic diffusivity (‘Full OD+’) substantially reduced precision, however. Precision for p₂ was high under all conditions.

Figure 4 –

Parameter precision illustrated by distributions of parameter estimates (point swarms) simulated using the in vivo protocol under priors denoted on the x-axes. Precision was highest for ‘Zero OD’ and decreased slightly for the ‘Mid OD’ and the ‘Full OD’ priors. The Full OD+ priors, featuring full orientation dispersion together with equal compartment isotropic diffusivities and T₂ values, had a large detrimental impact on precision.

4.2 |. In vivo results

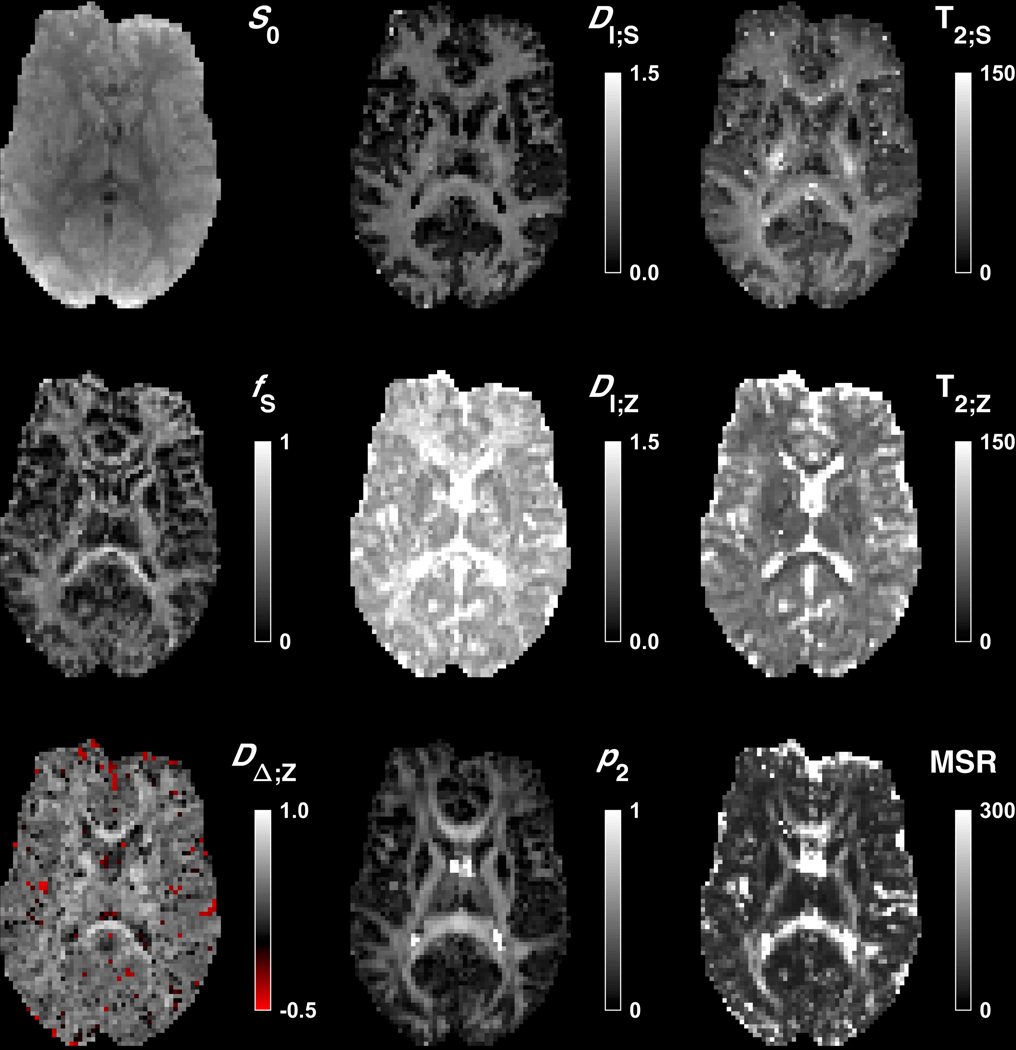
Maps of the kernel parameters are presented in Figure 5 and in Supporting Information Figure S2 together with p₂ and the mean squared residuals (MSR). Parameter estimates were generally precise, indicated by the lack of visible noise in the parameter maps and confirmed by a test-retest experiment (Supporting Information Figure S3). The exception was D_Δ;Z, with somewhat noisier maps. The maps of f_S, D_I;S, D_I;Z, D_Δ;Z, T_2;S and p₂ were brighter in white matter than in gray matter, although the D_I;Z maps were brightest in the ventricles and the T_2;S maps were particularly bright in the cerebrospinal tract. The T_2;Z maps were relatively homogeneous but darker in iron-rich deep gray matter and brightest in the ventricles. The p₂ maps were bright in coherent white matter and appeared to correlate with larger fit residuals. The median SNR in the non-cortical brain (Figure 1C) was approximately 50 at TE = 63 ms and b = 0.1 ms/μm² based on the MSR (thus including both noise and model errors).

Figure 5 –

Maps of the kernel parameters in an adult volunteer together with p₂ and mean squared residuals (MSR) from the fitting. Additional slices are shown in Supporting Information Figure S2. Isotropic diffusivities are in μm²/ms, T₂ values are in ms and remaining parameters are dimensionless. All maps were masked to exclude voxels outside of the brain. In addition, the D_I;S, T_2;S, and p₂ maps were masked to exclude voxels where f_S < 0.1. The S₀ maps exhibited proton density-weighting and lacked typical T₂-related hypointensities. The f_S (‘stick’ fraction) maps were bright in white matter and dark in deep gray matter, although somewhat brighter in the lateral thalamus. The D_I;S and D_I;Z (the ‘stick’ and ‘zeppelin’ isotropic diffusivities) maps were brightest in white matter, with D_I;S maps being very dark in deep gray matter. The D_Δ;Z (‘zeppelin’ shape) maps appeared somewhat noisy and were brightest in white matter and in orientationally coherent structures such as the corpus callosum. Negative D_Δ;Z values (red) were sparse. The T_2;S (‘stick’ T₂ value) maps were brightest in white matter and particularly in the cerebrospinal tract. The T_2;Z (‘zeppelin’ T₂ value) maps were homogenous but darker in deep gray matter and brighter close to CSF. The p₂ maps were smooth and resembled FA maps, being bright in white matter except in crossing-fiber regions such as the anterior corona radiata. The MSR maps were similar to p₂ maps, possibly reflecting the ‘bluntness’ of the spherical harmonic ODF truncated at l_max = 2.

Parameter values are presented in Table 3 from the adults, children, and white matter lesions of the elderly subjects. In adults, white matter showed similar ‘stick’ properties across all regions with f_S ≈ 0.5, D_I;S ≈ 0.6 μm²/ms and T_2;S ≈ 80 ms, with somewhat higher values in the internal capsule. ‘Zeppelins’ featured higher isotropic diffusivities and lower T₂ values, with D_I;Z ≈ 1.3 μm²/ms and T_2;Z ≈ 65 ms, respectively. The properties of ‘sticks’ were similar also between deep gray matter regions, although the ‘stick’ fractions and isotropic diffusivities were lower than in white matter, with f_S ≈ 0.15, D_I;S ≈ 0.25 μm²/ms and T_2;S ≈ 80 ms. ‘Zeppelins’ in deep gray matter featured lower isotropic diffusivities and T₂ values than in white matter, with D_I;Z ≈ 0.9 μm²/ms and T_2;Z ≈ 50 ms. In children, most values were similar to in adults, but white matter ‘stick’ fractions were 10–30% lower and deep gray matter ‘zeppelin’ T₂ values were 10–30% higher. Markedly high ‘stick’ T₂ values and low ‘stick’ fractions were seen in the head of the caudate nucleus and the putamen of children, possibly due to imaging artifacts. In white matter lesions, we found elevated ‘zeppelin’ isotropic diffusivities and T₂ values, with D_I;Z = 1.68 μm²/ms and T_2;Z = 149 ms, respectively, and a tendency towards more isotropic diffusion (D_Δ;Z closer to zero). The ‘stick’ fractions and the diffusivities and T₂ values of ‘sticks’ were similar to those found in adults, however. The lesion parameters also exhibited high inter-subject variance.

Table 3 –

ROI parameter values with means and inter-subject standard deviations for adults (Ad; n = 5), children (Ch, n = 5) and elderly subjects with white matter lesions (Le; n = 5).

Non-cortical brain tissue		fS	DI;S	DI;Z	DΔ;Z	T2;S	T2;Z	p2	D||;Z	D⊥;Z
	Ad	0.40 (0.01)	0.54 (0.03)	1.23 (0.05)	0.47 (0.01)	77 (2)	67 (2)	0.37 (0.01)	2.41 (0.10)	0.64 (0.02)
	Ch	0.34 (0.02)	0.51 (0.03)	1.22 (0.02)	0.49 (0.01)	81 (2)	72 (4)	0.40 (0.01)	2.43 (0.06)	0.61 (0.01)
White matter		fS	DI;S	DI;Z	DΔ;Z	T2;S	T2;Z	p2	D||;Z	D⊥;Z
Centrum semiovale	Ad	0.49 (0.02)	0.62 (0.03)	1.31 (0.04)	0.46 (0.03)	82 (3)	62 (3)	0.29 (0.03)	2.54 (0.10)	0.69 (0.05)
	Ch	0.46 (0.02)	0.61 (0.05)	1.28 (0.07)	0.49 (0.03)	77 (3)	69 (7)	0.36 (0.03)	2.55 (0.17)	0.64 (0.05)
Posterior leg of internal capsule	Ad	0.53 (0.03)	0.66 (0.04)	1.41 (0.16)	0.63 (0.05)	107 (8)	65 (6)	0.48 (0.03)	3.20 (0.38)	0.52 (0.10)
	Ch	0.41 (0.07)	0.58 (0.05)	1.37 (0.12)	0.65 (0.02)	102 (17)	66 (3)	0.55 (0.02)	3.15 (0.25)	0.48 (0.06)
Optic radiations	Ad	0.45 (0.01)	0.62 (0.04)	1.30 (0.08)	0.50 (0.04)	79 (3)	68 (5)	0.49 (0.04)	2.60 (0.23)	0.64 (0.04)
	Ch	0.39 (0.03)	0.58 (0.03)	1.30 (0.04)	0.48 (0.02)	74 (1)	80 (11)	0.51 (0.05)	2.55 (0.05)	0.67 (0.04)
Anterior corona radiata	Ad	0.45 (0.04)	0.58 (0.04)	1.36 (0.09)	0.44 (0.03)	69 (3)	60 (4)	0.30 (0.03)	2.57 (0.23)	0.75 (0.04)
	Ch	0.40 (0.03)	0.59 (0.03)	1.32 (0.04)	0.46 (0.05)	68 (3)	61 (7)	0.32 (0.02)	2.56 (0.11)	0.70 (0.08)
	Le	0.44 (0.11)	0.57 (0.04)	1.68 (0.16)	0.37 (0.05)	71 (30)	149 (29)	0.23 (0.02)	2.70 (0.18)	1.05 (0.11)
Deep gray matter		fS	DI;S	DI;Z	DΔ;Z	T2;S	T2;Z	p2	D||;Z	D⊥;Z
Thalamus	Ad	0.15 (0.02)	0.33 (0.05)	0.99 (0.03)	0.52 (0.03)	97 (16)	53 (3)	0.31 (0.01)	2.01 (0.10)	0.47 (0.03)
	Ch	0.13 (0.01)	0.28 (0.03)	1.02 (0.02)	0.50 (0.01)	115 (17)	64 (3)	0.32 (0.02)	2.06 (0.06)	0.50 (0.02)
Head of caudate nucleus	Ad	0.14 (0.03)	0.25 (0.05)	0.81 (0.03)	0.34 (0.05)	77 (19)	60 (3)	0.18 (0.03)	1.38 (0.11)	0.53 (0.04)
	Ch	0.07 (0.02)	0.29 (0.07)	0.82 (0.02)	0.32 (0.04)	172 (42)	68 (3)	0.19 (0.03)	1.35 (0.08)	0.56 (0.03)
Putamen	Ad	0.10 (0.02)	0.20 (0.02)	0.83 (0.02)	0.41 (0.03)	77 (13)	51 (3)	0.16 (0.01)	1.53 (0.08)	0.49 (0.02)
	Ch	0.10 (0.03)	0.27 (0.09)	0.85 (0.04)	0.36 (0.05)	108 (22)	67 (3)	0.13 (0.01)	1.47 (0.14)	0.54 (0.03)
Globus pallidus	Ad	0.15 (0.04)	0.26 (0.08)	1.06 (0.05)	0.54 (0.03)	80 (16)	41 (5)	0.20 (0.01)	2.23 (0.16)	0.48 (0.01)
	Ch	0.15 (0.01)	0.31 (0.05)	1.09 (0.06)	0.51 (0.03)	84 (9)	55 (2)	0.23 (0.02)	2.23 (0.17)	0.52 (0.01)

Diffusivities are in μm²/ms and T₂ values are in ms.

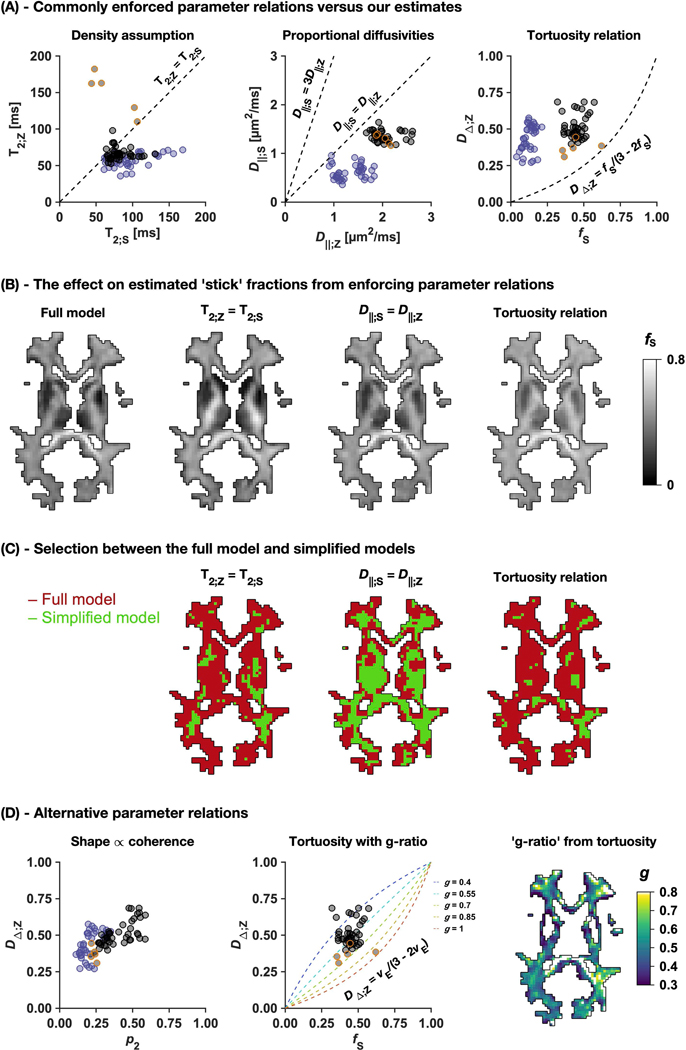
Parameter relations are explored in Figure 6. Three commonly enforced parameter relations were contradicted by our estimates (Figure 6A). The density assumption predicts equal compartment T₂ values (Eq. 16) but data indicated higher T₂ values for ‘sticks’ than for ‘zeppelins’ in healthy white matter and the opposite in white matter lesions. Proportional diffusivities link compartment axial diffusivities by a constant (Eq. 17) but data did not suggest a simple linear relationship between these parameters. The tortuosity relation connects the ‘zeppelin’ shape to the ‘stick’ fraction (Eq. 18), but again, observations did not agree with assumptions. Enforcing these relations yielded ‘stick’ fraction maps that were smoother but featured rather different values compared with using the full model (Eq. 12; Figure 6B). Enforcing equal T₂ values resulted in different ‘stick’ fractions (f_S´) that were higher in healthy white matter (f_S´ – f_S = Δf_S ≈ 0.05–0.15), and particularly in the cerebrospinal tract, but lower in white matter lesions (Δf_S ≈ –0.30), and thus substantially exaggerating their effect. Enforcing equal axial diffusivities resulted in ‘stick’ fractions that were similar in white matter but higher in white matter lesions (Δf_S ≈ 0.15). Enforcing the tortuosity relation resulted in higher ‘stick’ fractions both within normal (Δf_S ≈ 0.05–0.10) and lesioned (Δf_S ≈ 0.15) white matter. Using the full model yielded a significantly better fit within most regions of the healthy brain compared with enforcing equal compartment T₂ values or the tortuosity relation, although enforcing equal axial diffusivities appeared acceptable in many regions (Figure 6C).

Figure 6 –

Evaluation of model simplification through enforcing parameter relations. Panel A shows commonly enforced relations (dashed lines) together with our estimates (dots). The estimates are ROI-averages from adults and children in white matter regions (black) and deep gray matter regions (blue), and from elderly subjects in white matter lesions (orange-bordered black). Panel B compares ‘stick’ fraction maps obtained either using the full model or simplified models enforcing different parameter relations. Panel C shows model selection maps (F-statistics thresholded at a level corresponding to a significance level of 5%, uncorrected for multiple comparisons) between the full model and the simplified models in panel B. Panel D shows alternative parameter relations that may be compatible with data, including the tortuosity relation allowing a variable g-ratio (Eq. 20) together with a fitted ‘g-ratio’ map.

Data suggested some alternative parameter relations (Figure 6D). The ‘zeppelin’ shape appeared positively related to the orientation coherence in white matter. Furthermore, allowing different g-ratios (Eq. 20) may explain variation unaccounted for by the ‘ordinary’ tortuosity relation (g = 1; Eq. 18). Finally, a tortuosity-based ‘g-ratio’ map is shown within white matter from fitting g using Eq. 20 and our estimates of f_S and D_Δ;Z. Although noisy, the map featured a median of approximately 0.5, which is close to the value of 0.6 where conduction velocities are theoretically optimized (86). The shown data points are available at https://github.com/belampinen/lampinen_mrm_2019/tree/master/estimates.

5 |. DISCUSSION

In this paper, we show what is required of a diffusion-relaxation sampling protocol to enable precise estimation of compartment-specific fractions, diffusivities and T₂ values, and present a 15-minute whole-brain imaging protocol. Three protocol features were critical to parameter precision. First, at least seven unique b/b_Δ/TE-combinations (shells) were required for robust estimation of seven kernel parameters (counting S₀; Figure 2D). Using fewer shells resulted in parameters becoming undetermined under high orientation dispersion (starting with D_Δ;Z for six shells; Supporting Information Figures S4 and S5). Second, using at least two shapes of the b-tensor substantially enhanced precision (Figure 2B). This was expected, because the two-compartment ‘standard model’ is degenerate for data acquired with a single b-tensor shape (LTE) (32, 33, 37, 38), even when using very high b-values (33, 87) or multiple echo times (40). With multiple b-tensor shapes, this degeneracy is resolved (37, 38). Third, multiple echo times for high b-values were required to distinguish the T₂ values of compartments with different anisotropy but similar isotropic diffusivities (Figure 3A/B) (28, 40). Protocols with these three features allowed estimation of seven kernel parameters, compared with three kernel parameters allowed by contemporary approaches using multi-shell dMRI (27, 28, 31). The estimates were robust to full orientation dispersion (Figure 4; Supporting Information Figure S4), where the ‘standard model’ is degenerate even for data acquired with multiple shapes of the b-tensor (37, 38). This confirms that diffusion-relaxation experiments improve precision in diffusion parameters, at least in the presence of compartmental differences in T₂ values (88).

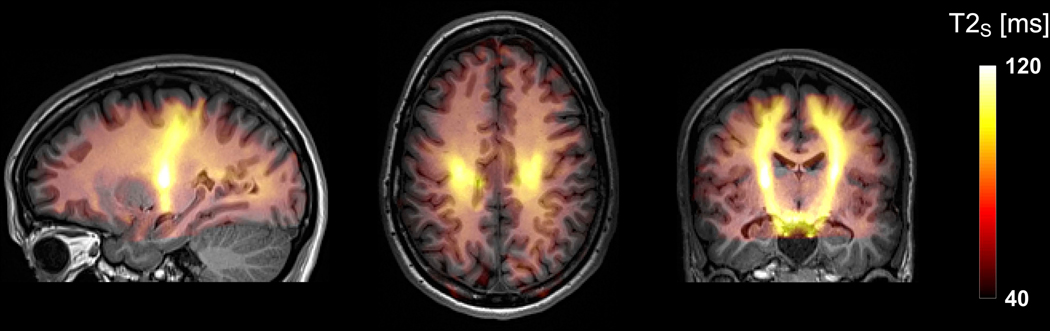
In vivo parameter maps were smooth, indicating precise estimates (Figure 5), which invites a tentative interpretation of the parameters in terms of microstructure. In white matter, the ‘stick’ fractions close to 50% are consistent with estimates from similar approaches (40), and are aligned with axonal volume fractions from histology (30, 71, 89) if corrected for the space occupied by MR-invisible myelin, according to f_S = v_A / (1 – v_M). In children, white matter ‘stick’ fractions were lower than in adults (Table 3), potentially reflecting incomplete maturation (90). The ‘stick’ axial diffusivities were low (D_||;S ≈ 1.8 μm²/ms; Table 3) in comparison with estimates for intra-axonal water obtained using planar signal filtering (D_|| ≈ 2.25 μm²/ms) (91). Potential explanations include the comparatively longer TE used in Dhital (91), if longer axonal T₂ are related to higher axial diffusivities. The ‘stick’ axial diffusivities were low also compared with those of ‘zeppelins’ (D_||;Z ≈ 2.7 μm²/ms), possibly indicating obstruction of intra-axonal diffusion from, for example, variation in axonal caliber (92). The axial diffusivities were more similar between compartments in previous studies (33, 40), possibly due to model differences and undetected bias in those or the present study. The ‘zeppelin’ shape assumed negative values only sparsely and incoherently (Figure 5), indicating an absence of ‘oblate’ diffusion tensors in healthy brain. The ‘stick’ T₂ values (Table 3) are largely consistent with previous observations (40, 93), including high values in the internal capsule. Higher T₂ values within the more anisotropic (stick) compartment is also consistent with previous findings both in the human brain (40, 93, 94) and in ex vivo animal nervous tissue (95–98), possibly reflecting a reduction of ‘zeppelin’ T₂ from exchange between the extracellular space and myelin water (99). Additionally, we found that T_2;S yielded a plausible segmentation of the cerebrospinal tract all the way from the brainstem to the motor cortex (Figure 7). This suggests that diffusion-relaxation experiments increase specificity to particular fiber bundles, which could potentially improve regional segmentation or aid separating crossing fibers in tractography (100).

Figure 7 –

Maximum intensity projections of the T_2;S parameter in three planes shown on top of a coregistered T₁-weighted image. The result yielded a plausible segmentation of the cerebrospinal tract all the way from the brainstem to close to the motor cortex.

In gray matter, ‘stick’ fractions between 10 and 20% are consistent with previous findings (28, 33). However, the findings are not consistent with interpreting ‘sticks’ as neurites, because the combined (neurite) density of axons and dendrites is approximately 60% according to histology (101–103). We hypothesize, as in Lampinen (28), that this discrepancy is due to dendrites not exhibiting stick-like diffusion, due to, for example, exchange with soma or between short segments with different orientations. Thus, the model may be too simplistic for gray matter.

In white matter lesions, the increased ‘zeppelin’ isotropic diffusivities and T₂ values are consistent with demyelination enlarging the extracellular space (104). Disambiguating between demyelination and axonal loss requires either data with independent sensitivity to myelin or the use of assumptions, however. By the tortuosity assumption extended to variable g-ratios (Eq. 20), and excluding the outlier lesion in Fig. 6, our results would suggest similar axonal volume fractions (v_A ≈ 0.2) but lower myelin volume fractions (v_M ≈ 0.4 versus 0.5) in lesions versus in the healthy anterior corona radiata, which is in line with the results of Coelho (105).

This study had limitations. First, for efficiency reasons, the optimization used a small set of priors (Table 1). One may be concerned that the choice of priors could have a strong effect on the protocol and in some way bias the fitting procedure. However, using different priors revealed similar sampling requirements and no bias towards particular solutions was seen in the fitting. Second, CLRB-optimized protocols can be susceptible to local minima (Figure 3A/B). However, these can be avoided by using multiple random initial guesses in the fitting, and the manually adjusted in vivo protocol appeared robust. Third, we did not address reproducibility. Future studies should investigate the impact on parameter values from changing the sampling protocol. Fourth, the gradient waveforms used to generate linear and prolate tensor encoding differed with respect to time-dependent diffusion encoding, which may lead to bias (106, 107). Such time dependence is only expected for very short encoding times (108), however. For the longer encoding times used in this study, we have not been able to detect time dependence in the healthy brain (20, 28). Fifth, a spherical harmonic expansion truncated at l_max = 2 may be insufficient for representing sharp ODFs, as indicated by the fit being worst in regions with high orientation coherence (Figure 5). However, comparing our estimates with those obtained using the ‘RotInv’ approach suggests that this is not likely to bias the kernel parameters (Supporting Information Figure S6). Finally, even the relatively unconstrained model used here is simplistic compared with the complexity of neural tissue and does not account for myelin (71), soma (109), the microvasculature (50), glial cells (110) or CSF (111), wherefore parameters should be interpreted with care. Preliminary results indicate that our present data would support an additional free parameter to include a free water compartment (Supporting Information Figure S7), and that bias from neglecting free water is small but non-negligible also within non-cortical brain, possibly indicating contributions from perivascular spaces (112). This should be further investigated and validated in future studies using the b/b_Δ/TE measurement space to drive models with higher capacity.

5 |. CONCLUSIONS

Optimized diffusion-relaxation sampling enabled precise and efficient whole-brain estimation of compartment-specific fractions, diffusivities and T₂ values. Acquiring data using the independent dimensions of b-value, b-tensor shape and echo time expands the set of microstructure parameters measurable with MRI, as well as the range of conditions in which they may be accurately estimated. According to our findings, the conventional approach of improving precision through enforcing parameter relations causes bias even in the healthy brain. Future studies could use diffusion-relaxation MRI with tensor-valued diffusion encoding for enhanced specificity to microstructural quantities. Our in vivo results showed that ‘stick’ fractions were lower in the white matter of children than in adults, and that white matter lesions featured changes compatible with demyelination.

Supplementary Material

Supporting Information

FIGURE S1 Validation of the CRLB by comparing the V_W metric based on variance estimates from either CRLB or simulations.

FIGURE S2 A multi-slice version of Figure 5.

FIGURE S3 A test-retest experiment on an adult volunteer, showing test and retest parameter maps, difference maps, and Bland-Altman plots.

FIGURES S4 and S5 The importance of the number of ‘shells’ versus the degree of orientation dispersion for the ability to determine all model parameters.

FIGURE S6 Comparison of parameter maps obtained by fitting Eq. 12 directly to data versus those obtained using the ‘RotInv’ approach.

FIGURE S7 Comparison of parameter maps obtained using the two-compartment model (Eq. 12) versus a model extended to include a free water compartment.