Sustainable fuzzy multi-trip location-routing problem for medical waste management during the COVID-19 outbreak

Abstract

The performance of waste management system has been recently interrupted and encountered a very serious situation due to the epidemic outbreak of the novel Coronavirus (COVID-19). To this end, the handling of infectious medical waste has been particularly more vital than ever. Therefore, in this study, a novel mixed-integer linear programming (MILP) model is developed to formulate the sustainable multi-trip location-routing problem with time windows (MTLRP-TW) for medical waste management in the COVID-19 pandemic. The objectives are to concurrently minimize the total traveling time, total violation from time windows/service priorities and total infection/environmental risk imposed on the population around disposal sites. Here, the time windows play a key role to define the priority of services for hospitals with a different range of risks. To deal with the uncertainty, a fuzzy chance-constrained programming approach is applied to the proposed model. A real case study is investigated in Sari city of Iran to test the performance and applicability of the proposed model. Accordingly, the optimal planning of vehicles is determined to be implemented by the municipality, which takes 19.733 h to complete the processes of collection, transportation and disposal. Finally, several sensitivity analyses are performed to examine the behavior of the objective functions against the changes of controllable parameters and evaluate optimal policies and suggest useful managerial insights under different conditions.

Graphical abstract

Highlights

• •Addressing the sustainability of location-routing problem under the pandemic situation
• •Applying fuzzy chance-constrained programming technique to address the uncertainty
• •Implementing weighted goal programming method to deal with the mutli-objectiveness
• •Investigating applicability of the proposed methodology using a real case study.

1. Introduction

The most recent epidemic outbreak that caused a pandemic and public health emergencies is the spread of the novel coronavirus disease (COVID-19), threatening the health of the world population (Kargar et al., 2020). The COVID-19 has quickly spread from Wuhan to other regions and influenced >200 countries throughout the world by the end of March 2020 (Ahmadi et al., 2020; Govindan et al., 2020). It is now a pandemic due to the rapid rise in the number of infected people and the lack of initial attention to the COVID-19 pandemic from world's leaders (Mardani et al., 2020).

So, we have encountered a critical and challenging period for the control and prevention of the pandemic. One of the serious concerns about the outbreak of COVID-19 is the incubation period, which fluctuates from 3 to 14 days (Issa and Abd Elaziz, 2020). It is obvious that the spread of COVID-19 may be increased through an inefficient waste management system (Sarkis et al., 2020).

In line with the significance of providing medical items, another substantial issue is handling the infectious medical waste related to COVID-19 generated in diagnosing and treating patients at health centers including hospitals and infirmaries. With the growing rate of confirmed cases, the amount of medical waste related to COVID-19 increases significantly, which is now considered as critical hazardous materials (HAZMAT). In other words, medical waste disposal is regarded as a significant way to handle the source of infection, strict establishment and standardization of the waste management of COVID-19 (Peng et al., 2020). On the other hand, since most of this waste is made out of plastic, it can put the environment in danger, if it is not processed properly and timely. Therefore, a careful consideration should be made to decrease the risk of the epidemic in hospitals and infirmaries as much as possible. This study designs a waste management system to efficiently deal with the collection (from hospitals and infirmaries), transportation (through the road network) and disposal of the COVID-19 related waste at pre-established disposal sites.

The main idea is to provide a decision support system (DSS) ensuring that COVID-19 related medical waste is timely, regularly, harmlessly and effectively is disposed by considering sustainable development. To this end, the sustainable multi-trip location-routing problem with time windows (MTLRP-TW) is introduced to address the collection, transportation and disposal processes considering the priorities of services and available budget of the system. Here to address the sustainable development, the objectives are defined to concurrently minimize the total traveling time of waste-collection vehicles, total violation from time windows (service priorities) and the number of people live around disposal sites. Accordingly, a novel MOMILP model is developed to formulate the problem and then to be validated using a real-life case study problem.

2. Survey on related research

The location-routing problem (LRP) is an extension of the classic routing problem that integrates the strategic and operational decisions by facility location problem (FLP) and vehicle routing problem (VRP), respectively. Each of these problems has been frequently investigated in the literature as can be seen in Erkut et al. (2008) and Tirkolaee et al., 2018, Tirkolaee et al., 2019, Tirkolaee et al., 2020a. Due to the high application of LRP in supply chain and waste management systems, it has been studied by many researchers in different cases (Drexl and Schneider, 2015). To be more specific, Zografros and Samara (1989), as one of the pioneering research, suggested an LRP model for transportation and disposal of HAZMAT considering three minimization-type objectives of routing risk, disposal risk and travel time. They applied a goal programming (GP) approach to solve the model.

Alumur and Kara (2007) worked on a new model for the HAZMAT LRP to simultaneously minimize total cost and transportation risk. They could evaluate the performance of their proposed model on a real case study in Turkey using CPLEX. Xie et al. (2012) developed a multi-modal LRP model for HAZMAT transportation considering long distances. They implemented the proposed model on two case studies to represent the applicability of their proposed model. Das et al. (2012) designed a multi-objective framework for routing of HAZMAT between generating nodes and disposal sites with the aim of total transportation cost and risk minimization. They conducted a real case study using posteriori technique with multi-objective programming approach to provide non-dominated solutions for the waste management system. A multi-objective mixed-integer linear programming model (MOMILP) was designed by Samanlioglu (2013) to address the industrial HAZMAT LRP. The objectives were to minimize total cost, total transportation risk and total risk for the population around treatment facilities. They investigated a real case study in Turkey using lexicographic weighted Tchebycheff formulation and CPLEX software.

Zhao and Ke (2017) analyzed the incorporation of inventory risks in LRP for explosive waste management. They developed a bi-objective model to concurrently minimize total cost and total risk. They investigated some numerical experiments using real-world data in China. Aydemir-Karadag (2018) offered a profit-oriented model for HAZMAT LRP considering energy recovery and the application of polluter pays principle. She tested the applicability of the proposed model using hypothetical problem instances based on a real-life case study. Two meta-heuristic algorithms were proposed by Rabbani et al. (2018) to tackle an industrial HAZMAT LRP considering incompatible waste types. The objectives were to simultaneously minimize total cost, total site risk for people and total transportation risk. Beneventti et al. (2019) introduced a multi-product maximin HAZMAT LRP with multiple origin-destination pairs. They formulated the problem as a MOMILP model to simultaneously maximize the minimum weighted distance between facilities and vulnerable population sites, and minimum weighted distance from HAZMAT transportation routes to vulnerable population sites, and concurrently minimize total hazard inflicted on non-vulnerable population and total cost. A multi-period industrial HAZMAT LRP was suggested by Rabbani et al. (2019) using Monte Carlo simulation and non-dominated sorting genetic algorithm II (NSGA-II). They formulated the problem using a stochastic MOMILP to minimize total cost and environmental risk in transportation and location phases. A comprehensive investigation on solid waste management was conducted by Singh (2019) considering the application of mathematical models. Saeidi-Mobarakeh et al. (2020) developed a bi-objective robust framework for a HAZMAT LRP considering two stakeholders and uncertain demand. The objectives were to minimize total risk to population and total cost of waste management system. They investigated a real medical waste case study in Iran to test the applicability of the proposed methodology.

Recently, some efforts have been made to study the effects of the COVID-19 pandemic on the waste and wastewater services but not at operational levels. Saadat et al. (2020) reviewed the environmental aspects of the COVID-19 pandemic. They discussed the disposal of medical wastes in the environment as a big challenging issue. Kitajima et al. (2020) found that ribonucleic acid (RNA) in wastewater can be employed to monitor the COVID-19 pandemic. Accordingly, they examined state-of-the-knowledge and research requirements. The potential effects of the COVID-19 pandemic on waste/wastewater services were investigated by Nghiem et al. (2020). They demonstrated that monitoring viral RNA in wastewater can evaluate disease prevalence and spread. Wang et al. (2020) suggested some disinfection strategies for hospital waste/wastewater during the COVID-19 pandemic in China. Nzediegwu and Chang (2020) clarified the importance of appropriate waste management to decrease the potential of the COVID-19 spread in developing countries.

To the best of our knowledge, there is no study yet dealing with the efficient treatment of COVID-19 related medical waste at the operational level; i.e., in terms of timely collection, transportation and disposal within a waste management system. Moreover, this is the first study that introduces the MTLRP-TW under uncertain conditions. Therefore, due to the instability and uncertainty of the demand parameter, fuzzy chance-constrained programming approach is applied. Furthermore, a weighted goal programming (WGP) technique is then implemented to deal with the multi-objectiveness of the model.

3. Methodology

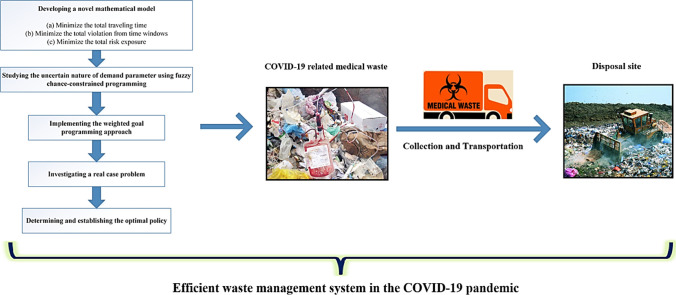
This section describes the suggested methodology of the study to establish an efficient waste management system during the COVID-19 pandemic. To have an overall view, Fig. 1 represents the execution steps.

Fig. 1.

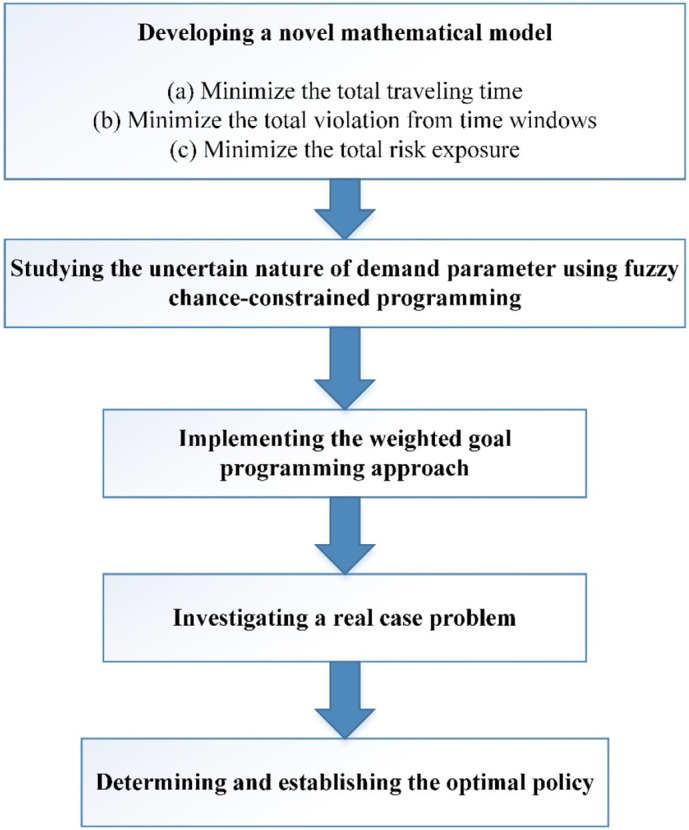
Proposed DSS of the study.

3.1. Problem description and mathematical model

Consider a network including parking site, demand nodes (hospitals and infirmaries) and pre-established and post-established disposal sites. The aim is to make locational and routing decisions under a specific situation imposed by the COVID-19 pandemic. Accordingly, at the first stage, the required additional disposal sites are established at the beginning of the time horizon, which are called post-established disposal sites. Vehicles routing plan is made at the second stage such that a fleet of vehicles is considered to start their first trip from the parking and end it at one of the available disposal sites. Furthermore, the next possible trips of these vehicles start from that disposal site and end at available disposal sites. It means that the destination and departure can be different, so the concept of “intermediate depots” is associated. For more information, see Tirkolaee et al. (2020b).

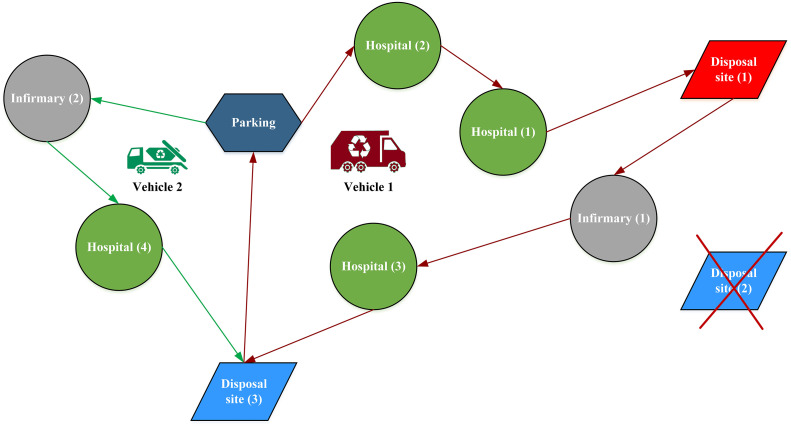
According to this pandemic situation, it is necessary that the waste should be instantly collected, transported and disposed. Each demand node has its own service time window that should be served. So, the objective functions are to simultaneously (i) minimize the total traveling time, (ii) minimize total violation from time windows and (iii) minimize total infection/environmental risk imposed on the population around disposal sites. Fig. 2 illustrates a hypothetical example to schematically describe the proposed network of the study. Here, red and blue disposal sites denote the pre- and post-established disposal sites, respectively. To serve these 6 demand nodes (4 hospitals and 2 infirmaries), 2 vehicles are used. The first vehicles have 2 trips which are highlighted in orange. The first trip of Vehicle 1 includes Parking → Hospital (2) → Hospital (1) → Disposal site (1), and its second trip includes Disposal site (1) → Infirmary (1) → Hospital (3) → Disposal site (3) → Parking.

Fig. 2.

Proposed transportation network of the study.

The second vehicle has just 1 trip which is highlighted in black and consists of Parking → Infirmary (2) → Hospital (4) → Disposal site (3) → Parking.

The main assumptions of the problem are as follows:

• I.Vehicles are heterogeneous and may have several trips.
• II.Time windows are defined for each demand node.
• III.Each vehicle has a maximum service time.
• IV.Demand parameters are considered as triangular fuzzy numbers.
• V.There are both pre- and post-established disposal sites that have limited capacity.
• VI.Candidate disposal site can be established just at the beginning of the planning periods.
• VII.Each demand node should be served only by one vehicle.
• VIII.From second trips onwards, vehicles may unload the collected waste in a different disposal site from which the trip has been already started.

Now, the mathematical notations of the proposed model including sets and indices, parameters and variables are listed as follows.

3.1.1. Sets and indices

N

Set of nodes (i, j ∈ N); N = {1, 2, …,  n}; here, 1 represents the parking,

R

Set of demand nodes (i, j ∈ R),

F

Set of pre-established disposal sites (i, j ∈ F),

G

Set of candidate (post-established) disposal sites (i, j ∈ G),

K

Set of vehicles (k ∈ K),

P

Set of vehicle trips (p ∈ P),

T

Set of planning periods (t ∈ T),

S

An arbitrary set of nodes.

3.1.2. Parameters

c_ij

Distance between node i and j (km),

v_k

Average speed of vehicle k (km/h),

W_k

Capacity of vehicle k (kg),

T_max

Maximum available time for vehicles (min),

ϒ

Budget of the waste management system ($),

cv_k

Variable cost of vehicle k ($),

cf_k

Fixed cost of vehicle k ($),

Fv_i

Variable cost to processing the waste at disposal site i ($),

Fx_i

Fixed cost to establishing disposal site i ($),

Ca_i

Capacity of disposal site i at each period (kg),

${\tilde{D}}_{\mathit{it}}$

Demand of demand node i in period t (kg),

(e_it, l_it)

Time window for serving demand node i in period t,

Po_i

Population size (number of people) around disposal site i,

θ

Conversion factor of distance to cost ($/km),

M

An optional large number.

3.1.3. Variables

y_i

Binary variable indicating whether candidate disposal site i is established or not,

x_ijkpt

Binary variable indicating whether vehicle k traverses arc (i, j) in trip p at period t or not,

z_kt

Binary variable indicating whether vehicle k is used in period t or not,

Lw_kpt

Amount of waste collected and transported by vehicle k in trip p at period t (kg),

Uw_it

Amount of waste unloaded and processed at disposal site i in period t (kg),

AT_it

Arrival time at demand node i in period t,

VT_it

Violation amount from the time window of demand node i in period t (hr).

Now, the proposed MILP model is as follows:

$$minimize\mathit{Obj}1=\sum _{i\in N}\sum _{j\in N}\sum _{k\in K}\sum _{p\in P}\sum _{t\in T}\frac{c_{\mathit{ij}}}{v_k}{x}_{\mathit{ijkpt}}$$ (1)

$$minimize\mathit{Obj}2=\sum _{i\in N}\sum _{t\in T}{\mathit{VT}}_{\mathit{it}}$$ (2)

$$minimize\mathit{Obj}3=\sum _{i\in N}{\mathit{Po}}_i{y}_i$$ (3)

subject to

$$\sum _{j\in R}{x}_{\mathit{ijkpt}}=\sum _{j\in R}{x}_{\mathit{jikpt}}\forall i\in N;i\ne j,k\in K,p\in P,t\in T,$$ (4)

$$\sum _{i\in N}\sum _{p\in P}\sum _{k\in K}{x}_{\mathit{ijkpt}}=1\forall j\in R;i\ne j,t\in T,$$ (5)

$$\sum _{i\in N}\sum _{j\in R}{\tilde{D}}_{\mathit{jt}}{x}_{\mathit{ijkpt}}\le W_k\forall k\in K,p\in P,t\in T,$$ (6)

$${\mathit{Lw}}_{\mathit{kpt}}=\sum _{i\in N}\sum _{j\in R}{\tilde{D}}_{\mathit{jt}}{x}_{\mathit{ijkpt}}\forall k\in K,p\in P,t\in T,$$ (7)

$${\mathit{Uw}}_{\mathit{it}}=\sum _{j\in R}\sum _{k\in K}\sum _{p\in P}{\mathit{Lw}}_{\mathit{ktp}}{x}_{\mathit{jikpt}}\forall i\in F\cup G,t\in T,$$ (8)

$${\mathit{Uw}}_{\mathit{it}}\le {\mathit{Ca}}_i{y}_i\forall i\in F\cup G,t\in T,$$ (9)

$$y_i=1\forall i\in F,$$ (10)

$$\sum _{i\in N}\sum _{j\in N}\sum _{p\in P}\frac{c_{\mathit{ij}}}{v_k}{x}_{\mathit{ijkpt}}\le T_{\mathit{max}}\forall k\in K,t\in T,$$ (11)

$$\sum _{i\in S}\sum _{\begin{array}{c}j\in S\\ i\ne j\end{array}}{x}_{\mathit{ijkpt}}\le \left|S\right|-1\forall S\in N\backslash \left\{1\right\}\cup F\cup G;S\ne \varnothing ,k\in K,p\in P,t\in T,$$ (12)

$$\sum _{j\in R}{x}_{1\mathit{jk}1t}\ge \sum _{j\in R}{x}_{\mathit{ijk}2t}\forall i\in F\cup G,k\in K,t\in T,$$ (13)

$$\sum _{j\in R}{x}_{\mathit{ijk}p-1t}\ge \sum _{j\in R}{x}_{\mathit{ijkpt}}\forall i\in F\cup G,p\in P\backslash \left\{1\right\},k\in K,t\in T,$$ (14)

$\begin{array}{l}A{T}_{\mathit{jt}}-\sum _{i\in N}\sum _{k\in K}\sum _{p\in P}\left(1-x_{\mathit{ijkpt}}\right)M\le \sum _{i\in N}\sum _{k\in K}\sum _{p\in P}\left(A{T}_{\mathit{it}}+\frac{c_{\mathit{ij}}}{v_k}\right)\le A{T}_{\mathit{jt}}+\sum _{i\in N}\sum _{k\in K}\sum _{p\in P}\left(1-x_{\mathit{ijkpt}}\right)M\\ \forall j\in R,t\in T,\end{array}$ (15)

$${\mathit{AT}}_{1t}=0\forall t\in T,$$ (16)

$$e_{\mathit{it}}\le {\mathit{AT}}_{\mathit{it}}\le l_{\mathit{it}}\forall i\in R,t\in T,$$ (17)

$${\mathit{VT}}_{\mathit{it}}\ge max\left\{{\mathit{AT}}_{\mathit{it}}-l_{\mathit{it}},e_{\mathit{it}}-{\mathit{AT}}_{\mathit{it}},0\right\}\forall i\in R,t\in T,$$ (18)

$$\sum _{j\in R}{x}_{1\mathit{jk}1t}=z_{\mathit{kt}}\forall k\in K,t\in T,$$ (19)

$$\sum _{j\in R}\sum _{i\in F\cup G}{x}_{\mathit{jik}1t}=z_{\mathit{kt}}\forall k\in K,t\in T,$$ (20)

$$\sum _{i\in F\cup G}\sum _{j\in R}{x}_{\mathit{ijkpt}}\le z_{\mathit{kt}}\forall k\in K,p\in P\backslash \left\{1\right\},t\in T,$$ (21)

$$\sum _{j\in R}\sum _{i\in F\cup G}{x}_{\mathit{jikpt}}\le z_{\mathit{kt}}\forall k\in K,p\in P\backslash \left\{1\right\},t\in T,$$ (22)

$$x_{i1\mathit{kpt}}\ge x_{i1kp-1t}\forall i\in F\cup G,p\in P\left\{1\right\},k\in K,t\in T,$$ (23)

$$\sum _{i\in F\cup G}\sum _{p\in P}{x}_{i1\mathit{kpt}}=z_{\mathit{kt}}\forall k\in K,t\in T,$$ (24)

$\begin{array}{l}\theta \left(\sum _{i\in N}\sum _{j\in N}\sum _{k\in K}\sum _{p\in P}\sum _{t\in T}{c}_{\mathit{ij}}{x}_{\mathit{ijkpt}}\right)+\sum _{k\in K}\sum _{t\in T}c{f}_k{z}_{\mathit{kt}}+\sum _{k\in K}\sum _{t\in T}\sum _{p\in P}c{v}_{k}L{w}_{\mathit{ktp}}+\sum _{i\in G}F{x}_i{y}_i\\ +\sum _{i\in F\cup G}\sum _{t}F{v}_{i}U{w}_{\mathit{it}}\le \Upsilon ,\end{array}$ (25)

$$\sum _{i\in N}\sum _{j\in N}\sum _{p\in P}{x}_{\mathit{ijkpt}}\le M{z}_{\mathit{kt}}\forall k\in K,t\in T,$$ (26)

$$y_i,x_{\mathit{ijkpt}},z_{\mathit{kt}}\in \left\{01\right\}\forall i,j\in N,k\in K,p\in P,t\in T,$$ (27)

$${\mathit{Lw}}_{\mathit{ktp}},{\mathit{Uw}}_{\mathit{it}},{\mathit{AT}}_{\mathit{it}},{\mathit{VT}}_{\mathit{it}}\ge 0\forall i,j\in N,k\in K,p\in P,t\in T.$$ (28)

Objective function (1) minimizes the total traveling time of vehicles. Objective function (2) minimizes the total violation from time windows defined by demand nodes. Objective function (3) minimizes the disposal sites risk; i.e., the number of people around disposal sites is minimized. Constraint (4) represents the flow balance equation for each node. Constraint (5) guarantees that each demand node should be served in each period. Constraint (6) indicates the capacity limitation of each vehicle in each trip. Constraints (7), (8) calculate the amount of waste collected by each vehicle and transported to each disposal facility, respectively. Constraint (9) represents the capacity limitation of disposal sites. Constraint (10) ensures that pre-established disposal sites are located in the network at the beginning of the time horizon. Constraint (11) states the maximum available time for vehicles. Constraint (12) eliminates any possible sub-tours. Constraints (13), (14) ensure that the trip number of vehicles takes value based on the numerical order from 1 to P. Constraints (15), (16), (17), (18) are related to the calculation of time windows. Constraint (15) calculates the arrival time at demand points. Constraint (16) expresses that the arrival time at parking is zero. Constraint (17) reflects the time window of demand nodes. Constraint (18) computes the violation amount from time windows. Constraints (19), (20) guarantee that vehicles should start the first trip from parking and end it at a disposal site, respectively. Constraints (21), (22) ensure that vehicles start the potential next trips from the disposal site (as the final node of its first trip) and end it at a disposal site, respectively. Constraints (23), (24) guarantee that vehicles should move back to the parking in their last trip to complete their tour in each period. Constraint (25) indicates the budget limitation of the waste management system. Constraint (26) expresses that vehicles can construct a route only when they are already assigned. Constraints (27), (28) show the types of the variables.

3.2. Linearization of the model

Constraint (8) contains a non-linear equation due to the multiplication of a positive continuous variable by a binary variable. To this end, it should be linearized by applying the following equations:

$${\mathit{Lx}}_{\mathit{jikpt}}={\mathit{Lw}}_{\mathit{kpt}}{x}_{\mathit{jikpt}}\forall i\in F\cup G,j\in R,t\in T,k\in K,p\in P,$$ (29)

$${\mathit{Uw}}_{\mathit{it}}=\sum _{j\in R}\sum _{k\in K}\sum _{p\in P}{\mathit{Lx}}_{\mathit{jikpt}}\forall i\in F\cup G,t\in T,$$ (30)

$${\mathit{Lx}}_{\mathit{jikpt}}\le M{x}_{\mathit{jikpt}}\forall i\in F\cup G,j\in R,t\in T,k\in K,p\in P,$$ (31)

$${\mathit{Lx}}_{\mathit{jik}\mathrm{p}t}\le {\mathit{Lw}}_{\mathit{kpt}}\forall i\in F\cup G,j\in R,t\in T,k\in K,p\in P,$$ (32)

$${\mathit{Lx}}_{\mathit{jikpt}}\ge {\mathit{Lw}}_{\mathit{kpt}}-M\left(1-x_{\mathit{jikpt}}\right)\forall i\in F\cup G,j\in R,t\in T,k\in K,p\in P,$$ (33)

$${\mathit{Lx}}_{\mathit{ijkpt}}\ge 0\forall i\in F\cup G,j\in R,t\in T,k\in K,p\in P,$$ (34)

The proposed model can easily be linearized by replacing Eq. (8) with Eqs. (30), (31), (32), (33), (34).

3.3. Fuzzy chance-constrained programming

To deal with the uncertain nature of parameters and to develop a more realistic model, fuzzy mathematical programming is applied as an efficient approach (Tirkolaee et al., 2020c). Here, the fuzzy chance-constrained programming model is employed to address the uncertainty of demand parameter, which is implemented based on strong mathematical concepts (Liu and Liu, 2002; Khishtandar, 2019). For example, the expected value of a fuzzy number and its credibility can support a variety of fuzzy numbers, including triangular and trapezoidal numbers, and enables a decision-maker to achieve minimum levels of confidence with chance constraints. The triangular fuzzy numbers have the appropriate applicability to cope with data which suffer from accuracy or information (Li et al., 2012). If $\tilde{x}=\left(x^p,x^m,x^o\right)$is taken into account as a triangular fuzzy number and the confidence level (ρ) is >0.5, considering the confidence level of the fuzzy number versus the random number r, we have:

$$\mathit{Cr}\left\{\tilde{x}\le r\right\}\ge \rho \iff r\ge \left(2\rho -1\right)x^p+2\left(1-\rho \right)x^m,$$ (35)

$$\mathit{Cr}\left\{\tilde{x}\ge r\right\}\ge \rho \iff r\le \left(2\rho -1\right)x^o+2\left(1-\rho \right)x^m.$$ (36)

Eqs. (35), (36) are directly used to convert fuzzy chance-constrained programming model into a defuzzified model with crisp values by comparing critical ρ values (Liu and Liu, 2002).

In the proposed model, demand parameter ${\tilde{D}}_{\mathit{jt}}=\left({D_{\mathit{jt}}}^p,{D_{\mathit{jt}}}^m,{D_{\mathit{jt}}}^o\right)$ is the uncertain parameter of the model as an independent triangular fuzzy number. Now, the constraints that include this parameter are rewritten based on the fuzzy chance-constrained programming model. Therefore, Eqs. (6), (7) are reformulated based on the chance-constrained planning approach.

$$\mathit{Cr}\left\{\sum _{i\in N}\sum _{j\in R}{\tilde{D}}_{\mathit{jt}}{x}_{\mathit{ijkpt}}\le W_k\right\}\ge {{\rho }^1}_{\mathit{kpt}}\forall k\in K,\forall p\in P,t\in T,$$ (37)

$$\mathit{Cr}\left\{{\mathit{Lw}}_{\mathit{kpt}}=\sum _{i\in N}\sum _{j\in R}{\tilde{D}}_{\mathit{jt}}{x}_{\mathit{ijkpt}}\right\}\ge {{\rho }^2}_{\mathit{kt}}\forall k\in K,p\in P,t\in T.$$ (38)

Now, based on Eqs. (35), (36), Eqs. (37), (38) are defuzzified. It is noticeable that Eq. (38) should be regarded as two inequalities:

$${\sum }_{i\in N}{\sum }_{j\in R}\left[\left(2{{\rho }^1}_{\mathit{kpt}}-1\right){D_{\mathit{jt}}}^p{x}_{\mathit{ijkpt}}+2\left(1-{{\rho }^1}_{\mathit{kpt}}\right){D_{\mathit{jt}}}^m{x}_{\mathit{ijkpt}}\right]\le W_k$$

$$\forall k\in K,\forall p\in P,t\in T,$$ (39)

$${\mathit{Lw}}_{\mathit{kpt}}\le \left(2{{\rho }^2}_{\mathit{kt}}-1\right)\sum _{i\in N}\sum _{j\in R}{D_{\mathit{jt}}}^o{x}_{\mathit{ijkpt}}+2\left(1-{{\rho }^2}_{\mathit{kt}}\right)\sum _{i\in N}\sum _{j\in R}{D_{\mathit{jt}}}^m{x}_{\mathit{ijkpt}}$$

$$\forall k\in K,p\in P,t\in T,$$

$${\mathit{Lw}}_{\mathit{kpt}}\ge \left(2{{\rho }^2}_{\mathit{kt}}-1\right)\sum _{i\in N}\sum _{j\in R}{D_{\mathit{jt}}}^p{x}_{\mathit{ijkpt}}+2\left(1-{{\rho }^2}_{\mathit{kt}}\right)\sum _{i\in N}\sum _{j\in R}{D_{\mathit{jt}}}^m{x}_{\mathit{ijkpt}}$$

$$\forall k\in K,p\in P,t\in T.$$ (40)

The final developed model is now given as follows:

$$minimize\mathit{Obj}1=\sum _{i\in N}\sum _{j\in N}\sum _{k\in K}\sum _{p\in P}\sum _{t\in T}\frac{c_{\mathit{ij}}}{v_k}{x}_{\mathit{ijkpt}}$$ (41)

$$minimize\mathit{Obj}2=\sum _{i\in N}\sum _{t\in T}{\mathit{VT}}_{\mathit{it}}$$ (42)

$$minimize\mathit{Obj}3=\sum _{i\in N}{\mathit{Po}}_i{y}_i$$ (43)

subject to

$$\begin{array}{l}\mathrm{Eqs}.\left(4\right)–\left(5\right),\\ \mathrm{Eqs}.\left(9\right)–\left(27\right),\\ \mathrm{Eqs}.\left(29\right)–\left(33\right),\\ \mathrm{Eqs}.\left(38\right)–\left(39\right)\end{array}$$ (44)

3.4. Weighted goal programming

One of the most attractive multi-objective programming approaches is GP that was introduced by Charnes and Cooper (1977). This method addresses optimization problems with multiple conflicting objectives. The main advantage of GP over other multi-objective programming techniques is the concurrent consideration of different objectives, and also permissibility of deviation from ideal objectives (goals) which makes the decision-making process flexible.

On the other hand, since we usually encounter multiple objectives with multiple units and importance degrees, it is required to normalize the objective function of GP and assign weights to the objectives to tackle the importance levels. Accordingly, WGP is proposed with the following mathematical structure:

$$minimize{\sum }_{o=1}^O{W}_o\left(\frac{d_o^{+}+d_o^{-}}{b_o}\right)$$

subject to

$$H_g\left(X\right)=\left(\le \text{or}\ge \right)0g=1,2,\dots ,G,$$

$$f_o-d_o^{+}+d_o^{-}=b_{o}o=1,2,\dots ,O,$$

$$d_o^{+},d_o^{-}\ge 0o=1,2,\dots ,O.$$ (45)

Based on the objective function of WGP, the sum of weighted negative deviation (d _o ⁻) and positive deviations (d _o ⁺) must be minimized. Here, o is an index to indicate the objective functions of the model. In Model (45), H _g(X) and b _o stand for the gth constraint set and the ideal value of oth objective function, and f _o shows the oth objective function. Note that b _o cannot take the value of 0. Moreover, the positive and negative deviations are computed as follows:

$$d_o^{-}=\left\{\begin{array}{c}{b}_o-f_o\text{if}{f}_o<b_o,\\ 0\text{otherwise}.\end{array}\right)$$ (46)

$\begin{array}{l}{d}_o^{+}=\{\begin{array}{ll}{f}_o-b_o& \mathit{if}{f}_o>b_o,\\ 0& \mathit{otherwise}.\end{array}\end{array}$

Here, $W_o\mid \sum _o{W}_o=1$represents the importance of oth objective function. It should be noted that these weights are determined based on the decision-maker attitude.

Hence, the following modifications are made in the proposed model to concurrently take into account the three objective functions. The final model is developed as follows:

$$minimize\mathrm{\Psi }=W_1\left(\frac{d_1^{+}}{b_1}\right)+W_2\left(\frac{d_2^{+}}{b_2}\right)+W_3\left(\frac{d_3^{+}}{b_3}\right)$$ (47)

subject to

$$\mathit{Obj}1-d_1^{+}+d_1^{+}=b_1,$$ (48)

$$\mathit{Obj}2-d_2^{+}+d_2^{+}=b_2,$$ (49)

$$\mathit{Obj}3-d_3^{+}+d_3^{+}=b_3,$$ (50)

Eqs. (4), (5),

Eqs. (9), (10), (11), (12), (13), (14), (15), (16), (17), (18), (19), (20), (21), (22), (23), (24), (25), (26), (27), (28),

Eqs. (30), (31), (32), (33), (34),

Eqs. (38), (39).

where Ψ is the objective function of the WGP model. Since all the objective functions are of minimization type, the objective function of WGP model is formulated as a weighted sum of normalized positive deviations.

4. Computational results

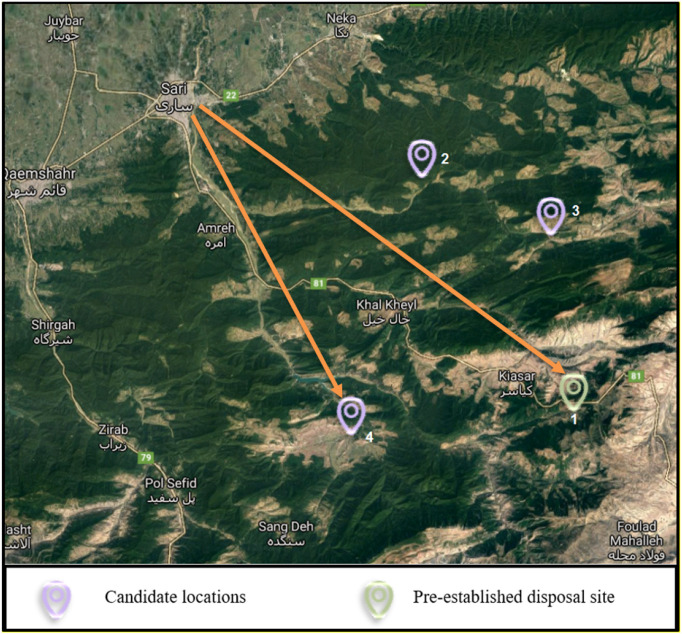
This section investigates the validation of the proposed model using a real case study problem in Sari, the capital of Mazandaran province, Iran. According to Fig. 3 , 1 pre-established disposal site (node number 1) and 3 candidate locations (nodes numbers 2, 3 and 4) are given in the map. It should be noted that the candidate locations are adapted from the study conducted by Lahmian (2018). He evaluated the potential locations to establish disposal sites considering the criteria of i. geology, ii. land use, iii. slope, iv. vegetation, v. access roads, and vi. distance from towns of Sari city. Finally, the land use and distance from towns of Sari city were determined as the main effective criteria.

Fig. 3.

Geographical area and information of the disposal sites outside Sari city.

Moreover, based on Fig. 4 , 16 hospitals and infirmaries are distributed within the city networks which generate COVID-19 related medical waste. Moreover, 4 vehicles are available at the parking site. The confidence levels of Eqs. (6), (7); i.e., ${{\rho }^1}_{\mathit{kpt}}$ and ${{\rho }^2}_{\mathit{kt}}$ are set to 0.7. The maximum available time for vehicles and available budget are set to 480 min and 1 million USD, respectively. Furthermore, ${D_{\mathit{jt}}}^p$ = 0.8 ${D_{\mathit{jt}}}^m$ and ${D_{\mathit{jt}}}^o$ = 1.2${D_{\mathit{jt}}}^m$. All the required input data were collected from the health department of Mazandaran University of Medical Sciences (2020) for a week. Furthermore, the weights assigned to the objective functions are W ₁ = 0.4, W ₂ = 0.3 and W ₃ = 0.3. These weights were set as the average of the values proposed by 5 experts from the waste management department of Sari Municipality (2020) and the health department of Mazandaran University of Medical Sciences (2020).

Fig. 4.

Geographical area and information of the hospitals, infirmaries and parking within Sari city.

To obtain the values of the triple goals, the single-objective model is separately solved by each objective function. The proposed model is implemented using CPLEX solver/GAMS software. Table 1 represents these values.

Table 1.

Ideal values of the goals.

Goals	Values
b1	36.484
b2	1.250
b3	13,214

Now, the proposed MILP model in Section is implemented to attain the optimal policy for the case study problem and evaluate its performance and complexity. Table 2 shows the obtained results of the objective functions and main variables. It should be noted that the reported run time is 1029.739 s.

Table 2.

Values of the goal variables.

Variables	Ψ	Obj1	Obj2	Obj3	d1+	d1−	d2+	d2−	d3+	d3−
Values	0.234	39.466	2.090	13,214	2.982	0	0.840	0	0	0

As it is obvious from Table 2, all hospitals and infirmaries are served within 19.733 h by 3 vehicles. Moreover, the total violation time is equal to 2.982 h within a working weak and total infection risk size is 13,214 people. Since the pre-established disposal site is also used for household waste, the 4th candidate location is established.

Table 3 represents the optimal routing plans of vehicles in the first time period.

Table 3.

Optimal routing plans at the first time period.

Vehicle no.	Trip 1	Trip 2
1	Parking-3-5-10-9-DS1	DS1-1-11-2-4-6-DS4
2	Parking-12-13-14-15-DS4	–
4	Parking-7-8-16-DS4	–

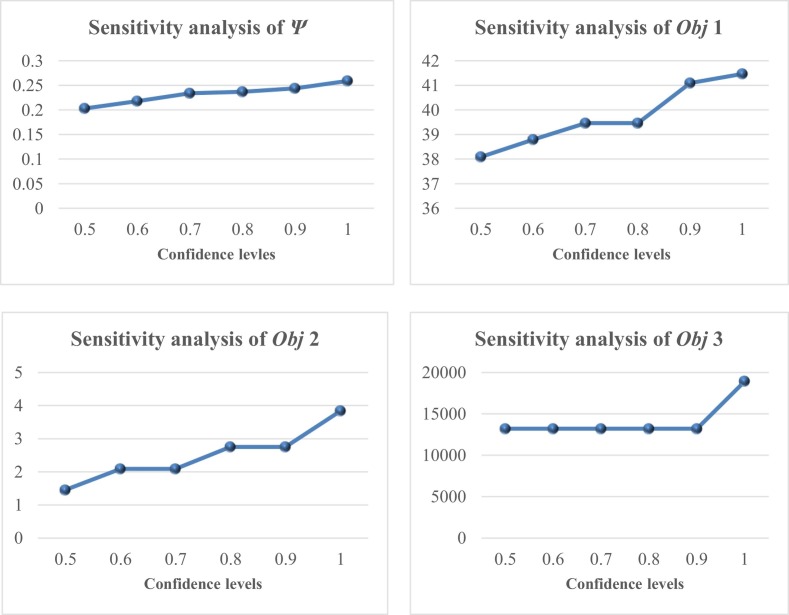
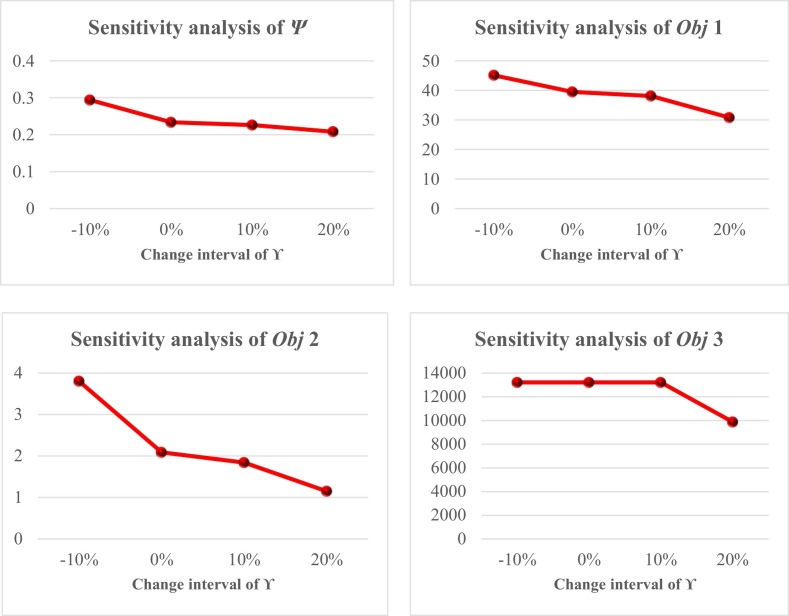
Now, to investigate the effects of key parameters on the objective functions, a sensitivity analysis is performed on the confidence levels (${{\rho }^1}_{\mathit{kpt}}$, ${{\rho }^2}_{\mathit{kt}}$) and budget level of the waste management system (ϒ). The obtained results are given in Table 4, Table 5 and Fig. 5, Fig. 6 .

Table 4.

Sensitivity analysis results of confidence levels.

Variables	Values of ${{\rho }^1}_{\mathit{kpt}}$ and ${{\rho }^2}_{\mathit{kt}}$
	0.5	0.6	0.7	0.8	0.9	1
Ψ	0.203	0.218	0.234	0.237	0.244	0.259
Obj1	38.090	38.792	39.466	39.466	41.094	41.467
Obj2	1.455	2.090	2.090	2.752	2.752	3.84
Obj3	13,214	13,214	13,214	13,214	13,214	18,941

Table 5.

Sensitivity analysis results of available budget level.

Variables	Change interval of ϒ
	−20%	−10%	0%	+10%	+20%
$\mathsf{\Psi }$	NFS⁎	0.294	0.234	0.226	0.208
Obj1	NFS	45.095	39.466	38.120	30.795
Obj2	NFS	3.803	2.090	1.843	1.150
Obj3	NFS	13,214	13,214	13,214	9872

^⁎No feasible solution.

Fig. 5.

Sensitivity analysis of the objective functions against confidence levels.

Fig. 6.

Sensitivity analysis of the objective functions against budget level.

As can be seen in Fig. 5, the objective functions reflect a direct behavior against the increase of the confidence levels. In other words, the objective functions grow with a different range of fluctuations in various change intervals. It means that reaching high confidence levels needs more resources and management should analyze and consider these behaviors to prevent any potential failures in the system.

On the other hand, according to Fig. 6, the objective functions show an indirect behavior against the increase of budget level. As an interesting point, the problem becomes infeasible for the 20% decrease in the budget level and the waste management system cannot provide a solution. So, it is indispensable that management considers the amount of available budget as an effective and critical parameter, and provides the required level under different real-world conditions, particularly for the COVID-19 pandemic.

5. Discussion and conclusion

The COVID-19 pandemic is still far from the over, and it is not certain that the future trends would confront any region of the world. Getting closer to the peak of the pandemic, waste management has not been receiving the priority which is required to minimize the detrimental impacts on the health and environment. The collected information from Mazandaran University of Medical Science and Sari Municipality demonstrates a variable trend on the decreasing or increasing in COVID-19 related medical waste amount. Designing and establishing an efficient DSS for controlling this problem can help the Sari city and provide a useful example for other cities and countries so that they can handle the spread of the disease using the same DSS. Hence, this study tried to efficiently collect, transport and dispose the COVID-19 related medical waste by modeling the problem as an MTLRP-TW.

The following main conclusions are yielded according to the numerical results of this study:

• (1)A novel MOMILP formulation was proposed for the MTLRP-TW considering real-life assumptions for the waste management application, such as multiple planning periods and separate locations for the disposal sites and parking,
• (2)Fuzzy chance-constrained programming was utilized to study the significant uncertainty of demand parameter that denotes the amount of COVID-19 related medical waste generated at hospitals and infirmaries,
• (3)To make a useful link between the research contributions and computational results, it can be stated that sustainable development by optimizing Obj1, Obj2 and Obj3 does not exist in the literature, the obtained results tried to show the relationship between the possible optimal values of the objective functions by implementing WGP technique,
• (4)A real-life case study problem was implemented by the developed DSS and the results included the optimal planning in locational and routing decisions and the optimal values of objectives were reported,
• (5)The results of sensitivity analysis demonstrated that the objective functions are directly dependent on the budget level, such that the problem became infeasible for the 20% decrease in the budget level. Accordingly, the management can assess the required level of resources to be assigned to the waste management system.

As it is clear, this study has some limitations as well as other research works. Here, some useful recommendations for future studies are given based on these main limitations. Other objective functions can be studied in the model, such as total cost and/or transportation risk minimization. Moreover, other uncertainty techniques can be applied to the model; e.g., robust optimization techniques and stochastic programming to investigate the uncertainty situation and be compared with the fuzzy chance-constrained programming method. Finally, to solve the problem in larger scales, heuristic and meta-heuristic algorithms should be designed and implemented. CPLEX solver/GAMS software cannot be regarded as an efficient solution tool in large-sized problems.

CRediT authorship contribution statement

Erfan Babaee Tirkolaee: Writing - original draft, Conceptualization, Methodology, Formal analysis, Software, Supervision. Parvin Abbasian: Data curation, Formal analysis, Validation. Gerhard-Wilhelm Weber: Project administration, Writing - review & editing.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Editor: Huu Hao Ngo