Quantitative Structure-Based Prediction of Electron Spin Decoherence in Organic Radicals

Abstract

The decoherence of electron spins in paramagnetic molecules limits sensitivity and resolution in electron paramagnetic resonance (EPR) spectroscopy, and it represents a challenge for utilizing paramagnetic molecules as qubit building blocks for quantum information devices. Traditionally, electron spin decoherence is modeled as driven by an external dynamic stochastic process with a phenomenological rate constant. Here, we show that the electron spin decoherence behavior of organic radicals in frozen aqueous solution can be quantitatively predicted from just molecular structure and solvation geometry using a fully deterministic quantum model with a static spin Hamiltonian that includes nucleus-nucleus couplings. We present experiments and simulations on two nitroxide radicals and one trityl radical, which have decoherence time scales of 4-5 μs below 60 K. We show that nuclei within 12 Å contribute to decoherence, with the strongest impact from protons 4-7 Å from the electron spin.

Graphical Abstract

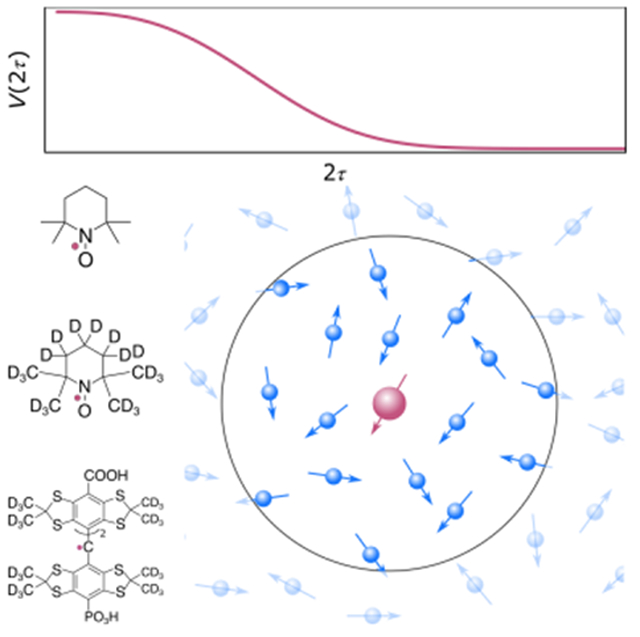
The spins of unpaired electrons in organic radicals and metal ions are extensively used in pulse electron paramagnetic resonance (EPR) spectroscopy to probe the structure and dynamics of the nano-environment around the electrons.^1-3 Molecule-based unpaired electrons are also investigated as potential building blocks for materials useful to quantum information science (QIS).^4-6 In this context, they are often referred to as “molecular spin qubits”. In both cases, a key limitation is the fact that excited electron spins lose coherence over time. This process, called decoherence, dephasing, or transverse relaxation, results in the loss of signal.⁷ In EPR, decoherence limits sensitivity and spectral resolution. In QIS applications, it impacts the efficient transfer of information between coupled qubits, and it limits the complexity of algorithms that can be executed. Extending coherence times is therefore an important development goal in both fields. For this, a detailed understanding of the physical origin of decoherence is crucial.

There are two classes of processes that drive electron spin decoherence: motion and magnetic interactions. It is possible to eliminate the effect of motion (librations, thermal methyl rotations, etc.) on decoherence by operating at cryogenic temperatures, i.e. below about 50 K. Magnetic interactions between electron spins, and between electron spins and nearby nuclear spins, also contribute to decoherence. At low temperatures and low electron spin concentrations, decoherence is driven by nearby nuclear spins.^8,9 This mechanism has been described semi-classically as arising from stochastic flip-flops of pairs of nuclei, leading to spectral diffusion of the electron spin resonance frequency and consequently to decoherence.^10-12 The problem with this stochastic model is that it is not predictive and does not provide insight into the physical origin of the assumed flip-flop rate. Given the key challenge of extending coherence times, a method for quantitatively predicting decoherence is needed to guide materials design.

Here, we experimentally determine the decoherence behavior of three prototypical organic radicals in dilute frozen aqueous solutions and show that their nuclear-spin-driven decoherence behaviors can be quantitatively predicted from their molecular geometry and solvation structure, using a combination of molecular dynamics (MD) and quantum spin dynamics, without the need for any adjustable free parameters.

Electron spin decoherence can be measured using various pulse EPR techniques. The most straightforward is the Hahn echo decay (Figure 1). This technique uses the pulse sequence π/2 − τ − π − τ – echo and records the decay of echo amplitude resulting from increasing the interpulse delay τ.

Figure 1.

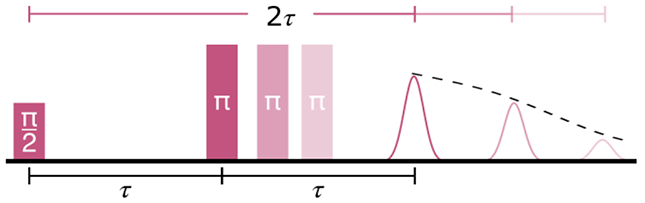
Hahn echo pulse sequence. For a decoherence experiment, the value of τ is increased and the decreasing echo amplitude is recorded.

We investigated the decoherence characteristics of three different radicals systems: 2,2,6,6-tetramethylpiperidine-1-oxyl (TEMPO), its perdeuterated isotopologue (d₁₈-TEMPO), and a perdeuterated trityl radical (p₁TAM)¹³ (Figure 2). TEMPO and d₁₈-TEMPO both are N/O-centered radicals with four neighboring methyl groups and differ only in that all the ¹H atoms in TEMPO are replaced with ²H atoms in d₁₈-TEMPO. The trityl radical, p₁TAM, is a C-centered radical and has 12 deuterated methyl groups. The concentrations of the radicals were kept low enough to minimize additional decoherence effects arising from electron-electron couplings (instantaneous diffusion).^14,15 All samples were prepared in a solution of 1:1 (w:w) H₂O:glycerol and were snap frozen in liquid nitrogen. The experiments were performed from 20-60 K at Q-band frequencies (ca. 33 GHz).

Figure 2.

Prototypical molecular spin qubits used in this study. From left to right, TEMPO, d₁₈-TEMPO, and p₁TAM.

Figure 3 shows the experimental Hahn echo decays at 20 K, presented in black. For all samples, the coherence decays on a similar timescale and is completely lost within 12 μs. The decays are phenomenologically fitted well by stretched exponentials of the form: V(2τ) = V₀ · exp(−(2τ/T_M)^x), shown in gray. Here, T_M is the phase memory time, and x is a stretching exponent. This stretched exponential is predicted by the semiclassical model that uses stochastic nuclear flip-flops to describe the loss of electron spin coherence.^10-12

Figure 3.

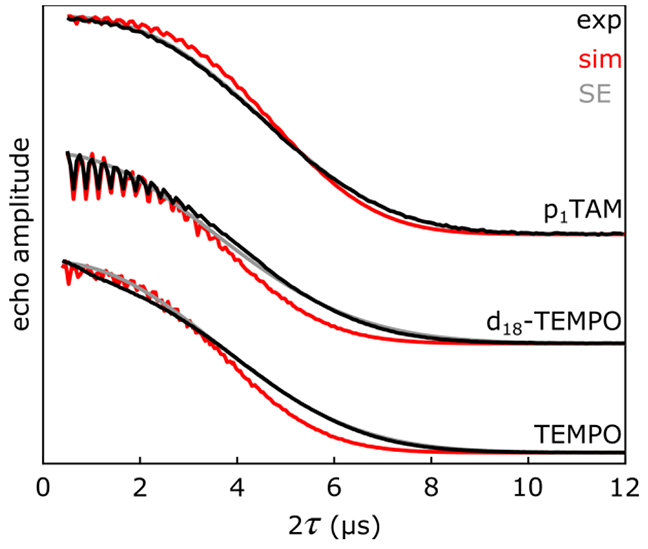
Experimental decoherence behavior of the molecules used in tins study (black), stretched exponential (SE) fits (gray), and the structure-based simulations (red). From top to bottom, approximately 10 μM p₁TAM, 100 μM d₁₈-TEMPO, and 200 μM TEMPO. The experiments were performed in 1:1 (w:w) H₂O:glycerol at 20 K and ca. 33 GHz. The SE fits gave x values of 3.37, 2.81, and 2.77 and T_M values of 5.37, 4.23, and 4.33 μs for p₁TAM, d₁₈-TEMPO, and TEMPO, respectively.

The experimental decay shape of p₁TAM (Figure 3, top) is the closest of the three molecules used in this study to a pure stretched exponential. p₁TAM does not have hydrons (protons or deuterons) neighboring the C-centered unpaired electron; the closest hydrons are about 4 Å away. The d₁₈-TEMPO decay (Figure 3, middle) shows oscillations at short times resulting from nuclear electron spin echo envelope modulations (ESEEM). This effect arises from the pseudo-secular parts of the hyperfine coupling to nearby nuclei, the deuterons on the radicals in this case.^2,16 No ESEEM oscillations are visible in the TEMPO sample (Figure 3, bottom). Instead, the TEMPO decay shows a slight deviance from the shape of a stretched exponential at early times that may be the result of thermal or tunneling methyl rotations.^17,18

To investigate the temperature dependence of the decoherence behavior at cryogenic temperatures, we performed experiments from 20-60 K; the decoherence behavior is unaffected by temperature in this range (Figures S2 and S3). This is consistent with previous experimental results.⁸

To predictively model the experimental decoherence behavior, we performed explicit structure-based spin quantum dynamics simulations of the Hahn echo decays. Structures of the solvated radicals were generated using molecular structures optimized by density functional theory (DFT) and solvation geometries obtained by molecular dynamics (MD). The ensemble of spins used in the spin dynamics calculation includes the unpaired electron, all magnetic nuclei on the radicals, and up to 1600 solvent protons within a radius of up to 20 Å of the electron spin. Full nucleus-nucleus coupling tensors as well as both secular and pseudo-secular parts of hyperfine coupling tensors between nuclei and the electron spins were included in the static spin Hamiltonian:

$${\widehat{H}}_0={\mu }_{\mathrm{B}}{g}_{\mathrm{e}}{B}_0{\widehat{S}}_z+\sum _{n=1}^N\left(-{\mu }_{\mathrm{N}}{g}_n{B}_0{\widehat{I}}_{z,n}+{\widehat{S}}_z({\mathit{z}}^{\mathrm{T}}{\mathit{A}}_n){\widehat{\mathit{I}}}_n+{\widehat{\mathit{I}}}_n^{\mathrm{T}}{\mathit{P}}_n{\widehat{\mathit{I}}}_n\right)+\sum _{m=1}^{N-1}\sum _{n=m+1}^N{\delta }_{g_n,g_m}{\widehat{\mathit{I}}}_m^{\mathrm{T}}{\mathit{b}}_{m,n}{\widehat{\mathit{I}}}_n$$

The individual terms in this Hamiltonian mostly follow standard notation and are described in the Supporting Information. Microwave pulses were modelled as ideal (i.e. infinitely short).

To handle the enormous state space, we employed the ensemble cluster correlation expansion (CCE) method^19,20 that has been developed for predicting the decoherence behavior of defects in crystals.^21-23 This method simulates spin dynamics in Hilbert space using a truncated expansion approach and is conceptually similar to the truncated Liouville space methods employed in nuclear magnetic resonance (NMR).^24-28 It is important to note that the simulation is structure-based and does not contain any additional free physical parameters, neither static nor dynamic. Algorithmic truncation parameters of the CCE method are the size of the spin system, a neighbor cutoff to exclude clusters that do not contribute, the maximum cluster size used, and the number of orientation of the magnetic field to be averaged over. They are shown in Figure 4 and have been optimized to assure convergence of the result. Further details are given in the Supporting Information.

Figure 4.

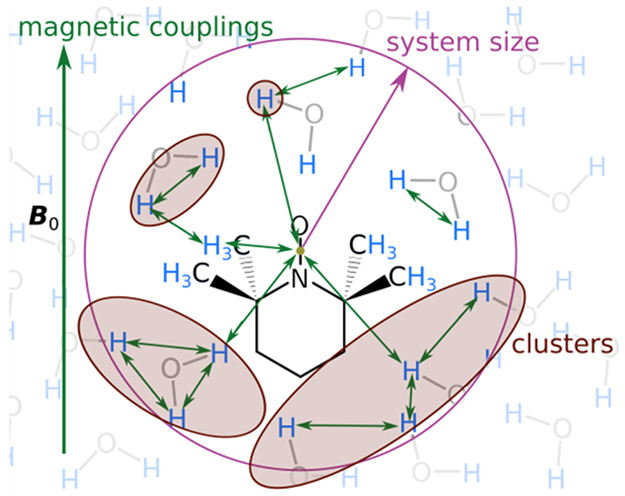
Illustration of the truncation parameters, which are the system size r_Sys (purple circle and arrow), the cluster sizes used (rust areas), and the clustering based on neighbor cutoff (green arrows).

The structure-based simulated echo decays are shown in red in Figure 3. In all, the decoherence behaviors of all three radicals are quantitatively predicted both in shape and timescale. All three simulations result in a stretched exponential decay with oscillations from ESEEM at early times. Eliminating nucleus-nucleus couplings from the simulation completely eliminates the decays, showing that these couplings are key to the mechanism of electron spin decoherence for the systems under investigation in this study. For systems in which T_M is limited by T₁, this method would not be successful in predicting phase memory times of molecular spin systems. The slight timescale discrepancies between simulated and experimental decays may arise from errors in the MD prediction of the solvation geometries and solvent proton densities. The p₁TAM simulation is in most agreement with experiment with or without the inclusion of ESEEM-generating terms in the Hamiltonian. The d₁₈-TEMPO simulation required the inclusion of ESEEM-generating terms in the Hamiltonian to reproduce the oscillations at early times in the experimental decays. Inclusion of ESEEM in the TEMPO simulation did not reproduce the early time shape of the experimental decay. The simulations show increased ESEEM oscillation amplitudes that are likely due to incomplete averaging over solvation geometries. A measurement and simulation of d₁₈-TEMPO at X-band (Fig. S4) show that the mechanism is field independent.

To gain more insight into the structural aspects that determine decoherence timescales, we devised a method to attribute decoherence effects to individual nuclei in the systems. To do so for a particular nucleus i, we simulated the echo decay of the system without nucleus i (i.e. assuming it as non-magnetic). This results in a slightly prolonged echo decay compared to the full system. We capture this by the difference in phase memory times, ΔT_M,i, between the full system and the reduced system (Figure S7); ΔT_M,i quantifies by how much the presence of nuclear spin i shortens the phase memory time. It is important to note that individual ΔT_M values are not additive, as the decoherence mechanism is a cooperative effect driven by nucleus-nucleus couplings. Still, they allow the assessment of the relative importance of individual nuclei to electron spin decoherence, within their context of neighboring nuclear spins.

The results of this analysis for TEMPO are depicted in Figure 5. Figure 5(a) shows a 3D cartoon of the solvated radical, with each proton colored according to ΔT_M,i, where darker indicates larger values. No clear geometric patterns are discernible, although it is evident that some protons in the vicinity of the electron contribute much more than others. Figure 5(b) shows a scatterplot of ΔT_M for all nuclei as a function of their distance from the electron spin. The protons 4-8 Å from the electron have the largest effect upon electron spin decoherence. Their presence each shortens the predicted phase memory time by up to 28 ns. Protons that are less than about 4 Å from the electron, such as the methyl protons, contribute much less to decoherence. This volume of suppressed decoherence contributions corresponds to the notion of the diffusion barrier observed in nuclear spin diffusion. The value obtained here (4 Å), however, is smaller than those reported for nuclear diffusion barriers (7-10 Å,^8,11 4-6.6 Ų⁹, < 6 ų⁰).^31,32 This direct comparison is not entirely valid, since we model loss of electron spin coherence, whereas the diffusion barrier relates to spatial transfer of nuclear polarization. Beyond 8 Å, the individual ΔT_M taper off rapidly with increasing distance. Figure 5(b) also plots the calculated overall T_M as a function of system size and shows that in order to obtain a converged T_M, all nuclei up to at least 12 Å from the electron spin need to be included. The conclusions are similar for d₁₈-TEMPO and p₁TAM (Figure S8).

Figure 5.

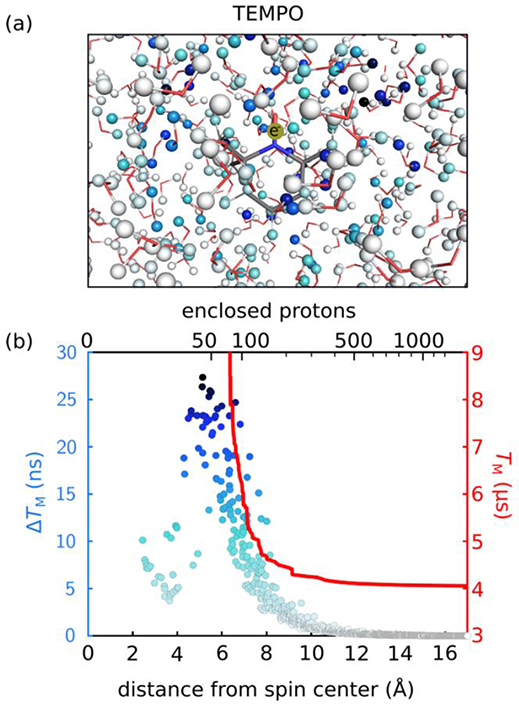
(a) Map of decoherence effects ΔT_M of individual nuclei for TEMPO in H₂O demonstrating which nuclei contribute most to the dephasing of the electron spin. The color scale corresponds to that in (b), with darker blue indicating larger values of ΔT_M. (b) Individual ΔT_M values as a function of distance (blue, left vertical scale) and calculated T_M as a function of system size (red, right vertical scale).

In combination with the experimentally validated simulations, the ability to examine decoherence effects due to individual nuclei greatly enhances insight into the structural origins of nuclear-spin-driven electron spin decoherence. As mentioned, this decoherence mechanism has traditionally been described semi-classically by a stochastic process of nuclear flip-flops involving pairs of surrounding nuclei, with an ad hoc flip rate constant. Within the quantum model presented herein, however, electron spin decoherence is the result of a coherent, deterministic evolution of a large ensemble of nuclear spins coupled to each other and to the electron spin, without any external stochastic influence.

Extending the simulation methodology to fully deuterated solvents is not straightforward. Deuterons lead to prolonged time scales of the echo decays, and the presence of nuclear quadrupole couplings results in deeper echo modulations. Both the longer time scales as well as the increased modulation depths create convergence challenges for the CCE method.³³ This is an area needing more investigation.

In summary, we have shown that the electron spin decoherence behavior of radicals in frozen aqueous solutions at cryogenic temperatures can be quantitatively predicted directly from the solvation structure of the radicals using explicit spin quantum dynamics with a static spin Hamiltonian, without any free parameters. This methodology can be useful for designing molecules and platforms that maximize electron spin coherence lifetimes, both to increase sensitivity and resolution in EPR spectroscopy as well as to improve molecular spin qubits for potential QIS applications.