Assessing XMT-Measurement Variability of Air-Water Interfacial Areas in Natural Porous Media

Abstract

This study investigates the accuracy and reproducibility of air-water interfacial areas measured with high-resolution synchrotron x-ray microtomography (XMT). Columns packed with one of two relatively coarse-grained monodisperse granular media, glass beads or a well-sorted quartz sand, were imaged over several years, encompassing changes in acquisition equipment, improved image quality, and enhancements to image acquisition and processing software. For the glass beads, the specific solid surface area (SSSA-XMT) of 31.6 ±1 cm⁻¹ determined from direct analysis of the segmented solid-phase image data is statistically identical to the independently calculated geometric specific solid surface area (GSSA, 32 ±1 cm⁻¹) and to the measured SSSA (28 ±3 cm⁻¹) obtained with the N₂BET method (NBET). The maximum specific air-water interfacial area (A_max) is 27.4 (±2) cm⁻¹, which compares very well to the SSSA-XMT, GSSA, and SSSA-NBET values. For the sand, the SSSA-XMT (111 ±2 cm⁻¹) and GSSA (113 ±1 cm⁻¹) are similar. The mean A_max is 96 ±5 cm⁻¹, which compares well to both the SSSA and the GSSA values. The XMT-SSSA values deviated from the GSSA values by 7–16% for the first four experiments, but were essentially identical for the later experiments. This indicates that enhancements in image acquisition and processing improved data accuracy. The A_max values ranged from 74 cm⁻¹ to 101 cm⁻¹, with a coefficient of variation (COV) of 9%. The maximum capillary interfacial area ranged from 12 cm⁻¹ to 19 cm⁻¹, for a COV of 10%. The COVs for both decreased to 5–6% for the latter five experiments. These results demonstrate that XMT imaging provides accurate and reproducible measurements of total and capillary interfacial areas.

1. INTRODUCTION

The importance of fluid-fluid interfaces for fluid-flow processes, contaminant transport and fate, oil and gas recovery, CO₂ sequestration, and many other applications is now clearly established. Advancements in microtomographic image acquisition and processing methods over the past two decades have provided the means to accurately characterize fluid-fluid interfacial area in three-dimensional porous-media systems. High-resolution industrial x-ray microtomography and in particular synchrotron x-ray microtomography have been used to measure air-water and organic liquid-water interfacial areas for synthetic media (Culligan et al. 2004, 2006; Al Raoush and Wilson 2005; Prodanovic et al., 2006; Lu et al., 2010; Narter and Brusseau, 2010; Porter et al. 2010; Aferka et al. 2011; Landry et al., 2011; Lyu et al., 2017; Patmonoaji et al., 2018; Wang et al., 2019) and natural porous media (Schnaar and Brusseau, 2005, 2006a, 2006b; Brusseau et al., 2006, 2007, 2008, 2009; Costanza-Robinson et al., 2008; Al-Raoush, 2009, 2014; Russo et al., 2009; Willson et al., 2012; Carroll et al., 2015; McDonald et al., 2016; Lyu et al., 2017, Patmonoaji et al., 2018).

Measured XMT data are used to test theoretical and mathematical pore-scale models for multiphase fluid flow. The prior investigations noted above have relied almost exclusively on single sets of image measurements. Accordingly, studies testing theoretical and mathematical models have also relied on single sets of measured data, with no consideration of potential data variability or measurement uncertainty. One question of interest then is the variability and reproducibility of measurements for fluid-fluid interfacial area obtained with imaging methods. Clearly, outcomes from model testing are dependent upon the robustness of the measured data obtained from imaging.

The objective of this work is to investigate the reproducibility of air-water interfacial area measurements obtained with x-ray microtomography (XMT). Columns packed with glass beads or a well-sorted quartz sand were imaged at multiple drainage steps to measure total and capillary air-water interfacial area. Multiple columns were imaged over several years, encompassing changes in acquisition equipment, improved image quality, and enhancements to image acquisition and processing software.

2. MATERIALS AND METHODS

2.1. Experiment Set-Up

A well-sorted 45–50 mesh quartz sand (Accusand, Unimin Co.) and borosilicate glass beads (Sigma-Aldrich) were used for the experiments. Physical properties of these two media are presented in Table 1. The glass beads were used to help examine the efficacy of the image acquisition and processing methods. Both of these media are water wetting. The wetting phase comprised distilled water containing 12% potassium iodide (KI) (Fisher Scientific) as a contrast agent, to better distinguish between the phases in the system.

Table 1.

Physical Properties of the Porous Media^†.

	ad50	bU	cn	cnXMT	dρb	dρb,XMT	eAmax	fSSSAXMT	gSSSA-NBET	hGSSA
	(mm)	(d60/d10)	(--)	(--)	(g/cm3)	(g/cm3)	(cm−1)	(cm−1)	(cm−1)	(cm−1)
Glass Beads	1.1	1.0	0.38±0.08	0.37±0.008	1.37±0.20	1.40±0.03	27.4±2	31.6±1	28±3	32±1
Sand	0.35	1.1	0.36±0.02	0.34±0.002	1.72±0.05	1.76±0.02	96±5	111±2	2997±66	113±1

^†All values determined using segmented XMT data with the exception of n and ρ_b.

^aMedian particle diameter

^bCoefficient of Uniformity, (d₆₀/d₁₀)

^cporosity (n) from bulk density (ρ_b) of sample.

^dρ_b bulk density.

^eMaximum measureable specific interfacial area, A_max=A_nw(1-S_w), ± indicates upper and lower 95% confidence interval.

^fSpecific solid surface area obtained directly from image analysis normalized by imaged volume.

^gN₂-Brunauer, Emmet and Teller (NBET) surface area. This value represents the total external solid surface area available in the system and incorporates surface area associated with microscopic surface roughness.

^hGeometric specific solid surface area based on smooth-sphere assumption, (=6(1-n)/d₅₀, where d₅₀ is median particle diameter, and n is porosity).

Thin-walled polycarbonate columns, L = 3.2 cm, ID = 0.63 cm, or aluminum columns, of similar dimensions (L= 3 cm, ID ≈ 0.6 cm), were used for the experiments. The polycarbonate columns, used for the majority of the sand experiments, have minimal dead volume (i.e. water volume that is not part of the porous-medium pack), with less than 0.05 mL compared to a fluid capacity of 1.14 mL (<4%). This attribute allows for quantitative comparison between column-wide gravimetric water saturations and image-based values. A hydrophilic capillary membrane (5–15 μm pore diameter) was attached to the bottom of the column and a fine mesh was used at the top of the column to retain the solids.

The aluminum columns were dry-packed with the selected porous medium whereas the polycarbonate columns were packed under slurry conditions. Both methods achieved reasonably uniform bulk densities (Table 2). A programmable electronic syringe pump (KD Scientific) with a 2.5 mL gas-tight syringe was connected to a pressure transducer and to the bottom of the column. The columns were saturated by injecting aqueous solution into the bottom of the column at a low flow rate. Image data collected for each column prior to initiating drainage demonstrated that the columns were fully saturated.

Table 2.

Column Properties for each experiment^†

	Exp. 1	Exp. 2	Exp. 3	Exp. 4	Exp. 5	Exp. 6	Exp. 7	Exp. 8	Exp. 9	GB 1	GB2
Year	2007	2/2009	6/2009	2010	11/2011	11/2011	2012	7/2013	7/2013	2008	2015
aAmax, (cm−1)	74±2	101±5	84±2	91±2	101±5	101±6	94±2	87±2	95±2	28±1	27±1
bSSSAXMT, (cm−1)	95±1	109±3	99±1	105±1	112±1	113±1	114±1	107±1	111±1	31±1	32±1
cGSSA, (cm−1)	112±1	116±1	114±1	113±1	113±3	114±1	113±1	111±1	113±1	31±1	34±1
ρb, XMT, (g/cm3)	1.75	1.80	1.77	1.76	1.76	1.77	1.76	1.73	1.77	1.31±0.004	1.44±0.005
ρb, (g/cm3)	1.75	1.72	1.74	1.64	1.60	1.70	1.79	1.78	n/a	1.3	1.45
dnXMT, (--)	0.34	0.32	0.33	0.33	0.33	0.33	0.33	0.34	0.33	0.41±0.002	0.35±0.002
dn, (--)	0.34	0.35	0.34	0.38	0.40	0.35	0.35	0.33	n/a	0.42	0.34

^†XMT-subscript indicates values calculated solely from segmented imaged data.

^aMaximum measureable specific interfacial area, A_max=A_nw(1-S_w)

^bSpecific solid surface area obtained directly from image analysis normalized by imaged volume, ±indicates upper and lower 95% confidence interval.

^cGeometric specific solid surface area based on smooth-sphere assumption, (=6(1-n)/d₅₀, where d₅₀ is mean particle diameter, and n is porosity).

^dporosity (n) from bulk density (ρ_b) of sample.

Each experiment comprised a series of image collection and drainage steps. First, each column was imaged prior to drainage. Then a drainage step was induced by removing a small increment of the wetting fluid from the column at a low flow rate of ~0.05 ml/min. The column was then left to equilibrate for at least 15 minutes, after which it was imaged again. This procedure was repeated several times per drainage experiment. Final saturation was established when the weight of the column remained unchanged after application of a drainage step, which means no additional water was removed. The mass of the column was measured with an analytical balance for each drainage step after data acquisition. The column was sealed and weighed to calculate the final gravimetric water content for future processing. The data presented in this study reflect a compilation of replicate data sets subject to changes in image collection and processing components beyond our control.

2.2. Image Acquisition

Synchrotron X-ray microtomography images were collected at the GeoSoilEnviroCARS (GSECARS) BM-13D beamline of the Advanced Photon Source at Argonne National Laboratory, Il. The resolution for all experiments conducted with the sand ranged between 9.7–11 μm/pixel. For the glass beads, the resolution for GB1 was 10 μm/pixel versus 7.5 μm/pixel for GB2. Hence, the resolutions did not change significantly over the course of the study. The field of view for the samples was approximately 7 (h) by 5 (w) mm. The images were collected from the vertical centers of the columns, to minimize the potential influence of end effects. The imaged-domain volumes fulfilled representative elementary volume requirements (Culligan et al., 2004; Brusseau et al., 2006; Razavi et al. 2007; Narter and Brusseau, 2010; Costanza-Robinson et al., 2011).

Sequential images of the columns were collected above and below the iodide absorption edge, at 33.269 and 33.069 keV, respectively. The above-edge image highlights the wetting phase, whereas the below-edge image distinguishes the solid phase. The image set that best represented all three phases was used for simultaneous multiphase segmentation. A particular focus was placed on imaging the solid phase directly. This is in contrast to previous studies (e.g., Wildenschild et al. 2002, 2004, Schnaar and Brusseau 2006a, Costanza-Robinson et al. 2008) wherein image processing focused solely on the segmentation of the fluid phases. In these studies, the solid phase was inferred based on segmentation of the fluids, thereby avoiding the complexities inherent in the analysis of natural geomedia grains (i.e. Wildenschild et al. 2004; Kaestner et al. 2008).

The images were preprocessed with GSECARS-developed software (Rivers et al., 2010; Rivers, 2012). The program is a set of IDL© (ITT, Visual Information Solutions) routines that were designed to view the raw image data, remove artifacts, correct for dark currents, and to perform a white-field correction. Furthermore, it aligns the rotation axis based on alignment of the sinograms, removes ring artifacts, and filters noise. Finally, the program writes the reconstructed data as a single three-dimensional volume file (16-bit integer files), which can be exported into a series of individual slices or imported into a 3D viewer such as ImageJ (Schneider et al., 2012). The resulting exported image sets are used for analysis. These consist of grayscale values ranging from 0 (black) to 255 (white) for 8-bit resolution, which corresponds to low and high X-ray attenuation, respectively. Further details regarding the facility are available at the GSECARS webpage, (http://cars9.uchicago.edu/software/idl/tomography.html).

2.3. Image Processing and Analysis

The multiple steps required to process a reconstructed data volume were combined into a single MatLab Program. Initially, the original grayscale images were cropped with Matlab (The MathWorks Inc.). A circular cropping area was chosen such that it encompasses a large portion of the sample and removes the column wall, while maintaining a reasonable REV. After cropping, the grayscale volumes were normalized for intensity differences with a sequential algorithm developed by Iassonov and Tuller (2010). The relevance of this approach is that it accounts for intra-phase spatial variations of grayscale intensities. The particular mechanics of the algorithms used are beyond the scope of this work. Details regarding the algorithm and respective routines are described in Iassonov et al. (2009), Kulkarni et al. (2012), and Tuller et al. (2013). Prior to segmentation, the data were pre-processed using standard unsharp masking filters and median smoothing steps. A connected component-labeling (CCM) algorithm was also applied after segmentation of all samples to remove small unrealistic voxel clusters, such as voxels enclosed by another phase due to residual noise or the presence of dense metal oxides.

Phase volumes were determined by means of voxel counting, and are used to obtain porosity and volumetric water contents. Surface areas were determined using the method presented by Lindblad (2005). This method is based on the Marching Cube surface reconstruction algorithm, modified to avoid topological ambiguities (Lindblad, 2005).

2.4. Interfacial Area Determination

The total surface area of air, the non-wetting phase, was used to determine total air-water interfacial area (A_nw). This is based on the fact that the surfaces of the solids are water wetting, and that thin water films are present that cannot be resolved by microtomography. The interfacial areas reported in this work represent the specific interfacial area, unless otherwise noted, wherein the areas are normalized by the volume of the imaged domain (with units of cm²/cm³ or cm⁻¹).

Specific capillary interfacial area (C_nw) was calculated as one half of the difference between the combined sum of the water phase and air phase surface areas and the solid phase surface area (e.g., Montemagno and Ma, 1997; Dalla et al., 2002); where a_a, a_s, a_w, indicate the specific total surface areas of air, solid, and water phases, respectively:

$${\text{C}}_{\text{nw}}=\frac{1}{2}({\text{a}}_{\text{a}}+{\text{a}}_{\text{w}}-{\text{a}}_{\text{s}})$$ (1)

The capillary interfacial area calculated from equation (1) refers to interfaces associated with the menisci of contacts between air and “bulk” water residing in intergranular pore domains (partially filled capillaries, pendular rings, and wedges). The surface areas were determined individually for each phase, obtained directly from the simultaneous multi-phase segmentation procedure.

2.5. Independent Validation

The efficacy of the image-acquisition, raw-image processing, and data-segmentation procedures was assessed based on phase-balance complementarity and comparison to independently measured parameters. The porosity from image analysis is determined as the quotient of the volume of void space (i.e., sum of air and water volumes) and the total imaged sample volume (n_XMT = V_v/V_t). The n_XMT is compared to porosity (n) calculated using the gravimetrically measured bulk density (ρ_b) value obtained during column preparation and the measured particle densities reported in Table 1. The segmented volume of solids in conjunction with the measured particle densities (ρ_p) can be used to calculate bulk densities for the image domain (ρ_{b, XMT}). These values are also referenced to the gravimetrically measured bulk densities (ρ_b). Water saturation (S_w) can be calculated using either the volume of water, V_w/V_v, or the volume of air (1-(V_a/V_v)).

The volume-normalized specific solid surface areas (SSSA) can be calculated directly from the solid surface areas determined from analysis of the segmented solid-phase image data. These values can be compared to independently determined solid surface areas. One such area is the geometric smooth-sphere specific surface area (GSSA, =6(1-n)/d₅₀), calculated using the median particle diameter (d₅₀) and the porosity (n) obtained from the image data (Table 1). Another relevant solid surface area is a measured value obtained using the N₂-Brunauer, Emmet and Teller (NBET) method. This value represents the total external solid surface area available in the system as measured by adsorption of gas molecules onto the solid surface (e.g., Orchiston 1953; Brunauer et al., 1938), and incorporates surface area associated with microscopic surface roughness, if present.

The maximum specific air surface area is defined as the theoretical maximum total air surface area associated with vanishingly small water saturation (S_w→0). Similarly, the specific maximum interfacial area (A_max) is defined as the theoretical maximum total interfacial area associated with vanishingly small water saturation (Brusseau et al., 2009; 2010; Araujo and Brusseau 2019). Under this condition, a wetting-phase film of a few molecules thick will be present on the solid surfaces. It is expected that under this condition the specific surface area of the non-wetting phase, and the corresponding non-wetting/wetting interfacial area, will be similar to the specific solid surface area. This provides a means to compare measured total interfacial areas to independent measurements of specific solid surface areas. The A_max values are calculated from linear regression of the relationship between A_nw and S_w.

3. RESULTS AND DISCUSSION

3.1. Benchmark Analysis of Glass-bead Data

The measured SSSA is 28 cm⁻¹ (±3, 95% confidence interval) for the glass beads, determined from NBET characterization. The specific solid surface area calculated using the geometric smooth-sphere approach is 32 (±1) cm⁻¹, which is similar to the NBET-measured value. This equivalence is consistent with the fact that these glass beads have no measurable surface roughness within the resolution limits of the measurement methods. The absence of measurable surface roughness has been confirmed via scanning electron microscopy (SEM) and phase-contrast microscopy (Araujo and Brusseau, 2019).

Table 1 presents the gravimetric porosity (n) and imaged-based porosity (n_XMT) values for both glass-bead experiments. The two sets of values are observed to be statistically identical considering the overlapping 95% confidence intervals. Similarly, the bulk densities obtained using XMT data are consistent with those determined gravimetrically. The SSSA determined from direct analysis of the XMT solid-phase data is 31.6 (±1) cm⁻¹. This value is consistent with both the NBET-measured SSSA and the GSSA values reported above.

Figure 1 shows the total volume-normalized air-water interfacial areas (A_nw) as a function of wetting saturation (S_w) for the glass-bead experiments. The A_max (27.4 ±2 cm⁻¹) is calculated based on the mean of linear regressions of the two individual data sets. The A_max is very similar to all three specific solid surface areas, the NBET-measured SSSA, the XMT-measured SSSA, and the GSSA. Similar results were reported by Brusseau et al. (2009) and Narter and Brusseau (2010) for XMT measurements of organic liquid-water interfacial areas for the same glass beads as used herein. The measured A_max values were consistent with the SSSA-XMT, SSSA-NBET, and GSSA specific solid surface areas in both studies. Additionally, Narter and Brusseau independently determined A_max from interfacial partitioning tracer test (IPTT) measurements, and the resultant value (28 cm⁻¹) was consistent with the XMT-based A_max as well as the SSSA-NBET and GSSA. Zhong et al. (2016) used a two-phase flow IPTT method to measure organic liquid-water interfacial areas for the same glass beads, and the A_max (34 cm⁻¹) is comparable to the values above. Finally, Lyu et al. (2017) used the gas-absorption/chemical reaction (GACR) method to measure air-water interfacial areas for the same glass beads. The A_max (29 cm⁻¹) they determined is similar to the A_max and specific solid surface areas discussed above.

Figure 1.

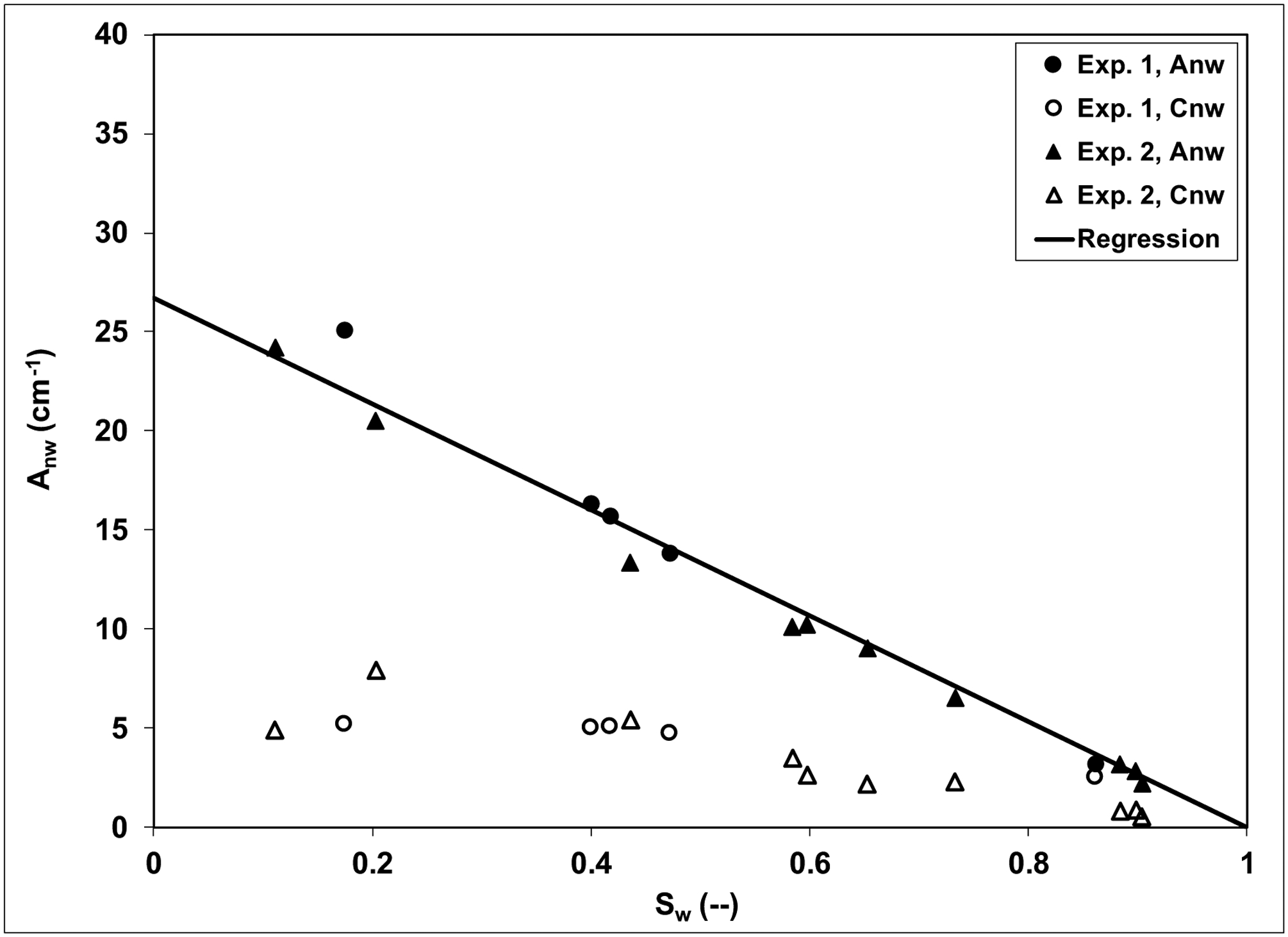
Total and capillary air-water interfacial area for glass beads. Regression-based maximum A_max is equal to the mean for both experiments (Table 1).

The capillary interfacial areas (C_nw) as a function of water saturation (S_w) for the glass bead experiments are also presented in Figure 1. Unlike the total A_nw, there are no independent measurements to which to reference these results. The profiles exhibited by the C_nw-S_w data are consistent with the expected behavior for capillary interfacial area wherein the area first increases during drainage and then decreases at lower saturations. The magnitudes of the values (C_max~7.5 cm⁻¹ for S_w~0.2) are consistent with prior data reported for glass-bead systems (Culligan et al., 2004, 2006; Porter et al., 2010).

In total, the observed excellent consistency between XMT-measured values and those obtained from independent measurements indicate that the image acquisition and processing methods were robust and produced accurate results. Pore-scale studies of porous media, whether computational or experimental, typically focus on analysis of fluid phases only, indirectly inferring solid-phase properties (e.g., Costanza-Robinson et al., 2008; Baveye et al 2010; Guan et al. 2018). The results presented above illustrate the advantages associated with including solid-phase analyses for pore-scale studies, wherein they are particularly useful for benchmarking analysis and helping to ensure the image acquisition and analysis methods employed are robust.

3.2. Benchmark Analysis of Sand Data

Table 1 presents the mean gravimetric and imaged-based porosities and bulk densities for the sand. The two sets of values are observed to be statistically identical, just as they were for the glass beads. The specific solid surface area (SSSA) obtained from direct analysis of the solid phase is also presented in Table 1. The mean SSSA for the sand is 111 ±2 cm⁻¹ for the latter five experiments (discussed further below), which is statistically identical to the GSSA (113 ±1 cm⁻¹). It is noted that the SSSA-NBET for the sand is much greater than the SSSA_XMT or the GSSA. This disparity reflects the presence of microscopic surface roughness, which is not captured by the latter two measurements.

The total volume-normalized air-water interfacial areas (A_nw) as a function of saturation (S_w) for the sand are presented in Figure 2. The mean A_max is 96 (±5) cm⁻¹, determined from the latter five experiments. This value is approximately 17% smaller than the SSSA-XMT and GSSA specific solid surface areas. Similar results have been reported in prior studies (Costanza-Robinson et al., 2008; Willson et al., 2012). The observation of A_max values being somewhat smaller than specific solid surface areas is to be expected given the impact of grain-to-grain contacts and the possible under-prediction of interfacial area due to limited resolution of smaller pore domains.

Figure 2.

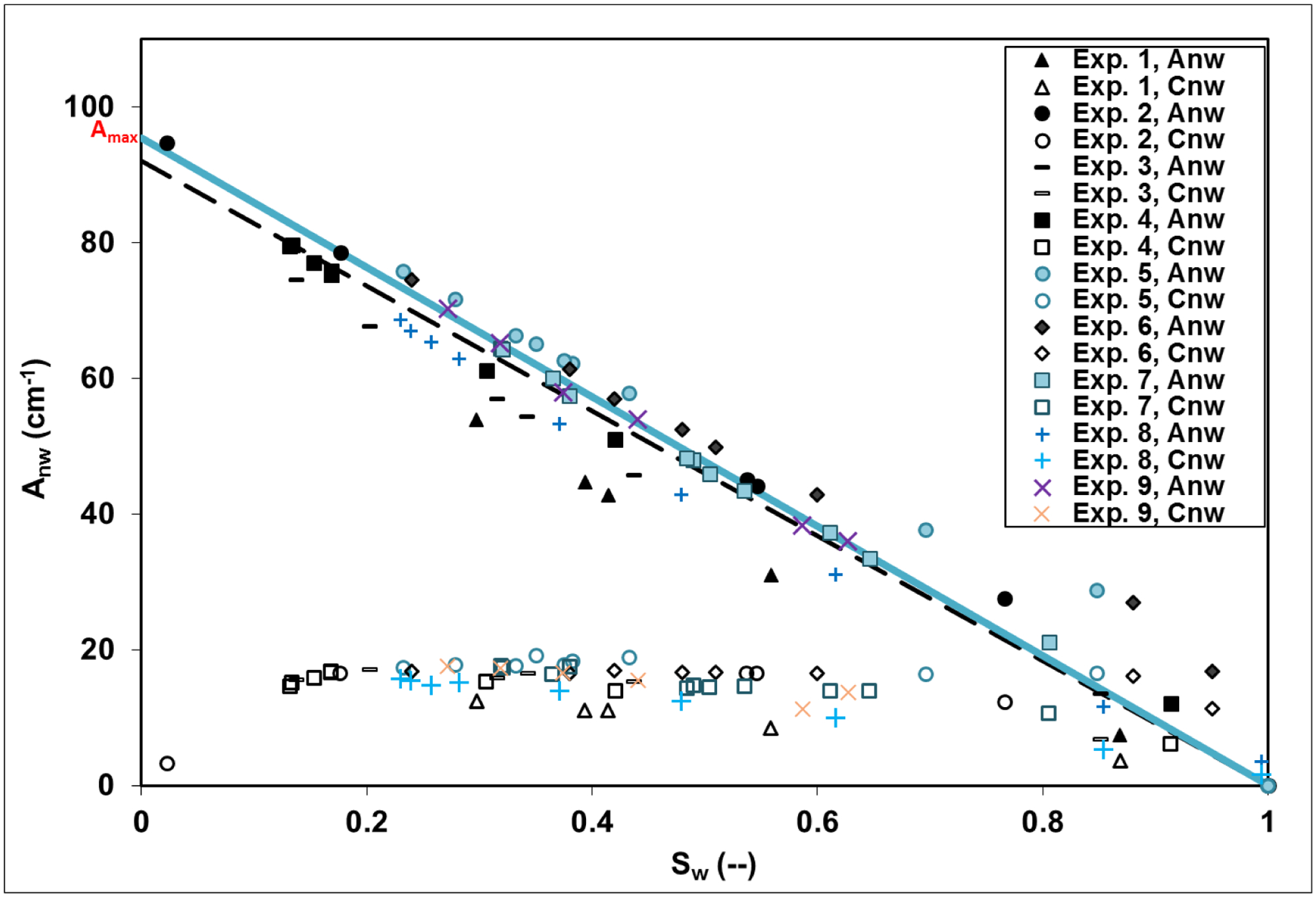
Total and capillary air-water interfacial area for 45–50 sand. Regression line calculated using compilation of all data sets (black dash line), and for experiments 5–9 (blue line).

Figure 2 also shows the volume-normalized capillary interfacial area (C_nw) as a function of S_w for each experiment. The profiles exhibited by the C_nw-S_w relationships match the expected behavior for capillary interfacial area, wherein the area first increases during drainage and then decreases at lower saturations as noted above. The calculated maximum C_nw for the sand is approximately 17 cm⁻¹ for the sand at S_w~0.34. As would be expected, this value is larger than the value determined for the glass beads.

3.3. Reproducibility of Measured Interfacial Areas

Table 2 shows gravimetric porosity (n) and imaged-based porosity (n_XMT) values for each replicate sand experiment. The corresponding COV for image-based porosity (n_XMT) is 2%, and the COV is 6% for gravimetric porosity. The two values are very similar for most of the experiments, but 10–20% differences between image-based and gravimetric porosities are observed for a few of the experiments. This is to be expected given that local porosities vary spatially to some degree within the column. Similar overall results are observed for bulk densities (Table 2).

The SSSA-XMT values are compared to the GSSA values for all nine experiments in Table 2. It is observed that the two sets of values differ by approximately 7–16% for the first four trips, with the SSSA-XMT values consistently smaller than the GSSA. However, the two sets of values are essentially identical for all later trips, with a mean difference of 2% between the two sets. This suggests that ongoing enhancements in image acquisition and processing improved data accuracy. These improvements included changes in acquisition setup, as well as software changes for optimization of the data collection and reconstruction process (Rivers, 2012, 2016). In addition, a major upgrade occurred in 2010 (after experiment 4) with a switch in the scintillator crystal from Yttrium Aluminum Garnet to Lutetium Aluminum Garnet (Rivers et al., 2010). This reduced blurriness around grains, as quantified by improved greyscale histograms.

The improved image clarity led to improved characterization of the solids, consistent with the observed increase in SSSA-XMT values for experiments 5–9. An increase in A_max values is also observed for the data collected after the image enhancements, wherein the mean value is 87 for experiments 1–4 versus 96 for the latter five (as noted below). In addition to improved characterization of solid-phase boundaries, the improved image clarity allows for better characterization of the pore-network configuration (e.g. shape, size, connectivity) and of macro-features on the surfaces of solid grains. Overall, these improvements are expected to affect the determination of SSSA-XMT and A_max, but would have minimal impact on the GSSA since it is a function only of porosity and median grain size. Interestingly, the SSSA-XMT and GSSA values are essentially identical for the glass beads for both experiment 1 and 2. Noting that experiment 1 was conducted prior to 2011 (and therefore prior to the system improvements), the consistency between the two experiments demonstrates that the pre-2011 limitations influencing characterization of the sand did not affect the glass beads. This is consistent with the fact that the glass beads comprise near-perfect spheres with no measurable surface roughness.

Greater discrepancies between independent and imaged-based values are generally expected to occur when examining the solid phase. Segmentation of the solid phase is particularly sensitive to grayscale variations that occur at the boundary with the wetting phase (e.g., Kaestner 2008). Furthermore, natural media are affected by non-uniform illumination that occurs because of physical and geochemical heterogeneity and beam variability. The consistency in XMT-SSSA and GSSA values observed for the later trips in this study indicate that the improvements reduced the uncertainty associated with imaging analysis of solid phases.

Figure 3 shows the A_nw for each sand experiment as a function of S_w. The estimated A_max was calculated for each data set, along with the 95% confidence interval for each data set (Table 2). The individual A_max values range from 74 to 101 cm⁻¹, with a mean of 92 ±6 cm⁻¹ and a coefficient of variation (COV) of 9% for all 9 experiments. The mean A_max is 96 ±5 cm⁻¹ with a COV of 5% for experiments 5–9. Brusseau et al. 2008 reported a COV of 8% for total specific organic liquid-water interfacial areas determined from eight XMT experiments. This variability is similar to that reported herein.

Figure 3:

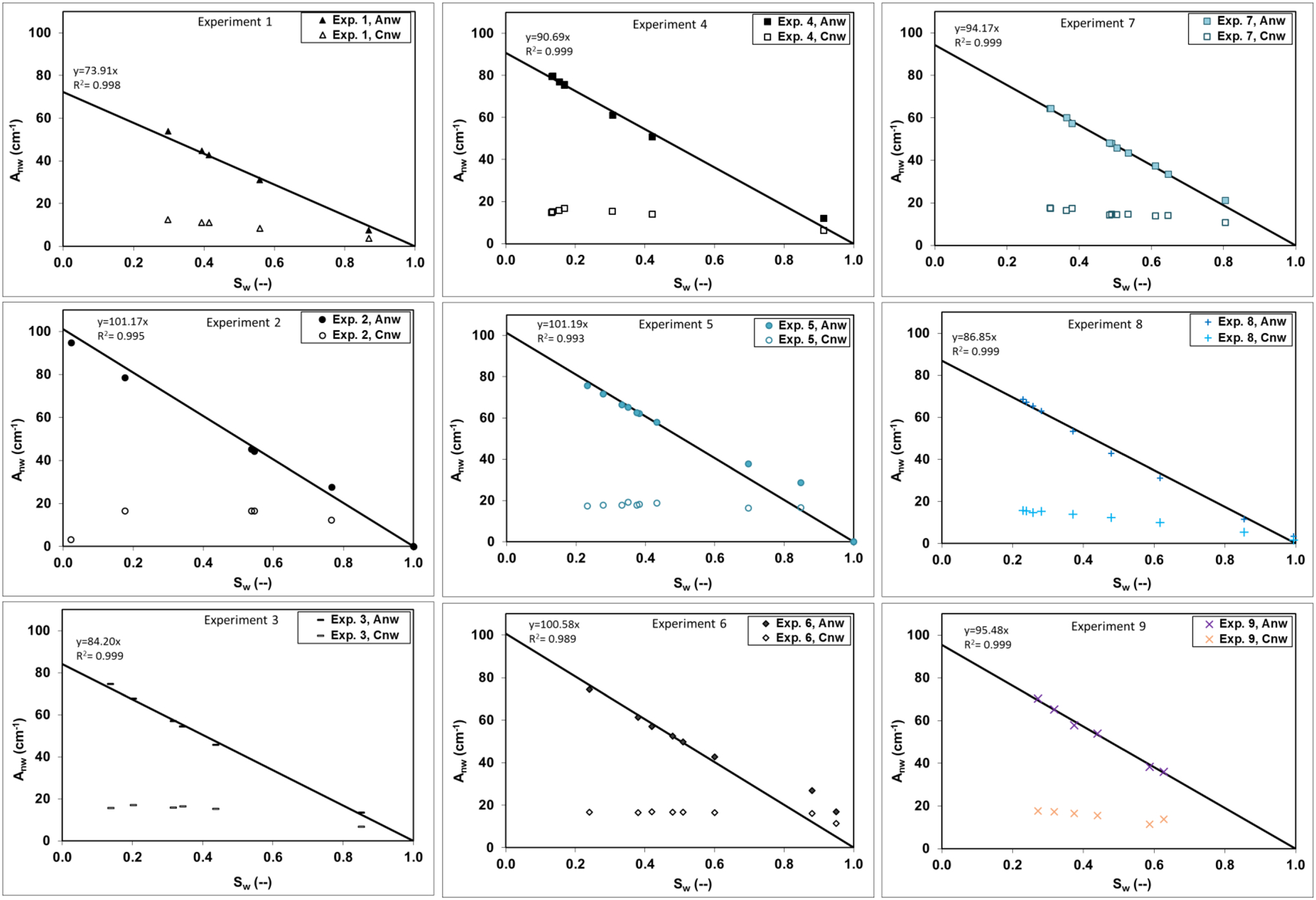
Total and capillary air-water interfacial area for each experiment. Regression line calculated for each experiment set and represents, A_max at S_w=0.

Figure 3 also shows the capillary interfacial area (C_nw) as a function of water saturation (S_w) for all nine experiments. The mean maximum capillary interfacial area is 16 (±1 cm⁻¹), with a COV of 10%, for all data sets. The maximum capillary interfacial area for experiments 5–9 is 17 ±1 cm⁻¹, with a reduction in COV to 6%. The reduced variabilities for both A_nw and C_nw is consistent with the lower variability for specific solid surface areas observed for experiments 5–9.

The small degrees of variability observed for A_max and maximum C_nw may originate from a number of factors. As discussed above, values for SSSA, porosity, and bulk density all vary slightly between experiments. The COVs for the XMT-determined SSSA, ρ_b, and n are 2%, 1%, and 2%, respectively, for the sand. This variability is a natural consequence of the impacts of variations in properties of the source media from sample to sample and differences in column packs, as well as variability in the imaging.

4. SUMMARY

The accuracy and reproducibility of capillary and total air-water interfacial areas determined from high-resolution synchrotron microtomography data was examined in this study. The accuracy of image-based results was evaluated by benchmarking porosity, bulk density, specific solid surface area, and A_max to independently determined values. Reproducibility was investigated by conducting a total of 11 separate imaging experiments over the course of seven years.

Analysis of data collected for ideal glass beads confirmed that the image acquisition and processing methods produced accurate results. For the sand, porosities and bulk densities obtained from image analysis were statistically identical to independent (gravimetric) parameters. The SSSA-XMT values were consistently smaller than the GSSA values by 7–16% for the first four trips, but were essentially identical for the later experiments. This indicates that enhancements in image acquisition and processing improved data accuracy primarily through better resolution of the solid phase. The A_max values ranged from 74 cm⁻¹ to 101 cm⁻¹, with a coefficient of variation (COV) of 9%. The maximum capillary interfacial area ranged from 12 cm⁻¹ to 19 cm⁻¹, for a COV of 10%. The COVs for both A_max and C_max decreased to 5–6% for the last five experiments.

These results indicate that the XMT method provided robust measurements of total and capillary interfacial areas for the two tested porous media. The magnitude of measurement variability was relatively small, especially for the later experiments. This provides a degree of confidence in the standard practice of using single measured data sets for experiment and modeling investigations. However, it should be noted that the two media used for this work are relatively coarse-grained, monodisperse granular media. Additional investigation of reproducibility is warranted for media that are finer grained and polydisperse. In addition, the benchmarking employed in the present work helped to demonstrate that the image acquisition and processing methods were robust. It is possible that measurement variability will be greater for conditions in which sub-optimal methods are used. It is important to incorporate measurement variability in experimental and modeling investigations of pore-scale processes, in recognition that such variability contributes to uncertainty in calculated and simulated values. Hence, it is recommended that the magnitude of variability be determined in future studies by conducting multiple replicate measurements, at least for a representative subset of samples.

Keypoints:

Air-water interfacial areas measured with XMT have low variability

XMT-measured values are robust based on comparison to independently measured benchmarks