Breaking the entanglement barrier: Tensor network simulation of quantum transport

Abstract

The recognition that large classes of quantum many-body systems have limited entanglement in the ground and low-lying excited states led to dramatic advances in their numerical simulation via so-called tensor networks. However, global dynamics elevates many particles into excited states, and can lead to macroscopic entanglement and the failure of tensor networks. Here, we show that for quantum transport – one of the most important cases of this failure – the fundamental issue is the canonical basis in which the scenario is cast: When particles flow through an interface, they scatter, generating a “bit” of entanglement between spatial regions with each event. The frequency basis naturally captures that – in the long–time limit and in the absence of inelastic scattering – particles tend to flow from a state with one frequency to a state of identical frequency. Recognizing this natural structure yields a striking – potentially exponential in some cases – increase in simulation efficiency, greatly extending the attainable spatial- and time-scales, and broadening the scope of tensor network simulation to hitherto inaccessible classes of non-equilibrium many-body problems.

Tensor networks enable the systematic search for ground states of certain many-body Hamiltonians, as well as numerical time evolution, provided that there is a limited amount of entanglement present [1-6]. Quantum quenches – when a parameter of the Hamiltonian is suddenly changed – can, though, generate highly-entangled states, seen both experimentally [7] and theoretically [8-13]. The large amount of entanglement creates a challenge for tensor network simulation and the efficient representation of the underlying quantum state [4, 12]. There are many approximate approaches under development to truncate further the description of the state and maintain control over the size of the tensor network [14-16], but these rely on additional assumptions, such as the thermalizing nature of the dynamics. We will here develop a controllable approach to break the entanglement barrier for an important class of problems in transport.

Quantum transport through an impurity $\mathcal{S}$ is a paradigmatic example of a “pathological” quench. A global bias μ drives particles through an interface where they scatter, see Fig. 1a. For particles around the Fermi level (ω = 0), each scattering event gives rise to an entangled electron-hole pair [17, 18]

$$\sqrt{T(0)}\mid 0_{\mathcal{L}}{1}_{\mathcal{R}}\rangle +\sqrt{1-T(0)}\mid 1_{\mathcal{L}}{0}_{\mathcal{R}}\rangle$$ (1)

across the left ($\mathcal{L}$) and right ($\mathcal{R}$) reservoir regions. The left component of the state represents a particle transmitted from $\mathcal{L}$ to $\mathcal{R}$ with transmission probability T(0) and the right component the reflected particle (the phase is unimportant here). Given that the attempt frequency is μ/2π [19], the entanglement entropy S increases as

$$S\approx H[T(0)]\frac{\mu t}{2\pi },$$ (2)

where H[T(0)] is the binary entropy of the transmission probability and t the time [17, 18]. This linear growth of spatial entanglement – and its “light cone” spread [20] (see the heat map in Fig. 1a) – is due to the linear increase in the number of entangled electron-hole pairs, as expressed by Eqs. (1),2).

FIG. 1. Entanglement, transport, and simulation.

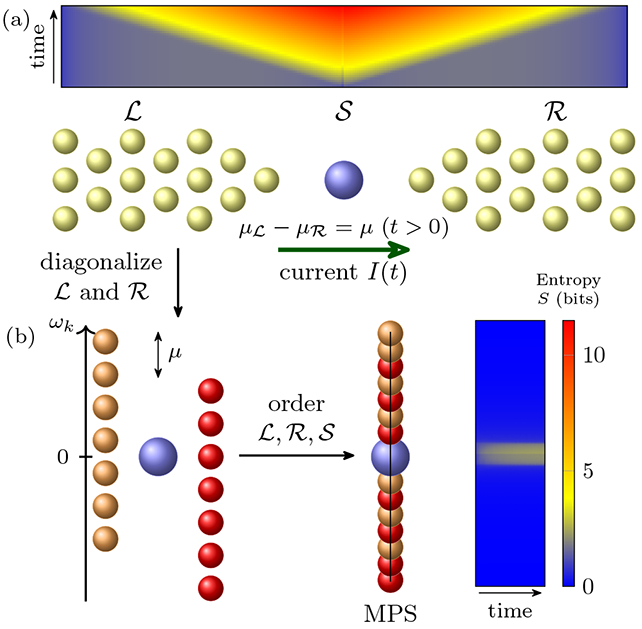
(a) A bias or particle imbalance between the $\mathcal{L}$ and $\mathcal{R}$ reservoirs drives a current I through the impurity system $\mathcal{S}$. This spatial structure, though, has an entanglement “light cone” (over top heat map), leading to macroscopic entanglement and simulation failure. (b) Separately diagonalizing the single-particle eigenstates in the $\mathcal{L}$ and $\mathcal{R}$ regions (of arbitrary spatial dimension) and combining them into a joint $\mathcal{L}\mathcal{R}$ environment circumvents this issue by naturally structuring the simulated system. The entanglement then becomes localized within the bias window and highly suppressed (right heat map). The heat map scale is for both entanglement plots and the simulation details are the same as in Fig. 2.

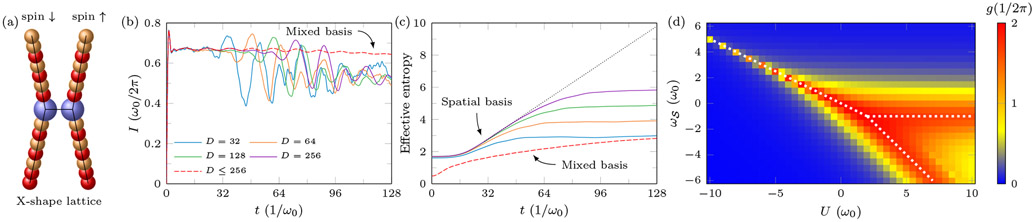
This growth results in the failure of one-dimensional tensor networks – matrix product states (MPS) – beyond a “hard wall”: The required matrix product dimension D increases exponentially with the timescale. Figure 2 shows this spectacular failure for the non-interacting Anderson impurity model (see the caption for its definition). This intrinsic, physically-based limitation restricts MPS to short timescales and small/moderately-sized lattices [21-31], or linear response via an equilibrium correlation function [32, 33]. Simulating time-dependent problems (artificial gauge fields, Floquet states, etc.), more complex many-body regions, or long relaxation times, requires a new approach.

FIG. 2. Failure and success.

(a) The particle current I versus time for both the exact simulation via the single-particle correlation matrix (black line) and MPS simulations (colored lines). In the spatial basis, the simulation abruptly fails and successive doubling of D only gives a linear increase of the achievable time scale, an exponential relationship that negates the primary advantage of MPS. In the mixed energy/spatial basis, however, a modest D of 128 (necessary only around the bias window) allows for the time dynamics to be accurately captured (red, dashed line). The Hamiltonians are $H_{\mathcal{S}}=\hslash {\omega }_{\mathcal{S}}{\sum }_{\sigma }{n}_{\sigma }$, $H_{\mathcal{L}(\mathcal{R})}=\hslash {\omega }_0{\sum }_{j\in \mathcal{L}(\mathcal{R})}\left(b_j^{†}{b}_{j+1}+b_{j+1}^{†}{b}_j\right)+{\mu }_{\mathcal{L}(\mathcal{R})}{\sum }_{j\in \mathcal{L}}{b}_j^{†}{b}_j$, and $H_{\mathcal{I}}=\hslash v{\sum }_{\sigma ,l=1_{\mathcal{L}},1_{\mathcal{R}}}\left(c_{\sigma }^{†}{b}_{l\sigma }+b_{l\sigma }^{†}{c}_{\sigma }\right)$ for $\mathcal{S}$, $\mathcal{L}(\mathcal{R})$($v={\omega }_0∕\sqrt{2}$), and the interaction, respectively [36]. The parameters are ${\omega }_S={\omega }_0$, ω_S = ω₀, $N_{\mathcal{L}}=N_{\mathcal{R}}=256$, and $\mu ={\omega }_0∕2=2{\mu }_{\mathcal{L}}=-2{\mu }_{\mathcal{R}}$, where ω₀ sets the frequency scale. For these parameters, T(0) = 1/2, thus giving a rapid increase in spatial entanglement. The initial state has μ = 0 (half-filling). (b) Intuitively (although not precisely [4, 37]), the failure of the spatial basis is due to the conflict between a linearly growing entanglement entropy (black line, see Eq. (2)) and the maximal amount of entanglement, S* = log₂ D, an MPS can hold with a given bond dimension D (colored lines saturating near S*). (c) Simulations of very large systems (512+1+512 sites) and long times (extensive in $N_{\mathcal{L}(\mathcal{R})}$ are made possible by this basis, which is also reflected in the ability to capture the linear growth in spatial entanglement (red, dashed line in b). The inset shows the error in the current versus time, normalized by the exact steady-state current $I_{\text{ss}}^{\text{ex}}$ [36].

The linear growth in entanglement entropy – or its consequence, the uncontrolled growth in matrix product dimension – is deceptive: The paradigmatic impurity model will, in the long time limit, have particles go from a state of frequency ω (on the left) to a state of the same frequency ω on the right, albeit with some characteristic spread. This entails that if one instead works with the single-particle eigenbasis of $\mathcal{L}$ and $\mathcal{R}$, ordered on a lattice as shown in Fig. 1b, the entanglement should be limited (in higher dimensions, momentum conservation can play this role). In fact, recently it was shown, in the context of dynamical mean-field theory, that for real-time single-particle correlation functions (and equilibrium) the so-called star geometry, where the energy basis for the bath is used, suppresses entanglement from logarithmic into a localized structure with smaller overall magnitude [34]. For quenches in the Anderson impurity model, it was shown that energy basis ordering naturally delineates the bad (linear entanglement growth) and good (limited entanglement) scenarios [35].

Unlike these cases, we address simulating the bad scenario and show that it can be transformed to a scenario with logarithmic growth, and thus intermediate between the bad and good. To do so, we use a mixed energy and spatial basis, reflecting the entanglement structure in Eq. (1) and incorporating the energy basis in two separate spatial regions. Figure 1 shows the steps leading to this mixed basis (diagonalizing the separate $\mathcal{L}$ and $\mathcal{R}$ spatial regions and then ordering them). Entanglement in this mixed basis is localized to the bias window and mostly between pairs of (iso- or nearly iso-energetic) sites, see the heat map in Fig. 1b. The strength of the couplings to the impurity, as well as many-body interactions and inelastic scattering, determine the spread of entanglement. At the same time, the low dimensionality of $\mathcal{S}$ and the scattering nature of the states limits the amount of entanglement between the impurity and the reservoirs. We will comment on alternative structural representations later.

We note here that various approaches can perform computations with matrix product states, such as the density matrix renormalization group (DMRG) [38], the time-dependent variational principle (TDVP) [39], or Krylov-based methods [40]. Unlike the schemes based on the Trotter decomposition of the Hamiltonian into local gates, they allow treating any Hamiltonian represented as a matrix product operator (MPO). Thus, we use DMRG to find the initial ground state in the preferred basis and TDVP for the subsequent time evolution. Since we work with the MPO of the Hamiltonian, its dimension is important since the formal scaling for time evolution in, e.g., 1D is $\mathcal{O}(D^{3}Md+D^2{M}^2{d}^2)$, where M is the MPO bond dimension and d is the local Hilbert space dimension. When the reservoirs are non-interacting, the MPO of the mixed basis has a small, fixed M for both the initial state and time evolution regardless of bias [36].

Since there is overhead associated with the presence of long-range interactions, we also work under a guiding principle that both the Hamiltonian MPO and the state MPS should have limited D. The mixed basis, in contrast to the spatial basis (exponentially large MPS D) and the global single particle basis (extensive MPO D when interactions are present), respects this principle in addition to capturing the natural structure of impurity transport [36]. Optimality questions aside, it permits an advantageous extension to open systems [41] where a bias is maintained by external contacts to $\mathcal{L}$ and $\mathcal{R}$ eigenstates separately [42-44], as well as a suitable structure for fine–graining the reservoirs [45].

Figure 2a shows the result of employing this mixed-basis MPS. An inhomogeneous and modest D ≤ 128 already gives excellent results out to a time extensive in the system size (a time equal to the reservoir length divided by the Fermi velocity, 2ω₀, at which the current “front” hits the open boundary and travels backwards toward the impurity [20, 46]). This mixed basis captures the linear growth in spatial entanglement entropy, Fig. 2b, and allows for very large systems, Fig. 2c.

As a consequence of naturally representing the entanglement structure, the majority of the lattice in the mixed basis has little entanglement across bipartite cuts with correlations predominantly between modes in the bias window (see Fig. 1b). Thus, the computational speedup is not just a consequence of a reduced D, but also an inhomogeneous D. As a point of comparison, the mixed-basis simulations in Fig. 2a took only 15 hours, whereas the spatial-basis simulation with the same D = 128 took 44 hours, both on the same single core computer. While implementation choices affect this comparison, the empirical scaling follows from Fig. 2: To bring the spatial-basis simulation out to t = 128 ω₀ requires five more doublings of D just to move the breaking point (forgetting about overall error). The dominant D³Md contribution to the computational cost then indicates an approximate computational time of (2⁵)³ · 44 hours, or 165 years.

Even for a large bias, the mixed-basis MPS still out performs the spatial basis, a direct consequence of the more local nature of entanglement in energy. Figure 3a shows the conductance and current versus time traces for μ = 0 to 4 ω₀ (after which the $\mathcal{L}$ and $\mathcal{R}$ bands go out of alignment and there is no steady state current and entanglement saturates). In all cases, the mixed basis yields accurate results. Figure 3b shows that the effective entanglement entropy [36] grows logarithmically opposed to linear. The advantages of the mixed basis also extend to interacting reservoir models, where Fig. 3c,d show the current versus time and effective entanglement entropy for the same $\mathcal{L}\mathcal{S}\mathcal{R}$ system but with interactions in $\mathcal{L}\mathcal{R}$. The Hamiltonian’s MPO dimension grows with the system size in this case, and in some parameter regimes we expect a spatial basis may be more suitable (such as in a localized regime), but the mixed basis enables stable time evolution. Further work will be necessary to assess the efficiency gains across different parameter regimes, since many-body interactions in $\mathcal{L}$ and $\mathcal{R}$ modify both the MPO and entanglement structure of the problem.

FIG. 3. mixed-basis simulation.

(a,b) The conductance, g = I_ss/μ, versus bias for the mixed-basis simulation (data points) and the exact (black line) for the non-interacting model of Fig. 2, as well as the entanglement growth with time for the mixed basis. We obtain the steady-state current by fitting I(t) = I_ss + δ sin(ϕt + ϕ₀) within the window of ω₀t ∈ [32, 128] [29]. The 95 % confidence intervals are smaller than the symbol line widths. The inset shows the current versus time for several applied biases. The entanglement growth is logarithmic in time for the mixed basis, unlike the linear in time growth for the spatial basis. Here, $N_{\mathcal{L}}=N_{\mathcal{R}}=256$ and D = 256 except for μ/ω₀ = 1 and 2, for which D = 512. (c,d) The current versus time for interacting $\mathcal{L}$ and $\mathcal{R}$ reservoirs that have the additional contribution $\hslash U_r{\sum }_{j\in \mathcal{L}\mathcal{R}}(n_j-1∕2)(n_{j+1}-1∕2)$ to the Hamiltonian, as well as the effective entanglement entropy for the spatial and mixed bases (black, dotted line extrapolates the linear region of the entropy for the largest D). The MPO of the Hamiltonian increases when U_r ≠ 0, but the mixed-basis simulation enables stable evolution that is not possible in the spatial basis. The advantage of the mixed basis becomes substantial as $\mathcal{L}\mathcal{R}$ entanglement increases with time or with the transport parameters (e.g., with the bias). For this interacting model, the results are for μ/ω₀ = 2 and $N_{\mathcal{L}}=N_{\mathcal{R}}=64$.

The above can be straightforwardly applied to higher dimensional non-interacting reservoirs (since only their energy/momentum bases matter) and to interacting spinless fermions, including larger dimensional systems $\mathcal{S}$. For many-body systems of typical interest, though, one has to have spin, which requires simulating multiple channels. The Anderson impurity problem [47] with electron-electron interaction Un_↑n_↓ at the impurity (where n_↑(↓) is $\mathcal{S}$’s spin up (down) number operator), and its extension to larger $\mathcal{S}$ [48, 49], is the paradigmatic example.

In the non-interacting limit the two spin channels are fully independent. In the presence of interactions, U ≠ 0, the interchannel entanglement originates from the many-body contact at $\mathcal{S}$, which is in addition to the intrachannel entanglement around the bias window [36]. This suggests an X-shape MPS (i.e., a tree tensor network [50, 51]) depicted in Fig. 4a as a natural ansatz (a structure also supported by results of other recent works [52]). Tree tensor networks, similarly to a one-dimensional MPS, possess a normal form. As such, the TDVP integration scheme of Ref. [39] directly extends to such tensor network geometries [36].

FIG. 4. Many-body transport in a mixed, multi-channel basis.

(a) The “X-lattice” we employ when multiple channels are present. (b) Current versus time for spatial- and mixed-basis simulations, showing abrupt failure of the spatial basis. (c) Effective entanglement versus time, which accounts also for the inhomogeneity of D [36]. The spatial basis shows a linear growth in spatial entanglement (black, dotted line extrapolates the linear region of the entropy for the largest D), similarly to its non–interacting counterpart. The mixed basis, however, has only moderate growth in entanglement and essentially does not change as D increases beyond the value shown. (d) Conductance diagram for the Anderson impurity model versus the system’s on-site frequency ${\omega }_{\mathcal{S}}$ and interaction strength U. White dashed lines indicate high conductance states, see the main text for discussion. The steady state is found in the same way as Fig. 3a but using the window ω₀t ∈ [32, 64] for $N_{\mathcal{L}}=N_{\mathcal{R}}=128$. The parameters are $v={\omega }_0∕\sqrt{2}$ and μ = ω₀/5. Note that the broken U < 0 line is due to the resolution of the figure. For (b) and (c), $N_{\mathcal{L}}=N_{\mathcal{R}}=256$, U = 5 ω₀, ω_S = 0, and μ = ω₀/2.

Figure 4b shows the X-lattice simulated in both the spatial and mixed bases. Just as with the non-interacting case, the spatial basis abruptly fails and increasing D only gives logarithmic increase in the achievable simulation time. The mixed basis, though, enables the simulation to go out to a time extensive in the reservoir size. When D is too small, it will lose accuracy, but it does not abruptly fail. This is reflected in the limited growth in entanglement, Fig. 4c, which behaves similarly to the non-interacting case.

Figure 4d shows the conductance diagram of the paradigmatic Anderson impurity problem. For negative U, $\mathcal{S}$ is approximately half occupied in each channel, giving a U/2 contribution to $\mathcal{S}$’s on-site energy in the other channel. This results in a single high conductance state when the level energy is pushed into the bias window at ${\omega }_{\mathcal{S}}\approx -U∕2$. As ${\omega }_{\mathcal{S}}$ becomes negative, the conductance peak bifurcates into two particle-hole dual, correlated high-conductance states. For one, there is a correlated state between one channel being occupied and current flowing in the other channel, giving ${\omega }_{\mathcal{S}}\approx -U$ to effectively push the current-carrying channel state into the bias window. The other is a correlated state between one channel being empty and current flowing in the other channel. This occurs at ${\omega }_{\mathcal{S}}\approx -{\omega }_0$ instead of ${\omega }_{\mathcal{S}}=0$ due to residual many-body correlations increasing the energy (a residual also present in the ${\omega }_{\mathcal{S}}\approx -U$ state). The accurate calculation of the whole conductance diagram enables the identification of these features.

Finally, we comment on the computational speedup. The spatial basis requires exponentially large D in the total simulation time T, already alluded to above: Each doubling of D increments the breaking point by Δt (independent of the value of D), giving Δt ln D ≈ T or D ≈ e^T/Δt. For the mixed-basis simulation of the single channel model, we examine the error versus D for several simultaneous multiples of the reservoir size and time [36]. The simultaneously, e.g., doubling of size and time is the method by which one achieves the long-time limit. The error decay suggests that doubling of the simulation time (and size) requires increasing D to αD, where α is bounded, to keep the overall error fixed. Thus, the computational cost is brought from e^3T/Δt to T^p, where p ≈ 3 [36]. We note, however, that for fermions with spin, the X-lattice configuration requires also evolution between the two channels. The entropy across this bond is the same in the spatial and mixed basis, and can itself increase linearly in time. For the range of parameters here, it is still quite small. In principle, this will dominate the scaling for long times. However, one will still get an exponential improvement in the prefactor of this contribution, since that prefactor depends in the intrachannel entanglement and thus is suppressed when going to the mixed basis. Other structures besides the X-lattice may improve this further.

The above general considerations demonstrate that difficult computational problems can be broached so long as the natural entanglement structure is recognized – here, by changing the canonical basis. This enables the accurate simulation of quantum transport that underlies many applications, from quantum dot platforms for computing to molecular and nanoscale electronic devices, and fundamental studies with cold-atom emulators. The long times achievable will be conducive to simulating transport through systems undergoing time-dependent driving to generate artificial gauge fields or Floquet states. Combining the approach here with other recent methods [53-55] will push further the limits of simulation, as will developing algorithms to locally optimize the canonical basis [56]. As such, our results open new avenues to study the behavior and simulation of non-equilibrium many-body systems, from fermionic impurities to bosonic baths to the inherent structure of tensor networks.