Spatiotemporal Antialiasing in Photoacoustic Computed Tomography

Abstract

Photoacoustic computed tomography (PACT) based on a full-ring ultrasonic transducer array is widely used for small animal wholebody and human organ imaging, thanks to its high in-plane resolution and full-view fidelity. However, spatial aliasing in full-ring geometry PACT has not been studied in detail. If the spatial Nyquist criterion is not met, aliasing in spatial sampling causes artifacts in reconstructed images, even when the temporal Nyquist criterion has been satisfied. In this work, we clarified the source of spatial aliasing through spatiotemporal analysis. We demonstrated that the combination of spatial interpolation and temporal filtering can effectively mitigate artifacts caused by aliasing in either image reconstruction or spatial sampling, and we validated this method by both numerical simulations and in vivo experiments.

I. Introduction

Photoacoustic computed tomography (PACT) is an imaging modality that provides tomographic images of biological tissues. By converting highly scattered photons into ultrasonic waves, which are much less scattered than light in biological tissues, PACT forms high-resolution images of the tissues’ optical properties at depths [1]–[8]. In PACT, the photon-induced acoustic waves, called photoacoustic waves, are detected by an ultrasonic transducer array. The detected acoustic signals are used to reconstruct the target tissue’s optical absorption via inverse algorithms. Commonly used reconstruction algorithms include forward-model-based iterative methods [9]–[18], time reversal methods [19]–[23], and the universal back-projection (UBP) method [1], [4], [6], [24]–[27].

In PACT, the ultrasonic transducer array should provide dense spatial sampling (SS) around the object to satisfy the Nyquist sampling theorem [4], [28]. The SS interval on the tissue surface should be less than half of the lowest detectable acoustic wavelength. Otherwise, artifacts may appear in image reconstruction (IR), a problem we call spatial aliasing. In practice, due to the high cost of a transducer array with a large number of elements or limited scanning time, spatially sparse sampling is common.

In this work, we analyze the spatial aliasing in PACT using the UBP reconstruction [24]. We use a circular geometry (a full-ring ultrasonic transducer array or its scanning equivalent) with point elements as an example for analysis. In addition, we discuss only acoustically homogeneous media. Starting from the reconstruction at a source point, we identify two types of spatial aliasing: aliasing in SS and aliasing in IR. Then we demonstrate that aliasing in IR can be eliminated through spatial interpolation, while aliasing in SS can be mitigated through temporal filtering. Finally, we validate the proposed spatiotemporal antialiasing methods via both numerical simulations and in vivo experiments.

II. Background

In a homogeneous medium, a photoacoustic wave can be expressed as [29], [30]

$$p(\mathbf{r},t)=\frac{1}{4\pi c^2}\frac{\partial }{\partial t}\left(\frac{1}{ct}{\int }_V\text{d}{\mathbf{r}}^{\prime }{p}_0\left({\mathbf{r}}^{\prime }\right)\delta \left(t-\frac{\Vert {\mathbf{r}}^{\prime }-\mathbf{r}\Vert }{c}\right)\right).$$ (1)

Here, p (r, t) is the pressure at location r and time t, c is the speed of sound (SOS), V is the volumetric space occupied by the tissue, and p₀ (r′) is the initial pressure at r′. For convenience in the following discussion, we rewrite Equation (1) as

$$p(\mathbf{r},t)=\frac{1}{4\pi c^2}{\int }_V\frac{p_0\left({\mathbf{r}}^{\prime }\right)}{\Vert {\mathbf{r}}^{\prime }-\mathbf{r}\Vert }\frac{\partial }{\partial t}\delta \left(t-\frac{\Vert {\mathbf{r}}^{\prime }-\mathbf{r}\Vert }{c}\right)\text{d}{\mathbf{r}}^{\prime }.$$ (2)

Discretizing Equation (2) in space, we obtain

$$\begin{gathered} p\left({\mathbf{r}}_n,t\right)=\frac{1}{4\pi c^2}\sum _{m=1}^M{v}_m\frac{p_0\left({\mathbf{r}}_m^{\prime }\right)}{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }\frac{\partial }{\partial t}\delta \left(t-\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}\right), \\ n=1,2,\dots ,N. \end{gathered}$$ (3)

Here, we assume M source points distributed at ${\mathbf{r}}_m^{\prime }$, m = 1, 2, …, M, and N point detection elements distributed at r_n,n = 1, 2, …, N. The term v_m is the volume of the m-th source point.

The response of an ultrasonic transducer can be described by the equation

$$\widehat{p}\left({\mathbf{r}}_n,t\right)=p\left({\mathbf{r}}_n,t\right){\ast }_t{h}_e(t),n=1,2,\dots ,N.$$ (4)

Here, $\widehat{p}\left({\mathbf{r}}_n,t\right)$ is the pressure impinging on the n-th point detection element at time t, and h_e (t) is the ultrasonic transducer’s electric impulse response (EIR). Substituting Equation (3) into Equation (4), we obtain

$$\widehat{p}\left({\mathbf{r}}_n,t\right)=\frac{1}{4\pi c^2}\sum _{m=1}^M{v}_m\frac{p_0\left({\mathbf{r}}_m^{\prime }\right)}{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{h}_e^{\prime }\left(t-\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}\right).$$ (5)

The term $h_e^{\prime }\left(t-\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}\right)$ is a function of both the time and space, where the first prime denotes temporal derivative. The following discussion is based on the spatiotemporal analysis of this term. When acoustic signals are digitized by a data acquisition system (DAQ), an antialiasing filter for a sufficiently high temporal sampling rate avoid temporal aliasing. Thus, for simplicity, the time variable is assumed to be continuous here. The spatial variables are discretized, allowing for further discussion of SS.

For the three common detection geometries—planar, spherical, and cylindrical surfaces, an image mapping the initial pressure p₀ (r″) can be reconstructed through the UBP formula [24]:

$$p_0\left({\mathbf{r}}^{″}\right)={\int }_{{\mathrm{\Omega }}_0}b\left(\mathbf{r},t=\frac{\Vert {\mathbf{r}}^{″}-\mathbf{r}\Vert }{c}\right)\frac{\text{d}\mathrm{\Omega }}{{\mathrm{\Omega }}_0},$$ (6)

where the back-projection term $b(\mathbf{r},t)=2p(\mathbf{r},t)-2t\frac{\partial p(\mathbf{r},t)}{\partial t}$, $\text{d}\mathrm{\Omega }=\frac{\text{d}S}{{\Vert {\mathbf{r}}^{″}-\mathbf{r}\Vert }^2}\frac{{\mathbf{n}}_S(\mathbf{r})\cdot \left({\mathbf{r}}^{″}-\mathbf{r}\right)}{\Vert {\mathbf{r}}^{″}-\mathbf{r}\Vert }$ is the solid angle for detection element at r with respect to reconstruction location r″, dS is the detection element surface area, and n_S (r) is the ingoing normal vector. The total solid angle is denoted as Ω₀. In practice, the true pressure p (r, t) is approximated by the detected pressure $\widehat{p}\left({\mathbf{r}}_n,t\right)$, leading to a discretized form of Equation (6):

$${\widehat{p}}_0\left({\mathbf{r}}^{″}\right)\approx \sum _{n=1}^N{w}_n\widehat{b}\left({\mathbf{r}}_n,t=\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}\right).$$ (7)

Here, ${\widehat{p}}_0\left({\mathbf{r}}^{″}\right)$ is the reconstructed initial pressure and $\widehat{b}\left({\mathbf{r}}_n,t\right)=2\widehat{p}\left({\mathbf{r}}_n,t\right)-2t\frac{\partial \widehat{p}\left({\mathbf{r}}_n,t\right)}{\partial t}$ is the back-projection term computed from the detected pressure. The weights w_n, n = 1, 2, …, N come from $\frac{\text{d}\mathrm{\Omega }}{{\mathrm{\Omega }}_0}$ in Equation (6).

III. Spatial Aliasing in SS and IR

Given a detection geometry, the SS frequency is determined by the reciprocals of the distances between the adjacent sampling positions. Here, we use a full-ring ultrasonic transducer array with point detection elements as an example for spatiotemporal analysis. We assume that the full-ring transducer array with a radius of R has N evenly distributed detection elements, shown as the red circle in Fig. 1(a). The center O of the circle is the origin of a coordinate system for IR. The upper cutoff frequency of the ultrasonic transducer is f_c (the estimation of f_c is discussed in Appendix B), and the corresponding lower cutoff wavelength ${\lambda }_c=\frac{c}{f_c}$. The acquired signals were first filtered by a third-order lowpass Butterworth filter and a sinc filter (both with a cutoff frequency of f_c). Thus, the frequency components with frequencies higher than f_c were removed. We define S₀, called the detection zone here, as

$$S_0=\left\{{\mathbf{r}}^{\prime }\mid \Vert {\mathbf{r}}^{\prime }\Vert \le R\right\}.$$ (8)

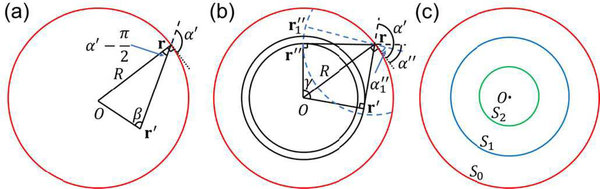
Fig. 1.

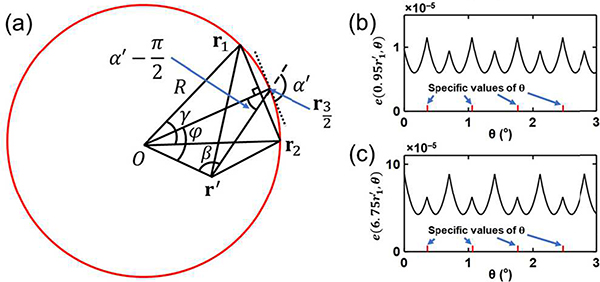
Analysis of the spatial aliasing for a circular geometry. (a) A full-ring transducer array of radius R (red circle), where a detection element location r and a source point location r′ are marked. The locations r and r′ are also seen as vectors from the origin to these locations. Vectors -r′ and r−r′ form an angle β, while the extension of line segment r−r′ forms an angle α′ with the tangential dotted line that is perpendicular to r. The angle formed by vectors −r and r′−r can be expressed as ${\alpha }^{\prime }-\frac{\pi }{2}$. This graph is used to analyze the aliasing in SS. (b) A full-ring transducer array with a detection element location r, two reconstruction locations r″ and ${\mathbf{r}}_1^{″}$ and a source point location r′ marked. Extensions of the line segments r−r″, $\mathbf{r}-{\mathbf{r}}_1^{″}$ and r′−r can be expressed as α″, ${\alpha }_1^{″}$ and α′, respectively, with the tangential dotted line that is perpendicular to r. Vectors r″ and r′ form an angle $\gamma =\arccos \left(\frac{r^{″}}{R}\right)+\arccos \left(\frac{r^{\prime }}{R}\right)$ where r″ = ‖r″‖. Points r″ and ${\mathbf{r}}_1^{″}$ are on the same circle centered at r. This graph is used to analyze aliasing in IR. (c) Regions in the field of view representing different types of aliasing. In S₂ (green circle), which contains all source points and reconstruction locations, UBP reconstruction yields no aliasing. In S₁ (blue circle), aliasing does not exist in SS but may exist in UBP reconstruction. In S₀ (red circle), aliasing may exist in SS.

We first analyze aliasing in SS. When the detection element location r varies discretely, the step size along the perimeter is $\frac{2\pi R}{N}$. The tangential direction is marked by a dotted line (Fig. 1(a)), which is perpendicular to vector r. We consider a source point at r′, and extend the line segment r−r′ as a dashed line (Fig. 1(a)). Vectors −r′ and r−r′ form an angle β, while vector r−r′ forms an angle α’ with the tangential dotted line. Then the angle formed by vectors −r and r′−r can be expressed as ${\alpha }^{\prime }-\frac{\pi }{2}$. The local sampling step size of ‖r−r^′‖ is approximately

$$\frac{2\pi R}{N}\cos {\alpha }^{\prime },$$ (9)

whose absolute value means the length of the local sampling step size, while the sign means the sampling direction. This approximation is proven to be accurate enough in Appendix C. From Equation (5), at a given time t, and with the lower cutoff wavelength λ_c, we can express the Nyquist criterion as

$$\frac{2\pi R\left|\cos {\alpha }^{\prime }\right|}{N}<\frac{{\lambda }_c}{2}.$$ (10)

To transform this inequality to a constraint for the source point location r′, we use the Law of Sines:

$$\frac{R}{\sin \beta }=\frac{r^{\prime }}{\sin \left({\alpha }^{\prime }-\frac{\pi }{2}\right)}=\frac{r^{\prime }}{-\cos {\alpha }^{\prime }}.$$ (11)

Here r^′ = ‖r^′‖. Using Equation (11), Expression (9) can be transformed to

$$\frac{2\pi R\cos {\alpha }^{\prime }}{N}=\frac{-2\pi r^{\prime }\sin \beta }{N}.$$ (12)

Combining Inequality (10) and Equation (12), we obtain

$$r^{\prime }<\frac{N{\lambda }_c}{4\pi \left|\sin \beta \right|},$$ (13)

which must be satisfied for any β ∈ [0, 2π).

When $\beta =\frac{\pi }{2}$ or $\frac{3\pi }{2}$, Equation (13) leads to the smallest r′:

$$r^{\prime }<\frac{N{\lambda }_c}{4\pi },$$ (14)

and the length of the local step size maximizes to $\frac{2\pi r^{\prime }}{N}$. Obviously, if r′ satisfies Equation (14), the length of the local step size of ‖r−r′‖ given by Equation (12) also satisfies the Nyquist criterion:

$$\frac{2\pi R\left|\cos {\alpha }^{\prime }\right|}{N}=\frac{2\pi r^{\prime }\left|\sin \beta \right|}{N}\le \frac{2\pi r^{\prime }}{N}<\frac{{\lambda }_c}{2}.$$ (15)

We define the region S₁, called the one-way Nyquist zone here, as

$$S_1=\left\{{\mathbf{r}}^{\prime }\mid \Vert {\mathbf{r}}^{\prime }\Vert <\frac{N{\lambda }_c}{4\pi }\right\}.$$ (16)

Equivalently, we can consider the boundary of S₁ as a virtual detection surface, where the sampling spacing is scaled down from the actual detection spacing by $\frac{R_1}{R}$ with R₁ being the radius of S₁. For any source point inside S₁, there is no spatial aliasing during SS because the sampling spacing is less than half of the lower cutoff wavelength, which agrees with the result in Xu et al. [28].

Next, we analyze the spatial aliasing in IR. Substituting Equation (5) into Equation (7), we obtain

$$\begin{gathered} {\widehat{p}}_0\left({\mathbf{r}}^{″}\right)\approx \frac{1}{2\pi c^2}\sum _{n=1}^N{w}_n\sum _{m=1}^M{v}_m\frac{p_0\left({\mathbf{r}}_m^{\prime }\right)}{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert } \\ \times \left(1-\left(t+\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}\right)\frac{\partial }{\partial t}\right)h_e^{\prime } \\ \times \left(\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}-\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}\right). \end{gathered}$$ (17)

Here, we use the differential operator

$$\begin{gathered} \left(1-\left(t+\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}\right)\frac{\partial }{\partial t}\right)h_e^{\prime }(t) \\ =h_e^{\prime }(t)-\left(t+\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}\right)h_e^{″}(t). \end{gathered}$$ (18)

In Equation (17), we need to analyze only the expression $\left(1-\left(t+\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}\right)\frac{\partial }{\partial t}\right)h_e^{\prime }\left(\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}-\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}\right)$, which consists of two terms: $h_e^{\prime }\left(\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}-\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}\right)$ and $\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}{h}_e^{″}\left(\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}-\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}\right)$. As analyzed in Appendix A, the difference between the spectra of $\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}{h}_e^{″}\left(\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}-\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}\right)$ and $h_e^{″}\left(\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}-\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}\right)$ is negligible. Thus we only need to analyze the spatial aliasing in $h_e^{\prime }\left(\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}-\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}\right)$ and $h_e^{″}\left(\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}-\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}\right)$.

If $h_e^{\prime }(t)$ has an upper cutoff frequency f_c (the estimation of f_c is discussed in Appendix B), $h_e^{″}(t)$ will have the same upper cutoff frequency (Appendix B). Given a reconstruction location r″ and a source point location r′ (Fig. 1(b)), we need to analyze the sampling step size of ‖r″−r‖ − ‖r′−r‖ while the detection element location r varies. In fact, the lengths of the step sizes of both ‖r″−r‖ and ‖r′−r‖ reach maxima when r″−r and r′−r are perpendicular to r″ and r′, respectively. If the angle γ between vectors r″ and r′ satisfies $\gamma =\arccos \left(\frac{r^{″}}{R}\right)+\arccos \left(\frac{r^{\prime }}{R}\right)$, where r″ = ‖r″‖ and r′ = ‖r″‖, then the lengths of the step sizes of ‖r″−r‖ and ‖r′−r‖ achieve maxima of $\frac{2\pi r^{″}}{N}$ and $\frac{2\pi r^{\prime }}{N}$, respectively, with r at the same location, as shown in Fig. 1(b). In addition, as r passes this location clockwise, ‖r″−r‖ increases while ‖r′−r‖ decreases. Thus, the length of the step size of ‖r″−r‖ − ‖r′−r‖ achieves its maximum of

$$\frac{2\pi r^{″}}{N}+\frac{2\pi r^{\prime }}{N}=\frac{2\pi \left(r^{″}+r^{\prime }\right)}{N}.$$ (19)

The Nyquist criterion requires that

$$\frac{2\pi \left(r^{″}+r^{\prime }\right)}{N}<\frac{{\lambda }_c}{2},$$ (20)

which is equivalent to

$$r^{″}+r^{\prime }<\frac{N{\lambda }_c}{4\pi }.$$ (21)

One may interpret this condition as follows. The physical propagation of the photoacoustic wave in the object to the detectors is succeeded by a time-reversal propagation for the IR. The combined region encompasses a disc with a radius of r″ + r′. On the perimeter of this disc, the Nyquist sampling criterion requires that the sampling spacing be less than half of the lower cutoff wavelength, i.e., Equation (20).

We denote S₂, referred to as the two-way Nyquist zone here, as

$$S_2=\left\{{\mathbf{r}}^{\prime }\mid \Vert {\mathbf{r}}^{\prime }\Vert <\frac{N{\lambda }_c}{8\pi }\right\}.$$ (22)

Again, we can consider the boundary of S₂ as a virtual detection surface, where the sampling spacing is scaled down from the actual detection spacing by $\frac{R_2}{R}$ with R₂ being the radius of S₂. If the source points are inside S₂ and we reconstruct at points within S2, then $r^{\prime }<\frac{N{\lambda }_c}{8\pi }$ and $r^{″}<\frac{N{\lambda }_c}{8\pi }$, respectively, and Inequality (21) is satisfied. Thus, there is no spatial aliasing during reconstruction, and we call S₂ an aliasing-free region. It needs to be pointed out that, due to the finite duration of the transducer’s temporal response, the function $\left(1-\left(t+\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}\right)\frac{\partial }{\partial t}\right)h_e^{\prime }(t)$ has nonzero value only when t is within a finite interval, denoted as T_e. The broader the bandwidth of h_e (t), the shorter T_e. When $\frac{\Vert {\mathbf{r}}^{″}-\mathbf{r}\Vert }{c}-\frac{\Vert {\mathbf{r}}^{\prime }-\mathbf{r}\Vert }{c}$ is out of T_e, signals from source point r′ that are detected by the element at r have no contribution to the reconstruction at r″.

In the following discussion, we assume that $\frac{\Vert {\mathbf{r}}^{″}-\mathbf{r}\Vert }{c}-\frac{\Vert {\mathbf{r}}^{\prime }-\mathbf{r}\Vert }{c}$ belongs to T_e. Even with source points inside S₂, we may still have aliasing when reconstruction locations are outside S₂ but inside S₁. To demonstrate this, we assume that both r″ and r′ are on the boundary of S₂, and that the length of the step size of ‖r″−r‖ − ‖r′−r‖ achieves the maximum value of $\frac{2\pi R(\cos \alpha ″-\cos \alpha \prime )}{N}=\frac{{\lambda }_c}{2}$. Here, α″ and α′ denote the angles formed by the line segments r−r″ and r−r′ respectively, with the tangential dotted line that is perpendicular to r. We move the reconstruction location r″ to a new position ${\mathbf{r}}_1^{″}$ outside S₂ but inside S₁, as shown in Fig. 1(b). We keep the distance $\Vert {\mathbf{r}}_1^{″}-\mathbf{r}\Vert =\Vert {\mathbf{r}}^{″}-\mathbf{r}\Vert$ constant. Thus $\frac{\Vert {\mathbf{r}}_1^{″}-\mathbf{r}\Vert }{c}-\frac{\Vert {\mathbf{r}}^{\prime }-\mathbf{r}\Vert }{c}=\frac{\Vert {\mathbf{r}}^{″}-\mathbf{r}\Vert }{c}-\frac{\Vert {\mathbf{r}}^{\prime }-\mathbf{r}\Vert }{c}$ still belongs to T_e. As r″ moves to ${\mathbf{r}}_1^{″}$, the angle α″ decreases to ${\alpha }_1^{″}$. Both α″ and ${\alpha }_1^{″}$ belong to $\left(0,\frac{\pi }{2}\right)$, then we have $\cos {\alpha }_1^{″}>\cos {\alpha }^{″}$. Thus, for the local step size of $\Vert {\mathbf{r}}_1^{″}-\mathbf{r}\Vert -\Vert {\mathbf{r}}^{\prime }-\mathbf{r}\Vert$, we have the estimation $\frac{2\pi R\left(\cos {\alpha }_1^{″}-\cos {\alpha }^{\prime }\right)}{N}>\frac{2\pi R\left(\cos {\alpha }^{″}-\cos {\alpha }^{\prime }\right)}{N}=\frac{{\lambda }_c}{2}$, which means that spatial aliasing appears in reconstruction. Switching the source and reconstruction locations, we can repeat the analysis and draw a similar conclusion: with source points inside S₁ but outside S₂, we may have aliasing when reconstruction locations are inside S₂.

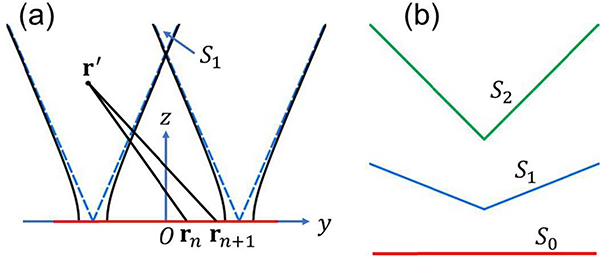
We visualize the relative sizes of the three regions S₀, S₁, and S₂ in Fig. 1(c). Spatial aliasing in SS does not appear for objects inside S₁, but appears for objects outside S₁. Spatial aliasing in IR does not appear for objects and reconstruction locations inside S₂, but appears for other combinations of objects and reconstruction locations. A detailed classification is shown in Fig. 2(a).

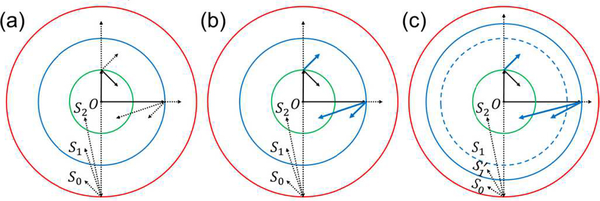
Fig. 2.

Different combinations of source locations and reconstruction locations subject to spatial aliasing in SS and IR. Three regions S₀, S₁, and S₂ are defined in Equations (8), (16), and (22), respectively. The first line radiating from the origin O represents the range of source locations for SS, while the second line radiating from the tip of the first line represents the range of reconstruction locations for IR. A solid line means no aliasing, while a dotted line means aliasing. (a) Spatial aliasing in UBP. The innermost two-way Nyquist zone S₂ is an aliasing-free region. (b) Spatial aliasing in UBP with spatial interpolation. Spatial interpolation removes spatial aliasing in three cases of IR, making the one-way Nyquist zone S₁ an aliasing-free region. The dotted lines representing the three cases in (a) are changed to blue-solid lines in (b). (c) Spatial aliasing in UBP with temporal filtering and spatial interpolation. Temporal filtering extends the one-way Nyquist zone S₁ in (b) to $S_1^{\prime }$ in (c), and the original S₁ is marked as a blue-dashed circle for reference. Spatial interpolation further makes $S_1^{\prime }$ an aliasing-free region.

IV. Spatial Antialiasing in SS and IR

Spatial aliasing solely in IR but not in SS can be removed by spatial interpolation. In fact, without spatial aliasing in SS, spatially continuous signals can be accurately recovered from spatially discrete signals through Whittaker–Shannon interpolation. Then, in theory, no aliasing would occur in reconstructing the image using the spatially continuous signals. In practice, the number of detection elements is numerically increased. To clarify the process, at any given time t, we define

$$f_R(\theta )=\widehat{p}(\mathbf{r},t),$$ (23)

where r = (Rcosθ, Rsinθ), θ ∈ [0, 20π_,). The function f_R(θ) is sampled at ${\theta }_n=\frac{2\pi n}{N}$, n = 0, 1, 2, …, N − 1. For objects inside the region S₁, SS has no aliasing. Thus, the function f_R (θ) can be well recovered from f_R(θ_n), n = 0, 1, 2, …, N −1 through spatial Whittaker–Shannon interpolation. To extend the region S₂, we can numerically double the number of detection elements N′ = 2N based on the interpolation. Substituting N′ for N in Equation (22), we obtain a larger region:

$$S_2^{\prime }=\left\{{\mathbf{r}}^{\prime }\mid \Vert {\mathbf{r}}^{\prime }\Vert <\frac{N^{\prime }{\lambda }_c}{8\pi }\right\}=\left\{{\mathbf{r}}^{\prime }\mid \Vert {\mathbf{r}}^{\prime }\Vert <\frac{N{\lambda }_c}{4\pi }\right\}=S_1.$$ (24)

From the above discussion about Equation (22), we know that with source and reconstruction locations inside $S_2^{\prime }$, IR has no aliasing. From $S_1=S_2^{\prime }$, we can see that spatial interpolation successfully removes spatial aliasing in IR. Fig. 2(a) is now replaced by Fig. 2(b). For source points outside the region S₁, SS has aliasing, and spatial interpolation cannot recover the lost information, which is mitigated by the next method.

Spatial aliasing in SS can be eliminated by temporal lowpass filtering. We consider a region larger than S₁:

$$S_1^{\prime }=\left\{{\mathbf{r}}^{″}\mid \Vert {\mathbf{r}}^{″}\Vert <r^{\prime }\right\}\text{with}{r}^{\prime }>\frac{N{\lambda }_c}{4\pi }.$$ (25)

We have already shown that source points in this region can produce spatial aliasing during SS. To avoid this concern, before spatial interpolation and reconstruction, we process the signals using a lowpass filter with upper cutoff frequency $f_c^{\prime }=\frac{Nc}{4\pi r^{\prime }}$. Replacing λc in Equation (16) with ${\lambda }_c^{\prime }=\frac{c}{f_c^{\prime }}$, we extend the region S₁ to

$$S_1^{\prime }=\left\{{\mathbf{r}}^{″}\mid \Vert {\mathbf{r}}^{″}\Vert <\frac{N{\lambda }_c^{\prime }}{4\pi }\right\}=\left\{{\mathbf{r}}^{″}\mid \Vert {\mathbf{r}}^{″}\Vert <r^{\prime }\right\}.$$ (26)

Based on the above discussion about Equation (16), for source points inside $S_1^{\prime }$, using spatial interpolation, we can reconstruct any points inside $S_1^{\prime }$ without aliasing artifacts. Thus, we extend the one-way Nyquist zone through temporal lowpass filtering at the expense of spatial resolution, and replace Fig. 2(b) with Fig. 2(c).

An ideal antialiasing method should extend the region $S_1^{\prime }$ in Fig. 2(c) to the whole region S₀. However, lowpass filtering removes the high-frequency signals, and blurs the reconstructed images. Directly extending $S_1^{\prime }$ to S₀ would greatly compromise the image resolution. As a balance between spatial antialiasing and high resolution, to reconstruct the image at r′ ∈ S₀, we design the lowpass filter based on its distance to the center r′ = ‖r′‖. If $r^{\prime }<\frac{N{\lambda }_c}{4\pi }$, we apply spatial interpolation, then perform reconstruction. If $r^{\prime }\ge \frac{N{\lambda }_c}{4\pi }$, we first filter the signals with upper cutoff frequency $f_c^{\prime }=\frac{Nc}{4\pi r^{\prime }}$, then perform spatial interpolation and reconstruction. We call this method radius-dependent temporal filtering.

V. Numerical Simulation

To visualize the artifacts caused by spatial aliasing, we first simulated a 3D case with a hemispherical detection geometry, where the antialiasing methods were not applied. The k-wave toolbox [12] was used for the forward problem.

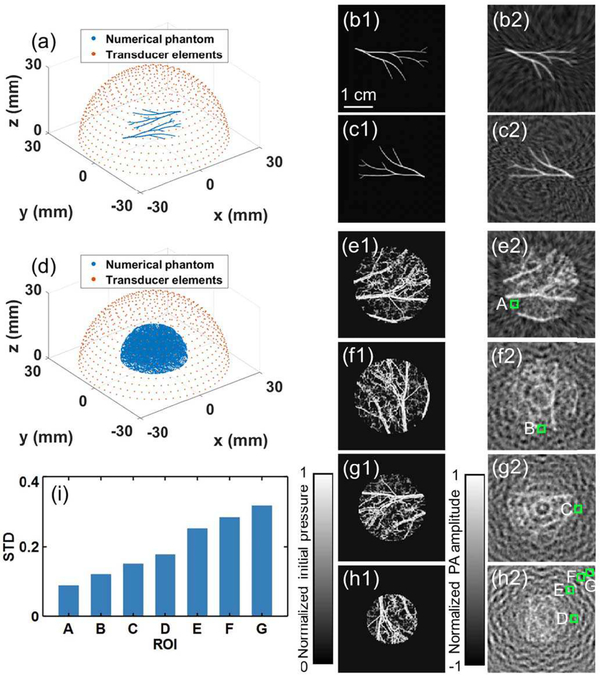
The simulation parameters were set as follows: the frequency range of the ultrasonic transducer is from 0.1 MHz to 4.5 MHz (2.3-MHz central frequency, 191% bandwidth, f_c = 4.5MHz), the SOS c= 1.5mm · μs⁻¹, the number of detection elements N= 651 (evenly distributed on the hemisphere based on the method in [31]), the radius of the hemisphere R = 30 mm, and the simulation grid size is 0.1× 0.1× 0.1 mm³). The elements are shown as red dots in Fig. 3(a). A simple numerical phantom with nonzero initial pressure from two layers with distances of 0 and 6.8 mm from the xy plane was analyzed first. The phantom is shown as blue dots in Fig. 3(a). The ground-truth images of the two layers are shown in Fig. 3(b1) and (c1), respectively, and the reconstructions are shown in Fig. 3(b2) and (c2), respectively. As can be seen, artifacts appear in both layers and seem stronger in the layer further from the xy plane.

Fig. 3.

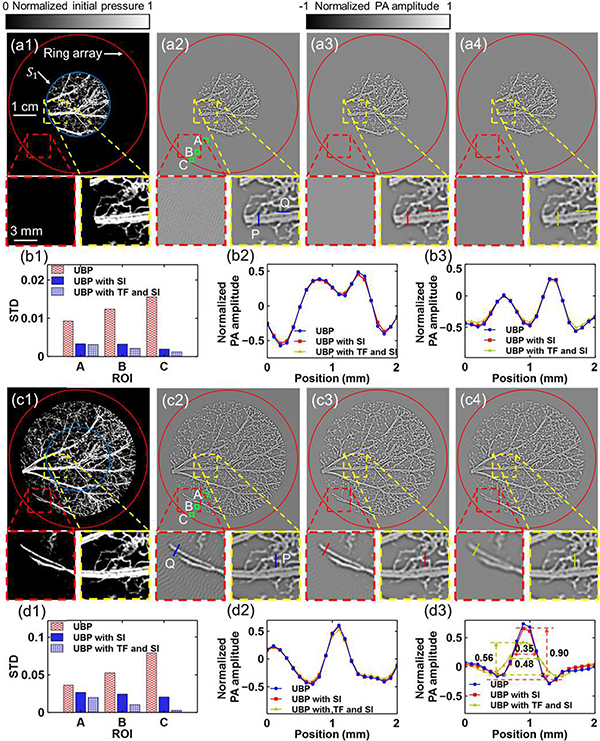
Aliasing artifacts in 3D reconstruction in a numerical simulation. (a) An array with 651 detection elements evenly distributed on a hemisphere and a simple numerical phantom covered by the array. (b1)–(b2), (c1)–(c2) Ground-truth slices (Column 1) of a simple phantom at z = 0 (Row b) and 6.8 mm (Row c), respectively, and their corresponding reconstructed images (Column 2). (d) The same array with a complex numerical phantom. (e1)–(e2), (f1)–(f2), (g1)–(g2), and (h1)–(h2) Ground-truth slices (Column 1) of the phantom at z = 0, 3.4, 6.8, and 10.2 mm (Rows e–h), respectively, and their corresponding reconstructed images (Column 2). (i) STD values of the pixel values in the ROIs outlined in the green boxes.

Using the same array, we further simulated a complex phantom with nonzero initial pressure from four layers with distances of 0, 3.4, 6.8, and 10.2 mm from the xy plane, shown as blue dots in Fig. 3(d). The ground-truth images of the four layers are shown in Fig. 3(e1), (f1), (g1), and (h1), respectively, and the reconstructions are shown in Fig. 3(e2), (f2), (g2), and (h2), respectively. Strong aliasing artifacts appear in all reconstructed images, and the artifacts tend to be more obvious in layers further from the origin. Regions of interest (ROIs) A–G (1.5×1.5 mm²) with increasing distances from the origin were picked from the four layers at locations with zero initial pressure. The standard deviations (STDs) of the pixel values inside these regions were calculated to quantify the aliasing artifacts. As can be seen in Fig. 3(i), the artifacts become stronger as the ROI moves away from the origin.

The 3D simulation provides a direct observation of the aliasing artifacts. Furthermore, we give a simplified estimation of the one-way Nyquist zone of the hemisphere geometry. We consider the planes crossing the center of the hemisphere. On each plane, we calculate the one-way Nyquist zone for the 2D case. All the detection elements for this plane lie on its intersection with the hemisphere, which is a semicircle with length π R (subset of a full circle with length 2π R). Based on the above analysis, we only need to estimate the number of detection elements for this plane. In fact, given the area of the hemisphere 2π R² and the number of elements N, we know that the distance between two neighboring elements is approximately $\sqrt{\frac{2\pi R^2}{N}}$. Thus, the number of elements (in a full circle) for this plane is approximately

$$N^{\prime }=\frac{2\pi R}{\sqrt{\frac{2\pi R^2}{N}}}=\sqrt{2\pi N}.$$ (27)

Using Equation (15), we obtain the one-way Nyquist zone on this plane:

$$S_1^{\prime }=\left\{{\mathbf{r}}^{\prime }\mid \Vert {\mathbf{r}}^{\prime }\Vert \le \frac{N^{\prime }{\lambda }_c}{4\pi }\right\}=\left\{{\mathbf{r}}^{\prime }\mid \Vert {\mathbf{r}}^{\prime }\Vert \le \frac{c}{4f_c}\sqrt{\frac{2N}{\pi }}\right\}.$$ (28)

For a 3D simulation, we vary the plane’s normal vector: All the 2D regions $S_1^{\prime }$ form a half ball with radius $\frac{c}{4f_c}\sqrt{\frac{2N}{\pi }}$ ≈ 1.70 mm, which is much smaller than the radius R = 30 mm. This large difference explains the prevalence of the artifacts in the reconstructed 3D image.

To simplify the problem and clarify the key points, in the following simulations, we focus on the 2D case with a full-ring transducer array of radius R = 30 mm. The frequency range of the transducer is from 0.1 MHz to 4.5 MHz. We set the number of detection elements N= 512 and the SOS c = 1.5 mm·μs⁻¹. The radius of the one-way Nyquist zone S₁ is thus $r=\frac{Nc}{4\pi f_c}\approx 13.6\text{mm}$.

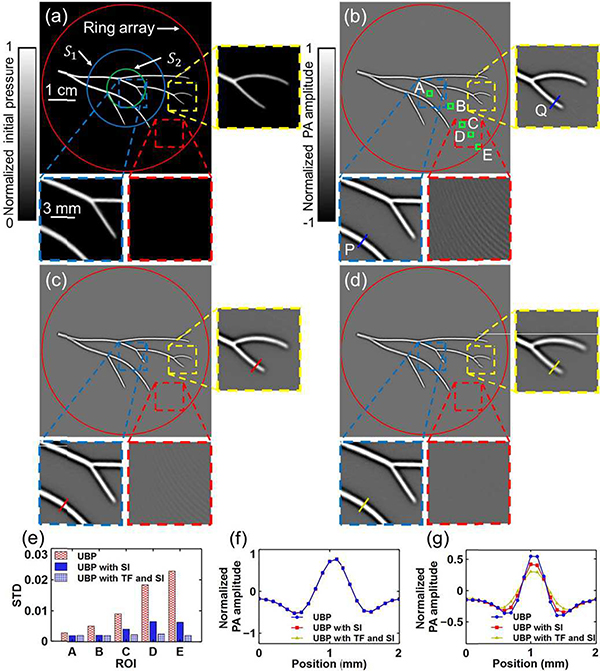
We used 0.1 × 0.1 mm² grid size, and we first simulated a simple initial pressure distribution shown in Fig. 4(a), with closeups of the blue-dashed, red-dashed, and yellow-dashed boxed regions. The full-ring transducer array and the boundaries of S₁ and S₂ are marked by red, blue, and green circles, respectively. The reconstruction of the object in Fig. 4(a) using UBP is shown in Fig. 4(b). Despite the clean ground-truth background boxed in Fig. 4(a), obvious aliasing-induced artifacts appear in the reconstructed image outside S₁ (red box) but not inside (blue box). It should be noticed that the yellow-boxed region in Fig. 4(b) is outside S₁, but it does not show strong artifacts. In fact, based on the above discussion, spatial aliasing only appears for certain combinations of source and reconstruction locations. Due to the specific distribution of the source, the artifacts turn out to be much stronger in the red-boxed region than that in the yellow-boxed region. We used spatial interpolation to remove aliasing solely in IR. Given a time t, signals from all the detection elements formed a vector with length N. The fast Fourier transformation (FFT) was then applied to the vector, and zeros were padded behind the highest frequency components to double the vector length to 2N. Finally, the inverse FFT was applied to the new vector to interpolate the data. This process is the frequency domain implementation of Whittaker–Shannon interpolation. Spatial interpolation numerically doubled the number of detection elements. The reconstruction of the object in Fig. 4(a) using UBP with spatial interpolation is shown in Fig. 4(c). To remove the spatial aliasing during SS, we applied a radius-dependent lowpass filter to the temporal signals before spatial interpolation. We used a third-order lowpass Butterworth filter and a sinc filter (with the same cutoff frequency) for radius-dependent filtering. The reconstruction of the object in Fig. 4(a) using UBP with temporal filtering and spatial interpolation is shown in Fig. 4(d).

Fig. 4.

Spatial interpolation and temporal filtering’s effects on IR in numerical simulations for a simple phantom. The full-ring transducer array and the boundaries of S₁ and S₂ are marked by red, blue, and green circles, respectively. (a) Ground truth of a simple initial pressure p₀ distribution. (b)–(d) Reconstructions of the object in (a) using (b) UBP, (c) UBP with SI, and (d) UBP with TF and SI, respectively. SI, spatial interpolation; TF, temporal filtering. (e) Comparison of the STDs in the ROIs A–E marked with the green boxes. (f)–(g) Comparisons of the profiles of lines (f) P and (g) Q, respectively, based on the three methods.

To quantify the amplitude of artifacts, we chose ROIs A–E (1.2×1.2mm²) at locations with zero initial pressure. The STDs of the pixel values inside these regions were calculated. As can be seen in the red-boxed regions and Fig. 4(e), spatial interpolation mitigates the aliasing artifacts significantly, while adding temporal filtering before spatial interpolation further diminishes the artifacts. This observation agrees with the above demonstration about both methods’ effects on extending the aliasing-free region. To quantify the impact of the antialiasing methods on image resolution, we picked two lines at P and Q, respectively, in each reconstructed image, and compared their profiles in Fig. 4(f) and (g), respectively. For signals from source points inside S₁, there is no spatial aliasing in SS, and spatial interpolation is accurate at the interpolation points. Moreover, radius-dependent temporal filtering does not affect the signals when reconstructing inside S₁. Thus, the antialiasing methods have negligible impact on the profile of line P (inside S₁), as shown in Fig. 4(f). For signals from source points outside S₁, the spatial interpolation is inaccurate due to spatial aliasing. Thus, directly applying spatial interpolation affects the profile of line Q (outside S₁). Radius-dependent temporal filtering smooths the signals before reconstructing outside S₁, thus it further smooths the profile of line Q, as shown in Fig. 4(f).

Next, we simulated two complex cases. For the first case, the object is completely within S₁, as shown in Fig. 5(a1). The reconstructions of the object in Fig. 5(a1) using UBP, UBP with spatial interpolation, and UBP with temporal filtering and spatial interpolation are shown in Fig. 5(a2)–(a4), respectively. ROIs A–C (1.2×1.2 mm²) were chosen at locations with zero initial pressure. The STDs were calculated and compared, as shown in Fig. 5(b1). Profiles of lines P and Q are shown in Fig. 5(b2) and (b3), respectively. For the second case, the object is beyond S₁, and covers most of the area inside the full-ring transducer array, as shown in Fig. 5(c1). The reconstructions of the object in Fig. 5(c1) using the three methods are shown in Fig. 5(c2)–(c4), respectively. The STDs of ROIs A–C are compared in Fig. 5(d1), while the profiles of lines P and Q are shown in Fig. 5(d2) and (d3), respectively. Although spatial interpolation mitigates the aliasing artifacts in both Fig. 5(a2) and (c2), visible artifacts remain in the red-boxed region in Fig. 5(c3) but not in Fig. 5(a3). It can also be seen in Fig. 5(b1) and (d1) that spatial interpolation has more obvious antialiasing effects on Fig. 5(a2) than on Fig. 5(c2), while temporal filtering’s effect on Fig. 5(c2) is more obvious than on Fig. 5(a2). In fact, the aliasing artifacts in Fig. 5(a2) are solely from the IR, while those in Fig. 5(c2) are from both the SS and the IR. Thus, spatial interpolation works well in antialiasing for Fig. 5(a2), for which temporal filtering’s smoothing effect slightly helps; but not as well for Fig. 5(c2) due to the spatial aliasing in SS, for which temporal filtering is necessary. In general, the aliasing artifacts are mitigated by spatial interpolation and further diminished by temporal filtering, as shown in both Fig. 5(b1) and (d1). The antialiasing methods maintain the image resolution well inside S₁, as shown in Fig. 5(b2), (b3), and (d2). Due to spatial aliasing in SS for objects outside S₁, the profile of line Q is affected by spatial interpolation. Adding temporal filtering further smooths the profile. The full width at half maximum (FWHM) of the main lobe in line Q’s profile was increased by temporal filtering while the amplitude was reduced, as shown in Fig. 5(d3). All these observations regarding the complex phantoms agree with the discussions about the simple phantom in Fig. 4.

Fig. 5.

Spatial interpolation and temporal filtering’s effects on IR in numerical simulations for two complex phantoms. (a1) Ground truth of a complex initial pressure p₀ distribution confined to S₁. (a2)–(a4) Reconstructions of the object in (a1) using (a2) UBP, (a3) UBP with SI, and (a4) UBP with TF and SI, respectively. SI, spatial interpolation; TF, temporal filtering. The artifacts in the red-boxed region are caused by spatial aliasing in IR, and they are mainly mitigated by SI. (b1) Comparison of the STDs in the ROIs A–C. (b2) and (b3) Comparisons of the profiles of lines P and Q, respectively, for the three methods. (c1) Ground truth of a complex initial pressure p₀ distribution beyond S₁. (c2)–(c4) Reconstructions of the object in (c1) using (c2) UBP, (c3) UBP with SI, and (c4) UBP with TF and SI, respectively. The artifacts in the red-boxed region are caused by spatial aliasing in SS and IR, and the artifacts are mitigated by TF and SI. (d1) Comparison of the STDs in the ROIs A–C. (d2) and (d3) Comparisons of the profiles of lines P and Q, respectively, for the three methods. The FWHM of the main lobe at Q was increased from 0.35 mm to 0.48 mm by temporal filtering, while the amplitude was changed from 0.90 to 0.56, respectively.

VI. In Vivo Experiment

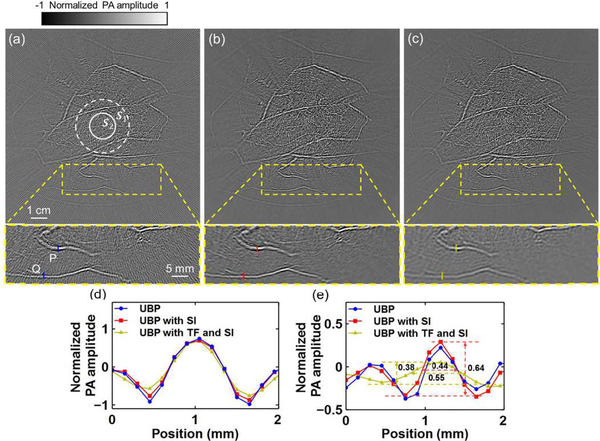
Finally, we applied the spatial interpolation and temporal filtering methods to human breast imaging. The imaging system, as previously reported by Lin et al. [6], employed a 512element full-ring ultrasonic transducer array (Imasonic, Inc., 110-mm radius, 2.25-MHz central frequency, 95% one-way bandwidth). Based on point source measurements (Appendix B), the cutoff frequency is estimated to be f_c ≈ 3.80 MHz. The acquired signals were filtered by a third-order lowpass Butterworth filter and a sinc filter (both with cutoff frequency 3.80 MHz). Thus, the one-way Nyquist zone S₁ has a radius $r=\frac{Nc}{4\pi f_c}\approx 16.0\text{mm}$, while the two-way Nyquist zone S₂ has a radius of 8.0 mm. Here we use the speed of sound c = 1.49 mm · μs⁻¹.

Using UBP, we reconstructed a cross-sectional image of a breast, shown in Fig. 6(a). The aliasing artifacts are obvious in the peripheral regions, as shown in Fig. 6(a)’s closeup subset in a yellow-boxed region. After spatial interpolation of the raw data, the reconstructed image is shown in Fig. 6(b). Applying temporal filtering and spatial interpolation, we obtained Fig. 6(c). As can be seen from these subsets, the image quality is improved by spatial interpolation, and the aliasing artifacts are further mitigated by temporal filtering. For comparison, the profiles of lines P and Q for the three images are shown in Fig. 6(d) and (e), respectively. As shown by the numerical simulation, image resolution outside S₁ is compromised by both spatial interpolation and temporal filtering. Temporal filtering smooths the profiles, as shown in Fig. 6(d) and (e). Quantitatively, as shown in Fig. 6(e), temporal filtering increases the FWHM of the main lobe of line Q’s profile and reduces the amplitude.

Fig. 6.

Spatial interpolation and temporal filtering’s effects on IR in an in vivo human breast image. (a) Reconstructed image using UBP without either spatial interpolation or temporal filtering, and a closeup subset in the yellow-boxed region. Boundaries of S₁ and S₂ are shown as white-dashed and white-solid circles, respectively. (b) and (c) Reconstructions of the same region as (a) using (b) UBP with SI, and (c) UBP with TF and SI, respectively. SI, spatial interpolation; TF, temporal filtering. (d) and (e) Comparisons of the profiles of lines P and Q, respectively, for the three methods. The FWHM of the main lobe at Q was increased from 0.44 mm to 0.55 mm by temporal filtering, while the amplitude was changed from 0.64 to 0.38, respectively.

VII. Conclusions and Discussion

In this work, we clarified the source of spatial aliasing in PACT through spatiotemporal analysis. Then we classified the aliasing into two categories: aliasing in SS, and aliasing in IR. Using a circular geometry as an example, we demonstrated two antialiasing methods to remove aliasing artifacts. The methods were validated by numerical and in vivo studies. Spatial interpolation maintains the resolution in the one-way Nyquist zone S₁ while mitigating the artifacts caused by aliasing in IR. It extends the aliasing-free zone from S₂ to S₁. For objects outside S₁, spatial interpolation is inaccurate due to spatial aliasing in SS, thus compromises the resolution. Adding radius-dependent temporal filtering does not affect the resolution inside S₁. For objects outside S₁, temporal filtering suppresses high-frequency signals to satisfy the temporal Nyquist sampling requirement. Although reducing the spatial resolution in the affected regions, temporal filtering mitigates aliasing in SS and makes the spatial interpolation accurate, thus further extends the aliasing-free zone.

The spatiotemporal analysis used here is not limited to circular geometry. It can also be applied to the linear array geometry, as shown in Appendix D. Based on the basic 1D circular and linear geometries, one can analyze 2D geometries, such as, the planar geometry and the spherical geometry, through decomposition. Moreover, the conclusions drawn are also applicable to other IR algorithms. For example, spatial interpolation has been used in time reversal methods to generate a dense enough grid for numerical computation [20]–[23]. Now we prove that it can mitigate the aliasing artifacts caused in reconstruction. Furthermore, location-dependent temporal filtering can be incorporated into a wave propagation model and be used in time reversal methods and iterative methods to mitigate aliasing in SS.

Appendix A

Spectrum Analysis of $\frac{\Vert {\mathbf{R}}^{″}-{\mathbf{R}}_n\Vert }{c}{h}_e^{″}\left(\frac{\Vert {\mathbf{R}}^{″}-{\mathbf{R}}_n\Vert }{c}-\frac{\Vert {\mathbf{R}}_m^{\prime }-{\mathbf{R}}_n\Vert }{c}\right)$ in equation (17)

To analyze the spatial aliasing in IR, we first analyze the expression $\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}{h}_e^{″}\left(\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}-\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}\right)$, which is a multiplication of a fast-change variable $h_e^{″}\left(\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}-\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}\right)$ and a slow-change variable $\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}$. Considering that the multiplication is equivalent to a convolution in the frequency domain, the multiplication of $\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}$ causes spectrum change. In this appendix, we analyze this spectrum change and prove that it is negligible.

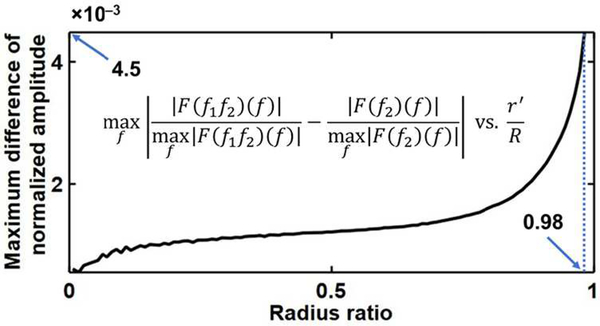
To simplify the problem, we only consider the case with ${\mathbf{r}}_m^{\prime }=\left(r^{\prime },0\right)$ and ${\mathbf{r}}^{″}=\left(r^{\prime }\cos \left(2\arccos \frac{r^{\prime }}{R}\right),r^{\prime }\sin \left(2\arccos \frac{r^{\prime }}{R}\right)\right)$. In this case, $\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}-\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}$ can achieve the maximum sampling step size $\frac{4\pi r^{\prime }}{N}$ as n varies (Equation (19)), where spatial aliasing is the most severe. Given an element location r(θ) = R(cos θ, sin θ), we define $f_1(\theta )=\frac{\Vert {\mathbf{r}}^{″}-\mathbf{r}(\theta )\Vert }{c}$ and $f_2(\theta )=h_e^{″}\left(\frac{\Vert {\mathbf{r}}^{″}-\mathbf{r}(\theta )\Vert }{c}-\frac{\Vert {\mathbf{r}}_m^{\prime }-\mathbf{r}(\theta )\Vert }{c}\right)$. Then, the continuous form of $\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}{h}_e^{″}\left(\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}-\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}\right)$ can be expressed as f₁ (θ) f₂ (θ). Applying the Fourier transformation to f₁ (θ) f₂ (θ) and f₂ (θ), we obtain F (f₁f₂) (f) and F (f₂)(f), respectively. Here F denotes the Fourier transformation operator. The difference between the two normalized spectra is expressed as $\underset{f}{\max }\left|\frac{\left|F\left(f_1{f}_2\right)(f)\right|}{\underset{f}{\max }\left|F\left(f_1{f}_2\right)(f)\right|}-\frac{\left|F\left(f_2\right)(f)\right|}{\underset{f}{\max }\left|F\left(f_2\right)(f)\right|}\right|$, which is a function of r^′ ∈ [0, R). We calculated the difference between the two normalized spectra for a full-ring array geometry with a radius R = 110 mm, and a point source response $h_e^{\prime }$ measured through experiments. We used a speed of sound c = 1.49 mm · μs⁻¹ in the computation. As shown in Fig. 7, for r′ ∈ [0, 0.98R], which is large enough for this research, we have $\underset{f}{\max }\left|\frac{\left|F\left(f_1{f}_2\right)(f)\right|}{\underset{f}{\max }\left|F\left(f_1{f}_2\right)(f)\right|}-\frac{\left|F\left(f_2\right)(f)\right|}{\underset{f}{\max }\left|F\left(f_2\right)(f)\right|}\right|<4.5\times {10}^{-3}$. When r′ approaches R, singularity occurs. For a system with a frequency-dependent SNR smaller than $\frac{1}{4.5\times {10}^{-3}}\approx 222$, which is almost always true for our experimental cases, the difference between the two normalized spectra is negligible. Therefore, to simplify the problem, we analyze the spatial aliasing in $h_e^{″}\left(\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}-\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}\right)$ to respresent the spatial aliasing in $\underset{f}{\max }\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}{h}_e^{″}\left(\frac{\Vert {\mathbf{r}}^{″}-{\mathbf{r}}_n\Vert }{c}-\frac{\Vert {\mathbf{r}}_m^{\prime }-{\mathbf{r}}_n\Vert }{c}\right)$.

Fig. 7.

Difference between the normalized spectra $\frac{\left|F\left(f_1{f}_2\right)(f)\right|}{\underset{f}{\max }\left|F\left(f_1{f}_2\right)(f)\right|}$ and $\frac{\left|F\left(f_2\right)(f)\right|}{\underset{f}{\max }\left|F\left(f_2\right)(f)\right|}$ for r′ ∈ [0,0.98R]. We have $\underset{f}{\max }\left|\frac{\left|F\left(f_1{f}_2\right)(f)\right|}{\underset{f}{\max }\left|F\left(f_1{f}_2\right)(f)\right|}-\frac{\left|F\left(f_2\right)(f)\right|}{\underset{f}{\max }\left|F\left(f_2\right)(f)\right|}\right|\le 4.5\times {10}^{-3}$ for any r′ ∈ [0,0.98R].

Appendix B

Estimation of the Upper Cutoff Frequency

In this appendix, we estimate f_c using point source measurements. From these measurements, we obtain an estimation of the point source response. We quantify the response’s amplitude and noise level in the frequency domain, then calculate the frequency-dependent signal-to-noise ratio (SNR). We choose the upper cutoff frequency f_c, higher than the central frequency, where the frequency-dependent SNR decreases to one for the first time.

We used the full-ring transducer array to acquire the PA signals generated by a point source located at the array center for J repetitions (J = 100). From each acquisition, we obtained N measurements from N transducer elements (N= 512). Based on Equation (5), by ignoring a constant factor, we can express the point source response as $h_e^{\prime }(t)$. We denote the measurement of $h_e^{\prime }(t)$ by the n-th element in the j-th acquisition as $h_{e,j,n}^{\prime }(t)$. In each acquisition, the mean response is denoted as

$$h_{e,j}^{\prime }(t)=\frac{1}{N}\sum _{n=1}^N{h}_{e,j,n}^{\prime }(t),t>0,j=1,2,\dots ,J.$$ (29)

We can further estimate the point source response $h_e^{\prime }(t)$ using

$$\overline{h_e^{\prime }}(t)=\frac{1}{J}\sum _{j=1}^J{h}_{e,j}^{\prime }(t),t>0.$$ (30)

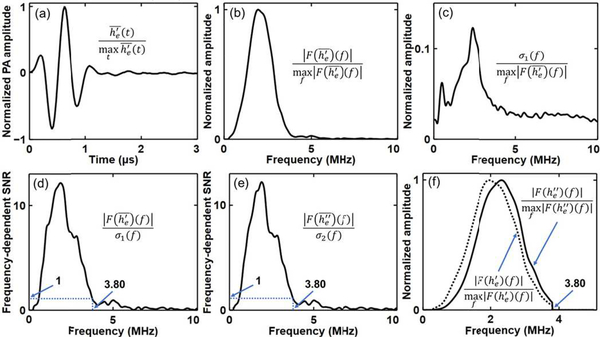
The normalized value of $\overline{h_e^{\prime }}(t)$ is shown in Fig. 8(a). Applying the Fourier transformation to $h_{e,j}^{\prime }(t)$ and $\overline{h_e^{\prime }}(t)$, we obtain $F\left(h_{e,j}^{\prime }\right)(f)$ and $F\left(\overline{h_e^{\prime }}\right)(f)$, respectively. The normalized amplitude of $F\left(\overline{h_e^{\prime }}\right)(f)$ is shown in Fig. 8(b).

Fig. 8.

Estimation of the upper cutoff frequency. (a) Normalized estimated point source response $(\frac{\overline{h_e^{\prime }}(t)}{\underset{t}{\max }\overline{h_e^{\prime }}(t)})$. (b) Normalized frequency spectrum of the estimated point source response $(\frac{\left|F\left(\overline{h_e^{\prime }}\right)(f)\right|}{\underset{f}{\max }\left|F\left(\overline{h_e^{\prime }}\right)(f)\right|})$. (c) Normalized frequency spectrum of the noise $\mathrm{STD}(\frac{{\sigma }_1(f)}{\underset{f}{\max }\left|F\left(\overline{h_e^{\prime }}\right)(f)\right|})$. (d) Frequency-dependent SNR $({\text{SNR}}_1(f)=\frac{\left|1\left(\overline{h_e^{\prime }}\right)(f)\right|}{{\sigma }_1(f)})$. The upper cutoff frequency is estimated to be f_c = 3.80 MHz, where the SNR equals to one. (e) Frequency-dependent SNR of the derivative of the point source response $({\text{SNR}}_2(f)=\frac{\left|F\left(\overline{h_e^{″}}\right)(f)\right|}{{\sigma }_2(f)})$. The upper cutoff frequency is also estimated to be f_c = 3.80 MHz. (f) Normalized frequency spectra of $h_e^{\prime }$ (frequency components with frequencies higher than 3.80 MHz are removed) and $h_e^{″}$ ($\frac{\left|F\left(h_e^{\prime }\right)(f)\right|}{\underset{f}{\max }\left|F\left(h_e^{\prime }\right)(f)\right|}$ and $\frac{\left|F\left(h_e^{″}\right)(f)\right|}{\underset{f}{\max }\left|F\left(h_e^{″}\right)(f)\right|}$, respectively).

Considering that each pixel value in a reconstructed image is obtained by a weighted summation of the signals from N elements, we can use the noise in $h_{e,j}^{\prime }(t)$ (rather than $h_{e,j,n}^{\prime }(t)$) to approximate the noise in the reconstructed image. At a frequency of f, the noise STD in $h_{e,j}^{\prime }(t)$ can be estimated as

$${\sigma }_1(f)\approx \sqrt{\frac{1}{J-1}\sum _{j=1}^J{\left|F\left(h_{e,j}^{\prime }\right)(f)-F\left(\overline{h_e^{\prime }}\right)(f)\right|}^2}.$$ (31)

Thus, we can define the frequency-dependent SNR as

$${\text{SNR}}_1(f)=\frac{\left|F\left(\overline{h_e^{\prime }}\right)(f)\right|}{{\sigma }_1(f)}.$$ (32)

The normalized value of σ₁ ( f ) and the value of SNR₁ ( f ) are shown in Fig. 8(c) and (d), respectively. We choose the cutoff frequency f_c to be 3.80 MHz (higher than the central frequency 2.25 MHz), where SNR ( f ) decreases to one for the first time.

To observe the temporal differentiation effect on the spectrum of $\overline{h_e^{\prime }}$, we replace $\overline{h_e^{\prime }}$ in Equation (31) and (32) with $\overline{h_e^{″}}$, and obtain σ₂ ( f ) and SNR₂ ( f ), respectively. As can be seen in Fig. 8(e), the upper cutoff frequency we obtain from SNR₂ ( f ) is the same as that from SNR₁ ( f ). In practice, before the UBP reconstruction, we filter the acquired signals with a third-order lowpass Butterworth filter and a sinc filter (both with a cutoff frequency of f_c). Thus, the frequency components with frequencies higher than 3.80 MHz are removed from $h_e^{\prime }$. The normalized frequency spectrum of $h_e^{\prime }$ and $h_e^{″}$ are shown in Fig. 8(f). As can be seen, although the spectrum is positively shifted by the temporal differentiation for f < 3.80 MHz, the cutoff frequency 3.80 MHz doesn’t change.

Appendix C

Accuracy of the Sampling Step Size Approximation

This research is based on an approximation of the sampling step size, as shown in Expression (9), especially its maximum value $\frac{2\pi r^{\prime }}{N}$. In this appendix, we discuss the accuracy of this approximation by expressing the sampling step size as a Taylor expansion with the Lagrange remainder. The first-order term is the approximation we use. By analyzing the higher-order terms, we prove that the differences are negligible.

For a full-ring transducer array with a radius R and centered at the origin O, we consider a source point at r′ and two adjacent detection element locations r₁ and r₂ (Fig. 9(a)). The bisector of the angle formed by vectors r₁ and r₂ intersects with the ring at ${\mathbf{r}}_{\frac{3}{2}}$. Vectors r₁ and r₂ form an angle γ; vectors ${\mathbf{r}}_{\frac{3}{2}}$ and r′ form an angle φ; while vectors ${\mathbf{r}}_{\frac{3}{2}}-{\mathbf{r}}^{\prime }$ and −r^′ form an angle β. Vector ${\mathbf{r}}_{\frac{3}{2}}-{\mathbf{r}}^{\prime }$ forms an angle α^′ with the tangential dotted line crossing point ${\mathbf{r}}_{\frac{3}{2}}$. Thus, the angle formed by vectors $-{\mathbf{r}}_{\frac{3}{2}}$ and ${\mathbf{r}}^{\prime }-{\mathbf{r}}_{\frac{3}{2}}$ can be expressed as ${\alpha }^{\prime }-\frac{\pi }{2}$. Based on the Law of Cosines in triangles Or₁r′ and Or₂r′, we have

$$\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_1\Vert =\sqrt{R^2+r^{\prime 2}-2R{r}^{\prime }\cos \left(\phi +\frac{\gamma }{2}\right)},$$ (33)

and

$$\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_2\Vert =\sqrt{R^2+r^{\prime 2}-2R{r}^{\prime }\cos \left(\phi -\frac{\gamma }{2}\right)},$$ (34)

respectively. To simplify the following expression, we define functions

$$f_{k,\phi }(\gamma )=\frac{\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_1\Vert }{R}=\sqrt{1+k^2-2k\cos \left(\phi +\frac{\gamma }{2}\right)},$$ (35)

$$g(k,\phi )=k{\left(1+k^2-2k\cos \phi \right)}^{-\frac{1}{2}}\sin \phi ,$$ (36)

and

$$q(k,\phi )=\frac{1-k^2}{1+k^2-2k\cos \phi }\in \left[\frac{1-k}{1+k},\frac{1+k}{1-k}\right].$$ (37)

Here, we let $k=\frac{r^{\prime }}{R}$. Using the Law of Sines in triangle $O{\mathbf{r}}_{\frac{3}{2}}{\mathbf{r}}^{\prime }$

$$\frac{\sin \phi }{R\sqrt{1+k^2-2k\cos \phi }}=\frac{\sin \beta }{R}=\frac{\sin \left({\alpha }^{\prime }-\frac{\pi }{2}\right)}{r^{\prime }}=\frac{-\cos {\alpha }^{\prime }}{r^{\prime }},$$ (38)

we have

$$g(k,\phi )=-\cos {\alpha }^{\prime },$$ (39)

and

$$|g(k,\phi )|=\left|k\sin \beta \right|\le k,k\in [0,1),\phi \in [0,2\pi ).$$ (40)

One can prove that

$$f_{k,\phi }(-\gamma )=\frac{\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_2\Vert }{R},$$ (41)

$$f_{k,\phi }^{\prime }(\gamma )=\frac{1}{2}g\left(k,\phi +\frac{\gamma }{2}\right),$$ (42)

and

$$f_{k,\phi }^{″\prime }(\gamma )=-\frac{g\left(k,\phi +\frac{\gamma }{2}\right)}{8}\left(\frac{1}{4}+\frac{3}{4}{q}^2\left(k,\phi +\frac{\gamma }{2}\right)\right).$$ (43)

Then, based on the Taylor expansion of f_k,φ (γ)− f_k,φ (−γ), we can express the sampling step size as

$$\begin{gathered} \left|\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_1\Vert -\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_2\Vert \right| \\ =R\left|f_{k,\phi }(\gamma )-f_{k,\phi }(-\gamma )\right| \\ =R\left|2f_{k,\phi }^{\prime }(0)\gamma +\frac{f_{k,\phi }^{″\prime }\left({\gamma }^{\prime }\right)+f_{k,\phi }^{″\prime }\left(-{\gamma }^{\prime }\right)}{6}{\gamma }^3\right| \\ =\mathrm{sgn}(\sin \phi )g(k,\phi )R\gamma \\ -\frac{\mathrm{sgn}(\sin \phi )g\left(k,\phi +\frac{{\gamma }^{\prime }}{2}\right)}{48}\left(\frac{1}{4}+\frac{3}{4}{q}^2\left(k,\phi +\frac{{\gamma }^{\prime }}{2}\right)\right)R{\gamma }^3 \\ -\frac{sgn(\sin \phi )g\left(k,\phi -\frac{{\gamma }^{\prime }}{2}\right)}{48}\left(\frac{1}{4}+\frac{3}{4}{q}^2\left(k,\phi -\frac{{\gamma }^{\prime }}{2}\right)\right)R{\gamma }^3, \\ \text{for}\text{some}\gamma \prime \in (0,\gamma ). \end{gathered}$$ (44)

Here, we use the sign function

$$\mathrm{sgn}(x)=\{\begin{array}{ll}-1,\hfill & x<0,\hfill \\ 0,\hfill & x=0,\hfill \\ 1,\hfill & x>0.\hfill \end{array}$$ (45)

Fig. 9.

Accuracy of the sampling step size approximation. (a) A full-ring transducer array with a radius R (red circle), where two adjacent detection element locations r₁ and r₂, and a source point location r′ are marked. These and the following locations are also regarded as vectors from the origin O to them. Vectors r₁ and r₂ form an angle γ, whose bisector intersects with the ring at ${\mathbf{r}}_{\frac{3}{2}}$. Vector ${\mathbf{r}}_{\frac{3}{2}}-{\mathbf{r}}^{\prime }$ forms an angle α′ with the tangential dotted line that is perpendicular to vector ${\mathbf{r}}_{\frac{3}{2}}$. Vectors ${\mathbf{r}}_{\frac{3}{2}}$ and r′ form an angle φ, while vectors ${\mathbf{r}}_{\frac{3}{2}}-{\mathbf{r}}^{\prime }$ and −r′ form an angle β. The angle formed by vectors $-{\mathbf{r}}_{\frac{3}{2}}$ and ${\mathbf{r}}^{\prime }-{\mathbf{r}}_{\frac{3}{2}}$ can be expressed as ${\alpha }^{\prime }-\frac{\pi }{2}$. This graph is used to estimate the sampling step size |‖r′−r₁‖ − ‖r′−r₂‖|. (b) and (c) Errors of using $r^{\prime }\gamma =\frac{2\pi r^{\prime }}{N}$ to approximate s(r′, θ) for r′ = 0.95 $r_1^{\prime }\approx 15.2\text{mm}$ and $r^{\prime }=6.75r_1^{\prime }\approx 107.8\text{mm}$, respectively.

In practice, it is the maximum sampling step size that affects spatial aliasing. To have a finer estimation of the maximum sampling step size, we first estimate the upper bound of |‖r′−r₁‖ − ‖r′−r₂‖|. For $\phi \in \left[\frac{\gamma }{2},\pi -\frac{\gamma }{2}\right]\cup \left[\pi +\frac{\gamma }{2},2\pi -\frac{\gamma }{2}\right]$, we have $sgn(\sin \phi )g\left(k,\phi \pm \frac{{\gamma }^{\prime }}{2}\right)\ge 0$. Thus, the high order terms in Equation (44) are nonpositive, and we have

$$\begin{gathered} \left|\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_1\Vert -\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_2\Vert \right| \\ \le |g(k,\phi )|R\gamma =\left|\cos {\alpha }^{\prime }\right|R\gamma , \\ k\in [0,1),\phi \in \left[\frac{\gamma }{2},\pi -\frac{\gamma }{2}\right]\cup \left[\pi +\frac{\gamma }{2},2\pi -\frac{\gamma }{2}\right], \\ \gamma =\frac{2\pi }{N}\le \frac{\pi }{4}. \end{gathered}$$ (46)

Here we assume that N ≥ 8. For $\phi \in \left[-\frac{\gamma }{2},\frac{\gamma }{2}\right]$, we have $\phi +\frac{\gamma }{2}\in [0,\gamma ]$ and $\phi -\frac{\gamma }{2}\in [-\gamma ,0]$, which means that both f_k,φ(γ) and f_k,φ(−γ) belong to $\left[\sqrt{1+k^2-2k},\sqrt{1+k^2-2k\cos \gamma }\right]$. Thus, we have

$$\begin{gathered} \left|\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_1\Vert -\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_2\Vert \right| \\ \le R\left|\sqrt{1+k^2-2k}-\sqrt{1+k^2-2k\cos \gamma }\right| \\ =R\left|f_{k,\frac{\gamma }{2}}(-\gamma )-f_{k,\frac{\gamma }{2}}(\gamma )\right|\le \left|g\left(k,\frac{\gamma }{2}\right)\right|R\gamma \le r^{\prime }\gamma . \end{gathered}$$ (47)

Here, we use Inequality (46) with $\phi =\frac{\gamma }{2}$. Similarly, for $\phi \in \left[\pi -\frac{\gamma }{2},\pi +\frac{\gamma }{2}\right]$, we have

$$\left|\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_1\Vert -\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_2\Vert \right|\le \left|g\left(k,\pi -\frac{\gamma }{2}\right)\right|R\gamma \le r^{\prime }\gamma .$$ (48)

Combining Inequalities (46)–(48), we obtain the upper bound of the sampling step size

$$\begin{gathered} \left|\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_1\Vert -\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_2\Vert \right| \\ \le r^{\prime }\gamma =\frac{2\pi r^{\prime }}{N},N\ge 8,r^{\prime }\in [0,R),\phi \in [0,2\pi ). \end{gathered}$$ (49)

Next, we estimate the lower bound of |‖r′ − r₁‖| − ‖r′ − r₂‖ for $\beta =\frac{\pi }{2}$. In fact, for each r′ > 0, there exist N locations of r′ evenly distributed on the circle ‖r′‖ = r′ such that $\beta =\frac{\pi }{2}$. For each location, we have φ = arccos k, sgn(sin φ) = 1, and g (k, arccos k) = k. In general, we may have singularities in $q\left(k,\phi +\frac{{\gamma }^{\prime }}{2}\right)$. To avoid the singularities, we assume k ≤ cos γ, which means that $\phi =\arccos k\in \left[\gamma ,\frac{\pi }{2}\right]$. Thus, we have $\cos \left(\phi +\frac{{\gamma }^{\prime }}{2}\right)<\cos \phi$ and $\cos \left(\phi -\frac{{\gamma }^{\prime }}{2}\right)<\cos \left(\phi -\frac{\gamma }{2}\right)$, leading to

$$q\left(k,\phi +\frac{{\gamma }^{\prime }}{2}\right)<q(k,\arccos k)=1,$$ (50)

and

$$\begin{gathered} q\left(k,\phi -\frac{{\gamma }^{\prime }}{2}\right)<q\left(k,\arccos k-\frac{\gamma }{2}\right) \\ =\frac{1-k^2}{1+k^2-2k^2\cos \frac{\gamma }{2}-2k\sqrt{1-k^2}\sin \frac{\gamma }{2}}, \end{gathered}$$ (51)

respectively. One can validate that $\frac{\partial q\left(k,\arccos k-\frac{\gamma }{2}\right)}{\partial k}\ge 0$ is equivalent to $k^2\le \frac{1+\cos \frac{\gamma }{2}}{5-3\cos \frac{\gamma }{2}}$. Thus $q\left(k,\arccos k-\frac{\gamma }{2}\right)$, as a function of k, is monotonically increasing on $\left[0,\sqrt{\frac{1+\cos \frac{\gamma }{2}}{5-3\cos \frac{\gamma }{2}}}\right)$. Note that ${\cos }^2\frac{\gamma }{2}<\frac{1+\cos \frac{\gamma }{2}}{5-3\cos \frac{\gamma }{2}}$ is equivalent to ${\left(\cos \frac{\gamma }{2}-1\right)}^2\left(3\cos \frac{\gamma }{2}+1\right)\ge 1$, which is valid for any $\gamma =\frac{2\pi }{N}\le \frac{\pi }{4}$. Thus, for any k ≤ cos γ, we have $k^2\le {\cos }^2\gamma <{\cos }^2\frac{\gamma }{2}\le \frac{1+\cos \frac{\gamma }{2}}{5-3\cos \frac{\gamma }{2}}$. Based on the monotonicity of $q\left(k,\arccos k-\frac{\gamma }{2}\right)$ as a function of k, we have

$$\begin{gathered} q\left(k,\arccos k-\frac{\gamma }{2}\right)\le q\left(\cos \gamma ,\arccos (\cos \gamma )-\frac{\gamma }{2}\right) \\ =\frac{1-{\cos }^2\gamma }{1+{\cos }^2\gamma -2\cos \gamma \cos \frac{\gamma }{2}}. \end{gathered}$$ (52)

Further, one can prove that $q\left(\cos \gamma ,\frac{\gamma }{2}\right)<4$ is equivalent to ${\left(\cos \frac{\gamma }{2}-1\right)}^2\left(5{\cos }^2\frac{\gamma }{2}+6\cos \frac{\gamma }{2}+2\right)>0$, which is valid for any $\gamma =\frac{2\pi }{N}\le \frac{\pi }{4}$. In summary, for any k ≤ cos γ, we have

$$0<q\left(k,\arccos k+\frac{{\gamma }^{\prime }}{2}\right)<1,$$ (53)

and

$$0<q\left(k,\arccos k-\frac{{\gamma }^{\prime }}{2}\right)<4.$$ (54)

Combining Inequalities (53) and (54) with Equation (44), we obtain

$$\begin{gathered} \mid \Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_1\Vert -\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_2\Vert \mid \\ \ge r^{\prime }\gamma -\frac{53r^{\prime }}{192}{\gamma }^3=\frac{2\pi r^{\prime }}{N}-\frac{53r^{\prime }}{192}{\left(\frac{2\pi }{N}\right)}^3, \\ N\ge 8,r^{\prime }\le R\cos \gamma ,\phi =\arccos \frac{r^{\prime }}{R}. \end{gathered}$$ (55)

For any source point r^′ = (r′ cos θ, r′ sin θ), the maximum sampling step size can be expressed as

$$s\left(r^{\prime },\theta \right)=\underset{\phi }{\max }\left|\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_1\Vert -\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_2\Vert \right|.$$ (56)

From Inequality (49) we have

$$s\left(r^{\prime },\theta \right)\le \frac{2\pi r^{\prime }}{N},N\ge 8,r^{\prime }\in [0,R).$$ (57)

According to Inequality (55), there exist at least N values of θ evenly distributed in [0, 2π) such that

$$s\left(r^{\prime },\theta \right)\ge \frac{2\pi r^{\prime }}{N}-\frac{53r^{\prime }}{192}{\left(\frac{2\pi }{N}\right)}^3,N\ge 8,r^{\prime }\le R\cos \gamma .$$ (58)

As can be seen in Equation (57), using $r^{\prime }\gamma =\frac{2\pi r^{\prime }}{N}$ to approximate s (r′, θ) is sufficient for the antialiasing analysis; while $\frac{53r^{\prime }}{192}{\left(\frac{2\pi }{N}\right)}^3{\left(\frac{{\lambda }_c}{2}\right)}^{-1}$ in Equation (58) can be used to estimate the necessity to further reduce the upper bound of s (r′, θ) for the N specific values of θ. For general values of θ, numerical simulation can be used to estimate.

Next, we analyze these estimations in our numerical simulations tions and in vivo experiments. In both cases, we use N = 512. The radius constraint, from Inequality (58) $\frac{r^{\prime }}{R}\le \cos \gamma =\cos \frac{2\pi }{N}\approx 1-7.5\times {10}^{-5}$ is close enough to the intrinsic $\text{constraint}\left(\frac{r^{\prime }}{R}<1\right)$. For the numerical simulations, we set c = 1.5mm · μs⁻¹, R = 30mm, and f_c = 4.5MHz, thus we have $\frac{53r^{\prime }}{192}{\left(\frac{2\pi }{N}\right)}^3{\left(\frac{{\lambda }_c}{2}\right)}^{-1}<\frac{53R}{192}{\left(\frac{2\pi }{N}\right)}^3\left(\frac{2f_c}{c}\right)<9.2\times {10}^{-5}$. For in vivo experiments, we use c = 1.49mm · μs⁻¹, R = 110mm, and f_c = 3.80MHz, then we have $\frac{53r^{\prime }}{192}{\left(\frac{2\pi }{N}\right)}^3{\left(\frac{{\lambda }_c}{2}\right)}^{-1}<2.9\times {10}^{-4}$. In both cases, for the N specific values of θ, using $\frac{2\pi r^{\prime }}{N}$ to approximate s (r′, θ) is accurate enough. For general values of θ, we use numerical simulation to observe the approximation error for source locations on two circles (in vivo experiment cases): one with a radius of $0.95r_1^{\prime }=0.95\frac{N{\lambda }_c}{4\pi }\approx 15.2\text{mm}$ ($r_1^{\prime }$ is the radius of S₁), the other with a radius of $6.75r_1^{\prime }\approx 107.8\text{mm}$ (98% of R). We plot $e\left(r^{\prime },\theta \right)=\left(r^{\prime }\gamma -s\left(r^{\prime },\theta \right)\right){\left(\frac{{\lambda }_c}{2}\right)}^{-1}$ $\text{against}\theta \in \widehat{E}\left[0,\frac{\pi }{60}\right]$ for $r^{\prime }=0.95r_1^{\prime }$ and $6.75r_1^{\prime }$ in Fig. 9(b) and (c), respectively. Each red bar marks a choice of θ assumed in Inequality (58). One can see from Fig. 9(b) and (c) that, for general values of θ, to further reduce the upper bound of s (r′, θ) is unnecessary.

Appendix D

Spatiotemporal Antialiasing for the Linear Array

As another application of the proposed spatiotemporal analysis, we consider a linear array with N(N ≥ 4) point elements, pitch d, and lower cutoff wavelength λc < 2d. Using the linear array center O as the origin, the array (marked as the red line) as one axis and its normal as another axis, we construct a cartesian coordinate, as shown in Fig. 10(a). For a source point location r′ = (y, z) and two adjacent element locations ${\mathbf{r}}_{\text{n}}=\left(\left(n-\frac{N-1}{2}\right)d,0\right)$ and ${\mathbf{r}}_{\text{n}+1}=\left(\left(n-\frac{N-3}{2}\right)d,0\right)$, n = 0, …, N – 2, the sampling step size can be expressed as

$$\left|\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_{\mathbf{n}}\Vert -\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_{n+1}\Vert \right|=\left|\begin{array}{l}\sqrt{z^2+{\left(y-\left(n-\frac{N-1}{2}\right)d\right)}^2}-\hfill \\ \sqrt{z^2+{\left(y-\left(n-\frac{N-3}{2}\right)d\right)}^2}\hfill \end{array}\right|.$$ (59)

We first consider the sampling step size of $\frac{{\lambda }_c}{2}$

$$\left|\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_{\text{n}}\Vert -\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_{n+1}\Vert \right|=\frac{{\lambda }_c}{2},$$ (60)

which is a hyperbola with a standard form:

$$\frac{{\left(y-\left(n-\frac{N-2}{2}\right)d\right)}^2}{{\left(\frac{{\lambda }_c}{4}\right)}^2}-\frac{z^2}{{\left(\frac{d}{2}\right)}^2-{\left(\frac{{\lambda }_c}{4}\right)}^2}=1.$$ (61)

For source points lie in between the two curves of this hyperbola, the spatial Nyquist criterion

$$\left|\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_{\text{n}}\Vert -\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_{n+1}\Vert \right|<\frac{{\lambda }_c}{2},$$ (62)

is satisfied. Based on this geometric perception, the spatial Nyquist criterion for all element pairs can be simplified into two cases: the leftmost one $\mid \Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_0\Vert -\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_1\Vert \Vert <\frac{{\lambda }_c}{2}$, and the rightmost one $\left|\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_{N-2}\Vert -\Vert {\mathbf{r}}^{\prime }-{\mathbf{r}}_{N-1}\Vert \right|<\frac{{\lambda }_c}{2}$. Illustrations of these two hyperbolas with z ≥ 0 are shown in Fig. 10(a) as black-solid curves, while their asymptotes are shown as blue-dashed lines. Due to the symmetry between these two hyperbolas, they intersect with z axis at the same point $\left(0,z_1^{\prime }\right)=\left(0,\sqrt{\left({\left(\frac{2d}{{\lambda }_c}\right)}^2-1\right)\left({\left(\frac{N-2}{2}d\right)}^2-{\left(\frac{{\lambda }_c}{4}\right)}^2\right)}\right)$, while their asymptotes intersect with z axis at

$$\left(0,z_1\right)=\left(0,\frac{N-2}{2}d\sqrt{{\left(\frac{2d}{{\lambda }_c}\right)}^2-1}\right).$$ (63)

We approximate the one-way Nyquist zone using

$$S_1=\left\{(y,z)\mid z>\max \left\{\mid \begin{array}{l}\left|y-\frac{N-2}{2}d\right|\hfill \\ y+\frac{N-2}{2}d\mid \hfill \end{array}\right\}\sqrt{{\left(\frac{2d}{{\lambda }_c}\right)}^2-1}\right\},$$ (64)

which is the region above the two intersecting asymptotes, as shown in Fig. 10(a). At y = 0, the approximation error achieves the maximum value

$$\left|z_1-z_1^{\prime }\right|\le \frac{{\left(\frac{{\lambda }_c}{4}\right)}^2\sqrt{{\left(\frac{2d}{{\lambda }_c}\right)}^2-1}}{\sqrt{{(N-2)}^2{d}^2-{\left(\frac{{\lambda }_c}{2}\right)}^2}}<\frac{{\left(\frac{{\lambda }_c}{4}\right)}^2\sqrt{{\left(\frac{2d}{{\lambda }_c}\right)}^2-1}}{d\sqrt{(N-1)(N-3)}}.$$ (65)

Assuming c = 1.5 mm · μs⁻¹, f_c = 4.5 MHz, N = 256, and d = 0.25 mm, we have z₁ ≈ 35.5 mm and $\frac{2\left|z_1-z_1^{\prime }\right|}{{\lambda }_c}<7.4\times {10}^{-4}$, which proves the accuracy of using S₁ as the one-way Nyquist zone. Further, we approximate the two-way Nyquist zone using

$$S_2=\left\{(y,z)\mid z>\max \left\{\left|\begin{array}{l}y-\frac{N-2}{2}d\hfill \\ y+\frac{N-2}{2}d\hfill \end{array}\right|,\right\}\sqrt{{\left(\frac{4d}{{\lambda }_c}\right)}^2-1}\right\}.$$ (66)

One can prove that spatial interpolation extends S₂ to S₁, whereas further extending S₁ requires temporal filtering. The linear array (with the whole imaging domain S₀) and the boundaries of the two zones (S₁ and S₂) are shown in Fig. 10(b) as red, blue, and green lines, respectively.

Fig. 10.

Spatial aliasing in a linear array. (a) A linear array (marked as the red line) with N elements and pitch d. A Cartesian coordinate is formed with the array’s center O as the origin, the array direction as y axis, and its normal vector as z axis. Two adjacent element locations r_n, r_n+1, and a source point location r′ are marked. Two symmetric hyperbolas (with sampling step size $\frac{{\lambda }_c}{2}$) with z ≥ 0 are shown as black-solid curves and their asymptotes as blue-dashed lines. The one-way Nyquist zone S₁ is formed by the points above the two asymptotes crossing z axis. (b) The whole imaging domain S₀, the one-way Nyquist zone S₁, and the two-way Nyquist zone S₂ are outlined with red, blue, and green lines, respectively.