Non-circular CT orbit design for elimination of metal artifacts

Abstract

Metal artifacts are a well-known problem in computed tomography - particularly in interventional imaging where surgical tools and hardware are often found in the field-of-view. An increasing number of interventional imaging systems are capable of non-circular orbits providing one potential avenue to avoid metal artifacts entirely by careful design of the orbital trajectory. In this work, we propose a general design methodology to find complete data solution by applying Tuy’s condition for data completeness. That is, because metal implants effectively cause missing data in projections, we propose to find orbital designs that will not have missing data based on arbitrary placement of metal within the imaging field-of-view. We present the design process for these missing-data-free orbits and evaluate the orbital designs in simulation experiments. The resulting orbits are highly robust to metal objects and show greatly improved visualization of features that are ordinarily obscured.

1. INTRODUCTION

Metal artifacts commonly occur in diagnostic and image-guided cone-beam CT procedures due to the presence of surgical tools and hardware including embolization materials, dental fillings, artificial joints, fixation hardware, etc. Metal objects often result in photon starvation and beam hardening which appear as bright and dark streaks in the reconstructed images that confound visualization of anatomical features surrounding the metal. The artifact is especially severe when multiple metal objects are present, where anatomical features lying in-between metal objects are completely obliterated. Many algorithmic solutions have been proposed to mitigate the severity of streaks to produce a visually acceptable image. Classic corrections interpolate over metal regions in the projection data, effectively treating those projections as missing data. However, without additional prior information there is no way to guarantee accurate interpolations of this missing information.

Increasingly, modern interventional imaging systems are capable of non-circular orbits (e.g., robotic C-arms, etc.). This provides a potential solution to the metal artifact problem – by using non-circular orbits one can potentially eliminate missing data from the CT acquisition. Specifically, we design source sampling patterns that maximizes the number of locations that satisfy Tuy’s condition¹ for arbitrary metal placement in the object. This work is significantly different from previous work by our group^2–4 in task-driven orbit design in the following aspects: 1) the design objective considers considers data completeness rather than noise, resolution, or task-based metrics; 2) the non-circular orbit may leverage multiple degrees of freedom including out-of-plane angles and shifts along axes; 3) the proposed design methods do not require redesigns based on prior knowledge of the patient anatomy, and is generally applicable for metal placement in arbitrary locations. We demonstrate the proposed method in a physical phantom with a 2cm diameter spherical metal implant, and compare the resulting reconstructions with a circular and a helical orbit.

2. METHODS

2.1. Design Principle

For each location in the object, we trace the source trajectory on a spherical support centered at that location with spherical coordinates denoted as (ϕ^l, θ^l) [Fig.1(a)]. To satisfy Tuy’s condition, the source trajectory must intersect every great circle on the spherical support. Great circles on a unit sphere is given by:

$$\text{cot}\varphi =\text{tan}\gamma \text{cos}\left(\theta -{\theta }_0\right)$$ (1)

with examples shown in Fig.1(b). By discrete sampling the great circles in γ and θ₀, we may calculate the total percentage of great circles intersected by an orbit as a sampling completeness metric to quantify the extent to which a point satisfies Tuy’s condition. Similar metrics have been previously used in nuclear imaging and cone-beam CT to quantify data completeness.^5–7

Figure 1.

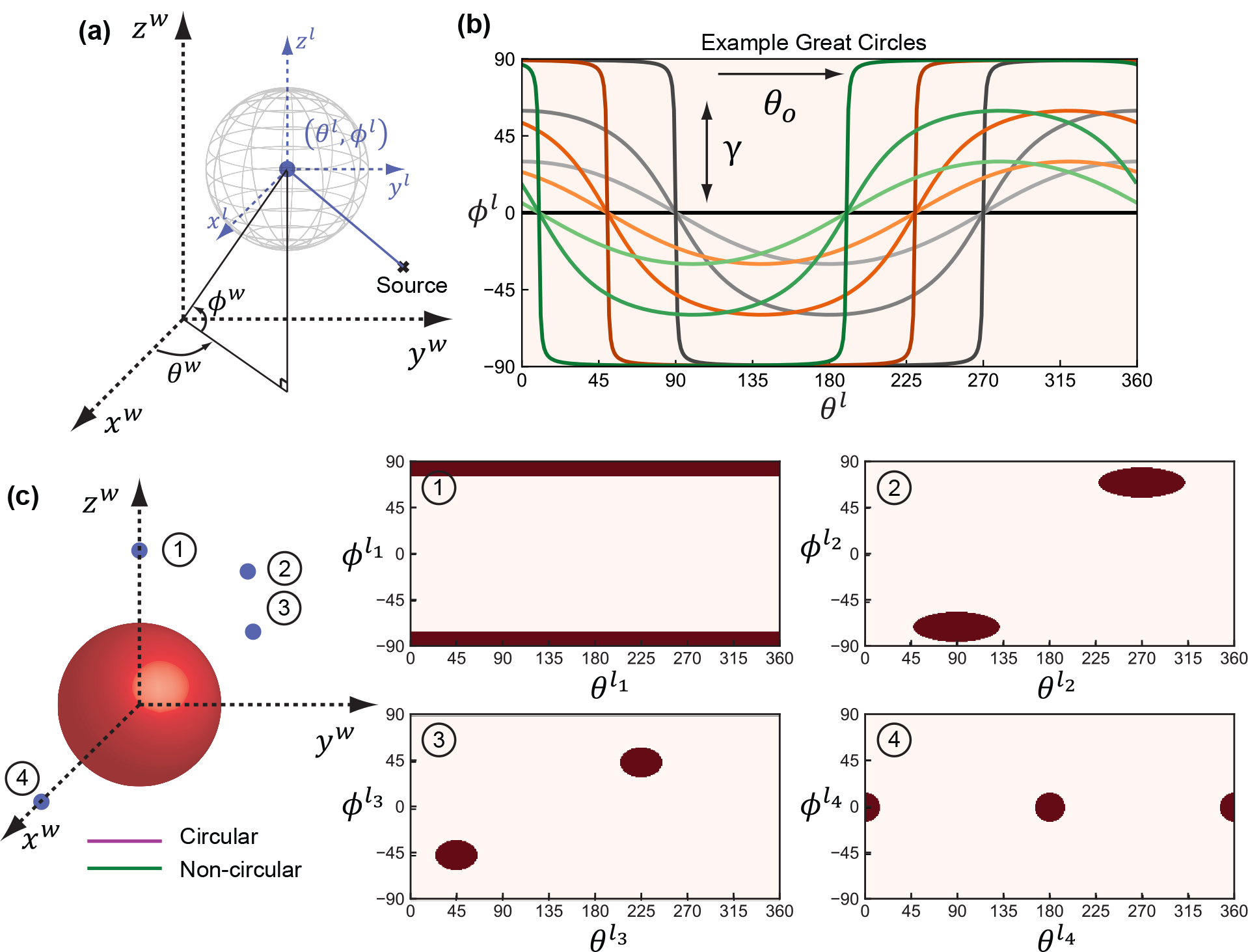
(a) Spherical coordinate systems centered at each location, (ϕ^l, θ^l), and world coordinates, (ϕ^w, θ^w), for defining source trajectory. (b) Example great circles of different o sets and amplitudes in (ϕ^l, θ^l). (c) Metal creating “gaps” in (ϕ^l, θ^l) for two example locations in (a), resulting in incomplete sampling when an orbit intersectings both “gaps”.

In the presence of metal, rays traversing the metal object are highly attenuated and may be considered to no longer contribute information - i.e., metal objects create missing data “gaps” in (ϕ^l, θ^l). If a great circle intersects the orbit only in these “gaps”, we no longer count it towards the sampling completeness percentage. However, if the orbit intersects this particular circle elsewhere, it can still contributes to the percentage. The shape and location of the “gaps” are dependent on the shape and size of the metal, as well as the relative position of the metal and the location at which sampling completeness is evaluated. For a simple spherical metal object, the “gaps” can be quickly computed efficiently using equirectangular projection formulations⁸s without forward projection.

The goal of this work is to develop a methodology to design general non-circular orbits that maximizes sampling for all locations in the image in the presence of metal objects in arbitrary locations.

2.2. Design parameters, Objective Function and Optimizer

2.2.1. Orbit parameterization

We constrain the acquisition to 360 projections evenly spaced over a single 360° rotation, i.e., the in-plane angles, θ, are fixed for all orbits. For orbit design, we allow the out-of-plane angle, ϕ, and a longitudinal x-ray source shift, z, to change from view to view. To reduce redundancy, z shift as a function of θ is assumed to be evenly spaced from −5cm to 5cm along the axis of rotation, z. Therefore, the orbit design parameter amounts to finding ϕ^w(θ^w). We further adopted a low-dimensional representation of ϕ^w(θ^w) as a linear combination of 31 local Gaussian basis functions and assume a mechanical constraint on ϕ^w to be within ±50°.

2.2.2. Sampling of great circles and locations

We performed discrete sampling of great circles over different phase offsets and amplitudes. For initial investigations, we assume the maximum size of the metal object to be a sphere of 2 cm diameter which may be placed in arbitrary locations on the central axial plane within a 16 cm radius support. We sampled 45 metal locations along a square grid as shown in Fig.2 (a). For each metal location, we evaluated Tuy’s condition over a shell of 50 points that are 10 mm from the surface of the metal ball as shown in Fig.2 (b).

Figure 2.

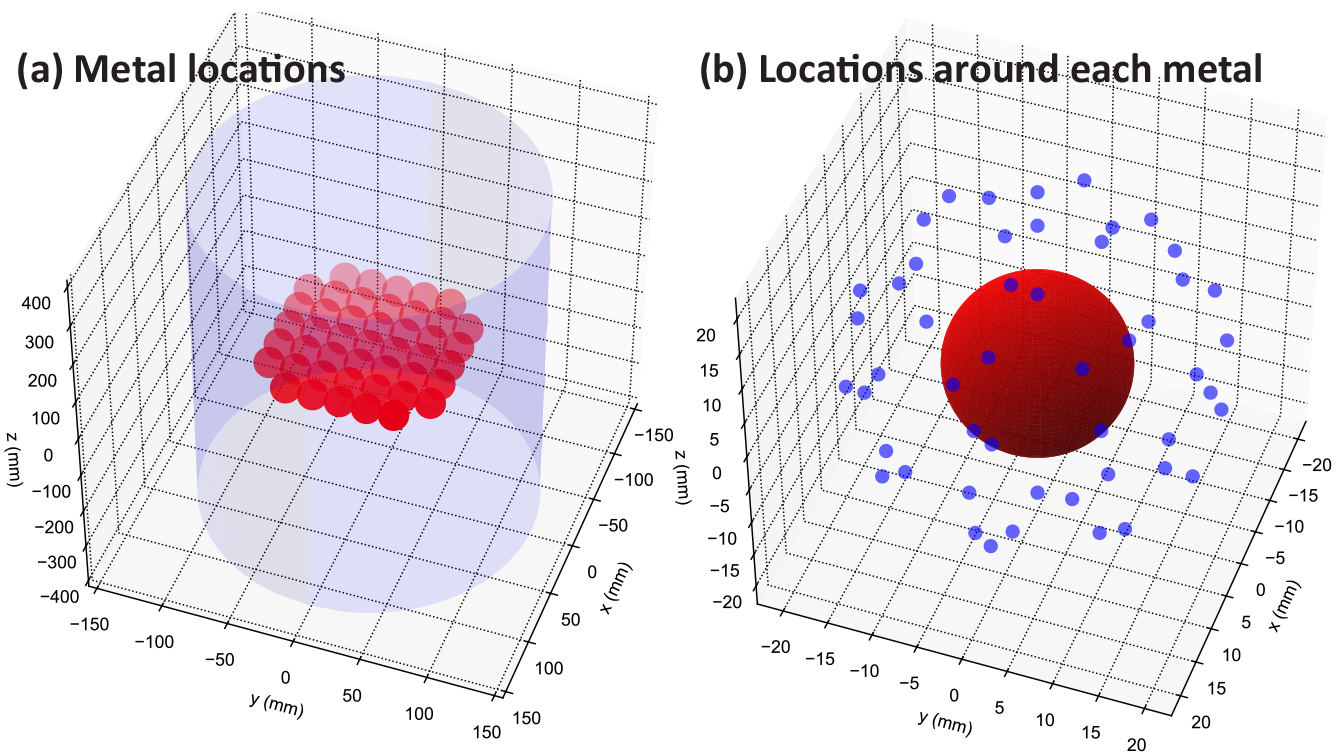
(a) Locations of metal balls and (b) locations around each metal ball for which Tuy’s condition is evaluated.

2.2.3. Objective function and optimizer

We chose to maximize the minimum percentage of sampled great circles that intersect the orbit over all metal and evaluation locations. We used a covariance matrix adaptation evolution strategy (CMA-ES) optimizer to optimize the coefficients for ϕ^w(θ^w).

2.3. Experimental Evaluation

As shown in Fig.3, we simulated a cylindrical phantom (25×25×100cm) filled with spheres simulating soft tissue contrast levels (0.005 mm⁻¹ and 0.01 mm⁻¹). We inserted a single metal ball of 2 cm diameter at the central axial plane together with line pairs in-plane and out-of-plane to demonstrate sampling effects. Although not explicitly designed for multiple metal objects, the orbits were also used to reconstruct a phantom with two metal balls. The designed non-circular orbit is compared with a circular orbit and a helical orbit. The pitch for the helical orbit is 10 cm and is equal to the total z-translation of the designed orbit.

Figure 3.

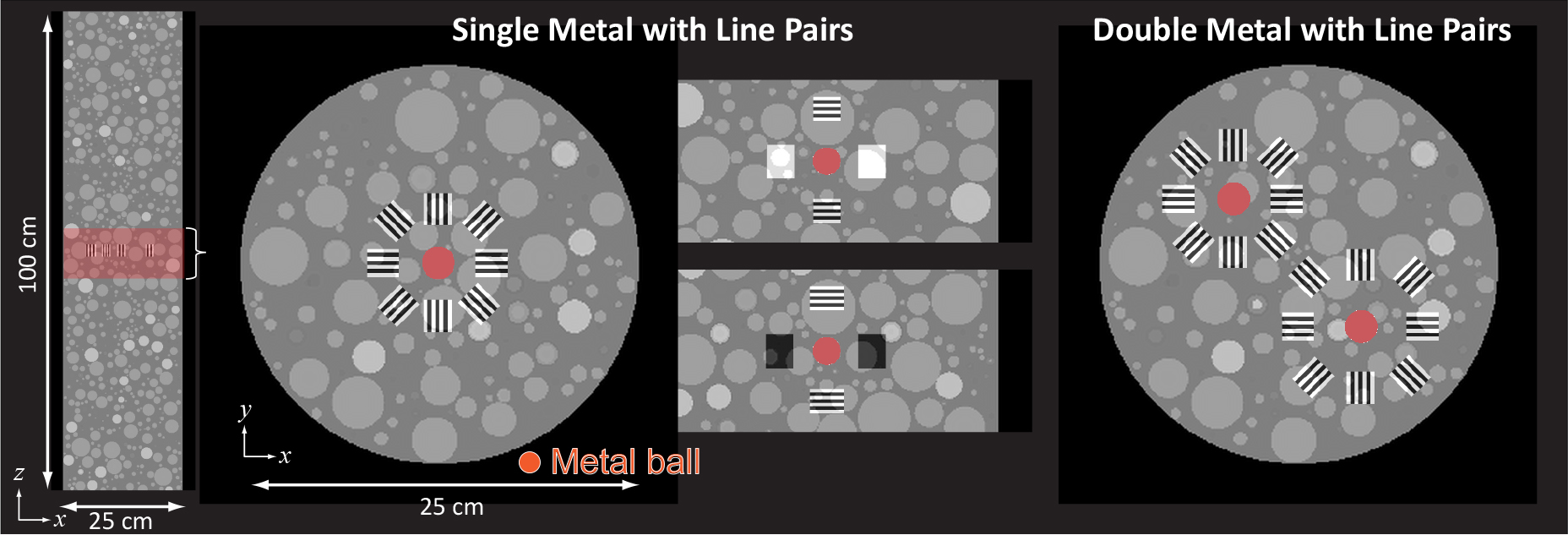
Phantoms used for evaluation of different orbits.

2.4. Reconstruction Algorithm

A penalized-likelihood (PL) reconstruction algorithm with a Huber penalty was employed for image reconstruction. We used separable footprint forward and back projector. Images were reconstructed at an isotropic voxel size of 2 mm.

3. RESULTS

Figure 4 shows the circular, helical, and designed orbit as source locations connected to the center of rotation. The objective function - minimum percentange of great circles sampled over all locations (denoted as “Min %”), is the highest for the designed orbit at 99%. We further evaluated the percentage of locations that satisfy Tuy’s condition (e.g., where 100% of great circles are sampled, denoted as “% complete”). Not surprisingly, the circular and helical orbits do not offer complete sampling of any locations when the metal is in-plane or at the center of the helix. The designed orbit completely samples 79% of the locations.

Figure 4.

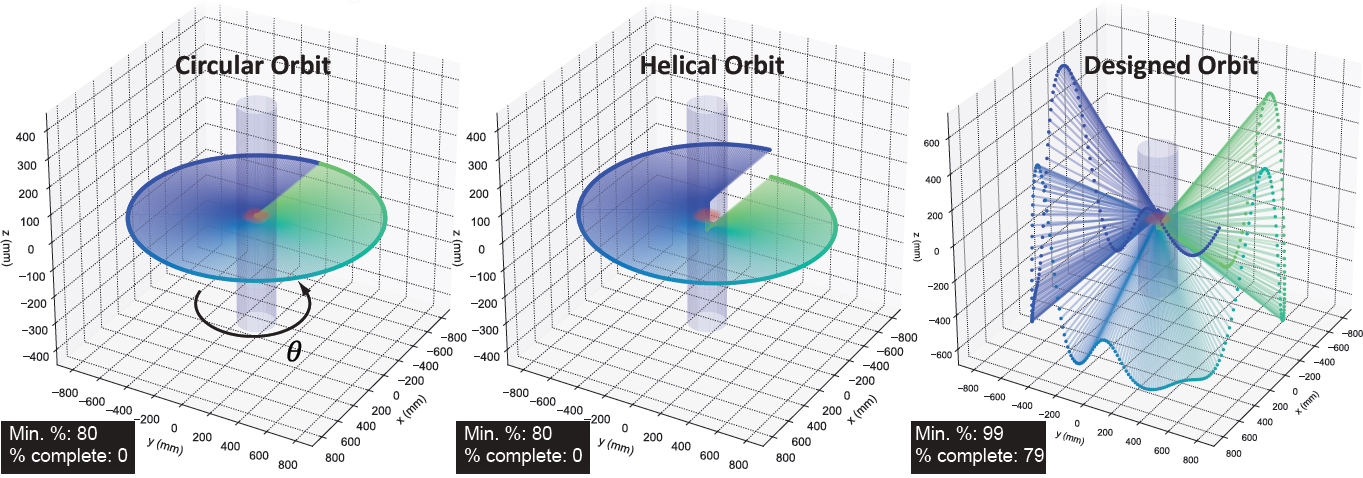
A circular, helical and designed orbit plotted as source location connected to the center of rotation.

Reconstructions using the three orbits for the single and double metal cases are shown in Fig.5. For the single metal case, the in-plane line pairs are invisible for the circular and helical orbits, but are clearly visible for the designed orbit. The out-of-plane line pairs are visible for all three orbits. A similar trend is shown in the double metal case where all in-plane line pairs are reconstructed for the designed orbit.

Figure 5.

Reconstructions of the single metal and double metal phantoms using three orbits.

4. DISCUSSION AND CONCLUSION

This work presents a general non-circular orbit design that aims to maximum Tuy’s condition in the presence of metal objects (treating projections through metal as fundamentally missing data). Designed orbits are demonstrated to greatly improve on the percentage of locations in the object for which complete data is collected. Consequently, image reconstructions show greatly reduced metal artifacts and visible in-plane structures that would be otherwise obscured by metal. Because the orbital design objective searched for solutions over arbitrary metal locations, the orbital trajectory is generally useful regardless of where metal is found in the object. More-over, there appears to be resilience to multiple metal objects in the field. Thus the proposed methodology has the potential for broad application in CT imaging systems with non-circular orbital capability.

Future work will consider orbit optimization over multiple rotations – offering greater potential to satisfy Tuy’s condition for all locations. Similarly, prior to translation of these methods onto physical imaging systems, we will incorporate the velocity and acceleration constraints of C-arm systems into the design.