Abstract
Coronavirus disease 2019 is caused by severe acute respiratory syndrome coronavirus 2. Kenya reported its first case on March 13, 2020 and by March 16, 2020 she instituted physical distancing strategies to reduce transmission and flatten the epidemic curve. An age-structured compartmental model was developed to assess the impact of the strategies on COVID-19 severity and burden. Contacts between different ages are incorporated via contact matrices. Simulation results show that 45% reduction in contacts for 60-days period resulted to 11.5–13% reduction of infections severity and deaths, while for the 190-days period yielded 18.8–22.7% reduction. The peak of infections in the 60-days mitigation was higher and happened about 2 months after the relaxation of mitigation as compared to that of the 190-days mitigation, which happened a month after mitigations were relaxed. Low numbers of cases in children under 15 years was attributed to high number of asymptomatic cases. High numbers of cases are reported in the 15–29 years and 30–59 years age bands. Two mitigation periods, considered in the study, resulted to reductions in severe and critical cases, attack rates, hospital and ICU bed demands, as well as deaths, with the 190-days period giving higher reductions.
Keywords: Coronavirus, Non-pharmaceutical intervention, Age structured, Contact matrix, Mathematical model
Introduction
The coronavirus disease 2019 (COVID-19) is caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). The first reported case was in mainland China, City of Wuhan, Hubei on the December 29, 2019 (Li et al., 2020). Subsequently the disease spread at an exponential rate to countries in contact with China resulting to World Health Organization (WHO) declaring it as a Public Health Emergency of International Concern (PHEIC) on January 30, 2020 (WHO Africa, 2020). As of May 31, 2020 there were over six million infections globally, with the European region taking lead in these infections (WHO, 2020c, p. 2633). In Africa, the first case was reported in Egypt then followed by Algeria (WHO, 2020a). The first Kenyan case was reported on the 13th of March and by May 31, 2020 there were about 1900 confirmed cases, with Nairobi and Mombasa taking the lead in these infections (MoH-Kenya, 2020).
There are mainly three kinds of infections; asymptomatic, pre-asymptomatic and symptomatic. The incubation period for COVID-19, which is the time between after exposure to the virus and symptoms onset, is on average 5–6 days, however it can be as high as 14 days. For COVID-19 symptomatic case, the disease manifests itself through symptoms such as fever, coughs, sneezes and headaches, whereas for asymptomatic case the infected individual does not develop symptoms (WHO, 2020b). The basic reproduction number, defined as the average number of secondary infections produced by an infectious individual in a population where everyone is susceptible (Li et al., 2020), is affected by the rate of contacts in the host population, the probability of transmission during contact and the duration of infectiousness. It can also vary for different age bands since the attack rates are age-dependent. The basic reproduction number for COVID-19 in Kenya ranges from 1.78 (95% CI 1.44–2.14) to 3.46 (95% CI 2.81–4.17) (Brand et al., 2020). Reduction of the reproduction number can definitely be achieved by instituting appropriate Non-Pharmaceutical Interventions (NPIs) or use of a vaccine.
In the absence of a vaccine, social/physical distancing strategies have globally become the most appropriate Non-Pharmaceutical Interventions (NPIs) (Ferguson et al., 2020). These mitigations can be implemented by reducing social contacts in workplaces, schools, markets and other public areas. Social contacts are influenced by age structure of the population and the frequency of contacts across population (Prem et al., 2017). Mathematical models that describe the impact of the NPIs in reducing morbidity, infection peak sizes, and excess mortality are vital in public-health planning (Singh & Adhikari, 2020). In their first step towards developing a credible model for COVID-19 dynamics in Kenya, the authors of this paper studied the impact of social distancing and contaminated environment in the article (Mwalili et al., 2020). The current study presents an improved model with the aim of predicting the possible trajectory of COVID-19 infections in Kenya.
Similar to other countries in sub-Saharan Africa, the Kenyan government has imposed travel restrictions across counties, dusk-to-dawn curfew and school closure to ensure social distancing in the population and consequently slowed transmission of COVID-19. Although it is not clear for how long these measures should be in place to eradicate the epidemic in Kenya, we state that premature and sudden lifting of interventions could potentially lead to a new peak of infections. However, intermittent application of the interventions can flatten the infections curve (Prem et al., 2020). Previous study of COVID-19 in Kenya also predicted the risk of epidemic rebound after the social distancing measures are lifted (Brand et al., 2020).
In this study, an age-structured SEIR mathematical model that examines the impact of NPIs in curbing COVID-19 severity and deaths in Kenya is developed, with the aim of achieving the following; (i) assessing the impact of reducing social contacts in different age-groups, (ii) examining the trend in infections during and after the NPIs, (iii) providing plausible period for lifting the NPIs. We postulate that this study can form a basis for policy formulation to enable Kenya delay the disease transmission and eventually flatten the epidemic curve.
Materials and methods
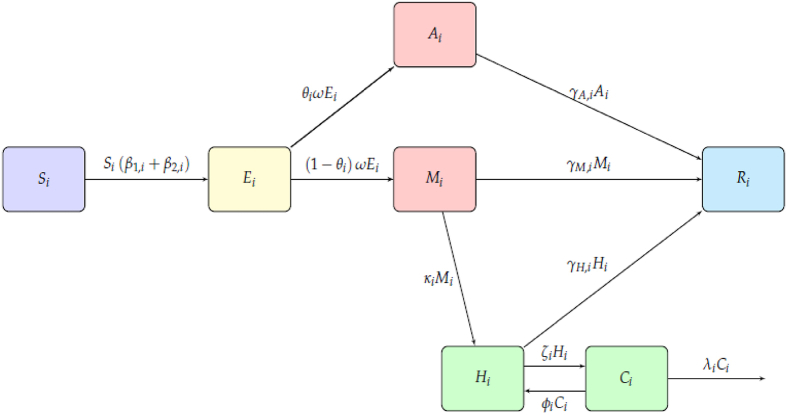
The Kenya population is split into the four broad age groups (KNBS, 2019): those below 15 years, 15–29 years, 30–59 years, and above 59 years. These are denoted by subscript respectively. Each population of age group is classified as either susceptible , exposed , asymptomatic , mild , severe , critical or recovered . The sum of the compartments gives the size of the population in age group .
| (1) |
The exposed compartment represents the individuals infected with coronavirus but are not yet infectious, since the virus is in incubation stage. The asymptomatic compartment has those individuals who are infectious, but do not exhibit the disease symptoms. The mild compartment has infectious individuals who exhibit symptoms of COVID-19, but their condition does not require hospitalization. The severe compartment has infected individuals who need to be hospitalized so as to manage their condition better. Finally, the critical compartment contains infected individuals whose situation is much worse as compared to a severe case; in that they are required to be in intensive care unit. The susceptible individuals are exposed/infected through contact with infectious individuals from any of the age-groups. After the disease incubation period, exposed individuals progress into either the asymptomatic or mild compartment. Infectious individuals who are asymptomatic, are assumed to recover over time whereas the mild cases either recover or progress to the severe compartment. Depending on the disease severity, the individuals in either recover or become critically ill. These critical cases, now in either die or their condition improves to a severe case, no longer requiring ventilation.
The dynamics of the epidemic in our age-structured model is governed by the flow diagram in Fig. 1. The flow diagram yields the following model equations:
Fig. 1.
| (2) |
Description of the age-dependent model parameters are presented in Table 1.
Table 1.
Description of model parameters and their values. The age-specific parameter values are determined based on the references provided against the values.
| Model Parameter Name | Symbol | 0–15 years | 15–29 years | 30–59 years | 59+ years | Reference |
|---|---|---|---|---|---|---|
| Proportion of Asymptomatic | 0.95 | 0.90 | 0.85 | 0.8 | MoH-Kenya (2020) | |
| Proportion of Mild progressing to Severe | 0.03 | 0.06 | 0.09 | 0.12 | MoH-Kenya (2020) | |
| Basic Reproduction Number | 2.5 | 2.5 | 2.5 | 2.5 | Ferguson et al. (2020) | |
| Proportion of Severe progressing to Critical | 0.1 | 0.13 | 0.16 | 0.19 | MoH-Kenya (2020) | |
| Proportion of Critical progressing to Severe | 0.35 | 0.25 | 0.15 | 0.05 | MoH-Kenya (2020) | |
| Reciprocal of the average incubation period | 0.2 | 0.2 | 0.2 | 0.2 | Brand et al. (2020) | |
| Recovery proportion of Asymptomatic | 1 | 1 | 1 | 1 | Assumed | |
| Recovery proportion of Severe | 0.9 | 0.87 | 0.84 | 0.81 | MoH-Kenya (2020) | |
| Recovery proportion of Mild | 0.97 | 0.94 | 0.91 | 0.88 | Assumed | |
| Proportion of fatalities of Critical | 0.65 | 0.75 | 0.85 | 0.95 | van Zandvoort et al. (2020) |
Human-human transmission of coronavirus depends on whom one is in contact with and where. The place of contact could be at home, school, work, or within the community e.g. markets, restaurants etc. Therefore, we assume the susceptible individuals will acquire the virus when they come into contact with an infectious individual, and express the rate of infections and as follows:
| (3) |
| (4) |
For . denotes contact matrices and describe the interactions between the considered age-group with other age-groups . The constants and represent the likelihood of infection upon contact, and based on the basic reproduction number for COVID-19. The parameter denotes the proportion of mild (symptomatic) infectives who self-isolate to minimize their contacts, which is a control measure encouraged by the health experts during the coronavirus pandemic.
Specification of the contact matrix
Contact matrix comprises of contacts at home , workplace , school and other contact which is not happening at home, work or in school. Therefore, we express as follows:
| (5) |
where for instance the home contact matrix for is expressed as follows:
| (6) |
such that the matrix elements range between and ; with value implying no contact and value implying maximum contact.
During the coronavirus epidemic the contact patterns are definitely not the same as compared to the no epidemic times (Prem et al., 2020).
Implementation of social distancing strategies
The mixing of different age-group populations has been incorporated in our model equations through contact matrices, which are used in (4). The goal of social distancing measures is to reduce individuals’ contacts in schools, workplaces, and the general community. These measures are imposed at different times and remain in place for a given duration. In order to implement the control measures adequately by specifying when the measure was started and for how long it will be in place, as well as its effectiveness in reducing contacts, we introduce the following time-dependent control, a similar approach is found in Singh & Adhikari (2020):
| (7) |
where and are respectively the day of imposing and lifting the control measure. is a shape parameter whereas the constant is chosen such that the desired reduction in contact is achieved. When it implies zero contacts, as is the case with closure of schools, and when it means no mitigation measure is in place. We apply this function to the non-household contact matrices as follows:
| (8) |
where the constant captures the fact that in the absence of “stay at home” measures, adults and school-going children will spend less time at home, hence less interactions in homes. In this study, we assume for the unmitigated scenario so as to reflect the less interactions at home and let for restricted movement, in which people are advised to stay at home.
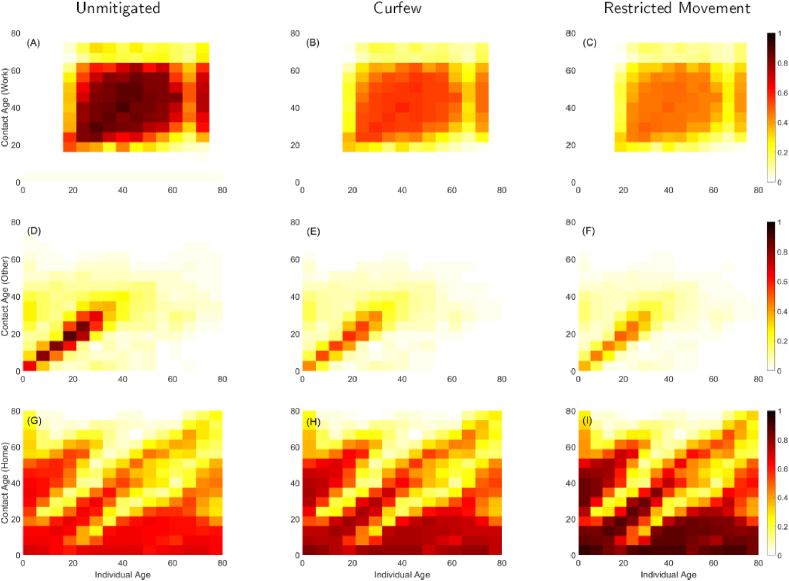
Using (8) in (4) enables us to implement the interventions of school closure, dusk-to-dawn curfew, and movement restriction independently and at the precise time they were instituted. The dusk-to-dawn curfew is whereby the Kenyan government imposed a national wide curfew requiring the citizens to be at home by 7:00 p.m. and should only leave their homes after 5:00 a.m. The term movement restriction implies the partial lock down of travel in/out of Nairobi, Mombasa, Kilifi and Kwale counties that the government imposed on 7th April 2020. Closure of schools yields a 100% reduction in the school contacts, as such will be a matrix of zeros since . We assume that imposing a dusk-to-dawn curfew and restricting movement in and out of hotspots reduces the social mixing in workplaces and in other places (besides home, school, and work) by 35% and 45% respectively. Then we choose such that for the curfew, and for the restricted movement. Using these minimum values to scale down the non-household contact matrices, we obtain the contact patterns depicted in Fig. 2. The actual contact matrices for Kenya were unavailable to the authors, so we produced synthetic contact matrices guided by Prem et al., (2017) and Prem et al., (2020) by approximating the mean number of contact per day from the matrices in Prem et al., (2017), normalizing and adjusting accordingly to best reflect the Kenyan situation. Panels (A), (B), and (C) depicts the contacts at workplaces between working age groups. Panel (B) show a 35% reduction in contacts at work due to the time constraints brought about by the dusk-to-dawn curfew, in which the working hours are reduced to allow individuals get home before dusk.
Fig. 2.
Effect of social distancing strategies on synthetic contact matrices for Kenya population. In the unmitigated scenario, there will be maximum contacts in workplaces and other locations (excluding home, schools and workplace). This results to less contacts at home. The dusk-to-dawn curfew results to a 35% reduction in contacts at workplaces and other locations, but assumed to increase the home contacts. The movement restriction yields a 45% reduction in contacts at workplaces and other locations, but presumed to increase the home contacts by 25%.
When the movement restriction is instituted for non-essential services, whereby people are not allowed to travel in and out of certain regions, we see much less contacts at work in panel (C). Panels (D), (E), and (F) show contacts which are dominant along the diagonal and in age groups less than 50 years. These contacts are happening in places that are not work, school or home. Therefore, they constitute contacts in marketplaces, entertainment places, or other social gatherings such as weddings. Hence the mixing is highly assortative and is likely to bring into contact individuals of same age groups but from distant regions. Therefore, it is imperative to control interactions in this category of contacts, otherwise the epidemic would spread very fast in the communities. As shown in panels (E) and (F), the social distancing measures imposed on through (7) are effective in minimizing these contacts by 35% and 45% respectively. In Africa, majority of the population is generally less than 35 years, and often in contact with children and their (grand)parents as indicated by the main diagonal and off-diagonals in panels (G), (H), and (I). Noting that ministry of health is advising people to stay at home, we postulate that imposing the curfew and movement restriction increases home contacts by 12.5% and 25% respectively, as shown in panels (H) and (I).
Simulation set-up
To show the impact of the highlighted measures in Kenya, we present results for daily and cumulative infections, severe and critical cases, deaths, as well as peak demand for hospital and ICU beds. The simulation was done for a one year starting from 13th March 2020, but we present results for up to December 2020 since the evolution of the epidemic after this period is subject to uncertainties. To initialize the simulation, we assumed , , , , and while all other compartment populations were taken as zero, but . The populations , , , and are respectively obtained as , , , and of , Kenya’s total population. The parameter values used are presented in Table 1. For the unmitigated scenario we assumed , which is within the range in the study (Brand et al., 2020), of COVID-19 in Kenya. The transmissions of infection were obtained from (3), (4), where the contact matrices are implemented through (8) and , . The basic reproduction number for asymptomatics is determined as that of mild individuals as . The time lag (in days) before the instituted social measure took effect was assumed to be days, and added to value. The schools were closed in Kenya only three days after the first confirmed case of COVID-19 i.e. on 16th March 2020. Then on 27 March 2020 the government imposed a dusk-to-dawn curfew, and on 7th April 2020 travel was restricted in/out of Nairobi, Mombasa, Kilifi and Kwale counties (MoH-Kenya, 2020). These dates informed the start date for the three interventions, such that days for the curfew and days for the restricted movement, with the time lag of days for a curfew and days for restricted movement. We assumed the infectiousness of asymptomatic individuals to be 33% while the symptomatic individuals to be 67%. Finally, we assume that 30% of confirmed symptomatic individuals will self-isolate (van Zandvoort et al., 2020) to reduce their contact with susceptible population i.e. . This control measure is uniform across all the age-groups and assumed part of Kenya’s mitigation efforts alongside the school closure, curfew and travel restrictions.
Results and discussions
Simulation results of effects of social distancing measures
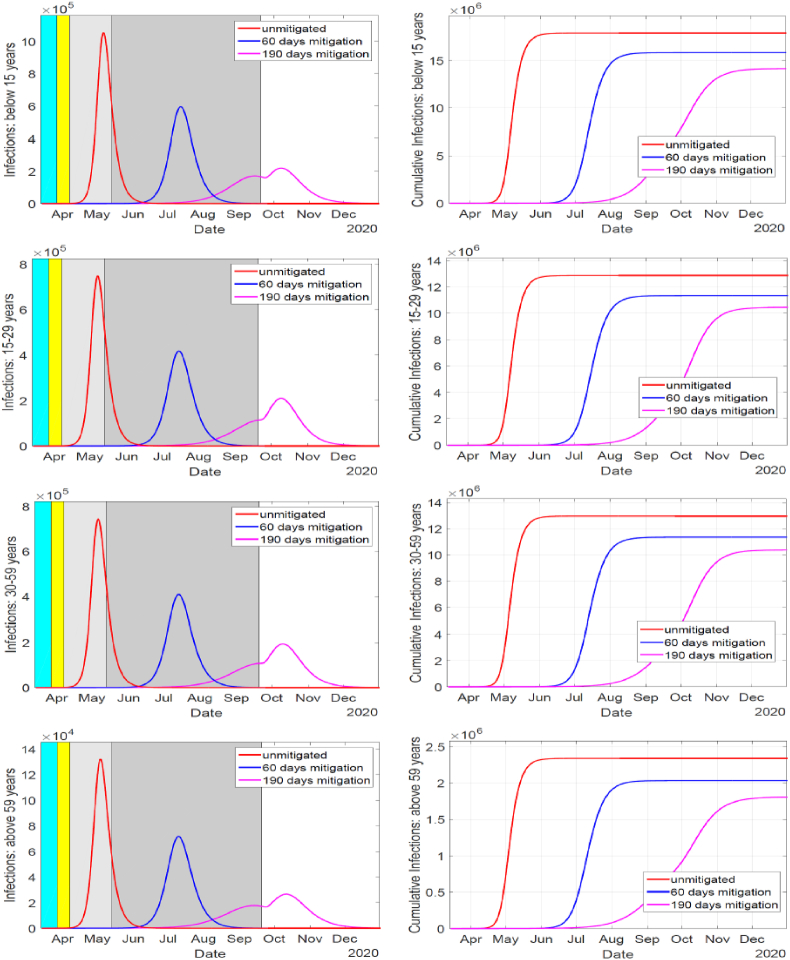
The simulation results are depicted in Fig. 3 and Table 2. In Fig. 3, the duration of school closure is indicated by cyan shaded region and is overlapped by the duration of implementing the dusk-to-dawn curfew indicated by yellow shaded region. The gray shaded region indicate duration of implementing travel restriction across counties. The interventions begin at different days but they all end at the same day, as shown by the light-gray region for the 60-days mitigation and darker-gray for the 190-day mitigation. The social distancing measure lasting for 60 days resulted to a delay of the epidemic peak for about 2 months compared to the unmitigated situation which peaked within 52–55 days. The 45% reduction in contacts for 60 days resulted to between 11.5 and 13% reduction of cumulative infections. When the social distancing measures were in place for 190 days the epidemic peak was delayed for about 5 months compared to the unmitigated scenario. Also, the 45% reduction in contacts for the 190 days resulted to between 18.8 and 22.7% reduction of cumulative infections.
Fig. 3.
Effect of social distancing strategies on mitigating the spread of COVID-19 infections in Kenya. Applying the measures for up to 190 days, yielded a much significant reduction in epidemic as compared to the 60 days. The measures are quite effective in suppressing the disease transmission such that substantial levels of herd-immunity are not realized in the 60-days mitigation period, but in the 190-days mitigation period. This results to high number of infections in the 60-days mitigation once the measures are relaxed, while the herd-immunity realized in the 190-days period resolves the epidemic in the observed rise of infections after the measures are lifted.
Table 2.
Simulation outputs of the epidemic in Kenya in unmitigated and mitigated situations. Age-specific cumulative symptomatic, severe, critical and death cases are displayed. The peak of infections, in days, and peaks of demands for hospital and ICU beds, and deaths are also shown. The table also shows age-specific overall (symptomatic) attack rates, which are calculated as the number of infections (symptomatic cases) over the total population of that age band.
| Age | Output | Unmitigated | 60-days mitigation | 190-days mitigation |
|---|---|---|---|---|
| Below 15 years | Cumulative Symptomatic cases | 923,100 | 817,000 | 729,750 |
| Cumulative Severe cases | 27,749 | 24,559 | 21,937 | |
| Cumulative Critical cases | 2775 | 2456 | 2194 | |
| Cumulative Deaths | 1804 | 1596 | 1426 | |
| Symptomatic Attack Rate | 4.97% | 4.40% | 3.93% | |
| Overall Attack Rate | 96.33% | 85.26% | 76.15% | |
| Infections Peak (days) | 54 | 121 | 209 | |
| Peak of Deaths | 103 | 59 | 22 | |
| Peak of Hospital Beds demand | 14,452 | 13,360 | 12,044 | |
| Peak of ICU Beds demand | 1445 | 1335 | 1204 | |
| 15–29 years | Cumulative Symptomatic cases | 1,368,300 | 1,204,400 | 1,111,300 |
| Cumulative Severe cases | 79,296 | 69,798 | 64,406 | |
| Cumulative Critical cases | 10,308 | 9074 | 8373 | |
| Cumulative Deaths | 7731 | 6805 | 6280 | |
| Symptomatic Attack Rate | 10.27% | 9.04% | 8.34% | |
| Overall Attack Rate | 96.61% | 04% | 78.47% | |
| Infections Peak (days) | 55 | 124 | 211 | |
| Peak of Deaths | 436 | 248 | 125 | |
| Peak of Hospital Beds demand | 39,623 | 33,903 | 32,700 | |
| Peak of ICU Beds demand | 5151 | 4413 | 4252 | |
| 191. 30–59 years | Cumulative Symptomatic cases | 2,117,800 | 1,853,400 | 1,696,100 |
| Cumulative Severe cases | 176,420 | 154,390 | 141,290 | |
| Cumulative Critical cases | 28,227 | 24,702 | 22,607 | |
| Cumulative Deaths | 23,993 | 20,997 | 19,216 | |
| Symptomatic Attack Rate | 15.89% | 13.91% | 12.73% | |
| Overall Attack Rate | 97.23% | 85.09% | 77.87% | |
| Infections Peak (days) | 54 | 123 | 211 | |
| Peak of Deaths | 1341 | 749 | 356 | |
| Peak of Hospital Beds demand | 86,043 | 79,473 | 75,008 | |
| Peak of ICU Beds demand | 13,767 | 12,721 | 12,001 | |
| 241. Above 59 years | Cumulative Symptomatic cases | 519,800 | 452,080 | 401,680 |
| Cumulative Severe cases | 55,039 | 47,869 | 42,531 | |
| Cumulative Critical cases | 10,457 | 9095 | 8081 | |
| Cumulative Deaths | 9935 | 8640 | 7677 | |
| Symptomatic Attack Rate | 21.84% | 18.99% | 16.88% | |
| Overall Attack Rate | 98.19% | 85.40% | 75.88% | |
| Infections Peak (days) | 52 | 119 | 212 | |
| Peak of Deaths | 547 | 302 | 113 | |
| Peak of Hospital Beds demand | 27,591 | 26,593 | 22,546 | |
| Peak of ICU Beds demand | 5242 | 4475 | 4284 |
The peak of infections in the 60-days mitigation is higher and happens about 2 months after the mitigation is relaxed as compared to that of the 190-days mitigation, which happens a month after mitigation is relaxed. This is due to insufficient herd-immunity since the infections are quite suppressed during the 60 days as compared to significant presence of infections for the 190-days mitigation before the measures are relaxed, as shown in Fig. 3. Also shown is a notable rise in infections after the interventions are lifted. However, due to herd-immunity and the depletion of susceptible in the population the rise in infections is not sustained.
Simulated severe, critical cases, hospital demands and deaths
From Table 2 we show the age dependence in the simulated cases and peaks. In all the cases presented in the table, the numbers for those under 15 years are low. This is the age group with a high number of asymptomatic infections, which are more likely to remain undetected. High number of cases are reported for the 15–29 years and 30–59 years age bands since majority of individuals in these age bands have wider interaction spheres (outside of schools and home), and they form a significant percentage of Kenya population. The considered mitigation periods yielded reductions in the key health outputs, although applying the mitigation for entire simulation time of 365 days would have resulted into more significant reductions. However, in reality the population might not withstand the long-term imposing of dusk-to-dawn curfew and travel restrictions. The high numbers of severe and critical cases translate to high demands for hospital and ICU beds, and also deaths. In the 190-day mitigation in Table 2 there is an increase in hospital and ICU beds peak demands which is likely due to the notable rise in infections after the measures have been relaxed, as shown in Fig. 3.
Simulated attack rates
The overall and symptomatic attack rates are presented in Table 2 and they exhibit age-dependency. The younger population have lower attack rates (and lower epidemic peak sizes) as compared to the older population whereby those older than 59 years have the highest overall attack rate, as well as the highest symptomatic attack rate. This result shows the age-dependency of exposed individuals progressing to symptomatic cases. The 190-days mitigation period reduces the attack rates and subsequently flattens the epidemic curve. However, imposing these stringent measures for a prolonged period has adverse effects on the socio-economics of the country. The dependency of the attack rates on age underscores the variability of across the age bands (van Zandvoort et al., 2020).
Conclusions
The dependency of COVID-19 transmissions, severity and deaths on age is crucial to the design of social distancing measures and projection of the expected disease burden in the country. Indeed, the considered interventions do not completely avert the epidemic, but they significantly slow down the transmissions and reduce the infection peak sizes, and deaths. We note that if there is no self-isolation of symptomatic cases, the number of cases and deaths will increase, which will result to the peaks happening earlier in all cases. Prolonged implementation of social distancing measures will definitely resolve the epidemic; however, it will damage the country economically. It is not fully known how the epidemic would spread to various counties in Kenya, and how people in these counties will react to the NPIs. There is need for coordination and frequent exchange of information between modeling and surveillance groups in order to refine predictions of the epidemic trajectory.
Credit authorship contribution statement
Kimathi: Conceptualization of this study, Methodology, Software, Results Discussion. Mwalili: Conceptualization of this study, Data curation, Writing - Original draft preparation. Ojiambo: Conceptualization of this study, Writing - review and editing. Gathungu: Conceptualization of this study, Writing - review and editing.
Declaration of competing interest
No conflict of interest.
Acknowledgements
The authors appreciate the valuable advice offered by Peter Young and Thomas Achia of Centers for Disease Prevention and Control (CDC), Mozambique and Kenya respectively.
Handling editor: Dr. J Wu
Footnotes
Peer review under responsibility of KeAi Communications Co., Ltd.
Contributor Information
Mark Kimathi, Email: mark.kimathi@mksu.ac.ke.
Samuel Mwalili, Email: smusili@jkuat.ac.ke, smwalili@strathmore.edu.
Viona Ojiambo, Email: vojiambo@jkuat.ac.ke.
Duncan Kioi Gathungu, Email: dkioi@jkuat.ac.ke.
References
- Brand S., Aziza R., Kombe I., Agoti C., Hilton J., Rock K. 2020. Forecasting the scale of the COVID-19 epidemic in Kenya. [DOI] [Google Scholar]
- Ferguson N.M., Laydon D., Nedjati-Gilani G., Imai N., Ainslie K., Baguelin M., Bhatia S., Boonyasiri A., Cucunubá Z., Cuomo-Dannenburg G., Dighe A., Dorigatti I., Fu H., Gaythorpe K., Green W., Hamlet A., Hinsley W., Okell L.C., Van Elsland S.…Ghani A.C. 2020. Report 13: Estimating the number of infections and the impact of non-pharmaceutical interventions on COVID-19 in 11 European countries. Imperial College COVID-19 Response Team, March. [DOI] [Google Scholar]
- Knbs . Vol. 2. 2019. Distribution of population by administrative units.http://www.knbs.or.ke (2019 Kenya population and housing census). [Google Scholar]
- Li Q., Guan X., Wu P., Wang X., Zhou L., Tong Y., Ren R., Leung K.S.M., Lau E.H.Y., Wong J.Y., Xing X., Xiang N., Wu Y., Li C., Chen Q., Li D., Liu T., Zhao J., Liu M.…Feng Z. Early transmission dynamics in Wuhan, China, of novel coronavirus–infected pneumonia. New England Journal of Medicine. 2020;382(13):1199–1207. doi: 10.1056/nejmoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MoH-Kenya . Vol. 148. 2020. pp. 1–16. (Covid-19 outbreak in Kenya). July. [Google Scholar]
- Mwalili S., Kimathi M., Ojiambo V., Gathungu D., Mbogo R. SEIR model for COVID-19 dynamics incorporating the environment and social distancing. BMC Research Notes. 2020 doi: 10.1186/s13104-020-05192-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prem K., Cook A.R., Jit M. Projecting social contact matrices in 152 countries using contact surveys and demographic data. PLoS Computational Biology. 2017 doi: 10.1371/journal.pcbi.1005697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prem K., Liu Y., Russell T.W., Kucharski A.J., Eggo R.M., Davies N., Flasche S., Clifford S., Pearson C.A.B., Munday J.D., Abbott S., Gibbs H., Rosello A., Quilty B.J., Jombart T., Sun F., Diamond C., Gimma A., van Zandvoort K.…Klepac P. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: A modelling study. The Lancet Public Health. 2020;5(5):e261–e270. doi: 10.1016/S2468-2667(20)30073-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh R., Adhikari R. 2020. Age-structured impact of social distancing on the COVID-19 epidemic in India; pp. 1–9.http://arxiv.org/abs/2003.12055 [Google Scholar]
- Who . 2020. 20200425-Sitrep-96-Covid-19. 2019(April) [Google Scholar]
- Who . WHO Newsletter; 2020. Statement on the meeting of the international health regulations (2005) emergency committee regarding the outbreak of novel coronavirus (2019-nCoV) [Google Scholar]
- Who . World Health Organization; 2020. WHO siterep 73; p. 2633. 2019(March) [DOI] [Google Scholar]
- Who Africa A second COVID-19 case is confirmed in Africa. 2020. https://www.afro.who.int/news/second-covid-19-case-confirmed-africa 28 February, 2–4.
- van Zandvoort K., Jarvis C.I., Pearson C.A.B., Davies N.G., Ratnayake R., Russell T.W. Response strategies for COVID-19 epidemics in african settings: A mathematical modelling study. BMC Medicine. 2020;18(1):1–19. doi: 10.1186/s12916-020-01789-2. [DOI] [PMC free article] [PubMed] [Google Scholar]