Analyzing population structure for forensic STR markers in next generation sequencing data

Abstract

Match probabilities calculated during the evaluation of DNA evidence profiles rely on appropriate values of the population structure quantity θ. NGS-based methods will enhance forensic identification and with the transformation to such methods comes the need to facilitate NGS-based population genetics analysis. If NGS data are to be used for match probabilities there needs to be a way to accommodate population structure, which requires values for θ for those data. Such estimates have not been available. This study assesses population structure for sequence-based data using a relatively new approach applied to STR data over 27 loci in five different geographic groups. Matching proportions between individuals or groups are used to obtain locus-specific θ estimates as well as estimates per geographic group and a global measure. The results demonstrate similar effects of sequencing data on θ estimates compared to what has been seen for CE-based results.

1. Introduction

Forensic DNA interpretation is currently centered on the analysis of short tandem repeats (STRs), relying on capillary electrophoresis (CE) to gain access to the allele types contained in a DNA sample. To evaluate such DNA evidence profiles, match probabilities can be calculated and these depend on appropriate values of the population structure quantity θ. It is common in forensic DNA evidence evaluations to use values of 1% – 5% [1].

With the introduction of next generation sequencing (NGS) more discrimination is provided through the ability of this technique to reveal variation within the STR. STR analysis has been well established in the forensic community so backward compatibility with CE-based STR profiles is needed to allow the use of existing DNA databases [2]. As long as this is the case, it is expected that NGS methods will continue to be implemented, stressing the need to facilitate NGS-based population genetics analysis.

In recent years, studies have reported population statistics demonstrating the increase in discrimination power by differentiating the nucleotide sequences of STR alleles with identical size [3, 4, 5]. Such statistics include allele frequencies, observed and expected heterozygosity, and tests for Hardy-Weinberg equilibrium and linkage disequilibrium. Freely accessible tools like STRAF [6] and Arlequin [7] provide a whole range of statistics, including F-statistics [8]. F-statistics, or more specifically values for F_ST, written here as θ, for NGS data, are required if sequence data are to be used for match probabilities. However, as with most published estimates of θ, F-statistics from these tools are produced using the Weir and Cockerham estimator [9] and a less restrictive estimator is recommended nowadays. This updated framework is detailed in Weir and Goudet [10] and applied to CE-based STR data in [1].

The Scientific Working Group on DNA Analysis Methods (SWGDAM) reported in an addendum from April, 2019, that “Currently, guidance does not exist regarding θ values for sequence-based data; therefore the existing NRC II guidance should be followed (NRC II 4.4a, where typically θ = 0.01 for most U.S. groups or 0.03 for some isolated populations).” [11]. This paper addresses this gap.

2. Materials and methods

2.1. Estimation of θ

The parameter θ is needed for the Balding-Nichols [12] expressions for match probabilities. The probability an untyped person has homozygous genotype AA when a different person in the same population has been found to have the same type, for example, is

$$\mathrm{Pr}(AA|AA)=\frac{[3\theta +(1-\theta \left){\pi }_A\right][2\theta +(1-\theta \left){\pi }_A\right]}{(1+\theta )(1+2\theta )}$$ (1)

Here θ is specific to the population to which the two people belong and π_A is the probability an allele is of type A. Equation 1 can be used to assign a probability for an unknown perpetrator having the evidence profile AA after a suspect has been found to have that type.

The motivation for Equation 1 is that alleles within a population may have some dependencies because of shared evolutionary history. These dependencies will be small in populations with large population sizes and long histories, such as an African population, where mutation has had many opportunities to reduce the equality of different alleles. Allelic dependencies will be great in populations with small population sizes and few founders, such as Native American populations, where many alleles have the same ancestral allele type. The dependence of alleles in the same population is described by θ, the probability of two alleles taken randomly from a population are identical by descent (ibd), meaning that they are both copies of the same allele in an ancestral reference population. Larger θ values increase the probability of a person’s genotype once that genotype has already been seen.

There are two problems with implementing Equation 1: neither θ nor π_A is known. It is not generally possible to specify the relevant population for a particular situation, so that population cannot be sampled to directly observe the proportion of pairs of individuals with the same genotype, or estimate matching probabilities from the equation. Instead, use is made of databases representing many populations, generally for a single continental ancestry. A single database by itself, however, does not provide information about the variance in allele frequencies among populations so that it does not indicate how different allele frequencies may be among populations.

The sample frequencies ${\tilde{p}}_A$ for alleles A in a large database are good estimates of the probabilities π_A for the populations represented in the database but there is a variance of ${\tilde{p}}_A$ around π_A. In Appendix A we show that $\text{Var}\left({\tilde{p}}_A\right)={\pi }_A(1-{\pi }_A){\theta }_B$, where θ_B is an average of the probabilities of two alleles, one from each of two populations represented by the database, being ibd. This means that if ${\tilde{p}}_A$ is used instead of π_A in Equation 1, then the expression is estimating something that depends on θ_B. Buckleton et al.[1] offered a work-around to this problem, by introducing the average θ_W of population-specific θ values and using $\beta =({\theta }_W-{\theta }_B)/(1-{\theta }_B)$ instead of θ in Equation 1 when ${\tilde{p}}_A$ is used instead of π_A. The parameter β is the probability of two alleles in one population are ibd, relative to the probability of alleles in different populations are ibd. There is no need to specify the ancestral reference population implicit in the definition of ibd, and there is no requirement that β is positive. It was estimates of β that were given by Buckleton et al. [1], and are given here for NGS data.

Buckleton et al. [1] adopted two sampling frameworks: global and single continental ancestry. In the second case, a set of populations with similar ancestry, such as “European”, was used to estimate θ for that ancestry with the thought that it would provide guidance to a forensic analyst who wished to use allele frequencies from their own European ancestry database to estimate match probabilities with Equation 1. The other framework used data from all available ancestries, and that is the framework we use here as we had limited data within each ancestral group.

A formal justification for the Buckleton et al. [1] procedure for implementing Equation 1 is difficult to give, but a related situation is quite straightforward. The probability two alleles taken randomly from a random-mating population are both of type A is

$$\mathrm{Pr}\left(AA\right)=\theta {\pi }_A+(1-\theta ){\pi }_A^2$$

If this equation is averaged over a set of populations, then θ is replaced by its average, θ_W, over populations and π_A is not changed as this probability is assumed to hold for all the populations. If π_A is replaced by a database frequency ${\tilde{p}}_A$, then an unbiased estimator of the average Pr(AA) is

$$\widehat{\mathrm{Pr}\left(AA\right)}=\beta {\tilde{p}}_A+(1-\beta ){\tilde{p}}_A^2$$

This expression follows from the expresion above for the variance of ${\tilde{p}}_A$ and it applies as an average for any population represented by the database, provided the database is large.

Estimation of β can be based on allele counts from a set of at least two populations, as implied in the discussion of the variation of allele frequencies $\tilde{p}$ about the probabilities π, or it can be based on genotype counts to allow for departures from Hardy-Weinberg equilibrium (HWE) in sample data. For allelic data, the estimates are written as ${\hat{\beta }}_{WT}$ and are functions of sample proportions $\tilde{M}$ of pairs of alleles that match, corresponding to probabilities of identity by descent θ. Starting with allele counts n_iu of allele A_u sampled from population i, the within-population sample matching proportion is ${\tilde{M}}_W^i={\sum }_u{n}_{iu}(n_{iu}-1)/[n_i(n_i-1)]$, where $n_i={\sum }_u{n}_{iu}$. For populations i and i′, the between-population sample matching proportions are ${\tilde{M}}_B^{{ii}^{\prime }}={\sum }_u{n}_{iu}{n}_{i^{\prime }u}/(n_i{n}_{i^{\prime }})$. For sets of r populations, averaging over populations of within-population allele matching proportions gives ${\tilde{M}}^W={\sum }_i{\tilde{M}}_W^i/r$, and the average over pairs of populations of between-population matching proportions ${\tilde{M}}^B={\sum }_{i\ne i\prime }{\tilde{M}}_B^{ii\prime }/[r(r-1)]$.

Population-specific θ measures for allelic data can then be estimated relative to allele matching proportions between populations as ${\hat{\beta }}_{WT}^i=({\tilde{M}}_W^i-{\tilde{M}}^B)/(1-{\tilde{M}}^B)$. An overall estimate for allelic data is obtained as ${\hat{\beta }}_{WT}=({\tilde{M}}^W-{\tilde{M}}^B)/(1-{\tilde{M}}^B)$. These are locus-specific estimates, which are expected to vary among loci. The average β estimates over loci are calculated as the ratio of averages of numerators and denominators rather than the average of ratios, with the former leading to smaller variances. The reader is referred to [1, 10] for a more detailed discussion on this approach. The overall β estimates are used in Equation 1.

Equivalent genotypic expressions define within-population sample matching between individuals j and j′ in population i as ${\tilde{M}}_{jj\prime }^i={\sum }_u{X}_{ju}^i{X}_{j\prime u}^i/4$, where X_ju denotes the dosage, i.e. number of copies, of allele u for individual j. The average between-individual matching in a sample of N_i individuals from population i ${\tilde{M}}_S^i={\sum }_{j\ne j\prime }{\tilde{M}}_{jj\prime }^i/[N_i(N_i-1)]$ can then be averaged over populations to get ${\tilde{M}}^S={\sum }_i{\tilde{M}}_S^i/r$. Similarly, matching between individual j from population i and individual j′ from population i′ ${\tilde{M}}_{jj\prime }^{ii\prime }={\sum }_u{X}_{ju}^i{X}_{j\prime u}^{i\prime }/4$ leads to average between-population sample matching proportions ${\tilde{M}}_B^{ii\prime }={\sum }_{j\ne j\prime }{\tilde{M}}_{jj\prime }^{ii\prime }/(N_i{N}_{i\prime })$. Averaging over pairs of populations yields ${\tilde{M}}^B={\sum }_{i\ne i\prime }{\tilde{M}}_B^{ii\prime }/[r(r-1)]$.

Population-specific θ values for genotypic data are given by ${\hat{\beta }}_{ST}^i=({\tilde{M}}_S^i-{\tilde{M}}^B)/(1-{\tilde{M}}^B)$, with an overall estimate of ${\hat{\beta }}_{ST}=({\tilde{M}}^S-{\tilde{M}}^B)/(1-{\tilde{M}}^B)$ per locus. Taking the ratio of averages of numerator and denominator over these locus-specific estimates again yields an average β estimate. Such genotype-based estimates allow for for departures from HWE in the data, although we note that HWE is assumed in Equation 1.

Software to perform these allele-based estimates is simple to prepare as it requires only the number of copies of each allele in each population. More detail was given by Weir and Goudet [10]. There are some good packages now available, including SNPRelate [13] and hierFstat [14].

2.2. Data

DNA from 350 individuals, over five geographic groups, included in the 1000 Genomes Project Phase 3 (http://www.1000genomes.org) were obtained from the Coriell Institute for Medical Research (Camden, New Jersey, USA) and sequenced using Illumina’s MiSeq FGx™ and ForenSeq™ DNA Signature Prep Kit. Genotype calls were obtained through their Universal Analysis Software (UAS) over 27 autosomal loci for both the length-based (LB) allele callings, equivalent to CE, as well as the sequence-based (SB) allele callings. The geographic groups being distinguished are: African (AFR), admixed American (AMR), East Asian (EAS), European (EUR), and South Asian (SAS) groups.

Out of the 9,450 genotype calls (350 individuals over 27 STR markers) 7,485 are classified as heterozygotes, 1,772 as homozygotes and the remaining types contain either drop-ins or complete locus drop-outs and are excluded from further analysis. The 7,485 heterozygous types can be distinguished further into isoalleles, showing variation only in the STR repeat region, corresponding to homozygous in the CE case, and alleles of different length. In addition, some flanking region variation can be observed as the UAS incorporates a small amount of sequence variation in these regions for a subset of the markers [15].

3. Results

3.1. Sequence variation

Table 1 displays the number of individuals per geographic group and the observed number of unique alleles obtained by length compared to STR sequence after genotype calling. As expected, more variation has been observed for larger sample sizes and sequence-based allele callings as compared to length-based allele callings. Overall, 316 unique length-based alleles have been observed and the amount increases to 593 for sequence-based alleles, indicating differences in allele frequencies over the geographic groups.

Table 1:

Number of individuals per geographic group together with observed number of length-based (LB) alleles and sequence-based (SB) alleles over the set of 27 markers.

		# Alleles
Group	Sample size	LB	SB	Increase
African	88	260	408	57%
American	75	239	337	41%
East Asian	74	234	331	41%
European	58	228	318	40%
South Asian	55	225	317	41%

The first four columns of Table 2 show the number of unique alleles obtained by length compared to STR sequence per locus combined over all individuals, sorted based on the increase in number of alleles. Similarities can be seen between our results and the observations reported by Gettings et al. [3]. An overview of all unique sequences per locus is presented in Supplemental Table 1, together with their corresponding frequencies overall and per geographic group within the data set.

Table 2:

Number of unique alleles obtained by length compared to sequence for N = 350 individuals for 27 autosomal markers, as well as locus-specific global β estimates based on length-based (LB) genotypic data and sequence-based (SB) genotypic data.

	# Alleles			${\hat{\beta }}_{ST}$
Locus	LB	SB	Difference	LB	SB
D21S11	17	65	+48	0.0259	0.0383
D12S391	17	64	+47	0.0074	0.0064
D2S1338	13	50	+37	0.0148	0.0149
vWA	10	30	+20	0.0228	0.0260
D1S1656	18	34	+16	0.0174	0.0146
D3S1358	10	25	+15	0.0081	0.0399
D8S1179	11	25	+14	0.0153	0.0209
D13S317	7	19	+12	0.0404	0.0421
D9S1122	9	19	+10	0.0063	0.0130
D2S441	10	19	+9	0.0426	0.0368
D5S818	8	16	+8	0.0396	0.0250
D18S51	13	20	+7	0.0145	0.0141
FGA	22	28	+6	0.0049	0.0046
D19S433	15	19	+4	0.0091	0.0091
D6S1043	19	23	+4	0.0380	0.0377
PentaE	21	25	+4	0.0207	0.0210
CSF1PO	9	12	+3	0.0016	0.0019
D16S539	9	12	+3	0.0224	0.0213
D4S2408	6	9	+3	0.0787	0.0724
D7S820	9	11	+2	0.0199	0.0195
D10S1248	8	9	+1	0.0131	0.0133
D17S1301	8	9	+1	0.0102	0.0101
D22S1045	9	10	+1	0.0524	0.0515
PentaD	14	15	+1	0.0286	0.0288
TH01	7	8	+1	0.0642	0.0640
D20S482	9	9	0	0.0059	0.0059
TPOX	8	8	0	0.0402	0.0402
All				0.0245	0.0257

3.2. Locus-specific θ

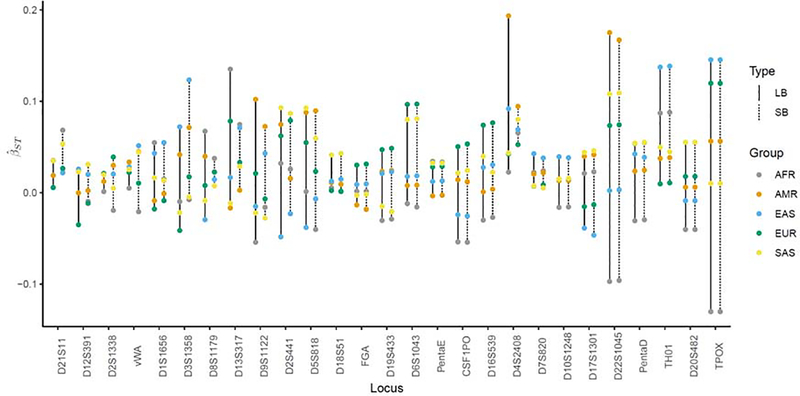
We regard the data we generated from the 1000 Genomes samples as a database. The data are from five groups, the five identified continental ancestry designators. All estimates based on genotypic data are depicted graphically in Figure 1 and locus-specific estimates, obtained as an unweighted average over geographic groups, are displayed in Table 2. It can be seen that there is a considerable variation of estimates over loci and length-based versus sequence-based estimates may increase, decrease, or stay the same. The latter happens when loci show no additional sequence variation, as is the case for locus D20S482 and TPOX.

Figure 1:

β estimates per geographic group (African (AFR), admixed American (AMR), East Asian (EAS), European (EUR), South Asian (SAS)) and locus using length-based (LB) and sequence-based (SB) genotypic data over 27 autosomal STR loci. LB estimates are connected with a solid line, while SB estimates are connected with a dotted line.

Locus D21S11 shows the highest increase in number of alleles, from 17 different LB alleles to 65 different SB alleles, as well as an increase in the β estimate from 0.0259 to 0.0383. This happens since the extra variation leads to relatively less matching between groups as compared to within groups. From a population genetics perspective, this may occur when populations or groups share the same length-based allele, but the underlying nucleotide sequences differ. If no additional sequence variation is observed within a group, within-group matching is higher for sequence-based genotypic data relative to the global group, leading to higher β estimates for such groups.

An increase in the observed number of alleles does not necessarily translate to an increase in the β estimates, as can be seen for locus D1S1656. In this case, the extra variation leads to relatively less matching within a group as compared to between. This may happen in a situation where an allele originally unique to a group shows additional sequence variation. The heterozygosity within the group increases more than the overall heterozygosity, yielding smaller estimates.

3.3. Geographic-group-specific θ

Estimated matching proportions based on length-based genotype matching yield an average within-group matching, averaged over groups and loci, of ${\tilde{M}}^S=0.2165$, while the average between-group matching is ${\tilde{M}}^B=0.1968$, yielding an overall estimate of ${\hat{\beta }}_{ST}=0.0245$.

Group-specific estimates range from 0.0035 for the African group to 0.0347 for the American group (Table 3). An advantage of having population- or group-specific estimates is that the variation among the estimates reflects differences among θ values, which can be regarded as a signature of different evolutionary histories, such as age and population size. Such effects are not possible when using the Weir & Cockerham model, as it is assumed there that the populations have equal evolutionary histories [10].

Table 3:

β estimates per geographic group using length-based (LB) and sequence-based (SB) genotype counts.

	${\hat{\beta }}_{ST}$
Group	LB	SB
African	0.0035	−0.0016
American	0.0347	0.0312
East Asian	0.0239	0.0332
European	0.0302	0.0327
South Asian	0.0302	0.0327
All	0.0245	0.0257

Our length-based results can be compared to those in the worldwide survey by Buckleton et al. [1] and show concordance, for example, in showing the smallest values for Africa as compared to the rest of the world, as expected from our understanding of higher genetic diversity within those older populations pre-dating the migration of modern humans out of Africa. In addition, the largest values are for the American group, and the Asian and European values are lying between the African and American values.

Matching proportions based on sequence-based genotypes show somewhat lower values of ${\tilde{M}}^S$ = 0.1878 and ${\tilde{M}}^B$ = 0.1664 due to the increase in the number of observed types as a result of the additional variation. The global estimate is in this case ${\hat{\beta }}_{ST}$ = 0.0257, which is an increase from the length-based estimate, albeit small. Not all geographic groups show an increase in the estimated values. For the African group, the average within-group matching proportion is now ${\tilde{M}}_S$ = 0.1651. Relative to the between-group matching ${\tilde{M}}^B$ = 0.1664 individuals in the African group are less similar to each other, leading to a negative β for the African group with all geographic groups as reference set. For both sequence-based as well as length-based results, the “θ-correction” has little effect when applied to the African group. The estimate for the admixed American group has decreased as well, while the Asian and European groups all show an increase in the estimate with values now larger than the American geographic group.

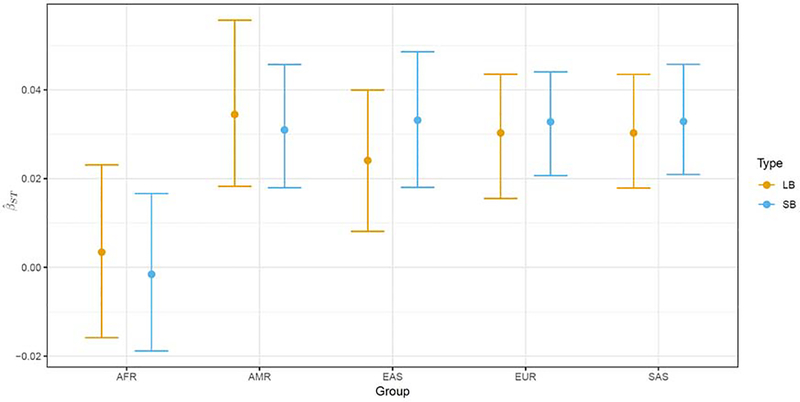
To check the impact of these differences 95% confidence intervals were obtained based on bootstrapping over loci. The Balding-Nichols formulation refers to profile matching caused by evolutionary processes in previous generations. It reflects what Weir [16] referred to as “genetic sampling.” The formulation also has an implicit recognition of variation of allele frequencies among replicates of these evolutionary histories: the only information generally available about these replicates is provided by multiple loci typed on the same individuals and this led Weir [16] to explain why properties of β estimates are obtained by bootstrapping over loci, rather than over individuals. This latter procedure would accommodate the “statistical sampling” of drawing individuals from the same population, but would provide no information about genetic sampling variation. Figure 2 demonstrates a great deal of overlap for all intervals and this also holds for the global β estimates (not shown). Overall, comparing the interval for length-based results (0.0179, 0.0315) with the sequence-based results (0.0191, 0.0329) suggests that the usual recommended value of around 3% is appropriate for DNA evaluations based on NGS data. A value of 5% is expected to yield conservative results for each system.

Figure 2:

Group-specific β estimates for length-based (LB) and sequence-based (SB) genotypic data together with 95% confidence intervals obtained by bootstrapping over loci.

4. Discussion and conclusion

We presented here an analysis of forensic STR markers to give guidance on θ values for sequence-based data. Since we have access to genotype data, all results have been obtained using genotypic matching proportions. Allelic data may be used if there is Hardy-Weinberg equilibrium within the samples from populations, and results when applying the framework to this type of data (not shown) are almost indistinguishable from the results as presented here.

Although locus-specific estimates are interesting, we recommend averaging θ estimates over loci to reduce the bias and variance of ratio estimators. The values using all loci as shown in the last row of Table 2 should be used as a global estimate for θ in match probabilities. If no assumption is made on the ancestry of the true source of the DNA evidence, results may be reported for each of the different groups using group-specific estimates as displayed in Table 3. It is important to note that these estimates per geographic group do not reflect substructure within those groups and they are intended to be used in conjunction with global allele frequencies.

NGS-based methods will enhance forensic identification and since such data are subject to population structure, the impact on θ, a measure integral to DNA evidence evaluations, should be checked. This study gives guidance as to what values are appropriate for the population structure quantity used in match probability calculations for sequence-based data. If match probabilities are wanted for use with a single-ancestry database, a study parallel to this one would be needed with data from several populations within that ancestry group.

Although the data used in this study are limited as compared to other studies and an analysis has been performed only on a geographic basis, results for length-based data show patterns concordant with CE-based results. Availability of sequencing data is expected to increase in the upcoming years, so it is recommended to replicate this study more thoroughly. As NGS-based data better reflect the true variation among individuals, population structure estimates based on such data will be more accurate. So far, our results show similar effects of sequencing data on θ estimates as what has been seen for CE-based data.

Highlights.

• Population structure is assessed for sequence data.

• Results demonstrate similar effects of sequencing data on θ estimates as what has been seen for CE-based results.

• θ values of around 3% are appropriate for DNA evaluations based on NGS data.

Appendix A

If a database has n_i alleles from population i and if x_ijA is 1 when allele j from population i is of type A, and is 0 otherwise:

$$\begin{gathered} {\tilde{p}}_{iA}=\frac{1}{n_i}\sum _{j=1}^{n_i}{x}_{ijA} \\ {\tilde{p}}_{iA}^2=\frac{1}{n_i^2}(\sum _{j=1}^{n_i}{x}_{ijA}^2+\underset{j\ne j\prime }{\sum _{j=1}^{n_i}\sum _{j\prime =1}^{n_i}}{x}_{ijA}{x}_{ij\prime A}) \end{gathered}$$

If each population i is in Hardy-Weinberg equilibrium, then the expectation of ${\tilde{p}}_{iA}^2$ from Weir and Goudet [10] is

$$\begin{gathered} \mathcal{E}({\tilde{p}}_{iA}^2)=\frac{1}{n_i^2}(\sum _{j=1}^{n_i}{\pi }_A+\underset{j\ne j\prime }{\sum _{j=1}^{n_i}\sum _{j\prime =1}^{n_i}}[{\pi }_A^2+{\pi }_A(1-{\pi }_A){\theta }_i]) \\ ={\pi }_A^2+{\pi }_A(1-{\pi }_A)({\theta }_i+\frac{1-{\theta }_i}{n_i}) \\ \mathrm{Var}({\tilde{p}}_{iA})={\pi }_A(1-{\pi }_A)({\theta }_i+\frac{1-{\theta }_i}{n_i}) \end{gathered}$$

where θ_i applies to any pair of distinct alleles from population i.

For allele frequencies from two populations:

$$\begin{gathered} {\tilde{p}}_{iA}{\tilde{p}}_{i\prime A}=\left(\frac{1}{n_i}\sum _{j=1}^{n_i}{x}_{ijA}\right)\left(\frac{1}{n_{i\prime }}\sum _{j\prime =1}^{n_{i\prime }}{x}_{i\prime j\prime A}\right) \\ \mathcal{E}({\tilde{p}}_{iA}{\tilde{p}}_{i\prime A})=\frac{1}{n_i{n}_{i\prime }}\sum _{j=1}^{n_i}\sum _{j\prime =1}^{n_{i\prime }}[{\pi }_A^2+{\pi }_A(1-{\pi }_A){\theta }_{ii\prime }] \\ ={\pi }_A^2+{\pi }_A(1-{\pi }_A){\theta }_{ii\prime } \\ \mathrm{Cov}({\tilde{p}}_{iA},{\tilde{p}}_{i\prime A})={\pi }_A(1-{\pi }_A){\theta }_{ii\prime } \end{gathered}$$

where ${\theta }_{ii\prime }$ applies to any pair of distinct alleles, one from population i and one from population $i\prime$.

To combine information over the r populations contributing to a database, for sample allele frequencies and for ibd measures, population i receives a weight w_i:

$$\begin{gathered} {\tilde{p}}_A=\frac{1}{\left(\sum _{i=1}^r{w}_i\right)}\sum _{i=1}^r{w}_i{\tilde{p}}_i\mathrm{overall}\mathrm{average} \\ {\theta }_W=\frac{1}{\left(\sum _{i=1}^r{w}_i\right)}\sum _{i=1}^r{w}_i{\theta }_i\mathrm{within}\mathrm{population}\mathrm{average} \\ {\theta }_B=\frac{1}{\left({\sum }_{i=1}^r{\sum }_{i^{\prime }=1,i\ne i^{\prime }}^r{w}_i{w}_{i\prime }\right)}\underset{i\ne i\prime }{\sum _{i=1}^r\sum _{i\prime =1}^r}{w}_i{w}_{i\prime }{\theta }_{ii\prime }\text{between}\text{population}\text{average} \end{gathered}$$

An “unweighted” analysis sets w_i = 1 and it allows each population to contribute equally to ibd averages as may be important when the θ_i are different. A “weighted” analysis sets w_i = n_i so that populations with more alleles in the database contribute more to average ibd measures. This is the weighting scheme used when the database allele frequencies are simply the proportions of each allele in the whole database but frequencies for the contributing populations are not available.

The variance of the sample allele frequencies, for all weighting schemes, is

$$\begin{gathered} \mathrm{Var}({\tilde{p}}_A)=\frac{1}{{\left({\sum }_{i=1}^r{w}_i\right)}^2}\left(\sum _{i=1}^r{w}_i^2\mathrm{Var}({\tilde{p}}_{iA})+\underset{i\ne i\prime }{\sum _{i=1}^r\sum _{i=1}^r}{w}_i{w}_{i\prime }\mathrm{Cov}({\tilde{p}}_{iA},{\tilde{p}}_{i\prime A})\right) \\ ={\pi }_A(1-{\pi }_A)({\theta }_B+\frac{{\sum }_{i=1}^r{w}_i^2({\theta }_i-{\theta }_B)}{{\left({\sum }_{i=1}^r{w}_i\right)}^2}+\frac{{\sum }_{i=1}^r\frac{w_i^2}{n_i}(1-{\theta }_i)}{\left({\sum }_{i=1}^r{w}_i\right)}) \end{gathered}$$

The weighted and unweighted weighting schemes are the same when each population has the same number n of alleles in the database:

$$\mathrm{Var}({\tilde{p}}_A)={\pi }_A(1-{\pi }_A)({\theta }_B+\frac{{\theta }_W-{\theta }_B}{r}+\frac{1-{\theta }_W}{nr})$$

but for both schemes, when the database is large and it contains alleles from many populations, $\text{Var}\left({\tilde{p}}_A\right)\approx {\pi }_A(1-{\pi }_A){\theta }_B$.