Improved phase-field models of melting and dissolution in multi-component flows

Abstract

We develop and analyse the first second-order phase-field model to combine melting and dissolution in multi-component flows. This provides a simple and accurate way to simulate challenging phase-change problems in existing codes. Phase-field models simplify computation by describing separate regions using a smoothed phase field. The phase field eliminates the need for complicated discretizations that track the moving phase boundary. However, standard phase-field models are only first-order accurate. They often incur an error proportional to the thickness of the diffuse interface. We eliminate this dominant error by developing a general framework for asymptotic analysis of diffuse-interface methods in arbitrary geometries. With this framework, we can consistently unify previous second-order phase-field models of melting and dissolution and the volume-penalty method for fluid–solid interaction. We finally validate second-order convergence of our model in two comprehensive benchmark problems using the open-source spectral code Dedalus.

1. Introduction

Many scientific and industrial questions involve fluid flows coupled with phase changes; including sea-ice formation [1], semiconductor crystal manufacture [2], binary alloy solidification [3] and geophysical mantle dynamics [4]. Multi-phase interaction combines the challenges of nonlinear multi-component convection [5] and evolution of phase boundaries [6], creating entirely new effects. Quantifying this complexity demands appropriate mathematical tools.

Moving boundary problems are the standard method to model phase change phenomena. Separate partial differential equations (PDEs) exist in the liquid and solid regions and moving boundary conditions are applied at the interface (figure 1a). A dynamically shifting interface means that the boundary conditions form an essential (often nonlinear) part of the solution [7]. Moving boundaries present many challenges, complicating numerical algorithms [8] and mathematical proofs [9].

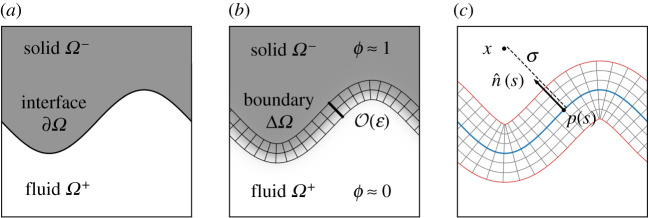
Figure 1.

(a) A moving boundary formulation in which the domain is partitioned into the fluid Ω⁺, solid Ω⁻ and interface ∂Ω. (b) A phase-field approximation, where the phase ϕ smoothly varies between fluid and solid. The ϕ = 1/2 contour approximates the true interface. We illustrate the asymptotic fluid Ω⁺, solid Ω⁻ and size $\mathcal{O}(\epsilon )$ boundary ΔΩ regions of our analysis. (c) The signed-distance coordinate system used to analyse the boundary region ΔΩ. Points on the interface p(s) (blue) are parameterized by arbitrary surface coordinates s. A point off the boundary x can be reached by moving a distance σ in the normal direction $\hat{n}(s)$ from the closest point on the manifold p(s). Coordinate singularities (the corners of the outermost red curves) will occur, but the coordinate system remains well behaved in the interface region (b). The figure is in two dimensions for clarity, though the analysis of §3 is done in three dimensions. (Online version in colour.)

As a possible remedy, it is useful to recall that boundary conditions are a mathematical abstraction; they result from limiting cases of rapid transitions in material properties. There is a long history of reinterpreting discontinuous boundary conditions as smoothed phenomena. Where Gibbs treated capillarity with infinitesimal surfaces [10], van der Waals understood the importance of smoothness at phase boundaries [11]. Where Stefan treated solid–liquid phase boundaries as discontinuous [12], Cahn and Hilliard modelled phase separation as smoothed [3]. Readopting a physics-based viewpoint of boundary conditions allows new possible techniques for addressing complex multi-phase problems. As well as providing a firmer mathematical and physical foundation, smoothed models also simplify numerical implementations by removing the need to track the infinitesimal boundary.

This paper focuses on phase-field models, one of the foremost examples of this smoothed approach. Phase-field models represent distinct phases using a single smoothed phase field ϕ, illustrated in figure 1b [13,14]. The evolution of the phases is then determined by a single set of equations that apply over the entire domain. Many other methods also model phase changes, such as enthalpy methods [15,16], level set methods [17,18], diffuse-domain approaches [19,20] or some immersed-boundary methods [21]. Yet phase-field models stand out for combining several key benefits:

• —They are physically motivated, introduced by Fix [22] and Langer [23] to model free energy near phase boundaries (following from Hohenburg and Halperin’s model C [24]).
• —They generalize canonical models of phase separation, reducing to Allen–Cahn and Hele-Shaw flow (among others) in various asymptotic limits [25,26].
• —They are easily extensible to more general systems, including two-component alloys [27–30], convection [31,32] or multi-phase flows [20,33].
• —They can be made thermodynamically consistent [34–38].
• —They are mathematically rigorous, with well-posedness and convergence results [39,40].
• —They are simple to simulate as they avoid explicit tracking of the interface [22,41–49].

We emphasize this last point. The simulation of moving boundary problems requires specialized algorithms designed to track and apply boundary conditions at the interface. These algorithms can be difficult or impossible to implement in existing codes. For example, spectral methods are popular for their efficiency, but cannot easily handle non-trivial geometries or topologies. Phase-field models (and other diffuse-interface methods) alleviate these difficulties by removing boundary conditions from the problem formulation. By replacing boundary conditions with simple source terms, they can be implemented in general codes for little effort. More general effects can be modelled by changing source terms, as opposed to developing and integrating new algorithms into the codebase. Phase-field models extend the range of phenomena that existing codes can simulate, and accelerate the development of codes to study new scientific problems.

However, phase-field models possess one important drawback for simulation: they must resolve the diffuse interface. For small-scale simulations, this is feasible. But there is a vast disparity between the microscopic scale of the smoothed interface and the macroscopic scale of interest in most problems. This disparity is what makes discontinuous boundary conditions appropriate models in most circumstances. Throughout this paper, we denote this ratio, also known as the Cahn number [50,51], by ε

$$\epsilon =\text{Cahn number}=\frac{\text{microscopic interface width}}{\text{bulk system size}}.$$ 1.1

Feasible numerical values of ε are orders of magnitude larger than reality. Straightforward analysis implies a commensurate $\mathcal{O}(\epsilon )$ error with respect to the limiting boundary conditions.

The only way to perform accurate phase-field simulations with achievable values of ε is to accelerate the convergence of the model itself. This can be done through second-order asymptotic analysis in the limit ε → 0. While the first order is sufficient to determine the limiting behaviour, it is the second order that reveals the dominant error of the model. It is then possible to find optimal prescriptions that cancel the dominant error and boost convergence from $\mathcal{O}(\epsilon )$ to $\mathcal{O}({\epsilon }^2)$.

This strategy leads to various ‘quantitative’ (i.e. second order) phase-field models, beginning with a correction for arbitrary interface kinetics in pure materials [52,53], and since extended to unequal diffusivities [36,54], multiple components [29], and the combination thereof [55,56]. An introduction to this asymptotic procedure can be found in [57]. Despite much success, progress is difficult. Second-order asymptotic analysis has not yet ascertained a quantitative phase-field model of multi-component convection.¹

This paper presents the first second-order phase-field model of buoyancy-forced convecting binary mixtures. The model, given in §2, builds on first-order models of multi-component convection [31], second-order models of pure melts [59], the diffuse-domain method for Robin boundary conditions [60], and the smooth volume-penalty method for no-slip boundary conditions [61]. We verify second-order convergence in §3 by developing a straightforward asymptotic procedure suitable for general equations and geometries in three dimensions. This procedure allows us to consistently analyse and unify previous second-order phase-field and diffuse-interface methods. We also implement this procedure in the symbolic computing language Mathematica. For brevity, we assume somewhat simplified thermodynamical properties in our model, such as uniform temperature diffusivity, negligible solute within the solid, and Boussinesq buoyancy. Each assumption could be relaxed and analysed using the framework of §3. We finally validate the improved convergence in two comprehensive benchmark problems implemented in the Dedalus numerical code [62] in §4.

2. Models of melting in binary mixtures

(a). Conventional moving boundary formulation

Melting in binary mixtures, such as ice in sea water, is often modelled as a moving boundary problem. We partition the domain into fluid Ω⁺ and solid Ω⁻ regions, pose separate PDEs on each subdomain, and apply boundary conditions at the evolving interface ∂Ω (as in figure 1a).

In the fluid, the temperature T⁺ and dissolved solute concentration C satisfy advection–diffusion equations, and the fluid velocity u and pressure p satisfy incompressible Navier–Stokes equations with Boussinesq buoyancy forcing $g\rho (T^{+},C)\hspace{0.17em}\hat{z}$,

$$\begin{array}{rl}{\mathrm{\partial }}_t{T}^{+}+u\cdot \mathrm{\nabla }{T}^{+}-\kappa {\mathrm{\nabla }}^2{T}^{+}& =0,\\ {\mathrm{\partial }}_{t}C+u\cdot \mathrm{\nabla }C-\mu {\mathrm{\nabla }}^{2}C& =0,\\ {\mathrm{\partial }}_{t}u+u\cdot \mathrm{\nabla }u-\nu {\mathrm{\nabla }}^{2}u+\mathrm{\nabla }p+\frac{g\rho (T^{+},C)}{{\rho }_0}\hat{z}& =0,\\ \mathrm{\nabla }\cdot u& =0,\text{in}\hspace{0.17em}{\mathit{\Omega }}^{+},\end{array}$$ 2.1

where κ, μ and ν are the thermal, solutal and momentum diffusivity (each assumed constant), and g, ρ and ρ₀ are the gravitational acceleration, the density of the fluid and a reference density. In the solid only the temperature T⁻ is defined, which follows a diffusive equation,

$${\mathrm{\partial }}_t{T}^{-}-\kappa {\mathrm{\nabla }}^2{T}^{-}=0,\text{in}\hspace{0.17em}{\mathit{\Omega }}^{-}.$$ 2.2

We require several boundary conditions at the moving interface [7]. The Gibbs–Thompson relation relates departure of thermosolutal equilibrium (T + mC, where m is the liquidus slope) to a mean-curvature $\overline{K}$ dependent surface energy, and kinetic undercooling proportional to the interfacial normal velocity v. The Stefan condition expresses heat conservation, equating latent heat L release with a discontinuity in temperature flux. The Robin concentration condition ensures total solute conservation. Zero velocity boundary conditions maintain mass conservation,

$$T+mC-\gamma \overline{K}+\alpha v=0,{[\kappa \hat{n}\cdot \mathrm{\nabla }T]}_{-}^{+}+Lv=0,\mu \hat{n}\cdot \mathrm{\nabla }{C}^{+}+C^{+}v=0,u=0.$$ 2.3

This model involves several idealizations, namely Boussinesq buoyancy forcing, constant diffusivities and densities that are phase, temperature, and concentration invariant, and a linear liquidus relation. We can include more general thermodynamic properties into our framework, but we continue with the current model as it captures many aspects of melting and dissolution in multi-component flows. Kinetic undercooling is only relevant for rapidly solidifying supercooled liquids so we set α = 0. Note that the neglect of density change during melting means the fluid velocity is equal to zero at the moving interface.

(b). Phase-field model

Phase-field models are an alternative approach that is physically motivated and simple to simulate. They represent distinct phases with a smoothed phase field ϕ. This field obeys an Allen–Cahn type equation which forces the phase to ϕ ≈ 1 in the solid and ϕ ≈ 0 in the fluid [31]. The interface is represented implicitly by the level set ϕ = 1/2. The new equations are

$$\begin{array}{rl}{\mathrm{\partial }}_{t}T+u\cdot \mathrm{\nabla }T-\kappa {\mathrm{\nabla }}^{2}T& =L{\mathrm{\partial }}_t\varphi ,\\ {\mathrm{\partial }}_{t}C+u\cdot \mathrm{\nabla }C-\mu {\mathrm{\nabla }}^{2}C& =\frac{C{\mathrm{\partial }}_t\varphi -\mu \mathrm{\nabla }\varphi \cdot \mathrm{\nabla }C}{1-\varphi +\delta },\\ {\mathrm{\partial }}_{t}u+u\cdot \mathrm{\nabla }u-\nu {\mathrm{\nabla }}^{2}u+\mathrm{\nabla }p+\frac{g\rho (T,C)}{{\rho }_0}\hat{z}& =-\frac{\nu }{{(\beta \epsilon )}^2}\varphi \hspace{0.17em}u,\\ \mathrm{\nabla }\cdot u& =0,\\ \epsilon \frac{5}{6}\frac{L}{\kappa }{\mathrm{\partial }}_t\varphi -\gamma {\mathrm{\nabla }}^2\varphi & =-\frac{1}{{\epsilon }^2}\varphi (1-\varphi )(\gamma (1-2\varphi )+\epsilon (T+mC)).\end{array}$$ 2.4

The new source terms of equation (2.4) can be understood heuristically. At leading order, the phase-field equation develops a tanh-like profile around the interface with thickness ε. Beyond this distance, the phase ϕ tends to its limiting values of zero in the fluid and one in the solid. In the fluid, equation (2.4) reproduces equation (2.1). In the solid, the advective and diffusive solute flux tend to zero (with δ ≪ 1 regularizing the concentration equation for numerical stability), and the velocity is damped by Darcy drag terms for porous media. At next order, thermosolutal forcing perturbs the interface to generate latent heat. For a clear derivation of a similar first-order model, see [31].

Our goal is to surpass this approximate understanding and demonstrate improved convergence of this optimized phase-field model to the original moving boundary formulation. We achieve this with an asymptotic analysis of equation (2.4) as the interface length-scale ε tends to zero. Some approaches focus on a variational derivation of phase-field equations [34–38]; however, we follow the view of [31], which states ‘phase-field equations are only quantitatively meaningful in the sharp-interface limit where they can be ultimately related to experiment’. While variational derivations are useful, it is asymptotic analysis, tested with numerical experiments, that best determines the accuracy of phase-field models. Proving these equations converge to the moving boundary formulation at $\mathcal{O}({\epsilon }^2)$ in general geometries is nontrivial, but builds on second-order models of each individual boundary condition; a phase-field model which optimizes the mobility term for zero interface kinetics [59], a concentration equation similar to [31] and the diffuse domain method for Robin boundary conditions [60], and the smooth volume penalty method (which gives β = 1.51044385) [61].

3. Analysis of the phase-field model

In order to understand the phase-field model and demonstrate second-order accuracy, we use a multiple-scales matched-asymptotics framework, which we break into several modular steps:

• (i)Partition the solid Ω⁻, fluid Ω⁺ and size $\mathcal{O}(\epsilon )$ boundary ΔΩ regions (figure 1b).
• (ii)Adopt signed distance coordinates in the boundary region (§3a(i), figure 1c).
• (iii)Rescale normal coordinate and operators by ε near the interface (§3a(ii), figure 1b).
• (iv)Expand the variables in an asymptotic power series in ε in each region (§3a(iii)).
• (v)Connect regions with asymptotic matching conditions in the limit ε → 0 (§3a(iv)).
• (vi)Iterate to solve the zeroth-, first- and second-order problems (§3b–d).

This procedure follows our previous analysis of the volume-penalty method [61]. The philosophy of our approach is to determine the evolution of the phase-field model up to and including $\mathcal{O}({\epsilon }^2)$ in each region. We show that the variables in the fluid and solid regions, as well as the location of the interface itself, evolve with only $\mathcal{O}({\epsilon }^2)$ divergence from the moving boundary formulation. Errors of $\mathcal{O}(\epsilon )$ in the temperature and tangential velocity do occur in the boundary region ΔΩ. But this deviation is a necessary consequence of smoothly approximating discontinuous gradients across the interface, and is localized to the boundary region. We thereby derive a second-order accurate phase-field model. We now summarize the key components of this procedure.²

(a). Summary of asymptotic procedure

(i). (Signed-distance coordinate system)

We build a simple orthogonal coordinate system in the boundary region ΔΩ using the signed-distance function from the ϕ = 1/2 level set. The signed distance σ is the minimum distance of a point x to the interface. It follows that the point x must lie in the direction of the unit normal vector $\hat{n}$ from the nearest point on the interface p, which we label with surface coordinates s,

$$x=p(s)+\sigma \hspace{0.17em}\hat{n}(s).$$ 3.1

The surface coordinates induce a tangent vector basis t_i. Given orthogonal surface coordinates, we also derive the dual vector basis $\mathrm{\nabla }{s}_i$ and a unique orthonormal tangent basis ${\hat{t}}_i$,

$$t_i=\frac{\mathrm{\partial }p}{\mathrm{\partial }{s}_i},{\hat{t}}_i=\frac{t_i}{|t_i|}\text{and}\mathrm{\nabla }{s}_i=\frac{{\hat{t}}_i}{|t_i|}.$$ 3.2

We can then write the surface area measure dA = |t₁||t₂| ds₁ ds₂ and surface gradient ${\mathrm{\nabla }}_{\mathrm{\perp }}$,

$${\mathrm{\nabla }}_{\mathrm{\perp }}=\mathrm{\nabla }{s}_1\frac{\mathrm{\partial }}{\mathrm{\partial }{s}_1}+\mathrm{\nabla }{s}_2\frac{\mathrm{\partial }}{\mathrm{\partial }{s}_2}={\hat{t}}_1{\mathrm{\nabla }}_1+{\hat{t}}_2{\mathrm{\nabla }}_2.$$

It is not difficult to show the normal $\hat{n}$ is everywhere equal to the gradient of the signed distance. The gradient of the normal is therefore symmetric and diagonalizable. The eigenvectors are the principal directions of curvature (which must align with orthogonal surface coordinates), and the eigenvalues are the principal curvatures κ_i,

$$\hat{n}=\mathrm{\nabla }\sigma ,{\mathrm{\nabla }}_{\mathrm{\perp }}\hat{n}=-{\kappa }_1{\hat{t}}_1{\hat{t}}_1-{\kappa }_2{\hat{t}}_2{\hat{t}}_2=-K.$$ 3.3

We use this orthonormal frame to describe all geometric quantities near the interface. We can then express the gradient using the surface and normal derivatives and the scale tensor J

$$\mathrm{\nabla }=\hat{n}{\mathrm{\partial }}_{\sigma }+J^{-1}\cdot {\mathrm{\nabla }}_{\mathrm{\perp }},\text{where}\hspace{0.17em}J=I-\sigma K.$$ 3.4

It is straightforward to derive the remaining vector calculus operators from the gradient, which we list in appendix A. Finally, the Cartesian partial time derivative ∂_t can be rewritten in a moving coordinate system using the signed-distance partial time derivative ${\mathrm{\partial }}_{\tau }$,

$${\mathrm{\partial }}_t={\mathrm{\partial }}_{\tau }-v{\mathrm{\partial }}_{\sigma }+\sigma {\mathrm{\nabla }}_{\mathrm{\perp }}v\cdot J^{-1}\cdot {\mathrm{\nabla }}_{\mathrm{\perp }}.$$ 3.5

(ii). (Rescaling interfacial coordinates)

We analyse the size ε interfacial region using the rescaled coordinate ξ and derivative ${\mathrm{\partial }}_{\xi }$,

$$\sigma =\epsilon \xi ,{\mathrm{\partial }}_{\sigma }=\frac{1}{\epsilon }{\mathrm{\partial }}_{\xi }.$$ 3.6

This rescales vector calculus operators (listed in appendix A) through scale factors of the gradient

$$J=I-\epsilon \xi K,J^{-1}=\sum _{k=0}^{\mathrm{\infty }}{\epsilon }^k{\xi }^k{K}^k.$$ 3.7

(iii). (Variable expansions with formal power series)

After splitting the domain into the fluid Ω⁺, solid Ω⁻ and interfacial ΔΩ regions, each variable f in each region (fluid f⁺, solid f⁻ and interfacial f) is expressed as a power series in ε,

$$f^{+}(x,t)=\sum _{k=0}^{\mathrm{\infty }}{\epsilon }^k{f}_k^{+}(x,t),f^{-}(x,t)=\sum _{k=0}^{\mathrm{\infty }}{\epsilon }^k{f}_k^{-}(x,t)\text{and}\hspace{0.17em}f(\xi ,s,\tau )=\sum _{k=0}^{\mathrm{\infty }}{\epsilon }^k{f}_k(\xi ,s,\tau ).$$ 3.8

We do so for the temperature T, solute concentration C, fluid velocity $u=u_{\sigma }\hat{n}+u_{\mathrm{\perp }}$, pressure p, phase field ϕ and interface velocity $v\hspace{0.17em}\hat{n}$ (which does not depend on ξ). We substitute these series into the hierarchy of equations generated by §3a(ii) to derive a system of equations at each order of ε. Solving each order requires a matching procedure between adjacent regions.

(iv). (Asymptotic matching)

To ensure agreement between different regions, we specify asymptotic matching boundary conditions. This subtle notion requires asymptotic agreement in intermediate zones ξ ∼ ε^−1/2 in the limit that ε → 0. We can then let ξ approach infinity for the inner problem without encountering coordinate singularities (provided $\epsilon \ll \underset{i}{min}|{\kappa }_i^{-1}|$), and let σ approach zero for the outer problem without entering the interfacial region. That is, for any variable f, we require

$$\underset{\epsilon \to 0}{lim}f(\pm {\epsilon }^{-1/2}\xi ,s,t)\sim \underset{\epsilon \to 0}{lim}{f}^{\pm }(p(s,t)\pm {\epsilon }^{+1/2}\hspace{0.17em}\xi \hspace{0.17em}\hat{n}(s,t),t).$$ 3.9

Each variable is already expressed as an asymptotic series. Each series term in the outer variables can be further expanded as a Taylor series about the interface at ϕ = 1/2 using the signed distance σ. The matching conditions at each order of ε then simplify to

$$\underset{\xi \to \pm \mathrm{\infty }}{lim}f(\xi )=\underset{\xi \to \pm \mathrm{\infty }}{lim}\sum _{k=0}{\epsilon }^k{f}_k\sim \underset{\xi \to \pm \mathrm{\infty }}{lim}\sum _{k=0}{\epsilon }^k\left(\sum _{\ell =0}^k\frac{{\xi }^{\ell }}{\ell !}{\mathrm{\partial }}_{\sigma }^{\ell }{f}_{k-\ell }^{\pm }{|}_{\sigma =0}\right).$$ 3.10

Equipped with our multiple-scales matched-asymptotics procedure, we can now verify second-order convergence of our phase-field model in general smooth geometries.

(b). Zeroth order

At leading order, the phase-field equation reduces to the condition ${\varphi }_0^{\pm }(1-{\varphi }_0^{\pm })(1-2{\varphi }_0^{\pm })=0$. We define the solid by ${\varphi }_0^{-}=1$, the liquid by ${\varphi }_0^{+}=0$, with the boundary region separating them.

Fluid problem—Noting that the phase is zero in the fluid, we recover the desired sharp interface equations for the remaining leading order variables,

$$\begin{array}{rl}{\mathrm{\partial }}_t{T}_0^{+}+u_0^{+}\cdot \mathrm{\nabla }{T}_0^{+}-\kappa {\mathrm{\nabla }}^2{T}_0^{+}& =0,\\ {\mathrm{\partial }}_t{C}_0^{+}+u_0^{+}\cdot \mathrm{\nabla }{C}_0^{+}-\mu {\mathrm{\nabla }}^2{C}_0^{+}& =0,\\ {\mathrm{\partial }}_t{u}_0^{+}+u_0^{+}\cdot \mathrm{\nabla }{u}_0^{+}-\nu {\mathrm{\nabla }}^2{u}_0^{+}+\mathrm{\nabla }{p}_0^{+}-B(T_0^{+}-N{C}_0^{+})\hat{z}& =0,\\ \mathrm{\nabla }\cdot u_0^{+}& =0.\end{array}$$

For brevity, we approximate the buoyancy relationship as being linear in temperature and concentration, with proportionality constants B and −NB respectively. This simplification does not affect the convergence results. The solutions may also require external boundary conditions to complete the system.

Solid problem— Within the solid, we reproduce the diffusion equation for the temperature, and zero velocity in the solid. The divergence of the momentum equation reveals a Poisson equation for the pressure. The concentration equation depends sensitively on the decay of the phase to zero, but in the region 1 − ϕ ≪ δ the concentration forcing terms vanish, giving

$${\mathrm{\partial }}_t{T}_0^{-}-\kappa {\mathrm{\nabla }}^2{T}_0^{-}=0,{\mathrm{\partial }}_t{C}_0^{-}-\mu {\mathrm{\nabla }}^2{C}_0^{-}=0,u_0^{-}=0,{\mathrm{\nabla }}^2{p}_0^{-}=B{\mathrm{\partial }}_z(T_0^{-}-N{C}_0^{-}).$$

Similarly, internal ice boundary conditions may be necessary.

Boundary problem—The boundary region is defined relative to the interface ϕ = 1/2. To hold true for all ε when expanded into its power series, this implies that

$${\varphi }_0(\xi =0)=\frac{1}{2}\text{and}{\varphi }_k(\xi =0)=0\text{for all }k>0.$$

In this region, the phase-field equation balances the diffusion and reaction terms. The limiting boundary conditions ϕ₀(ξ → +∞) = 0 and ϕ₀(ξ → −∞) = 1 imply a tanh profile for ϕ₀,

$${\mathrm{\partial }}_{\xi }^2{\varphi }_0={\varphi }_0(1-{\varphi }_0)(1-2{\varphi }_0),\underset{\xi \to \pm \mathrm{\infty }}{lim}{\varphi }_0(\xi )\sim {\varphi }_0^{\pm }{|}_{\sigma =0},\hspace{0.17em}⟹\hspace{0.17em}{\varphi }_0(\xi )=\frac{1}{2}\left(1-\tanh \frac{\xi }{2}\right).$$

Matching the inner heat equation to the outer temperature requires T₀ to be constant in ξ,

$${\mathrm{\partial }}_{\xi }^2{T}_0=0,\underset{\xi \to \pm \mathrm{\infty }}{lim}{T}_0(\xi )\sim T_0^{\pm }{|}_{\sigma =0},\hspace{0.17em}⟹\hspace{0.17em}{T}_0=T_0^{\pm }{|}_{\sigma =0}.$$

The identity ${\mathrm{\partial }}_{\xi }{\varphi }_0=-{\varphi }_0(1-{\varphi }_0)$ simplifies the concentration equation. The limiting behaviour of the operator implies exponential growth of the kernel into the solid. This is unphysical, implying that the operand ${\mathrm{\partial }}_{\xi }{C}_0$ is zero. Matching to the outer variables requires a constant concentration,

$$(1-{\varphi }_0)({\mathrm{\partial }}_{\xi }+{\varphi }_0){\mathrm{\partial }}_{\xi }{C}_0=0,\underset{\xi \to \pm \mathrm{\infty }}{lim}{C}_0(\xi )\sim C_0^{\pm }{|}_{\sigma =0}\hspace{0.17em}⟹\hspace{0.17em}{C}_0=C_0^{\pm }{|}_{\sigma =0}.$$

The divergence constraint and matching to the solid implies zero normal velocity,

$${\mathrm{\partial }}_{\xi }{u}_{\sigma 0}=0,\underset{\xi \to \pm \mathrm{\infty }}{lim}{u}_{\sigma 0}(\xi )\sim u_{\sigma 0}^{\pm }{|}_{\sigma =0},\hspace{0.17em}⟹\hspace{0.17em}{u}_{\sigma 0}=u_{\sigma 0}^{\pm }{|}_{\sigma =0}=0.$$

The tangential momentum equation balances diffusion with damping. The kernel is spanned by an unphysical solution that grows exponentially into the solid, and a physical solution $\mathcal{U}(\xi )$ that decays exponentially into the solid and is affine in the fluid. Calibrating β [61] allows linear (rather than affine) behaviour of $\mathcal{U}(\xi )$ in the fluid. Matching to the fluid implies u_⊥0 is zero,

$$\left({\mathrm{\partial }}_{\xi }^2-\frac{1}{{\beta }^2}{\varphi }_0\right)u_{\mathrm{\perp }0}=0,\underset{\xi \to \pm \mathrm{\infty }}{lim}{u}_{\mathrm{\perp }0}(\xi )\sim u_{\mathrm{\perp }0}^{\pm }{|}_{\sigma =0},\hspace{0.17em}⟹\hspace{0.17em}{u}_{\mathrm{\perp }0}=u_{\mathrm{\perp }0}^{\pm }{|}_{\sigma =0}=0.$$

In summary, the zeroth-order asymptotics shows that the phase field has a tanh profile near the boundary, and that the leading order outer velocities satisfy no-slip boundary conditions. The next order problem reproduces the remaining boundary conditions.

(c). First order

The first-order perturbation of the phase-field equation away from the interface takes the form

$$(1-6{\varphi }_0^{\pm }+{6{\varphi }_0^{\pm }}^2){\varphi }_1^{\pm }=(T_0^{\pm }+m{C}_0^{\pm }){\varphi }_0^{\pm }(1-{\varphi }_0^{\pm }).$$

At subsequent orders, the leading order operator $(1-6{\varphi }_0^{\pm }+{6{\varphi }_0^{\pm }}^2)$ pairs with the highest order ${\varphi }_k^{\pm }$. The forcing terms contain lower-order factors. As the first inhomogeneity is zero, all remaining forcing terms, and therefore all outer phase-field expansions ${\varphi }_{k\ge 1}^{\pm }$, are zero.

Fluid problem—The remaining fluid equations are linear and homogeneous,

$$\begin{array}{rl}{\mathrm{\partial }}_t{T}_1^{+}+u_0^{+}\cdot \mathrm{\nabla }{T}_1^{+}+u_1^{+}\cdot \mathrm{\nabla }{T}_0^{+}-\kappa {\mathrm{\nabla }}^2{T}_1^{+}& =0,\\ {\mathrm{\partial }}_t{C}_1^{+}+u_0^{+}\cdot \mathrm{\nabla }{C}_1^{+}+u_1^{+}\cdot \mathrm{\nabla }{C}_0^{+}-\mu {\mathrm{\nabla }}^2{C}_1^{+}& =0,\\ {\mathrm{\partial }}_t{u}_1^{+}+u_0^{+}\cdot \mathrm{\nabla }{u}_1^{+}+u_1^{+}\cdot \mathrm{\nabla }{u}_0^{+}-\nu {\mathrm{\nabla }}^2{u}_1^{+}+\mathrm{\nabla }{p}_1^{+}-B(T_1^{+}-N{C}_1^{+})\hat{z}& =0,\\ \mathrm{\nabla }\cdot u_1^{+}& =0.\end{array}$$

The external boundary conditions are satisfied by the zeroth-order outer solutions. The first-order corrections therefore have homogeneous external boundaries. They are only perturbed at the melting interface. We show this interfacial perturbation is zero at first order.

Solid problem—The solid equations are the same at first order,

$${\mathrm{\partial }}_t{T}_1^{-}-\kappa {\mathrm{\nabla }}^2{T}_1^{-}=0,{\mathrm{\partial }}_t{C}_1^{-}-\mu {\mathrm{\nabla }}^2{C}_1^{-}=0,\hspace{0.17em}{u}_1^{-}=0,\hspace{0.17em}{\mathrm{\nabla }}^2{p}_1^{-}=B{\mathrm{\partial }}_z(T_1^{-}-N{C}_1^{-}).$$

Boundary problem—The differential operator of the first-order phase-field equation has a two-dimensional kernel spanned by ${\mathrm{\partial }}_{\xi }{\varphi }_0$ and 6ϕ₀(1 − ϕ₀)(ξ + sinhξ) + sinhξ. The inhomogeneity must be orthogonal to the kernel, implying the Gibbs–Thomson condition,

$$\gamma ({\mathrm{\partial }}_{\xi }^2-(1-6{\varphi }_0+6{\varphi }_0^2)){\varphi }_1=-{\mathrm{\partial }}_{\xi }{\varphi }_0(T_0+m{C}_0-\gamma \overline{K})\hspace{0.17em}⟹\hspace{0.17em}(T_0^{\pm }+m{C}_0^{\pm }){|}_{\sigma =0}-\gamma \overline{K}=0.$$

Matching implies ϕ₁ = 0. Integrating the temperature equation recovers energy conservation,

$$\kappa {\mathrm{\partial }}_{\xi }^2{T}_1=v_{0}L{\mathrm{\partial }}_{\xi }{\varphi }_0,\hspace{0.17em}⟹\hspace{0.17em}{T}_1=\frac{-v_{0}L}{\kappa }{\int }_{\xi }^{\mathrm{\infty }}{\varphi }_0\hspace{0.17em}\text{d}\eta +{\mathrm{\partial }}_{\sigma }{T}_0^{+}(0)\xi +T_1^{+}(0),{[\kappa {\mathrm{\partial }}_{\sigma }{T}_0^{\pm }]}_{\sigma =0}+L{v}_0=0.$$

Solving the homogeneous concentration equation and matching gives the solute conservation condition,

$$[({\mathrm{\partial }}_{\xi }+{\varphi }_0)(\mu {\mathrm{\partial }}_{\xi }{C}_1+v_0{C}_0)=0,\hspace{0.17em}⟹\hspace{0.17em}{C}_1=\frac{-v_0}{\mu }{C}_0^{+}(0)\xi +C_1^{+}(0),\mu {\mathrm{\partial }}_{\sigma }{C}_0^{+}{|}_{\sigma =0}+C^{+}{|}_{\sigma =0}{v}_0=0.$$

The divergence condition when matched with the solid again implies zero normal velocity,

$${\mathrm{\partial }}_{\xi }{u}_{\sigma 1}=0,\hspace{0.17em}⟹\hspace{0.17em}{u}_{\sigma 1}=u_{\sigma 1}^{\pm }{|}_{\sigma =0}=0.$$

The tangential velocity is proportional to the physical solution $\mathcal{U}(\xi )$. We choose β [61] to ensure linear behaviour in the fluid,

$$\left({\mathrm{\partial }}_{\xi }^2-\frac{{\varphi }_0}{{\beta }^2}\right)u_{\mathrm{\perp }1}=0\hspace{0.17em}⟹\hspace{0.17em}{u}_{\mathrm{\perp }1}(\xi )={\mathrm{\partial }}_{\sigma }{u}_{\mathrm{\perp }0}^{+}{|}_{\sigma =0}\mathcal{U}(\xi ),\hspace{0.17em}{u}_{\mathrm{\perp }1}(\xi \to \mathrm{\infty })\sim {\mathrm{\partial }}_{\sigma }{u}_{\mathrm{\perp }0}^{+}{|}_{\sigma =0}\xi ,\hspace{0.17em}{u}_{\mathrm{\perp }1}^{+}{|}_{\sigma =0}=0.$$

We finally use the normal momentum equation to show the pressure is constant at leading order

$${\mathrm{\partial }}_{\xi }{p}_0+\nu \frac{{\varphi }_0}{{\beta }^2}{u}_{\sigma 1}=0\hspace{0.17em}⟹\hspace{0.17em}{p}_0=p_0^{\pm }(0).$$

The first-order asymptotics have reproduced the Gibbs–Thomson condition with zero interface kinetics and the solute and energy conservation boundary conditions. Hence the phase-field equations will tend to the sharp interface equations in the limit. Calibrating β ensures the first-order outer fluid velocity satisfies homogeneous boundary conditions $u_{\sigma 1}^{+}{|}_{\sigma =0}=u_{\mathrm{\perp }1}^{+}{|}_{\sigma =0}=0$. We now solve the second-order asymptotics to show that the mobility coefficient ε(5/6)(L/κ) ensures homogeneous boundary conditions for the first-order outer temperature and concentration, and that the first-order interfacial velocity error is zero—allowing second-order convergence.

(d). Second order

Fluid problem—At second order, the fluid equations are sourced by the first-order errors,

$$\begin{array}{rl}{\mathrm{\partial }}_t{T}_2^{+}+u_0^{+}\cdot \mathrm{\nabla }{T}_2^{+}+u_2^{+}\cdot \mathrm{\nabla }{T}_0^{+}-\kappa {\mathrm{\nabla }}^2{T}_2^{+}& =-u_1^{+}\cdot \mathrm{\nabla }{T}_1^{+},\\ {\mathrm{\partial }}_t{C}_2^{+}+u_0^{+}\cdot \mathrm{\nabla }{C}_2^{+}+u_2^{+}\cdot \mathrm{\nabla }{C}_0^{+}-\mu {\mathrm{\nabla }}^2{C}_2^{+}& =-u_1^{+}\cdot \mathrm{\nabla }{C}_1^{+},\\ {\mathrm{\partial }}_t{u}_2^{+}+u_0^{+}\cdot \mathrm{\nabla }{u}_2^{+}+u_2^{+}\cdot \mathrm{\nabla }{u}_0^{+}-\nu {\mathrm{\nabla }}^2{u}_2^{+}+\mathrm{\nabla }{p}_2^{+}-B(T_2^{+}-N{C}_2^{+})\hat{z}& =-u_1^{+}\cdot \mathrm{\nabla }{u}_1^{+},\\ \mathrm{\nabla }\cdot u_2^{+}& =0.\end{array}$$

Solid problem—The solid velocity is now non-zero from interior pressure and forces,

$$\begin{array}{rl}& {\mathrm{\partial }}_t{T}_2^{-}=\kappa {\mathrm{\nabla }}^2{T}_2^{-},{\mathrm{\partial }}_t{C}_2^{-}=\mu {\mathrm{\nabla }}^2{C}_2^{-},\\ & {\mathrm{\nabla }}^2{p}_2^{-}=B{\mathrm{\partial }}_z(T_2^{-}-N{C}_2^{-}),\frac{\nu }{{\beta }^2}{u}_2^{-}=B(T_0^{-}-N{C}_0^{-})\hat{z}-\mathrm{\nabla }{p}_0^{-}.\end{array}$$

Boundary problem—The phase-field equation now has a more complex inhomogeneous term:

$$\gamma ({\mathrm{\partial }}_{\xi }^2-(1-6{\varphi }_0+6{\varphi }^2)){\varphi }_2=-{\mathrm{\partial }}_{\xi }{\varphi }_0\left(\frac{5}{6}\frac{L}{\kappa }{v}_0+(T_1+m{C}_1)-\xi \gamma \overline{K^2}\right).$$

We again apply a solvability condition. The odd terms drop out, and integration shows ${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}-{\mathrm{\partial }}_{\xi }{\varphi }_0{\varphi }_0(1-{\varphi }_0)\hspace{0.17em}\text{d}\xi =\frac{1}{6}$ and ${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}-{\mathrm{\partial }}_{\xi }{\varphi }_0{\varphi }_0(1-{\varphi }_0){\int }_{\xi }^{\mathrm{\infty }}{\varphi }_0\hspace{0.17em}\text{d}\eta \hspace{0.17em}\text{d}\xi =\frac{5}{36}$. The interfacial velocity term thus vanishes, giving a constraint between first-order concentration and temperature:

$${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\mathrm{\partial }}_{\xi }{\varphi }_0^2\left(T_1^{\pm }(0)+m{C}_1^{\pm }(0)+\frac{L{v}_0}{\kappa }\left(\frac{5}{6}-{\int }_{\xi }^{\mathrm{\infty }}{\varphi }_0\hspace{0.17em}\text{d}\eta \right)\right)\hspace{0.17em}\text{d}\xi =0\hspace{0.17em}⟹\hspace{0.17em}(T_1^{\pm }+m{C}_1^{\pm }){|}_{\sigma =0}=0.$$

An explicit formula for ϕ₂ (using variation of parameters) is non-trivial but it decays exponentially to zero in either direction. The temperature equation is then integrated. If initially $T_1^{\pm }{|}_{\sigma =0}=0$, then matching prevents linear asymptotic behaviour of T₂, implying v₁ = 0,

$$\begin{array}{rl}\kappa {\mathrm{\partial }}_{\xi }^2{T}_2& =L{v}_1{\mathrm{\partial }}_{\xi }{\varphi }_0+{\mathrm{\partial }}_t{T}_0-\kappa {\mathrm{\nabla }}_{\mathrm{\perp }}\cdot {\mathrm{\nabla }}_{\mathrm{\perp }}{T}_0+(\kappa \overline{K}-v_0){\mathrm{\partial }}_{\xi }{T}_1,\\ \kappa T_2& =({\mathrm{\partial }}_t-\kappa {\mathrm{\nabla }}_{\mathrm{\perp }}\cdot {\mathrm{\nabla }}_{\mathrm{\perp }}+(\kappa \overline{K}-v_0){\mathrm{\partial }}_{\sigma })T_0^{+}{|}_{\sigma =0}\frac{{\xi }^2}{2}+(\kappa \overline{K}-v_0)\frac{v_{0}L}{\kappa }{\int }_{\xi }^{\mathrm{\infty }}{\int }_{\eta }^{\mathrm{\infty }}{\varphi }_0\hspace{0.17em}\text{d}\zeta \hspace{0.17em}\text{d}\eta +T_2^{\pm }{|}_{\sigma =0}.\end{array}$$

The concentration equation is similarly integrated. The inhomogeneity is constant in ξ, and explicitly solvable. Using previous solutions and $C_1^{\pm }{|}_{\sigma =0}=T_1^{\pm }{|}_{\sigma =0}=v_1=0$, we find C₂,

$$\begin{array}{rl}({\mathrm{\partial }}_{\xi }+{\varphi }_0)(\mu {\mathrm{\partial }}_{\xi }{C}_2+v_0{C}_1+v_1{C}_0)& ={\mathrm{\partial }}_t{C}_0+\mu \overline{K}{\mathrm{\partial }}_{\xi }{C}_1-\mu {\mathrm{\nabla }}_{\mathrm{\perp }}\cdot {\mathrm{\nabla }}_{\mathrm{\perp }}{C}_0,\\ \mu C_2=\frac{v_0^2}{{\mu }^2}{C}_0^{+}{|}_{\sigma =0}\frac{{\xi }^2}{2}+({\mathrm{\partial }}_t+\overline{K}{v}_0& -\mu {\mathrm{\nabla }}_{\mathrm{\perp }}\cdot {\mathrm{\nabla }}_{\mathrm{\perp }})\hspace{0.17em}{C}_0^{\pm }{|}_{\sigma =0}{\int }_0^{\xi }\frac{-\log \varphi }{1-\varphi }\hspace{0.17em}\text{d}\eta +C_2^{\pm }{|}_{\sigma =0}.\end{array}$$

The divergence equation implies the second-order normal velocity is now no longer zero,

$${\mathrm{\partial }}_{\xi }{u}_{\sigma 2}=-{\mathrm{\nabla }}_{\mathrm{\perp }}\cdot u_{\mathrm{\perp }1},\hspace{0.17em}⟹\hspace{0.17em}{u}_{\sigma 2}=u_{\sigma 2}(-\mathrm{\infty })-{\mathrm{\nabla }}_{\mathrm{\perp }}\cdot ({\mathrm{\partial }}_{\sigma }{u}_0^{+}(0)){\int }_{-\mathrm{\infty }}^{\xi }\mathcal{U}\hspace{0.17em}\text{d}\zeta .$$

The second-order tangential velocity can then be solved using variation of parameters

$$\begin{array}{rl}\nu \left({\mathrm{\partial }}_{\xi }^2-\frac{{\varphi }_0}{{\beta }^2}\right)u_{\mathrm{\perp }2}& ={\mathrm{\nabla }}_{\mathrm{\perp }}{p}_0+(\nu \overline{K}-v_0){\mathrm{\partial }}_{\xi }{u}_{\mathrm{\perp }1}+B(T_0-N{C}_0){\hat{z}}_{\mathrm{\perp }}=\mathcal{R},\\ u_{\mathrm{\perp }2}& =(\mathcal{Q}+c)\hspace{0.17em}\mathcal{U},\text{where}\hspace{0.17em}\mathcal{Q}\equiv {\int }_0^{\xi }-\frac{{\int }_{-\mathrm{\infty }}^{\eta }\mathcal{R}\mathcal{U}\hspace{0.17em}\text{d}\zeta }{{\mathcal{U}}^2}\hspace{0.17em}\text{d}\eta ,\end{array}$$

where c is a constant of integration that cancels the linear part of the solution into the fluid. The normal momentum equation can then be integrated to determine p₁. Matching requires no constant term in the limiting behaviour of the pressure into the fluid,

$$\begin{array}{rl}{\mathrm{\partial }}_{\xi }{p}_1& =\nu {\mathrm{\nabla }}_{\mathrm{\perp }}\cdot ({\mathrm{\partial }}_{\sigma }{u}_{\mathrm{\perp }0}^{+}{|}_{\sigma =0})\left(\frac{{\varphi }_0}{{\beta }^2}\left({\int }_{-\mathrm{\infty }}^{\xi }\mathcal{U}\hspace{0.17em}\text{d}\eta -{\mathcal{U}}^{\prime }(\xi )\right)\right)-\frac{\nu {\varphi }_0}{{\beta }^2}{u}_{\sigma 2}^{-}{|}_{\sigma =0}-B(T_0^{+}-N{C}_0^{+}){|}_{\sigma =0}{\hat{z}}_{\sigma },\\ p_1& =\nu {\mathrm{\nabla }}_{\mathrm{\perp }}\cdot ({\mathrm{\partial }}_{\sigma }{u}_{\mathrm{\perp }0}^{+}{|}_{\sigma =0})\mathcal{U}(\xi )-B(T_0^{+}-N{C}_0^{+}){|}_{\sigma =0}{\hat{z}}_{\sigma }\xi \\ & +\frac{\nu }{{\beta }^2}\left({\mathrm{\nabla }}_{\mathrm{\perp }}\cdot ({\mathrm{\partial }}_{\sigma }{u}_{\mathrm{\perp }0}^{+}{|}_{\sigma =0})\left({\int }_{\xi }^{\mathrm{\infty }}{\varphi }_0{\int }_{-\mathrm{\infty }}^{\zeta }\mathcal{U}(\eta )\hspace{0.17em}\text{d}\eta \hspace{0.17em}\text{d}\zeta \right)+u_{\sigma 2}^{-}{|}_{\sigma =0}{\int }_{\xi }^{\mathrm{\infty }}{\varphi }_0\hspace{0.17em}\text{d}\eta \right).\end{array}$$

The second-order asymptotic analysis shows that calibrating the mobility and damping parameters ensures homogeneous boundary conditions of the first-order outer solutions at the interface. Combined with homogeneous external boundary conditions and homogeneous linear evolution equations at first order, this implies that if the outer solutions are initialized correct to $\mathcal{O}({\epsilon }^2)$, then the fields and interfacial velocity will evolve accurate to $\mathcal{O}({\epsilon }^2)$ over time. In reality, the chaotic nature of many fluid dynamics problems prevents convergence beyond the Lyapunov timescale of the flow, but at each point in time the system behaves correctly to within second-order accuracy.

4. Numerical validation of the model

We now validate the asymptotic arguments of §3 in two benchmark problems. In each problem, we calculate a numerical reference solution corresponding to the ‘sharp interface’ equations of §2a. We then show the optimal phase-field equations of §2b achieve convergence of $\mathcal{O}({\epsilon }^2)$ to these reference solutions. Both the reference and phase-field problems are simulated using the flexible and efficient spectral code Dedalus [62].³ Dedalus is a general-purpose code that takes PDEs in plain text and automatically discretizes them using spectral series (including Fourier series, Chebyshev polynomials and other orthogonal polynomials). Linear terms in the equations are converted into sparse banded matrices and nonlinear terms are treated pseudospectrally. Included implicit–explicit timesteppers integrate the linear terms implicitly, and the nonlinear terms explicitly. Dedalus is written in the Python programming language to aid rapid development, and uses compiled libraries (including BLAS, LAPACK and MPI) to perform efficient parallelized simulations at scale.

(a). Melting and dissolution at a stagnation point

The first benchmark problem examines warm liquid with dissolved solute flowing towards a melting interface at a stagnation point (similar to §5 of [63] and 5.6 of [61]). We compare the sharp interface and phase-field approximations to this problem, as illustrated in figure 2. The symmetries of the system allow us to significantly simplify equation (2.1), revealing a steady travelling wave similarity solution for the moving boundary and phase-field formulations. We do this by transforming to a frame moving leftward at the steady interface melting speed −v. We solve the system as a nonlinear boundary value problem in Dedalus.

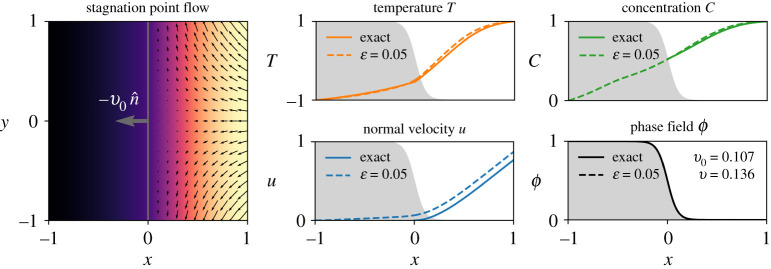
Figure 2.

On the left, we illustrate stagnation point flow towards a melting interface. The fluid velocity decreases to zero at the interface (black arrows x > 0), and the vertical velocity is proportional to y. The interface velocity (grey arrow at x = 0) uniformly recedes to the left. The temperature (in colour) decreases towards the left, and is invariant in y (as are all quantities excepting the vertical fluid velocity). The concentration (not shown) decreases similarly. We also plot reference and phase-field solutions for temperature T, solute concentration C, normal velocity u and phase field ϕ as a function of x in the second and third columns. Only the temperature exists inside the solid in the reference solution. We negate the normal fluid velocity u for clarity. (Online version in colour.)

Sharp interface model—We solve a diffusion equation for the solid temperature T⁻, advection–diffusion equations for the liquid temperature T⁺ and solute concentration C and a nonlinear third-order equation for the horizontal fluid velocity u,

$$\begin{array}{rlr}{T}^{-}(-1)=-1,& T^{+}(0)=T^{-}(0),{[{\mathrm{\partial }}_{x}T(0)]}_{-}^{+}=-\frac{Lv}{\kappa },\hspace{0.17em}u(0)=0,& {\mathrm{\partial }}_{x}u(0)=0,\\ T^{+}(1)=1,& T^{\pm }(0)=-mC(0),{\mathrm{\partial }}_{x}C(0)=-\frac{C(0)v}{\mu },\hspace{0.17em}C(1)=0,& {\mathrm{\partial }}_{x}u(1)=-1.\end{array}$$ 4.2

Phase-field model—The phase field instead implicitly models the interfacial boundary conditions through various equation terms, which reduce equation (2.4) to

$$\begin{array}{rl}\nu {\mathrm{\partial }}_x^{2}T& =((1-\varphi )u-v){\mathrm{\partial }}_{x}T+Lv{\mathrm{\partial }}_x\varphi ,\\ \mu {\mathrm{\partial }}_x^{2}C& =(u-v){\mathrm{\partial }}_{x}C-{\mathrm{\partial }}_x\log (1-\varphi +\delta )(\mu {\mathrm{\partial }}_{x}C+vC),\\ \nu {\mathrm{\partial }}_x^{3}u& =1+(u-v){\mathrm{\partial }}_x^{2}u-{({\mathrm{\partial }}_{x}u)}^2+\frac{\nu }{{(\beta \epsilon )}^2}\varphi {\mathrm{\partial }}_{x}u,\\ \gamma {\mathrm{\partial }}_x^2\varphi & =-\epsilon \frac{5}{6}\frac{L}{\kappa }v{\mathrm{\partial }}_x\varphi +\frac{\gamma }{{\epsilon }^2}\varphi (1-\varphi )(1-2\varphi )+\frac{1}{\epsilon }\varphi (1-\varphi )(T+mC).\end{array}$$ 4.3

We now only require the Dirichlet outer boundary conditions of before to solve the problem

$$T(-1)=-D,C(-1)=0,\hspace{0.17em}\varphi (-1)=1,\hspace{0.17em}u(-1)=0,\hspace{0.17em}{\mathrm{\partial }}_{x}u(-1)=0$$ 4.4

and

$$T(1)=1,C(1)=1,\hspace{0.17em}\varphi (1)=0,\hspace{0.17em}\varphi (0)=\frac{1}{2},\hspace{0.17em}{\mathrm{\partial }}_{x}u(1)=-1.$$ 4.5

Requiring ϕ(0) = 1/2 is necessary to fix the problem in the moving frame to determine v.

Results—We solve each problem as a nonlinear boundary value problem in Dedalus. We discretize each variable on the solid (−1 < x < 0) and fluid (0 < x < 1) domains using Chebyshev polynomials. Newton–Kantorovich iteration then converges on a solution with a tolerance of 10⁻¹² (see [64, appendix C]). We reproduce example phase field and reference snapshots in figure 2 for ε = 0.05, κ = μ = ν = 1/10 and D = m = L = γ = 1, using 64 grid points for each subdomain. We set δ = 2 × 10⁻⁵ to regularize the solute equation within the solid. The disagreement (though small) is visible by eye for the temperature, concentration and normal velocity.

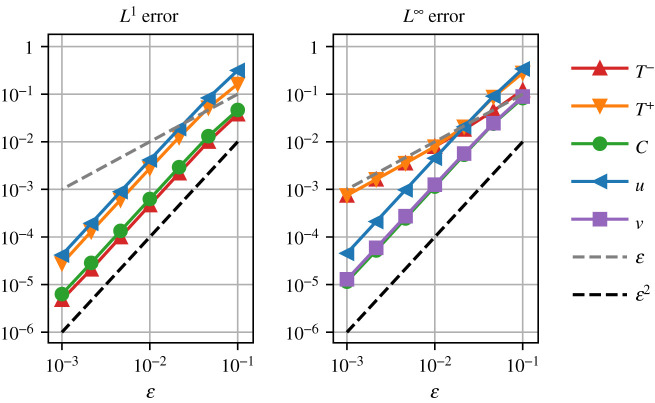
We then perform a quantitative analysis of convergence in figure 3. We test seven logarithmically spaced values of ε from 10⁻¹ to 10⁻³, for the previous control parameters, and using 256 grid points in each subdomain. We quantify the difference between the reference and phase-field solutions with the L¹ and L^∞ error norms of each variable (u, T⁺, T⁻, C, v) as a function of ε. We find clear $\mathcal{O}({\epsilon }^2)$ convergence in the L¹ error norm of each field variable, as well as for the L^∞ error norm of the u, C and v variables. The L¹ convergence demonstrates the quantitative accuracy of the phase-field model. The reason for the apparently restricted $\mathcal{O}(\epsilon )$ L^∞ convergence of the temperature fields is the jump in temperature gradient of the reference solution at the interface. The smooth phase-field model cannot follow this kink leading to an $\mathcal{O}(\epsilon )$ disagreement that is localized to the boundary. Tangential velocities also suffer from this reduced continuity in general.

Figure 3.

Plot of convergence in L¹ and L^∞ error norm of the velocity u, liquid temperature T⁺, solid temperature T⁻, solute concentration C and interface melting speed v as a function of ε. Each norm is calculated within the appropriate domain of the reference variable. Clear $\mathcal{O}({\epsilon }^2)$ convergence is observed in L¹ norm using optimal parameters. $\mathcal{O}(\epsilon )$ convergence in L^∞ norm occurs for the temperature because of the non-differentiability of the reference solution. (Online version in colour.)

(b). Double diffusive melting

In our second benchmark, we examine buoyancy driven flow of warm liquid with dissolved solute underneath a melting solid layer. This problem develops non-trivial geometries from the evolution of the flow. To simulate the reference formulation in Dedalus, we use an evolving coordinate system that maps the fluid and solid regions to a stationary rectangular domain. This transformation allows an efficient spectral discretization using Dedalus, and is used in similar spectral solvers [65]. We repeat this remapping for the phase-field formulation as it concentrates resolution near the ϕ = 1/2 level set. This allows us to efficiently and accurately simulate much smaller ε. By comparing the phase-field simulation to the reference problem as we decrease ε, we demonstrate second-order accuracy of the model.

Sharp differential equations—The full domain exists between 0 < z < 2 and 0 < x < 4. It is partitioned by the interface at height z = h(t, x). Above the interface, we solve the heat equation for the solid temperature field T⁻ with diffusivity κ. Below the interface, we solve incompressible Boussinesq hydrodynamics (using a first-order formulation in terms of velocity u, vorticity q and augmented pressure $p=P+\frac{1}{2}|u{|}^2$), with advection and diffusion of temperature T⁺ and solute concentration C,

$$\begin{array}{rl}& {\mathrm{\partial }}_t{T}^{-}-\kappa {\mathrm{\nabla }}^2{T}^{-}=0,\hspace{0.17em}\mathrm{\nabla }\cdot u=0,\\ & {\mathrm{\partial }}_t{T}^{+}-\kappa {\mathrm{\nabla }}^2{T}^{+}=-u\cdot \mathrm{\nabla }{T}^{+},q-\mathrm{\nabla }\times u=0,\\ & {\mathrm{\partial }}_{t}C-\mu {\mathrm{\nabla }}^{2}C=-u\cdot \mathrm{\nabla }C,{\mathrm{\partial }}_{t}u+\mathrm{\nabla }p-\nu \mathrm{\nabla }\times q=q\times u+(T^{+}-NC)\hspace{0.17em}{\hat{e}}_z,\end{array}$$ 4.6

where ν, κ and μ are the momentum, temperature and solute diffusivity. This first-order reformulation is required in the Dedalus solver, and has the added benefit of simplifying the mathematical details of the coordinate transformation. We set the buoyancy parameter B = 1.

Boundary conditions—At the top, we specify conservative temperature boundary conditions. At the bottom, we specify no-slip boundaries with no-flux temperature and solute conditions. The zeroth mode for the vertical velocity is replaced by a choice of pressure gauge,

$${\mathrm{\partial }}_z{T}^{-}(t,x,2)=0,{\mathrm{\partial }}_z{T}^{+}(t,x,0)=0,\hspace{0.17em}{\mathrm{\partial }}_{z}C(t,x,0)=0,\hspace{0.17em}u(t,x,0)=0,\hspace{0.17em}p(t,x,0)=0.$$

At the interface z = h(t, x), we have a Gibbs–Thomson boundary condition, matching temperature boundary conditions, energy and solute conservation boundary conditions and zero velocity boundary conditions required for mass conservation,

$$\begin{array}{rlr}{T}^{+}+mC=-\gamma \mathrm{\nabla }\cdot \hat{n},& \hat{n}\cdot \mathrm{\nabla }{T}^{+}-\hat{n}\cdot \mathrm{\nabla }{T}^{-}+\frac{L}{\kappa }\hat{n}\cdot {\mathrm{\partial }}_{t}h\hspace{0.17em}{\hat{e}}_z=0,& u_x=0,\\ T^{+}-T^{-}=0,& \hat{n}\cdot \mathrm{\nabla }C+\frac{C}{\mu }\hat{n}\cdot {\mathrm{\partial }}_{t}h\hspace{0.17em}{\hat{e}}_z=0,& u_z=0.\end{array}$$ 4.7

Initial conditions—We initialize the problem with h(0, x) = 1 and zero velocity and pressure, and a decreasing concentration profile with height. We apply a large perturbation to the linearly decreasing temperature field to initiate convection,

$$[T(0,x,z)=1-z+\exp (5^2({(x-2)}^2+{(z-0.5)}^2))$$

and

$$[C(0,x,z)=0.05+(1-0.05)\frac{1}{2}(1-\tanh (10(z-0.5))).$$

Phase-field equations—The phase-field equations are a similar reformulation of equation (2.4):

$$\begin{array}{rl}{\mathrm{\partial }}_{t}T-\kappa {\mathrm{\nabla }}^{2}T-L{\mathrm{\partial }}_t\varphi =-u\cdot \mathrm{\nabla }T,& {\mathrm{\partial }}_{t}C-\mu {\mathrm{\nabla }}^{2}C=-u\cdot \mathrm{\nabla }C+\frac{{\mathrm{\partial }}_t\varphi C-\mathrm{\nabla }C\cdot \mathrm{\nabla }\varphi }{1-\varphi +\delta },\\ \mathrm{\nabla }\cdot u=0,& \epsilon \frac{5}{6}\frac{L}{\kappa }{\mathrm{\partial }}_t\varphi -\gamma {\mathrm{\nabla }}^2\varphi =-\frac{1}{{\epsilon }^2}\varphi (1-\varphi )(\gamma (1-2\varphi )+\epsilon (T+mC)),\\ q-\mathrm{\nabla }\times u=0,& {\mathrm{\partial }}_{t}u+\mathrm{\nabla }p-\nu \mathrm{\nabla }\times q=q\times u+(T^{+}-NC)\hspace{0.17em}{\hat{e}}_z-\frac{\nu }{{(\beta \epsilon )}^2}\varphi \hspace{0.17em}u.\end{array}$$ 4.8

We use the optimal damping prescription β = 1.51044385 [61] and choose δ = 10⁻⁴. We specify the same insulating no-slip boundary conditions at z = 0 and z = 2. The boundary conditions at z = h(t, x) require continuity of each field and its derivatives. We initialize using the same initial conditions as for the remapped simulation, plus the initial conditions for the phase field

$$\varphi (0,x,z)=\frac{1}{2}\left(1+\tanh \left(\frac{1}{2\epsilon }\right)(z-1)\right).$$

Remapped coordinates—To solve the melting problem, we remap our evolving domain in Cartesian space to a fixed rectangular domain with the new coordinates τ, ξ and ζ^±,

$$\tau (t,x,z)=t,\xi (t,x,z)=x,\hspace{0.17em}{\zeta }^{+}(t,x,z)=\frac{z}{h(t,x)},\hspace{0.17em}{\zeta }^{-}(t,x,z)=\frac{z-h}{2-h(t,x)},$$

for which we plot equally spaced level set contours in figure 4. The differential geometry of the new coordinates is presented in appendix B. We solve the phase-field equations on the remapped domains of the reference problem to concentrate resolution near the phase-field interface and speed up comparison of quantities between simulations.

Figure 4.

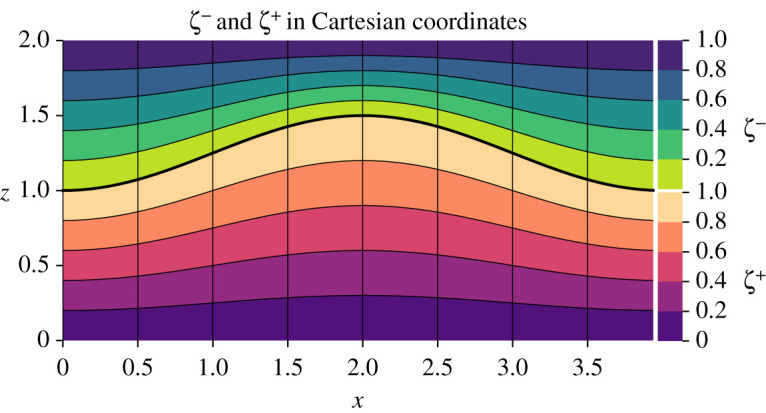
Contour plot of ξ (vertical) and ζ coordinates (horizontal) for $h(x)=\frac{3}{4}+\frac{1}{5}\cos (\pi x)$. (Online version in colour.)

Model and numerical parameters—We simulate these equations using model parameter values from table 1. We simulate the reference equations using 64 Chebyshev polynomials in the vertical direction and 128 Fourier modes in the periodic horizontal direction. After determining the reference solution, we discretize the phase-field equations on the same evolving domain of the reference simulation for several values of ε. To interpolate the reference geometries into the phase-field simulations between the saved time and grid points, we use third-order interpolating splines. The phase-field simulations discretize the vertical ζ basis using three compound Chebyshev bases $[0,10\hspace{0.17em}\epsilon ]\cup [10\hspace{0.17em}\epsilon ,1-10\hspace{0.17em}\epsilon ]\cup [1-10\hspace{0.17em}\epsilon ,1]$, with resolutions of 32, 64 and 32 modes, respectively. This greatly reduces the simulation cost. We use a time step size of Δt = 10⁻³, 5 × 10⁻⁴, 2.5 × 10⁻⁴, 2 × 10⁻⁴, 5 × 10⁻⁵ for decreasing choice of ε, and integrate in time using a second-order multistep semi-implicit backwards difference formula (SBDF2).

Table 1.

Model parameters used in the second benchmark problem.

ν	κ	μ	γ	L	m	N	ε
10−2	10−2	10−2	10−2	1${}^{\phantom{{\int }^{\int }}}$	0.2	0	$\sqrt{5}\times {10}^{-3},{10}^{-2.5},\sqrt{2}\times {10}^{-2.5},\sqrt{5}\times {10}^{-2.5},{10}^{-2}$

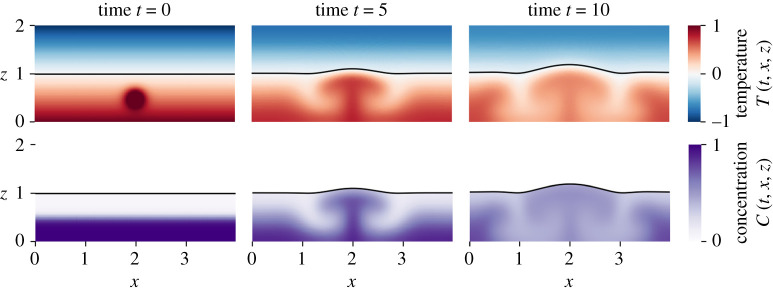
Results—A time series of the temperature and concentration fields of the reference solution is given in figure 5, which illustrates a rising buoyant plume from the initial temperature anomaly in the fluid. The warm solute-laden liquid melts the interface in the middle more rapidly than the ambient liquid at the sides, causing a trough to develop.

Figure 5.

Time series of temperature and concentration fields in reference simulation. (Online version in colour.)

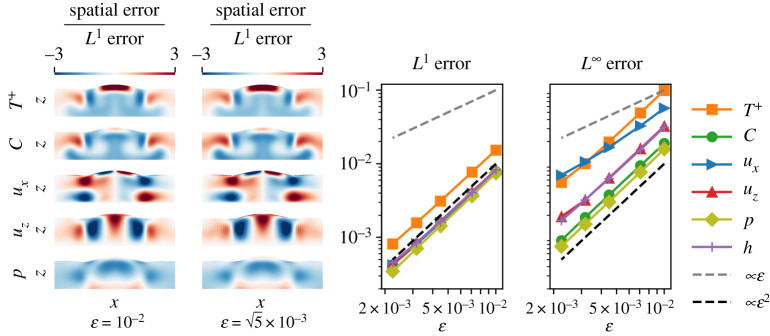
In figure 6, we plot several error metrics of the phase-field simulations. In the first two columns, we plot the spatial error normalized by the L¹ error for the liquid temperature T⁺, solute concentration C, Cartesian velocity components u_x and u_z, and true pressure $P=p-\frac{1}{2}|u{|}^2$. We plot these normalized spatial errors for the smoothest (ε = 10⁻²) and sharpest ($\epsilon =\sqrt{5}\times {10}^{-3}$) phase-field simulations at the final time t = 10. These plots reveal a consistent spatial error profile between simulations. To understand the amplitude of the spatial error, we plot the L¹ and L^∞ error norms of each variable as a function of ε in the third and fourth columns of figure 6. We see clear second-order convergence of all variables in L¹ norm. We note that the structure of the boundary layer of the tangential velocity and temperature affects the L^∞ norm. The phase-field model causes a kink in the temperature and tangential velocity near the interface, which leads to an O(ε) error of these variables in the interfacial region. However, this error is localized to the boundary, and does not propagate outward. (This trend is difficult to notice in the temperature plot as the error within the fluid still dominates the $\mathcal{O}(\epsilon )$ boundary error for the moderate choices of ε chosen.) We therefore achieve second-order convergence in the fluid and solid regions due to our optimal calibration of the phase-field model parameters.

Figure 6.

Columns 1 and 2 plot normalized spatial errors of the liquid temperature T⁺, concentration C, horizontal and vertical Cartesian velocity u_x, u_z and pressure p at time t = 10. Columns 3 and 4 plot the L¹ and L^∞ error norms for the fluid temperature T⁺, concentration C, vertical u_x and horizontal velocity u_z, pressure p and interface height h as a function of ε at time t = 10. (Online version in colour.)

5. Conclusion

In this paper, we provide a general framework for analysing the convergence of phase-field models. We use this procedure to develop a second-order phase-field model of melting and dissolution in multi-component flows. This is a concrete advancement that showcases second-order accurate approximations of many common boundary conditions; no-slip Dirichlet boundaries, Neumann boundaries, Robin boundaries and Stefan boundaries. We also verify these prescriptions in two thorough benchmark problems with accurate reference solutions. By developing a framework to validate this model, we now possess the machinery required to create second-order accurate extensions to more general thermodynamic properties. We can also consider yet higher-order analyses of this and other models. An automated approach of Richardson sequence extrapolation could also be considered to generate higher-order accurate models, as was done by the authors for the volume-penalty method [61]. To be clear, phase-field models are not necessarily the most appropriate choice for any problem. Remapping was also shown to be an effective strategy for sufficiently simple geometries in §4b. However, our second-order phase-field model is simple to implement, is more accurate than standard phase-field models, and is applicable in much more challenging geometries than remapping approaches.

Appendix A. Signed-distance coordinates

The signed distance σ of the point x is the minimum distance to the surface. Labelling surface points p and unit normals $\hat{n}$ with orthogonal surface coordinates s, we have

$$[x=p(s)+\sigma \hspace{0.17em}\hat{n}(s).$$

This gives a tangent vector basis t_i, dual basis $\mathrm{\nabla }{s}_i$ and orthonormal tangent basis ${\hat{t}}_i$:

$$[t_i=\frac{\mathrm{\partial }p}{\mathrm{\partial }{s}_i},{\hat{t}}_i=\frac{t_i}{|t_i|}\text{and}\mathrm{\nabla }{s}_i=\frac{{\hat{t}}_i}{|t_i|}.$$

These give the surface gradient ${\mathrm{\nabla }}_{\mathrm{\perp }}$, area measure dA = |t₁||t₂| ds₁ ds₂ and surface divergence,

$${\mathrm{\nabla }}_{\mathrm{\perp }}=\mathrm{\nabla }{s}_1\frac{\mathrm{\partial }}{\mathrm{\partial }{s}_1}+\mathrm{\nabla }{s}_2\frac{\mathrm{\partial }}{\mathrm{\partial }{s}_2}={\hat{t}}_1{\mathrm{\nabla }}_1+{\hat{t}}_2{\mathrm{\nabla }}_2\text{and}{\mathrm{\nabla }}_{\mathrm{\perp }}\cdot u_{\mathrm{\perp }}=\frac{1}{|t_1||t_2|}\left(\frac{\mathrm{\partial }}{\mathrm{\partial }{s}_1}(|t_2|u_1)+\frac{\mathrm{\partial }}{\mathrm{\partial }{s}_2}(|t_1|u_2)\right).$$

The normal $\hat{n}$ is everywhere equal to the gradient of the signed distance, and therefore its gradient is symmetric and diagonalizable. The eigenvectors are the principal directions of curvature (which align with orthogonal surface coordinates), and the eigenvalues are the principal curvatures κ_i,

$$\hat{n}=\mathrm{\nabla }\sigma ,{\mathrm{\nabla }}_{\mathrm{\perp }}\hat{n}=-{\kappa }_1{\hat{t}}_1{\hat{t}}_1-{\kappa }_2{\hat{t}}_2{\hat{t}}_2=-K.$$

We express the gradient using the orthonormal frame $(\hat{n},{\hat{t}}_1,{\hat{t}}_2)$ and the scale tensor J

$$\mathrm{\nabla }=\hat{n}{\mathrm{\partial }}_{\sigma }+J^{-1}\cdot {\mathrm{\nabla }}_{\mathrm{\perp }},\text{where}\hspace{0.17em}J=I-\sigma K.$$

The determinant |J| relates mean curvature $\overline{K}$, Gaussian curvature |K | and volume measure dV,

$$\overline{K}={\kappa }_1+{\kappa }_2,|K|={\kappa }_1{\kappa }_2,\hspace{0.17em}|J|=1-\sigma \overline{K}+{\sigma }^2|K|\text{and}\text{d}V=|J|\hspace{0.17em}\text{d}\sigma \hspace{0.17em}\text{d}A.$$

We define the adjugate tensors $\hat{J}$ and $\hat{K}$,

$$\hat{K}=|K|K^{-1}={\kappa }_2{\hat{t}}_1{\hat{t}}_1+{\kappa }_1{\hat{t}}_2{\hat{t}}_2,\hat{J}=|J|J^{-1}=I-\sigma \hat{K}.$$

We also define the cross product with the unit normal, which admits simple identities,

$$\begin{array}{rl}{\mathrm{\nabla }}^{\mathrm{\perp }}=\hat{n}\times {\mathrm{\nabla }}_{\mathrm{\perp }},& {\mathrm{\nabla }}^{\mathrm{\perp }}\cdot {\mathrm{\nabla }}_{\mathrm{\perp }}={\mathrm{\nabla }}_{\mathrm{\perp }}\cdot {\mathrm{\nabla }}^{\mathrm{\perp }}=0,\hat{n}\times (J{u}_{\mathrm{\perp }})=\hat{J}{u}^{\mathrm{\perp }},\\ u^{\mathrm{\perp }}=\hat{n}\times u_{\mathrm{\perp }},& u^{\mathrm{\perp }}\cdot u_{\mathrm{\perp }}=u_{\mathrm{\perp }}\cdot u^{\mathrm{\perp }}=0,\hat{n}\times u^{\mathrm{\perp }}=-u_{\mathrm{\perp }}.\end{array}$$

We next find the gradient of the basis vectors, and define Ricci rotation coefficients,

$$\begin{array}{rl}{\mathrm{\nabla }}_{\mathrm{\perp }}\hat{n}=-{\kappa }_1{\hat{t}}_1{\hat{t}}_1-{\kappa }_2{\hat{t}}_2{\hat{t}}_2,& {\mathcal{R}}_i^{jk}={\hat{t}}_j\cdot (\mathrm{\nabla }{\hat{t}}_i)\cdot {\hat{t}}_k,\hspace{0.17em}{\mathcal{R}}_1^{12}={\hat{t}}_1\cdot (\mathrm{\nabla }{\hat{t}}_1)\cdot {\hat{t}}_2={\omega }_1,\\ {\mathrm{\nabla }}_{\mathrm{\perp }}{\hat{t}}_i={\kappa }_i{\hat{t}}_i\hat{n}+{\mathcal{R}}_i^{jk}{\hat{t}}_j{\hat{t}}_k,& {\mathcal{R}}_i^{jk}=-{\mathcal{R}}_k^{ji},{\mathcal{R}}_2^{21}={\hat{t}}_2\cdot (\mathrm{\nabla }{\hat{t}}_2)\cdot {\hat{t}}_1=-{\omega }_2.\end{array}$$

These relations allow us to calculate all relevant vector calculus operators,

$$\begin{array}{rl}\mathrm{\nabla }\cdot u& =\frac{{\mathrm{\partial }}_{\sigma }(|J|u_{\sigma })}{|J|}+\frac{{\mathrm{\nabla }}_{\mathrm{\perp }}\cdot (\hat{J}{u}_{\mathrm{\perp }})}{|J|},\\ {\mathrm{\nabla }}^{2}f& =\frac{{\mathrm{\partial }}_{\sigma }(|J|{\mathrm{\partial }}_{\sigma }f)}{|J|}+\frac{{\mathrm{\nabla }}_{\mathrm{\perp }}\cdot (\hat{J}{J}^{-1}{\mathrm{\nabla }}_{\mathrm{\perp }}f)}{|J|},\\ \mathrm{\nabla }\times u& =-\hat{n}\frac{{\mathrm{\nabla }}_{\mathrm{\perp }}\cdot (\hat{J}{u}^{\mathrm{\perp }})}{|J|}+{\hat{J}}^{-1}({\mathrm{\partial }}_{\sigma }(\hat{J}{u}^{\mathrm{\perp }})-{\mathrm{\nabla }}_{\mathrm{\perp }}{u}_{\sigma })\\ & -\mathrm{\nabla }\times \mathrm{\nabla }u=\frac{\hat{n}}{|J|}(-{\mathrm{\nabla }}_{\mathrm{\perp }}\cdot (\hat{J}{J}^{-1}({\mathrm{\partial }}_{\sigma }(J{u}_{\mathrm{\perp }})-{\mathrm{\nabla }}_{\mathrm{\perp }}{u}_{\sigma })))\\ & +{\hat{J}}^{-1}{\mathrm{\partial }}_{\sigma }(\hat{J}{J}^{-1}({\mathrm{\partial }}_{\sigma }(J{u}_{\mathrm{\perp }})-{\mathrm{\nabla }}_{\mathrm{\perp }}{u}_{\sigma }))+{\hat{J}}^{-1}{\mathrm{\nabla }}_{\mathrm{\perp }}\left(\frac{{\mathrm{\nabla }}^{\mathrm{\perp }}\cdot (J{u}_{\mathrm{\perp }})}{|J|}\right),\\ \mathrm{\nabla }u& =\hat{n}\hspace{0.17em}\hat{n}\hspace{0.17em}{\mathrm{\partial }}_{\sigma }{u}_{\sigma }+\hat{n}{\mathrm{\partial }}_{\sigma }{u}_{\mathrm{\perp }}+J^{-1}({\mathrm{\nabla }}_{\mathrm{\perp }}{u}_{\sigma }+K{u}_{\mathrm{\perp }})\hspace{0.17em}\hat{n}+J^{-1}({\mathrm{\nabla }}_{\mathrm{\perp }}{u}_{\mathrm{\perp }}-K{u}_{\sigma }),\\ u\cdot \mathrm{\nabla }f& =u_{\sigma }{\mathrm{\partial }}_{\sigma }f+u_{\mathrm{\perp }}\cdot J^{-1}{\mathrm{\nabla }}_{\mathrm{\perp }}f,\\ u\cdot \mathrm{\nabla }u& =\hat{n}\hspace{0.17em}(u_{\sigma }{\mathrm{\partial }}_{\sigma }{u}_{\sigma }+u_{\mathrm{\perp }}\cdot J^{-1}({\mathrm{\nabla }}_{\mathrm{\perp }}{u}_{\sigma }+K{u}_{\mathrm{\perp }}))+u_{\sigma }{\mathrm{\partial }}_{\sigma }{u}_{\mathrm{\perp }}+u_{\mathrm{\perp }}\cdot J^{-1}({\mathrm{\nabla }}_{\mathrm{\perp }}{u}_{\mathrm{\perp }}-K{u}_{\sigma }),\\ {\mathrm{\partial }}_{t}f& ={\mathrm{\partial }}_{\tau }f-v{\mathrm{\partial }}_{\sigma }f+\sigma {\mathrm{\nabla }}_{\mathrm{\perp }}v\cdot J^{-1}\cdot {\mathrm{\nabla }}_{\mathrm{\perp }}f,\\ {\mathrm{\partial }}_{t}u& =({\mathrm{\partial }}_{\tau }{u}_{\sigma }-v{\mathrm{\partial }}_{\sigma }{u}_{\sigma }+\sigma {\mathrm{\nabla }}_{\mathrm{\perp }}v\cdot J^{-1}\cdot ({\mathrm{\nabla }}_{\mathrm{\perp }}{u}_{\sigma }+K{u}_{\mathrm{\perp }}))\hat{n}\\ & +({\mathrm{\partial }}_{\tau }{u}_{\mathrm{\perp }}-v{\mathrm{\partial }}_{\sigma }{u}_{\mathrm{\perp }}+\sigma {\mathrm{\nabla }}_{\mathrm{\perp }}v\cdot J^{-1}\cdot ({\mathrm{\nabla }}_{\mathrm{\perp }}{u}_{\mathrm{\perp }}-K{u}_{\sigma })).\end{array}$$

Rescaling—Rescaling the normal coordinate by ξ = σ/ε gives the following operators:

$$\begin{array}{rl}\mathrm{\nabla }& ={\epsilon }^{-1}\hat{n}{\mathrm{\partial }}_{\xi }+{\sum }_{k=0}^{\mathrm{\infty }}{\epsilon }^k{\xi }^k{K}^k{\mathrm{\nabla }}_{\mathrm{\perp }},\\ |J|\mathrm{\nabla }\cdot u& ={\epsilon }^{-1}{\mathrm{\partial }}_{\xi }{u}_{\sigma }-{\mathrm{\partial }}_{\xi }(\xi \overline{K}{u}_{\sigma })+{\mathrm{\nabla }}_{\mathrm{\perp }}\cdot u_{\mathrm{\perp }}+\epsilon ({\mathrm{\partial }}_{\xi }({\xi }^2|K|u_{\sigma })-\xi {\mathrm{\nabla }}_{\mathrm{\perp }}\cdot (\hat{K}{u}_{\mathrm{\perp }})),\\ {\mathrm{\nabla }}^{2}f& ={\epsilon }^{-2}{\mathrm{\partial }}_{\xi }^{2}f+{\epsilon }^{-1}(-\overline{K}{\mathrm{\partial }}_{\xi }f)+{\epsilon }^0(-\xi \overline{K^2}{\mathrm{\partial }}_{\xi }f+{\mathrm{\nabla }}_{\mathrm{\perp }}\cdot {\mathrm{\nabla }}_{\mathrm{\perp }}f)+\mathcal{O}(\epsilon )\\ & -\mathrm{\nabla }\times \mathrm{\nabla }\times u={\epsilon }^{-2}{\mathrm{\partial }}_{\xi }^2{u}_{\mathrm{\perp }}+{\epsilon }^{-1}(-\overline{K}{\mathrm{\partial }}_{\xi }{u}_{\mathrm{\perp }}-{\mathrm{\partial }}_{\xi }{\mathrm{\nabla }}_{\mathrm{\perp }}{u}_{\sigma }-\hat{n}{\mathrm{\nabla }}_{\mathrm{\perp }}\cdot ({\mathrm{\partial }}_{\xi }{u}_{\mathrm{\perp }}))+\mathcal{O}({\epsilon }^0),\\ u\cdot \mathrm{\nabla }f& ={\epsilon }^{-1}{u}_{\sigma }{\mathrm{\partial }}_{\xi }f+{\sum }_{k=0}^{\mathrm{\infty }}{\epsilon }^k{\xi }^k{K}^k{u}_{\mathrm{\perp }}\cdot {\mathrm{\nabla }}_{\mathrm{\perp }}f,\\ u\cdot \mathrm{\nabla }u& ={\epsilon }^{-1}(u_{\sigma }{\mathrm{\partial }}_{\xi }{u}_{\mathrm{\perp }}+\hat{n}{u}_{\sigma }{\mathrm{\partial }}_{\xi }{u}_{\sigma })\\ & +{\sum }_{k=0}^{\mathrm{\infty }}{\epsilon }^k{\xi }^k{u}_{\mathrm{\perp }}{K}^k\cdot (({\mathrm{\nabla }}_{\mathrm{\perp }}{u}_{\mathrm{\perp }}-K{u}_{\sigma })+({\mathrm{\nabla }}_{\mathrm{\perp }}{u}_{\sigma }+K{u}_{\mathrm{\perp }})\hat{n}),\\ {\mathrm{\partial }}_t& =-{\epsilon }^{-1}v{\mathrm{\partial }}_{\xi }+{\epsilon }^0{\mathrm{\partial }}_{\tau }+{\epsilon }^1(\xi {\mathrm{\nabla }}_{\mathrm{\perp }}v\cdot \sum _{k=0}^{\mathrm{\infty }}{\epsilon }^k{\xi }^k{K}^k{\mathrm{\nabla }}_{\mathrm{\perp }}).\end{array}$$

Appendix B. Differential geometry of remapped coordinates

We solve §4b by remapping to a fixed rectangular domain with coordinates τ, ξ and ζ^±,

$$\tau (t,x,z)=t,\xi (t,x,z)=x,\hspace{0.17em}{\zeta }^{+}(t,x,z)=\frac{z}{h(t,x)},\hspace{0.17em}{\zeta }^{-}(t,x,z)=\frac{z-h(t,x)}{2-h(t,x)},\hspace{0.17em}\eta (\tau ,\xi )=h(t,x),$$

where η is the interface height in the new coordinates. We now develop the differential geometry required to write equations (2.1) and (2.4) in the new coordinates. We give explicit formulae for the ζ⁺ remapping. The ζ⁻ remapping is analogous and straightforward to derive. We use a tangent vector basis derived from the Jacobian $\mathcal{J}$ of our transformation and its inverse $\mathcal{K}$,

$${\mathcal{J}}^{+}\equiv \left[\begin{array}{ccc}{\mathrm{\partial }}_t\tau & {\mathrm{\partial }}_t\xi & {\mathrm{\partial }}_t\zeta \\ {\mathrm{\partial }}_x\tau & {\mathrm{\partial }}_x\xi & {\mathrm{\partial }}_x\zeta \\ {\mathrm{\partial }}_z\tau & {\mathrm{\partial }}_z\xi & {\mathrm{\partial }}_z\zeta \end{array}\right]=\left[\begin{array}{ccc}1& 0& -\zeta \frac{{\mathrm{\partial }}_{\tau }\eta }{\eta }\\ 0& 1& -\zeta \frac{{\mathrm{\partial }}_{\xi }\eta }{\eta }\\ 0& 0& \frac{1}{\eta }\end{array}\right]\text{and}{\mathcal{K}}^{+}\equiv \left[\begin{array}{ccc}{\mathrm{\partial }}_{\tau }t& {\mathrm{\partial }}_{\tau }x& {\mathrm{\partial }}_{\tau }z\\ {\mathrm{\partial }}_{\xi }t& {\mathrm{\partial }}_{\xi }x& {\mathrm{\partial }}_{\xi }z\\ {\mathrm{\partial }}_{\zeta }t& {\mathrm{\partial }}_{\zeta }x& {\mathrm{\partial }}_{\zeta }z\end{array}\right]=\left[\begin{array}{ccc}1& 0& \zeta {\mathrm{\partial }}_{\tau }\eta \\ 0& 1& \zeta {\mathrm{\partial }}_{\xi }\eta \\ 0& 0& \eta \end{array}\right].$$

The tangent vector components are the rows of the spatial component of the inverse Jacobian $e_i={{\mathcal{K}}_i}^j{\hat{e}}_j$. We use Einstein notation to sum over the spatial indices i = 1, 2. These tangent vectors induce dual vectors ${\omega }^i={{\mathcal{J}}_j}^i\hspace{0.17em}{\hat{e}}^j$ which satisfy ${\omega }^i\cdot e_j={\delta }_j^i$, with components from the column vectors of the spatial component of the Jacobian. We record the length of the vectors using the metric, with co/contravariant components g_ij = e_i · e_j, g^ij = Ωⁱ · Ω^j,

$$\begin{array}{rl}{e}_1^{+}={\hat{e}}_1+\zeta {\mathrm{\partial }}_{\xi }\eta \hspace{0.17em}{\hat{e}}_2,& e_2^{+}=\eta \hspace{0.17em}{\hat{e}}_2,{{\omega }^1}^{+}={\hat{e}}_1,{{\omega }^2}^{+}=\frac{{\hat{e}}_2-\zeta {\mathrm{\partial }}_{\xi }\eta \hspace{0.17em}{\hat{e}}_1}{\eta },\\ g_{11}^{+}=(1+{\zeta }^2{\mathrm{\partial }}_{\xi }{\eta }^2),& g_{12}^{+}=\zeta \eta {\mathrm{\partial }}_{\xi }\eta ,{g^{11}}^{+}=1,{g^{12}}^{+}=-\zeta \frac{{\mathrm{\partial }}_{\xi }\eta }{\eta },\\ g_{21}^{+}=\zeta \eta {\mathrm{\partial }}_{\xi }\eta ,g_{22}^{+}={\eta }^2,& {g^{21}}^{+}=-\zeta \frac{{\mathrm{\partial }}_{\xi }\eta }{\eta },{g^{22}}^{+}=\frac{1}{{\eta }^2}(1+{\zeta }^2{\mathrm{\partial }}_{\xi }{\eta }^2).\end{array}$$

These give ‘Jacobian’ $||\mathcal{K}||$ determinants of $||{\mathcal{K}}^{+}||\equiv \sqrt{||g_{ij}||}=\eta$. The completely antisymmetric tensor can be transformed from Cartesian coordinates,

$$\mathcal{E}=[ij]{\hat{\omega }}^i{\hat{\omega }}^j=[ij]{\mathcal{K}}_k^i{\mathcal{K}}_l^j\hspace{0.17em}{\omega }^k{\omega }^l=||\mathcal{K}||[kl]\hspace{0.17em}{\omega }^k{\omega }^l=\frac{1}{||\mathcal{K}||}[kl]\hspace{0.17em}{e}_k{e}_l,$$

where [ij] is the antisymmetric symbol. We project the gradient to the tangent basis with the covariant derivative ${\mathrm{\nabla }}_i=e_i\cdot \mathrm{\nabla }\hspace{0.17em}⟺\hspace{0.17em}\mathrm{\nabla }={\omega }^i{\mathrm{\nabla }}_i$. We measure spatial variation of the basis with the connection coefficients ${\mathrm{\Gamma }}_{ij}^k={\omega }^k\cdot {\mathrm{\nabla }}_j{e}_i\hspace{0.17em}⟺\hspace{0.17em}{e}_j\cdot \mathrm{\nabla }{e}_i={\mathrm{\Gamma }}_{ij}^k{e}_k$. For the tangent basis, the connection coefficients take a particularly simple and symmetric form

$$[{{\mathrm{\Gamma }}_{11}^1}^{+}={{\mathrm{\Gamma }}_{12}^1}^{+}={{\mathrm{\Gamma }}_{21}^1}^{+}={{\mathrm{\Gamma }}_{22}^1}^{+}=0,\hspace{0.17em}{{\mathrm{\Gamma }}_{11}^2}^{+}=\frac{\zeta {\mathrm{\partial }}_{\xi }^2\eta }{\eta },\hspace{0.17em}{{\mathrm{\Gamma }}_{12}^2}^{+}={{\mathrm{\Gamma }}_{21}^2}^{+}=\frac{{\mathrm{\partial }}_{\xi }\eta }{\eta },\hspace{0.17em}{{\mathrm{\Gamma }}_{22}^2}^{+}=0.$$

We note the connection coefficients for the dual vectors are related to those for the tangent basis by $0={\mathrm{\nabla }}_k({\omega }^i\cdot e_j)={\mathrm{\nabla }}_k({\omega }^i)\cdot e_j+{\omega }^i\cdot {\mathrm{\nabla }}_k(e_j)={\mathrm{\nabla }}_k({\omega }^i)\cdot e_j+{\mathrm{\Gamma }}_{jk}^i$. The partial time derivative ∂_t changes as defined in zeroth row of the Jacobian, and the basis vectors also evolve in time,

$${\mathrm{\partial }}_{\tau }{e}_1^{+}\equiv {{\mathrm{\Gamma }}_{10}^i}^{+}{e}_i^{+}=\frac{\zeta }{\eta }{\mathrm{\partial }}_{\tau }{\mathrm{\partial }}_{\xi }\eta \hspace{0.17em}{e}_2^{+},{\mathrm{\partial }}_{\tau }{e}_2^{+}\equiv {{\mathrm{\Gamma }}_{20}^i}^{+}{e}_i^{+}=\frac{{\mathrm{\partial }}_{\tau }\eta }{\eta }\hspace{0.17em}{e}_2^{+}.$$

These geometric quantities allow us to calculate all the relevant vector calculus quantities,

$$\begin{array}{rl}\mathrm{\nabla }u& ={\mathrm{\nabla }}_i(u^j\hspace{0.17em}{e}_j){\omega }^i=({\mathrm{\nabla }}_i{u}^j+u^k{\mathrm{\Gamma }}_{ki}^j)\hspace{0.17em}{e}_j\hspace{0.17em}{\omega }^i,\\ \mathrm{\nabla }\cdot u& =\mathrm{\nabla }u:I=({\mathrm{\nabla }}_i{u}^j+u^k{\mathrm{\Gamma }}_{ki}^j)\hspace{0.17em}{e}_j\cdot {\omega }^i={\mathrm{\nabla }}_i{u}^i+u^k{\mathrm{\Gamma }}_{ki}^i,\\ \mathrm{\nabla }\times u& ={\mathcal{E}}^{\mathrm{\top }}:\mathrm{\nabla }u=({\mathcal{E}}_{ij}{\omega }^i{\omega }^j):{\omega }^k({\mathrm{\nabla }}_k)(u^l\hspace{0.17em}{e}_l)=||\mathcal{K}||[ij]u_{;k}^l({\omega }^i\cdot {\omega }^k)({\omega }^j\cdot e_l)=||\mathcal{K}||[ij]g^{ik}{u}_{;k}^j,\\ \mathrm{\nabla }\times q& ={\mathcal{E}}^{\mathrm{\top }}\cdot \mathrm{\nabla }q=({\mathcal{E}}^{ij}{\mathrm{\nabla }}_{k}q)(e_j\cdot {\omega }^k)e_i=\frac{1}{||\mathcal{K}||}[ij]q_{,j}{e}_i=\frac{1}{||\mathcal{K}||}(q_{,2}{e}_1-q_{,1}{e}_2),\\ {\mathrm{\nabla }}^{2}f& ={\mathrm{\nabla }}_i({\mathrm{\nabla }}_{j}f\hspace{0.17em}{\omega }^j)\hspace{0.17em}{\omega }^i:I=({\mathrm{\nabla }}_i{\mathrm{\nabla }}_{j}f)\hspace{0.17em}{\omega }^j\cdot {\omega }^i-{\mathrm{\nabla }}_{j}f{\mathrm{\Gamma }}_{ki}^j{\omega }^k\cdot {\omega }^i=g^{ji}{\mathrm{\nabla }}_i{\mathrm{\nabla }}_{j}f-g^{ki}{\mathrm{\nabla }}_{j}f{\mathrm{\Gamma }}_{ki}^j,\\ \mathrm{\nabla }p& =g^{ji}{p}_{,j}{e}_i,\\ u\times q& =\mathcal{E}\cdot uq=({\mathcal{E}}_{ij}{\omega }^i{\omega }^j)\cdot (q{u}^k{e}_k)=||\mathcal{K}||g^{jk}[ij]u^i{e}_k=||\mathcal{K}||q(g^{2k}{u}^1-g^{1k}{u}^2)e_k,\\ \mathrm{\nabla }\times \mathrm{\nabla }\times u& =[ij]{\mathrm{\partial }}_j([kl]{\mathrm{\partial }}_k{u}_l)\hspace{0.17em}{\hat{e}}_i=({\delta }_{ik}{\delta }_{jl}-{\delta }_{il}{\delta }_{jk}){\mathrm{\partial }}_j{\mathrm{\partial }}_k{u}_l{\hat{e}}_i=\mathrm{\nabla }(\mathrm{\nabla }\cdot u)-{\mathrm{\nabla }}^{2}u,\\ (\mathrm{\nabla }\times u)\times u& =[ij][kl]{\mathrm{\partial }}_k{u}_l{u}_j{\hat{e}}_i=({\mathrm{\partial }}_i{u}_j-{\mathrm{\partial }}_j{u}_i)u_j{\hat{e}}_i=\frac{1}{2}\mathrm{\nabla }(u\cdot u)-(u\cdot \mathrm{\nabla })u,\\ \mathrm{\nabla }\cdot (uu)& =(u\cdot \mathrm{\nabla })u+(\mathrm{\nabla }\cdot u)u,\\ {\mathrm{\partial }}_t& ={\mathrm{\partial }}_{\tau }+{{\mathcal{J}}_0}^i{\mathrm{\nabla }}_i,\\ {\mathrm{\partial }}_{t}u& ={\mathrm{\partial }}_t{u}^i{e}_i+u^i{\mathrm{\partial }}_t{e}_i=({\mathrm{\partial }}_{\tau }+{\mathcal{J}}_0^i{\mathrm{\nabla }}_i)u^j{e}_j+{{\mathcal{J}}_0}^{i\ge 0}{\mathrm{\Gamma }}_{ki\ge 0}^j{u}^k{e}_j.\end{array}$$

The normal vector at the interface is proportional to the ζ dual vector. This gives us the normal gradient and normal velocity at the interface,

$$\hat{n}=\frac{{\omega }^2}{\sqrt{g^{22}}}\hat{n}\cdot \mathrm{\nabla }=\frac{g^{2i}}{\sqrt{g^{22}}}{\mathrm{\nabla }}_i,v={\mathrm{\partial }}_{t}h\hspace{0.17em}{\hat{e}}_z,\hat{n}\cdot v=\frac{1}{\sqrt{g^{22}}}\frac{{\mathrm{\partial }}_{t}h}{h}.$$

We finally write the interfacial curvature as $\kappa ={\mathrm{\partial }}_{\xi }^2\eta /{(1+{\mathrm{\partial }}_{\xi }{\eta }^2)}^{3/2}$. This completes the relations used to simulate the sharp interface and phase-field equations in remapped geometries.

Data accessibility

The Dedalus code is free and open-source and available at http://dedalus-project.org/. All simulation code, data and analysis scripts and plots are available at https://github.com/ericwhester/phase-field-code. The Mathematica asymptotics script is also available at that link.

Authors' contributions

E.W.H. project conception and design, writing, mathematics (asymptotics and remapping), simulation code, data analysis and visualization; L.-A.C. project design and conception; B.F. project design and conception, phase-field expertise; K.J.B. domain remapping simulation expertise, Dedalus code; G.M.V. mathematics of signed distance coordinates, Dedalus code. All authors provided critical revision of the manuscript, approve the final version of the paper and agree to be held accountable for the work.

Competing interests

We declare that we have no competing interests.

Funding

E.W.H. acknowledges support from The University of Sydney Phillip Hofflin International Research Travel Scholarship, Postgraduate Research Support Scheme and William and Catherine McIlrath Scholarship. L.-A.C. acknowledges support from the European Union’s Horizon 2020 research and innovation programme under Marie Skłodowska-Curie grant agreement no. MIMOP 793450.