Development of a Physiologically-Based Pharmacokinetic Model for Ocular Disposition of Monoclonal Antibodies in Rabbits

Abstract

Development of protein therapeutics for ocular disorders, particularly age-related macular degeneration (AMD), is a highly competitive and expanding therapeutic area. However, the application of a predictive and translatable ocular PK model to better understand ocular disposition of protein therapeutics, such as a physiologically-based pharmacokinetic (PBPK) model, is missing from the literature. Here, we present an expansion of an antibody platform PBPK model towards rabbit and incorporate a novel anatomical and physiologically relevant ocular component. Parameters describing all tissues, flows, and binding events were obtained from existing literature and fixed a priori. First, translation of the platform PBPK model to rabbit was confirmed by evaluating the model’s ability to predict plasma PK of a systemically administered exogenous antibody. Then, the PBPK model with the new ocular component was validated by estimation of serum and ocular (i.e. aqueous humor, retina, and vitreous humor) PK of two intravitreally administered monoclonal antibodies. We show that the proposed PBPK model is capable of accurately (i.e. within 2-fold) predicting ocular exposure of antibody-based drugs. The proposed PBPK model can be used for preclinical-to-clinical translation of antibodies developed for ocular disorders, and assessment of ocular toxicity for systemically administered antibody-based therapeutics.

Introduction

Diseases of the eye have significant impacts on the lives of patients ranging from transient irritation to irreversible vision loss. Of the ocular disorders, age-related macular degeneration (AMD) and diabetic retinopathy (DR) are among the leading causes of blindness and are primary indications for protein therapeutics[1,2]. In fact, all four FDA-approved therapies for AMD and DR are macromolecules: Macugen (pegaptanib, Gilead Sciences, Inc), Lucentis (ranibizumab, Genentech, Inc), Eylea (aflibercept, Regeneron Pharmaceuticals, Inc.), and Beovu (brolucizumab, Novartis International AG). With AMD alone expected to reach a global market of $10.4 billion by 2024, research in eye disease remains active and will benefit greatly from new tools that accelerate protein therapeutic drug development[3]. One such tool is pharmacokinetic (PK) models, which can help in characterization and a priori prediction of the ocular PK of protein therapeutics.

Existing ocular PK models for protein therapeutics take empiric or traditional compartmental approaches, although recent efforts incorporate more mechanistic aspects, such as tissue permeability and fixed anatomical volumes[4-7]. Currently, there are no mathematical models that characterize PK of protein therapeutics in the eye using purely physiologic parameters. Moreover, as most preclinical studies (e.g. in rabbits) collect only vitreous humor (VH), aqueous humor (AH), and occasionally retina for analysis, the PK in the rest of the ocular tissues is neglected. A physiologically-based pharmacokinetic (PBPK) model for the eye will help in accurately predicting the PK of a drug in all ocular tissues, including the retina and the frequently overlooked cornea, iris-ciliary body (ICB), and choroid. Thus, modelling the exposure in all the tissues of the eye will aid in the development of protein therapeutics for numerous ocular disorders, not just retinopathies.

Predicting the ocular exposure of protein therapeutics with the PBPK model can also help in evaluating the potential of drug induced toxicities in the eye. Antibodies for chemotherapy are targeted agents that are meant to be efficacious against cancerous cells that overexpress a specific antigen. However, presence of the target in healthy tissue, even at low levels, carries the risk of off-target, ocular toxicities, such as corneal microcysts, keratitis, and blurred vision [8-11], Several antibodies against various anti-cancer antigens currently used in therapy have shown potential ocular toxicities including Herceptin (trastuzumab, Genentech, Inc), Kadcyla (trastuzumab emtansine, Genentech, Inc.), Yervoy (ipilimumab, Bristol-Myers Squibb), and Erbitux (cetuximab, Eli Lilly). Ideally, the ocular PBPK model predicts concentrations in the eye tissues based on systemic exposure and can provide a risk assessment for ocular toxicity potential.

Since the 1980s, pharmacometricians have had great interest in the development of PBPK models for protein therapeutics[12-16]. In addition to predicting concentrations at the tissue level, PBPK models also take into account complex interactions between the drug and the proteins in the body, such as FcRn and antigen targets. With a PBPK model, the plasma and tissue-specific PK of a therapeutic can be predicted based on drug-specific parameters that can be obtained in vitro. Furthermore, PBPK models are easily translated between species. Characterization of a drug’s PK in one species can be used to predict the PK in another species, simply by changing the physiological parameters of the system.

In 2012, Shah and Betts[16], proposed a platform PBPK model to characterize the plasma and tissue PK of several monoclonal antibodies in mice, rats, monkeys, and human. In this manuscript we have presented the expansion of this platform PBPK model to include rabbit as an additional species. Specifically, rabbits were chosen as they are a predominant species used in ocular research[17,18] and in antivenom research[19-22], both fields that focus on the development of immunoglobulin (IgG)-based therapies.

In particular, the capabilities of PBPK modelling are currently underutilized in ocular research. Thus, our goal is to expand the platform PBPK model for antibody disposition into rabbit and incorporate a novel ocular component in the model. This PBPK model will help in preclinical to clinical translation of new therapies for ocular disorders and will help in the assessment of potential ocular toxicity for systemically administered antibody-based therapies.

Methods

Experimental Data.

We utilized data from several publications investigating the PK of full-size IgG antibodies in rabbits. All studies were carried in accordance with the Animal Welfare Act and were approved by the applicable Institutional Animal Care and Use Committee.

Data for the systemic PK of antibody comes from two studies in anthrax research. The first, is from a subset of data from Malkevich et al. [23]. In the relevant experiments, the authors dosed New Zealand White rabbits with Anthrivig (polyclonal human anthrax immunoglobulin, AIGIV), by intravenous infusion at 14.2 or 21.3 mg/kg bodyweight. Serial plasma samples were collected over 29 days and analyzed by ELISA[23]. In the second study, Nagy et al.[24]. investigators dosed New Zealand White rabbits with obiltoxaximab (chimeric monoclonal antibody) at 3, 10, or 30 mg/kg. Serum was collected over 28 days and analyzed by electrochemiluminescent assay[24].

Four additional sets of data contained intraocular PK of antibody after intravitreal administration in rabbits. The first, from Bakri et al.[25], provided the PK of bevacizumab (humanized antivascular endothelial growth factor, VEGF) in 20 Dutch-belted rabbits after intravitreal injection of 1.25 mg in one eye. On days 1, 3, 8, 15, and 29,terminal samples of serum, vitreous humor, and aqueous humor were collected [25]. The second data set comes from Nomoto et al.[26], who administered 1.25 mg bevacizumab intravitreally to a single eye in each of 24 Dutch-belted rabbits and collected plasma, retina, iris/ciliary body, vitreous humor, and aqueous humor at 1, 2, 4, and 12 weeks post-injection. In the third data set, Sinapis et al.[27] unilaterally injected 1.25 mg bevacizumab in 20 New Zealand White Rabbits and collected serum, vitreous humor, and aqueous humor on days 1, 2, 8, 15, and 29 after injection. The final data set comes from Gadkar et al. [28] (obtained from publication in Hutton-Smith et al.[5]) in which New Zealand White rabbits were administered one of several human antibodies or antibody fragments. The current study only utilizes the dataset for full-length IgG against glycoprotein D (α-gD). Rabbits received intravitreal injections of 0.5 mg/eye in both eyes. Terminal samples of serum, vitreous humor, aqueous humor, and retina were obtained at 0.25, 2, 8, 14, 21, and 28 days [28]. In all studies, antibody concentrations where determined by ELISA [26-28] or chemiluminescent immunoassay [25].

Platform PBPK Model.

The structure of the whole-body PBPK model, originally developed by Shah and Betts[16], is described in Figure 1. The model incorporates plasma and blood cell compartments, as well as 16 major tissues and an optional tumor compartment (not utilized in the present study). The 17th “other” compartment comprises all the remaining tissues not explicitly identified in the model. All tissues are connected by anatomical plasma/blood flow and lymphatic recirculation through the lymph nodes. Each of the 16 tissue compartments (except for the eye) is further sub-divided into the following 6 components: blood cells, plasma space, endosomal space, interstitial space, cell membrane, and cellular space (Figure 2)[16]. In this manner, we describe the flow of plasma (Q) into the tissue and the outward flow of plasma (Q-L) and lymph (L). IgG within the plasma space enters the tissue by two processes: (1) via paracellular pores using convective lymph flow, where the vascular reflection coefficient (σv) represents resistance to IgG convection by the vascular endothelial cells, or (2) via pinocytosis (CLup) into the endosomal space, where IgG may bind to FcRn and be recycled back into the plasma space (FR) or into the interstitial space (1-FR) via exocytosis. Unbound IgG in the endosomal space is degraded by a first-order process (Kdeg) in the lysosome. Once in the interstitial space, IgG is cleared by the flow of lymph where the interstitial reflection coefficient (σi) represents resistance to IgG convection by the lymphatic openings. Should the antibody in the interstitial space have a cellular target, it is tree to bind to antigen (Ag) expressed on the cell surface and be internalized (Kint_Ag-IgG). However, the antibodies selected as part of this study do not have targets expressed in rabbits. Therefore, parameters associated with antigen binding and internalization are set to zero.

Fig. 1.

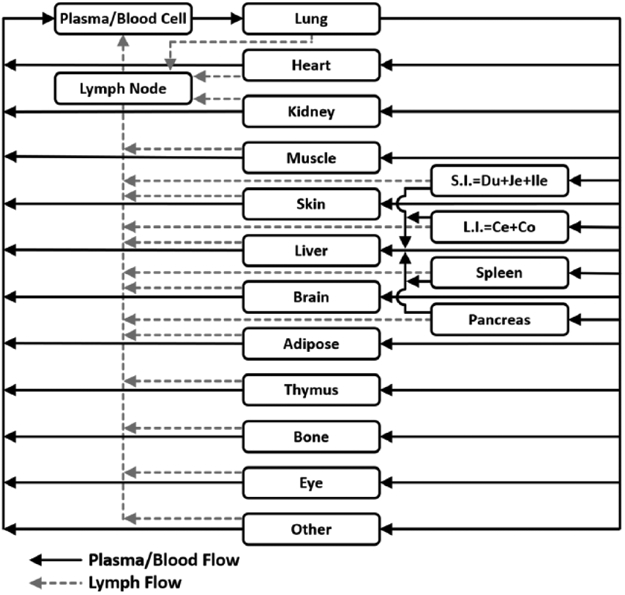
Schematic of the whole body PBPK model for antibody distribution. Rectangular compartments represent organs and solid and dashed arrows represent blood and lymph flow, respectively. Each tissue contains several sub-compartments as shown in Figure 2.

Fig. 2.

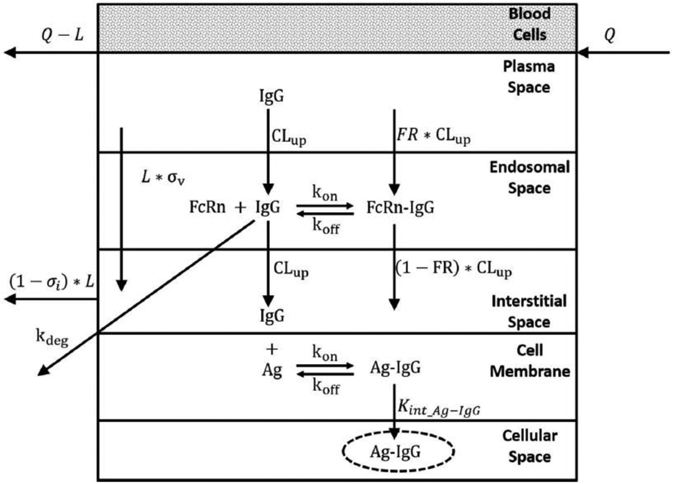
Schematic of tissue-level structure of the PBPK model. Please refer to the text for description of the processes involved in antibody disposition.

The physiological parameters related to tissue volumes and fluid flows in the PBPK model were obtained from a variety of sources[29-32]. The values and descriptions for physiological parameters of the platform model are shown in Tables 1 and 2. The lymph flow for all tissues was set to 0.2% of plasma flow and the endosomal volume was set to 0.5% of the total tissue volume[33,15]. The fraction of IgG bound to FcRn that recycles back to the plasma space (FR) was set to 0.715[34]. The vascular reflection coefficients (σv) for each tissue were set a priori and are as follows: 0.85 for spleen, liver, and bone; 0.9 for kidney, thymus, small intestine, and pancreas; 0.95 for lung, heart, muscle, skin, adipose, large intestine, and other; and 0.99 for brain[35]. The interstitial reflection coefficient (σi) was set to 0.2 in all tissues[15]. The association (K_on) and dissociation (K_off) rates for human/humanized IgG binding to rabbit FcRn are 2.85x10⁷ M⁻¹h⁻¹ and 1.4 h⁻¹, respectively[36], Pinocytosis and exocytosis rate (CL_up), lysosomal degradation rate (K_deg), and FcRn concentration were set to 0.55 L/h, 32.2 h⁻¹, and 4.98x10⁻⁵ M, as reported previously [37,16], The proportionality constant (C_LNLF) between the rate at which IgG transfers into the plasma from the lymph node and the plasma flow itself was set to 9.1, as determined by Shah and Betts[16]. Equations for the platform PBPK model are provided below.

Table 1.

Physiological model parameters for rabbit.

	Total Volume (L)	Plasma Volume (L)	Blood Cell Volume (L)	Interstitial Volume (L)	Endosomal Volume (L)	Cellular Volume (L)	Plasma Flow (L/h)	Blood Cell Flow (L/h)
Lung	0.0170	0.00247	0.00123	0.00320	0.0000850	0.0100	21.2	10.6
Heart	0.00600	0.000231	0.000116	0.000600	0.0000300	0.00502	0.768	0.384
Kidney	0.0150	0.00158	0.000788	0.00300	0.0000750	0.0103	3.69	1.85
Muscle	1.35	0.0351	0.0176	0.162	0.00675	1.13	6.21	3.11
Skin	0.110	0.00209	0.00105	0.0332	0.000550	0.0711	1.63	0.813
Brain	0.0140	0.000518	0.000259	5.60E-06	0.0000700	0.0134	0.380	0.190
Adipose	0.120	0.00120	0.000600	0.0162	0.000600	0.10128	1.28	0.641
Thymus S.	0.00410	0.000228	0.000114	0.000697	2.05E-05	0.00374	0.0224	0.0112
Intestine L.	0.0600	0.00144	0.000720	0.00564	0.000300	0.0524	2.21	1.10
Intestine	0.0300	0.000720	0.000360	0.00282	0.000150	0.0262	0.564	0.282
Spleen	0.00100	0.000282	0.000141	0.000150	0.00000500	0.000583	0.360	0.180
Pancreas	0.00360	0.000648	0.000324	0.000432	0.0000180	0.00263	0.144	0.0720
Liver	0.100	0.0115	0.00575	0.0163	0.000500	0.0690	0.163	0.0815
Bone	0.310	0.0127	0.00636	0.0310	0.00155	0.264	1.86	0.930
Ly. Node	0.0103	--	--	--	--	0.0103	--	--
Other	0.2493	0.0103	0.00517	0.0422	0.00123	0.230	1.89	0.943
Plasma	0.110	--	--	--	--	--	21.2	--
Blood Cells	0.055	--	--	--	--	--	--	10.6

Table 2.

Glossary of parameters used in the PBPK model

Parameter	Units	Definition
PLQi	L /h	Plasma flow to the tissue “i”
BCQi	L /h	Blood cell flow to the tissue “i”
Li	L /h	Lymph flow from the tissue “i”
VPlasma, VBC, VLymphNode	L	Volumes of the central plasma, central blood cell, and lymph node compartments
$V_i^V$, $V_i^{BC}$, $V_i^E$, $V_i^{IS}$, $V_i^C$	L	Volumes of the vascular, blood cell, endosomal, interstitial, and cellular compartments for the tissue “i”
CPlasma, CBC, CLymphNode	nM	Concentrations in the central plasma, central blood cell, and lymph node compartments
$C_i^V$, $C_i^{BC}$, $C_i^{E_{Unbound}}$, $C_i^{E_{Bound}}$, $C_i^{IS}$, $C_i^{C_{Bound}}$	nM	Concentrations in the vascular, blood cell, endosomal (Unbound and Bound), interstitial, and cellular (Bound) compartments for the tissue “i”
FcRn	M	Concentration of FcRn in the endosomal space
${\sigma }_i^V$, ${\sigma }_i^{IS}$	–	Vascular and lymph reflection coefficients
$K_{on}^{FcRn}$, $K_{on}^{Ag}$	1 /M/h	Association rate constants between mAb and FcRn and mAb and Antigen
$K_{off}^{FcRn}$, $K_{off}^{Ag}$	1/h	Dissociation rate constants between mAb and FcRn and mAb and Antigen
FR	–	Fraction of FcRn bound mAb that recycles to the vascular space
CLup	L/h/L	Rate of pinocytosis and exocytosis per unit endosomal space of the vascular endothelium
Kdeg	1/h	First-order degradation rate constant of FcRn-unbound mAb in the endosomal space

Blood Compartment

Plasma Space

$$\begin{gathered} \frac{d}{dt}{C}_{plasma}=(PL{Q}_{Heart}-L{F}_{Heart})\ast C_{Hear{t}_V}+(PL{Q}_{Kidney}-L{F}_{Kidney})\ast C_{Kidne{y}_V} \\ +(PL{Q}_{Muscle}-L{F}_{Muscle})\ast C_{Muscl{e}_V}+(PL{Q}_{Skin}-L{F}_{Skin})\ast C_{Ski{n}_V} \\ +(PL{Q}_{Brain}-L{F}_{Brain})\ast C_{Brai{n}_V}+(PL{Q}_{Adipose}-L{F}_{Adipose})\ast C_{Adipos{e}_V} \\ +(PL{Q}_{Thymus}-L{F}_{Thymus})\ast C_{Thymu{s}_V} \\ +((PL{Q}_{Liver}-L{F}_{Liver})+(PL{Q}_{S.Intestine}-L{F}_{S.Intestine})\phantom{)} \\ +(PL{Q}_{L.Intestine}-L{F}_{L.Intestine})+(PL{Q}_{Spleen}-L{F}_{Spleen}) \\ \phantom{(}+(PL{Q}_{Pancreas}-L{F}_{Pancreas}))\ast C_{Live{r}_V}+(PL{Q}_{Bone}-L{F}_{Bone})\ast C_{Bon{e}_V} \\ +(PL{Q}_{Other}-L{F}_{Other})\ast C_{Othe{r}_V}+2\left((PL{Q}_{Eye}-L{F}_{Eye})\ast f_{cho}\ast C_{Ey{e}_V}\right) \\ +2\left((PL{Q}_{Eye}-L{F}_{Eye})\ast f_{ret}\ast C_{Ey{e}_V}\right) \\ +2\left((PL{Q}_{Eye}-L{F}_{Eye})\ast (1-f_{cho}-f_{ret})\ast C_{Ey{e}_V}\right)-(PL{Q}_{Lung}+L{F}_{Lung}) \\ \ast C_{Plasma}+L{F}_{LymphNode}\ast C_{LymphNod{e}_V}\ast \left(\frac{1}{V_{Plasma}}\right) \end{gathered}$$ (1)

Blood Cell Space

$$\begin{gathered} \frac{d}{dt}{C}_{BC}=(BC{Q}_{Heart}\ast C_{Hear{t}_{BC}}+BC{Q}_{Kidney})\ast C_{Kidne{y}_{BC}}+BC{Q}_{Muscle}\ast C_{Muscl{e}_{BC}}\phantom{)} \\ +BC{Q}_{Skin}\ast C_{Ski{n}_{BC}}+BC{Q}_{Brain}\ast C_{Brai{n}_{BC}}+BC{Q}_{Adipose}\ast C_{Adipos{e}_{BC}} \\ +BC{Q}_{Thymus}\ast C_{Thymu{s}_{BC}} \\ +(BC{Q}_{Liver}+BC{Q}_{S.Intestine}+BC{Q}_{L.Intestine}+BC{Q}_{Spleen}+BC{Q}_{Pancreas}) \\ \ast C_{Live{r}_{BC}}+BC{Q}_{Bone}\ast C_{Bon{e}_{BC}}+BC{Q}_{Other}\ast C_{Othe{r}_{BC}} \\ +2(BC{Q}_{Eye}\ast f_{cho}\ast C_{Ey{e}_{BC}})+2(BC{Q}_{Eye}\ast f_{ret}\ast C_{Ey{e}_{BC}}) \\ \phantom{(}+2(BC{Q}_{Eye}\ast (1-f_{cho}-f_{ret})\ast C_{Ey{e}_{BC}})-BC{Q}_{Lung}\ast C_{BC})\ast \left(\frac{1}{V_{BC}}\right) \end{gathered}$$ (2)

Lymph Node Compartment

$$\begin{gathered} \frac{d}{dt}{C}_{LymphNode} \\ =((1-ISR{C}_{Heart})\ast L{F}_{Heart}\ast C_{Hear{t}_I}+(1-ISR{C}_{Kidney})\ast L{F}_{Kidney}\phantom{)} \\ \ast C_{Kidne{y}_I}+(1-ISR{C}_{Muscle})\ast L{F}_{Muscle}\ast C_{Muscl{e}_I}+(1-ISR{C}_{Skin})\ast L{F}_{Skin} \\ \ast C_{Skin}+(1-ISR{C}_{Brain})\ast L{F}_{Brain}\ast C_{Brai{n}_I}+(1-ISR{C}_{Adipose})\ast L{F}_{Adipose} \\ \ast C_{Adipos{e}_I}+(1-ISR{C}_{Thymus})\ast L{F}_{Thymus}\ast C_{Thymu{s}_I}+(1-ISR{C}_{Liver}) \\ \ast L{F}_{Liver}\ast C_{Live{r}_I}+(1-ISR{C}_{S.Intestine})\ast L{F}_{S.Intestine}\ast C_{S.Intestin{e}_I} \\ +(1-ISR{C}_{L.Intestine})\ast L{F}_{L.Intestine}\ast C_{L.Intestin{e}_I}+(1-ISR{C}_{Spleen}) \\ \ast L{F}_{Spleen}\ast C_{Splee{n}_I}+(1-ISR{C}_{Pancreas})\ast L{F}_{Pancreas}\ast C_{Pancrea{s}_I} \\ +(1-ISR{C}_{Bone})\ast L{F}_{Bone}\ast C_{Bon{e}_I}+(1-ISR{C}_{Other})\ast L{F}_{Other}\ast C_{Othe{r}_I} \\ +2(1-ISR{C}_{Eye})\ast L{F}_{Eye}\ast (1-f_{Cho}-f_{Ret})\ast C_{IC{B}_I}+2(1-ISR{C}_{Eye}) \\ \ast L{F}_{Eye}\ast f_{Ret}\ast C_{Re{t}_I}+2(1-ISR{C}_{Eye})\ast L{F}_{Eye}\ast f_{Cho}\ast C_{Ch{o}_I} \\ \phantom{(}+(1-ISR{C}_{Lung})\ast L{F}_{Lung}\ast C_{Lun{g}_I}-L{F}_{LymphNode}\ast C_{LymphNode}) \\ \ast \frac{1}{V_{LymphNode}} \end{gathered}$$ (3)

Typical Tissue Compartment

Vascular Space

$$\begin{gathered} \frac{d}{dt}{C}_{Tissu{e}_V}=(PL{Q}_{Tissue}\ast C_{Lun{g}_V}-(PL{Q}_{Tissue}-L{F}_{Tissue})\ast C_{Tissu{e}_V}-(1-VR{C}_{Tissue}) \\ \ast L{F}_{Tissue}\ast C_{Tissu{e}_V}-C{L}_{u{p}_{Tissue}}\ast C_{Tissu{e}_V}+C{L}_{u{p}_{Tissue}}\ast FR\ast C_{Tissu{e}_{EB}}) \\ \ast \frac{1}{V_{Tissu{e}_V}} \end{gathered}$$ (4)

Endosomal Space mAb unbound to FcRn

$$\begin{gathered} \frac{d}{dt}{C}_{Tissu{e}_{EU}}=\frac{C{L}_{u{p}_{Tissue}}\ast (C_{Tissu{e}_V}+C_{Tissu{e}_I})}{V_{Tissu{e}_E}}-K_{o{n}_{FcRn}}\ast C_{Tissu{e}_{EU}}\ast (FcR{n}_{Tissue}+FcRn) \\ +K_{of{f}_{FcRn}}\ast C_{Tissu{e}_{EB}}-K_{de{g}_{IgG}} \\ \ast C_{Tissu{e}_{EU}} \end{gathered}$$ (5)

Endosomal Space mAb bound to FcRn

$$\begin{gathered} \frac{d}{dt}{C}_{Tissu{e}_{EB}}=K_{o{n}_{FcRn}}\ast C_{Tissu{e}_{EU}}\ast (FcR{n}_{Tissue}+FcRn)-K_{of{f}_{FcRn}}\ast C_{Tissu{e}_{EB}} \\ -\frac{C{L}_{u{p}_{Tissue}}\ast C_{Tissu{e}_{EB}}}{V_{Tissu{e}_E}} \end{gathered}$$ (6)

Endosomal space FcRn

$$\begin{gathered} \frac{d}{dt}FcR{n}_{Tissue}=K_{of{f}_{FcRn}}\ast C_{Tissu{e}_{EB}}-K_{o{n}_{FcRn}}\ast C_{Tissu{e}_{EU}}\ast (FcR{n}_{Tissue}+FcRn) \\ +\frac{C{L}_{u{p}_{Tissue}}\ast C_{Tissu{e}_{EB}}}{V_{Tissu{e}_E}} \end{gathered}$$ (7)

Interstitial Space

$$\begin{gathered} \frac{d}{dt}{C}_{Tissu{e}_I}=((1-VR{C}_{Tissue})\ast L{F}_{Tissue}\ast C_{Tissu{e}_V}-(1-ISR{C}_{Tissue})\ast L{F}_{Tissue}\ast C_{Tissu{e}_I}\phantom{)} \\ \phantom{(}+C{L}_{u{p}_{Tissue}}\ast (1-FR)\ast C_{Tissu{e}_{EB}}-C{L}_{u{p}_{Tissue}}\ast C_{Tissu{e}_I})\ast \frac{1}{V_{Tissu{e}_I}} \end{gathered}$$ (8)

Blood Cell Space

$$\frac{d}{dt}{C}_{Tissu{e}_{BC}}=\frac{BC{Q}_{Tissue}\ast (C_{Lun{g}_{BC}}-C_{Tissu{e}_{BC}})}{V_{Tissu{e}_{BC}}}$$ (9)

Lung Compartment

Vascular Space

$$\begin{gathered} \frac{d}{dt}{C}_{Lun{g}_V}=((PL{Q}_{Lung}+L{F}_{Lung})\ast C_{Lun{g}_V}-PL{Q}_{Lung}\ast C_{Lun{g}_V}-(1-VR{C}_{Lung})\ast L{F}_{Lung}\phantom{)} \\ \phantom{(}\ast C_{Lun{g}_V}-C{L}_{u{p}_{Lung}}\ast C_{Lun{g}_V}+C{L}_{u{p}_{Lung}}\ast FR\ast C_{Lun{g}_{EB}}) \\ \ast \frac{1}{V_{Lun{g}_V}} \end{gathered}$$ (10)

Liver Compartment

Vascular Space

$$\begin{gathered} \frac{d}{dt}{C}_{Live{r}_V}=(PL{Q}_{Liver}\ast C_{Lun{g}_V}-(PL{Q}_{Liver}-L{F}_{Liver})+(PL{Q}_{S.Intestine}-L{F}_{S.Intestine}) \\ +(PL{Q}_{L.Intestine}-L{F}_{L.Intestine})+(PL{Q}_{Spleen}-L{F}_{Spleen}) \\ +(PL{Q}_{Pancreas}-L{F}_{Pancreas})\ast C_{Live{r}_V}+(PL{Q}_{S.Intestine}-L{F}_{S.Intestine}) \\ \ast C_{S.Intestin{e}_V}+(PL{Q}_{L.Intestine}-L{F}_{L.Intestine})\ast C_{L.Intestin{e}_V} \\ +(PL{Q}_{Spleen}-L{F}_{Spleen})\ast C_{Splee{n}_V}+(PL{Q}_{Pancreas}-L{F}_{Pancreas})\ast C_{Pancrea{s}_V} \\ -(1-VR{C}_{Liver})\ast L{F}_{Liver}\ast C_{Live{r}_V}-C{L}_{u{p}_{Liver}}\ast C_{Live{r}_V}+C{L}_{u{p}_{Liver}}\ast FR \\ \ast C_{Live{r}_{EB}}) \\ \ast \frac{1}{V_{Live{r}_V}} \end{gathered}$$ (11)

Blood Cell Space

$$\begin{gathered} \frac{d}{dt}{C}_{Tissu{e}_{BC}}=(BC{Q}_{Liver}\ast C_{Lun{g}_{BC}}+BC{Q}_{S.Intestine}\ast C_{S.Intestin{e}_{BC}}+BC{Q}_{L.Intestine} \\ \ast C_{L.Intestin{e}_{BC}}+BC{Q}_{Spleen}\ast C_{Splee{n}_{BC}}+BC{Q}_{Pancreas}\ast C_{Pancrea{s}_{BC}} \\ -(BC{Q}_{Liver}+BC{Q}_{S.Intestine}+BC{Q}_{L.Intestine}+BC{Q}_{Spleen}+BC{Q}_{Pancreas}) \\ \ast C_{Live{r}_{BC}}) \\ \ast \frac{1}{V_{Live{r}_{BC}}} \end{gathered}$$ (12)

Lung and liver compartments not explicitly shown, share the same equations as a typical tissue.

Physiologically-Based Ocular Compartment.

As a novel expansion to the platform PBPK model, we have incorporated an anatomically and physiologically relevant ocular compartment. The overall structure of the new compartment is shown in Figure 3, and the physiologic parameters are provided in Tables 3, 4 and 5. The major tissues of the eye are represented, which include cornea, iris-ciliary body (ICB), aqueous humor (AH), lens, vitreous humor (VH), retina, and choroid. Plasma flow to the eye is fractionally divided into the ICB, choroid, and retina, and equal flow exits these tissues by both plasma and lymph flow.

Fig. 3.

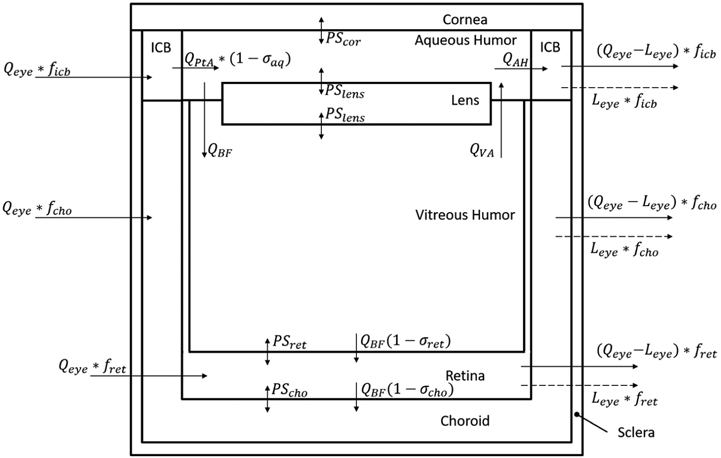
Structural schematic of the physiologically-based ocular compartment. The compartments are connected in an anatomical manner including blood, lymph, and intraocular fluid flows, and accounts for permeation at interfaces between tissues. The vascularized tissues are further divided in sub compartments as shown in Figure 5.

Table 3.

Physiological parameters for the ocular component of the rabbit PBPK model.

Parameter	Value	Source
VCornea (mL)	0.0887	[49]
VAH (mL)	0.306	Struble et al. [49]
VVH (mL)	1.41	[49]
Qeye (L/h)	0.0483	[50]
Leye (L/h)	Q_eye*0.002	Calculated
ficb	0.131	[51]
fret	0.00911	[51]
fcho	0.860	[51]
QBF (L/h)	0.00003	[52]
QVA (L/h)	0.000008	[53]
QPtA (L/h)	QAH – QVA + QBF	Calculated
QAH (L/h)	0.000212	[50]
σret	0.95	Fixed
σcho	0.99	Fixed
σaq	0.99	Fixed
PScor (L/h)	1.19 x 10−8	[54]
PSlens (L/h)	0	Fixed
PSret (L/h)	2.64 x 10−6	[5]
PScho (L/h)	2.88 x 10−6	[5]

Table 4.

Physiological parameters for tissue sub-compartments in the ocular model.

		Fraction of Total Volume comprising
	Total Volume (μL)	Plasma Volume	Blood Cell Volume	Interstitial Volume	Endosomal Volume	Cellular Volume
Retina	42.0	0.287[55]	0.1435	0.32[56]	0.005	0.245
Choroid	28.4	0.23[57]	0.115	0.4[58]	0.005	0.25
ICBa	87.8	0.23	0.115	0.4	0.005	0.25

^aICB was assumed to have the same composition as choroid due to structural similarity

Table 5.

Glossary of parameters used in the ocular compartment of the PBPK model.

Parameter	Units	Definition
VCornea, VAH, VVH	L	Volumes of the cornea, aqueous humor, and vitreous humor compartments
Qeye	L /h	Blood flow to the eye
Leye	L /h	Lymph flow from the eye
ficb, fret, fcho	–	Fraction of total blood and total lymph flow entering and exiting the iris-ciliary body, retina, and choroid
QBF	L /h	Bulk flow of fluid from the anterior eye to the posterior eye
QVA	L /h	Flow of fluid from vitreous chamber to aqueous chamber
QPtA	L /h	Flow of fluid from plasma to aqueous humor (i.e. rate of aqueous humor production)
QAH	L /h	Flow of fluid from aqueous humor returning to plasma (i.e. rate of aqueous humor drainage)
σret, σcho	–	Bulk flow reflection coefficients in the retina and choroid
σaq	–	Plasma-to-aqueous humor reflection coefficient
PScor, PSlens, PSret, PScho	L/h	Permeability Surface Area products for mAb in cornea, lens, retina, and choroid

Convection of fluid within the ocular humor compartments is also incorporated in the model. Aqueous humor produced by the ICB enters the aqueous chamber (QPtA) and exits via Schlemm’s canal (QAH) or flows into the vitreous chamber (QBF). Fluid entering the vitreous chamber recirculates back into the aqueous chamber (QVA), undergoing anterior elimination, or undergoes bulk flow (QBF) to the retina and subsequently the choroid, undergoing posterior elimination. Furthermore, the model allows for permeation of IgG at several major intraocular tissue interfaces.

As with the tissues in the platform PBPK model, the vascularized tissues of the eye are subdivided into smaller spaces (Figure 4), and the major mechanisms of antibody disposition described above are present. However, each intraocular tissue also contains components representing the unique fluid flows and interfaces found in the eye. As with the systemic reflection coefficients, reflection coefficients within the eye represent the level of resistance to IgG convection by the blood-aqueous barrier (σaq), the inner limiting membrane of the retina (σret), and the retinal pigment epithelium (σcho). These values are assumed to be high (i.e. 0.95, 0.99, and 0.99, respectively). Similar to the brain, the eye is known to be shielded from systemic circulation by the blood-aqueous barrier and the blood-retina barrier, thus the vascular reflection coefficient in the ocular tissues was set to 0.99 (the interstitial reflection coefficient remains 0.2). Equations for the ocular PBPK model are included below.

Fig. 4.

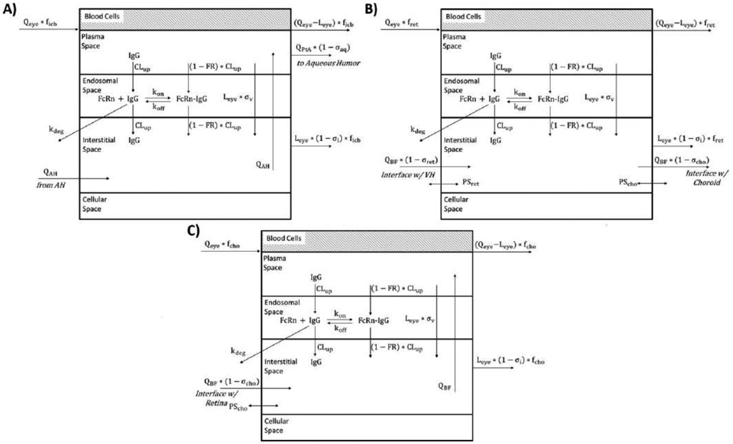
Schematic of tissue-level model for vascularized tissues in the ocular compartment, including (A) Iris-Ciliary Body, (B) Retina, and (C) Choroid.

Cornea Compartment

$$\frac{d}{dt}{C}_{Cor}=(C_{Aq}-C_{Cor})\ast P{S}_{Cor}$$ (13)

Aqueous Humor Compartment

$$\begin{gathered} \frac{d}{dt}{C}_{Aq}=(C_{Cor}-C_{Aq})\ast P{S}_{Cor}+(C_{Lens}-C_{Aq})\ast P{S}_{Lens}+\frac{C_{Vit}\ast Q_{VA}}{V_{Aq}} \\ +\frac{C_{IC{B}_V}\ast Q_{PtA}\ast (1-R{C}_{Aq})}{V_{Aq}}-\frac{C_{Aq}\ast (C{L}_{AH}+Q_{BF}+Q_{VA})}{V_{Aq}} \end{gathered}$$ (14)

Iris-Ciliary Body Compartment

Vascular Space

$$\begin{gathered} \frac{d}{dt}{C}_{IC{B}_V}=(PL{Q}_{Eye}\ast (1-f_{cho}-f_{ret})\ast C_{Lun{g}_V}-(PL{Q}_{Eye}-L{F}_{Eye})\ast (1-f_{cho}-f_{ret}) \\ \ast C_{IC{B}_V}-(1-VR{C}_{Eye})\ast L{F}_{Eye}\ast (1-f_{cho}-f_{ret})\ast C_{IC{B}_V}-C{L}_{u{p}_{ICB}}\ast C_{IC{B}_V} \\ \ast \frac{1}{V_{IC{B}_V}} \end{gathered}$$ (15)

Endosomal Space mAb unbound to FcRn

$$\begin{gathered} \frac{d}{dt}{C}_{IC{B}_{EU}}=\frac{C{L}_{u{p}_{ICB}}\ast (C_{IC{B}_V}+C_{IC{B}_I})}{V_{IC{B}_E}}-K_{o{n}_{FcRn}}\ast C_{IC{B}_{EU}}\ast (FcR{n}_{ICB}+FcRn)+K_{of{f}_{FcRn}} \\ \ast C_{IC{B}_{EB}}-K_{de{g}_{IgG}}\ast C_{IC{B}_{EU}} \end{gathered}$$ (16)

Endosomal Space mAb bound to FcRn

$$\frac{d}{dt}{C}_{IC{B}_{EB}}=K_{o{n}_{FcRn}}\ast C_{IC{B}_{EU}}\ast (FcR{n}_{ICB}+FcRn)-K_{of{f}_{FcRn}}\ast C_{IC{B}_{EB}}-\frac{C{L}_{u{p}_{ICB}}\ast C_{IC{B}_{EB}}}{V_{IC{B}_E}}$$ (17)

Endosomal Space FcRn

$$\begin{gathered} \frac{d}{dt}FcR{n}_{ICB}=K_{of{f}_{FcRn}}\ast C_{IC{B}_{EB}}-K_{o{n}_{FcRn}}\ast C_{IC{B}_{EU}}\ast (FcR{n}_{ICB}+FcRn) \\ +\frac{C{L}_{u{p}_{ICB}}\ast C_{IC{B}_{EB}}}{V_{IC{B}_E}} \end{gathered}$$ (18)

Interstitial Space

$$\begin{gathered} \frac{d}{dt}{C}_{IC{B}_I}=((1-VR{C}_{Eye})\ast L{F}_{Eye}\ast (1-f_{Cho}-f_{Ret})\ast C_{IC{B}_V}-(1-ISR{C}_{Eye})\ast L{F}_{Eye}\phantom{)} \\ \ast (1-f_{Cho}-f_{Ret})\ast C_{IC{B}_I}+C{L}_{U{p}_{ICB}}\ast (1-FR)\ast C_{IC{B}_{EB}}-C{L}_{U{p}_{ICB}}\ast C_{IC{B}_I} \\ \phantom{(}+C_{Aq}\ast C{L}_{AH}-C_{IC{B}_I}\ast C{L}_{AH})\ast \frac{1}{V_{IC{B}_I}} \end{gathered}$$ (19)

Blood Cell Space

$$\frac{d}{dt}{C}_{IC{B}_{BC}}=\frac{BC{Q}_{Eye}\ast (1-f_{Cho}-f_{Ret})\ast (C_{Lun{g}_{BC}}-C_{IC{B}_{BC}})}{V_{IC{B}_{BC}}}$$ (20)

Lens Compartment

$$\frac{d}{dt}{C}_{Lens}=(C_{AQ}-C_{Lens})\ast P{S}_{Lens}+(C_{Vit}-C_{Lens})\ast P{S}_{Lens}$$ (21)

Vitreous Humor Compartment

$$\begin{gathered} \frac{d}{dt}{C}_{Vit}=(C_{Re{t}_I}-C_{Vit})\ast P{S}_{Ret}+(C_{Lens}-C_{Vit})\ast P{S}_{Lens}-\frac{C_{Vit}\ast Q_{VA}}{V_{Vit}} \\ -\frac{C_{Vit}\ast Q_{BF}\ast (1-R{C}_{Ret})}{V_{Vit}}+\frac{C_{Aq}\ast (Q_{BF}+Q_{VA})}{V_{vit}} \end{gathered}$$ (22)

Retina Compartment

Vascular Space

$$\begin{gathered} \frac{d}{dt}{C}_{Re{t}_V}=(PL{Q}_{Eye}\ast f_{Ret}\ast C_{Lun{g}_V}-(PL{Q}_{Eye}-L{F}_{Eye})\ast f_{Ret}\ast C_{Re{t}_V}-(1-VR{C}_{Eye}) \\ \ast L{F}_{Eye}\ast f_{Ret}\ast C_{Re{t}_V}-C{L}_{u{p}_{Ret}}\ast C_{Re{t}_V}+C{L}_{u{p}_{Ret}}\ast FR\ast C_{Re{t}_{EB}})\ast \frac{1}{V_{Re{t}_V}} \end{gathered}$$ (23)

Endosomal Space mAb unbound to FcRn

$$\begin{gathered} \frac{d}{dt}{C}_{Re{t}_{EU}}=\frac{C{L}_{u{p}_{Ret}}\ast (C_{Re{t}_V}+C_{Re{t}_I})}{V_{Re{t}_E}}-K_{o{n}_{FcRn}}\ast C_{Re{t}_{EU}}\ast (FcR{n}_{Ret}+FcRn)+K_{of{f}_{FcRn}} \\ \ast C_{Re{t}_{EB}}-K_{de{g}_{IgG}}\ast C_{Re{t}_{EU}} \end{gathered}$$ (24)

Endosomal Space mAb bound to FcRn

$$\begin{gathered} \frac{d}{dt}{C}_{Re{t}_{EB}}=K_{o{n}_{FcRn}}\ast C_{Re{t}_{EU}}\ast (FcR{n}_{Ret}+FcRn)-K_{of{f}_{FcRn}}\ast C_{Re{t}_{EB}} \\ -\frac{C{L}_{u{p}_{Ret}}\ast C_{Re{t}_{EB}}}{V_{Re{t}_E}} \end{gathered}$$ (25)

Endosomal Space FcRn

$$\begin{gathered} \frac{d}{dt}FcR{n}_{Ret}=K_{of{f}_{FcRn}}\ast C_{Re{t}_{EB}}-K_{o{n}_{FcRn}}\ast C_{Re{t}_{EU}}\ast (FcR{n}_{Ret}+FcRn) \\ +\frac{C{L}_{u{p}_{Ret}}\ast C_{Re{t}_{EB}}}{V_{Re{t}_E}} \end{gathered}$$ (26)

Interstitial Space

$$\begin{gathered} \frac{d}{dt}{C}_{Re{t}_I}=((1-VR{C}_{Eye})\ast L{F}_{Eye}\ast f_{Ret}\ast C_{Re{t}_V}-(1-ISR{C}_{Eye})\ast L{F}_{Eye}\ast f_{Ret}\ast C_{Re{t}_I}\phantom{)} \\ \phantom{(}+C{L}_{U{p}_{Ret}}\ast (1-FR)\ast C_{Re{t}_{EB}}-C{L}_{U{p}_{Ret}}\ast C_{Re{t}_I})\ast \frac{1}{V_{Re{t}_I}}+(C_{Vit}-C_{Re{t}_I}) \\ \ast P{S}_{Ret}+(C_{Ch{o}_I}-C_{Re{t}_I})\ast P{S}_{Cho}+\frac{C_{Vit}\ast Q_{BF}\ast (1-R{C}_{Ret})}{V_{Re{t}_I}} \\ -\frac{C_{Re{t}_I}\ast Q_{BF}\ast (1-R{C}_{Cho})}{V_{Re{t}_I}} \end{gathered}$$ (27)

Blood Cell Space

$$\frac{d}{dt}{C}_{Re{t}_{BC}}=\frac{BC{Q}_{Eye}\ast f_{Ret}\ast (C_{Lun{g}_{BC}}-C_{Re{t}_{BC}})}{V_{Re{t}_{BC}}}$$ (28)

Choroid Compartment

Vascular Space

$$\begin{gathered} \frac{d}{dt}{C}_{Ch{o}_V}=(PL{Q}_{Eye}\ast f_{Cho}\ast C_{Lun{g}_V}-(PL{Q}_{Eye}-L{F}_{Eye})\ast f_{Cho}\ast C_{Ch{o}_V}-(1-VR{C}_{Eye}) \\ \ast L{F}_{Eye}\ast f_{Cho}\ast C_{Ch{o}_V}-C{L}_{u{p}_{Cho}}\ast C_{Ch{o}_V}+C{L}_{u{p}_{Cho}}\ast FR\ast C_{Ch{o}_{EB}}+C_{Ch{o}_I} \\ \ast Q_{BF})\ast \frac{1}{V_{Ch{o}_V}} \end{gathered}$$ (29)

Endosomal Space mAb unbound to FcRn

$$\begin{gathered} \frac{d}{dt}{C}_{Ch{o}_{EU}}=\frac{C{L}_{u{p}_{Cho}}\ast (C_{Ch{o}_V}+C_{Ch{o}_I})}{V_{Ch{o}_E}}-K_{o{n}_{FcRn}}\ast C_{Ch{o}_{EU}}\ast (FcR{n}_{Cho}+FcRn)+K_{of{f}_{FcRn}} \\ \ast C_{Ch{o}_{EB}}-K_{de{g}_{IgG}}\ast C_{Ch{o}_{EU}} \end{gathered}$$ (30)

Endosomal Space mAb bound to FcRn

$$\begin{gathered} \frac{d}{dt}{C}_{Ch{o}_{EB}}=K_{o{n}_{FcRn}}\ast C_{Ch{o}_{EU}}\ast (FcR{n}_{Cho}+FcRn)-K_{of{f}_{FcRn}}\ast C_{Ch{o}_{EB}} \\ -\frac{C{L}_{u{p}_{Cho}}\ast C_{Ch{o}_{EB}}}{V_{Ch{o}_E}} \end{gathered}$$ (31)

Endosomal Space FcRn

$$\begin{gathered} \frac{d}{dt}FcR{n}_{Cho}=K_{of{f}_{FcRn}}\ast C_{Ch{o}_{EB}}-K_{o{n}_{FcRn}}\ast C_{Ch{o}_{EU}}\ast (FcR{n}_{Cho}+FcRn) \\ +\frac{C{L}_{u{p}_{Cho}}\ast C_{Ch{o}_{EB}}}{V_{Ch{o}_E}} \end{gathered}$$ (32)

Interstitial Space

$$\begin{gathered} \frac{d}{dt}{C}_{Ch{o}_I}=((1-VR{C}_{Eye})\ast L{F}_{Eye}\ast f_{Cho}\ast C_{Ch{o}_V}-(1-ISR{C}_{Eye})\ast L{F}_{Eye}\ast f_{Cho}\ast C_{Ch{o}_I}\phantom{)} \\ \phantom{(}+C{L}_{U{p}_{Cho}}\ast (1-FR)\ast C_{Ch{o}_{EB}}-C{L}_{U{p}_{Cho}}\ast C_{Ch{o}_I})\ast \frac{1}{V_{Ch{o}_I}}+(C_{Re{t}_I}-C_{Ch{o}_I}) \\ \ast P{S}_{Cho}+\frac{C_{Re{t}_I}\ast Q_{BF}\ast (1-R{C}_{Cho})}{V_{Ch{o}_I}}-\frac{C_{Ch{o}_I}\ast Q_{BF}}{V_{Ch{o}_I}} \end{gathered}$$ (33)

Blood Cell Space

$$\frac{d}{dt}{C}_{Ch{o}_{BC}}=\frac{BC{Q}_{Eye}\ast f_{cho}\ast (C_{Lun{g}_{BC}}-C_{Ch{o}_{BC}})}{V_{Ch{o}_{BC}}}$$ (34)

PBPK Model Estimation and Simulation.

Model fitting was carried out in ADAPT 5 [38] with the intravitreal dose parameter being estimated. Data from collected tissues were fit simultaneously to estimate the dose in each study utilizing intravitreal dosing. Model simulations were carried out in Berkeley Madonna (version 8.3.23.0) software[39]. All values for parameters in the PBPK model are ascertained from previously published literature sources and the intravitreal dose amount estimated using ADAPT 5. Initially, performance of the platform PBPK model was evaluated by simulation of plasma PK of exogenous antibody after intravenous administration. After addition of the novel ocular component, the model was validated by estimation of PK in the serum, aqueous humor, vitreous humor, and retina after intravitreal administration of antibody. Predictive capability of the model was assessed quantitatively by calculation of symmetric mean absolute percentage error (SMAPE) (Equation 1) between the AUC of the simulated PK profile (AUC_sim) and the average AUC of the observed PK profiles for indicated niAbs (AUC_obs). Using this method, a 2-fold overprediction or a 2-fold under-prediction would give an SMAPE of 33%.

$$SMAPE=\frac{\mid AU{C}_{sim}-AU{C}_{obs}\mid }{\frac{1}{2}(\mid AU{C}_{sim}\mid +\mid AU{C}_{obs}\mid )}\ast 100\%$$ (35)

Results

In general, all plasma and tissue PK datasets in rabbit were well characterized by the PBPK model. The simulated AUC of the concentration vs time curve was within 2-fold of the average observed AUC in almost all cases as determined by SMAPE.

Dose Estimation with the PBPK Model.

As outlined in the “Experimental Data” section above, three of the four studies administered bevacizumab to one eye at a dose of 1.25 mg. However, the PK profiles for each study showed variability in the observed concentration vs. time course. Moreover, in the Sinapis et al. [27] study, serum was collected by allowing blood to clot at room temperature for 1 hr before centrifugation rather than immediate centrifugation, potentially resulting in bevacizumab loss and low observed serum concentrations of the antibody. Therefore, serum data was not used when estimating the dose parameter for the Sinapis et al. [27] dataset. The dose parameters for each intravitreal dose study was estimated with confidence and are shown in Table 6.

Table 6.

Estimated dose amount administered in intravitreal dosing studies and SMAPE of the PBPK model in prediction of AUC in ocular tissues.

			SMAPE
Estimated Dose (mg)	CV%	Study	Vitreous Humor	Aqueous Humor	Retina	Plasma	Iris/Ciliary Body
0.754	8.03	Gadkar[28]	11.0	4.19	9.43	19.3
0.926	14.1	Bakri[25]	23.4	30.5		23.4
0.696	2.39	Sinapis[27]	15.4	14.7		72.7
0.343	15.6	Nomoto[26]	5.09	89.6	11.2	12.5	15.1

Performance of the Platform PBPK Model.

Figure 5 shows the simulated and observed concentration vs. time profile of AIGIV and obiltoxaximab after an intravenous infusion. Both the simulated and observed data are dose normalized. In general, the simulation captures the observed profiles, with some discrepancy at earlier time points, but minimal deviation from most of the data. The average SMAPE of the prediction was 5.34%. The excellent performance of the model validates the successful translation of the platform model to rabbits.

Fig. 5.

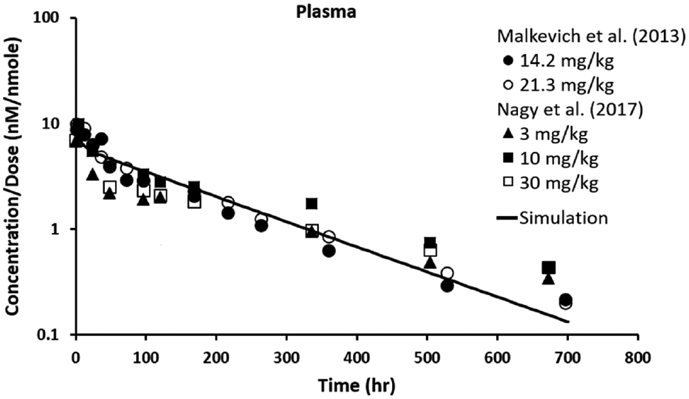
Observed (icons) and simulated (line) pharmacokinetics of intravenously-dosed monoclonal antibodies in rabbits. Data and simulation are dose normalized.

Performance of the Ocular PBPK Model.

Figure 6 shows the simulated and observed concentration vs. time profiles of all α-gD and bevacizumab data sets after intravitreal injection. In plasma, the slow appearance of antibody is recapitulated, although the terminal phase shows large variability between the two molecules. Furthermore, rapid appearance of antibody in the aqueous humor, iris/ciliary body, and retina are simulated in accordance with observed effects. Lastly, pharmacokinetics in the vitreous humor are simulated appropriately with the terminal decline parallel in all the ocular tissues. The SMAPE of the predictions in in all ocular tissues are in Table 6. Despite slight variation in the PK of α-gD and the three bevacizumab data sets, the model performs very well showing no systematic over- or under-prediction.

Fig. 6.

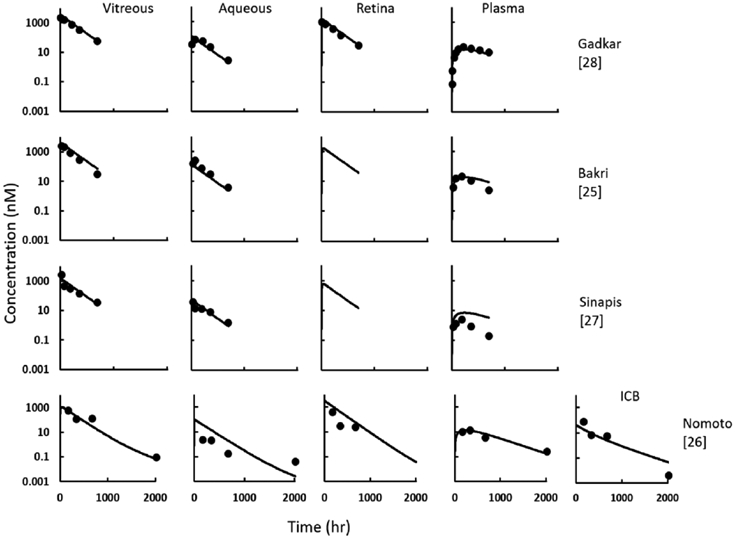
Observed (circles) and simulated (line) pharmacokinetics of intravitreally-dosed monoclonal antibodies that are non-targeting in rabbits.

Discussion

PBPK models are an important tool in translating preclinical pharmacology of antibodies to the clinic. An important objective of PBPK modelling is to characterize the system with physiologically relevant parameters so that the plasma and tissue PK of a drug can be accurately characterized simply with the knowledge of drug specific parameters obtained in vitro (e.g. affinity with FcRn). While PBPK models of antibody disposition have been well established in many species, such as mice, rats, monkeys, and human, to date, there is no validated PBPK model for antibody disposition in rabbits. In this manuscript, we sought to develop a PBPK model for rabbit because is a widely used species, particularly in development of antibody therapeutics for ocular disorders.

The platform PBPK model proposed by Shah and Betts[16] and presented in Figures 1 and 2 provides a basis for developing PBPK models for new species, as we have done here with rabbits. As an important validation step, the rabbit PBPK model accurately simulates the time course of antibody concentration in plasma after intravenous dosing with minimal predictive error (Figure 5). A key attribute of these simulations is that all parameters, both related to the system and to the drug, were fixed a priori. However, rabbits are rarely used with the intention of measuring whole body tissue pharmacokinetics. Therefore, tissue-level data for antibody PK is not readily available, with reported studies having few collection times or unclear dosing regimens, which is unsuitable to use for our modeling endeavors[40,41]. Nevertheless, reliable data in rabbit is available from the literature regarding ocular disposition of antibodies.

Rabbits are the most common species used in assessing ocular pharmacokinetics and toxicity[18,17]. Thus, a rabbit PBPK model including a detailed eye component would be a valuable tool in ocular drug development. As a frequently used species, the ocular anatomy and physiology of the rabbit is well known and has been incorporated into the PBPK model. While maintaining the whole-body and drug parameters, the ocular model accurately simulates the pharmacokinetics of IgG in both the serum and several individual ocular tissues: aqueous humor, iris/ciliary body, vitreous humor, and retina (figure 6). Such prediction across tissues is extremely advantageous in ocular research where some individual tissues, such as retina or iris-ciliary body, are difficult to isolate and analyze. For example, taps of the aqueous and/or vitreous chamber (i.e. direct sampling) can be used for data collection in a single animal over time, and the concentration in the hard-to-reach tissues can then be simulated using the ocular PBPK model. This predictive capability is of even greater importance in the clinical setting, where aqueous taps are the only samples typically available.

While our proposed model focuses on full-length IgG therapies (150 kDa), smaller molecular weight biologics are of more interest for treating ocular disease. Indeed, all FDA-approved macromolecules for ocular disorders have molecular weights below 150 kDa: aflibercept (115 kDa), pegaptanib (50 kDa), ranibizumab (48 kDa), ocriplasmin (27.2 kDa), and brolucizumab (26 kDa). The current iteration of the platform PBPK model is unsuited to model smaller biologics as it assumes a single pore exists in the vascular endothelium through which a therapeutic antibody enters tissues. For lower molecular weight protein therapeutics, a model incorporating the “two pore hypotheses” of extravasation would be more appropriate[42,43]. Recently, our lab has applied the “two pore hypothesis” to the platform PBPK model[37]. The next step is to integrate the “two pore hypotheses” with the ocular PBPK model to predict the PK of smaller compounds after intravitreal administration.

Although ocular therapy currently centers on lower molecular weight protein therapeutics, modelling full-length IgG exposure in the eye is critical in assessing ocular toxicities. Targeted cancer therapies carry a risk of toxicity in healthy tissues that express the target antigen even at low levels. In phase I and phase II trials of the anti-HER2 ADC trastuzumab emtansine, between 31.3 and 46.4% of patients had ocular adverse events[44,45]. For ipilimumab, Maker et al. [46] observed severe ocular toxicities in 35% of patients treated with the anti-CTLA-4 antibody. For cetuximab, the anti-EGFR antibody has been associated with several ocular adverse events including dry eye, blepharitis, and trichomegaly[47,48]. Our ocular PBPK model has the potential to predict drug concentrations in various tissues of the eye after systemic administration, and, when combined with knowledge of antigen expression, it provides a tool to assess potential risk of ocular toxicity.

Conclusions

In summary, we have presented a new platform PBPK model for antibody disposition in rabbits. Additionally, we have incorporated a novel physiologically relevant ocular compartment to the whole-body model, which incorporates the unique anatomy of the eye. Our ocular PBPK model successfully predicts the PK of an exogenous antibody in the plasma and the ocular tissues after intravitreal administration. Prediction of ocular PK with our model will aid in the preclinical to clinical translation of novel ocular therapeutics, and assessment of potential drug-induced ocular toxicities. In the future, the capabilities of the ocular PBPK model can be expanded by incorporating the “two pore hypothesis” to accurately predict the PK of smaller molecular weight protein therapeutics.