Abstract
Alchemical free energy simulations have long been utilized to predict free energy changes for binding affinity and solubility of small molecules. However, while the theoretical foundation of these methods is well established, seamlessly handling many of the practical aspects regarding the preparation of the different thermodynamic end states of complex molecular systems and of the numerous processing scripts often remain a burden for successful applications. In this work, we present CHARMM-GUI Free Energy Calculator (http://www.charmm-gui.org/input/fec) that provides various alchemical free energy perturbation molecular dynamics (FEP/MD) systems with input and post-processing scripts for NAMD and GENESIS. Four submodules are available: Absolute Ligand Binder (for absolute ligand binding FEP/MD), Relative Ligand Binder (for relative ligand binding FEP/MD), Absolute Ligand Solvator (for absolute ligand solvation FEP/MD), and Relative Ligand Solvator (for relative ligand solvation FEP/MD). Each module is designed to build multiple systems of a set of selected ligands at once for high-throughput FEP/MD simulations. The capability of Free Energy Calculator is illustrated by absolute and relative solvation FEP/MD of a set of ligands and absolute and relative binding FEP/MD of a set of ligands for T4 lysozyme in solution and adenosine A2A receptor in a membrane. The calculated free energy values are overall consistent with the experimental and published free energy results (within ~1 kcal/mol). We hope that Free Energy Calculator is useful to carry out high-throughput FEP/MD simulations in the field of biomolecular sciences and drug discovery.
Graphical Abstract

INTRODUCTION
Accurate predictions of ligand binding affinity are essential for computer-aided drug discovery.1-6 Since the early 1990’s, considerable efforts have been invested to develop and use alchemical free energy methods with the goal of aiding structure-based drug design. Simulation methodologies based on alchemical free energy perturbation (FEP) molecular dynamics (MD) with explicit solvent, in particular, have proven to be a powerful and robust tool to calculate the binding affinity of drug compounds to protein targets.7-10 Advances in simulation techniques, including incorporation of enhanced sampling algorithms11, 12 and carefully parametrized force fields13, 14 together with MD packages15 optimized on state-of-the-art high performance computing architectures, now make it possible to exploit more advanced physics-based all-atom free energy simulation (FES) methods in drug discovery.
Ligand binding FES can be categorized into absolute and relative ones, depending on the thermodynamic end states.16 Both approaches play an important, albeit, different role in drug discovery, and invoke contrasting computing cost and simulation setup due to the difference in these end states. Relative alchemical FES, as they consider modest changes relative to a given common chemical core structure, is expected to play a critical role during the final stages of a drug development. Because the chemical perturbations are fairly modest and the overall binding pose of the ligand is assumed to remain unchanged,6, 19 it is reasonable to hope that relative FES converge sufficiently fast to yield the rapid turnaround, which is needed to influence the decision process during lead optimization. This information is also extremely useful to better understand the key interactions affecting the binding affinity. In contrast, absolute FES are computationally more ambitious and expected to converge more slowly because one end state corresponds to the fully decoupled noninteracting ligand. Compared to relative FES, this requires a relatively large number of intermediate states as well as careful considerations of restraining potentials of the uncoupled ligand. Furthermore, issues of alternative binding pose may come into play if restraints are introduced to enhance the sampling of the orientation and conformation of the ligand.7, 17-19 Reasonably, the most rational use of absolute FES should be toward the final stages of high-throughput docking and screening efforts, where it can serve as a more accurate form of scoring.
Implementing and advancing these FES methods and making them freely accessible to academic and non-academic researchers are key to improve in silico prediction of ligand binding affinities. Alchemical FES algorithms have been implemented in popular MD software packages, such as NAMD,20 CHARMM,21 GROMACS,22 Amber,23 GENESIS,24 and Desmond.25 These algorithms rely either on a single- or dual-topology setup of ligand(s) with robust sampling strategy and free energy estimator.26-29 In particular, together with external hybrid structure building tools,23, 30 single-topology based hybrid ligand structure has been exclusively adopted in popular MD software. In addition to the advanced FES algorithms themselves, user-friendly platforms for FES, integrating automated script generation, ligand force field generation, and system setup, are also essential for large-scale drug discovery campaigns.
Aside from the simplest modeling, most MD simulations require much more than a single proverbial “click” to be executed properly. In particular, advanced computational tasks like ligand solvation and binding FES rely on sophisticated theory and system preparation. Handling all relevant information to correctly prepare a complex simulation system often requires a considerable amount of human time and experience, which can be challenging even to experts. Therefore, together with the automated and streamlined system building, the generation of all necessary input files and post-processing scripts not only significantly lowers the entry barrier both for beginners and experts, but also guarantees the reproducibility of FES results.
Since 2006, CHARMM-GUI31 has established itself as a widely-used web-based platform for automated complex molecular system setup,32-40 as well as simulation input script generation with well-established simulation protocols.41, 42 Previously, we implemented Ligand Binder43 to provide the standardized input files for absolute ligand binding FEP/MD using CHARMM and various biasing energy restraints to enhance the calculation convergence.7, 17 In this work, we extend Ligand Binder and present Free Energy Calculator to handle absolute and relative ligand solvation and binding FES protocols, construction of enhanced sampling strategy, parameterization of binding complexes, and free energy estimators. Free Energy Calculator consists of four submodules: Absolute Ligand Binder (for absolute protein-ligand binding FES), Relative Ligand Binder (for relative protein-ligand binding FES), Absolute Ligand Solvator (for absolute ligand solvation FES), and Relative Ligand Solvator (for relative ligand solvation FES). In particular, Free Energy Calculator supports contemporary HPC (high performance computing) software NAMD44 and GENESIS24, 45 for all four submodules. In the subsequent sections, the implementation of Free Energy Calculator is presented and the FEP/MD simulation setup in NAMD and GENESIS is discussed. The Free Energy Calculator functionality is illustrated in a series of representative absolute and relative ligand solvation and binding FEP/MD using NAMD and GENESIS.
METHODS
Workflow of Free Energy Calculator
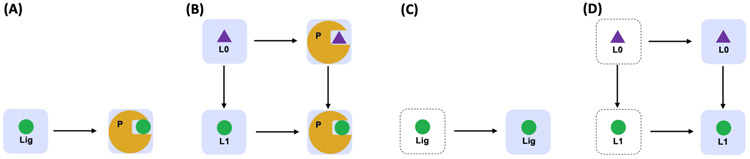
To cover a broad range of FEP/MD applications, Free Energy Calculator is designed with valid system setup protocols for Absolute Ligand Binder (ALB; Figure 1A), Relative Ligand Binder (RLB; Figure 1B), Absolute Ligand Solvator (ALS; Figure 1C), and Relative Ligand Solvator (RLS; Figure 1D). In particular, these modules are designed to build multiple FES systems for a set of ligands at once, as they need the same condition and simulation protocol for the successful high-throughput FES.
Figure 1.
Thermodynamic pathway used for (A) absolute and (B) relative binding free energy, and (C) absolute and (D) relative solvation free energy calculations. The protein is depicted in yellow, the aqueous solvent in blue, the initial ligand in purple, and the end ligand in green. Each Free Energy Calculator module requires two distinct systems for alchemical transformations.
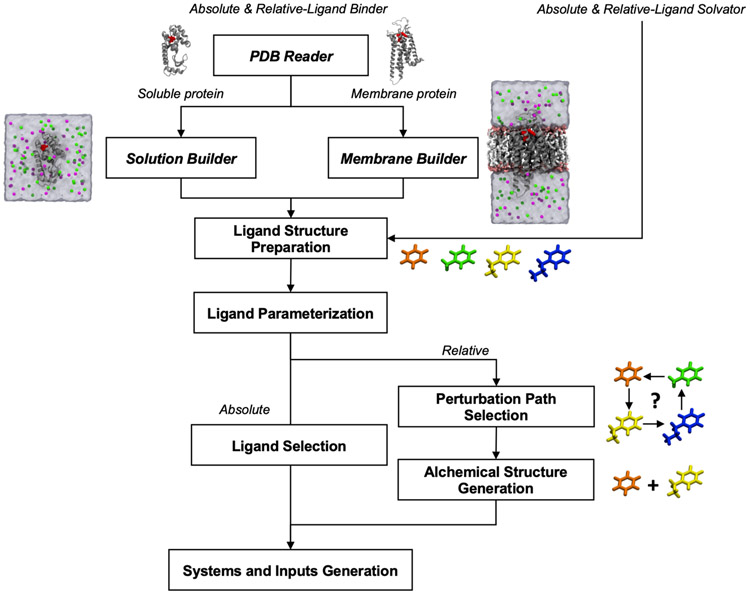
Free Energy Calculator has an automated workflow that ensures reproducible FEP/MD system and input generation (Figure 2). For ALB and RLB, Free Energy Calculator utilizes Solution Builder41 and Membrane Builder36, 39 to prepare a protein-ligand system in solution or in a bilayer. PDB Reader & Manipulator46 can be used to properly handle missing residues, protonation, mutation, disulfide bonds, and glycosylation to generate a reasonable initial protein-ligand complex structure. Note that the PDB structure should have at least one bound ligand for reference. Since a bound system is not required, ALS and RLS start with the ligand uploading step (Figure 2). In the following sections, the key implementation features of Free Energy Calculator are discussed in detail. To help users for successful practical applications, the video demonstrations of the four Free Energy Calculator submodules are available in the CHAMM-GUI website (http://www.charmm-gui.org/demo/fec).
Figure 2.
Schematic overview of Free Energy Calculator. Users need to prepare a protein-ligand complex structure (from RCSB or docking programs) and additional ligand structures. At the final step, two end-state systems are generated for all selected ligands with all necessary topology and force field files.
Ligand Structure Preparation
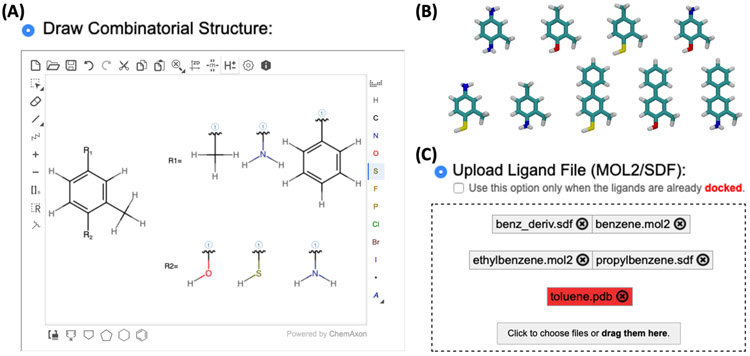
For high-throughput FEP/MD, a set of ligand structures is necessary, but it is a daunting task to prepare them from scratch. To ease the ligand preparation process, "Draw Combinatorial Structure" option (powered by ChemAxon MarvinJS) can be utilized to generate multiple structures from a core scaffold using functional groups and attachment sites (Figure 3A).35, 47 All combinatorial structures are automatically generated based on the substitution sites and substituents’ information (Figure 3B). In ALB and RLB, a reference ligand chemical structure is displayed on the sketchpad for easy drawing and editing. As an alternative option, ligand structure files (SDF or MOL2) can be separately prepared and uploaded using “Upload Ligand File” option (Figure 3C). If the files are pre-docked in the binding pose, users can use the ligand coordinate by clicking the “docked” option in Figure 3C. Note that Free Energy Calculator can handle an SDF file that contains multiple ligands.
Figure 3.
(A) Multiple ligands can be generated from a core scaffold by drawing functional groups and attachment sites in the sketchpad. (B) Based on the drawing in (A), nine combinatorial structures are generated. (C) MOL2 or SDF files are allowed for “Upload Ligand File” option, and unsupported file format is displayed with red box.
Ligand Parameterization
The latest version of the CHARMM General Force Field (CGenFF v2.x) includes additional lone-pair dummy atoms for all halogen atoms,48 which is not handled by the free energy modules in NAMD and GENESIS. For this reason, CGenFF v1.x is utilized to generate topology and parameter files for all ligand structures. Free Energy Calculator checks if a force field for a given ligand set can be parameterized by CGenFF, and users are asked to remove any ligand that CGenFF cannot handle properly. When NAMD and GENESIS FEP/MD support lone-pair atoms, CGenFF v2.x will be available.
Perturbation Path Selection for RLS and RLB
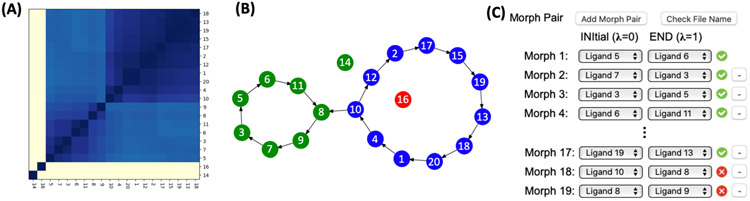
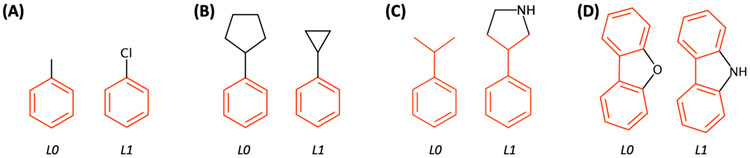
In relative FEP/MD, selection of optimal perturbation path for a set of ligands is crucial to get reliable outcomes as the calculated free energy (FE) value strongly depends on the path selection.49 In this context, two ligands need to be as structurally similar as possible to maximize the unperturbed region and minimize the perturbed region (and thus errors and/or sampling issues). In this context, Free Energy Calculator provides two pre-defined perturbation path algorithms and helps users to set up an optimal perturbation path. The first option is a “Closed minimal perturbation path” that groups ligands of the same charge and minimally connects paths as a spanning circle based on the similarity of all pairs in a given ligand set.49 For fast similarity scoring between all pairs, a fingerprint algorithm is applied for the pair having the same net charge, and the pair having a different net charge is excluded. Based on the similarity score matrix, a hierarchical clustering50 is applied to group similar ligands (Figure 4A). Finally, a row-wise maximum in the cluster matrix is searched and the paths are generated sequentially using the ligands in the row. In the case of multiple clusters, each disconnected cluster is linked through the two ligands with the highest similarity between two clusters. (Figure 4B). Another option is a "Radial shape perturbation path".49 This option makes the pairwise path between a reference ligand and all other ligands, which appears to be an appropriate path selection when an experimental free energy value of the reference ligand is available.49 Both path algorithms exclude the path between ligands that have different net charges. The two end-state ligands of all resulting pairs (L0 at λ = 0 and L1 at λ = 1, where λ is the thermodynamic coupling parameter) are displayed (Figure 4C). Note that the suggested paths can be modified to add more paths or delete suggested paths.
Figure 4.
(A) Re-ordered similarity matrix by using a hierarchical clustering method; navy and ivory colors represent high and low similarity scores of ligand pairs, respectively. (B) Result of the “Closed minimal perturbation path”, where a filled circle and an arrow represent a ligand and a perturbation path, respectively. Ligands having different charges (14th and 16th ligands) are separated from other ligands, and each cluster is colored in blue, green, and red. (C) Illustrative snapshot of suggested pairs. A pair having ligand(s) unsupported by the CGenFF is marked in red, and these pairs should be removed to go to the system and input generation step.
Alchemical Structure Generation for RLS and RLB
Structural mapping of L0 and L1 is essential to define perturbed/unperturbed atoms and bonds during relative FEP/MD. The maximum common structure (MCS) algorithm51, 52 is applied to find a maximum overlap between paired ligands, which leads to a minimal number of perturbed atoms. Both NAMD and GENESIS FEP/MD use a hybrid single-dual topology that considers unperturbed and perturbed atoms as single and dual topology regions, respectively. Hence, the explicit creation of a dummy atom for the perturbed one is not necessary, and the unperturbed region is unaffected by holonomic constraints. For this reason, the similarity criteria of RLS and RLB are broader than other single-topology based mapping, so that RLS and RLB can cover a broken ring and a mismatched ring consisting of the same size between L0 and L1 (Figure 5). During MCS search, all hydrogen atoms are explicitly included. Particularly, for ring topology transformation53 and macrocyclic-acyclic transformation,54 we provide an option to treat the decoupled (dummy) atoms, which retain some of the bonded terms (angles and dihedral angles) of the original atom,55, 56 at either end state of the relative FES. By default, we turn this option off, as its contribution in practice still is in debate.
Figure 5.
Exemplary maximum common structure mapping results between L0 and L1 for 4 ligand pairs. Red and black represent single-topology (unperturbed) and dual-topology (perturbed) regions, respectively. (A) The mismatched atom and (B) the atoms in different ring size are considered as the dual-topology region. (C) Ring formation is allowed. (D) Matched atoms in the same size of a mismatched ring are considered as the single-topology region.
Based on the MCS results, a specific atom-to-atom structural mapping between L0 and L1 is performed. The unperturbed atoms of L1 are renamed based on the atom name of L0. And the atom index of unperturbed atoms in both L0 and L1 are renumbered from 1 with the same order. The perturbed atoms of L0 and L1 are renumbered in order from the last unperturbed atom number. For alignment of L1 to L0, the unperturbed region of L1 is set to have the same coordinate as that of L0, and the perturbed atoms are regenerated using the internal coordinate values of L1. Note that a pair having dissimilar structures may result in an error-prone alignment of L1.
System and Input Generation
At the final stage, Free Energy Calculator generates two end-state systems; “Complex” and “Ligand” systems in ALB or RLB, and “Ligand” and “Vacuum” systems in ALS or RLS. To generate “Complex” system(s), the selected ligand(s) (in ALB) or ligand pair(s) (in RLB) are inserted into the initial complex structure by replacing the reference ligand. The binding pose of each ligand is determined by aligning MCS to the reference ligand. To generate "Ligand" system, each ligand (in ALB and ALS) or ligand pair (in RLB and RLS) is solvated in a water box. The size of water box can be adjusted by users. For "Vacuum" system, each ligand is in vacuum with the same dimension as in the “Ligand” system. All the generated systems are neutralized by counter ions (KCl). Together with input files and post-process scripts, all generated systems are provided in separate directories.
Algorithms and Methodologies
GENESIS
The hybrid single-dual topology scheme (for relative binding and solvation FEP/MD)20 and the soft-core potential functions to reduce the instability at end states57 are used. FEP/MD can be performed sequentially or in parallel. In the latter, FEP/MD can be combined with the replica-exchange MD (FEP/REMD) to enhance the convergence. The current version of GENESIS FEP/MD also supports a hybrid CPU/GPU acceleration for FEP/MD simulations.58 The short-range non-bonded interactions (Lennard-Jones (LJ) and particle mesh Ewald (PME)59, 60 real part) are calculated using GPU, while the long-range interactions (PME reciprocal part) are calculated using CPU. The multiple time-step rRESPA integrator with the 2.5-fs time-step can also be used to further accelerate FEP/MD. The output data are readily processed with GENESIS analysis tool (mbar_analysis) for MBAR analysis.
Absolute binding FE can be calculated in two ways: double annihilation method (DAM) and double decoupling method (DDM). DDM applies restraining potentials to restrain ligand’s position relative to a receptor during FEP/MD, which is similar to NAMD implementation. DAM in GENESIS calculates the FE of binding, ΔGbind, as:
| (1) |
where ΔGcomplex and ΔGligand correspond to the FE changes when the ligand in the complex and the ligand in solvent are transferred to gas phase, respectively. They are calculated by gradually annihilating the interactions between a ligand and its surrounding by applying a series of coupling parameters λ: 1.0, 0.9, 0.75, 0.6, 0.45, 0.35, 0.275, 0.2, 0.125, 0.05, and 0.0 (electrostatic interactions), 1.0, 0.9, 0.8, 0.7, 0.6, 0.525, 0.45, 0.4, 0.35, 0.325, 0.3, 0.275, 0.25, 0.225, 0.2, 0.175, 0.15, 0.125, 0.1, 0.05, and 0.0 (LJ interactions). The DAM in GENESIS is the same protocol as the MP-CAFEE method proposed by Fujitani et al.61 This method applies no restraint potentials and the calculated ΔGbind depends on the simulation system volume. This dependency is removed by applying the standard state correction, giving the binding affinity .62
| (2) |
where V is the volume of the simulation box (in periodic boundary conditions) and V0 is the volume of the standard state of 1 mol/L (1,660 Å3). In the current scheme, we do multiple simulations to reduce the sampling error as much as possible. The convergence of free energy calculations using MP-CAFEE is discussed in the original article.61
Relative binding FE between two ligands (L0 to L1, ) is calculated as:
| (3) |
where is the FE change upon transforming L0 to L1 in the complex, and is that in solution. The interactions of L0 with surrounding are slowly changed to those of L1 by applying six coupling parameters, λElecL0 and λElecL1 (electrostatic), λLJL0 and λLJL1 (LJ), and, λBondL0, and λBondL1 (bonded interactions). For 12 default windows, λElecL0, λLJL0, and λBondL0 are set to 1.0, 0.909, 0.818, 0.727, 0.636, 0.545, 0.455, 0.364, 0.273, 0.182, 0.091, and 0.0, while λElecL1, λLJL1, and λBondL1 are set to 0.0, 0.091, 0.182, 0.273, 0.364, 0.455, 0.545, 0.636, 0.727, 0.818, 0.909. and 1.0. Exchanges of λElecL0, λElecL1, λLJL0, λLJL1, λBondL0, and λBondL1 between adjacent windows (λ-exchange FEP or FEP/λ-REMD) are also available to enhance the convergence of FEP/MD.
Solvation FE, ΔGsolv, can be calculated in the same way as in the absolute binding FE:
| (4) |
where ΔGligand and ΔGvacuum correspond to the FE changes upon annihilation of the ligand in solution and in vacuum, respectively. Similarly, relative solvation FE, , is also calculated as in the relative binding FE.
| (5) |
where and are the FE change upon transforming L0 to L1 in solvent and in vacuum, respectively. Users can change the default number and values of coupling parameters by directly editing the configure file, although the coupling parameters in MP-CAFEE scheme have been well tuned.61 The spacing and the order of parameter change affect the stability/accuracy of the simulations, and these changes could be done in users’ responsibility.
The presented FE values from GENESIS FEP/MD in this work were obtained as follows. By using the inputs generated by Free Energy Calculator, each system was first equilibrated in NPT ensemble at 300 K and 1 bar using the Bussi thermostat and barostat.63, 64 Long-range electrostatic interactions were evaluated using smooth PME summation, while LJ interactions were truncated at a cutoff distance of 12 Å with a force switch function for the CHARMM force field.65, 66 All bonds involving hydrogen atoms were kept rigid using SHAKE and SETTLE algorithms.67, 68 Final configurations were used for subsequent FEP/MD. For the calculation of absolute binding FEs, we conducted 10 independent FEP/MD with different random seeds using the DAM (i.e., MP-CAFEE) and the rRESPA integrator with 2.5-fs time-step for fast motions and 5-fs for slow ones. In each calculation, the simulation was run for 5 ns per each window, and trajectories from 3 to 5 ns were used for analysis. For the calculations of relative binding, absolute solvation, or relative solvation FEs, the 5-ns FEP/λ-REMD simulations were performed, and the last 4 ns of the trajectories were used to calculate relative binding affinities. Only for vacuum systems, the calculations were performed in the NVT ensemble without the PME summation (both electrostatic and LJ interactions were calculated with no cutoff). In FEP/λ-REMD, the λ-exchanges between adjacent windows were attempted every 2 ps. Finally, the FE differences were estimated by the BAR method.69 In the MP-CAFEE method, the mean of the FE difference and its standard error were estimated from the FEs of 10 independent simulations. In the FEP/λ-REMD simulations, the obtained trajectories were decomposed into three blocks, and the mean and standard error were calculated using the blocks.
NAMD
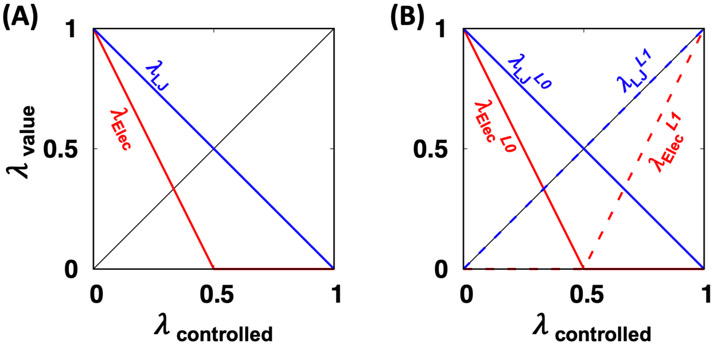
Like GENESIS, a hybrid single-dual topology scheme20 is used (for relative FES) with the soft-core potential70, 71 to avoid end-point catastrophe. During the alchemical transformation, two coupling parameters λLJ and λElec are controlled through a switching nonbonded (NB) scheduler (Figure 6). All FEP windows are launched together and run concurrently by the multiple-partition module72 of charm++/NAMD managed by a replica-exchange algorithm following the conventional Metropolis–Hastings exchange criterion.73 By using the simple overlap sampling (SOS) FE estimator,27 the collected potential energy evaluation of each replica-exchange is post-processed.
Figure 6.
Applied thermodynamic coupling parameters (λ) for LJ and electrostatic interactions of (A) absolute and (B) relative FEP/λ-REMD simulation in NAMD. The λ scaling is controlled using "alchElecLambdaStart” and “alchVdwLambdaEnd” keywords.
For the absolute FEP/λ-REMD calculations (Equations (1) and (4)), 32 windows are linearly employed (0.0, 0.03225, 0.06451, 0.09677, 0.12903, 0.16129, 0.19354, 0.22580, 0.25806, 0.29032, 0.32258, 0.35483, 0.38709, 0.41935, 0.45161, 0.48387, 0.51612, 0.54838, 0.58064, 0.61290, 0.64516, 0.67741, 0.70967, 0.74193, 0.77419, 0.80645, 0.83870, 0.87096, 0.90322, 0.93548, 0.96774, 1.0). Two coupling parameters λLJ and λElec are controlled by the NB scheduler, as shown in Figure 6A. Note that users can modify the number and values of two coupling parameters by directly editing the NAMD configure files. For the “Complex” system, a distance restraint is applied to restrain ligand’s position in decoupled states. And, the positional restraint for the ligand in “Ligand” and “Vacuum” is applied to prevent ligand’s drift. Note that these restraints are applied using “tclForces”, so that the restraint energies are separated and not added to the FE calculation results.
The relative binding and solvation FEs are calculated using Equations (3) and (5). For the relative FEP/λ-REMD simulation, 16 windows are employed (0.0000, 0.045, 0.090, 0.14546, 0.22425, 0.30303, 0.38182, 0.46061, 0.5394, 0.61819, 0.6970, 0.77576, 0.85455, 0.910, 0.955, 1.0000). During L0 to L1 transformation, two coupling parameters λLJ and λElec are exquisitely controlled by the switching NB scheduler, as shown in Figure 6B. Note that λElecL1 is turned on later than λLJL1, and λElecL0 is turned off earlier than λLJL0. During relative FEP/λ-REMD, a holonomic constraint is utilized to the coordinates of the single-topology atoms of L0 and L1 to maintain identical coordinates during simulation.20 To distinguish single and dual-topology atoms in L0 and L1, the different indices ("−2" and "−1" for single and dual-topology atoms in L0, and "2" and "1" for the atoms in L1) are used in the B-factor column of the structure (PDB) file. The four identifiers need to be segmented in an order of "−2", "−1", "2", and "1", and also the single-topology atoms in L0 and L1 should have the same atom name and order, which is automatically handled by RLS and RLB.
NAMD FEP/MD simulations in this work were performed as follows. By using the inputs generated by Free Energy Calculator, the equilibration was performed in NPT ensemble at 300 K and 1 atm (1.01325 bar) with Langevin piston pressure74 (for "Complex" and "Ligand"). RATTLE algorithm was used for TIP3P water model.68 For "Vacuum" system, NVT ensemble was used for both equilibration and FEP/MD simulation. During FEP/λ-REMD, the FE values were saved in history files, which were collected by SOS.75 For each of all relative FEs and absolute solvation FEs, 5-ns relative FEP/λ-REMD simulations were performed, and the last 4 ns of the simulation results were utilized for the final FE values. For each absolute binding simulation, 10-ns FEP/λ-REMD simulations were performed, and the last 5 ns of the FE values were measured for the final FE values.
APPLICATIONS
To validate the generated systems and necessary files by four Free Energy Calculator modules (ALB, RLB, ALS, and RLS), we performed absolute and relative FEP/λ-REMD simulations with NAMD and GENESIS (see Methods) using various test cases that were previously published by other authors. After FEP/MD simulations, the FE values were extracted from the saved configurations by using the provided post-processing scripts, and the FE values were averaged with the standard error of the mean (SEM) to estimate reliability and convergence of the results. All results are compared with the experimental and previously calculated FE values.
Ligand Solvation
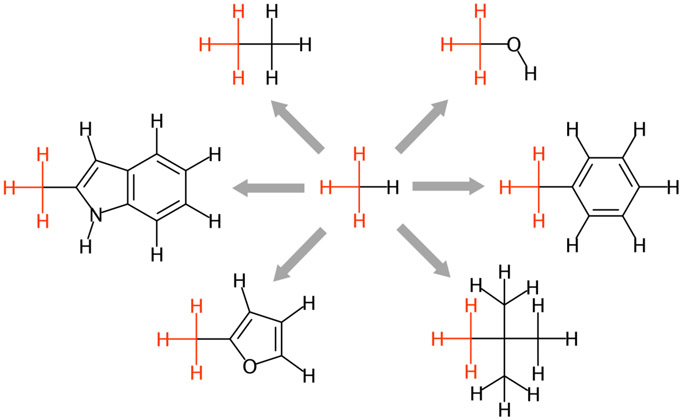
To test the ALS module, we chose seven organic molecules (Figure 7) that were used for in-depth FE calculations using the generalized Amber force field (GAFF) and various molecular simulation packages by Loeffler et al.76 All end-state systems (“Ligand” and “Vacuum”) were prepared at once through ALS and simulated using the protocols in Methods. Table 1 shows the ΔGsolv from NAMD and GENESIS FEP/λ-REMD simulations. Although the same CHARMM force field has been used, the methodology, λ schedule, and post-processing methods of two programs are different, yielding slightly different FE values. The biggest difference is less than 1 kcal/mol for the 2-methylindole. The SEM of all ΔGsolv show less than 0.03 kcal/mol, indicating that all systems are converged within 5-ns FEP/λ-REMD. In comparison of NAMD results with the experimental data, ΔGsolv of neopentane is closest to ΔGexp by 0.05 kcal/mol, and ΔGsolv of toluene is most deviated from ΔGexp by 0.78 kcal/mol. The GENESIS results also show a small difference of 0.1 kcal/mol for neopentane, and 1.1 kcal/mol difference for toluene that is most deviated among the seven ligands. All results from NAMD and GENESIS are in good agreement with the previous simulation results of Loeffler et al.76
Figure 7.
Seven ligands for testing ALS and RLS modules. For the relative solvation FEP/MD, the gray arrows and the red colors (atoms and bonds) are used for the perturbation paths and the single topology (unperturbed) region, respectively.
Table 1.
Absolute solvation FE results (kcal/mol) of ligands in Figure 7.
| Ligand | ΔGexp77 | ΔG76 | ΔG (NAMD) | ΔG (GENESIS) |
|---|---|---|---|---|
| Methane | 1.93 | 2.44 ~ 2.52 | 2.42 ± 0.01 | 2.46 ± 0.01 |
| Ethane | 1.77 | 2.48 ~ 2.56 | 2.28 ± 0.00 | 2.39 ± 0.02 |
| Methanol | −4.86 | −3.73 ~ −3.51 | −4.64 ± 0.01 | −4.38 ± 0.01 |
| Toluene | −0.76 | −0.72 ~ −0.55 | 0.01 ± 0.03 | 0.34 ± 0.02 |
| Neopentane | 2.68 | 2.58 ~ 2.71 | 2.63 ± 0.01 | 2.79 ± 0.01 |
| 2-methylfuran | −0.51 ~ −0.39 | −0.61 ± 0.01 | −0.36 ± 0.03 | |
| 2-methylindole | −6.35 ~ −6.06 | −7.02 ± 0.03 | −6.31 ± 0.05 |
For testing RLS, the six pairs were chosen as a radial shape having methane as a reference ligand L0 (Figure 7). Thus, the number of atoms in the single topology region are all same, and the number of perturbed atoms varies as many as 15. Nonetheless, the ΔΔGsolv results of both NAMD and GENESIS show a good agreement to each other, as well as with the previous simulation results (Table 2). Also, ΔΔGsolv of all pairs are remarkably consistent with the values taken from the absolute FE values ( from Table 1) with low SEM (~0.16 kcal/mol).
Table 2.
Relative solvation FE results (kcal/mol) of ligands in Figure 7.
| Ligand 0 | Ligand 1 | ΔΔGexp77 | ΔΔG76 | NAMD | GENESIS | ||
|---|---|---|---|---|---|---|---|
| ΔΔG | ΔΔG | ||||||
| Ethane | −0.16 | −0.19 ~ 0.01 | −0.12 ± 0.11 | −0.14 ± 0.10 | −0.06 ± 0.01 | −0.07 ± 0.02 | |
| Methanol | −6.79 | −6.20 ~ 6.00 | −7.15 ± 0.12 | −7.06 ± 0.13 | −6.76 ± 0.01 | −6.84 ± 0.01 | |
| Methane | Toluene | −2.70 | −3.52 ~ 3.06 | −2.40 ± 0.17 | −2.40 ± 0.19 | −2.11 ± 0.03 | −2.12 ± 0.02 |
| Neopentane | 0.75 | −0.40 ~ 0.13 | 0.23 ± 0.11 | 0.22 ± 0.15 | 0.37 ± 0.04 | 0.33 ± 0.01 | |
| 2-methylfuran | −3.10 ~ −2.84 | −3.03 ± 0.14 | −3.03 ± 0.11 | −2.81 ± 0.02 | −2.82 ± 0.03 | ||
| 2-methylindole | −9.14 ~ −8.64 | −9.40 (±0.16) | −9.44 (±0.20) | −8.80 ± 0.06 | −8.77 ± 0.05 | ||
Ligand Binding to Protein in Solution
We generated protein-ligand bound structures using benzene derivatives and T4-lysozyme L99A that were used to investigate the influence of protein conformational states on FEP/MD results by Lim et al.78 In their work, the binding cavity of T4-lysozyme was incrementally reorganized into three discrete conformational states referring to the closed, intermediate, and open states depending on the growth of acyl chain length attached to benzene. Thus, the simulation involving benzene with a long acyl chain results in inadequate sampling in the closed conformation, compared to an open conformation. For this reason, we chose benzene, toluene, ethylbenzene, and propylbenzene (Figure 8A) that are not critically affected by the closed conformation form of T4-lysozyme. To build a reference structure of the protein-ligand complex systems, the crystal structure of the closed T4-lysozyme conformation complexed with toluene (PDB ID 4W53) was chosen, and the toluene was used as the reference ligand (Figure 8B). All end-state systems ("Complex" and "Ligand") for both NAMD and GENESIS were prepared at once through ALB and RLB. For GENESIS systems, the MP-CAFEE (i.e., DAM) method was chosen.
Figure 8.
(A) (A) Four ligands for testing ALB and RLB modules. For the relative binding FEP/MD, the gray arrows and the red colors (atoms and bonds) are used for the perturbation paths and the single topology (unperturbed) region, respectively. (B) Overlaid stick representations of four ligand initial structures (benzene in orange, toluene in yellow, ethylbenzene in green, and propylbenzene in blue) in T4 lysozyme (gray). The aromatic ring of four ligands was well aligned based on the reference ligand (toluene). (C) A representative snapshot of T4-lysozyme-toluene complex in a solution box: gray cartoon for T4-lysozyme, yellow sphere for toluene, magenta and green beads for K+ and Cl− ions, respectively.
Table 3 shows the calculated ΔGbind obtained from NAMD and GENESIS FEP/λ-REMD. In NAMD results, ΔGbind of benzene is closest to ΔGexp with 0.08 kcal/mol difference, and ΔGbind of propylbenzene shows the largest difference with 1.45 kcal/mol to ΔGexp. In GENESIS results, ΔGbind of toluene is most similar to ΔGexp (0.45 kcal/mol difference), and the ΔGbind of propylbenzene is least similar (0.82 kcal/mol difference). In particular, the ΔGbind values of GENESIS show the sequential decrease of ΔGbind values as the acyl chain grows, which is consistent with ΔGexp. The SEM of all results are less than 0.5 kcal/mol, indicating that all systems are well converged within 10-ns (NAMD) or 5-ns (GENESIS) FEP/λ-REMD. According to the experiments,79 the occupancy of propylbenzene in the closed and intermediate protein conformations is 60% and 40%, respectively. For this reason, we speculate that the discrepancy of the initial structure (closed) and the intermediate conformation could affect ΔGbind of propylbenzene.
Table 3.
Absolute binding FE results (kcal/mol) of benzene derivatives in T4-Lysozyme L99A (Figure 8).
| Ligand | ΔGexp79 | ΔG (NAMD) | ΔG (GENESIS) |
|---|---|---|---|
| Benzene | −5.19 | −5.11 ± 0.25 | −5.80 ± 0.13 |
| Toluene | −5.52 | −5.01 ± 0.35 | −5.97 ± 0.18 |
| Ethylbenzene | −5.76 | −4.96 ± 0.31 | −6.22 ± 0.23 |
| Propylbenzene | −6.55 | −5.10 ± 0.46 | −7.37 ± 0.14 |
As shown in Table 4, the overall ΔΔGbind values from NAMD and GENESIS FEP/λ-REMD show less than 1 kcal/mol differences compared to ΔΔGexp . In NAMD results, ΔΔGbind of all three pairs show similar tendency with ΔΔGexp in that the longer acyl chain decreases ΔΔGbind more. The relative NAMD FEP/λ-REMD for propylbenzene yielded a FE value closer to ΔΔGexp than the absolute FE. In GENESIS results, all pairs of ΔΔGbind show good agreement with ΔΔGexp, and the transformation from toluene to ethylbenzene shows most similar ΔΔGbind to ΔΔGexp. In comparison with ΔΔG from the absolute values, GENESIS shows more consistent values that differ in ~0.5 kcal/mol. In both NAMD and GENESIS, ΔΔGbind for transformation from toluene to propylbenzene show the largest differences with ΔΔGexp (NAMD with ~1 kcal/mol and GENESIS with ~0.44 kcal/mol), which could be caused by protein conformations mentioned above. Nonetheless, the discrepancy less than 1 kcal/mol is sufficiently acceptable values for searching candidates in the lead optimization stage.6
Table 4.
Relative binding FE results (kcal/mol) of benzene derivatives (in T4-Lysozyme L99A (Figure 8).
| Ligand 0 | Ligand 1 | ΔΔGexp79 | NAMD | GENESIS | ||
|---|---|---|---|---|---|---|
| ΔΔG | ΔΔG | |||||
| Benzene | 0.33 | −0.23 ±0.10 | −0.09 ± 0.77 | −0.10 ± 0.07 | 0.17 ± 0.22 | |
| Toluene | Ethylbenzene | −0.24 | −0.66 ±0.03 | 0.06 ± 0.81 | −0.43 ± 0.02 | −0.25 ± 0.29 |
| Propylbenzene | −1.03 | −2.14 ±0.06 | −0.08 ± 0.81 | −1.57 ± 0.08 | −1.40 ± 0.23 | |
Ligand Binding to a Membrane Protein
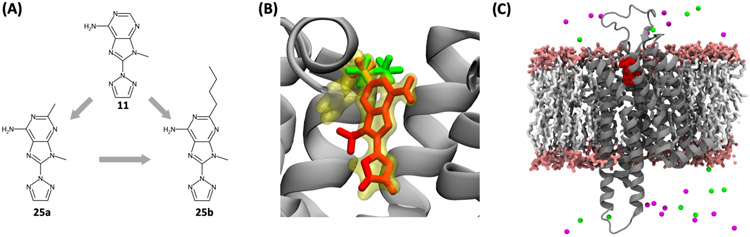
For testing the “bilayer” option provided by RLB, we prepared three relative binding systems for NAMD and GENESIS FEP/λ-REMD using the congeneric ligands bound to a G-protein-coupled receptor (GPCR) in a lipid bilayer environment. The three ligands (Figure 9A) were chosen from the previous experimental and computational study.80 We used a crystal structure of adenosine A2A receptor (PDB ID 3PWH)81 that was co-crystallized with ligand ZM241385 (yellow in Figure 9B) in the binding site. The missing residues in 3PWH and four disulfide bonds were generated automatically through PDB Reader & Manipulator, and a homogeneous POPC bilayer (55 lipids in each leaflet) was built through Membrane Builder. As the chemical structure of three congeneric ligands (11, 25a, 25b) have a large difference with ZM241385, ZM241385 was used only for positioning three alchemical structures (Figure 9B). To check the reliability of the FES results, all three pairs of the closed perturbation paths were selected. After equilibration runs through the Membrane Builder 6-step protocol,36 5-ns relative FEP/λ-REMD simulation was performed, and the last 4 ns of the simulation results were utilized for ΔΔGbind.
Figure 9.
(A) Three congeneric ligands for testing membrane systems; gray arrows represent the path directions for relative binding FEP/MD. (B) Overlaid stick representations of three ligand initial structures (11 in red, 25a in orange, and 25b in green) in A2A GPCR (gray). All ligands are well aligned based on the reference ligand (yellow) in the crystal structure. (C) Representative snapshot of A2A GPCR-11 complex embedded in a POPC bilayer (water is not shown for clarity): gray cartoon for GPCR, red sphere for compound 11, white stick for POPC tail, pink stick for POPC head, magenta and green beads for K+ and Cl− ions, respectively.
Table 5 shows the calculated ΔΔGbind. In the previous FEP/MD study of various types of GPCRs by Lenselink et al,82 the authors observed that the FE results of GPCR were highly target-dependent. The misassignment of some residues near binding sites and the conformation of the extracellular loop were responsible for the overprediction for some receptors. Nonetheless, the ΔΔGbind results from the automatically generated systems by RLB show good agreement with the experimental values. The error along the closed path is also quite low (0.44 kcal/mol for NAMD and 0.22 kcal/mol for GENESIS).
Table 5.
Relative binding FE results (kcal/mol) of the three congeneric ligands bound to A2A GPCR in a POPC bilayer (Figure 9).
| Transformation | ΔΔGexp80 | ΔΔG(NAMD) | ΔΔG(GENESIS) | |
|---|---|---|---|---|
| 11 | 25a | 0.25 | 0.41 ± 0.42 | 0.40 ± 0.05 |
| 11 | 25b | −1.15 | −0.10 ± 0.69 | −0.87 ± 0.12 |
| 25a | 25b | −1.40 | −0.95 ± 0.46 | −1.05 ± 0.10 |
Unlike the above T4-lysozme case with chemically simple ligand structures, the absolute binding FE calculations require additional orientional restraints of ligands relative their binding site.83 In other words, a simple distance restraint implemented in ALB for NAMD and GENESIS is not sufficient for accurate absolute FE calculations (see LIMITATIONS and FUTURE DIRECTIONS below). However, GENESIS provides another option, the MP-CAFEE (i.e., DAM) method, that does not require any restraints. Therefore, we calculated the absolute binding FE of three ligands for GPCR to test this option. As shown in Table 6, the MP-CAFEE method implemented in GENESIS successfully reproduced the experimental absolute binding FEs (and their trend) within 1.5 kcal/mol even in a complex membrane environment. The small SEM of less than 0.5 kcal/mol indicates that GENESIS MP-CAFEE simulations are well converged.
Table 6.
Absolute binding FE results (kcal/mol) of the three congeneric ligands bound to A2A GPCR in a POPC bilayer (Figure 9).
| Ligand | ΔGexp80 | ΔΔG(GENESIS) |
|---|---|---|
| 11 | −10.06 | −8.50 ± 0.25 |
| 11 | −9.81 | −8.60 ± 0.50 |
| 25a | −11.22 | −10.48 ± 0.47 |
LIMITATIONS and FUTURE DIRECTIONS
There are some limitations in the current version of Free Energy Calculator, which will be improved in the future. (1) In general, once system and input files are prepared for FEP calculations, using different ligand force fields becomes a daunting task because of the following reasons. Users need to specify their own ligand parameters (top & par files), and also edit the atom types to match with those in the already-built PSF files. Users must take care of nonbonded options specific to the parameter sets. For these reasons, we plan to support other small molecule force fields such as OPLS,84 GAFF,14 and CGenFF v2.x will be available. (2) In addition, uploading a custom ligand force field will be allowed, so that one can use other tools such as MATCH85 and GAAMP.86 (3) For neutralizing end-state systems "Ligand" and "Vacuum", only KCl ions are available, and other ion types will be supported. (4) For the "Radial shape perturbation path", a centered ligand is always the initially bound ligand (for Binder) or firstly uploaded ligand (for Solvator). Later, the centered ligand can be selectable by users. (5) The current version does not support the transformations between ligands carrying different net charges. The co-alchemical water approach,87 where a water molecule is alchemically mutated to an ion simultaneously during changing the net charge of a ligand (or ion) to maintain the neutrality of the system, will be supported. (6) In ALB, NAMD and GENESIS only support a distance restraint for ligands, and additional RMSD and orientational restraint option will be available. (7) The current version of CHARMM-GUI only produces the configure file for λ-REMD. FEP/T-REMD88 (replica-exchange along temperature) will be supported.
In general, if a user has access to parallel computing to launch FEP/λ-REMD for common drug-like ligands, the restraint setup provided by Free Energy Calculator is sufficient. In practice, a distance-only restraint requires λ-REMD to achieve thorough sampling/convergence on 3D spherical surface at alchemically decoupled states. A distance-only restraint can fail to sample some pivotal torsional motions of large flexible ligands, including therapeutic peptides, macrocycles, and inhibitors of protein-protein interactions. Sampling such binding associated with slow degrees of freedom requires sampling enhancement algorithms. The RMSD and orientational restraints are designed to assist sampling of ligand binding pose at decoupled states and accelerate conformational sampling of ligand. FEP with RMSD and orientational restraints can be run on a single computer node and does not need any special skill from general users.
CONCLUSIONS
In this work, we have described Free Energy Calculator that provides a broad range of standardized alchemical systems and necessary files for absolute binding, relative binding, absolute solvation, and relative solvation FEP/MD simulations using NAMD and GENESIS. A stepwise system generation workflow is designed to provide a flexible and easy-to-use interface and customizable workspaces. Furthermore, a set of congeneric ligands are accepted or generated to produce multiple FEP/MD systems at once, which alleviates time-consuming and repetitive tasks and assures the reproducibility.
To validate and illustrate the functionality of Free Energy Calculator, we have generated and performed various absolute and relative solvation FEP/MD simulations with a set of ligands and absolute and relative binding FEP/MD simulations with a set of ligands for T4 lysozyme in solution and adenosine A2A receptor in a membrane. In particular, NAMD and GENESIS utilized different approaches (DDM for NAMD and DAM for GENESIS) for the absolute FEP/MD simulation of T4 lysozyme to examine various embedded functions of Free Energy Calculator. Therefore, there is no reason to expect that both approaches give the same results. The goal of the current work is not to compare both approaches, but it is of interest to further investigate such differences as a follow-up work. Nonetheless, the calculated free energy values are overall consistent with the experimental and published free energy results (within ~1 kcal/mol). We hope that Free Energy Calculator is useful to carry out high-throughput FEP/MD simulations in the field of biomolecular sciences and drug discovery.
ACKNOWLEDGMENT
This work was supported in part by the grants from NSF MCB-1810695, DBI-1660380, and NIH GM138472 (WI), NIH P41-GM104601 and the Advanced Scientific Computing Research program, DOE Office of Science (WJ), NSF MCB-1517221 (BR), and KIAS individual grant (CG080501) (SK). For NAMD simulations, this research used resources of the Argonne Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC02-06CH11357. The computer resources for GENESIS simulations were provided through HPCI System Research projects (hp190097, hp200129, hp200135). Additional support for GENESIS development was supported in part by “Program for Promoting Researches on the Supercomputer Fugaku (Biomolecular dynamics in a living cell / MD-driven precision medicine)” and MEXT/KAKENHI (19H05645) (YS). We thank Dr. Chigusa Kobayashi for her technical advices to GPCR simulations using GENESIS.
REFERENCES
- 1.Jorgensen WL, The many roles of computation in drug discovery. Science 2004, 303, 1813. [DOI] [PubMed] [Google Scholar]
- 2.Jorgensen W, Efficient drug lead discovery and optimization. Accounts of Chemical Research 2009, 42 (6), 724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gilson M; Given J; Bush B; McCammon J, The statistical-thermodynamic basis for computation of binding affinities: a critical review. Biophys J 1997, 72 (3), 1047–1069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gilson M; Zhou H, Calculation of protein-ligand binding affinities. Annu Rev Biophys Biomol Struct 2007, 36, 21–42. [DOI] [PubMed] [Google Scholar]
- 5.Mobley D; Dill K, Binding of small-molecule ligands to proteins: "what you see" is not always "what you get". Structure 2009, 17 (4), 489–498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chodera JD; Mobley D; Shirts M; Dixon R; Branson K; Pande VS, Alchemical free energy methods for drug discovery: Progress and challenges. Curr Opin Struct Biol. 2011, 21 (2), 150–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Deng Y; Roux B, Calculation of standard binding free energies: Aromatic molecules in the t4 lysozyme l99a mutant. J. Chem. Theory Comput 2006, 2, 1255–1273. [DOI] [PubMed] [Google Scholar]
- 8.Deng Y; Roux B, Hydration of amino acid side chains: Nonpolar and electrostatic contributions calculated from staged molecular dynamics free energy simulations with explicit water molecules. J. Phys. Chem 2004, 108, 16567–16576. [Google Scholar]
- 9.Mobley DL; Graves AP; Chodera JD; Mcreynolds AC; Shoichet BK; Dill KA, Predicting absolute ligand binding free energies to a simple model site. J. Mol. Biol 2007, 371, 1118–1134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mobley DL; Vhodera JD; Dill KA, Confine-and-release method: obtaining correct binding free energies in the presence of protein conformational change. J. Chem. Theory Comput 2007, 3, 1231–1235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jiang W; Roux B, Free energy perturbation hamiltonian replica-exchange molecular dynamics (FEP/H-REMD) for absolute ligand binding free energy calculations J. Chem. Theory Comput 2010, 6 (9), 2559–2565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jiang W; Thirman J; Jo S; Roux B, Reduced free energy perturbation/Hamiltonian replica exchange molecular dynamics method with unbiased alchemical thermodynamic axis. J. Phys. Chem. B 2018, 122, 9435–9442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Vanommeslaeghe K; Hatcher E; Acharya C; Kundu S; Zhong S; Shim J; Darian E; Guvench O; Lopes P; MacKerell ADJ, CHARMM general force field (cgenff): A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem 2010, 31 (4), 671–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang J; Wolf R; Caldwell J; Kollman P; Case D, Development and testing of a general amber force field. J Comput. Chem 2004, 25 (9), 1157–1174. [DOI] [PubMed] [Google Scholar]
- 15.Lee T-S; Cerutti DS; Mermelstein D; Lin C; LeGrand S; Giese TJ; Roitberg A; Case DA; Walker RC; York DM, GPU-accelerated molecular dynamics and free energy methods in Amber18: performance enhancements and new features. J. Chem. Inf. Model 2018, 58 (10), 2043–2050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cournia Z; Allen BK; Beuming T; Pearlman DA; Radak BK; Sherman W, Rigorous Free Energy Simulations in Virtual Screening. J Chem Inf Model 2020. [DOI] [PubMed] [Google Scholar]
- 17.Wang J; Deng Y; Roux B, Absolute binding free energy calculations using molecular dynamics simulations with restraining potentials. Biophys. J 2006, 91, 2798–2814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Mobley DL; Chodera JD; Dill KA, On the use of orientational restraints and symmetry corrections in alchemical free energy calculations. J. Chem. Phys 2006, 125 (8), 084902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Boresch S; Tettinger F; Leitgeb M; Karplus M, Absolute binding free energies: A quantitative approach for their calculation. J. Phys. Chem. B 2003, 107, 9535–9551. [Google Scholar]
- 20.Jiang W; Chipot C; Roux B, Computing relative binding affinity of ligands to receptor: An effective hybrid single-dual-topology free-energy perturbation approach in NAMD. J. Chem. Inf. Model 2019, 59 (9), 3794–3802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Brooks BR; C. L. B III; A. D. M Jr.; Nilsson L; Roux B; Won Y; Archontis G; Boresch S; Im W; Karplus M, CHARMM: The biomolecular simulation program. J. Comput. Chem 2009, 30 (10), 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hess B; Kutzner C; Spoel D; Lindahl E, Gromacs 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput 2008, 4, 435–447. [DOI] [PubMed] [Google Scholar]
- 23.Kaus J; Pierce L; Walker R; McCammon A, Improving the efficiency of free energy calculations in the Amber molecular dynamics package. J. Chem. Theory Comput 2013, 9, 4131–4139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Jung J; Mori T; Kobayashi C; Matsunaga Y; Yoda T; Feig M; Sugita Y, GENESIS: a hybrid-parallel and multi-scale molecular dynamics simulator with enhanced sampling algorithms for biomolecular and cellular simulations. Wiley Interdiscip Rev Comput Mol Sci 2015, 5 (4), 310–323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wang L; Berne BJ; Friesner RA, On achieving high accuracy and reliability in the calculation of relative protein–ligand binding affinities. PNAS 2012, 109 (6), 1937–1942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Souaille M; Roux B, Extension to the weighted histogram analysis method: Combining umbrella sampling with free energy calculations. Computer Physics Communications 2001, 135 (2001), 40–57. [Google Scholar]
- 27.Lu N; Kofke D; Woolf T, Improving the efficiency and reliability of free energy perturbation calculations using overlap sampling methods. J Comput Chem 2004, 25 (28-39). [DOI] [PubMed] [Google Scholar]
- 28.Bennett CH, Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys 1976, 22, 245–268. [Google Scholar]
- 29.Shirts MR; Pande VS, Comparison of efficiency and bias of free energies computed by exponential averaging, the Bennett acceptance ratio, and thermodynamic integration. J. Chem. Phys 2005, 122, 144107. [DOI] [PubMed] [Google Scholar]
- 30.Loeffler HH; Michel J; Woods C, FESetup: Automating setup for alchemical free energy simulations. J. Chem. Inf. Model 2015, 55, 2485–2490. [DOI] [PubMed] [Google Scholar]
- 31.Jo S; Kim T; Iyer VG; Im W, CHARMM-GUI: a web-based graphical user interface for CHARMM. J Comput Chem 2008, 29 (11), 1859–65. [DOI] [PubMed] [Google Scholar]
- 32.Park SJ; Lee J; Qi Y; Kern NR; Lee HS; Jo S; Joung I; Joo K; Lee J; Im W, CHARMM-GUI Glycan Modeler for modeling and simulation of carbohydrates and glycoconjugates. Glycobiology 2019, 29 (4), 320–331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Qi Y; Lee J; Klauda JB; Im W, CHARMM-GUI Nanodisc Builder for modeling and simulation of various nanodisc systems. J Comput Chem 2019, 40 (7), 893–899. [DOI] [PubMed] [Google Scholar]
- 34.Lee J; Patel DS; Stahle J; Park SJ; Kern NR; Kim S; Lee J; Cheng X; Valvano MA; Holst O; Knirel YA; Qi Y; Jo S; Klauda JB; Widmalm G; Im W, CHARMM-GUI Membrane Builder for Complex Biological Membrane Simulations with Glycolipids and Lipoglycans. J Chem Theory Comput 2019, 15 (1), 775–786. [DOI] [PubMed] [Google Scholar]
- 35.Kim S; Lee J; Jo S; Brooks CL; Lee HS; Im W, CHARMM-GUI ligand reader and modeler for CHARMM force field generation of small molecules. Journal of Computational Chemistry 2017, 38 (21), 1879–1886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wu EL; Cheng X; Jo S; Rui H; Song KC; Davila-Contreras EM; Qi YF; Lee JM; Monje-Galvan V; Venable RM; Klauda JB; Im W, CHARMM-GUI Membrane Builder Toward Realistic Biological Membrane Simulations. Journal of Computational Chemistry 2014, 35 (27), 1997–2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Cheng X; Jo S; Lee HS; Klauda JB; Im W, CHARMM-GUI micelle builder for pure/mixed micelle and protein/micelle complex systems. J Chem Inf Model 2013, 53 (8), 2171–80. [DOI] [PubMed] [Google Scholar]
- 38.Jo S; Lim JB; Klauda JB; Im W, CHARMM-GUI Membrane Builder for mixed bilayers and its application to yeast membranes. Biophys J 2009, 97 (1), 50–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Jo S; Kim T; Im W, Automated Builder and Database of Protein/Membrane Complexes for Molecular Dynamics Simulations. Plos One 2007, 2 (9). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Park SJ; Lee J; Patel DS; Ma H; Lee HS; Jo S; Im W, Glycan Reader is improved to recognize most sugar types and chemical modifications in the Protein Data Bank. Bioinformatics 2017, 33 (19), 3051–3057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lee J; Cheng X; Jo S; MacKerell AD; Klauda JB; Im W, CHARMM-GUI Input Generator for NAMD, Gromacs, Amber, Openmm, and CHARMM/OpenMM Simulations using the CHARMM36 Additive Force Field. Biophysical Journal 2016, 110 (3), 641a–641a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lee J; Hitzenberger M; Rieger M; Kern NR; Zacharias M; Im W, CHARMM-GUI supports the Amber force fields. The Journal of Chemical Physics 2020, 153 (3), 035103. [DOI] [PubMed] [Google Scholar]
- 43.Jo S; Jiang W; Lee HS; Roux B; Im W, CHARMM-GUI ligand binder for absolute binding free energy calculations and its application. J. Chem. Inf. Model 2013, 53 (1), 267–277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Phillips J; Braun R; Wang W; Gumbart J; Tajkhorshid E; Villa E; Chipot C; Skeel R; Kale L; Shulten K, Scalable molecular dynamics with NAMD. J. Comput. Chem 2005, 26, 1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Kobayashi C; Jung J; Matsunaga Y; Mori T; Ando T; Tamura K; Kamiya M; Sugita Y, GENESIS 1.1: A hybrid-parallel molecular dynamics simulator with enhanced sampling algorithms on multiple computational platforms. J Comput Chem 2017, 38 (25), 2193–2206. [DOI] [PubMed] [Google Scholar]
- 46.Jo SW; Cheng X; Islam SM; Huang L; Rui H; Zhu A; Lee HS; Qi YF; Han W; Vanommeslaeghe K; MacKerell AD; Roux B; Im W, CHARMM-GUI PDB Manipulator for Advanced Modeling and Simulations of Proteins Containing Nonstandard Residues. Adv Protein Chem Str 2014, 96, 235–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Marvin JS was used for drawing chemical structures. Marvin JS 20.14.0. 2021. [Google Scholar]
- 48.Soteras Gutierrez I; Lin FY; Vanommeslaeghe K; Lemkul JA; Armacost KA; Brooks CL 3rd; MacKerell AD Jr., Parametrization of halogen bonds in the CHARMM general force field: Improved treatment of ligand-protein interactions. Bioorg Med Chem 2016, 24 (20), 4812–4825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Yang Q; Burchett W; Steeno GS; Liu S; Yang M; Mobley DL; Hou X, Optimal designs for pairwise calculation: An application to free energy perturbation in minimizing prediction variability. J Comput Chem 2020, 41 (3), 247–257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ward JH, Hierarchical Grouping to Optimize an Objective Function. Journal of the American Statistical Association 1963, 58 (301), 236–244. [Google Scholar]
- 51.Raymond JW; Willett P, Maximum common subgraph isomorphism algorithms for the matching of chemical structures. J Comput Aid Mol Des 2002, 16 (7), 521–533. [DOI] [PubMed] [Google Scholar]
- 52.Dalke A; Hastings J, FMCS: a novel algorithm for the multiple MCS problem. Journal of Cheminformatics 2013, 5 (1), O6. [Google Scholar]
- 53.Wang L; Deng Y; Wu Y; Kim B; LeBard DN; Wandschneider D; Beachy M; Friesner RA; Abel R, Accurate Modeling of Scaffold Hopping Transformations in Drug Discovery. J Chem Theory Comput 2017, 13 (1), 42–54. [DOI] [PubMed] [Google Scholar]
- 54.Yu HS; Deng Y; Wu Y; Sindhikara D; Rask AR; Kimura T; Abel R; Wang L, Accurate and Reliable Prediction of the Binding Affinities of Macrocycles to Their Protein Targets. J Chem Theory Comput 2017, 13 (12), 6290–6300. [DOI] [PubMed] [Google Scholar]
- 55.Boresch S; Karplus M, The Role of Bonded Terms in Free Energy Simulations: 1. Theoretical Analysis. The Journal of Physical Chemistry A 1999, 103 (1), 103–118. [Google Scholar]
- 56.S S; Roux B; Andersen OS, Free Energy Simulations: Thermodynamic Reversibility and Variability. The Journal of Physical Chemistry B 2000, 104 (21), 5179–5190. [Google Scholar]
- 57.Re SY; Oshima H; Kasahara K; Kamiya M; Sugita Y, Encounter complexes and hidden poses of kinase-inhibitor binding on the free-energy landscape. P Natl Acad Sci USA 2019, 116 (37), 18404–18409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Oshima H; Re S; Sugita Y, Prediction of Protein–Ligand Binding Pose and Affinity Using the gREST+FEP Method. Journal of Chemical Information and Modeling 2020. [DOI] [PubMed] [Google Scholar]
- 59.Darden T; York D; Pedersen L, Particle Mesh Ewald - an N.Log(N) Method for Ewald Sums in Large Systems. J Chem Phys 1993, 98 (12), 10089–10092. [Google Scholar]
- 60.Essmann U; Perera L; Berkowitz ML; Darden T; Lee H; Pedersen LG, A Smooth Particle Mesh Ewald Method. J Chem Phys 1995, 103 (19), 8577–8593. [Google Scholar]
- 61.Fujitani H; Tanida Y; Matsuura A, Massively parallel computation of absolute binding free energy with well-equilibrated states. Phys Rev E 2009, 79 (2). [DOI] [PubMed] [Google Scholar]
- 62.Deng Y; Roux B, Computations of standard binding free energies with molecular dynamics simulations. J Phys Chem B 2009, 113 (8), 2234–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Bussi G; Donadio D; Parrinello M, Canonical sampling through velocity rescaling. J Chem Phys 2007, 126 (1). [DOI] [PubMed] [Google Scholar]
- 64.Bussi G; Zykova-Timan T; Parrinello M, Isothermal-isobaric molecular dynamics using stochastic velocity rescaling. J Chem Phys 2009, 130 (7). [DOI] [PubMed] [Google Scholar]
- 65.Best RB; Zhu X; Shim J; Lopes PE; Mittal J; Feig M; Mackerell AD Jr., Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone phi, psi and side-chain chi(1) and chi(2) dihedral angles. J Chem Theory Comput 2012, 8 (9), 3257–3273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Klauda JB; Venable RM; Freites JA; O'Connor JW; Tobias DJ; Mondragon-Ramirez C; Vorobyov I; MacKerell AD Jr.; Pastor RW, Update of the CHARMM all-atom additive force field for lipids: validation on six lipid types. J Phys Chem B 2010, 114 (23), 7830–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Ryckaert J-P; Ciccotti G; Berendsen HJC, Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. Journal of Computational Physics 1977, 23 (3), 327–341. [Google Scholar]
- 68.Miyamoto S; Kollman PA, Settle - an Analytical Version of the Shake and Rattle Algorithm for Rigid Water Models. Journal of Computational Chemistry 1992, 13 (8), 952–962. [Google Scholar]
- 69.Shirts MR; Chodera JD, Statistically optimal analysis of samples from multiple equilibrium states. J Chem Phys 2008, 129 (12). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Beutler TC; Mark AE; Vanschaik RC; Gerber PR; Vangunsteren WF, Avoiding Singularities and Numerical Instabilities in Free-Energy Calculations Based on Molecular Simulations. Chem Phys Lett 1994, 222 (6), 529–539. [Google Scholar]
- 71.Zacharias M; Straatsma TP; Mccammon JA, Separation-Shifted Scaling, a New Scaling Method for Lennard-Jones Interactions in Thermodynamic Integration. J Chem Phys 1994, 100 (12), 9025–9031. [Google Scholar]
- 72.Jiang W; Phillips JC; Huang L; Fajer M; Meng YL; Gumbart JC; Luo Y; Schulten K; Roux B, Generalized scalable multiple copy algorithms for molecular dynamics simulations in NAMD. Computer Physics Communications 2014, 185 (3), 908–916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Murata K; Sugita Y; Okamoto Y, Free energy calculations for DNA base stacking by replica-exchange umbrella sampling. Chem Phys Lett 2004, 385 (1-2), 1–7. [Google Scholar]
- 74.Feller SE; Zhang YH; Pastor RW; Brooks BR, Constant-Pressure Molecular-Dynamics Simulation - the Langevin Piston Method. J Chem Phys 1995, 103 (11), 4613–4621. [Google Scholar]
- 75.Kumar S; Bouzida D; Swendsen RH; Kollman PA; Rosenberg JM, The Weighted Histogram Analysis Method for Free-Energy Calculations on Biomolecules .1. The Method. Journal of Computational Chemistry 1992, 13 (8), 1011–1021. [Google Scholar]
- 76.Loeffler HH; Bosisio S; Matos GDR; Suh D; Roux B; Mobley DL; Michel J, Reproducibility of Free Energy Calculations across Different Molecular Simulation Software Packages. J Chem Theory Comput 2018, 14 (11), 5567–5582. [DOI] [PubMed] [Google Scholar]
- 77.Bennaim A; Marcus Y, Solvation Thermodynamics of Nonionic Solutes. J Chem Phys 1984, 81 (4), 2016–2027. [Google Scholar]
- 78.Lim NM; Wang LL; Abel R; Mobley DL, Sensitivity in Binding Free Energies Due to Protein Reorganization. J Chem Theory Comput 2016, 12 (9), 4620–4631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Morton A; Matthews BW, Specificity of ligand binding in a buried nonpolar cavity of T4 lysozyme: linkage of dynamics and structural plasticity. Biochemistry 1995, 34 (27), 8576–88. [DOI] [PubMed] [Google Scholar]
- 80.Minetti P; Tinti MO; Carminati P; Castorina M; Di Cesare MA; Di Serio S; Gallo G; Ghirardi O; Giorgi F; Giorgi L; Piersanti G; Bartoccini F; Tarzia G, 2-n-Butyl-9-methyl-8-[1,2,3]triazol-2-yl-9H-purin-6-ylamine and analogues as A2A adenosine receptor antagonists. Design, synthesis, and pharmacological characterization. J Med Chem 2005, 48 (22), 6887–96. [DOI] [PubMed] [Google Scholar]
- 81.Dore AS; Robertson N; Errey JC; Ng I; Hollenstein K; Tehan B; Hurrell E; Bennett K; Congreve M; Magnani F; Tate CG; Weir M; Marshall FH, Structure of the Adenosine A(2A) Receptor in Complex with ZM241385 and the Xanthines XAC and Caffeine. Structure 2011, 19 (9), 1283–1293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Lenselink EB; Louvel J; Forti AF; van Veldhoven JPD; de Vries H; Mulder-Krieger T; McRobb FM; Negri A; Goose J; Abel R; van Vlijmen HWT; Wang LL; Harder E; Sherman W; IJzerman AP; Beuming T, Predicting Binding Affinities for GPCR Ligands Using Free-Energy Perturbation. Acs Omega 2016, 1 (2), 293–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Lee HS; Seok C; Im W, Potential Application of Alchemical Free Energy Simulations to Discriminate GPCR Ligand Efficacy. J Chem Theory Comput 2015, 11 (3), 1255–1266. [DOI] [PubMed] [Google Scholar]
- 84.Harder E; Damm W; Maple J; Wu CJ; Reboul M; Xiang JY; Wang LL; Lupyan D; Dahlgren MK; Knight JL; Kaus JW; Cerutti DS; Krilov G; Jorgensen WL; Abel R; Friesner RA, OPLS3: A Force Field Providing Broad Coverage of Drug-like Small Molecules and Proteins. Journal of Chemical Theory and Computation 2016, 12 (1), 281–296. [DOI] [PubMed] [Google Scholar]
- 85.Yesselman JD; Price DJ; Knight JL; Brooks CL 3rd, MATCH: an atom-typing toolset for molecular mechanics force fields. J Comput Chem 2012, 33 (2), 189–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Huang L; Roux B, Automated Force Field Parameterization for Non-Polarizable and Polarizable Atomic Models Based on Ab Initio Target Data. J Chem Theory Comput 2013, 9 (8). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Chen W; Deng YQ; Russell E; Wu YJ; Abel R; Wang LL, Accurate Calculation of Relative Binding Free Energies between Ligands with Different Net Charges. J Chem Theory Comput 2018, 14 (12), 6346–6358. [DOI] [PubMed] [Google Scholar]
- 88.Wang L; Berne BJ; Friesner RA, On achieving high accuracy and reliability in the calculation of relative protein-ligand binding affinities. P Natl Acad Sci USA 2012, 109 (6), 1937–1942. [DOI] [PMC free article] [PubMed] [Google Scholar]