Signal propagation in the dendrites of many neurons, including cortical pyramidal neurons in sensory cortex, is characterized by strong attenuation toward the soma. In contrast, using dual whole-cell recordings from the apical dendrite and soma of layer 5 (L5) pyramidal neurons in the anterior cingulate cortex (ACC) of adult male mice we found good coupling, particularly of slow subthreshold potentials like NMDA spikes or trains of EPSPs from dendrite to soma.
Keywords: anterior cingulate cortex, biophysical model, dendrite, electrical properties, NMDA spike, pyramidal neuron
Abstract
Signal propagation in the dendrites of many neurons, including cortical pyramidal neurons in sensory cortex, is characterized by strong attenuation toward the soma. In contrast, using dual whole-cell recordings from the apical dendrite and soma of layer 5 (L5) pyramidal neurons in the anterior cingulate cortex (ACC) of adult male mice we found good coupling, particularly of slow subthreshold potentials like NMDA spikes or trains of EPSPs from dendrite to soma. Only the fastest EPSPs in the ACC were reduced to a similar degree as in primary somatosensory cortex, revealing differential low-pass filtering capabilities. Furthermore, L5 pyramidal neurons in the ACC did not exhibit dendritic Ca2+ spikes as prominently found in the apical dendrite of S1 (somatosensory cortex) pyramidal neurons. Fitting the experimental data to a NEURON model revealed that the specific distribution of Ileak, Iir, Im, and Ih was sufficient to explain the electrotonic dendritic structure causing a leaky distal dendritic compartment with correspondingly low input resistance and a compact perisomatic region, resulting in a decoupling of distal tuft branches from each other while at the same time efficiently connecting them to the soma. Our results give a biophysically plausible explanation of how a class of prefrontal cortical pyramidal neurons achieve efficient integration of subthreshold distal synaptic inputs compared with the same cell type in sensory cortices.
SIGNIFICANCE STATEMENT Understanding cortical computation requires the understanding of its fundamental computational subunits. Layer 5 pyramidal neurons are the main output neurons of the cortex, integrating synaptic inputs across different cortical layers. Their elaborate dendritic tree receives, propagates, and transforms synaptic inputs into action potential output. We found good coupling of slow subthreshold potentials like NMDA spikes or trains of EPSPs from the distal apical dendrite to the soma in pyramidal neurons in the ACC, which was significantly better compared with S1. This suggests that frontal pyramidal neurons use a different integration scheme compared with the same cell type in somatosensory cortex, which has important implications for our understanding of information processing across different parts of the neocortex.
Introduction
Pyramidal neurons are the most abundant cell type in the neocortex, among which layer 5 (L5) pyramidal cells are the main output neurons of a cortical column projecting to other cortical and subcortical brain regions (Markram, 1997; Larsen et al., 2007). They possess a specific complex morphology with distinct apical, tuft and basal dendritic arborizations, which integrate and propagate synaptic inputs to generate action potential (AP) output (Markram et al., 1997; Häusser et al., 2000; London and Häusser, 2005). Indeed, synaptic integration within the dendritic tree is essential for the understanding of neuronal function (Spruston, 2008). The electrotonic structure of pyramidal neurons has therefore been extensively studied (Stuart and Spruston, 1998; London and Häusser, 2005; Larkum and Nevian, 2008; Major et al., 2013; Wybo et al., 2019). Dendrites of most L5 pyramidal neurons in sensory cortices are characterized by strong attenuation of synaptic inputs toward the soma (S; Berger et al., 2001; Williams and Stuart, 2002) that can be explained by the passive spread of potentials in a leaky cable (Rall, 1967; Norman, 1972; London et al., 1999). In human neocortical pyramidal neurons, the compartmentalization of the tuft dendrites is even more pronounced (Beaulieu-Laroche et al., 2018). In this scheme, distal synaptic inputs are electrotonically remote from the soma and have little impact on axonal AP generation (Zador et al., 1995). Hundreds of distal synapses would be required to trigger an AP, unless active dendritic mechanisms, like NMDA and Ca2+ spikes (Schiller et al., 1997, 2000), are activated by specific synaptic activity patterns (Larkum et al., 1999, 2009). Temporally and spatially correlated activity in thin dendritic branches can lead to the generation of NMDA spikes, which are more efficiently propagated along the dendrites compared with subthreshold EPSPs because of their slow kinetics (Nevian et al., 2007; Major et al., 2013). This illustrates that the frequency-dependent dendritic filtering properties are an essential determinant of neuronal integration.
It is well established that although the morphology of L5 pyramids in different brain regions might be homologous, their dendritic arborization can contain differential sets of ion channels that endow their dendrites with different electrical properties (Häusser et al., 2000; Lörincz et al., 2002; Dembrow et al., 2015). Often, these differences in ion channel composition depend on the projection target (Hattox and Nelson, 2007; Dembrow et al., 2010). Furthermore, pyramidal neurons in the hippocampus or in cortical L2/3 behave differently from cortical L5 pyramidal neurons (Robinson and Siegelbaum, 2003; Spruston, 2008). Accordingly, not all pyramidal neurons show the same electrotonic behavior. For example, we have recently described a type of pyramidal neuron in the anterior cingulate cortex (ACC), in which slow dendritic depolarizations are efficiently propagated to the somato–axonic integration site with little attenuation (Santello and Nevian, 2015). Also, hippocampal pyramidal neurons in CA1 have been reported to propagate steady-state subthreshold signals well (Magee, 1998). This could favor global integration of synaptic inputs within the dendritic tree (Tran-Van-Minh et al., 2015). The biophysical implementation for this “inverse propagation efficiency” (i.e., good propagation toward the soma) can be explained by cable theory, which states that good voltage transfer is observed when signals move from regions with low impedance to regions with high impedance values (Rall, 1962, 1967; London et al., 1999). The overall dendritic cable properties depend on the axial resistance, length, diameter, taper, and branching pattern. Additionally, the distribution of ionic conductances along the dendrites determining the membrane resistance might enhance or counteract the morphology. There is evidence that some types of pyramidal neurons possess a low-impedance apical dendrite and a more compact perisomatic region, but the consequence on signal propagation have not been explored in detail (Gulledge and Stuart, 2003; Kalmbach et al., 2013). Thus, it is relevant to determine and define the electrical properties of the different types of pyramidal neurons to characterize their integration scheme.
To understand the details of the electrotonic structure of L5 pyramidal neuron in the ACC, we studied signal propagation along dendrites with dual whole-cell recordings and compared it to recordings from pyramidal neurons in L5 of the somatosensory cortex. We used the experimental data to construct a computational model that provided a biophysically plausible explanation for the observed electrical behavior. The low impedance in the distal portion of the apical dendrite compared with the higher impedance in the perisomatic region favored good voltage transfer toward the soma. Only a few conductances were required to establish the corresponding impedance gradient. We report an integration scheme of these neurons that is based on low-pass filtering favoring the propagation of summed EPSPs and NMDA plateau potentials, without the necessity of Ca2+ spikes, which are apparently absent in this cell type. In conclusion, we describe a simple biophysical implementation of good coupling of distal synaptic inputs toward the soma in a cortical pyramidal neuron of the prefrontal cortex that contrasts with the electrotonic structure of other pyramidal neurons. These findings might be relevant for large-scale computational models of different areas of the neocortex (Markram et al., 2015).
Materials and Methods
Electrophysiology
Coronal slices (300 μm thick) containing the ACC were prepared from 10- to 12-week-old C57BL/6 male mice using a vibratome on a block angled at 15° to the horizontal in ice-cold oxygenated artificial CSF (ACSF) and then maintained in the same solution at 37°C for 15–120 min. Recordings from L5 pyramidal neurons in the primary somatosensory cortex (S1) were performed from parasagittal brain slices containing S1. Normal ACSF contained the following (in mm): NaCl 125, NaHCO3 25, KCl 2.5, NaH2PO4 1.25, MgCl2 1, glucose 25, and CaCl2 2, pH 7.4. Individual neurons were visualized with a Nikon Eclipse E600FN or Leica DMLFSA fit with a combination of oblique infrared illumination optics and epifluorescence, the switch between optical configurations was software triggered (DanCam 2013; Sieber et al., 2013). Pyramidal neurons were selected on the clearly visible, proximal apical dendrite. This selection criterion resulted in a homogeneous population of pyramidal neurons based on their firing properties and shape of the AP (i.e., all cells possessed a prominent afterhyperpolarization and a significant sag ratio at the soma). Dual somatic and dendritic whole-cell patch-clamp recordings were performed from identified L5 pyramidal neurons in the rostroventral ACC (1.1–1.4 mm below the pial surface, 1.1–0.2 mm rostral to the Bregma) using two Dagan BVC-700 amplifiers. During current injection experiments, the external recording solution (normal ACSF) contained 0.5 mm CNQX and 0.5 mm AP-5, while during extracellular stimulation experiments contained 0.5 mm gabazine. Experiments were performed at physiological temperatures between 34 and 37°. Whole-cell recording pipettes (somatic, 4–8 MΩ; dendritic, 12–32 MΩ) were pulled from borosilicate glass. The internal pipette solution consisted of the following (in mm): potassium gluconate 135, KCl 7, HEPES 10, Na2-phosphocreatine 10, Mg-ATP 4; GTP 0.3, and 0.2% biocytin, pH 7.2 (with KOH), 291–293 mosmol/L. For somatic recordings, 10–20 μm of Alexa Fluor 594 was added to the intracellular solution, as follows: first, the soma was patched (whole-cell configuration by negative pressure) after 5 min of intracellular perfusion, the fluorescent signal allowed for the clear identification of the apical dendritic tree, then an extracellular stimulation electrode was placed next to a tuft dendrite, and afterward the dendritic region of interest was patched with a smaller pipette. Compensation was performed in current-clamp mode by recovering the fast, initial square voltage response to a hyperpolarizing current injection (−100 pA, 50 ms). First, the pipette capacitance as compensated to the level that the voltage response showed an immediate voltage drop because of the series resistance of the pipette that was adjusted subsequently. Compensation of dendritic series resistance yielded values between 30 and 60 MΩ for pipettes with a resistance between 17 and 21 MΩ. On average, series resistance was 2.3 times larger than the pipette resistance. Series resistance of both somatic and dendritic recording electrodes was monitored frequently, and experiments were terminated when proper compensation was not possible anymore (i.e., reached values of more than four times the pipette resistance). In a set of experiments, we tested whether this compensation procedure yielded accurate voltage recordings. We performed dual whole-cell recordings from the soma of pyramidal neurons with a somatic and dendritic recording electrode. Measuring the voltage deflections with both electrodes while injecting current with the higher resistance dendritic recording electrode yielded an underestimation of the true voltage of <10%.
The stimulation techniques used in this study were intended to stimulate release from a few axon terminals localized close to the dendrite, and focal electrical synaptic stimulation was achieved by placing a theta patch pipette (diameter, 3–5 μm) located 2–4 μm from a dendrite in the apical tuft. All cells were filled with biocytin, and PFA-fixed slices were developed with the avidin–biotin–peroxidase method for Neurolucida reconstructions (Egger et al., 2008).
For optogenetic stimulation of afferent inputs, pyramidal neurons of the ACC were transfected by unilateral pressure injection of channelrhodopsin-2 (ChR2; AAV2_CamKIIa_hChR2(H134R)-mCherry) using a Pico spritzer. A total volume of 400 µl was injected in the ACC, using four separate injections of 100 µl at different coordinates (from bregma: 0.2/0.5/0.8/1.1 rostral, 0.3 lateral, −1.7/−1.7/−1.8/−1.9 ventral). Mice were anesthetized with isoflurane (1.5–2%) and locally anesthetized using lidocaine during the procedure. After an induction period of at least 3 weeks, coronal brain slices (300 μm thick) containing the ACC were prepared from 9- to 14-week-old mice. All recordings were performed at 30–32°C. Whole-cell dendritic and somatic recordings were obtained from L5 pyramidal neurons in the ACC as described above. EPSPs were evoked by stimulation of the ChR2-transfected axons with blue light (470 nm, 2 ms).
Data analysis
Data analysis was performed using Igor software (WaveMetrics) and Excel (Microsoft). For injected steady-state square pulses and EPSP-like currents, recorded events were automatically detected (threshold-crossing protocol) and analyzed (local maximum protocol). For extracellularly evoked synaptic potentials, individual events were visually identified and automatically analyzed (local maximum protocol). Amplitude, half-width, and rise and decay times were measured and compared for both the dendritic and the somatic events. The linearity of the recorded signals was assessed by comparing the amplitudes of depolarizing and hyperpolarizing responses normalized to the maximal amplitude of the injected current steps, voltages in the steady state were plotted against each other; reciprocity was evaluated by plotting the dendritic response to a current pulse delivered to the soma against the somatic response to the same current pulse delivered to the dendrite. Attenuation ratios were defined for dendrite-to-soma attenuation as Vmax,soma/Vmax,dendrite and for the soma-to-dendrite attenuation as Vmax,dendrite/Vmax,soma. In the case of distance-dependent attenuation, kinetics-dependent attenuation, and input resistance spatial gradient, the data were fit by either an exponential or linear function. The effective length constants λ were derived from the exponential fit of the experimental data. The distance dependency of attenuation in the compartmental model was captured by sigmoid fits, as was the case for the recruitment of NMDA conductances by extracellular stimulation. All statistical analyses used Student's t test (two sided).
Modeling
Simulations were performed in NEURON (Carnevale and Hines, 2004) using the biocytin-filled and -reconstructed cell shown in Figure 1. The resulting multicompartmental model consisted of 111 dendrites. The λ rule was used to obtain the number of segments for each compartment, except across the main apical dendrite where spatial resolution was refined to keep segment length below 5 μm. We used two independent modeling approaches to evaluate the robustness of our results.
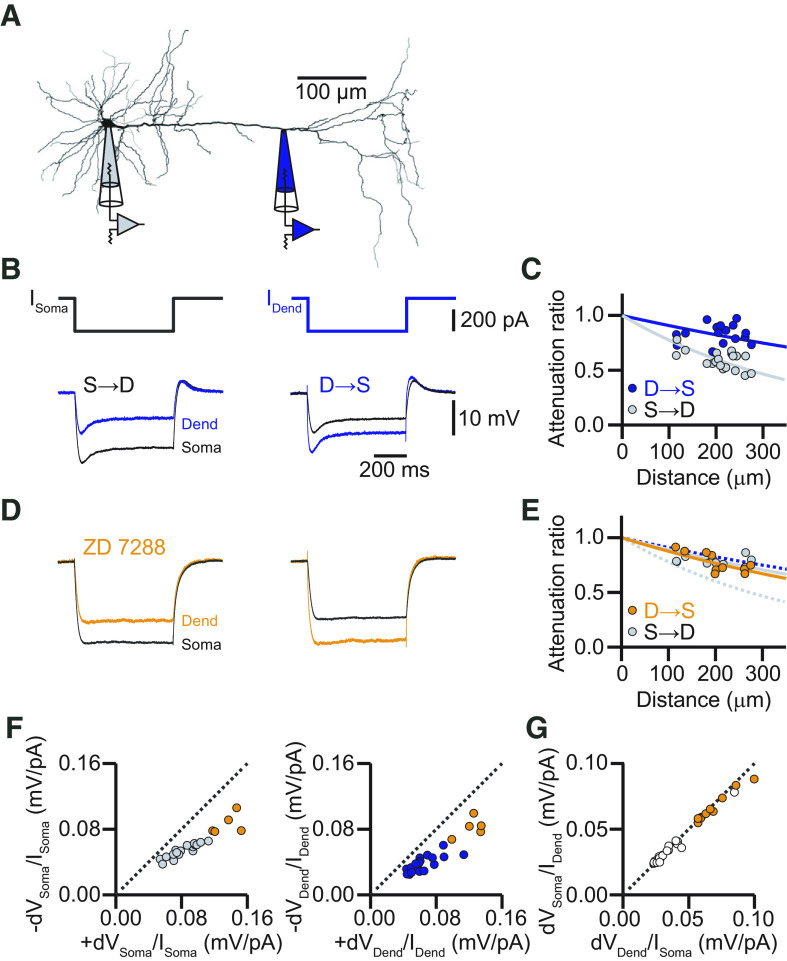
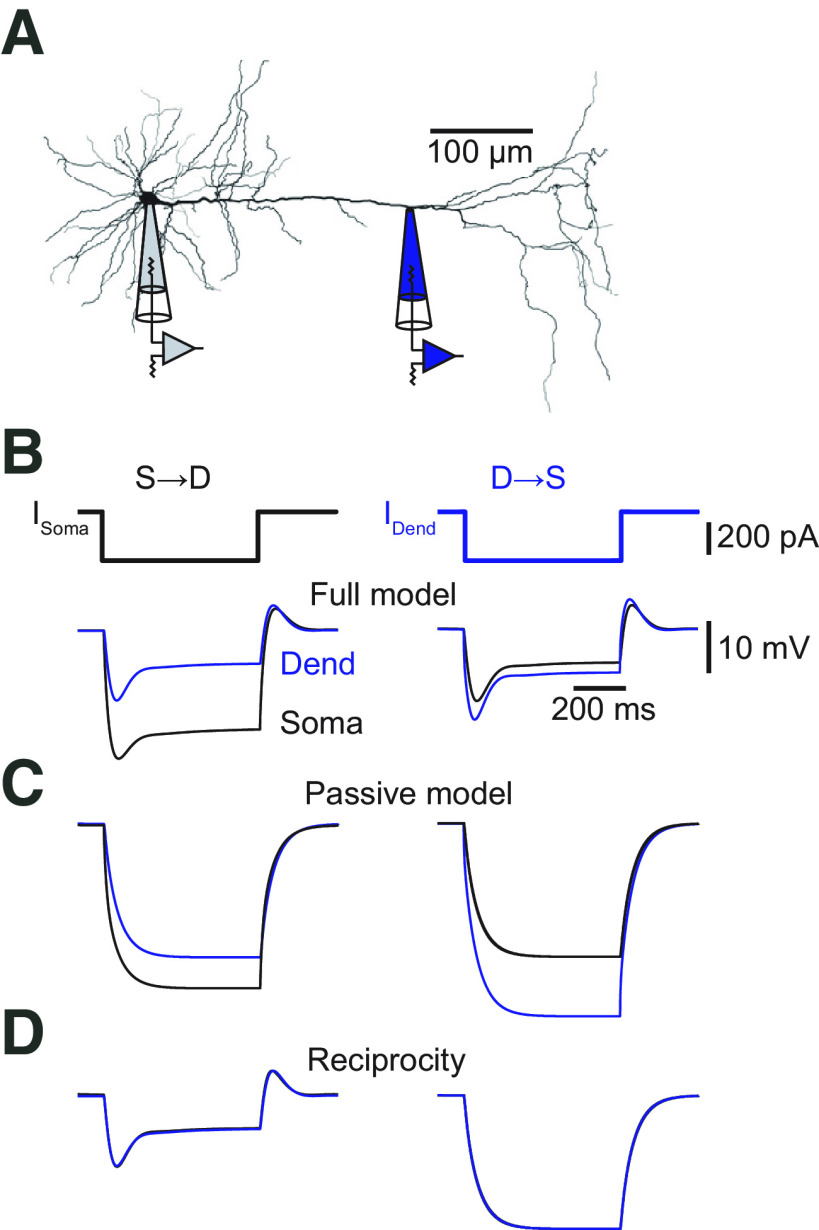
Figure 1.
Steady-state voltage attenuation along the apical dendrite of L5 pyramidal neurons in the ACC is small in the dendro-somatic direction. A, Neurolucida reconstruction of a biocytin-labeled L5 neuron in the ACC with the recording locations indicated. The dendritic recording had a distance of 262 μm from the soma. B, Voltage responses to somatic (left) and dendritic (right) current injections (600 ms, −300 pA). Somatic recordings are in black, and dendritic recordings are in blue. Resting membrane potential at the soma was −70 mV, and at the dendrite was −65 mV. C, Distance dependency of steady-state voltage attenuation for signals propagating from soma to dendrite (S→D, gray) and from dendrite to soma (D→S, blue). Solid lines represent exponential fits with effective length of constants of λS→D = 392 μm (gray) and λD→S = 1033 μm (blue). D, Voltage responses to somatic (left) and dendritic (right) current injections in the presence of the HCN channel blocker ZD-7288. Somatic recordings are in black, and dendritic recordings are in orange. Resting membrane potential at the soma was −80 mV, and at the dendrite was −75 mV. E, Distance dependency of steady-state voltage attenuation for signals propagating S→D (gray) and D→S (orange) in the presence of ZD-7288. Solid lines represent exponential fits with effective length constants of λS→D = 862 μm (gray) and λD→S = 750 μm (orange). Dashed lines indicate the corresponding fits determined in the control condition in C. F, Plot of voltage responses to hyperpolarizing current injections versus voltage responses to depolarizing current injections at the soma (left, gray circles) and the dendrite (right, blue circles). Orange circles represent responses in the presence of ZD-7288. The dashed unity line indicates equal responses to hyperpolarizing and depolarizing currents. The data points deviate from the unity line, indicating that the dendrites did not respond fully linearly. G, Plot of the steady-state voltage response amplitude at the soma to current injection at the dendrite versus steady-state voltage response amplitude at the dendrite to current injections at the soma. All data points (control, white; ZD-7288, orange) fall on the unity line, indicating reciprocity of the dendritic cable. Dend, Dendrite.
The first modeling approach was implemented in the NEURON simulator through NEAT (Wybo et al., 2020) and optimized with an evolutionary algorithm using the BluePyOpt library (Van Geit et al., 2016), where we ran 100 iterations with an offspring size of 100 for each combination of ion channels. Goodness of fit was evaluated in a multiobjective manner as the root mean square error of the resting voltage (computed as the average voltage 100 ms before each current step) and the final step voltage amplitudes after sag (computed as the average voltage during the last 100 ms after the DC current injection). We fixed the specific membrane capacitance at 1 μF/cm2 and the axial resistance at 113 Ω/cm. The membrane currents followed an exponential distribution , with the distance from the soma, the conductance at the soma, and the length constant of the distribution. Initial values (with bounds in square brackets) were for Km and the inward rectifying current Kir: = 4000 [0, 10,000] pS/μm2, = −100 [,−10] µm, = −85 [−95, −80] mV; for Ih: = 1 [0, 10,000] pS/μm2, = 100 [10, ] µm, = −40 [−50, −30] mV; and for Ileak: = 40 [0, 300] pS/μm2, = 200 [20, ] µm, and = −90 [−100, −50] mV. Negative means a distribution that decreases centrifugally, and indicates a constant current density. The reversal potential was spatially uniform, except for one case where we aimed to fit the data with only a leak current. To account for the difference in dendritic and somatic resting voltage in this case, we allowed to vary linearly with (, with the following initial values (with bounds in square brackets): −90 [−100, −50] mV and 0 [−1/15, 1/15] mV/μm).
In the second model, axial resistance (Ri) was set to 113 Ω/cm (within the range 80–150 Ω/cm established for neocortical pyramidal cells; Stuart and Spruston, 1998), membrane resistance (Rm) distribution was defined by the spatial profile of the leak conductance. Membrane capacitance (Cm) was also heterogeneously distributed as it increased distally as specified by the spinefactor as follows: f(x) = SomaticCm + [spinefactor * x]. Ri and Cm were obtained by finding the combination of the parameters that produced the best fit to experimentally recorded somatic and dendritic current step injections. The other passive biophysical parameters of the first model were as follows: Eleak = −70 mV, ENa = 50 mV, and EK = −87 mV. The active conductances Km, Kir, and Ih, and the passive leak followed an exponential distribution with the two free parameters and denoting the conducatance at the soma and the length constant of the distribution, respectively. The density of hyperpolarization-activated cyclic nucleotide-gated (HCN) channels was initially set to increase from soma to dendrite, Km channel density was set to decrease from soma to dendrite and the density of Kir and leak conductances was set as uniform. The experimentally acquired voltage responses to hyperpolarizing (600 ms, −300 pA) and depolarizing (600 ms, +100 pA) steady-state current injections from the dual recordings and the corresponding reconstructed morphology were used to constrain the compartmental model. The initial distributions were fit to the experimental data through a succession of iterations. After every iteration, dendritic and somatic voltage responses were simulated for both directions of propagation (dendrite-to-soma and soma-to-dendrite, respectively), then the resulting goodness of the fit was quantified by comparison with the experimental data. and were obtained by systematically exploring the combination of parameters that produced the best fit to experimentally recorded somatic and dendritic current step injections. Before the next round of fitting the values of the free parameters were tweaked to diverge randomly from their initial values to achieve a thorough exploration of the parameter space, which was implemented through the simulated annealing procedure. After a minimum discrepancy was found between the model and the experimental data, the corresponding point in the parameter space was taken for initiating Brent's algorithm to probe the parameter space locally in a systematic and more accurate manner. The exploration of the parameter space was sequential, as follows: first, Km, Kir, and leak, simulated annealing in Ih blockade conditions; second, Km, Kir, and leak, Brent's algorithms in Ih blockade conditions; third, only Ih (other conductances fixed), simulated annealing in control conditions; and fourth, only Ih (other conductances fixed), Brent's algorithm in control conditions. The densities of all the heterogeneously distributed parameters were kept constant across the tuft (taking the density value measured at the apical bifurcation). The final fitted values were as follows: (in pS/μm2) _leak = 0.004, _Km = 41.3, _Kir = 6.6, and _Ih = 0.05; (in µF/ cm2) SomaticCm = 1; (unitless) _leak = 27.5, _Km = −39.9, _Kir = −167.9, _Ih = 44.5, and spinefactor = 0.012904.
EPSP-like currents were modeled as double exponential functions with the appropriate rise and decay time constants (fast: τrise = 0.5 ms, τdecay = 2 ms; medium fast: τrise = 1 ms, τdecay = 4 ms; medium slow: τrise = 2 ms, τdecay = 8 ms; and slow: τrise = 4 ms, τdecay = 16 ms), and with a peak conductance of 0.0093211 μS.
To investigate synaptic integration under different HCN distributions, we took the model that was optimized with Ileak and the potassium conductances (Km and Kir) to fit the voltage response to step current injection under the application of ZD-7288, and added Ih (see Fig. 12A). We used the synapse model from Branco et al. (2010) to implement excitatory synapses with AMPA and NMDA components.
Figure 12.
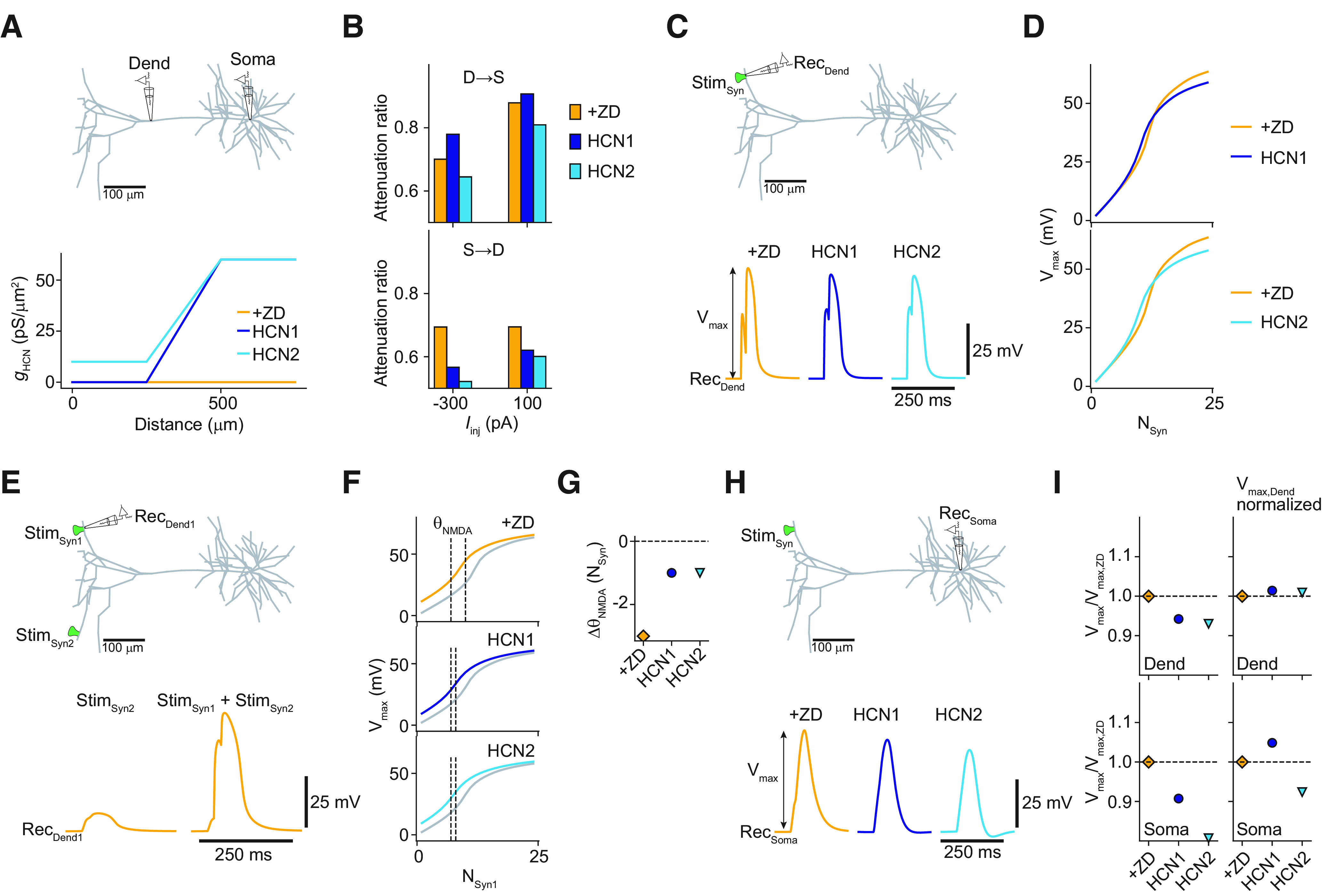
Effect of HCN distribution on dendrite-to-soma coupling and synaptic integration. A, Top, Sketch indicating dendritic (Dend) and somatic recording configuration. Bottom, Comparison of different HCN distributions (piecewise linear as a function of distance to soma). One distribution had no HCN channels proximally (<250 μm; HCN 1, purple), and the other one had a small constant proximal HCN density (10 pS/μm2; HCN 2, turquoise). Both distributions increased linearly between 250 and 500 μm from their respective proximal densities to 60 pS/μm2, which was kept constant from there on to the most distal branches (>500 μm). The experimental block of all HCN channels with ZD-7288 was modeled as zero HCN density throughout the cell (ZD, orange). B, Voltage attenuation under step current application from dendrite to soma (top) and from soma to dendrite (bottom) for the different HCN distributions. Note that HCN1 replicated the experimental results best (more attenuation in the presence of ZD from dendrite to soma, but less attenuation in the other direction). C, Top, Sketch of recording configuration at a distal synapse. Bottom, Local voltage responses for a paired-pulse activation protocol (time delay, 20 ms) for a cluster of 18 identical synapses for the different HCN distributions. D, Maximal amplitude of the local voltage responses (Vmax) as a function of the number of activated synapses. E, Top, Sketch of recording configuration to evaluate the interaction of synapse clusters on different branches. Bottom left, Voltage response measured at synapse cluster 1 (RecDend1) evoked by paired-pulse activation (20 ms) of 18 synapses at cluster 2 (StimSyn2). Bottom right, Voltage response to the sequential activation of both clusters. The activation of cluster 2 preceded activation of cluster 1 by 20 ms. Only the ZD case is shown. F, Vmax as a function of the number of activated synapses at cluster 1, while 18 synapses at cluster 2 were activated 20 ms before the activation of cluster 1 for the different HCN distributions. Activation curves without the activation of cluster 2 shown in gray for reference. NMDA thresholds (ΘNMDA, quantified as the minimal number of synapses for which Vmax exceeded the linear extrapolation of the response for the activation of one and two synapses by 20%) are indicated by the dashed black lines. G, Shift in NMDA threshold (ΔΘNMDA) at synapse cluster 1 when synapse cluster 2 was activated 20 ms before. H, Somatic voltage responses for the same paired-pulse activation protocol as in C. I, Top, Sketch of recording configuration to evaluate the dendrite-to-soma coupling. Bottom, Relative Vmax normalized to the ZD case for the local voltage responses (top) and the somatic voltage responses (bottom). Left column shows the relative Vmax when the synaptic weights were identical for ZD, HCN 1, and HCN 2 (as was the case for the results shown in C–H). Right column shows the relative Vmax when synaptic weights were rescaled to yield the same dendritic peak amplitude as in the ZD case (for the paired-pulse activation of 18 synapses). Stim, Stimulation.
Data availability
The code of the simulations can be found at https://github.com/unibe-cns/ACCPyr or can be made available on request.
Results
Electrophysiological characterization of L5 pyramidal neuron dendrites in the ACC
To evaluate the passive properties of the apical dendrite of L5 pyramidal neurons in the ACC of adult mice, we performed simultaneous dual whole-cell voltage recordings from the soma and the apical dendrite. The propagation of steady-state voltage deflections was measured by injecting hyperpolarizing (−300 pA) square pulses in current-clamp mode (Fig. 1A,B). When current was injected in the dendrite and recorded at the soma, the steady-state voltage amplitude was reduced by only ∼15% after propagation [average attenuation factor (AF): AFD→S = 0.83 ± 0.05, n = 22; distance: 193 ± 19 μm]; in the opposite direction, from soma to dendrite, attenuation was much stronger with ∼40% (AFS→D = 0.58 ± 0.03, n = 22, p < 0.0001 by Student's t test). From all the attenuation measurements at different dendritic locations, we estimated the dendrite-to-soma and soma-to-dendrite effective length constants of λD→S = 1033 ± 19 μm and λS→D = 392 ± 9 μm, respectively (Fig. 1C). This propagation asymmetry was largely equalized after blocking the hyperpolarization-activated current Ih by bath application of the selective blocker ZD-7288 (Fig. 1D,E). The effective length constant from dendrite to soma decreased (λD→S = 750 ± 16 μm; p < 0.01, one-way ANOVA of bootstrapped attenuation curves; n = 10) but increased from soma to dendrite (λS→D = 862 ± 27 μm; p < 0.0001, one-way ANOVA of bootstrapped attenuation curves; n = 10).
The cable properties of ACC L5 pyramidal cells as characterized in its steady-state followed the rule of reciprocity (mean slope: control, 1.07 ± 0.09; ZD-7288, 1.20 ± 0.09) but deviated from linearity (Hu et al., 2010) for positive current injections, indicating a boosted response to depolarizing pulses (linearity at the soma: control mean slope, 0.71 ± 0.11; ZD-7288, 0.66 ± 0.08; linearity at the dendrite: control mean slope, 0.64 ± 0.03; ZD-7288, 0.59 ± 0.06; Fig. 1F,G). The measured linearity and reciprocity revealed that the apical dendrite of L5 pyramidal neurons in the ACC behave as nearly passive cables in the steady state. Nevertheless, steady-state voltages propagate very well from the dendrite to the soma.
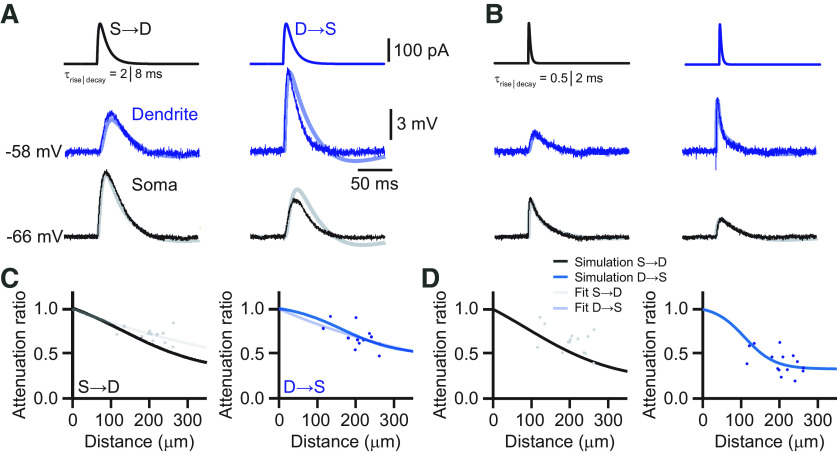
Next, we characterized the propagation of EPSP-like voltage deflections. EPSP-shaped currents (τrise = 2 ms, τdecay = 8 ms) were injected into the dendrite or soma through the corresponding patch electrode and recorded at the other site (Fig. 2A). EPSPs propagated well from dendrite to soma with an average attenuation of only ∼30% (AFD→S = 0.69 ± 0.02, n = 12). The propagation of EPSPs from soma to dendrite was similar (AFS→D = 0.72 ± 0.01, n = 12; p = 0.27, Student's t test). As expected, the corresponding effective length constants (λD→S = 539 μm, λS→D = 622 μm) were shorter than in the steady-state case (Fig. 2B). Although the EPSP amplitude was little affected, the shape of the EPSP as characterized by its rise time was filtered during propagation. The rise time was slowed down by a factor of 2.4 (τrise,dend = 2.9 ± 0.08 ms; τrise,soma = 6.9 ± 0.34 ms). Bath application of ZD-7288 left the propagation of the transient signals largely unaffected, suggesting that Ih had little effect on the propagation of individual EPSPs (Fig. 2C). Signal propagation in dendrites depends on its frequency components (Hu et al., 2009). To describe the distinctive dendritic filtering of L5 pyramids in the ACC, we quantified the impact of the kinetics of an EPSP on its attenuation. EPSP-shaped currents with a range of different rise and decay times were injected into the dendrite or soma, respectively (fast: τrise = 0.5 ms, τdecay = 2 ms; medium fast: τrise = 1 ms, τdecay = 4 ms; medium slow: τrise = 2 ms, τdecay = 8 ms; slow: τrise = 4 ms, τdecay = 16 ms, corresponding to half-widths of 5.5, 10, 19.6, and 41.25 ms, respectively). We found that the EPSP kinetics had a strong influence on the attenuation of EPSP amplitude in the dendrite-to-soma direction, as expected from cable theory (Fig. 2D). Peak amplitude attenuation ranged from ∼60% for fast signals to 20% for slow signals, corresponding to effective length constants of λD→S = 252 μm, λD→S = 399 μm, λD→S = 539 μm, and λD→S = 811 μm for the fastest to slowest EPSPs, respectively. In contrast, the attenuation of signals propagating from the soma to the dendrite was largely independent of signal kinetics with effective length constants of λS→D = 468 μm, λS→D = 561 μm, λS→D = 621 μm, and λS→D = 673 μm for the fastest to slowest EPSPs. Interestingly, dendrite-to-soma propagation was better in the opposite direction for the slowest EPSP, but fast signals traveled more efficiently away from the soma.
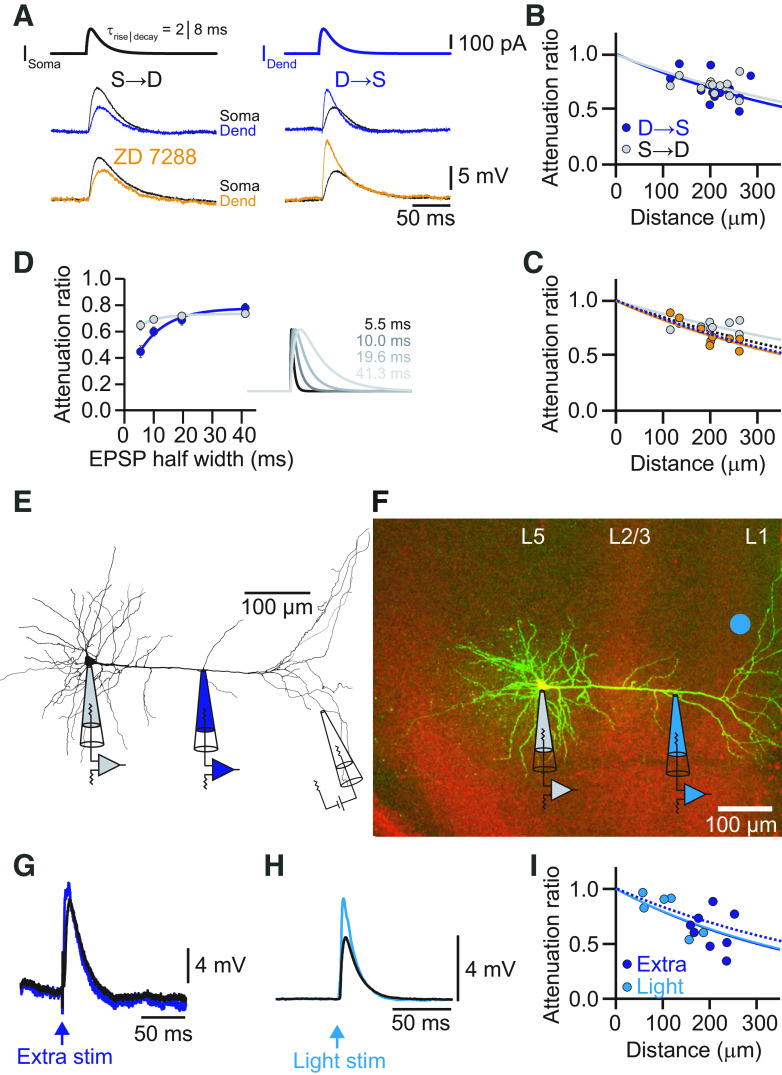
Figure 2.
EPSP attenuation in the apical dendrite of ACC L5 pyramidal neurons. A, Voltage responses to somatic (left) and dendritic (right) current injections of EPSP-like currents (τrise = 2 ms, τdecay = 8 ms) from the cell shown in Figure 1. Somatic recordings are in black. Dendritic recordings in the control condition are in blue, and in the presence of ZD-7288 in orange. Note the moderate attenuation of the EPSP amplitude from dendrite to soma. B, Distance dependency of EPSP attenuation for signals propagating S→D (gray) and D→S (blue). Solid lines represent exponential fits with effective lengths constants of λS→D = 622 μm (gray) and λD→S = 539 μm (blue). C, Distance dependence of EPSP amplitude attenuation for signals propagating S→D (gray) and D→S (orange) in the presence of ZD-7288. Solid lines represent exponential fits to the data points. Dashed lines indicate the corresponding fits determined in the control condition in B. D, Plot of the average voltage attenuation of injected EPSP-like currents with different kinetics as a function of the corresponding EPSP half-width. On the right, τrise, τdecay, and the corresponding half-width are indicated. E, Neurolucida reconstruction of a biocytin-labeled L5 neuron in the ACC with the recording locations indicated. The dendritic recording had a distance of 185 μm from the soma. EPSPs were evoked by an extracellular stimulation electrode placed close to the tuft dendrites. F, Confocal fluorescence image of an L5 pyramidal neuron in the ACC in green and the ChR2-positive axons from the contralateral ACC in red. The dendritic recording was a distance of 248 μm from the soma. The blue dot indicates the site of optogenetic stimulation with blue light in L1. G, Synaptically evoked EPSP by extracellular electrical stimulation recorded at the dendrite (blue) and the soma (black). H, Optogenetically evoked EPSP recorded at the dendrite (light blue) and the soma (black). I, Distance dependency of EPSP amplitude attenuation for signals propagating from dendrite to soma for electrically (blue) and optogenetically (light blue) evoked EPSPs. Solid lines represent exponential fits to the data points. The dashed line indicates the exponential fit to the dendrite-to-soma attenuation of an injected EPSP-like current (τrise = 2 ms, τdecay = 8 ms) from B. Note that electrical and light-evoked EPSPs yielded identical attenuation profiles. Stim, Stimulation.
Finally, we measured the attenuation of EPSPs evoked synaptically by electrical extracellular stimulation of axons in L1 (Fig. 2E,G). Evoked EPSPs had similar rise times to the second fastest injected EPSPs (τrise = 1.05 ± 0.02 ms). Distally evoked EPSPs still showed good dendrite-to-soma propagation (AFD→S = 0.55 ± 0.06 μm, n = 7) with an effective length constant of λD→S = 445 μm that was comparable to the corresponding injected EPSP (Fig. 2I). Additionally, we evoked EPSPs by optogenetic activation of axons from the contralateral ACC, virally transduced with ChR2, that projected prominently to the tuft dendrites of L5 pyramidal neurons on the ipsilateral side. Optogenetically evoked EPSPs were similar in terms of kinetics (τrise = 1.7 ± 0.3 ms) compared with the electrically evoked ones and had a comparable attenuation with an effective length constant of λD→S = 437 μm (Fig. 2F,H,I).
Comparison to EPSP attenuation in L5 pyramidal neurons in the somatosensory cortex
Our findings about EPSP attenuation in ACC suggested a difference to previous results of EPSP propagation in L5 pyramidal neurons in sensory cortices, in which the attenuation of fast EPSPs of synaptic origin was determined to range between 85% and 95%, and in which slow signals were also propagating less efficiently toward the soma (Berger et al., 2001; Williams and Stuart, 2002; Nevian et al., 2007). We performed dual whole-cell recordings from the soma and apical dendrites of cells in L5 of the S1 of adult mice for comparison with ACC (Fig. 3A). EPSP-like current injections at the dendritic electrode, with different kinetic profiles, as described above, resulted in voltage deflections that were more strongly attenuated toward the soma for fast than slow signals (Fig. 3B,C) with effective length constants of λD→S = 251 μm, λD→S = 338 μm, λD→S = 400 μm, and λD→S = 464 μm, respectively (Fig. 3D). In contrast, evoked EPSPs propagated better from the soma into the dendrite for all EPSP kinetics (λS→D = 433 μm, λS→D = 499 μm, λS→D = 557 μm, and λS→D = 568 μm).
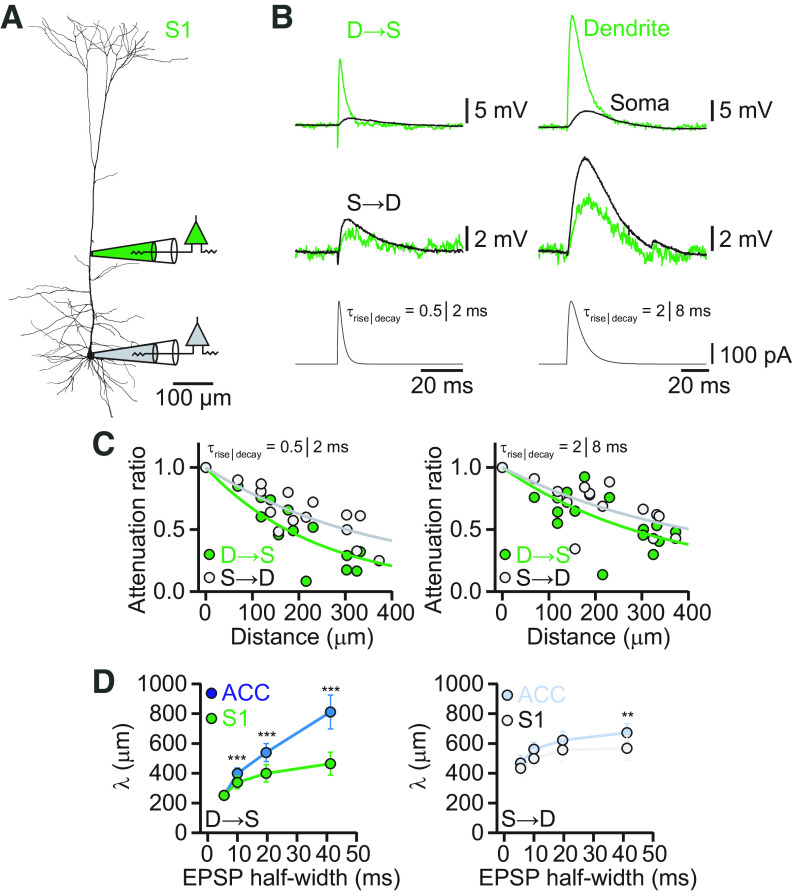
Figure 3.
EPSP attenuation in the apical dendrite of S1 L5 pyramidal neurons. A, Neurolucida reconstruction of a biocytin-labeled L5 neuron in S1 with the recording locations indicated. The dendritic recording had a distance of 210 μm from the soma. B, Voltage responses to dendritic (top) and somatic (bottom) current injections of EPSP-like currents with different kinetics. Somatic recordings are in black and dendritic recordings in green. C, Distance dependency of EPSP amplitude attenuation for signals propagating S→D (gray) and D→S (green). Solid lines represent exponential fits to the data points. D, Plot of the effective length constant of attenuation for EPSPs with different kinetics as a function of the corresponding EPSP half-width from dendrite to soma in the ACC (blue) and S1 (green). The plot on the right shows the corresponding effective length constants for the soma-to-dendrite direction. **p < 0.01, ***p < 0.001.
Comparing the length constants of L5 pyramidal neurons in S1 to ACC revealed significantly better propagation of slow EPSPs from dendrite to soma in ACC than in S1 (p < 0.001, one-way ANOVA of bootstrapped attenuation curves; n = 10). Only the fastest EPSP was identically attenuated from dendrite to soma in ACC and S1, suggesting differential low-pass filtering properties of L5 pyramidal neurons in these two brain regions (Fig. 3D). Functionally, this indicates that fast EPSPs of monosynaptic origin are equally attenuated, suppressing spontaneous and random synaptic noise, whereas slow potentials in the ACC are much less attenuated than in S1. EPSP propagation from soma to dendrite was very similar in the two cell types, showing only a significantly better propagation of the slowest EPSPs in ACC compared with S1 (p < 0.001, one-way ANOVA of bootstrapped attenuation curves; n = 10). In summary, ACC and S1 apical dendrites of L5 pyramidal neurons show quantitatively different degrees of signal propagation, particularly for slow signals, suggesting variable low-pass filtering properties in this cell type across cortical areas.
Modeling of steady-state signal propagation in L5 pyramidal neuron dendrites in ACC
To elucidate the underlying biophysical mechanism for the good propagation of slow subthreshold signals from dendrite to soma, we constructed a morphologically realistic model of an L5 pyramidal neuron in the ACC with NEURON (Figs. 4, 5). The choice of ion channels and their initial distribution was based on previous work suggesting Ileak, Km, Kir, and Ih as essential and sufficient to explain subthreshold signal propagation. Particularly, Ih is a key conductance for shaping the integration of EPSPs (Magee, 1998), which is modulated by the interplay with Kir channels (Day et al., 2005) and Km channels (George et al., 2009).
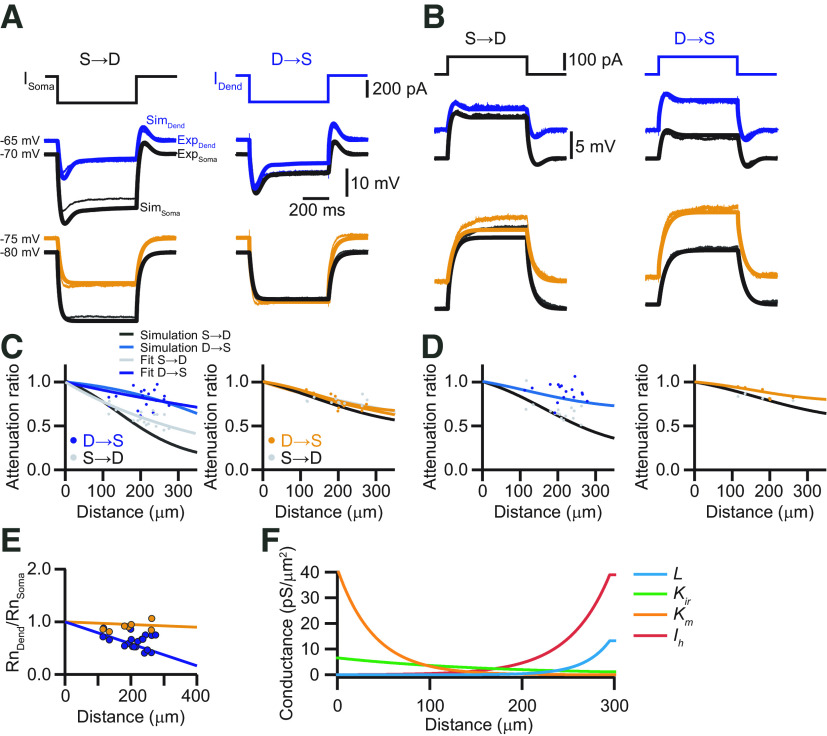
Figure 4.
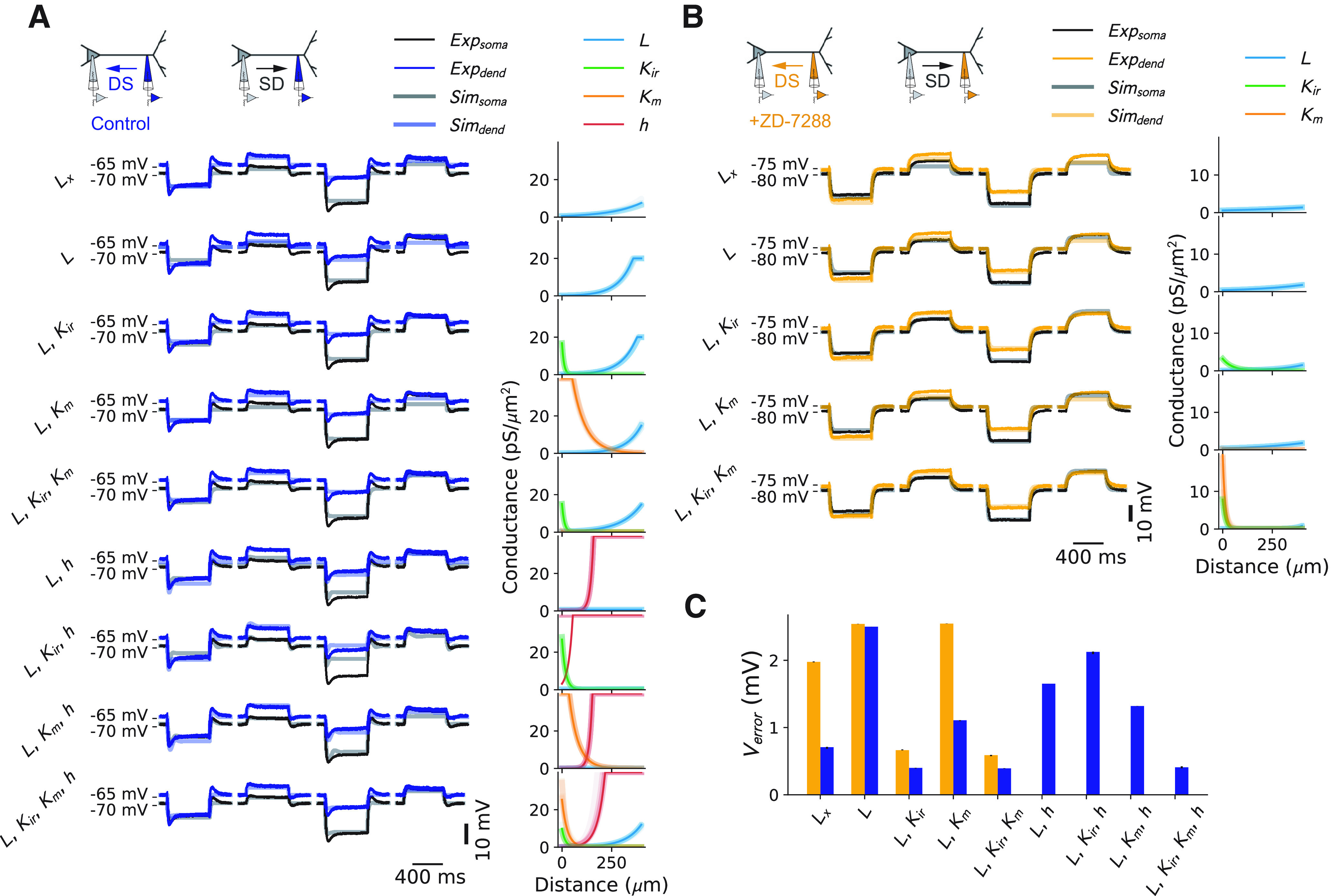
Fitting of the recorded dendritic and somatic voltage responses to steady-state current injections with various ion channel combinations. A, Control data. Left, Fit was performed with Lx (leak current with spatially varying reversal potential) or different combinations of Ileak (L), Kir, Km, and Ih (h). Middle, Temporal trace of data (Exp) and best fitting model (Sim). Right, Ion channel distributions for the 10 best fitting models. B, Same as A, but in the presence of the HCN channel antagonist ZD-7288. C, Average voltage error for each of the ion channel combinations (defined as the average between the resting voltage error and the final voltage errors during the current steps), for both control (blue) and ZD-7288 (orange) conditions. Averages were computed for the 10 best fitting models. Error bars are shown but are very small compared with error size. dend, Dendrite.
Figure 5.
Modeling of the steady-state voltage attenuation in the apical dendrite of L5 pyramidal neurons in the ACC. A, Dendritic (blue) and somatic (black) voltage responses to hyperpolarizing current injections (600 ms, −300 pA) and the corresponding modeling results (dendrite, light blue; soma, light gray) of the full model. Bottom traces show experimental (dendrite, orange; soma, black) and modeling (dendrite, light orange; soma, gray) results in the presence of the HCN channel blocker ZD-7288. For the morphologic realistic model, the neuron shown in Figure 1A was used. B, Same as in A, but for depolarizing current injections (600 ms, +100 pA). C, Modeling of the steady-state voltage attenuation in response to hyperpolarizing current injections as a function of the distance from the soma. Dots represent the measured attenuation in soma to dendrite (gray) and dendrite to soma (blue) direction with the corresponding exponential fits (S→D, gray; D→S, light blue). The solid black and blue lines represent the attenuation as a function of dendritic distance obtained from the model. The right graph shows the experimental and modeling results in the presence of ZD-7288. D, Same as in C, but for depolarizing current injections. E, Normalized dendritic Rn as a function of distance from the soma in control (blue) and in the presence of ZD-7288 (orange). Solid lines represent the corresponding modeling results. F, Channel distribution for Ileak (L), Kir, Km, and Ih as a function of dendritic distance obtained from fitting the experimental voltage responses in the dendrite and soma, as shown in A and B to a morphologically realistic compartment model in NEURON with the second modeling approach.
To confirm the necessity of these four conductances, we fitted the experimentally measured dendritic and somatic voltage responses to steady-state current injections consecutively with only Ileak, Ileak + potassium (Kir, Km) currents, Ileak + Ih or Ileak + Ih + potassium currents for control, and without HCN channels in the presence of ZD-7288 (Fig. 4). We used an evolutionary algorithm using the BluePyOpt library for optimizing the channel distribution (Van Geit et al., 2016). Each configuration was fitted independently from all others. Starting with the ZD-7288 condition, we found that Kir was required to obtain satisfactory fits (Fig. 4). This conductance was necessary since the voltage deflection for a negative current was larger in absolute values than for a positive current. Adding Km in this case did not improve the accuracy of the fit, but a slightly increasing density of Ileak was observed. In contrast, our fits in the control condition without adding Ih resulted in a large increase in Ileak distally. In these fits (without HCN channels), Kir was again required to obtain satisfactory fits, whereas Km did not improve accuracy. Finally, on adding HCN channels to the fits, we saw a marked decrease in Ileak. Ih itself took on a sharply increasing distribution. Interestingly, only combining Ileak and Kir with Ih did not result in an accurate fit. In this condition, Km was needed as well to recover the same accuracy as without HCN channels. These results indicated that a centrifugally increasing total leak was sufficient to explain the experimentally observed steady-state attenuation in the dendritic tree, and thus to keep the apical arborization electrically close to the soma. To further substantiate this idea, we implemented an artificial leak current (Lx) whose reversal could vary linearly with distance from soma, so as to implement the resting voltage difference between dendrite and soma (Fig. 4A). With this simplified, artificial current, we could also obtain a good fit in the control case (Fig. 4C), indicating that a minimal model of the observed steady-state attenuation was indeed attributable to a centrifugally increasing leak conductance in the membrane. Nevertheless, the systematic evaluation of the performance of the model with different combinations of Ileak, Kir, Km, and Ih revealed that the best fits required the presence of all these conductances. Investigating the influence of further channels, like persistent Na+ channels, which are present in L5 pyramidal neurons (Stuart and Sakmann, 1995) did not improve the model any further. The final values of the best fitting model were as follows: for Km: = 25.3 pS/μm2, = −26.6 µm, = −82.9 mV; for Kir: = 9.83 pS/μm2, = −17.1 µm, = −91.3 mV; for Ih: = 0.099 pS/μm2, = 36.3 µm, = −43.7 mV; and for Ileak: = 0.089 pS/μm2, = 81.7 µm, = −60 mV.
To test the robustness of the results, we used a second, independent fitting strategy. In this approach, we used simulated annealing for optimization of the model to the experimentally recorded voltage responses to depolarizing and hyperpolarizing current steps (see Materials and Methods). To begin with, the model was adjusted to the recordings with HCN channels blocked by ZD-7288, and, therefore, the density for Ih was set to zero (Fig. 5A,B). After optimizing the distribution for Ileak, Kir, and Km in this way, their values were fixed for the subsequent fitting of Ih to reproduce the voltage responses recorded under control conditions. At the end of this sequential fitting procedure, this model also faithfully replicated the distance dependency of steady-state voltage attenuation (Fig. 5C,D). The difference between experimental and simulated traces was always <2 mV, independent of the cell domain assessed or the propagation direction (sum of squares for errors: soma: SSED→S = 1.2 mV; SSES→D = 1.16 mV; dendrite: SSED→S = 1.74 mV; SSES→D = 0.69 mV). The finally established distributions of conductances followed exponential gradients from the soma of g0,Ih = 0.05 pS/µm2, g0,Kir = 6.6 pS/µm2, g0,Km = 41.3 pS/µm2, and g0,leak = 0.004 pS/µm2 to the main apical bifurcation with length constants of dIh = 44.5 µm, dKir = −167.9 µm, dKm = −39.9 µm, and dleak = 27.5 µm, respectively (Fig. 5F). In the apical tuft, the channel densities remained constant. The distribution of these conductances was quantitatively and qualitatively similar to the values obtained from the first fitting approach, suggesting robustness of the results.
The model replicated the gradient of the input resistance Rn along the somato-dendritic axis under both control and Ih blockade conditions (Fig. 5E). It was apparent that Rn decreased linearly from 64.6 MΩ at the soma to 26.8 MΩ at a distance of 295 µm from the soma in the apical dendrite because of the increasing leak in the apical dendrite. In a fully passive model, the morphology of the dendritic arborization would result in Rn at the distal dendritic location of 181.7 MΩ. Subsequently introducing Km, Kir, and Ih with their determined distributions in succession resulted in dendritic Rn values of 171.5, 78.5, and 42.6 MΩ, respectively. Thus, the specific distribution of Kir and Ih contributed dominantly to the decrease in input resistance. The decrease of Rn with distance from soma was the main determinant of the good relative voltage transfer (London et al., 1999) within the apical dendrite of L5 pyramidal neurons in the ACC. In the fully passive version of the model, steady-state voltage deflections were less well transferred from dendrite to soma as compared with the full model because of the increase of Rn with distance from the soma (Fig. 6). In contrast, soma-to-dendrite propagation became better in the passive case. Importantly, both models obeyed the reciprocity condition (Fig. 6).
Figure 6.
Comparison of the full model to the passive model. A, Neurolucida reconstruction of a biocytin-labeled L5 neuron in the ACC with the recording locations indicated. The dendritic recording had a distance of 262 μm from the soma. Same as in Figure 1A. B, Modeling results to hyperpolarizing current injections in the soma (black) and dendrite (blue) in the full model with all relevant conductances present. Attenuation in the steady state from dendrite to soma is smaller compared with attenuation in the other direction. C, In the passive model, steady-state voltage attenuation in the dendrite to soma direction is larger compared with the attenuation from soma to dendrite. D, In the full model as well as in the passive model, the rule of reciprocity is obeyed.
The model predicts EPSP propagation
Our model did not only replicate the voltage responses to steady-state current injections that were used for the fitting procedure, but it also predicted the behavior of faster and physiologically more relevant voltage deflections, like EPSPs, which were not used for the adjustment of any of the model parameters. We simulated the propagation of EPSP-shaped current injections with different kinetics along the apical dendrite (Fig. 7). The simulated EPSPs displayed rising and decaying phases very similar to the experimentally obtained traces (Fig. 7A,B). The distance dependence of EPSP attenuation in both directions was also well reproduced by the model (Fig. 7C,D).
Figure 7.
Modeling of EPSP propagation in the apical dendrite. A, Comparison of voltage responses to EPSP-like current injections (τrise = 2 ms, τdecay = 8 ms) in the soma and dendrite obtained from experiment (soma, black; dendrite, blue) and modeling (soma, gray; dendrite, light blue). B, Same as in A, but with faster EPSP kinetics (τrise = 0.5 ms, τdecay = 2 ms). The model replicated the EPSPs before and after propagation along the dendrite very well. C, Modeling of EPSP voltage attenuation as a function of the distance from the soma. Dots represent the measured attenuation in soma to dendrite (gray, left graph) and dendrite to soma (blue, right graph) directions with the corresponding exponential fits (S→D, gray; D→S, light blue). The solid black and blue lines represent the attenuation as a function of dendritic distance obtained from the model. D, Same as in C, but for EPSPs with faster kinetics. The solid black and blue lines represent the attenuation as a function of dendritic distance obtained from the model.
Our morphologically realistic model allowed further for the exploration of hardly accessible neuronal processes such as the apical tuft branches, which possess rather thin diameters <1 μm in mouse cortex. Simulated fast EPSP-like currents (τrise = 0.5 ms, τdecay = 2 ms) generated in those distal locations lead to large local voltage deflections that equally rapidly rose and decayed (Fig. 8A,B). These signals propagated from the most distal terminal branches (570 µm from soma) to the soma with a large attenuation factor of 0.04. Interestingly, most of the attenuation occurred within the tuft dendrites. Voltage signals were attenuated by 96% at the main bifurcation, whereas the remaining signal was only attenuated by 33% from there onward to the soma, consistent with our previous results (Fig. 8E,F). These simulations suggested that the main apical dendrite possesses different electrical properties compared with the tuft dendrites, which seem to behave similarly to tuft and basal dendrites of S1 pyramidal neurons (Nevian et al., 2007; Larkum et al., 2009). Indeed, input resistance in the tuft dendrites appeared to increase from the main apical bifurcation (27.8 MΩ at 295 µm from the soma) toward more distal sites (66.4 MΩ at 567 µm in the tuft).
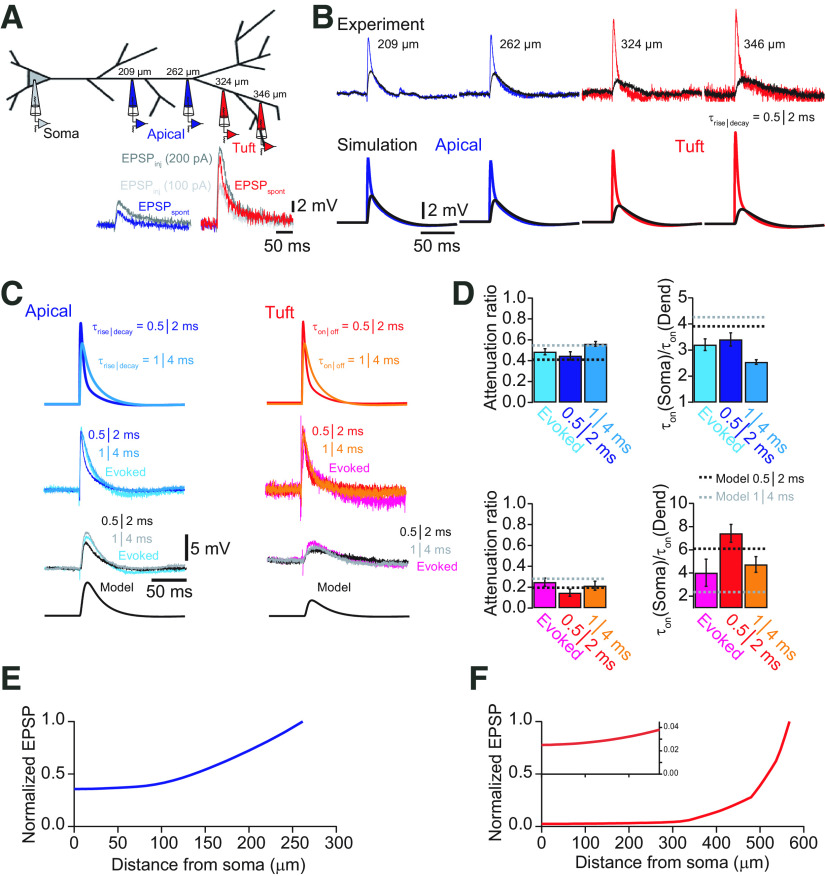
Figure 8.
The model predicts EPSP propagation in tuft dendrites. A, Schematic of recording configurations. Dual whole-cell recordings were performed in different cells at the indicated distances. Recordings from the apical dendrite are shown in blue, and recordings from tuft dendrites beyond the main bifurcation are shown in red. In the inset examples of spontaneous EPSPs from apical dendrite (blue) and tuft dendrite (red) are compared with EPSP-like current injections (τrise = 0.5 ms, τdecay = 2 ms) with amplitudes of 100 pA (gray) and 200 pA (black), suggesting that spontaneous EPSPs can be approximated by fast current injections. B, Comparison of measured somatic (black) and dendritic EPSPs evoked by EPSP-like current injections and the corresponding responses simulated in the model. Good agreement between experiment and simulation was found for both apical dendrite and distal tuft dendrite recordings in terms of local EPSP size and propagation toward the soma. C, Comparison of synaptically evoked EPSPs recorded in the soma and simultaneously in either the apical dendrite (left traces) or tuft (right traces) with EPSP-like current injections with different kinetics. Synaptically evoked EPSPs are well described by fast current injections. Modeling traces are shown after propagation to the soma. D, Bar graphs of average attenuation and change in EPSP slope for evoked EPSPs and EPSP-like current injections (τrise = 0.5 ms, τdecay = 2 ms; and τrise = 1 ms, τdecay = 4 ms, respectively). Dashed lines indicate the corresponding values obtained from the model. E, Plot of normalized EPSP amplitude as a function of distance from the soma for a modeled EPSP (τrise = 0.5 ms, τdecay = 2 ms) originating in the apical dendrite at the main bifurcation. F, Plot of normalized EPSP amplitude as a function of distance from the soma for a modeled EPSP (τrise = 0.5 ms, τdecay = 2 ms) originating in the distal part of the apical tuft. Most attenuation occurs within the tuft dendrite. Inset shows the evolution of the EPSP amplitude in the main apical dendrite on an expanded scale. Note that the EPSP, once it reaches the apical dendrite, is only little attenuated.
Retrospectively, we performed dual whole-cell voltage recordings from secondary or tertiary tuft branches and the soma (n = 4). Spontaneous as well as evoked EPSPs could be well approximated by EPSP-like current injections with τrise = 0.5 ms and τdecay = 2 ms or τrise = 1 ms and τdecay = 4 ms (Fig. 8A,C). Comparing the experimentally acquired recordings with simulations obtained for corresponding locations yielded a very good agreement with our model (Fig. 8B,C, Table 1). The attenuation from the recorded tuft dendrites to the soma was ∼80% (324 µm from soma) in both cases. This comparison revealed good predictive power of the compartmental model for the soma/dendrite ratios of the amplitude and rise time kinetics of EPSPs originating in the distal tuft dendrites that were not used for the fitting procedure (AFTuft-Soma,exp = 0.25 ± 0.04, AFTuft-Soma,sim = 0.20; rise timesoma = 3.20 ± 0.62 ms, rise timetuft = 1.14 ± 0.30 ms; dendritic filteringtuft-soma,exp = 4.02 ± 1.17, dendritic filteringtuft-soma,sim = 6.12; Fig. 8C,D). Furthermore, our model suggested that the electrical properties of the apical dendrite of L5 pyramidal neurons in the ACC promote the propagation of subthreshold signals with little attenuation once distal inputs have propagated there. At this location, EPSPs originating in the tuft are already slowed down in their kinetics and thus subsequently propagate well along the apical dendrite. Nevertheless, substantial depolarization at the main bifurcation can mainly be achieved by spatial and temporal summation of distal tuft synapses as well as dendritic plateau potentials like NMDA spikes. Therefore, we investigated these phenomena next.
Table 1.
Comparison of model and experimental EPSP propagation from tuft (d = 324 µm) and apical dendrite (d = 210 µm) toward the soma
| Model |
Experiments |
|||||||
|---|---|---|---|---|---|---|---|---|
| Normalized amplitude | Attenuation | Normalized amplitude | Attenuation | |||||
| EPSP (0.5 | 2) | EPSP (1 | 4) | EPSP (0.5 | 2) | EPSP (1 | 4) | EPSP (0.5 | 2) | EPSP (1 | 4) | EPSP (0.5 | 2) | EPSP (1 | 4) | |
| EPSP in tuft dendrite | ||||||||
| Tuft | 1 | 1 | 1 | 1 | ||||
| Bifurcation | 0.373 | 0.443 | 63% | 56% | ||||
| Soma | 0.194 | 0.281 | 81% (48%) | 72% (37%) | 0.143 | 0.201 | 85% | 80% |
| EPSP in apical dendrite | ||||||||
| Bifurcation | 1 | 1 | 1 | 1 | ||||
| Soma | 0.410 | 0.549 | 59% | 45% | 0.483 | 0.573 | 52% | 43% |
Subthreshold EPSP summation
The specific dendritic properties might influence the summation of EPSPs. Therefore, we measured the summation and propagation of bursts of five EPSPs at 50 Hz. The fifth-to-first EPSP amplitude ratio was used to quantify temporal summation (Fig. 9B,C). At the dendrite, the five EPSPs summed sublinearly with a summation ratio of 1.82 ± 0.06. After propagation to the soma, the summation was significantly larger there (2.32 ± 0.11; p < 0.001, Student's t test, n = 19). Current injections of EPSPs at the soma resulted in a local summation of 2.21 ± 0.14 and a similar value after propagation to the dendritic recording site (2.26 ± 0.09; p = 0.39, Student's t test, n = 18). Since the last EPSP-shaped current injection rode on top of the depolarization generated by the preceding EPSPs, its peak amplitude could be seen as a very slow voltage deflection, with kinetics in between the slowest EPSPs tested (τrise = 4 ms, τdecay = 16 ms) and the steady state (square pulse, 600 ms). The attenuation factor for the peak amplitude of the summed EPSP was 0.81 ± 0.02 in the dendrite-to-soma direction, and 0.68 ± 0.02 for summed EPSPs propagating from soma to dendrite (Fig. 9E). Quantifying the distance dependence of the attenuation gave an effective length constant of λD→S = 933 μm for signals propagating from dendrite to soma and λD→S = 566 μm for signals propagating in the opposite direction (Fig. 9D). We also evaluated temporal summation and propagation from our secondary and tertiary tuft recordings. Temporal summation in the tuft dendrites was small (1.79 ± 0.28) because of an almost complete decay of each EPSP within the 50 ms before the next EPSP was evoked. The corresponding summation at the soma was (2.93 ± 0.61). The amplitude attenuation of the signals traveling from dendrite to soma was 0.5 ± 0.06, consistent with considerable attenuation of each EPSP within the tuft dendrites and small attenuation of the remaining depolarization in the apical dendrite.
Figure 9.
Temporal summation and propagation of EPSPs. A, Schematic of recording configurations of either simultaneous soma–apical dendrite or soma–tuft dendrite recordings. B, Voltage recordings at the soma (black), apical dendrite (blue), and tuft dendrite (red) in response to EPSP-like current injections of five EPSPs (τrise = 2 ms, τdecay = 8 ms) at 50 Hz in the soma (S→D) or dendrite (D→S). Note, that the burst of EPSPs injected into the apical dendrite propagates very well toward the soma, whereas the same pattern injected into the tuft is considerably attenuated. C, Bar graphs quantifying the temporal summation of the five EPSPs. Temporal summation is in all cases sublinear. D, Attenuation of the peak amplitude of five EPSPs versus distance from the soma in soma-to-dendrite (left) and dendrite-to-soma (right) directions. Solid lines represent exponential fits to the data. E, Bar graph of the average attenuation of the peak amplitude of five EPSPs from apical dendrite (blue) and tuft dendrite (red). Dend, Dendrite.
Local dendritic autoregenerative potentials
Active dendritic properties can generate local spikes with either fast kinetics driven by Na+ conductances (Na+ spikes) or slow plateau potentials mediated by NMDA receptors (NMDA spikes) or voltage-dependent Ca2+ channels (Ca2+ spikes). The dendritic properties determined above suggested that the kinetics of each of these local autoregenerative events should result in different propagation efficiencies within the dendritic tree. We investigated the ability of L5 pyramidal cell dendrites in the ACC to generate local spikes by dual whole-cell recordings and either synaptic stimulation in L1 in close proximity to tuft dendrites or direct current injections (Fig. 10A). NMDA receptors were progressively recruited by increasingly stronger extracellular stimulation. NMDA spikes emerged in a nonlinear manner characterized by a sigmoid increase in EPSP amplitude at the dendritic as well as the somatic recording location (Fig. 10B,C). Bath application of APV abolished the NMDA spike (Fig. 10B). Evaluating the amplitude attenuation from dendrite to soma for increasing synaptic stimulus strength also revealed a nonlinear jump in propagation efficiency (Fig. 10C). Subthreshold potentials were moderately attenuated (AFD→S = 0.48 ± 0.05) consistent with our previous analysis. In contrast, the nonlinear NMDA spikes were significantly less attenuated (AFD→S = 0.82 ± 0.06, n = 9; p < 0.01, Student's paired t test). The corresponding distance dependence of NMDA spike attenuation was very similar to the attenuation of steady-state signals with an effective length constant of λD→S = 848 μm (Fig. 10D). Furthermore, given that the average half-width of the evoked NMDA spikes was ∼90 ms, the attenuation of the NMDA spikes was exactly predicted by the previously obtained exponential fit to the EPSP kinetics attenuation dependency (Fig. 10G).
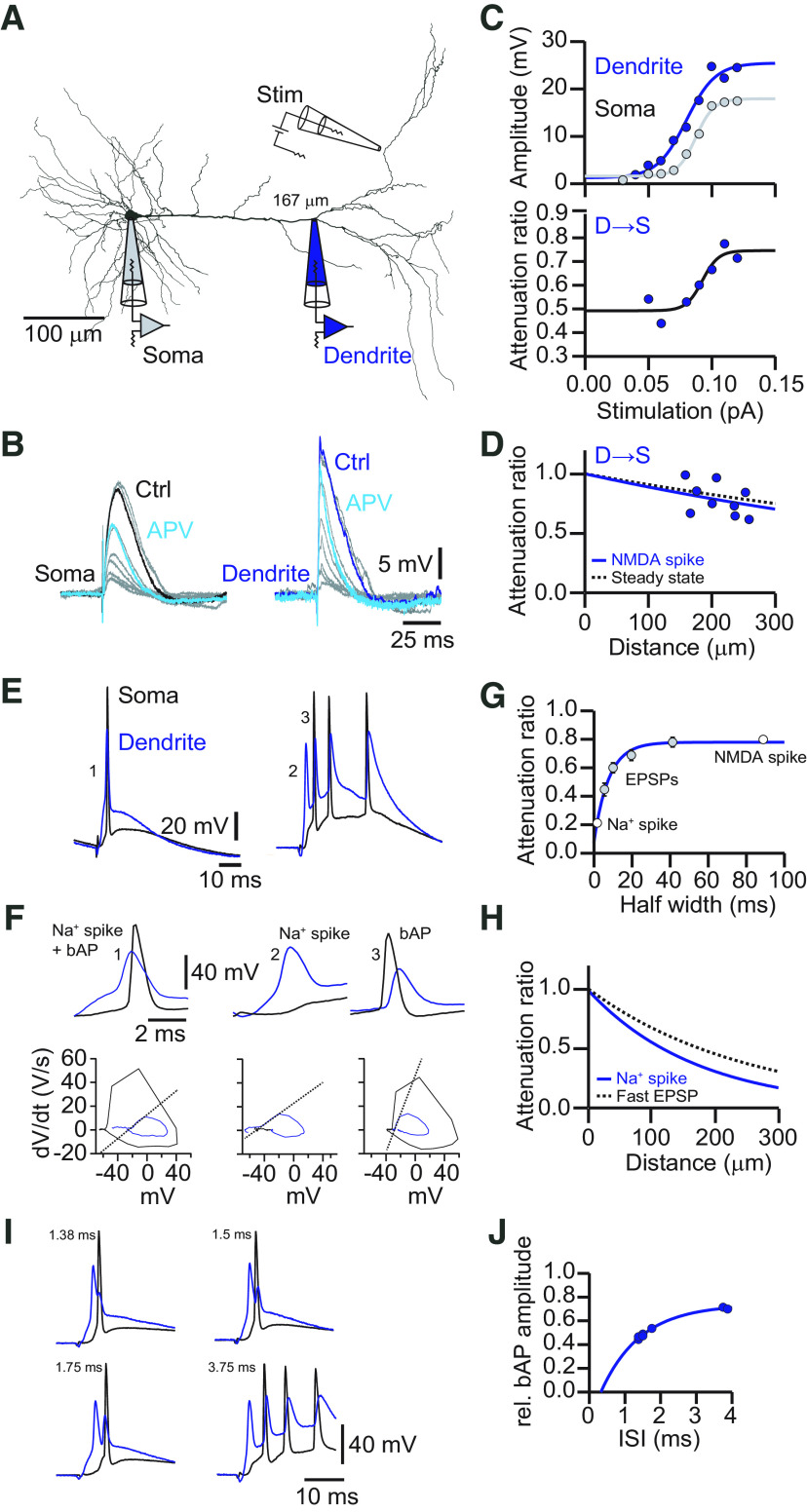
Figure 10.
Propagation of dendritic spikes in the apical dendrite. A, Neurolucida reconstruction of a biocytin-labeled L5 neuron in the ACC with the recording location indicated. The dendritic recording had a distance of 167 μm from the soma. An extracellular stimulation (Stim) pipette was placed close to a tuft dendrite. B, Voltage responses to increasing extracellular simulation strength recorded at the soma (left) and the apical dendrite (right). Bath application of the NMDA receptor antagonist APV reduced the suprathreshold plateau potentials at the soma [control (Ctrl), black; APV, turquoise] and the apical dendrite (Ctrl, blue; APV, turquoise) to a subthreshold EPSP, suggesting the presence of a NMDA spike in the control condition. C, EPSP amplitude versus extracellular stimulation strength. Dendritic (blue) and somatic (gray) amplitudes were fitted with a sigmoid function illustrating a nonlinear increase in EPSP amplitude with increasing stimulation strength. The lower graph shows the corresponding attenuation of the EPSP amplitude toward the soma versus stimulation strength. The solid line represents a sigmoid fit to the data points. The attenuation decreases concurrently with the occurrence of dendritic NMDA spikes. D, Attenuation of NMDA spikes versus distance from the soma. NMDA spikes were little attenuated toward the soma. The solid blue line represents an exponential fit to the data with an effective length constant of λ = 848 μm. The dashed black line represents the exponential fit to the attenuation of steady-state signals (λ =1033 μm). E, Example traces of synaptically evoked local Na+ spikes in the dendrite (blue) and the corresponding somatic response (black). F, Example traces from E on an expanded timescale, as indicated by the corresponding numbers. Left, The dendritic Na+ spike precedes a somatic AP. Middle, Isolated dendritic Na+ spike that is strongly attenuated toward the soma. Right, Somatic AP that backpropagates to the dendritic recording site. Local dendritic Na+ spikes can be distinguished from bAPs by a different rising slope, as indicated by the dV/dt-Vm plot shown below the corresponding traces. G, Plot of attenuation versus half-width of the event. Na+ spikes were the shortest dendritic membrane depolarizations and correspondingly were strongly attenuated. In contrast, NMDA spikes were long lasting and much less attenuated. H, Attenuation of Na+ spikes versus distance from the soma. Na+ spikes were strongly attenuated toward the soma. The solid blue line represents an exponential fit to the data with an effective length constant of λ = 173 μm. The dashed black line represents the exponential fit to the attenuation of the fastest EPSPs (λ =236 μm). I, Example traces of dendritic Na+ spikes (blue) followed by a somatic AP (black) that backpropagated to the dendritic recording site. Depending on the timing of Na+ spike and AP, the amplitude of the bAP in the dendrite was modulated, presumably because of the refractory period of voltage-dependent Na+ channels. J, Plot of the relative bAP amplitude versus the interspike interval (ISI) between dendritic Na+ spike and the bAP.
Local Na+ spikes could also be evoked by synaptic stimulation of distal tuft dendrites (Fig. 10E). They were recorded at the dendritic electrode as very fast voltage deflections with rising and decaying kinetics similar to those of backpropagating APs (bAPs; Fig. 10F). In ∼63% of the cases, Na+ spikes were triggered in close temporal proximity to a somatic AP. They could, however, be distinguished from bAPs by comparing the voltage response at the somatic and dendritic electrodes (Fig. 10F). The Na+ spike rising phase and peak amplitude always preceded the somatic AP and probably served as its trigger. In the remaining 37% of the cases, Na+ spikes were unequivocally identified as local dendritic spikes as they were only detected at the dendritic recording electrode. EPSP-like current injections into the apical dendrite always triggered local Na+ spikes concomitantly with somatic APs (Fig. 10I). Interestingly, variable time delays between the local Na+ spike and the bAP revealed a timing-dependent shunting of the bAP, presumably because of inactivation of the dendritic Na+ channels following the local spike (Fig. 10I). In distal tuft dendrites, more isolated Na+ spikes were observed (in ∼51% of the cases). The isolated Na+ spikes were used to quantify the distance dependency of amplitude attenuation (Fig. 10H). As expected from the fast kinetics of local Na+ spikes with a typical half-width of 1.8 ms, attenuation was substantial. We determined an effective length constant for Na+ spike propagation of λD→S = 173 μm. As in the case of the NMDA spikes, the attenuation of the Na+ spikes was exactly predicted by the exponential fit to the EPSP kinetics–attenuation dependency (Fig. 10G).
In none of our recordings were we able to elicit a dendritic Ca2+ spike that would be characterized by a dendritic plateau potential and somatic burst firing of APs as apparent in L5 pyramidal neurons in sensory cortex (Fig. 11; Larkum et al., 1999; Pérez-Garci et al., 2013). This finding is consistent with previous results reporting little Ca2+ regenerativity in the apical dendrites of L5 pyramidal neurons in the ACC (Santello and Nevian, 2015). In conclusion, our experiments suggest that the dendrites of L5 pyramidal neurons in the ACC support NMDA and Na+ spikes, but no Ca2+ spikes. NMDA spikes are reliably propagated, while Na+ spikes are strongly attenuated. The filtering properties of L5 pyramidal neuron dendrites in the frontal cortex strongly favor the propagation of slow signals (NMDA spikes or summed EPSPs) over signals with fast kinetics (Na+ spikes, fast EPSPs).
Figure 11.
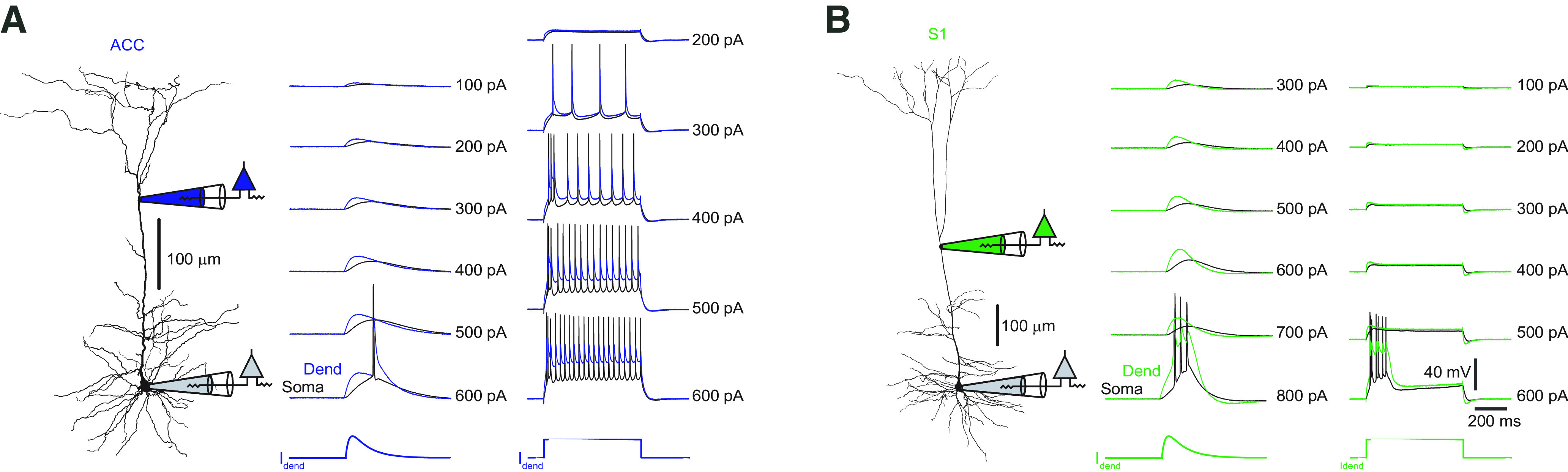
The apical dendrite of ACC pyramidal neurons does not generate Ca2+ spikes. A, Left, Neurolucida reconstruction of an L5 pyramidal neuron in the ACC. Positions of recording electrodes are indicated. Middle, EPSP-like current injections (τrise = 4 ms, τdecay = 16 ms) with increasing amplitude-evoked somatic APs above a certain threshold that backpropagate to the dendritic (Dend) recording site, but no plateau potentials that would be indicative of a dendritic Ca2+ spike were observed. Somatic traces are shown in black, dendritic traces in blue. Right, Steady-state current injections with increasing amplitude resulted in a regular discharge of somatic APs. Again, no plateau potentials were observed. B, Left, Neurolucida reconstruction of an L5 pyramidal neuron in S1. Positions of recording electrodes are indicated. Middle, EPSP-like current injections with increasing amplitude evoked a sudden dendritic Ca2+ spike that triggered somatic APs. Somatic traces are shown in black, dendritic traces are in green. Right, Steady-state current injections with increasing amplitude resulted in a sudden occurrence of a dendritic plateau potential that triggered bursts of somatic APs.
Consequences of HCN channel distribution on dendritic computation
The described electrotonic structure with a leakier apical dendrite compared with the perisomatic region has the effect of an apparently good coupling of slow dendritic signals, like NMDA spikes, to the soma. Nevertheless, the increased distal leak should make it more difficult to depolarize the dendritic membrane, and thus the impact of distal synapses on somatic depolarization might still be marginal despite good dendrite-to-soma coupling. As shown above, blocking Ih with ZD-7288 resulted in a larger dendritic voltage response compared with control for the same hyperpolarizing dendritic current injection (Fig. 1B,D). To disentangle the effects of Ih on dendritic computation in the specific electrotonic structure of L5 pyramidal neurons in the ACC, we performed further simulations.
To evaluate the influence of Ih, particularly in the apical trunk, we simplified the HCN channel distribution to a piecewise linear function (Fig. 12A) while keeping the distribution of the other channels as determined with the evolutionary optimization (Fig. 4). In the proximal part (<250 μm from the soma), the HCN channel density was kept constant. From there, it increased linearly between 250 and 500 μm to 60 pS/μm2. Then it was kept constant at this value up to the dendritic tips. The experimental block of all HCN channels with ZD-7288 was modeled as zero HCN density throughout the dendritic tree. We varied the proximal constant HCN channel density from 0 to 10 pS/µm2. The former value is consistent with an apparent lack of HCN channels in the perisomatic region of L5 pyramidal neurons in the ACC, as determined by immunohistochemistry (Santello and Nevian, 2015; Santello et al., 2017), whereas the latter value matches a low density of HCN channels in the initial apical dendrite of L5 pyramidal neurons in somatosensory cortex (Berger et al., 2001). First, we investigated the effect of ZD-7288 on the two simplified HCN channel distributions (Fig. 12B). We found that blocking Ih in the model with no perisomatic HCN channels (HCN1) increased the attenuation from dendrite to soma, while decreasing attenuation in the other direction. This behavior was consistent with our experimental results (Fig. 1). In contrast, blocking Ih in the second model that had a low HCN channel density in the proximal apical dendrite (HCN2) decreased attenuation from dendrite to soma and also from soma to dendrite. This behavior is consistent with the experimental ZD-7288 results in somatosensory cortex (Berger et al., 2001). These findings suggest that the density of HCN channels in the initial apical trunk can determine the attenuation between the tuft and the soma. This might provide a mechanism to tune the effective coupling between these two compartments.
Next, we investigated synaptic integration in the distal apical dendrites. A paired-pulse stimulation (Δt = 20 ms) of an increasing number of synapses on the same branch was simulated (Fig. 12C,D). We found that local integration and generation of NMDA spikes, as observed from the local postsynaptic potential and the peak amplitude as a function of the number of activated synapses, was not influenced by the two different HCN channel densities in the apical trunk. Blocking all HCN channels increased the peak amplitude of the local postsynaptic potential, as expected. However, cross talk between synapses on separate tuft branches was strongly influenced by Ih (Fig. 12E–G). We observed a shift to a lower number of synapses required to generate a NMDA spike at the recording site when distal synapses were activated concomitantly. Both HCN channel distributions resulted in the same small shift (ΔΘNMDA = −1 synapse), whereas in the presence of ZD the shift in threshold was larger (ΔΘNMDA = −3 synapses). These findings are expected from the membrane leak imposed by the HCN channels in the tuft dendrites, which reduces interaction between dendritic branches (Wybo et al., 2019).
Finally, we evaluated the propagation of distal synaptic inputs toward the soma (Fig. 12H,I). In line with the differential behavior of the change in attenuation for the two HCN channel distributions compared with the ZD case (Fig. 12B), propagation to the soma was better for the case with no HCN channels proximally (Fig. 12H,I). Since the neurons with HCN channels were leakier as a whole compared with the ZD case, the peak amplitude in the dendrite and at the soma for both distributions was lower in comparison (Fig. 12I, left). However, normalization of synaptic inputs in the presence of HCN channels to the same local response amplitude as in the ZD case, resulted in a larger somatic depolarization for the distribution with no HCN channels proximally compared with ZD (Fig. 12I, right). In summary, we conclude that part of the role of apical HCN channels is to decouple branches in the apical tuft, while, depending on the trunk channel density, controlling the coupling to the soma. Under the assumption of synaptic scaling to reach the same local NMDA spike amplitude compared with ZD or under conditions of strong stimulation that reaches the synaptic reversal potential, it seems that Ih has the mutually opposite effects of decoupling distal tuft branches from each other while at the same time efficiently connecting them to the soma.
Discussion
We characterized the electrical properties of L5 pyramidal neuron dendrites in the ACC, a brain region in the frontal cortex, using a combination of dual whole-cell patch-clamp recordings and modeling. We found good dendrite-to-soma propagation of slow dendritic membrane depolarizations such as temporally summed EPSPs and NMDA spikes. Faster individual EPSPs are progressively more attenuated, but still exhibit a significant depolarization at the soma. All of these findings are predicted from cable theory and are consistent with the idea that dendrites act as low-pass filters (Zador et al., 1995; Carnevale et al., 1997). Comparison to dendrites of S1 pyramidal neurons yielded a significant difference in the filtering properties, as slow signals in S1 were more strongly attenuated than in ACC. Thus, our data contribute to the well known notion that not all L5 pyramidal neurons possess the same electrotonic structure, but that quite different dendrite-to-soma coupling efficiencies and filtering characteristics can be found (Berger et al., 2001; Williams and Stuart, 2002). We describe a biophysical implementation for the good coupling of distal synaptic inputs toward the soma for pyramidal neurons in the ACC that will help to understand differences in synaptic integration in pyramidal neurons across the cortex.
Good dendrite-to-soma coupling of slow dendritic signals
The efficient dendrite-to-soma propagation observed here for slow signals is different from our findings in S1, and it is distinct from what has been established for some types of neocortical pyramidal cells and other neuronal types so far. Considerable voltage attenuation along dendrites is thought to be a design principle for many L5 pyramidal neuron types (Stuart and Spruston, 1998; Berger et al., 2001; Williams and Stuart, 2002; Nevian et al., 2007; Larkum et al., 2009; Harnett et al., 2013; 2015) as well as for CA1 pyramidal neurons (Andrasfalvy and Magee, 2001; Smith et al., 2003; Spruston, 2008). In human neocortical pyramidal neurons, the compartmentalization of the tuft dendrites is even more pronounced (Beaulieu-Laroche et al., 2018). Also in hippocampal basket cells (Hu et al., 2010) and granule cells in the dentate gyrus (Krueppel et al., 2011) strong attenuation of dendritic potentials has been observed. Nevertheless, recently it was reported that pyramidal neurons in the primary visual cortex (V1) show different dendritic properties depending on their location within V1 (Fletcher and Williams, 2019). Pyramidal neurons in the caudal V1 are more compact than pyramidal neurons in the rostral V1, resulting in better voltage transfer from dendrite to soma in the former compared with the latter case. Also hippocampal pyramidal neurons in CA1 propagate steady-state subthreshold signals well (Magee, 1998).
When comparing the electrical properties of pyramidal neurons in different brain areas, one also has to consider the kinetics of the signals investigated in these studies. Fast synaptic EPSPs are similarly attenuated in ACC compared with sensory cortices. Accordingly, individual distal synapses have a minor influence on axonal AP generation unless active dendritic events, like NMDA spikes, are generated (Schiller et al., 1997, 2000). This mode of operation results in a very good coupling of distal synapses in the tuft to the soma in the ACC. The effective length constant derived from the attenuation recorded at different distances from the soma in this case was λNMDA = 848 μm, which was similar to the effective length constant for the attenuation of 5 EPSPs of λ5EPSPs = 933 μm and the steady-state effective length constant of λsteady = 1033 μm. Given that the apical dendrite of L5 pyramidal neurons in the ACC is 265 ± 14 µm long, the good coupling from dendrite to soma becomes apparent and corresponds to an electrotonic length of 0.26 in the steady-state case. In comparison, the steady-state effective length constant in L5 pyramidal neurons in a sensory cortex has been determined to be much shorter (λsteady = 457 μm; Williams, 2004; Ledergerber and Larkum, 2010). Considering an average length of the apical dendrite in this case of 739 µm, this corresponds to an electrotonic length of 1.62. L2/3 and L6 pyramidal neurons in somatosensory cortex possess steady-state effective length constants of λsteady = 302 μm (Larkum et al., 2007) and λsteady = 334 μm (Ledergerber and Larkum, 2010), respectively, resulting in electrotonic lengths of 1.07 and 2.31 for L2/3 and L6, respectively. Thus, the dendrites of L5 pyramidal neurons in the ACC are particularly compact and can be considered to have a specific electrotonic profile that propagates slow signals much better compared with other pyramidal neuron dendrites. There is some evidence that this might be a general feature of L5 pyramidal neurons in the prefrontal cortex. In the prelimbic cortex, a similar decrease in input resistance in the apical dendrite compared with the soma was reported (Gulledge and Stuart, 2003). In the medial prefrontal cortex, bursts of EPSPs lead to a slow underlying dendritic membrane potential change, which is modulated by the fast EPSPs. This slow depolarization is apparently also well propagated to the soma of these cells (Dembrow et al., 2015).
Modelling of dendritic properties in the ACC
Our model can qualitatively and quantitatively explain the good dendrite-to-soma coupling of slow signals. A minimal set of four conductances known to be involved in shaping subthreshold signal propagation in dendrites (Day et al., 2005) were sufficient to capture the properties of the dendrites in L5 pyramidal neurons of the ACC. The fitting of the experimental data resulted in an increase of Ih from the soma to the dendrite as expected from immunohistochemistry (Lörincz et al., 2002; Santello et al., 2017) and direct electrical recordings (Magee, 1998; Harnett et al., 2015). The derived length constant of dIh = 44.5 µm is similar to the immunohistochemically measured distribution of Ih with a length constant of 50 µm (Santello et al., 2017). Also, a general leak conductance increased distally, whereas Kir and Km decreased from soma to dendrite. These distributions yielded a good reproduction of our experimental data, including the propagation of EPSPs within the apical dendrite and even in the distal tuft dendrites that were not used to constrain the model. The decrease in input resistance with distance from the soma was also captured. Since we kept the intracellular resistivity constant to fit the model, we suggest that the main determinant of good dendrite-to-soma coupling of slow voltage deflections in the ACC is because of the specific ion channel distribution in the main apical dendrite. In contrast, caudal pyramidal neurons in V1 possess a smaller intracellular resistivity compared with the larger pyramidal neurons in the rostral part of V1 that determines their good dendrite-to-soma coupling (Fletcher and Williams, 2019). Thus, there might be different cellular mechanisms (ion channel distribution vs intracellular resistivity) that pyramidal neurons across the cortex use to ensure good propagation of subthreshold EPSPs toward the soma. In this regard, intracellular resistivity of the apical dendrite is a fixed determinant of the electrical properties of the pyramidal neurons in V1, whereas neuromodulators can variably alter the function of ion channels, like Ih, and thus could dynamically modulate signal propagation.
What influence does this particular distribution of ion channels have in the dendrites of L5 pyramidal neurons in the ACC? The apical dendrite behaves linearly and obeys reciprocity, which is indicative of a passive system that can be described in the framework of cable theory. The latter predicts an increase in input resistance distally for tapered cylinders (Klee and Rall, 1977). However, in the dendrites studied here, we observed a decrease in input resistance despite a narrowing of the dendrite diameter with distance from the soma. Accordingly, the ion channel distribution compensates for increases in axial resistance that would otherwise hinder signal propagation. This particularity is at the core of the dendritic properties observed. Hence, according to cable theory, a cylinder with a heterogeneously distributed leak results in an input resistance gradient that enhances relative voltage transfer from the leakier toward the more compact end (London et al., 1999). In the case of the apical dendrite of L5 pyramidal neurons in the ACC, a passive leak (Ileak) combined with an Ih-dependent leak ensures keeping the dendritic input resistance below somatic input resistance values. Nevertheless, one has to note that a low dendritic input resistance also influences the local depolarization evoked by synaptic currents. Thus, larger currents are needed in the distal dendrite to achieve the same depolarization compared with the perisomatic region. Therefore, although the attenuation is small for slow signals, the actual impact of distal synapses might still be small because of their small local depolarization. Here, the local dendritic nonlinearity induced by a NMDA spike can overcome this problem as dendritic depolarizations are considerable (up to 50 mV), and we demonstrated that their attenuation was small. Our simulations suggest that the electrotonic structure of L5 pyramidal neurons in the ACC that is determined by the distribution of Ih in the apical trunk limits cross talk between tuft branches while ensuring good communication between tuft and soma. Certainly, without the presence of HCN channels the influence of a given synapse on somatic depolarization would be larger (mainly because of the increased local depolarization in a more compact dendrite), but this would come at the cost of increased interactions between synapses on different dendritic branches. Thus, Ih might be balanced to preferentially ensure dendrite-specific integration with good transmission of these results toward the soma.
Dendritic integration scheme in L5 pyramidal neurons in the ACC
The different electrotonic structure of the L5 pyramidal neuron dendrites in the ACC compared with S1 L5 pyramids suggests different integration schemes for information processing in these different classes of neurons. The good propagation of slow signals along the apical dendrite toward the soma results in an “electrical proximity” of the tuft dendrites to the soma. With a morphoelectrotonic transformation (Zador et al., 1995), the apical dendrite shrinks substantially and the tuft dendrites become equivalent to the basal dendrites. Thus, inputs arriving in these two compartments might have a similar impact on axonal AP generation. The apical dendrite with its low-pass filtering properties would favor the transmission of slow signals in a similar way as the basal dendrites of pyramidal neurons (Nevian et al., 2007). Nevertheless, it would suppress spontaneous and random synaptic noise originating from tuft synapses, but faithfully transmit more salient synaptic events that result from burst firing of afferent axons or synchronized synaptic activation leading to NMDA spikes. In contrast, in sensory cortex, the tuft dendrites are electrically more remote from the AP initiation zone (Williams and Stuart, 2002; Larkum et al., 2009). In this case, the initiation of Ca2+ spikes has been suggested to play a major role in the information transfer from tuft to soma (Larkum et al., 2009; Larkum, 2013). These differences might reflect the different type of information that is processed in primary versus higher-order cortices, particularly in the prefrontal cortex (but see Fletcher and Williams, 2019). The ACC receives inputs from a large number of brain areas (Fillinger et al., 2017), which represent already highly processed information. In contrast, primary cortex receives bottom-up sensory input from primary sensory thalamic nuclei and, in addition, top-down input from higher cortical brain areas (Xu et al., 2012; Larkum, 2013). In this comparison, ACC L5 pyramidal neurons might perform temporal summation of inputs (Dembrow et al., 2015) generating an internal model or prediction of the outside world that changes on a slow timescale, whereas sensory L5 neurons compare sensory inputs (bottom-up) to this internal model (provided by top-down inputs) on a more rapid timescale (Fiser et al., 2016). For sensory L5 neurons, an electrotonic separation of inputs in the apical and basal dendrites might be required, whereas for ACC neurons this separation is less important and the low-pass filtering properties of the apical dendrite are used instead. Thus, the different function of cortical L5 pyramidal neurons across the cortical hierarchy might determine their electrical properties.
Footnotes
This work was supported by the Swiss National Science Foundation (Grant 159872 to T.N.; Grant 156863 and 180316 to W.S.), the European Union's Horizon 2020 Framework Programme (Grant 720270, 785907 and 945539 to W.S.) and the European Research Council (Grant 682905 to T.N.). We thank Natalie Nevian for Neurolucida reconstructions and excellent technical assistance.
The authors declare no competing financial interests.
References
- Andrasfalvy BK, Magee JC (2001) Distance-dependent increase in AMPA receptor number in the dendrites of adult hippocampal CA1 pyramidal neurons. J Neurosci 21:9151–9159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beaulieu-Laroche L, Toloza EHS, van der Goes MS, Lafourcade M, Barnagian D, Williams ZM, Eskandar EN, Frosch MP, Cash SS, Harnett MT (2018) Enhanced dendritic compartmentalization in human cortical neurons. Cell 175:643–651.e14. 10.1016/j.cell.2018.08.045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger T, Larkum ME, Lüscher HR (2001) High I(h) channel density in the distal apical dendrite of layer V pyramidal cells increases bidirectional attenuation of EPSPs. J Neurophysiol 85:855–868. 10.1152/jn.2001.85.2.855 [DOI] [PubMed] [Google Scholar]
- Branco T, Clark BA, Häusser M (2010) Dendritic discrimination of temporal input sequences in cortical neurons. Science 329:1671–1675. 10.1126/science.1189664 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carnevale NT, Hines M (2004) The neuron book. Cambridge, UK: Cambridge UP. [Google Scholar]
- Carnevale NT, Tsai KY, Claiborne BJ, Brown TH (1997) Comparative electrotonic analysis of three classes of rat hippocampal neurons. J Neurophysiol 78:703–720. 10.1152/jn.1997.78.2.703 [DOI] [PubMed] [Google Scholar]
- Day M, Carr DB, Ulrich S, Ilijic E, Tkatch T, Surmeier DJ (2005) Dendritic excitability of mouse frontal cortex pyramidal neurons is shaped by the interaction among HCN, Kir2, and Kleak channels. J Neurosci 25:8776–8787. 10.1523/JNEUROSCI.2650-05.2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dembrow NC, Chitwood RA, Johnston D (2010) Projection-specific neuromodulation of medial prefrontal cortex neurons. J Neurosci 30:16922–16937. 10.1523/JNEUROSCI.3644-10.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dembrow NC, Zemelman BV, Johnston D (2015) Temporal dynamics of L5 dendrites in medial prefrontal cortex regulate integration versus coincidence detection of afferent inputs. J Neurosci 35:4501–4514. 10.1523/JNEUROSCI.4673-14.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egger V, Nevian T, Bruno RM (2008) Subcolumnar dendritic and axonal organization of spiny stellate and star pyramid neurons within a barrel in rat somatosensory cortex. Cereb Cortex 18:876–889. 10.1093/cercor/bhm126 [DOI] [PubMed] [Google Scholar]
- Fillinger C, Yalcin I, Barrot M, Veinante P (2017) Afferents to anterior cingulate areas 24a and 24b and midcingulate areas 24a' and 24b' in the mouse. Brain Struct Funct 222:1509–1532. 10.1007/s00429-016-1290-1 [DOI] [PubMed] [Google Scholar]
- Fiser A, Mahringer D, Oyibo HK, Petersen AV, Leinweber M, Keller GB (2016) Experience-dependent spatial expectations in mouse visual cortex. Nat Neurosci 19:1658–1664. 10.1038/nn.4385 [DOI] [PubMed] [Google Scholar]
- Fletcher LN, Williams SR (2019) Neocortical topology governs the dendritic integrative capacity of layer 5 pyramidal neurons. Neuron 101:76–90.e4. 10.1016/j.neuron.2018.10.048 [DOI] [PubMed] [Google Scholar]
- George MS, Abbott LF, Siegelbaum SA (2009) HCN hyperpolarization-activated cation channels inhibit EPSPs by interactions with M-type K(+) channels. Nat Neurosci 12:577–584. 10.1038/nn.2307 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gulledge AT, Stuart GJ (2003) Action potential initiation and propagation in layer 5 pyramidal neurons of the rat prefrontal cortex: absence of dopamine modulation. J Neurosci 23:11363–11372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harnett MT, Xu NL, Magee JC, Williams SR (2013) Potassium channels control the interaction between active dendritic integration compartments in layer 5 cortical pyramidal neurons. Neuron 79:516–529. 10.1016/j.neuron.2013.06.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harnett MT, Magee JC, Williams SR (2015) Distribution and function of HCN channels in the apical dendritic tuft of neocortical pyramidal neurons. J Neurosci 35:1024–1037. 10.1523/JNEUROSCI.2813-14.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hattox AM, Nelson SB (2007) Layer V neurons in mouse cortex projecting to different targets have distinct physiological properties. J Neurophysiol 98:3330–3340. 10.1152/jn.00397.2007 [DOI] [PubMed] [Google Scholar]
- Häusser M, Spruston N, Stuart GJ (2000) Diversity and dynamics of dendritic signaling. Science 290:739–744. 10.1126/science.290.5492.739 [DOI] [PubMed] [Google Scholar]
- Hu H, Vervaeke K, Graham LJ, Storm JF (2009) Complementary theta resonance filtering by two spatially segregated mechanisms in CA1 hippocampal pyramidal neurons. J Neurosci 29:14472–14483. 10.1523/JNEUROSCI.0187-09.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu H, Martina M, Jonas P (2010) Dendritic mechanisms underlying rapid synaptic activation of fast-spiking hippocampal interneurons. Science 327:52–58. 10.1126/science.1177876 [DOI] [PubMed] [Google Scholar]
- Kalmbach BE, Chitwood RA, Dembrow NC, Johnston D (2013) Dendritic generation of mGluR-mediated slow afterdepolarization in layer 5 neurons of prefrontal cortex. J Neurosci 33:13518–13532. 10.1523/JNEUROSCI.2018-13.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klee M, Rall W (1977) Computed potentials of cortically arranged populations of neurons. J Neurophysiol 40:647–666. 10.1152/jn.1977.40.3.647 [DOI] [PubMed] [Google Scholar]
- Krueppel R, Remy S, Beck H (2011) Dendritic integration in hippocampal dentate granule cells. Neuron 71:512–528. 10.1016/j.neuron.2011.05.043 [DOI] [PubMed] [Google Scholar]
- Larkum M. (2013) A cellular mechanism for cortical associations: an organizing principle for the cerebral cortex. Trends Neurosci 36:141–151. 10.1016/j.tins.2012.11.006 [DOI] [PubMed] [Google Scholar]
- Larkum ME, Nevian T (2008) Synaptic clustering by dendritic signalling mechanisms. Curr Opin Neurobiol 18:321–331. 10.1016/j.conb.2008.08.013 [DOI] [PubMed] [Google Scholar]
- Larkum ME, Zhu JJ, Sakmann B (1999) A new cellular mechanism for coupling inputs arriving at different cortical layers. Nature 398:338–341. 10.1038/18686 [DOI] [PubMed] [Google Scholar]
- Larkum ME, Waters J, Sakmann B, Helmchen F (2007) Dendritic spikes in apical dendrites of neocortical layer 2/3 pyramidal neurons. J Neurosci 27:8999–9008. 10.1523/JNEUROSCI.1717-07.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larkum ME, Nevian T, Sandler M, Polsky A, Schiller J (2009) Synaptic integration in tuft dendrites of layer 5 pyramidal neurons: a new unifying principle. Science 325:756–760. 10.1126/science.1171958 [DOI] [PubMed] [Google Scholar]
- Larsen DD, Wickersham IR, Callaway EM (2007) Retrograde tracing with recombinant rabies virus reveals correlations between projection targets and dendritic architecture in layer 5 of mouse barrel cortex. Front Neural Circuits 1:5. 10.3389/neuro.04.005.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ledergerber D, Larkum ME (2010) Properties of layer 6 pyramidal neuron apical dendrites. J Neurosci 30:13031–13044. 10.1523/JNEUROSCI.2254-10.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- London M, Häusser M (2005) Dendritic computation. Annu Rev Neurosci 28:503–532. 10.1146/annurev.neuro.28.061604.135703 [DOI] [PubMed] [Google Scholar]
- London M, Meunier C, Segev I (1999) Signal transfer in passive dendrites with nonuniform membrane conductance. J Neurosci 19:8219–8233. 10.1523/JNEUROSCI.19-19-08219.1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lörincz A, Notomi T, Tamás G, Shigemoto R, Nusser Z (2002) Polarized and compartment-dependent distribution of HCN1 in pyramidal cell dendrites. Nat Neurosci 5:1185–1193. 10.1038/nn962 [DOI] [PubMed] [Google Scholar]
- Magee JC. (1998) Dendritic hyperpolarization-activated currents modify the integrative properties of hippocampal CA1 pyramidal neurons. J Neurosci 18:7613–7624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Major G, Larkum ME, Schiller J (2013) Active properties of neocortical pyramidal neuron dendrites. Annu Rev Neurosci 36:1–24. 10.1146/annurev-neuro-062111-150343 [DOI] [PubMed] [Google Scholar]
- Markram H. (1997) A network of tufted layer 5 pyramidal neurons. Cereb Cortex 7:523–533. 10.1093/cercor/7.6.523 [DOI] [PubMed] [Google Scholar]
- Markram H, Lübke J, Frotscher M, Roth A, Sakmann B (1997) Physiology and anatomy of synaptic connections between thick tufted pyramidal neurones in the developing rat neocortex. J Physiol 500:409–440. 10.1113/jphysiol.1997.sp022031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markram H, Muller E, Ramaswamy S, Reimann MW, Abdellah M, Sanchez CA, Ailamaki A, Alonso-Nanclares L, Antille N, Arsever S, Kahou GAA, Berger TK, Bilgili A, Buncic N, Chalimourda A, Chindemi G, Courcol J-D, Delalondre F, Delattre V, Druckmann S, et al. (2015) Reconstruction and simulation of neocortical microcircuitry. Cell 163:456–492. 10.1016/j.cell.2015.09.029 [DOI] [PubMed] [Google Scholar]
- Nevian T, Larkum ME, Polsky A, Schiller J (2007) Properties of basal dendrites of layer 5 pyramidal neurons: a direct patch-clamp recording study. Nat Neurosci 10:206–214. 10.1038/nn1826 [DOI] [PubMed] [Google Scholar]
- Norman RS. (1972) Cable theory for finite length dendritic cylinders with initial and boundary conditions. Biophys J 12:25–45. 10.1016/S0006-3495(72)86069-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pérez-Garci E, Larkum ME, Nevian T (2013) Inhibition of dendritic Ca2+ spikes by GABAB receptors in cortical pyramidal neurons is mediated by a direct Gi/o-β-subunit interaction with Cav1 channels. J Physiol 591:1599–1612. 10.1113/jphysiol.2012.245464 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rall W. (1962) Theory of physiological properties of dendrites. Ann N Y Acad Sci 96:1071–1092. 10.1111/j.1749-6632.1962.tb54120.x [DOI] [PubMed] [Google Scholar]
- Rall W. (1967) Distinguishing theoretical synaptic potentials computed for different soma-dendritic distributions of synaptic input. J Neurophysiol 30:1138–1168. 10.1152/jn.1967.30.5.1138 [DOI] [PubMed] [Google Scholar]
- Robinson RB, Siegelbaum SA (2003) Hyperpolarization-activated cation currents: from molecules to physiological function. Annu Rev Physiol 65:453–480. 10.1146/annurev.physiol.65.092101.142734 [DOI] [PubMed] [Google Scholar]
- Santello M, Nevian T (2015) Dysfunction of cortical dendritic integration in neuropathic pain reversed by serotoninergic neuromodulation. Neuron 86:233–246. 10.1016/j.neuron.2015.03.003 [DOI] [PubMed] [Google Scholar]
- Santello M, Bisco A, Nevian NE, Lacivita E, Leopoldo M, Nevian T (2017) The brain-penetrant 5-HT7 receptor agonist LP-211 reduces the sensory and affective components of neuropathic pain. Neurobiol Dis 106:214–221. 10.1016/j.nbd.2017.07.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schiller J, Schiller Y, Stuart G, Sakmann B (1997) Calcium action potentials restricted to distal apical dendrites of rat neocortical pyramidal neurons. J Physiol 505:605–616. 10.1111/j.1469-7793.1997.605ba.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schiller J, Major G, Koester HJ, Schiller Y (2000) NMDA spikes in basal dendrites of cortical pyramidal neurons. Nature 404:285–289. 10.1038/35005094 [DOI] [PubMed] [Google Scholar]
- Sieber AR, Min R, Nevian T (2013) Non-Hebbian long-term potentiation of inhibitory synapses in the thalamus. J Neurosci 33:15675–15685. 10.1523/JNEUROSCI.0247-13.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith MA, Ellis-Davies GC, Magee JC (2003) Mechanism of the distance-dependent scaling of Schaffer collateral synapses in rat CA1 pyramidal neurons. J Physiol 548:245–258. 10.1113/jphysiol.2002.036376 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spruston N. (2008) Pyramidal neurons: dendritic structure and synaptic integration. Nat Rev Neurosci 9:206–221. 10.1038/nrn2286 [DOI] [PubMed] [Google Scholar]
- Stuart G, Sakmann B (1995) Amplification of EPSPs by axosomatic sodium channels in neocortical pyramidal neurons. Neuron 15:1065–1076. 10.1016/0896-6273(95)90095-0 [DOI] [PubMed] [Google Scholar]
- Stuart G, Spruston N (1998) Determinants of voltage attenuation in neocortical pyramidal neuron dendrites. J Neurosci 18:3501–3510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tran-Van-Minh A, Cazé RD, Abrahamsson T, Cathala L, Gutkin BS, DiGregorio DA (2015) Contribution of sublinear and supralinear dendritic integration to neuronal computations. Front Cell Neurosci 9:67. 10.3389/fncel.2015.00067 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Geit W, Gevaert M, Chindemi G, Rössert C, Courcol JD, Muller EB, Schürmann F, Segev I, Markram H (2016) BluePyOpt: leveraging open source software and cloud infrastructure to optimise model parameters in neuroscience. Front Neuroinform 10:17. 10.3389/fninf.2016.00017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams SR. (2004) Spatial compartmentalization and functional impact of conductance in pyramidal neurons. Nat Neurosci 7:961–967. 10.1038/nn1305 [DOI] [PubMed] [Google Scholar]
- Williams SR, Stuart GJ (2002) Dependence of EPSP efficacy on synapse location in neocortical pyramidal neurons. Science 295:1907–1910. 10.1126/science.1067903 [DOI] [PubMed] [Google Scholar]
- Wybo WAM, Torben-Nielsen B, Nevian T, Gewaltig MO (2019) Electrical compartmentalization in neurons. Cell Rep 26:1759–1773.e7. 10.1016/j.celrep.2019.01.074 [DOI] [PubMed] [Google Scholar]
- Wybo WAM, Jordan J, Ellenberger B, Mengual UM, Nevian T, Senn W (2020) Data-driven reduction of dendritic morphologies with preserved dendro-somatic responses. BioRxiv. Advance online publication. Retrieved October 14, 2020. doi: 10.1101/2020.04.06.028183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu NL, Harnett MT, Williams SR, Huber D, O'Connor DH, Svoboda K, Magee JC (2012) Nonlinear dendritic integration of sensory and motor input during an active sensing task. Nature 492:247–251. 10.1038/nature11601 [DOI] [PubMed] [Google Scholar]
- Zador AM, Agmon-Snir H, Segev I (1995) The morphoelectrotonic transform: a graphical approach to dendritic function. J Neurosci 15:1669–1682. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The code of the simulations can be found at https://github.com/unibe-cns/ACCPyr or can be made available on request.