Abstract
COVID-19, as an infectious disease, has shocked the world and still threatens the lives of billions of people. Recently, the detection of coronavirus (COVID-19) is a critical task for the medical practitioner. Unfortunately, COVID-19 spreads so quickly between people and approaches millions of people worldwide in few months. It is very much essential to quickly and accurately identify the infected people so that prevention of spread can be taken. Although several medical tests have been used to detect certain injuries, the hopefully detection efficiency has not been accomplished yet. In this paper, a new Hybrid Diagnose Strategy (HDS) has been introduced. HDS relies on a novel technique for ranking selected features by projecting them into a proposed Patient Space (PS). A Feature Connectivity Graph (FCG) is constructed which indicates both the weight of each feature as well as the binding degree to other features. The rank of a feature is determined based on two factors; the first is the feature weight, while the second is its binding degree to its neighbors in PS. Then, the ranked features are used to derive the classification model that can classify new persons to decide whether they are infected or not. The classification model is a hybrid model that consists of two classifiers; fuzzy inference engine and Deep Neural Network (DNN). The proposed HDS has been compared against recent techniques. Experimental results have shown that the proposed HDS outperforms the other competitors in terms of the average value of accuracy, precision, recall, and F-measure in which it provides about of 97.658%, 96.756%, 96.55%, and 96.615% respectively. Additionally, HDS provides the lowest error value of 2.342%. Further, the results were validated statistically using Wilcoxon Signed Rank Test and Friedman Test.
Keywords: COVID-19, Classification, Fuzzy logic, Feature selection
Highlights
-
•
A new Hybrid Diagnose Strategy (HDS) to detect COVID-19 patients.
-
•
HDS relies on fuzzy logic and deep neural network.
-
•
Ranked features are used to derive the proposed classification model.
-
•
The proposed strategy has been validate using 10-fold cross validation.
-
•
An accuracy of 97.658% for COVID-19 patients detection.
1. Introduction
The new coronavirus (also called COVID-19) has resulted in a global epidemic problem due to its quick spread from one individual to another in society [1]. The terrifying spread of COVID-19 is the greatest challenge humanity has faced since the Second World War. World Health Organization (WHO) declared COVID-19 as a global Pandemic in March 2020 [2]. The most common symptoms of COVID-19 are dry cough, sore throat, and fever [3]. Symptoms can progress to a severe form of pneumonia with critical complications, including septic shock, pulmonary edema, acute respiratory distress syndrome, and multi-organ failure [1]. Unfortunately, clinical characteristics alone cannot determine the diagnosis of COVID-19, especially for patients at the early-onset of symptoms. Among nucleic acid-based tests, Reverse Transcription Polymerase Chain Reaction (RT-PCR) test has been used as the ‘gold standard’ for confirming COVID-19 positive patients [4]. However, sometimes RT-PCR fails to diagnose several corona patients and accordingly, those patients will not receive the appropriate treatment on time [3]. Such uninformed patients are extremely dangerous as they represent a direct cause of infection given the highly contagious nature of the virus. Generally, RT-PCR test has high specificity, but low sensitivity. Thus, a negative result of RT-PCR test does not negate the possibility of COVID-19 infection [3].
Recently, care providers have decided to use imaging tests to diagnose COVID-19, which is usually done with a CT scan or chest x-ray. However, recent studies advise against the use of an imaging test to diagnose or rule out COVID-19 as it suffers from false positive and false negative cases [5]. Again, due to COVID-19 exponential spread, such undiagnosed cases can cause catastrophic effects [6]. Alternative diagnose techniques should be found for early detection of COVID-19 patients.
Rapid and accurate detection of COVID-19 is increasingly vital to prevent the sources of infection as well as helping patients to prevent disease progression. Soft Computing (SC) techniques, such as; fuzzy logic, neural networks, and genetic have proven as potential tools in the disease detection [7], [8]. They can support decision making, providing for immediate isolation and appropriate patient treatment [9]. Several techniques have been proposed for detecting COVID-19 infections, however, the hopefully detection accuracy has not been reached yet. Fuzzy Logic (FL) describes systems in terms of a combination of numeric and linguistic (symbolic) [10], [11]. This has advantages over pure mathematical (numerical) approaches or pure symbolic approaches because very often system knowledge is available in such a combination.
FL is the selected soft computing approach for implementing the proposed COVID-19 diagnose system based on the following reasons; (i) fuzzy algorithms are often robust, the reasoning process is often simple, so computing power is saved, (ii) fuzzy methods usually have a shorter development time than conventional methods. This is a very interesting feature, especially in real time systems such as online diagnose applications, (iii) FL is flexible and easy to implement machine learning techniques, (iv) It is a very convenient method for uncertain or approximate reasoning. However, FL suffers from a difficulty to find suitable membership values for fuzzy systems and it suffers from a difficulty to store the rule-base that might require a significant amount of memory. Additionally, FL should be built with the full guidance of experts [10], [11].
Medical experts take the diagnostic decision depending on familiarity, experience, knowledge, capability and perception of the medical scientist. On dealing with the global corona pandemic, it is not easy to follow a specific diagnostic way without any error. Fuzzy logic offers a powerful thinking way that can deal with uncertainty and imprecision. Uncertainty interval not only provides confident description of the detection results, but also offers double control limits for the detection process, thereby leading to less false negative or false positive and more effective strategy for detecting COVID-19 patients [12]. Combination of knowledge, observation and experience from medical experts is the backbone of a fuzzy models based medical diagnostic system [13].
Recently, several techniques have been proposed for COVID-19 diagnose, however, none of them considers the impact of the feature weight on the employed classifier decision [14], [15], [16], [17], [18], [19]. All techniques treats all features equally, which results in degraded performance. Wrong diagnose of COVID-19 cases will result in the pandemic spread of the disease [20]. On the other hand, assigning a weight or a rank to each feature will assist the employed classifier to take accurate decisions, and certainly promoting the diagnose accuracy.
The main contribution of this paper is to introduce a new Hybrid Diagnose Strategy (HDS). In fact, the proposed HDS can solve the classification problem by assigning a weight to each feature that enables the classification model to take accurate decisions in which it can promote the diagnose accuracy. It recognizes a several input features that are resulted from patient’s laboratory findings. HDS has new techniques for identifying effective features as well as assigning a rank for each feature. HDS is implemented through three sequential phases, which are; (i) pre-processing phase, (ii) feature ranking phase, and (iii) Classification Phase (CP). The main objective of pre-processing phase is to filter patients data from both outlier items and irrelevant features. The aim of the outlier rejection process is to detect and reject the hasted data that have very exceptional behavior when compared to other data. Irrelevant features should be eliminated from the patient laboratory findings to select only the best subset of features to enable the feature ranking phase to work well. Then, the weight is assigned to each identified feature based on its effect on the classification accuracy. Ineffective features are then discarded using feature distiller.
During the second phase (e.g., feature ranking), the selected features are ranked. The feature rank is calculated based on two factors, namely; (i) feature weight, and (ii) feature amount of convergence to other features, which is calculated by projecting features in a patient space (PS). Ranking features can be accomplished with the aid of Feature Connectivity Graph (FCG). FCG is a partially connected undirected graph that can be used to indicate the weight of each feature as well as the connection strength among each feature and its friends. As the feature rank is a measure to the feature effect in the final diagnose decision, the calculated ranks for the effective features are used for the next classification phase.
On the other hand, during the classification phase (e.g., CP) as a third and final phase in the proposed HDS, two classifiers called fuzzy inference engine and deep neural network are implemented in parallel manner to take the final decision. Hence, the final decision is taken by calculating average value from the outputs of the used classifiers. The fuzzy inference engine is applied in five steps, namely; (i) fuzzification, (ii) Normalization, (iii) Fuzzy Rule Induction, (iv) defuzzification, and (v) decision making. Deep neural network (DNN) is a powerful model with a wide range of applications. It was used to help the fuzzy inference engine for making a correct final decision. The proposed HDS has been compared against recent COVID-19 detection strategies, which are DarkCovidNet model [21], Group Method of Data Handling (GMDH) model [22], KNN Variant (KNNV) algorithm [23], Automated Detection and Patient Monitoring (ADPM) algorithm [24], proposed Convolutional Neural Network (CNN) model [25], and Corona Patients Detection Strategy (CPDS) [26].
This paper is organized as follows; Section 2 describes a problem definition about COVID-19. Section 3 discuss HDS applicability for COVID-19 diagnose. Section 4 introduces the previous efforts about COVID-19 patients classification. Section 5 focuses on the proposed Hybrid Diagnose Strategy (HDS) in details. Section 6 explains the experimental results. Finally, conclusions are presented in Section 7.
2. Problem definition
A recent study has shown that once the coronavirus epidemic starts, it will take around four weeks to break the basic healthcare system. As soon as the hospital capacity overwhelmed, the death rate jumps [27], [28]. Cases detection and isolation is the golden solution for protecting the healthcare system from becoming overwhelmed, and accordingly will flat the epidemic curve as illustrated in Fig. 1. Accordingly, all patients get the resources they need as capacity of the underlying healthcare system can occupy the diagnosed cases. On the other hand, the late detection of COVID-19 cases will break the system as it will have no ability to occupy the exponential growth in diagnosed cases.
Fig. 1.
COVID-19 epidemic curve with and without protective measures.
To show the spread of the novel coronavirus crisis, we can use a simple approximate mathematical model to understand the mechanism of virus spread among the population. The susceptible individuals can catch infection through either direct or indirect way. The direct way is by contacting with infectious individuals and the indirect way is by contacting with an environment affected by the virus. It is believed that, at the early stages of the COVID-19 epidemic, the proportion of the population with immunity to COVID-19 is negligible. Then, a small number of infected people can transmit the disease to many other people.
Mathematical model’s definition about the COVID-19’s problem based on four parameters, which are; (i) basic reproductive number () that refers to the expected number of new infectious cases per infectious case, (ii) case fatality rate () that refers to the proportion of cases who die within the symptomatic period, (iii) incubation period (m) that refers to the time from infection to symptom, and (v) duration of disease (n) that refers to the time from symptom to recovery or death. Actually, to predict the number of COVID-19 cases, only two parameters are used which are; basic reproductive number () and incubation period (m). Assume that, after one incubation period (m), one infectious case produces new infectious cases. The cumulative total number of cases at this time is . After two incubation periods (2 m), there are cases produced by the previous cases. The total number of cases is 2. Assuming that the predicted number of cases based on is , hence, total number of cases can be expressed by (1).
| (1) |
where is the predicted total number of cases, the predicted number of incident cases on , and t is the time expressed in the number of incubation periods. Additionally, m is the incubation period. Table 1 illustrates the application of the model to calculate the predicted number of COVID-19 cases, using 3 and days.
Table 1.
Predicted number of COVID-19 cases using X 3 and m 5 days.
| Number of incubation period (m) | Day | Predicted incident cases (E) | Predicted total cases(E) |
|---|---|---|---|
| 0 | 0 | 1() | 1 |
| 1 | 5 | 3 () | 4 (13) |
| 2 | 10 | 9 () | 13 (139) |
| 3 | 15 | 27 () | 40 (13927) |
Additionally, to predict number of COVID-19 deaths, assuming that after one disease duration n, the cases are removed with death or recovery. is the percentage of die cases while 1-D is the percentage of recover cases. Consequently, the predicted number of deaths based on and the predicted number of deaths can be calculated by (2), (3).
| (2) |
| (3) |
where is the predicted number of deaths based on , is the predicted total number of deaths, and t is the time expressed in the number of incubation periods. the predicted number of incident cases on , is the percentage of die cases, m is the incubation period, and n is the duration of disease. Table 2 illustrates the application of the model to calculate the predicted number of COVID-19 deaths, using , days, , and days.
Table 2.
Predicted number of COVID-19 deaths using X 3, m 5 days, D 10% and n 14 days.
| Number of incubation period (t) |
Day | Predicted incident cases (E) | Predicted new deaths (S) | Predicted total deaths (S) |
|---|---|---|---|---|
| 0 | 0 ( t*m) | 1 | 0 | 0.0 |
| 1 | 5 | 3 | 0 | 0.0 |
| 2 | 10 | 9 | 0 | 0.0 |
| 14 | 0 | 0.1 ( 1*Dr) | 0.1 | |
| ( t*m+n) | ||||
| 3 | 15 | 27 | 0 | 0.1 |
| 19 | 0 | 0.3 ( 3*Dr) | 0.4 | |
As shown in Table 2, cases from day 0 are removed on day 14, after one disease duration (14 days). The one case from day 0 is expected to produce 0.1 death (110%) and 0.9 recovered people. Likewise, the three cases from day 5 are expected to produce on day 19 (after 14 days) 0.3 death and 2.7 recovered people. The value of n can be determined from patient’s epidemiological studies. The optimal value of can be determined in a particular situation, given the optimal values of , m, and n can be determined by trying multiple values to see which combination of , , m, and n produces the predicted number of COVID-19 deaths that most closely matches the observed total number of COVID-19 deaths. Finally, it can be concluded from the illustrated model that COVID-19 can spread very quickly in the absence of interventions.
In spite of its sensitivity and diagnose speed, RT-PCR test suffers from the risk of eliciting false-positive and false-negative results, and accordingly, it does not pick up all infections. This may have no great impact in slow infection diseases, however, in the case of COVID-19, only one undiagnosed case may cause a devastating pandemic. Several COVID-19 diagnose systems based on artificial intelligence and soft computing techniques have been recently introduced [7], [8], however, the desired diagnose precision to flatten COVID-19 epidemic curve has not been reached yet. The aim of the work introduced in this paper is to provide fast, accurate, and reliable COVID-19 diagnose system, called Hybrid Diagnose Strategy (HDS). We hope that applying HDS for diagnose COVID-19 patients will protect the healthcare system from becoming overwhelmed.
3. HDS applicability for COVID-19 diagnose
What a pandemic represented by the terrifying spread of the COVID-19 virus. No doubt, it is the greatest challenge the humanity has faced since World War Two. In March 2020, World Health Organization (WHO) declared COVID-19 as a global Pandemic. However, COVID-19 is much more than a health crisis, it has the impact to create devastating economic, political, and social crises that will certainly leave deep scars [28].
Generally, COVID-19 diagnosis can be accomplished via three different treatments as illustrated in Fig. 2, which are; (i) Using Real-Time reverse transcriptase-Polymerase Chain Reaction (RT-PCR), (ii) using chest CT imaging scan, and (iii) using numerical laboratory tests. Among nucleic acid tests, polymerase chain reaction (PCR) laboratory test, and more precisely, Real-time reverse transcriptase-PCR (RT-PCR) is currently used as the ‘gold standard’ for confirming COVID-19 positive patients. RT-PCR tests are fairly quick, sensitive and reliable. A sample is collected from a person’s nose or throat, chemicals are used to remove any fats, proteins and other molecules, leaving only RNA behind [4]. Such separated RNA is a mixture of a person’s own genetic material and, if present, the coronavirus’ RNA. However, RT-PCR test suffers from the risk of eliciting false-positive and false-negative results, and accordingly, it does not pick up all infections [29]. Thus, a negative result of RT-PCR test does not negates the possibility of COVID-19 infection. Due to COVID-19 exponential spread, such undiagnosed cases can cause catastrophic effects. Accordingly, RT-PCR should not be used as the only criterion for detecting COVID-19 patients [30].
Fig. 2.
Different COVID-19 diagnosis techniques.
Chest CT has become a critical diagnostic tool for COVID-19, which detects hazy, patchy, “ground glass” white spots in the lung, a telltale sign of COVID-19. Several studies observed that the sensitivity of CT in diagnosing COVID-19 is significantly higher than that of RT-PCR [31]. However, current evidence suggests that CT scans and x-rays are not specific enough to either diagnose or rule out COVID-19, this is due to the following reasons; (i) CT Scans sometimes fail to detect coronary lung tissue. Like ultrasounds, a CT scan is unable to differentiate coronary tissue from non-coronary tissue. Therefore, CT scans can lead to a false negative and accordingly it negatively impacts the ability to get the best treatment or prolongs the time to get treatment. Accordingly, coronavirus can progress to destroy the patient lung and infection is allowed. (ii) CT Scans Lack Detail as it cannot identify the most aggressive tumors, hence it is unable to differentiate between cancerous tissue, cysts (or fibroids), and coronary tissue. While patients with COVID-19 can show an abnormality on either a chest x-ray or CT scan, many other lung problems can look very similar. Additionally, the absence of an abnormality on either a chest x-ray or CT scan does not necessarily exclude COVID-19. (iii) Although CT scan can result in rapid diagnose of COVID-19, rapid results mean rapid false-negatives and rapid false reassurance. This also means the rapid release of people with COVID-19, allowing them to mingle with people without the infection who may be potentially vulnerable.
Moreover, the American College of Radiology (ACR), which represents nearly 40,000 radiologists in USA, has issued guidance that CTs and x-rays should not be used as a first-line tool for diagnosing COVID-19. There are three basic reasons for the ACR’s recommendation, which are; (i) a chest CT or x-ray cannot accurately distinguish between COVID-19 and other respiratory infections, like seasonal flu. Unlike RT-PCR test, which lead to specific diagnoses of COVID-19, imaging findings are not specific enough to confirm COVID-19. They can only point to signs of an infection. Those signs could be due to other reasons such as seasonal flu. (ii) A significant number of patients with COVID-19 have normal chest CTs or x-rays, which falsely convince them that they are healthy. Hence, those uninformed patients are at greater risk of spreading the virus to others. (iii) Because COVID-19 is highly contagious, using imaging equipment on COVID-19 patients is a serious hazard for healthcare providers and other patients. CT scanners are large and complex pieces of machinery. They need to be thoroughly cleaned between each potential COVID-19 patient. But even with careful cleaning, there is a risk that the virus could remain on a surface in a CT scanner room. Additionally, moving potential COVID-19 patients to and from a CT scanner room increases the risk of spreading the virus inside of healthcare facilities.
In [32], the authors studied 104 patient with COVID-19 from the infamous Diamond Princess cruise ship. They found that half of asymptomatic patients and one-fifth of symptomatic patients had normal CT scans. They also reported that CT scans produce an unacceptably high false-negative rate and thus will fail to pick up a significant fraction (up to half) of patients with COVID-19.
In real-world practice, claiming that a person is infected with COVID-19 based on the presence of a minor abnormality on a CT both ignores the common subclinical lung inflammation that radiologists frequently encounter and the other diseases that patients may have instead of COVID-19 [33]. In [34] the diagnosis of COVID-19 pneumonia by CT imaging alone is not sufficient enough, especially in the case of coinfection with other pathogens. Moreover, there is no clear pattern in chest CT images of patients with COVID-19, making the virus detection process more difficult than other causes of viral pneumonia [35].
Based on the above discussion, we conclude that COVID-19 diagnoses and treatment plans based on a CT scan or RT-PCR are not recommended as primary screening tools [32], [33], [34], [35]. On the other hand, the use of accurate Numerical Laboratory Tests (NLTs) can be considered as the most preferred method for diagnosing COVID-19 as they are used in recent Covid-19 diagnose researches [36], [37], [38], [39]. Recently, the use of NLTs is the only method that the Centers for Disease Control (CDC) currently endorses [40]. Hence, it makes perfect sense that the use of NLTs will provide more accurate diagnosis with less waiting time. To the best of our knowledge, Hybrid Diagnose Strategy (HDS), the proposed diagnose strategy proposed in this paper, is the first to use NLTs as the main criteria for detecting COVID-19 patients. It relies on data mining techniques and more precisely on classification for diagnosing COVID-19. Although several classification techniques can be used, HDS relies on a new technique for feature ranking that can efficiently derive the proposed classification model.
As a predictive model, we hope that FL is a viable classifier that can be used for COVID-19 diagnosis because of the following reasons; (i) FL is powerful, simple, flexible, fast, and appropriate to the real world applications, (ii) FL can handle problems with imprecise and incomplete data, hence, it can make accurate predictions even with small amount of training data, (iii) FL is less sensitive to missing data, it is also resistive resistance to noisy data which avoids over-fitting the dataset, and (iv) when new data or rules are added to the system, there is no need to re-train the system, mainly just adding new rules (besides rule conflict check). As will be seen in the experimental results, the implementation of HDS reflects this issue and proves the applicability of the proposed HDS as the first COVID-19 diagnose strategy that completely relies on accurate NLTs rather than CT chest imaging or RT-PCR test.
To clarify the applicability of the proposed HDS, if a person has a similar symptoms of COVID-19 disease, a blood test is a faster, safer and cheaper way than PCR test or CT chest imaging. In this paper, the proposed system can be used to pre-diagnose the patient according to his laboratory findings to decide whether the patient is infected with COVID-19 or not. Based on that, it will be decided whether the patient should be sent to the isolation hospital or isolate himself at home. Consequently, early detection of COVID-19 patients is a critical task to prevent the sources of infection as well as helping patients to prevent disease progression. Hence, applying HDS for diagnose COVID-19 patients will protect the healthcare system from becoming overwhelmed.
4. Related work
In this section, previous research efforts to classify COVID-19 patients will be reviewed. In [21], an automated COVID-19 detection model called DarkCovidNet was introduced as a new detection method based on using chest X-ray images. DarkCovidNet model represented a development of deep learning technique to be able to perform binary and multi-class classification. The experimental results in [21] proven that the proposed model could perform binary tasks better than multi-class tasks in which the accuracy of binary is higher than multi-class.
As presented in [22], the Group Method of Data Handling (GMDH) was used as binary classification model. GMDH is a type of artificial neural networks that used to predict the number of confirmed COVID-19 cases in Hubei province. In fact, many different features were used as inputs to GMDH to predict the confirmed number of COVID-19 patients in the next 30 days. These features (factors) such as maximum, minimum, and average daily temperature, the density of city, humidity and wind speed. The results in [22] demonstrated that the proposed model introduced higher performance capacity in predicting the confirmed number of COVID-19 patients.
As depicted in [23], a KNN Variant (KNNV) algorithm was introduced to accurately and efficiently classify COVID-19 patients using incomplete and heterogeneous COVID-19 data. KNNV algorithm inherited the merits of KNN in which different K values were calculated for each unknown patient independently and efficient computations for the distances between patients were implemented. The experimental results in [23] illustrated that KNNV algorithm greatly outperforms the related algorithms in terms of precision, recall, accuracy, and F-score metrics. In [24], Automated Detection and Patient Monitoring (ADPM) algorithm was proposed for the detection, quantification, and tracking of COVID-19 patients. ADPM algorithm depended on using a deep learning model to classify COVID-19 from CT images. Additionally, this algorithm could distinguish COVID-19 patients from other patients.
As depicted in [25], an automated COVID-19 diagnosis method using the implementation of a convolutional neural network (CNN) was introduced as a new classification method. The proposed CNN has been developed using EfficientNet architecture to be able to perform binary and multi-class classification using X-ray images. The 10-fold cross-validation was used to evaluate the performance of the proposed system. Experimental results in [25] showed that the average accuracy values for binary and multiclass are 99.62% and 96.70%, respectively.
As presented in [26], a new Corona Patients Detection Strategy (CPDS) was introduced to detect COVID-19 patients. CPDS consists of two phase called Data Preprocessing (DP) and Patient Detection Phase (PDP). During DP, two main processes which are; feature extraction and feature selection were performed to extract and then select the most informative feature from CT images. On other hand, during PDP, fast and accurate detection of COVID-19 patients based on the selected features was provided by the proposed Enhanced KNN (EKNN) classifier. Experimental results in [26] proven that CPDS outperforms recent ones in which it introduces the best detection accuracy with the minimum time penalty.
As illustrated in [41], a Hybrid COVID-19 Detection (HCD) model was proposed to accurately detect COVID-19 patients. HCD composed of two methods called an Improved Marine Predators Algorithm (IMPA) and a Ranking-based Diversity Reduction (RDR) strategy. In fact, IMPA was used as a detection method, and RDR was used to improve the performance of the IMPA to reach better solutions in fewer iterations. The proposed model was implemented on the X-ray images to extract similar small regions to obtain areas that might contain COVID-19. The results in [41] proven that HCD outperforms the related algorithms.
As illustrated in [42], a new forecasting model to estimate and forecast the number of confirmed cases of COVID-19 based on the previously confirmed cases recorded in China was proposed. The proposed model is an improved Adaptive Neuro-Fuzzy Inference System (ANFIS) using an enhanced Flower Pollination Algorithm (FPA) by using the Salp Swarm Algorithm (SSA). The main idea of the proposed model (FPASSA-ANFIS) is to improve the performance of ANFIS by determining the parameters of ANFIS using FPASSA. Experimental results in [42] shown that the proposed model outperforms other forecasting models in terms of mean absolute percentage error, root mean squared relative error, root mean squared relative error, coefficient of determination, and computing time.
In [43], a proposed model for Forecasting of COVID-19 Spread was introduced. The proposed model called Wavelet-coupled Random Vector Functional Link (WCRVFL) networks. WCRVFL is a hybrid method between random vector functional link (RVFL) and 1-D discrete wavelet transform. The proposed method focuses on modeling and forecasting of COVID-19 spread in the top 5 worst-hit countries as per the reports on 10th July 2020. RVFL with wavelet provide a consistent prediction performance. Experimental results in [43] indicate the effectiveness of the WCRVFL model for COVID-19 spread forecasting. Table 3 shows a brief comparison about previous works on COVID-19 classification techniques.
Table 3.
Comparison about previous works on COVID-19 classification techniques.
| Used technique | Description | Advantages | Disadvantages |
|---|---|---|---|
| DarkCovidNet model [21] | DarkCovidNet model is an automated COVID-19 detection model that was introduced as a new detection method based on using chest X-ray images. It represented a development of deep learning technique to be able to perform binary and multi-class classification. | DarkCovidNet can be used in remote places in countries affected by COVID-19 to overcome a shortage of radiologists. Also, it can be used to diagnose other chest-related diseases including tuberculosis and pneumonia. | A limitation of this model is the use of a limited number of COVID-19 X-ray images. |
| Group Method of Data Handling (GMDH) model [22] | GMDH model was used as binary classification model. It is a type of artificial neural networks that used to predict the number of confirmed COVID-19 cases in Hubei province. | GMDH has the ability to work with inadequate knowledge and it have fault tolerance. | Unexplained behavior of the network represents the most problem of GMDH. |
| KNN Variant (KNNV) algorithm [23] | KNNV algorithm was introduced to accurately and efficiently classify COVID-19 patients using incomplete and heterogeneous COVID-19 data. It inherited the merits of KNN in which different K values were calculated for each unknown patient independently and efficient computations for the distances between patients were implemented | KNNV is a simple technique that used the merits of KNN method to classify COVID-19 patients. | KNNV is a lazy learning method that has a high computational time. |
| Automated Detection and Patient Monitoring (ADPM) algorithm [24] | ADPM was proposed for the detection, quantification, and tracking of COVID-19 patients. It depended on using a deep learning model to classify COVID-19 from CT images | ADPM could distinguish COVID-19 patients from other patients in which it efficient to classify positive cases. | ADPM cannot provide the optimal accuracy. |
| Proposed Convolutional Neural Network (CNN) [25] | CNN was proposed to accurately detect COVID-19 patients using EfficientNet architecture. CNN was used to perform binary and multi-class classification using X-ray images | CNN can accurately detect COVID-19 patients. | More complex |
| Corona Patients Detection Strategy (CPDS) [26] | CPDS was proposed to detect COVID-19 patients using enhanced KNN classifier based on the most effective and significant features. these features were selected using Hybrid Feature Selection Methodology (HFSM). | CPDS can accurately detect infected patients with minimum time penalty. | KNN is a lazy learner. |
5. The proposed Hybrid Diagnose Strategy (HDS)
In this section, the proposed Hybrid Diagnose Strategy (HDS) will be explained in details. The main target of HDS is to quickly and accurately diagnose COVID-19 cases. Quick detection of COVID-19 cases allows a fast treatment and isolation of patients and accordingly breaks down infection spread of the disease. The input of HDS is a training set in the form of laboratory findings of both COVID-19 and non COVID-19 persons. After the model is trained, it can receive new cases (also in the form of laboratory findings) for classification. HDS decides whether the input case is infected with COVID-19 or not. As illustrated in Fig. 3, HDS composed of three sequential phases, which are; (i) pre-processing phase, (ii) feature ranking phase, and (iii) Classification Phase (CP). The next subsections will depicts the details of each phase.
Fig. 3.
The proposed hybrid diagnose strategy.
5.1. Pre-processing phase
The main task in pre-processing phase is to filter patients data by using data mining techniques. To accomplish such aim, two main processes are performed, which are; outlier rejection and features selection. These two processes are depending on data mining techniques to give a meaningful pattern of data. Initially, patient features are extracted from the input training set. Several features can be considered for diagnose COVID-19 cases as presented in Table 4. Although feature selection process can enhance the performance of the medical system, the training dataset may have many rare data comparing to another large group that may reduce the efficiency of the classification method. Thus, outlier rejection process is an essential process to enable the classifier to be correctly learned and to provide accurate results. There are numerous outlier rejection methods categorized into two classes, which are; (i) classic outlier approach and (ii) spatial outlier approach [44], [45], [46], [47]. On the other hand, features selection methods can be categorized to filter and wrapper method. In this paper, outlier rejection process has been performed by using Genetic Algorithm (GA) technique [48].
Table 4.
Some of laboratory findings of patients infected with COVID-19.
| Features | Description |
|---|---|
| C-Reactive Protein (CRP) | CRP is one of the plasma proteins known as acute-phase proteins (p). The pooled effect size showed that CRP level was significantly higher in patients with severe COVID-19 than patients with non-severe COVID-19. |
| Lactate Dehydrogenase (LDH) | LDH is a type of protein, known as an enzyme. LDH plays an important role in making your body’s energy. The pooled effect size showed that LDH level was significantly higher in patients with severe COVID-19 than patients with non-severe COVID-19. |
| Eosinophil | Eosinophils are a type of disease-fighting white blood cell. |
| Leukocytes (WBC) | WBC means the number of white blood cells in a sample of blood. COVID-19 patients have low WBC count in the first day. |
| Neutrophils | Neutrophils are the most abundant type of granulocytes and make up 40% to 70% of all white blood cells in humans. |
| Basophils | Basophils are a type of white blood cell. Although they are produced in the bone marrow, they are found in many tissues throughout your body. |
| Lymphocyte (LYM) | LYM is a small white blood cell (leukocyte) that plays a large role in defending the body against disease. It was significantly lower in patients with severe COVID-19 than patients with non-severe COVID-19. |
| Platelets | Platelets are tiny blood cells that help your body form clots to stop bleeding. |
| Monocytes | Monocytes are a type of leukocyte, or white blood cell. They are the largest type of leukocyte and can differentiate into macrophages and myeloid lineage dendritic cells. |
| Alanine Aminotransferase (ALT) | ALT is an enzyme found primarily in the liver and kidney. It was originally referred to as serum glutamic pyruvic transaminase (SGPT). Normally, a low level of ALT exists in the serum. |
Additionally, it is an important to select the most effective features for COVID-19 diagnose. Hence, the core of the pre-processing phase is a feature distiller module. However, for saving classification time, it will be better to select only those effective features. Feature selection is the process of selecting those features which contribute most to the prediction problem. It is reasonable to ignore those input features with little effect on the output, so as to keep the size of the prediction model small. Having irrelevant features can decrease the accuracy of the models and make the model learn based on irrelevant features [44], [45], [46], [47]. As the feature selection process reduces the number of input variables when developing the predictive model, it results in minimizing the computational cost of modeling, reduces model complexity, and, in many cases, it improves the performance of the model. From another point of view, an irrelevant input feature may lead to overfitting problem especially in the domain of medical diagnosis in which the purpose is to infer the relationship between the symptoms and their corresponding diagnosis. If an irrelevant feature is included, an over-tuned machine learning process may come to the conclusion that the illness is determined by , which leads to degraded classification accuracy during the model testing.
Generally, there are two main types of feature selection algorithms, namely; filter and wrapper [44], [45], [46], [47]. In the former, the selection of features is independent of machine learning techniques. Instead, features are selected on the basis of their scores in several statistical tests for their correlation with the outcome variable. On the other hand, wrapper methods use a classification performance of a classifier (like accuracy) to evaluate the features. Wrapper methods are advantageous for giving better performances but they suffer from being costly. On the other hand, filter methods are less accurate but faster to compute [49].
As the efficiency is essential in disease diagnoses system, during the pre-processing phase, the employed feature distiller relies on the wrapper based algorithm to calculate the feature weight [50], [51]. The relative long time for weighting features in wrapper based method has no effect on the system performance as it takes place only one time. The weight of the feature , denoted as; w(f ) is an indication to the feature impact and is defined as the degradation percentage of the model accuracy after discarding from the input feature set. Table 5 gives an illustration of estimating the feature impact as well as the corresponding action that will be taken by the employed feature distiller. Several classifiers can be used to implement the underlying model such as; Naïve Bayes (NB), K-Nearest Neighbors (KNN), and Support Vector Machines (SVM). Only those features which have –ve impact on the model (e.g., cause accuracy degradation of the employed classifier when it is removed from the input feature set) are the considered ones. On the other hand, features with no or +ve impact on the classification accuracy will be discarded. The feature weight can be calculated by (4).
| (4) |
where w() is the weight (impact) of feature , accuracy () is the accuracy of the model when the feature is included in the feature set, and accuracy () is the accuracy of the model when is removed.
As illustrated in Table 5, should be kept in the input features as removing it will decrease the model accuracy. On the other hand, features and should be removed as they have no effect or decrease the model accuracy respectively. Sometimes, it wondrous that how the addition of a new feature will decrease the model accuracy. For illustration, if by mistake the patient ID number is included as one input feature, as the model is falsely trained, it may come to the conclusion that the illness is determined by the ID number, which will certainly degrades the model accuracy during the testing phase. After applying the pre-processing phase, four different features will be included, which are; White Blood Cell (WBC), Lymphocyte (LYM), Monocytes (MON), and Locate Dehydrogenase (LDH).
Table 5.
An illustration of estimating the feature impact.
| Feature (f) | Accuracy(f) | Accuracy(f) | w(f) | Action |
|---|---|---|---|---|
| f | 0.86 | 0.83 | 0.03 | Keep |
| f | 0.88 | 0.88 | 0.0 | Remove |
| f | 0.85 | 0.87 | −0.02 | Remove |
5.2. Feature ranking
The selected features are then ranked. The feature rank is calculated based on two factors, which are; (i) feature weight, and (ii) feature amount of convergence to its friends. Ranking features can be accomplished with the aid of Feature Connectivity Graph (FCG). FCG is a partially connected undirected graph that can be used to indicate the weight of each feature as well as the connection strength among each feature and its friends. As all graphs, FCG can be expressed as; where nodes represent the selected features and edges E represent relations between them. These relations are weight matrix given by a weight matrix W: IFW(, ), where (, ) is the Inter-Feature Weight between and . (, ) is non-zero if and are “friends”, i.e. the edge (i, j) is in E (weighted by (, )). In FCG, the feature is connected only to its friends. An illustration of a FCG is shown in Fig. 4 considering the feature set .
Fig. 4.
Feature Connectivity Graph (FCG) illustrative example.
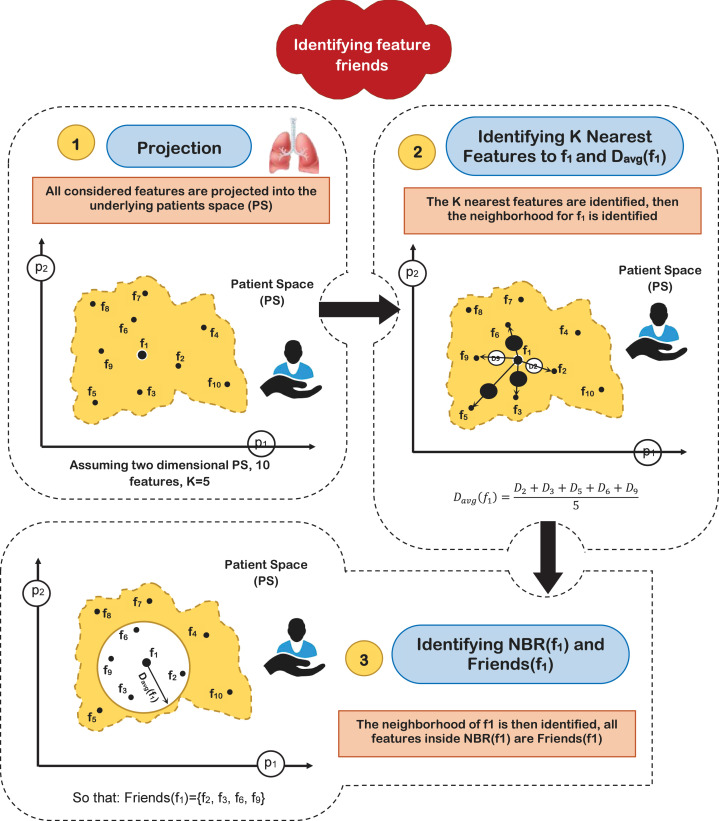
Two important issues should be discussed in more details, which are; (i) how to identify the feature friends, and (ii) how to calculate the inter-feature weight that can be considered as an indication to the amount of convergence between each pair of the selected features. Identifying the friend of each features can be accomplished by considering a Patients Space (PS) in which each patient in the training set represent a dimension in PS. The different considered features are projected as points in PS. To identify the friends of the feature , denoted as friends(f ), the K nearest features are picked. The average distance between and the K neighboring features is calculated, which is denoted as; . A neighborhood around denoted as NBR(f ) is then recognized whose radius is set to (). Finally, all features located inside NBR(f ) are considered as friends(f ). Fig. 5 gives an illustration of how to recognize the friends of the feature in two dimensional patient space assuming K 5 and a feature set of 10 features denoted as; .
Fig. 5.
Identifying the friends of a feature (illustrative example).
Definition 1 Friend Features —
In fact, friend features represent the closest neighbors of features which are the most closely related to each other. By identifying the nearest features, only qualified features are considered for classification. This guarantees the maximum classification accuracy and minimizes the classification time.
After identifying the friends of each feature, the task now is to calculate the inter-feature weight between each feature and each of its friends so that FCG for the underlying problem can be constructed. The inter-feature weight between a pair of feature (, ), denoted as (, ), indicates the bending strength between , and can be calculated by (5).
(5) where (, ) is inter feature weight between the pair (, ), accuracy (, ) is the accuracy of the employed base classifier when the features and are included in the input feature set, accuracy (, ) is the accuracy of the employed base classifier when the features and are removed in the input feature set. The Normalized IFW (NIFW) between each pair of friend features is then calculated by (6).
(6) where NIFW(f , ) is the normalized inter feature weight between the pair (, ), IFW(f , ) inter feature weight between the pair (, ), (, ) inter feature weight between the pair (, ), (, ) belongs to the selected set of input features F. Finally, the feature rank can be calculated by (7) :
(7) where is the rank of , is the weight (impact) of feature , NIFW() is the normalized inter feature weight between the pair (, ), is the weight (impact) of feature , and and are weighting factors and .
5.3. Classification Phase (CP)
The last phase in the proposed HDS is the classification phase in which the final decision is taken for classifying the input case to be infected by COVID-19 virus or not. In classification tasks, it may be wise to collect feedback from various sources, as it not only reduces training time, but also increase the performance of classification model. In this paper, the classification model consists of two classifier, which are; fuzzy inference engine, and deep neural network. Final result from both classifiers is often provided by just calculating the average value from the outputs of the used classifiers to take the final decision. Firstly, HDS receives laboratory findings of the patients. Then, the features are extracted from the collected laboratory findings, and then the extracted features are selected by the distiller after rejecting the outliers. Finally, the classification model will be implemented on the ranked features to take the final decision by calculating the average value from the outputs of both classifiers.
5.3.1. Fuzzy inference engine
In HDS, applying the fuzzy inference system is implemented through five steps, as depicted in Fig. 6, which are; (i) fuzzification, (ii) Normalization, (iii) Fuzzy Rule Induction, (iv) High defuzzification, and (v) decision Making. More details about each step will be discussed in the next subsections.
Fig. 6.
The employed fuzzy inference engine for COVID-19 detection.
A. Fuzzification
Based on the feature distiller employed in the pre-processing phase, four different fuzzy sets, which are; White Blood Cell (WBC), Lymphocyte (LYM), Monocytes (MON), and Locate Dehydrogenase (LDH) will be considered. During the fuzzification process, the crisp values of the input case to be tested are transformed into grades of membership for linguistic terms, “Low”, “Medium”, and “High” of the employed fuzzy sets. A membership function is used for each fuzzy set to provide the similarity degree of the crisp input value to the underlying fuzzy set. Such employed function returns a value between 0.0 (for non-membership) and 1.0 (for full-membership). The membership functions for the considered four fuzzy sets are illustrated in Fig. 7, while the used values of , , and are illustrated in Table 6.
Fig. 7.
The membership functions for the considered fuzzy sets.
Table 6.
The assigned values of , , and .
| Parameter | Assigned value |
|---|---|
| 2 | |
| 4 | |
| 6 | |
| 6.5 | |
| 12 | |
| 19.5 | |
| 0.5 | |
| 1.3 | |
| 2 | |
| 450 | |
| 530 | |
| 650 |
Really, any data generated in the real-world has some degree of uncertainty (i.e. both systematic and random error). Accordingly, it is an important to use any learning system to cope with such uncertainty. The definition of uncertainties is represented as the vagueness and lack of the information or data [52]. There are three types of uncertainties called epistemic, stochastic, and error [53]. In fact, epistemic uncertainty exists as a result of incomplete information and lack of knowledge or data. When the dealing with the lack of data, it is most appropriate to interpret the uncertainty compared to statistical approach. The reason is that the theory of fuzzy system is a non-probabilistic method.
A lot of stochastic simulation models need input distributions which are precisely fitted using samples of real-world data. Usually, a fitted distribution is almost surely not a perfect representation of the reality because the number of samples is finite. In a simulation model, the misspecification of an input distribution affects the quality of its output. A consequence of not knowing the true input distributions that drive a simulation model is known as input uncertainty. In fact, input uncertainty refers to the effect of driving a simulation with input distributions that are based on real-world data. Fig. 8 illustrates many sources of input uncertainty.
Fig. 8.
Sources of input data uncertainty.
There are two types of fuzzy logic systems to deal with uncertainties, which are; Type-1 Fuzzy Logic Systems (T1 FLSs) and Type-2 Fuzzy Logic Systems (T2 FLSs). T1 FLSs can deal with the linguistic uncertainty originating in the imprecise and vague meaning of words. Although the effectiveness of T1 FLSs, there are dynamic uncertainties such as the uncertainty about the training data used to tune the respective fuzzy system and uncertainties about the measurements activating the system that can lead to performance deterioration. Accordingly, this deterioration means that T1 FLSs use precise T1 fuzzy membership functions. Additionally, the parameters of these membership functions are fixed once the design process is completed.
On the other hand, T2 FLSs have the ability to be applied in many engineering areas in which these systems can deal with dynamic uncertainties [54]. Hence, T2 FLSs are better than T1 FLSs when facing dynamic uncertainties. The major difference depends on the model of individual fuzzy sets, which use membership degrees. Actually, these membership degrees are themselves fuzzy sets. Such new uncertainty dimension introduces additional degree of freedom. This degree of freedom has been provide for modeling and coping with dynamic input uncertainties. The input uncertainty should be carefully studied because it can promote the performance of the overall system. Although input uncertainty is not handled here, extra work can be added to enhance the performance by studying the input uncertainty.
B. Normalization
The output of the fuzzification step, e.g., the degree of membership of each input crisp value to the corresponding fuzzy set, is multiplied by the rank of the related feature calculated in the feature rank phase. For illustration, (WBC) is multiplied by FR(WBC), which resulted in a new value called ranked membership value to WBC fuzzy set and denoted as; (WBC). Hence, (WBC) (WBC) FR(WBC). The same is done for the remaining three membership degrees to the fuzzy sets LYM, MON, and LDH. Generally, the ranked membership value for the fuzzy set X is calculated by (8).
| (8) |
where the ranked membership value for the fuzzy set X, (X) is the degree of membership corresponding to X fuzzy set, and FR(X) is the rank of the feature corresponding to X fuzzy set. Through normalization step, the ranked membership values for each fuzzy set is normalized to obtain a value between 0.0 and 1.0. The normalized membership value for a fuzzy set X, denotes as (X) can be calculated by (9).
| (9) |
where The normalized membership value for a fuzzy set X, is the ranked membership value for the fuzzy set X, and is the ranked membership value for the fuzzy set .
C. Fuzzy Rule Induction
The output of the normalization step is the input for the fuzzy rule base. The considered rules are in the form; if (A is X) AND (B is Y) AND (C is Z) …… THEN (R is M), where A, B, and C represent the input variables (e.g., WBC, LYM, MON, and LDH), while X, Y, and Z represent the corresponding linguistic terms (e.g., low, medium, and high), R represents the rule output. The R.H.S of the rule (e.g., the part before THEN) is called “antecedent”, while the L.H.S (e.g., the part after THEN) is called “consequent”. 81 rules have been conducted, which are illustrated in Table 7, in which; ‘L’ refers to “Low”, ‘H’ refers to “High”, and ‘M’ refers to “Medium”. For illustration, the second rule in Table 7 indicates that; IF WBC(Item) is Low AND LYM(Item) is Low AND MON(Item) is Low AND LDH(Item) is Medium THEN Output is Low.
Table 7.
The considered fuzzy rules.
| ID | WBC | LYM | MON | LDH | Rule output | ID | WBC | LYM | MON | LDH | Rule output | ID | WBC | LYM | MON | LDH | Rule output |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | L | L | L | L | L | 28 | M | L | L | L | L | 55 | H | L | L | L | M |
| 2 | L | L | L | M | L | 29 | M | L | L | M | L | 56 | H | L | L | M | L |
| 3 | L | L | L | H | M | 30 | M | L | L | H | L | 57 | H | L | L | H | H |
| 4 | L | L | M | L | L | 31 | M | L | M | L | L | 58 | H | L | M | L | L |
| 5 | L | L | M | M | M | 32 | M | L | M | M | M | 59 | H | L | M | M | M |
| 6 | L | L | M | H | L | 33 | M | L | M | H | M | 60 | H | L | M | H | H |
| 7 | L | L | H | L | M | 34 | M | L | H | L | L | 61 | H | L | H | L | H |
| 8 | L | L | H | M | L | 35 | M | L | H | M | M | 62 | H | L | H | M | H |
| 9 | L | L | H | H | M | 36 | M | L | H | H | H | 63 | H | L | H | H | H |
| 10 | L | M | L | L | L | 37 | M | M | L | L | M | 64 | H | M | L | L | L |
| 11 | L | M | L | M | M | 38 | M | M | L | M | M | 65 | H | M | L | M | M |
| 12 | L | M | L | H | L | 39 | M | M | L | H | M | 66 | H | M | L | H | H |
| 13 | L | M | M | L | M | 40 | M | M | M | L | M | 67 | H | M | M | L | M |
| 14 | L | M | M | M | M | 41 | M | M | M | M | M | 68 | H | M | M | M | M |
| 15 | L | M | M | H | M | 42 | M | M | M | H | M | 69 | H | M | M | H | M |
| 16 | L | M | H | L | L | 43 | M | M | H | L | M | 70 | H | M | H | L | H |
| 17 | L | M | H | M | M | 44 | M | M | H | M | M | 71 | H | M | H | M | M |
| 18 | L | M | H | H | H | 45 | M | M | H | H | M | 72 | H | M | H | H | H |
| 19 | L | H | L | L | M | 46 | M | H | L | L | L | 73 | H | H | L | L | H |
| 20 | L | H | L | M | L | 47 | M | H | L | M | M | 74 | H | H | L | M | H |
| 21 | L | H | L | H | H | 48 | M | H | L | H | H | 75 | H | H | L | H | H |
| 22 | L | H | M | L | L | 49 | M | H | M | L | M | 76 | H | H | M | L | H |
| 23 | L | H | M | M | M | 50 | M | H | M | M | M | 77 | H | H | M | M | M |
| 24 | L | H | M | H | H | 51 | M | H | M | H | M | 78 | H | H | M | H | H |
| 25 | L | H | H | L | H | 52 | M | H | H | L | H | 79 | H | H | H | L | H |
| 26 | L | H | H | M | H | 53 | M | H | H | M | M | 80 | H | H | H | M | H |
| 27 | L | H | H | H | H | 54 | M | H | H | H | H | 81 | H | H | H | H | H |
Four different techniques of fuzzy rules inference can be considered, namely; max–min, max-product, drastic product, and sum-dot [10], [11]. The max–min technique is considered in this paper, which is based on choosing a min operator for the conjunction in the premise of the rule and for the implication function, on the other hand, the max operator is used for aggregation. For illustration, consider a simple case of two items of evidence per rule, then, the corresponding rules are illustrated in Table 8.
Table 8.
The fuzzy rules using two items of evidence per rule.
| Rule ID | Rule |
|---|---|
| 1 | IFANDTHEN |
| 2 | IFANDTHEN |
| … | … |
| N | IFANDTHEN |
Hence, the max–min compositional inference rule can be illustrated in (10), which yield (11).
| (10) |
| (11) |
D. Defuzzification
Generally, the output of the inference engine is a fuzzy set, however, crisp values are usually required for most real life applications. Accordingly, the output of the fuzzy rules should be defuzzified. Defuzzification process is the mapping from a fuzzy space of into a non-fuzzy space of actions. Several defuzzification techniques can be considered such as; mean of maxima, center-of-gravity, and max-criterion [10], [11]. To the best of our knowledge, the Center of Gravity (COG) method is the most popular one at which the weighted average of the area bounded by the membership function curve is considered the crisp value of the fuzzy quantity. According to the work in this paper, defuzzification has been done using the output membership function illustrated in Fig. 9. Hence, consider a person whose input parameters are; , LYM, MON, and . The result of the defuzzification process is a crisp value that combines evidence from the considered input parameters (e.g., features) and accordingly indicates the person’s Diagnosis Value (DV), which is denoted DV(p ).
Fig. 9.

The output membership function.
E. Decision Making
After calculating the diagnose value of the input case (person), it is needed to identify the initial belonging score of the input case to be classified into each class label (patient and normal). To accomplish such aim, a threshold diagnose value, and diagnostic constant are calculated, denoted as; DV and . Hence, once the diagnose value of the input case obtained, then the belonging score of the input case is determined. Consequently, the output can be interpreted as the probability of a particular input case (person) belonging to each of the considered classes. However, calculating the precise value of DV and are a challenge. Calculating DV and are carried out be empirically. Initially, a set of 2 training cases are prepared, which consists of equal number of COVID-19 patients and normal persons (e.g., cases for COVID-19 patients and cases for normal persons). The features (e.g., WBC, LYM, MON, and LDH) of each case is extracted. The corresponding diagnose value for each case in the set is calculated using the procedure illustrated in the previous subsections. Then, the average diagnose value is calculated, which constitutes the values of DV. Such scenario has been conducted using 200 case (), the calculated value for DV equals 5.836 and diagnostic constant () equals 2. A simple step function is used to estimate the belonging score of the input new case as illustrated in Fig. 10. DV calculation steps is illustrated in algorithm 1.
Fig. 10.
The output membership function.
5.3.2. Deep Neural Network (DNN)
Deep Neural Network (DNN) is an artificial neural network with multiple layers between input and outputs. It helps us to create a model and define its complex hierarchies in a simple form. Thus, DNN consists of input layer, n- hidden layers, and output layer in which each layer consists of nodes [55]. While the input layer receives input data, the hidden layers perform mathematical computations on the inputs. Number of nodes in input and output layer, bias, learning rate, initial weights for adjustment, number of hidden layers, number of nodes in every hidden layers, and stop condition for terminating the epochs while execution are the basic parameters used in DNN. In this paper, after the features are extracted and selected, the classification step using DNN with 5-hidden layers of processing is performed on the resulted feature vector to determine the belonging degree of the input item to be classified according to each class label. The used DNN model is illustrated in Fig. 11.
Fig. 11.
DNN architecture.
In DNN model, the bias value is assigned to be l, which is usually assigned to be 1 in any neural network to avoid nullified network results and learning rate is assigned as 0.15 which is the default value. Additionally, the initial weight of the nodes can be generated randomly and changed by the network during back propagation by calculating error rate and updated periodically after every epoch. Number of hidden layers and number of nodes in every hidden layer are decided based on the number of inputs and size of the data. Also, the termination condition is satisfied either reach the number of epochs or achieve the expected result from the learning model. In fact, the output is predicted as a probability, so sigmoid activation function is the right choice to train the model. Since probability of anything exists only between the range of 0 and 1, sigmoid is the best choice.
5.3.3. Final decision
Finally, it is the time to decide whether the person is infected or normal. To accomplish such aim, the final belonging degree for each considered class can be calculated by calculating the average value from the outputs of the two classifiers using (12), (13).
| (12) |
| (13) |
where (Infected) is the probability that the input case (person) is infected with Coronavirus, (Infected) is the output probability from fuzzy inference engine representing that the input case is infected with coronavirus, and (infected) is the output probability from DNN classifier representing that the person is infected with virus. Additionally, (Normal) is the probability that the input case (person) is uninfected with Coronavirus. (Normal) is the output probability from fuzzy inference engine representing that the person is uninfected with coronavirus, and (Normal) is the output probability from DNN classifier representing that the input case is uninfected with coronavirus. Finally, the input case is targeted to the class in which it has the maximum belonging score. According to (12), (13), the final decision is taken by calculating the average value from the outputs of the used classifiers to overcome the drawbacks of both classifiers in order to obtain the most accurate diagnosis. Fig. 12 shows in details the sequential steps that should be followed to calculate the diagnostic value for a person’s input case .
Fig. 12.
Illustrative example showing how to diagnose an input case for a person using the proposed HDS.
6. Experimental results
In this section, a new Hybrid Diagnosis Strategy (HDS) will be evaluated. HDS is implemented through three sequential phases, which are; Pre-processing, Feature Ranking, and classification. In pre-processing phase, outlier items are rejected and the best features are selected. Then, NB classifier has been implemented as a base classifier to assign a weight to each identified feature based on its effect on the classification accuracy. Accordingly, ineffective features are discarded using feature distiller. Then, the selected features from preprocessing phase are ranked during feature ranking phase to the next classification phase to quickly and correctly diagnose patients. Our implementation is based on a set of laboratory findings for COVID-19 and NON-COVID-19 patients [56]. This collected data (patients dataset) was used to produce the results presented in this paper. Due to the small number of available dataset, cross-validation is used to validate the classification model. In this paper, 10-fold cross-validation is used to divide the dataset into 10 equal partitions in which it uses one of these sets as a testing set and the remaining nine as training sets. Hence, the number of training and testing patients are 251 (90%) and 28 (10%) respectively. Table 9 shows the parameters applied with the corresponding used values.
Table 9.
The parameters applied with the corresponding used values.
| Parameter | Description | Applied value |
|---|---|---|
| for white blood cell | 2 | |
| for white blood cell | 4 | |
| for white blood cell | 6 | |
| for Lymphocyte | 6.5 | |
| for Lymphocyte | 12 | |
| for Lymphocyte | 19.5 | |
| for Monocytes | 0.5 | |
| for Monocytes | 1.3 | |
| for Monocytes | 2 | |
| for Locate Dehydrogenase | 450 | |
| for Locate Dehydrogenase | 530 | |
| for Locate Dehydrogenase | 650 | |
| for output (Diagnose) | 3 | |
| for output (Diagnose) | 6 | |
| o | for output (Diagnose) | 9 |
| Weighting factors | 1 | |
| 0.5 |
6.1. Dataset description
Dataset represents medical records of data collected on patients and contains a set of laboratory findings from various cases who have different ages, sex (male or female), and diseases. The number of the collected dataset equals 279 cases. In fact, the cases in the collected dataset are categorized into COVID-19 patients and non COVID-19 patients as presented in Table 10. COVID-19 patients are people who suffer from COVID-19 disease. On the other hand, non COVID-19 patients are people who do not suffer from COVID-19 disease. The number of used features in both training and testing datasets is twelve features routine blood exams. These features are; White Blood Cell (WBC), Alanine Aminotransferase (ALT), Lymphocytes (LYM), Basophils,….etc. as provided in [56]. The distribution of the used cases in the collected dataset has been represented according to “Age”, “Sex”, and “type of disease” as shown in Fig. 13, Fig. 14, Fig. 15.
Fig. 13.
The total number of cases according to age.
Fig. 14.
The total number of cases according to age and sex.
Fig. 15.
The presentation of COVID-19 patient and non COVID-19 patient distribution.
Table 10.
Dataset description.
| Criteria | Value/Description | ||||
|---|---|---|---|---|---|
| Total number of cases | Male | Female | |||
| 188 | 91 | ||||
| Sick cases | COVID-19 | Non COVID-19 | |||
| 177 | 102 | ||||
| COVID-19 patients | 20 | 20–40 | 41–60 | 61–80 | >80 |
| 5 | 9 | 63 | 78 | 22 | |
6.2. Evaluation parameters
During the following experiments; accuracy, error, precision, and sensitivity are four evaluation that will be calculated. Then, also F-measure, macro-average, and micro-average will be measured as additional criteria to clear the application results. To calculate the values of these measurements, a confusion matrix is applied as presented in Table 11. Noticeably, various formulas are used as a summarization of the confusion matrix as depicted in Table 12.
Table 12.
Confusion matrix formulas.
| Measure | Formula | Intuitive meaning |
|---|---|---|
| Precision (P) | TP/(TP FP) | The percentage of positive predictions those are correct. |
| Recall/ Sensitivity (R) |
TP/(TP FN) | The percentage of positive labeled instances that were predicted as positive. |
| Accuracy (A) | (TPTN)/(TP TN FP FN) | The percentage of predictions those are correct. |
| Error (E) | 1-Accuracy | The percentage of predictions those are incorrect. |
| Macro-average | “for Precision” | The average of the precision and recall of the system on different c classes. |
| “for Recall” | ||
| Micro-average | (TP1 TP2)/(TP1 TP2 FP1 FP2) “for precision” | The summation up to the individual true positives, false positives, and false negatives of the system for different classes and the apply them to get the statistics |
| (TP1 TP2)/(TP1 TP2 FN1 FN2) “for Recall” | ||
| F-measure | 2*PR/(P+R) | The weighted harmonic mean of Precision and Recall |
Table 11.
Confusion matrix.
| Predicted label |
|||
|---|---|---|---|
| Positive | Negative | ||
| Known label | Positive | True Positive (TP) | False Negative (FN) |
| Negative | False Positive (FP) | True Negative (TN) | |
6.3. Testing the proposed Hybrid Diagnosis Strategy (HDS)
During this subsection, it is the time to test the proposed HDS and the results are shown in Table 13, Table 14. Also, to argue the effectiveness of HDS, it is compared against some of the recently used COVID-19 classification methods as presented in Table 3. Those recent methods are DarkCovidNet [21], GMDH [22], KNNV [23], ADPM [24], CNN [25], and CPDS [26]. Additionally, the proposed HDS method was compared to the rule based method called Rule Based-Fuzzy Logic (RBFL) classifier [57]. Results are shown in Table 15, Table 16.
Table 13.
Performance of HDS in terms of accuracy, precision, recall, and error.
| Fold | Accuracy | Precision | Recall | Error |
|---|---|---|---|---|
| 1 | 98% | 97% | 97% | 2% |
| 2 | 96.86% | 96% | 96% | 3.14% |
| 3 | 96.86% | 95.5% | 95.5% | 3.14% |
| 4 | 98% | 97% | 97% | 2% |
| 5 | 98% | 97% | 97% | 2% |
| 6 | 98% | 96.6% | 96.5% | 2% |
| 7 | 96.86% | 95.86% | 95% | 3.14% |
| 8 | 98% | 97.5% | 97% | 2% |
| 9 | 98% | 97% | 96.5% | 2% |
| 10 | 98% | 98.1% | 98% | 2% |
| Average | 97.658% | 96.756% | 96.55% | 2.342% |
Table 14.
Performance of HDS in terms of Macro-average (precision& recall) and Micro-average (precision& recall), and F-measure.
| Fold | Macro-average precision | Macro-average recall | Micro-average precision | Micro-average recall | F-measure |
|---|---|---|---|---|---|
| 1 | 96% | 97% | 96.5% | 96.8% | 97% |
| 2 | 95.6% | 95.9% | 96% | 96% | 96% |
| 3 | 95% | 95.8% | 95% | 95% | 95% |
| 4 | 96.5% | 97% | 96.9% | 97.2% | 97% |
| 5 | 96.5% | 97% | 96.9% | 96.9% | 96.9% |
| 6 | 96% | 96.5% | 96.6% | 97% | 96.5% |
| 7 | 95.55% | 95.3% | 95.5% | 95.8% | 95.75% |
| 8 | 97.1% | 96.3% | 97.8% | 96.9% | 97% |
| 9 | 96% | 96% | 96.9% | 97% | 96.5% |
| 10 | 97.1% | 98% | 97% | 96.9% | 98.5% |
| Average | 96.135% | 96.44% | 96.51% | 96.55% | 96.615% |
Table 15.
Comparison between HDS and the existing classification technique in terms of accuracy, precision, recall, and error.
| Used technique | Accuracy | Precision | Recall | Error |
|---|---|---|---|---|
| DarkCovidNet | 84.26% | 85.6% | 82.5% | 15.74% |
| GMDH | 92.48% | 93% | 91.4% | 7.52% |
| KNNV | 91.5% | 92.3% | 93.6% | 8.5% |
| ADPM | 90.4% | 89.9% | 89.9% | 9.6% |
| CNN | 85.6 | 87.42% | 85.6% | 14.4% |
| CPDS | 94.9% | 90.86% | 91% | 5.1% |
| RBFL | 95.97% | 92.6% | 93.48% | 4.03% |
| HDS | 97.658% | 96.756% | 96.5% | 2.342% |
Table 16.
Comparison between HDS and the existing classification technique in terms of Macro-average (precision& recall), Micro-average (precision& recall), and F-measure.
| Used technique | Macro-average precision | Macro-average recall | Micro-average precision | Micro-average recall | F-measure |
|---|---|---|---|---|---|
| DarkCovidNet | 83% | 84.6% | 82% | 87.6% | 82.5% |
| GMDH | 92% | 90% | 90.6% | 89.95% | 90.3% |
| KNNV | 89.5% | 85.7% | 87.6% | 88.5% | 90.1% |
| ADPM | 89.5% | 88.9% | 87.98% | 89.56% | 83% |
| CNN | 85.7 | 86.4% | 83.6% | 83.9% | 87% |
| CPDS | 90.1% | 92.16% | 91.8% | 89.8% | 93.42% |
| RBFL | 94.7% | 93.6% | 93. 8% | 94.7%% | 94.8%% |
| HDS | 96.035% | 96.42% | 96.5% | 96.52 | 96.615% |
As shown in Table 13, Table 14, the results are presented for each fold, and the average values are also calculated. Table 13 presents the accuracy, precision, recall, and error for HDS to detect COVID-19 patient. The average accuracy is 97.658% while the average value of error is 2.342%. As presented in Table 13, the lower performance values of the HDS model are presented for 2, 3, and 7-fold, while the best values are presented for 1,4,5,6,8,9, and 10-fold. The lower precision values are introduced in the 3- fold and 7-fold with values equal 95.5%, and 95.86% respectively. Moreover, the lower recall value is 95% in 7-fold. The least value of F-measure is 95% occurred in the 3-fold. The average precision, recall, and F-measure are 96.756%, 96.55%, and 96.615%. Additionally, the average values of macro-average precision and macro-average recall are 96.135% and 96.44% respectively. The average values of micro-average precision and micro-average recall are 96.51% and 96.55% respectively as presented in Table 14.
According to Table 15, Table 16, HDS is much better than DarkCovidNet, GMDH, KNNV, ADPM, CNN, CPDS and RBFL. The reason is that the proposed HDS does not depend on the original features, but it depends on most informative features which are selected by using a very accurate method, which is wrapper method therefore, it increased the accuracy and helped the classifiers to give a quick and accurate decision to detect COVID-19 patients. The receiver operating characteristic is presented in Fig. 16. Finally, HDS is much better than other recent methods according to many metrics of measurement as it has the ability to quickly and accurately diagnose COVID-19 patients. Also, HDS is more simple, flexible, and able to manage problems with inaccurate data. HDS has proven to be a safe decision-making system for detecting COVID-19 patients. Consequently, it protects the healthcare system from becoming overwhelmed.
Fig. 16.
ROC curve of the validation testing.
6.4. Statistical tests
Measuring model performance should be validated statistically. Therefore, Friedmann test and Wilcoxon Signed Rank Test (WSRT) are applied to compare and analyze the predictive capability of the proposed strategy [58]. The Wilcoxon signed-rank test was performed at 5% significant level and 95% confidence intervals. The results of Wilcoxon signed-rank test are shown in Table 17. In this analysis, a null hypothesis was assumed that there is no significant difference between mean values of the two strategies. This statistical analysis was implemented in Minitab software. The results showed that p value is less than 0.05 (5% significance level) which is a strong evidence against the null hypothesis. It means that there is a statistical difference between the proposed strategy and other strategies. It can be concluded that, the proposed hybrid diagnose strategy has a performance effectiveness better than other traditional strategies for detecting COVID-19 patients. Additionally, Friedman test metric is a non-parametric statistical tool that ranks the performance of the each strategy. This approach would determine the difference between the proposed HDS and DarkCovidNet, GMDH, KNNV, ADPM, CNN, CPDS, and RBFL at significant level (.05). The results are presented in Table 18.
Table 17.
WSRT results.
| Model 1 vs. Model 2 | WSRT | p- value | Estimated median difference |
|---|---|---|---|
| HDS vs. DarkCovidNet | 0.0 | 0.00 | 0.003 |
| HDS vs. GMDH | 0.0 | 0.00 | 0.0017 |
| HDS vs. KNNV | 0.0 | 0.00 | 0.0018 |
| HDS vs. ADPM | 0.0 | 0.00 | 0.0025 |
| HDS vs. CNN | 0.0 | 0.00 | 0.0031 |
| HDS vs. CPDS | 0.0 | 0.00 | 0.0016 |
| HDS vs. RBFL | 0.0 | 0.00 | 0.0015 |
Table 18.
Friedman mean ranking.
| Used technique | Rank |
|---|---|
| DarkCovidNet | 6.0 |
| GMDH | 2.3 |
| KNNV | 3.36 |
| ADPM | 3.8 |
| CNN | 4.8 |
| CPDS | 2.1 |
| RBFL | 1.5 |
| HDS | 1.2 |
The results showed that the p value is less than 0.05. As shown in Table 18, it concluded that there is a difference between the proposed HDS and other traditional strategies. The proposed HDS achieves the best rank among all. It means that the effectiveness of the proposed HDS is better than other traditional strategies.
6.5. Testing HDS using different feature selection techniques
In this subsection, the proposed Hybrid Diagnose Strategy (HCD) will be tested using different features selection techniques which are; are Hybrid Fuzzy ARTMAP and Brain storm optimization (FAR-BSO) [59], Opposition-based Crow Search (OCS) algorithm [60], Filter–Wrapper Feature Subset Selection (FWFSS) [61], and Parallelized hybrid feature selection (HFS) [62] to prove the effectiveness of the used feature selection method with the proposed strategy. Consequently, the used feature selection method in our proposed strategy will be replaced with different features selection techniques. Results are depicted in Table 19, Table 20.
Table 19.
Comparison between HDS with different feature selection techniques in terms of accuracy, precision, recall, and error.
| Used technique | Accuracy | Precision | Recall | Error |
|---|---|---|---|---|
| Method1: HDS-(FAR-BSO) | 90.4% | 86.5% | 84.5% | 9.6% |
| Method 2: HDS-OCS | 92.98% | 92.9% | 92.4% | 7.02% |
| Method 3: HDS-FWFSS | 93.8% | 93.4% | 93.6% | 6.2% |
| Method 4: HDS-HFS | 95.5% | 94.9% | 93.9% | 4.5% |
| HDS | 97.658% | 96.756% | 96.5% | 2.342% |
Table 20.
Comparison between HDS with different feature selection techniques e in terms of Macro-average (precision& recall), Micro-average (precision& recall) and F- measure.
| Used technique | Macro-average precision | Macro-average recall | Micro-average precision | Micro-average recall | F-measure |
|---|---|---|---|---|---|
| Method1: HDS-(FAR-BSO) | 85% | 86.6% | 85.9% | 89.6% | 86.5% |
| Method 2: HDS-OCS | 93% | 91% | 90.6% | 89.95% | 90.9% |
| Method 3: HDS-FWFSS | 93.5% | 94.7% | 91.46% | 90.5% | 91.1% |
| Method 4: HDS-HFS | 94.5% | 94.9% | 92.08% | 92.56% | 92.8% |
| HDS | 96.035% | 96.42% | 96.5% | 96.52 | 96.615% |
As presented in Table 19, Table 20, the results are presented for the proposed strategy using different feature selection techniques. Table 19, presents the accuracy, precision, recall, and error for each method. According to Table 19, each of HDS-(FAR-BSO), HDS-OCS, HDS-FWFSS, HDS-HFS, and HDS provides about 90.4%, 92.98%, 93.8%, 95.5%, and 97.658% accuracy respectively. These methods also provide at the same order about 9.6%, 7.02%, 6.2%, 4.5%, and 2.342% error. The precision values of them are 86.5%, 92.9%, 93.4%, 94.9% and 96.756% respectively. Finally, the recall values of them are 84.5%, 92.4%, 93.6%, 93.9%, and 96.5% respectively. According to Table 19, it is noticed that; the proposed FCDS demonstrates the maximum “Accuracy”, “Precision”, “Recall”, and the minimum “Error”. The reason is that the proposed HDS does not depend on the original features, but it depends on most informative features which are elected by using a very accurate method, which is wrapper method therefore, it increased the accuracy and helped the classifier to give a quick and accurate decision to detect COVID-19 patients. As shown in Table 20, HDS is much better than HDS-(FAR-BSO), HDS-OCS, HDS-FWFSS, and HDS-HFS. HDS introduces the highest macro-average precision, macro-average recall, micro-average precision, micro-average recall, and F- measure.
7. Conclusions
COVID-19 infection was grown at rapid rate and still threatens the lives of billions of people. Therefore, early detection of COVID-19 patients is a vital for disease cure and control. The literature review work shows that no optimal technique can be determined yet. Generally, there are three types of COVID-19 diagnose, which are; (i) using RT-PCR test, (ii) using CT test, and (iii) using numerical laboratory tests. The first two diagnose methods are based on nominal data for diagnosing COVID-19. However, recent studies have proven that the use of such nominal tests may suffer from false positive or false negative, which will degrades COVID-19 diagnose accuracy. We have decided to rely on the numerical laboratory tests which are based on accurate numerical data.
In this work, fast and accurate diagnose strategy based on patients laboratory findings was introduced. In our diagnose strategy, Hybrid Diagnose Strategy (HDS) relied on three essential parts, which are; pre-processing, feature ranking, and classification phase. In pre-processing, the outlier items are rejected and the most informative features are selected using wrapper method that use a classification performance of NB classifier to evaluate features. Then, the selected features have been ranked based on its weight, and convergence to its friends to enable classification model to make a quick and accurate decision. Experimental results showed that the proposed HDS provides fast and accurate results comparing to other recent methods in terms of accuracy, error, precision, sensitivity/recall, macro-average, micro-average, and F-measure.
As a future work, the element of uncertainty is one of the biggest challenges in the field of engineering. Studying the input uncertainty can be added to the work introduced in this paper, which refers to the effect of driving a simulation with input distributions that are based on real-world data. This will have a great effect in promoting the performance of the overall system.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors are so pleased to introduce their great thanks to all staff members of Nile higher institute for engineering and technology for the great support. Most of the work introduced in this paper has been done in the laboratories of the institution. Special thanks of gratitude to doctor Salah Abd Elghafar Mansour for his endless support and kindness.
References
- 1.Zaim S., Chong J., Sankaranarayanan V., Harky A. COVID-19 and Multiorgan response. Curr. Probl. Cardiol. 2020;45(8):1–22. doi: 10.1016/j.cpcardiol.2020.100618. Elsevier. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Rubin G., Ryerson C., Haramati L. The role of Chest imaging in patient management during the COVID-19 Pandemic: A multinational consensus statement from the Fleischner Society. Radiology. 2020:172–180. doi: 10.1148/radiol.2020201365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wang Y., Kang H., Liu X., Tong Z. Combination of RT-PCR testing and clinical features for diagnosis of COVID-19 facilitates management of SARS-CoV-2 outbreak. J. Med. Virol. 2020;22(6):538–539. doi: 10.1002/jmv.25721. Wiley. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Li Y., Yao L., Li Jiawei, Chen Lei. Stability issues of RT-PCR testing of SARS-CoV-2 for hospitalized patients clinically diagnosed with COVID-19. J. Med. Virol. 2020:1–6. doi: 10.1002/jmv.25786. Wiley. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Li L., Qin L., Xu Z. Using artificial intelligence to Detect COVID-19 and Community-acquired Pneumonia based on pulmonary CT: Evaluation of the diagnostic accuracy. Radiology. 2020;296(2):65–72. doi: 10.1148/radiol.2020200905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bertone E., JuncaL L. Effectiveness of the early response to COVID-19: Data analysis and modelling. Syst. Multidiscip. Digit. Publ. Inst. (MDPI) 2020;8(2):1–17. doi: 10.3390/systems8020021. [DOI] [Google Scholar]
- 7.Aydin N., Yurdakul G. Assessing countries’ performances against COVID-19 via WSIDEA and machine learning algorithms. Appl. Soft Comput. 2020;97:1–18. doi: 10.1016/j.asoc.2020.10679. Elsevier. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gayathri G., Satapathy S. A survey on techniques for prediction of Asthma. Smart Intell. Comput. Appl. 2020;159:751–758. doi: 10.1007/978-981-13-9282-5_72. Springer. [DOI] [Google Scholar]
- 9.Pegoraro F., Santos E. A hybrid model to support decision making in emergency department management. Knowl. Based Syst. 2020;203:1–16. doi: 10.1016/j.knosys.2020.106148. Elsevier. [DOI] [Google Scholar]
- 10.Rabie A., Ali S., Ali H., Saleh A. A fog based load forecasting strategy for smart grids using big electrical data. Cluster Comput. 2019;22(1):241–270. doi: 10.1007/s10586-018-2848-x. Springer. [DOI] [Google Scholar]
- 11.Rebrovs O., Kuļešova G. Comparative analysis of fuzzy set Defuzzification Methods in the context of ecological risk assessment. Inf. Technol. Manage. Sci. J. Riga Tech. Univ. 2017;20(1):25–29. doi: 10.1515/itms-2017-0004. [DOI] [Google Scholar]
- 12.Liu Y., Liu B. A mixture of variational canonical correlation analysis for nonlinear and quality-relevant Process Monitoring. IEEE Trans. Ind. Electron. 2018;65(8):6478–6486. doi: 10.1109/TIE.2017.2786253. [DOI] [Google Scholar]
- 13.Awotunde1 J., Matiluko O., Fatai O. Medical diagnosis system using fuzzy logic. Afr. J. Comput. ICT. 2014;7(2):99–106. IEEE, https://eprints.lmu.edu.ng/id/eprint/185. [Google Scholar]
- 14.El Asnaoui K., Chawki Y. Using X-ray images and deep learning for automated detection of coronavirus disease. J. Biomol. Struct. Dyn. 2020:1–12. doi: 10.1080/07391102.2020.1767212. Taylor and Francis. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Barstugan M., Ozkaya U., Ozturk S. 2020. Coronavirus (COVID-19) Classification using CT images by machine learning methods; pp. 1–10. arXiv preprint arXiv:2003.09424, https://arxiv.org/abs/2003.09424. [Google Scholar]
- 16.Brunese L., Mercaldo A. Reginelli F., Santone A. Explainable deep learning for Pulmonary Disease and coronavirus COVID-19 detection from X-rays. Comput. Methods Programs Biomed. 2020;196:1–11. doi: 10.1016/j.cmpb.2020.105608. Elsevier. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.slam Z., Asraf A. A combined deep CNN-LSTM network for the detection of novel coronavirus (COVID-19) using X-ray images. Inform. Med. Unlocked. 2020;20:1–11. doi: 10.1016/j.imu.2020.100412. Elsevier. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Salehi A., Baglat P., Gupta G. Review on machine and deep learning models for the detection and prediction of Coronavirus. Mater. Today: Proc. 2020:1–6. doi: 10.1016/j.matpr.2020.06.245. Elsevier. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Apostolopoulos I., Mpesiana T. Covid-19: automatic detection from X-ray images utilizing transfer learning with convolutional neural networks. Phys. Eng. Sci. Med. 2020;43:635–640. doi: 10.1007/s13246-020-00865-4. Springer. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Guo L., Ren L., Yang S., Xiao M. Profiling early humoral response to Diagnose Novel Coronavirus Disease (COVID-19) Clin. Infect. Dis. 2020:1–8. doi: 10.1093/cid/ciaa310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ozturk T., Talo M., Yildirim E. Automated detection of COVID-19 cases using deep neural networks with X-ray images. Comput. Biol. Med. 2020;121:1–11. doi: 10.1016/j.compbiomed.2020.103792. Elsevier. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Pirouz B., Haghshenas S., Haghshenas S., Piro P. Investigating a Serious challenge in the sustainable development process: Analysis of confirmed cases of COVID-19 (new type of Coronavirus) through a binary classification using artificial intelligence and regression analysis. Sustainability. 2020;2(6):1–22. doi: 10.3390/su12062427. [DOI] [Google Scholar]
- 23.Hamed A., Sobhy A., Nassar H. 2020. Accurate classification of COVID-19 based on incomplete heterogeneous data using a KNN variant Algorithm; pp. 1–13. Research Square, Preprints, https://www.researchsquare.com/article/rs-27186/v1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gozes O., Frid-Adar M., Greenspan H. 2020. Rapid AI development cycle for the coronavirus (COVID-19) Pandemic: Initial results for automated detection & patient monitoring using deep learning CT image analysis; pp. 1–22. arXiv preprint, https://arxiv.org/abs/2003.05037. [Google Scholar]
- 25.Marques G., Agarwal D., Diez I. Automated medical diagnosis of COVID-19 through Efficientnet convolutional neural network. Appl. Soft Comput. 2020;96:1–11. doi: 10.1016/j.asoc.2020.106691. Elsevier. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Shaban W., Rabie A., Saleh A. A new COVID-19 Patients Detection Strategy (CPDS) based on hybrid feature selection and enhanced KNN classifier. Knowl. Based Syst. 2020;205:1–18. doi: 10.1016/j.knosys.2020.106270. Elsevier. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Piva S., Filippini M. Clinical presentation and initial management critically ill patients with severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infection in Brescia, Italy. J. Crit. Care. 2020;58:29–33. doi: 10.1016/j.jcrc.2020.04.004. Elsevier. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Singhal T. A review of Coronavirus disease-2019 (COVID- 2019) Indian J. Pediatrics. 2020;87(4):281–286. doi: 10.1007/s12098-020-03263-6. Springer. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Fan L., Liu S. CT and COVID-19: Chinese experience and recommendations concerning detection, staging and follow-up. Eur. Radiol. 2020;30:5214–5216. doi: 10.1007/s00330-020-06898-3. Springer. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Tahamtan A., Ardebili A. Real-time RT-PCR in COVID-19 detection: issues affecting the results. Expert Rev. Mol. Diagn. 2020;20(5):453–454. doi: 10.1080/14737159.2020.1757437. Taylor & Francis. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ye Z., Zhang Y. Chest CT manifestations of new coronavirus disease 2019(COVID-19): a pictorial review. Eur. Radiol. 2020;30:4381–4389. doi: 10.1007/s00330-020-06801-0. Springer. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Inui S., Fujikawa A., Jitsu M. Chest CT findings in cases from the Cruise ship Diamond princess, with Coronavirus Disease 2019 (COVID-19) Radiol.: Cardiothorac. Imaging. 2020;2(2):1–17. doi: 10.1148/ryct.2020200110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Yang R., Li X., Liu H. Chest CT severity score: An imaging tool for assessing severe COVID-19. Radiol.: Cardiothorac. Imaging. 2020;2(2):1–23. doi: 10.1148/ryct.2020200047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Xia W., Shao J., Guo Y. Clinical and CT features in pediatric patients with COVID-19 infection: Different points from adults. Pediatr. Pulmonol. 2020:1–6. doi: 10.1002/ppul.24718. Wiley Online Library. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Derakhshanfar H., Sobouti B., Fallah S. A review on the effect of Coronavirus infections on respiratory problems in Children. J. Crit. Rev. 2020;7(7):1–5. doi: 10.31838/jcr.07.07.205. [DOI] [Google Scholar]
- 36.Brinati D., Compagner A. Detecting of COVID-19 infection from routine blood exams with machine learning: A feasibility study. J. Med. Syst. 2020;44:1–12. doi: 10.1101/2020.04.22.20075143. Springer. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ferrari D., Motta A., Strollo M. Routine blood tests as a potential diagnostic tool for covid-19. Clin. Chem. Lab. Med. 2020;85(7):1095–1099. doi: 10.1515/cclm-2020-0398. [DOI] [PubMed] [Google Scholar]
- 38.Qiu P., Zhou Y., Wang F. Clinical characteristics, laboratory outcome characteristics, comorbidities, and complications of related COVID-19 deceased: a systematic review and meta-analysis. Aging Clin. Exp. Res. 2020;32:869–1878. doi: 10.1007/s40520-020-01664-3. Springer. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Cabitza F., Campagner A., Ferrari D. Development, evaluation, and validation of machine learning models for COVID-19 detection based on routine blood tests. Clin. Chem. Lab. Med. (CCLM) 2020:1–11. doi: 10.1515/cclm-2020-1294. [DOI] [PubMed] [Google Scholar]
- 40.Patel A., Jernigan D. Initial public health response and interim clinical guidance for the 2019 novel coronavirus outbreak—United States, December 31, 2019–February 4, 2020. Morb. Mortal. Wkly. Rep. (MMWR) 2020;69(5):140–146. doi: 10.15585/mmwr.mm6905e1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Abdel-Basset M., Mohamed R., Elhoseny M. A hybrid COVID-19 detection model using an improved marine predators algorithm and a ranking-based diversity reduction strategy. IEEE Access. 2020;8:79521–79540. doi: 10.1109/ACCESS.2020.2990893. IEEE. [DOI] [Google Scholar]
- 42.Al-qaness M., Ewees A., Fan H., Abd El Aziz M. Optimization Method for forecasting Confirmed cases of COVID-19 in China. J. Clin. Med. 2020;9(3):1–15. doi: 10.3390/jcm9030674. Multidisciplinary Digital Publishing Institute (MDPI) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hazarika B., Gupta D. Modelling and forecasting of COVID-19 spread using wavelet-coupled random vector functional link networks. Appl. Soft Comput. 2020;96:1–17. doi: 10.1016/j.asoc.2020.106626. Elsevier. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Rabie A., Saleh A., Abo-Al-Ez K. A new strategy of load forecasting technique for smart grids. Int. J. Mod. Trends Eng. Res. (IJMTER) 2015;2(12):332–341. https://ijmter.com/papers/volume-2/issue-12/a-new-strategy-of-load-forecasting-technique-for-smart-grids-2.pdf. [Google Scholar]
- 45.Saleh A., Rabie A., Abo-Al-Ezb K. A data mining based load forecasting strategy for smart electrical grids. Adv. Eng. Inform. 2016;30(3):422–448. doi: 10.1016/j.aei.2016.05.005. Elsevier. [DOI] [Google Scholar]
- 46.Rabie A., Ali S., Saleh A., Ali H. A new outlier rejection me thodology for supporting load forecasting in smart grids based on big data. Cluster Comput. 2019:1–27. doi: 10.1007/s10586-019-02942-0. Springer. [DOI] [Google Scholar]
- 47.Rabie A., Ali S., Saleh A., Ali H. A fog based load forecasting strategy based on multi-ensemble classification for smart grids. J. Ambient Intell. Hum. Comput. 2020;11(1):209–236. doi: 10.1007/s12652-019-01299-x. Springer. [DOI] [Google Scholar]
- 48.Duraj A., Chomątek Ł. Outlier detection using the multiobjective Genetic Algorithm. J. Appl. Comput. Sci. 2017;25(2):29–42. doi: 10.34658/jacs.2017.2.29-42. [DOI] [Google Scholar]
- 49.Ansari G., Ahmad T., Doja M. Hybrid Filter–Wrapper feature selection method for sentiment classification. Arab. J. Sci. Eng. 2019;44:9191–9208. doi: 10.1007/s13369-019-04064-6. Springer. [DOI] [Google Scholar]
- 50.Wang L., Meng J., Huang R. Incremental feature weighting for fuzzy feature selection. Fuzzy Sets Syst. 2019;368:1–19. doi: 10.1016/j.fss.2018.10.021. Elsevier. [DOI] [Google Scholar]
- 51.Zhanga L., Jiang L., Li C. Two feature Weighting approaches for Naive Bayes text classifiers. Knowl. Based Syst. 2016;100:137–144. doi: 10.1016/j.knosys.2016.02.017. Elsevier. [DOI] [Google Scholar]
- 52.Farkas L., Moens D., Vandepitte D. Fuzzy finite element analysis based on reanalysis technique. Struct. Saf. 2010;32(6):442–448. doi: 10.1016/j.strusafe.2010.04.004. Elsevier. [DOI] [Google Scholar]
- 53.He L., Huang H., Du L. A review of possibilistic approaches to reliability analysis and optimization in engineering design. Hum. Comput. Interact. 2007;4553:1075–1084. doi: 10.1007/978-3-540-73111-5_118. Springer. [DOI] [Google Scholar]
- 54.Zadeh L. Fuzzy logic = computing with words. IEEE Trans. Fuzzy Syst. 1996;4(2):103–111. doi: 10.1109/91.493904. [DOI] [Google Scholar]
- 55.Mohsen H., El-Dahshan E., El-Horbaty et.al E. Classification using deep learning neural networks for brain tumors. Future Comput. Inform. J. 2018;3(1):68–71. doi: 10.1016/j.fcij.2017.12.001. Elsevier. [DOI] [Google Scholar]
- 56.Zenodo . 2020. https://zenodo.org/record/3886927#.X0gYnnWxXIV. [Last Access: 1 September, 2020] [Google Scholar]
- 57.Reddy G., Khare N. Heart disease classification system using optimized fuzzy rule based algorithm. Int. J. Biomed. Eng. Technol. 2018;27(3):183–201. doi: 10.1504/IJBET.2018.094122. Science Publishing Group. [DOI] [Google Scholar]
- 58.Ribeiro M., Coelho L. Ensemble approach based on bagging, boosting and stacking for short-term prediction in agribusiness time series. Appl. Soft Comput. 2020;86:1–17. doi: 10.1016/j.asoc.2019.105837. Elsevier. [DOI] [Google Scholar]
- 59.Pourpanah F., Shi Y., Lim Ch. Feature selection based on brain storm optimization for data classification. Appl. Soft Comput. 2019;80:761–775. doi: 10.1016/j.asoc.2019.04.037. Elsevier. [DOI] [Google Scholar]
- 60.Raj R., Shobana S., Pustokhina I., Shankar H. Optimal feature selection-based medical image classification using deep learning model in Internet of Medical Things. IEEE Access. 2020;8:58006–58017. doi: 10.1109/ACCESS.2020.2981337. [DOI] [Google Scholar]
- 61.Shukla A., Singh P., Vardhan M. A hybrid framework for optimal feature subset selection. J. Intell. Fuzzy Syst. 2019;36(2):2247–2259. doi: 10.3233/JIFS-169936. IOS Press. [DOI] [Google Scholar]
- 62.Venkataramana L., Jacob S., Ramadoss R. Improving classification accuracy of cancer types using parallel hybrid feature selection on microarray gene expression data. Genes Genom. 2019;41:1301–1313. doi: 10.1007/s13258-019-00859-x. Springer. [DOI] [PubMed] [Google Scholar]