Skip to main content
PMC home page
Patterns logoLink to Patterns
. 2020 May 4;1(3):100035. doi: 10.1016/j.patter.2020.100035

A Random Matrix Theory Approach to Denoise Single-Cell Data

Luis Aparicio 1,2,4, Mykola Bordyuh 1,2,4, Andrew J Blumberg 3, Raul Rabadan 1,2,5,∗
PMCID: PMC7660363  PMID: 33205104

Summary

Single-cell technologies provide the opportunity to identify new cellular states. However, a major obstacle to the identification of biological signals is noise in single-cell data. In addition, single-cell data are very sparse. We propose a new method based on random matrix theory to analyze and denoise single-cell sequencing data. The method uses the universal distributions predicted by random matrix theory for the eigenvalues and eigenvectors of random covariance/Wishart matrices to distinguish noise from signal. In addition, we explain how sparsity can cause spurious eigenvector localization, falsely identifying meaningful directions in the data. We show that roughly 95% of the information in single-cell data is compatible with the predictions of random matrix theory, about 3% is spurious signal induced by sparsity, and only the last 2% reflects true biological signal. We demonstrate the effectiveness of our approach by comparing with alternative techniques in a variety of examples with marked cell populations.

Keywords: single cell, random matrix theory, universality, eigenvector localization, denoising, sparsity

Graphical Abstract

graphic file with name fx1.jpg

Open in a new tab

Highlights

  • •

    Sparse random matrix theory provides a suitable framework to study single-cell biology

  • •

    Eigenvector localization disentangles sparsity-induced signals from biological signals

  • •

    95% of the information is a random matrix, 3% sparsity-induced signal, and 2% true signal

  • •

    The method improves clustering and identification of cell populations

The Bigger Picture

Single-cell technologies are able to capture information of a biological system cell by cell. Such a level of precision is changing the way we understand complex systems such as cancer or the immune system. However, a major challenge in studying single-cell systems and their underlying biological phenomena is their inherently noisy nature due to their complexity. Random matrix theory is a field with many applications in different branches of mathematics and physics. In the words of one of its developers, the theoretical physicist Freeman Dyson, it describes a “black box in which a large number of particles are interacting according to unknown laws.” A complex system with a large number of components (such as genes, biomolecules, or cells) interacting according to unknown laws is the epitome of systems biology. Therefore, random matrix theory looks like a suitable framework to mathematically describe the noise and complexity of gene-cell expression data coming from single-cell biology.

We demonstrate the effectiveness of (sparse) random matrix theory for studying the spectrum of the covariance matrix of single-cell genomic data. We show that single-cell data have a 3-fold structure: a random matrix, a sparsity-induced signal, and a biological signal. Most of the spectrum follows the expectations from random matrix theory (95%), but there exist deviations due to artifacts generated by a sparsity-induced signal (∼3%) and a biological signal (∼2%).

Introduction

Characterizing different cellular subtypes in heterogeneous populations and describing their evolution plays a central role in understanding complex systems such as cancer or the immune system. Single-cell technologies offer the opportunity to identify previously unreported cell types and cellular states and explore the relationship between new and known cell states.1, 2, 3, 4, 5, 6, 7 However, there exist several significant biological and technical challenges that complicate the analysis. The first challenge is the lack of a complete quantitative understanding of the different sorts of noise that arise in single-cell measurements, such as intrinsic cell-to-cell variability and spatial and temporal fluctuations within a cell. Moreover, different technologies show biases arising from the process of detecting, amplifying, and sequencing genomic material that significantly vary across different genomic loci. Correctly estimating noise and distinguishing between biological and technical sources of signal is essential for any further analysis, otherwise it is difficult to reliably distinguish states or identify potential variations of a single state. A second complicating factor for single-cell analysis is the sparsity of data (i.e., the large fraction of zero values in the original data matrix), typically caused by the very small amounts of genomic material being amplified.

A number of computational and statistical approaches have been designed to address these challenges.4,8, 9, 10, 11, 12, 13 Imputation methods try to infer the “true” expression levels of missing values from the sample data by empirically modeling the underlying distributions; for instance, using negative binomial plus zero inflation (dropout) for single-cell data. These techniques usually assume that all values are generated by the same distribution (i.e., they assume independent and identically distributed random variables, or i.i.d.). Although there have been efforts to understand the intrinsic stochastic nature of gene expression,14,15 we currently do not have predictive quantitative models of gene expression. Therefore, it is not clear what the correct distribution is, or whether it is reasonable to make the i.i.d. assumption. Given the lack of a quantitative microscopic description of cell transcription, we would ideally like to have a statistical description of the noise in single-cell data that does not rely on specific details of the underlying distributions of expression.

Universality and Random Matrix Theory in Single-Cell Biology

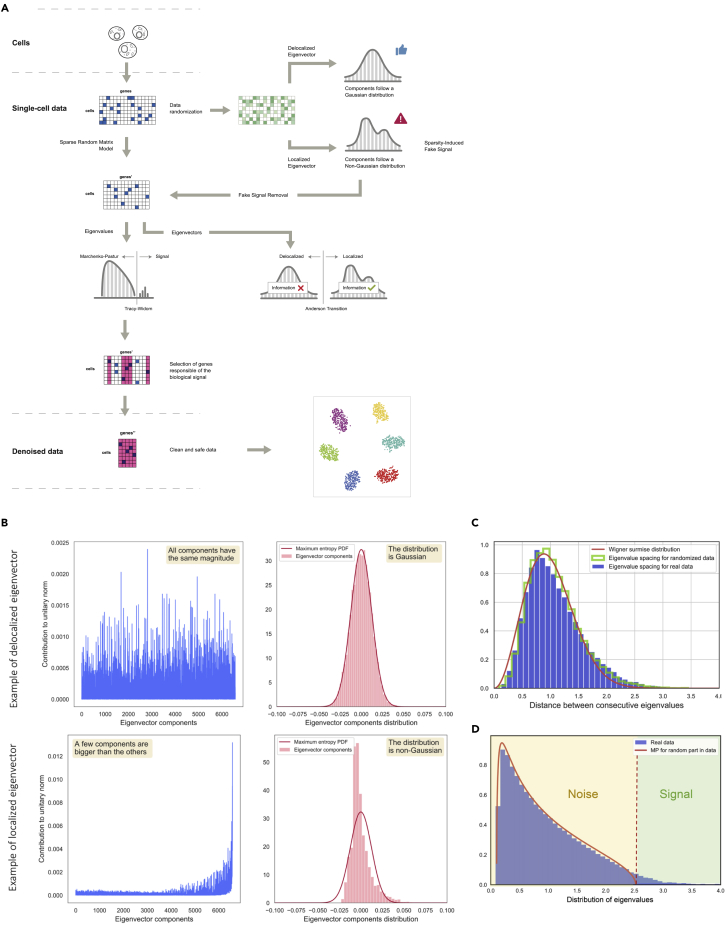
Historically a similar problem arose in the 1950s in nuclear physics, when the lack of quantitative models of complex nuclei precluded accurate predictions of their energy levels. However, simple theoretical models based on experimental data showed that some observables, such as the spacing between two consecutive energy levels, followed distributions that could be derived from random matrices, i.e., matrices whose entries are independently sampled from a given probability distribution.16, 17, 18 The same distributions were subsequently identified in a variety of complex systems including quantum versions of chaotic systems19 and patterns of zeros of the Riemann zeta function.20,21 In this paper, we show that these distributions also appear in the context of single-cell biology and that their properties can be used to denoise single-cell data (Figure 1A).

Figure 1.

Figure 1

Open in a new tab

Random Matrix Theory Applications to Single-Cell Sequencing Data

(A) Schematic of the analysis based on random matrix theory (RMT). Single-cell data can be modeled using sparse random matrix theory (sRMT), showing a 3-fold structure: a random matrix, a sparsity-induced signal, and a biological signal. The strategy proposed here is to identify the biological signal using the predictions from sRMT applied to the covariance matrix of the data.

(B) Deviations from the Tracy-Widom (TW) distribution have been associated to the phenomenon of eigenvector localization. Delocalized eigenvectors are randomly distributed in an N sphere, whereas localized eigenvectors are localized along some directions in the N sphere. Localization can be identified as deviations in components of the eigenvectors from the expected distribution, which is approximately Gaussian in high dimensions. If we think of the components of the eigenvector as a random variable, its probability density function (PDF) (the Gaussian) corresponds to a maximum entropy PDF.

(C) The Wigner surmise distribution captures the spacing between eigenvalues of Wishart matrix across single-cell RNA-sequencing experiments.

(D) Departures from universal distributions predicted by RMT indicate interesting potential biological signals. In red is the non-parametric Marchenko-Pastur (MP) distribution. Deviations from universality can be found by analyzing the larger eigenvalues in relation to the expected TW distribution.

Random matrix theory (RMT) studies the statistical properties of the eigenvalues and eigenvectors of an ensemble of random matrices. These statistical properties exhibit a phenomenon known as universality, where under mild hypotheses the specific details of the underlying probability distribution generating the entries of the matrix become irrelevant (akin to the central limit theorem).22,23 Specifically, the observed distributions depend only on the finiteness of the first few moments of the distribution generating the matrix entries.24, 25, 26 RMT universality implies that the density of eigenvalues of covariance matrices obtained from a random matrix follows the Marchenko-Pastur (MP) distribution.22,27 It also implies that the eigenvectors of a random matrix are delocalized, i.e., their norm is equally distributed across all their components (see Figure 1B and Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 for an extensive discussion).

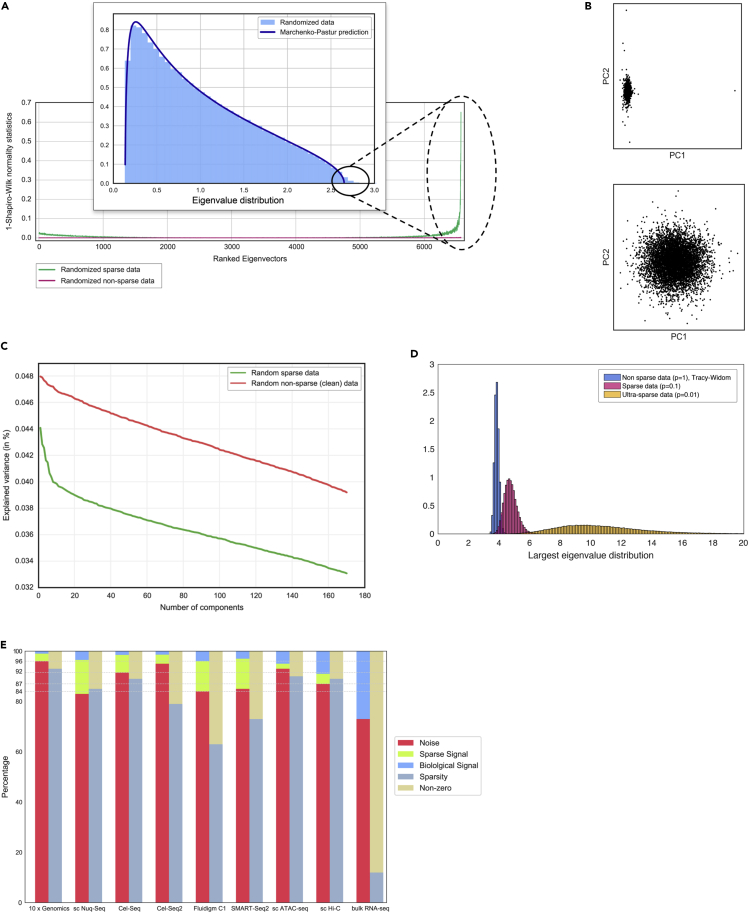
Figure 2.

Figure 2

Open in a new tab

Sparse Random Matrices and Sparsity-Induced Eigenvector Localization

(A) Randomized sparse dataset, corresponding to PBMCs in Kang et al.,32 where there exist deviations from MP distribution at the eigenvalue level, and presence of localized eigenvectors.

(B) The localization phenomenon due to sparsity can bias the lower-dimensional representations (up). Eliminating the genes that cause eigenvector localization in the randomized dataset generates a more homogeneous distribution in the lower-dimensional representation (down), reflecting the random nature of the data.

(C) The effects of sparsity can also be appreciated in the classical elbow plots: sparsity can introduce an artifactual elbow in randomized data.

(D) Deviations from TW distributions can be easily seen in sparse matrices. In this case, 100-by-100 random matrices are drawn a mixture of a normal and a Dirac-delta at zero. Similar results are obtained with other sparse distributions.

(E) Departures from universality amount to near 5% of eigenvalues. However, most of these can be explained by the sparsity of data, suggesting that Sparse Random Matric Theory can provide a better model to understand single-cell sequencing data. Truly potential biological signal amounts to only ~2% of eigenvalues.

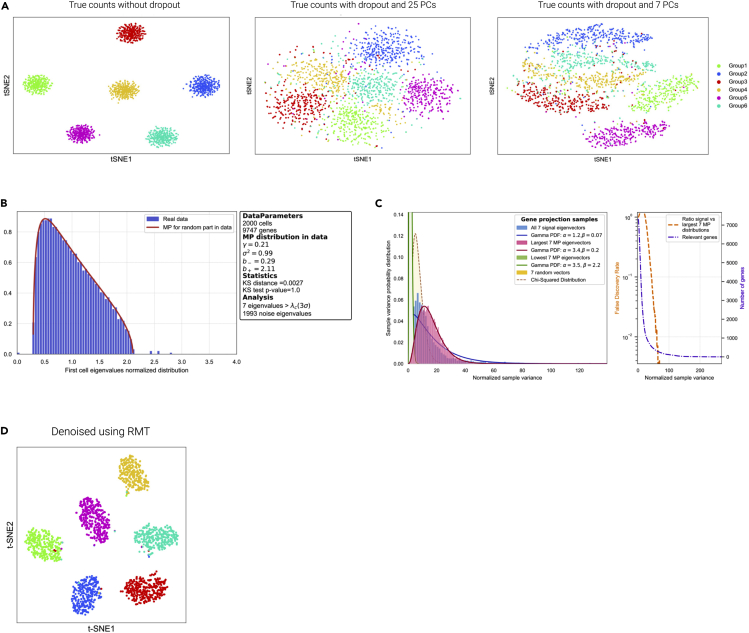
Figure 3.

Figure 3

Open in a new tab

Application to Simulations of Single-Cell and Comparison with Standard PCA

(A) t-SNE representation of a six-cell population single-cell simulation using Splatter33 for the cases with and without noise associated with dropout effects, and for different selection of principal components after applying a standard PCA technique. The colors correspond to the label of each group of cells simulated, and no clustering has been performed.

(B) MP prediction and identification of the relevant components.

(C) Selection of features (genes) responsible for signal.

(D) t-SNE representation after results after processing through the RMT.

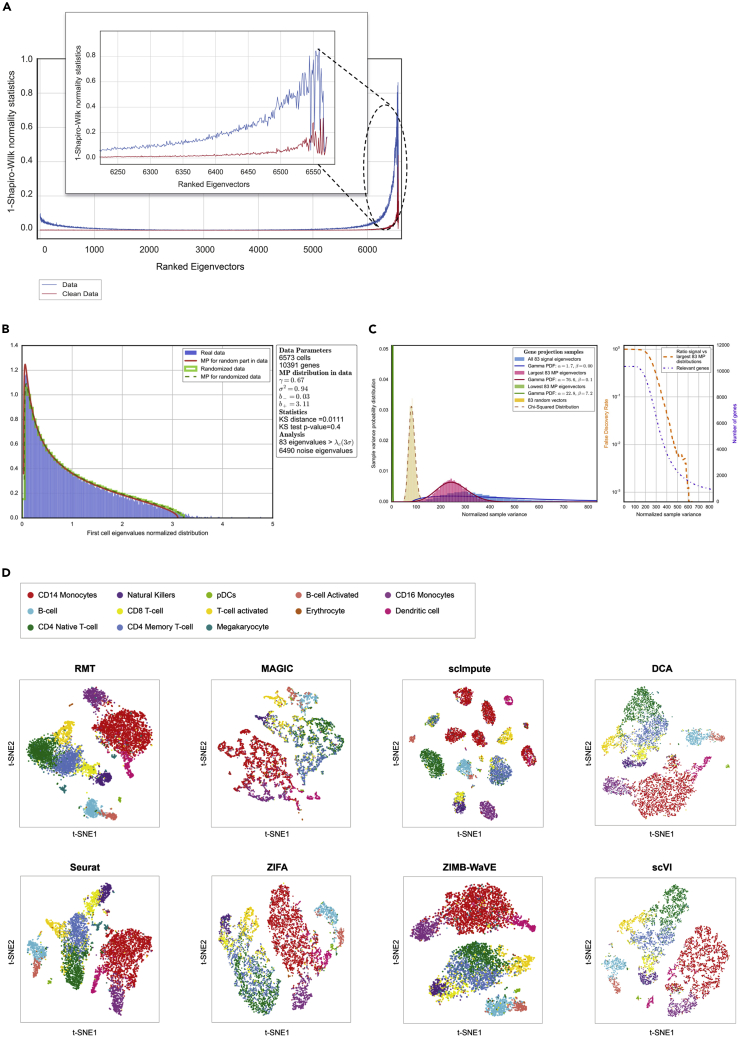
Figure 4.

Figure 4

Open in a new tab

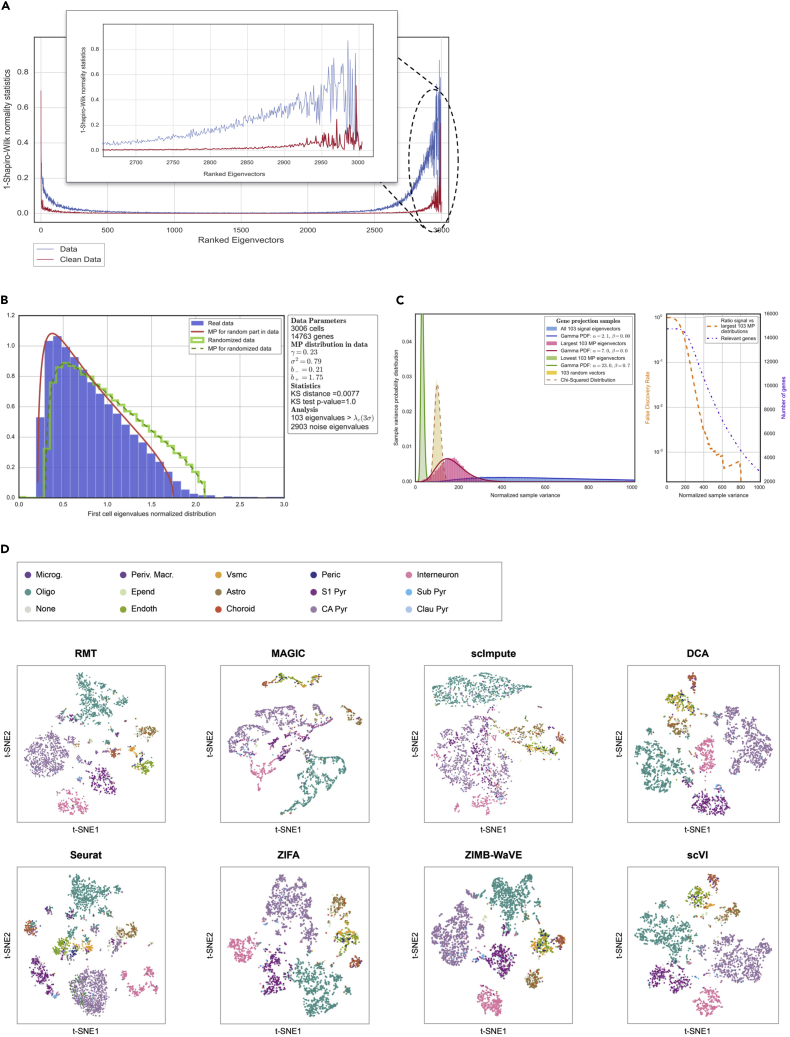
Application to PBMC Single-Cell Expression

(A) Localization properties of the eigenvectors in a single-cell dataset of PBMCs.32 The blue line represents the system dominated by sparsity and the red line corresponds to the system after removing sparsity. This figure also shows how some eigenvectors corresponding to eigenvalues out of MP distribution are delocalized (red line) and therefore do not carry any information.

(B) MP prediction and identification of relevant components.

(C) Study of the chi-squared test for the variance (normalized sample variance) in signal and noise gene projections. In the left panel, the distributions correspond to a projection of genes into the 83 signal eigenvectors (corresponding to the 83 eigenvalues of A) and the projection into the 83 lowest and 83 largest MP eigenvectors. There is also a projection into 83 random vectors. Finally, the lines show how gamma functions can fit the distributions discussed. The right panel shows the number of relevant genes in terms of the test discussed above, together with a false discovery rate. Higher values for the chi-squared test for variance indicate that the genes are less responsible for the signal.

(D) Comparison of the t-SNE representation for different public algorithms. This case corresponds to 13 different PBMC phenotypes sequenced in Kang et al.32 and described in Butler et al.11

Figure 5.

Figure 5

Open in a new tab

Application to Mouse Cortex Single-Cell Expression

(A) Localization properties of the eigenvectors in a single-cell dataset of PBMCs.32 The blue line represents the system dominated by sparsity and the red line corresponds to the system after removing sparsity. This figure also shows how some eigenvectors corresponding to eigenvalues out of MP distribution are delocalized (red line) and therefore do not carry any information.

(B) MP prediction and identification of relevant components.

(C) Study of the chi-squared test for the variance (normalized sample variance) in signal and noise gene projections. In the left panel, the distributions correspond to a projection of genes into the 103 signal eigenvectors (corresponding to the 103 eigenvalues of A) and the projection into the 103 lowest and 103 largest MP eigenvectors. There is also a projection into 103 random vectors. Finally, the lines show how gamma functions can fit the distributions discussed. The right panel shows the number of relevant genes in terms of the test discussed above together with a false discovery rate. Higher values for the chi-squared test for variance indicate that the genes are less responsible for the signal.

(D) Comparison of the t-SNE representation for different methods and algorithms. This case corresponds to 15 different mouse cortex cell phenotypes described in Zeisel et al.34

Figure 6.

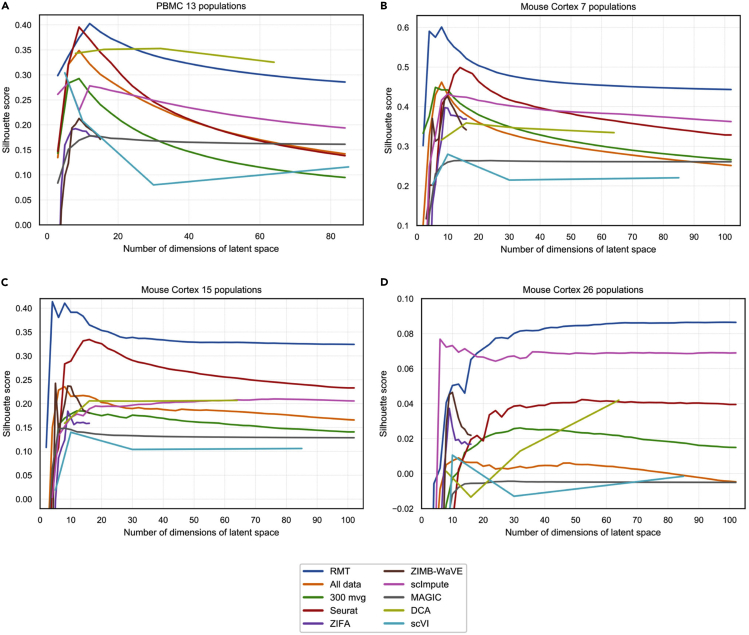
Figure 6

Open in a new tab

Comparison of Alternative Approaches for Single-Cell Analysis

(A) Mean silhouette score for different methods as a function of the number of dimensions of the latent space for the case of 13 PBMC cell phenotypes described in Butler et al.11

(B–D) Mean silhouette score for different methods as a function of the reduced space number of dimensions for the case of 7 (B), 15 (C), and 26 (D) mouse cortex cell phenotypes described in Zeisel et al.34

We propose here to apply this universality phenomenon to identify statistical features of noise present in single-cell biology (Figure 1). In particular, we claim that any single-cell dataset can be modeled as a random matrix (that encodes the noise) plus a low-rank perturbation (which is the signal). As a consequence, we expect the noise of the system follows the distributions predicted by RMT universality. Large deviations from these distributions indicate the presence of a signal that can be further analyzed. At the level of eigenvalues, random deviations from the MP distribution are described by the Tracy-Widom (TW) distribution, which is the probability distribution for fluctuations on the value of the largest eigenvalue of a random matrix (Figure 1C). Similar strategies using TW and MP distributions have been already discussed in previous works.28, 29, 30

Eigenvector Localization in Single-Cell Biology

One of the main novelties of this work is the application of the eigenvector statistics predicted by RMT to single-cell sequencing. For the eigenvectors, the transition between noise and signal is described by a phase transition: the delocalized eigenvectors give way to localized eigenvectors, i.e., eigenvectors characterized by having their norm concentrated in a few components (Figure 1B and Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6). In condensed matter physics this phenomenon is known as Anderson localization.31 In the single-cell context, localization can be interpreted as groups of cells whose gene expression is correlated. An essential feature of the situation is that the distribution of components for delocalized eigenvectors approximates a Gaussian distribution, whereas the localized eigenvector components have a non-Gaussian distribution (Figure 1B and Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6). Eigenvalues that lie outside of the MP distribution are associated with localized eigenvectors (Figures 4 and 5).

As noted above, single-cell data are often very sparse. Sparsity introduces a subtlety in the analysis because sparse random matrices can present deviations from the eigenvalue distributions predicted by RMT universality and can have localized eigenvectors (Figure 2A). As a consequence, in a sparse dataset the deviations from the MP distribution and the localized eigenvectors will be partially induced by the sparsity. A way to identify the effects of sparsity is to randomize the dataset (permuting the cell labels for each gene independently) and observe that, although the entire dataset is now uncorrelated, it still might show localized eigenvectors and potentially also significant deviations in the eigenvalues from the MP prediction (Figure 2A) due to sparsity. We can therefore conclude that single-cell data can be thought of as decomposing into three parts: a random matrix, a sparsity-induced non-biological signal, and a biological signal. To distinguish the biological signal from the sparsity-induced eigenvectors, we propose a feature selection method that discards the features (genes) that are responsible for the localized eigenvectors in the randomized case. This method increases the power for identifying potentially interesting biological signals (Figures 3, 4, and 5). Our approach leads directly to an estimate of the latent space. We show that this procedure is better able than alternative techniques to capture marked single-cell clusters across a variety of datasets (Figure 6).

Results

Quasi-Universality of Single-Cell Sequencing Data

We observed that the distribution of spacing between two consecutive eigenvalues of the sample covariance matrix in different single-cell RNA-sequencing experiments35, 36, 37, 38, 39, 40 resembles the Wigner surmise distribution conjectured by Wigner in 195518 in the study of the difference between resonant peaks in slow neutron scattering (Figure 1D). This observation prompted us to investigate the connection between RMT and the spectra of single-cell data, guided by the hypothesis that departures from RMT universality distributions indicate potential biological signals (Figures 1A–1C). We observed that across single-cell datasets these deviations amount to 5% of eigenvalues (Figure 2E). We also demonstrate (Supplemental Experimental Procedures) that the level of localization can be identified as deviations from normality in the distribution of eigenvector components (Figure 2A). Alternatively, localization can be detected using Shannon entropy (Figures S3A–S3C) or by the inverse participation ratio (IPR) (Figures S3D–S3F).

Sparsity-Induced Eigenvector Localization

Single-cell data are usually sparse. Thus, we investigated how sparsity could induce deviations from RMT universality (Figure 2A). By introducing zeros in a random matrix with entries generated with Gaussian or Poisson distributions, we observed deviations in the fluctuations of the eigenvalues from the TW distribution (Figure 2D). A similar phenomenon has been reported in the context of sparse random matrix ensembles, a generalization of RMT to the setting of random matrices with a significant fraction of zero entries. It has been shown24,41, 42, 43 that for the case of sparse Wishart random matrices, the density distribution of eigenvalues deviates from MP and some eigenvectors become localized. We show that this phenomenon can be observed in sparse single-cell data. To this end, we randomized a 95% sparse cell-gene expression matrix corresponding to 6,573 human peripheral blood mononuclear cells (PBMCs) from Kang et al.32 and analyzed the statistics of its eigenvalues and eigenvectors. Although the bulk of the eigenvalue density seems to follow an MP distribution, it is easily seen that deviations on the upper edge appear. Using a normality test we detected localization in the corresponding eigenvectors (Figures 2A, 4A, and 5A). Eigenvector localization due to sparsity generates artifacts that could potentially be interpreted as true signal in standard application of principal component analysis (PCA). For instance, the highest components of sparse random data show a bias toward the first component (Figure 2B). Another effect of sparsity is the generation of an artifactual “elbow” in randomized sparse data (Figure 2C). Therefore, the first step in our algorithm is to suppress these effects by removing genes that introduce spurious effects due to sparsity. We identify such genes in terms of deviation from normality after random projection (Supplemental Experimental Procedures).

Feature Selection and Application to Single-Cell Transcriptomic Datasets

In this section we explain the application of the RMT analysis to two marked single-cell datasets: 6,573 human PBMCs from Kang et al.32 (Figure 4) and 3,005 mouse cortex cells from Zeisel et al.34 (Figure 5). The first step is to remove the sparsity-induced signal. Figures 4A and 5A show the normality test for the eigenvectors before (blue line) and after (red line) removing the sparsity-induced signal. There is a substantial number of eigenvectors that become delocalized once the genes responsible for the sparsity are trimmed out (Supplemental Experimental Procedures). Once the sparsity-induced signal has been removed, the second step in the algorithm is to detect the part of the dataset that corresponds to a random matrix. We first compute the Wishart matrix and then use gradient descent to find the MP distribution in the eigenvalue distribution (Figures 4B and 5B; Supplemental Experimental Procedures). At the same time, the analysis of the normality of the eigenvectors (red line in Figures 4A and 5A) provides an estimate of the amount of information contained in each eigenvector. As mentioned before, the components of delocalized eigenvectors follow a Gaussian distribution; Figures 4A and 5A show the Gaussian profile of each eigenvector through a normality test (Shapiro-Wilk). Interestingly, even some of the eigenvectors corresponding to eigenvalues outside the MP distribution are delocalized and hence do not carry information. A similar argument can be made in terms of other eigenvector features, such as Shannon entropy or IPR (Figure S3). The strategy of our analysis is to detect and remove these delocalized (non-informative) eigenvectors. Filtering the eigenvectors complements and improves the analysis based only on the eigenvalues.

The third step consists in projecting the dataset onto the eigenvectors that carry signal and also onto different subsets of the eigenvectors that correspond to eigenvalues in the MP distribution (Supplemental Experimental Procedures). Using a chi-squared test for the variance of each gene projected onto the signal and noise eigenvectors, we use a false discovery rate to evaluate which genes are responsible for signal or noise (Figures 4C and 5C). The end result is a selection of features (genes) and a projection of the dataset onto the signal directions. Finally, Figures 4D and 5D (see also Figure S4) show t-distributed stochastic neighbor embedding (t-SNE) representations to visualize in two dimensions the latent space after denoising using our approach. The colors represent the cell populations described in Kang et al.32 and Butler et al.11 for human PBMCs, and for marked mouse cortex cell populations described in Zeisel et al.34 In the same figures we also show a comparison with other methods used to denoise single-cell datasets based on imputation and zero-inflated dimensionality reduction.

Biological Interpretation

We have performed a gene set enrichment analysis on the genes that the algorithm selects as responsible for the biological signal. Using a hypergeometric test on reported biological processes in our mouse brain dataset, the top pathways in the signal gene list correspond to specific brain functions (transmission across chemical synapses, q value = 1.4 × 10−23, Neural system q value = 2.8 × 10−23) while in the PBMC dataset the top pathways correspond to immune-system-related processes (immune system q value = 1.9 × 10−32, cytokine signaling in immune system q value = 2.0 × 10−21). On the other hand, taking the genes that were not selected by our algorithm, the most significant pathways are associated with generic biological processes (S-phase q value = 4.1 × 10−12; cell-cycle q value = 2.0 × 10−11). These results support the contention that eigenvector localization can be used to identify biological processes that are specific to independent cell populations within each experiment.

Simulations and Comparison of Alternative Approaches

We now proceed to evaluate the performance of the algorithm for the identification of potential relevant biological signals. We first perform a single-cell RNA-sequencing simulation of six cell populations using Splatter33 (Supplemental Experimental Procedures). Figure 3A shows a t-SNE representation of a simulation without and with noise associated with dropout effects. Here, 25 and 7 principal components have been selected. The colors correspond to each cell group simulated (no clustering has been performed). Figure 3D shows the result after our algorithm, and Figures 3B and 3C the associated MP statistics. The first example illustrates the challenge of identifying structures based on t-SNE plots before performing the algorithm (Figure 3A); in contrast, after the algorithm has been applied, we see clearly separated clusters (Figure 3D).

We now perform a comparison with some published algorithms in terms of cell-phenotype cluster resolution. We again use the datasets from Kang et al.32 (human PBMCs) and Zeisel et al.34 (mouse cortex) described in the previous section. As explained in the previous sections, these references together with Butler et al.11 have cells already labeled by phenotype. We claimed in previous sections that our method is able to remove system noise such that the cell-phenotype clusters are better resolved. This noise is partially generated due to the missing values in single-cell experiments. For this reason, we compare the two main approaches in the field that address this: imputation (MAGIC8 and scImpute10) and zero-inflated dimensionality reduction (ZIFA13 and ZIMB-WaVE9). We also perform a comparison with non-linear neural networks methods: scVI44 and DCA.45 For completeness, we also compare the raw data with a selection of genes based on higher variance (top 300 genes) and with Seurat.46 The comparison is performed using the knowledge of cell phenotypes in the studies by Butler et al., Kang et al., and Zeisel et al.11,32,34 and by computing the mean silhouette score in the reduced space, whereby higher values would indicate a better (less noisy) cell-phenotype cluster resolution. In Figures 6A–6D we represent the mean silhouette score as a function of the latent space number of dimensions for 13 PBMC phenotypes described in Butler et al.11(Figure 6A) and for 7 (Figure 6B), 15 (Figure 6C), and 26 (Figure 6D) marked mouse cortex cell populations described in Zeisel et al.34 We have selected the 1,500 most signal-like genes using RMT and we can observe how RMT outperforms other methods in the identification of known marked populations. Notice also how this becomes more dramatic as we increase the number of populations. Although this exercise is done with known populations in order to give a comparative quantitative measure, from Figures 6A–6D we can also conclude that RMT method is a suitable one to better disentangle cell populations by noise removal and hence to find new potential cell populations. Moreover, the performance advantage of the RMT method increases with the dimension of the latent space. This last feature is particularly interesting since in the future, the number of required dimensions in the latent space for an accurate analysis is expected to grow due to continuing improvements in resolution and the number of cells that can be measured.

Discussion

In this paper, we demonstrate the effectiveness of (sparse) RMT for studying the spectrum of the covariance matrix of single-cell genomic data. We have shown that single-cell data shows a 3-fold structure: a random matrix, a sparsity-induced signal, and a biological signal. We also show that while most of the spectrum follows the expectations from RMT (95%), there exist deviations due to artifacts generated by a sparsity-induced signal (∼3%) and due to a biological signal (∼2%). The large contribution of the random component to the spectral properties of the covariance matrix of single-cell expression data could be due to the stochastic nature of gene expression at single-cell level, as has been studied in a variety of biological contexts.14,47

We have introduced a method to denoise single-cell sequencing data studying eigenvalue and eigenvector properties based on RMT. This method uses RMT universality properties of eigenvalue distributions, e.g., the TW and MP distributions, and extends it to the study of the eigenvector properties, based on the localization/delocalization phase transition. This method is also able to select genes responsible for potentially interesting biological signals. The algorithm provides a powerful tool to identify this signal and produce a low-rank representation of single-cell data that may be used for further interpretation. Additionally, we should point out that the universality we observed in Wishart/covariance matrices is also observable in the spectra of graph Laplacians (including sparse graphs48) and kernel random matrices,49 which are used in other single-cell analytic techniques, suggesting that the approach followed here could be applied more broadly. The code for the algorithm is publicly available on https://rabadan.c2b2.columbia.edu/html/randomly/.

Acknowledgments

We want to thank Carlos Aparicio, Francesco Brundu, Andrew Chen, Tim Chu, Oliver Elliott, Ioan Filip, Karen Gomez, Antonio Iavarone, Zhaoqi Liu, and Richard Wolff. We would like to especially thank Ivan Corwin for helpful discussions about mathematical aspects and implications of this work. This work was funded in part by R01CA185486-01, R01CA179044-01A1, U54CA209997, U54CA193313, and a Chan-Zuckerberg pilot grant.

Author Contributions

L.A., M.B., and R.R. developed the application of localization and sparse RMT concepts into single-cell biology. L.A. and M.B. have developed the RMT-based algorithm and applied it to the single-cell datasets described in the main text and methods under the supervision of R.R. L.A., M.B., and R.R. wrote the manuscript. A.J.B. provided valuable mathematical insights and strategies and helped during the writing of the manuscript.

Declaration of Interests

The authors declare no competing financial interests.

Published: May 4, 2020

Footnotes

Supplemental Information can be found online at https://doi.org/10.1016/j.patter.2020.100035.

Supplemental Information

Document S1. Figures S1–S5 and Supplemental Experimental Procedures
mmc1.pdf (2.1MB, pdf)
Document S2. Article plus Supplemental Information
mmc2.pdf (6.6MB, pdf)

References

  • 1.Patel A.P., Tirosh I., Trombetta J.J., Shalek A.K., Gillespie S.M., Wakimoto H., Cahill D.P., Nahed B.V., Curry W.T., Martuza R.L. Single-cell RNA-seq highlights intratumoral heterogeneity in primary glioblastoma. Science. 2014;344:1396–1401. doi: 10.1126/science.1254257. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Bintu L., Yong J., Antebi Y.E., McCue K., Kazuki Y., Uno N., Oshimura M., Elowitz M.B. Dynamics of epigenetic regulation at the single-cell level. Science. 2016;351:720–724. doi: 10.1126/science.aab2956. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Cao J., Packer J.S., Ramani V., Cusanovich D.A., Huynh C., Daza R., Qiu X., Lee C., Furlan S.N., Steemers F.J. Comprehensive single-cell transcriptional profiling of a multicellular organism. Science. 2017;357:661–667. doi: 10.1126/science.aam8940. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Rizvi A.H., Camara P.G., Kandror E.K., Roberts T.J., Schieren I., Maniatis T., Rabadan R. Single-cell topological RNA-seq analysis reveals insights into cellular differentiation and development. Nat. Biotechnol. 2017;35:551–560. doi: 10.1038/nbt.3854. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Azizi E., Carr A.J., Plitas G., Cornish A.E., Konopacki C., Prabhakaran S., Nainys J., Wu K., Kiseliovas V., Setty M. Single-cell map of diverse immune phenotypes in the breast tumor microenvironment. Cell. 2018;174:1293–1308.e36. doi: 10.1016/j.cell.2018.05.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Cusanovich D.A., Reddington J.P., Garfield D.A., Daza R.M., Aghamirzaie D., Marco-Ferreres R., Pliner H.A., Christiansen L., Qiu X., Steemers F.J. The cis-regulatory dynamics of embryonic development at single-cell resolution. Nature. 2018;555:538–542. doi: 10.1038/nature25981. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Farrell J.A., Wang Y., Riesenfeld S.J., Shekhar K., Regev A., Schier A.F. Single-cell reconstruction of developmental trajectories during zebrafish embryogenesis. Science. 2018;360 doi: 10.1126/science.aar3131. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.van Dijk D., Sharma R., Nainys J., Yim K., Kathail P., Carr A.J., Burdziak C., Moon K.R., Chaffer C.L., Pattabiraman D. Recovering gene interactions from single-cell data using data diffusion. Cell. 2018;174:716–729.e27. doi: 10.1016/j.cell.2018.05.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Risso D., Perraudeau F., Gribkova S., Dudoit S., Vert J.P. A general and flexible method for signal extraction from single-cell RNA-seq data. Nat. Commun. 2018;9:284. doi: 10.1038/s41467-017-02554-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Li W.V., Li J.Y.J. An accurate and robust imputation method scImpute for single-cell RNA-seq data. Nat. Commun. 2018;9:997. doi: 10.1038/s41467-018-03405-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Butler A., Hoffman P., Smibert P., Papalexi E., Satija R. Integrating single-cell transcriptomic data across different conditions, technologies, and species. Nat. Biotechnol. 2018;36:411–420. doi: 10.1038/nbt.4096. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Stegle O., Teichmann S.A., Marioni J.C. Computational and analytical challenges in single-cell transcriptomics. Nat. Rev. Genet. 2015;16:133–145. doi: 10.1038/nrg3833. [DOI] [PubMed] [Google Scholar]
  • 13.Pierson E., Yau C. ZIFA: dimensionality reduction for zero-inflated single-cell gene expression analysis. Genome Biol. 2015;16 doi: 10.1186/s13059-015-0805-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Elowitz M.B., Levine A.J., Siggia E.D., Swain P.S. Stochastic gene expression in a single cell. Science. 2002;297:1183–1186. doi: 10.1126/science.1070919. [DOI] [PubMed] [Google Scholar]
  • 15.Peccoud J., Ycart B. Markovian modeling of gene-product synthesis. Theor. Popul. Biol. 1995;48:222–234. [Google Scholar]
  • 16.Dyson F.J. Statistical theory of energy levels of complex systems .1. J. Math. Phys. 1962;3:140–&. [Google Scholar]
  • 17.Dyson F.J. A brownian-motion for eigenvalues of a random matrix. J. Math. Phys. 1962;3:1191. [Google Scholar]
  • 18.Wigner E.P. Characteristic vectors of bordered matrices with infinite dimensions. Ann. Math. 1955;62:548–564. [Google Scholar]
  • 19.Bohigas O., Giannoni M.J., Schmit C. Characterization of chaotic quantum spectra and universality of level fluctuation laws. Phys. Rev. Lett. 1984;52:1–4. [Google Scholar]
  • 20.Odlyzko A.M. On the distribution of spacings between zeros of the zeta-function. Math. Comput. 1987;48:273–308. [Google Scholar]
  • 21.Mehta M.L., editor. Pure and Applied Mathematics. Vol. 142. Academic Press; 2004. [Google Scholar]
  • 22.Tracy C.A., Widom H. Level-spacing distributions and the airy kernel. Phys. Lett. B. 1993;305:115–118. [Google Scholar]
  • 23.Tao T., Vu V. Random matrices: universality of local eigenvalue statistics up to the edge. Commun. Math. Phys. 2010;298:549–572. [Google Scholar]
  • 24.Mirlin A.D., Fyodorov Y.V. Universality of level correlation-function of sparse random matrices. J. Phys. A Math Gen. 1991;24:2273–2286. [Google Scholar]
  • 25.Ben Arous G., Peche S. Universality of local eigenvalue statistics for some sample covariance matrices. Commun. Pur Appl. Math. 2005;58:1316–1357. [Google Scholar]
  • 26.Pillai N.S., Yin J. Universality of covariance matrices. Ann. Appl. Probab. 2014;24:935–1001. [Google Scholar]
  • 27.Marchenko V.A.P., Pastur L.A. Distribution of eigenvalues for some sets of random matrices. Math. USSR Sb. 1967;72:457–483. [Google Scholar]
  • 28.Kiselev V.Y., Kirschner K., Schaub M.T., Andrews T., Yiu A., Chandra T., Natarajan K.N., Reik W., Barahona M., Green A.R., Hemberg M. SC3: consensus clustering of single-cell RNA-seq data. Nat. Methods. 2017;14:483–486. doi: 10.1038/nmeth.4236. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Klein A.M., Mazutis L., Akartuna I., Tallapragada N., Veres A., Li V., Peshkin L., Weitz D.A., Kirschner M.W. Droplet barcoding for single-cell transcriptomics applied to embryonic stem cells. Cell. 2015;161:1187–1201. doi: 10.1016/j.cell.2015.04.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Shekhar K., Lapan S.W., Whitney I.E., Tran N.M., Macosko E.Z., Kowalczyk M., Adiconis X., Levin J.Z., Nemesh J., Goldman M. Comprehensive classification of retinal bipolar neurons by single-cell transcriptomics. Cell. 2016;166:1308–1323.e30. doi: 10.1016/j.cell.2016.07.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Anderson P.W. Absence of diffusion in certain random lattices. Phys. Rev. 1958;109:1492–1505. [Google Scholar]
  • 32.Kang H.M., Subramaniam M., Targ S., Nguyen M., Maliskova L., McCarthy E., Wan E., Wong S., Byrnes L., Lanata C.M. Multiplexed droplet single-cell RNA-sequencing using natural genetic variation. Nat. Biotechnol. 2018;36:89–94. doi: 10.1038/nbt.4042. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Zappia L., Phipson B., Oshlack A. Splatter: simulation of single-cell RNA sequencing data. Genome Biol. 2017;18 doi: 10.1186/s13059-017-1305-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Zeisel A., Muñoz-Manchado A.B., Codeluppi S., Lönnerberg P., La Manno G., Juréus A., Marques S., Munguba H., He L., Betsholtz C. Cell types in the mouse cortex and hippocampus revealed by single-cell RNA-seq. Science. 2015;347:1138–1142. doi: 10.1126/science.aaa1934. [DOI] [PubMed] [Google Scholar]
  • 35.Lawlor N., George J., Bolisetty M., Kursawe R., Sun L., Sivakamasundari V., Kycia I., Robson P., Stitzel M.L. Single-cell transcriptomes identify human islet cell signatures and reveal cell-type-specific expression changes in type 2 diabetes. Genome Res. 2017;27:208–222. doi: 10.1101/gr.212720.116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Grun D., Muraro M.J., Boisset J.C., Wiebrands K., Lyubimova A., Dharmadhikari G., van den Born M., van Es J., Jansen E., Clevers H., de Koning E.J.P. De novo prediction of stem cell identity using single-cell transcriptome data. Cell Stem Cell. 2016;19:266–277. doi: 10.1016/j.stem.2016.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Muraro M.J., Dharmadhikari G., Grün D., Groen N., Dielen T., Jansen E., van Gurp L., Engelse M.A., Carlotti F., de Koning E.J., van Oudenaarden A. A single-cell transcriptome atlas of the human pancreas. Cell Syst. 2016;3:385–394.e3. doi: 10.1016/j.cels.2016.09.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Ramani V., Deng X., Qiu R., Gunderson K.L., Steemers F.J., Disteche C.M., Noble W.S., Duan Z., Shendure J. Massively multiplex single-cell Hi-C. Nat. Methods. 2017;14:263–266. doi: 10.1038/nmeth.4155. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Nestorowa S., Hamey F.K., Pijuan Sala B., Diamanti E., Shepherd M., Laurenti E., Wilson N.K., Kent D.G., Göttgens B. A single-cell resolution map of mouse hematopoietic stem and progenitor cell differentiation. Blood. 2016;128:e20–e31. doi: 10.1182/blood-2016-05-716480. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Buenrostro J.D., Wu B., Litzenburger U.M., Ruff D., Gonzales M.L., Snyder M.P., Chang H.Y., Greenleaf W.J. Single-cell chromatin accessibility reveals principles of regulatory variation. Nature. 2015;523:486–490. doi: 10.1038/nature14590. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Fyodorov Y.V., Mirlin A.D. Localization in ensemble of sparse random matrices. Phys. Rev. Lett. 1991;67:2049–2052. doi: 10.1103/PhysRevLett.67.2049. [DOI] [PubMed] [Google Scholar]
  • 42.Evangelou S.N., Economou E.N. Spectral density singularities, level statistics, and localization in a sparse random matrix ensemble. Phys. Rev. Lett. 1992;68:361–364. doi: 10.1103/PhysRevLett.68.361. [DOI] [PubMed] [Google Scholar]
  • 43.Rodgers G.J., Bray A.J. Density of states of a sparse random matrix. Phys. Rev. B Condens Matter. 1988;37:3557–3562. doi: 10.1103/physrevb.37.3557. [DOI] [PubMed] [Google Scholar]
  • 44.Lopez R., Regier J., Cole M.B., Jordan M.I., Yosef N. Deep generative modeling for single-cell transcriptomics. Nat. Methods. 2018;15:1053–1058. doi: 10.1038/s41592-018-0229-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Eraslan G., Simon L.M., Mircea M., Mueller N.S., Theis F.J. Single-cell RNA-seq denoising using a deep count autoencoder. Nat. Commun. 2019;10:390. doi: 10.1038/s41467-018-07931-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 46.Satija R., Farrell J.A., Gennert D., Schier A.F., Regev A. Spatial reconstruction of single-cell gene expression data. Nat. Biotechnol. 2015;33:495–U206. doi: 10.1038/nbt.3192. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 47.Kaern M., Elston T.C., Blake W.J., Collins J.J. Stochasticity in gene expression: from theories to phenotypes. Nat. Rev. Genet. 2005;6:451–464. doi: 10.1038/nrg1615. [DOI] [PubMed] [Google Scholar]
  • 48.Tran L.V., Vu V.H., Wang K. Sparse random graphs: eigenvalues and eigenvectors. Random Struct. Algor. 2013;42:110–134. [Google Scholar]
  • 49.El Karoui N. The spectrum of kernel random matrices. Ann. Stat. 2010;38:1–50. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Document S1. Figures S1–S5 and Supplemental Experimental Procedures
mmc1.pdf (2.1MB, pdf)
Document S2. Article plus Supplemental Information
mmc2.pdf (6.6MB, pdf)

Articles from Patterns are provided here courtesy of Elsevier

RESOURCES