Integrated Value of Influence: An Integrative Method for the Identification of the Most Influential Nodes within Networks

Summary

Biological systems are composed of highly complex networks, and decoding the functional significance of individual network components is critical for understanding healthy and diseased states. Several algorithms have been designed to identify the most influential regulatory points within a network. However, current methods do not address all the topological dimensions of a network or correct for inherent positional biases, which limits their applicability. To overcome this computational deficit, we undertook a statistical assessment of 200 real-world and simulated networks to decipher associations between centrality measures and developed an algorithm termed Integrated Value of Influence (IVI), which integrates the most important and commonly used network centrality measures in an unbiased way. When compared against 12 other contemporary influential node identification methods on ten different networks, the IVI algorithm outperformed all other assessed methods. Using this versatile method, network researchers can now identify the most influential network nodes.

Graphical Abstract

Highlights

• •The Integrated Value of Influence (IVI) is a novel influential node detection method
• •IVI algorithm is the synergistic product of Hubness and spreading values
• •IVI captures all topological dimensions of the network
• •IVI improves the performance of current tools and accurately detects influential nodes

The Bigger Picture

Decoding the information buried within the interconnection of components could have several benefits for the smart control of a complex system. One of the major challenges in this regard is the identification of the most influential individuals that have the potential to cause the highest impact on the entire network. This knowledge could provide the ability to increase network efficiency and reduce costs. In this article, we present a novel algorithm termed the Integrated Value of Influence (IVI) that combines the most important topological characteristics of the network to identify the key individuals within it. The IVI is a versatile method that could benefit several fields such as sociology, economics, transportation, biology, and medicine. In biomedical research, for instance, identification of the true influential nodes within a disease-associated network could lead to the discovery of novel biomarkers and/or drug targets, a process that could have a considerable impact on society.

The study of networks, and identification of key players within them, is a constant challenge in fields ranging from transportation to biological systems. As experimental methods are often too costly and inefficient in large networks to assign value to particular network components, several algorithms have been designed to identify the most influential nodes computationally. However, current methods do not address the multi-dimensionality of networks and their inherent biases. Here, we present a novel method, the Integrated Value of Influence (IVI), that effectively handles such challenges and accurately calculates the influence of each individual within a network.

Introduction

The computational theory of complex systems aims to provide a holistic, top-down view of network interactions with the purpose of identifying critical network properties that reductionist approaches are incapable of identifying. Network science has been used for the investigation of complex networks within a broad variety of scientific fields, including social networks, road traffic, telecommunications, cartography, chemistry, biochemistry, and biology in general.1, 2, 3, 4 In the age of high-throughput biological assays, systems biology techniques are being used extensively for the analysis of a variety of biological networks, including gene regulatory networks, protein-protein interactions (PPI), and neural signals.⁵ In these approaches, the topology of a network is analyzed, and its different centrality measures (metrics demonstrating the influence of each node within a network) are calculated to find deeper biological meanings and identify the most influential regulatory molecules. While hub nodes have high connections with other nodes within a network, the spreader nodes are predicted to have the greatest impact on the flow of information throughout the network.⁶ Also, both of these features (i.e., hubness and spreading potential) are commonly, but independently, used to identify network influential nodes. Nodes with a simultaneously large number of connections and high spreading potential are the most influential or vital nodes in a network.

Most influential nodes can be identified by measurements of the centralities of a network, which themselves are calculated by analyzing the overall topology of the network. Network basic features and centrality measures are general and apply to all network domains, including biological ones. A network (graph) can be formulated as $N=(n,e)$, where $n$ and $e$ are indicative of nodes (also known as vertices) and edges, respectively. Nodes are parts of a network that are connected to each other by edges. To date, more than 100 centrality measures have been identified during the assessment of different network nodes, and several tools, plugins, and packages have been developed for the calculation of these measures.^7,8 Furthermore, some tools have been developed for the identification of the most influential nodes of a network based on its centrality measures.^9,10 The simplest local centrality measure of a graph is the degree centrality (DC) ${\text{DC}}_i={\sum }_{j\ne i}{A}_{ij}$, where $A$ is representative of the adjacency matrix of the corresponding network and $A_{ij}=1$ if nodes $i$ and $j$ are connected and $A_{ij}=0$ otherwise.¹¹ ClusterRank is another local centrality measure that makes an intermediation between local and semi-local characteristics of a node by removing the negative effects of local clustering. The ClusterRank for node $i$ is mathematically defined as $s_i=f\left(c_i\right){\sum }_{j\in {\Gamma }_i}\left(k_j^{\text{out}}+1\right)$, where the term $f\left(c_i\right)$ accounts for the effect of $i$’s local clustering, ${\Gamma }_i$ is the set of neighbors of vertex $i$ and the term $+1$ results from the contribution of $j$ itself. The ClusterRank, although it considers the degree of first neighbors of each node as well, as explained in its corresponding paper, is a local centrality index due to its multiplication by $f\left(c\right)$, which accounts for the local clustering of each node.¹² Betweenness centrality and collective influence are two global centrality measures and among the most widely adopted for the identification of network influencers.^13,14 Betweenness is defined as the tendency of a node to be on the shortest path between nodes in a graph.¹ Nodes with high betweenness are considered as influencers of information flow within a network. If $S_{mn}$ is the number of shortest paths between nodes m and n, and $S_{mn}\left(i\right)$ is the number of shortest paths between nodes $m$ and $n$ that pass through node $i$, then the betweenness centrality of node $i$ is ${\text{BC}}_i={\sum }_{m\ne i,m\ne n,n\ne i}\left(S_{mn}\left(i\right)/S_{mn}\right)$.¹¹ Collective influence is a novel global centrality metric that measures the collective number of nodes that can be reached from a given node $i$ and is mathematically defined as ${\text{CI}}_{\ell }\left(i\right)=\left(k_i-1\right){\sum }_{j\in \delta B\left(i,\ell \right)}\left(k_j-1\right)$, where $k_i$ is defined as the degree of node $i$ and $\delta B\left(i,\ell \right)$ represents the set of nodes at distance $\ell$ from node $i$. Neighborhood connectivity is a semi-local centrality measure of a network that deals with the connectivity (number of neighbors) of nodes. It is defined as a semi-local metric because it is not restricted to only first neighbors of a node and encompasses a broader environment. The neighborhood connectivity of a vertex $i$ is defined as the average connectivity of all neighbors of $i$ and could be formulated as ${\text{NC}}_i=\left({\sum }_{k\in N\left(i\right)}N\left(k\right)\right)/N\left(i\right)$, where $N$ is representative of neighbors and $N\left(i\right)$ is the set of neighbors of vertex $i$.¹⁵ It is also reported that not only the number of first connections of a node (degree centrality) but also the extent to which the immediate neighbors of the node are connected with each other and other nodes (neighborhood connectivity) are determinants of the importance of a node in the network.¹⁶ The H index is another semi-local centrality measure that was inspired by its application in assessing the impact of scholars and was first introduced by Korn et al.¹⁷ as a network centrality index; its superiority to some other methods was further explained by Lü et al.¹⁸. The H index of node $i$ is defined as the maximum value $h$ such that there exist at least h neighbors of a degree larger than or equal to $h$. Mathematically, the H index of node $i$ is defined as $H_{{\text{index}}_i}=\mathcal{H}\left(k_{j_1},k_{j_2},\dots ,k_{j_{k_i}}\right)$, where $\mathcal{H}$ is an operator that calculates the H index of node $i$ based on the degree of its immediate neighbors, and $k_i$ and $k_j$ are the degrees of nodes $i$ and $j$, respectively.¹⁸ However, the H index has a resolution limit such that it assigns the same value to too many nodes. To remove this problem, an improved version of the H index, named the local H index, was introduced; it is defined mathematically as ${\text{LH}}_{{\text{index}}_i}=H_{{\text{index}}_i}+{\sum }_{\upsilon \in N\left(i\right)}{H}_{{\text{index}}_{\upsilon }}$, where $N\left(i\right)$ is the set of neighbors of node $i$.¹⁹ Contrary to its name, the local H index is a semi-local centrality measure, because it leverages the H index centrality to the second-order neighbors of a given node. All of the above centrality metrics (i.e., degree centrality, ClusterRank, local H index, neighborhood connectivity, betweenness centrality, and collective influence) are the most important metrics for the identification of a network’s most influential nodes. However, other network metrics such as network density,²⁰ size,²⁰ path length,²¹ PageRank versatility,²² and modularity²¹ can also be used to evaluate the topology of networks. For extensive review of network measures and influential node identification methods, the reader is referred to the following comprehensive review and research articles.23, 24, 25, 26, 27, 28

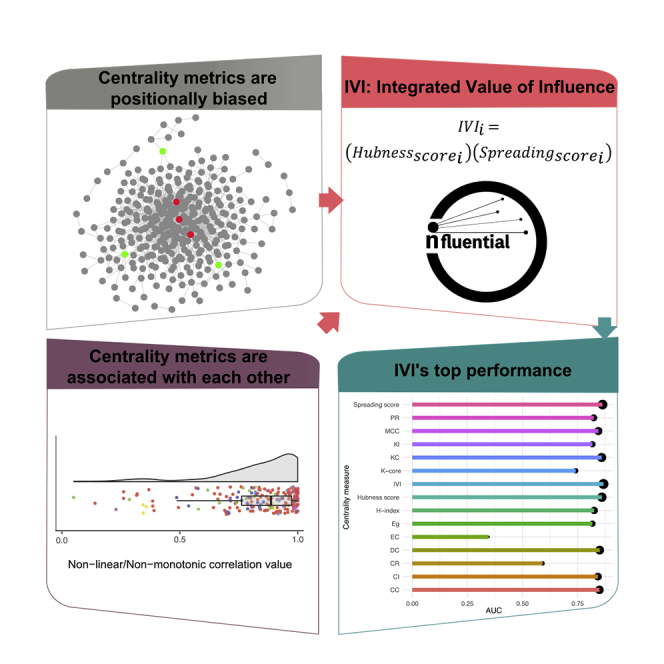
The simultaneous consideration of a set of centrality measures has been previously used as a strategy to find the most influential network nodes. del Rio et al.,²⁹ by analyzing 16 well-known centrality measures, demonstrated that while identification of network vital nodes based on a single centrality measure is not statistically significant, the combination of two centrality measures that involve both local and global features of the network could more reliably predict the most influential nodes. In systems biology studies, nodes with high degree and betweenness centrality are usually represented as network influential nodes in the context of defining both local significance and global network flow.^30,31 However, some novel influential node identification algorithms, such as collective influence, local H index, and ClusterRank have been developed recently but are not so widely adopted, particularly in biological-based studies. Furthermore, no method or algorithm has been developed to date that integrates these centrality measures with the purpose of synergizing their effects. In addition, in many networks, there are nodes that are topologically positioned in the center of the network and consequently have a high degree centrality but low betweenness centrality due to their lack of connections to nodes outside the main module.¹¹ Specifically, nodes may exhibit a high local centrality but low global centrality, or vice versa, depending on their position in the network.³² Betweenness centrality measurement is therefore biased by a node's position in the network and consequently should be carefully used for identification of network spreaders or in developing new influential node identification algorithms. Furthermore, the positional bias of betweenness centrality has not been clearly addressed in previous studies, and no solution has been proposed to correct for this computationally.

To overcome these problems, we developed a novel formula termed the Integrated Value of Influence (IVI) that integrates the most significant network centrality measures in order to synergize their effects and simultaneously remove their biases to identify the most essential regulatory molecules in a network. The IVI is the first method that truly integrates the effect of six important network centrality measures. To address the issue of positional bias of betweenness centrality, we utilized one of the other network centrality measures named neighborhood connectivity. Also, precise assessment of the association of each pair of the selected centrality measures helped to define the proper functions needed for their integration. Considering all centrality metrics represented in the literature, we selected six metrics, including degree centrality, ClusterRank, neighborhood connectivity, local H index, betweenness centrality, and collective influence, which are the most important ones for the identification of a network’s most influential nodes. Each of these centrality measures captures a different topological dimension of the graph, including local, semi-local, and global topology. One of the other advantages of these centrality measures is that none of them require a fully connected graph or module to be calculated. In this study, we addressed the problems and gaps in integration of centrality measures and identification of true network influential nodes. We first precisely interrogated the association of each pair of these six centrality measures and determined that neighborhood connectivity is an effective method for removing positional bias in the context of betweenness centrality and collective influence measurements. Next, we compared the IVI method with 12 other current methods of influential node identification. Overall, our results reveal that the IVI algorithm outperforms all methods tested in the identification of the most influential network nodes.

Results

We aimed to integrate the most commonly used local, semi-local, and global measures of network centrality, namely degree centrality and ClusterRank, neighborhood connectivity and local H index, and betweenness centrality and collective influence, respectively, and to synergize their effect for the identification of influential nodes in the network in an unbiased way. For this purpose, we recruited the Addition and Multiplication functions, two mathematical operations of arithmetic. Using the Addition function, the effect of two associated indices is combined in a way that they compensate for each other's deficiencies. By contrast, when two indices are multiplied, this results in a synergistic product that reflects the effect of both indices. Taking ${\text{Pair}}_1=\left\{a,b\right\}$, ${\text{Pair}}_2=\left\{c,d\right\}$, and ${\text{Pair}}_3=\left\{e,f\right\}$, where $a$, $b$, $c$, $d$, $e$, and $f$ are 30, 30, 25, 35, 20, and 40, respectively, as an example of three pairs of indices, all of which their additive product equals 60. This indicates that the indices involved in an additive product make up each other's deficits. By contrast, while the multiplicative product of ${\text{Pair}}_1$ equals 900, that of ${\text{Pair}}_2$ and ${\text{Pair}}_3$ equals 875 and 800, respectively. This demonstrates that the effect of two indices is synergized when using the Multiplication function for their integration, and the less the difference value of a pair of indices with the same additive product, the more the value of their multiplicative product. Although Addition and Multiplication functions are not new methods, they have been ignored for too long for scoring measurements in an integrative manner. Furthermore, using the Multiplication method, no normalization is required before the integration and, consequently, the source of subjectivity concerning the use of the appropriate normalization method is removed.³³ However, proper application of these arithmetic functions requires prior knowledge on the nature of the association of the indices to be integrated. Accordingly, we first inspected the association of every possible pair of the selected centrality measures from different aspects, including linearity, monotonicity, and dependence, which together revealed the nature of their associations and helped identify the proper functions to be used for their integration.

All Selected Centrality Measures Were Variously Correlated with Each Other

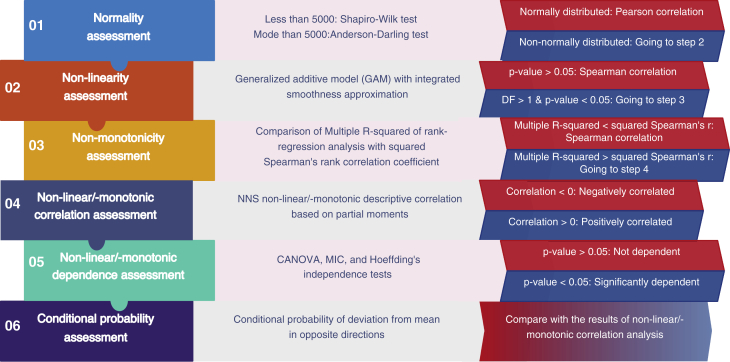
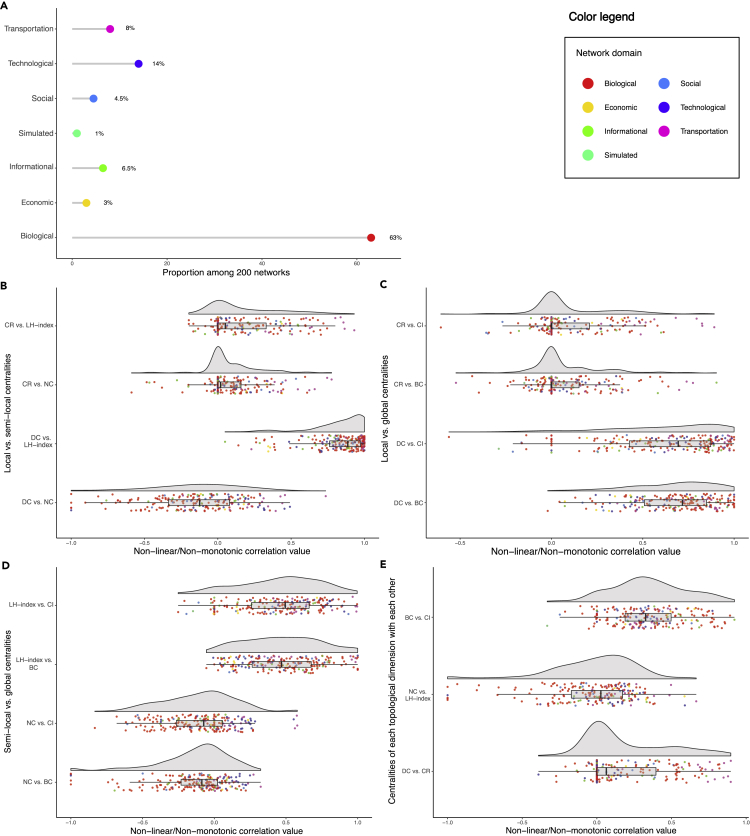
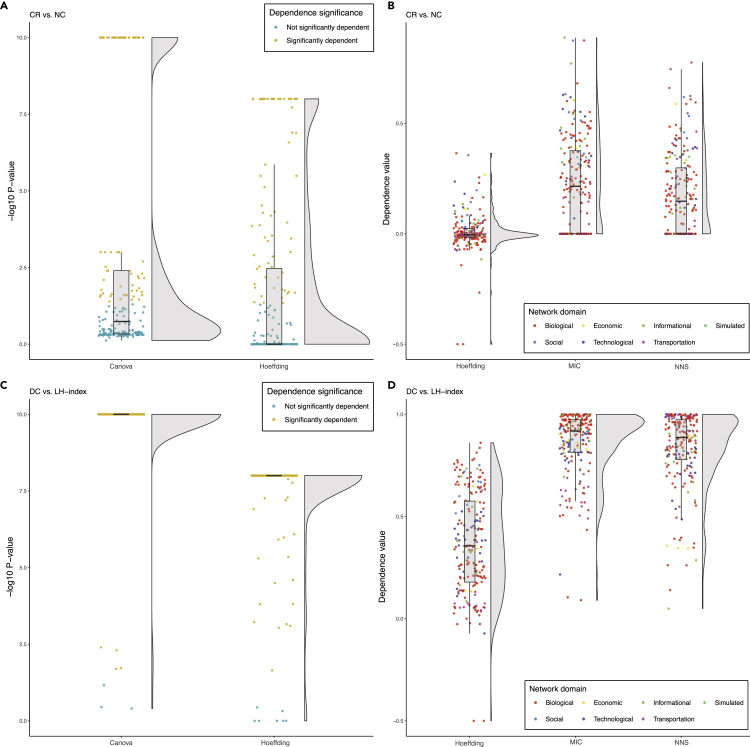
In order to examine the correlation of six selected centrality measures with each other and to investigate the nature of their associations, we built a computational pipeline through which the innate features of these metrics and their dependence were carefully assessed (Figure 1). The normality assessments demonstrated that all selected centrality measures were non-normally distributed (p value ≅ 0) in the majority of studied networks (Table 1). Also, non-linearity/monotonicity assessments indicated that all six centrality measures were non-linearly/non-monotonically correlated with each other (estimated degree of freedom of smooth terms >2.29, p < 0.0395) in both of the independent real-world biological networks analyzed. Similarly, non-monotonicity evaluations revealed that the selected centrality measures were more non-monotonically correlated (multiple R-squared from rank-regression > squared Spearman's rank correlation coefficient) with each other rather than monotonically. Accordingly, the non-linear non-parametric statistics (NNS) were used for the correlation analyses between each pair of the selected centrality measures. The NNS is a statistical method for the assessment of dependence and correlation between two variables based on higher-order partial moment matrices. According to the assessment of 200 networks (Figure 2A), most of the centrality pairs had a considerable non-linear/non-monotonic correlation with each other. Considering the positional bias reduction and for index integration purposes, we focused on the remarkable correlation between four pairs, including degree centrality and local H index (Figure 2B), betweenness centrality/collective influence and neighborhood connectivity (Figure 2D), and betweenness centrality and collective influence (Figure 2E). In addition, ClusterRank was the only centrality measure that was positively correlated with neighborhood connectivity in the majority of networks (Figure 2B).

Figure 1.

The Assessment Workflow of the Association of Two Network Centrality Measures

This workflow illustrates the stepwise assessment of innate characteristics and association/dependence of two centrality metrics of a network. CANOVA, continuous analysis of variance; DF, degree of freedom; MIC, maximum information coefficient; NNS, non-linear non-parametric statistic.

Table 1.

List of Selected Centrality Measures and Their Characteristics

Centrality Measure	Topological Scale	% Normalitya
Degree centrality	Local	100% non-normally distributed
ClusterRank	local	95% non-normally distributed
LH index	semi-local	96% non-normally distributed
Neighborhood connectivity	semi-local	84.5% non-normally distributed
Betweenness centrality	global	97% non-normally distributed
Collective influence	global	97% non-normally distributed

^aThe normality percentage of each centrality measure among 200 networks studied.

Figure 2.

The Non-linear/-monotonic Correlation of Selected Centrality Measures across 200 Networks

(A) The proportion of network domains among 200 networks. See also Table S2.

(B) The correlation of local versus semi-local centrality measures.

(C) The correlation of local versus global centrality measures.

(D) The correlation of semi-local versus global centrality measures.

(E) The correlation of centrality measures of each topological dimension with each other.

The correlation analyses were done using the non-linear non-parametric statistics (NNS), and the data was illustrated using the Raincloud method.³⁴ BC, betweenness centrality; CI, collective influence; CR, ClusterRank; DC, degree centrality; LH index, local H index; NC, neighborhood connectivity.

Betweenness Centrality and Collective Influence Were Dependent on Neighborhood Connectivity

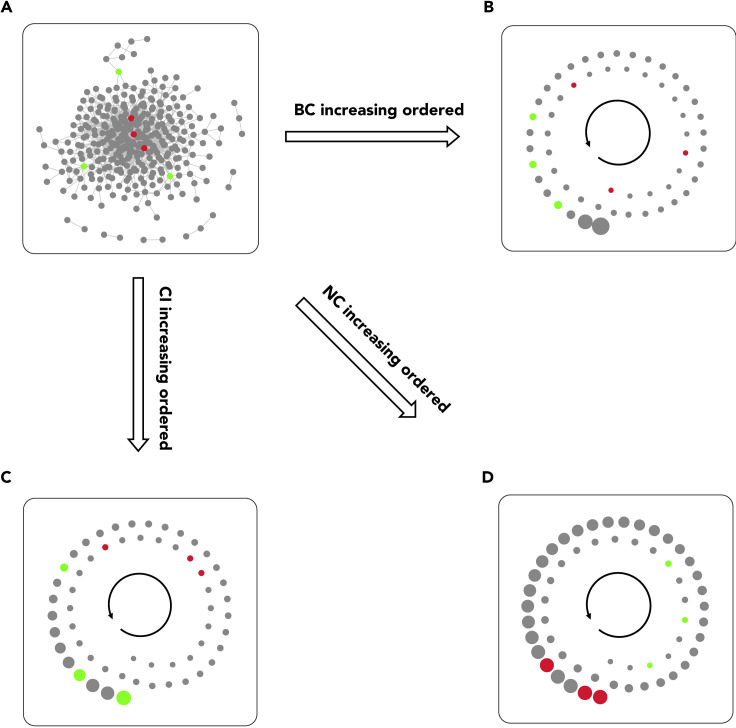
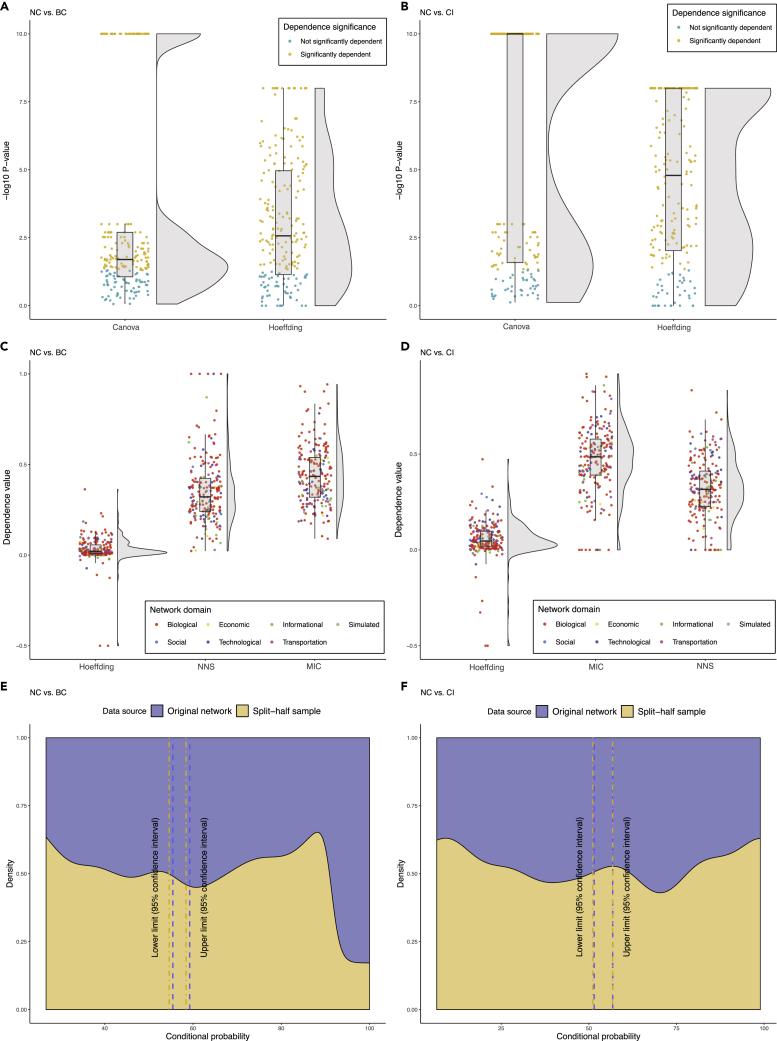
Betweenness centrality is biased by a node's position in the network.^11,32 Also, betweenness centrality and collective influence are both global centrality metrics and remarkably positively correlated with each other (Figure 2E). Considering the guilt-by-association principle,^35,36 which explains that correlated objects share common features, we may conclude that collective influence has the same positional bias as betweenness centrality. In other words, betweenness centrality and its associated other global centrality measure, namely collective influence, are biased by a node's position in the network and the edge numbers of its surrounding local environment. By contrast, neighborhood connectivity represents the average number of edges connected to immediate neighbors and consequently, is a good candidate metric for removing the positional bias introduced by betweenness centrality and collective influence measures. Also, looking at the correlation of these two global centrality measures with neighborhood connectivity (Figure 2D), we see the same pattern in both pairs; both of these global indices are notably negatively correlated with neighborhood connectivity. As an example, the topological analysis of a PPI network of adrenocortical carcinoma (ACC) clearly depicted that there is a positional bias in the distribution of betweenness centrality and collective influence scores between nodes in the network, which is contrary to neighborhood connectivity distribution. While the selected nodes in the center of the network (red nodes) with a high number of connections have high neighborhood connectivity and low betweenness centrality and collective influence scores, this is exactly opposite for (green) nodes at the edge of the network (Figure 3). Also, continuous analysis of variance (CANOVA) and Hoeffding's independence analyses indicated that betweenness centrality (Figure 4A) and collective influence (Figure 4B) were significantly dependent on, and non-linearly/non-monotonically correlated with, neighborhood connectivity in the majority of networks (p < 0.05). Moreover, the maximal information coefficient (MIC), NNS descriptive dependence, and Hoeffding's independence analyses demonstrated that betweenness centrality (Figure 4C) and collective influence (Figure 4D) were dependent on neighborhood connectivity. In addition, conditional probability assessment has been proposed as a complementary test to dependence analysis for the investigation of causality.³⁷ Accordingly, in order to further test if neighborhood connectivity is a good candidate for removing the positional bias of betweenness centrality and collective influence, we performed conditional probability assessments. As a result, the measurements based on whole networks as well as their split-half random samples determined that betweenness centrality/collective influence and neighborhood connectivity deviate from their corresponding means in opposite directions (Figures 4E and 4F). Altogether, we concluded that neighborhood connectivity has the ability to remove bias from betweenness centrality and collective influence.

Figure 3.

The Positional Bias of Betweenness Centrality and Collective Influence

This network has been reconstructed using the interactions presented by the STRING database and based on genes in the blue module provided by Xia et al.³⁸ according to the weighted gene co-expression network analysis (WGCNA) as seed proteins. Red nodes are three examples of nodes with a high number of connections positioned in the center of the network; green nodes are representative of nodes with a lower number of connections at the edges of the network. A module of interacting nodes, including all red and green ones, was extracted from the entire network for the visualization of (B)–(D) in the spiral layout. Also, for simplicity and clear visualization, node connections are not shown in (B)–(D).

(A) The entire protein-protein interaction network of adrenocortical carcinoma. The nodes were automatically organized using the Inverted Self-Organizing Map Layout with some slight alterations to make the selected nodes visible.

(B) The vertices of extracted module ordered based on their betweenness centrality values.

(C) The vertices of extracted module ordered based on their collective influence values.

(D) The vertices of extracted module ordered based on their neighborhood connectivity values.

The network was analyzed by the influential R package and illustrated using the Cytoscape software. BC, CI, and NC represent betweenness centrality, collective influence, and neighborhood connectivity, respectively.

Figure 4.

The Association of Betweenness Centrality/Collective Influence, and Neighborhood Connectivity in 200 Networks

(A) Statistical significance of the dependence of betweenness centrality on neighborhood connectivity based on two different dependence tests, including CANOVA and Hoeffding across all networks.

(B) Statistical significance of the dependence of collective influence on neighborhood connectivity based on two different dependence tests, including CANOVA and Hoeffding across all networks.

(C) Descriptive dependence of betweenness centrality on neighborhood connectivity based on three different tests, including Hoeffding, MIC, and NNS across all networks.

(D) Descriptive dependence of collective influence on neighborhood connectivity based on three different tests, including Hoeffding, MIC, and NNS across all networks.

(E) The conditional probability of deviation of betweenness centrality from its mean given that neighborhood connectivity has deviated from its corresponding mean in the opposite direction based on both original networks as well as their split-half random samples.

(F) The conditional probability of deviation of collective influence from its mean given that neighborhood connectivity has deviated from its corresponding mean in the opposite direction based on both original networks as well as their split-half random samples.

BC, CI, NC, Canova, NNS, and MIC represent betweenness centrality, collective influence, neighborhood connectivity, continuous analysis of variance, non-linear non-parametric statistic, and maximum information coefficient, respectively.

Spreading Score Emerged as the Product of Four Centrality Measures

Although neighborhood connectivity is a good means for unbiasing the selected global centrality measures, its association with other metrics should also be interrogated. As mentioned above, ClusterRank is the only centrality measure among all the indices under investigation in this study that was positively correlated with neighborhood connectivity in the majority of networks (Figure 2B). Furthermore, the dependence analysis of ClusterRank and neighborhood connectivity using four statistical methods, including CANOVA, Hoeffding, MIC, and NNS, demonstrated that these two indices were dependent on each other in a considerable proportion of networks (Figures 5A and 5B). In addition, betweenness centrality and collective influence are negatively correlated with ClusterRank in a significant number of networks (Figure 2C). Thus, based on the mathematical rules explained above, we considered recruiting the additive product of ClusterRank and neighborhood connectivity as a tool for removing the bias of the additive product of betweenness centrality and collective influence. Also, as different centrality measures have different scales, their integration without any normalization would result in a biased product inclined toward the index with the wider range. Accordingly, we used the Min-Max feature scaling method to bring all the centrality measures in the same range while keeping their relative weight ratio intact.³⁹ Also, concerning the basis of these four measurements, highlighted in the introduction, and the topological dimensions they capture, we named their final product as the Spreading score, which could be reflective of the potential of vertices in spreading of information within a network.

$${\text{Spreading}}_{{\text{score}}_i}=\left(\text{N}{\text{C}}_i^{\prime }+\text{C}{\text{R}}_i^{\prime }\right)\left(\text{B}{\text{C}}_i^{\prime }+\text{C}{\text{I}}_i^{\prime }\right)\text{,}$$

where $\text{N}{\text{C}}_i^{\prime }$, $\text{C}{\text{R}}_i^{\prime }$, $\text{B}{\text{C}}_i^{\prime }$, and $\text{C}{\text{I}}_i^{\prime }$ are range normalized neighborhood connectivity, ClusterRank, betweenness centrality, and collective influence of node $i$, respectively.

Figure 5.

The Association of ClusterRank and Degree Centrality with Neighborhood Connectivity and Local H Index, Respectively, in 200 Networks

(A) Statistical significance of the dependence of ClusterRank and neighborhood connectivity on each other based on two different dependence tests, including CANOVA and Hoeffding, across all networks.

(B) Descriptive dependence of ClusterRank and neighborhood connectivity on each other based on three different tests, including Hoeffding, MIC, and NNS, across all networks.

(C) Statistical significance of the dependence of degree centrality and local H index on each other based on two different dependence tests including CANOVA and Hoeffding, across all networks.

(D) Descriptive dependence of degree centrality and local H index on each other based on three different tests, including Hoeffding, MIC, and NNS, across all networks.

Canova, continuous analysis of variance; CR, ClusterRank; DC, degree centrality; LH index, local H index; MIC, maximum information coefficient; NC, neighborhood connectivity; NNS, non-linear non-parametric statistic.

Hubness Score Was Achieved by the Integration of Degree Centrality and Local H Index

Among six selected centrality measures, the local H index was remarkably positively correlated with degree centrality in all 200 networks analyzed (Figure 2B). The association between local H index and degree centrality was further demonstrated by dependence analyses. According to the significance analysis of the dependence of local H index and degree centrality using CANOVA and Hoeffding's independence tests, these two centrality indices were significantly dependent on each other in the majority of the networks studied (Figure 5C). Likewise, the analysis of dependence level using Hoeffding, MIC, and NNS indicated that local H index and degree centrality were dependent on each other with a noticeably high dependence value across the majority of networks (Figure 5D). Altogether, using the same mathematical rules and normalization methods explained above, the Addition function was used to combine the effect of local H index and degree centrality. Moreover, considering the same rationale used for the denomination of Spreading score, the additive product of local H index and degree centrality was named as the Hubness score, which could be reflective of the sovereignty of a vertex in it surrounding local territory.

$${\text{Hubness}}_{{\text{score}}_i}=\text{D}{\text{C}}_i^{\prime }+\text{L}{{\text{H}}^{\prime }}_{{\text{index}}_i}\text{,}$$

where $\text{D}{\text{C}}_i^{\prime }$ and $\text{L}{{\text{H}}^{\prime }}_{{\text{index}}_i}$ are range normalized degree centrality and local H index of node $i$, respectively.

IVI Synergized the Effect of Hubness and Spreading Scores

Each of the scores described above, namely Spreading and Hubness scores, represent an important but different characteristic of each node. While the Hubness score reflects the power of each vertex in its surrounding environment, the Spreading score is indicative of the spreading potential. Evidently, according to the same mathematical rules explained in this paper, the higher the multiplicative product of Spreading and Hubness scores, the more influential the vertex is in the entire network. Thus, in order to integrate Spreading and Hubness scores and calculate their synergistic effect, the Multiplication function was used and the IVI was produced. In other words, IVI is the synergistic product of the most important local (i.e., degree centrality and ClusterRank), semi-local (i.e., neighborhood connectivity and local H index), and global (i.e., betweenness centrality and collective influence) centrality measures in a way that simultaneously removes positional biases.

$${\text{IVI}}_i=\left({\text{Hubness}}_{{\text{score}}_i}\right)\left({\text{Spreading}}_{{\text{score}}_i}\right)\text{,}$$

which could be mathematically expanded as

$${\text{IVI}}_{i_{\ell }}=\left(\sum _{j\ne i}{A}_{ij}+\mathcal{H}\left(k_{j_1},k_{j_2},\dots ,k_{j_{k_i}}\right)+\sum _{\upsilon \in N\left(i\right)}\mathcal{H}\left(k_{y_1},k_{y_2},\dots ,k_{y_{k_{\upsilon }}}\right)\right)\left(\left(\frac{{\sum }_{\upsilon \in N\left(i\right)}N\left(\upsilon \right)}{N\left(i\right)}+f\left(c_i\right)\sum _{j\in N\left(i\right)}\left(k_j^{\text{out}}+1\right)\right)\left(\sum _{m\ne i,m\ne n,n\ne i}\frac{S_{mn}\left(i\right)}{S_{mn}}+\left(k_i-1\right)\sum _{j\in \delta B\left(i,\ell \right)}\left(k_j-1\right)\right)\right)$$

where $A$ is representative of the adjacency matrix of the corresponding network, and $A_{ij}=1$ if nodes $i$ and $j$ are connected and $A_{ij}=0$ otherwise. $k$ and $N$ are two operators for measuring the degree and set of first-order neighbors of a node, respectively. $\mathcal{H}$ is an operator that calculates the H index of node $i$ based on the degree of its immediate neighbors. The term $f\left(c_i\right)$ accounts for the effect of $i$’s local clustering. $S_{mn}$ is the number of shortest paths between nodes $m$ and $n$, and $S_{mn}\left(i\right)$ is the number of shortest paths between nodes $m$ and $n$ that pass through node $i$. The term $\delta B\left(i,\ell \right)$ represents the set of nodes at distance $\ell$ from node $i$.

It should also be recalled that all of the centrality measures used in the above formula should be normalized using the Min-Max feature scaling method to bring them all in the same range and remove weight biases while maintaining their relative weight ratio. In short,

$${\text{IVI}}_i=\left(\text{D}{\text{C}}_i^{\prime }+\text{L}{{\text{H}}^{\prime }}_{{\text{index}}_i}\right)\left(\left(\text{N}{\text{C}}_i^{\prime }+\text{C}{\text{R}}_i^{\prime }\right)\left(\text{B}{\text{C}}_i^{\prime }+\text{C}{\text{I}}_i^{\prime }\right)\right)\text{.}$$

IVI Outperformed Other Methods in Detecting Influential Network Nodes

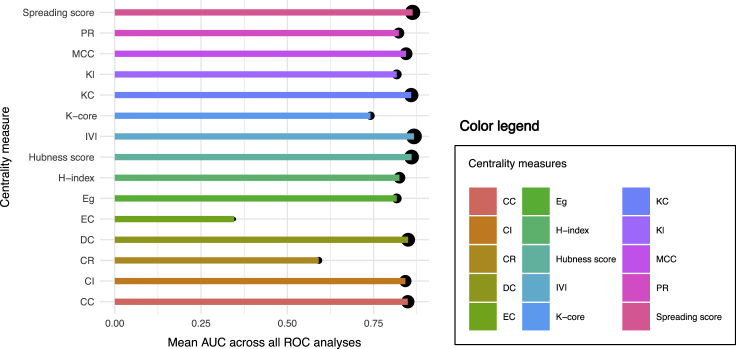
To assess the performance of IVI, we calculated the IVI value and the Spreading and Hubness scores involved in the generation of IVI, as well as 12 other contemporary centrality measures in ten networks, including two real-world biological networks, which were also used in association analyses of centrality measures, and eight randomly simulated networks with different number of vertices and edges (Table S1). The 12 influential node identification methods used for evaluation purposes in this paper included degree centrality, Kleinberg's hub centrality score,⁴⁰ ClusterRank, collective influence, K core (coreness⁴¹), H index, PageRank, closeness centrality,⁴² eigenvector centrality,⁴³ Katz centrality,⁴⁴ eccentricity centrality,⁴⁵ and maximal clique centrality (MCC⁴⁶). Then, in order to assess the performance of IVI in comparison with other methods in an unsupervised manner, we developed a novel ranking method we termed SIRIR (SIR-based influence ranking), which is the combination of the conventional susceptible-infected-recovered (SIR⁴⁷) model with the leave-one-out cross-validation technique. In the SIR model, the nodes or individuals within a network can adopt three states, including susceptible (S), infected (I), and recovered (R). For each single experiment, we assumed that one random individual was initially infected and all the other individuals were susceptible to the disease. Each infected individual can transmit the disease to any of its susceptible neighbors, with probability β at each time step (infection rate) and at the same time, it can recover from the disease and become immune, with probability γ (recovery rate). In this paper, without lack of generality, we set β = 0.5 and γ = 1. In the SIRIR method, the spread of the disease in the original network is measured using the SIR model, the network is perturbed by removing one of its nodes, the SIR model is run for the perturbed network, and finally the spread of the disease in the perturbed network is subtracted from that of the original network. This process is repeated until all of the nodes have been removed from, and involved in, the network one time and k − 1 times, respectively, where k is the number of nodes within the original network. In the end, all of the nodes of the network are ranked based on their difference values; the higher the difference value, the higher (more significant) the node's rank. As the transmission from an infected node to its susceptible neighbors and the overall spread of the disease within the network is a random process, simulation should be done to increase the accuracy of the model, and the higher the number of simulations, the more accurate the estimation of spread. In all of our experiments, on both the original and perturbed networks, we simulated the SIR model 100N times, where N is the number of nodes in the network under investigation, and averaged the measured spread of all simulations. This means that all of the nodes within a network have an equal chance of being selected as the seed (starter) for 100 times. Also, using the SIRIR method, not only the spreading potential but also the true influence of each node on the overall topology and structure of the network as well as its probable role in inter-modular connectivities were considered. Altogether, the SIRIR model-based ranking was considered as the “ground truth” and the top 50% ranked nodes in each network were selected as real positives and the bottom 50% as real negatives. Subsequently, the sensitivity and specificity of each of 15 influential node identification methods was assessed and plotted as a receiver operating characteristic (ROC) curve, and the average area under the curve (AUC) of each metric across all ten networks was calculated. Interestingly, the results illustrated that the IVI generally outperformed other methods in detecting the most influential nodes (Figures 6 and S1). The Spreading and Hubness scores, the components of the IVI formula, were the second- and third-ranked metrics, respectively.

Figure 6.

Performance of IVI in Comparison with 14 Other Current Methods in Practice

The average area under the curve (AUC) of 15 different influential node identification methods across ten interrogated networks. The size of the points on the top of the bars corresponds to the ranking of the influential node identification methods based on their average AUC values; the higher (first) ranked methods have larger point sizes and vice versa. CC, closeness centrality; CR, ClusterRank; CI, collective influence; DC, degree centrality; EC, eccentricity centrality; Eg, eigenvector centrality; IVI, Integrated Value of Influence; KC, Katz centrality; Kl, Kleinberg's hub centrality score; MCC, maximal clique centrality; PR, PageRank; ROC, receiver operating characteristics.

See also Figure S1 and Table S3.

Discussion

Identification of the most influential nodes is a necessity in all network analyses across all fields, and different centrality measures are being used for this purpose. Several methods and algorithms have also been proposed for the identification of network hubs in previous decades. However, these methods could be further improved by (1) integrating more centrality measures to capture all topological dimensions of the network and (2) by addressing the positional biases of global centrality measures. Thus, integration of common centrality measures in a way that captures all topological dimensions of a network and synergizes their impacts could be a big step toward identification of the most influential nodes. However, some centrality measures, including betweenness centrality and collective influence, two of the most common global centrality metrics, are biased by their positions (the edge numbers of their surrounding local environment) in the network. Freeman⁴² has proposed a formula for the normalization of betweenness centrality; however, this formula adjusts the betweenness centrality for the network size, not its positional bias. This issue is also properly addressed in the IVI formula. Firstly, neighborhood connectivity is highly representative of the size of surrounding local environment. In addition, according to the methodology applied for the assessment of dependence and correlation of betweenness centrality/collective influence and neighborhood connectivity, these two global centrality measures are dependent on, and negatively correlate with, neighborhood connectivity. Therefore, the additive product of neighborhood connectivity and its associated index, namely ClusterRank, which showed the same but a milder association with betweenness centrality and collective influence, performs better in removing the positional bias introduced by the aforementioned global centrality measures and consequently was used in the Spreading score and IVI formula. By contrast, the association and dependence analyses of degree centrality and local H index demonstrate that these two centrality measures are highly positively correlated with and dependent on each other, and accordingly, these indices could be combined to generate the Hubness score.

The concept of IVI, while being very simple, represents an unsupervised method that generates the synergistic product of the most important local, semi-local, and global centrality measures in a way that simultaneously removes the positional biases for the identification of most influential nodes in the whole network as well as its functional modules. This is achieved by synergizing the effect of Spreading and Hubness scores. Moreover, the IVI is not dependent on an arbitrary threshold selection. On the contrary, a list of the most influential nodes of a particular network can be identified by sorting the set of nodes based on their IVI values. We also developed an R package named “influential” (https://cran.r-project.org/package=influential) to calculate the required centrality measures and the IVI of each node in the R environment. The “influential” package is the first R package that can calculate neighborhood connectivity, H index, local H index, and collective influence in the R environment. In addition, the centrality measures calculated by other tools such as Cytoscape software could be imported into the R environment for the calculation of IVI of nodes.

Comparison of the IVI formula with 12 other influential node identification methods, as well as the Spreading and Hubness scores using the SIRIR method, confirmed that the IVI method outperforms all other algorithms. Interestingly, the Spreading and Hubness scores, the two components of the IVI, had the second and third highest average AUC values, respectively, across all networks assessed. This is further confirmation of the fact that IVI synergizes the impact of Spreading and Hubness scores. The superiority of the IVI method to other contemporary influential node identification methods is due to its characteristics, including its network-wide dimensionality and inherent unbiasing potential. Also, we believe that the SIRIR model is a precise and powerful method for ranking the true influence of nodes within a network. The SIRIR method is based on the SIR model, which assesses the spread of information or disease within a network. In contrast, the SIRIR method utilizes the leave-one-out cross-validation technique to remove each node of a network and interrogates its impact on the whole network and the spread of disease within it. Removing a vertex not only eliminates a point of information diffusion from a network but also could make varying levels of structural and topological alterations depending on its original position and topological characteristics. In addition, elimination of a node that resides in the interconnection between two modules would weaken their association. Altogether, these alterations have significant impacts on the flow of information and could help assess the true influence of vertices within a network.

In conclusion, the IVI method we describe here is based on the accurate evaluation of the association of the most important network centrality measures in order to integrate them in such a way that their strengths are synergized and positional biases are removed. Furthermore, the workflow depicted in Figure 1 could be used as a reference for the assessment of association and dependence of network centrality measures as well as any other two continuous variables. Our results demonstrate that the IVI formula outperforms other algorithms in identifying the most influential nodes in terms of both accuracy and specificity. Moreover, IVI is an unbiased synergistic product of six centrality measures, some of which could involve the weight of vertices and direction of edges in their measurements. Accordingly, IVI is very general and is not dependent on either directedness or weightedness of the network and can be calculated for directed and weighted networks as well. This broadness of applicability is a further advantage of the IVI method in comparison with other influential node identification methods that are not applicable to all network types and cannot simultaneously involve all of the features of vertices and edges. In addition, the IVI method is applicable to both the statistically inferred networks as well as the experimental real-world ones. All in all, the IVI is an unbiased synergistic product of the most important centrality measures that together cover all topological dimensions of the network and according to our results, we believe that the IVI could accurately identify the most influential nodes in a network, which could be a great benefit for all future network analyses, including systems biology studies.

Experimental Procedures

Resource Availability

Lead Contact

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Peter D. Currie (peter.currie@monash.edu).

Materials Availability

This study did not generate new unique reagents.

Data and Code Availability

All datasets generated/analyzed for this study are included in the manuscript and the Supplemental Information files. The “influential” R package was developed for calculating the Spreading and Hubness scores, IVI value, and all required centrality metrics and is available on CRAN (https://cran.r-project.org/package=influential). Moreover, some functions have been provided for the assessment of dependence and correlation of two network centrality measures as well as the conditional probability of deviation from their corresponding means in opposite directions. In addition, a function has been included in the “influential” R package for running the SIRIR model on a network, which outputs the unsupervised influence ranking of vertices. Collectively, assessment of the basic statistics of centrality measures as well as their association and dependence, measurement of the Hubness and Spreading scores, and identification and ranking of the most influential nodes can be accomplished in the same environment using the “influential” R package.

Method Details

Data Preparation

A total of 200 connectivity tables including 198 real adjacency matrices as well as two random ones generated via the igraph R package⁴⁸ were gathered for the analysis of the topology of networks and the association of their selected centrality measures. The real-world networks included 196 adjacency matrices compiled by Ghasemian et al.⁴⁹ from the Index of Complex Networks (ICON) (https://icon.colorado.edu) and two of them were downloaded from independent biological studies, which included a PPI from Xia et al.³⁸ and an miRNA expression dataset from Yepes et al.⁵⁰ The connectivity matrices were retrieved from different domains to ensure the reliability of our analyses. A list of all networks is provided in Table S2. In addition, ten networks, including the same two independent biological networks used for the assessment of centrality measures associations, as well as eight simulated networks with different number of vertices and edges, generated by the igraph R package, were gathered to compare and assess the applicability of our method in comparison with other available methods in identification of nodes with the highest impact in the network. A list of all networks used for the evaluation of the IVI method and their characteristics are provided in Table S3. The key resources used for the statistical assessment and visualization purposes are provided in Table S4.

Network Reconstruction and Analysis

A correlation analysis was done based on the Pearson algorithm for the identification of co-expressed genes in an miRNA dataset. Next, an undirected network was reconstructed for each of the co-expression/PPI datasets, all other real-world connectivity matrices retrieved from ICON, as well as the random adjacency matrices via the igraph R package. Then, the topology of each network and its centrality measures, including degree centrality, ClusterRank, neighborhood connectivity, local H index, betweenness centrality, and collective influence were analyzed using the igraph, centiserve,⁷ and influential R packages (https://cran.r-project.org/package=influential). Cytoscape software v3.7.1 was also used for network visualization purposes.⁵¹ All the downstream quantifications and statistical analyses and assessments were done independently for each network.

Interrogation of the Non-monotonic Association of Selected Centrality Measures

Although a single regression line does not fit all models with a certain degree of freedom and consequently is not applicable in high-throughput assessments, regression analysis was used to precisely evaluate non-linearity and non-monotonicity of the association of each possible pair of selected centrality measures of two real-world independent biological networks. For this purpose, the non-linear correlation between each pair of metrics was interrogated by fitting a generalized additive model (GAM), with integrated smoothness approximation using the mgcv R package,⁵² which estimates non-parametric functions of the predictor (independent) variable. GAM is a technique for regression analysis of non-linear/non-monotonic associations.⁵³ Subsequently, the most squares strategy was used to decipher if the association of selected centrality measures is more of a monotonic or a non-monotonic form. Accordingly, squared coefficients of the correlation of each pair of centrality measures based on Spearman's rank correlation analysis and ranked regression test with non-linear splines were compared, and the correlation was designated as monotonic if the squared coefficient of Spearman's rank correlation was higher compared with the other test and was identified as non-monotonic if the argument was inverse. For the ranked regression analysis, the splines R package was used to generate a basis matrix for natural cubic splines of the predictor variable.

Assessment of the Association of Selected Centrality Measures

From a statistical viewpoint, the intrinsic features of variables should be inspected before association analyses. Similar to real-world networks that have interdependent parts and follow non-linear associations,^54,55 their centrality measures might also be non-linearly/non-monotonically correlated to each other. Thus, although previously done by other researchers,^11,56 ranking-based monotonic correlation tests such as Spearman's rank correlation test does not produce correct and reliable enough results. On the other hand, assessment of local associations of two continuous variables with a subsequent global assessment of all local correlations would more reliably and correctly assess non-linear non-monotonic correlations. However, the correlation between two variables is not enough for proving causality. While correlation analysis could indicate a desired predictive relationship, dependence analysis, which is one of the sub-branches of correlation tests, could reveal the statistical relationship between two variables.⁵⁷ Also, conditional probability assessment is a complementary test to dependence analysis for proving causality.³⁷ Accordingly, subsequent to the interrogation of the innate characteristics of selected centrality measures and the nature of their associations, we considered assessing their correlation, dependence, and the conditional probability of their opposite behaviors in order to reach more reliable conclusions. A schematic workflow of the methods implemented for the assessment of innate features and association of selected network centrality measures is shown in Figure 1.

First, Gaussian distribution of selected centrality measures was assessed using the Shapiro-Wilk test or Anderson-Darling test for variables with less than or more than 5,000 objects, respectively. Next, the following association analyses was done for every possible pair of the selected centrality measures. Firstly, based on the NNS statistics, descriptive correlation and dependence of the selected centrality measures were analyzed using the NNS R package (https://cran.r-project.org/package=NNS). The NNS is a robust method for the assessment of dependence and correlation of two variables with non-linear/non-monotonic association and uses higher-order partial moment matrices instead of global measurements. In other words, the NNS method calculates the correlation coefficient by combining linear segments resulting from ordered partitions without the need to perform a linear transformation. Subsequently, the statistical significance of dependence of each pair of centrality metrics and the non-linear/non-monotonic correlation between them was assessed by three methods, including CANOVA, MIC, and Hoeffding's independence tests using CANOVA,⁵⁷ Minerva,⁵⁸ and Hmisc (https://CRAN.R-project.org/package=Hmisc) R packages, respectively. The CANOVA test is able to detect dependence and non-linear/non-monotonic correlation between two continuous variables.⁵⁹ Furthermore, CANOVA works well and is robust in non-linear correlation cases, especially when the association between two continuous variables is non-monotonic.⁵⁷ Hoeffding is a non-parametric test for the independence of two random variables with continuous distribution.⁶⁰ MIC is a maximal information-based nonparametric statistics for identifying relationships and measuring dependence, especially in many-dimensional datasets.⁶¹ Also, as a complementary test, the conditional probability of deviation of betweenness centrality/collective influence and neighborhood connectivity from their corresponding means in opposite directions was calculated in each network. In addition, the split-half random sampling method was used for each network for reliability assessment of conditional probability assessments. Finally, the 95% confidence interval of all conditional probability assessments was calculated using the Rmisc R package (https://cran.r-project.org/package=Rmisc).

Evaluation of the Performance of the IVI Formula in Comparison with Other Methods

To evaluate the functioning of the IVI formula in comparison with other contemporary influential node identification indices, ten networks, including two real-world biological networks and eight randomly simulated ones generated by the igraph R package with varying number of edges and vertices (Table S3), were assessed. Next, the IVI and Hubness and Spreading scores as well as 12 other influential node identification methods, including degree centrality, Kleinberg's hub centrality score, ClusterRank, collective influence, K core (coreness), H index, PageRank, closeness centrality, eigenvector centrality, Katz centrality, eccentricity centrality, and MCC (the recommended method by the authors of the cytoHubba plugin⁴⁶) were calculated for all of the vertices of each network. Degree centrality, Kleinberg's hub centrality scores, K core, PageRank, closeness centrality, eigenvector centrality, Katz centrality, and eccentricity centrality were calculated by the igraph R package; IVI, Hubness score, Spreading score, collective influence, and H index were measured by the influential R package; ClusterRank was calculated using the centiserve R package; and MCC was calculated by the cytoHubba plugin of Cytoscape software. Subsequently, the SIRIR model, which is achieved by applying the leave-one-out cross-validation technique on the conventional SIR model, was developed to generate a “ground truth” ranking for all of the vertices within a network. The SIRIR model was run on each network using the influential R package. In the end, considering the top and bottom 50% of SIRIR model-based ranked nodes as real positives and real negatives, respectively, an ROC analysis was done using the plotROC R package⁶² to assess the performance of all 15 influential node identification algorithms mentioned above in an unsupervised manner. Also, the AUC of each influential node identification method across all ten networks was averaged to compare the overall performance of the indices.

Published: June 22, 2020