A Review of Super-Resolution Single-Molecule Localization Microscopy Cluster Analysis and Quantification Methods

Abstract

Single-molecule localization microscopy (SMLM) is a relatively new imaging modality, winning the 2014 Nobel Prize in Chemistry, and considered as one of the key super-resolution techniques. SMLM resolution goes beyond the diffraction limit of light microscopy and achieves resolution on the order of 10–20 nm. SMLM thus enables imaging single molecules and study of the low-level molecular interactions at the subcellular level. In contrast to standard microscopy imaging that produces 2D pixel or 3D voxel grid data, SMLM generates big data of 2D or 3D point clouds with millions of localizations and associated uncertainties. This unprecedented breakthrough in imaging helps researchers employ SMLM in many fields within biology and medicine, such as studying cancerous cells and cell-mediated immunity and accelerating drug discovery. However, SMLM data quantification and interpretation methods have yet to keep pace with the rapid advancement of SMLM imaging. Researchers have been actively exploring new computational methods for SMLM data analysis to extract biosignatures of various biological structures and functions. In this survey, we describe the state-of-the-art clustering methods adopted to analyze and quantify SMLM data and examine the capabilities and shortcomings of the surveyed methods. We classify the methods according to (1) the biological application (i.e., the imaged molecules/structures), (2) the data acquisition (such as imaging modality, dimension, resolution, and number of localizations), and (3) the analysis details (2D versus 3D, field of view versus region of interest, use of machine-learning and multi-scale analysis, biosignature extraction, etc.). We observe that the majority of methods that are based on second-order statistics are sensitive to noise and imaging artifacts, have not been applied to 3D data, do not leverage machine-learning formulations, and are not scalable for big-data analysis. Finally, we summarize state-of-the-art methodology, discuss some key open challenges, and identify future opportunities for better modeling and design of an integrated computational pipeline to address the key challenges.

The Bigger Picture

Recent developments in super-resolution SMLM imaging techniques enable researchers to study macromolecular structures at the nanometer scale. However, SMLM data quantification and interpretation methods have yet to keep pace with the rapid advancement of SMLM imaging. This article provides a balanced and comprehensive review of state-of-the-art SMLM image analysis methods and ties disparate approaches together in a cohesive manner. Researchers are actively exploring new computational methods to analyze SMLM data, including recent approaches to use data-driven and machine-learning approaches. However, the validation of the SMLM clustering methods remains an open challenge. Potential future directions using multi-modality imaging (e.g., SMLM and electron microscopy) might help validate quantitative SMLM image analysis methods.

Super-resolution single-molecule localization microscopy (SMLM) enables localization of components of macromolecular complexes at the nanometer scale. However, determining a complex structure from SMLM data-clustering analysis faces challenges of imaging artifacts, big data, 2D versus 3D data, and so forth. In this Review, we provide a holistic overview of state-of-the-art computational methods leveraged to quantify SMLM data. We classify the methods and list their pros and cons to help the researcher optimally consider the most appropriate quantification method. Finally, we show how the field is growing and draw conclusions about the applicability of data-driven approaches as well as methods validation and benchmarking.

Main Text

Introduction

Cells are the structural and functional units of living organisms. Studying the cell requires an understanding of its different compartments and their relationship to one other inside and outside the cell. With the aid of microscopes, researchers can visualize, identify, and study cell organelles and molecular components, which is critical to understanding cell function in health and malfunction in different diseases. The recent advent of super-resolution microscopy, which provides an order-of-magnitude improvement in resolution compared with light microscopy, allows visualization and quantification of the organization of proteins to form macromolecular complexes in situ in intact cells, facilitating our understanding of molecular interactions in different biological structures that drive cell behavior. This revolutionary discovery advances science to better understand cellular function and the machinery of its subcellular compartments.

Resolution Limit

Optical microscopy (also known as a light microscopy) uses visible light and a series of lenses to image and magnify cell and tissue samples. Light is usually used in non-invasive imaging of cells in vitro and in vivo for various imaging applications, which helps researchers magnify and visualize biological structures within the optical resolution of the imaging system. The resolution of the imaging system is affected by physical phenomena such as lens misalignment and the diffraction of light, known as the diffraction limit of the imaging system (i.e., the microscope). The diffraction limit of the light microscope, which was theoretically described by Abbe in 1873,¹ is proportional to the wavelength of the light (λ) being observed and inversely proportional to the numerical aperture (NA) of the objective lens. The formulation of Abbe's diffraction limit is given in Equation 1:^2,3

$$d=\frac{\lambda }{2{\text{NA}}_{\text{obj}}}\text{.}$$ (Equation 1)

For example, if we use visible light with a wavelength of 500 nm (green light) and an objective lens with NA_obj of 1.0, the minimum theoretical distance d will be 250 nm that defines two separable objects.² However, practically, the resolution can be less than that due to various experimental reasons. Abbe's diffraction limit of light microscopy (i.e., 250 nm) is a major barrier that has prevented researchers from studying multiple biological structures and macromolecular complexes below the diffraction barrier. Breaking this barrier has been achieved finally with development of super-resolution microscopy (next section) and improvements in fluorescent probes and labeling techniques for super-resolution microscopy.⁴

Super-Resolution Nanoscopy Methods

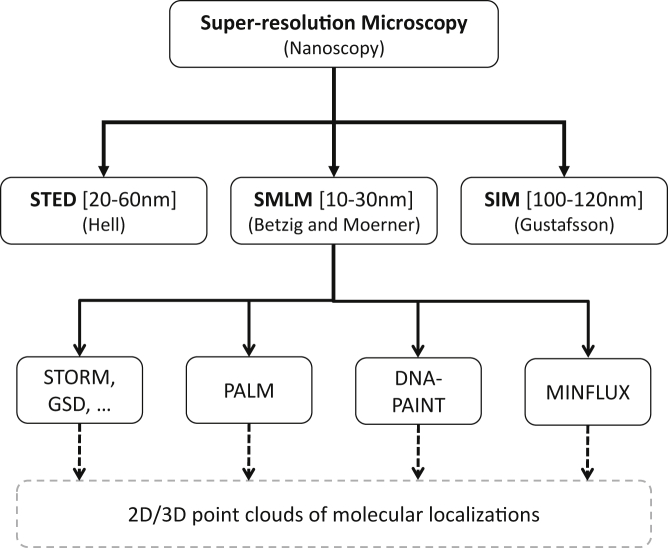
The invaluable contribution of super-resolution microscopy was acknowledged by the 2014 Nobel Prize in Chemistry awarded jointly to three scholars for their contribution to bringing light microscopy into the nanometer scale (i.e., nanoscopy). Eric Betzig, William E. Moerner, and Stefan W. Hell shared the prize.^3,5,6 Betzig and Moerner developed the principles of single-molecule localization microscopy (SMLM)^7,8 and Hell worked on stimulated emission depletion (STED) microscopy.⁹ Another microscopy method, structured illumination microscopy (SIM),¹⁰ developed by Mats Gustafsson, lately gained rapid popularity.⁶ Another super-resolution method, super-resolution optical fluctuation imaging (SOFI),¹¹ has been developed to overcome the diffraction limit of light. SOFI is faster than SMLM but has lower resolution. Schidorsky et al.¹² combined SOFI and SMLM to improve the overall imaging performance. They showed that by rejecting common background sources, SOFI-assisted SMLM can be used to improve image reconstruction. Figure 1 depicts the various super-resolution methods developed to break the diffraction limit barrier of light microscopy.

Figure 1.

Classification of Super-Resolution Nanoscopy Methods

All SMLM methods generate localizations as 2D or 3D point clouds.

SMLM methods include photoactivated localization microscopy (PALM),^7,13 stochastic optical reconstruction microscopy (STORM),¹⁴ direct STORM (dSTORM),¹⁵ ground state depletion (GSD),¹⁶ DNA-based point accumulation for imaging in nanoscale topography (DNA-PAINT),¹⁷ and MINFLUX.¹⁸ SMLM achieved the highest resolution among the super-resolution methods (Figure 1). The lateral resolution of SMLM could be from 10 to 30 nm (MINFLUX achieves 2 nm resolution). The STED lateral resolution reaches 60–100 nm, while it is about 100–120 nm for SIM. On the other hand, the analysis complexity of SMLM is ranked as the most complex according to Owen and Gaus,¹⁹ followed by SIM as intermediate in the analysis complexity and, finally, STED as the simplest. Wegel et al.²⁰ experimentally studied the super-resolution methods, including SMLM, and applied them to image various subcellular structures. They showed the weakness and strength of each method on the studied structures (e.g., vesicles and filaments).

Super-resolution microscopy has allowed for unprecedented high-resolution visualization of various biological structures such as microtubules, actin, clathrin-coated pits, mitochondria, chromatin complexes, neurons, ER, and focal adhesion complexes.²¹ However, the initial demand for high-resolution images of biological structures has been replaced by a need for quantitative methods and analysis.²² SMLM imaging methods produce spatial coordinates of molecular localizations, called “point clouds” in this survey, that are ideally suited for the application of cluster analysis algorithms and tools. We focus this survey on state-of-the-art super-resolution SMLM cluster analysis methods and their capabilities and shortcomings. Note that we do not intend to survey all possible data-clustering methods but rather limit the presented works to those methods that have been applied to SMLM data clustering.

From Imaging to Quantification

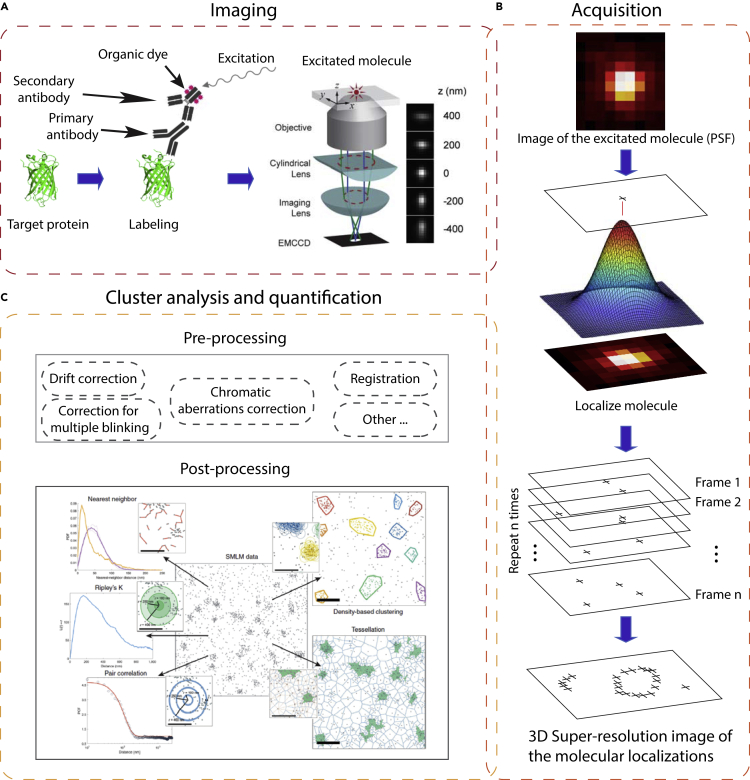
Figure 2 gives an overview of the imaging-to-quantification pipeline for SMLM, which starts with fluorescent labeling of the target molecule, then determining molecular localization from the acquired SMLM images, and ends with post-processing and quantification of the imaged and localized proteins. Our focus in this survey will be on cluster analysis and quantification of SMLM data.

Figure 2.

Overview of SMLM Quantification Pipeline

An overview of the whole framework from imaging to quantification of super-resolution STORM SMLM data: (A) 3D SMLM imaging of the target protein,²³ (B) acquiring the protein localizations and getting a map for the molecular coordinates, and (C) analyzing the super-resolved image to quantify the SMLM clusters. (C) is produced with permission from Nicovich et al.²⁴

Acquisition and Localization

The first step in imaging or tracking a protein is to label the target protein with a fluorescent dye. The labeling process varies depending on the SMLM imaging technique. For example, for STORM imaging the target molecule is labeled via antibodies conjugated to organic dyes (e.g., Alexa 647 molecules) (Figure 2). In PALM, genetically modified fluorescent proteins (FPs) are used in the labeling of the target proteins (e.g., mEos2). Also, the labeling strategy may depend on the binding proteins/antibodies used in the labeling. We show the primary-secondary labeling strategy in Figure 2A as an example. Other labeling strategies, including using fragment antigen-binding (Fab) antibodies (that can be obtained for both primary and secondary labeling) and nanobody labeling, might be used to reduce the size of the fluorescent probe and improve the resolution.25, 26, 27, 28

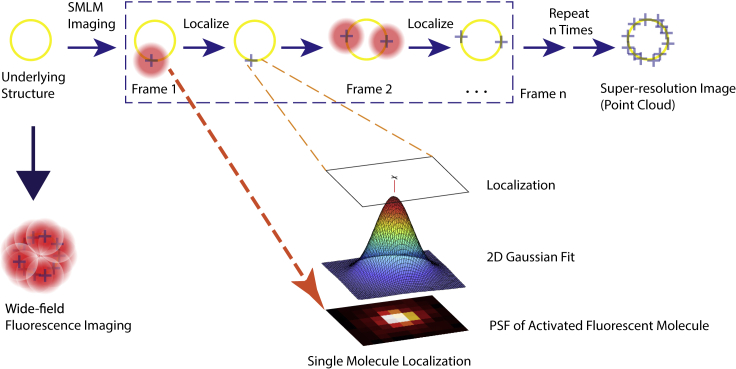
Although the exact implementation may vary, all SMLM methods fundamentally rely on temporal separation of the emissions of the excited fluorophores,^4,29 where the fluorophores are sparsely activated and forced to switch between on “bright state” and off “dark state” stochastically during the imaging session. Stochastic “blinking” of non-overlapping point spread functions (PSFs), formed due to diffraction of light, are recorded by the imaging system. Positional localization of individual fluorophores is approximated to be at the center of a Gaussian fitting of the PSF, as shown in Figure 3, resulting in significantly improved (~10×) resolution. By repeating this process thousands of times and compiling the fluorophore localizations from all the acquired frames, we obtain a high-resolution image. This is in contrast to diffraction-limited fluorescence microscopy in which, due to the single-shot approach, the PSFs of molecules at distances below the diffraction limit overlap (Figure 3), resulting in reduced resolution of the image.

Figure 3.

Illustration of the SMLM Imaging Principle

Labeling the yellow circle (i.e., biological structure below the diffraction limit) efficiently with fluorescent dye to be imaged with a fluorescence microscope. The conventional diffraction-limited wide-field microscope produces a blurred image. The SMLM imaging produces a super-resolved image that is constructed from a set of time-separated images, wherein each time frame image a sparse set of excited labeled proteins can be localized using Gaussian PSF to form the final point-cloud super-resolution image for the structure.

dSTORM is based on the use of standard fluorophores that are commercially available conjugated to a wide range of antibodies, and are therefore applicable to common immunofluorescent labeling of multiple cellular constituents. For dSTORM, fluorophores are induced to enter a weakly emissive or dark state by high-powered laser illumination from which fluorophores will spontaneously return to the ground state and emit fluorescence.² Choice of fluorophore is based on photon output, as higher photon output improves localization accuracy as well as the relative time the fluorophore spends in the dark and bright states (duty cycle) and how many times the fluorophore can cycle between the dark and bright states (switching cycle). Fluorophore blinking is enhanced using buffers containing thiol reducing agents and oxygen scavengers. The dSTORM dye of choice is Alexa 647, which exhibits high levels of blinking and photon yield that are critical for analysis approaches described later in this review.

In addition to localizing the photon events of the excited fluorophores in the plane, i.e., x and y coordinates, introducing a cylindrical lens in the light path of the imaging system will deform the PSF according to the depth (i.e., z) of the molecule within the imaged sample. Arriving at the depth value of a single molecule involves fitting a multi-variate Gaussian PSF to the deformed shape of PSF.²³ Other three-dimensional (3D) localization methods include biplane,³⁰ PSF engineering as in (1) double-helix PSF,³¹ (2) phase ramp,³² and (3) Zernike optimized localization approach in 3D (ZOLA-3D),³³ and dual opposed objective interferometry as in (1) iPALM³⁴ and (2) 4Pi detection scheme,³⁵ and supercritical-angle fluorescence recovery.³⁶

The imaging process is repeated thousands of times using a Gaussian PSF fit to determine the localization of the individual molecules at high resolution. Every molecular location might have other information such as the localization uncertainty (fitting error of the Gaussian PSF), frame number, and number of photons. The final super-resolved image is formed by recombining all the localizations from all of the imaged frames. A number of methods have been designed for this purpose, such as ThunderSTORM,³⁷ QuickPALM,³⁸ RapidSTORM,³⁹ and RainSTORM⁴⁰ (see EPFL SMLM Software Directory, http://bigwww.epfl.ch/smlm/software/index.html). As shown in Figure 2B, the localization of the molecules is obtained from every frame image individually enabling the user to map locations in two-dimensional (2D) or 3D coordinate space. The set of molecular localizations and their associated metadata are known as point clouds, events-list, pointillist, and so forth. The point clouds representation is used as input to the cluster analysis and quantification as shown in Figure 2C. We guide the reader's attention to many of the excellent references and reviews on super-resolution microscopy, especially the SMLM imaging techniques.^{2,7,13,14,22,26} In Figure 2A, we show 3D STORM imaging as an example of imaging a single molecule.²³

Imaging Artifacts

Quantification of super-resolution SMLM data might be biased due to some imaging artifacts. Some of the artifacts are challenging⁴¹ and should be accounted for before analyzing the data. There are common pitfalls in super-resolution microscopy specimen preparation and imaging acquisition that should be avoided and optimized to ensure data reproducibility.⁴² However, there are computational methods to address some of the artifacts and mitigate their effects to produce artifact-free super-resolution images. To enlighten readers about the super-resolution imaging artifacts and challenges that facing the cluster analysis and quantification, we guide them to further references.41, 42, 43, 44, 45, 46, 47 We list here the main artifacts as they appear in recent papers.41, 42, 43

Labeling Errors

Labeling of the protein of interest in SMLM is done primarily by expression of a photoactivatable FP directly linked to the protein of interest or via an antibody-conjugated fluorescent organic dye by means of immunolabeling. The photoactivatable FP, used in PALM, has a large size and may alter the localization and function of the protein of interest. For the immunolabeling approach adopted for STORM, the dye is conjugated to an antibody specific for the protein of interest. This method might include unspecific labeling, and antibody specificity for the protein of interest should be validated.⁴¹ In both labeling methods, the location of the imaged dye/FP can differ from the true location of the protein of interest and in a random direction. These localization errors create limitations to the quantification methods such that the protein clusters appear enlarged.

Detection Efficiency

Several methods have been proposed to quantify the percentage of proteins that are properly active. Not all the photoconvertible FP and molecules/fluorophores used in protein labeling are mature or successfully photoconvert. Hence, no algorithm can count the proteins that never appear.⁴³

Localization Uncertainty

Several methods⁴⁸ have been used to determine the position of the emitting molecule. The localization algorithms estimate the localization of the formed PSF of the fluorescent molecule. For example, in the Gaussian PSF model, the localization uncertainty is inversely proportional to the square root of the number of collected photons from the molecule.

Blinking

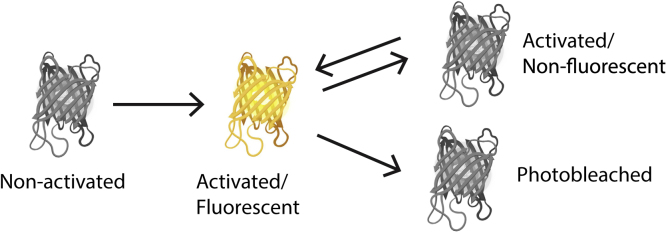
The blinking artifact, also known as multiple blinking of a single fluorophore, is considered a serious artifact and has been studied extensively.^45,49, 50, 51, 52, 53 Multiple blinking affects molecular counting and creates pseudoclusters. For example, in PALM imaging, according to the four-state photokinetic model for photoswitchable fluorescent protein (Figure 4), once the fluorescent probe is activated, it can switch between non-fluorescent and fluorescent state before photobleaching irreversibly occurs,⁵⁰ resulting in overcounting.

Figure 4.

The Four-State Photokinetics Model for Photoswitchable Fluorescent Proteins

The image used in this illustration is adapted from Frick et al.⁵⁰

Drift

Super-resolution SMLM images consist of thousands of stacked frames collected over time. Changes in temperature, the vibration of the microscope base, or air current, among others, might cause sample drift in both lateral and axial directions.⁴¹ Hence, the consequent drift can introduce localization (or spatial translation) errors by dozens of nanometers for different molecules relative to each other during the data acquisition.

Chromatic Aberrations

This occurs in multi-color imaging whereby light undergoes wavelength-dependent distortions. Motion artifacts (e.g., mechanical movements) and imperfections in the optical imaging system are the main sources of the chromatic aberration artifacts that affect co-localization of fluorophores of different colors.⁵⁴ The chromatic aberration correction is thus required on top of the drift.

Cluster Analysis and Quantification

Using point-cloud representation for SMLM data analysis is not trivial. Point-cloud representation is fundamentally different from the intensity grid valued pixel or voxel image representation used in conventional microscopy. Consequently, the computational tasks such as image processing, segmentation, and registration applied for SMLM data analysis are different⁵⁵ from the ones applied for conventional microscopy data analysis. Researchers have been working for decades to develop computational methods designed for conventional microscopy image analysis. However, these methods are not necessarily applicable to the point-cloud data. Analysis of SMLM point-cloud data is more complex^19,55 and therefore requires new approaches. In particular, cluster analysis methods are most appropriate for analysis of super-resolution SMLM data point clouds generated by the localization methods that produce the data.

The SMLM data analysis literature uses pre-processing and post-processing terms interchangeably. We believe that a clear distinction between the two terms should be made. Hence, in Figure 2C, we have included the methods used to correct for imaging artifacts in a pre-processing sub-box and the analysis methods used to quantify the biological clusters in a post-processing sub-box. For better quantification and interpretation of biological clusters, as opposed to artifactual pseudoclusters, we believe that pre-processing should be applied first to obtain artifact-free data. In this survey, we focus on the post-processing methods used for SMLM cluster analysis as discussed in the next section. Specifically, this work focuses on reviewing the post-processing methods used to cluster and analyze point-cloud SMLM data. However, some other methods, i.e., image-based cluster analysis, have been utilized to analyze the SMLM data and do not utilize the intrinsic pointillist properties of SMLM data. Examples of image-based cluster analysis methods that include extracting statistical measures are provided by several studies.56, 57, 58, 59, 60

SMLM Cluster Analysis Methods

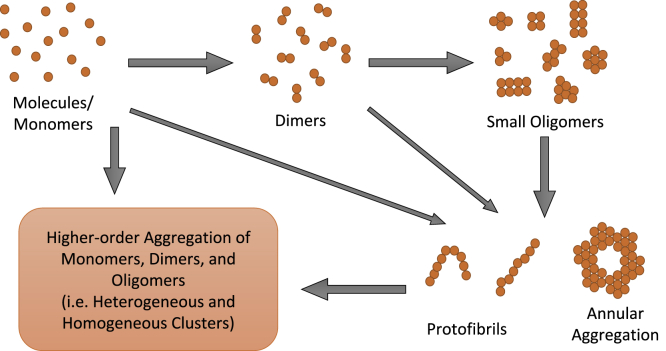
Protein-to-protein interactions produce heterogeneous and dynamic multi-molecular protein complexes.⁶¹ The complex arrangements might consist of multiple molecules that vary in sizes; ranging from few to tens of nanometers. Studying protein cluster structure and organization is important to determine their function in the cell. Figure 5 shows how the protein molecules could cluster together in many ways to form more complex structures. In this section, we focus on the cluster analysis methods used to specifically understand the molecular clusters in super-resolution SMLM data.

Figure 5.

Illustration of How the Protein Molecules Cluster Together to Form Complexes

Monomers aggregate to form dimers which aggregate to form the small oligomers. Monomers could also cluster directly to form the large mutants and oligomers.

Not all the clusters in SMLM data are related to biological structures. Some of the clusters in SMLM data are due to imaging artifacts (i.e., pseudoclusters) caused by the uncertainty of the photophysical properties of the fluorescent reporters²⁷ as mentioned in Imaging Artifacts, as well as labeling of the target molecule by more than one antibody probe. Pseudoclusters could bias the quantification and the interpretation of detected molecular clusters. Hence, pre-processing analysis is required to correct for multi-blinking artifacts.

SMLM Molecular Localizations Clustering Task

SMLM data are a point cloud in 2D or 3D coordinate space where fluorophore events, or localizations, of the labeled target protein are output as an eventlist or pointillist $\mathbf{P}=\left\{{\mathbf{p}}_1,{\mathbf{p}}_2,\dots ,{\mathbf{p}}_L\right\}$, where L is the total number of localizations. Each ${\mathbf{p}}_i$records the reconstructed spatial location of the event as a coordinate vector $\left(x_i,y_i\right)$in 2D or $\left(x_i,y_i,z_i\right)$in 3D. Additionally, metadata associated with each fluorophore event are recorded, which can vary from SMLM imaging technique to another (e.g., STORM, PALM, GSD) or from one microscope to another. Examples of fluorophore event ${\mathbf{p}}_i$ metadata are $photon-coun{t}_i$, $frame-I{D}_i$, $error-in-x_i$, and $error-in-y_i$. These metadata may be leveraged during the pre-processing of the eventlist. For example, $photon-count$ could be used as a confidence measure for an event where events with low photon counts are discarded. Following attempts to correct for imaging artifacts (e.g., diminishing the multiple blinking that causes pseudoclusters and the offsets due to the length of antibody chain), one can obtain a reconstructed point cloud that provides estimates of molecular localizations. Each reconstructed molecular localization ${\mathbf{m}}_i$ is represented as a 2D or 3D spatial coordinate. Mathematically, we write $\mathbf{M}=\mathcal{R}\left(\mathbf{P}\right)$, where $\mathbf{M}$ is a set of reconstructed molecular localizations, $\mathcal{R}$ represents the correction process, and ${\mathbf{m}}_i\in \mathbf{M},i=\mathrm{1,2},\cdots ,N$, where N is the total number of reconstructed molecular localizations (i.e., $N=\left|\mathbf{M}\right|,L=\left|\mathbf{P}\right|$). ${\mathbf{m}}_i$ has coordinate vector $\left(x_i,y_i\right)\in {\mathbb{R}}^2$ for a 2D point or $\left(x_i,y_i,z_i\right)\in {\mathbb{R}}^3$ in 3D. Notice that typically N ≤ L.

The molecular cluster analysis task is to apply various mathematical operators to find relations, patterns, curves (e.g., Ripley's H function that shows a cluster of molecular localizations) over the entire set $\mathbf{M}$ to detect, segment, and classify the molecular clusters that represent the different protein complexes in the imaged SMLM data. Formally, a cluster of molecular localizations is a dense group of molecules that are, loosely speaking, closer in some way to each other than to the localizations outside the cluster. Clustering analysis is the task of decomposing a given point cloud of molecular localizations $\mathbf{M}$ into smaller disjoint (non-overlapping) subsets, such that their union covers the whole set $\mathbf{M}$. Each subset (i.e., cluster/blob $b_i$) implies some underlying macromolecular biological structure. Sometimes the process of isolating a given set of point clouds of molecular localizations $\mathbf{M}$ into smaller disjoint subsets is called segmentation.

Formally, let $\mathcal{C}$ represent the clustering operation applied to the set of localizations $\mathbf{M}$. $\mathcal{C}$ takes every localization in $\mathbf{M}$ and bins into one of K bins or clusters denoted $b_j,j=\mathrm{1,2},\cdots ,K$. If the set of K clusters or bins is denoted $\mathbf{B}$, and when ${\mathbf{m}}_i$ can only belong to one cluster (i.e., disjoint, non-intersecting bins), we write the mapping $\mathcal{C}:\mathbf{M}\to \mathbf{B}$ as $\mathcal{C}\left({\mathbf{m}}_i\right)=b_j\in \mathbf{B},{\cup }_j{b}_j=\mathbf{M},b_j\cap b_k=\phi ,\forall j,k$, where $\cup$ and $\cap$ are union and intersection, respectively.

Sometimes, the cluster analysis is applied directly to the raw SMLM data (i.e., $\mathbf{P}$).

In this section, we dig deeper into the cluster analysis methods used to quantify the molecular clusters (i.e., post-processing) obtained through super-resolution SMLM. The methods include statistical, Bayesian, density-based, Voronoi tessellation-based, and graph-based approaches.

Statistical Methods

Over the past few years, researchers have started to apply statistical methods that are based on second-order statistics and spatial point analysis methods to quantify the SMLM clusters. The statistical methods have been applied to ecological spatial data and adopted for SMLM analysis. In this section, we cover the main statistical methods used in the literature to analyze super-resolution SMLM data as listed in Table 2. Given its large popularity in analyzing SMLM data, we describe Ripley's functions next as well as some of its variants. We then describe a class of statistical methods that are based on correlation techniques.

Table 2.

Super-Resolution SMLM Cluster Analysis and Quantification Methods (Post Processing)

Study			Acquisition						Analysis
Ref	Year	App	ImgMeth	Dim	Res (nm)	#FPI	#Loc	DataSz	CAM	A/V (μm2/μm3)	WAV	SRIC	CP	ICA	ML & CC	MSA	SW
Owen et al.73	2010	Lck and Src in T cells	PALM dSTORM	2D	~20	15K	1,500/μm2	NR	Ripley	2 × 2	✓		2–5			✓
Lillemeier et al.74	2010	TCR and Lat in T cells	hsPALM	2D	~25	1K	140–150/μm2	5–10 cells per exp. (3 exp.)	Ripley	NR	✓		2–5			✓
Williamson et al.93	2011	Lat in T cells	PALM dSTORM	2D	NR	150–200K	NR	3–25 exp.	Ripley, G&F	3 × 3			3–4			✓
Pereira et al.75	2012	HIV-1 amtrix in HIV-1 virus	dSTORM	2D	15–20	20K	NR	5–6 cells per exp. (2 exp.)	Ripley, G&F	10 × 10	✓		2–5			✓
Owen et al.92	2012	LAT in T; HeLa cells	PALM	2D	NR	15K	NR	7 cells per cond. (4 cond.)	Ripley, G&F	3 × 3			2			✓
Pageon et al.76	2013	NKG2D in NK T cells	PALM GSD	2D	20–30	20–25K	1,140–1,920/μm2	16–23 cells (2–4 exp.)	Ripley	2 × 2 3 × 3	✓		2–5			✓
Rossy et al.77	2013	Lck and CD45 in T cells	PALM dSTORM	2D	21	15–20K	NR	10–13 cells (3 exp.)	Ripley	3 × 3 4 × 4	✓		2–5			✓
Owen et al.80	2013	DiI, Lat vesicles in T cells HIV-1 Gag	HILO-PALM	3D	NR	NR	NR	NR	Ripley, G&F	2 × 2	✓	✓	3–5
Malkusch et al.81	2013	polyprotein in T cells	dSTORM	2Da	~20	4–10K	NR	NR	Ripley, NN	2 × 2	✓		2–3			✓
Rossy et al.99	2014	Lck and CD45 in T cells	PALM dSTORM	2D	20–30	NR	NR	NR	G&F	2 × 2b	✓		2			✓
Wee et al.89	2015	CD37,β2-integrin in HL-60 cells	dSTORM	2D	NR	8K	NR	20 cells	Ripley, G&F	3 × 3	✓
Stone and Veatch104	2015	Lyn kinase, BCR in CH27 cells	STORM	2D	NR	NR	NR	5 cells	steady-state cross-correlation	NR	✓					✓	MATLAB func.
Gao et al.85	2016	STAT1, STAT3 in HeLa cells; CENP-A in U2OS cells	dSTORM	2D	29	5K	NR	20 cells per cond. (5 exp.)	Ripley, G&F	4 × 4	✓		2–3			✓
Oszmiana et al.91	2016	KIR, KIR2DL1, KIR2DS1 in NKL cells	GSD	2D	NR	20K	NR	14–35 cells per exp. (24 exp.)	Ripley, G&F	3 × 3	✓		8
Krüger et al.149	2017	TLR4 in HEK 293 cells	PALM	2D	50	NR	NR	9–10 cells per cond.	NN histogram	NR	✓
Lopes et al.88	2017	FcγRI, FcγRII, SIRPα in T, B cells	dSTORM	2D	25	5K	NR	10–30 cells	Ripley, G&F, CBC	5 × 5	✓		2–3			✓
Bálint et al.87	2018	NKG2D in T cells	dSTORM	2D	NR	5K	NR	12–500 cells	Ripley, G&F	5 × 5	✓		2–3			✓
Peters et al.94	2018	actin cytoskeleton in T cells	iPALM dSTORM	2D, 3D	NR	50–100K	NR	NR	angular Ripley	3 × 3			2–3			✓	MATLAB func.
Rubin-Delanchy et al.78	2015	CD3 in T cells	PALM dSTORM	2D	10–30	20K	2 × 2b	30 ROIs (per cond.)	Bayesian; Ripley	3 × 3	✓		4			✓	R func.
Griffié et al.90	2015	LFA-1 in T cells	dSTORM	2D	NR	NR	NR	10 cells	Ripley, G&F, Bayesian	2 × 2b			4
Griffié et al.105	2016	ZAP-70 in T cells	PALM dSTORM	2D	20–30	NR	15–20K	12 cells	Bayesian	2 × 2 3 × 3			3			✓	MATLAB, R
Griffié et al.83	2017	LAT vesicles in T cells	iPALM	3D	10–30	30K	2 × 2b	5 cells per cond.	Ripley, Bayesian	2 × 2b			5			✓
Griffié et al.55	2018	CD4 in T cells	Live-cell PALM	2D	NR	NR	4K	6 cells	Ripley, Bayesian	2 × 2b			3
Pengo et al.109	2014	GaG data HIV, Nef	PALM	2D	NR	NR	NR	NR	DBSCAN	NR	✓	✓					PALMsiever
Caetano et al.79	2015	PACS-1, LAMP1, etc. in HeLa cells	GSD	2D	20	5–30K	NR	5 cells per exp. (3 exp.)	density– based; Ripley	1.5 × 1.5 3.5 × 3.5 4 × 4	✓		4			✓	MIiSR
Mazouchi and Milstein107	2015	RNAP II in cortex cells; H-NS in E. coli	PALM dSTORM	2D	~10	NR	NR	NR	density-based; DBSCAN	2 × 2b	✓		2			✓	FOCAL
Pageon et al.82	2016	TCR, VD45 in T cells	dSTORM	2D	20–30	20K	NR	NR	Ripley, DBSCAN	4 × 4	✓		13			✓	Clus-DoC
Malkusch and Heilemann96	2016	HIV, gag, env in T cells	SMLM	2D	NR	NR	NR	1 cell	DBSCAN, Ripley, OPTICS	NR			5			✓	LAMA
Barna et al.111	2016	mitochondrial protein Tom20 in neuroblast brain cells	STORM	3D	40	20K	NR	NR	DBSCAN	NR	✓		3				VividSTORM
Mollazade et al.112	2017	RGD peptides	dSTORM	2D	16	20K	NR	NR	DBSCAN, NND	2 × 2b	✓		3			✓
Zhang et al.113	2017	Salmonella typhimurium mutants in bacterial cells	FPALM	2D, 3D	~35	6–18K	NR	58–600 cells	DBSCAN wavelet	NR	✓		3			✓
Lukeš et al.150	2017	CD4 glycoprotein mutants in T cells	SOFI; simulated PALM	2D	NR	5K	NR	20 cells per cond.	SOFI density analysis	3 × 3	✓		3				codec
Schnitzbauer et al.102	2018	cis-Golgi, GRASP65, GM130, trans-Golgi, TGN46 in RPE cells	STORM	2D	NR	NR	NR	NR	DBSCAN, histogram correlation	NR	✓		2–3				Python func.
Lagache et al.95	2018	synapsin, VGLUT in primary hippocampal neurons	SIM STORM	3D	NR	30K	0.5M	NR	DBSCAN, Ripley, SODA	20 × 20 × 2	✓		3–5				Icy Plugin
Sieben et al.110	2018	proteins within centrioles and procentrioles in KE37 cells	STORM	3D	32–65	30–60K	NR	NR	DBSCAN	2 × 2	✓	✓	8		✓		SPARTAN
Tobin et al.103	2018	trastuzumab (HER2 receptor) in breast cancer cell lines (BT-474, SK-BR-3, MDA-MB-468)	dSTORM	2D	NR	20–40K	230–360 locs/μm2	17–23 cells	density pair correlation	20 × 20	✓		6		✓		ClusterOccupancy
Nino et al.108	2019	nuclear pore complex in U-2 human OS cells	dSTORM	3D	NR	NR	2 × 2b	NR	density-based; DBSCAN	2 × 2b	✓		2			✓	FOCAL3D
Paul et al.151	2019	DSB foci in human (U2Os) cells	dSTORM	2D	NR	NR	NR	NR	KDE DBSCAN, Voronoi	NR			3				SMoLR
Levet et al.115	2015	microtubules in COS7 cells; GluA1, tubulin, integrin-β3 in neuronal cells	PALM dSTORM	2D	33.9	NR	0.024–0.277M	3 cells per cond.	Voronoi	2 × 2b	✓		4				SR-Tesseler
Andronov et al.116	2016	microtubules, chromatin in HeLa cells	GSD	2D	NR	NR	0.230M	NR	Voronoi	2 × 2b	✓		5				ClusterVisu
Andronov et al.84	2016	β-tubulin in HeLa cells TPR	GSD	2D	20	NR	NR	NR	Ripley, Voronoi	1.5 × 1.5	✓					✓	SharpViSu
Andronov et al.118	2018	β-tubulin in HeLa cells; CENP-A in U2OS cells	dSTORM	3D	NR	28–50K	NR	3 exp.	Voronoi	ROIs from 18 × 18	✓	✓	2–4				3DClusterViSu
Haas et al.86	2018	RAD51, RPA in HeLa cells; HPNE, LN9, EUFA423	dSTORM	2Da	~30–40	25K	NR	5 exp.	Ripley, Delaunay, Voronoi	NR	✓		2–5				Grafeo
Peters et al.97	2018	F-actin in T cells; microtubule network in fixed HeLa cell	dSTORM	2D	60	100K	NR	3–5 cells	Voronoi; angular Ripley	3 × 3	✓		4
Levet et al.140	2019	nuclear pore complex; microtubules; actin cytoskeleton regulators	DNA-PAINT dSTORM PALM	2D, 3D	20–60	40K	20K-8.3M	3–18 cells per cond.	Voronoi	NR	✓		4				Coloc-Tesseler
Khater et al.126	2018	Cav1, Cavin-1 in PC3 cells	GSD	3D	20–50	32–40K	0.45–1.2M	9–11 cells per cond. 2 cond. (4 exp.)	network graph mean-shift	18 × 18 × 0.8	✓	✓	28	✓	✓	✓
Khater et al.128	2019	Cav1, Cavin-1 in PC3 cells	GSD	3D	20–50	32–40K	1.17–1.43M	10 cells per cond. (2 cond.)	network graph mean-shift graphlet	18 × 18 × 0.8	✓		11–47	✓	✓	✓

The nomenclature used in this table is as follows. Ref, reference to the method; App, application; ImgMeth, imaging method; Dim, dimensionality; Res, resolution; #FPI, number of frames per image; #Loc, number of localizations; DataSz, dataset size; CAM, cluster analysis method; A/V, area/volume; WAV, whole-area visualization; SRIC, surface reconstruction for individual clusters; CP, cluster properties; ICA, intra-cluster analysis; ML & CC, machine learning and cluster classification; MSA, multi-scale analysis; SW, software; NR, information not reported.

^aData acquisition is 3D but the analysis is applied to the projected 2D data.

^bInformation is reported for simulated data.

^cCode available upon request.

Ripley's Functions

Ripley's K, H, and L functions are gaining popularity in cluster analysis of the SMLM membrane proteins. These functions are used increasingly due to the point-cloud nature of SMLM data (localization of molecules). Ripley⁶² studied the stochastic models that have been proposed for spatial point patterns. Ripley's K function is a tool used for analyzing spatial point process data.^62,63 It is usually used for analyzing 2D data, but may be used to analyze locations along a line (one dimension) or may be extended to 3D spatial data.^63,64

The density of points in an area (number of points per unit area) is known as the first moment property.⁶⁵ The second moment property (also known as a bivariate or multi-variate generalization) is used to describe the relationships between two or more point patterns by finding the expected number of points N within a distance r of another point.^63,65 Ripley's K function⁶² is a second moment property (second-order statistics). Theoretically, the K function is given in Equation 2:⁶³

$$K\left(r\right)={\lambda }^{-1}E\left[\text{number}\text{of}\text{points}\text{within}\text{distance}r\text{of}\text{randomly}\text{chosen}\text{point}\right]\text{,}$$ (Equation 2)

where λ is the density normalization of points (number of points per area A, $\lambda =N/A$). Formally, the K function is given in Equation 3:^62,65

$$K\left(r\right)=\frac{1}{n}\sum _{i=1}^n{N}_{p_i}\left(r\right)/\lambda \text{,}$$ (Equation 3)

where $p_i$ is the ith point in the data and the sum is taken over n points. For a homogeneous Poisson process, which is known as complete spatial randomness (CSR), the expected value of function $K\left(r\right)$ is given in Equation 4:⁶³

$$\text{K}\left(r\right)=\pi r^2\text{.}$$ (Equation 4)

Note that deviation from the CSR expected value indicates scales of clustering and dispersion. So Ripley's K function is typically used to find the level of clustering by comparing a given distribution with a random distribution.

Other Ripley's functions can be derived from the K function. The complete derivation for all the other functions can be found in other papers.^63,65 The L function was proposed by Besag⁶⁶ as a normalization for the K function, as seen in Equation 5:

$$L\left(r\right)=\sqrt{K\left(r\right)/\pi }\text{.}$$ (Equation 5)

The L function and its derivative can be used to identify the radius of the clusters.⁶⁵ Normalizing the L function will produce another function called the H function.⁶⁷ Hence, the H function is a further normalization of the original K function. The H function is given in Equation 6:

$$H\left(r\right)=L\left(r\right)-r\text{.}$$ (Equation 6)

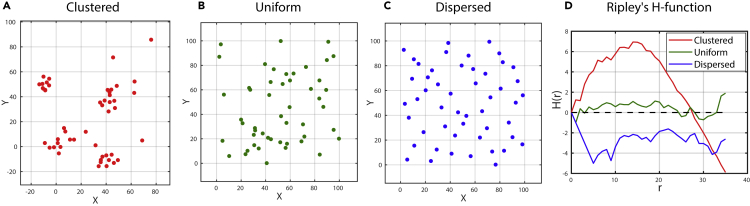
Note that the H function may result in a positive value, which indicates clustering over the spatial scale; on the other hand, the negative value indicates dispersion. The value is zero when we have CSR distributed points (not clustered or dispersed points). This is because for a CSR distribution, $L\left(r\right)=r$ for all values of r. Figure 6 shows three cases of spatial point patterns and the corresponding Ripley's H-function behavior. The pattern of the H function fluctuates around zero for uniformly distributed points, above zero for clustered points, and below zero for dispersed points.

Figure 6.

An Example Showing the Behavior of the $H\left(r\right)$ Function for the Different Distributions of Spatial Point Patterns

The $H\left(r\right)$ function (D) has positive values for clustered points (A), fluctuates around 0 for uniformly distributed (random) points (B), and has negative values for dispersed points (C). The generated data consist of 50 points for each one of the patterns shown in (A) to (C).

To estimate $K\left(r\right)$, the numerator of Equation 3 can be written as $N^{-1}{\sum }_i{\sum }_{j\ne i}I\left(d_{ij}<r\right)$,^63,68 where $d_{ij}$ is the distance between the ith and jth points. $I(.)$ is an indicator function that is equal to 1 if $d_{ij}\le r$ and is zero otherwise.

In its current formulation, the K function does not consider the effect of the points close to the border of the study area. This issue, which is called the edge effect of Ripley's K function, causes underestimation of K.^63,68, 69, 70 Hence, Ripley's K function requires more elaborate methods for edge correction. Many methods have been proposed to correct the edge effect of Ripley's K function.69, 70, 71, 72 Generally, the corrected K function ($\hat{K}\left(r\right)$) can be written as Equation 7:

$$\hat{K}\left(r\right)=\frac{A}{N}\sum _i\sum _{j\ne i}\frac{I\left(d_{ij}<r\right)}{w_{ij}}\text{,}$$ (Equation 7)

where $w_{ij}$ is a weight function that provides the edge correction.

Ripley's functions are becoming increasingly popular in analyzing SMLM data. The functions have been utilized in many biological applications to find the level of molecular clustering. They are used either alone or in combination with the other cluster analysis methods.^53,73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97 We summarize how the methods are adopted for SMLM cluster analysis of the different biological applications in Table 2.

Getis and Franklin's Local Point Pattern

Getis and Franklin published a paper and proposed a new $L\left(r\right)$ function. Their function is a variant of Ripley's K function, called second-order neighborhood analysis. The goal of their $L\left(r\right)$ function is to quantify the clustering of the points (molecules in SMLM context) at various spatial scales.⁹⁸ The values of $L\left(r\right)$ function are calculated for each point as described in Equation 8:

$$L{\left(r\right)}_j=\sqrt{A\sum _{i=1}^n\frac{{\delta }_{ij}}{n-1}/\pi }\text{,}$$ (Equation 8)

where A is the region area (e.g., rectangular region) under study and n is the total number of points in the region. The indicator function delta ${\delta }_{ij}=1$ if the distance between point i and point j is <r and zero otherwise. ${\sum }_{i=1}^n{\delta }_{ij}$ is the summation over all points within distance r from point j (i.e., all points within a circle of radius r centered at localization j). Thus, $L\left(r\right)$ is another way of normalizing Ripley's K function by finding the local point patterns normalized by the average point density in the whole analyzed region. The property of $L\left(r\right)=r$ for all values of r when having a CSR distribution still holds.

The Getis and Franklin (G&F) function could be used to find the local descriptor (patterns) of every localization, while Ripley's function is used to describe all the points in the region globally. Therefore, the G&F function has been used in combination with Ripley's K function to analyze the localization of molecules from SMLM data.^75,80,83,85,87, 88, 89, 90, 91, 92, 93^,99 For example, a G&F point pattern was used in double protein-labeling analysis⁹⁹ to investigate the co-clustering of membrane proteins. It was also used for generating a topographic map of the level of clustering to determine the heights of peaks in the map across a region⁹⁰ and then using the relative heights of the peaks to determine the clustering characteristics and avoid inaccurate thresholding.

Correlation-Based Methods

Correlation-based analysis methods (pair correlation, autocorrelation, cross-correlation, co-localization) have been applied to super-resolution SMLM data for both pre-processing and post-processing quantification (Figure 2C). Pre-processing methods^53,100, 101, 102 address imaging artifacts such as the multiple blinking of a single fluorophore that may cause molecular overcounting. Overcounting, as well as the other implications of imaging artifacts, might bias SMLM cluster analysis and should be corrected before post-processing the SMLM data for quantifying the biological clusters. For example, Malkusch et al.¹⁰¹ used a correlation coefficient framework, coordinate-based co-localization, to analyze every single localization within a certain radial distance and assign to it a score ranging from –1 to 1. In their formulation, –1 is assigned to perfectly segregated localizations, 0 for uncorrelated (randomly distributed), and +1 for perfect co-localization. The same coordinate-based co-localization idea has also been used to analyze the protein localizations of biological clusters.^82,88,96 Many other correlation functions have been used to quantify the localization clustering for post-processing SMLM data.^82,88,96,99,102, 103, 104 The proposed correlation functions are used to analyze biological clusters rather than the biologically irrelevant pseudoclusters (also known as nanoclusters). For example, Schnitzbauer et al.¹⁰² derived a cross-correlation function for the localization coordinates inspired by the translational cross-correlation function in pixel-based image representation. They mathematically showed that the point-to-point distance distribution in super-resolution SMLM is equivalent to the pixel-based correlation function. They then extended cross-correlation to quantify the spatial relationship between complicated structures by considering the point-to-set distance.

Bayesian Methods

The SMLM cluster analysis methods usually depend on a set of user-defined parameters. Sometimes, the subjectivity and the ambiguity of selecting the parameters affect the performance of the SMLM clustering task. The main goal of the Bayesian approach for super-resolution SMLM data is to design a clustering method that alleviates the need for arbitrary user-selected analysis parameters. A well-defined prior Bayesian will replace the arbitrary user-selected parameters. Bayesian is a model-based approach which is used for spatial point clustering generated by SMLM. The model is used to evaluate the assignment of every molecule to clusters by its marginal posterior probability. The posterior probability is computed based on a specified model for the molecular data and their uncertainties.⁷⁸ Therefore, the mechanism is to select clusters from a set of generated clustering proposals. Usually, clustering proposals are generated with variable spatial scale and threshold using statistical methods such as Ripley's K function⁸³ or the G&F function.⁷⁸ After generating thousands of candidate proposals per region of interest (ROI), the optimum number of proposals is then selected by scoring them against the Bayesian model.^55,78,83,105 For example, in their generative model, Griffié et al.⁸³, considered an ROI containing clustered and non-clustered localizations. The user sets the probability that localization is non-clustered, and this is the prior parameter for the model. They also assume that the molecular positions in the cluster are following spherical Gaussian distribution. The radius (Gaussian standard deviation) of the cluster is drawn from a user-specified histogram of sizes. They claim that the aforementioned model reflects the a priori knowledge of the molecular distribution. The Bayesian approach is not limited to quantifying 2D, and it was extended by Griffié et al. to analyze 3D SMLM data.⁸³

Density-Based Methods

Density-based clustering methods are popular in data mining and spatial data clustering. Ester et al. proposed density-based spatial clustering of applications with noise (DBSCAN),¹⁰⁶ a density-based clustering algorithm that is capable of discovering clusters of arbitrary shapes. This can be used to filter out noisy events from the SMLM data when its parameters are set correctly.

DBSCAN is based on two parameters for detecting and segmenting the clusters in SMLM data. It requires a neighborhood radius ε and the minimum number of localizations/points ($MinPts$) within ε to qualify as a cluster (Figure 7). The algorithm can start from any molecular localization that has not been visited. The connectivity of the molecules of the qualified clusters should maintain the $MinPts$ condition within ε while propagating from one molecule to another within the same cluster until reaching the boundary molecules, where the $MinPts$ condition no longer holds. Otherwise, the cluster is considered an outlier. It is clear that the clustering is conditioned on the minimum density of molecules within neighborhood radius ε. Figure 7 shows an example of how the DBSCAN clustering method works and the required parameters to cluster the localizations.

Figure 7.

An Example Illustrating the Density-Based DBSCAN Clustering Method Applied to SMLM Data

For instance, DBSCAN algorithm is applied when using ε and $MinPts=3$ parameters. Sometimes the subjectivity of selecting the parameters might change the clustering results dramatically. For example, pseudoclusters in SMLM complicate the selection of the algorithm parameters.

According to Mazouchi and Milstein,¹⁰⁷ leveraging DBSCAN to analyze super-resolution SMLM data has certain limitations. The algorithm is slow scaling with the number of localizations and it has $O\left(n\text{log}\left(n\right)\right)$ at best. The ambiguity and subjectivity in selecting the algorithm parameters affect its performance and makes the algorithm general. The imaging artifacts and the multiple blinking of a single fluorophore cause the formation of pseudoclusters. DBSCAN may not be sufficient to differentiate between protein clusters (i.e., biologically relevant clusters) and the non-biologically relevant pseudoclusters.¹⁰⁷ To address the limitations of DBSCAN, Mazouchi and Milstein¹⁰⁷ propose a density-based clustering algorithm, fast optimized cluster algorithm for localizations (FOCAL). FOCAL is a grid-based method optimized for fast analysis of SMLM data. It has one parameter that needs to be optimized, density threshold ($minL$). It has a linear time complexity ($O\left(n\right)$). FOCAL has limitations in dealing with small clusters and requires the setting of fine grids. The problem becomes more severe with high levels of noise. Moreover, FOCAL has issues with high-density SMLM data and the overlapped clusters. FOCAL3D¹⁰⁸ is an extension for the FOCAL method that is capable of analyzing 3D SMLM data.

In SMLM data cluster analysis, DBSCAN is used either alone^107,109, 110, 111 or in combination with other clustering algorithms^{82,95,96,102,112,113} to quantify the SMLM clusters.

Voronoi Tessellation-Based Methods

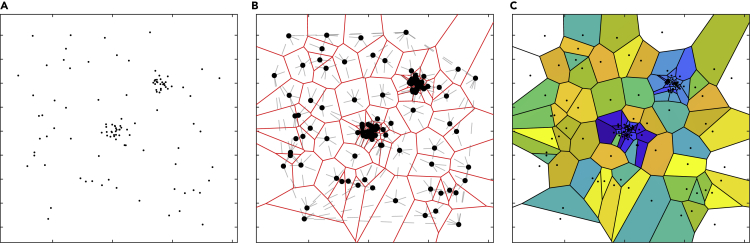
The Voronoi diagram, or tessellation of point clouds, has been used in many applications for various goals, including computational geometry, computational physics, astrophysics, computational chemistry, and biology. In SMLM, a Voronoi diagram is a method used to partition the input space of molecular localizations into regions according to the Euclidean distance between the seed points (i.e., molecules). The resultant polygonal regions are called Voronoi cells, where each cell is centered around one of the molecules. Figure 8A shows a set of points in 2D space, where each point might represent a molecular localization. Figure 8B depicts the Voronoi diagram for the molecular localizations shown in Figure 8A. The Voronoi cells are shown in different colors in Figure 8C. Notice that the Voronoi edges are equidistant from the two nearest molecules. Specifically, the projected perpendicular line from every molecule to any one of its Voronoi cell edges is the shortest distance between every neighboring pair of molecules. Hence, there is no intersection between any Voronoi cells. To learn more about the methods used to find the Voronoi polygons, we draw the reader's attention to the work of Okabe et al.¹¹⁴

Figure 8.

Voronoi Tessellation-Based Method Used to Segment the Clustered SMLM Molecular Localizations

(A) The input space of molecular localization. It has two clusters and noisy/background localizations.

(B) Voronoi tessellation and partitioning the space into polygonal regions (Voronoi cells) in red. The Delaunay triangulation (dual of Voronoi) is shown by gray dashed connections.

(C) The Voronoi cells colored with different colors. The white regions are the Voronoi cells with open regions.

Segmenting SMLM molecular clusters using geometric properties (e.g., area, shape) of the Voronoi cell was done by Levet et al. and Andronov et al.^115,116 The Voronoi geometric characteristics could be used to describe the neighborhood of the molecules. The Voronoi geometric characteristics for every molecule might be different based on the density and data organization. Both of these studies^115,116 depended on the Voronoi cell area to segment the SMLM molecular clusters, where the Voronoi cell area is inversely proportional to the density of the molecules (regions with high molecular densities are composed of Voronoi cells with smaller areas). Both works designed a method to cluster SMLM localizations by comparing their Voronoi cell areas with a reference distribution chosen to be either a spatially uniform¹¹⁵ or CSR distribution.¹¹⁶ Figure 8 explains the concept of the Voronoi diagram method when applied to point-cloud data. Note that the clustered points (Figure 8A) have Voronoi cell areas (Figure 8C) that are smaller than the non-clustered points.

Voronoi tessellation for clustering molecular localization has been applied to structures with various shapes, such as tubular-shaped structures (e.g., microtubules, filamentous, fibrous).^115,116 Voronoi tessellation was also adopted in other super-resolution SMLM cluster analysis applications.^84,86,97

Delaunay triangulation is the companion of the Voronoi tessellation (Figure 8B). It has also been used for analyzing and quantifying super-resolution SMLM data.^86,117 However, Voronoi tessellation methods are different from the Delaunay triangulation with respect to the former's ability to provide a direct estimation of the region of influence,¹¹⁸ and hence is preferable for analyzing SMLM data. Recently, a 3D extension of the Voronoi tessellation method has been proposed by Andronov et al.,¹¹⁸ who used Voronoi volumes as a characteristic of 3D Voronoi cells to segment 3D SMLM clusters. Andronov et al.¹¹⁸ claim that the Voronoi-based methods are able to handle the edge effect (see Ripley's Functions). This is because the border molecules have larger or infinite Voronoi cell areas that prevent them from contributing to the clustering.

Clustering molecular localizations is therefore based on the geometrical properties of the Voronoi cells such as the cell area. Some molecules are considered as part of a cluster based on their individual Voronoi cell areas. This leads to crude segmentation of the clusters. Moreover, some of the border molecules might be excluded from being part of a cluster as they might have very large Voronoi cell areas (e.g., white cells in Figure 8C) compared with inner molecules. In addition, the Voronoi tessellation-based methods might fail in extracting the true molecular clusters from SMLM data with multiple blinking of single fluorophore artifact. Leveraging Voronoi cell area for segmenting clusters from SMLM data with varying cluster densities might be another problem in such methods because the cell areas hugely depend on the underlying molecular densities and the closeness of the nearby clusters.

Graph-Based Methods

Graphs are strong mathematical structures employed to model the interaction between objects or entities of a system. The entities are represented as graph nodes and their interactions are represented as edges.¹¹⁹ Hence, the graphs are considered powerful and rich data structures that encode the connectivity relationships between the different entities of a system. In real-world problems, graphs are frequently complex networks because they have many properties that make them different from other types of graphs such as random graphs.¹²⁰ For example, real-world networks have many subgraphs, modules, patterns, and small-worldness that are not frequent in other types of graphs. Networks are ubiquitous and they are used to study and model many real-world problems effectively. Recently, network analysis methods have been successfully adopted in many fields of study such as the brain, social, computer, road, metabolic, and Internet.121, 122, 123, 124, 125

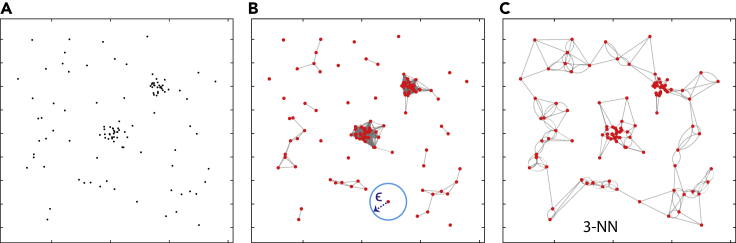
Leveraging graph theory to analyze SMLM data is infrequent in the surveyed literature. Few recent works have been proposed to utilize complex networks and graphs for cluster analysis of super-resolution SMLM data. Various neighborhood networks/graphs can be constructed from the spatial SMLM data. Figure 9 shows two types of neighborhood graphs that can be adopted for analyzing the SMLM data.

Figure 9.

Network/Graph-Based Method Used to Model the SMLM Molecular Localizations for Cluster Analysis

(A) The input space of molecular localization. It has two clusters and noisy/background localizations.

(B) The ε-graph used to construct the network, where every node is connected to all the other nodes within the proximity distance ε.

(C) The kNN graph used to construct the network, where every node is connected to only the k closest neighboring nodes. We constructed the 3-NN graph for illustration.

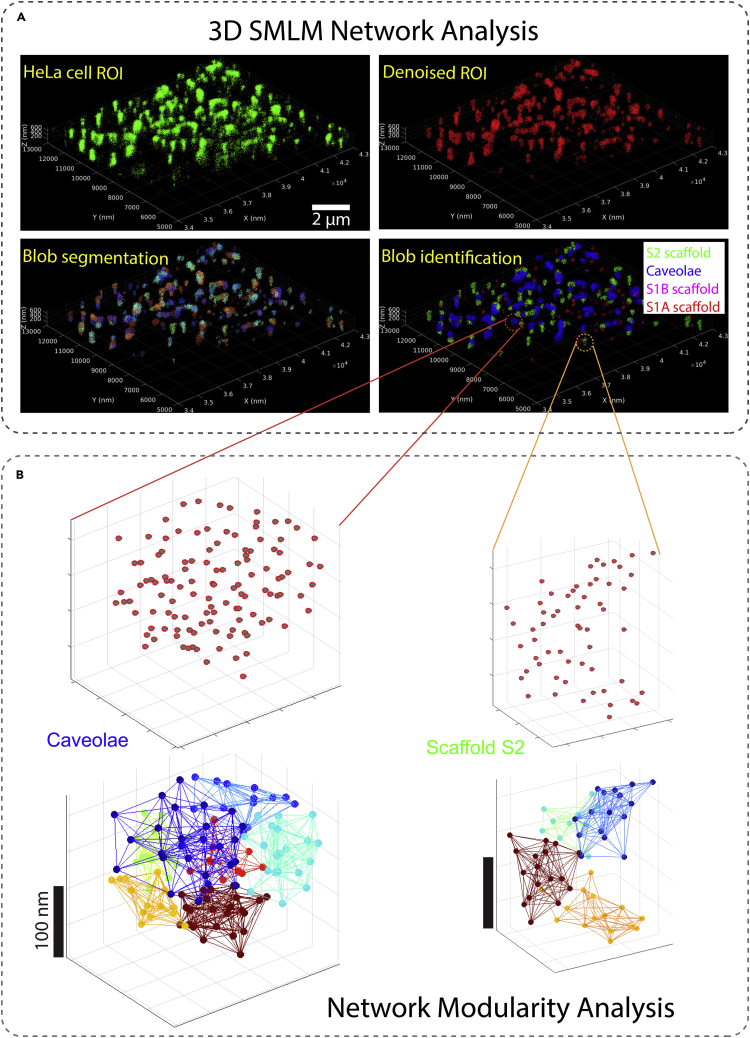
Networks have been adopted to analyze large datasets of prostate cancer data as well as cardiac data from various SMLM modalities.^126,127 A graph-based network method has been proposed by Khater et al. to model SMLM data,¹²⁶ where the nodes represent the molecules and the molecular interactions are represented as edges connecting the nodes. Various network features have been leveraged to pre-process the SMLM data (e.g., correcting for multiple blinking of a single fluorophore artifact) as well as post-processing (e.g., denoising the SMLM data and extracting its constituent molecular clusters). A combination of network analysis and the mean-shift algorithm are leveraged to segment the clusters and obtain 3D representation of molecular localization of diffraction-limited cellular structures, in this case plasma membrane invagination called caveolae. Khater et al.¹²⁸ also proposed a graph-based method to extract graphlet features from SMLM molecular clusters for automatic identification and quantification of various biological structures. Network community detection and modularity analysis have been proposed to decipher the architecture of the molecular clusters.¹²⁹ Communities represent subclusters of molecules within a larger cluster. An example of modular detection within caveolae is shown in Figure 10.

Figure 10.

Graph-Based Network Analysis Methods for SMLM Data Proposed by Khater et al.

(A) Khater et al.^126,129 proposed the 3D SMLM Network Analysis pipeline¹²⁶ to correct for multiple blinking of a single fluorophore, filter out noisy localizations, segment the biological structures into clusters/blobs, and identify the cluster/blob classes.

(B) Network community/modularity analysis¹²⁹ detecting the modules within caveola and S2 scaffold domains.

Some other very recent graph-based methods to analyze and quantify SMLM data are posted as preprints and are still unpublished. We cover them briefly in this survey and categorize them under the graph-based methods. Researchers are exploring new computational methods to analyze the SMLM data. For example, community detection has also been exploited for extracting SMLM clusters.¹³⁰ A segmentation protocol based on persistence homology and DBSCAN has been employed to segment and quantify the topological structure within SMLM data.¹³¹ In this persistence homology method, the density modes were constructed from a graph that connects all the localizations within the same search radius.

Machine-Learning-Based Methods

Machine-learning algorithms (including deep learning) are data-driven approaches. Deep-learning approaches typically require relatively large data that could capture the variations in the dataset. Supervised machine-learning approaches require ground-truth data for training the different learning models, which is difficult to obtain in SMLM data. Machine-learning models can be trained to perform various computational tasks such as predicting, segmenting, and classifying the molecular complexes.

We have not witnessed a large amount of work leveraging machine learning for super-resolution SMLM data for the aforementioned computational tasks. However, some works have applied deep learning for the localization and data acquisition132, 133, 134 but not for cluster analysis.

Khater et al.^126,128 designed a graph-based machine-learning method to automatically identify the class of the molecular complexes from super-resolution SMLM data. They leveraged machine learning for many computational tasks such as determining the scale of clustering, finding the biosignatures for several biological structures, and identifying patterns of the isolated and multiple antibody proteins. They also leveraged deep learning for the biological structures classification task¹³⁵ applied to several SMLM data representations. Sieben et al.¹¹⁰ used machine learning to identify the class of the biological structures from SMLM data. Another recent work that utilized machine learning to detect clustered and unclustered (background) molecules was proposed by Tobin et al.¹⁰³ Williamson et al.¹³⁶ proposed a supervised machine-learning method that is capable of classifying all the localizations from microscopy datasets into clustered or non-clustered classes. Their model is trained on several simulated clustered datasets.

Validation

Validation of the cluster analysis method is critical when applying the various algorithms to find the biological clusters from SMLM data. There is no publicly available dataset with ground-truth class labels for the membership of the localizations to the various cluster types. Hence, most of the methods are unsupervised approaches whereby the ground truth is not provided along with the data. The ground truth might include information such as the number of clusters and their features (e.g., sizes and densities). Also, comparing the different clustering methods requires having benchmark SMLM data with known cluster features. We summarize the main methods used to validate the super-resolution SMLM clustering methods in the following subsections.

Computer Simulations (In Silico)

Synthetic Data

Generating synthetic data with known cluster features (e.g., density, size/volume, shape) has been widely used to mimic SMLM data. Background and noise signals with known distributions are also generated along with the synthetic clusters. Some methods generate synthetic data that is based on specific assumptions, such as generating Gaussian clusters, and the minimum distance between the generated clusters should be greater than some threshold value.^65,118

Given synthetic data, a clustering method is tested on extracting the synthetic clusters first. It could then be used for cluster analysis in experimental SMLM data. To assess the quality of a clustering method, the extracted clusters and their features are compared with the known clusters used in the data generation.

Simulated Data

Simulation could be used to mimic super-resolution SMLM imaging for known biological structures. Simulators have the ability to imitate the SMLM imaging by varying several parameters (e.g., labeling strategy, labeling efficiency, epitope length, number of frames, imaging time, density, background) that might be useful for optimizing the imaging of the experimental sample. Hence, simulation gives more control to study all the possible scenarios that might lead to less imaging artifacts in the data. Moreover, simulation could help in assessing the quality of the adopted clustering analysis methods.

Recently, many SMLM simulators have been developed and posted as publicly available software tools. The simulators facilitate the generation of data for use in cluster analysis applied to various biological structures. Popular SMLM simulators software includes SuReSim,¹³⁷ TestSTORM,¹³⁸ and SMeagol.¹³⁹ Synthetic data generation offers controlled creation of clusters and background with known density distributions (e.g., Gaussian, uniform) and cluster shapes (e.g., circular, tubular). For example, Levet et al.¹⁴⁰ generated synthetic two-color 2D and 3D clusters of circular and square shapes. They also simulated multiple scenarios by varying the number of clusters, their relative positions, their diameters, their density ratios, and background/noise levels.

Data simulators, on the other hand, are designed to mimic realistic labeling and imaging conditions.^46,47 SMLM data simulation considers the inner workings of the SMLM imaging technique and labeling parameters (e.g., epitope length, labeling efficiency, localization precision, number of frames, blinking events per frame) in the data generation, but does not give direct control of the resulting data. For example, Spahn et al.¹⁴¹ used the SuReSim simulator¹³⁷ with specific SMLM imaging parameters (e.g., cluster diameter of 100 nm and various numbers of epitopes per cluster) to generate an image with a field of view of 15 × 15 μm², of some biological structures (e.g., clathrin-coated pits). Sieben et al.¹¹⁰ also used simulation to validate their work. They mimicked their real experimental conditions to generate ground-truth models by controlling the labeling efficiency, localization positions, noise molecules, and fluorophore parameters (e.g., distributions for photon count, localization precision). To evaluate their ERGO emitter density estimation method, Cardoen et al.¹³⁴ used the in silico sequence of 2,500 frames (each 64 × 64 grayscale pixels corresponding to a 2D view of 100 × 100 nm²) from Sage et al.,⁴⁸ which simulates a realistic acquisition of microtubules labeled with the commonly used Alexa 647 fluorophore. They verified their approach on real-world data¹⁴² with a markedly different microscope configuration whereby they showed that aligning the intensity distribution between training and real-world data is sufficient to obtain consistent results without retraining.

Validation via Physical Phantoms

DNA Origami and Nanorulers

DNA origami and nanorulers have been developed to validate many of the SMLM imaging and analysis methods. They are used in super-resolution imaging and microscope calibration.⁴⁷ The DNA origami is designed to allow placing of a known number of fluorescent molecules to nanostructures in defined geometries.¹⁴³ In addition, DNA origami has been used to quantify the protein copy number in the cells using super-resolution microscopy.¹⁴⁴

Validation via Knowledge of Biology and Other Imaging Modalities

Real experimental super-resolution SMLM data can be used in clustering methods validation if the studied clusters of biological complexes have been studied before with other imaging modalities. Biological structures, imaged using electron microscopy (EM), with known size and number of molecules, can be used as ground truths for super-resolution cluster analysis methods. Generally, researchers use simulation or synthetic data to validate their methods and then apply their methods to real experimental data. For example, Sieben et al.^110,145 used EM imaging to validate their multi-color 3D SMLM reconstruction and analysis method. They used dual-color SMLM to image around 300 centrioles per field of view. They then used masking to segment the localizations and DBSCAN to separate adjacent particles. The 3D volumes were reconstructed by EM routines and classified by applying 2D clustering. Khater et al.^126,129 used known information about the cell surface invagination, caveolae, to validate their work. For example, they compared their findings with known topology, size, and number of predicted proteins per segmented structure.

Summary and Discussion

In this paper, we surveyed the state-of-the-art cluster analysis and quantification works applied to super-resolution SMLM. We depended on various criteria to study the papers and tabulate them in Table 2 according to: (1) the biological application of the study; (2) the data acquisition; and (3) the data analysis technique adopted. We then categorized the different clustering methods for easy reference and comparison and identified the pros and cons of these categories in Table 1. Looking at the various methods/algorithms listed in Table 2, we note the following:

• •2D or 3D analysis. Some algorithms have been used only for 2D super-resolution SMLM data analysis, while some other algorithms were used for 2D and then extended to 3D. Dealing with 3D SMLM data is challenging because the axial resolution is usually poorer than the lateral resolution. Also, some biological structures depict structural properties evident in 3D (e.g., hollow structures), so the analysis methods should be designed with care to handle such 3D structures in the denoising, clustering, and identification stages.
• •Pre-processing. Few methods could effectively handle some of the imaging artifacts, such as the multiple blinking of a single fluorophore artifact (e.g., graph-based, statistical methods), while some other methods could not (e.g., Voronoi tessellation-based, density-based methods).
• •Localization uncertainties. Few methods utilized the localization uncertainties (e.g., Bayesian methods) in the analysis, while the majority of the methods did not.
• •Parameterization. The majority of the methods have parameters, while the Bayesian methods are claimed to be parameter-free models. However, Bayesian methods are relatively much slower (e.g., Griffié et al.¹⁰⁵ reported that the processing time for one dataset consisting of 30 small 2D ROIs is ~19 h with user input). Voronoi tessellation-based clustering is parameter-free method if the segmentation threshold is determined by Monte Carlo simulations.¹¹⁶
• •Intra-cluster analysis. The intra-cluster features (features of molecular interaction within a cluster and its subclusters such as network analysis of the molecules, modularity analysis, and subnetworks) lead to understanding the architecture of the biological complexes. Very few methods are equipped with capabilities to extract the intra-cluster features (e.g., graph-based), while the majority of the methods do not have this capability.
• •Machine-learning integration. Most of the methods are not equipped to be integrated with machine-learning approaches for further analysis. Machine-learning approaches require associating features with samples/clusters to train a model. Subtle features could be extracted from graph-based methods (e.g., network measures) and used to train a machine-learning model. Also, some recent deep-learning approaches for graphs^146,147 could be leveraged for analysis of SMLM data.
• •Big-data analysis. The majority of the methods do not scale well to handle the big data generated from the super-resolution SMLM imaging techniques, while some methods are highly efficient and scale up efficiently with big data (e.g., graph-based and Voronoi tessellation-based methods).
• •Cluster shape variation. Some of the methods could discover the clusters with various shapes (e.g., density-based methods). Some methods are more suitable for identifying tubular-like shapes (e.g., Voronoi tessellation-based methods).
• •FOV/ROI analysis. The majority of the surveyed methods were used to analyze small ROIs rather than the whole field of view (FOV). Also, in most methods the ROIs were either selected manually or randomly from the whole FOV. We believe that selecting a small ROI is not a good strategy and will bias the cluster analysis. Analyzing ROI is dependent on its location in the cell. For example, selecting an ROI very close to the periphery of the cell could reveal structures that are different to those in an ROI in the middle of the cell, because the structures at the periphery might have different functions (e.g., focal adhesion) than the structures in the middle of the cell.
• •Software. Some published software is designed to visualize SMLM data with very limited analysis capabilities, such as ViSP.¹⁴⁸ Some published software is limited to analyzing 2D regions of the SMLM data, is unstable, cannot handle the whole FOV but is limited to small ROIs, and is not robust to noise. Some software packages implement more than one method for analyzing SMLM data. In general, we noted limited work on automatic quantification and analysis methods applied to super-resolution SMLM data.
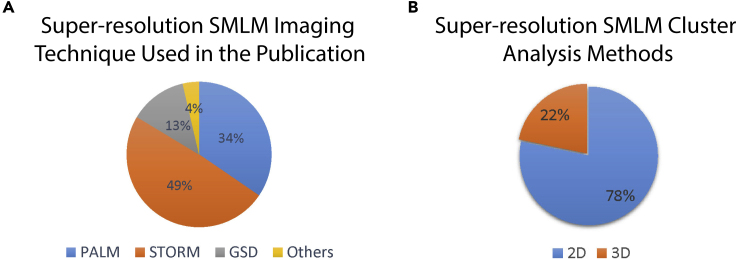
• •2D methods for 3D data. We noted that some methods acquire 3D super-resolution SMLM images; then, in order to leverage existing 2D super-resolution SMLM cluster analysis methods, they project the 3D data to 2D.^81,86 Projecting 3D data to 2D for analysis is not a good idea. Processing data in its 3D native format is much better to (1) avoid artifacts and (2) filter the noisy background localizations. About 78% of the super-resolution SMLM cluster analysis methods are 2D, as shown in Figure 11B. Around 49% of the SMLM imaging used STORM-based techniques as depicted in Figure 11A.
• •Validation. Various ways to validate the methods were used, such as using DNA origami and nanorulers, synthetic data generation, SMLM simulators, and, finally, using real experimental cellular data with known biosignatures. Validation and evaluation of the different methods remains a challenging task for all surveyed methods, as no public dataset is available for benchmarking and assessing the performance of different (post-localization) analysis methods.

Table 1.

Summary of the Main Categories of the Super-Resolution Cluster Analysis and Quantification Methods

Method	Pros (+)	Cons (–)
Statistical	simple and easy to implement; could be used to detect the level of clustering; could be used for both pre- and post-processing	restricted to analyze homogeneous clusters; edge effect; some normalization based on Poisson point process assumption
Bayesian	can handle SMLM localizations and their associated uncertainties; parameter-free model	very slow; sensitive to the prior settings; used in combination with other methods; requires generation of thousands of cluster proposals; very sensitive to imaging artifacts
Density-based	efficient in noise removal; could be used to discover clusters with various shapes	clustering is conditioned on the minimum density of molecules within neighborhood radius; slow scaling with the number of localizations; ambiguity and subjectivity in selecting the algorithm parameters affect its performance; cannot deal with varying cluster densities and hollow clusters
Voronoi-based	fast and scalable to handle big data; efficient in noise removal; sensitive to clusters of specific geometry (e.g., tubular-like structures).	might cause problems in segmenting data with non-isotropic distribution; limited multi-scale capabilities; might not be good for segmenting hollow clusters
Graph-based	fast and scalable to handle big data; easy to be integrated with machine/deep learning; robust to noise; capable to extract per-point and per-cluster features; topological graph is invariant to the dimensionality of the data; extracting heterogeneous clusters capability; can be used for both pre- and post-processing; all the other methods can be derived from the graph-based method	graph construction is not straightforward for big data; might cause problems in segmenting data with non-isotropic distribution; clustering results are highly dependent on the graph construction method

The cons (+) and pros (–) for each of the clustering analysis methods are also shown for comparison.

Figure 11.

SMLM Imaging Techniques and Dimensionality Used in Various Publications

(A) The distribution of the publications based on the super-resolution SMLM imaging technique used in the study.

(B) The distribution of the publications based on the dimensionality of the super-resolution SMLM cluster analysis method.

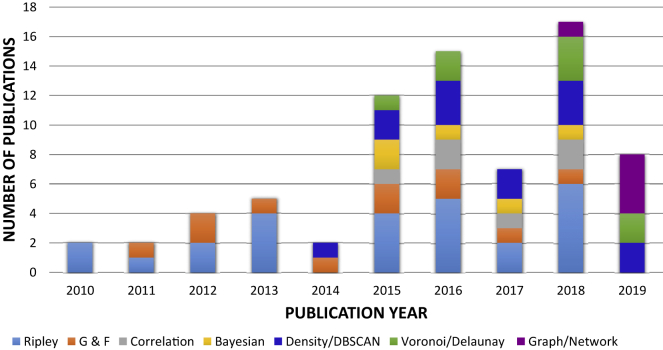
We summarize the number of publications (listed in Table 2) per year categorized according to super-resolution SMLM cluster analysis methods used in the study in Figure 12. Our survey shows that before 2014, only a couple of methods (i.e., statistical) and few studies addressed analysis of SMLM data. After 2014, researchers started exploring new clustering methods and, at the same time, the number of publications per year started growing, except for 2017. Graph-based cluster analysis methods applied to super-resolution SMLM data started appearing in 2018. We expect that more clustering methods based on graphs will appear in 2020 and onward. Ripley's functions are the most popular methods used for super-resolution SMLM cluster analysis over the years, as depicted in Figure 12. Furthermore, given their successes in analyzing other imaging modalities, we anticipate growth in the number of methods that leverage and adapt machine-learning (and particularly deep-learning) methods for SMLM analysis.

Figure 12.

Number of Publications per Year (Starting from 2010) Categorized According to Super-Resolution SMLM Cluster Analysis Methods Used in the Study

Conclusions

The SMLM imaging modality is relatively new and is creating exciting opportunities to help us understand the structure and function of many macromolecular complexes below the diffraction limit of fluorescence microscopy. The data it provides can enable discoveries, but we note that there is still a need and an opportunity to develop methods and tools that can (1) read data from different super-resolution microscopes and pre-process the data to handle image-acquisition artifacts, (2) provide different visualization alternatives, (3) analyze a large number of datasets in 3D, (4) extract and quantitatively describe the structural geometry and interaction of the underlying biological structures, and (5) do so in a way that is either robust to parameter settings or provide intuitive descriptions of parameters easily communicated to and understandable by the end user.

Our observations from conducting this review revealed that studying the various methods adopted for cluster analysis and quantification requires a benchmarking dataset and evaluation measures for the assessment of the quality of clusters. The benchmark dataset should be available to validate both 2D and 3D cluster analysis methods. It should have several types of clusters with various densities, shapes, sizes, and noise levels.

Our review also motivated us to highlight the importance of strong interdisciplinary collaborations between computational scientists, biophysicists, biochemists, and biologists for novel breakthrough discoveries. Furthermore, artificial intelligence algorithms (e.g., machine learning) need to be incorporated in the analysis to (1) get rid of the subjectivity and bias, (2) robustly analyze the generated big data, and (3) automatically identify the distinct biological structures and their constituent biosignatures.

In this Review, we have summarized and compared the various computational methods for SMLM cluster analysis and quantification. We note that network/graph-based methods have more capabilities such that they could be used for pre-processing (e.g., correcting for multiple blinking of a single fluorophore artifact) and post-processing (e.g., filtering, segmenting, and identifying the biological structures) of the SMLM data. Graph-based methods could be applied to extract per-point and per-cluster features for analyzing 3D SMLM data, analyze the whole FOV, process big data (millions of localizations), and extract heterogeneous clusters. Graph-based methods are well suited to extract intra-cluster features and could be integrated with the machine-learning algorithms for automatic analysis and quantification of the underlying clusters.

In the end, we believe that synergy and harmony across research disciplines such as biophysics, biology, imaging, biochemistry, and artificial intelligence, among others, are required to improve our understanding of the underlying protein cluster structure and function. The extraordinary SMLM imaging modality and elegant computational methods will lead to a better understanding of protein interactions in several subcellular structures, consequently enhancing the modeling of antibodies and drug design to obtain better disease therapies.

Details of the criteria used in Table 2 are as follows:

• •Application: the main biological application of the related studies. The imaged protein and biological model
• •Imaging method: imaging technique applied in the study (the study may apply more than one imaging method; we are here focusing on the SMLM super-resolution methods only)
• –PALM: photoactivated localization microscopy
• –hsPALM: high-speed version of PALM
• –iPALM: interferometric PALM
• –FPALM: fluorescence PALM
• –STORM: stochastic optical reconstruction microscopy
• –dSTORM: direct STORM
• –GSD: ground state depletion
• –GSDIM: GSD followed by individual molecule return
• –HILO: highly inclined and laminated optical sheet
• –SOFI: super-resolution optical fluctuation imaging
• –SIM: structured illumination microscopy
• •Dimensionality: is either 2D data analysis (for 2D acquisition) or 3D data analysis (for 3D acquisition) applied for the provided method?
• •Resolution/localization precision: the resolution of the images on which the reported analysis is applied. (We report the localization precision if the resolution is missing.) The localization precision is much smaller than the spatial image resolution
• •Area/volume: the total area or volume where the analysis is applied
• •#frames per image: number of frames per super-resolution image (in thousands [K]).
• •#localizations (blinks, events, pointillist, etc.): the total number or density of acquired blinks/molecules (in PALM-based methods)/localization events as described in the study
• •Dataset size: dataset size (how many cells, how many experiments used in the work)
• •Cluster analysis method: the clustering analysis method(s) used in the work
• •Whole-area visualization: is cluster visualization of the whole analyzed area provided (after cluster analysis)?
• •Surface reconstruction for individual clusters: is surface reconstruction for individual clusters provided?
• •Cluster properties/descriptors: does the study provide analysis on any cluster properties? Yes or no. If yes, how many features have been used in the analysis?
• •Intra-cluster analysis: does the study provide detailed analysis at intra-cluster levels (network analysis of the molecules, modularity analysis, subnetworks, etc.)?
• •Machine learning and cluster classification: is machine learning used to automatically classify the clusters?
• •Multi-scale analysis: is multi-scale analysis supported and used by the method?
• •Software: is software available for the method/algorithm? Yes (software name) or no.