Avoid Oversimplifications in Machine Learning: Going beyond the Class-Prediction Accuracy

Abstract

Class-prediction accuracy provides a quick but superficial way of determining classifier performance. It does not inform on the reproducibility of the findings or whether the selected or constructed features used are meaningful and specific. Furthermore, the class-prediction accuracy oversummarizes and does not inform on how training and learning have been accomplished: two classifiers providing the same performance in one validation can disagree on many future validations. It does not provide explainability in its decision-making process and is not objective, as its value is also affected by class proportions in the validation set. Despite these issues, this does not mean we should omit the class-prediction accuracy. Instead, it needs to be enriched with accompanying evidence and tests that supplement and contextualize the reported accuracy. This additional evidence serves as augmentations and can help us perform machine learning better while avoiding naive reliance on oversimplified metrics.

Graphical Abstract

The Bigger Picture

There is a huge potential for machine learning, but blind reliance on oversimplified metrics can mislead. Class-prediction accuracy is a common metric used for determining classifier performance. This article provides examples to show how the class-prediction accuracy is superficial and even misleading. We propose some augmentative measures to supplement the class-prediction accuracy. This in turn helps us to better understand the quality of learning of the classifier.

Class-prediction accuracy is an evaluative method for machine-learning classifiers. However, this method is simple and may produce spurious interpretations when used without caution. Contextualization, dimensionality reduction approaches, and bootstrapping with Jaccard coefficients are possible strategies that can be used to better inform the learning outcome.

Main Text

Introduction: Classification and Class-Prediction Accuracy

Classification, a common task in machine learning, is the process of predicting the identity of a new sample using a trained machine learner. The sample identity is referred to as the class label, e.g., in a scenario where we are training a machine-learning algorithm to differentiate gender, “male” and “female,” are class labels that are attached to each person. A trained machine learner, having learned decision rules from training data, is referred to as a classifier. Classification is also referred to as “class prediction.”

Before it can be used for prediction, a machine learner must be trained with data. These data are known as training data (or a training set). The class labels associated with samples in the training set are known. The objective is to identify rules and feature sets that allow differentiation of the various class labels. For example, if the purpose is to predict biological gender, the class labels could be “Male” and “Female” and the feature set, which is a set of informative variables, may consist of quantitative measurements such as “height,” “weight,” and “hair length,” and qualitative observations such as “presence of facial hair.” If the samples, rules, and the feature set are informative, the classifier's predictions on new samples should be often, if not always, correct.

The set of new samples meant for evaluating prediction is known as test data. In test data, the class labels are known but not supplied to the classifier. Instead, the classifier makes a “guess” based on its “previous experiences.” There can only be two outcomes, correct or wrong. The sum of correct guesses over all guesses is the class-prediction accuracy.

The class-prediction accuracy provides a snapshot of learning performance: If the classifier has learned well, the class-prediction accuracy is expected to be high. However, the class-prediction accuracy does not inform on the quality of learning. As in humans, high examination scores do not necessarily imply that students truly understand the subject matter; the same may also be said in machine learning. The class-prediction accuracy does not inform on the mechanism and processes undertaken in order to arrive at the prediction, and thus offers limited explainability.

Elaborating on the exam-taking analogy, suppose two individuals, pA and pB, were preparing to take an exam but differed in learning style: pA learned by critical evaluation of the teachings across her existing knowledge while pB simply memorized. Both scored 99% on the test; thus, we cannot use grades to inform that A has learned better. Suppose too we have two machine learners mX and mY, both of which were trained on the same dataset and were demonstrated to exhibit 99% class-prediction accuracy during validation. This also does not mean that mX and mY have learned in the same way. In fact, when challenged with future datasets, both mX and mY may exhibit wildly different class-prediction accuracies, suggesting that they have not learned from the data in the same way.¹ As with human learners, when we judge the value and depth of machine learning using a highly reductionist metric, we risk oversimplification, and this oversimplification does not inform us about mechanism or applicability of the classifier in real-world scenarios. To understand the implications of oversimplification, here we cover six problems associated with the class-prediction accuracy and also offer some remedies (or augmentative tests) to help analysts better understand the machine-learning models.

Problem 1: High Accuracy Does Not Imply Reproducibility

Consider Table 1. Five different statistical approaches (single protein t-test [SP], hypergeometric enrichment test [HE], subnetwork testing [SNET], fuzzy subnetwork testing [FSNET], and paired fuzzy subnetwork testing [PFSNET]) were used to obtain five different feature sets for training a naive Bayes machine-learning method to differentiate normal tissue from kidney cancer tissue. The full details on how the statistical methods differ are irrelevant (but can be accessed in Goh and Wong²). One might note that while the feature sets are of different sizes across different methods, they all give rise to relatively high cross-validation accuracy (this is the average of class-prediction accuracies based on the N-fold cross-validation approach3, 4, 5).

Table 1.

Number of Selected Features and Consequent Cross-Validation Accuracy of the Five Statistical Approaches Used and Discussed in This Paper

Method	No. of Features	CV Accuracy
SP	2,662	1.00
HE	570	0.75
SNET	130	0.98
FSNET	141	1.00
PFSNET	200	1.00

Superficially, it would seem that when class-prediction accuracy, based on the N-fold cross-validation (CV accuracy; Table 1) is high, the classifiers are working well. However, high variation in the number of reported features should give us pause, as each method is saying different things about which features are important. It turns out that high CV accuracy says nothing about the stability of the feature set (Figure 1). Why is this important? Deriving a good-quality feature set is crucial toward developing a sound model that is based on highly relevant variables. While each of the five statistical methods all give good CV accuracy, this metric alone tells us nothing about the quality of the feature set. It only informs that these feature sets can be used for predicting the class labels.

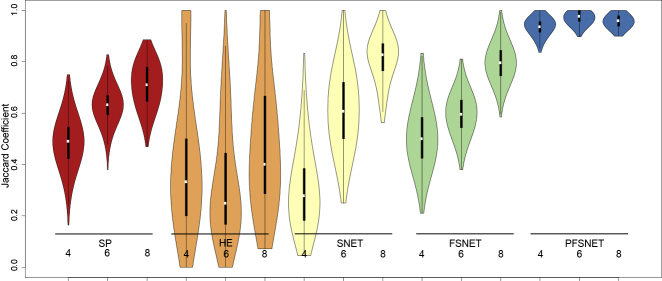
Figure 1.

Agreement of Feature Sets Selected from Different Samples of the Same Population Is Much Poorer for Methods that Use No or “Wrong” Domain Knowledge

Colors denote different statistical approaches. For each approach, bootstrap resampling is performed 1,000 times on three sampling sizes (4, 6, and 8). Each resampling is compared against one another, and their similarity denoted by the Jaccard coefficient (y axis). Some methods exhibit high agreement (e.g., PFSNET) while in others, agreement rates are highly fluctuating (e.g., HE).

To know whether or not a statistical or a machine-learning method is generating a good-quality feature set (which in turn suggests that it is using the “correct” domain knowledge), a combination of the bootstrap with the Jaccard coefficient is useful (Figure 1). The bootstrap is a random sampling procedure that allows us to repeatedly resample our data at a given n. With each resampling i, we apply a statistical test and then identify its feature set i. We may compare all pairwise resamplings using the Jaccard coefficient. Given the feature sets of two resamplings i and j, the Jaccard coefficient J is the intersection of feature sets i and j divided by the union of feature sets i and j. J is bound between 0 and 1, where 0 means complete dissimilarity and 1 means perfect similarity. A J distribution concentrated near 1 is a proxy for reproducibility, i.e., the tendency to obtain similar feature sets (and hopefully, consequent predictions) in analysis. Since the comparisons are performed pairwise, given 1,000 resamplings, (1,000 × 999)/2 Jaccard coefficients are generated.

Graphical visualizations are useful for summarizing the J distribution, especially when numerous. One may use violin plots with embedded box plots (Figure 1). The box plot readily conveys information on the median, interquartile range, and first and 99th percentiles. The undulations of the “violin,” which is really a symmetrized version of the density plot, conveys information on potential subpopulations. (If a double bump is observed, this would suggest two underlying populations. The box plot's median would not capture this.)

There is no immediate relationship between the size of the feature set and feature set stability (Table 1 and Figure 1). We can see that even for methods that provide similar CV accuracies (FSNET and PFSNET both have CV accuracies of 1.00), they exhibit different feature set stabilities.

Conversely, if a statistical method provides similar feature sets consistently during the bootstrap and is associated with an overall decent CV accuracy, one may have higher confidence that the statistical method is a good one. In addition, when the feature set is stable and gives rise to good CV accuracy, it is likely that it would also make for more reliable and generalizable performance in future.

Problem 2: High Accuracy Does Not Imply Meaningfulness

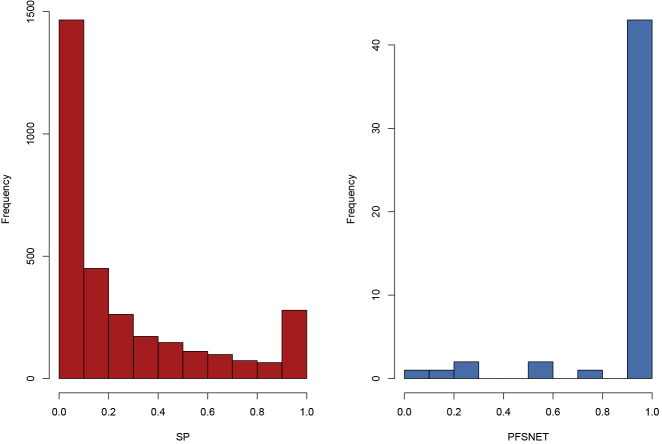
In Problem 1, we assert that an overall higher Jaccard coefficient is indicative of feature set stability and, therefore, reproducibility. Meaningfulness, on the other hand, is determined by the relevance of each feature, i.e., how it contributes directly toward class differentiation instead of being merely “correlated.” This can be assayed by the “recurrence distribution” of individual features. (The identities of all features are known. What is being measured is the number of times each feature is reported as significant per bootstrap.) To obtain this, one may combine the bootstrap with a histogram (Figure 2), where the y axis is a frequency count of the variables and the x axis is a proportion from 0 to 1, where a peak near 0 means a strong majority of variables are only observed once or rarely across all bootstrap resamplings. Conversely, a peak at 1 means that a strong majority of variables recurs. Besides assaying the presence or absence of a peak at 1.0 on the x axis (Figure 2), we can infer a high-quality feature set by only using variables that recur 100% of the time.

Figure 2.

Recurrence Distributions across Different Feature-Selection Methods

The y axis corresponds to the frequency count of the variables, and the x axis is a proportion from 0 to 1, where a peak near 0 means that a strong majority of variables are only observed once or rarely, across all bootstrap resamplings.

Comparing Table 1 with Figure 2, it is seen that although SP has high CV accuracy, this does not translate to good recurrence distributions. A good proportion of features is rarely observed across resamplings, and even with increment of sampling size the left peak remains persistent. This is in contrast with approaches such as PFSNET, which shows a positive effect by sample size increment, with its peak on the right side (100% recurrence rates). If a statistical or machine-learning method uses the correct intuition or correct domain information, recurrence should be high.

In another example where we can use a similar concept of recurrence and meaningfulness, a high-quality feature set was obtained by taking the intersections among the best-performing published breast cancer signatures.^2,6, 7, 8 This is similar to the use of the recurrence distribution, except that we did not do the bootstrap ourselves (we merely considered each published cancer signature as an independent sampling of the underlying population, and treated those genes that are found in common as “high recurrence”). This feature set inferred from high recurrence, the Super-Proliferation Set, is found to be highly predictive of aggressive breast cancers and is also highly generalizable, even when tested against seven rounds of independent validation.^7,8

Again, comparing Table 1 with Figure 2, a higher CV accuracy does not imply high recurrence distribution. SP has a CV accuracy of 1.00 but the recurrence distribution suggests that many of the features are non-recurrent. If SP is being used anyway as the feature-selection method, one can still isolate a high-quality feature set by simply considering only those variables that give rise to the right peak (near to the x axis value of 1.00; Figure 2). This higher-quality feature set, when used for training the classifier, will provide a good CV accuracy but is also likely to be more generalizable in real-world applications as it is often detected despite many different rounds of resampling.

Problem 3: High Accuracy Does Not Imply that Features Used Are Better Than Random

Statistics is undergoing an image crisis: from attacks on the instability of the p value9, 10, 11, 12, 13 and general non-reproducibility of expensive high-profile studies¹³ to inane proposals such as further reducing statistical cutoffs from the generally accepted 0.05 to 0.005,¹² never-ending debates on whether the confidence interval is the more intuitive alternative to the p value,¹⁴ and even the complete abolition of statistical significance testing with nothing tangible to offer in its place.¹⁵ Besides the general imperfections of statistical tools, we also know that hidden confounders due to batch effects and hidden subpopulations¹⁶ can produce spurious associations.¹⁷ The implication is that these issues percolate to machine learning by creating misleading decision rules or diluting the information value of the feature set.

In 2011, Venet et al. reported that published breast cancer signatures did not do better at prediction than randomly generated signatures or irrelevant signatures.⁶ Although they did not formally use any machine-learning methods (instead relying on the p value provided by the Cox hazard ratio), the lessons apply to machine learning nonetheless. For each signature, they compared the performance (based on the significance of the p value with the phenotypes) of a published signature against a distribution of randomly generated signatures (which are obviously non-clinically relevant) of the same size as the published signature, whereby it was shown that many reported signatures did worse than half of the randomly generated signatures.⁶ We later clarified that this effect is dependent on the size of the published signature and also the proportion of growth-related proliferation genes.⁸ We also demonstrated that a truly meaningful signature can never be beaten by randomly generated signatures.⁷ This insight is useful because it means that the information quality of a feature set can be inferred by comparison not by its direct correlation with the class labels but against randomly generated versions of itself. This does not require a novel test in itself; rather, using Fisher's permutation test (also known as the randomization test) suffices.¹⁸

We have applied the idea of comparing the performance of a feature set in machine learning against randomized variants of itself. The CV p value is the proportion of the number of times a random feature set beats the inferred feature set over all randomization trials (Table 2). For example, a CV p value of 0.01 means that out of 1,000 trials, 10 randomly generated feature sets trained a classifier that produced a CV accuracy equal to or higher than the CV accuracy of the actual feature set.

Table 2.

Classifiers Trained on Feature Sets Selected by Statistical Approaches

Method	No. of Features	CV Accuracy	CV p value
SP	1,124	0.98	0.91
HE	162	0.98	0.91
SNET	21	0.84	0.06
FSNET	36	0.96	0.06
PFSNET	65	0.92	0.06

All approaches have high CV accuracy, but this does not mean that this good CV accuracy in itself is meaningful or specific.

Given the five different statistical feature-selection methods, a high CV accuracy does not imply significant CV p values. This may be due to issues with confounding,^17,19,20 poor information value of features,² sheer chance in what is sometimes also referred to as the winner's curse,^9,21 or high class-effect proportion, whereby most of the evaluated features are correlated with class labels such that it does not matter statistically which is picked.²²

Since class-prediction accuracy, inferred from the CV accuracy, does not imply that randomized feature sets will not do just as well, the randomization test is useful for providing this information. Interestingly, the CV p value is in itself also a useful indicator of statistical significance, whereby we are assured that random feature sets do not outperform the actual feature set (the CV p value is in fact equivalent to an empirically derived p value). Therefore, we state that high accuracy does not imply significance.

Problem 4: Same Accuracy Does Not Imply that Classifiers Have Learned in the Same Way

So far, we have seen that class-prediction accuracy does not imply reproducibility, meaningfulness, or significance. But what if we have two classifiers, trained on the same data, and reporting the same high class-prediction accuracy on the same test data?

It turns out that two classifiers reporting the same accuracy on a specific test set can disagree greatly in future test sets.¹ In one example, two models reporting 90% accuracy on a test set can disagree on ∼80% of future cases (B. Teodora, personal communication). This means that two classifiers reporting the same accuracy does not mean they have learned in the same way.

So, what is happening here? The class-prediction accuracy is a highly reductionistic measure, and so does not provide any information on decision rules or learning mechanism. This is intuitive if we simply think about the human condition: two students who happened to score the same grade on an exam should not be expected to perform similarly in all future exams.

However, if the two individuals are probed and examined further to ensure that they used similar modes of learning and have adopted similar mechanisms for understanding the subject matter, it is likely that in future exams their performance will also be consistently similar. In other words, besides simply relying on a single point measure, it is better to try to understand the mechanisms that gave rise to the result. Indeed, even if similar mechanisms of understanding are utilized, it also does not ensure that every single time the same class-prediction accuracy will be reported. After all, the winner's curse can strike at any time.⁹

Interestingly, this problem of performance divergence is quite readily solvable. In the first place, we should not assume that the performance of two classifiers can be readily benchmarked on a single test dataset. This is, unfortunately, a limitation of the single independent validation approach. Since the divergence in performance is observable in future test cases, it is the distribution of multiple test cases that may be useful in informing about the learning of the classifier. We may assert that a classifier that has learned well is one that universally or consistently reports high accuracy when challenged repeatedly with future test cases.⁷

Problem 5: High Accuracy Does Not Come with Explainability

The internal learning processes of many machine-learning and artificial intelligence (AI) models are “black boxes.” Simpler machine-learning models try to formulate rules based on the input variables while advanced ones, e.g., neural networks, may try to construct higher-level features from the more basic input features. These higher-level features are further aggregated across different learning layers before the final prediction is assimilated in the final layer.

Many machine-learning algorithms do not allow their decision-making layer to be examined, yet it is the soundness and quality of features used by a prediction model that is crucial for understanding the model and assessing its soundness. If the features themselves, and the interactions among these features, make sense, it is highly likely that the classifier will do well in any validation test. If it does not, we may suspect that there is something wrong with the validation data instead.

So far, the manifestations of reproducibility, meaningfulness, significance, and divergence are symptomatic proxies for explainability. However, obtaining information on explainability from classifiers cannot be achieved easily if the model does not permit inspection of its decision-making layers.

Therefore, until such models come along we suggest temporary work-arounds. In Table 1, we see methods such as PFSNET performing strongly in terms of reproducibility, meaningfulness, and significance while other approaches such as SP stumble, despite both approaches performing similarly in accuracy. So, what is different? The difference is in terms of the information value of the variables. SP uses information from individual proteins while PFSNET looks at information on the level of protein complexes. In biology, proteins are organized into higher functional units known as protein complexes, where there are many useful information constraints: members are involved in the same process; if members are missing, the complex cannot form; and members in the same complex are autocorrelated. In other words, the protein complex is a natural higher-order feature that can be looked at without the aid of a machine learner. We refer to the process of transforming a lower-order feature set into higher-order features as “contextualization.”

So why does contextualization help? First, looking at autocorrelated structures where members must be involved in a shared process helps in reducing the likelihood of false positives seeping into the feature set. Suppose the basal false-discovery rate is 25%. This implies that in a given feature set, we expect a quarter of these to be false positives. However, we may reduce this likelihood of admitting false positives by considering higher-level constructs. Suppose there is a complex C comprising members a, b, c, d, and e. We may express the likelihood of the complex existing as a function of its observed components. If only a, b, c, and d are reported as present (subject to the 25% false-discovery rate), we may then say that the likelihood of C existing is 4/5 × (1 − 0.25) = 0.6. However, if all components are reported as present, the likelihood of C existing is 5/5 × (1 − 0.25) = 0.75. We may also assert that P(a exists|C exists) = 100%; that is, if the complex C exists, its constituent members must also exist. Moreover, assuming all five components of C are reported as present, the likelihood that a given reported component exists is no longer 75%, it is P(a exists|C exists) × P(C exists) + P(a exists|∼C exists) × P(∼C exists) = 0.75 + 0.75 × 0.25 = 0.94.

A second advantage of contextualization is dimensionality reduction. This is particularly useful for overcoming curse-of-dimensionality problems when there are a limited number of samples (or observations) relative to high numbers of measured variables. When there are a limited number of observations given many variables, the chance of incurring false positives and false negatives becomes higher. Correction techniques in statistics for such problems tend to be conservative, favoring reductions in false positives over reducing false negatives. For example, multiple test corrections, such as the Bonferroni, limit false positives by adjusting the p value threshold according to the number of tests performed. This tends to be lead to overkill, as it mistakenly assumes independence among variables. If the variables exhibit some degree of collinearity, such approaches can unintentionally shrink the feature set such that it is no longer comprehensive. Reorganizing proteins into higher-order complexes means that within each complex, genes are expected to be highly correlated and are treated as a single entity (instead of multiple). Because there are fewer complexes relative to proteins, it also reduces the overkill impact from multiple test correction.²³

Besides being higher-level organizations, complexes can also offer explainability because these entities are highly enriched with meta-information and annotations.²⁴ Knowledge about where they exist, what they do, and the various pathways and mechanisms associated with them already exist. These can be leveraged to achieve explainability.²⁵ For example, if our feature set contains complexes associated with cancer pathways in a study of breast cancer, we should feel quite assured. Conversely, if the feature set instead comprises hibernation pathways, it is likely that errors in computation might have occurred.

However, what if we do not have good-quality context? Ordination-based approaches such as principal components analysis (PCA) can also help. PCA is a technique that resolves high-dimensional variable space into a reduced set of principal components (PCs) that are orthogonal to each other. This means that each PC acts independently of others and can be effectively considered a variable in its own right. Indeed, using PCs as feature sets have been proposed in the literature as a possible statistical strategy,^26,27 and have been proved to work in actual practice.²⁸ To provide explainability, each PC can be annotated with some meta-information; the easiest way of achieving this is to apply a statistical test on each PC to check for correlation with a specific co-variate.^28,29

Although most machine learners do not offer explainability, some do, a classic example being decision trees. While not as powerful as more recent implementations based on ensemble approaches or neural networks, decision trees nonetheless offer highly interpretable insights such that if the order of rules makes sense, this means that the classifier has learned in a sensible manner and is therefore not likely to falter in future validations (Figure 3). A key weakness of the decision tree is that it does not scale well when there are many variables and/or the variables offer similar information value due to autocorrelation. Another weakness is that when there are two or more key independent explanations for the class labels a decision tree forces these to be merged, thus convoluting two independent sets of rules. For example, suppose bad genes cause lung cancer and smoking too many cigarettes also cause lung cancer. These are independent causes. There should thus be two rules: (1) if got bad genes, then lung cancer; and (2) if smoke a lot, then lung cancer. However, it is not possible to express this knowledge in a standard decision tree: the tree forces us to pick one of the conditions to be the “root,” so we obtain a tree such as: if got bad genes then lung cancer else {if smoke a lot then lung cancer else no lung cancer}; or a tree such as: if smoke a lot then lung cancer else {if got bad genes then lung cancer else no lung cancer}. Both weaknesses can lead toward tree structure instability or create unnecessary complexity whereby the tree becomes very deep by attempting to force-fit as many variables as possible. In such cases, it is useful to transform the variables into higher-order features (e.g., using context or ordination methods) before input to the decision tree.

Figure 3.

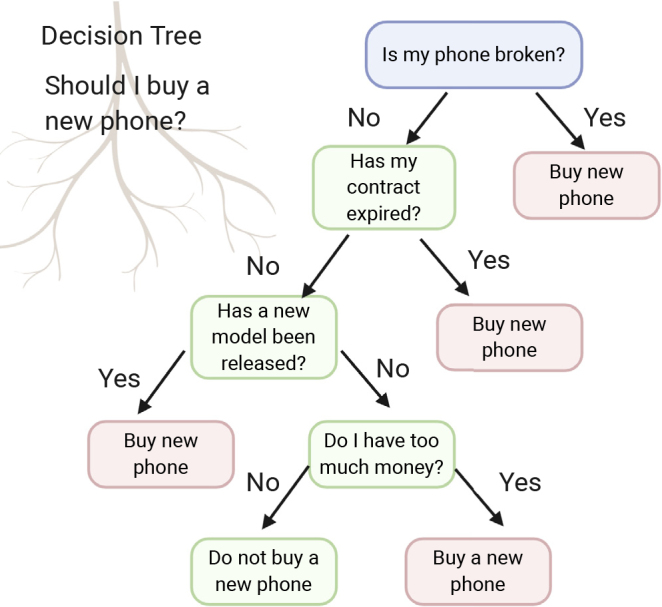
Decision Tree Using Realistic Rules to Determine Phone-Buying Considerations Made Using BioRender (biorender.com)

Explainability provides a rational basis for machine learning and is far more important than a blind reliance on traditionally used metrics such as CV accuracy. This is because any cross-validation on an AI's performance is inherently limited in its world view, and that when challenged with all possibilities no one AI or method should be expected to be superior to another. This is also known as the “no-free-lunch” theorem.¹ The no-free-lunch results are subtle and can generally mean, over all possible inputs, that two separate models are likely to disagree over a large fraction of these inputs. Not all inputs are necessarily real or correct, but these do constitute a subset of all possible inputs. The models only need to be shown to agree on real inputs (while their disagreement on other irrelevant inputs can be disregarded). This approach is analogous to the way class-label permutations are performed to compute values in a network-based feature method such as PFSNET.³⁰ We do not generate null samples by arbitrary permutations. We generate only by class-label permutations. This is because null samples are required to satisfy or are assumed to satisfy the null hypothesis (which in PFSNET's case is that the feature is irrelevant to class).

As discussed by Giraud-Carrier and Provost,³¹ if cross-validation is to be used for inducing meaningful performance differentials, it requires incorporation of a meaningful meta-learning component during the training process. However, in large part no-free-lunch critics did not or were unable to formally characterize which subset of input to restrict it to. Therefore, they cannot find a reasonable way to escape the no-free-lunch theorem.

Problem 6: Accuracy Depends on Class Proportion of the Test Set

The final issue is that accuracy depends on class proportion (the relative representation of class labels). For example, if male and female are equally represented in an evaluation of gender, the class proportion would be one-half for either gender of the test set. If this differs too much from real-world proportions, it can be misleading.

In fact, ensuring a test set's fidelity to actual population distributions is an important methodological point that is often overlooked. If a test set is not faithful to actual population distributions, some typical performance measures (e.g., accuracy and precision) determined from the test set may considerably deviate in new data. For example, let us say we have a well-trained classifier C with 80% sensitivity and 90% specificity. On a test set A where the positive samples fully reflect the properties of positive population and negative samples fully reflect the properties of negative population but the proportion of positive to negative samples is 100:1,000, the precision of this classifier C on test set A will be 80/(80 + 100) = 44% and its accuracy will be (80 + 900)/(100 + 1,000) = 89%. On a test set B where the positive samples fully reflect the properties of positive population and negative samples fully reflect the properties of negative population but the proportion of positive to negative samples is 1,000:100, the precision of this classifier C on test set B will be 800/(800 + 10) = 99% and its accuracy will be (800 + 90)/(1,000 + 100) = 81%.

As we can see, the performance changes dramatically with different class proportions. If the actual population distribution is 1,000:100, the performance on test set B is one that will give a better sense of what the performance of classifier C will be on real data, whereas the performance on test set A will completely mislead.

Given an actual 1,000:100 population distribution, test set A can be calibrated so that every positive sample counts as 100 while every negative sample counts as 1. After this calibration, the “proportion” of positive to negative in test set A becomes 100 × 100:1000 (= 10,000:1,000 = 1,000:100), faithful to the actual population distributions, and the calibrated precision becomes 99% and accuracy 81%, more closely reflecting the performance of classifier C that one can expect with real data (assuming the positive and negative samples in test set A are indeed respectively representative of the positive and negative populations).

Conclusion

Class-prediction accuracy is an oversimplified measure that does not inform on the reproducibility of the results or meaningfulness of the feature set. It is also not a proxy for statistical significance, as high accuracy can also at times be achieved with meaningless, randomly assimilated feature sets. Similar accuracies, given a single benchmark, are also an unreliable indicator of future performance. Therefore, we propose the use of additional measures to augment the class-prediction accuracy. While additional measures provide informative proxies on how learning is achieved, the best way is to extract explainability from the classifier. When it is not possible to isolate the decision-making layers, using context or ordination approaches helps. One should also note that class-prediction accuracy is sensitive to class-proportion effects.

Given the limitations of evaluative metrics (the class-prediction accuracy is not the only oversummarization-type metric), a “black box” produced by a machine-learning method may not be all that we think it is. We advise that it is used with caution and avoided unless there is no choice: if the data are sound and the feature set is informative, good results will be obtained even with simple statistical tests anyway.

Experimental Procedures

Lead Contact

The lead contact is W.W.B.G. E-mail: wilsongoh@ntu.edu.sg.

Materials Availability

This study did not use any materials or unique reagents.

Data and Code Availability

This study did not generate datasets.

Biographies

About the Authors

Sung Yang Ho is a Research Assistant in Dr Goh's BioData Science and Education laboratory at the School of Biological Sciences, Nanyang Technological University (NTU). His research interests are in psychology and machine learning applications on education technology. He received his BSc (Biological Sciences) in 2019 from NTU.

Limsoon Wong is Kwan-Im-Thong-Hood-Cho-Temple Chair Professor in the School of Computing at the National University of Singapore (NUS). He was also a professor (now honorary) of pathology in the Yong Loo Lin School of Medicine at NUS. He currently works mostly on knowledge discovery technologies and their application to biomedicine. He has also done, in the earlier part of his career, significant research in database query language theory and finite model theory, as well as significant development work in broad-scale data integration systems. Limsoon is a Fellow of the ACM, named in 2013 for his contributions to database theory and computational biology.

Wilson Wen Bin Goh leads the BioData Science and Education laboratory at the School of Biological Sciences, NTU. His research interests include themes in resolving practice-theory gaps in statistics and machine learning, computational biology with focus on mass spectra analysis and network theory, and in education technology supporting experiential and (human) deep learning.