Spectral Jaccard Similarity: A New Approach to Estimating Pairwise Sequence Alignments

Summary

Pairwise sequence alignment is often a computational bottleneck in genomic analysis pipelines, particularly in the context of third-generation sequencing technologies. To speed up this process, the pairwise k-mer Jaccard similarity is sometimes used as a proxy for alignment size in order to filter pairs of reads, and min-hashes are employed to efficiently estimate these similarities. However, when the k-mer distribution of a dataset is significantly non-uniform (e.g., due to GC biases and repeats), Jaccard similarity is no longer a good proxy for alignment size. In this work, we introduce a min-hash-based approach for estimating alignment sizes called Spectral Jaccard Similarity, which naturally accounts for uneven k-mer distributions. The Spectral Jaccard Similarity is computed by performing a singular value decomposition on a min-hash collision matrix. We empirically show that this new metric provides significantly better estimates for alignment sizes, and we provide a computationally efficient estimator for these spectral similarity scores.

Highlights

• •Current pairwise sequence alignment schemes suffer from short common subsequences
• •Frequent k-mers skew Jaccard similarity-based aligners
• •Our scheme, Spectral Jaccard Similarity, implicitly detects these spurious similarities
• •This provides more accurate and computationally efficient estimates for alignments

The Bigger Picture

Pairwise sequence alignment is often a computational bottleneck in genomic analysis pipelines, particularly in the context of third-generation sequencing technologies. To speed up this process, k-mer Jaccard similarities are often used as a proxy for alignment size to filter pairs of reads, and min-hashes are employed to efficiently estimate these similarities. However, when the k-mer distribution of a dataset is significantly non-uniform (e.g., due to GC biases or repeats), Jaccard similarity is no longer a good proxy for alignment size. We introduce a min-hash-based approach to estimate alignment sizes called Spectral Jaccard Similarity, which naturally accounts for uneven k-mer distributions. The Spectral Jaccard Similarity is computed by performing a singular value decomposition on a min-hash collision matrix. We show that this metric provides significantly better estimates for alignment sizes, and we provide a computationally efficient estimator for these spectral similarity scores.

To speed up pairwise sequence alignment, pairwise k-mer Jaccard similarities are often used as a proxy for alignment size. However, Jaccard similarity ceases to be a good proxy for alignment size when the k-mer distribution of the dataset is significantly non-uniform (e.g., due to GC biases and repeats). We introduce a min-hash-based approach for estimating alignment sizes called Spectral Jaccard Similarity, which accounts for uneven k-mer distributions leading to significantly better performance.

Introduction

The advent of long-read sequencers such as PacBio and Oxford Nanopore has made the goal of obtaining gold-standard genome assemblies a reality. Unlike short-read technologies, which provide reads of length 100–200 bp with an error rate of $1\text{\%}$, chiefly substitution errors, long-read technologies provide reads of lengths in the tens of thousands with a nominal error rate of 13%–$15\text{\%}$, consisting mostly of insertions and deletions.¹ While the long reads make resolving repeated sequences easier, the higher error rates make the computational tasks required for assembly significantly more challenging.

Genome assembly is usually performed based on one of two main approaches: de novo assembly, whereby one attempts to assemble a new genome “from scratch” using only the reads obtained, and reference-based assembly, whereby one assembles the reads using a pre-assembled genome of a related organism. Alignment is an integral part of most pipelines in either approach, and is often the most time-consuming step (Figure S11). In both settings naive dynamic-programming-based alignment2, 3, 4 is impractical due to its quadratic time complexity.

In reference-based assembly pipelines,^5,6 where one has a reference of a related organism, the first step usually consists of aligning all reads to the reference; i.e., read-to-reference alignment. For n reads each of length L and a reference of length G, the time complexity of aligning all reads to the reference via dynamic programming is $O\left(nLG\right)$, which is impractical in settings where there are $n\sim {10}^5$ reads, each of length $L\sim {10}^4$, with G on the order of ${10}^6$–${10}^{11}$ depending on the organism.

Similarly, the first step in most de novo assembly pipelines7, 8, 9, 10, 11, 12 is the pairwise alignment of all reads, which is computationally very costly. For n reads each of length L, the time complexity of aligning all pairs of reads would be $O\left(n^2{L}^2\right)$. Even for bacterial genome datasets where the number of reads obtained is on the order of $n\sim {10}^5$, with $L\sim {10}^4$, this is impractical. For most of this work we discuss alignment in the context of pairwise read alignment. However, our ideas can be adapted to the read-to-reference alignment paradigm.

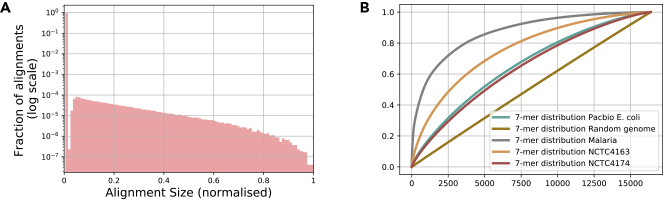
One key observation that helps alleviate this computational burden is that in practice one only cares about alignment between reads when there is a significant overlap. Furthermore, as shown in Figure 4A, in a typical dataset more than $99.99\text{\%}$ of pairs of reads do not have a significant overlap. Hence, most practical read aligners follow a “seed-and-extend” paradigm. The “seeding” step typically involves identifying pairs of reads that share many k-mers (length-k contiguous substrings). This step can be understood as a way to “filter” the set of read pairs to select those that share a reasonable number of k-mers and are thus likely to have a significant overlap.^7,12, 13, 14 Once these “candidate pairs” (whose number can be orders of magnitude smaller than the total number of read pairs) are obtained, computationally expensive dynamic-programming-based algorithms are used to obtain detailed alignment maps.

Figure 4.

Alignment Size Distribution for PacBio Datasets and k-mer Distribution for Several Bacterial Genomes

(A) A histogram of the alignment size (measured in terms of fraction of shared sequence) detected by Daligner¹⁴ in reads of E. coli K-12 dataset of Pacific Biosciences.³⁰ We note that more than $99.9\text{\%}$ of pairs of reads have no alignment between them. We also note that practical aligners are not able to capture small overlaps, which are difficult to distinguish from spurious alignments generated by noise, creating the “notch” in the histogram.

(B) Cumulative distribution function (CDF) of the k-mer distributions for various genomes. For each genome, we sort the k-mers in decreasing order of frequency to help with visualization. We see that the distributions deviate significantly from a uniform distribution (dark-yellow line). In particular, we remark that the CDFs for NCTC 4163 and NCTC 4174 have the largest and smallest deviation from the uniform distribution among the NCTC datasets analyzed in this paper.

The idea of using the number of shared k-mers as a metric for filtering pairs of reads is equivalent to viewing the Jaccard similarity between the set of k-mers of each read as a proxy for the alignment size. Under standard implementations whereby computing set unions and set intersections has a linear time complexity in the sizes of the sets, this filtering step has a time complexity of $O\left(n^{2}L\right)$ for pairwise read alignment. Recently Jaccard similarity has been used in a variety of applications such as genome skimming,¹⁵ and in new methods to compare whole genomes and study taxonomic diversity in the microbiome.^16,17

One very attractive property of Jaccard similarity in the context of filtering pairs of reads is that this metric is amenable to efficient estimation through the use of min-hashes. This is done by hashing all k-mers on a read (the total number of k-mers in a length-L read is $L-k+1$) and computing the minimum hash value (the min-hash) for each read. For a randomly chosen hash function, the collision probability for the min-hashes of two reads is precisely their Jaccard similarity. Hence, one can estimate the Jaccard similarity by computing the fraction of min-hash collisions out of the set of hash functions considered. For pairwise read alignment, if one uses H hashes to estimate the Jaccard similarity, this requires $O\left(nLH\right)$ to compute the min-hashes and $O\left(n^{2}H\right)$ to compute the collisions giving us a time complexity of $O\left(n^{2}H\right)$ for the filtering step as generally, for regimes of interest, $n\gg L$. We note that this general approach is related to the minimizers method, which has been used both in the context of document fingerprinting and reducing storage requirements for biological sequence comparison18, 19, 20 and to locality-sensitive hashing.^21,22

The idea of using min-hashes to estimate the Jaccard similarity provides significant computational savings and is particularly effective when the genome where the reads come from is close to a random genome, i.e., a genome where every k-mer is equally likely to appear on a read. However, when the k-mer distribution of the reads being considered is significantly non-uniform, the Jaccard similarity is no longer a good proxy for the alignment size. In particular, genome-wide GC biases and the presence of common k-mers increase the probability of a min-hash collision, thus biasing the estimate of alignment size provided by the Jaccard similarity. In this work, we introduce a min-hash-based approach for estimating alignment sizes called Spectral Jaccard Similarity (SJS), which naturally accounts for an uneven k-mer distribution in the reads being compared. The SJS is computed by considering a min-hash collision matrix (where rows correspond to pairs of reads and columns correspond to different hash functions), removing an offset, and performing a singular value decomposition (SVD). As illustrated in Figure 1, the leading left and right singular vectors can be seen as providing a rank-one approximation to the min-hash collision matrix. The leading left singular vector provides the SJS for each pair of reads, while the corresponding right singular vector can be understood as a measure of the “unreliability” or noise level of each hash function. Intuitively, a hash function that assigns low values to common k-mers is more unreliable for estimating alignment sizes, since it is more likely to create spurious min-hash collisions. Implicitly, this approach leads to a kind of weighted Jaccard similarity, where the weight of different hash functions is learned from the dataset.

Figure 1.

Overview of the Spectral Jaccard Similarity Computation

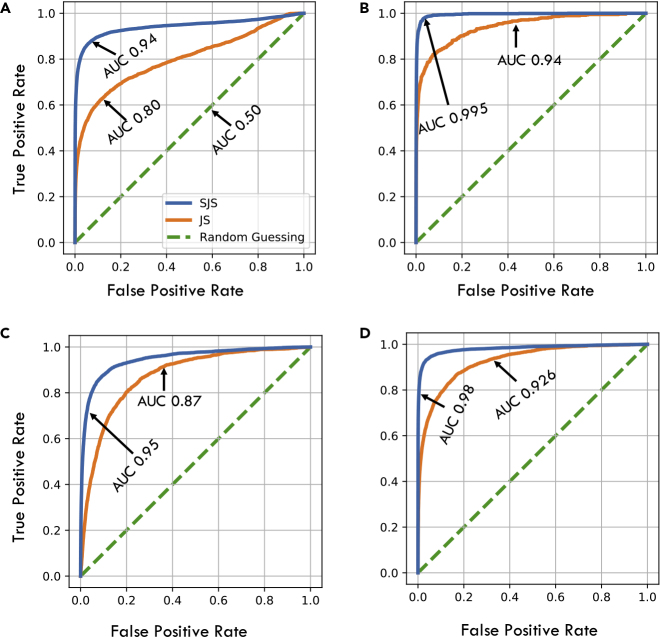
Experiments on PacBio long-read sequencing data from several bacterial genomes, spanning a variety of k-mer distributions, show that the SJS is significantly more correlated with alignment size than the standard Jaccard similarity. When used as a metric to filter out pairs of reads that are unlikely to have a large alignment, SJS outperforms Jaccard similarity on standard classification performance metrics. As an example, when applied to filtering pairs of reads which have an overlap of at least 30%, the area under the receiver-operating characteristic (ROC) curve (AUC) obtained by SJS filtering was consistently higher than the AUC obtained for Jaccard similarity on 40 datasets of the NCTC collection of Public Health England,²³ as shown in Figure 2. These results are obtained using $k=7$, which is an appropriate choice for the PacBio error rates.¹⁴

Figure 2.

SJS Has Uniformly Higher Area under the ROC Curve for Experiments on 40 PacBio Bacterial Datasets from the NCTC Library²³

In these experiments, SJS and Jaccard similarity were used to filter pairs of reads with an overlap of at least $30\text{\%}$. SJS was used with 1,000 hash functions while Jaccard similarity was computed exactly. By varying a second threshold determining which values of Jaccard similarity (or SJS) are selected, we can obtain ROC curves describing the performance of each filter, from which the AUC can be computed.

(A) AUC values using Daligner alignments as ground truth.

(B) The same results using Minimap2 alignments as ground truth.

This paper is organized as follows. First, we present a brief review of Jaccard similarity and its application to seed-and-extend algorithms for pairwise read alignment. Then we present the basis for SJS and provide results on real and simulated datasets, concluding with a discussion.

Results and Discussion

Jaccard Similarity

In general terms, the Jaccard similarity (denoted in equations as JS) is a similarity metric between sets. For two sets A and B, the Jaccard similarity between them, $\text{JS}\left(A,B\right)$, is defined as the size of their intersection divided by the size of their union. This is a very convenient measure as it is bounded between 0 and 1, $\text{JS}\left(A,B\right)=0$ if and only if $A\cap B=\varnothing$, and $\text{JS}\left(A,B\right)=1$ if and only if $A=B$. It has gained recent interest in its applications to finding documents (or web-pages) that are very similar but not the same as each other and in plagiarism detection. We refer the interested reader to Leskovec et al.,²⁴ Chapter 3, for a detailed review of the topic.

The Jaccard similarity was applied to the problem of pairwise read alignment in Berlin et al.⁷ by considering the sets of k-mers of each read. For a fixed parameter k, the k-mer Jaccard similarity between reads $S_0$ and $S_1$ is given by

$${\text{JS}}_k\left(S_0,S_1\right)=\frac{\left|\text{Γ}\left(S_0\right)\cap \text{Γ}\left(S_1\right)\right|}{\left|\text{Γ}\left(S_0\right)\cup \text{Γ}\left(S_1\right)\right|},$$ (Equation 1)

where $\text{Γ}\left(S_i\right)$ is defined as the set of k-mers for read $S_i$. This is the same as k-shingle Jaccard similarity in the data mining literature.^25,26 In this case, Jaccard similarity can be viewed as a proxy for the size of the overlap (if any) between reads $S_0$ and $S_1$.

For instance, consider length-L reads $S_0$ and $S_1$ with an overlap of size ${\alpha }_{\mathrm{0,1}}L$, for $0\le {\alpha }_{\mathrm{0,1}}\le 1$, as illustrated in Figure 3, and let $p_{\mathrm{0,1}}$ be the fraction of overlap; i.e.,

$$p_{\mathrm{0,1}}=\frac{{\alpha }_{\mathrm{0,1}}}{2-{\alpha }_{\mathrm{0,1}}}.$$ (Equation 2)

Figure 3.

The k-mer Jaccard Similarity Can Be Seen as a Proxy for the Alignment Size

If not many k-mers are shared by the non-overlapping parts of $S_0$ and $S_1$, we have ${\text{JS}}_k\left(S_0,S_1\right)\approx p_{\mathrm{0,1}}$, making this a useful metric to filter pairs of reads with a high overlap. Note that this approach is in a sense robust to errors in the reads. If we assume that each base is independently corrupted by noise (substitution, insertion, or deletion) with probability z, then a k-mer is not corrupted with probability ${\left(1-z\right)}^k$. Ignoring the unlikely event of collision of an erroneous k-mer with some other k-mer, ${\text{JS}}_k\left(S_0,S_1\right)$ is approximated as

$${\text{JS}}_k\left(S_0,S_1\right)\approx \frac{{\alpha }_{\mathrm{0,1}}{\left(1-z\right)}^k}{2-{\alpha }_{\mathrm{0,1}}{\left(1-z\right)}^k}\approx \frac{{\alpha }_{\mathrm{0,1}}{\left(1-z\right)}^k}{2},$$ (Equation 3)

where the last approximation holds when ${\left(1-z\right)}^k$ is small. Therefore, the k-mer Jaccard similarity is intuitively still a good proxy for the overlap size in the presence of errors, as this expression is monotone increasing in the true alignment. The parameter k should be large enough to guarantee that not too many spurious k-mer collisions occur, but small enough so that a reasonable number of k-mers per read are not corrupted by noise.^7,12,14 For a relative noise rate of $30\text{\%}$ (which results from both reads having error rates of around $15\text{\%}$), Myers¹⁴ argues that $k=7$ achieves the optimal trade-off. In the remainder of this paper, we utilize $k=7$.

While Figure 3 depicts an overlap between $S_0$ and $S_1$ (i.e., a suffix of $S_0$ that matches a prefix of $S_1$), the general alignment problem is concerned with finding long matches between $S_0$ and $S_1$, which need not be proper overlaps. In general, one may think of ${\alpha }_{\mathrm{0,1}}\in \left[\mathrm{0,1}\right]$ as the total size of the matches between $S_0$ and $S_1$, which may include an overlap and repeats. For simplicity, we will focus our discussion on overlaps, and show that this is a sufficiently good model to predict alignment well.

Computing the Jaccard similarity between two reads of length L takes $O\left(L\right)$ time. Hence, computing this metric for all pairs of reads would take $O\left(n^{2}L\right)$ time, which is quite expensive. An attractive feature of the Jaccard similarity metric is that it can be efficiently estimated. A probabilistic approach for estimating Jaccard similarity through the use of min-hashes was originally proposed by Broder et al.²⁷ In essence, one takes a random hash function h, hashes all k-mers in a read $S_i$, and picks the minimum hash value. Define

$$h\left(\text{Γ}\left(S_i\right)\right):=\text{min}\left\{h\left(x\right):x\in \text{Γ}\left(S_i\right)\right\},$$

for some hash function h and read $S_i$. We then observe that, for a randomly chosen hash function h,

$$\text{Pr}[h\left(\text{Γ}\left(S_0\right)\right)=h\left(\text{Γ}\left(S_1\right)\right)]={\text{JS}}_k\left(S_0,S_1\right),$$ (Equation 4)

since h is equally likely to have any of the k-mers on both reads as its minimizer. This surprising fact is elaborated upon and proved in Section 3.3.3 of Leskovec et al.²⁴ This means that we can use a random hash function to get an unbiased estimate of the Jaccard similarity between two strings. More precisely, if we sample random hash functions $h_1,h_2,\dots ,h_H$, we can estimate the Jaccard Similarity as

$$\frac{1}{H}\sum _{i=1}^{H}1\left\{h_i\right(\text{Γ}\left(S_0\right))=h_i\left(\text{Γ}\right(S_1\left)\right)\left\}\stackrel{\left(a\right)}{\approx }{\text{JS}}_k\right(S_0,S_1)\stackrel{\left(b\right)}{\approx }\frac{{\alpha }_{\mathrm{0,1}}{\left(1-z\right)}^k}{2}.$$ (Equation 5)

Hence, by choosing H moderately large, one should be able to accurately estimate ${\text{JS}}_k\left(S_0,S_1\right)$, which provides a proxy for the alignment size. With H hashes, one would take $O\left(nLH\right)$ time to compute the hashes and $O\left(n^{2}H\right)$ time to compute collisions, which is $O\left(n^{2}H\right)$ time in regimes of interest where $n\gg L$.

Drawbacks of Jaccard Similarity

The key assumption that drives the approximation in Equation 5 is that that all k-mers are roughly equally likely to occur in the reads. On real datasets, however, k-mer distributions are far from uniform, as illustrated in Figure 4B for several genomes.

An uneven distribution of the k-mers throughout a genome increases the likelihood that the non-overlapping parts of two reads $S_0$ and $S_1$ share k-mers. In this case, for a randomly drawn hash function h, Equation 4 still holds but Equation 5 no longer holds. In particular, if the hash function h is such that common k-mers are given low hash values, the min-hash collision probability, given by $\text{Pr}[h\left(\text{Γ}\left(S_0\right)\right)=h\left(\text{Γ}\left(S_1\right)\right)]$, can be significantly higher than the right-most expression in Equation 5. For this reason, when the k-mer distribution throughout a genome is uneven, Equation 5 yields a poor estimate for the read overlap size. This is illustrated in Figure 6A for PacBio Escherichia coli reads,³⁰ where we show that Jaccard similarity is a poor predictor of alignment sizes.

Figure 6.

Comparison between Alignment Estimates and True Alignments

Linear regression fit to positive alignments found by Daligner to (A) Jaccard similarity between corresponding reads and (B) SJS between the reads, which provides a better fit.

One simple way to address this issue is to “mask” common k-mers^11,24 and then compute the Jaccard similarity on the remaining k-mers. However, these approaches are arbitrary and require the tuning of parameters that can in general depend on the distribution. Intuitively, they can be thought of as applying a hard threshold to determine which k-mer matches are due to noise and which are actual signals.

Another approach is to consider a soft version of this thresholding, where different k-mers are given different weights in the computation of a weighted Jaccard similarity. This idea has been explored in the context of detecting near duplicate images in image databases. In particular, a tf-idf (term frequency-inverse document frequency) weighting was used to weight visual words (i.e., image features) according to the inverse of their frequency in the database.²⁸ This way, image features that are very common across the images in the database count less toward determining whether two images are similar.

The approach we present in the next section bears similarities with the method by Chum et al.²⁸ A key difference is that we assign weights to hash functions rather than individual k-mers. Moreover, these weights are assigned in an implicit way by a spectral approximation to a min-hash collision matrix, which allows the weights to adjust to the specific reads being aligned.

Spectral Jaccard Similarity

We propose a new Jaccard-similarity-inspired approach to estimate the overlap between reads that avoids the need for hard thresholds for determining “common k-mers” or “bad hashes” and instead assigns soft penalties to individual hash functions according to how biased an estimator they are for alignment size.

Suppose reads $S_0$ and $S_1$ of length L have an overlap of size $\alpha L$ for some $0\le \alpha \le 1$, and no other significant repeats across them. If there were no shared k-mers in the non-overlapping part of the reads, we would model the min-hash collision event for a random hash function h, as

$$1\{h\left(\text{Γ}\left(S_0\right)\right)=h\left(\text{Γ}\left(S_1\right)\right)\}\sim \text{Ber}\left(p_{\mathrm{0,1}}\right),$$ (Equation 6)

where $p_{\mathrm{0,1}}=\frac{\alpha }{2-\alpha }$ (this expression can be modified to account for errors as in Equation 3). However, when the distribution of k-mers is uneven, the min-hash collision probability is larger than $p_{\mathrm{0,1}}$. Moreover, some hash functions are worse than others: if h assigns lower values to common k-mers, it is more likely to overestimate $p_{\mathrm{0,1}}$. We model this effect by rewriting Equation 6 as

$$1\{h\left(\text{Γ}\left(S_0\right)\right)=h\left(\text{Γ}\left(S_1\right)\right)\}\sim \text{Ber}\left(p_{\mathrm{0,1}}\right)\vee \text{Ber}\left(q_h\right),$$ (Equation 7)

where $\vee$ is the Boolean “or” operator and $q_h\in \left[\mathrm{0,1}\right]$ is a hash-specific parameter that can be intuitively understood as how unreliable h is due to common k-mers. Notice that the hash-specific noise term always leads to overestimation of $p_{\mathrm{0,1}}$. We also emphasize that the $q_h$ values are unknown. Therefore, we cannot directly estimate the $p_{i,j}$ and instead we need to jointly estimate all model parameters.

To perform this joint estimation, we define the min-hash collision matrix as follows. For a fixed reference read $S_0$, a list of target reads $S_1,S_2,\dots ,S_n$, and a list of hash functions $h_1,\dots ,h_H$, the $\left(i,j\right)$th entry of the min-hash collision matrix is the binary indicator variable for whether there is a min-hash collision between $S_0$ and $S_i$ when using hash function $h_j$; i.e., $1\{h_j\left(\text{Γ}\left(S_0\right)\right)=h_j\left(\text{Γ}\left(S_i\right)\right)\}$. Note that ${\text{JS}}_k\left(S_0,S_i\right)$ can be directly estimated from the min-hash collision matrix by computing the fraction of 1s in the ith row.

As it turns out, if we assume that the entries in the min-hash collision matrix were generated according to Equation 7, we can jointly estimate the $p_{0,i}$s and the $q_{h_j}$s by performing an SVD on an offset version of the min-hash collision matrix. This allows us to use efficient algorithms for computing the SVD in order to obtain estimates for the parameters $p_{0,i}$.

We refer to the parameter $p_{0,i}$ in the model given by Equation 7 as the “Spectral Jaccard Similarity” (SJS) between $S_0$ and $S_i$. Note that the definition of these parameters in itself does not depend on the estimation procedure based on SVD outlined above. In that sense, the use of the word “spectral” in SJS refers to the fact that the model in Equation 7 provides a decomposition of the standard Jaccard similarity (modeled by Equation 6) into two components: one due to the alignment between $S_0$ and $S_1$ and one due to k-mers that are common throughout the genome.

As we describe in Appendix A in Supplemental Information, the model described in this section can be alternatively described in terms of a generative model for the sequences that are being aligned. Under this alternative description, $p_{\mathrm{0,1}}$ is precisely the alignment fraction between $S_0$ and $S_1$ (i.e., the size of the alignment between them divided by the total span of unique sequence segments in $S_0$ and $S_1$). Next, we describe the computation of the SJS in more detail.

Computing the Spectral Jaccard Similarity

Algorithmically, we approximate all pairwise alignments by iterating over each read in the dataset, treating it as the reference read, and computing the SJS between the reference and all other reads. For a reference read $S_0$, we define the min-hash collision matrix as $A_0\in {\left\{\mathrm{0,1}\right\}}^{n\times H}$ where

$$A_0[i,j]=1\{h_j\left(\text{Γ}\left(S_0\right)\right)=h_j\left(\text{Γ}\left(S_i\right)\right)\}\sim \text{Ber}\left(p_{0,i}\right)\vee \text{Ber}\left(q_{h_j}\right).$$ (Equation 8)

For cleanliness of notation, we will write $p_{0,i}=p_i$ and $q_{h_j}=q_j$. Note that both the $p_i$s and the $q_j$s depend on the choice of $S_0$, but we do not make that dependence explicit in the notation.

The key observation about our model is that, in expectation, the matrix $A_0$ defined in Equation 8 is rank one after accounting for offset. More precisely, since $\mathbb{E}{A}_0[i,j]=p_i+q_j-p_i{q}_j=\left(1-p_i\right)\left(q_j-1\right)+1$, we have that for $\mathbf{p}\triangleq \left(p_1,\dots ,p_n\right)$ and $\mathbf{q}\triangleq \left(q_1,\dots ,q_H\right)$,

$$\mathbb{E}{A}_0-{11}^{\top }=\left(1-\mathbf{p}\right){\left(\mathbf{q}-1\right)}^{\top }.$$ (Equation 9)

We illustrate this point by comparing the sorted singular values of $A_i-{11}^{\top }$ for the PacBio E. coli K-12 dataset, shown in Figure S7. We note that the fact that $A_0-{11}^{\top }$ is in expectation a rank-one matrix allows us to estimate $\mathbf{p}$ and $\mathbf{q}$ through an SVD on $A_0-{11}^{\top }$. More precisely, if we let $\mathbf{u}$ and $\mathbf{v}$ be respectively the leading left and right singular vectors of $A_0-{11}^{\top }$, then we expect $\mathbf{u}$ to be approximately proportional to $\left(1-\mathbf{p}\right)$ and $\mathbf{v}$ to be approximately proportional to $\left(\mathbf{q}-1\right)$, up to flipping signs. We normalize the $q_j$s to be between 0 and 1 for plotting purposes, noting that algorithmically we are only interested in the SJS values (the $p_i$s). We require a slightly more sophisticated normalization method for the $p_i$s. See Appendix B in Supplemental Information for more details on the normalization of $p_i$s and $q_j$s.

To illustrate the comparison between Jaccard similarity and SJS, we consider the example shown in Figure 5. The standard min-hash Jaccard similarity approach would estimate ${\text{JS}}_k\left(S_0,S_i\right)$ to be the fraction of 1s in the ith row. We see that while rows 1 and 3 have the same estimated Jaccard similarity, they have different SJS values. This is because columns 2 and 5 are found to be noisier (i.e., worse hash functions), and so while rows 1 and 3 have two collisions each, a collision on column 1 is deemed more indicative of alignment, and thus row 3 has a higher SJS than row 1.

Figure 5.

Example of Comparison between Jaccard Similarity and SJS on a Small Matrix

While the standard Jaccard similarity approach would assign the same value to rows 1 and 3, SJS takes into account the fact that columns 2 and 5 are seen as less reliable indicators of alignment.

It turns out that the estimates of $p_i$ obtained via SVD are a much better proxy for the size of the alignment between reads $S_0$ and $S_i$ than the standard Jaccard similarity, particularly when the k-mer distribution is uneven. To illustrate this point, we computed the SJS values $p_i$ (from a min-hash collision matrix with $n=1004$ and $H=1000$) and the exact Jaccard similarity ${\text{JS}}_k\left(S_0,S_i\right)$ for the corresponding pairs of reads, for the E. coli PacBio dataset. As illustrated in Figure 6, while the $R^2$ coefficient between (exact) Jaccard similarity and overlap size is only 0.18, for SJS the $R^2$ coefficient is 0.48.

While $p_i$ parameters, or the SJS values, track the alignment between pairs of reads, we have not given a precise meaning to the $q_j$s we recover. Intuitively, a large $q_j$ means that the corresponding hash function is more likely to create a spurious min-hash collision, thus being a less reliable estimator for the alignment size. We provide a more in-depth interpretation in Validating the Model. In Figures 10A and 10B, we plot the frequency of the argmin k-mer for different hash functions, and verify that large $q_j$s correspond to hash functions whose argmin k-mers have high frequency. We point out that we compute SJS on a reference-by-reference basis instead of considering a single matrix with all $\left(\begin{array}{c}n\\ 2\end{array}\right)$ rows at once. Note that, in principle, SJS can be computed on the matrix with all $\left(\begin{array}{c}n\\ 2\end{array}\right)$ read pairs as rows. However, as illustrated in Appendix C in Supplemental Information, allowing the $q_j$ hash parameters to be reference specific increases their ability to capture the discriminative power of each hash function, as this depends on which k-mers are present in the reference read. Furthermore, this reference-by-reference approach avoids the computation of an SVD for a very large matrix.

Figure 10.

Comparison between Collision Probability and Hash Unreliability Parameter

For each hash function $h_j$, we compared the collision probability on hash $h_j$ with the corresponding $q_j$ for (A) the E. coli dataset and (B) the K. pneumoniae dataset (NCTC 5047).

From a computational perspective, this algorithm computes all H hashes in $O\left(nLH\right)$ time, collisions in $O\left(n^{2}H\right)$ time, and performs n $\left(n\times H\right)$ SVDs. In regimes of interest where $n\gg L$, this last term dominates. Computing a full $\left(n\times H\right)$ SVD requires $O\left(\text{min}\left(n^{2}H,n{H}^2\right)\right)=O\left(n{H}^2\right)$, giving a computational complexity of $O\left(n^2{H}^2\right)$, which naively is slower than the min-hash based Jaccard similarity computation. However, note that we only need to compute the principal left singular vector, which can be done efficiently via power iteration, reducing the $O\left(n{H}^2\right)$ run time to $\tilde{O}\left(nH\right)$, where $\tilde{O}$ suppresses logarithmic factors in n and H. Further improvement is available in the practical case whenever most of the $\left(S_0,S_i\right)$ pairs have no overlap, as most of the $p_i$s are expected to be close to zero. When this holds true, we are able to approximate the principal right singular vector $\mathbf{q}$ efficiently, allowing us to approximate $\mathbf{p}$ via a single matrix-vector product, speeding up our method significantly to $O\left(n^{2}H\right)$, the same complexity of Jaccard similarity. This approach is discussed in more detail in Approximation in the Case where Most pis Are Zero.

We point out that it may be possible to modify the approach described in this section in order to further improve the computational efficiency of computing SJS. In particular, since we are typically only interested in identifying pairs of reads with a significant overlap, we can reduce the overall number of min-hash comparisons needed by performing fewer min-hash comparisons for pairs of reads with small alignments. In particular, the adaptive Monte Carlo method²⁹ can be used to adaptively decide the number of min-hash comparisons performed for each pair of reads. Another strategy that can lead to computational savings is to explore the use of “bottom sketches” as done by Ondov et al.¹⁶ More precisely, for a single hash function, one can compute s minimizers per read (the bottom-s sketch). As explained by Ondov et al.,¹⁶ the bottom sketches can be compared to produce a direct estimate of the Jaccard similarity between the reads. This offers the potential to significantly reduce the overall number of hash functions needed to estimate pairwise sequence alignments. Note, however, that based on this approach each of the entries in the min-hash collision matrix is no longer in $\left\{\mathrm{0,1}\right\}$ (it is instead a number describing the similarity between the bottom sketches). Hence, the binary model described in Equation 7 would need to be updated to allow a larger set of output values.

Results

To compare the performance of Jaccard similarity and SJS at estimating alignment sizes, we highlight experimental results on three PacBio datasets: a standard E. coli dataset,³⁰ and two NCTC datasets,²³ NCTC 4163 and NCTC 4174, which represent distinct levels of deviation from a uniform k-mer distribution, as illustrated by the k-mer CDFs in Figure 4B.

As a first experiment, for the E. coli dataset, we plot the Daligner¹⁴ alignment sizes versus Jaccard similarity and SJS scores in Figure 6. By comparing the linear regression fit for Jaccard similarity and SJS we see that SJS has a significantly stronger linear relationship with the Daligner alignments. However, we note that the $R^2$ values are not necessarily indicative of performance in this scenario, as they only indicate how well we can fit a linear relationship to the data. For the goal of identifying pairs of reads with an alignment larger than a certain threshold, a better way to assess the performance of SJS is to analyze ROC curves.

We consider the problem of identifying pairs of reads with an overlap of size at least θ. We compute exact Jaccard similarity values and compare them with SJS values computed based on 1,000 hash functions (see Trade-Off between Filter Accuracy and Number of Hash Functions for results with different numbers of hash functions). We discuss the preprocessing steps performed on these datasets in Appendix E of Supplemental Information. In Figure 7, we plot ROC curves for different values of θ and different datasets. We utilize Daligner alignments as ground truth for the alignment sizes. We point out that using the Daligner outputs as ground truth is not ideal, since the tool itself utilizes an empirical Jaccard-similarity-based filter to align reads; this choice of ground truth biases the result in favor of the conventional Jaccard similarity. Despite this, we note that SJS performs significantly better than Jaccard similarity on all datasets tested, even when the output metric inherently favors Jaccard similarity. In addition, we obtain similar results when Minimap2 is used to generate ground truth alignments in place of Daligner (Figure S6). The fact that Minimap2 and Daligner use different procedures to filter pairs of reads provides additional evidence that the superior performance of SJS over Jaccard similarity is not simply due to using Daligner to define the ground truth.

Figure 7.

Comparison of ROC Curves on Various Datasets

ROC curves across different PacBio datasets and different θ thresholds using Daligner ground truth and 1,000 hashes.

(A) ROC of E. coli (K-12 from PacBio website) for alignment threshold $\theta =0.3$.

(B) ROC of E. coli for alignment threshold $\theta =0.8$.

(C) ROC of NCTC 4174—the least repetitive dataset we consider —with alignment threshold $\theta =0.3$.

(D) ROC of NCTC 4163—the most repetitive dataset we consider—with alignment threshold $\theta =0.3$.

Figure S8 shows a similar plot with Minimap2 as ground truth. AUCs across a variety of datasets are shown in Figure 8.

We note that the performance of both Jaccard similarity and SJS filters degrades as the k-mer distribution becomes skewed. To formally capture this skew for a dataset of reads $D=\left\{S_1,\dots ,S_n\right\}$ with an average read length of L, we let the k-mer distribution of D be defined as the empirical distribution of the $\approx nL$ k-mers in the reads of D. We then have the following definitions.

Definition 1: For a dataset D and hash function h, the collision probability of read S, denoted ${\text{colprob}}_{D,h}\left(S\right)$, is the probability that a set of $L-k+1$ randomly chosen k-mers drawn independently and uniformly at random from the k-mer distribution of D has the same min-hash on hash h as S.

This collision probability of read S in a dataset D with hash h can be computed in closed form, as discussed in Appendix D in Supplemental Information. Furthermore, we can extend this definition in order to capture the overall hardness of approximating pairwise alignments in a dataset D as follows.

Definition 2: The mean collision probability of a dataset $D=\left\{S_1,\dots ,S_n\right\}$ is given by

$$\frac{1}{n}\sum _{i=1}^n{\mathbb{E}}_h\left[{\text{colprob}}_{D,h}\left(S_i\right)\right],$$ (Equation 10)

where ${\mathbb{E}}_h$ is the expectation with respect to a randomly chosen hash function h.

While computing the expectation ${\mathbb{E}}_h$ over hash functions h is computationally infeasible, it can be approximated by an average over a set of randomly chosen hash functions $h_1,\dots ,h_m$. As we discuss in Appendix D in Supplemental Information, we can use the set of hash functions that were used to compute the min-hashes to give a closed form approximation of the mean collision probability of a dataset.

In Figure 8A we plot the performance of SJS and Jaccard similarity as a function of the computed collision probabilities for 40 datasets from the NCTC 3000 project.²³ This shows the uniform improvement in performance afforded by SJS, in that for every dataset the SJS AUC is higher than the Jaccard similarity AUC. Furthermore, it shows that as the k-mer distribution becomes more skewed, the degradation in performance suffered by SJS is smaller than that suffered by Jaccard similarity. We plot the ratio of the improvement of the two AUCs over random guessing in Figure 8B. This shows that the improvement of SJS over Jaccard similarity is larger when the k-mer distribution is more skewed.

Figure 8.

Impact of the Dataset Collision Probability on the SJS Performance

(A) The higher the min-hash collision probability is, the worse both methods perform, indicating a “harder” dataset. However, the performance of the SJS filter degrades less than that of the Jaccard similarity filter.

(B) Ratio between the improvement of the SJS filter over random guessing and the improvement of the Jaccard similarity filter over random guessing, as a function of collision probability of the reads' k-mer distribution.

The results in both plots were computed for $\theta =0.3$ using 1,000 hashes. A similar plot with Minimap2 providing ground truth alignments can be found in Figure S5.

Discussion

In this paper, we introduced the notion of SJS as an alternative to the standard k-mer Jaccard similarity for estimating the overlap size between pairs of noisy, third-generation sequencing reads. SJS is a probabilistic approach that utilizes min-hash collisions as a way to estimate the size of the overlap between pairs of reads. However, unlike previous approaches, SJS attempts to learn how good different hash functions are at estimating overlap size for that specific dataset. In particular, when the k-mer distribution of the dataset in question is very uneven, the gain of SJS over Jaccard similarity is greater.

We conclude the paper by discussing some additional aspects of the algorithm implementation and providing some further validation of the model. First, we show how the fact that the columns of the A matrix are typically sparse can be exploited in order to approximate the SVD using a single matrix-vector multiplication, which can significantly speed up the computation of SJS. Second, we validate our earlier claim that $q_j$s represent how bad a hash function is for the purpose of alignment. Third, we examine the performance of SJS as a function of the number of hashes used and show that it can match the performance of exact Jaccard similarity with around 150 hashes, as shown in Figure 10B.

A final implementation-related point, the calibration of the SJS values across different reference reads, is discussed in Appendix B in Supplemental Information. More precisely, we describe how we normalize the $p_i$s obtained for different reference reads (i.e., from the SVD of different matrices $A_i$ and $A_j$) so that the SJS values are comparable. We also point out that, when computing SJS for two reads A and B, the choice of reference read matters, as illustrated in Figure S3.

Approximation in the Case where Most $p_i$s Are Zero

Given a min-hash collision matrix $A\in {\left\{\mathrm{0,1}\right\}}^{n\times H}$, define

$$\overline{p}=\frac{1}{n}\sum _{i=1}^n{p}_i,{\overline{q}}_j=\frac{1}{n}\sum _{i=1}^n{A}_{i,j},$$

for $1\le j\le H$; i.e., $\overline{p}$ is the average $p_i$ value and ${\overline{q}}_j$ is the fraction of ones in column j. We note that, since $A_{i,j}\sim \text{Ber}\left(p_i\right)\vee \text{Ber}\left(q_j\right)$, when most $p_i$s are zero, most of the entries in column j are distributed as $\text{Ber}\left(q_j\right)$. It follows that $\mathbb{E}\left[{\overline{q}}_j\right]=q_j+\overline{p}-\overline{p}{q}_j\approx q_j$ since $\overline{p}\approx 0$. This means that the leading right singular vector is approximately $\overline{\mathbf{q}}={[{\overline{q}}_1,\dots ,{\overline{q}}_H]}^{\top }$. Since the rank-one approximation is

$$A-{\mathbf{11}}^{\top }\approx \left(\mathbf{1}-\mathbf{p}\right){\left(\mathbf{q}-\mathbf{1}\right)}^{\top }\approx \left(\mathbf{1}-\mathbf{p}\right){\left(\overline{\mathbf{q}}-\mathbf{1}\right)}^{\top },$$

by multiplying both sides by $\left(\overline{\mathbf{q}}-\mathbf{1}\right)$, we obtain

$$\left(A-{\mathbf{11}}^{\top }\right)\left(\overline{\mathbf{q}}-\mathbf{1}\right)\approx {\left||\overline{\mathbf{q}}-\mathbf{1}|\right|}_2^2\left(\mathbf{1}-\mathbf{p}\right)$$

$$\Rightarrow \mathbf{p}\approx \mathbf{1}-\frac{1}{\overline{\mathbf{q}}-{\mathbf{1}}_2^2}\left(A-{\mathbf{11}}^{\top }\right)\left(\overline{\mathbf{q}}-\mathbf{1}\right),$$ (Equation 11)

which gives us a method to compute the SJS with a matrix-vector multiplication rather than an SVD. This can intuitively be understood as follows. We wish to approximate the principal left singular vector of the matrix $A-{\mathbf{11}}^{\top }$. We are, however, given some side information; we are able to easily obtain a high-quality approximation of the principal right singular vector as $\overline{\mathbf{q}}-\mathbf{1}$. This allows us to effectively perform one step of the Power Iteration method, as $\left(A-{\mathbf{11}}^{\top }\right)\left(\overline{\mathbf{q}}-\mathbf{1}\right)$ which, after normalization, gives us a very good approximation of the principal left singular vector.

In Figure 9A, we show that for an E. coli dataset where most reads do not have any overlap, $\overline{\mathbf{q}}$ is very correlated with $\mathbf{q}$. In Figure 9B, we show that the approximate SJS values computed using Equation 11 are highly correlated with those computed through a full SVD.

Figure 9.

Approximating Right Singular Vector with Column Averages

When most $p_i\approx 0$, it is possible to approximate the SVD by a simple matrix-vector multiplication as described in Equation 11. In particular, we verify empirically that (A) $\overline{\mathbf{q}}\approx \mathbf{q}$ and that (B) the $\mathbf{p}$ obtained from Equation 11 is nearly the same as the one computed by SVD. If one instead tries to approximate $\mathbf{p}$ by considering row averages (C), the approximation is not as good.

We note that one could have attempted to use row averages instead of column averages in this approximation procedure. However, this would correspond to computing the standard Jaccard similarities. Jaccard similarity is not as well correlated with the SJS, as we show in Figure 9C. Furthermore, we note that Equation 11 implies that $p_i\underset{˜}{\propto }{\left[A\left(1-\overline{\mathbf{q}}\right)\right]}_i$, which is expanded as

$$p_i\underset{˜}{\propto }\frac{1}{H}\left(\sum _{j=1}^H{A}_{i,j}\left(1-\frac{1}{n}\sum _{\ell =1}^n{A}_{\ell ,j}\right)\right),$$ (Equation 12)

where $\underset{˜}{\propto }$ indicates “monotonic function of.” Since ${\text{JS}}_k\left(S_0,S_i\right)\approx \frac{1}{H}{\sum }_{j=1}^H{A}_{i,j},$ our method can be understood as downweighting the contribution of hash functions that yield many collisions. We call this scheme approximate SJS (aSJS), and show that this approximation performs nearly as well as SJS in Figures S9 and S4.

While performing a spectral decomposition is costly, the approximation method provided by Equation 11 is efficient. Comparing the running time of the different approaches, after the common min-hash computation step, we see that on the E. coli dataset with $n=\mathrm{1,000}$ reads and $H=\mathrm{1,000}$ hashes, SJS takes 1352.9 s, min-hash approximation of Jaccard similarity takes 4.47 s, and aSJS takes 10.88 s. Experiments were run on one core of an AMD Opteron Processor 6378 with 500 Gb of memory. We point out that performing the same experiment on different datasets leads to similar results, as the operations involved (SVD and matrix-vector multiplication) depend almost exclusively on the matrix dimensions, not the content of the collision matrices themselves.

Validating the Model

In the section Spectral Jaccard Similarity, we proposed the model in Equation 7 with the interpretation that $q_j$ represented how likely were min-hash collisions given the hash function $h_j$. In this section, we empirically verify that claim. In Figure 10, we show the collision probability of a reference read on a hash function $h_j$ as a function of our computed $q_j$ for the E. coli and Klebsiella pneumoniae (NCTC 5047) datasets. We see a very strong correlation between the computed collision probability and the $q_j$ parameters, validating our model.

Trade-Off between Filter Accuracy and Number of Hash Functions

While throughout this paper we present results for SJS using 1,000 hash functions, our method performs well even with a smaller number of hash functions. In Figure S10, we plot ROC curves for SJS and aSJS (described in Approximation in the Case where Most pis Are Zero) using different numbers of hashes to compare the performance of these filters on the E. coli K-12 dataset. We note that as few as 150 hashes are enough for SJS to dominate the exact Jaccard-similarity-based filter. The performance of the approximation is similar.

Experimental Procedures

See Supplemental Experimental Procedures for full details.

Resource Availability

Lead Contact

Ilan Shomorony, ilans@illinois.edu.

Materials Availability

This study did not generate new unique materials or reagents.

Data and Code Availability

The code generated during this study are available at https://github.com/TavorB/spectral_jaccard_similarity. This study used only publicly available datasets.

Published: July 31, 2020