Ion Specific Effects on the Stability of Halloysite Nanotube Colloids—Inorganic Salts versus Ionic Liquids

Abstract

Charging and aggregation processes were studied in aqueous dispersions of halloysite nanotubes (HNTs) in the presence of monovalent inorganic electrolytes and ionic liquid (IL) constituents. The same type of co-ion (same sign of charge as HNT) was used in all systems, while the type of counterions (opposite sign of charge as HNT) was systematically varied. The affinity of the inorganic cations to the HNT surface influenced their destabilizing power leading to an increase in the critical coagulation concentration (CCC) of HNT dispersions in the Cs⁺ < K⁺ < Na⁺ order. This trend agrees with the classical Hofmeister series for negatively charged hydrophobic surfaces. For the IL cations, the CCCs increased in the order BMPY⁺ < BMPIP⁺ < BMPYR⁺ < BMIM⁺. An unexpectedly strong adsorption of BMPY⁺ cations on the HNT surface was observed giving rise to charge neutralization and reversal of the oppositely charged outer surface of HNT. The direct Hofmeister series was extended with these IL cations. The main aggregation mechanism was rationalized within the classical theory developed by Derjaguin, Landau, Verwey, and Overbeek, while ion specific effects resulted in remarkable variation in the CCC values. The results unambiguously proved that the hydration level of the surface and the counterions plays a crucial role in the formation of the ionic composition at the solid–liquid interface and consequently, in the colloidal stability of the HNT particles in both inorganic salt and IL solutions.

Introduction

Halloysite nanotubes (HNTs) represent an interesting class of materials due to their advantageous properties such as biocompatibility, abundant surface functional groups, and availability in large scale, which are exploited in various applications.¹⁻³ HNTs are aluminosilicates of tubular structure with two different surface charge states.⁴ The outer surface is negatively charged due to the presence of the deprotonated silanol groups, while the protonation of the aluminol groups results in a positively charged inner surface.⁵ Recent reviews indicate a widespread contemporary interest in HNTs and their composites.⁶⁻¹⁰ Despite the fact that numerous applications take place in liquid medium,¹¹⁻¹⁴ the main focus was made on the structural properties in the solid state, and less attention was paid to the colloidal features. In the handful of papers released on this topic,^2,15−18 low colloidal stability of the commercially available HNTs was reported, which leads to aggregation and subsequent sedimentation of the HNT materials. In some studies, the aggregation was suppressed by surface modification with polyelectrolytes.^15,17,18

Ion specific effects particularly influence charging and aggregation of colloidal particles in aqueous samples;¹⁹⁻²³ however, this issue was not explored for HNT dispersions so far. Accordingly, ions of dissolved salts are able to interact specifically with surfaces, thereby modifying the charge density to different extents.²⁴⁻²⁶ Such a variation in the surface charge affects the aggregation processes and, thus, the colloidal stability of the samples. These phenomena prompted the establishment of the Hofmeister series of cations and anions to order their effect on particle aggregation processes. This theory was originally developed for the destabilization of protein solutions by inorganic salts,²⁷ but it has also proven to be a powerful tool to predict the stability of particle dispersions on the basis of the type of co- and counterions.^{19−21,28−32} The original Hofmeister series were established as follows:

Note that only monovalent ions are presented in the above series, since the Schulze–Hardy rule³³ has to be applied once the effects of the multivalent ions are discussed. The above sequences for anions and cations indicate that negatively charged colloidal particles form stable aqueous dispersions even in the presence of a high concentration of ions located on the right-hand side of the series, while the ions from the left-hand side induce their aggregation at lower concentrations. This is the so-called direct Hofmeister series. For positively charged surfaces, the reversed Hofmeister series applies, since the effect of ions on the colloidal stability of dispersions is just the opposite; i.e., the ions from the right side of the series destabilize the dispersions at low concentrations, while they are more stable in solutions of salt constituents located on the left side. The charge density and hydrophobicity of the colloidal particle also play an important role in determining the order of ions in this series. Accordingly, the above rules are valid only for hydrophobic particles, while the order is reversed for hydrophilic surfaces.^31,34,35

However, there are cases in which water is not a suitable continuous medium in colloidal dispersions. Instead, ionic liquids (ILs)^36,37 are organic salts of low melting point with many advantageous properties including wide electrochemical window, low vapor pressure, and high chemical stability.^36,38 An important class of systems is particle suspensions in ILs, as they are relevant in many applications.³⁹⁻⁴² Among them, HNT-IL systems were studied and applied as catalysts,⁴³ anticorrosion agents,⁴⁴ supercapacitors,⁴⁵ sensors,⁴⁶ and building blocks in batteries.⁴⁷ Despite the considerable interest in studying colloid–IL systems, studies concerning particle aggregation in ILs have begun only recently.⁴⁸⁻⁵⁴ It was soon realized that the interfacial assembly of the IL constituents greatly influences the interparticle forces⁵⁵⁻⁵⁷ and, hence, the stability of colloidal dispersions. This issue can be adequately addressed in diluted IL solutions by investigating the effect of the interfacial properties on the forces between the particles. Therefore, interparticle forces and the subsequent particle aggregation mechanism in samples containing aqueous solutions of IL constituents were explored by different experimental techniques.^{49,56,58−60} For diluted IL solutions, the measured trends in colloidal stability resembled the one described by the theory of Derjaguin, Landau, Verwey, and Overbeek (DLVO),⁶¹ implying that ILs dissociate in the solutions causing charge screening and subsequent destabilization of the dispersion at high IL concentrations. Nevertheless, ILs of different compositions destabilized the particle dispersions at different concentrations, which contrasts with the DLVO theory. Such an ion specific effect in IL solutions is analogous to the one discussed for simple ions previously. In this way, a Hofmeister series can be established for IL cations and anions as well.⁶²⁻⁶⁴ However, only a limited number of quantitative data are available for particle dispersions,^59,60 and such investigations for HNT-IL systems have not been performed so far.

In the present study, therefore, the colloidal stability of HNTs was investigated in the presence of different monovalent inorganic electrolytes (KCl, NaCl, and CsCl) and aqueous solutions of ILs (1-butyl-3-methylimidazolium chloride (BMIMCl), 1-butyl-2-methylpyridinium chloride (BMPYCl), 1-butyl-1-methylpyrrolidinium (BMPYRCl), and 1-butyl-1-methylpiperidinium chloride (BMPIPCl)). Based on the results, an extended Hofmeister series was proposed for the nanotubes, and the aggregation mechanism was compared to the predictions of existing theories.

Methods

Materials

The ILs (BMIMCl, ≥99%, BMPYCl, >98%, BMPYRCl, 99%, and BMPIPCl, 99%, see Figure 1 for the structure of the cations) were purchased from Iolitec GmbH. Inorganic salts such as potassium chloride (KCl), sodium chloride (NaCl), and cesium chloride (CsCl) were bought from VWR. The raw HNT powder was purchased from Sigma-Aldrich. High purity water from a VWR Purity TU+ device was used for all the sample preparations. The measurements were carried out at 25 °C, and the HNT concentration was set to 10 mg/L. The water, salt, and IL solutions were filtered with a 0.1 μm syringe filter (Millex) prior to the sample preparation to avoid dust contamination.

Figure 1.

Chemical structure of IL constituent cations used in the present study (BMIM⁺, 1-butyl-3-methylimidazolium; BMPY⁺, 1-butyl-2-methylpyridinium; BMPIP⁺, 1-butyl-1-methylpiperidinium; BMPYR⁺, 1-butyl-1-methylpyrrolidinium; chloride was used as the anion).

Alkaline Treatment of HNTs

Before use, the raw HNTs were treated with an alkaline solution in order to improve their surface properties and polydispersity.¹⁸ Briefly, the HNTs were dispersed at a concentration of 20 g/L in a 14.5 mM KOH solution under magnetic stirring for 24 h. The hydroxylated HNTs were then washed several times with ultrapure water by centrifugation at 10 000 rpm for 10 min. The supernatant was removed, and the slurry was dried in an oven at 110 °C for 15 h. The dry powder was redispersed into water to obtain the HNT stock dispersions (denoted as h-HNT thereafter) at a concentration of 10 g/L.

Electrophoresis

The electrophoretic measurements were performed with a Litesizer 500 instrument (Anton Paar) equipped with a 40 mW semiconductor laser (658 nm wavelength). The samples were prepared by the following procedure. IL solutions of 1.8 mL volume and of calculated concentration were mixed with 0.2 mL of h-HNT of 10 mg/L. The suspensions were prepared by mixing the required amounts of water, salt, or IL solutions and the particle suspension to get the desired concentrations. The sample was allowed to rest overnight before performing the electrophoretic mobility measurements, which were carried out in an Univette (Anton Paar) accessory. The obtained electrophoretic mobility (u) values were converted to zeta potentials (ζ) with the Smoluchowski equation:⁶⁵

1

where η is the viscosity, ε is the dielectric constant of the medium, and ε₀ is the permittivity of the vacuum. Note that the Henry equation could be used below 1 mM ionic strengths in the BMPYCl system. However, the difference between the zeta potentials calculated by the two methods is comparable to the accuracy of our measurements. Therefore, the Smoluchowski equation was applied for all electrophoretic mobility–zeta potential conversions because of simplicity reasons. The concentration dependence of the η values is known for the inorganic salts^19,66 and was measured for the aqueous IL solutions, as detailed below. The average error of the zeta potentials determined in the electrophoretic measurements is about 5%.

Dynamic Light Scattering

Dynamic light scattering (DLS) was used to determine the hydrodynamic radius (R_h) of the particles. The experiments were carried out with a Litesizer 500 instrument (Anton Paar) at a scattering angle of 175°. The correlation function was fitted with the cumulant method to obtain the decay rate constant (Γ). The diffusion coefficient (D) was calculated as follows:⁶⁷

2

where q is the scattering vector, which can be calculated using the parameters of the experimental setup:

3

where n is the refractive index of the medium, λ is the wavelength of the laser beam, and Θ is the scattering angle. The refractive indices of the IL solutions were determined, as detailed later. The R_h was then calculated by the Stokes–Einstein equation:

4

where k_B is the Boltzmann constant and T is the absolute temperature. The sample preparation procedure was the same as in the electrophoretic studies with the exception that the DLS measurements were started immediately after adding the h-HNTs stock suspension and mixing for 25 s. The samples were equilibrated for 30 s in the instrument before data collection began.

Refractive Index

The n values of the IL solutions were measured with an Abbemat 3200 automatic one-wavelength refractometer (Anton Paar) at 589 nm. The data used in eq 3 were interpolated with a linear fit on the n versus IL concentration values (Figure 2a):

5

where C_IL is the molar concentration of the ILs, while a and b are the fitting parameters given in Table 1.

Figure 2.

Refractive indices (a) and viscosities (b) of aqueous IL (BMIMCl, BMPYCl, BMPYRCl, and BMPIPCl) solutions at different concentrations. The solid lines are fits using eqs 5 (a) and 6(b) applied for data interpolation.

Table 1. Fitting Parameters Used to Interpolate the Refractive Indices and Viscosities of the IL Solutions.

	refractive indexa		viscosityb
composition	a (M–1)	b	A (M–1/2)	B (M–1)	D (M–2)
BMIMCl	3.10 × 10–2	1.3310	0.3774	2.87 × 10–4	0.3894
BMPYCl	3.94 × 10–2	1.3308	0.7738	3.47 × 10–2	0.6350
BMPIPCl	3.74 × 10–2	1.3294	0.1724	–7.70 × 10–1	1.4782
BMPYRCl	3.12 × 10–2	1.3311	0.7915	–5.95 × 10–1	0.7591

^aFitting parameters of eq 5.

^bFitting parameters of eq 6.

Viscosity

The η data of the IL solutions were measured in a cone–plate geometry (CPE-40 cone) with a LVDV-II+ ProC/P viscometer (Brookfield). The η of the different IL–water mixtures was obtained by fitting the shear stress versus shear rate data with the Casson model.⁶⁸ The measured η values were then plotted against C_IL and fitted with the following equation⁶⁶

6

where η₀ is the viscosity of water, while A, B, and D constants are listed in Table 1. The above relation was applied for interpolation of η used in eqs 1 and 4. The experimental data determined in the IL concentration regimes applied and the fits with eq 6 are shown together in Figure 2b.

Electron Microscopy

Morphology studies of bare h-HNTs were carried out using transmission electron microscopy (TEM, FEI TECNAI G²20 X-TWIN). For the TEM measurements, the dispersions of the particles were dried on copper–carbon mesh grids, and 200 kV accelerating voltage was used for imaging in the bright field mode.

Results

Surface charge and aggregation rates of negatively charged halloysite nanotubes (h-HNTs) were investigated in the presence of inorganic electrolytes and ILs by electrophoresis and DLS. The principal aim of these experiments was to assess the affinities of the cations (which act as counterions) to the h-HNT surface and their effects on the stability of colloidal dispersions. Based on these results, the validity of the Hofmeister series will be clarified for simple ions, and the series will be extended with IL cations.

Characterization of the h-HNT

The morphology of the h-HNTs was studied with TEM (Figure 3), and the elongated structure was confirmed. The outer diameter and length of the h-HNTs vary in the range of 50–60 and 200–500 nm, respectively, indicating moderate polydispersity in both dimensions.

Figure 3.

TEM micrographs of the bare h-HNTs. The images were taken after drying the dispersions.

The pH-dependent charge and size of h-HNT were investigated in the 3–11 pH regime. The zeta potentials were negative under the conditions applied due to the abundance of the deprotonated silanol groups on the outer surface (Figure 4). Although positive zeta potentials were reported earlier with a point of zero charge of 2,¹⁶ this condition is out of the pH range studied here. The overall negative charge originates from the higher number of deprotonated silanol groups compared to the protonated aluminol groups.⁵ However, one cannot determine this relation quantitatively on the basis of the zeta potential results. A significant decrease was observed in the pH range of 4–6, as the pK_a of the silanol groups falls in this range. Subsequently, the zeta potentials of h-HNT indicate a relatively high magnitude of surface charge over a wide pH range in the alkaline regime. The further colloidal stability studies were carried out at pH 7. At this condition the particles possess considerable negative charge (−33 mV zeta potential), while the pH is low enough to avoid possible carbon dioxide absorption into the samples, which would be a significant error source in the ion specificity studies.

Figure 4.

Zeta potentials (circles, left axis) and hydrodynamic radii (squares, right axis) of h-HNT as a function of the pH. The measurements were performed at 1 mM ionic strength.

The trend in the pH-dependent size of h-HNTs is analogous to the above-discussed zeta potential tendency. The hydrodynamic size decreased with the pH due to the increase of the surface charge and, consequently, the lowering of the tendency of the particles toward aggregation. The presence of some aggregates at lower pHs is due to the weaker double layer repulsion between the particles giving rise to higher average hydrodynamic radii in these samples. At pH 7 the hydrodynamic radius was obtained as 442 nm, and the polydispersity index was 0.15. These data indicate that the h-HNT dispersions are suitable for time-resolved DLS measurements, discussed later.

Surface Charge Properties

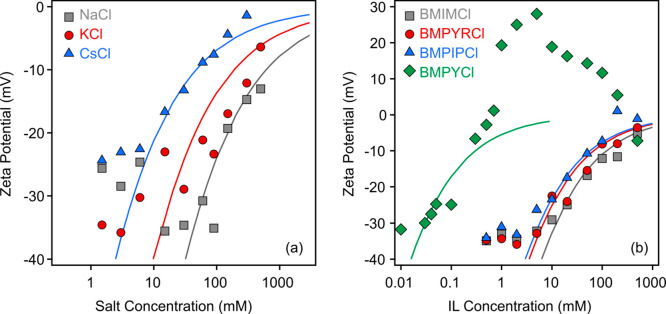
First, the charging features of h-HNT particles were investigated in the presence of NaCl, KCl, and CsCl, as no literature data were reported for these systems so far. In general, the magnitude of the zeta potentials decreased with the salt concentration, and they remained negative in the entire regime investigated (Figure 5a). However, at a given ionic strength, the measured potentials are system specific. An increase in magnitude can be observed in the Cs⁺ < K⁺ < Na⁺ order indicating ion specific interactions with the surface of h-HNT particles.

Figure 5.

Zeta potentials of negatively charged h-HNTs at different concentrations of monovalent salts (a) and IL solutions (b). The lines are the results of calculations using eq 9.

Subsequently, the effect of the IL cations on the charging conditions of h-HNT was investigated by measuring the zeta potential in a wide range of IL concentrations (Figure 5b). It was assumed that ILs completely dissociate to hydrated anions and cations under these experimental conditions.^50,56,58 It is obvious from the measured data that the system containing BMPY⁺ cations behaved rather differently from the other systems. Accordingly, charge neutralization and reversal behavior of the h-HNT particles were observed, indicating high affinity of BMPY⁺ cations to adsorb on the surface of the colloidal particles. A similar phenomenon has been already reported with some other IL cations with both hydrophilic⁵⁹ and hydrophobic⁶⁰ surfaces; however, it is rather exceptional behavior within monovalent counterions. For the BMIMCl, BMPYRCl, and BMPIPCl solutions, the absolute value of the zeta potential decreased with increasing the IL concentration, and the values remained in the negative regime even at high IL levels. Looking at the zeta potential at the same IL concentrations, their magnitude followed the BMPY⁺ < BMPIP⁺ < BMPYR⁺ < BMIM⁺ order indicating a decreasing adsorption tendency of the cations to the surface in this sequence. Note that BMPY⁺ is the only cation in which the methyl group is connected to a carbon atom (and to nitrogen in all other ILs). This fact may explain the different affinity to the surface; however, no unambiguous experimental evidence exists to underline this implication.

Particle Aggregation

The aggregation properties of systems containing h-HNT particles were investigated by time-resolved DLS experiments by following the change in the hydrodynamic radius under the same experimental conditions (pH, particle concentration, and ionic strength range) as for zeta potential measurements. The rate of aggregation was expressed in terms of stability ratio (W), which was calculated as follows:⁶⁹

7

where Δ is the apparent aggregation rate constant calculated from the initial increase in the hydrodynamic radii and Δ_fast is the rate constant determined in 1 M KCl solutions, in which fast aggregation of the particles occurs. Thus, stability ratios close to unity indicate unstable samples, and higher values refer to more stable dispersion and slower particle aggregation.

In general, the trends in the stability ratio values were the same for both inorganic salts and ILs (Figure 6a and Figure 6b, respectively). Accordingly, slow aggregation was observed at low ionic strengths, which is illustrated by the high stability ratio values. Then, in parallel with the increase in ionic strength, the stability ratio decreases until it reaches a unit value and remains constant within the experimental error at higher concentrations. This behavior resembles the one predicted by the DLVO theory,⁷⁰ which states that the overlap of the electrical double layers around the charged particles leads to the rise of repulsive electrostatic forces at low salt concentrations, which are stronger than the attractive van der Waals forces. This situation results in stable dispersions. Besides, the double layer forces weaken progressively with increasing the electrolyte level due to the surface charge screening, and thus van der Waals forces become predominant at high electrolyte concentrations leading to aggregation of the particles. These observations are generic for all colloidal systems, but the actual values of the stability ratios vary by changing the composition of the electrolytes. Such an influence of the type of electrolyte on the colloidal stability is not included in the DLVO theory.

Figure 6.

Stability ratios of h-HNTs at different concentrations of monovalent salt (a) and IL solutions (b). The lines are the results of calculations using eq 8.

Note that the charge reversal process may cause restabilization of the particles in certain systems;⁶⁰ however, this was not observed with the h-HNT-BMPYCl samples. This is due to the joint effect of the relatively low magnitude of the zeta potentials and charge screening by the nonadsorbed IL constituents. Similar results were also reported with titania particles dispersed in aqueous IL solutions.⁵⁹

Discussion

Ion Specific Effects

To quantify the deviations in the aggregation tendencies for the different systems, the critical coagulation concentration (CCC) values were calculated from the stability ratio versus ionic strength plots with the following equation:⁶⁹

8

where c is the molar concentration and the exponent β was calculated from the slope of the stability ratios in the slow aggregation regime. Note that CCC defines the electrolyte concentration, at which the transition between the slow and fast aggregation regimes occurs.⁷⁰ The fitted curves are shown in Figure 6a and 6b, while the obtained CCCs are shown in Table 2 and Figure 7a.

Table 2. Characteristic Aggregation and Charging Data of h-HNTs Particles Measured in Monovalent Salt and IL Solutions.

salt/IL	NaCl	KCl	CsCl	BMIMCl	BMPYRCl	BMPIPCl	BMPYCl
CCC (mM)a	300	80	15	50	20	17	1
σ (mC/m2)b	–16	–10	–5	–8	–6	–5	–1
ζ (mV)c	–13	–15	–17	–15	–20	–19	–6

^aCritical coagulation concentration calculated by eq 8.

^bCharge density determined with eq 9.

^cZeta potential at the CCC.

Figure 7.

CCC values of h-HNT particles determined in the presence of monovalent salts and ILs (a). CCC versus the charge density data (b). The experimental CCCs and charge densities were calculated with eqs 8 and 9, respectively. The lines in (a) are just to guide the eyes, while in (b), it was calculated by eq 10.

The fitted CCC values for the h-HNTs in inorganic salt and IL solutions decrease in the following order:

Considering only the inorganic cations, the sequence corresponds to the direct Hofmeister series for negatively charged hydrophobic surfaces.¹⁹ Once the IL cations are included, the presence of BMPY⁺ leads to the lowest CCC. This remarkable effect stems from the strong adsorption of BMPY⁺ to the surface of h-HNT resulting in charge neutralization and reversal, as discussed before. The CCCs in the case of other IL cations are located between K⁺ and Cs⁺ in the above order, which is considered as the Hofmeister series for h-HNT particles extended with IL cations.

Charge–Aggregation Relation

Earlier studies carried out with different colloid particle dispersions shed light on the importance of ion adsorption in the stability of colloids.¹⁹⁻²¹ Therefore, this issue was explored by calculating the charge density (σ) values from the zeta potential versus concentration plots using the Debye–Hückel model:⁷⁰

9

where κ is the inverse Debye length, which contains the contribution of the ionic species to the electrical double layer.⁶⁵ Note that this model is valid in the case of moderate zeta potentials, and thus deviation between the experimental and calculated values occurs at low ionic strength. The results of the calculations are shown in Figures 5, and the determined charge densities are given in Table 2. One can notice that they follow the same order as the CCCs discussed above. Accordingly, the lowest charge was determined for BMPY⁺ and the highest for Na⁺.

Plotting the CCC values against the charge densities (Figure 7b), the charge–aggregation relation is unambiguous. The strength of cation adsorption is the highest for BMPY⁺ and the lowest for Na⁺. The repulsive electrical double layer forces are the weakest in the former case due to the higher extent of charge compensation upon adsorption; hence, destabilization takes place at a low CCC. The situation in the case of Na⁺ is the opposite. Weak adsorption on the oppositely charged surface does not significantly decrease the charge of h-HNT leading to strong double layer forces, which can be screened only at higher salt concentrations giving rise to a higher CCC value. In summary, the extent of the ion specific adsorption determines the location of the CCCs in the individual systems.

As discussed above, such a dependence of the CCC on the type of ions is not predicted by the DLVO theory, once the same particles are dispersed in different monovalent salt solutions. However, in the case of ion specific adsorption, the surface charge of the particle changes; thus, one cannot consider the properties of h-HNT to be the same in all systems. In other words, the significant adsorption of BMPY⁺ leads to different charging properties and strength of double layer forces than in the case of Na⁺, where the charge is close to that of the bare h-HNT. The origin of the interparticle interactions can be further investigated by the relation derived from the DLVO theory, which allows the calculation of CCC values from the charge densities:⁷⁰

10

where N_A is Avogadro’s number, H is the Hamaker constant, and L_B is the Bjerrum length, which is equal to 0.72 nm for monovalent electrolytes in water.¹⁹ To obtain the best fit to the experimental data, a Hamaker constant of 7.0 × 10^–21 J was used in eq 10.

Based on the relatively good agreement between the experimental and calculated CCCs (Figure 7b), one can conclude that DLVO theory predicts the CCC values rather well, once the appropriate charge densities are entered in eq 10. Such an agreement indicates that the aggregation mechanism, i.e., the origin of major interparticle forces, can be derived from the DLVO model. Nevertheless, the locations of the CCCs are system specific, and they are determined by the affinity of the counterions to the surface, which affects the strength of the double layer repulsion. Such a synergistic influence of DLVO forces and ion specific adsorption on the colloidal stability led to different CCCs and the establishment of the Hofmeister series of cations for the h-HNT particles.

Conclusions

The effect of simple monovalent electrolytes (NaCl, KCl, and CsCl) and water-soluble ILs (BMIMCl, BMPYCl, BMPYRCl, and BMPIPCl) on the surface charge and aggregation of h-HNT particles in dilute aqueous solutions was investigated by light scattering techniques. Very similar generic trends were observed in zeta potentials and stability ratios determined at different ionic strengths except for the BMPY⁺ cation. In that case, the unexpectedly strong adsorption gave rise to charge neutralization and reversal behavior of the negatively charged h-HNT. For the other systems, the magnitudes of both zeta potentials and stability ratios decreased with increasing the ionic strength leading to rapidly aggregating particles beyond the CCCs, whose order was determined as follows:

This sequence corresponds to the direct Hofmeister series suggested for cations in the presence of negatively charged hydrophobic surfaces. However, this is the first time when such a series is established for HNTs and extended with IL cations. Comparison of the CCCs determined by the experiments and those calculated by the DLVO theory sheds light on the origin of the interparticle forces. It was found that the aggregation mechanism is controlled by the interplay between the repulsive electrical double layer and attractive van der Waals forces, which is in line with the DLVO theory. In addition, the variation of the CCC in different salt solutions results from the different extent of counterion adsorption on the h-HNT surface, which follows the opposite order than the CCC data shown above. These findings bring considerable new knowledge useful for designing the processable h-HNT dispersions in electrolyte solutions or in their mixtures. The interfacial assembly of IL constituents is of paramount importance to tune and predict the stability of colloidal systems including dispersions of HNT or other inorganic particles in ILs.

The authors declare no competing financial interest.