Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Oct 21;16(11):6938–6949. doi: 10.1021/acs.jctc.0c00744

A GPU-Accelerated Fast Multipole Method for GROMACS: Performance and Accuracy

Bartosz Kohnke 1, Carsten Kutzner 1, Helmut Grubmüller 1,*
PMCID: PMC7660746  PMID: 33084336

Abstract

graphic file with name ct0c00744_0017.jpg

An important and computationally demanding part of molecular dynamics simulations is the calculation of long-range electrostatic interactions. Today, the prevalent method to compute these interactions is particle mesh Ewald (PME). The PME implementation in the GROMACS molecular dynamics package is extremely fast on individual GPU nodes. However, for large scale multinode parallel simulations, PME becomes the main scaling bottleneck as it requires all-to-all communication between the nodes; as a consequence, the number of exchanged messages scales quadratically with the number of involved nodes in that communication step. To enable efficient and scalable biomolecular simulations on future exascale supercomputers, clearly a method with a better scaling property is required. The fast multipole method (FMM) is such a method. As a first step on the path to exascale, we have implemented a performance-optimized, highly efficient GPU FMM and integrated it into GROMACS as an alternative to PME. For a fair performance comparison between FMM and PME, we first assessed the accuracies of the methods for various sets of input parameters. With parameters yielding similar accuracies for both methods, we determined the performance of GROMACS with FMM and compared it to PME for exemplary benchmark systems. We found that FMM with a multipole order of 8 yields electrostatic forces that are as accurate as PME with standard parameters. Further, for typical mixed-precision simulation settings, FMM does not lead to an increased energy drift with multipole orders of 8 or larger. Whereas an ≈50 000 atom simulation system with our FMM reaches only about a third of the performance with PME, for systems with large dimensions and inhomogeneous particle distribution, e.g., aerosol systems with water droplets floating in a vacuum, FMM substantially outperforms PME already on a single node.

1. Introduction

The evaluation of mutual interactions in many-body systems is a crucial and limiting task in many scientific fields such as biomolecular simulations,1 astronomy,2 and plasma physics.3 Here, we consider molecular dynamics (MD) simulations, where electrostatic forces

1. 1

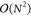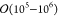acting on N atoms at positions xi with partial charges qi are calculated to determine new positions of the atoms in subsequent discrete time steps. ∥·∥ denotes the Euclidean norm. A direct calculation of the forces has Inline graphic complexity; thus only systems of limited size can be computed directly in equitable time. Additionally, a typical MD simulation employs periodic boundary conditions (PBC) to avoid surface artifacts, making the direct calculation unfeasible even for small systems. In contrast to cosmological calculations, which are usually limited by the available memory due to enormous particle numbers,1 many interesting biomolecular systems consist of Inline graphic particles. Recently, however, the demand to study increasingly large systems has grown markedly, and systems of 108–109 particles could become routine soon.4−7 Nevertheless, biomolecular systems, independent of their size, require long trajectories where the length of a time step can be no longer than a few femtoseconds for numerical stability reasons. Thus, the time required to finish one simulation step needs to be shortened to a millisecond or less so that long enough trajectories can be produced in reasonable time. To overcome these bottlenecks, the solution of eq 1 requires efficient approximation.

The prevalent method for such approximation in the field is particle mesh Ewald (PME).8 PME uses Ewald summation to split up the calculation into a short-range part, for which all interactions up to a cutoff radius rc are directly evaluated, and a long-range part, which is solved in reciprocal space. To take advantage of fast Fourier transforms (FFTs) for the conversions to and from reciprocal space, the charges are interpolated onto a uniform grid using cardinal B-splines. Higher interpolation orders and finer grids yield higher accuracy for the reciprocal part. PME scales with 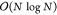Inline graphic and by construction provides a PBC solution, but does not allow for nonperiodic calculations.

MD packages like GROMACS9−11 or NAMD12 have PME implementations that are highly performance optimized. With GROMACS, typical MD systems reach iteration rates of 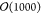Inline graphic steps per second currently;11 hence all forces are computed in less than a millisecond. However, with increasing parallelization, as required for high performance applications, PME runs into a communication bottleneck. Because the FFTs require all-to-all communication, which implies quadratic scaling with the number of processes, PME scaling breaks down at an intermediate number of processes.13−15 A further limitation is that the FFT grid becomes memory intensive, particularly if high accuracy is required or for highly inhomogeneous charge distributions.

An alternative way for rapid evaluation of Coulomb forces is the fast multipole method16 (FMM), which is not impaired by the aforementioned limitations and even scales with 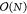Inline graphic. Therefore, while PME is fast for small to medium sized MD systems at moderate parallelization, FMM will be competitive for large number of particles, large simulation boxes, inhomogeneous charge distributions, and high parallelization.11,13 Further, FMM can be used for both periodic and open boundaries.

FMM splits the calculation into a near field, which is directly evaluated, and into a far field. For the far field, groups of sufficiently separated point charges are combined and described as truncated multipole expansions. The grouping is accomplished by recursively subdividing the simulation box into sub-boxes in an octree fashion; i.e., each parent box is subdivided into eight equal child boxes when the tree depth d is increased. This yields 8d boxes on the lowermost level. For d = 0, there is no subdivision. Interactions between particles residing in the same or in directly neighboring boxes at the lowest tree level are calculated directly as in eq 1, whereas interactions between particles in distant boxes are approximated via far field calculations. FMM can also allow for direct interactions between particles in boxes with a larger distance from each other. The distance is controlled by the well-separateness criterion “ws”. Larger ws improves the accuracy of the method but it impairs its performance markedly since eq 1 scales quadratically with respect to the number of particles.17 In this work we exclusively consider ws = 1; hence, only particles of nearest neighbor boxes interact directly.

For the far field interactions, the inverse distance between charged particles with index i and j is approximated as18

1. 2

where Y and Y* are spherical harmonics and their complex conjugate, respectively. The multipole order p controls the accuracy of the approximation. FMM achieves linear scaling with respect to N by performing hierarchical far field operations on multipoles expanded in octree boxes. Computationally, the most demanding part of the far field evaluation is the multipole-to-local (M2L) transformation. 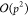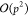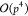It requires Inline graphic dot products with Inline graphic complexity, yielding an overall complexity of Inline graphic.

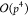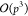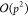The spherical harmonics based FMM (eq 2) was developed by Greengard and Rokhlin.18 Following this, other approximations of the inverse distance have been developed, such as the plane wave expansion approach19 to reduce operational costs of the M2L operator from Inline graphic or Inline graphic to Inline graphic or the black-box FMM,20 which utilizes Chebyshev interpolation to minimize the far field representation of the multipoles.

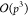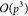One of the first parallel GPU implementations of the spherical harmonics based FMM21 used Inline graphic operators and achieved accuracy dependent speedups of 30–70 relative to a serial run on a single CPU core. Recently, the Inline graphic M2L operator for a single GPU was optimized further.22 GPUs were used to speed up the kernel independent FMM20,23 and the black-box FMM.24 A single-GPU implementation of the spherical harmonics FMM25 was also parallelized over a cluster26 with 32 GPUs where it reached parallel efficiencies of 44% for 106 particles and 66% for 107 particles. Larger, multinode, multi-GPU parallelization27 for a 256 million particle system over 256 GPUs followed. Blanchard et al.28 and Agullo et al.24 presented task based parallelization strategies.

The FMM has been successfully used to compute Coulomb or gravitational interactions in a wide range of applications,1−3 whereas its use for biomolecular simulations is still limited with a few exceptions.29,30 We have therefore developed, implemented, and optimized an FMM for MD simulations with GROMACS.

As GROMACS usually runs in mixed precision, using double precision only for accumulation order sensitive tasks, consumer GPUs are extremely attractive for the force computation, as they offer a high single-precision FLOP rate at a low price, especially compared to CPUs.31 Therefore, we implemented the complete FMM workflow on the GPU. Whereas rotational M2L operators with complexity Inline graphic have been proposed,18 here we consider an Inline graphic approach for the M2L operator as it is better suited for GPU parallelization.32

Our GPU version is based on the ScaFaCoS FMM,2 which we fully parallelized with CUDA33 and optimized for GROMACS. Here, we assess the performance of our GPU FMM implementation34 and evaluate its accuracy in comparison to GROMACS’ PME implementation.

2. Benchmark Methods

In a first step, we verified that our CUDA FMM implementation yields accurate energies and forces by comparing against known reference solutions for several input systems. Subsequently, we used typical MD systems to compare FMM vs PME performance in GROMACS 2019.

2.1. Accuracy of FMM Results

The forces and energies computed with the FMM deviate from their exact values mainly due to truncation of the multipole expansion at finite order p, which for small p causes the main contribution to the numerical error. Additionally, the errors in the energies vary due to different accumulation orders in the parallelized reductions. To quantify the magnitude of these errors, we compared FMM derived forces, potentials, and energies with reference solutions.

Given a reference solution vi, i = 1, ..., N, with N values of the potential at the atomic positions, or the 3N individual scalar values x, y, and z force components, we estimated the approximation error with the cumulative relative L2 error norm:

2.1. 3

where ṽi are the approximated values.

2.2. Benchmark Systems

To assess the correctness and performance of our FMM implementation, we created five benchmark systems, which were then used to check different aspects of our implementation. We first verified that the FMM forces and energies for open and periodic boundaries are correct; then we found the FMM parameters yielding the same accuracy as the existing GROMACS PME implementation. Finally, we compared the performance of both methods at the same accuracy.

GROMACS benchmark systems were set up with GROMACS10 2019 using the AMBER03 force field,35 the TIP3P36 water model, and an integration time step of 4 fs. Note that this force field and water model are just an example—in fact, all force fields and water models supported by GROMACS can be combined with FMM electrostatics.

2.2.1. Infinite Ideal Crystal

The “ideal crystal” benchmark represents an infinite lattice of alternating positive and negative elementary charges. The charges were arranged as in an NaCl crystal in a 32 × 32 × 32 nm3 large box containing alternating +1e and −1e charges at 0.5, 1.5, 2.5, ..., 30.5, 31.5 nm in each dimension, in total 323 = 32 768 point charges. The shortest distance between nearest charges is exactly 1.0 nm, allowing for direct comparison with an analytical solution.

Considering the PBC, such a system of size 2 × 2 × 2 nm3 would be sufficient to compare against an analytical solution. However, the number of charges was chosen in a way that allows for flexibility during the tests regarding the choice of parameters. For instance, with PME a larger range of real-space cutoffs can be used, and with FMM various tree depths d = 1, 2, 3, 4 can be tested having a significant number of charges even on the lowest levels.

The potential energies at each charge center were calculated analytically with Madelung’s constant M.37 Its value was obtained by summing a specific, three-dimensional Epstein zeta function

2.2.1. 4

for the case of s = 1/2, where ∑′ excludes the origin sum to avoid singularity. The sum is absolutely convergent when summing over expanding cubes.38 For comparison we used the value M = −1.74756459..., which is given with 60 digits by Crandall.37

2.2.2. Salt Water

Our “salt water” benchmark consists of 16 861 water molecules with 46 Na+ and 46 Cl– ions in an ≈8 × 8 × 8 nm3 periodic simulation box, yielding 50 675 atoms in total. We used it to compare PME versus FMM errors and to determine which FMM parameters are needed to obtain a desired accuracy. Considering the Coulomb forces, we expect this system to reasonably well approximate the error behavior of typical MD systems of macromolecules embedded in water. However, setups with highly nonuniform charge distributions, e.g., membrane systems, could differ in their error distribution and magnitude.

An initial trajectory was generated with cutoffs set to 1 nm. PME was used for electrostatic interactions with a grid spacing of 0.135 nm and fourth order B-spline interpolation.8 Temperature coupling to a heat bath of 300 K was done with the V-rescale algorithm,39 while the pressure was kept at 1 bar with the use of Berendsen coupling.40

2.2.3. Salt Water Droplet

The “salt water droplet,” as shown in Figure 1, contains the same number of molecules as the periodic salt water system, but in open boundaries. It was built by centering a snapshot of the above system in a larger box of size 14 × 14 × 14 nm3. Apart from the fixed volume and therefore variable pressure, the simulation parameters are identical to those of the periodic case. With open boundaries, the system adopted an approximately spherical shape within ≈50 ps.

Figure 1.

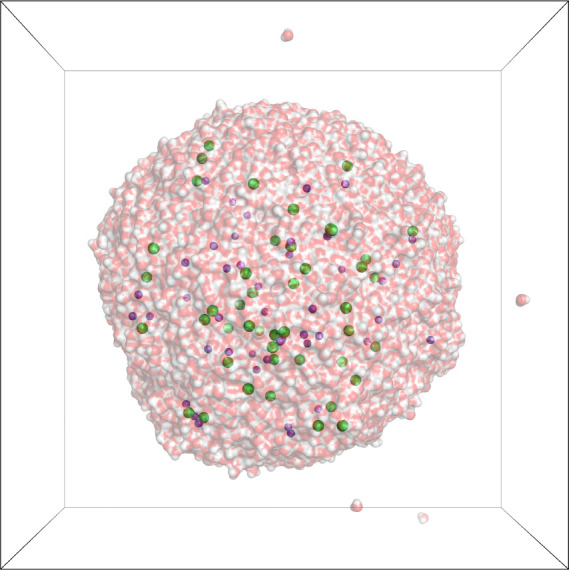
Figure 1

Open in a new tab

Salt water droplet test system. Water molecules are shown in surface representation (oxygens, red; hydrogens, white), with Na+ ions in magenta, Cl– ions in green, simulation box in black.

In principle, the box size is only relevant with PBC; technically, however, we used the box to treat the individual single water molecules that did occasionally evaporate from the droplet, as if they were in PBC, simply to keep them from flying too far away. A 130 ns long trajectory of the droplet was simulated, of which snapshots for later analysis were extracted.

The droplet system with open boundaries allows for computation of the reference Coulomb energy and forces by direct summation. It was, therefore, used assess the correctness of the complete FMM implementation apart from the periodic part, which is computed with an additional lattice operator.

2.2.4. Aerosol/Multidroplet Evaporation System

The “multidroplet system” (Figure 2) was built to demonstrate the advantages of the FMM for systems with highly nonuniform particle distributions, as occur in the atomistic simulation of, e.g., electrospray ionization as a prerequisite for mass spectrometric analysis,41−43 ion mobility spectrometry,44 laser-induced liquid beam ion desorption,45,46 and various naturally occurring47 or artificially produced48 aerosols.

Figure 2.

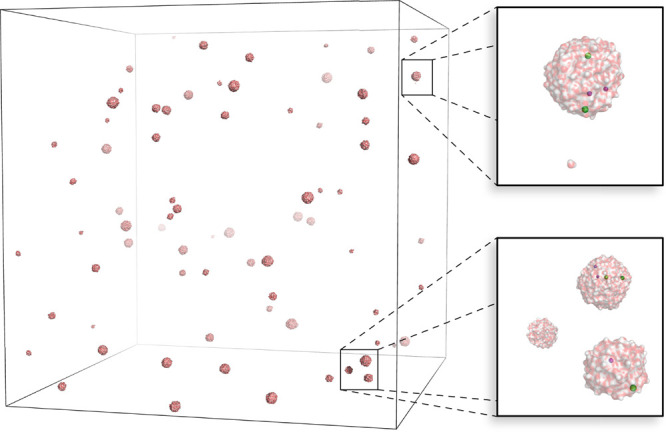
Figure 2

Open in a new tab

Aerosol/multidroplet system. Water surface representation as in Figure 1; close-ups to the right show individual droplets with Na+ ions in magenta and Cl– ions in green.

MD simulations can significantly complement these experiments by providing a detailed picture of the involved processes, e.g., the various aspects of droplet formation and evolution, charge migration, ion/lipid/protein desolvation, collisions with the background gas, and gas-phase unfolding. Simulating proteins, lipids, ion, and waters in the gas phase49 implies spatially extended simulation systems consisting mostly of vacuum.

In the gas phase, due to the lack of shielding, the correct treatment of long-range electrostatic forces is even more crucial than for fully solvated species to avoid artifacts50 and to correctly describe experimental conditions.51 With such extended systems, PME often reaches its limits, as memory requirements become prohibitive for the underlying large FFT grids. Sometimes the use of PME is precluded because, for optimal agreement with experiment, open boundaries may be more appropriate than PBC.43

Being a prototype for such sparse systems, our multidroplet benchmark contains 75 small water droplets in a box of side length 135.6 nm with 108 663 atoms. Sixty-three Na+ and 63 Cl– ions were distributed within the droplets. The system was run in the NVE ensemble with PBC. The van der Waals cutoff was set to 2 nm. For PME, to prevent a prohibitively large FFT grid, a Coulomb cutoff of 2.943 nm was used in combination with a grid spacing of 0.353 nm. This results in a Fourier grid of 3843 points.

2.2.5. Water Boxes of Different Sizes

To assess how our FMM implementation scales with respect to the number of particles N, we have build cubic boxes of edge lengths 3.13–67.4 nm containing 1000–10 000 000 TIP3P water molecules,36 i.e., N = 3000–30 000 000 particles. Benchmarks were run in the NVT ensemble with the use of Berendsen temperature coupling40 at a reference temperature of 300 K. Coulomb and van der Waals cutoffs were set to 1 nm. With PME, a mesh spacing of 0.135 nm was used with fourth order interpolation.

2.2.6. Random Charges

To assess the FMM performance and scaling in a standalone setting, i.e., without being coupled to GROMACS, we used 1000 < N < 286 000 000 randomly distributed charges in a box of a constant size of 100 nm. FMM standalone tests estimate the overhead introduced by integration of the FMM into GROMACS.

2.3. Benchmarking Procedure

All performance benchmarks were run on a node with Intel E5-2630v4 @ 2.2 GHz CPU, and NVIDIA RTX 2080Ti GPU running Scientific Linux 7.6 GROMACS 2019 was compiled with GCC 7.4.0, CUDA 10.0, thread-MPI, and AVX2_256 SIMD instructions, and with OpenMP and hwloc52 1.11 support. For the runs with PME on the CPU, the FFTW 3.3.753 library was used.

For optimum performance in a single-CPU, single-GPU setting,11,31 we used a single thread-MPI rank with either as many OpenMP threads as physical CPU cores (10) or as many OpenMP threads as CPU hardware threads (20). On modern Intel CPUs, using all available hardware threads can provide a performance benefit of up to ≈15% for cases with at least a few thousand atoms per core. We tested both settings in our benchmarks and report the performance of the fastest setting. It turned out that our benchmark systems with 50 000 atoms or more were faster with 20 threads instead of 10.

Additionally, the FMM vs PME scaling benchmarks were run on a node with 20-core Intel Xeon Gold 6148F CPU and NVIDIA V100-PCIE-32GB GPU running SLES 12.4. Here, GROMACS was compiled with GCC 8.4.0, CUDA 10.1, Intel MPI 2019, and AVX_512 SIMD instructions, and with OpenMP and hwloc 2.1.

Each benchmark ran for several minutes, i.e., several thousand time steps. Because the initial time steps often require long execution times due to memory allocations and load balancing effects, all times were recorded for the second half of each run.

3. Results and Discussion

3.1. FMM Convergence and Correctness

In this section we quantify the errors resulting from the FMM evaluation of the Coulomb interactions. We will first show that, with increasing order p of the multipole expansion, FMM converges to the correct solution. This was done in two steps. First, we used a system with open boundaries, where the correct solution (within numerical limits) can be obtained by a direct summation. Second, a simple periodic crystal with analytically derived solution was used as a reference to verify the correctness of the FMM PBC solution.

The Coulomb potential VC for a system of N charges is

3.1. 5

with k = 1/(4πϵ0) and ϵ0 is the vacuum permittivity. Our FMM implementation uses dimensionless values with k set to unity, whereas in GROMACS, k ≈ 138.935 kJ nm/(mol e2), with e the elementary charge. If an axis of a plot shows kilojoules per mole units for the potential energy and kilojoules per mole per nanometer for a force, the GROMACS unit system is used; otherwise energy and forces will be dimensionless.

3.1.1. Comparison to the Direct Summation for Open Boundaries

We first asked how accurate the FMM is for open boundaries. For an exemplary snapshot of the salt water droplet (Figure 1), we compared the FMM result for different parameters to a reference solution, which was determined by directly summing all Coulomb interactions in double precision.

Figures 3 and 4 quantify the FMM errors in the Coulomb forces for double and single precision, respectively. The upper rows (black) show the distribution of the 3N individual components of the forces firef (i = 1, ..., 3N) as absolute values. The colored histograms show error distributions computed from the differences to the reference values |fi – fiFMM| for various multipole orders for depths d = 2, 3, and 4.

Figure 3.

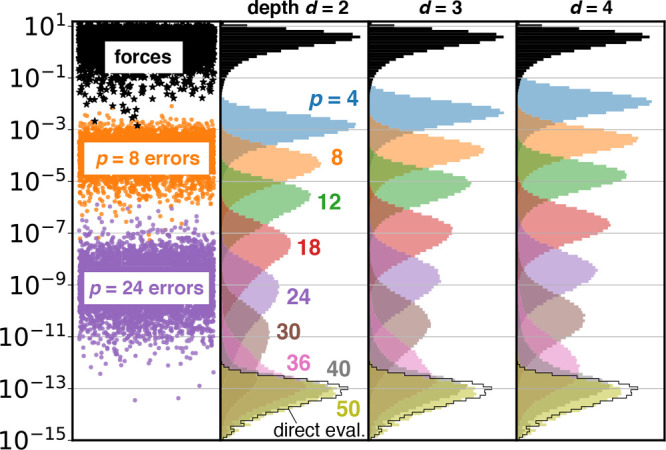
Figure 3

Open in a new tab

FMM errors for the 50 675 atom salt water droplet (Figure 1) using double precision. (left) Absolute values of individual force components (black stars, index on x-axis), and deviations from reference values for exemplary cases p = 8 (orange dots) and p = 24 (purple dots). Colored histograms show distributions of absolute errors in the forces for multipole approximations p = 4–50 and tree depths d = 2, 3, and 4. For comparison, black histograms show distributions of actual forces (in absolute values). The black outline near the bottom shows the error for directly evaluating all interactions. Note that the black force histograms were scaled by 0.75 to fit in the panels.

Figure 4.

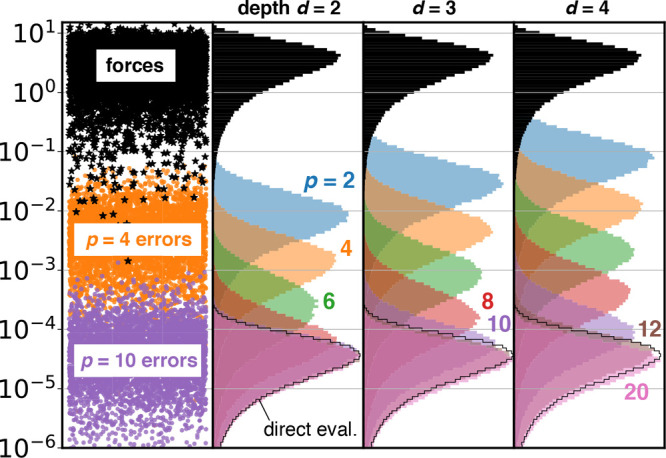
Figure 4

Open in a new tab

FMM errors for 50 675 atom salt water droplet (Figure 1). Same as Figure 3, but for single-precision FMM.

As can be seen, the force errors decrease exponentially with growing multipole order p and begin to saturate at p = 40 and p = 10 in double and single precision, respectively. With single precision, as commonly used for MD simulations, increasing the multipole order to p > 12 does not result in a further reduction of the error in the Coulomb forces for d ≤ 4. Increasing the tree depth d by 1 increases the errors by approximately 1/2 order of magnitude; however, this effect is less pronounced for higher multipole orders.

The black-outlined histograms at the bottom of Figures 3 and 4 quantify the error distributions between different runs of a direct summation. These errors reach maximal relative machine precision,54 which is 2.22 × 10–16 and 5.96 × 10–8 for double and single precision, respectively. Hence, since the FMM errors with multipole orders p = 40 in double precision and p = 12 in single precision saturate in the region of a direct summation error, for both precisions FMM reaches the numerical limits at these multipole orders.

Figures 5 and 6 show L2rel error norms of potentials and energies for an exemplary snapshot of the salt water droplet system. In single precision, increasing the multipole order to p > 12 does not reduce the error any further as the error reaches the limited machine representation.

Figure 5.

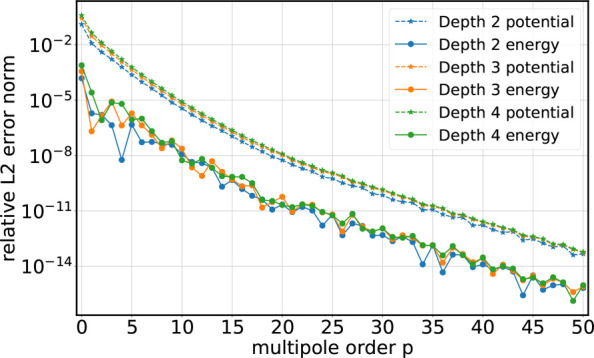
Figure 5

Open in a new tab

Relative L2rel error norm (eq 3) of the total electrostatic energy (solid lines with circles) and of the potentials at the atomic positions (dashed lines with stars) for the salt water droplet with open boundaries (double precision).

Figure 6.

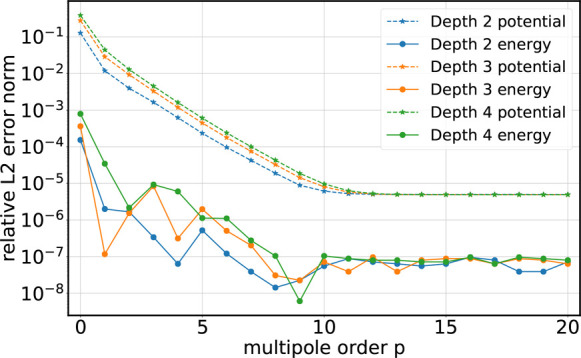
Figure 6

Open in a new tab

Relative L2rel error norm (eq 3) of the total electrostatic energy (solid lines with circles) and of the potentials at the atomic positions (dashed lines with stars) for the salt water droplet with open boundaries (single precision).

In summary, for open boundaries we conclude that FMM forces are as accurate as forces from a direct summation for high multipole orders p. In double precision, p ≳ 40 yields as accurate forces as a direct summation, whereas for single precision, p ≳ 12 suffices to reach the numerical limits. The relative accuracy of the Coulomb potential energy is about 10–7 for p ≥ 8 in single precision, whereas with double precision, accuracies of 10–14 are reached for p > 40. For p < 50 in double precision and p < 12 in single precision, the errors in forces and energies are larger for higher tree depth d.

3.1.2. Comparison to Analytic Solution for Periodic Boundaries

Next, we compared the FMM electrostatic energy for the ideal crystal with the analytical results. Figure 7 shows the relative error in the energy for a double-precision computation. The energy error decays exponentially with increasing multipole order. Note that the decay of the energy (compare also Figures 6 and 5) is not strictly monotonic, which follows from the evaluation of the Coulomb integral on cuboids and has been described elsewhere.17,55 Reaching the relative accuracies at the numerical limit for p ≳ 40 verifies that the treatment of the periodic boundaries in our FMM implementation is correct and that the FMM approximated energy with full PBC converges to the true value for growing multipole orders.

Figure 7.

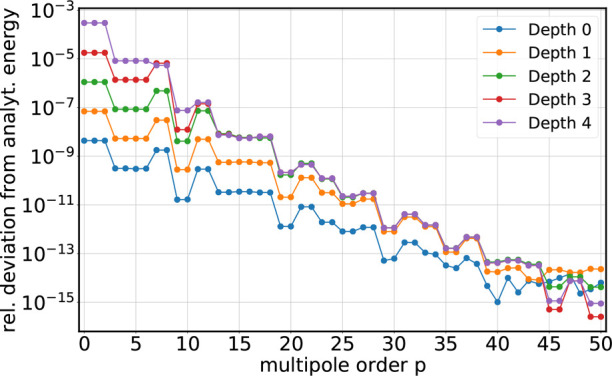
Figure 7

Open in a new tab

FMM energy error for the ideal crystal (double precision). Circles show the relative deviation of the energy computed with FMM from its correct value as a function of multipole order p and tree depth d.

3.2. Comparison of FMM to PME

After establishing the correctness of our FMM implementation, we compared it to PME by asking which FMM parameters p and d yield accuracies similar to those of several representative PME parameter settings, e.g., the spacing s of the Fourier grid and the B-splines interpolation order (also called PME order). In GROMACS’ PME implementation, the ewald-rtol parameter controls the relative strength of the direct potential at the cutoff rc and thereby how accurate the real space part is in relation to the reciprocal space part.56 Smaller values yield a more accurate real space contribution but a less accurate reciprocal space contribution. The default PME parameters use 10–5 for ewald-rtol, which minimizes the error for typical MD settings with cutoffs of rc ≈ 1 nm and PME grid spacings of s ≈ 0.12 nm. To reach optimal PME accuracy, however, a much smaller value of the ewald-rtol parameter is required in combination with a very fine PME grid and a sufficiently large interpolation order.

3.2.1. PME and FMM for the Ideal Crystal

Figure 8 shows how much the energy of the ideal crystal computed using several different PME parameters deviates from the reference values. For the used very fine grids with spacing s = 0.05–0.1 nm (corresponding to 3203–6403 grid points) combined with a high interpolation order of 12, PME accuracy mainly depends on the value of the ewald-rtol parameter. For ewald-rtol ≲ 10–13, the energy error achieves roughly 10–14, whereas FMM reaches this error bound for p ≥ 40. Hence, we have shown that both PME and FMM reach a relative accuracy of ≈10–14 in double precision in a periodic system.

Figure 8.

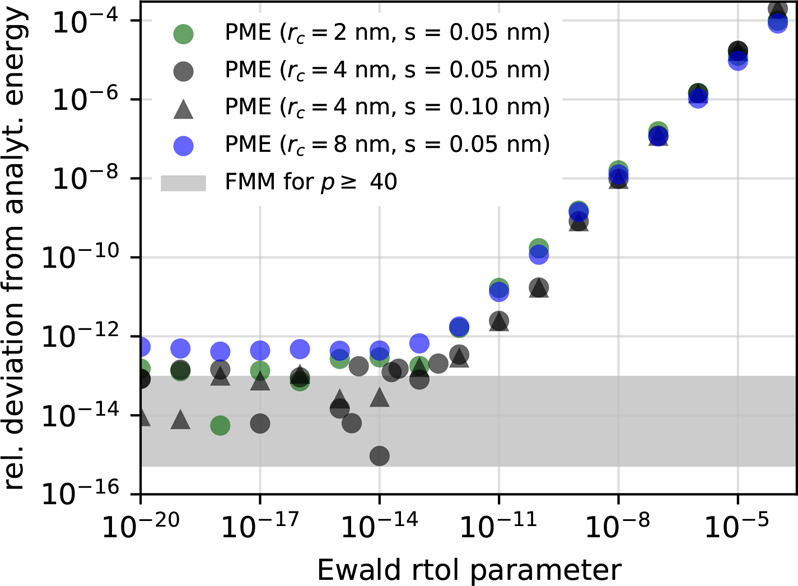
Figure 8

Open in a new tab

PME energy error for the ideal crystal (double precision). Circles show the relative deviation of the energy computed with PME from its correct value as a function of the ewald-rtol parameter for interpolation order 12 for four parameter sets (see legend, rc = real-space cutoff, s = PME grid spacing) For comparison, the corresponding FMM errors for p ≥ 40 are indicated by the shaded region (compare Figure 7).

3.2.2. PME vs FMM for the Salt Water System

Having shown that FMM and PME yield the same numerical accuracy for the potential energy for a simple periodic system, we switch to a more typical MD setting, namely the periodic salt water box with 50 675 atoms. For this system, we used a reference solution computed with the FMM in double precision using p = 50 and d = 0.

The colored histograms in Figure 9 show the errors in the Coulomb forces for various FMM and PME parameters. For PME, we selected four different parameter sets, two of which are representative for typical MD settings, another which pushes the parameters toward maximum accuracy, and an intermediate one. The “default” set uses the GROMACS default values of PME parameters, which are typical settings for many biomolecular simulations, i.e., a Coulomb cutoff of rc = 1.0 nm with a PME grid spacing of s = 0.12 nm and a B-spline interpolation order of 4. The “high precision” set uses rc = 1.2 nm with s = 0.1 nm and an interpolation order of 6. We also test a “maximal” parameter set using the largest possible cutoff that still respects the minimum image convention (rc = 4.0 nm) with s = 0.04 nm and an interpolation order of 12, which is the highest order supported by GROMACS. The “extreme” parameter set yields a precision between the “high” and “maximal” settings; see the legend of Figure 10. For each of the four PME parameter sets we have selected the ewald-rtol parameter such that it yields the minimal error in the Coulomb energy in double precision, as summarized in Figure 10.

Figure 9.

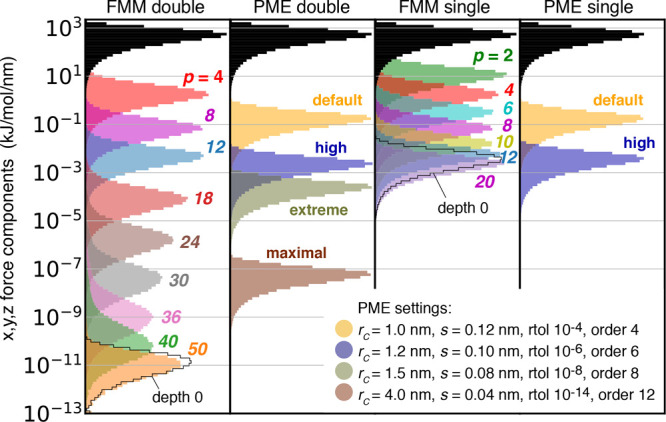
Figure 9

Open in a new tab

Accuracy of FMM and PME Coulomb forces for a snapshot of the 50 675 atom periodic salt water system for double precision (left two panels) and single precision (right two panels). Black histograms show distributions of actual forces (in absolute values). For FMM, colored histograms show distributions of absolute errors in forces for multipole approximations p = 2–50 at d = 3. For PME, values for four representative parameter sets are shown color coded (see legend). Note that the black force histograms were multiplied by 0.9 to fit in the panels. The black outline in the FMM panels shows the error for a direct evaluation of all interactions that are in the simulation box (d = 0) combined with a p = 50 (for double precision, p = 20 for single) multipole approximation for the surrounding periodic images.

Figure 10.

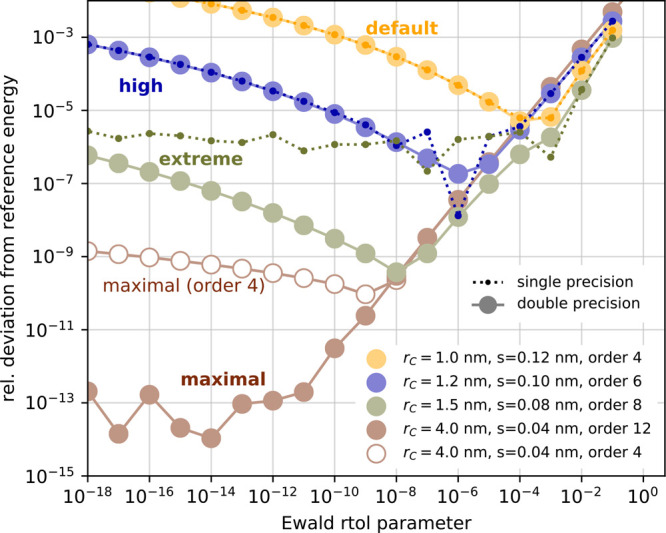
Figure 10

Open in a new tab

Coulomb energy error for various PME parameters, as in Figure 8but for a snapshot of the salt water system for double precision (solid lines with large circles) and single precision (dotted lines with darker small circles). For each combination of rc, s, and PME order, there is one value of the ewald-rtol parameter that minimizes the PME error. The reference energy was determined using a double-precision FMM calculation with p = 50 at d = 0. As almost all energy errors are ≥10–6 for single precision, they were omitted from the graph for the “maximal” parameter set (brown).

For the typical use case with single-precision forces, the accuracy of the Coulomb forces for “default” PME parameters is similar to that of FMM for p ≈ 7 at d = 3. The “high precision” PME parameters require an FMM with p = 14.

3.2.3. Periodic Boxes with Noncubic Geometry

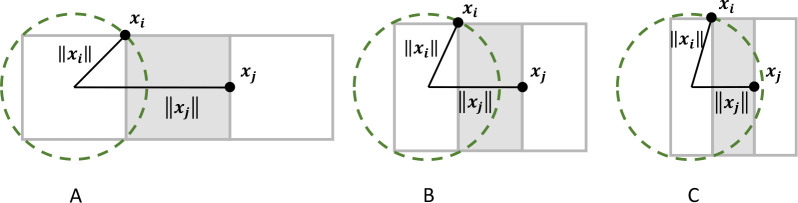
With PBC, our implementation is currently limited to cubic box shapes. Noncubic simulation boxes require modified octree subdivision,57 as eq 2 converges only if ∥xi∥ < ∥xj∥. As shown in Figure 11A, this condition is always fulfilled for cubic boxes. A slight deviation from cubicity, Figure 11B, does not violate this condition, but a larger ratio s ≔ ∥xi∥/∥xj∥ affects the convergence rate of the approximation. With decreasing s, the approximation error decreases with ∥xj – xi∥–1sp+1 for given p.19 As a rough guideline, a rectangular box with a 1.2:1 aspect ratio should achieve an accuracy similar to that of a cubic box with p = 8 (or p = 12), if the multipole order is raised to p = 10 (or p = 25). Slight deviations from cubicity, i.e., a few percent, should however not markedly affect the accuracy at constant p.

Figure 11.

Figure 11

Open in a new tab

Chosen strict octree subdivision requires the simulation box to be approximately cubic; otherwise the convergence criterion is not fulfilled. (A) Exactly cubic box; (B) slightly noncubic box; (C) extremely noncubic box. A source particle xi and a target particle xj are positioned in a way that maximizes the ∥xi∥/∥xj∥ ratio reflecting the worst-case scenario.

3.3. Energy Conservation with FMM

For NVE simulations without temperature and pressure control, all employed algorithms must be energy conserving to prevent a gradual, unphysical heating (or cooling) of the simulation system. But even when a thermostat is in place to absorb excess heat, algorithms should in general not introduce or remove significant amounts of heat from the system as that could cause artifacts. In practice, however, slight deviations from perfect energy conservation may be tolerated and, in fact, many of the employed algorithms contribute (with positive or negative sign) to an overall energy drift. The drift is caused by accumulated numerical and integration errors due to, e.g., the finite integration step size, the finite numerical precision, the constraint algorithm(s), or the various approximations during force calculations.

One such approximation is the pair lists for the Coulomb and van der Waals interactions within the cutoff. For enhanced performance, these lists are constructed from the cutoff plus an added buffer region (called Verlet buffer) so that they do not need to be updated every step. However, with list lifetimes > 1 step, even with such a radial buffer, occasionally a distant nonbonded interaction may be missed, thus contributing to the overall energy drift.58

In contrast, for FMM-computed Coulomb interactions, energy drift results from octree space discretization. Whereas PME uses a smooth switching function between interactions computed in direct versus reciprocal space, FMM particles contribute either completely or not at all to an octree box. Hence, particles crossing the octree box boundaries produce small discontinuities in the forces over time.

When substituting PME with FMM, we need to make sure that FMM does not increase the total energy drift. Therefore, we have determined the energy drift over time in a typical, mixed-precision simulation with PME and compared it to the same simulation with FMM for various FMM parameters. Figure 12 shows the drift of the total energy for the salt water benchmark with FMM in comparison to PME with “default” parameters (rc = 1.0 nm, s = 0.12 nm, fourth order interpolation, ewald-rtol = 10–4). With FMM, at the depth that yields the highest performance (d = 3), the PME default drift level is met for multipole orders p ≥ 8. The values of the total drift smaller than the black dashed line are due to cancellation of the positive FMM contribution with negative contributions as, e.g., result from the water SETTLE constraints.58 Whereas with double precision and a large enough Verlet buffer, the total drift can be reduced to <10–7 kJ/mol/ps per atom for both PME and FMM (see Figure 11 in Kohnke et al.32), typical mixed-precision MD settings yield drifts of (5–8) × 10–5 kJ/mol/ps per atom. Regularizing the FMM could help to meet the energy conservation requirements of MD simulation at even lower p, as shown by Shamshirgar et al.59

Figure 12.

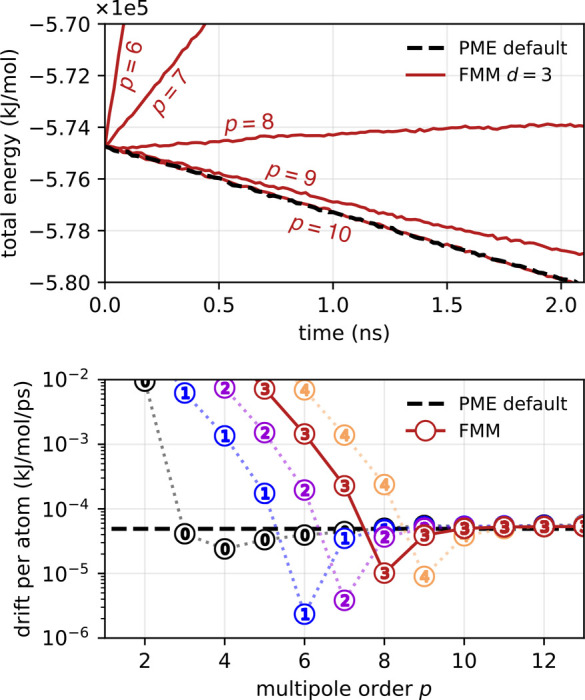
Figure 12

Open in a new tab

Drift of total energy at typical mixed-precision settings for the periodic salt water system. Dashed black lines show the total (in this case negative) energy drift with PME (Δt = 4 fs, “default” PME parameters as given in Figure 9, default Verlet buffer tolerance of 0.005 kJ/mol/ps). (top) Evolution of total energy with FMM at depth 3 (red) compared to PME (black). (bottom) Absolute drift of total energy derived from a linear fit. At depth d = 3 (encircled numbers), which results in optimal FMM performance for this system, for p ≥ 8, the positive drift component from the FMM does not lead to an increased total drift.

3.4. Performance of GPU FMM in GROMACS

3.4.1. FMM vs PME Performance

With previous tests we have established that the FMM with p = 8 and d = 3 achieves the same approximation quality as the PME with “default” parameters (see Figure 9). Therefore, we compared the performances of the two methods at these parameters.

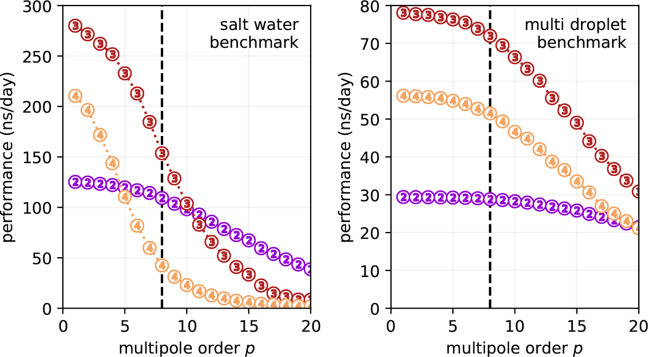
We first determined the FMM performance as a function of p and d for simulations in mixed precision (Figure 13). At p = 8, the salt water and multidroplet benchmarks achieve 153 and 72 ns/day, respectively. For both benchmarks d = 3 maximizes the performance. However, the scaling behaviors with respect to p notably differ when comparing both systems.

Figure 13.

Figure 13

Open in a new tab

GROMACS performance with FMM electrostatics for the 50 675 atom periodic salt water system (left) and for the 108 663 atom aerosol/multidroplet benchmark (right). Encircled numbers indicate FMM tree depth. With p = 8 as indicated by the dashed vertical line, FMM offers an accuracy of the electrostatic interactions that is comparable to the “default” PME parameter set (i.e., rc = 1.0 nm, PME grid spacing s = 0.12 nm, fourth order interpolation, see Figure 9). Benchmarks were run with 20 OpenMP threads on the CPU.

The inhomogeneity of the particle distribution in the multidroplet system changes the near field to far field calculation intensity ratio. Clustered particles occupy only a few FMM boxes; hence, for the far field, the empty boxes are skipped to enhance performance. We can observe that performance dependency on p is significant only for higher multipoles as the calculation is dominated by a very large number of directly interacting particles clustered into only a few boxes.

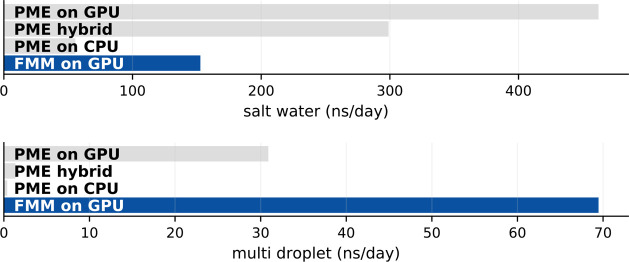
Figure 14 shows a performance comparison between FMM and PME for both systems. For the periodic salt water system, GROMACS with GPU FMM achieves about a third of the GPU PME performance. The situation reverses for the strongly inhomogeneous multidroplet system: here, FMM outperforms PME by more than a factor of 2.

Figure 14.

Figure 14

Open in a new tab

FMM versus PME performance in GROMACS for salt water (top) and multidroplet (bottom) benchmarks. Settings were chosen such that PME and FMM yield similar accuracies of electrostatic forces as well as comparable energy drifts. FMM used p = 8 and d = 3, whereas PME used the “default” parameter set (rc = 1.0 nm, PME grid spacing s = 0.12 nm, fourth order interpolation, see Figure 9). For the multidroplet system, for optimal PME performance, both rc and s were scaled by a factor of 2.943, which leaves the PME accuracy essentially unchanged.

We finally compared the FMM and PME scaling behaviors with respect to the number of particles for N = 3000–30 000 000. To ensure optimal scaling, we determined the proper FMM depth for each system size at p = 8. As can be seen in Figure 15, for both methods we can identify two different slopes with polynomial scaling 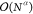Inline graphic, where α describes the slope of the curve. For small systems (N < 30 000), α is approximately 0.5. This indicates that with growing N in this region the GPU utilization increases leading to a better scaling behavior than linear. For N > 30 000 both methods achieve α ≈ 1 on the Tesla V100 GPU with 32 GB memory in the entire tested particle range. However, when the RTX 2080Ti GPU with 11 GB memory is used, the scaling begins to worsen already by ≈300 000 particles. Here the FMM scales slightly better (α = 1.02) whereas the PME achieves α = 1.08, indicating a performance decrease due to higher memory requirement.

Figure 15.

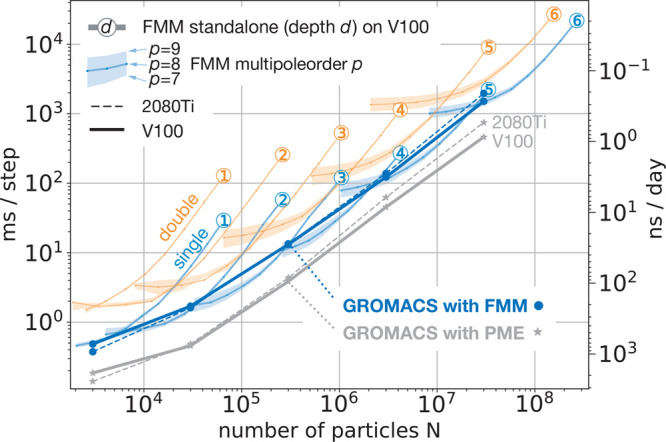
Figure 15

Open in a new tab

FMM and PME scaling with respect to system size N for up to 268 million charges. Benchmarks were run on an NVIDIA Tesla V100 GPU with 32 GB RAM (solid lines) and on an RTX 2080Ti GPU (dashed lines). Blue (single precision) and orange (double precision) colors denote FMM standalone timings for the random charge benchmark (left scale) with depths d = 1–6 (encircled numbers) and multipole order p = 8, whereas the lower and upper boundaries of the shaded regions indicate timings for p = 7 and p = 9. Gray and dark blue lines show wall clock time per MD step (left scale) and resulting GROMACS performance (right scale) for PME (gray stars) and FMM (blue circles) for water boxes of different sizes. GROMACS benchmarks were run on a 10-core E5-2630v4 node with RTX 2080Ti GPU (dashed lines) and on a 20-core Xeon Gold 6148F with V100 GPU (solid lines) with all nonbonded interactions offloaded to the GPU.

From the FMM standalone tests, also shown in Figure 15, we can clearly see that our FMM is tightly integrated into the GROMACS time stepping over the whole tested N range, as the runtimes of the FMM with GROMACS are not significantly longer than the FMM standalone runtimes.

Furthermore, on the Tesla V100 GPU, with the standalone FMM implementation we were able to run performance tests for an even larger number of particles as, in contrast to PME, where the simulation box size is limited by the available memory, FMM is limited only by the number of particles. Figure 15 shows that standalone FMM scales linearly up to ≈270 000 000 and ≈160 000 000 particles in single and double precision, respectively. The ability to perform efficient double-precision calculations on a GPU introduces a new asset as GROMACS is limited to run double-precision simulations only on a CPU.

3.4.2. Comparison to Other FMM Implementations

Finally, we compared the performance of our implementation with that of GemsFMM,25 which is another GPU FMM implementation written in CUDA. It uses spherical harmonics for the far field evaluation and 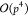Inline graphic operators to shift and transform the moments. Unfortunately, we were unable to find any other complete GPU FMM implementations (i.e., that compute both the far field and the near field) that can be tested and provide verifiable results.

Figure 16 compares FMM runtimes for particle numbers N = 104–107. The optimal depth for each N was chosen separately for each implementation to ensure optimal performance. Both implementations show a linear scaling with respect to N. The FMM implementation described in this work outperforms GemsFMM by a factor of 5.5 to 13.

Figure 16.

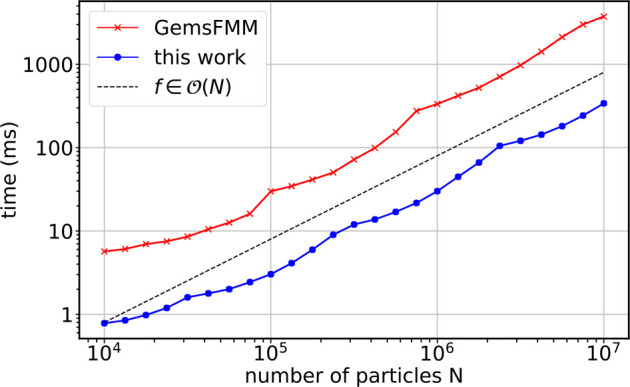
Figure 16

Open in a new tab

Performance of our FMM (blue) compared to the GemsFMM implementation (red). Shown are the average runtimes for a single complete FMM evaluation (far field plus near field) at p = 8 on an NVIDIA RTX 2080 GPU. The black dashed line depicts linear scaling.

4. Conclusions and Outlook

Here we have assessed the accuracy and performance of our GPU FMM described in detail by Kohnke et al.34 We demonstrated that our implementation provides correct electrostatic energies and forces for single and double numerical precisions by comparison to high-precision reference solutions for open and periodic systems. Using benchmark systems of various sizes and compositions, ranging from 3000 to 286 000 000 particles, we measured and compared FMM and PME performances in GROMACS on up-to-date GPU models.

As a prerequisite to calculating Coulomb interactions in MD simulations with the FMM, as well as for a proper performance comparison, we have determined the FMM parameters that yield results as accurate as those with typical PME settings. For a representative biomolecular simulation system of about 50 000 particles in size, a multipole order of 7 yields a similar accuracy for the Coulomb energies and forces as standard PME parameters in a mixed-precision simulation. The error distribution for the Coulomb forces is comparable for both solvers. Limiting the energy drift to the level present in a standard PME simulation requires raising the multipole order to about 8.

For typical biomolecular systems (proteins in solution) of up to 30 million particles in size, the GROMACS 2019 performance with our CUDA FMM is about a third of that with PME on a single GPU node. However, for systems with larger dimensions and nonuniform particle distributions, such as our ≈100 000 atom aerosol/multidroplet example, FMM easily outperforms PME already at small particle numbers. Here, the huge memory requirements for the FFT grid become the limiting factor for PME.

GemsFMM is a completely independent FMM implementation, which also runs exclusively on the GPU and which uses the same operators for the far field evaluations as our implementation. Our GPU FMM outperforms GemsFMM by a factor of about 8. Unfortunately, further comparisons were not possible because we did not find additional ready-to-use FMM codes that provide verifiable results.

One of the drawbacks of the FMM is that it does not intrinsically allow for noncubic simulation boxes with periodic boundaries. For noncubic boxes the governing octree structure of the FMM would have to be redesigned,60 requiring further optimizations if the level of achieved performance is to be maintained. Moreover, for typical biomolecular simulation systems of proteins in solution, the single-node GPU FMM is still slower than the highly optimized GROMACS GPU PME implementation; however, single-node GPU FMM can handle larger particle systems and larger simulation boxes.

One of the advantages of FMM electrostatics over PME is that also open boundaries can be handled; however, the FMM’s main strength will become apparent on larger exascale clusters of GPU nodes, where PME scaling breaks down due to its inherent communication bottleneck. In combination with the demonstrated high single-GPU performance of this implementation, the performance of a parallelized FMM should eventually beat that of PME. For large sparse systems, FMM already outperforms PME on a single GPU. Additionally, due to FMM’s flexible octree structure that allows one to easily evaluate local energy differences, λ-dynamics calculations, as needed for MD simulations at constant pH, can be implemented without much computational overhead.32

The next step toward higher FMM performance will be a parallel implementation for multiple GPUs. As the FMM communication requirement is small compared to that of PME, we expect a parallelized FMM to scale significantly better than PME with the number of GPUs. Additionally, harnessing new CUDA programming features such as persistent threads and CUDA graphs should be beneficial also for single-node GPU performance. Considering large sparse systems, additional optimizations should yield even more speedup because the current implementation was only slightly adopted to handle nonuniform particle distributions.

Acknowledgments

This study was supported by the DFG priority program Software for Exascale Computing (SPP 1648). The multidroplet system was provided by Frank Wiederschein. Many thanks to Ivo Kabadshow for sharing his insights on FMM error behavior.

Appendix

A modified version of GROMACS that includes our CUDA FMM is available for download; please follow the instructions at https://www.mpibpc.mpg.de/grubmueller/sppexa.

The authors declare no competing financial interest.

References

  1. Potter D.; Stadel J.; Teyssier R. PKDGRAV3: Beyond trillion particle cosmological simulations for the next era of galaxy surveys. Comput. Astrophys. Cosmol. 2017, 4, 2. 10.1186/s40668-017-0021-1. [DOI] [Google Scholar]
  2. Arnold A.; Fahrenberger F.; Holm C.; Lenz O.; Bolten M.; Dachsel H.; Halver R.; Kabadshow I.; Gähler F.; Heber F.; Iseringhausen J.; Hofmann M.; Pippig M.; Potts D.; Sutmann G. Comparison of scalable fast methods for long-range interactions. Phys. Rev. E 2013, 88, 063308 10.1103/PhysRevE.88.063308. [DOI] [PubMed] [Google Scholar]
  3. Dawson J. M. Particle simulation of plasmas. Rev. Mod. Phys. 1983, 55, 403–447. 10.1103/RevModPhys.55.403. [DOI] [Google Scholar]
  4. Bock L.; Blau C.; Schröder G.; Davydov I.; Fischer N.; Stark H.; Rodnina M.; Vaiana A.; Grubmüller H. Energy barriers and driving forces in tRNA translocation through the ribosome. Nat. Struct. Mol. Biol. 2013, 20, 1390–1396. 10.1038/nsmb.2690. [DOI] [PubMed] [Google Scholar]
  5. Zink M.; Grubmüller H. Mechanical properties of the icosahedral shell of southern bean mosaic virus: A molecular dynamics study. Biophys. J. 2009, 96, 1350–1363. 10.1016/j.bpj.2008.11.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Perilla J. R.; Goh B. C.; Cassidy C. K.; Liu B.; Bernardi R. C.; Rudack T.; Yu H.; Wu Z.; Schulten K. Molecular dynamics simulations of large macromolecular complexes. Curr. Opin. Struct. Biol. 2015, 31, 64–74. 10.1016/j.sbi.2015.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Jung J.; Nishima W.; Daniels M.; Bascom G.; Kobayashi C.; Adedoyin A.; Wall M.; Lappala A.; Phillips D.; Fischer W.; Tung C.-S.; Schlick T.; Sugita Y.; Sanbonmatsu K. Y. Scaling molecular dynamics beyond 100,000 processor cores for large-scale biophysical simulations. J. Comput. Chem. 2019, 40, 1919–1930. 10.1002/jcc.25840. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Essmann U.; Perera L.; Berkowitz M.; Darden T.; Lee H.; Pedersen L. G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
  9. Hess B.; Kutzner C.; van der Spoel D.; Lindahl E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
  10. Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindahl E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1-2, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
  11. Páll S.; Abraham M. J.; Kutzner C.; Hess B.; Lindahl E.. Tackling Exascale Software Challenges in Molecular Dynamics Simulations with GROMACS. In Solving Software Challenges for Exascale. EASC 2014; Markidis S., Laure E., Eds.; Lecture Notes in Computer Science 8759; Springer International Publishing: Cham, Switzerland, 2015; pp 1–25. 10.1007/978-3-319-15976-8_1. [DOI] [Google Scholar]
  12. Phillips J. C.; Braun R.; Wang W.; Gumbart J.; Tajkhorshid E.; Villa E.; Chipot C.; Skeel R. D.; Kale L.; Schulten K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Board J. A.; Humphres C. W.; Lambert C. G.; Rankin W. T.; Toukmaji A. Y.. Ewald and Multipole Methods for Periodic N-Body Problems. In Computational Molecular Dynamics: Challenges, Methods, Ideas; Deuflhard P., Hermans J., Leimkuhler B., Mark A. E., Reich S., Skeel R. D., Eds.; Springer: Berlin, 1999; pp 459–471. [Google Scholar]
  14. Kutzner C.; van der Spoel D.; Fechner M.; Lindahl E.; Schmitt U.; de Groot B.; Grubmüller H. Speeding up parallel GROMACS on high-latency networks. J. Comput. Chem. 2007, 28, 2075–2084. 10.1002/jcc.20703. [DOI] [PubMed] [Google Scholar]
  15. Kutzner C.; Apostolov R.; Hess B.; Grubmüller H.. Scaling of the GROMACS 4.6 molecular dynamics code on SuperMUC. In Parallel Computing: Accelerating Computational Science and Engineering; Bader M., Bode A., Bungartz H. J., Eds.; IOS Press: Amsterdam, Netherlands, 2014; pp 722–730. [Google Scholar]
  16. Greengard L.; Rokhlin V. A fast algorithm for particle simulations. J. Comput. Phys. 1987, 73, 325–348. 10.1016/0021-9991(87)90140-9. [DOI] [Google Scholar]
  17. Kabadshow I.Periodic Boundary Conditions and the Error-Controlled Fast Multipole Method; IAS Series 11; Forschungszentrum Jülich: 2012. [Google Scholar]
  18. Greengard L.; Rokhlin V. A new version of the Fast Multipole Method for the Laplace equation in three dimensions. Acta Numer. 1997, 6, 229–269. 10.1017/S0962492900002725. [DOI] [Google Scholar]
  19. Cheng H.; Greengard L.; Rokhlin V. A Fast Adaptive Multipole Algorithm in Three Dimensions. J. Comput. Phys. 1999, 155, 468–498. 10.1006/jcph.1999.6355. [DOI] [Google Scholar]
  20. Fong W.; Darve E. The black-box fast multipole method. J. Comput. Phys. 2009, 228, 8712–8725. 10.1016/j.jcp.2009.08.031. [DOI] [Google Scholar]
  21. Gumerov N. A.; Duraiswami R. Fast multipole methods on graphics processors. J. Comput. Phys. 2008, 227, 8290–8313. 10.1016/j.jcp.2008.05.023. [DOI] [Google Scholar]
  22. Garcia A. G.; Beckmann A.; Kabadshow I.. Accelerating an FMM-Based Coulomb Solver with GPUs. In Software for Exascale Computing – SPPEXA 2013–2015; Bungartz H.-J., Neumann P., Nagel W. E., Eds.; Springer International Publishing: Berlin, 2016; pp 485–504. [Google Scholar]
  23. Takahashi T.; Cecka C.; Fong W.; Darve E. Optimizing the multipole-to-local operator in the fast multipole method for graphical processing units. Int. J. Numer. Methods Eng. 2012, 89, 105–133. 10.1002/nme.3240. [DOI] [Google Scholar]
  24. Agullo E.; Bramas B.; Coulaud O.; Darve E.; Messner M.; Takahashi T. Task-based FMM for heterogeneous architectures. Concurrency and Computation: Practice and Experience 2016, 28, 2608–2629. 10.1002/cpe.3723. [DOI] [Google Scholar]
  25. Yokota R.; Barba L. A.. Chapter 9 – Treecode and Fast Multipole Method for NBody Simulation with CUDA. In GPU Computing Gems Emerald Edition; Hwu W. W., Ed.; Applications of GPU Computing Series; Morgan Kaufmann: Boston, 2011; pp 113–132. [Google Scholar]
  26. Yokota R.; Narumi T.; Sakamaki R.; Kameoka S.; Obi S.; Yasuoka K. Fast multipole methods on a cluster of GPUs for the meshless simulation of turbulence. Comput. Phys. Commun. 2009, 180, 2066–2078. 10.1016/j.cpc.2009.06.009. [DOI] [Google Scholar]
  27. Lashuk I.; Chandramowlishwaran A.; Langston H.; Nguyen T.-A.; Sampath R.; Shringarpure A.; Vuduc R.; Ying L.; Zorin D.; Biros G.. A Massively Parallel Adaptive Fast-Multipole Method on Heterogeneous Architectures. In SC ’09: Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis; Association for Computing Machinery: New York, NY, 2009; pp 1–12. [Google Scholar]
  28. Blanchard P.; Bramas B.; Coulaud O.; Darve E.; Dupuy L.; Etcheverry A.; Sylvand G.. ScalFMm: A Generic Parallel Fast Multipole Library. Presented at the SIAM Conference on Computational Science and Engineering, 2015. [Google Scholar]
  29. Ohno Y.; Yokota R.; Koyama H.; Morimoto G.; Hasegawa A.; Masumoto G.; Okimoto N.; Hirano Y.; Ibeid H.; Narumi T.; Taiji M. Petascale molecular dynamics simulation using the fast multipole method on K computer. Comput. Phys. Commun. 2014, 185, 2575–2585. 10.1016/j.cpc.2014.06.004. [DOI] [Google Scholar]
  30. Andoh Y.; Yoshii N.; Fujimoto K.; Mizutani K.; Kojima H.; Yamada A.; Okazaki S.; Kawaguchi K.; Nagao H.; Iwahashi K.; Mizutani F.; Minami K.; Ichikawa S.-i.; Komatsu H.; Ishizuki S.; Takeda Y.; Fukushima M. MODYLAS: A Highly Parallelized General-Purpose Molecular Dynamics Simulation Program for Large-Scale Systems with Long-Range Forces Calculated by Fast Multipole Method (FMM) and Highly Scalable Fine-Grained New Parallel Processing Algorithms. J. Chem. Theory Comput. 2013, 9, 3201–3209. 10.1021/ct400203a. [DOI] [PubMed] [Google Scholar]
  31. Kutzner C.; Páll S.; Fechner M.; Esztermann A.; de Groot B. L.; Grubmüller H. More bang for your buck: Improved use of GPU nodes for GROMACS 2018. J. Comput. Chem. 2019, 40, 2418–2431. 10.1002/jcc.26011. [DOI] [PubMed] [Google Scholar]
  32. Kohnke B.; Ullmann T. R.; Beckmann A.; Kabadshow I.; Haensel D.; Morgenstern L.; Dobrev P.; Groenhof G.; Kutzner C.; Hess B.; Dachsel H.; Grubmüller H.. GROMEX – A scalable and versatile Fast Multipole Method for biomolecular simulation. In Software for Exascale Computing – SPPEXA 2016–2019; Bungartz H.-J., Reiz S., Uekermann B., Neumann P., Nagel W. E., Eds.; Springer International Publishing: Berlin, 2020; pp 517–543. [Google Scholar]
  33. Nickolls J.; Buck I.; Garland M.; Skadron K. Scalable Parallel Programming with CUDA. Queue 2008, 6, 40–53. 10.1145/1365490.1365500. [DOI] [Google Scholar]
  34. Kohnke B.; Kutzner C.; Beckmann A.; Lube G.; Kabadshow I.; Dachsel H.; Grubmüller H. A CUDA Fast Multipole Method with highly efficient M2L far field evaluation. Int. J. High Perform. Comput. Appl. 2020, 10.1177/1094342020964857. [DOI] [Google Scholar]
  35. Duan Y.; Wu C.; Chowdhury S.; Lee M. C.; Xiong G.; Zhang W.; Yang R.; Cieplak P.; Luo R.; Lee T.; Caldwell J.; Wang J.; Kollman P. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J. Comput. Chem. 2003, 24, 1999–2012. 10.1002/jcc.10349. [DOI] [PubMed] [Google Scholar]
  36. Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
  37. Crandall R. E. New Representations for the Madelung Constant. Experimental Mathematics 1999, 8, 367–379. 10.1080/10586458.1999.10504625. [DOI] [Google Scholar]
  38. Borwein D.; Borwein J. M.; Taylor K. F. Convergence of lattice sums and Madelungs constant. J. Math. Phys. 1985, 26, 2999–3009. 10.1063/1.526675. [DOI] [Google Scholar]
  39. Bussi G.; Zykova-Timan T.; Parrinello M. Isothermal-isobaric molecular dynamics using stochastic velocity rescaling. J. Chem. Phys. 2009, 130, 074101 10.1063/1.3073889. [DOI] [PubMed] [Google Scholar]
  40. Berendsen H. J.; Postma J.; van Gunsteren W. F.; DiNola A.; Haak J. R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
  41. Daub C. D.; Cann N. M. How are completely desolvated ions produced in electrospray ionization: insights from molecular dynamics simulations. Anal. Chem. 2011, 83, 8372–8376. 10.1021/ac202103p. [DOI] [PubMed] [Google Scholar]
  42. Kim D.; Wagner N.; Wooding K.; Clemmer D. E.; Russell D. H. Ions from solution to the gas phase: a molecular dynamics simulation of the structural evolution of substance P during desolvation of charged nanodroplets generated by electrospray ionization. J. Am. Chem. Soc. 2017, 139, 2981–2988. 10.1021/jacs.6b10731. [DOI] [PubMed] [Google Scholar]
  43. Konermann L.; Metwally H.; McAllister R. G.; Popa V. How to run molecular dynamics simulations on electrospray droplets and gas phase proteins: Basic guidelines and selected applications. Methods 2018, 144, 104–112. 10.1016/j.ymeth.2018.04.010. [DOI] [PubMed] [Google Scholar]
  44. Marklund E. G.; Benesch J. L. Weighing-up protein dynamics: the combination of native mass spectrometry and molecular dynamics simulations. Curr. Opin. Struct. Biol. 2019, 54, 50–58. 10.1016/j.sbi.2018.12.011. [DOI] [PubMed] [Google Scholar]
  45. Abel B.; Charvat A.; Diederichsen U.; Faubel M.; Girmann B.; Niemeyer J.; Zeeck A. Applications, features, and mechanistic aspects of liquid water beam desorption mass spectrometry. Int. J. Mass Spectrom. 2005, 243, 177–188. 10.1016/j.ijms.2005.02.008. [DOI] [Google Scholar]
  46. Meyer T.; Gabelica V.; Grubmüller H.; Orozco M. Proteins in the gas phase. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2013, 3, 408–425. 10.1002/wcms.1130. [DOI] [Google Scholar]
  47. Caleman C.; Hub J. S.; van Maaren P. J.; van der Spoel D. Atomistic simulation of ion solvation in water explains surface preference of halides. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 6838–6842. 10.1073/pnas.1017903108. [DOI] [Google Scholar]
  48. Schoolcraft T. A.; Constable G. S.; Zhigilei L. V.; Garrison B. J. Molecular dynamics simulation of the laser disintegration of aerosol particles. Anal. Chem. 2000, 72, 5143–5150. 10.1021/ac0007635. [DOI] [PubMed] [Google Scholar]
  49. van der Spoel D.; Marklund E. G.; Larsson D. S.; Caleman C. Proteins, lipids, and water in the gas phase. Macromol. Biosci. 2011, 11, 50–59. 10.1002/mabi.201000291. [DOI] [PubMed] [Google Scholar]
  50. Schreiber H.; Steinhauser O. Cutoff size does strongly influence molecular dynamics results on solvated polypeptides. Biochemistry 1992, 31, 5856–5860. 10.1021/bi00140a022. [DOI] [PubMed] [Google Scholar]
  51. Luedtke W.; Landman U.; Chiu Y.-H.; Levandier D.; Dressler R.; Sok S.; Gordon M. S. Nanojets, electrospray, and ion field evaporation: Molecular dynamics simulations and laboratory experiments. J. Phys. Chem. A 2008, 112, 9628–9649. 10.1021/jp804585y. [DOI] [PubMed] [Google Scholar]
  52. Broquedis F.; Clet-Ortega J.; Moreaud S.; Furmento N.; Goglin B.; Mercier G.; Thibault S.; Namyst R.. hwloc: A generic framework for managing hardware affinities in HPC applications. In Parallel, Distributed and Network-Based Processing, 2010, 18th Euromicro International Conference on; IEEE: 2010; pp 180–186. 10.1109/PDP.2010.67. [DOI] [Google Scholar]
  53. Frigo M.; Johnson S. G. The design and implementation of FFTW3. Proc. IEEE 2005, 93, 216–231. 10.1109/JPROC.2004.840301. [DOI] [Google Scholar]
  54. IEEE Standard for Floating-Point Arithmetic. In IEEE Standard 754-2008; IEEE: 2008; pp 1–70. 10.1109/IEEESTD.2008.4610935. [DOI] [Google Scholar]
  55. Mura M. E.; Handy N. C. Cuboidal basis functions. Theor. Chim. Acta 1995, 90, 145–165. 10.1007/BF01113845. [DOI] [Google Scholar]
  56. Abraham M. J.; Gready J. E. Optimization of parameters for molecular dynamics simulation using smooth particle-mesh Ewald in GROMACS 4.5. J. Comput. Chem. 2011, 32, 2031–2040. 10.1002/jcc.21773. [DOI] [PubMed] [Google Scholar]
  57. Kudin K. N.; Scuseria G. E. A fast multipole method for periodic systems with arbitrary unit cell geometries. Chem. Phys. Lett. 1998, 283, 61–68. 10.1016/S0009-2614(97)01329-8. [DOI] [Google Scholar]
  58. Páll S.; Hess B. A flexible algorithm for calculating pair interactions on SIMD architectures. Comput. Phys. Commun. 2013, 184, 2641–2650. 10.1016/j.cpc.2013.06.003. [DOI] [Google Scholar]
  59. Shamshirgar D.; Yokota R.; Tornberg A.-K.; Hess B. Regularizing the fast multipole method for use in molecular simulation. J. Chem. Phys. 2019, 151, 234113. 10.1063/1.5122859. [DOI] [PubMed] [Google Scholar]
  60. Andoh Y.; Yoshii N.; Okazaki S. Extension of the fast multipole method for the rectangular cells with an anisotropic partition tree structure. J. Comput. Chem. 2020, 41, 1353–1367. 10.1002/jcc.26180. [DOI] [PubMed] [Google Scholar]

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES