Abstract
The COVID-19 pandemic has resulted in worldwide shortages of nasopharyngeal swabs required for sample collection. While the shortages are becoming acute due to supply chain disruptions, the demand for testing has increased both as a prerequisite to lifting restrictions and in preparation for the second wave. One of the potential solutions to this crisis is the development of 3D printed nasopharyngeal swabs that behave like traditional swabs. However, the opportunity to digitally conceive and fabricate swabs allows for design improvements that can potentially reduce patient pain and discomfort. The study reports the progress that has been made on the development of auxetic nasopharyngeal swabs that can shrink under axial resistance. This allows the swab to navigate through the nasal cavity with significantly less stress on the surrounding tissues. This is achieved through systematically conceived negative Poisson's ratio () structures in a biocompatible material. Finite element (FE) and surrogate modelling techniques were employed to identify the most optimal swab shape that allows for the highest negative strain () under safe stress (). The influence and interaction effects of the geometrical parameters on the swab's performance were also characterised. The research demonstrates a new viewpoint for the development of functional nasopharyngeal swabs that can be 3D printed to reduce patient discomfort. The methodology can be further exploited to address various challenges in biomedical devices and redistributed manufacturing.
Keywords: 3D printing, Nasopharyngeal swabs, COVID-19, Auxetic, Negative Poisson's ratio, Meta-biomaterials
1. Introduction
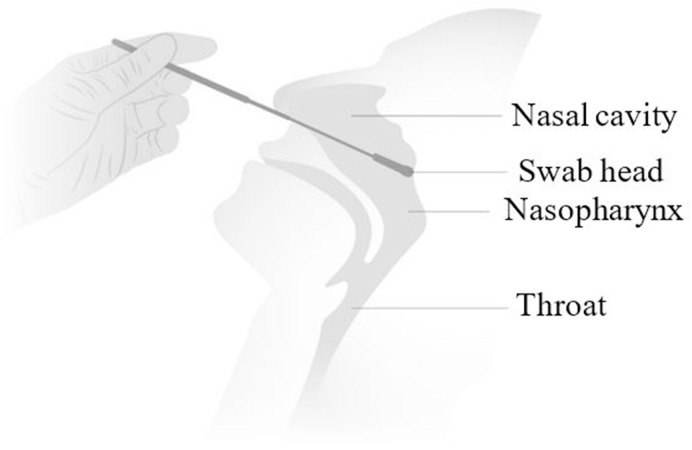
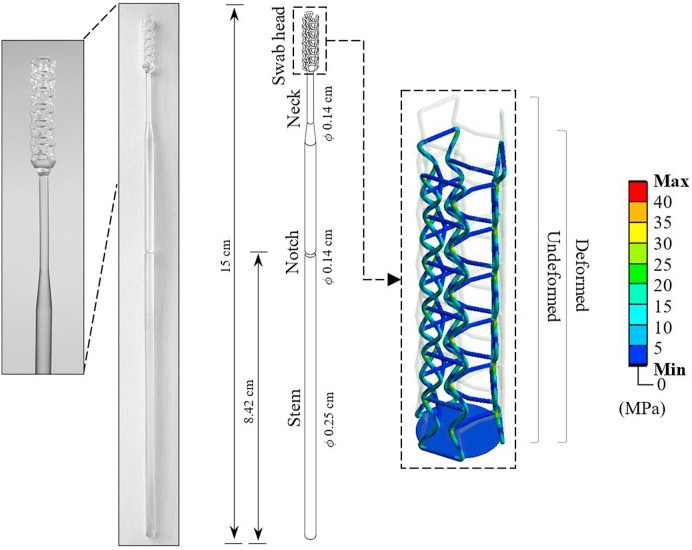
At the time of writing this article, more than 17.9 million (D-19 situation update) people have been diagnosed with COVID-19 across the world. All of these diagnoses were confirmed using nasopharyngeal swabs, which is the reference sampling method recommended by WHO (Péré et al., 2020). The nasopharyngeal swabs required for the coronavirus tests are different from standard cotton swabs; they are usually 15 cm long with a tip diameter of 0.35–0.40 cm suitable to get to the nasopharynx as shown in Fig. 1 . According to the guidelines issued by the centre for disease control and prevention (Interim Guidelines for Cl), the swabs must be made of synthetic fibre without a wooden shaft. Also, the swab material should not contain calcium alginate or any antimicrobial materials that are usually present in wound care swabs, as that can kill the virus. Usually, the nasopharyngeal swabs are inserted through the nostril until they reach the inferior concha and the back of the nasopharyngeal cavity. The swabs are then rotated five times and removed. Post-sampling, the swabs are inserted into a vial containing 3 ml of suitable virus transport medium.
Fig. 1.
A schematic illustration of the nasopharyngeal swab testing for coronavirus adapted from Borresen (Borresen, 2020).
There have been numerous reports regarding the shortages of nasopharyngeal swabs required for sample collection associated with COVID-19 testing across many countries (Coronavirus Testing Delay; Coronavirus Test Obstacle; Singapore's Nasal Swab St). Anecdotal evidence suggests that these shortages are expected to become even more critical in the coming months because of increased testing and global concerns over a COVID-19 s wave. The situations can be further worsened due to supply chain disruption requiring clinicians and local agencies to identify alternative sources for essential supplies such as test swabs. A potential solution that is being investigated across the world in this regard is the digital fabrication of nasopharyngeal swabs through various 3D printing (additive manufacturing) techniques.
The key advantages of 3D printing essential supplies such as swabs go beyond meeting the current shortage or forecasted demand. The capability to digitally transport print files over the internet means that these healthcare innovations can transcend supply chain disruption and reach the user. This would mean that key innovation in product design and print parameters can reach the end-user almost instantly without any delay. The multistep swab manufacturing process, storage, and transport can be drastically simplified through print-on-demand keeping the printers and material versatile for generating a range of relevant products. Lastly and most importantly the widespread availability of 3D printers means that iterative innovation in open-source designs can happen more drastically than closed-cycle product development.
This research, therefore, is the first step in starting an open and collaborative process to drastically improve the existing concepts in nasopharyngeal swabs at the interface of digital fabrication and mechanical meta-biomaterials. As part of this process, the research develops the first auxetic nasopharyngeal swab that can be 3D printed in a biocompatible material, where the innovation pipeline is kept open allowing for collective innovation. A biocompatible photopolymer (FLSGAM01) developed by ‘Formlabs’ is the base material of choice as it is readily available and compatible with desktop printers used to manufacture biomedical devices.
According to Kolken and Zadpoor (2017), rationally designed complex, arbitrary, and meta-structures enabled by the advances in 3D printing techniques can offer numerous benefits in terms of their mechanical performance. Examples of this include the work by Gao et al. where the performance of cylindrical double-arrow (Gao et al., 2018a, 2020) and double-V (Gao et al., 2018b) honeycomb auxetic structures where demonstrated. Mechanical metamaterials (Duoss et al., 2014; Ahmadi et al., 2018; Yuan et al., 2017; Hedayati et al., 2017; Janbaz et al., 2017) exhibit unusual properties allowing for advanced functionalities, with applications ranging from biomedicine (Ahmadi et al., 2018; Arjunan et al., 2020a; Robinson et al., 2020a, 2020b; de Krijger et al., 2017), soft robotics (Chen et al., 2017; Clegg et al., 2019), crashworthiness (Nikkhah et al., 2020; Baroutaji et al., 2019; Harris and McShane, 2020; Lee et al., 2019), and sound transmission (Arjunan, 2019a, 2019b; Arjunan et al., 2019).
Scarpa et al. (2008) used the finite element method to investigate the mechanical performance of auxetic tubular structures to show the dependence of the curvature‐bending moment versus the Poisson's ratio of the core. Later, Karnessis and Burriesci (2013) investigated the collapse under pure bending of auxetic tubes, with the aim to identify design strategies suitable for improving their kinking response. More recent studies include the one from Lee et al. (2019) and Yang and Ma (2020) where different types of auxetic structures were investigated for energy absorption applications. When it comes to biomedical devices, Chen et al. (2019a) developed mechanically superior tubular structures based on re-entrant honeycomb for microcatheters. As can be seen, the concept of auxetic structures are gaining significant attention for numerous applications.
Auxetic mechanical metamaterials are identified by a negative Poisson's ratio () which is a direct consequence of their geometrical architecture. Poisson's ratio is a mechanical property that represents the lateral behaviour of materials under an axial load. In contrast to traditional materials with positive Poisson's ratio, auxetic materials have , translated to unilateral shrinkage. This means that if such a concept can be successfully applied to nasopharyngeal swabs, the swab can shrink under axial load to navigate easily through the nasal cavity into nasopharynx. Although the designs are different, similar concepts can be seen to be exploited by Ma and Liu (2011) for the development stents based upon negative Poisson's ratio.
The research is directed towards a process-structure–property relationship into two main classes of auxetic metamaterials, namely, chiral (Hu et al., 2019; Wang et al., 2020), and re-entrant (Zhang et al., 2015; Geng et al., 2019; Ling et al., 2020) structures. While the deformation mechanisms of the above-mentioned types of structures are auxetic, their suitability and parametric combinations to be used as nasopharyngeal swabs are unknown. Furthermore, the influence of the 3D printing process on the structure-property relationship at the sub-millimetre are also required to be analysed (Goh et al., 2020). While the development of such a structure at the sub-millimetre level is highly challenging through traditional manufacturing, 3D printing makes it accessible. The study, therefore, attempts the development, analysis, and optimisation of 3D printable nasopharyngeal swabs that can exhibit auxetic behaviour for the first time. The effect of various geometrical parameters on the performance of the swab such as lateral strain (), von Mises stress (), Poisson's ratio () and relative density () are also carried out. This was done using Finite Element (FE) and Design of Experiments (DoE) based surrogate modelling to allow for open innovation through data sharing. The combined numerical modelling approach also allowed to perform parametric analysis required to identify the order of significance of the geometric parameters while paying critical attention to lateral shrinkage and stress generated. The study therefore not only introduces a novel auxetic geometry but also its most optimal case to yield the best performance informed by the desirability optimisation approach.
2. Materials and methods
2.1. Swab head design scope and focus
The focus of the project was on developing a nasopharyngeal swab head that exhibits auxetic behaviour and can be 3D printed. The first step was to identify a suitable unit cell for the lattice structure to establish auxetic behaviour from which a suitable variant can be derived for further optimisation. The scope of this unit cell selection was based on the mechanics of metamaterial concepts (Bertoldi et al., 2017; Zhang et al., 2018; Yang et al., 2019) that adds new functionalities such as broadening the behaviour of lattice structures. When a traditional material is compressed, expansion takes place along the lateral direction to the load applied. Quantifying this phenomenon is the material property called Poisson's ratio, which is the negative ratio of transverse to longitudinal strain.
The Poisson's ratio of a traditional micro-lattices is therefore positive. However, when a material deviates from the norm and gives rise to a negative Poisson's ratio (), such structures can be classified auxetic (Evans, 1991; Choi et al., 2019; Mirzaali et al., 2018, 2019; Wojciechowski, 2003). Micro-lattices that exhibit are increasingly being sought due to their peculiar effects which often cannot be achieved through traditional lattices (Jin et al., 2019; El Dhaba and Shaat, 2019; Shufrin et al., 2019; Jeong and Yoo, 2019). These effects then translate to their tremendous potential in applications such as the ones explores in this study. Though there are exceptions, widely studied structures fall under one of the two categories namely re-entrant (Spagnoli et al., 2015; Lekesiz et al., 2017; Alomarah et al., 2018; Jiang et al., 2019; Wang et al., 2018; Nečemer et al., 2019) and chiral (Kolken and Zadpoor, 2017; Jiang and Li, 2018; Han et al., 2019; Wojciechowski, 1987, 1989; Mizzi et al., 2015). Although 3D printing allows conceiving structures that fall under any categories, the most studied variant is the re-entrant category. The primary reason for this is the simplicity of the re-entrant architecture allowing it to be used for a wide range of structural applications.
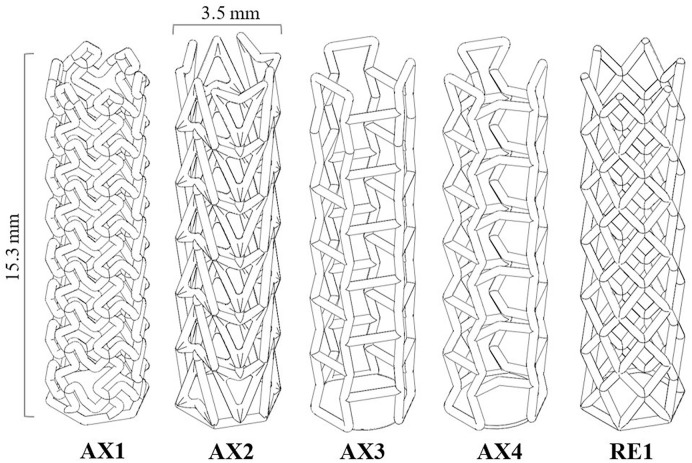
A total of four different auxetic lattices (AX1 to AX4) and one regular (RE1) lattice are investigated in this study (Fig. 2 ). Out of the four auxetic designs, the first one (AX1) was inspired by chiral helix structures. Although the rest of designs AX2, AX3 and AX4 were inspired by the traditional re-entrant architecture, AX2 is commonly referred to as the arrowhead design due to its distinct shape. AX3 and AX4 both share fundamental bowtie re-entrant architecture with the latter featuring an angled cross-link resulting in a novel architecture. The regular structure RE1 is based on the well-established cross-hatch diamond architecture, which is included in this study as a benchmark design. All the structures featured a global diameter and height of 3.5 mm and 15.3 mm respectively at a strut diameter of 0.3 mm. The relative density for all the structures was within a range of 0.08–0.13 to allow effective comparison and for data normalisation.
Fig. 2.
Different designs analysed to identify their suitability to be used as the foundation for the auxetic nasopharyngeal swab head. The designs AX1 to AX4 are auxetic variants while RE1 is a regular geometry designed as a control specimen for comparative study.
2.2. Numerical modelling
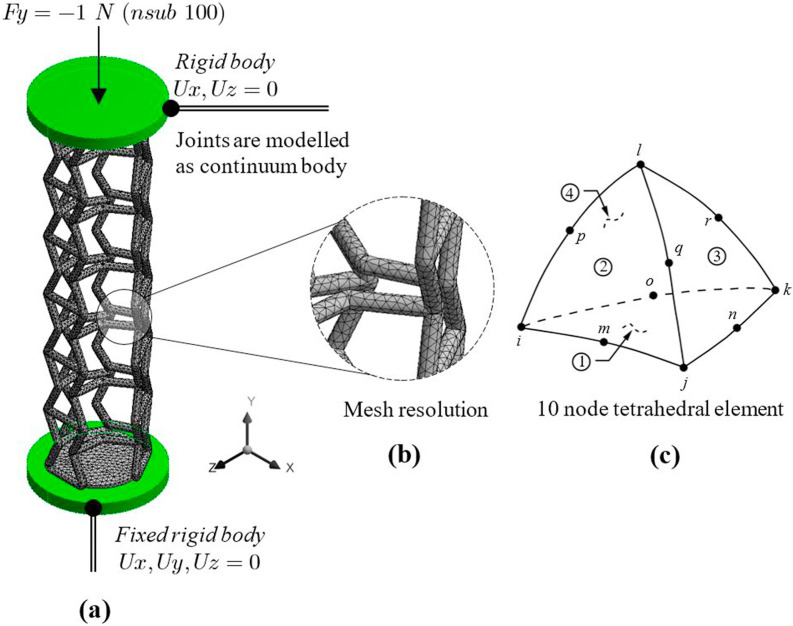
Structural performance analysis of the designs was carried out using the Finite Element Method (FEM). The solver of choice was Ansys non-linear mechanical to mimic a quasi-static experimental compression test. The compression platens were modelled as rigid bodies with a diameter and thickness of 5 mm and 0.5 mm respectively as shown in Fig. 3 . The boundary conditions for bottom platens were assigned fixed in all directions and a 1 N vertical load ramped at 100 substeps (nsub) was applied along the - (compression) direction. For patient safety and to prevent injury to the nasopharynx, it was critical that the swabs are designed for a safe load. Since there were no standards available regarding the safe load for nasopharyngeal swabs, inhouse tests were carried out on commercially available traditional swabs, which showed plastic deformation between 0.8 and 1.2 N approximately. As a result, 1 N was identified as a suitable safe load to develop the first prototype. Overall, the design load needs careful consideration as higher loads, especially for designs featuring thin walls may cause microtears along the nasopharynx causing a burning sensation, pain, and the risk of infection. The contact between the rigid body platens and the swab head was modelled as frictionless for computational efficiency.
Fig. 3.
Finite element numerical model showing (a) boundary conditions (b) mesh resolution and (c) element type used to predict the mechanical behaviour of the lattice structures considered for swab head.
The structural components were modelled using a solid tetrahedral elemental type (SOLID187) with a Bilinear Isotropic Strain Hardening (BISO) material model. A 3D solid tetrahedral was the element of choice as lower-order elements such as beam offer less accuracy. For the geometries under consideration, it was important to study both the local stress concentration effects at joints in addition to the global deformation of the lattices. The element was defined by 10 nodes having three degrees of freedom (DOF) at each node: translations in the nodal x, y, and z directions as shown in Fig. 3c. The element has plasticity, creep, stress stiffening, large deflection, and large strain capabilities. The element is also suitable for modelling quadratic displacement behaviour making it well suited for modelling irregular meshes in top-down FE modelling approaches such as the ones in this study. All elements of the lattice structure were modelled as a continuum body rather than an assembly to avoid spurious rotational effects at joints.
The BISO material model was the most appropriate for this study hence the exact plastic behaviour of the structure is not of interest in this study. The BISO model represents the material behaviour using a bilinear stress-strain () curve where the initial slope is described using Young's modulus (E). As the focus of the simulation is limited to the elastic performance of the structure, the BISO curve is represented perfectly plastic after the yield strength () of the material. Based on the numerical results, the lateral strain () to characterise the radial shrinkage was evaluated as the average elastic strain across the two radial directions which in this case are and . The strains were calculated independently for all the six lattice layers and an average was taken to characterise the overall shrinkage. The normalised lateral strain () with respect to relative density was then evaluated by dividing with the respective and converting it into a percentage. The relative density of the structures was classified using the method described in previous studies (Vance et al., 2018, 2019). Lastly, the Poisson's ratio was calculated using Eq. (1):
| (1) |
Although numerous biocompatible polymers such as Polyjet exists (Chen et al., 2019b), the choice of material selection for the study was informed by three primary criteria: (i) biocompatibility, (ii) accessibility, and (iii) affordability. During the initial discussion with academics and industry specialists, it became apparent that both the 3D printing technique and the material should be both low cost and accessible to be adopted across the globe. Consequently, the decision was taken to use the globally used stereolithography (SLA) technique in a ready to print biocompatible material that can be used in a low-cost plug and play desktop printer Form2. The surgical guide biomedical resin (FLSGAM01) was the material of choice as it follows ISO 13485:2016 (BS EN ISO 13485, 2016) and 14971:2012 (BS EN ISO, 14971a) (replaced by 14971:2019 (BS EN ISO, 14971b)).
All material properties used for the structures are as summarised in Table 1 . The material properties were evaluated from post-cured tensile test specimens (Fig. 4 a) 3D printed in a ‘Form-2’ machine under identical conditions to that used to print the swab heads for validation (Fig. 4b). The material after printing was washed in a ‘Form Wash’ for 20 min in 99% isopropyl alcohol. The specimens were then cured at 60 °C for 30 min in a ‘Form Cure’. The accuracy of the numerical model was further validated by comparing the load to failure observed between the manufactured samples and the numerical model.
Table 1.
Material properties of the biocompatible photopolymer FLSGAM01.
| Material property | Value | Compliance/specification |
|---|---|---|
| Elastic modulus | 2.9 (GPa) | |
| Yield strength | 73 (MPa) | |
| Poisson's ratio | 0.3 | |
| Density | 1250 (kg/m3) | |
| Disinfection compatibility | Chemical | 70% Isopropyl Alcohol for 5 min |
| Steam | Autoclave at 134 °C at 20 min or 121 °C at 30 min. | |
| Biocompatibility | Not cytotoxic Non-irritant Non-sensitizer |
EN ISO 10993-5:2009 ISO 10993-10:2010/(R)2014 |
Fig. 4.
Samples used for mechanical tests where (a) shows the post-cured tensile test samples and (b) sample swab head used for numerical validation.
Mesh refinements were carried out using a mesh sensitivity analysis resulting in the optimum number of finite element nodes and elements as listed in Table 2 at a minimum edge length of 3.0712e-3 mm. The mesh sensitivity analysis was carried out using the strain energy convergence criterion until there was no variation in the average strain of elements. Strain energy was deemed appropriate as stress singularities do not significantly influence the average strain energy of elements. Consequently, the minimum edge length was determined as the smallest element size required to produce no further variations in result. The global elemental matrix was solved using a six-core ‘Intel Xeon’ processor at 2.10 GHz assisted by 64 GB RAM resulting in a solution time of approximately 17 min for convergence.
Table 2.
Optimum elemental and nodal distribution associated with the converged structural FE model.
| Parameters | Swab design |
||||
|---|---|---|---|---|---|
| AX1 | AX2 | AX3 | AX4 | RE1 | |
| Elements | 86888 | 61923 | 201863 | 41537 | 58782 |
| Nodes | 169837 | 133271 | 316460 | 98374 | 125873 |
Consideration was also given to non-linear geometrical behaviour of the auxetic design to capture a realistic behaviour. To accommodate this, the model uses the solid tetrahedron element that features large strain capabilities. Small deformation and strain analyses assume that displacements are small enough that the resulting stiffness changes are insignificant, which is not the case in this analysis. Therefore, a large strain formulation is used to account for the stiffness changes that result from changes in an element's shape and orientation. This is further enforced through prescribing the non-linear geometry formulation (nlgeom, on) that ensures large strain effects are captured. This procedure is coupled with the use of substeps (nsub, 100) so the load is discretised into smaller steps that are solved using the Newton-Raphson non-linear formulation.
Before each solution, the Newton-Raphson method evaluates the out-of-balance load vector, which is the difference between the restoring forces (the loads corresponding to the element stresses) and the applied loads. The program then performs a linear solution, using the out-of-balance loads, and checks for convergence. If convergence criteria are not satisfied, the out-of-balance load vector is re-evaluated, the stiffness matrix is updated, and a new solution is obtained. This iterative procedure continues until the problem converges. Several convergence-enhancement and recovery features, such as line search, automatic load stepping, and bisection, were also activated to help the problem converge in a computationally efficient manner.
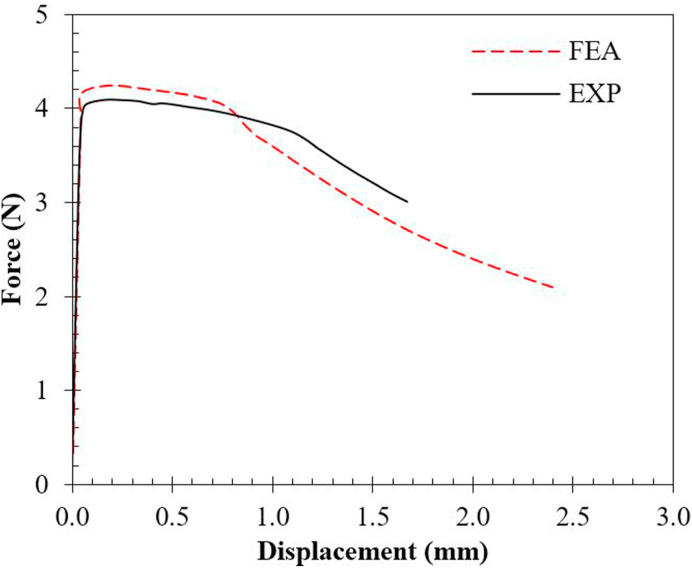
The validation of the finite element model was carried out by comparing the numerical predictions with experimentally measured force-displacement () curve of the swab heads shown in Fig. 4b. Fig. 5 shows that the numerical model is capable of predicting both the elastic and plastic behaviour of the swab heads being analysed. The finite element elastic deformation can be seen to closely follow the experimental trend. In both cases, failure was observed through barrel-shaped shrinking followed by buckling. Comparing the parametric values as shown in Table 3 shows that the FE model overestimates the yield and peak forces by 4.30% and 3.87% respectively. This can be attributed to the idealised geometry and the thin struts of the lattice structures being studied. In summary, the curve shows that FEA model offers good agreement with experimental results.
Fig. 5.
Comparison between experimentally and numerically measured load-deflection data for model validation.
Table 3.
Finite element model validation.
| Item | AX4 () |
|
|---|---|---|
| Yield force (N) | Peak force (N) | |
| Validation experiment | 3.27 | 4.09 |
| FEA | 2.41 | 4.25 |
| % difference | 4.30% | 3.87% |
2.3. Multi-objective optimisation
2.3.1. Formulation of the optimisation problem
Generally, for a multi-objective optimisation problem, the relationship between the variables associated with the design and the objective function can be represented using Eq. (2):
| (2) |
where is the vector of design variables, and are the lower and upper limits of the design variables, respectively and is the objective function. After studying all the candidate designs as shown in Fig. 2 and selecting the best auxetic design to be used as the foundation for the swab head. The design must be optimised by identifying the best geometrical parameters to achieve the targeted properties of interests (responses). These responses are the characteristics that are considered most favourable for the problem for which the design is required to be optimised for.
For the best auxetic swab, the optimal design is the one that has the ideal geometrical dimensions to achieve the highest shrinkage while exhibiting safe stress. Understanding the relationship between these responses and the design parameters will allow for the generation of an optimised result. Based on the auxetic lattice selected, the geometrical parameters were selected as design variables while maximum elastic lateral strain () and von Misses stress as design responses (). These two responses were selected as the focus of the project is to create 3D printable auxetic swab that exerts the least lateral resistance without plastically deforming as it travels through the nasal cavity. Accordingly, maximising the elastic shrinkage will ensure that the structure exerts the least amount of stress on surrounding tissues. Besides, the influence of the chosen design parameters on Poisson's ratio () and relative density () are also studied for further characterisation of the structural performance and to understand the contribution from material mass, respectively.
2.3.2. Surrogate modelling
To generate the solution for the optimisation problem as represented in Eq. (1), the design parameters must be linked to the responses first. This is done through the development of a surrogate model, which uses response surfaces to characterise the influence of geometrical parameters and their interaction on the responses of interest. The surrogate model employs mathematical and statistical techniques that are based on the fit of empirical models to numerical data. This is done by employing polynomial functions to describe the behaviour of the auxetic lattice selected for the swab head and to explore their parametric influence.
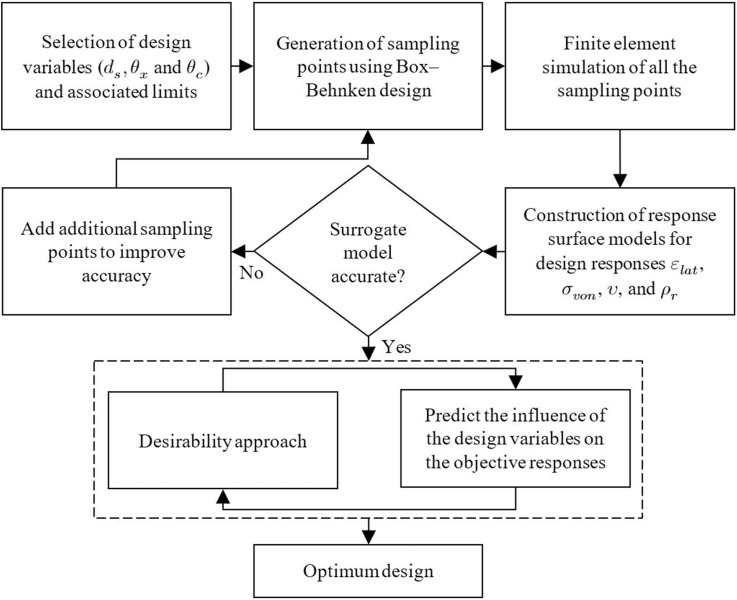
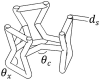
Numerous variables can affect the behaviour of the structure being studied; however, it is unfeasible to identify and control contributions from each one. Therefore, it was necessary to select those variables that allow for major effects on auxetic behaviour, which are the strut diameter (), auxetic angle () and cross link angle (). Accordingly, the model considered in this study is represented using four responses namely the lateral strain (), maximum von Mises stress (), Poisson's ratio () and relative density (). By fitting the simulation data to suitable polynomial equations, the surrogate model can provide a prediction that can be used to indicate which design parameter has the most influence on the performance of the swab head. The surrogate models can be also extended to understand the interaction effects between the geometrical parameters for each of the responses considered. A flowchart of the methodology considered for the development of the surrogate model and obtaining the optimal design is summarised in Fig. 6 .
Fig. 6.
Flow chart of the optimisation process using the desirability approach.
The surrogate model was developed using the Box–Behnken response surface modelling technique. Box-Behnken designs are used to generate accurate response surfaces using fewer required runs than a normal factorial technique (Rao and Kumar, 2012). Box–Behnken and the central composite techniques used in previous work (Arjunan et al., 2020b) identify runs required for developing response surface models. In general, the Box-Behnken design uses the twelve middle edge nodes and three centre nodes to fit a polynomial equation. Box-Behnken designs place points on the midpoints of the edges of the cubical design region, as well as points at the centre as listed in Table 5.
Table 5.
Design parameters selected for the surrogate model.
| Design | Variable | Code | −1 | 0 | 1 |
|---|---|---|---|---|---|
 |
(mm) | A | 0.1 | 0.2 | 0.3 |
| (deg.) | B | 65 | 75 | 85 | |
| (deg.) | C | 130 | 155 | 180 |
For this study, each factor is placed at one of three equally spaced values. The design is sufficient to fit a quadratic model, which includes square and interaction effects between factors. In this regard the ratio of the number of simulation points to the number of coefficients in the quadratic model is reasonable. When it comes to structural mechanics, often a certain relationship exists between output () and design variables () where a model can be written as shown in Eq. (3):
| (3) |
where represents the error associated with the response . Usually, a second-order model is used in response surface surrogate modelling represented by Eq. (4):
| (4) |
where the coefficients are calculated using the least-squares method. The response surface surrogate model can then be used to find values of the responses ( and ) that result in optimised multi-objective response or to discover what values of will satisfy the targeted requirements (point prediction).
3. Results and discussion
3.1. Selection of a suitable auxetic design
Using the numerical model, four auxetic candidates (AX1-4) were evaluated for their potential to be used as the foundation for the swab head. The regular design RE1 was conceived to act as a benchmark to demonstrate comparative behaviour between auxetic and regular design. For an effective design of the auxetic swab head, the balance between axial shrinkage and strength are crucial factors, which must be considered. The properties and associated responses for all the designs are summarised in Table 4 . As evident from the porosity range, the material distribution between the designs was comparable with the highest difference limited to 6%. Despite the slight difference in porosity between the designs considered, the strut, and the global diameter are kept constant to allow for a valid comparison.
Table 4.
Properties associated with all the lattice candidates that were being evaluated to design the swab head.
| Property | AX1 | AX2 | AX3 | AX4 | RE1 |
|---|---|---|---|---|---|
| 0.121 | 0.138 | 0.084 | 0.088 | 0.106 | |
| (vol. %) | 87.87 | 86.23 | 91.58 | 91.20 | 89.43 |
| (MPa) | 32.85 | 12.13 | 13.27 | 28.45 | 19.87 |
| −0.29 | −0.60 | −1.08 | −1.43 | 0.86 | |
| −0.12 | −0.23 | −0.29 | −0.29 | 0.27 |
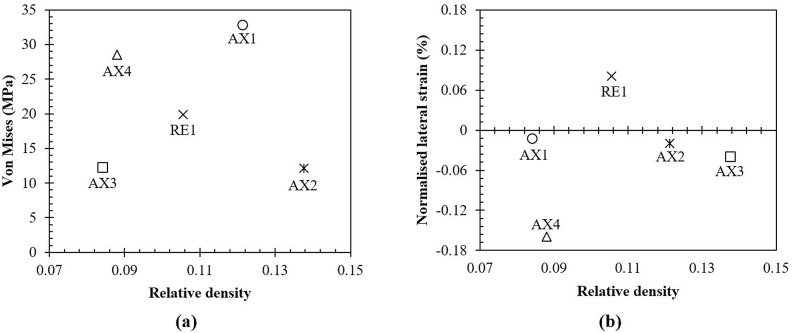
Two primary parameters namely lateral strain () and von Mises stress () were chosen to evaluate the performance of the cellular structures. While average lateral strain allowed to characterise the overall radial shrinkage, von Mises stress evaluated the structural integrity. Consequently, using these two parameters the most suitable design that demonstrate a balance between shrinkage and strength can be evaluated. Considering the load-bearing capacity of a traditional nasopharyngeal swab, which failed at 860 ± 50 mN, a compressive load of 1 N was used to study the structural integrity of the cellular structures. Under this circumstance, the resulting (Table 1) confirms that all the designs perform well below the yield strength (73 MPa) of the bulk material. The lowest and highest stresses were exhibited by designs AX2 and AX1 respectively. However, these designs show comparatively low performance when it comes to the lateral strain.
Looking at the influence of relative density on the structural performance as shown in Fig. 7 , it is clear that stresses are not dictated by , instead, by the shape of the unit cells. This is consistent with previous studies on microporous cellular structures where different unit cell shapes were evaluated under identical porosity and loading (Arjunan et al., 2020c). Nevertheless, for the application considered in this study, the capacity for lateral shrinkage of the structures was of prime importance.
Fig. 7.
Performance of the lattice designs considered showing (a) the von Mises stress observed and (b) the normalised lateral strain.
Though small, to disregard the variability offered by the porosity between the designs, the lateral strain was normalised () as shown in Fig. 7b. All the auxetic designs (AX1-4) exhibited a negative lateral strain (signifying radial shrinkage) with the regular design (RE1) showing a positive strain (expansion) as demonstrated in Fig. 8 . The highest lateral shrinkage was exhibited by AX4, a 23% improvement in comparison to AX3. Even though both of these designs (AX3 and AX4) are based on the traditional re-entrant architecture (Yu et al., 2018), AX4 allows for an increased bend dominance as a result of the chevron cross-link which is the reason for the enhanced shrinkage.
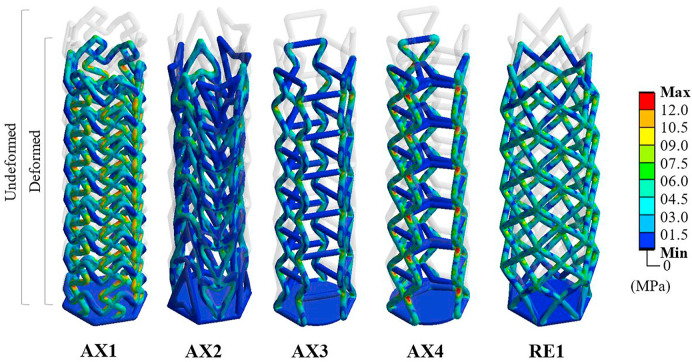
Fig. 8.
Von Mises stress profile and elastic deformation associated with the candidates tested for the swab head.
The increased bend dominance of the modified re-entrant architecture (AX4) can be confirmed also by studying the associated stress profile as shown in Fig. 8. When compared to AX3, the re-entrant beams can be seen to be experiencing comparatively higher stress that results in a higher lateral strain. However, when it comes to the design that is experiencing the highest stress that is AX1, the nature of the design means that most of the associated strain is being transmitted axially. This was not surprising as the chiral nature of the unit cell is known to exhibit rotational load transfer as demonstrated by Mousanezhad et al. (2016). The FE model also reveals the location in addition to the magnitude (Fig. 8) of the stress concentration. Here, a constant legend is used to aid the visual identification of areas with high stress. As can be seen, AX1 shows numerous areas of high stress facilitated by unique lattice followed by AX4 and RE1. While the additional stresses in AX4 facilitate increased lateral shrinkage, the opposite is true for RE1.
Therefore, the results so far established that the geometry of the cellular structures has a higher influence on mechanical performance, and an enhanced understanding of the stress distribution is required to derive effective design guidelines. For the structures investigated, every aspect of the mechanical performance and associated failure are dependent on the concentration of stress facilitated by the geometry as opposed to relative density (Wahid et al., 2019). Overall, considering that AX4 exhibited the highest lateral shrinkage while meeting the structural integrity criteria (), this design approach was selected to be used as foundation to develop the auxetic nasopharyngeal swab.
3.2. Influence of design parameters
3.2.1. Generation of the surrogate model
After selecting AX4 to act as the potential design candidate for the best auxetic swab head; the question becomes ‘what optimum combinations of the design parameters will result in the most favourable response?‘. To answer this question, the surrogate model is generated to study both the interaction effects and order of influence of the design variables on the mechanical performance. While the analysis so far was focused on establishing a suitable auxetic design, the role of the surrogate model is to identify the interaction effects of the geometric variables on the performance of the selected design.
For a systematic analysis, three geometrical parameters of AX4 that preserved the auxetic response were identified, namely the strut diameter (), auxetic angle () and cross link angle () as listed in Table 5. Consideration was also given when selecting the maximum and minimum limits of these geometrical parameters to make sure the overall shape remains unaffected. The surrogate model is then used to study both the influence and interaction of these parameters and their significance on four responses that characterises the performance of the structure, namely , , and . The results of the analysis were used to identify design parameters that had the most and least significance on the responses of interest. While the number of designs that demonstrate are being increasingly documented, the literature is rather scarce, when it comes to their optimum variants.
Before using the surrogate model for further analysis, the accuracy of the model was characterised using the analysis of variance (ANOVA). Once the model was confirmed valid, it was used to generate response surfaces (RS), that showed the relationship between the geometrical parameters (, , ) on the responses (, , , ) characterising the mechanical properties. The surrogate model developed was based on the Box–Behnken higher-order response surface methodology that represents the variables of interest as independent factors as listed in Table 6 . While the is the maximum von Misses stress under a constant load of 1 N, both and are evaluated from the elastic response of the structure.
Table 6.
Design matrix informing the surrogate model.
| Factor 1 A = (mm) |
Factor 2 B = (deg.) |
Factor 3 C = (deg.) |
Responses |
|||
|---|---|---|---|---|---|---|
| (MPa) | ||||||
| 0.3 | 75 | 130 | 0.084 | 14.72 | −1.32 | −0.29 |
| 0.1 | 85 | 155 | 0.011 | 134.44 | −4.80 | −0.30 |
| 0.1 | 65 | 155 | 0.012 | 324.46 | −2.63 | −0.22 |
| 0.2 | 65 | 130 | 0.042 | 78.07 | −2.41 | −0.25 |
| 0.3 | 85 | 155 | 0.080 | 7.83 | −1.83 | −0.31 |
| 0.1 | 75 | 180 | 0.011 | 271.02 | −2.76 | −0.30 |
| 0.2 | 75 | 155 | 0.039 | 52.37 | −4.45 | −0.28 |
| 0.2 | 75 | 155 | 0.039 | 52.37 | −4.45 | −0.28 |
| 0.2 | 75 | 155 | 0.039 | 52.37 | −4.45 | −0.28 |
| 0.1 | 75 | 130 | 0.011 | 278.04 | −2.69 | −0.29 |
| 0.3 | 75 | 180 | 0.082 | 14.25 | −1.33 | −0.29 |
| 0.3 | 65 | 155 | 0.086 | 17.49 | −1.27 | −0.29 |
| 0.2 | 75 | 155 | 0.039 | 52.37 | −4.45 | −0.28 |
| 0.2 | 85 | 180 | 0.038 | 22.25 | −4.21 | −0.30 |
| 0.2 | 65 | 180 | 0.041 | 85.23 | −2.41 | −0.25 |
| 0.2 | 75 | 155 | 0.039 | 52.37 | −4.45 | −0.28 |
| 0.2 | 85 | 130 | 0.038 | 21.64 | −3.75 | −0.30 |
Design variants of AX4 that met each of the factorial combinations dictate by the sampling points were generated. Finite element analysis was then carried out on each of the design variants and the responses , , and were evaluated as listed in Table 6. The best-fit indicators characterising the accuracy of the surrogate model revealed that and can be characterised using linear models listed in Eqs. (5), (6) respectively. On the other hand, effective prediction of and requires quadratic models as listed in Eqs. (7), (8) which implies significant interaction effects.
| (5) |
| (6) |
| (7) |
| (8) |
As shown in Table 7 , ANOVA can be used to represent the accuracy of the model, which are the probability (p-value), coefficient of determination R2, Adjusted R2, Predicted R2, and Adequate precision. The results show that all models feature significant F-values and very low p-values, which are the most common denominator demonstrating that all models are valid with negligible noise (Baroutaji et al., 2015).
Table 7.
Analysis of variance showing the significance and quality of the surrogate models developed.
| Model | F-value | p-value | Statistical measurements |
|||
|---|---|---|---|---|---|---|
| R2 | Adj-R2 | Pre-R2 | Adeq-precision | |||
| 167.13 | <0.0001 | 0.9747 | 0.9689 | 0.9540 | 34.1431 | |
| 71.72 | <0.0001 | 0.9893 | 0.9755 | 0.8283 | 26.9415 | |
| 60.95 | <0.0001 | 0.9874 | 0.9712 | 0.7984 | 21.4362 | |
| 9.07 | 0.0017 | 0.6767 | 0.6021 | 0.3287 | 9.5297 | |
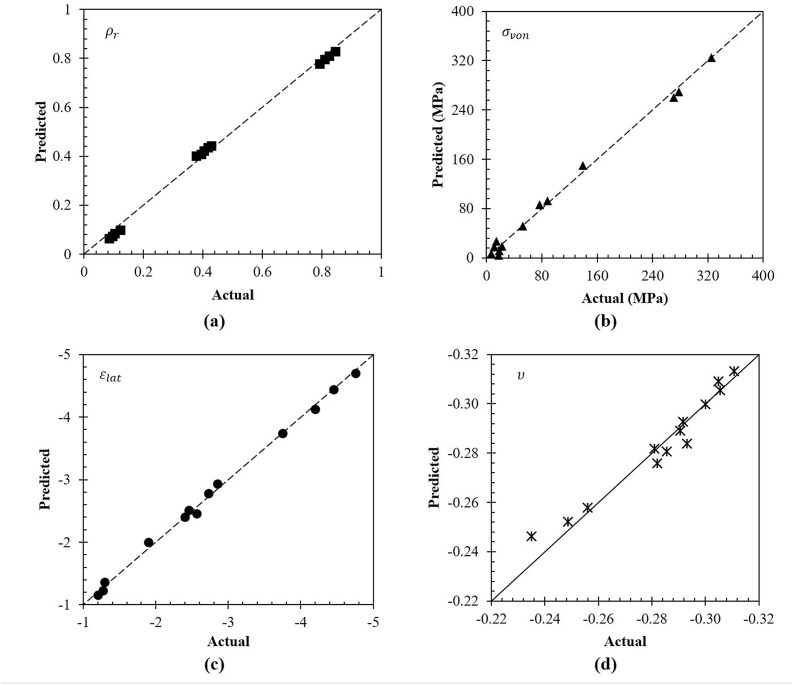
In general, models with a probability (p) value of less than 0.05 signifies that model terms are significant (Sthle and Wold, 1989). This in combination with a higher than 4 adequate precision ratios shows that the surrogate model has insignificant noise (Praveen and Arjunan, 2019). It can also be seen that all model terms show high R2 (>0.6) in addition to an excellent agreement between the predicted and adjusted R2, which are all commonly used credentials indicating the quality of the surrogate model. Overall, the analysis of variance shows that all the four models are significant and can be used to make valid predictions within the range listed in Table 5. After having evaluated the values through statistical parameters, the relationship between the finite element and surrogate model predictions were compared as shown in Fig. 9 a–d. For all responses being evaluated ( , and ), the predictions of the surrogate model (diagonal dotted line) can be seen to closely follow the numerical results. The comparatively small residuals as presented in Table 8 also shows that the models are valid. This means that Eqs. (4), (5), (6), (7) adequately represents the relationship between the geometrical variables and the responses.
Fig. 9.
Comparison between surrogate and finite element predictions for (a) relative density, (b) von Mises stress, (c) lateral strain, and (d) Poisson's ratio of the auxetic swab head.
Table 8.
Residuals for the response surface models developed.
| 0.0045 | −08.91 | −0.2388 | −0.0018 |
| 0.0054 | −20.85 | −0.1400 | 0.0001 |
| 0.0028 | −00.78 | −0.2425 | 0.0251 |
| −0.0035 | −11.94 | 0.0987 | 0.0106 |
| 0.0026 | 00.78 | 0.2425 | 0.0077 |
| 0.0045 | 08.91 | 0.2387 | −0.0241 |
| −0.0039 | 00.00 | 0.0000 | 0.0031 |
| −0.0039 | 00.00 | 0.0000 | 0.0031 |
| −0.0039 | 00.00 | 0.0000 | 0.0031 |
| 0.0037 | 12.72 | 0.1438 | −0.0203 |
| 0.0036 | −12.72 | −0.1438 | 0.0016 |
| 0.0058 | 20.85 | 0.1400 | −0.0268 |
| −0.0039 | 00.00 | 0.0000 | 0.0031 |
| −0.0031 | 11.94 | −0.0988 | 0.0061 |
| −0.0035 | −08.13 | 0.0037 | 0.0057 |
| −0.0039 | 00.00 | 0.0000 | 0.0031 |
| −0.0033 | 08.13 | −0.0038 | 0.0008 |
Although small, the agreement for Poisson's ratio at low thicknesses and high auxetic angles were found to deviate the furthest from the predicted performance. This was due to the buckling effects that were more prominent at lower strut thicknesses (0.1–0.2 mm) and higher auxetic angle (75–85°). Since the Poisson's ratio considers both the axial and radial strains, these effects had a higher effect showing a slight deviation from an otherwise ideal trend. Nevertheless, it can be seen from Table 7 that all the statistical parameters commonly used to evaluate the quality of the surrogate model indicate that the model is still valid. Overall, the analysis of variance shows that all the models including the one for Poisson's ratio are significant and can be used to make valid predictions. Therefore, it can be confirmed that the surrogate model developed in this study is appropriate.
3.2.2. Influence of design parameters on
Fig. 10 shows that the relative density of AX4 is primarily dependent on the strut diameter (Fig. 10a) with very small and almost no influence from auxetic and cross link angles respectively (Fig. 10b). The dependency of on is also linear with the lowest and highest amount of material within the structures relating to the lowest and highest respectively. This response is logical as the key parameter modulating the amount of material within the structures is the strut thickness.
Fig. 10.
Influence of the design parameters on the relative density showing (a) the effect of and when is constant and (b) the interaction effects of and when is constant.
Neither the variation in or can introduce large changes in the amount of material in comparison to , which was expected due to the overall geometry. The limited interaction between the design parameters can be further validated using Fig. 10b, where the trend in performance with varying and while keeping constant is not affected. This results in an almost flat performance slope (Fig. 10b) resulting in similar despite the changes in or . Therefore, for AX4, one can only make substantial changes to the relative density of the structure by changing . Overall, the most significant terms on are the first-order effects of .
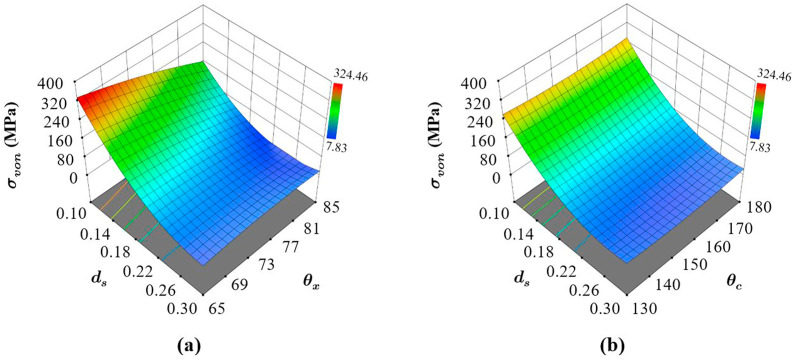
3.2.3. Influence of design parameters on
Fig. 11 a shows the influence of the strut diameter and auxetic angle on the von Mises stress experienced by the structure. As can be seen, as the strut diameter approaches the lowest limit of 0.1 mm, the structure is plastically deforming as the von Misses stress has well passed the yield strength of the material. This was expected and does not skew the lateral strain and Poisson's ratio calculations as they are evaluated from the elastic range of the structure. Furthermore, von Mises stress itself is composed of principal stresses, which are related to the magnitude of the load and area resisting the load. Consequently, comparing the von Mises stress to the yield strength of the material is the standard procedure to see where the design lies.
Fig. 11.
Influence of the design parameters on the von Mises stress experienced by the structures showing (a) the effect of and when is constant and (b) the effect of and when is constant. Comparing (a) and (b) also shows whether there are interaction effects between the structures.
It can be seen that is influenced not only by variations in but also by . Furthermore, the variation in the stresses follows a non-linear pattern, where the stress increases when both the strut diameter and auxetic angle decreases. An observation that is generally associated with auxetic lattice structures (Arjunan et al., 2020b; Ribeiro Filho et al., 2014) irrespective of the material. However, different from what was observed in the case of , the interaction between the parameters on the resulting is significant, which can be confirmed by comparing Fig. 11a to b.
The influence of on the von Mises stress varies with (Fig. 11a) and not with (Fig. 11b). This can be observed from the difference in the slope of the response surface concerning at different as shown in Fig. 11. On the contrary, when was varied the dependency of von Mises stress on was not affected as shown in Fig. 11b. Overall, it can be seen that has a higher influence on the von Mises stress when is higher, which means that the interaction effect between the design parameters and is significant and needs to be taken into consideration while designing the most effective AX4 structure. Accordingly, for improving the structural integrity of AX4, the most significant terms on are the first-order effects of and in the order where the strut diameter has a significantly higher influence in comparison to . Lastly, as evident from Fig. 11b the cross-link angle was found to have a very low influence on the structural integrity of the structure. This is not to say that had no influence, however comparing the influence of the other parameters, the effect of is smaller.
3.2.4. Influence of design parameters on
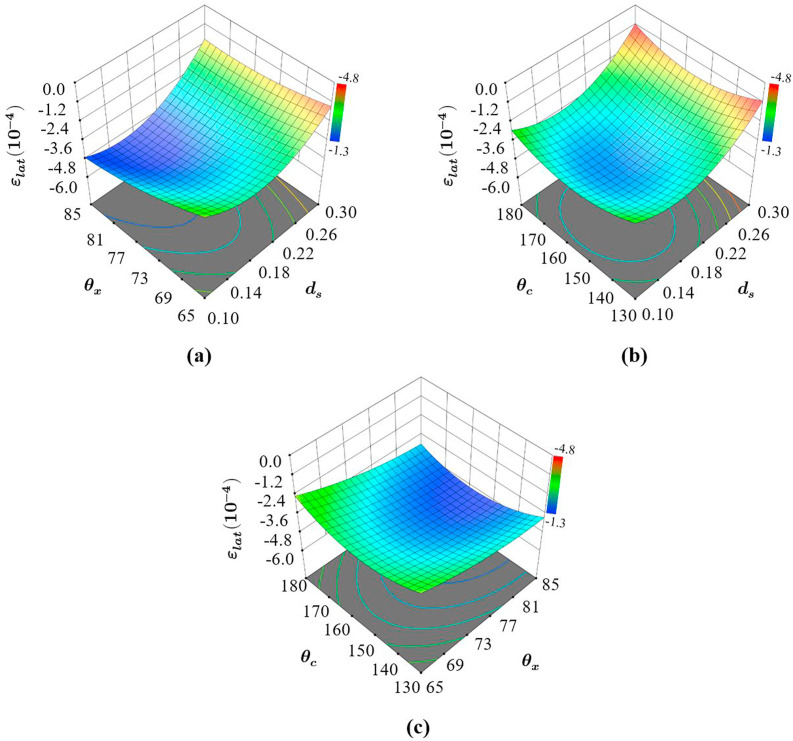
When it comes to lateral strain, the parameter that is used to characterises the radial shrinkage of the structure, all the design parameters were found to have a significant influence as shown in Fig. 12 . A combination of all three design parameters are required to obtain a targeted . Looking at the influence of and as shown in Fig. 12a it can be seen that is influenced by both and , where the highest absolute value in strain is when is at the highest and is the smallest. However, when is introduced as shown in Fig. 12b, the performance of the structure can be seen to be dependent on the interaction between and . Here, for the highest , it is also important that is somewhere between 150 and 170°. Different from what was observed in all the cases so far, Fig. 12c confirms that there is also a significant interaction between the parameters and where the best performance not only depends on the highest but also on a that is between 150 and 170.
Fig. 12.
Influence of the design parameters on the lateral strain stress showing (a) the effect of and when is constant, (b) the effect of on when is constant and (c) the effect of on when is constant. The comparison of (a), (b), and (c) also reveals the interaction effects between the design parameters taking place.
Therefore, the influence of on the lateral strain varies with both and . This can be observed from the difference in the slope of the response surface with respect to at different and as shown in Fig. 12a and b. When was varied the dependency of lateral strain on was also affected as shown in Fig. 12c. However, it can be seen that has a higher influence on the lateral strain followed by and . This means that the interaction effect between the design parameters , and are all significant and need to be taken into consideration to design the most effective AX4 to achieve maximum lateral shrinkage for the nasopharyngeal swab.
The influence of all three design parameters on elastic shrinkage also validates the design focus of this study and selection of the novel auxetic structure AX4. For example, the introduction of a new design component through the creation of AX4 allowed to achieve higher elastic strain along the radial direction in comparison to AX3. Looking at the order of influence, the most significant terms on are the effects of and followed by the interaction and in the order where the strut diameter has a significantly higher influence in comparison to and . This means that the structure AX4 is not only suitable for the swab head but can also be adopted for structures that require a high radial strain.
3.2.5. Influence of design parameters on
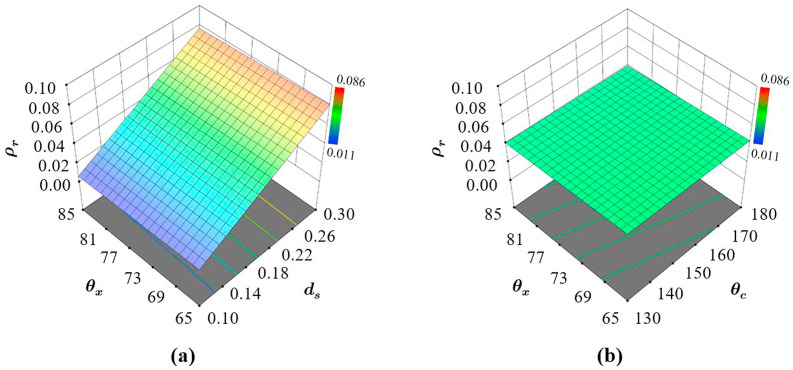
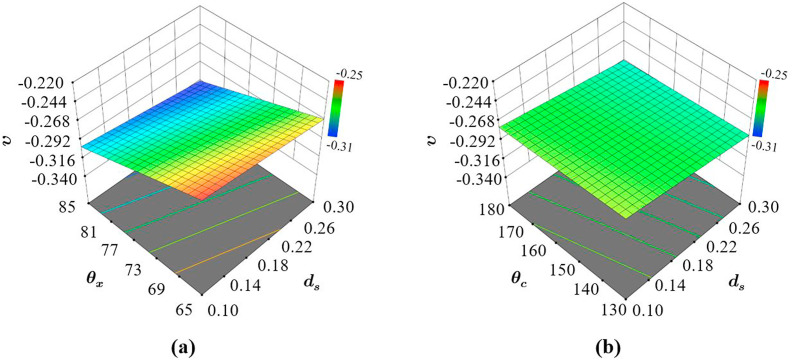
All the version derived from AX4 varying the design parameters , and exhibited negative Poisson's ratio () which is critical for this application. This validates the evolution of AX4 as a suitable structure inspired by a re-entrant unit cell. The surrogate model shows (Fig. 13 a) that when it comes to Poisson's ratio, the key parameter is the auxetic angle is . The absolute value of can be seen to increase linearly when increased as shown in Fig. 13a. Though comparatively smaller, the second most influential parameter was found to be . Nevertheless, this is the first response for the mechanical property of the structure that is primarily driven by the auxetic angle and not the strut thickness. Accordingly, the highest value of was observed at the highest auxetic angle and highest strut diameter as shown in Fig. 13a.
Fig. 13.
Influence of the design parameters on Poisson's ratio showing (a) the effect of and when is constant and (b) shows the interaction effects of and when is constant.
From a structural mechanics perspective, Poisson's ratio is defined as the negative ratio of transverse to axial strain. Therefore, to exhibit negative Poisson's ratio, the material must be allowed to laterally shrink under axial compression. Further to the shape of the unit cell, the amount of porosity or the void space dictates how much a structure can shrink. In this view, increasing the angle is beneficial as this allows more space for the structure to shrink and therefore reach a higher negative Poisson's ratio. Consequently, it is clear why the cross-link angle has a minimal influence as shown in Fig. 13b.
On the other hand, increasing the strut diameter decreases the porosity, which is less conducive to the absolute value of the Poisson's ratio in the negative direction. For the structure under consideration, has a higher significance in dictating the absolute value of the Poisson's ratio. The most significant terms on are the first-order effect of followed by . Consequently, the order of influence of the geometrical parameters when it comes to the Poisson's ratio is >. The effect of was found to be negligible for the geometrical range considered in this study. When it comes to the auxetic values for the swab heads studied, the range is comparable to elastic range performance exhibited by the tubular concepts proposed by Ren et al., 2016, 2019. Overall, it clear that AX4 offers new possibilities for targeted nasopharyngeal swab behaviour and properties at the same time allowing customisability, and scalability. Having established the interaction and influence of all the design parameters on the properties of interest, the next step is to derive the most optimal parametric combination using the surrogate model to design the auxetic nasopharyngeal swab.
3.3. Generation of the optimised design
3.3.1. Problem description
While the influence of geometrical parameters on the performance AX4 has been characterised, the optimum combination of the parametric values for optimum performance is still unknown. Accordingly, a problem description targeting the most important responses being investigated is required to identify an optimum design. However, to do this, the commonly used single-objective optimisation approach is inappropriate as multiple responses are involved. Consequently, a multi-objective description of the optimisation problem is conceived to identify an optimum solution.
An optimum auxetic nasopharyngeal swab should be able to convert as much of the axial load into lateral shrinkage () without plastic deformation. In other words, the optimised structure should allow for the highest while exhibiting a stress () around 50 MPa. A balance of these two parameters will allow the swab head to elastically shrink exerting less stress on the surrounding tissue as it travels to the nasopharyngeal cavity, which reduces the patient discomfort. Therefore, the objectives were to minimise (maximise the absolute value) while maintaining close to 50 MPa to prevent failure. The design stress of 50 MPa was selected considering a factor of safety of 1.4 at a tensile strength of 73 MPa. The resulting optimisation problem can be formulated as shown in Eq. (10):
| (10) |
An optimisation problem that involves multiple objectives as listed in Eq. (10) can be solved using two methods. The first one is to investigate all the objectives independently and look for an optimal solution generally referred to as the ‘Pareto optimal solution’. The second method incorporates multiple objectives functions into a single cost objective function, which is a measure of its relative performance. This method uses a desirability approach to identify a single solution to the optimisation problem. The second approach using the desirability criteria was the preferred approach in this study as it allows for flexibility in weighting the objective functions at a relatively low computational cost.
The optimisation is carried out using the response method called desirability as described by Myers et al. (2011). The method makes use of an objective function, , called the desirability function. It reflects the desirable ranges for each response . The desirable ranges are from zero to one (least to most desirable, respectively). The simultaneous objective function is a geometric mean of all transformed responses as shown in Eq. (11):
| (11) |
where n is the number of responses in the measure. If any of the responses or factors fall outside their desirability range, the overall function becomes zero.
For simultaneous optimisation each response must have a low and high value assigned to each goal which is represented by Eq. (10) solved using the desirability approach where Fig. 14 shows the results as a function of desirability objective concerning the design parameters considered. It appears that the optimal solution at the highest desirability (1.0) lies close to the maximum auxetic angle (Fig. 14a–c) and at midway for strut diameter (Fig. 14a–c) and cross link angle (Fig. 14b). As can be seen, there is not one but multiple optimal solutions that correspond to the desirability of 1 and one of which is shown in Table 9 .
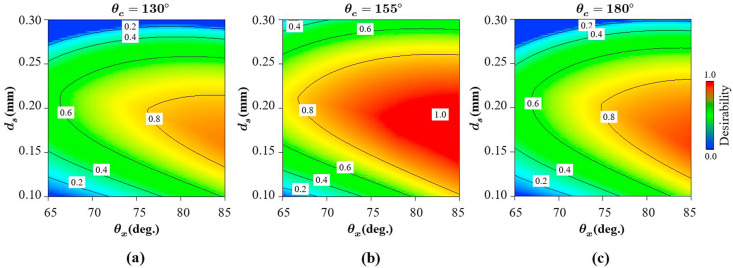
Fig. 14.
The desirability of the optimum solution against the design variables showing (a) the effect of strut diameter and the auxetic angle at a cross link angle of 130 (b) the effect of strut diameter and the auxetic angle at a cross link angle of 155 and (c) the effect of strut diameter and the auxetic angle at a cross link angle of 180. A desirability contour of 0.0 and 1.0 refers to the least and most optimum solution respectively that can be achieved between the geometrical ranges considered.
Table 9.
Optimal solution predicted by the surrogate model based on Eq. (10).
| Number | (mm) | (deg.) | (deg.) | Desirability |
|---|---|---|---|---|
| 1 | 0.18 | 80 | 160 | 1.0 |
Based on the predicted geometrical parameters, designs were developed, and numerical evaluation carried out as shown in Fig. 15 . As listed in Table 10 , the structural performance of the optimised design is very close to the design stress of 50 MPa. Besides, the deformed shape of the optimised design can be seen to allow for a significant increase (2.7 times) in lateral shrinkage in comparison to the regular AX4 design. Overall, the results of the optimised model in comparison to the surrogate model (Table 10) were in good agreement.
Fig. 15.
Performance of the optimum auxetic swab and the representative printed sample.
Table 10.
Confirmation runs for the optimum swab design.
| Item | (MPa) | |||
|---|---|---|---|---|
| Surrogate | −4.9 | 52.22 | −0.29 | 0.03 |
| FEM | −5.3 | 50.13 | −0.29 | 0.03 |
| % difference | 7.8 | 4.1 | – | – |
The surrogate model underestimated the lateral strain by 7.8% and overestimated the von Mises stress by 4.1%. However, no changes in Poisson's ratio and relative density were observed between the predictions carried out by the surrogate model in comparison to FEM. Consequently, the findings show that the optimum design is preferable and results in a much higher auxetic performance of the nasopharyngeal swab. Although the re-entrant architecture features a higher stress concentration effect, both the experimental and numerical analysis confirms that the optimised swab head can withstand a safe load. Furthermore, the use of von-Mises stress as a response parameter in the optimisation algorithm also accounts for the geometrical effects leading to stress concentration.
Using the optimised design, a representative example of a full auxetic nasopharyngeal swab that can be manufactured by 3D printing is shown in Fig. 15. The global dimensions of the swab are comparable to traditional nasopharyngeal swabs that are commercially available. Additional design feature includes a notch to allow for the user to easily break the swab to go into the transporter. Breaking the swab at the notch after use will also allow distinguishing between swabs that are used and new to avoid contamination.
Although a potential concept has been established, the design requires further improvements to achieve uniform auxetic behaviour. This includes further evaluation of the bending and twisting performance in addition to testing the effectiveness in swab collection itself. Furthermore, compression is not the only load experienced by the swab head and fretting/lateral loading are involved depending on both the usage and variation in the nasal cavity. However, having carefully evaluated various loading scenarios, compression was identified as the most prominent of all. Accordingly, the proof of concept was developed giving primary consideration to the most significant load case, which is compression.
Overall, this research is not aimed at developing a final product, rather a first step in examining the potential of using auxetic designs to improve the existing concepts in nasopharyngeal swabs. It is expected that the project will initiate new thinking which fellow researchers can adapt and improve to develop functional biomedical devices.
4. Conclusion
The supply-chain disruption associated with COVID-19 lockdown has compelled to identify alternative sources of essential biomedical devices that can be manufactured on-demand. The restriction on the movement of the workforce means that there is a need for innovation that can be conceived and manufactured digitally where 3D printing has an established advantage. There are also numerous reports of swab shortages across Europe, USA, and Asia calling for a time-sensitive approach. As a response, this study puts forward an open innovation framework to develop 3D printable nasopharyngeal swabs that can perform in an auxetic nature. The auxetic approach is considered to develop a one size fits all swab that has the potential for reducing patient discomfort by shrinking inward. This allows for the swab head to navigate the nasal cavity by exerting considerably reduced stress on surrounding tissue as opposed to a regular swab. Accordingly, the results of this study go well beyond the COVID-19 crisis and improve how nasopharyngeal swabs are conceived today. To achieve this various auxetic candidates were evaluated and a potential design designated AX4 was selected as it outperformed all other designs for its capacity for lateral shrinkage. The subsequent parametric analysis revealed that the performance of the selected design was dependent on the geometrical parameters , and at a Poisson's ratio range of −0.22 to −0.31 confirming auxeticity. Further analysis using the finite element method informed by the surrogate model showed that the von Mises stress experienced by the structure was primarily influenced by followed by . For lateral shrinkage, the most significant terms were and followed by the interaction effects of , in the order . Having captured these relationships using the surrogate model, a multi-objective optimisation was carried out to develop the most optimum design for the swab. The most desirable solution with the highest lateral strain around a 50 MPa design stress was found to be at a , and of 0.18, 180 and 160 respectively. The design stress of 50 MPa was selected at a factor of safety of 1.4 to account for material inconsistencies across manufacturers and machines around the world. The surrogate model developed in this study showed an accuracy of 92.2% in predicting and 95.9% for for the multi-objective design problem. Overall, the study suggests that the lateral shrinkage of the auxetic swabs can be maximised by the careful selection of design parameters considering their interaction. Using the surrogate model developed in this study, manufacturers and research institutions can further improve the design and generate alternate prototypes if necessary. As the pandemic evolves, various situations such as a second wave are likely to appear unpredictably were carefully conceived 3D printed products can achieve higher-order solutions. Although the focus was on developing an optimum auxetic nasopharyngeal swab, the design and analysis philosophy conceived in this study allows developing novel biomedical products using the auxetic concept that can be digitally transported and manufactured on demand.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
CRediT authorship contribution statement
Arun Arjunan: Conceptualization, Supervision, Methodology, Software, Investigation, Validation, Formal analysis, Writing - original draft, Writing - review & editing. Suhaib Zahid: Methodology, Software, Investigation, Validation. Ahmad Baroutaji: Methodology, Software, Investigation, Validation, Formal analysis, Writing - review & editing. John Robinson: Methodology, Software, Investigation, Validation, Formal analysis, Writing - review & editing.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This research was conducted with support from the CALMERIC grant [European Commission, Grant number: 32R19P03053]; 6DME Ltd. UK; and Formlabs GmbH.
References
- Ahmadi S.M.M., Hedayati R., Li Y., Lietaert K., Tümer N., Fatemi A., Rans C.D.D., Pouran B., Weinans H., Zadpoor A.A.A. Fatigue performance of additively manufactured meta-biomaterials: the effects of topology and material type. Acta Biomater. 2018;65:292–304. doi: 10.1016/j.actbio.2017.11.014. [DOI] [PubMed] [Google Scholar]
- Alomarah A., Ruan D., Masood S. Tensile properties of an auxetic structure with re-entrant and chiral features—a finite element study. Int. J. Adv. Manuf. Technol. 2018;99:2425–2440. doi: 10.1007/s00170-018-2637-y. [DOI] [Google Scholar]
- Arjunan A. Acoustic absorption of passive destructive interference cavities. Mater. Today Commun. 2019;19:68–75. doi: 10.1016/j.mtcomm.2018.12.012. [DOI] [Google Scholar]
- Arjunan A. Targeted sound attenuation capacity of 3D printed noise cancelling waveguides. Appl. Acoust. 2019;151:30–44. doi: 10.1016/J.APACOUST.2019.03.008. [DOI] [Google Scholar]
- Arjunan A., Baroutaji A., Praveen A.S., Olabi A.G., Wang C.J. Ref. Modul. Mater. Sci. Mater. Eng. Elsevier; 2019. Acoustic performance of metallic foams. [DOI] [Google Scholar]
- Arjunan A., Robinson J., Al Ani E., Heaselgrave W., Baroutaji A., Wang C. Mechanical performance of additively manufactured pure silver antibacterial bone scaffolds. J. Mech. Behav. Biomed. Mater. 2020;112:104090. doi: 10.1016/j.jmbbm.2020.104090. [DOI] [PubMed] [Google Scholar]
- Arjunan A., Singh M., Baroutaji A., Wang C. Additively manufactured AlSi10Mg inherently stable thin and thick-walled lattice with negative Poisson's ratio. Compos. Struct. 2020:112469. doi: 10.1016/j.compstruct.2020.112469. [DOI] [Google Scholar]
- Arjunan A., Demetriou M., Baroutaji A., Wang C. Mechanical performance of highly permeable laser melted Ti6Al4V bone scaffolds. J. Mech. Behav. Biomed. Mater. 2020;102 doi: 10.1016/j.jmbbm.2019.103517. [DOI] [PubMed] [Google Scholar]
- Baroutaji A., Gilchrist M.D.D., Smyth D., Olabi A.G.G. Crush analysis and multi-objective optimization design for circular tube under quasi-static lateral loading. Thin-Walled Struct. 2015;86:121–131. doi: 10.1016/j.tws.2014.08.018. [DOI] [Google Scholar]
- Baroutaji A., Arjunan A., Niknejad A., Tran T., Olabi A.-G. Ref. Modul. Mater. Sci. Mater. Eng. Elsevier; 2019. Application of cellular material in crashworthiness applications: an overview. [DOI] [Google Scholar]
- Bertoldi K., Vitelli V., Christensen J., Van Hecke M. Flexible mechanical metamaterials. Nat. Rev. Mater. 2017;2 doi: 10.1038/natrevmats.2017.66. [DOI] [Google Scholar]
- Borresen J. USA Today; 2020. What to Expect if You Are Being Tested for the Coronavirus.https://eu.usatoday.com/in-depth/news/2020/04/01/coronavirus-testing-what-expect-if-youre-tested/5077039002/ [Google Scholar]
- BS EN ISO 13485:2016 Medical devices. Quality management systems. Requirements for regulatory purposes, (n.d.). https://shop.bsigroup.com/ProductDetail?pid=000000000030353196&creative=435401337506&keyword=&matchtype=b&network=g&device=c&gclid=Cj0KCQjwjer4BRCZARIsABK4QeUcElo3_Mkyxo30nwEssp2M6-3tco78hTAGkiotCm-pC7hYkjce9EkaAgGZEALw_wcB (accessed July 24, 2020).
- BS EN ISO 14971:2012 Medical devices. Application of risk management to medical devices, (n.d.). https://shop.bsigroup.com/en/ProductDetail/?pid=000000000030268035 (accessed July 24, 2020).
- BS EN ISO 14971:2019 Medical devices. Application of risk management to medical devices, (n.d.). https://shop.bsigroup.com/ProductDetail/?pid=000000000030407615 (accessed July 24, 2020).
- Chen Y., Li T., Scarpa F., Wang L. Lattice metamaterials with mechanically tunable Poisson's ratio for vibration control. Phys. Rev. Appl. 2017;7 doi: 10.1103/PhysRevApplied.7.024012. [DOI] [Google Scholar]
- Chen S., Karthikeyan R., Ryu S.C. Towards the design of mechanically superior tubular structures for microcatheters. Smart Mater. Struct. 2019;28 doi: 10.1088/1361-665X/aaea45. [DOI] [Google Scholar]
- Chen Y.W., Fang H.Y., Shie M.Y., Shen Y.F. The mussel-inspired assisted apatite mineralized on PolyJet material for artificial bone scaffold. Int. J. Bioprinting. 2019 doi: 10.18063/ijb.v5i2.197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi M.-J., Kang S.-H., Oh M.-H., Cho S. Controllable optimal design of auxetic structures for extremal Poisson's ratio of −2. Compos. Struct. 2019;226:111215. doi: 10.1016/J.COMPSTRUCT.2019.111215. [DOI] [Google Scholar]
- Clegg J.R., Wagner A.M., Shin S.R., Hassan S., Khademhosseini A., Peppas N.A. Modular fabrication of intelligent material-tissue interfaces for bioinspired and biomimetic devices. Prog. Mater. Sci. 2019;106 doi: 10.1016/j.pmatsci.2019.100589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coronavirus Test Obstacles: A Shortage of Face Masks and Swabs - The New York Times, (n.d). https://www.nytimes.com/2020/03/18/health/coronavirus-test-shortages-face-masks-swabs.html (accessed July 18, 2020).
- Coronavirus testing delays fueled by swab Shortage : shots - health News : NPR, (n.d). https://www.npr.org/sections/health-shots/2020/03/18/817801222/testing-swabs-run-in-short-supply-as-makers-try-to-speed-up-production?t=1595078120724 (accessed July 18, 2020).
- COVID-19 situation update worldwide, as of 18 July 2020, (n.d). . https://www.ecdc.europa.eu/en/geographical-distribution-2019-ncov-cases (accessed July 18, 2020).
- de Krijger J., Rans C., Van Hooreweder B., Lietaert K., Pouran B., Zadpoor A.A. Effects of applied stress ratio on the fatigue behavior of additively manufactured porous biomaterials under compressive loading. J. Mech. Behav. Biomed. Mater. 2017;70:7–16. doi: 10.1016/j.jmbbm.2016.11.022. [DOI] [PubMed] [Google Scholar]
- Duoss E.B., Weisgraber T.H., Hearon K., Zhu C., Small W., Metz T.R., Vericella J.J., Barth H.D., Kuntz J.D., Maxwell R.S., Spadaccini C.M., Wilson T.S. Three-Dimensional printing of elastomeric, cellular architectures with negative stiffness. Adv. Funct. Mater. 2014;24:4905–4913. doi: 10.1002/adfm.201400451. [DOI] [Google Scholar]
- El Dhaba A.R., Shaat M. Modeling deformation of auxetic and non-auxetic polymer gels. Appl. Math. Model. 2019;74:320–336. doi: 10.1016/J.APM.2019.04.050. [DOI] [Google Scholar]
- Evans K.E. Auxetic polymers: a new range of materials. Endeavour. 1991;15:170–174. doi: 10.1016/0160-9327(91)90123-S. [DOI] [Google Scholar]
- Gao Q., Zhao X., Wang C., Wang L., Ma Z. Multi-objective crashworthiness optimization for an auxetic cylindrical structure under axial impact loading. Mater. Des. 2018 doi: 10.1016/j.matdes.2018.01.063. [DOI] [Google Scholar]
- Gao Q., Wang L., Zhou Z., Ma Z.D., Wang C., Wang Y. Theoretical, numerical and experimental analysis of three-dimensional double-V honeycomb. Mater. Des. 2018 doi: 10.1016/j.matdes.2017.11.024. [DOI] [Google Scholar]
- Gao Q., Liao W.H., Wang L. An analytical model of cylindrical double-arrowed honeycomb with negative Poisson's ratio. Int. J. Mech. Sci. 2020 doi: 10.1016/j.ijmecsci.2019.105400. [DOI] [Google Scholar]
- Geng L., Wu W., Sun L., Fang D. Damage characterizations and simulation of selective laser melting fabricated 3D re-entrant lattices based on in-situ CT testing and geometric reconstruction. Int. J. Mech. Sci. 2019;157–158:231–242. doi: 10.1016/j.ijmecsci.2019.04.054. [DOI] [Google Scholar]
- Goh G.D., Yap Y.L., Tan H.K.J., Sing S.L., Goh G.L., Yeong W.Y. Process–structure–properties in polymer additive manufacturing via material extrusion: a review. Crit. Rev. Solid State Mater. Sci. 2020;45:113–133. doi: 10.1080/10408436.2018.1549977. [DOI] [Google Scholar]
- Han S.C., Kang D.S., Kang K. Two nature-mimicking auxetic materials with potential for high energy absorption. Mater. Today. 2019;26:30–39. doi: 10.1016/j.mattod.2018.11.004. [DOI] [Google Scholar]
- Harris J.A., McShane G.J. Metallic stacked origami cellular materials: additive manufacturing, properties, and modelling. Int. J. Solid Struct. 2020;185–186:448–466. doi: 10.1016/j.ijsolstr.2019.09.007. [DOI] [Google Scholar]
- Hedayati R., Leeflang A.M., Zadpoor A.A. Additively manufactured metallic pentamode meta-materials. Appl. Phys. Lett. 2017;110 doi: 10.1063/1.4977561. [DOI] [Google Scholar]
- Hu H., Zhang M., Liu Y., Hu H., Zhang M., Liu Y. Auxetic structures and mechanisms. Auxetic Text. 2019:19–56. doi: 10.1016/B978-0-08-102211-5.00002-4. [DOI] [Google Scholar]
- Interim guidelines for clinical specimens for COVID-19 | CDC, (n.d.). . https://www.cdc.gov/coronavirus/2019-ncov/lab/guidelines-clinical-specimens.html (accessed July 18, 2020).
- Janbaz S., Noordzij N., Widyaratih D.S., Hagen C.W., Fratila-Apachitei L.E., Zadpoor A.A. Origami lattices with free-form surface ornaments. Sci. Adv. 2017;3 doi: 10.1126/sciadv.aao1595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeong S., Yoo H.H. Shape optimization of bowtie-shaped auxetic structures using beam theory. Compos. Struct. 2019;224:111020. https://www.sciencedirect.com/science/article/pii/S0263822319309377 [Google Scholar]
- Jiang Y., Li Y. 3D printed auxetic mechanical metamaterial with chiral cells and Re-entrant cores. Sci. Rep. 2018;8:2397. doi: 10.1038/s41598-018-20795-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang Y., Rudra B., Shim J., Li Y. Limiting strain for auxeticity under large compressive Deformation: chiral vs. re-entrant cellular solids. Int. J. Solid Struct. 2019;162:87–95. doi: 10.1016/J.IJSOLSTR.2018.11.035. [DOI] [Google Scholar]
- Jin S., Korkolis Y.P., Li Y. Shear resistance of an auxetic chiral mechanical metamaterial. Int. J. Solid Struct. 2019:174–175. doi: 10.1016/J.IJSOLSTR.2019.06.005. 28–37. [DOI] [Google Scholar]
- Karnessis N., Burriesci G. Uniaxial and buckling mechanical response of auxetic cellular tubes. Smart Mater. Struct. 2013;22 doi: 10.1088/0964-1726/22/8/084008. [DOI] [Google Scholar]
- Kolken H.M.A., Zadpoor A.A. Auxetic mechanical metamaterials. RSC Adv. 2017;7:5111–5129. doi: 10.1039/C6RA27333E. [DOI] [Google Scholar]
- Lee W., Jeong Y., Yoo J., Huh H., Park S.-J., Park S.H., Yoon J. Effect of auxetic structures on crash behavior of cylindrical tube. Compos. Struct. 2019;208:836–846. doi: 10.1016/J.COMPSTRUCT.2018.10.068. [DOI] [Google Scholar]
- Lekesiz H., Bhullar S.K., Karaca A.A., Jun M.B.G. Mechanical characterization of auxetic stainless steel thin sheets with reentrant structure. Smart Mater. Struct. 2017;26 doi: 10.1088/1361-665X/aa73a4. [DOI] [Google Scholar]
- Ling B., Wei K., Wang Z., Yang X., Qu Z., Fang D. Experimentally program large magnitude of Poisson's ratio in additively manufactured mechanical metamaterials. Int. J. Mech. Sci. 2020;173 doi: 10.1016/j.ijmecsci.2020.105466. [DOI] [Google Scholar]
- Ma Z.-D., Liu Y. This invention relates generally to medical/surgical stents and, in particular, to stents based upon negative Poisson's ratio (NPR) structures. 2011. https://patents.google.com/patent/US20110029063A1/en US20110029063A1.
- Mirzaali M.J., Caracciolo A., Pahlavani H., Janbaz S., Vergani L., Zadpoor A.A. Multi-material 3D printed mechanical metamaterials: rational design of elastic properties through spatial distribution of hard and soft phases. Appl. Phys. Lett. 2018;113:241903. doi: 10.1063/1.5064864. [DOI] [Google Scholar]
- Mirzaali M.J., Pahlavani H., Zadpoor A.A. Auxeticity and stiffness of random networks: lessons for the rational design of 3D printed mechanical metamaterials. Appl. Phys. Lett. 2019;115 doi: 10.1063/1.5096590. [DOI] [Google Scholar]
- Mizzi L., Attard D., Gatt R., Pozniak A.A., Wojciechowski K.W., Grima J.N. Influence of translational disorder on the mechanical properties of hexachiral honeycomb systems. 2015. [DOI]
- Mousanezhad D., Haghpanah B., Ghosh R., Hamouda A.M., Nayeb-Hashemi H., Vaziri A. Elastic properties of chiral, anti-chiral, and hierarchical honeycombs: a simple energy-based approach. Theor. Appl. Mech. Lett. 2016;6:81–96. doi: 10.1016/j.taml.2016.02.004. [DOI] [Google Scholar]
- Myers R.H., Montgomery D.C., Anderson-Cook C.M. Response surface methodology: process and product optimization using designed Experiments. Wiley. 2011 https://books.google.co.uk/books?id=F6MJeRe2POUC [Google Scholar]
- Nečemer B., Kramberger J., Vuherer T., Glodež S. Fatigue crack initiation and propagation in re-entrant auxetic cellular structures. Int. J. Fatig. 2019;126:241–247. doi: 10.1016/J.IJFATIGUE.2019.05.010. [DOI] [Google Scholar]
- Nikkhah H., Baroutaji A., Kazancı Z., Arjunan A. Evaluation of crushing and energy absorption characteristics of bio-inspired nested structures. Thin-Walled Struct. 2020;148:106615. doi: 10.1016/j.tws.2020.106615. [DOI] [Google Scholar]
- Péré H., Péré H., Péré H., Podglajen I., Podglajen I., Wack M., Wack M., Flamarion E., Mirault T., Mirault T., Goudot G., Goudot G., Hauw-Berlemont C., Le L., Le L., Caudron E., Caudron E., Carrabin S., Rodary J., Ribeyre T., Bélec L., Bélec L., Bélec L., Veyer D., Veyer D., Veyer D. Nasal swab sampling for SARS-CoV-2: a convenient alternative in times of nasopharyngeal swab shortage. J. Clin. Microbiol. 2020;58 doi: 10.1128/JCM.00721-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Praveen A.S., Arjunan A. Parametric optimisation of High-Velocity Oxy-Fuel Nickel-Chromium-Silicon-Boron and Aluminium-Oxide coating to improve erosion wear resistance. Mater. Res. Express. 2019 doi: 10.1088/2053-1591/ab301c. [DOI] [Google Scholar]
- Rao J.S., Kumar B. Inst. Mech. Eng. - 10th Int. Conf. Vib. Rotating Mach. Woodhead Publishing Limited; 2012. 3D Blade root shape optimization; pp. 173–188. [DOI] [Google Scholar]
- Ren X., Shen J., Ghaedizadeh A., Tian H., Xie Y.M. A simple auxetic tubular structure with tuneable mechanical properties. Smart Mater. Struct. 2016;25 doi: 10.1088/0964-1726/25/6/065012. [DOI] [Google Scholar]
- Ren X., Liu F.C., Zhang X.Y., Xie Y.M. Numerical investigation of tubular structures generated by cutting method and pattern scale factor (PSF) method, Pigment Resin Technol. 2019. [DOI]
- Ribeiro Filho S.L.M., Silva T.A.A., Vieira L.M.G., Panzera T.H., Boba K., Scarpa F. Geometric effects of sustainable auxetic structures integrating the particle swarm optimization and finite element method. Mater. Res. 2014;17:747–757. doi: 10.1590/S1516-14392014005000024. [DOI] [Google Scholar]
- Robinson J., Stanford M., Arjunan A. Correlation between selective laser melting parameters, pore defects and tensile properties of 99.9% silver. Mater. Today Commun. 2020;25:101550. doi: 10.1016/j.mtcomm.2020.101550. [DOI] [Google Scholar]
- Robinson J., Stanford M., Arjunan A. Stable formation of powder bed laser fused 99.9% silver. Mater. Today Commun. 2020:101195. doi: 10.1016/j.mtcomm.2020.101195. [DOI] [Google Scholar]
- Scarpa F., Smith C.W., Ruzzene M., Wadee M.K. Phys. Status Solidi Basic Res. 2008. Mechanical properties of auxetic tubular truss-like structures; pp. 584–590. [DOI] [Google Scholar]
- Shufrin I., Pasternak E., Dyskin A.V. Effective properties of layered auxetic hybrids. Compos. Struct. 2019;209:391–400. doi: 10.1016/J.COMPSTRUCT.2018.10.072. [DOI] [Google Scholar]
- Singapore's Nasal Swab Struggle Shows Why Test Kits Are Scarce - Bloomberg, (n.d). https://www.bloomberg.com/news/articles/2020-05-08/singapore-s-nasal-swab-struggle-shows-why-test-kits-are-scarce (accessed July 18, 2020).
- Spagnoli A., Brighenti R., Lanfranchi M., Soncini F. On the auxetic behaviour of metamaterials with Re-entrant cell structures. 2015. https://www.sciencedirect.com/science/article/pii/S187770581501214X
- Sthle L., Wold S. Analysis of variance (ANOVA) Chemometr. Intell. Lab. Syst. 1989;6:259–272. doi: 10.1016/0169-7439(89)80095-4. [DOI] [Google Scholar]
- Vance A., Bari K., Arjunan A. Compressive performance of an arbitrary stiffness matched anatomical Ti64 implant manufactured using Direct Metal Laser Sintering. Mater. Des. 2018;160:1281–1294. doi: 10.1016/j.matdes.2018.11.005. [DOI] [Google Scholar]
- Vance A., Bari K., Arjunan A. Investigation of Ti64 sheathed cellular anatomical structure as a tibia implant. Biomed. Phys. Eng. Express. 2019;5 doi: 10.1088/2057-1976/ab0bd7. [DOI] [Google Scholar]
- Wahid Z., Ariffin M.K.A.M., Baharudin B.T.H.T., Ismail M.I.S., Mustapha F. Abaqus simulation of different critical porosities cubical scaffold model. IOP Conf. Ser. Mater. Sci. Eng. 2019;530 doi: 10.1088/1757-899X/530/1/012018. [DOI] [Google Scholar]
- Wang T., Wang L., Ma Z., Hulbert G.M. Elastic analysis of auxetic cellular structure consisting of re-entrant hexagonal cells using a strain-based expansion homogenization method. Mater. Des. 2018;160:284–293. doi: 10.1016/J.MATDES.2018.09.013. [DOI] [Google Scholar]
- Wang H., Zhang Y., Lin W., Qin Q.H. A novel two-dimensional mechanical metamaterial with negative Poisson's ratio. Comput. Mater. Sci. 2020;171 doi: 10.1016/j.commatsci.2019.109232. [DOI] [Google Scholar]
- Wojciechowski K.W. Constant thermodynamic tension Monte Carlo studies of elastic properties of a two-dimensional system of hard cyclic hexamers. Mol. Phys. 1987;61:1247–1258. doi: 10.1080/00268978700101761. [DOI] [Google Scholar]
- Wojciechowski K.W. Two-dimensional isotropic system with a negative Poisson ratio. Phys. Lett. 1989;137:60–64. doi: 10.1016/0375-9601(89)90971-7. [DOI] [PubMed] [Google Scholar]
- Wojciechowski K.W. Remarks on “Poisson ratio beyond the limits of the elasticity theory. J. Phys. Soc. Japan. 2003;72:1819–1820. doi: 10.1143/JPSJ.72.1819. [DOI] [Google Scholar]
- Yang H., Ma L. Design and characterization of axisymmetric auxetic metamaterials. Compos. Struct. 2020;249:112560. doi: 10.1016/j.compstruct.2020.112560. [DOI] [Google Scholar]
- Yang H., Wang B., Ma L. Mechanical properties of 3D double-U auxetic structures. Int. J. Solid Struct. 2019;180–181:13–29. https://www.sciencedirect.com/science/article/pii/S002076831930318X [Google Scholar]
- Yu X., Zhou J., Liang H., Jiang Z., Wu L. Mechanical metamaterials associated with stiffness, rigidity and compressibility: a brief review. Prog. Mater. Sci. 2018;94:114–173. doi: 10.1016/j.pmatsci.2017.12.003. [DOI] [Google Scholar]
- Yuan S., Shen F., Bai J., Chua C.K., Wei J., Zhou K. 3D soft auxetic lattice structures fabricated by selective laser sintering: TPU powder evaluation and process optimization. Mater. Des. 2017;120:317–327. doi: 10.1016/J.MATDES.2017.01.098. [DOI] [Google Scholar]
- Zhang X.-C., An L.-Q., Ding H.-M., Zhu X.-Y., El-Rich M. The influence of cell micro-structure on the in-plane dynamic crushing of honeycombs with negative Poisson's ratio. J. Sandw. Struct. Mater. 2015;17:26–55. doi: 10.1177/1099636214554180. [DOI] [Google Scholar]
- Zhang D., Xiao J., Yu W., Guo Q., Yang J. Hierarchical metal/polymer metamaterials of tunable negative Poisson's ratio fabricated by initiator-integrated 3D printing (i3DP) Nanotechnology. 2018;29:505704. doi: 10.1088/1361-6528/aae283. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.