Lab on a rod: Size-based particle separation and sorting in a helical channel

Abstract

Size-based particle separation using inertial microfluidics in spiral channels has been well studied over the past decade. Though these devices can effectively separate particles, they require a relatively large device footprint with a typical outer channel radius of approximately 15 mm. In this paper, we describe a microfluidic device with a footprint diameter of 5.5 mm, containing a helical channel capable of inertial particle separation fabricated using abrasive jet micromachining. The separation of particles in several channel geometries was studied using wide-field fluorescence microscopy. A maximum separation efficiency of approximately 90% was achieved at a flow rate of 1.5 ml/min with a purity of approximately 95% at the outlet, where large particles were collected. An accompanying computational fluid dynamics model was developed to allow researchers to quickly assess the separation capability of their helical or spiral devices.

I. INTRODUCTION

Size-based particle separation is often a key step in the preparation, purification, and analysis of biomedical and environmental samples.^1,2 Traditional methods of particle separation involve the use of a filter such as a membrane, though this is prone to clog, and only particles smaller than a single size pass through the filter.³ In recent years, microfluidics-based particle separation approaches have also been developed. These microfluidic methods include dielectrophoretic,⁴ magnetophoretic,⁵ and acoustophoretic⁶ separation. Another emerging passive filtration method is inertial microfluidics, which has the advantage of relying solely on particle and fluid properties to manipulate the location of particles in the flow.^7–9

In a straight channel, inertial particle migration is achieved through the balance of two inertial forces, the shear-gradient lift, forcing particles to the walls, and the wall-induced lift, forcing particles away from the walls.^3,9 Balancing these forces yields distinct particle positions based on their size.⁷ There may, however, be several equilibrium positions for each particle size depending on the channel geometry.^8,10 For example, particles in a straight square or rectangular microchannel will focus along the midpoint of each wall, resulting in up to four equilibrium positions per particle size.¹⁰ To reduce the number of positions per particle size, microfluidic devices that utilize secondary flows have been proposed. The secondary flows are induced by the centrifugal forces generated by flows in serpentine⁷ or spiral channels,^11–21 making it feasible to extract particles through separate outlets. In the past decade, much of the focus in inertial microfluidics has been on the implementation and improvement of spiral microfluidic channels fabricated with soft lithography in a flat polydimethylsiloxane (PDMS) substrate.^{14,15,18–25}

Microfluidic devices featuring planar spiral channels are typically designed with an outer channel radius greater than 15 mm,^{15,17,22,25,26} resulting in a relatively large device footprint. Typically, flow rates up to 5 ml/min^{11–15,20,22,23,25,26} are used for the separation of cells or microspheres in such devices. Recently, Shen et al.²⁴ demonstrated a flow rate of 6.5 ml/min using ordered micro-obstacles along a spiral channel to manipulate the secondary flow fields, achieving separation efficiencies of 98.7%, 97.8%, and 85.8% for 15.5, 9.9, and 7.3 μm diameter particles, respectively, the best separation efficiencies to date, as reported in the literature. For this technology to be feasible for higher flow rate applications, devices may need to be connected in parallel; however, the relatively large footprint of spiral channels will make such assemblies quite large.

Recently, investigators have begun to study the feasibility of using three-dimensional helical channels for particle separation. Unlike planar spiral channels, the radius of curvature is constant throughout a helical channel. Since the Dean drag force is a function of channel curvature, maintaining a constant curvature may yield better control of particle separation along the channel length. In contrast to planar channels, fluid in a helical channel can be exposed to significant momentum exchange along the helix axis, resulting in complex secondary flows and distorting the Dean vortices in channels with a large helical pitch. To minimize this distortion, the helical pitch should be minimized. A numerical analysis will investigate this effect in an upcoming paper by our group.²⁷

To date, the only successful application of helical channels for size-based particle separation and sorting was in a channel with an outer radius of 15.5 mm made using stereolithography which was reported by Lee et al.²⁸ In that study, free magnetic nanoparticle clusters (MNCs) and MNCs bound with Escherichia coli with diameters of 200 nm and 1 μm, respectively, were separated using an inlet flow rate of 5 ml/min and a sheath flow rate of 5 ml/min. The sheath flow was required to move the 200 nm particles to the wall furthest from the helical axis so that they became entrained in the Dean vortices, while the 1 μm particles migrated toward the channel wall closest to the helix axis. Without the sheath flow, the 200 nm particles circulated throughout the entire channel cross section and the device was not capable of separating particles. Paiè et al.²⁹ used femtosecond laser irradiation followed by chemical etching to fabricate a low aspect ratio helical channel with a rectangular cross section (80 μm wide and 50 μm deep) and a helical radius of 80 μm in a 20 × 20 × 1 mm³ fused silica glass substrate. The purpose of the device was to focus 15 μm polystyrene beads at a flow rate of 0.3 ml/min into a single stream. However, focusing was not achieved because two particle streams were created, one in each of the Dean flow vortices that were induced at the center of the channel. Fabrication methods for helical microfluidic devices with circular cross sections have been developed for PDMS using soldering wire³⁰ and nylon thread³¹ for devices with helical radii in the range of 300–500 μm and cross-sectional diameters of 50–280 μm. However, these devices were designed to mimic biological environments, such as artificial blood vessels, and particle separation was not demonstrated. Jung et al.³² used a flexible PDMS channel wrapped around a rod to demonstrate the separation of 26 μm and 15 μm, and 26 μm and 10 μm diameter particles in two channels, with rectangular cross sections (100 μm wide and 400 μm deep) and inner channel diameters of 4 mm and 14 mm at flow rates of 1.5 and 3.0 ml/min. However, the separation efficiency through separate outlets was not reported and the separation distance between particle streamlines was small for each configuration (min. separation: 0 μm and max. separation: 70 μm). The 26 μm particles migrated toward the wall nearest the helix axis and the 15 μm and 10 μm particles were entrained in the Dean vortices in the center of the channel. As suggested by Guan et al.,¹⁵ the separation performance of the device can be improved by using a trapezoidal channel cross section, increasing the separation distance of particle streamlines by shifting the Dean vortices to the outer channel wall. As a result, the focusing and separation of small particles, which would not undergo inertial migration in a rectangular channel, may be achieved using a trapezoidal channel with similar dimensions. The capability of separating smaller particles in a larger channel makes the channels less prone to clogging and reduces the pressure drop through the channel, thus reducing the pumping requirements. Asghari et al.³³ used flexible PDMS wrapped around a rod to demonstrate streamlines for 6 μm particles in rectangular cross section helical channels (50 μm wide and 200 μm deep) with an inner channel diameter of 6 mm and helical pitches of 4 mm and 8 mm. Focusing was not achieved with a helical pitch of 4 mm, and particles were only focused at the center of the 8 mm pitch channel at flow rates between 0.33 and 0.67 ml/min. In both above-mentioned works using PDMS, the outlet ports were tangent to the helical channel, thus resulting in a relatively large overall device footprint. Therefore, despite the potential biotechnological utility of sheath-free particle separation in small-footprint helical trapezoidal microchannels with a small pitch, no such technology exists to date.

This present paper describes a sheath-free, helical microfluidic device with a trapezoidal channel cross section for inertial microfluidics that is fabricated using abrasive jet micromachining (AJM). AJM, which uses abrasive erodent particles in a high-speed air jet to micro-machine various materials, has been used to fabricate helical micro-channels in a 2–5 mm diameter glass and polymethylmethacrylate (PMMA) rods.³⁴ Steel springs were used as contact masks to shield the spaces between the channels from the erosive jet, producing helical channels with aspect ratios up to 1.2, and channels with widths of hundreds of micrometers. AJM has not yet been used to fabricate helical microchannels for a particle separation device, which is the focus of the present work.

In comparison with spiral channel devices having a rectangular cross section, the present devices with helical channels and a trapezoidal cross section may offer advantages for use in high-flow rate applications through parallelization because they have a smaller device footprint, they can separate smaller particles in a larger channel, and the constant radius of curvature generates an unchanging flow field. The only successful implementation of a helical channel for inertial particle separation and sorting had a relatively large device radius and required the use of an additional sheath flow at the device inlet.²⁸ The present paper presents an in-line inertial particle separation device featuring a helical channel with a trapezoidal cross section and a small pitch fabricated with AJM on a 4.76 mm diameter PMMA rod using wire wrapping to produce a novel contact mask. Separated particle streams were collected through novel outlet ports that intersected the channels at different locations and were parallel to the helix axis to reduce the device footprint. Two diameters of polystyrene microspheres were separated without the use of a sheath flow, in agreement with the predictions of an accompanying computational fluid dynamics (CFD) model.

II. MATERIALS AND METHODS

A. Device fabrication

The helical micro-channels were machined into the outer surface of a PMMA rod with a nominal diameter of 4.76 mm (McMaster-Carr, Douglassville, GA, USA). PMMA was chosen as the rod material for its ductility, which results in relatively steep channel sidewalls compared to more brittle materials when machined using AJM.³⁵

To accurately define the channel width during AJM, a stainless steel rectangular wire with dimensions of 0.254 × 0.508 mm (Radcliff Wire Inc., Bristol, CT, USA), with the long face against the rod, was used as a contact mask. The wire was wrapped on the rods using a lathe rotating at 125 rpm. To produce consistent wire spacing (mask opening), a custom jig in the tool holder was used to feed the wire at a specified pitch along the length of the rod. The pitch of the channel was determined by the wire winding pitch on the lathe. The pitch must be larger than the width of the wire in order to allow for a mask opening; therefore, the width of the channels was limited by the selected pitch on the lathe and the width of the wire. The smallest possible winding pitch settings were used to minimize the helical pitch and width of the channel, thus minimizing the distortion of the Dean vortices and minimizing the hydraulic diameter, D_h, to increase the inertial lift force acting on the particles, as will be discussed in Sec. II C. Consequently, the channel depth, expressed in terms of the aspect ratio, AR, was the principal variable in the fabrication of three test device geometries. The ends of the wire were clamped to the rod with two-piece aluminum shaft collars (McMaster-Carr, Douglassville, GA, USA). Approximately 80 mm of the rod was wrapped in this manner to allow for multiple devices to be cut from each rod. Vinyl tape was wrapped on sections of the rod to prevent unwanted erosion and to control the lengths of the channels.

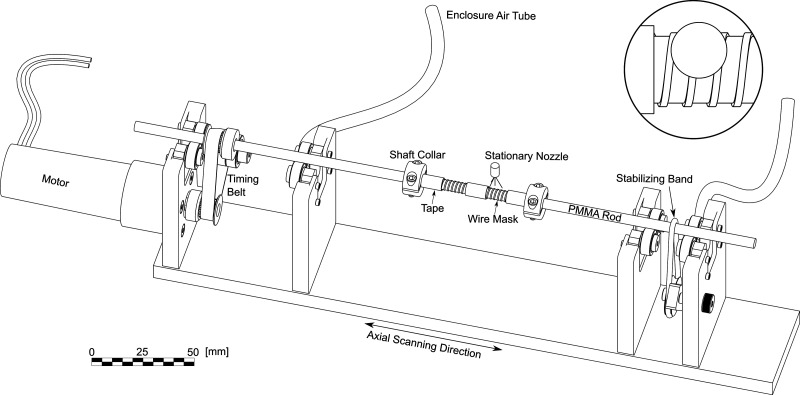
A miniature lathe was designed to rotate the rod under the abrasive jet during the AJM process, as shown in Fig. 1. An acrylic enclosure (not shown in the figure) was pressurized to 40 kPa to prevent abrasive particles from damaging the lathe components. A computer-controlled DC motor was used to drive the rod at 500 rpm (verified with a digital laser tachometer, accurate to ±0.05%) through a timing belt with identical pulleys on the motor shaft and the rod. The rod was supported by pairs of sealed ball bearings, and a second rubber band was used to stabilize the opposite end of the rod.

FIG. 1.

Schematic of the abrasive jet micromachining setup. Components are shown to scale except for the AJM nozzle which is enlarged. The inset image shows the nozzle offset relative to the rod axis.

The lathe was clamped to a computer-controlled linear stage to move the masked rod below a fixed round nozzle with a diameter of 0.760 mm, which was mounted 10 mm away from the rod. The erosion of ductile materials such as PMMA occurs due to plastic deformation and cutting wear, where erosion efficiency is increased at shallower impact angles.³⁶ Therefore, to increase the erosion rate by making the particle rod impact angle closer to the optimum value of 25°,³⁵ the nozzle axis was offset from the rod axis by 1.4 mm. The lathe moved at a scan speed of 0.2 mm/s relative to the stationary nozzle. The channel cross section shape was limited to that naturally produced by the AJM process. As a result of increased erosion efficiency at shallow impact angles, inclined sidewalls erode quickly to produce a trapezoidal channel with steep sidewalls. Further discussion of the effect of process parameters on the resulting channel geometry is provided by Nouhi et al.³⁴ The depth of the channels was controlled by the number of machining passes. A device with channel dimensions of 230 × 640 μm was machined with 15 passes using a contact mask wrapped with a 0.6 mm pitch, resulting in an initial mask opening of 92 μm. Devices with dimensions of 150 × 465 μm, 160 × 760 μm, and 168 × 883 μm were machined with 15, 17, and 19 machining passes, respectively, using a contact mask wrapped with a 0.575 mm pitch, giving an initial mask opening of 67 μm. Since the channel width was maintained at the practical minimum, the number of machining passes, and thus AR, was varied to improve device performance. Channel dimensions were chosen based on the experimental results that will be discussed in Sec. III A. Note that the channel widths for a given contact mask pitch were wider than the initial mask opening and increased with additional machining passes due to the additional erosion of the mask.

The abrasive jet was produced with an AccuFlo AF10 Micro-Abrasive Blaster (Comco Inc., Burbank, CA, USA). Aluminum oxide (Al₂O₃) powder (Comco Inc., Burbank, CA, USA) with a mean diameter of approximately 10 μm was delivered with a constant air pressure of 200 kPa and a powder mass flow rate of 2.2 g/min. Particles were taken from the bulk packages using the quartering method suggested by ASTM to ensure the correct size distribution.³⁷ Process repeatability was improved and the mass flow rate was measured by the processes and techniques described by Ghobeity et al.:³⁸ sacks of desiccant were placed in the sealed powder storage bottles, the particles within the pressurized blasting chamber were stirred continuously, and the powder level was maintained above 2/3 of the hopper volume.

Individual devices with a length of 13 mm were separated using a cut-off saw at a distance approximately 3 mm away from each end of the helical channel. Inlet and outlet ports were drilled into the end faces of the device to allow 20-gauge needles to be inserted parallel to the rod axis, maintaining a small device footprint (Fig. 2). Each port consisted of a 0.91 mm hole to hold and position the 20-gauge needles, with a smaller central hole leading to the helical channel. These smaller central holes were 0.61 mm in diameter in the inlet port and the second outlet port, to closely match the inner diameter of the needles and were placed near the beginning and end of the helical channel. The first outlet port was laterally offset and parallel to the second outlet port, intersecting the inner wall of the channel one half-turn upstream (Fig. 2). A smaller central hole of 0.34 mm was used for the first outlet to increase the flow resistance relative to the larger second outlet, thereby preventing the flow near the top of the channel from exiting through the first outlet. In this way, the two outlet ports diverted different portions of the particle flow.

FIG. 2.

(a) Schematic of the microfluidic device. The inset shows the intersection of outlet 1 with the helical channel. (b) Image of a fully assembled device, (c) close-up image of outlet ports. The top outlet is outlet 1 with a diameter of 0.34 mm and the bottom outlet is outlet 2 with a diameter of 0.61 mm.

Vinyl electrical tape was pressed onto the machined channels and then peeled off to remove residual dust and debris.³⁹ The channels were then cleaned ultrasonically (Branson 1510, Danbury, CT, USA) in de-ionized water for 15 min. To create a sealed microfluidic channel, clear heat-shrink polyvinylchloride (PVC) tubing with an initial diameter of 6.35 mm and a wall thickness of 0.64 mm (Insultab, Woburn, MA, USA) was placed on the rod and heated in an oven at 85 °C for 10 min. 20-gauge syringe needles were placed in the inlet and outlet ports and the end faces were sealed using an aluminum-filled epoxy (Hy-Poxy, Hilton Head Island, SC, USA). During the particle separation experiments, Tygon™ tubing was used to connect a 10 ml syringe containing the particle suspension to the device inlet and to the outlets for collecting the separated particles in separate Petri dishes.

B. Device characterization

1. Determination of optimum helical channel geometry

The separation performance of devices with various channel depths and widths fabricated by changing the number of AJM machining passes was studied with wide-field fluorescence microscopy (ZEISS, Oberkochen, Germany) to observe the locations of fluorescent microspheres at a cross section one turn before the channel outlet. Since the purpose of the initial experiments was to observe particle separation within the channel, these devices consisted of only one outlet. A particle solution was prepared by mixing fluorescent orange 26 μm (std. dev. 3.0 μm) and fluorescent green 9.9 μm polystyrene microspheres (Microgenics, Fremont, CA, USA) with excitation/emission wavelengths of 468/508 nm and 542/612 nm, respectively. These particle diameters were chosen as they are a representative of the size range of human cells and have been used in similar studies.^15,23,32 The particles were suspended in de-ionized water with a concentration of 10 000 particles per ml for each particle size. Tween 20 at 0.4 v/v% (Sigma Aldrich, St. Louis, MO, USA) was added to the particle suspension to prevent particle aggregation. A syringe pump delivered the solution containing both particle sizes through the channel at flow rates of 0.5–2.0 ml/min, with 0.5 ml/min increments between experiments. Imaging was performed using structured illumination microscopy to excite each particle diameter separately through the outer surface of the heat-shrink tubing, which was cleaned with isopropyl alcohol to improve image quality.

Sequential images were taken from the bottom to the top of the channel at a focal elevation spacing of 20 μm. To determine the relative particle positions, microspheres were excited at their respective wavelengths, and fluorescence images of the streaks generated by the passing particles were captured by the microscope (Fig. 3). Particle images could only be captured if the particle passed the current focal plane during the 5 ms exposure time of the image. This made the observation of the particle positions within the turns of the channels very time-consuming. As a result, it was a lengthy trial-and-error process to capture focused images of particles, and it was decided to report only the particle positions for 2.0 ml/min at a point in the channel, where the particles were in their final, separated equilibrium positions, as will be discussed in Sec. III A. The streak images were analyzed to determine the number of in-focus particles present at each focal position. Particles were considered in focus for a given image if the full-width half-max (FWHM) intensity of the streak width was less than 10.5 μm for 9.9 μm particles or 28.2 μm for 26 μm particles, and the signal to noise ratio was greater than 2.0 for 9.9 μm particles or 3.0 for 26 μm particles. Full-width half max was defined as the width of the fluorescent streak where the intensity was midway between the noise and the maximum intensity value. The signal-to-noise ratio was defined as the ratio of the peak intensity of a particle track by the average value of the background noise. Once the channel with the best particle separation was identified using fluorescence microscopy, the final particle separation device was fabricated using the optimal AJM process parameters with the addition of the outlet ports shown in Fig. 2.

FIG. 3.

Fluorescent images and fluorescent intensity of adjacent particle streaks defined as in focus and out of focus: (a) 9.9 μm and (b) 26 μm particles. The in-focus 9.9 μm particle (a) has a signal to noise ratio of 3.2 and an FWHM of 10.0 μm. The in-focus 26 μm particle (b) has a signal to noise ratio of 5.4 and an FWHM of 26.3 μm.

2. Evaluation of device performance

To determine the separation efficiency and purity of the outlet streams in the device, the particle solutions used in the above fluorescence experiments were introduced to the device at flow rates of 0.5–3.0 ml/min with increments of 0.5 ml/min. An upper limit of 3.0 ml/min was chosen as the separation efficiency began to decrease with increasing flow rate, as will be discussed in Sec. III D. Three experiments were performed at each flow rate. Particle solutions from each outlet were collected in separate Petri dishes. The device was primed for 2 min with de-ionized water at a flow rate of 1 ml/min prior to the first experiment at each flow rate. Particle solutions then flowed through the channel for 2 min prior to sample collection at intervals of 1 to 3 min, depending on the flow rate. To prevent particle aggregation over time, the collected particle suspension was re-suspended in the Petri dishes and the particles were allowed to settle for 5 min before taking images. A total of 40 images (1250 × 934 μm² field of view) were taken in three rows of 10–15 adjacent images spaced 2–3 mm apart for each experiment. An average of 1129 particles were then sized and counted for each experiment using image analysis (ImageJ software). Figure 4(a) shows a sample image from outlet 1, where there was a predominance of large particles. It is noted that the population of large particles displayed a significant fraction that were smaller than the nominal diameter of 26 μm. Figure 4(b) shows a sample image from outlet 2, where there was a predominance of small particles with a few larger ones.

FIG. 4.

Particle solutions at (a) outlet 1 showing the predominance of 26 μm particles, and (b) outlet 2, for a flow rate of 1.5 ml/min showing mostly 9.9 μm particles.

C. Operating principle and numerical simulation

The equilibrium position of a particle in a helical channel is determined by the balance between the shear-gradient lift force and the Dean drag force. Due to the parabolic nature of the velocity profile, a relatively large particle flowing through a microchannel will experience a lift force created by the shear gradient across the particle. This shear-induced lift force directs the particle toward the closest channel wall in the direction with the highest relative velocity between the particle and the flow. However, the particle will also interact with the walls of the microchannel, increasing the pressure between the particle and the wall as it approaches the wall, thus generating an opposing lift force, which tends to move the particle toward the center of the channel. The resultant of these two lift forces can be approximated by the following expression:^12,40

$$F_L=C_L{\displaystyle \frac{\rho U_{max}^2{a}^4}{D_h^2},}$$ (1)

where the lift coefficient C_L is a function of particle position in the channel and the fluid Reynolds number, ρ is the fluid density, U_max is the maximum fluid velocity in the channel, a is the particle diameter, and D_h is the channel hydraulic diameter.

Dean drag forces result from secondary flows created in curved channels as the fluid with the highest momentum, at the center of the channel, moves toward the outer wall as it travels through a curve. This generates a pair of counter-rotating vortices perpendicular to the main channel flow.⁴¹ The strength of this secondary flow is characterized by the Dean number, De,

$$De=Re\sqrt{{\displaystyle \frac{D_h}{2R}}},$$ (2)

where R is the radius of curvature of the channel centerline and Re is the Reynolds number, defined using the average fluid velocity in the channel, U, as

$$Re={\displaystyle \frac{\rho U{D}_h}{\mu }.}$$ (3)

This Dean flow imposes a drag force on the particles which tends to move them toward the outer wall of the channel, which can be approximated with the following expression:¹²

$$F_D=3\pi \mu U_{Dean}a,$$ (4)

where μ is the fluid viscosity and U_Dean is the average Dean flow velocity given by

$$U_{Dean}=1.8\times {10}^{-4}D{e}^{1.63}.$$ (5)

The inertial force ratio, R_f, expresses the relative magnitude of the net lift force and the Dean drag force acting on a particle in planes normal to the channel axis as

$$R_f={\displaystyle \frac{F_L}{F_D}.}$$ (6)

If the force ratio R_f  ∼ 1, an equilibrium position exists in the channel that is a function of the particle diameter. If $R_f\gg 1$ for a given particle diameter, the lift force will dominate, and those particles will tend to move to the channel wall closest to the helix axis. If $R_f\ll 1$, the Dean drag force will dominate and the particles will tend toward the centers of the Dean vortices near the outer wall. In the present device, the channel was designed such that the equilibrium position for the larger particles having R_f  ∼ 1 was close to the inner wall, and smaller particles having $R_f\ll 1$ were entrained by the Dean vortices close to the outer wall.

The flow field for the helical channel was calculated using the CFD software Fluent 19.2 (ANSYS Inc., Canonsburg, PA, USA). The fluid density and viscosity were set to those of water. A constant inlet velocity was used to simulate fluid Reynolds numbers of 5, 25, 50, 75, and 100, with an outlet condition of zero pressure. An incompressible laminar flow model was used since no simulation exceeded a Re of 100. The models were iterated until all residuals were below 10⁻⁶ at steady state. To validate the separation capability of the present device, particle trajectories were simulated in the calculated flow fields using the Lagrangian discrete phase model, as described in the ANSYS Fluent Theory Guide.⁴² Since particle concentrations were very low (<1%), particle–particle interactions were neglected. The particle density was set equal to the fluid density since the polystyrene particles were assumed to be neutrally buoyant. Particle–wall interactions were assumed to be perfectly elastic, thus a coefficient of restitution of 1 was used. Since the Lagrangian discrete phase model did not include inertial microfluidic forces such as the shear-gradient lift force, a custom code was added to incorporate the force in Eq. (1). A detailed explanation of the simulations and the implementation and validation of the custom code is found in the supplementary material.

III. RESULTS AND DISCUSSION

A. Fluorescence microscopy results

Three different devices were analyzed for particle separation using wide-field fluorescence microscopy;, i.e., channels with width and depth dimensions of 230 × 640 μm (AR = 2.8), 150 × 465 μm (AR = 3.1), and 160 × 760 μm (AR = 4.8). An average of 40 particles were examined in each channel to obtain an estimate of the separation capability. Figure 5 shows the normalized spatial distribution of observed particles at one turn from the outlet of the helical channels at a flow rate of 2 ml/min, where 0 and 1 represent the wall closest to the rod axis and shrink fit tubing, respectively. All particles in the AR = 2.8 channel appeared to be entrained in the Dean vortices and were therefore not separated. The channels with AR = 3.1 and 4.8 demonstrated progressively better separation capability as AR increased. In addition to these effects of increasing the channel depth an upcoming paper²⁷ will show: (i) that the separation distance between large and small particle streams is increased by decreasing channel width, increasing the channel depth, and minimizing the channel pitch; (ii) that the effect of increasing channel cross section taper angle is a shift of larger particles toward the Dean vortices; and (iii) that the effect of decreasing the diameter of the large particles causes them to shift toward entrainment in the Dean vortices. Although the same mask width was used for both the AR = 3.1 and 4.8 devices, the 17 machining passes required for the deeper channel (AR = 4.8) created a slight increase in the width due to additional mask erosion compared with the AR = 3.1 device which required 15 machining passes. To further increase the separation distance between the particles, the actual device used in the final separation experiments had AR = 5.2 (168 × 883 μm², 19 machining passes). The separation capability of the device with AR = 5.2 was confirmed with CFD, as will be described in Sec. III C.

FIG. 5.

Measured particle locations in various helical channels at a flow rate of 2 ml/min. The points represent the average location of each particle size, and the scatter bars represent the total height range over which particles were observed.

B. Channel characterization

Figure 6 shows an image of a microchannel taken with an optical microscope. To achieve the desired channel dimensions, the rod was machined with 19 passes (machining time of 13 min). The channel dimensions and roughness were measured using a confocal microscope (Sensofar Metrology, Terrassa, Spain) with a spatial resolution of 0.47 μm. The average depth and width of the grooves in the 11-loop channel used in the final separation experiments were 883 μm (standard deviation of 27 μm over 11 measurements) and 168 μm (standard deviation of 7 μm), respectively. Regarding the repeatability of the AJM process, four other devices made on the same day had an average channel depth of 866 μm with a standard deviation of 48 μm.

FIG. 6.

(a) Schematic of the AJM contact mask. The insets show a close-up of gaps at no offset and 1.4 mm offset from the rod axis. The shaded areas represent the portions of the PMMA rod exposed to the abrasive jet. Solid lines represent the upper edges of the masks and dashed lines represent the bottom edges. These are collinear at no abrasive jet offset and are separated at 1.4 mm offset due to the helical wrap of the wire. (b) Optical microscope image of helical channel cross sections, taken in a plane parallel to the rod axis.

As shown in the inset of Fig. 1, to increase the machining erosion rate, the axis of the blasting nozzle was offset from the rod axis by 1.4 mm. However, because of this and the helical path of the wire-wrapped mask, the gaps between the wires of the contact mask were asymmetric (Fig. 6), causing a small asymmetry in the machined channel such that the base of the channel was offset by 30 μm from the center of the top face of the channel. Only in the case of zero offset between the nozzle axis and the rod centerline was the gap between the masking wires symmetric about the nozzle axis, and then strictly for abrasive particles traveling on the axis. Nevertheless, the degree of asymmetry in the channel cross section was negligible in the present devices.

To determine the channel roughness, additional channels were machined using identical parameters and sectioned to expose a channel sidewall. Lengths of 5 mm were analyzed using the confocal microscope with a cut-off wavelength of 250 μm.⁴³ The average roughness was measured to be 0.4 μm on the sidewalls.

C. CFD results

A 10-loop helical channel, with the dimensions of the channel used in the final separation experiments (168 × 883 μm, taper angle of 3.5°, helical pitch of 575 μm) with a total length of 100 mm was modeled in SolidWorks 2018 (Dassault Systèmes, Vélizy-Villacoublay, France). A mesh independence study was conducted to find an optimal fluid domain average cell size of 1887 μm³, giving a total of 6.732 × 10⁶ quadrilateral cells. The Dean flow field was extracted in the final loop of the channel, in the plane normal to the local channel axis (i.e., the true channel cross section). Figure 7 shows the typical secondary flow vectors and the axial flow speeds from the numerical simulation.

FIG. 7.

CFD simulation results at a Re = 50 of the AR = 5.2 device. Large arrows represent inertial microfluidic forces acting on the large particles in the plane normal to the channel axis. Vectors represent the direction of Dean flow. The velocities of the axial flow are indicated by the shading. Particles represent approximate locations of 26 μm and 9.9 μm based on experiments.

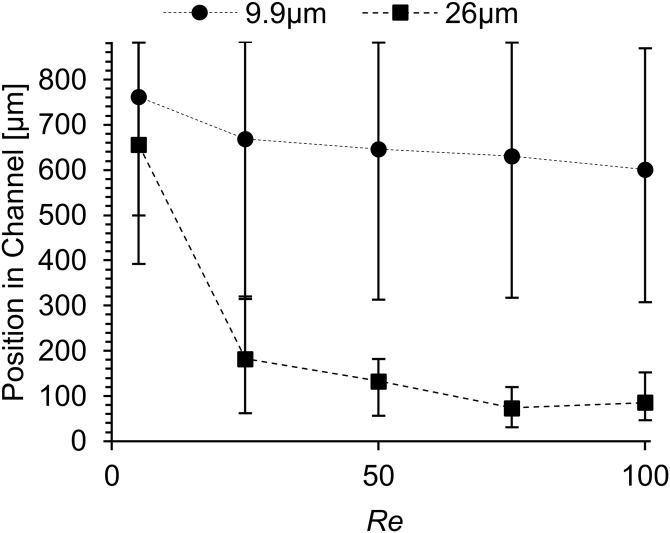
The CFD particle separation results are shown in Fig. 8, where each data point represents the average location of the specified particle size at the outlet, and the scatter bars represent the range of elevations in which particles were present. Fluorescence microscopy particle elevation results for the AR = 4.8 device at Re = 38 and Re = 76 were used to tune the particle trajectory model, shown in Fig. S1 of the supplementary material. The resulting model was then used to predict the approximate equilibrium positions for particles in the AR = 5.2 device.

FIG. 8.

CFD predictions of particle positions measured from the bottom of the channel (closest to rod axis) at the end of the 10-loop AR = 5.2 helical channel. The points represent the average location for each particle size and the scatter bars represent the range in elevation in which 95% of particles were present.

As expected, there was no particle separation predicted at low Re since the inertial lift forces were too small compared with the Dean drag force. As Re increased, the particles began to separate and adopt different equilibrium positions in the channel. This resulted from the growing influence of the inertial lift force on the 26 μm particles with increasing Re, resulting in a compact stream near the bottom of the channel (closest to the rod axis). In contrast, due to the size dependence of the inertial lift force, the 9.9 μm particles were subjected to relatively weak inertial lift forces relative to the drag imposed by the secondary flow. As a result, the 9.9 μm particles were entrained in the Dean vortices with their mean location at the vortex cores, but with trajectories that spanned a relatively large range of channel positions compared to the 26 μm particles, hence the much larger scatter bars for the smaller particles. The range in elevation of the 9.9 μm particles might in the future be decreased by reducing the channel width, thus decreasing the size of the Dean vortices, as will be discussed in an upcoming paper from our group.²⁷ From these results, low separation efficiency is expected at low Re, where most particles of both sizes will pass through outlet 2 since they tend to occupy the top of the channel. Particle separation is expected at Re = 50 and above, where the inertial lift force is sufficiently high for the 26 μm particles to migrate to the bottom of the channel. Sample purity through outlet 1 is expected to increase with increasing Re as the 26 μm particles become concentrated near the bottom of the channel.

D. Device performance

Figure 9 shows the separation efficiency at the two outlets. The separation efficiency of outlet 1 was defined as the percentage of 26 μm particles captured from outlet 1 relative to the total number of 26 μm particles captured through both outlets. Similarly, the separation efficiency of outlet 2 was defined as the percentage of 9.9 μm particles captured through outlet 2 relative to the total number of 9.9 μm particles captured from both outlets.

FIG. 9.

Measurements of outlet separation efficiency for outlet 1 (26 μm) and outlet 2 (9.9 μm). Scatter bars represent the range of measured efficiencies over three experiments.

As predicted in the CFD model, Fig. 9 shows that there was relatively low separation efficiency at low Re. The separation efficiency of both outlets increased to a maximum of approximately 90% at Re = 50, in agreement with the CFD model prediction of distinct streams for each particle size at Re = 50.

It is noted that the apparent performance of any device which is separating two particles on the basis of size is a function of the degree to which the two size distributions are well separated. Widely spaced means and small standard deviations yield a better separation. In the present case, the separation efficiency would improve if the relatively large standard deviation of 3 μm for the 26 μm particles were decreased by, for example, preliminary sieving.

Figure 9 shows that flows with Re > 50 resulted in a gradual increase in the separation efficiency of the 9.9 μm particles, however, the opposite trend was observed for the 26 μm particles. A potential cause for this decrease in separation efficiency was the geometry of the outlet. In traditional spiral channels, the channel is split using a physical barrier into two or more outlets in the direction of the channel. In the present device, the outlet is perpendicular to the helical channel without the addition of physical barriers to guide the particles. As a result, although particles were separated within the helical channel, they could not be collected unless they followed the fluid streamlines from the helical channel to the respective outlet port. At Re > 50, the inertia of the 26 μm particles was sufficient to cause a growing fraction to cross streamlines and bypass outlet 1, resulting in lower separation efficiencies. Introducing a physical barrier at outlet 1 would guide the particles along the streamline and through the outlet, preventing them from crossing streamlines and bypassing their intended outlet. In addition, Guan et al.¹⁵ have observed a flow rate threshold of 3 ml/min in their trapezoidal channel after which inertially focused particles become entrained in the Dean vortices, suggesting that a decrease in efficiency is expected at higher flow rates even with the presence of a physical barrier.

Figure 10 demonstrates the purity of each outlet, defined as the percentage of particles intended to exit from a given outlet that were actually collected at the outlet. As Re increased, the purity of outlet 1 increased to approximately 95%, while the purity of outlet 2 increased to a maximum of about 80% at Re = 50. For Re > 50, 26 μm particles began to bypass outlet 1, resulting in a decrease in purity. By exploiting the high purity of outlet 1, there is potential to improve the separation efficiency at higher flow rates by placing additional devices in series.

FIG. 10.

Measurements of outlet separation purity for outlet 1 (26 μm) and outlet 2 (9.9 μm). Scatter bars represent the range of purities measured over three experiments.

IV. CONCLUSIONS

The present paper describes a novel small-footprint helical microchannel capable of size-based particle separation without the use of a sheath flow. The device was fabricated using a novel, low-cost AJM methodology that utilized a steel contact mask to define the microchannels on a 4.76 mm diameter PMMA rod. In-line inlet and outlet ports were added parallel to the rod axis to reduce the device footprint for ease of parallelization. A CFD analysis predicted the separation of 9.9 μm and 26 μm particles in the helical microchannel at various Re, which is in agreement with the trends observed in the experiments.

The present device was capable of a separation efficiency of ∼90% through both outlets at a Re = 50 and a purity of ∼95% through the large particle outlet. The separation efficiency could be improved at higher flow rates by flowing the particle solution from the small particle outlet through the inlet of an identical device in order to collect unseparated large particles, thus exploiting the high purity of the large particle outlet. Additionally, the performance of the outlets at higher flow rates may be improved by introducing physical barriers in the channel near the outlets to prevent the larger particles from bypassing outlet 1. Additional experiments should also be performed to demonstrate cell separation in the present device.

SUPPLEMENTARY MATERIAL

See the supplementary material for a detailed description of the numerical model, including experimental validation and the code used to implement the inertial lift force.

DATA AVAILABILITY

The data that support the findings of this study are available within the article and its supplementary material and can be obtained from the authors upon request.