Enumeration of compact coalescent histories for matching gene trees and species trees

Abstract

Compact coalescent histories are combinatorial structures that describe for a given gene tree G and species tree S possibilities for the numbers of coalescences of G that take place on the various branches of S. They have been introduced as a data structure for evaluating probabilities of gene tree topologies conditioning on species trees, reducing computation time compared to standard coalescent histories. When gene trees and species tree have a matching labeled topology G = S = t, the compact coalescent histories of t are encoded by particular integer labelings of the branches of t, each integer specifying the number of coalescent events of G present in a branch of S. For matching gene trees and species trees, we investigate enumerative properties of compact coalescent histories. We report a recursion for the number of compact coalescent histories for matching gene trees and species trees, using it to study the numbers of compact coalescent histories for small trees. We show that the number of compact coalescent histories equals the number of coalescent histories if and only if the labeled topology is a caterpillar or a bicaterpillar. The number of compact coalescent histories is seen to increase with tree imbalance: we prove that as the number of taxa n increases, the exponential growth of the number of compact coalescent histories follows 4ⁿ in the case of caterpillar or bicaterpillar labeled topologies and approximately 3.3302ⁿ and 2.8565ⁿ for lodgepole and balanced topologies, respectively. We prove that the mean number of compact coalescent histories of a labeled topology of size n selected uniformly at random grows with 3.3750ⁿ. Our results contribute to the analysis of the computational complexity of algorithms for computing gene tree probabilities, and to the combinatorial study of gene trees and species trees more generally.

1. Introduction

The study of the relationships between gene trees, which represent the histories of individual genomic regions, and species trees, representing the histories of populations of organisms, has generated new combinatorial structures (Maddison, 1997; Degnan and Salter, 2005; Rosenberg and Tao, 2008; Than and Nakhleh, 2009; Degnan et al., 2012; Wu, 2012, 2016; Degnan and Rhodes, 2015). Among these structures are coalescent histories, structures that for a given gene tree topology G and species tree S represent possible pairings of the coalescences in G with the branches of S on which the coalescences take place (Degnan and Salter, 2005; Rosenberg, 2007). The use of coalescent histories in calculations of the probability Prob(G|S) (Degnan and Salter, 2005) has motivated the study of the number of coalescent histories possible for a given gene tree topology and species tree topology (Degnan and Salter, 2005; Rosenberg, 2007, 2013; Than et al., 2007; Rosenberg and Degnan, 2010; Disanto and Rosenberg, 2015, 2016). A variety of enumerative results have been derived, primarily in the case in which gene trees and species trees have a matching labeled topology.

Building on the approach of Degnan and Salter (2005), Wu (2016) introduced compact coalescent histories as a tool for simplifying gene tree probability computations (see also Degnan and Rhodes, 2015). Given G and S, Wu’s “CompactCH” algorithm computes Prob(G|S) by grouping into equivalence classes two (or more) coalescent histories h₁ and h₂ when, in each branch of S, the numbers of coalescences of G specified by h₁ and h₂ are the same. The resulting equivalence classes are the compact coalescent histories, or compact histories for short. Certain intermediate computations in the probability formula of Degnan and Salter (2005) are identical for all coalescent histories with the same compact history, simplifying the probability computation.

Compact coalescent histories appear in sets over which sums are computed (e.g. Eq. 5 of Wu (2016)). Hence, for a given G and S, similarly to the way that evaluation of Prob(G|S) by the method of Degnan and Salter (2005) depends on the number of coalescent histories, the complexity of the evaluation of Prob(G|S) in CompactCH is affected by the number of compact coalescent histories possible for G and S. By studying this number, Wu (2016) showed that when the size of the species tree is fixed and multiple gene lineages can be sampled per species, CompactCH calculates gene tree probabilities in polynomial time in the number of gene lineages. The approach of Wu (2016) exchanges the slower summation of Degnan and Salter (2005) over all coalescent histories with a given compact history for a faster computation that requires only the number of such coalescent histories.

Here, permitting the size of the species tree to grow, we investigate the number of compact coalescent histories for gene trees and species trees with a matching labeled topology G = S = t. In particular, we measure how the growth of the number of compact coalescent histories of t is affected by its number of taxa and its topology. In Section 3, we present a recursion for the number of compact coalescent histories of a matching gene tree and species tree. Extending a result of Wu (2016)—whose supplement reported that when t has a caterpillar topology of size |t| = n, the number of compact coalescent histories of t equals the number of coalescent histories of t—we show that the number of compact coalescent histories of t equals its number of coalescent histories if and only if t is a caterpillar or bicaterpillar topology. Next, in Section 4, we study the number of compact coalescent histories when t belongs to each of several families of trees with different degrees of imbalance. We demonstrate that unlike in the caterpillar and bicaterpillar cases, the number of compact coalescent histories can be much smaller than the number of coalescent histories when t is not a caterpillar or bicaterpillar. Moreover, we show that when the number of taxa increases, the number of compact coalescent histories grows exponentially faster in the families of more unbalanced trees. Section 5 reports the mean number of compact coalescent histories for a random labeled topology t of given size drawn under a uniform distribution. Our results can assist in relating the complexity of algorithms for computing gene tree probabilities based on compact coalescent histories to those that use an evaluation based on other combinatorial structures, such as coalescent histories and ancestral configurations (Wu, 2012; Disanto and Rosenberg, 2017, 2018).

2. Preliminaries

We investigate the number of compact coalescent histories for rooted binary labeled trees. We recall basic features of tree structures in Section 2.1. In Section 2.2, we give properties of generating functions that will be used for counting compact coalescent histories.

2.1. Labeled toplogies

A bifurcating rooted tree with labeled taxa (Fig. 1A) is termed a labeled topology, or “tree” for short. The size of a labeled topology t is its number of taxa |t|. We denote by [t] the unlabeled topology, or “tree shape,” underlying t. This shape is obtained by ignoring labels for the taxa of t.

Figure 1:

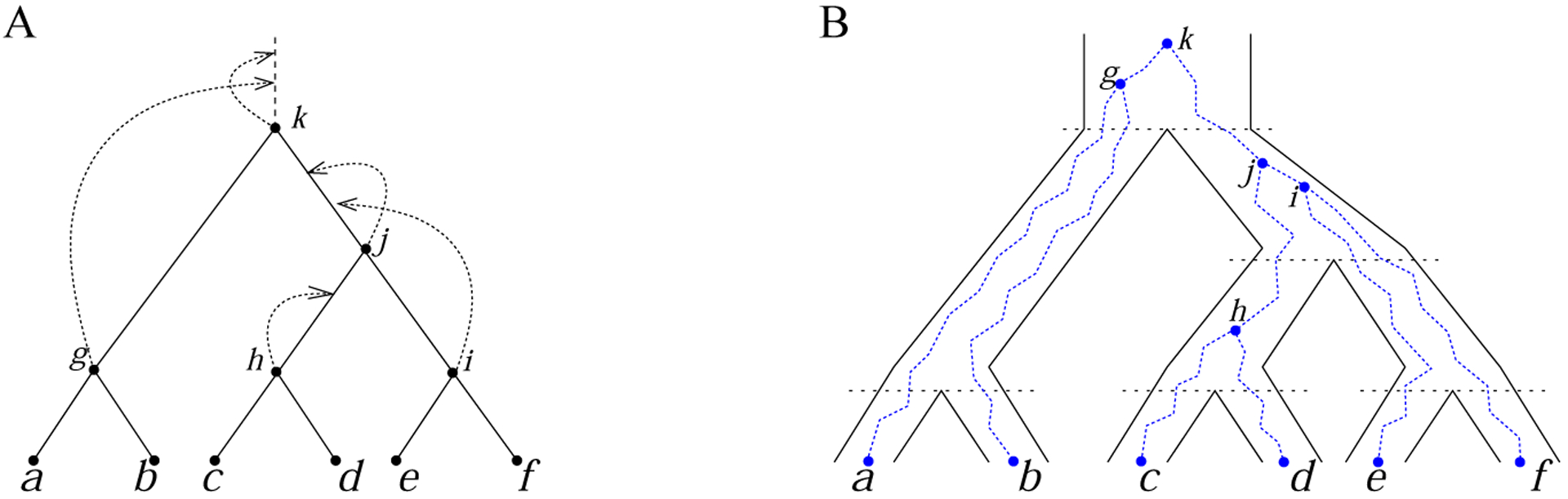
Coalescent histories for a gene tree and a species tree with a matching labeled topology G = S = t. (A) A coalescent history. Arrows map the internal nodes of t = ((a, b), ((c, d), (e, f))) to the branches of t. (B) The gene tree topology G = t realized in the matching species tree S = t according to the coalescent history in (A). The mapping in (A) specifies the branches of the species tree (thick lines) where the coalescent events of the gene tree (thin lines) take place.

Without loss of generality, we assume an alphabetical order a ≺ b ≺ c ≺ … over the set {a,b,c, …} of possible labels for the taxa of a labeled topology, using the first n labels for the leaves of a tree of size n.

As it is sometimes important to refer to internal nodes of a labeled topology, it is useful to assign distinct but arbitrary labels to these internal nodes. Unlike the taxon labels, the internal node labels need not be ordered. The labeling of internal nodes is merely a convenience that does not distinguish different trees, and only the taxon labels are important for characterizing if two labeled topologies with the same unlabeled topology are distinct. In enumerating labeled topologies, only leaves are considered to be labeled.

We let T_n be the set of labeled topologies of size n. We will require two results concerning T_n.

Proposition 1 (Felsenstein, 1978) For n ≥ 1, the cardinality of T_n is (2n)!/[2ⁿ(2n − 1)n!].

Proposition 2 (Flajolet and Sedgewick, 2009, Example II.19) The generating function $T(z)=\sum _{t:|t|\ge 1}{z}^{|t|}/|t|!={\sum }_{n=1}^{\infty }|T_n|z^n/n!$ of the sequence |T_n|/n! satisfies $T(z)=1-\sqrt{1-2z}$.

2.2. Exponential growth and analytic combinatorics

One of our main goals is to evaluate features of the growth of sequences of non-negative integers. Following Flajolet and Sedgewick (2009), we recall a number of results concerning the asymptotic behavior of sequences.

Definition 3 A sequence of non-negative numbers s_n is said to have exponential growth kⁿ, or equivalently, to have exponential order k, when limsup_n→∞ [(s_n)^1/n] = lim_n→∞ [sup_m≥n [(s_m)^1/m]] = k.

Equivalently, this relation can be written s_n = kⁿg(n), with g a subexponential factor. If the value k of the limit strictly exceeds 1, then sequence s_n grows exponentially in n, and we say that its exponential order is k.

By these definitions, if the exponential order k_s of a sequence s_n is strictly smaller than the exponential order $k_{\tilde{s}}$ of a sequence ${\tilde{s}}_n$, then the sequence of ratios $s_n/{\tilde{s}}_n$ converges to 0 exponentially fast as ${\left(k_s/k_{\tilde{s}}\right)}^n$. If instead s_n and ${\tilde{s}}_n$ have the same exponential order, then the increase or decrease of the sequence of ratios $s_n/{\tilde{s}}_n$ is at most polynomial in n, and we write $s_n\bowtie {\tilde{s}}_n$.

Some of our results will be obtained by applying methods of analytic combinatorics that concern singularities of generating functions (Sections IV and VI of Flajolet and Sedgewick (2009)). More precisely, entries of a sequence of integers (s_n)_n≥0 can be seen as coefficients ([zⁿ]f)_n≥0 of the power series expansion $f(z)={\sum }_{n=0}^{\infty }{s}_n{z}^n$ at z = 0 of a function f(z), the generating function of the sequence. Considering z as a variable in the complex plane $ℂ$, a correspondence exists between the dominant singularity z = ρ of f(z)—the singularity of smallest distance from the origin in $ℂ$—and the exponential growth of the coefficients s_n. In particular, for n → ∞, the exponential order of sequence s_n is the inverse of the modulus of the dominant singularity of f(z),

$$s_n=\left[z^n\right]f(z)\bowtie {\left(\frac{1}{\rho }\right)}^n.$$ (1)

For instance, consider the generating function T(z) of the sequence |T_n|/n! (Proposition 2). Due to the branching character of the square root function $\sqrt{1-2z}$, z = 1/2 is the point of smallest modulus in the complex plane where T(z) fails to be analytic. Hence, z = 1/2 is the dominant singularity of T(z). Using eq. 1, we have

$$\frac{|T_n|}{n!}\bowtie 2^n.$$ (2)

3. Compact coalescent histories for matching gene trees and species trees

In this section, we define compact coalescent histories, and we provide a characterization of the compact coalescent histories of a gene tree and species tree (Section 3.1). Next, we report a recursion for the number of compact coalescent histories of a matching gene tree and species tree (Section 3.2), using this recursion to analyze the number of compact coalescent histories for small trees (Section 3.3). We provide a characterization of the trees for which the numbers of coalescent histories and compact coalescent histories are the same (Section 3.4).

We consider a gene tree labeled topology G and a species tree labeled topology S with the same set of leaf labels. The gene tree labeled topology represents the sampling of a single gene lineage in each of n ≥ 1 species.

A partial order can be placed on nodes and branches of a tree, where we denote k₂ ≤ k₁ for a pair of nodes k₁, k₂ if k₂ is descended from k₁ in t; we write k₂ < k₁ if k₂ is descended from k₁ and k₁, k₂ are distinct. We also write b₂ ≤ b₁ if branch b₂ is descended from b₁ in t, and b₂ < b₁ if in addition, b₁, b₂ are distinct. A node or branch is trivially descended from itself.

Let t_k be the subtree of t generated by node k, including the branch immediately ancestral to k. Let |t_k| be the number of leaves in t_k; we identify node k with the branch immediately ancestral to it, so that we also describe t_k as the subtree generated by this branch.

3.1. A characterization of compact coalescent histories

We now formally define compact coalescent histories, recalling the definition of coalescent histories (e.g. Than et al., 2007; Rosenberg and Degnan, 2010).

Definition 4 Given a gene tree G and a species tree S, a coalescent history of (G, S) is a function h from the internal nodes of G to the internal branches of S, satisfying two conditions: (i) for each internal node k in G, all leaves descended from node k in G descend from branch h(k) in S; (ii) for all pairs of internal nodes k₁ and k₂ in G, if k₂ is a descendant of k₁ in G, then branch h(k₂) is descended from branch h(k₁) in S.

Here and in our subsequent analysis, we include the root of S as an internal node, and we consider that a branch b_root of S exists that is ancestral to the root. Note that in condition (ii), h(k₂) is permitted to equal h(k₁).

In the case of a matching labeled topology G = S = t, a coalescent history can be regarded as being associated with the single tree t, and the conditions can be simplified: a coalescent history of t is a function h from the internal nodes of t to the internal branches of t satisfying: (i) for each internal node k in t, node k descends from branch h(k) in t; (ii) for all pairs of internal nodes k₁ and k₂ in t, if k₂ is a descendant of k₁ in t, then branch h(k₂) is descended from branch h(k₁) in t.

Coalescent histories (Fig. 1A) represent the topologically distinct configurations that a gene tree labeled topology G can assume in the branching structure of a species tree labeled topology S (Fig. 1B). A coalescent history specifies a possible list of the species tree branches on which the gene tree coalescent events occur.

Following Wu (2016), an equivalence can be defined over the set of coalescent histories for (G, S).

Definition 5 Consider a relation in which two coalescent histories h₁, h₂ of (G, S) are equivalent when, for each branch b of S, considering all internal nodes k in G, |{k : h₁(k) = b}| = |{k : h₂(k) = b}|. Each equivalence class of this relation is termed a compact coalescent history, or a compact history for short.

In this equivalence relation, h₁ is equivalent to h₂ when, in each branch of S, h₁ and h₂ have the same numbers of coalescent events (Fig. 2A). We represent a compact history of (G, S) by an integer labeling of the internal branches of S, the branch b being labeled by the number ℓ_b of coalescent events in that branch (Fig. 2B). We denote by m = m(h) the number ℓ_root of coalescent events in the root branch b_root of compact history h.

Figure 2:

Equivalence classes of coalescent histories and compact coalescent histories for matching gene trees and species trees. (A) Two coalescent histories of the species tree G = S = t = ((a, b), ((c, d), (e, f))) in the same equivalence class. For each branch of t, the numbers of incoming arrows in the two coalescent histories, representing coalescences on the branch, are the same. (B) The compact coalescent history of the species tree t representing the equivalence class of the coalescent histories depicted in (A). The label for each branch corresponds to the number of incoming arrows in that branch.

Note that from a compact history, the numbers of lineages of G entering the branches of S from below and exiting them above can be extracted. Indeed, in Definition 5, we could instead define h₁ and h₂ to be equivalent if and only if for each branch of S, (i) h₁ and h₂ have the same numbers of entering lineages, and (ii) h₁ and h₂ have the same numbers of exiting lineages (Wu, 2016, Lemma 3.1). This alternative perspective is useful for computing the probability of the set of coalescent histories represented by the compact history, as gene tree probability computations rely on counts of entering and exiting lineages (Degnan and Salter, 2005; Wu, 2016).

Let (ℓ_b)_b be an integer labeling of the internal branches of S, where ℓ_b is the label of branch b. We will also treat the label of a branch of S as the label of its immediate descendant node, so that the labeling is associated with both the internal branches and the internal nodes of S.

For branch b of S, let G_b be the set of all internal nodes k in G with the following pair of properties: (i) k represents the most recent common ancestor in G of a group of two or more taxa descended from branch S_b of S; (ii) all taxa descended from k in G are descended from S_b. |G_b| is the number of such nodes. The set G_b represents the set of coalescences of G that have the possibility of occurring on branch b of S. For the root branch b_root of S, we have |G_root| = |G| − 1.

We can then characterize the labelings (ℓ_b)_b that represent compact histories for (G, S).

Proposition 6 A labeling (ℓ_b)_b of S identifies a compact history h of (G, S) if and only if (i) for all branches b of S other than the root branch, $0\le {\mathcal{l}}_b\le |G_b|-\sum _{b^{\prime }<b}{\mathcal{l}}_{b^{\prime }}$, and (ii) ${\mathcal{l}}_{\mathit{\text{root}}}=|G|-1-\sum _{b\ne \mathit{\text{root}}}{\mathcal{l}}_b$.

Proof First, we show that a labeling (ℓ_b)_b that represents a compact history satisfies (i) and (ii).

For a subtree S_b of S descended from branch b, the sum $\sum _{b^{\prime }\le b}{\mathcal{l}}_{b^{\prime }}$ is the total number of coalescent events in S_b. By definition of a coalescent history, this quantity is bounded above by the number of internal nodes of the gene tree all of whose descendant taxa in G descend from S_b in S, or |G_b|. Removing ℓ_b from the sum and noting that ℓ_b ≥ 0 because ℓ_b is a count, we obtain (i). For the case in which b is the root branch of S, the total number of internal nodes of G all of whose descendant taxa in G descend from S_root in S is exactly |G| − 1, so that the inequality ${\mathcal{l}}_b\le |G_b|-\sum _{b^{\prime }<b}{\mathcal{l}}_{b^{\prime }}$ becomes an equality, and we obtain (ii).

We must now show that any labeling (ℓ_b)_b that satisfies (i) and (ii) represents a compact history. It suffices to demonstrate that at least one coalescent history h lies in the equivalence class represented by (ℓ_b)_b. By postorder traversal of S, proceed through the internal branches of S, for each branch b assigning certain nodes k of G the value h(k) = b in the following manner. (1) If ℓ_b = 0, continue to the next branch of S. (2) If ℓ_b > 0, by postorder traversal of G, proceed through the internal nodes k of G all of whose taxa are descended from b in S. (3) Assign the value h(k) = b to the first node of G encountered that either has no internal node descendants in G or that already has all its descendant internal nodes in G assigned values of h. (4) Continue following (3) until ℓ_b nodes k of G have been assigned h(k) = b.

That this construction produces a coalescent history h can be seen as follows. Because (ℓ_b)_b satisfies (i) by assumption, for each non-root branch b of S, Steps (1)–(4) always find ℓ_b internal nodes of G to which the label b can be assigned: because of the postorder traversal of S, the number of unassigned internal nodes of G descended from b is initially $|G_b|-\sum _{b^{\prime }<b}{\mathcal{l}}_{b^{\prime }}$, and ℓ_b is no more than this quantity by (i). Condition (ii) guarantees that all |G| − 1 internal nodes k of G are assigned a value of h(k), with those unassigned when b_root is reached being assigned h(k) = b_root. Step (1) guarantees that condition (i) of the definition of a coalescent history is respected by h, and Step (2) guarantees that h respects condition (ii) of the definition of coalescent histories. □

In Proposition 6, condition (i) indicates that the maximal number of coalescent events that can happen in an internal branch b of the species tree, other than the root, is given by the difference between the number |G_b| of coalescences of the gene tree that could potentially occur on that branch and the number of coalescent events present in the internal branches descended from b in S. Condition (ii) states instead that the number of coalescences above the root of S is the total number of coalescences in G, or |G| − 1, minus the number of coalescences in the branches below the root. When b is a leaf of S, G_b is empty, as no coalescences occur in the branch above a leaf node. Note that although the definitions of coalescent histories and compact histories consider only the internal branches of S, we can extend the labeling in compact histories to include ℓ_b = 0 for branches b of S immediately ancestral to leaf nodes. Proposition 6 still applies if compact histories are taken to include leaf nodes of S with labels of 0; indeed, by (i), ℓ_b = 0.

Our main interest is in the case of G = S = t. In this case, the number of internal nodes of G that could potentially coalesce on branch b of S is |G_b| = |t_b| − 1, so that we have the following corollary.

Corollary 7 A labeling (ℓ_b)_b of t identifies a compact history h of t if and only if (i) for all internal branches b of t other than the root branch of t, $0\le {\mathcal{l}}_b\le |t_b|-1-\sum _{b^{\prime }<b}{\mathcal{l}}_{b^{\prime }}$, and (ii) ${\mathcal{l}}_{\mathit{\text{root}}}=|t|-1-\sum _{b\ne \mathit{\text{root}}}{\mathcal{l}}_b$.

Compact coalescent histories are closely related to the population histories of Degnan and Rhodes (2015). A compact coalescent history, like a coalescent history, is defined for a pair consisting of a gene tree topology and a species tree topology. A population history in the sense of Degnan and Rhodes (2015) is an integer labeling of the species tree branches that, like a compact coalescent history, tabulates the numbers of coalescences of a gene tree that occur on those branches. However, a population history is defined only given the species tree, and not all population histories of a species tree can represent possible sets of locations for the coalescences of a specified gene tree on that species tree; the population histories of a species tree are exactly the compact coalescent histories associated with the species tree and its matching gene tree.

3.2. Recursion for the number of compact coalescent histories

For a general pair of trees (G, S), the compact coalescent histories can be enumerated by classifying into equivalence classes the coalescent histories listed by the exhaustive recursive enumeration of Rosenberg (2007). In the case of G = S = t, we can provide a recursion for the number of compact coalescent histories itself.

We consider a concept of extended compact coalescent histories, which differ from compact coalescent histories in that it is possible that some of the gene tree coalescences of t have not yet occurred in t, including on the root branch of species tree t; this extension is useful in case t is a subtree of a larger tree (Fig. 3). Let u be the number of coalescences that occur in t, including on its root branch. Let m be the number of coalescences that occur on the root branch of t. The quantities u and m are constrained, with 0 ≤ m ≤ u ≤ |t| − 1. For compact coalescent histories, we have u = |t| − 1, as all coalescences of t occur in t, possibly on the root branch.

Figure 3:

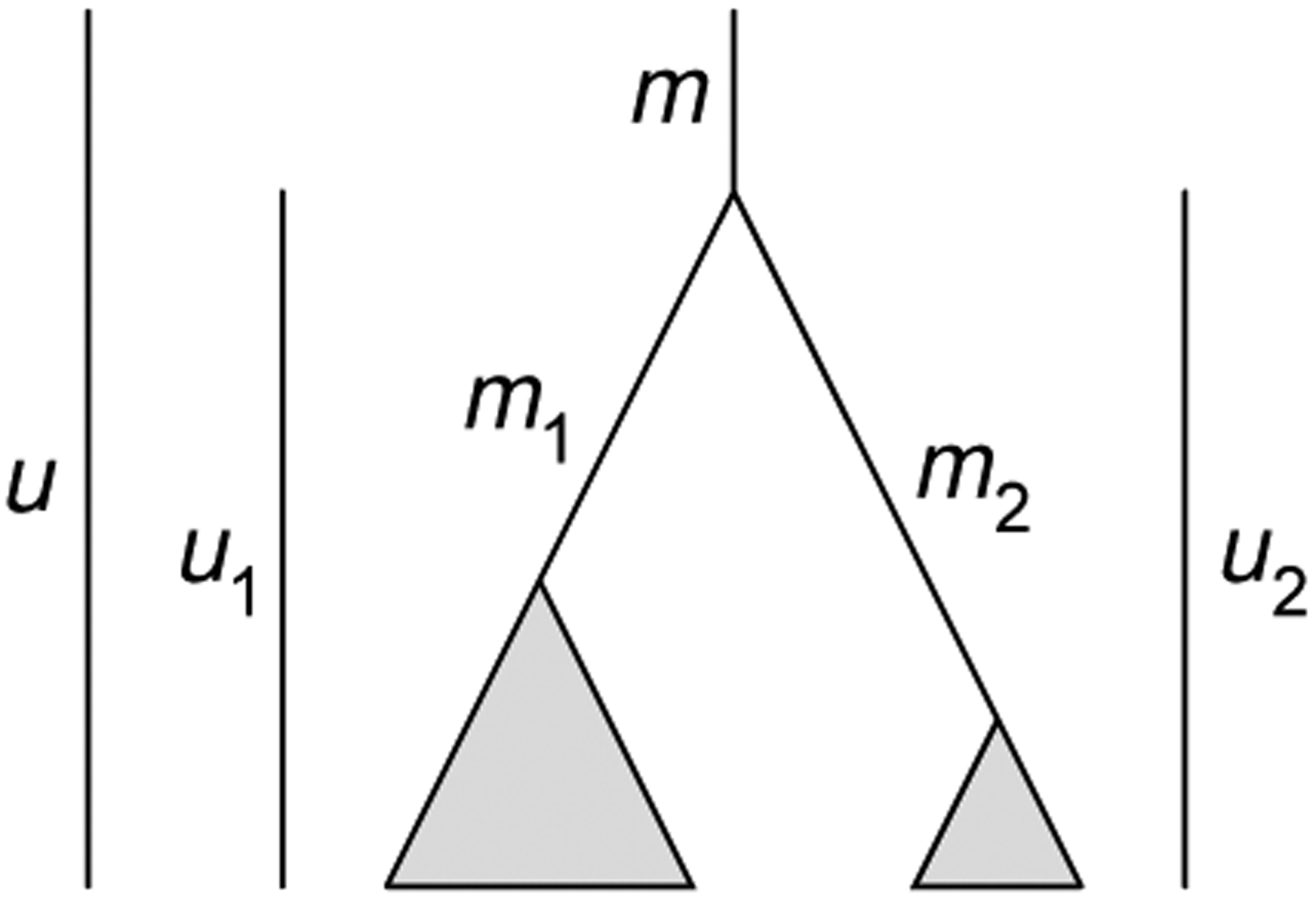
Schematic illustration of quantities in the recursion for the number of compact coalescent histories. The labels m, m₁, and m₂ represent the numbers of coalescences on the root branch of a tree t, the root branch of the left subtree t₁, and the root branch of the right subtree t₂, respectively. The quantities u, u₁, and u₂ represent the total numbers of coalescences in the tree, left subtree, and right subtree, respectively, including coalescences on the associated root branches.

Tree t has “left” and “right” subtrees t₁ and t₂, where we consider these subtrees to include their associated root branches. The quantities u₁, u₂, m₁, m₂, corresponding to the numbers of coalescences of the left subtree, the right subtree, the root branch of the left subtree, and the root branch of the right subtree, respectively, satisfy 0 ≤ m₁ ≤ u₁ ≤ |t₁| −1 and 0 ≤ m₂ ≤ u₂ ≤ |t₂| −1. The total number of coalescences in t is u = u₁ +u₂ +m, as each coalescence of t must occur in the left subtree of t, the right subtree of t, or on the root branch of t.

Let A_t,u,m be the number of extended compact coalescent histories of t in which u coalescences occur, of which m occur on the root branch. By definition of extended compact coalescent histories, A_t,0,0 = 1 for any tree t, as a tree has a single labeling—zeroes on all internal branches—if u = 0 and m = 0 and no coalescences occur. In addition, A_t,u,m = 0 when u,m fail to satisfy 0 ≤ m ≤ u ≤ |t| − 1. Let B_t denote the number of compact coalescent histories for a tree t with |t| taxa, and let B_t,m = A_t,|t|−1,m be the number among these compact coalescent histories in which m coalescences occur on the root branch.

Theorem 8 The number of compact coalescent histories for a tree t with |t| ≥ 2 taxa satisfies

$$B_t=\sum _{m=1}^{|t|-1}{A}_{t,|t|-1,m}.$$ (3)

The number of extended compact coalescent histories for a tree t with |t| ≥ 1 taxa satisfies

$$A_{t,u,m}=\sum _{u_1=\text{max}\left[0,u-m-\left(|t_2|-1\right)\right]}^{\text{min}\left(|t_1|-1,u-m\right)}\sum _{m_1=0}^{u_1}\sum _{m_2=0}^{u-m-u_1}{A}_{t_1,u_1,m_1}{A}_{t_2,u-m-u_1,m_2},$$ (4)

The base cases of the recursion are A_t,0,0 = 1 for the 1-taxon tree, A_t,0,0 = A_t,1,1 = 1 for the 2-taxon tree, and A_t,u,m = 0 when u,m fail to satisfy 0 ≤ m ≤ u ≤ |t| − 1.

Proof Eq. 3 follows from the fact that B_t,m = A_t,|t|−1,m, noting that the number of coalescences on the root branch of a tree with |t| ≥ 2 taxa satisfies 1 ≤ m ≤ |t| − 1.

For Eq. 4, we decompose each extended compact coalescent history for t into an extended compact coalescent history for t₁, an extended compact coalescent history for t₂, and a set of coalescences on the root branch of t. We must consider all assignments of (u₁, u₂, m₁, m₂) that produce an extended compact coalescent history with u total coalescences and m coalescences above the root. For each such assignment, the number of extended compact coalescent histories is $A_{t_1,u_1,m_1}{A}_{t_2,u_2,m_2}$.

To determine permissible values for (u₁, u₂), recall that the total number of coalescences in t₁ and t₂ together is u₁ + u₂ = u − m, so that 0 ≤ u₁, u₂ ≤ u − m. However, u₁ ≤ |t₁| − 1, as at most |t₁| − 1 coalescences occur in t₁, and similarly, u₂ ≤ |t₂| − 1. Hence, if as many coalescences as possible are placed in t₂ so that u₂ is as large as possible, u₁ remains bounded below by u − m − (|t₂| − 1). Once u₁ and u₂ = u − m − u₁ have been specified, (m₁, m₂) satisfies 0 ≤ m₁ ≤ u₁ and 0 ≤ m₂ ≤ u₂.

The nontrivial base case A_t,1,1 = 1 for the 2-taxon tree follows by noting from Corollary 7 that this tree has only a single labeling that represents a compact coalescent history, and that this labeling has u = m = 1. □

Using Theorem 8, we can compute the number of compact coalescent histories for arbitrary trees t by applying Eq. 3, recursively applying Eq. 4 to complete the calculation.

3.3. Number of compact coalescent histories for small trees

For small values of n, we use Theorem 8 to exhaustively compute the number of compact histories for representative labelings of the unlabeled topologies with n taxa. Table 1 reports these numbers of compact coalescent histories for each unlabeled topology of size 2 ≤ n ≤ 7, where an unlabeled topology is taken to have a specific but arbitrary labeling. For the tree shapes considered, the number of compact coalescent histories is always less than or equal to the number of coalescent histories, with equality only when the two root subtrees are caterpillar trees. As we will see, this characterization of the condition for equality of the numbers of compact coalescent histories and coalescent histories will be shown to hold for arbitrary tree size in Section 3.4.

Table 1:

Numbers of compact coalescent histories and coalescent histories for small trees.

Size	Unlabeled topology	Number of coalescent histories	Number of compact coalescent histories	Size	Unlabeled topology	Number of coalescent histories	Number of compact coalescent histories
2		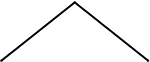1	1	6		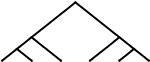25	25
3		2	2	7		132	132
4		5	5	7		138	118
4		4	4	7		130	108
5		14	14	7		112	98
5		13	12	7		113	86
5		10	10	7		106	90
6		42	42	7		84	84
6		42	37	7		84	74
6		37	33	7		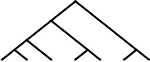74	66
6		28	28	7		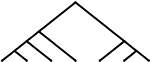70	70
6		26	24	7		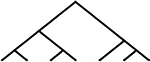65	60

Each unlabeled topology corresponds to a single representative labeled topology t.

From the table, we also observe that the number of compact coalescent histories does not always increase with the number of coalescent histories. The fifth tree shape of size 7 has more coalescent histories than the sixth tree shape of size 7, but the latter has more compact coalescent histories. In Section 4, we will observe this phenomenon on a larger scale, identifying two families of trees of increasing size, ${\mathcal{F}}_1$ and ${\mathcal{F}}_2$, such that the number of coalescent histories grows exponentially faster for trees in ${\mathcal{F}}_1$ than for trees in ${\mathcal{F}}_2$, whereas the growth of the number of compact coalescent histories for trees in ${\mathcal{F}}_1$ is exponentially slower than for trees in ${\mathcal{F}}_2$.

Our calculations suggest a correlation between the number of compact histories and tree balance, with more compact histories occurring for less balanced trees. We can examine this claim using the Colless (1982) index, i_C(t), which measures the degree of imbalance of a tree t, summing over all internal nodes k of t the absolute value of the difference between the sizes ℓ_k, r_k of the left and right subtrees of k. More precisely, $i_C(t)=s_t\sum _k|r_k-{\mathcal{l}}_k|$, where s_t = 2/[(|t|−1)(|t|−2)] is a rescaling factor. The index i_C(t) ranges in the interval i_C(t) ∈ [0, 1], assuming values close to 1 for more unbalanced trees and values close to 0 for more balanced trees.

Fig. 4 plots the number of compact histories against i_C(t) for the 98 unlabeled topologies with 10 taxa. Trees with a larger Colless index tend to have more compact histories. The Pearson correlation coefficient is 0.9691.

Figure 4:

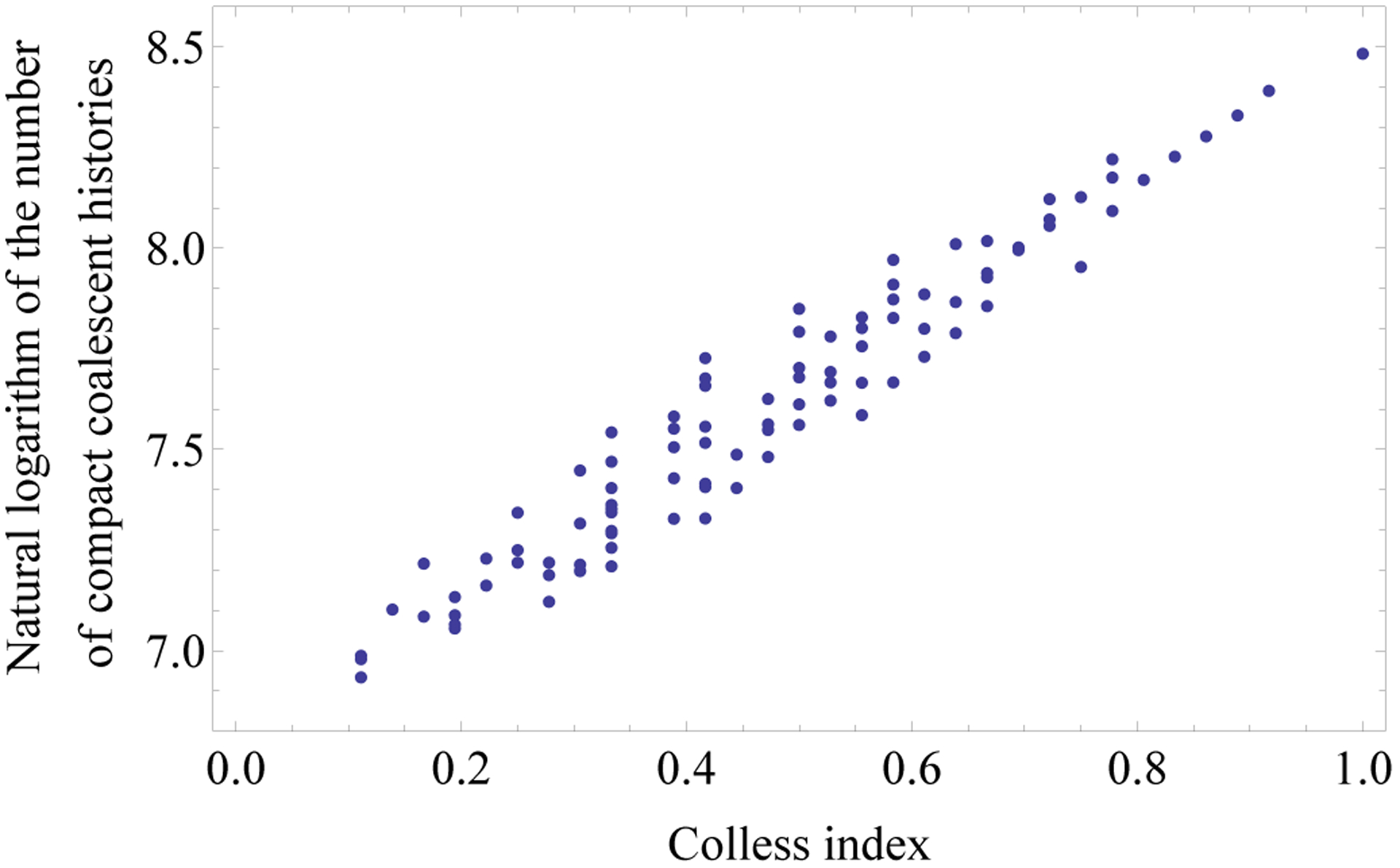
The natural logarithm of the number of compact coalescent histories for the 98 tree shapes of size n = 10, plotted against the Colless index of imbalance.

For n ≤ 15, we have identified the tree shapes underlying the labeled topologies with the largest and smallest numbers of compact histories among labeled topologies of size n. These shapes are not necessarily those with the largest and smallest numbers of coalescent histories; for example, in Table 1, the shapes with the fewest compact histories and the fewest coalescent histories differ for n = 6, and the shapes with the most compact histories and the most coalescent histories differ for n = 7.

For each n for 2 ≤ n ≤ 15, caterpillar shapes are seen to have the most compact histories, equal to the (n − 1)th Catalan number, their number of coalescent histories (see Section 4). Tree shapes associated with the fewest compact histories for each small n appear in Fig. 5. These shapes have a recursive structure: the nth tree t_n for 2 ≤ n ≤ 15 can be decomposed as

$$t_n=\left(t_d,t_{n-d}\right),$$ (5)

where d is the power of 2 nearest to n/2. In particular, when n is a power of 2, the observed tree decomposition defines t_n to be the completely balanced tree shape. Interestingly, the family of tree shapes (t_n)_n≥1 obtained by iteratively applying Eq. 5 already appears in the study of gene trees and species trees. As shown by Disanto and Rosenberg (2017), for fixed tree size n, the labeled topologies with shape t_n have the largest number of “root ancestral configurations,” and they also have the highest probability under the Yule model of speciation (Harding, 1971; Hammersley and Grimmett, 1974; Degnan and Rosenberg, 2006).

Figure 5:

Tree shapes of size 1 ≤ n ≤ 10 whose labeled topologies have the fewest compact histories among shapes of size n. In each tree with n ≥ 2, the two root subtrees each minimize the number of compact coalescent histories among trees of their size. From left to right, the numbers of compact histories are 1, 1, 2, 4, 10, 24, 60, 144, 396, and 1032. For 11 ≤ n ≤ 15, the shapes with the fewest compact histories continue to follow the recursive decomposition in Eq. 5, with 2796, 7200, 19800, 51600, and 139800 compact coalescent histories for n = 11, 12, 13, 14, and 15, respectively.

3.4. Trees with the same numbers of compact coalescent histories and coalescent histories

In this section, we characterize labeled topologies of matching gene trees and species trees for which the number of compact coalescent histories equals the number of coalescent histories. Because each compact coalescent history represents an equivalence class of coalescent histories, the number of compact histories is less than or equal to the number of coalescent histories. Wu (2016) showed that each compact coalescent history for a caterpillar labeled topology is associated with a single coalescent history, so that the numbers of compact histories and coalescent histories are equal. A caterpillar tree has only one possible sequence in which the coalescences can occur, so that once the locations of the coalescences are specified by the integer labeling of a compact coalescent history, the particular coalescences associated with the nodes are determined.

Following Rosenberg (2007), a bicaterpillar tree is a tree whose two root subtrees are both caterpillar trees (Fig. 6A). A caterpillar of size n ≥ 2 is trivially a bicaterpillar, with subtrees of size 1 and n−1. In a bicaterpillar, no internal node other than the root has the property that both of its immediate descendant nodes are internal nodes; in a caterpillar, not even the root has this property. Any non-bicaterpillar tree has at least one non-root internal node both of whose immediate descendant nodes are internal nodes.

Figure 6:

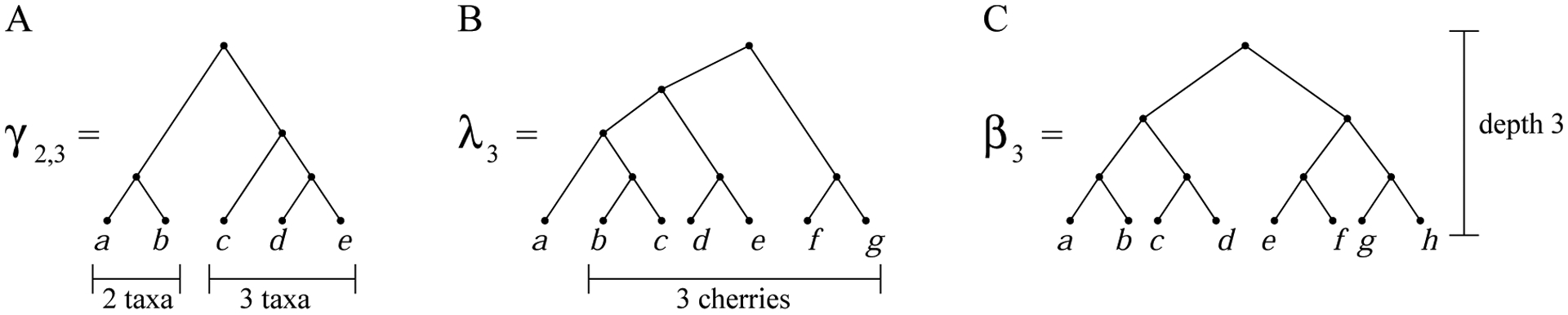
Families γ_p,q, λ_n, and β_n of labeled topologies. (A) The bicaterpillar labeled topology γ_2,3. Topology γ_p,q has |γ_p,q| = p + q taxa. (B) The lodgepole labeled topology λ₃, where |λ_n| = 2n + 1. (C) The completely balanced labeled topology β₃, where |β_n| = 2ⁿ.

Theorem 9 In a labeled topology t, the number of compact coalescent histories equals the number of coalescent histories if and only if t is a bicaterpillar.

Proof Consider a bicaterpillar tree t. We must show that each compact history of t is associated with only a single coalescent history. Consider a compact history of t. In that compact history, for each of the two caterpillar root subtrees, the list of integer labels for the nodes in that subtree, including the subtree root, uniquely specifies the locations of the coalescences in that subtree. The remaining coalescences necessarily occur above the root of t. Hence, the list of labels for the nodes of t specifies exactly where all coalescences occur, and only one coalescent history is possible for each compact history.

For the reverse direction, suppose t is not a bicaterpillar. Then there must exist an internal node κ other than the root of t whose immediate descendant nodes κ₁ and κ₂ are internal nodes. These nodes must each have as a descendant a cherry internal node, an internal node with exactly two leaf descendants. Denote these cherry nodes ${\kappa }_1^{\prime }$ and ${\kappa }_2^{\prime }$, with ${\kappa }_1^{\prime }$ possibly equal to κ₁ and ${\kappa }_2^{\prime }$ possibly equal to κ₂. Let a and b be leaves that descend from ${\kappa }_1^{\prime }$, and let c and d be leaves that descend from ${\kappa }_2^{\prime }$. The compact history in which the label for κ is 1, the label for the root of t is |t| − 2, and all other nodes have label 0 has at least two associated coalescent histories. In particular, it is possible that the single coalescence associated with node κ is (a, b), or that it is (c, d). Hence, we have two coalescent histories associated with a single compact history, and the number of compact histories is strictly less than the number of coalescent histories. □

As noted above, Table 1 illustrates that the number of compact coalescent histories is equal to the number of coalescent histories if and only if t is a bicaterpillar for trees t of size 2 ≤ n ≤ 7.

4. Number of compact coalescent histories for special families of trees

We now study the number of compact histories in three families of labeled topologies. We consider bicaterpillar, lodgepole, and completely balanced labeled topologies.

By γ_p,q, we denote a representative bicaterpillar labeled topology having root subtrees of size p ≥ 1 and q ≥ 1 (Fig. 6A). For fixed n ≥ 2, letting q ≥ p, the bicaterpillar trees have (p, q) = (1, n−1),(2, n−2), … , (⌊n/2⌋, ⌈n/2⌉).

Denote by λ_n a representative lodgepole labeled topology with n cherries and size |λ_n| = 2n+1 taxa (Fig. 6B). The shape [λ_n] satisfies the recursion [λ_n] = ([λ_n−1], (•, •)), with [λ₀] = •. In other words, [λ_n] is inductively defined by appending [λ_n−1] and a tree with two leaves—a cherry—to a common root, beginning with the 1-taxon tree [λ₀]. Lodgepole trees have been introduced by Disanto and Rosenberg (2015) as an example of a tree family for which the growth of the number of coalescent histories is faster than exponential in the number of taxa. In particular, the number of coalescent histories of λ_n grows asymptotically like the double factorial (2n + 1)!!.

Finally, in contrast with maximally unbalanced trees γ_1,n−1, we consider completely balanced trees. We denote by β_n a representative completely balanced labeled topology of size |β_n| = 2ⁿ taxa (Fig. 6C), with shape defined by [β₀] = • and [β_n] = ([β_n−1], [β_n−1]). The number of coalescent histories in the family β_n is available only by a recursion (Rosenberg, 2007), and the asymptotic growth of this number is not known.

Setting c(γ_p,n−p), c(λ_n), and c(β_n) as the numbers of compact histories for γ_p,n−p, λ_n, and β_n respectively, in Sections 4.1, 4.2, and 4.3 we show that for increasing values of n, the exponential growth of the sequences c(γ_p,n−p), c(λ_n), and c(β_n) with respect to tree sizes |γ_p,n−p|, |λ_n|, and |β_n| is given by

$$c\left({\gamma }_{p,n-p}\right)\bowtie {\left(k_{\gamma }\right)}^{\mid {\gamma }_p,n-p\mid },\text{ with }{k}_{\gamma }=4,$$ (6)

$$c\left({\lambda }_n\right)\bowtie {\left(k_{\lambda }\right)}^{|{\lambda }_n|},\text{ with }{k}_{\lambda }=\sqrt{\frac{5\sqrt{5}+11}{2}}\approx 3.3302,$$ (7)

$$c\left({\beta }_n\right)\bowtie {\left(k_{\beta }\right)}^{|{\beta }_n|},\text{ with }2.855<k_{\beta }<\mathrm{2.858.}$$ (8)

A remarkable consequence of Eq. 7 is that although the growth of the number of coalescent histories in the lodgepole family is faster than exponential, the number of compact histories in the family grows “only” exponentially, as determined by Eq. 7. Furthermore, although the number of coalescent histories in the lodgepole family grows much faster than in the caterpillar family (Disanto and Rosenberg, 2015), the growth of the number of compact histories in the lodgepole family is exponentially slower than for caterpillars.

In accord with the cases of the small trees illustrated in Fig. 4, we also observe a trend in the values of the exponential orders k_γ, k_λ, and k_β and the values of the Colless indices i_C(γ_1,n−1), i_C(λ_n), and i_C(β_n). For maximally unbalanced and completely balanced trees, we have i_C(γ_1,n−1) = 1 and i_C(β_n) = 0. For n ≥ 1, $i_C\left({\lambda }_n\right)=2/[2n(2n-1)]\times \left[1+{\sum }_{i=2}^n(2i-3)\right]=\left(n^2-2n+2\right)/[n(2n-1)]$, from which i_C(λ_n) → 1/2 as n → ∞. For large n, among the families we consider, the unbalanced caterpillars have the most compact histories, the completely balanced trees have the fewest, and the lodgepole trees, with an intermediate level of balance, have an intermediate number of compact histories.

4.1. Bicaterpillar trees γ_p,n−p

We showed in Section 3.4 that the number c(γ_p,n−p) of compact coalescent histories for γ_p,n−p equals the number of coalescent histories of γ_p,n−p. This fact enables the computation of c(γ_p,n−p) and its exponential growth.

Theorem 10 For the bicaterpillar tree γ_p,n−p, (i) the number of compact coalescent histories satisfies

$$c\left({\gamma }_{p,n-p}\right)=C_p{C}_{n-p},$$ (9)

where $C_n=\left(\begin{array}{c}2n\\ n\end{array}\right)/(n+1)$ is the nth Catalan number, and (ii) the exponential growth of the number of compact coalescent histories satisfies $c\left({\gamma }_{p,n-p}\right)\bowtie {\left(k_{\gamma }\right)}^{|{\gamma }_{p,n-p}|}$, where k_γ = 4.

Proof (i) The number of coalescent histories for c(γ_p,n−p) was shown by Rosenberg (2007, Theorem 3.10) to be C_pC_n−p. The claim follows from the equivalence of compact histories and coalescent histories for bicaterpillars.

(ii) We compute the exponential growth of the number of compact coalescent histories first for the caterpillar γ_1,n−1. Eq. 9 yields c(γ_1,n−1) = C_n−1. From $\left(\begin{array}{c}2n\\ n\end{array}\right)\bowtie 4^n$ and |γ_1,n−1| = n, it follows that c(γ_1,n−1) ⋈ 4ⁿ.

Rosenberg (2007, Corollary 3.11) showed that for fixed n ≥ 2, over the range 1 ≤ p ≤ ⌊n/2⌋, the number of coalescent histories for the bicaterpillar γ_p,n−p (Eq. 9) is greatest when p = 1, and it decreases monotonically from C_n−1 to C_⌊n/2⌋C_⌈n/2⌉ as p increases from 1 to ⌊n/2⌋. Hence, considering bicaterpillars with n taxa, the Catalan number C_n−1 is both the largest number of coalescent histories and the largest number of compact histories. Note that because C_n ⋈ 4ⁿ, the product C_⌊n/2⌋C_⌈n/2⌉, representing the smallest number of coalescent histories and compact histories possible for a bicaterpillar with n taxa, also satisfies C_⌊n/2⌋C_⌈n/2⌉ ⋈ 4^⌊n/2⌋4^⌈n/2⌉ = 4ⁿ. Thus, because the number of compact histories satisfies c(γ_p,n−p) ⋈ 4ⁿ both for the n-taxon bicaterpillar with the fewest compact histories and for the n-taxon bicaterpillar with the most compact histories, it does so for any n-taxon bicaterpillar, irrespective of the value of p. □

The pattern that the number of compact histories increases with increasing imbalance that is seen in comparing caterpillar, lodgepole, and completely balanced families is also observed with bicaterpillars as p changes. The Colless index for γ_p,n−p is

$$i_C\left({\gamma }_{p,n-p}\right)=\frac{(n-2p)+\left[\sum _{i=2}^p(i-2)\right]+\left[\sum _{i=2}^{n-p}(i-2)\right]}{(n-1)(n-2)}=\frac{2{\left[p-\left(\frac{n}{2}+1\right)\right]}^2+\frac{n^2-6n+4}{2}}{(n-1)(n-2)}.$$ (10)

For fixed n, this quantity decreases as p increases from 1 to ⌊n/2⌋. At p = 1, it has the maximal value of i_C(γ_1,n−1) = 1. At p = ⌊n/2⌋, it is near 1/2: i_C(γ_n/2,n/2) = (n−4)/[2(n−1)] for even n and i_C(γ_{(n−1)/2,(n+1)/2}) = (n² − 6n + 13)/[2(n − 1)(n − 2)] for odd n.

Fig. 7 plots the logarithm of the number of compact histories (Eq. 9) against the Colless index (Eq. 10) for each p from 1 to ⌊n/2⌋, for n = 10, 20, 30, 40, and 50. Following Eqs. 9 and 10, the values of both log c(γ_p,n−p) and i_C(γ_p,n−p) decrease as p increases. We can also observe from the figure the relatively constant value in p for log c(γ_p,n−p) suggested by the fact that c(γ_p,n−p) has exponential order 4 in n irrespective of p. For fixed p, with each increment of 10 in n, the figure illustrates that this constant value increases by a value close to log(4ⁿ⁺¹⁰/4ⁿ) = 10 log 4 ≈ 13.8629, the value predicted by the exponential order 4 of c(γ_p,n−p) at fixed p.

Figure 7:

The natural logarithm of the number of compact coalescent histories for bicaterpillar tree shapes γ_p,n−p (Eq. 9), plotted against the Colless index of imbalance (Eq. 10). For each of five values of n, the size of plotted points increases as p ranges from 1 to ⌊n/2⌋, indicating that bicaterpillars with larger p have smaller Colless indices and fewer compact histories.

4.2. Lodgepole trees λ_n

In this section, we study in detail the number c(λ_n) of compact histories of the lodgepole labeled topology λ_n. We prove Eq. 7, and we derive an explicit formula, Eq. 18, for c(λ_n).

We say that a compact history h of λ_n generates a compact history h′ of λ_n+1 if the restriction of h′ to the subtree λ_n of λ_n+1 agrees with h when we ignore the label assigned by h to the root branch of λ_n. For instance, exactly 6 of the 10 compact histories of λ₂ depicted in Fig. 8 are generated by the compact history h of λ₁ = (a, (b, c)) that has m(h) = 2 and label 0 for the branch above the cherry (b, c). According to this definition, each compact history h′ of λ_n+1 is generated by exactly one compact history h of λ_n.

Figure 8:

The 10 compact histories possible for the lodgepole labeled topology λ₂.

To enumerate the compact histories of the lodgepole family, we use a generating tree approach (Barcucci et al., 1999; Banderier et al., 2002). We associate each compact history with a labeled node in a tree that represents all possible choices for producing the compact histories: the generating tree. More precisely, the generating tree of the compact histories of the lodgepole family is characterized by the following properties.

Definition 11 The generating tree of the compact coalescent histories of the lodgepole family (λ_n)_n≥0 is the rooted tree in which (i) the node associated with a compact history h of λ_n for which m(h) = m has depth n and label (m), and (ii) a node (m′) directly descends from a node (m), written (m) ⇝ (m′), when (m′) is associated with a compact history of λ_n+1 generated by the compact history of λ_n corresponding to the node (m).

The first levels of the generating tree appear in Fig. 9B. Nodes correspond to the compact histories of λ₀, λ₁, and λ₂; each of the 10 depth-2 nodes is associated with a compact history of λ₂ from Fig. 8. As previously observed, 6 of the 10 compact histories of λ₂ are generated by the compact history of λ₁ with root label 2. Indeed, in Fig. 9B, 6 nodes at depth 2 descend directly from node (2) at depth 1. Different nodes in the generating tree can share the same label, as different compact histories can have the same label for their root branch (Fig. 8).

Figure 9:

Generation of compact coalescent histories of lodgepole labeled topologies. (A) Generation of compact histories of λ_n+1 from a compact history of λ_n. Let h be a compact history of λ_n with label m = m(h) for its root branch. The compact histories h′ of λ_n+1 generated by h are determined by choosing two parameters: (i) the label, 0 or 1, for the branch above the cherry root subtree of λ_n+1, and (ii) the label ℓ ∈ [0, m] for the branch above the root subtree λ_n of λ_n+1. If the label in (i) is chosen to be 0, then the label m(h′) = m + 2 − ℓ of the root branch in λ_n+1 ranges in the interval m(h′) ∈ [2, m + 2]. Similarly, if the label chosen in (i) is 1, then the label m(h′) = m + 1 − ℓ ranges in m(h′) ∈ [1, m + 1]. (B) The first levels of the generating tree (Eq. 11). A node (m) at depth n in the generating tree accounts for a compact history of λ_n with root branch labeled by m. The root of the generating tree has label (0), as the lodgepole λ₀ with 1 taxon has no coalescent events. Nodes descending from a generic node (m) are determined by Eq. 11. The 10 nodes at depth 2 account for the compact histories of λ₂ of Fig. 8.

For an arbitrary compact history h of λ_n, the value of m(h) = m provides information about the number of compact histories of λ_n+1 generated by h, or, equivalently, about the number of nodes at depth n + 1 in the generating tree that descend from the node (m) at depth n associated with h. Moreover, taking the integer m as input, the construction in Fig. 9A determines the value m(h′) for all the compact histories h′ generated by h.

The next result iteratively characterizes the structure of the generating tree.

Proposition 12 The generating tree of the compact coalescent histories of the lodgepole family (λ_n)_n≥0 can be produced iteratively, level by level, by the following rule: (i) the root of the generating tree is labeled by (0), and (ii) each node with label (m) in the generating tree has exactly 2m + 2 descendants, which are labeled by (2),(3), … , (m + 2) and (1),(2), … , (m + 1). In symbols,

$$\{\begin{array}{lll}(0)\hfill & \equiv \hfill & \mathit{\text{root}};\hfill \\ (m)\hfill & ⇝\hfill & (2),(3),\dots ,(m+2),(1),(2),\dots ,(m+1).\hfill \end{array}$$ (11)

Proof According to the construction of compact histories described in Fig. 9A, each compact history h of λ_n with root label m generates exactly 2m + 2 different compact histories h′ of λ_n+1: one for each value of m(h′) ∈ {2,3, … , m + 2}, when the node above the cherry root subtree of λ_n+1 has label 0, and one for each value of m(h′) ∈ {1,2, …, m + 1}, when the node above the cherry root subtree of λ_n+1 has label 1. In particular, this construction characterizes the nodes of the generating tree that directly descend from an arbitrary node (m): for each integer m ≥ 0, the descendants of each node (m) present in the generating tree are (2),(3), … , (m + 2),(1),(2), … , (m + 1). Setting to (0) the label for the root—the node at depth 0—of the generating tree, the characterization of descendant nodes yields the procedure given in Eq. 11 for iteratively producing the generating tree of the compact histories of the lodgepole family. □

As an example, starting from the root node (0) of the generating tree and applying Eq. 11, we find (0) ⇝ (2), (1), which gives the first level of the tree of Fig. 9B. A second application then gives (2) ⇝ (2), (3), (4), (1), (2), (3) and (1) ⇝ (2), (3), (1), (2), from which we recover the second level of the tree.

To count the number of compact histories of the nth lodgepole tree, we make use of the equivalence between the number of nodes with label (m) produced at depth n in the generating tree determined by Eq. 11 and the number c_m,n of compact histories of λ_n with root branch labeled by m.

Let $L(x,z)={\sum }_{n=0}^{\infty }{\sum }_{m=0}^{|{\lambda }_n|-1}{c}_{m,n}{x}^m{z}^n$ be the bivariate generating function counting nodes (m) at depth n in the generating tree. Note that for each n ≥ 0, because each compact history has label from 1 to at most |λ_n|−1 above the root, we have ${\sum }_{m=0}^{|{\lambda }_n|-1}{c}_{m,n}=c\left({\lambda }_n\right)$. Hence, $L(1,z)={\sum }_{n=0}^{\infty }c\left({\lambda }_n\right)z^n$ is the generating function associated with the sequence c(λ_n). A functional equation that characterizes L(1, z) can be determined from the structure of the generating tree described in Proposition 12.

Proposition 13 The generating function $L(1,z)={\sum }_{n=0}^{\infty }c\left({\lambda }_n\right)z^n$ satisfies the functional equation

$$L(1,z)=1+zL{(1,z)}^2+zL{(1,z)}^3\equiv \varphi (z,L(1,z)).$$ (12)

Proof We first derive an equation for the bivariate generating function L(x, z), which is then used to prove Eq. 12. From Proposition 12, each time that an expression x^mzⁿ is counted in the generating function L(x,z)—written x^mzⁿ ∈ L in what follows—the terms $\left({\sum }_{j=2}^{m+2}{x}^j+{\sum }_{j=1}^{m+1}{x}^j\right)z^{n+1}$ appear in L(x, z) as well. Summing over all possible x^mzⁿ ∈ L, we obtain

$$\begin{gathered} L(x,z)=1+\left[\sum _{x^m{z}^n\in L}\left(\sum _{j=2}^{m+2}{x}^j+\sum _{j=1}^{m+1}{x}^j\right)z^{n+1}\right] \\ =1+x^{2}z\sum _{x^m{z}^n\in L}\frac{\left(1-x^{m+1}\right)z^n}{1-x}+xz\sum _{x^m{z}^n\in L}\frac{\left(1-x^{m+1}\right)z^n}{1-x}=1+\left(x^{2}z+xz\right)\left[\frac{L(1,z)-xL(x,z)}{1-x}\right], \end{gathered}$$ (13)

where the 1 = x⁰z⁰ term in Eq. 13 accounts for the root of the generating tree (Eq. 11). The root does not appear in the sum on the right-hand side because it is not descended from any node; in summing over all x^mzⁿ ∈ L to produce L(x, z) on the left, no term gives rise to x⁰z⁰ on the right. Collecting terms yields

$$L(x,z)\left[1+\frac{x^{2}z(1+x)}{1-x}\right]=1+L(1,z)\left[\frac{xz(1+x)}{1-x}\right],$$ (14)

from which we can derive an equation for L(1, z) by applying the “kernel” method (Banderier et al., 2002).

Take X = X(z) such that

$$1+\frac{X^{2}z(1+X)}{1-X}=0.$$ (15)

By replacing x with X in Eq. 14, the left-hand side cancels, giving

$$0=1+L(1,z)\left(-\frac{1}{X}\right),$$

where we note that $\frac{Xz(1+X)}{1-X}=-\frac{1}{X}$ to produce the right-hand side. We then obtain L(1, z) = X, which together with Eq. 15 yields Eq. 12. □

From Eq. 12, it is possible to determine the dominant singularity ρ of L(1, z), and thus, from Eq. 1, the exponential growth of the sequence c(λ_n) ⋈ (1/ρ)ⁿ. Following Section VII.6.1 of Flajolet and Sedgewick (2009), given m ≥ 1 generating functions y₁(z), …, y_m(z) satisfying a system of m non-linear polynomial equations

$$\{\begin{array}{ccc}{y}_1& =& {\varphi }_1\left(z,y_1,\dots ,y_m\right)\\ ⋮& ⋮& ⋮\\ y_m& =& {\varphi }_m\left(z,y_1,\dots ,y_m\right),\end{array}$$ (16)

the value ρ of the common dominant singularity of y₁, …, y_m can be determined from the algebraic expressions for ϕ₁, …, ϕ_m through the “characteristic system” associated with Eq. 16. Eq. 64 in Section VII.6.1 of Flajolet and Sedgewick (2009) enables the calculation of the characteristic system of Eq. 16.

In our case, setting y₁(z) = L(1, z), ϕ₁ = ϕ, and m = 1, the associated characteristic system of Eq. 12 is

$$\{\begin{array}{l}\tau =\varphi (\rho ,\tau )=1+\rho {\tau }^2+\rho {\tau }^3\hfill \\ 0=1-\frac{\partial \varphi (\rho ,\tau )}{\partial \tau }=1-2\rho \tau -3\rho {\tau }^2,\hfill \end{array}$$ (17)

and the following theorem holds.

Theorem 14 In the lodgepole family (λ_n)_n≥0, (i) the exponential growth of the number of compact coalescent histories satisfies c(λ_n) ⋈ (k_λ)^|λn|, where

$$k_{\lambda }=\sqrt{\frac{5\sqrt{5}+11}{2}}\approx 3.3302,$$

and (ii) when n ≥ 1, the number c(λ_n) can be computed as

$$c\left({\lambda }_n\right)=\frac{1}{n}\sum _{i=0}^{n-1}{2}^{i+1}\left(\begin{array}{c}2n\\ i\end{array}\right)\left(\begin{array}{c}n\\ i+1\end{array}\right).$$ (18)

Proof (i) By solving Eq. 17 in positive real numbers, we obtain $\rho =(5\sqrt{5}-11)/2$, and c(λ_n) ⋈ (1/ρ)ⁿ. Because the lodgepole λ_n has |λ_n| = 2n + 1 taxa, the number of compact histories in the lodgepole family grows like (1/ρ)^{(|λn|−1)/2}, or

$$c\left({\lambda }_n\right)\bowtie {(\sqrt{1/\rho })}^{|{\lambda }_n|},$$ (19)

with respect to the number of taxa |λ_n|. Setting $k_{\lambda }=\sqrt{1/\rho }$, Eq. 19 yields the result.

(ii) The exact formula for c(λ_n) follows from an application of Lagrange inversion to the functional equation of Proposition 13. The complete derivation of Eq. 18 from Eq. 12 can be found in Deutsch (2000), where a class of lattice paths is shown to be enumerated by a generating function satisfying Eq. 12. □

Note that computing the exponential order 1/ρ of the sequence c(λ_n) directly from Eq. 18 is not straightforward, and the value of ρ is indeed not reported by Deutsch (2000). Fig. 10 shows numerical values of c(λ_n)^1/|λn| converging to the value of k_λ ≈ 3.3302 that determines the exponential growth of the sequence c(λ_n) with respect to tree size |λ_n|.

Figure 10:

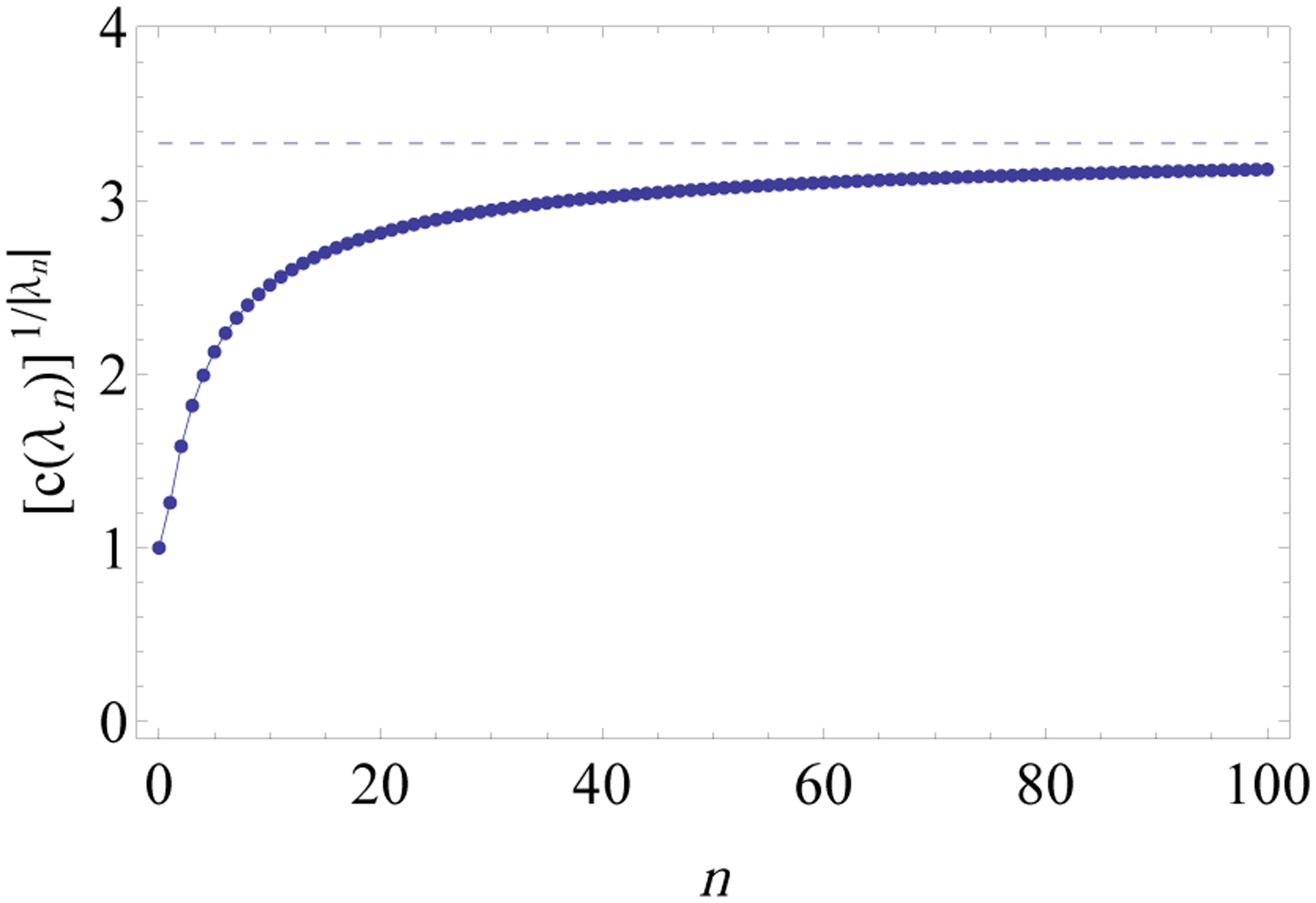
Values of $c{({\lambda }_n)}^{1/\left|{\lambda }_n\right|}$ for 0 ≤ n ≤ 100. The dashed horizontal line has ordinate k_λ, with k_λ ≈ 3.3302 as in Theorem 14. The integers c(λ_n) representing the number of compact coalescent histories for the lodgepole family are computed from Eq. 18. As $c({\lambda }_n)\bowtie k_{\lambda }^{\left|{\lambda }_n\right|}$, for increasing n, the sequence $c{({\lambda }_n)}^{1/\left|{\lambda }_n\right|}$ approaches k_λ.

4.3. Completely balanced trees β_n

This section studies the number c(β_n) of compact histories for the completely balanced labeled topology β_n. We prove Eq. 8, deriving a recursive procedure for calculating c(β_n).

Denote by c_m,n the number of compact histories of β_n with root branch labeled by m. Consider the family of polynomials $B_n(x)={\sum }_{m=0}^{|{\beta }_n|-1}{c}_{m,n}{x}^m$, where each term x^m in B_n(x), written x^m ∈ B_n, accounts for a compact history h of β_n with m(h) = m. Note that $B_n(1)={\sum }_{m=0}^{|{\beta }_n|-1}{c}_{m,n}=c\left({\beta }_n\right)$.

The next proposition gives a recursive procedure for calculating the polynomial B_n+1(x).

Proposition 15 The family of polynomials $B_n(x)={\sum }_{m=0}^{|{\beta }_n|-1}{c}_{m,n}{x}^m$ satisfies the recursion

$$B_{n+1}(x)=\frac{x{\left[B_n(1)-x{B}_n(x)\right]}^2}{{(1-x)}^2},$$ (20)

with B₀(x) = 1.

Proof The construction of compact histories described in Fig. 11 translates into algebraic terms, determining the following recurrence for the polynomial B_n+1(x):

$$B_{n+1}(x)=\sum _{x^{m_1}\in B_n}\sum _{x^{m_2}\in B_n}\sum _{{\mathcal{l}}_1=0}^{m_1}\sum _{{\mathcal{l}}_2=0}^{m_2}{x}^{m_1+m_2+1-{\mathcal{l}}_1-{\mathcal{l}}_2}$$ (21)

$$=x\left[\left(\sum _{x^{m_1}\in B_n}\sum _{j=0}^{m_1}{x}^j\right)\left(\sum _{x^{m_2}\in B_n}\sum _{j=0}^{m_2}{x}^j\right)\right]=x{\left(\sum _{x^m\in B_n}\frac{1-x^{m+1}}{1-x}\right)}^2=\frac{x{\left[B_n(1)-x{B}_n(x)\right]}^2}{{(1-x)}^2}.$$ (22)

In particular, the nested sums in Eq. 21 encode the generation of a generic compact history $h\equiv x^{m_1+m_2+1-{\mathcal{l}}_1-{\mathcal{l}}_2}\in B_{n+1}$ by appending to a common root two arbitrary compact histories $h_1\equiv x^{m_1}\in B_n$ and $h_2\equiv x^{m_2}\in B_n$ (step i of Fig. 11), and then choosing new labels ℓ₁ ∈ [0, m₁] and ℓ₂ ∈ [0, m₂] for the two branches descending from the root of h (step ii). Eq. 22 follows from Eq. 21 through algebraic manipulations. □

Figure 11:

Compact histories of completely balanced labeled topologies. Each compact history h of β_n+1 is uniquely obtained by (i) appending two compact histories h₁, h₂ of β_n to a common root node, and (ii) choosing labels ℓ₁ and ℓ₂ for the two branches descending from the root of h. If m₁ = m(h₁) and m₂ = m(h₂) are the labels of the root branches of h₁ and h₂ respectively, then ℓ₁ ranges in the interval ℓ₁ ∈ [0, m₁], and ℓ₂ ranges in the interval ℓ₂ ∈ [0, m₂]. Once ℓ₁, ℓ₂ have been fixed, the label of the root branch in h is determined by m(h) = m₁ + m₂ + 1 − ℓ₁ − ℓ₂. After step (ii), taxa of h₁ and h₂ are relabeled to obtain a proper completely balanced labeled topology (capital letters). The labeling is applied such that one set of labels is given to the taxa in h₁ and another set to the taxa in h₂. Note that even when h₁ = h₂ (as in the figure), if ℓ₁ =6 ℓ₂, then switching the values for ℓ₁ and ℓ₂ generates a different compact history of β_n+1.

By applying Eq. 20 four times, we obtain B₁(x) = x, B₂(x) = x + 2ײ + x³, B₃(x) = 16x + 32ײ + 40׳ + 32×⁴ + 17×⁵ + 6×⁶ + x⁷, and B₄(x) = 20736x + 41472ײ + 57600׳ + 64512×⁴ + 60160×⁵ + 47616×⁶ + 32480×⁷ + 19200×⁸ +9824×⁹+4288×¹⁰+1552×¹¹ +448×¹²+97×¹³+14×¹⁴+x¹⁵. For example, the term 448×¹² ∈ B₄ indicates that β₄ has exactly 448 compact histories with root branch labeled by m = 12. Using these calculations, we find that the first entries of the sequence c(β_n) = B_n(1) are c(β_n) = 1, 1, 4, 144, and 360000 for n = 0, 1, 2, 3, and 4, respectively. The sequence c(β_n) grows exponentially as specified by the following theorem.

Theorem 16 In the completely balanced family (β_n)_n≥0, (i) the exponential growth of the number of compact coalescent histories satisfies $c\left({\beta }_n\right)\bowtie {\left(k_{{\beta }_n}\right)}^{|{\beta }_n|}$, where

$$k_{\beta }=\text{exp}\left[\sum _{j=0}^{\infty }{2}^{-j}\text{\hspace{0.17em}log}\left(1+e_j\right)\right],$$

and $e_n=B_n^{\prime }(1)/B_n(1)=\left({\sum }_{m=0}^{|{\beta }_n|-1}m{c}_{m,n}\right)/c\left({\beta }_n\right)$ is the expected value of m(h) in a compact coalescent history h chosen uniformly at random from the set of compact coalescent histories of β_n. Furthermore, (ii) k_β satisfies the bounds 2.855 < k_β < 2.858.

Proof (i) From Eq. 20, we have

$$c\left({\beta }_{n+1}\right)=B_{n+1}(1)={\left[B_n(1)+B_n^{\prime }(1)\right]}^2={\left(1+e_n\right)}^2{B}_n{(1)}^2={\left(1+e_n\right)}^{2}c{\left({\beta }_n\right)}^2,$$ (23)

where the second equality follows from a double application of l’Hopital’s rule to the limit

$$B_{n+1}(1)=\underset{x\to 1}{\text{lim}}\frac{x{\left[B_n(1)-x{B}_n(x)\right]}^2}{{(1-x)}^2}.$$

Setting y_n = log c(β_n), from Eq. 23, we obtain

$$y_{n+1}=2y_n+2\text{\hspace{0.17em}log}\left(1+e_n\right).$$

This linear recursion has solution

$$y_n=2^n{y}_0+\sum _{j=0}^{n-1}{2}^{n-j}\text{\hspace{0.17em}log}\left(1+e_j\right)=2^n\left[y_0+\sum _{j=0}^{\infty }{2}^{-j}\text{\hspace{0.17em}log}\left(1+e_j\right)\right]-\sum _{j=n}^{\infty }{2}^{n-j}\text{\hspace{0.17em}log}\left(1+e_j\right),$$ (24)

where, because the two series in Eq. 24 have positive terms, they both converge being bounded from above. More precisely, for j ≥ 0, the inequality 1 + e_j ≤1 + (2^j – 1) = 2^j holds, from the interpretation of e_j as the mean value of m(h) for a random compact history h of a balanced tree with 2^j taxa. Hence, for each fixed n ≥ 0, the following upper bound for the series in Eq. 24 holds

$$\sum _{j=n}^{\infty }{2}^{n-j}\text{\hspace{0.17em}log}\left(1+e_j\right)\le 2^n\sum _{j=n}^{\infty }\frac{\text{log}\left(2^j\right)}{2^j}<2^n\sum _{j=n}^{\infty }\frac{j}{2^j}=2^n\left[\sum _{j=0}^{\infty }\frac{j}{2^j}-\sum _{j=0}^{n-1}\frac{j}{2^j}\right]=2^n\left[2-\frac{2^n-n-1}{2^{n-1}}\right]=2n+2.$$ (25)

The second equality in Eq. 25 uses the fact that ${\sum }_{j=0}^{k}j/2^j=2^{-k}\left(2^{k+1}-k-2\right)$ for each integer k ≥ −1, which follows by setting x = 1 into

$$\sum _{j=0}^k{\left(\frac{x}{2}\right)}^{j}j=\frac{x}{2}\sum _{j=0}^k{\left(\frac{x}{2}\right)}^{j-1}j=\frac{x}{2}{\left[2\sum _{j=0}^k{\left(\frac{x}{2}\right)}^j\right]}^{\prime }=x{\left[\frac{1-{(x/2)}^{k+1}}{1-x/2}\right]}^{\prime }=\frac{x\left[2^{k+1}-2(k+1)x^k+k{x}^{k+1}\right]}{2^k{(2-x)}^2}.$$

Switching back to $c({\beta }_n)=e^{y_n}$, and noting that c(β₀) = 1 and |β_n| = 2ⁿ, Eq. 24 yields

$$c\left({\beta }_n\right)={\left[c\left({\beta }_0\right)\text{exp}\left(\sum _{j=0}^{\infty }{2}^{-j}\text{\hspace{0.17em}log}\left(1+e_j\right)\right)\right]}^{2^n}\text{exp}\left[-\sum _{j=n}^{\infty }{2}^{n-j}\text{\hspace{0.17em}log}\left(1+e_j\right)\right]=\frac{1}{a_n}{\left(k_{\beta }\right)}^{|{\beta }_n|},$$

where $a_n=\text{exp}\left[{\sum }_{j=n}^{\infty }{2}^{n-j}\text{\hspace{0.17em}log}\left(1+e_j\right)\right]$ and k_β is the quantity defined in the statement of the theorem.

Note that the sequence a_n is bounded by polynomial functions of the size |β_n| = 2ⁿ. Indeed, from the trivial inequality e_j ≥ 1 (with j ≥ 1) and from Eq. 25, for n ≥ 1 we have

$$4=e^{2\text{\hspace{0.17em}log\hspace{0.17em}}2}\le a_n<e^{2n+2}=e^{2n}{e}^2=e^{2{\text{log}}_2|{\beta }_n|}{e}^2=e^{2\text{\hspace{0.17em}log}|{\beta }_n|/\text{log\hspace{0.17em}}2}{e}^2={|{\beta }_n|}^{2/\text{log\hspace{0.17em}}2}{e}^2.$$

Hence, the exponential growth of the sequence c(β_n) is determined by c(β_n) ⋈ (k_β)^|βn| as claimed.

(ii) The value of the constant k_β can be bounded by using the first terms of the sequence e_n. For n ≤ 14, we perform the exact computation of the values of e_n using the recursion of Proposition 15 for the polynomials B_n(x). By using the exact sequence of rational numbers (e_n)_0≤n≤14, symbolic calculations give

$$2.8550<\text{exp}\left[\sum _{j=0}^{14}{2}^{-j}\text{\hspace{0.17em}log}\left(1+e_j\right)\right]<\mathrm{2.8551.}$$

From this inequality, we obtain the bounds for k_β claimed in the statement of the theorem:

$$2.8550<\text{exp}\left[\sum _{j=0}^{14}{2}^{-j}\text{\hspace{0.17em}log}\left(1+e_j\right)\right]<k_{\beta }=\text{exp}\left[\sum _{j=0}^{14}{2}^{-j}\text{\hspace{0.17em}log}\left(1+e_j\right)\right]\text{exp}\left[\sum _{j=15}^{\infty }{2}^{-j}\text{\hspace{0.17em}log}\left(1+e_j\right)\right]<2.8551\text{\hspace{0.17em}exp}\left[\sum _{j=15}^{\infty }{2}^{-j}\text{\hspace{0.17em}log}\left(1+e_j\right)\right]<2.8551e^{1/1024}<2.8580,$$

where we have used the inequality ${\sum }_{j=15}^{\infty }{2}^{-j}\text{\hspace{0.17em}log}\left(1+e_j\right)=\left[{\sum }_{j=15}^{\infty }{2}^{15-j}\text{\hspace{0.17em}log}\left(1+e_j\right)\right]/2^{15}<32/2^{15}=1/1024$ derived directly from Eq. 25. □

Because the lower and upper bounds for k_β given in Theorem 16 are quite close to each other, we can take their mean as an approximation for k_β, that is, k_β ≈ (2.855 + 2.858)/2 = 2.8565 (Fig. 12). Finally, we observe that by computing more terms of the sequence e_n—here we have used the first n ≤ 14 terms—the same approach used in the proof of the theorem can be applied to obtain even more accurate estimates of k_β. In particular, because e_n increases slowly with respect to the number of taxa |β_n| = 2ⁿ—the values of e_n are 0, 1, and 2 for n = 0, 1, and 2, respectively, and they are approximated by 3.1667, 4.6033, 6.4180, 8.7404, 11.7342, 15.6085, 20.6332, 27.1578, 35.6357, 46.6559, 60.9835, and 79.6133 for n = 3,4, …, 14—the calculation of a few more terms of the sequence e_n can lead to stricter bounds for k_β.

Figure 12:

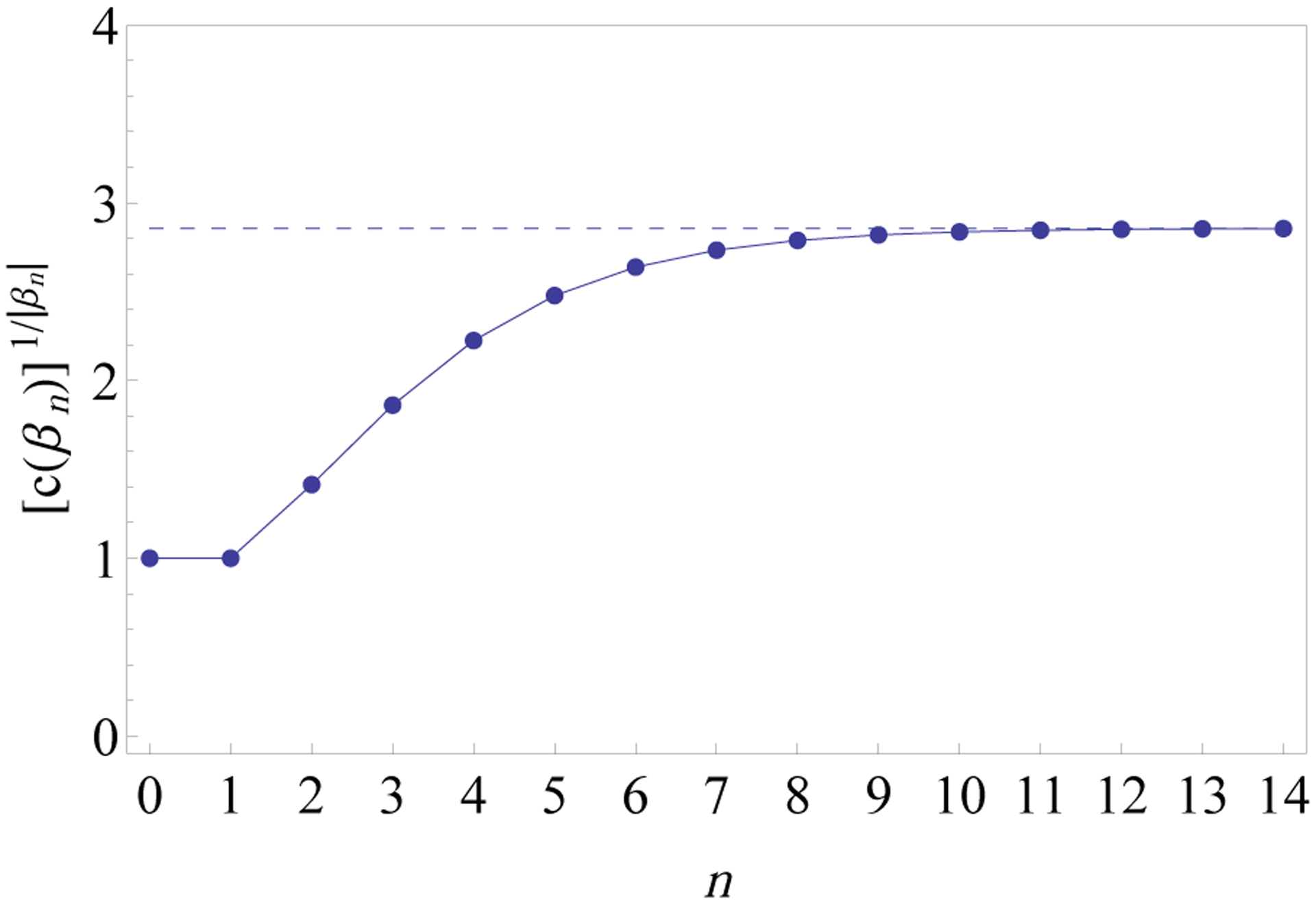
Values of $c({\beta }_n{)}^{1/|{\beta }_n|}$ for 0 ≤ n ≤ 14. The dashed horizontal line has ordinate 2.8565 given by the mean of the lower and upper bounds found for the exponential order k_β for the increase in the number of taxa of compact histories for the completely balanced trees (Eq. 8). The integers c(β_n) are computed as c(β_n) = B_n(1), that is, by setting x = 1 in the polynomials B_n(x) obtained recursively from Proposition 15. The last few points are very closely approximated by the horizontal line. As $c\left({\beta }_n\right)\bowtie k_{\beta }^{|{\beta }_n|}$, for increasing n, the sequence $c({\beta }_n{)}^{1/|{\beta }_n|}$ approaches k_β.

5. Mean number of compact coalescent histories

In Section 4, we found that the sequence of the number of compact histories can have different exponential orders for different tree families, as seen in the values of k_γ = 4 (Eq. 6), k_λ ≈ 3.3302 (Eq. 7), and k_β ≈ 2.8565 (Eq. 8) for the bicaterpillar, lodgepole, and balanced families, respectively. Motivated by these observations, we now study the exponential growth of the mean number ${\mathbb{E}}_n[c]$ of compact histories of a labeled topology selected uniformly at random in the set of labeled topologies T_n. By using generating functions, we show that the mean grows like

$${\mathbb{E}}_n[c]\bowtie {3.375}^n,$$ (26)

where the asymptotic constant 3.375 is close to the mean (k_γ + k_λ + k_β)/3 ≈ 3.3955.

We start our proof of Eq. 26 by considering all possible labeled topologies of size n, where c_m,n now denotes the total number of compact histories with root branch labeled by m. Define $c_n={\sum }_{m=0}^{n-1}{c}_{m,n}$ to be the total number of compact histories of all trees of size n. Let

$$F(x,z)=\sum _{n=1}^{\infty }\sum _{m=0}^{n-1}\frac{c_{m,n}{x}^m{z}^n}{n!}=z+\frac{x}{2}{z}^2+\left(\frac{x}{2}+\frac{x^2}{2}\right)z^3+\left(\frac{9x}{8}+\frac{5x^2}{4}+\frac{5x^3}{8}\right)z^4+\left(\frac{7x}{2}+4x^2+\frac{21x^3}{8}+\frac{7x^4}{8}\right)z^5+\dots$$

be the bivariate exponential generating function associated with integers c_m,n, where each term x^mzⁿ/n! in F(x, z), written x^mzⁿ/n! ∈ F, accounts for a compact history h of size n with m(h) = m. The function F(x, z) is characterized by the following proposition.

Proposition 17 The generating function $F(x,z)={\sum }_{n=1}^{\infty }{\sum }_{m=0}^{n-1}\frac{c_{m,n}{x}^m{z}^n}{n!}$ satisfies the functional equation

$$F(x,z)=z+\frac{x{[F(1,z)-xF(x,z)]}^2}{2{(1-x)}^2}.$$ (27)

Proof Observe that we can write F(x, z) as the sum

$$F(x,z)=z+\frac{1}{2}\sum _{\frac{x^{m}1z^{n}1}{n_1!}\in F}\sum _{\frac{x^{m}2z^{n}2}{n_2!}\in F}\sum _{{\mathcal{l}}_1=0}^{m_1}\sum _{{\mathcal{l}}_2=0}^{m_2}\frac{x^{m_1+m_2+1-{\mathcal{l}}_1-{\mathcal{l}}_2}{z}^{n_1+n_2}}{\left(n_1+n_2\right)!}\left(\begin{array}{c}{n}_1+n_2\\ n_1\end{array}\right).$$ (28)

The initial z in Eq. 28 accounts for the term x⁰z¹/1! in F associated with the compact history of the one-taxon tree. Mirroring the construction of compact histories of size larger than one from smaller compact histories described in Fig. 13, the nested sums and the factor 1/2 in Eq. 28 take into account the presence in F of exactly $\left(\begin{array}{c}{n}_1+n_2\\ n_1\end{array}\right)/2$ copies of the term $x^{m_1+m_2+1-{\mathcal{l}}_1-{\mathcal{l}}_2}{z}^{n_1+n_2}/\left(n_1+n_2\right)!$, for each fixed pair $\left(x^{m_1}{z}^{n_1}/n_1!,x^{m_2}{z}^{n_2}/n_2!\right)\in F\times F$ and for each choice of (ℓ₁, ℓ₂) ∈ [0, m₁]×[0, m₂]. Specifically, each copy of $x^{m_1+m_2+1-{\mathcal{l}}_1-{\mathcal{l}}_2}{z}^{n_1+n_2}/\left(n_1+n_2\right)!$ is associated with a compact history h that, as in Fig. 13A, can be decomposed into the compact histories h₁ and h₂ associated with terms $x^{m_1}{z}^{n_1}/n_1!$ and $x^{m_2}{z}^{n_2}/n_2!$, and in which the two branches descending from the root are labeled by ℓ₁ and ℓ₂, respectively.

Figure 13:

Generation of compact histories from compact histories of smaller trees. (A) Generation of a compact history for a tree from compact histories for its two root subtrees. (B) Generating the same compact history twice when h₁ = h₂ and ℓ₁ = ℓ₂. (C,D) Generating the same compact history twice when h₁ = h₂ and ℓ₁ ≠ ℓ₂. Each compact history h of size |h| > 1 is obtained as in (A) by (i) appending to a common root node a pair (h₁, h₂) of compact histories, and (ii) choosing labels ℓ₁, ℓ₂ for the two branches descending from the root of h. If m₁ = m(h₁) and m₂ = m(h₂) are the labels of the root branches of h₁ and h₂, respectively, then ℓ₁ ranges in the interval ℓ₁ ∈ [0,m₁], and ℓ₂ ranges in ℓ₂ ∈ [0, m₂]. The label of the root branch in h is thus m(h) = m₁ + m₂ + 1 − ℓ₁ − ℓ₂, which provides the exponent assigned to variable x in Eq. 28. After step (ii), taxa of h₁ and h₂ are relabeled to obtain a proper labeled topology underlying h. As in Section 2.1, we impose without loss of generality a linear order ≺ for the labels of the taxa of a tree. For the relabeling procedure, we choose |h₁| elements among the |h| = |h₁|+ |h₂| new labels possible for the taxa of h, where we are using |h|, |h₁|, and |h₂| here to indicate the number of taxa in the trees underlying h, h₁, and h₂, respectively. There are $\left(\begin{array}{c}|h|\\ |h_1|\end{array}\right)$ different choices, producing the binomial coefficient in Eq. 28. The elements chosen relabel h₁, and the remaining elements relabel h₂. With respect to the order ≺, the ith label of h₁ is assigned the ith label selected. Similarly, the ith label of h₂ is assigned the ith label that was not selected. This construction generates each compact history exactly twice. For this reason, the factor 1/2 appears in Eq. 28 before the summations. More precisely, if the pair (h₁, h₂) considered in step (i) of the procedure has h₁ ≠ h₂, then each resulting compact history has a copy when we take the pair (h₂, h₁). If h₁ = h₂, and we take ℓ₁ = ℓ₂ in step (ii), then the $\left(\begin{array}{c}|h|\\ |h_1|\end{array}\right)$ relabelings generate each compact history twice, as can be seen in (B) by switching the labels assigned to h₁ and h₂. Finally, if h₁ = h₂ and we set ℓ₁ ≠ ℓ₂ in step (ii), then each compact history generated has an equivalent one obtained as in (C) and (D) by switching both the values of ℓ₁ and ℓ₂ and the labels assigned to h₁ and h₂.

From Eq. 28, algebraic manipulations give

$$F(x,z)=z+\frac{1}{2}x\left[\left(\sum _{\frac{x^{m}1z^{n}1}{n_1!}\in F}\frac{z^{n_1}}{n_1!}\sum _{j=0}^{m_1}{x}^j\right)\left(\sum _{\frac{x^{m}2z^{n}2}{n_2!}\in F}\frac{z^{n_2}}{n_2!}\sum _{j=0}^{m_2}{x}^j\right)\right]=z+\frac{x{[F(1,z)-xF(x,z)]}^2}{2{(1-x)}^2},$$

where the last equality uses

$$\sum _{\frac{x^m{z}^n}{n!}\in F}\frac{z^n}{n!}\sum _{j=0}^m{x}^j=\sum _{\frac{x^m{z}^n}{n!}\in F}\frac{z^n\left(1-x^{m+1}\right)}{n!(1-x)}=\frac{1}{1-x}\left(\sum _{\frac{x^m{z}^n}{n!}\in F}\frac{z^n}{n!}-x\sum _{\frac{x^m{z}^n}{n!}\in F}\frac{x^m{z}^n}{n!}\right)=\frac{F(1,z)-xF(x,z)}{1-x}.$$

□

Setting

$$f\equiv F(1,z)=\sum _{n=1}^{\infty }\sum _{m=0}^{n-1}\frac{c_{m,n}{z}^n}{n!}=\sum _{n=1}^{\infty }\frac{c_n{z}^n}{n!},$$ (29)

the equation for F(x, z) given in Proposition 17 yields the next result.

Proposition 18 The exponential generating function $f\equiv F(1,z)={\sum }_{n=1}^{\infty }\frac{c_n{z}^n}{n!}$ of the total number of compact coalescent histories of all trees of size n satisfies the equation

$$f=z-(27/2)z^2-4f^2-4f^3+18zf\equiv \psi (z,f).$$ (30)

Proof From Eq. 27, we derive Eq. 30 by applying the “quadratic” method. As described by Flajolet and Sedgewick (2009, Section VII.8.2), this method can be used for solving functional equations of the form

$${\left[g_{1}F(x,z)+g_2\right]}^2=g_3,$$ (31)

where the functions g_j = g_j(x, z, f) are given explicitly, and both F(x, z) and f = f(z) are unknown generating functions. Rearranging terms and completing the square, Eq. 27 can be rewritten as

$${\left[\frac{x^{3/2}F(x,z)}{\sqrt{2}(1-x)}-\frac{1-2x+x^2+x^{2}f}{\sqrt{2}(1-x)x^{3/2}}\right]}^2={\left[\frac{1-2x+x^2+x^{2}f}{\sqrt{2}(1-x)x^{3/2}}\right]}^2-\frac{x{f}^2}{2{(1-x)}^2}-z.$$ (32)

This equation has the form given in Eq. 31 when we set

$$\left(g_1,g_2,g_3\right)=\left(\frac{x^{3/2}}{\sqrt{2}(1-x)},-\frac{1-2x+x^2+x^{2}f}{\sqrt{2}(1-x)x^{3/2}},{\left[\frac{1-2x+x^2+x^{2}f}{\sqrt{2}(1-x)x^{3/2}}\right]}^2-\frac{x{f}^2}{2{(1-x)}^2}-z\right).$$

Following the quadratic method, suppose there exists a substitution x = X = X(z) for which the left-hand side of Eq. 32, g₁(X, z, f)F(X, z) + g₂(X, z, f), cancels. This substitution cancels the right-hand side of Eq. 32 as well and, because of the square in the left-hand side of the equation, its derivative with respect to x. Note that because f is a function of z only, both the substitution x = X and the derivative of g₃ with respect x do not affect f. We thus have a system of two equations,

$$\{\begin{array}{ll}{g}_3(X,z,f)\hfill & =0\hfill \\ \frac{\partial g_3(X,z,f)}{\partial x}\hfill & =0,\hfill \end{array}$$ (33)

which implicitly determines the two unknown functions X and f. The derivative produces

$$\frac{\partial g_3(X,z,f)}{\partial x}=\frac{-3+4X-X^2-2X^{2}f}{2X^4}.$$

Solving Eq. 33 for f and z yields $f=-\frac{(X-1)(X-3)}{2X^2}$ and $z=\frac{X-1}{X^3}$, from which we eliminate X to obtain f = z − (27/2)z² − 4f² − 4f³ + 18zf, as claimed. □

Identifying f with its power series expansion (Eq. 29), we observe that the terms of f with order at most i ≥ 2 that appear in the left-hand side of Eq. 30 can be determined from the terms of f of order at most i − 1 present in the right-hand side of Eq. 30. For example, setting i = 3 and writing $c_n^{*}\equiv c_n/n!$, Eq. 30 gives

$$\left(c_1^{*}z+c_2^{*}{z}^2+c_3^{*}{z}^3+c_4^{*}{z}^4+\dots \right)=z-(27/2)z^2-4{\left(c_1^{*}z+c_2^{*}{z}^2+c_3^{*}{z}^3+c_4^{*}{z}^4+\dots \right)}^2-4{\left(c_1^{*}z+c_2^{*}{z}^2+c_3^{*}{z}^3+c_4^{*}{z}^4+\dots \right)}^3+18z\left(c_1^{*}z+c_2^{*}{z}^2+c_3^{*}{z}^3+c_4^{*}{z}^4+\dots \right),$$

where the terms of the right-hand side given in bold are the terms of the expansion of f that affect the computation of the terms in bold on the left-hand side. In other words, Eq. 30 can be used for recursively computing the coefficients [zⁿ]f = c_n/n! of the generating function f. Denoting by p⁽ⁱ⁾ the polynomial obtained from a polynomial p(z) by deleting terms of order larger than i in z, the polynomial f_i recursively defined by

$$\{\begin{array}{ll}{f}_0\hfill & =0\hfill \\ f_1\hfill & =z\hfill \\ f_i\hfill & ={\left[z-(27/2)z^2-4f_{i-1}^2-4f_{i-2}^3+18z{f}_{i-1}\right]}^{(i)},i\ge 2,\hfill \end{array}$$ (34)

gives the expansion of f up to the term of order i. For instance, for i = 2 and i = 3 we have f₂ = z + z²/2, and f₃ = z + z²/2 + z³, respectively.

Increasing the value of i, from the polynomials f_i we obtain the expansion

$$f=z+z^2/2+z^3+3z^4+11z^5+(91/2)z^6+204z^7+969z^8+4807z^9+(49335/2)z^{10}+\dots ,$$ (35)

in which coefficients c_n/n! grow like

$$\frac{c_n}{n!}\bowtie {(1/\rho )}^n,$$ (36)

with ρ corresponding to the dominant singularity of f. From the calculation of the value of ρ, the following theorem determines the exponential growth of the mean number of compact histories in a labeled topology of size n selected uniformly at random.

Theorem 19 The exponential growth of the mean number of compact coalescent histories in a labeled topology of size n selected uniformly at random satisfies ${\mathbb{E}}_n[c]\bowtie {3.375}^n$.

Proof We proceed as in Section VII.6.1 of Flajolet and Sedgewick (2009), calculating the value of ρ (Eq. 36) as the positive solution of the characteristic system associated with the functional equation (Eq. 30) satisfied by f:

$$\{\begin{array}{l}\tau =\psi (\rho ,\tau )=\rho -(27/2){\rho }^2-4{\tau }^2-4{\tau }^3+18\rho \tau \hfill \\ 0=1-\frac{\partial \psi (\rho ,\tau )}{\partial \tau }=1+8\tau +12{\tau }^2-18\rho .\hfill \end{array}$$ (37)

This characteristic system has been obtained by Eq. 64 of Flajolet and Sedgewick (2009), interpreting our Eq. 30 as their Eq. 61. By solving Eq. 37 in positive real numbers, we obtain ρ = 4/27, with 1/ρ = (27/4) = 6.75.

The mean number of compact histories in a labeled topology of size n selected uniformly at random can be computed as E_n[c] = c_n/|T_n|, with |T_n| as in Proposition 1. From Eqs. 36 and 2, the mean ${\mathbb{E}}_n[c]$ grows like

$${\mathbb{E}}_n[c]=\frac{c_n/n!}{|T_n|/n!}\bowtie \frac{{(27/4)}^n}{2^n}={(27/8)}^n={3.375}^n,$$

as claimed. □

Fig. 14 shows numerical values of ${\left({\mathbb{E}}_n[c]\right)}^{1/n}$ approaching the exponential order 3.375 of the sequence ${\mathbb{E}}_n[c]$.

Figure 14:

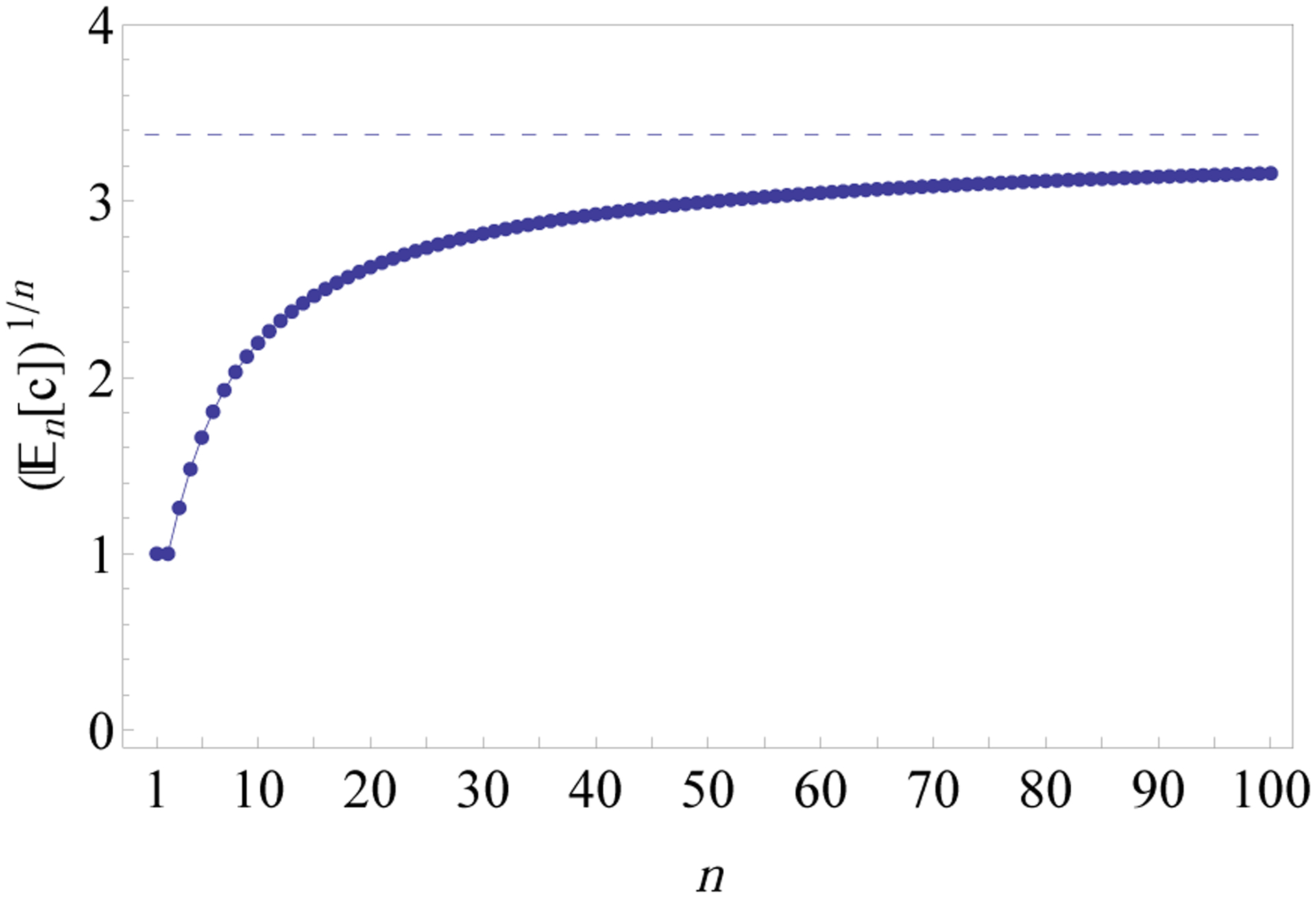
Values of ${\left({\mathbb{E}}_n[c]\right)}^{1/n}$ for 1 ≤ n ≤ 100. The dashed horizontal line has ordinate 3.375 given by the exponential order of the sequence ${\mathbb{E}}_n[c]$ (Theorem 19). The expectation ${\mathbb{E}}_n[c]$ is calculated as the ratio c_n/|T_n|, where c_n = n!([zⁿ]f) is the total number of compact histories of size n and |T_n| is the number of labeled topologies with n taxa (Proposition 1). The nth coefficient [zⁿ]f in the expansion (Eq. 35) is the coefficient of the term of order n in the polynomial f₁₀₀, obtained recursively as in Eq. 34. As ${\mathbb{E}}_n[c]\bowtie {3.375}^n$, for increasing n, the sequence ${\left({\mathbb{E}}_n[c]\right)}^{1/n}$ approaches 3.375.

6. Discussion

Considering gene trees and species trees with a matching labeled topology G = S = t, we have studied the number of compact histories of labeled topologies t. We have focused on the exponential growth of the number of compact histories, both when t belongs to special tree families of increasing size and when t is a random labeled tree topology of given size drawn under a uniform distribution. We also characterized the set of labeled topologies in which the coalescent histories are the same as the compact coalescent histories.

In Section 4, in addition to the caterpillar trees γ_1,n−1 already studied by Wu (2016), we considered three other tree families: the bicaterpillar trees γ_p,n−p, the lodgepole trees λ_n, and the completely balanced tress β_n. Whereas for the caterpillar and bicaterpillar trees, the number of compact histories grows like $c\left({\gamma }_{p,n-p}\right)\bowtie {\left(k_{\gamma }\right)}^{|{\gamma }_{p,n-p}|}$, with k_γ = 4, for the lodgepole trees, it grows exponentially like c(λ_n) ⋈ (k_λ)^|λn|, where k_λ ≈ 3.3302. Notably, although the growth of the number of coalescent histories in the family λ_n is faster than exponential (Disanto and Rosenberg, 2015), the number of compact histories grows “only” exponentially—in fact, exponentially slower than in the family γ_p,n−p. In terms of the relative complexity of the two gene tree probability algorithms CompactCH (Wu, 2016) and COAL (Degnan and Salter, 2005), this result demonstrates that when gene trees and species trees have a particular matching labeled topology t, the number of compact coalescent histories processed by CompactCH for calculating the gene tree probability can be much smaller—although still exponential in the size of t—than the number of coalescent histories used by COAL for computing the same probability.

The study of the number c(β_n) of compact histories in the family of completely balanced trees β_n appears to be more difficult. Indeed, whereas for the caterpillar γ_1,n−1 and the lodgepole λ_n, explicit formulas, Eqs. 9 and 18, could be obtained for enumerating compact histories, in the completely balanced case, the exact enumeration proceeds only recursively. However, the bounds given in Eq. 8 determine the numerical value of the exponential order k_β of the sequence c(β_n) with a precision of 2 decimal digits, k_β = 2.8565 ± 0.0015. Theoretical results describing the growth of the number of coalescent histories in the family β_n are not known. It is of interest to examine if the generating tree and generating function approaches used here for enumerating compact histories could be extended to the framework of coalescent histories.

By comparison of the values of k_γ, k_λ, and k_β, it can be observed that in more unbalanced trees, the number of compact histories tends to be larger. This correlation is supported by the exhaustive calculation of the number of compact histories for unlabeled topologies of small size (Section 3.3) and by the analysis of bicaterpillar trees with different levels of balance (Section 4.1). More generally, our results prove that for different tree families, the growth of the number of compact histories can be exponentially faster or slower than for other families. An average case analysis of the number of compact histories is conducted in Section 5, where it is shown that the expected number of compact histories of a labeled topology of size n selected uniformly at random grows like 3.3750ⁿ. Interestingly, the constant 3.3750 is not far from the mean (k_γ + k_λ + k_β)/3 ≈ 3.3955.

Note that because coalescent histories are at least as numerous as compact histories, the value 3.375 provides a lower bound for the exponential order of the sequence of the mean number of coalescent histories of a labeled topology of size n chosen uniformly at random. This lower bound is unlikely to be precise, as sequences of the number of coalescent histories in specific families substantially exceed this value in exponential order. For example, for caterpillar and bicaterpillar families, the agreement of the number of compact histories with the number of coalescent histories gives an exponential order of 4 for sequences of the number of coalescent histories. An exponential order of 4 has also been associated with caterpillar-like families that begin with a seed tree t⁽⁰⁾ and for n ≥ 1 sequentially build a family of trees t⁽ⁿ⁾ by appending t⁽ⁿ⁻¹⁾ and a single taxon to a shared root (Rosenberg, 2013; Disanto and Rosenberg, 2016). Moreover, as noted above, the number of coalescent histories for the lodgepole family grows faster than exponentially (Disanto and Rosenberg, 2015).

Many enumerative problems concerning compact histories remain open. For instance, to understand the computational complexity of gene tree probability algorithms, it would be of interest to obtain comparative results relating numbers of compact histories not only to numbers of coalescent histories, but also to enumerations of the ancestral configurations (Wu, 2012; Disanto and Rosenberg, 2017) and “nonequivalent” ancestral configurations (Wu, 2012; Disanto and Rosenberg, 2018) that arise in alternative probability methods. It would also be of interest to have an explicit characterization of those labeled topologies that, for a given number of taxa, possess the largest and smallest numbers of compact histories. Results from Section 3.3 suggest that the maximally asymmetric caterpillar trees might have the largest number of compact histories, whereas for small n, trees with the smallest number appear to follow a recursive decomposition that appears in other settings (Eq. 5).

We have considered compact coalescent histories only for matching gene trees and species trees. For non-matching trees, the characterization in Section 3.4 of cases in which the numbers of compact histories and coalescent histories are equal does not have a natural extension. For caterpillar gene trees and arbitrary species trees, they continue to be equal: because coalescences in a caterpillar gene tree must follow a unique sequence, the only nonzero labels in a compact history must be associated with species tree internal nodes that all lie on a single path in which any two distinct nodes k₁, k₂ satisfy k₁ < k₂ or k₂ < k₁. Proceeding from the “smallest” node in this path to the species tree root, the nonzero labels in the compact history indicate the gene tree coalescences in the specified unique sequence, identifying only one coalescent history. This reasoning of Wu (2016) for matching caterpillar gene trees and species trees applies to caterpillar gene trees with arbitrary species trees as well.

However, the equivalence of coalescent histories and compact coalescent histories seen with caterpillar gene trees and arbitrary species trees does not extend to the other settings in which the equivalence holds for matching trees. The case of bicaterpillar (and caterpillar) species tree (((((a, b), e), f), c), d), bicaterpillar gene tree ((((a, b), c), d),(e, f)), and a compact history with label 1 above subtree (((a, b), e), f), 4 above the species tree root, and 0 above all other species tree internal nodes provides a counterexample that shows that the numbers of compact histories and coalescent histories need not agree both for the case in which the species tree is a caterpillar or bicaterpillar and for the case in which the gene tree is a non-caterpillar bicaterpillar: two coalescent histories are indicated by the compact history, one with the coalescence above subtree (((a, b), e), f) joins (a, b), and the other in which it joins (e, f). At the same time, many combinations of a gene tree and a non-matching species tree, neither of which is caterpillar or bicaterpillar, can have the same numbers of compact histories and coalescent histories. In the many cases in which all cherries in the gene tree involve taxa on opposite sides of the species tree—gene tree (((a, b),(c, d)),((e, f),(g, h))) and species tree (((a, c),(e, g)),((b, d),(f, h))), for example—only one coalescent history exists, only one compact history exists, and the numbers of compact histories and coalescent histories are trivially equal.

We note that in parallel to the introduction of compact coalescent histories by Wu (2016), a related concept of the population histories of a species tree—equivalent to the compact coalescent histories for a species tree and matching gene tree—was defined by Degnan and Rhodes (2015) for analyzing non-matching caterpillar trees. Using population histories, Degnan and Rhodes (2015, Remark 15) demonstrated that given a caterpillar species tree, the number of coalescent histories, and hence the (equivalent) number of compact coalescent histories, is always larger for the matching gene tree than for a non-matching caterpillar gene tree. We have not compared compact histories for distinct gene trees with a fixed species tree, and we defer a deeper analysis of compact histories of non-matching gene trees and species trees for future work.