Motor constraints influence cultural evolution of rhythm

Abstract

While widely acknowledged in the cultural evolution literature, ecological factors—aspects of the physical environment that affect the way in which cultural productions evolve—have not been investigated experimentally. Here, we present an experimental investigation of this type of factor by using a transmission chain (iterated learning) experiment. We predicted that differences in the distance between identical tools (drums) and in the order in which they are to be used would cause the evolution of different rhythms. The evidence confirms our predictions and thus provides a proof of concept that ecological factors—here a motor constraint—can influence cultural productions and that their effects can be experimentally isolated and measured. One noteworthy finding is that ecological factors can on their own lead to more complex rhythms.

1. Introduction

Among the many factors that play a causal role in the evolution of cultural ideas, behaviours and artefacts, it is useful to distinguish psychological and ecological factors. Psychological factors are capacities and dispositions that may be universal, such as the ability to acquire a language, or specific to some cultural groups, such as the ability to read a given script. Ecological factors are aspects of the physical environment that impose constraints and offer opportunities to human action and interaction. Ecological factors can be universal, like gravity, or local, like the climate. They can consist of the presence of specific kinds of material objects or substances in the environment or of the spatial and temporal distribution of these objects. Many ecological factors are themselves large- or small-scale products of cultural activity, as for instance, a road network, or a set of kitchen tools [1].

While both psychological and ecological factors are involved in the evolution of any cultural trait, they are not equally important in all cases. Psychological factors, for instance, play the main role in the evolution of language, and ecological factors in the evolution of agriculture. In the laboratory, it is in principle possible to investigate the two types of factors separately. This has been done in particular in studies inspired by the cultural attraction framework [2,3]. In this framework, the evolution of a cultural trait can be explained not only in terms of competition and selection of faithfully reproduced variants but also in terms of transformations in the process of transmissions that, being biased rather than random, tend to converge toward ‘attractors.’ For instance, in a transmission chain experiment, a story on bloodletting in which bleeding is practised on a body part of the patient far from the localization of the pain tends to be recalled and transmitted with the bleeding being practised nearer to the localization of the pain. This transformation is then retained in chains of successive recall and transmission episodes, suggesting that this bias towards co-locating pain and cure has contributed to making the practice of bloodletting a cultural attractor [4]. This kind of convergence can secure the relative stability of a cultural trait at the population level over generations in spite of relatively low fidelity in individual episodes of transmission.

There has been a growing corpus of research on psychological factors of attraction (including, for instance, mechanisms involved in predicting other agents' actions and how they influence which spatial compositions are produced in human portraits [5]). Ecological factors of attraction have been occasionally discussed [6], in particular with reference to animal technical traditions [7,8], but they have not yet been experimentally investigated as such. Here, we demonstrate the feasibility of such an investigation by studying the role of a very simple ecological factor—the spatial arrangement of a set of drum pads—in the evolution of a simple rhythm.

Musicality is considered to be a biological and cognitive trait spontaneously developing in humans [9]. It makes possible and underlies musical practices, including singing [10], across human cultures [11]. A variety of major works in studying musical production have focused on more specific universal patterns or characteristics that are found in music productions from all human groups and societies. Exploring both universality and diversity of musical productions was already at the heart of Lomax's Cantometrics projects [12,13], and continued by more recent initiatives such as CantoCore [14]. Research has revealed the existence of statistical universals in human music [15,16] and demonstrated that humans are able to identify the different uses of songs even from cultures other than their own (e.g. lullabies) [17].

Such approaches have built on a more general scientific interest for the human species-wide capacity for music, its possible analogues and homologues in other species and its evolutionary basis [11,18–23]. Such fruitful approaches have mostly focused on psychological factors.

Here, we present a study of ecological factors of attraction in the transmission of rhythm using a transmission chain experiment. Transmission chain experiments (also called iterated learning experiments) mimic cultural transmission in the laboratory by borrowing the structure of the well-known children's game ‘telephone’ [24]. The experimenter gives the first participant some content as an input, which she is then asked to reproduce. This input given to the first generation of participants is referred to as the ‘seed’. Whatever is produced by the first participant is then given to the second participant in the chain, who is asked to reproduce it—and so on until the last participant in the chain (figure 1). This type of experimental paradigm has been proven useful in studying the interactions between cultural transmission and rhythm. In particular, one such experiment [25] focused on how transmission can magnify individual learning biases and thus produce outputs with universal features (such as an isochronous underlying beat, hierarchical organization of beats of unequal strength and grouping of beats in groups of 2 or 3) from random, computer-generated, rhythmic sequences.

Figure 1.

A schematic description of the experimental procedure. The participants first heard a sequence of 13 taps. This sequence was either a metronome-like sequence (for participants in the first generation) or a sequence produced by the previous participant in the chain (for participants in generations 2 to 6). The 24 trials were transmitted and their order randomized between each participant in a chain, and so on until the sixth participant of the chain.

Our study departs from previous transmission chain experiments in several key ways: (i) the topic of inquiry, i.e. the role of motor constraints in music-making has not been investigated with this methodology, and our design allows for both (ii) a pattern of divergence and (iii) an increase in complexity. Those last two aspects raise methodological questions related to paradigms commonly used in studying the evolution and emergence of language.

Previous studies used diffusion chain experiments to show how some priors in the participants' minds determine which contents remain stable through transmission (e.g. [26]). Here, we expect such biases to come from the spatial arrangement of the drums (i.e. ecological properties), which may influence the participants’ movements, rather than from a psychological prior. Motor constraints have been shown to influence melodic aspects in both human and bird songs [27,28]. By comparing anatomies and songs of humans and birds, Adam Tierney and colleagues were able to relate the predominance of arch-shaped and descending melodic contours in musical phrases to respiratory constraints, the tendency for phrase-final notes to be relatively long to articulatory constraints, and the bias toward small pitch movements between adjacent notes in a melody to vibratory constraints [27,28]. Yet, little is known about the impact of motor constraints on rhythmic aspects of music, which is the focus of this study. The possibility that ecological properties of tasks, and how they interact with human cognition, can bias transmission and thereby shape specific characteristics of cultural items, although acknowledged in theoretical works, has not been explored empirically using transmission chains. In this experiment, we test whether spatial properties and their effects on human movement can act as a factor of attraction, by predicting characteristics of participants' productions from parameters relating to the ease with which the required movements can be produced. We manipulate the order in which the drums have to be hit, and as a consequence, the size of the movements, i.e. the distance covered by the movements, required to produce taps. When, for example, a particular distance requires a large movement, it is harder to produce a short inter-onset interval (henceforth IOI) and easier to produce a longer one [29].

The transmission chain experiment we present here includes four conditions (figure 2). Two of our conditions are Equal Movements conditions with the same distance to cover for all movements, which is either small (Small small condition) or large (Large large condition). The two remaining conditions are Unequal Movements conditions. They include both types of distances to cover and differ by the order in which they must be covered—either as the first or third movement (leading to conditions respectively named Large small small and Small small large). All four conditions start with the same seed (a uniform metronome sequence). This study of motor constraints thus provides a demonstration of the possibility of experimentally singling out ecological factors and investigating their specific contribution to the evolution and stabilization of cultural traditions.

Figure 2.

Depictions of our four conditions. All conditions started by tapping on the rightmost pad. The upper row depicts the two Equal Movements conditions (Large large and Small small), and the lower row depicts the two Unequal Movements conditions (Small small large and Large small small).

Previous studies using iterated learning paradigms have demonstrated patterns of convergence between chains (i.e. convergence on a ‘universal-like’ property of the production, e.g. integer ratio intervals [30]). By contrast, we aim to test whether transmission chains can, because of differences in an ecological factor across conditions, lead to different stable ‘cultural items’ (recurrent rhythmic sequences) from the same seed. If motor constraints constitute a factor of attraction in this drumming task, then differences in spatial arrangements across chains that start from the same seed should result in a pattern of divergence. So, by contrast with previous experiments, we predict a divergence between conditions and the emergence of different rhythmic sequences.

Finally, previous experiments focusing on artificial languages [31,32] or musical sequences [25] have used transmission chains in order to demonstrate how structure can emerge from random experimental inputs [33,34]. This cumulative emergence of structure through transmission can be understood as a subtractive [35] ratchet effect on the basis of the assumption that complexity gets reduced over generations with no decrease in performance (e.g. in communication games, the duo or group guesses the correct target from the words used at least as frequently at the end of the experiment as at the beginning). By contrast, the transmission chains here start with a rhythmic sequence that is rhythmically as simple as possible, making it impossible for participants to produce a simpler sequence with the same number of taps. In particular, the seed rhythm is composed of the repetition of just one IOI. We expect transmission episodes to lead to stable and more complex rhythms, resulting from biases created by kinematic patterns in a drumming task. Such results would demonstrate an additive ratchet effect. Specifically, we predict an increase in complexity (from an isochronous beat using only one IOI to a structured rhythmic pattern mixing two different IOIs). We expect the transmitted content to gain, through repeated reproduction, a quality (here, complexity and a specific rhythmic structure) rather than getting rid of variability (coming from the random character of the seed in previous experiments). We record the evolution of the simple uniform rhythm used as a seed over six generations in a transmission chain.

Thus, in this study, we predict that the difference in kinematics between the different conditions will lead to qualitatively and quantitatively different productions. The overall predicted pattern is one of divergence, i.e. the rhythms produced in chains from different conditions will be less and less alike over time (i.e. experimental generations; hypothesis 1). This divergence will be explained by a combination of more specific hypotheses on how the physical affordances in the different conditions impact the rhythm produced.

Through all conditions, we hypothesize, smaller movements will produce shorter IOIs and larger movements longer IOIs. In Equal Movements conditions, the rhythm of the sequences produced should remain isochronous, while Unequal Movements conditions should move away from isochronous rhythms (hypothesis 2). In Equal Movements conditions, the size of the movement should predict the relative length of the IOIs: shorter in the condition that includes only small movements than in the condition that includes only large movements (hypothesis 3). In Unequal Movements, we can predict which IOI will be longer: it should be the first one in the sequence whenever the larger movement occurs first, and the third in the sequence whenever the larger movement occurs third (hypothesis 4). Together these four hypotheses predict, with precision, characteristics of the rhythmic sequence participants will produce at the end of the chains, based on the motor constraints they encounter in each condition.

Finally, we expect to have stable rhythms by the end of our transmission chains. The predicted emergence of stability means that we expect the amount of change—i.e. copying errors (differences between what a participant heard and what she produced)—to decrease through the chain (which corresponds to learnability or copying accuracy increasing) (hypothesis 5). This has been observed in previous experiments as well, e.g. [25], and is usually interpreted as an increasing match between what participants have to reproduce and their own biases. We expect this type of gradual change to occur in all conditions.

2. Methods

(a). Participants

A total of 120 participants (38 male, 80 female, 2 not known, mean age = 26, s.d. = 4.5) participated in this experiment. All participants were right-handed and had no musical training (they had neither learned to play an instrument, nor taken music lessons). All participants gave their informed consent and received gift vouchers as compensation. This research was approved by the United Ethical Review Committee for Research in Psychology (EPKEB) on behalf of the Central European University (ethics approval number 2018-18).

(i). Sample size and sample size rationale

We collected five transmission chains of six participants (generations) per condition. Each participant took part in 24 trials. These sample sizes were decided a priori on the basis of previous experiments and pre-registered¹. Our pre-registration is available here: https://osf.io/8p4mz/?view_only=ec41d8ed252d4cbf963aac4abc172a7b. Participants were randomly assigned to one of the four different conditions.

(b). Stimuli

(i). Seed and transmitted sequences

For the first generation, the seed—i.e. the first generation's input—was a regularly spaced beat, isochronous (metronome-like) sequence, of 13 beats. For all subsequent generations, the input consisted of whatever sequence was produced by the previous participant in the chain. The initial seed interval ratio of evenly spaced beats (1 : 1 : 1) also has one advantage: it is rather infrequent in most music our participants might be familiar with, thus avoiding biased priors or showing strong cultural variation [36,37].

The seed is played at a tempo of 120 beats per minute (BPM). This tempo was chosen based on the results from a pilot experiment which indicated that, with this tempo, it is possible, but not trivially easy to reproduce the given pattern, but the reproduction was not trivially easy with our task setup. Moreover, 120 BPM or an IOI of 500 ms is known to be a ‘preferred’ tempo for humans, being easy to process [38] and used in a variety of tasks, including serial interval production [39].

(ii). Physical setup

Participants were given headphones and a single drumstick and presented with a set of three independent Millenium drum pads connected to a MacBook Pro laptop via a trigger box (ddrum DDTi) that sent MIDI notes. The three drum pads had a diameter of 20.5 cm and were evenly spaced, by 20 cm (see also figures 1 and 2). Overall, our large movement had to cover twice the distance covered by small movements. All three drum pads used produced the same sound (same pitch): they were all set to a percussion sound with a sharp onset (MIDI Note 60 from the standard Mac OS sound bank).

(c). Procedure

Participants were asked to recreate a pattern of sounds by tapping different drum pads in a certain order. The experimental design used a linear transmission chain method, i.e. with output from a participant serving as input for the next participant, akin to the telephone game. Participants were explicitly asked to reproduce the audio they heard as faithfully as possible.

Each participant had to listen to and reproduce 24 sequences spread across 24 trials. In each trial, participants heard a sequence of 13 taps, which was either a metronome (for the first participant in each chain), or a sequence produced by the previous participant in a chain, which was the case for all participants in generations 2 to 6. Participants then had to reproduce the sequence using the drumstick and the drum pads in front of them. Depending on the condition they were assigned to, they had to reproduce the sequence they heard either using only movements covering the same distance (Equal Movements conditions, with only small or only large distances), or a mix of large and small distances, in a different order in each condition (Unequal Movements conditions, figure 2). They had to listen to and reproduce 24 sequences spread across 24 trials.

Each sequence was recorded and given to the next participant in the chain. Participants were unaware they would be listening to stimuli produced by a previous learner. All sequences produced by one participant were transmitted to the next participant in the chain, with no change and in their entirety. The order in which sequences were presented to participants was randomized at each transmission step. We recorded all taps produced by the participant with their velocity (ranging from 0 to 127) and with timestamps (from which we calculated IOIs).

After the behavioural task, participants completed a short questionnaire with the following questions: (i) how difficult was the task? (answered on a scale from 0, very easy, to 7, very difficult), and (ii) do you have any musical experience? (classes, played an instrument?); if yes, please specify.

The physical apparatus and the initial sequence were the same in all four conditions. The study had a between-subjects design such that each participant took part in only one of the four conditions. In total, the experiment took around 20 min per participant.

(d). Data analysis

(i). Data pre-processing

Whenever a sequence was missing or compromised owing to technical problems, one other trial among the 23 available ones from the same participant was randomly selected and passed on. This ensured that all participants went through the same number of trials, and no participants who had such doubles as input sequences noticed that they were actually identical. The total number of trials with problems (not recorded/recording not viable owing to software issues) was 22 (over a total of 480 trials, i.e. amounting to 4.58% of the total number of trials, and distributed over all four conditions).

3. Results

In order to illustrate our results, we created audio files that reflect the mean sequence produced by participants of each condition, at the first and the last generation, which can be listened to at https://osf.io/8p4mz/?view_only=ec41d8ed252d4cbf963aac4abc172a7b. These audio files were produced by averaging each IOI (out of the 12 included in each sequence of 13 taps) from all the sequences produced by all participants from all chains of the same condition at the same generation. An audio file is also available for the sequence used as the seed.

(a). Hypothesis 1: overall divergence between different conditions

We predicted that chains would become increasingly different between all four conditions. We tested this prediction by calculating the Jensen–Shannon divergence (JSD) on the sequence of IOIs. Here, we prefer the JSD as a measure of distance to the Kolmogorov–Smirnov distance (KSD) because of its sensitivity to the order of the IOIs. For instance, comparing the two sequences 500–550–600 and 600–500–550 would give a KSD of zero, but a JSD of 4.93. The JSD was calculated for each generation separately by comparing each trial in a given condition with all trials from the same generation but from the other conditions. The average distance of a chain to other chains that are not from the same condition (the divergence between conditions) increased over time. A Page trend test confirmed that the JSD between conditions increased over generations, whether we included the first generation (L = 1778, k = 6, N = 20, p < 0.001) or not (L = 1059, k = 5, N = 20, p < 0.001) (figure 3).

Figure 3.

Jensen–Shannon divergence (JSD) calculated between each trial and all trials from different conditions at each generation, by generation. Error bars represent the 95% confidence intervals.

(b). Hypothesis 2: Equal Movements conditions versus Unequal Movements conditions

Our experimental design builds on the assumption that larger movements tend to produce longer IOIs. We thus tested whether that assumption by use of a mixed effects model. IOI was the dependent variable. Size of the movement (large or small) was used as a fixed effect, while participant nested by generation was used as a random effect. The condition was not used in this model, as some conditions included only one type of movement, while others had both. The mixed effects model revealed a significant main effect of the movement's size, such that compared with large movements, small movements produce shorter IOIs (β = −192.423, s.e. = 2.833, t_16347.593 = −67.93, p < 0.001) (figure 4).

Figure 4.

Distributions of IOIs by condition, generation and movement size. (Online version in colour.)

We predicted that both conditions including all equal movements, which we refer to as Equal Movements conditions (Large large and Small small), would show an increase in complexity under the form of a bimodal distribution of IOIs (i.e. a non-isochronous rhythmic sequence), whereas both conditions in which not all movements are equal, Unequal Movements conditions (Large small small and Small small large conditions) would not (i.e. they would produce non-isochronous rhythmic sequences).

Visual inspection confirms that the distribution of IOIs in the Equal Movements conditions tended to become bimodal, whereas this was not the case for Unequal Movements conditions (figure 4).

Rhythmic structure was assessed using normalized pairwise calculations (nPCs) [40,41]. NPCs provide a ratio between two successive IOIs: they do not consider their absolute value, only the relationship between them. From [40], it can be calculated as

$$\mathrm{nPC}=200\times \left|\frac{\text{antecedent}\hspace{0.17em}\text{IOI}-\text{consequent}\hspace{0.17em}\text{IOI}}{\text{antecedent}\hspace{0.17em}\text{IOI + consequent}\hspace{0.17em}\text{IOI}}\right|.$$

Visual inspection suggests that the distribution of nPCs became bimodal for Unequal Movements conditions (i.e. Large small small and Small small large), but that this was not the case for Equal Movements conditions (Large large and Small small) (figure 5).

Figure 5.

Histogram of normalized pairwise calculations (nPCs) per condition and generation.

In order to test for a difference in the types of rhythm, we computed the normalized pairwise variability index (nPVI, see below) for each sequence produced by participants. The normalized pairwise variability index is a measure that has a minimal value of 0 when all IOIs are equal, and increases as a sequence gets more unequal IOIs. It can be calculated as follows, from [40]:

$$\mathrm{nPVI}=\frac{100}{m-1}\ast \sum _{k=1}^{m-1}\left|\frac{\text{IO}{\text{I}}_k-\text{IO}{\text{I}}_{k+1}}{(\text{IO}{\text{I}}_k+\text{IO}{\text{I}}_{k+1})/2}\right|,$$

where m is the total number of IOIs, and k stands for which IOI in the sequence is considered.

This distribution of nPVIs is used to test whether there is a change from the seed (i.e. metronome sequence): any divergence from this rhythm translates to an increase of the nPVIs. Overall, nPVI increased for both Equal Movements conditions (L = 829, k = 6, N = 10, p < 0.001 including the first generation; L = 478, k = 5, N = 10, p = 0.041 excluding the first generation) and Unequal Movements conditions (L = 870, k = 6, N = 10, p < 0.001 including the first generation; L = 511, k = 5, N = 10, p < 0.001 excluding the first generation) (figure 6).

Figure 6.

Normalized pairwise variability index (nPVI) by generation and conditions. Error bars represent standard 95% confidence intervals. (Online version in colour.)

A Kolmogorov–Smirnov test on the distribution of nPVI at the last generation confirmed that the Equal Movements conditions (Large large and Small small) had a different nPVI from the Unequal Movements conditions (Large small small and Small small large) (D = 0.84, p < 0.001). A t-test at the final generation suggested that Unequal Movements conditions (M = 50.54, s.d. = 14.96) had higher nPVIs than Equal Movements conditions (M = 15, s.d. = 15.41) (t_455.00 = 25.03, p < 0.001, d = 2.34).

(c). Hypothesis 3: movement size predicts the mean inter-onset interval of Equal Movements

We predicted that Equal Movements conditions (Large large and Small small) would show isochronous rhythms, but with different IOIs (Small small should have shorter IOIs than Large large). IOIs were not normally distributed (Shapiro–Wilk: W = 0.817, p < 0.001), but the differences between the IOIs produced in both conditions were also confirmed by a Mann–Whitney U-test (U = 332850, p < 0.001): IOIs produced in the Large large condition (median = 539 ms) were larger than the ones produced in the Small small condition (median = 472.5 ms) (figure 7).

Figure 7.

Mean inter-onset intervals (IOIs) by condition (Large large or Small small) and generation (first to sixth). Error bars represent 95% confidence intervals. The dashed line indicates the seed's IOI (500 ms). (Online version in colour.)

A mixed effects model², including condition and generation as main effects, and participants nested by chain as a random effect, showed that this pattern emerged over generations. There was a significant interaction effect between condition and generation (β = −18.991, s.e. = 9.387, t_55.971 = −2.023, p = 0.0479), indicating that as generations passed, the difference in IOI between the Large large and the Small small conditions increased. There was also a significant effect of generation (β = 19.791, s.e. = 6.638, t_55.984 = 2.982, p = 0.004), but not of condition (p = 0.28) (figure 7).

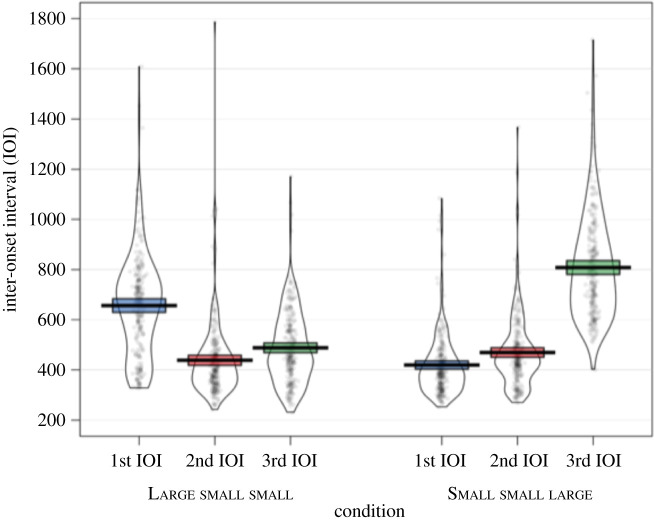
(d). Hypothesis 4: the order of movements of different sizes predicts the order of larger and smaller inter-onset intervals in Unequal Movements conditions

We predicted that while Unequal Movements conditions would show non-isochronous rhythms, they would have longer IOIs in different places. This longer IOI (out of three) should occur first when the large movement occurs first in the sequence (Large small small condition), and third when the large movement occurs last in the sequence (Small small large condition).

We predicted that the condition (Small small large or Large small small) should impact which order in the cycle (i.e. first, second or third) is associated with longer IOIs. We should observe an interaction effect between condition and order in a cycle. A cycle was understood as three consequent IOIs, to reflect the set of movements used, and the factor order in the cycle could thus take the values 1, 2 or 3. Because we analysed sequences of two such cycles (taps 4 to 10, i.e. six IOIs), there were two IOIs per order in the cycle of movements per trial.

Condition and Order in the cycle were used as fixed effects, and participants nested by chain were used as random effects in a linear mixed effects model. On the last generation, the mixed effects model revealed significant effects of both order in cycle (β = −84.50, s.e. = 7.705, t₁₃₇₄ = −10.967, p < 0.001) and condition (i.e. Small small large, compared with Large small small; –β = −521.824, s.e. = 57.073, t_10.952 = −9.143, p < 0.001). An interaction effect between condition and order of the IOIs in the cycle confirmed our prediction (β = 279.06, s.e. = 10.873, t₁₃₇₄ = 25.666, p < 0.001) (figure 8). This difference emerged over time (see electronic supplementary material).

Figure 8.

IOI by their order in the cycle, by condition, at the sixth (last) generation. The coloured bands represent the 95% confidence intervals, points the raw data, and the external curve is the distribution's density. (Online version in colour.)

(e). Hypothesis 5: stability over generations

We hypothesized that our experiment would produce stable rhythms, and that the rhythms produced by participants would become easier to reproduce. Because our prediction bore on the rhythmic sequence becoming stable, we used an edit nPC distance; by analogy with the (edit) time distance [25], it can be defined as the total cost of the minimal cost set of substitutions, insertions or deletions among nPCs necessary to transform the pattern of nPCs a participant has heard into the pattern they have reproduced.

The edit nPC distance increased over time, as confirmed by a Page trend test, both when including the first generation (L = 1668, k = 6, N = 20, p < 0.001) or excluding it (L = 978, k = 5, N = 20, p < 0.001). This result was unexpected. We had predicted an increase in stability, i.e. a decrease in the quantity of change, but we observed an increase in the quantity of change. Additional analyses revealed that edit distances depended, to some extent, on both generation and condition—see electronic supplementary material for additional analyses, figure and similar results on edit time distances.

4. Discussion

This study had four different conditions, which differed in the sequence of movements required to reproduce a rhythmic sequence. All conditions started with the same seed: an isochronous sequence of 13 taps equally spaced by 500 ms. We predicted that differences in physical affordances and movements produced by participants (an ecological factor of attraction) would determine which rhythmic sequences ended up being produced in the different conditions (different attractors). We observed, as predicted, an overall pattern of divergence between the different conditions.

Furthermore, the different conditions included in our study could either fit or not fit with the rhythm of the seed: Equal Movements conditions had only one size of movements, in the same way that the seed had only IOIs of the same duration. Unequal Movements conditions changed more than Equal Movements conditions. Motor constraints and their fit with different rhythmic sequences influenced both how much transformation took place and which productions were stable. Motor constraints had an effect on three features: (i) whether the rhythm produced remained isochronous or not over six generations of participants; (ii) the overall length of the IOIs; and (iii) the order in a cycle of movements in which longer or shorter IOIs occur. The differences in motor affordances created an overall pattern of divergence: the distance between rhythmic sequences produced by participants across different conditions increased over experimental generations. Participants could have reproduced the isochronous seed and kept IOIs identical throughout by moving faster for larger distances or slower for smaller distances, but instead they tended to keep a constant movement velocity and therefore tended to produce unequal IOIs. We did not observe the reverse tendency, that is, participants from the second generation onward hearing a pattern with unequal IOIs and tending to equalize them by speeding up some of their movements. With our hypotheses 1 to 4 confirmed, this study provides a proof of concept of the influence of a type of causal factor—an ‘ecological’ factor of attraction—instantiated by motor constraints in this particular case.

Hypothesis 5, by contrast, was not confirmed. We did not find an increase in learnability in participants' productions. Both measures of change between what participants heard and what they produced (either on the IOIs directly or a measure of rhythmic structure—nPCs) did not show a decrease over generations. The motor constraints impacted not only which rhythms were produced in our experimental populations, but also how stable these rhythms were.

In addition to ecological factors, psychological factors might have also played a role in at least some of our results. Most of the IOIs produced by the participants remained around 500 ms or 120 BPM (figure 3). By choosing this target IOI, which is known to be a ‘favoured’ tempo, we might have limited the potential for the sequences to drift further away from these initial IOIs. For the Unequal Movements conditions, the rhythmic sequences produced by participants moved closer to the next possible integer ratio (1 : 1 : 2 or 2 : 1 : 1, equivalent to an nPVI of 66.67). This could also correspond to an attractor, since such small integer ratios are known as a universal feature of human songs [16]. Participants tend to converge towards these ratios after a few iterations of reproducing an initially random rhythmic sequence [30].

A great deal of work has focused on psychological aspects of music-making (e.g. [30]). The present study provides a proof of concept of the role of motor constraints in musical production. If such constraints have played a role in the cultural evolution of musical practices, this should be observable through patterns of coevolution of music and instruments. Thus our results may have implications for the study of the evolution of instruments. Evolutionary changes should flow in both directions: from the instruments to the music produced, and from the music to be produced to the design of the instruments. The evolution of violins might provide a relevant example: when female voices became more popular in Baroque music, violins were made to produce a sound closer to such voices [44]. In our experiment, all three drum pads produced the same sound. In actual instruments, on the other hand, we should expect to see the physical characteristics of instruments to vary in relation to desired sound properties. Instruments themselves might exhibit spatial organizations making them easier to use, depending on characteristics of the music they are used to produce. One such example is the way some string instruments, like guitars, can be tuned so that some melodies become easier to play. More generally, our results also argue in favour of the existence of a large array of possible causal factors in explaining cultural phenomena, including psychological and ecological factors and, among the latter, apparently simple motor constraints. In particular, encountering or imposing different motor or material constraints can produce different cultural items—in our case, different rhythmic structures. This finding also echoes the observation of the emergence of different drumming patterns in chimpanzees depending on the medium used [45].

There are a number of features of the present study that might contrast with music-making in the wild. This study recruited novice participants, who are less able to overcome different motor constraints than experts. The question of the extent to which expert performance is influenced by motor constraints remains. Even if expert music production might be less influenced by such constraints, physical affordances might still play a role in the acquisition of expertise as it clearly does in the case of novices. Whereas in this study learners were provided with only an acoustic input from the previous generation, real-life transmission and the acquisition of expertise typically involves several modalities: acoustic, visual and often haptic. Music is also, more often than not, produced collectively, by two or more individuals involved in joint action [46]. Joint action, and coordination with one or several partners, is itself a complex, at least partly ecological factor of attraction [47]. It can be expected to have influenced the evolution of several aspects of musical productions, including, for instance, the tempo [48], in non-trivial ways.

Ethics

All participants gave their informed consent and received gift vouchers as compensation. This research was approved by the United Ethical Review Committee for Research in Psychology (EPKEB) on the behalf of the Central European University (ethics approval number 2018-18).

Data accessibility

All raw data and scripts used for analyses are available at https://osf.io/8p4mz/.

Authors' contributions

All authors discussed the experiment's design. H.M. and T.W. collected the data and made the figures. H.M. analysed the data and drafted the manuscript. All authors gave feeedback on the manuscript.

Competing interests

We declare we have no competing interests.

Funding

The research reported in this manuscript was supported by the European Research Council under the European Union's Seventh Framework Programme (FP7/2007-2013/ERC grant agreement no. 609819), SOMICS. H.M. was supported by a Complexity postdoctoral fellowship at the Santa Fe Institute.