SEIAQRDT model for the spread of novel coronavirus (COVID-19): A case study in India

Abstract

COVID-19 is a global pandemic declared by WHO. This pandemic requires the execution of planned control strategies, incorporating quarantine, self-isolation, and tracing of asymptomatic cases. Mathematical modeling is one of the prominent techniques for predicting and controlling the spread of COVID-19. The predictions of earlier proposed epidemiological models (e.g. SIR, SEIR, SIRD, SEIRD, etc.) are not much accurate due to lack of consideration for transmission of the epidemic during the latent period. Moreover, it is important to classify infected individuals to control this pandemic. Therefore, a new mathematical model is proposed to incorporate infected individuals based on whether they have symptoms or not. This model forecasts the number of cases more accurately, which may help in better planning of control strategies. The model consists of eight compartments: susceptible (S), exposed (E), infected (I), asymptomatic (A), quarantined (Q), recovered (R), deaths (D), and insusceptible (T), accumulatively named as SEIAQRDT. This model is employed to predict the pandemic results for India and its majorly affected states. The estimated number of cases using the SEIAQRDT model is compared with SIRD, SEIR, and LSTM models. The relative error square analysis is used to verify the accuracy of the proposed model. The simulation is done on real datasets and results show the effectiveness of the proposed approach. These results may help the government and individuals to make the planning in this pandemic situation.

Introduction

Many times, in the past, human pandemics and epidemics have destroyed humankind, usually, these pandemics have made many changes in the living of humankind. Similarly, due to the novel coronavirus, the whole world is again facing the deadly experience which affects human lives the most [1]. WHO declared the COVID-19 as an international pandemic on March 11, 2020 [2]. According to WHO, the continuing pandemic of novel coronavirus has asserted 5,31,806 deaths and 11,301,850 confirmed cases in the world, as of July 6, 2020 [2]. In India, 7,00,728 confirmed cases, and 19,721 deaths have been reported till July 6, 2020 [3]. The government of India also accepted it as pandemic and imposed a nation-wide lockdown on March 23, 2020. Almost the entire nation has been locked down and different preventative measures, like sanitization of containment zones, identifying close contacts, quarantining infected individuals, encouraging social consensus on individual-protection such as wearing a face-mask, using hand-sanitizer, and washing hands regularly, etc. have been employed. Although, the cases of novel coronavirus are continuing and the number of daily confirmed cases is making a new record.

COVID-19 has been showing unusual characteristics in comparison to earlier coronavirus (i.e., the SARS-CoV and MERS-CoV) epidemic [4]. A considerable number of transmissions of COVID-19 is observed via human-to-human contact with individuals having no symptoms or the mild symptom of the disease [5]. The Immense viral capacity of SARS-Cov-2 was observed within the upper respiratory system of patients with mild symptoms or without symptoms [6]. Therefore, the subclinical infection may play an important part in maintaining the epidemic. Mathematical modeling is one of the prominent techniques for predicting and controlling the spread of coronavirus [7–10]. The popular SIR model [11] characterized the spread of infection using susceptible, infected, and removed compartments. Generally, new factors are incorporated in the SIR model to obtain more relevant information is a common practice. Therefore, several mathematical models have been introduced by improving the SIR model to capture the dynamics of COVID-19. Lin et al. [12] developed a conceptual SEIR model which includes factors like individual reaction and government activity. Giordano et al. [4] developed the SIDARTHE model which incorporates undetected and detected infected individuals. Prem et al. [13] studied the impact of control strategies through the SEIR model. Peng et al. [14] developed a generalized SEIR model that covered the transmission of COVID-19 in the latent period. The novel coronavirus tends to transmit from human-to-human within the latent period [15]. Till today, no proper vaccine or treatment is available for the disease. Hence, the best way to control the spread of the pandemic is the prediction of the number of infected cases that benefit the authorities in better planning of control strategies. Commonly used models like SIR [16–18], SEIR [18], and SEIJR [19] are not appropriate to predict the impact of the epidemic because they include a limited number of factors and ignored some important factors like asymptomatic cases, quarantined cases, etc. Moreover, recurrent neural networks (RNN), such as long-short term memory (LSTM), models are generally focused on the number of infectious. The main drawback of the LSTM based models is that these models do not consider the effect of quarantined cases, asymptomatic cases, protected population, etc. Therefore, it motivates us to propose a model that includes the ignored factors to estimate the number of infected cases accurately. The high number of asymptomatic cases have been reported in India. So, it is important to incorporate asymptomatic cases in the mathematical model. In this paper, we proposed a new mathematical model (SEIAQRDT) by extending the generalized SEIR model given by Peng et al. [14] for India and its highly affected states. The proposed eight compartmental model incorporates factors such as susceptible, exposed, infected, asymptomatic, quarantined, recovered, dead, and insusceptible. In this model, asymptomatic and symptomatic patients are treated differently. The nation-wide lockdown and compulsion on wearing of face-mask to get an accurate prediction are also considered. The simulation results offered by the proposed model are very close to the actual data as compared to other models. This paper divided into 5 sections. Section 1 gives an introduction. A brief overview of the related works is given in Section 2. In Section 3, we discuss the newly proposed mathematical model and its parameter values. In Section 4, the simulation results and discussion for India and its majorly affected states are presented. The performance of the proposed model is compared with three different models (SIRD, SEIR, and LSTM models) for different countries. Section 5 gives the conclusion and possible future works.

Literature Review

In this section, currently available epidemiological models for prediction of coronavirus (COVID-19) are briefly discussed. These models help to estimate the number of COVID-19 patients. Some of the popular mathematical models (e.g. SIR, SEIR, SEIJR, SEIAR, and SEIRD) are widely used to estimate the future outbreak of communicable diseases.

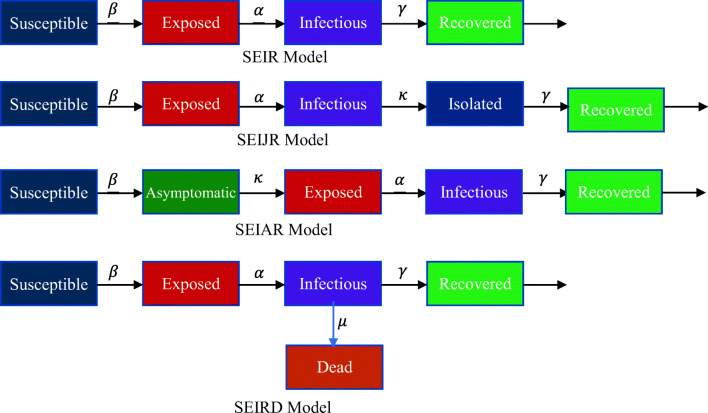
Zareie et al. [20] applied the SIR model to the prediction of coronavirus spread in Iran based on China parameters. Zhang et al. [21] proposed the SEIR model which illustrates the relation among susceptible, exposed, infectious, and recovered individuals. It is the widely used model that predicted the outbreak of coronavirus in China as well as in other countries. Fan et al. [22], Geng et al. [23] and Zhou et al. [24] used this model for the prediction of the outbreak of the coronavirus in China. This model accepts a limited amount of actual data and offers a correct prediction for the small period but the prediction for a long period is not much accurate. Yang et al. [25] proposed the modified SEIR model by introducing the two new parameters move-in and move-out for the inflow and outflow of susceptible individuals respectively. The basic structure of the different compartmental models for the prediction of infected cases is shown in Fig. 1. Lin et al. [12] discussed the conceptual SEIR model by incorporating the factors government action and public perception. Read et al. [26] proposed the extended version of the SEIR model.

Fig. 1.

4 different compartmental models for the prediction of the total number of infected cases

It includes one more factor asymptomatic individual during the incubation period in the SEIR model. It precisely segregates an isolated individual from the other populations. However, it is difficult to collect precise data for individuals which makes it difficult to get the best-fit parameters. Hence, the long-term forecasting is distant from the real data. The major difference between the SEIJR and the SEIAR is that isolated individuals are replaced with asymptomatic individuals. Bai et al. [27] applied this model and show similar properties to the SEIJR model. Additionally, this model deals with the zoonotic force of pneumonia and daily new infected cases. This model is applied by Wu et al. [28] and its simulation is very accurate to pandemic’s actual data at the starting stage.

The models discussed above have their specific properties. However, no one is perfect for long-range forecasting because of the number of parameters and model accuracy. Therefore, one more parameter i.e. the dead individual has been introduced by Huang et al. [29] in the SEIAR model to improve the accuracy of the model for long-term prediction. They also include two new factors, i.e., time of isolation initiation and intensity of isolation that the government has taken. The accuracy of this model is also better than the previously discussed models. Some artificial intelligence models are also applied to estimate the number of infected cases of coronavirus [30, 31]. Pathan et al. [32] applied the recurrent neural network-based LSTM model to predict the time-series of COVID-19 through mutation rate analysis. Kirbas et al. [33] predicted the total number of cases of Denmark, Belgium, Germany, France, United Kingdom, Finland, Switzerland, and Turkey with the help of the LSTM model. Jana et al. [34] studied the COVID-19 dynamics transmission for the USA and Italy with the help of the convolution LSTM model. Arora et al. [35] applied deep LSTM, convolutional LSTM, and Bi-directional LSTM to predict the confirmed cases for India and performed the comparative analysis for these models. LSTM models are generally focused on the number of infectious. The main drawback of the LSTM based models is that these models do not consider the effect of quarantined cases, asymptomatic cases, protected population, etc. These factors are essential to study the impact of COVID-19.

Model Formulation

In this section, we present a new mathematical model for the prediction of the number of coronavirus cases. In this model, we consider asymptomatic and quarantine as a separate compartment. The basic reproduction number and stability analysis is also discussed.

Generalized SEIR model with asymptomatic cases

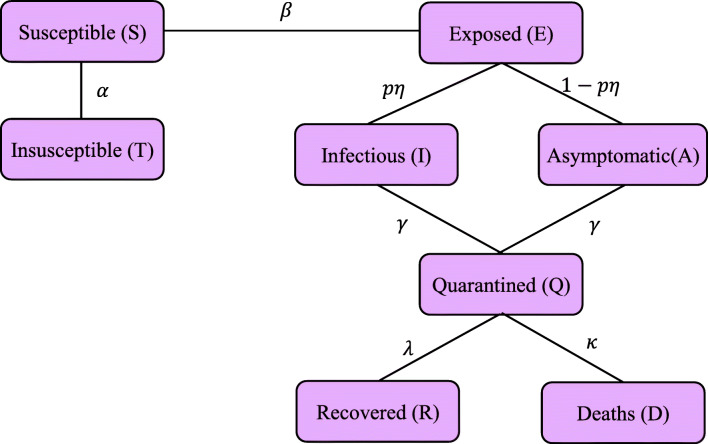
To describe the pandemic of a novel coronavirus in India and its states, eight compartmental mathematical model, namely SEIAQRDT, is proposed. In this model, S(t) represents the susceptible population at time t, E(t) represents the exposed population (population those are infected but do not infect others within the latent period), I(t) represents the infectious (symptomatic) population (that have the scope to infect others and still not quarantined), A(t) represents infectious (asymptomatic) population (that have scope to infect others, but have no symptoms of the disease), Q(t) represents the quarantined population (the confirmed population that is infectious), R(t) represents the recovered population, D(t) represents the death population, and T(t) represents the protected population. The systematic compartmental diagram is shown in Fig. 2.

Fig. 2.

Compartmental diagram for SEIAQRDT model

The system of differential equations which describe the COVID-19 epidemic in India and its states are as follows:

$${\displaystyle \begin{array}{c}\frac{dS(t)}{dt}=-\frac{\beta S(t)(I(t)+q(A(t)))}{N}-\alpha S(t)\\ \frac{dE(t)}{\mathrm{d}\mathrm{t}}=\frac{\beta S(t)(I(t)+q(A(t)))}{N}-\eta E(t)\\ \begin{array}{c}\frac{dI(t)}{dt}=p\eta E(t)-\gamma I(t)\\ \frac{dA(t)}{dt}=(1-p)\eta E(t)-\gamma I(t)\\ \begin{array}{c}\frac{dQ(t)}{dt}=\gamma (I(t)+A(t))-\lambda (t)Q(t)-\kappa (t)Q(t)\\ \frac{dR(t)}{dt}=\lambda (t)Q(t)\\ \begin{array}{c}\frac{dD(t)}{dt}=\kappa (t)Q(t)\\ \frac{dT(t)}{dt}=\alpha \mathrm{S}(t)\end{array}\end{array}\end{array}\end{array}}$$ 1

with initial conditions S(0) > 0, E(0) ≥ 0, I(0) > 0, Q(0) ≥ 0, R ≥ 0, D ≥ 0, T ≥ 0.

The total population of a particular region is assumed to be constant, which is represented by N = S + E + I + Q + R + D + T.

Parameters and their definition
Symbol	Definition
α	Protection rate
β	Infection rate
N	Total population
η	Inverse of the average latent time
𝑝	Probability of symptomatic infectious
γ	Quarantine rate
λ(t)	Recovery rate (time-dependent)
κ(t)	Mortality rate (time-dependent)

Where β is the transmission rate for infectious (symptomatic) individuals and qβ is transmission rate for asymptomatic individuals (qβ < β, i. e. , q < 1). α is the protection rate (it includes the effect of control measures). (1 − p) is the probability of asymptomatic infectious. To consider the dynamics of the proposed model, the recovery rate λ(t) and the mortality rate κ(t) are considered as a time-dependent function.

Basic Reproduction Number

The reproduction number is one of the prominent states in the investigation of contagious disease. It helps in deciding that the diseases disappear or it will continue with the time. Generally, it is illustrated by R₀, which provides the number of secondary cases. The Original infectious person can transmit disease in a population where each individual is susceptible. If R₀ > 1 disease will remain in the population and if R₀ < 1 disease is under control and it will die out. Therefore, in the case of the COVID-19 pandemic, there is a need to plan an effective strategy to make the reproduction number smaller than one [1, 8, 36, 37].

For system (1), a disease-free equilibrium point exists which is denoted by e₀. Where S = N (1 − α) and E = I = A = Q = R = D = 0. As α is the protection rate through which people are protected and therefore the susceptible population is calculated as S = N(1 − α). Thus, R₀ is computed mathematically, and to calculate the reproduction number, we employ the next generation matrix method [8]. The reproduction number for the proposed system is calculated using equation R₀ = ρ(FV⁻¹), where ρ represents the spectral radius of the matrix FV⁻¹ [17]. With

$$F{\left(\right|}_{e_0}=\left[\begin{array}{ccc}0& \beta \left(1-\alpha \right)& \mathit{\beta q}\left(1-\alpha \right)\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]$$

and

$$V{\left(\right|}_{e_0}=\left[\begin{array}{ccc}\eta & 0& 0\\ \mathit{p\eta }& -\gamma & 0\\ \left(1-p\right)\eta & 0& -\gamma \end{array}\right]$$

Hence, the reproduction number is

$$R_0=\rho \left(F{V}^{-1}\right)=\frac{\mathit{p\beta }\left(1-\alpha \right)}{\gamma }+\frac{\mathit{\beta q}\left(\mathit{\gamma \eta }-\mathit{p\gamma \eta }\right)\left(1-\alpha \right)}{{\gamma }^2\eta }=\frac{\beta \left(p+q-\mathit{pq}\right)\left(1-\alpha \right)}{\gamma }$$ 2

Theorem 1. If R₀ < 1, the disease-free equilibrium is locally asymptotically stable, and if R₀ > 1, then the disease-free equilibrium is unstable and a pandemic exists in the population [11].

Stability analysis of disease-free equilibrium

The Jacobian matrix for the model (1) at the disease-free equilibrium point is

$$\left[\begin{array}{cccccccc}-\alpha & 0& -\beta \left(1-\alpha \right)& -\mathit{\beta q}\left(1-\alpha \right)& 0& 0& 0& 0\\ 0& -\eta & 0& 0& 0& 0& 0& 0\\ 0& \mathit{p\eta }& -\gamma & 0& 0& 0& 0& 0\\ 0& \left(1-p\right)\eta & 0& -\gamma & 0& 0& 0& 0\\ 0& 0& \gamma & \gamma & -\lambda \left(t\right)-\kappa \left(t\right)& 0& 0& 0\\ 0& 0& 0& \lambda \left(t\right)& \lambda \left(t\right)& 0& 0& 0\\ 0& 0& 0& \kappa \left(t\right)& \kappa \left(t\right)& 0& 0& 0\\ \alpha & 0& 0& 0& 0& 0& 0& 0\end{array}\right]$$

The characteristic equation for the matrix J is:

$$\mathit{Ch}\left(J\right)=a_0{x}^8+a_1{x}^7+a_2{x}^6+a_3{x}^5+a_4{x}^4+a_5{x}^3+a_6{x}^2+a_{7}x+a_8$$ 3

where

$$a_0=1,a_1=\alpha +\gamma +2\delta +\kappa +\lambda$$

$$a_2=\mathit{\alpha \gamma }+2\mathit{\alpha \delta }+2\mathit{\gamma \delta }+{\delta }^2+\mathit{\alpha \kappa }+\mathit{\gamma \kappa }+2\mathit{\delta \kappa }+\dots \mathit{\alpha \lambda }+\mathit{\gamma \lambda }+2\mathit{\delta \lambda }$$

$$a_3=2\mathit{\alpha \gamma \delta }+\alpha {\delta }^2+\gamma {\delta }^2+\mathit{\alpha \gamma \kappa }+2\mathit{\alpha \delta \kappa }+2\mathit{\gamma \delta \kappa }+{\delta }^2\kappa +\mathit{\alpha \gamma \lambda }+2\mathit{\alpha \delta \lambda }+2\mathit{\gamma \delta \lambda }+{\delta }^2\lambda$$

$$a_4=\mathit{\alpha \gamma }{\delta }^2+2\mathit{\text{αγδκ}}+\alpha {\delta }^2\kappa +\gamma {\delta }^2\kappa +2\mathit{\text{αγδλ}}+\alpha {\delta }^2\lambda +\gamma {\delta }^2\lambda$$

$$a_5=\mathit{\alpha \gamma }{\delta }^2\kappa +\mathit{\alpha \gamma }{\delta }^2\lambda ,a_6=0,a_7=0,a_8=0$$

Since one of the eigenvalues of the matrix J is zero. Hence, the system is singular. Due to this, the stability of the system (1) near the disease-free equilibrium cannot be concluded using eigenvalues. However, from theorem 1, the system (1) is unstable. We obtained R₀ > 1 for India and its states.

Numerical simulations & discussion

In this section, we present the numerical simulations for India and its most affected states. The comparison of simulation results with real data is also made from March 14, 2020 to July 03, 2020. The real data of India, Maharashtra, Tamil Nadu, Gujarat, and Delhi [3] is used for comparison. We also compare the results of the proposed model with other state-of-the-art works reported by different authors [25, 31, 38, 39].

India

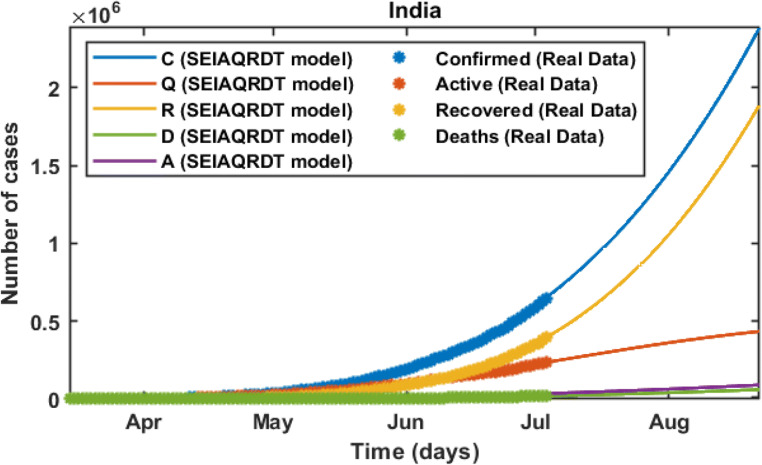
The model fitting of cumulative cases in India reported till July 03, 2020 shows a satisfactory estimation. The model also shows the fitting of recovered and death cases. The number of quarantined cases is also considered as active cases. The total active cases are the sum-up of quarantined, hospitalized, and self-isolation cases which are also fitted in our model. In addition to quarantined cases, asymptomatic cases are also incorporated. The data for fitting is examined from the second week of March. The evolution of the total number of cases, deaths, recovered and quarantined cases have been tracked very closely with the data up to July 03, 2020. The model predicts the peak of the daily number of cases in the first or second week of September with an estimation error may be less than 5%. The recent situation includes protective measures like nation-wide lockdown, wearing of face-mask, and identification of containment zones. Hence, it is observed that the number of cases is much higher if these restrictions were not imposed. Around 2.4 million cumulative cases are approximated till the second last week of August whereas 1.85 million people will be recovered from COVID-19 and around 0.06 million deaths are estimated in India by the second last week of August. The number of asymptomatic cases is approximated around 0.09 million based on the assumption that the probability of transmission of asymptomatic infectious is lower than symptomatic patients, whereas the recovery rate is assumed the same for both the cases. In the proposed model, recovery rate and mortality rate for India and its states are given as follows.

$$\kappa \left(t\right)=\kappa \left(1\right)\ast e^{\left\{-\kappa \left(2\right)t\right\}}$$

$$\lambda \left(t\right)=\lambda \left(1\right)\ast e^{\lambda \left(2\right)t}$$

All the parameters are fitted with the help of LSQCURVEFIT function in MATLAB. The error is minimized using minsum(FUN(X, XDATA) − YDATA). ^ 2 formula. The function FUN takes X and XDATA as inputs and returns a vector (or matrix) of function values FUN(X, XDATA) where FUN and YDATA (observed output) are of the same size. The function X = LSQCURVEFIT(FUN, X₀, XDATA, YDATA, LB, UB, OPTIONS) is used to optimize the parameters [40]. The function X starts at X₀ = [t_pop − Q(1) − R(1) − D(1) − E₀ − I₀ − A_0, E₀, I₀, Q(1), R(1), D(1)] where t_pop represents the total population. The terms Q(1), R(1), D(1), I_o, and A₀ represent the number of active, recovered, death, confirmed, and asymptomatic cases reported on March 14, 2020, respectively. It is assumed that initially there are no asymptomatic patients i.e. A₀ = 0 and the number of exposed cases is equal to the number of infected cases. For the simulation results of the proposed model, options are considered as follows:

• p. addoptional(‘tolX’, 1e⁻⁵) is option for optimset. It sets the tolerance for X to 10⁻⁵.

• p. addoptional(‘tolFUN’, 1e⁻⁵) is option for optimset. It also sets the tolerance for FUN to 10⁻⁵.

• p. addoptional(′dt′, 0.1) is option for optimset. It sets the time step for fitting to 0.1.

$$\mathit{\text{options}}=\mathit{\text{optimset}}\left(\prime \mathit{Tol}{X}^{\prime },\mathit{\text{tolX}}{,}^{\prime }\mathit{\text{TolFu}}{n}^{\prime },\mathit{\text{tolFun}},..{.}^{\prime }\mathit{\text{MaxFunEval}}{s}^{\prime },1200{,}^{\prime }\mathit{\text{Displa}}{y}^{\prime },\mathit{\text{Display}}\right).$$

The fitted parameters for India are given in Table 1.

Table 1.

Best-fitted Parameter values for India

α	β	p	q	γ	η	λ(1)	λ(2)	κ(1)	κ(2)
0.0043	1.4007	0.4	0.05	0.5393	0.8115	0.0217	0.0101	0.0029	0.0013

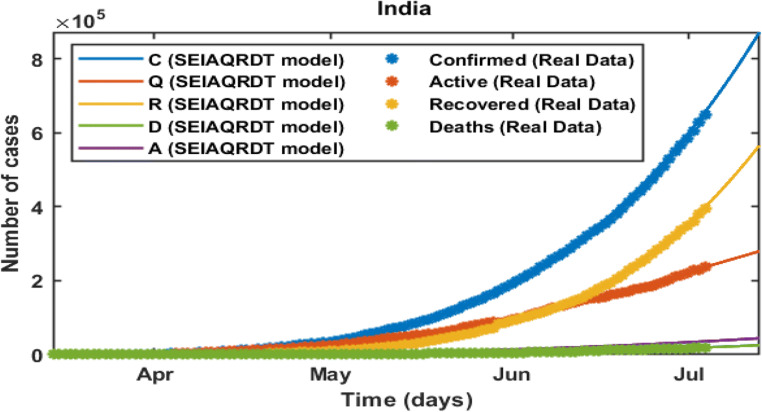
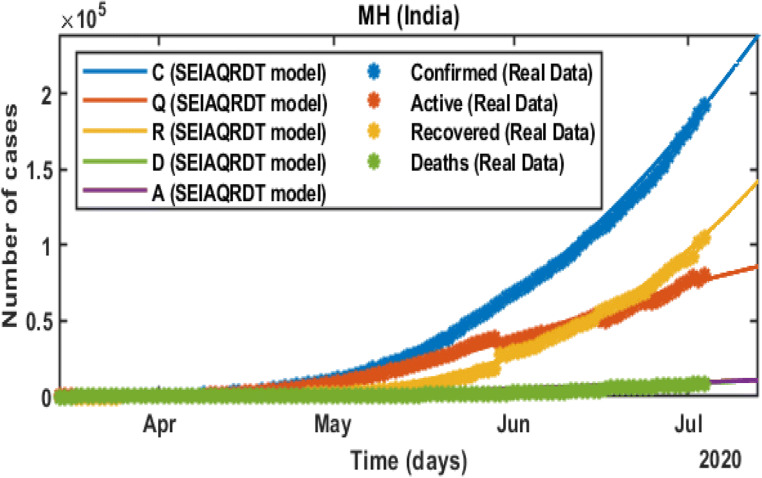
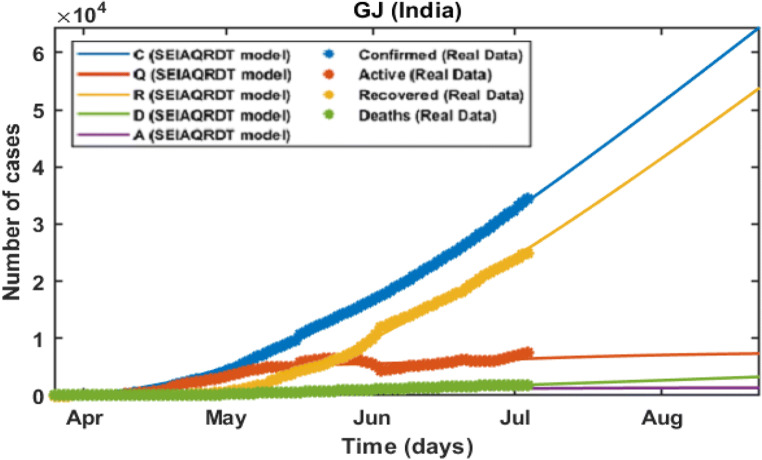
In Fig. 3, C represents the total number of cases, Q represents the total quarantined cases, R represents the total recovered, D represents the total deaths, and A represents estimated total asymptomatic cases from the SEIAQRDT model. The total number of cases in India initiating from March 14, 2020 to July 12, 2020 is shown in Fig. 3. The total number of cases observed in the second week of July is around 0.86 million whereas 0.57 million recovered. Asymptomatic cases are observed at around 0.045 million. In the current situation R₀ =1.1121 which is greater than one. It indicates that the epidemic exists and will remain in the population. The long-term prediction in India is shown in Fig. 4. With the help of the fitted parameters, the cumulative number of confirmed cases, quarantined cases, recovered and death cases are estimated.

Fig. 3.

Prediction and comparison in India till July 12, 2020 Cumulative (confirmed cases, recovered, deaths, quarantined and asymptomatic infectious with real data)

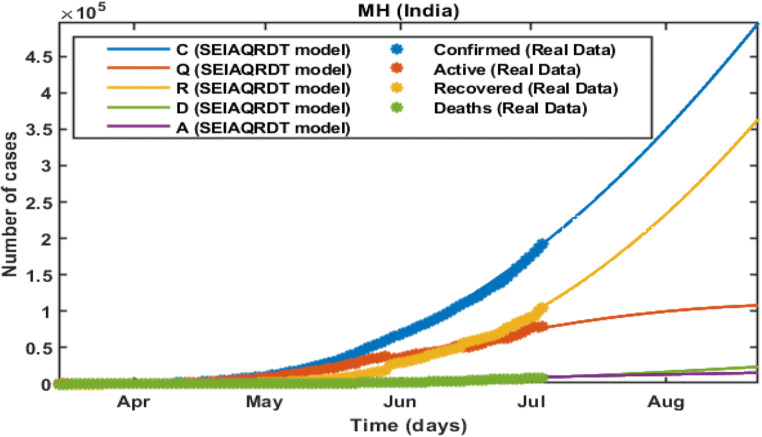
Fig. 4.

Prediction and comparison in India for long-term Cumulative (confirmed cases, recovered, deaths, quarantined and asymptomatic infectious with real-data)

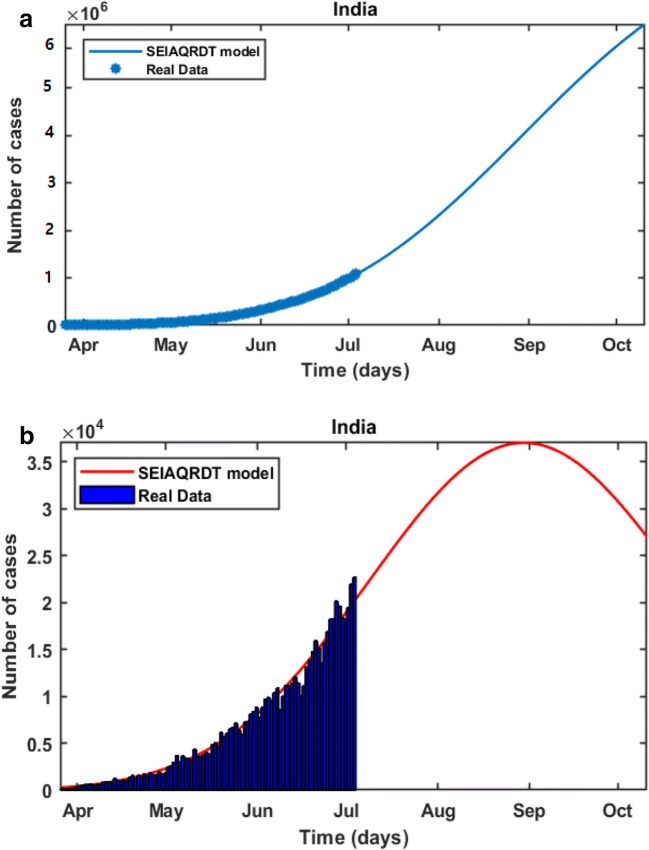
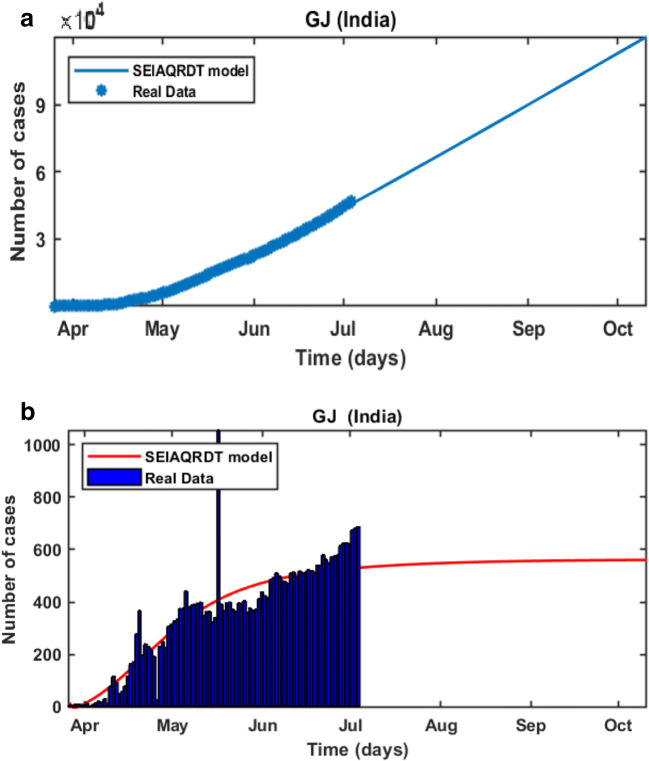
In Fig. 5(a), it is observed that the curve for cumulative cases starts to flatten at the end of October. In Fig. 5(b), daily-reported cases in India are shown in the bar diagram. The peak of the number of cases in India is observed in the first or second week of September. It is also noticed in Fig. 5(b) that around 23% of cases will be removed from the population in the second or third week of October.

Fig. 5.

Prediction in India (a) Cumulative cases in India in the first week of October (b) Bar diagram for daily new cases in India

Maharashtra

Maharashtra is the most affected state from COVID-19 in India from the beginning. Hence, it is very important to discuss the scenario of the state. The estimation of the cumulative number of cases, deaths, recovered, and quarantined cases are forecasted with data up to July 03, 2020. The model predicts the peak of the daily number of cases in the last week of July or the first week of August. Around 0.496 million cumulative cases are approximated at the second last August whereas 0.36 million people will be recovered from COVID-19 in the second last week of August and around 0.024 million deaths are estimated by the second last week of August in the recent circumstances. The number of asymptomatic cases is approximately 0.015 million. In this case, R₀ = 1.3733 which is larger than one. It indicates that the epidemic exists and will remain in the population. The fitted parameters for Maharashtra are shown in Table 2. The recovery and mortality rates are time-dependent functions which are the same as λ(t) and κ(t), respectively.

Table 2.

Best-fitted Parameter values for Maharashtra (India)

α	β	p	q	γ	η	λ(1)	λ(2)	κ(1)	κ(2)
0.0081	1.556	0.4	0.05	0.4832	0.7277	0.022	0.0066	0.0032	0.00013

In Fig. 6, the total number of cases in Maharashtra initiating from March 14, 2020 to July 12, 2020 is shown. The total number of cases observed at the end of the second week of July is around 0.24 million whereas 0.14 million recovered. Asymptomatic cases are observed at around 0.0105 million. Figure 7 shows the long-term forecast. With the help of the fitted parameter, the cumulative number of confirmed infectious cases, quarantined cases, recovered and death cases are estimated.

Fig. 6.

Prediction and comparison in Maharashtra till July 12, 2020 Cumulative (confirmed cases, recovered, deaths, quarantined and asymptomatic infectious with real data)

Fig. 7.

Prediction and comparison in Maharashtra for long-term Cumulative (confirmed cases, recovered, deaths, quarantined and asymptomatic infectious with real data)

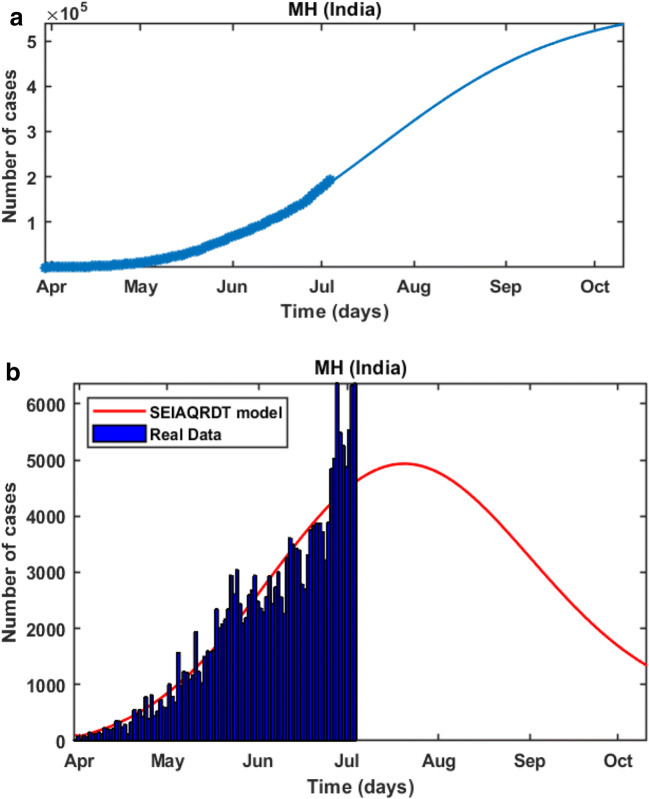
In Fig. 8(a), it is observed that the curve for cumulative cases starts to flatten at the end of October or the starting of November. In Fig. 8(b), daily-reported cases in Maharashtra are shown in the bar diagram. The model predicts the peak of the daily number of cases in the last week of July or the initial week of August. Around 90% of cases will be removed from the total population at the end of October.

Fig. 8.

Prediction in Maharashtra (a) Cumulative cases in Maharashtra in the first week of October (b) Bar diagram for daily new cases in Maharashtra

Tamil Nadu

In the initial stage of COVID-19 in India, the number of cases was less in Tamil Nadu, but presently it is the second most affected state. Nowadays, the daily count has reached near to 7000. Due to this, it is important to consider cases in Tamil Nadu separately. The estimation of the cumulative number of cases, deaths, recovered, and quarantined cases are forecasted with data up to July 03, 2020. The model predicts the peak of the daily number of cases in the first or second week of August. Around 0.42 million cumulative cases are observed in the second last week of August whereas 0.296 million people will be recovered from COVID-19 in the second last week of August and around 0.0038 million deaths may be reported till the second last week of August in the current scenario. The number of asymptomatic cases is approximately 0.017 million. R₀ = 1.361 is calculated for Tamil Nadu which is more than one. Therefore, the epidemic will exist in the population for a smaller period. The fitted parameters for simulation are taken from Table 3.

Table 3.

Best-fitted Parameter values for Tamil Nadu (India)

α	β	p	q	γ	η	λ(1)	λ(2)	κ(1)	κ(2)
0.0058	1.6761	0.4	0.05	0.5264	0.9999	0.0601	2.377*10−14	0.0026	0.0099

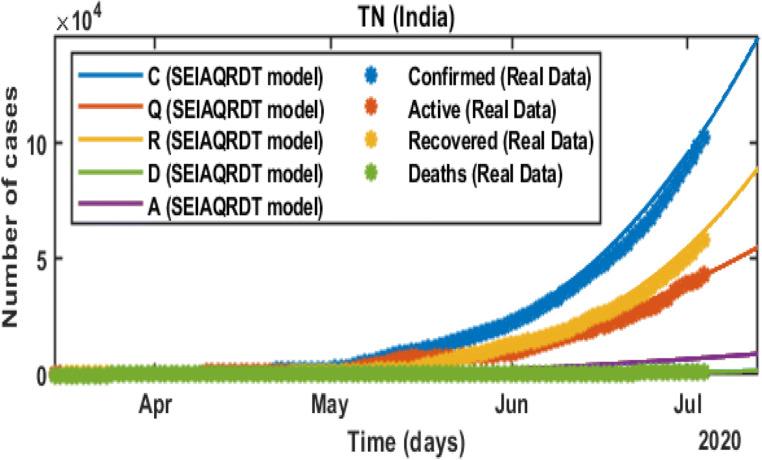
The total number of cases in Tamil Nadu starting from March 14, 2020 to July 03, 2020 is shown in Fig. 9. The total number of cases observed in the second week of July is around 0.142 million whereas 0.087 million recovered. Asymptomatic cases are observed at around 0.0085 million. In Fig. 10, long-term prediction in Tamil Nadu is shown. With the help of the fitted parameter, the cumulative number of confirmed infectious cases, quarantined cases, recovered and death cases are estimated.

Fig. 9.

Prediction and comparison in Tamil Nadu till July 12,2020 Cumulative (confirmed cases, recovered, deaths, quarantined and asymptomatic infectious with real data)

Fig. 10.

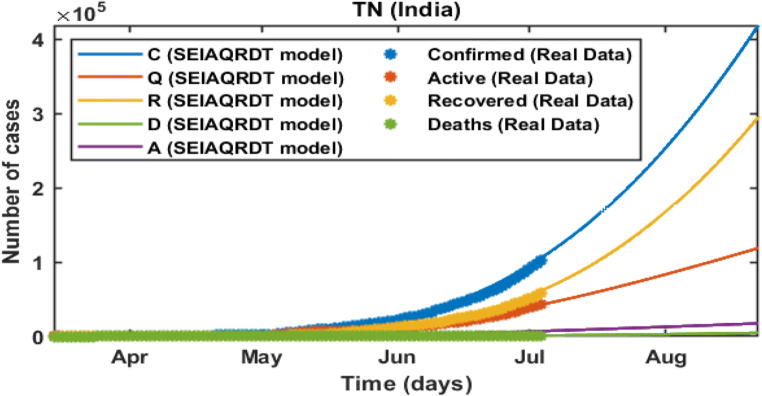
Prediction and comparison in Tamil Nadu for long-term Cumulative (confirmed cases, recovered, deaths, quarantined and asymptomatic infectious with real data)

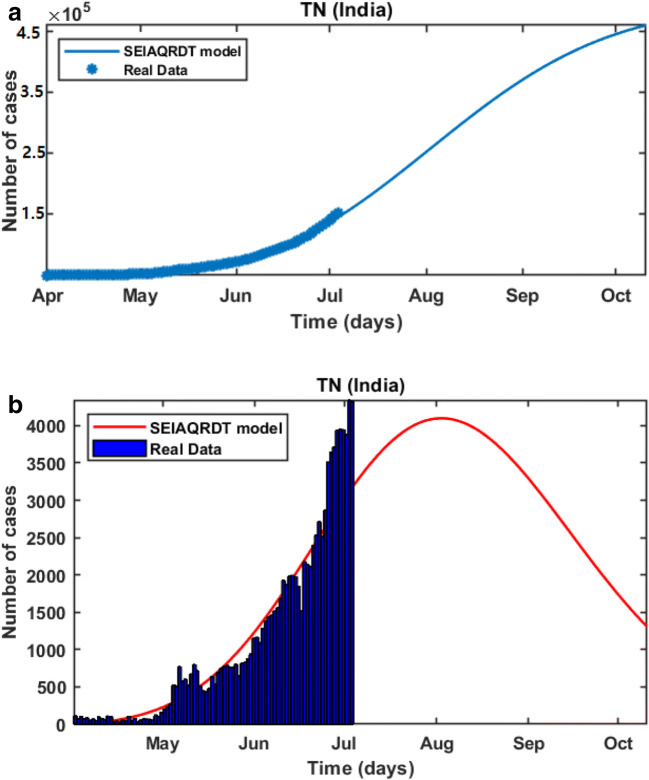
In Fig. 11(a), it is observed that the curve for cumulative cases starts to flatten in the last week of October or the first week of November. In Fig. 11(b), daily-reported cases in Tamil Nadu are shown in the bar diagram. The model predicts the peak of the daily number of cases in the second or third week of August. Around 90% of cases will be removed from the total population at the end of October.

Fig. 11.

Prediction in Tamil Nadu (a) Cumulative cases in Tamil Nadu in the first week of October (b) Bar diagram for daily new cases in Tamil Nadu

Gujarat

In the initial stage of COVID-19 in India, the number of cases is less in Gujarat. Gujarat reaches the third position in the list of most affected states which crosses the 0.01 million number of cases. The estimation of the cumulative number of cases, deaths, recovered, and quarantined cases are predicted with data up to July 03, 2020. The model predicts that the daily number of cases reported gets constant from the second week of July. Around 0.062 million cumulative cases are observed at the second last week of August whereas 0.053 million people will be recovered from COVID-19 s last week of August and around 0.0048 million deaths are estimated in Gujarat by the second last week of August in the current scenario including all the preventive measures that are imposed. The number of asymptomatic cases is approximately 0.0028 million. The fitted parameters for the model are given in Table 4. The recovery and mortality rate for Gujarat is different from other states. The time-dependent recovery and death rate are taken from Eq. (2).

$$\lambda \left(t\right)=\lambda \left(1\right)/\left(1+\mathit{exp}\left(-\lambda \left(2\right)\ast \left(t-\lambda \left(3\right)\right)\right)\right)$$

$$\kappa \left(t\right)=\lambda \left(1\right)+\mathit{exp}\left(-\lambda \left(2\right)\ast \left(t+\lambda \left(3\right)\right)\right)$$ 4

where λ(1), λ (2), λ (3), κ(1), κ(2) and κ(3) are fitted coefficient.

Table 4.

Best-fitted Parameter values for Gujarat (India)

α	β	η	p	q	γ
0.0731	1.4676	0.1916	0.09	0.508	0.5649
λ(1)	λ(2)	λ(3)	κ(1)	κ(2)	κ(3)
0.4946	0.0588	86.4685	0.0054	0.3109	1.9229*10−4

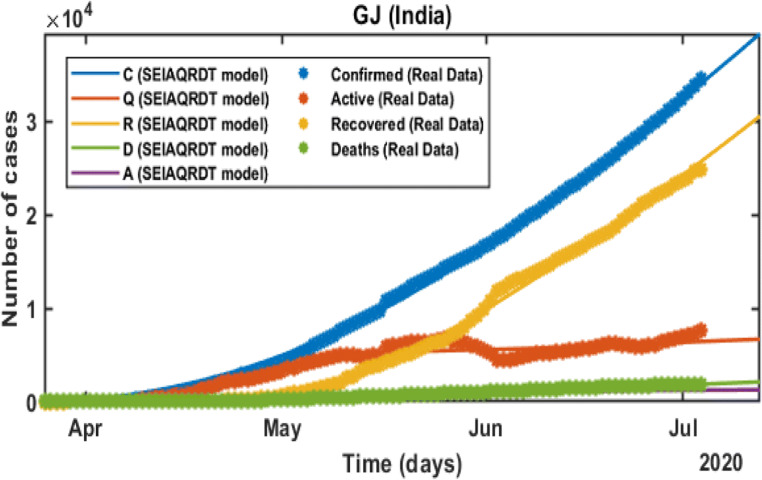
In Fig. 12, the total number of cases in Gujarat starting from March 21, 2020 to July 12, 2020 is shown. The total number of cases in the second week of July is estimated at around 0.039 million whereas 0.031 million will be recovered in the second week of July. Asymptomatic cases are observed at around 0.0023 million. In Fig. 13, long-term prediction is shown. With the help of the fitted parameter, the cumulative number of confirmed infectious, quarantined, recovered, and death cases are estimated.

Fig. 12.

Prediction and Comparison in Gujarat till July 12 Cumulative (confirmed cases, recovered, deaths, quarantined and asymptomatic infectious with real data)

Fig. 13.

Prediction and Comparison in Gujarat for long-term Cumulative (confirmed cases, recovered, deaths, quarantined and asymptomatic infectious with real data)

In Fig. 14(a), it is observed that the curve for cumulative cases does not start to flatten at the first end of October. In Fig. 14(b) daily-reported cases are shown in the bar diagram. It is observed that the daily new cases in Gujarat get constant from the second week of July.

Fig. 14.

Prediction in Gujarat (a) Cumulative cases in Gujarat till the first week of October (b) Bar diagram for daily new cases in Gujarat

Delhi

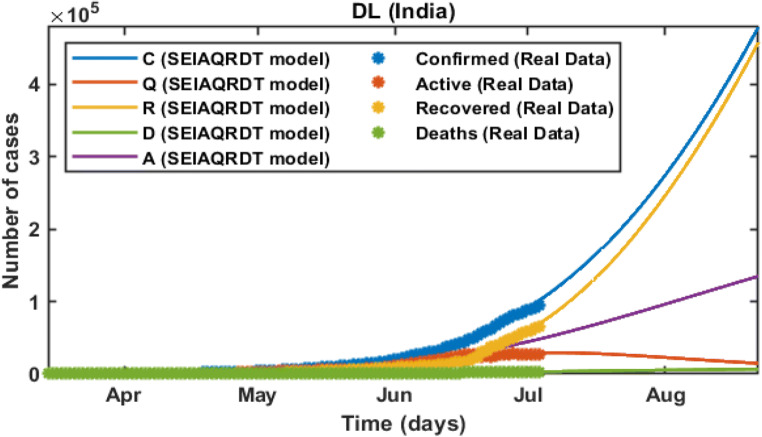
In the initial stage of COVID-19 in India, the number of cases is quite high in Delhi. The model predicts the peak of the daily number of cases at the end of September. Around 0.46 million cumulative cases are observed at the second last week of August whereas 0.44 million people will be recovered from COVID-19 at the second last week of August and around 0.007 million deaths are estimated by the second last week of August in the current scenario including all the preventive measures that are imposed. The number of asymptomatic cases is approximated to 0.05 million. In this case, R₀ = 2.3678 which is greater than one. Hence, the cases for novel coronavirus will remain in the population. The fitted parameters for the model are shown in Table 5.

Table 5.

Best-fitted Parameter values for Delhi (India)

α	β	p	q	γ	η	λ(1)	λ(2)	κ(1)	κ(2)
0.0071	1.0013	0.4	0.05	0.1805	0.2193	0.0027	0.0355	0.0035	9.549

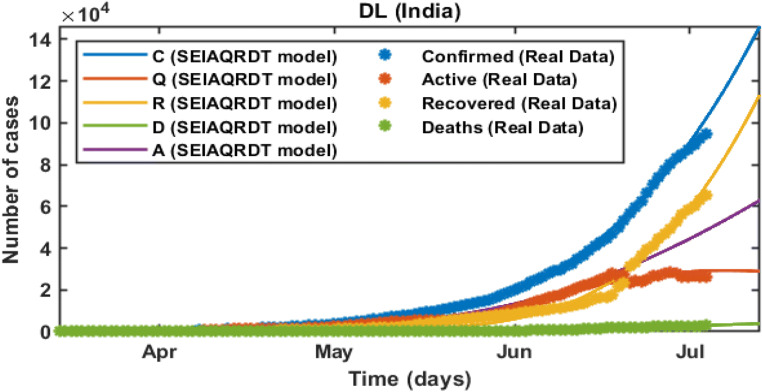
In Fig. 15, the total number of cases in Delhi starting from March 14, 2020 to July 12, 2020 is shown. The total number of cases is recorded at the end of July is around 0.145 million whereas 0.115 million will be recovered. Asymptomatic cases are observed at around 0.024 million. In Fig. 16, long-term prediction in Delhi is shown. With the help of the fitted parameter, the cumulative number of confirmed infectious, quarantined, recovered and death cases are estimated.

Fig. 15.

Prediction and comparison in Delhi till July 12 Cumulative (confirmed cases, recovered, deaths, quarantined and asymptomatic infectious with real data)

Fig. 16.

Prediction and Comparison in Delhi for long-term Cumulative (confirmed cases, recovered, deaths, quarantined and asymptomatic infectious with real data)

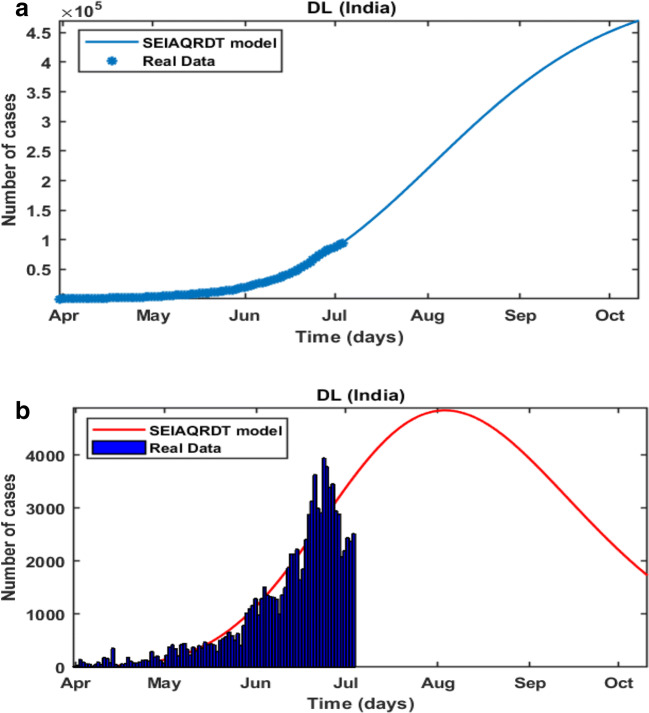
In Fig. 17(a), it is observed that the curve for cumulative cases starts to flatten at the end of October. In Fig. 17(b), daily-reported cases in Delhi are shown in the bar diagram. The peak of the number of cases in Delhi will be observed at the end of August. Around 63% of cases will be removed from the total population at the end of October. Table 6 shows the relative error between the actual data and the data obtained from the proposed model. The relative error (%) for India varies from 0.02 to 1.81 and the average relative error is only 0.699%. Moreover, the state’s relative error varies from 0 to 2.45 and the average relative error for states is 0.869%. Hence, the average relative error for the SEIAQRDT model is less than 1% for India and its states.

Fig. 17.

Prediction in Delhi (a) Cumulative cases in Delhi in the first week of October (b) Bar diagram for daily new cases in Delhi

Table 6.

Relative error between real and estimated cases of India, Maharashtra, Tamil Nadu, Gujarat, and Delhi

India	Date	Mar 21	Apr 04	Apr 18	May 02	May 16	May 30	June 13	June 27	July 11
	Total cases (predicated)	338	3648	15,652	40,545	90,668	181,910	321,710	529,592	841,029
	Total cases (Real -data) [3]	334	3684	15,725	39,826	90,648	181,860	321,638	529,590	850,361
	Relative Error (%)	1.2	0.98	0.47	1.81	0.03	0.022	0.0002	0.0004	1.097
MH	Total cases (predicated)	64	638	3663	12,381	30,752	65,172	105,821	161,850	243,083
	Total cases (Real -data) [3]	64	635	3648	12,296	30,706	65,168	104,568	159,133	246,600
	Relative Error (%)	0	0.48	0.42	0.7	0.15	0.006	1.198	1.71	1.44
TN	Total cases (predicated)	6	474	1354	2801	10,695	21,190	43,472	80,266	136,663
	Total cases (Real -data) [3]	6	485	1372	2757	10,585	21,184	42,687	78,835	134,226
	Relative Error (%)	0	2.27	1.32	1.6	1.04	0.028	1.84	1.82	1.82
GJ	Total cases (predicated)	14	107	1368	4818	10,567	16,130	22,852	30,553	39,951
	Total cases (Real -data) [3]	14	108	1376	4824	10,759	16,126	22,849	30,543	41,027
	Relative Error (%)	0	0.93	0.59	0.13	1.79	0.025	0.013	0.033	2.62
DL	Total cases (predicated)	27	439	1863	4202	9303	18,552	39,000	80,208	113,068
	Total cases (Real -data) [3]	27	445	1893	4122	9333	18,549	38,958	80,188	110,921
	Relative Error (%)	0	1.35	1.59	1.95	0.33	0.016	0.11	0.025	1.94

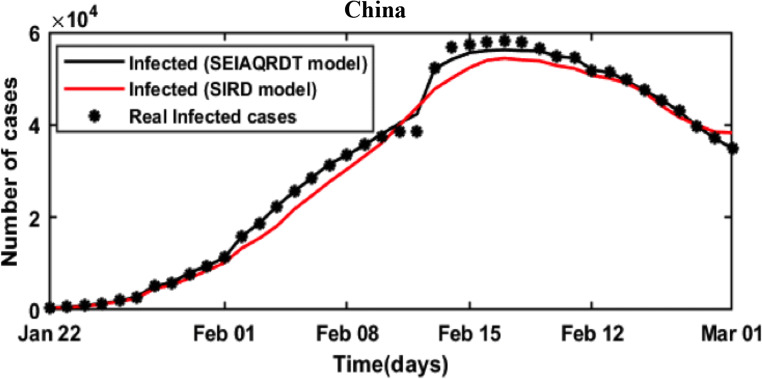
The simulation results of the proposed (SEIAQRDT) model and the SIRD model are compared with the real data of China. The estimated values of infected cases for China using SIRD are taken from [39] for comparison purposes. The data thief software [41] is used to extract the data from the figure. Table 7 shows China’s real infected cases (reported), infected cases estimated using the SIRD model with relative error, and infected cases estimated using SEIAQRDT model with relative error for the period from Feb 16 to March 1. The relative error for the proposed model varies from 0.01 to 3.39 and the average relative error is 0.86%, whereas the relative error for the SIRD model varies from 0.37 to 9.78 and the average relative error is 3.99%.

Table 7.

Relative error between the estimated cases using SIRD model [39] and the real data of China [42]

Date	Real Infected (China)	SIRD Model (China)	Relative error percentage (SIRD)	SEIAQRDT Model (China)	Relative error percentage (SEIAQRDT)
Feb 16, 20	57,992	53,955	6.97	56,084	3.36
Feb 17, 20	58,108	54,388	6.41	56,206	3.28
Feb 18, 20	58,002	54,040	6.84	56,037	3.39
Feb 19, 20	56,541	53,813	4.83	55,996	0.97
Feb 20, 20	54,825	52,785	3.73	54,792	0.07
Feb 21, 20	54,608	52,186	4.44	54,459	0.28
Feb 22, 20	51,859	50,686	2.27	51,856	0.01
Feb 23, 20	51,390	50,044	2.62	51,334	0.11
Feb 24, 20	49,631	48,966	1.34	49,445	0.38
Feb 25, 20	47,413	47,041	0.79	47,366	0.1
Feb 26, 20	45,365	44,045	2.91	45,371	0.02
Feb 27, 20	42,924	41,594	3.1	42,822	0.24
Feb 28, 20	39,809	39,956	0.37	39,721	0.23
Feb 29, 20	37,199	38,489	3.47	37,077	0.33
Mar 1, 20	34,898	38,311	9.78	34,929	0.09
Average Relative Error			3.99		0.86

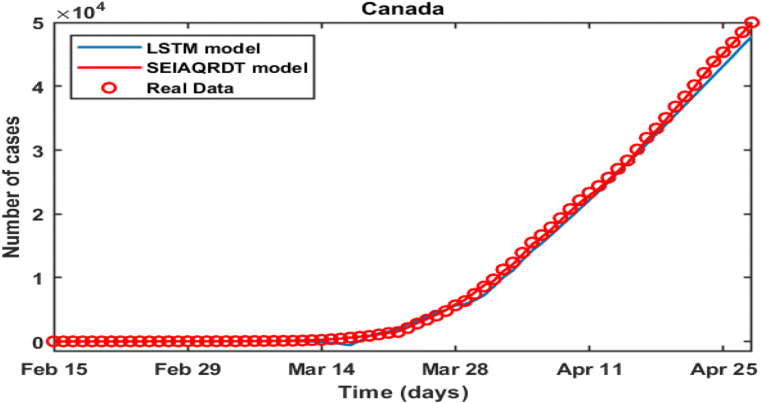
Figure 18 shows the comparison between the real infected cases, estimated infected cases with SEIAQRDT model, and estimated infected cases with SIRD model for China. In this figure, it can be seen that the estimated infected cases with SEIAQRDT model are either touching the real infected cases or very close to real infected cases. However, the estimated infected cases with SIRD are away (distant) from the real data points except starting and ending points. Table 8 shows Canada’s real infected cases (reported), infected cases estimated using SEIAQRDT model with relative error, and the infected cases estimated using LSTM model with relative error from April 14 to April 28. The relative error for the SEIAQRDT simulation model varies from 0.2578 to 1.356 and the average relative error is 0.78%, whereas relative error for the LSTM model varies from 1.4975 to 5.05 and the average relative error is 3.58%.

Fig. 18.

Comparison between the real infected cases [42], estimated infected cases with SEIAQRDT model and estimated infected cases with the SIRD model [39] for China

Table 8.

Relative error between the estimated cases using LSTM model [38] and the real data of Canada [43]

Date	Real Infected (Canada)	LSTM (Canada)	Relative error percentage (LSTM)	SEIAQRDT (Canada)	Relative error percentage (SEIAQRDT)
Apr 14, 20	27,063	26,475	2.1727	26,696	1.356
Apr 15, 20	28,379	27,954	1.4975	28,023	1.2544
Apr 16, 20	30,106	29,342	2.5377	29,754	1.1692
Apr 17, 20	31,927	30,976	2.9786	31,600	1.0242
Apr 18, 20	33,383	32,499	2.648	33,057	0.9765
Apr 19, 20	35,056	34,008	2.9895	34,744	0.89
Apr 20, 20	36,829	35,545	3.4863	36,514	0.8553
Apr 21, 20	38,422	37,079	3.4953	38,111	0.8094
Apr 22, 20	40,190	38,592	3.9761	39,894	0.7365
Apr 23, 20	42,110	40,127	4.709	41,827	0.672
Apr 24, 20	43,888	41,670	5.0537	43,666	0.5058
Apr 25, 20	45,354	43,200	4.7493	45,127	0.5005
Apr 26, 20	46,895	44,716	4.6465	46,729	0.3539
Apr 27, 20	48,500	46,342	4.4494	48,342	0.3257
Apr 28, 20	50,026	47,814	4.4217	49,897	0.2578
Average Relative Error			3.5874		0.7791

Figure 19 shows the comparison between SEIAQRDT model and the LSTM model with real infected cases of Canada. The real data is represented by the red dots and the predicted number of total infected cases by LSTM model is shown by the blue line. The red line represents the total number of infected cases estimated by the SEIAQRDT model. In this case, the prediction with SEIAQRDT model is very close to real data. The average relative error is higher for the LSTM model as compared to SEIAQRDT. Results show that the SEIAQRDT model fits the data better than LSTM model.

Fig. 19.

Comparison between the real infected cases [43], estimated infected cases with SEIAQRDT model and estimated infected cases with LSTM model [38] for Canada

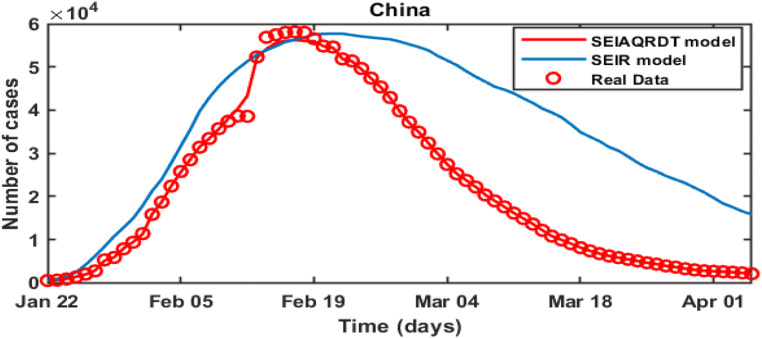
Table 9 shows China’s real infected cases (reported), infected cases estimated using SEIAQRDT model with relative error, and the infected cases estimated using SEIR model with relative error for the period from Feb 13 to Feb 27. The relative error for the SEIAQRDT model varies from 0.0057 to 4.7397, whereas relative error for SEIR model varies from 1.0343 to 17.4131. Figure 20 shows the comparison between the proposed model and the SEIR model with real infected cases of China. The average relative error of SEIR model is 7.1523% which is very high as compared to the average error of the proposed model i.e. 1.3657%. Figure 20 shows that the SEIAQRDT model predicts the total number of infected cases better than the SEIR model.

Table 9.

Relative error between the estimated cases using SEIR simulation model [25] and the real data of China [42]

Date	Real Infected (China)	SEIR (China)	Relative error percentage (SEIR)	SEIAQRDT (China)	Relative error percentage (SEIAQRDT)
Feb 13, 20	52,309	52,850.07	4.5963	52,128	0.3460
Feb 14, 20	56,860	53,912.21	3.7939	54,165	4.7397
Feb 15, 20	57,452	54,811.33	1.0343	55,584	3.2514
Feb 16, 20	57,992	55,791.83	5.1842	56,048	3.3522
Feb 17, 20	58,108	56,283.34	3.1401	56,206	3.2732
Feb 18, 20	58,002	56,856.36	1.9751	56,037	3.3878
Feb 19, 20	56,541	57,510.89	1.7153	55,996	0.9639
Feb 20, 20	54,825	57,676.43	5.2009	54,792	0.0601
Feb 21, 20	54,608	57,698.51	5.6594	54,459	0.2728
Feb 22, 20	51,859	55,714.92	7.4353	51,856	0.0057
Feb 23, 20	51,390	56,371.04	9.6926	51,334	0.1089
Feb 24, 20	49,631	55,068.97	10.9568	49,445	0.3747
Feb 25, 20	47,413	53,821.96	13.5173	47,366	0.0991
Feb 26, 20	45,365	52,610.07	15.9706	45,371	0.0132
Feb 27, 20	42,924	50,398.4	17.4131	42,822	0.2376
Average Relative Error			7.1523		1.3657

Fig. 20.

Comparison between the real infected cases [42], estimated infected cases with SEIAQRDT model, and estimated infected cases with SEIR model [25] for China

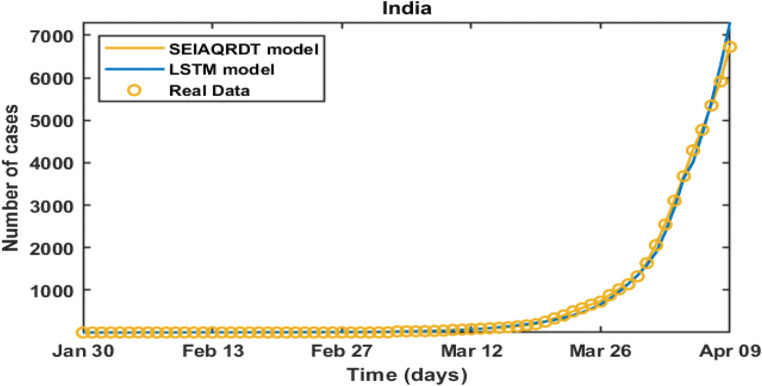
Table 10 shows India’s real infected cases (reported), infected cases estimated using SEIAQRDT model with relative error, and the infected cases estimated using LSTM model with relative error for the period from March 26 to April 09. The relative error for the SEIAQRDT model varies from 0.2787 to 1.084 and the average relative error is 0.6915%, whereas the relative error for LSTM model varies from 0.7733 to 8.62.

Table 10.

Relative error between the estimated cases using LSTM model [31] and the real data of India [3]

Date	Real Infected (India)	LSTM (India)	Relative error percentage (LSTM)	SEIAQRDT (India)	Relative error percentage (SEIAQRDT)
Mar 26, 20	730	682.9332	6.4475	738	1.084
Mar 27, 20	883	827.8121	6.25	889	0.6749
Mar 28, 20	1019	982.6909	3.5632	1030	1.0679
Mar 29, 20	1139	1147.809	0.7733	1150	0.9565
Mar 30, 20	1326	1347.226	1.6007	1340	1.0447
Mar 31, 20	1635	1587.665	2.8950	1647	0.7285
Apr 01, 20	2059	1918.252	6.8357	2079	0.962
Apr 02, 20	2545	2383.895	6.3302	2570	0.9727
Apr 03, 20	3105	2958.819	4.7079	3120	0.4807
Apr 04, 20	3684	3637.915	1.2509	3700	0.4324
Apr 05, 20	4293	4012	6.5455	4305	0.2787
Apr 06, 20	4777	4676	2.1142	4795	0.3753
Apr 07, 20	5350	5438	1.644	5359	0.1679
Apr 08, 20	5915	6311	6.6948	5948	0.5548
Apr 09, 20	6728	7308	8.62	6768	0.591
Average Relative Error			4.4182		0.6915

Figure 21 shows the comparison between SEIAQRDT model and the SEIR model with real infected cases of India. In this case, the average relative error of the LSTM model is 4.4182%, which is higher than the average relative error of the proposed model i.e. 0.6915%. The SEIAQRDT model is compared with SIRD, SEIR, and LSTM models for different country’s data. The LSTM models are mainly focused on the number of infectious. The main drawback of the LSTM based models is that these models do not consider the effect of quarantined cases and asymptomatic cases. In all the cases, simulation results show that the SEIAQRDT model fits the data better than the other models. The reason for this superiority is that the SEIAQRDT model takes suspected, infected with and without symptoms, recovered, quarantined, death, and exposed cases, whereas SIRD and SEIR model considered only four factors.

Fig. 21.

Comparison between the real infected cases [3], estimated infected cases with the SEIAQRDT model and estimated infected cases with the LSTM model [31] for India

Conclusion

The COVID-19 epidemic is exerting an unusual weight on social life in many countries, including India. Although nation-wide lockdown and other preventive majors are imposed in India still the number of cases is getting increased. In this study, we proposed the SEIAQRDT model including asymptomatic cases for the prediction of COVID-19 disease. The real data for total cumulative cases, daily infected cases, total recovered, total deaths, and total quarantined individuals have been incorporated. The numerical simulations are presented for India and four major states (Maharashtra, Tamil Nadu, Gujarat, and Delhi). The estimated number of cases using the SEIAQRDT model has been compared with SIRD, SEIR, and LSTM models. The estimated data with SEIARQDT model is very near to actual data. The relative error square analysis is used to verify the accuracy of the proposed model. The proposed model has average relative error of 0.86% (3.99% with SIRD) and 1.36% (7.15% with SEIR) for China, 0.69% (3.59% with LSTM) for India and 0.77% (4.42% with LSTM) for Canada. The average relative error for SEIAQRDT model with a higher number of factors is very less in comparison to the average relative error for the other models. These results may help to recognize the impact of coronavirus and to prevent the spread of the virus on a large scale. In the future, the proposed model can be extended by introducing additional factors like environmental transmission, effect of vaccines, treatment strategies, effect of delay, impact of unlocking, etc. Moreover, the fractional-order derivative can also be applied in the present model.