Colonic stem cell data are consistent with the immortal model of stem cell division under non‐random strand segregation

Abstract

Objectives:  Colonic stem cells are thought to reside towards the base of crypts of the colon, but their numbers and proliferation mechanisms are not well characterized. A defining property of stem cells is that they are able to divide asymmetrically, but it is not known whether they always divide asymmetrically (immortal model) or whether there are occasional symmetrical divisions (stochastic model). By measuring diversity of methylation patterns in colon crypt samples, a recent study found evidence in favour of the stochastic model, assuming random segregation of stem cell DNA strands during cell division. Here, the effect of preferential segregation of the template strand is considered to be consistent with the ‘immortal strand hypothesis’, and explore the effect on conclusions of previously published results.

Materials and methods:  For a sample of crypts, it is shown how, under the immortal model, to calculate mean and variance of the number of unique methylation patterns allowing for non‐random strand segregation and compare them with those observed.

Results:  The calculated mean and variance are consistent with an immortal model that incorporates non‐random strand segregation for a range of stem cell numbers and levels of preferential strand segregation.

Conclusions:  Allowing for preferential strand segregation considerably alters previously published conclusions relating to stem cell numbers and turnover mechanisms. Evidence in favour of the stochastic model may not be as strong as previously thought.

Introduction

DNA methylation is involved in many important biological processes, such as gene imprinting, X‐chromosome inactivation and regulation of gene expression (1, 2, 3). Gene expression patterns need to be stably transmitted to daughter cells during somatic cell division and, therefore, tissue‐specific methylation patterns (which are formed during foetal development) need to be accurately transmitted from parent to daughter cell. Evidence supports the case for somatic inheritance of methylation patterns (4). After DNA strands separate during somatic cell division, a new unmethylated strand is synthesized. DNA methyltransferases use the methylated template strand as a guide to replicate the methylation pattern of the template strand, on to the newly synthesized strand, but the process does not have complete fidelity (5, 6). Somatic inheritance but higher replication error rate of DNA methylation (compared to DNA mutation) makes using DNA methylation an attractive marker to make inferences about cell population histories (7, 8).

Epithelial mucosa of the colon contains indentations known as crypts. These, along with ‘villi’ (which project into the lumen, but not in the colon), increase the absorptive surface area. Crypts are thought to contain approximately 2000 cells in total and cell number is maintained by activity of colonic stem cells (9). Whenever stem cells divide asymmetrically to produce a single non‐stem cell, this founder differentiated cell, like all non‐stem cells, always produces further non‐stem cells. Non‐stem cell offspring of stem cells differentiate and migrate towards the lumen where they die. The number of cell divisions between birth and death for non‐stem cells is likely to be small as they can be replaced within a week (10).

There are two questions of interest relating to these stem cells: their number, and the process by which they divide to produce differentiated cells. There are two nested models of stem cell turnover proposed (11, 12). The first is the immortal model in which stem cells always divide asymmetrically into exactly one stem and one non‐stem cell. The second is the stochastic model in which at each cell division there is a fixed probability P (P < 1) that a stem cell divides asymmetrically and a probability (1 – P)/2 that it may divide symmetrically into two stem or two non‐stem cells. In the stochastic model, stem cells reside in specialized compartments in the crypts (niches) maintained by mesenchymal cells of the lamina propria (13, 14). In this model, it is residence in the niche that confers ‘stemness’ to cells rather than an intrinsic property of the cell itself. In the immortal model, certain cells are stem cells and remain as such indefinitely. Addressing the stem cell turnover mechanism experimentally is difficult to do, because stem cells remain unidentified as a result of their immature, undifferentiated phenotype (14).

In the absence of histological approaches to studying colonic stem cells, a method based on recreating crypt histories using DNA methylation as a marker has been proposed by Yatabe et al. (15). The investigators isolated a small number of crypts from colectomy specimens taken from patients aged between 40 and 88 years. From each crypt they sampled a small number of cells. For each patient, they looked at methylation patterns (or tags) of genomic sequences and calculated mean and variance of the number of unique methylation patterns between crypts. Using simulation they compared mean and variance to that expected under the immortal and the stochastic models of stem cell turnover, for various numbers of stem cells. Both stochastic and immortal models were consistent with mean number of methylation patterns (for certain numbers of stem cells), but only the stochastic model fits the variance data. The authors concluded that empirical evidence supported the stochastic model of colonic stem cell turnover.

In both models, the number of stem cells is fixed for each generation; it is ancestry that differs. The stochastic model is characterized by niche succession in which at some point in the population history all stem cells are likely to be descended from a common ancestor as a result of genetic drift. In the immortal model, every stem cell is unrelated and remains so throughout the lifetime of the crypt. The diversity of methylation patterns in the colonic crypt will differ under these two models. In the immortal model, stem cells will contain increasingly diverse methylation patterns. In the stochastic case, increased relatedness of the stem cells will reduce diversity of methylation patterns. The extent of methylation diversity will depend on the number of divisions since niche succession (when all stem cells have a common ancestor).

A key assumption by Yatabe et al. is that of random segregation of the template strand (15). During asymmetric division, this means that the template strand in the parent stem cell is equally likely to become the template in the stem cell or non‐stem cell offspring. There is considerable and long‐standing evidence supporting the ‘immortal strand hypothesis’ (16, 17) in which the parent stem cell template strand is preferentially transmitted to the offspring stem cell during stem cell renewal; the non‐stem cell offspring receives the synthesized strand as template. The immortal strand hypothesis was suggested as a means to slow accumulation of replication‐induced mutations in stem cells (18); differentiated cells acquire most of the replication errors, but this is not problematic as they are short‐lived; however, it remains a controversial subject (19, 20). To add to the debate, evidence using a new technical approach suggests that preferential template strand segregation is not limited to asymmetric division in renewing stem cells; it may also occur in multiple subsequent divisions of differentiated cells with multiple fates (21). The effect of preferential strand segregation is to slow the accumulation of methylation errors in stem cells so that different stem cells are more likely to have identical methylation patterns. For an individual of a given age, diversity of methylation tags in stem cells would be less under preferential compared to random segregation of the template strand.

In this paper, the model of effects of probabilistically preferential template strand segregation is examined in expectation and variance of number of unique methylation tags, in a sample of cells taken from a small number of colon crypts and it is investigated how this affects conclusions of previously published results relating to the colonic stem cell turnover mechanism.

Materials and methods

At birth, genome‐wide de‐methylation leaves all CpGs unmethylated (22, 23). The modelling process is started at birth and, therefore, assumes that all cytosines in the DNA sequence are initially unmethylated. It is further assumed, without loss of generality, that primers are designed to amplify only strand 1 so that only strand 1 is sequenced. If strand 1 is the template strand in the founder stem cell and there is preferential segregation, then in any daughter stem cell it is more likely that the template strand is strand 1 than strand 2. This asymmetry in template strand probabilities in any (nonfounder) generation, means that it is needed to keep track of the template strand through all stem cell divisions. σ is defined to represent conditional probability that the template strand in the parent stem cell becomes the template strand in the daughter stem cell, during asymmetric division (where σ ≥ 0.5). In Appendix 1 we show that the conditional probability that strand 1 is the template in a descendent stem cell in generation t given that strand 1 was the template in the ancestral founder stem cell in generation 1 is given by

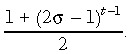(1)

Human colon stem cells divide approximately once a week (10), and because here consideration is of individuals between the ages of 40 and 80 years, the number of cell divisions between birth and sampling is between 2000 and 4000. This means that even if σ is high, the probability in eqn (1) is very close to 0.5. For example, with σ as high as 0.999, after 2000 generations probability in eqn (1) takes the value 0.5091. In practice, it is therefor not needed to keep track of which strand is the template strand as the stem cells divide; we assume that in a descendent stem cell (for the age range considered) there is an equal probability of either strand being the template even though one particular strand is the template in the founder ancestral stem cell. This avoids the need to place a condition on the template strand in the founder stem cell.

It is assumed that de novo and maintenance methylation error rates are low (2 × 10⁻⁵ per CpG site per cell division), and because number of generations between birth and death of differentiated cells is small, it is assumed that no methylation errors occur as differentiated cells progress from the base of the crypt towards the lining of the lumen. Under this assumption, all sampled cells will have the same pattern of methylation as the ancestral stem cell from which they descend. Essentially, it is assumed that all variability in methylation patterns is a result of cell divisions in the stem cells. This is a valid assumption with low rates of copying error and small sample sizes (Yatabe et al. (15) sampled between 7 and 9 from each crypt containing approximately 2000 cells). If a small number of pattern copying errors occurs in differentiated cells, there is a low probability that any of these are sampled.

The final assumption made is with regard to epithelial cells sampled. Figure 1 shows in white, cells that the results of Yatabe et al. are based on, for the artificial case where non‐stem cells die, after just three generations (15). These represent the cells present in the crypt at some time point. The oldest cells die and are replaced by younger, dividing epithelial cells. This means that sampled epithelial crypt cells are all descendents of the same stem cell but for some of the epithelial cells, the stem cell will have gone through several cycles of DNA division and replication. These sampled cells will also have a range of ages. Because methylation error rate is small, it is assumed that the methylation pattern of a descendent stem cell will be the same as the ancestral stem cell, a small number of generations back. For modelling convenience, it is therefore assumed that samples are from the cells in Fig. 1 with diagonal hatching (descendents of a single stem cell) and not from the cells in white (selected descendents from a group of related stem cells).

Figure 1.

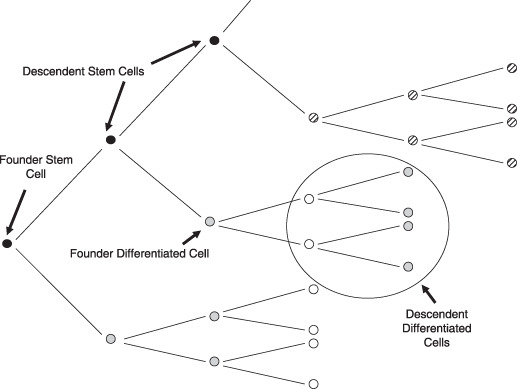
Stem cell turnover in the colon under the immortal model. Cells in white are the cells that are actually sampled. Hatched cells are the cells that are assumed to have been sampled.

Data presented by Yatabe et al. (15) relate to three loci: two autosomal loci, MYOD1 and CSX (5 and 8 CpG sites, respectively) and the larger X‐linked BGN locus (9 CpG sites). Here, methods are presented and results for the larger X‐linked BGN locus but please note that extending to the autosomal case is trivial and requires only a minor alteration to eqn (8) in Appendix 2. This amendment is discussed in the text following eqn (8).

Data presented for the BGN locus are for five adults aged 40, 41, 63, 76 and 87 years. Data of Yatabe et al. have been used to determine consistency of the immortal model of colonic stem cell division when allowing for nonrandom strand segregation (15). Consistency of the model (for a range of parameters) with the observed methylation data is determined by comparing both variance and expected value of the mean number of unique methylation patterns calculated for each model with that observed in Yatabe et al. (15). For the mean, consistency was determined by eye and no formal tests of consistency were performed. For variance, cumulative probability distribution of the variance of the number of unique tags was calculated and the standard hypothesis testing framework to determine consistency was used. Only a limited region of the possible parameter space was consider, not selecting the ‘best’ model as that most likely to reflect reality, but focus on determining whether there exists a subset of the parameter space that is consistent with the observed data.

In Appendix 2, how to derive an expression for the probability that a sample of cells from a single colon crypt was explained to contains exactly y unique methylation tags. In Appendix 2, P(Y) given in eqn (2) is the within‐crypt probability distribution for the number of unique tags. In a sample of (independent) crypts, joint probability of number of unique tags in a given number of crypts has a multinomial distribution. Probability that the mean (variance) of these unique tags over the sampled crypts takes a given value is then obtained by summing over the (multinomial) probabilities of within‐crypt tag configurations consistent with the given mean (variance).

Results

In their paper, Yatabe et al. only considered the case of two immortal stem cells as this was the only scenario consistent with the mean number of observed methylation tags per crypt (15). Figure 2 shows mean number of methylation tags per crypt for stem cell numbers ranging from 2 to 16 and σ between 0.5 and 0.99 calculated using the model described here. It is assumed that the DNA strands are initially unmethylated and use a methylation error rate (both maintenance and de novo) of 2 × 10⁻⁵ per CpG site per division; this is the same as that used in Yatabe et al. and allows assessment of the effect of preferential strand segregation on their results. Also the same rate of stem cell turnover, once per week, has been used. In each case it is assumed that seven cells were sampled from each of nine crypts. The only immortal scenario consistent with mean tags per crypt data when σ = 0.5 is the 2 stem cell model. Larger numbers of immortal stem cells are consistent as σ increases from 0.5. There are four pairs of stem cell numbers and σ values that are considered consistent with the observed mean data: (4, 0.75) (4, 0.9) (8, 0.9) (16, 0.9). None of the plots for σ = 0.99 are consistent for stem cell numbers considered here.

Figure 2.

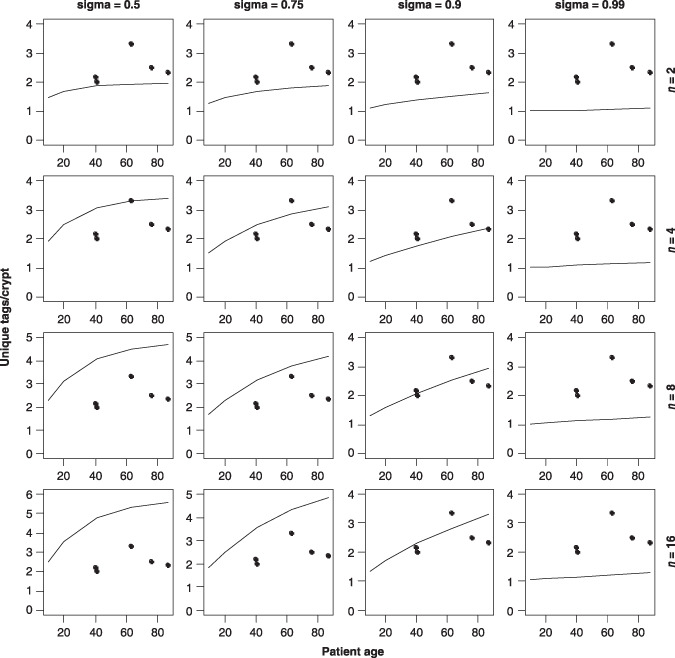
Observed mean tags per crypt (solid circles) compared to calculated mean tags per crypt (solid line) for different σ and stem cell numbers for the immortal model.

Yatabe et al. also looked at variance of the number of unique tags per crypt to further narrow down the range of stochastic and immortal models consistent with the observed data (15). They found a range of stem cell numbers consistent with data for the stochastic case, but for the two stem cell immortal model they consider, variance is too low to fit with observed variance data. For example, for the 41‐year‐old patient, observed variance was 0.67 and the simulated 95% confidence interval (CI) for the two stem cell model is (0, 0.33). Here it has been determined whether the increased set of stem cell immortal models consistent with the mean number of tags per crypt were also consistent with observed variance data. It has been calculated cumulative probability distribution for variance of the number of unique methylation tags per crypt for the 41‐, 63‐ and 87‐year‐old patients. The cumulative probability distribution was not calculated for the 40‐year‐old patient as the result would be very similar to that of the 41‐year‐old patient. Variance for the 76‐year‐old patient (4.3) did not fit any of the results for the models reported by the authors, neither immortal nor stochastic. Calculations here for the 63‐ and 87‐year‐old patients indicated that for the range of σ and stem cell numbers considered, the observed variance for the 76‐year‐old patient did not fit with models of this team either. This individual was excluded from the analysis here, for this reason.

Table 1 shows calculated 95% CI for variance of number of methylation tags per crypt for the four cases that were consistent with the observed mean tags per crypt data. The final column indicates whether the observed variance falls within the 95% CI. Observed variance data fit the 16 stem cell immortal model at all three ages considered. The eight stem cell and four stem cell model (both with σ = 0.9) are consistent for the 41‐ and 87‐year‐old patients but not for the 63‐year‐old patient, although in the eight stem cell case observed variance is not far from the 97.5th percentile. It is worth noting that observed variance for the 63‐year‐old patient is only just contained within the simulated 95% CI for stochastic models described in Yatabe et al.

Table 1.

Observed variance for the patients aged 41, 63 and 87 years and the calculated 95% confidence intervals (CI) calculated under various models. The final column indicates whether the observed variance is contained within the CI for the four models and different ages

N	Sigma	Age	Observed variance	95% CI for variance	Observed variance consistent with model?
4	0.75	41	0.67	(0.20, 1.28)	Yes
		63	2.3	(0.12, 1.25)	No
		87	1.4	(0.12, 1.11)	No
4	0.9	41	0.67	(0.12, 1.19)	Yes
		63	2.3	(0.20, 1.28)	No
		87	1.4	(0.20, 1.37)	Yes
8	0.9	41	0.67	(0.20, 1.77)	Yes
		63	2.3	(0.25, 2.03)	No
		87	1.4	(0.28, 2.25)	Yes
16	0.9	41	0.67	(0.25, 3.36)	Yes
		63	2.3	(0.28, 2.36)	Yes
		87	1.4	(0.36, 2.75)	Yes

Discussion

Figure 3 shows the cumulative probability distribution of the variance of the number of tags for the 87‐year‐old patient for the 16 stem cell model (σ from 0.5 to 0.99). The effect on cumulative distribution of varying σ is somewhat age dependent. In Fig. 3, increasing σ from 0.5 to 0.9 increased median variance; increasing beyond this value decreases median variance compared to the random segregation model (σ = 0.5). This pattern of increasing variance with σ up to some threshold followed by decreasing variance beyond this point is observed at all three ages considered and the threshold is observed to increase with age.

Figure 3.

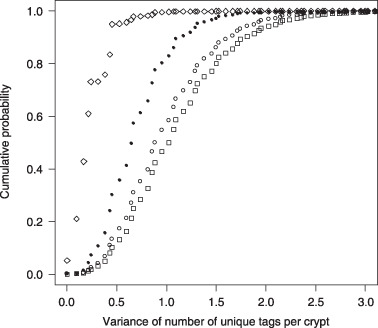
Cumulative probability distribution for the variance of the number of tags per crypt for an 87‐year‐old patient for the 16 stem cell immortal model for σ = 0.5 (solid circle); σ = 0.75 (open circle); σ = 0.9 (square) and σ = 0.99 (diamond).

Probability distribution for variance is concentrated around lower values when σ is 0.99 compared to when σ is 0.5. This is to be expected since an increase in variance of tags across crypts is a consequence of a more uniform within‐crypt probability distribution for the number of tags. When σ takes the value 0.99, the template strand in the parent stem cell is passed to the offspring cell with probability 0.99. Because the template strand is error‐free, this reduces accumulation of methylation errors compared to the case when σ is 0.5 (this is one of the motivations for Cairns (18) proposing the immortal strand hypothesis). This means that when σ takes the value 0.99, the within‐crypt probability distribution for the number of tags is heavily concentrated around a single value (one tag per crypt representing the unmethylated state). This results in a low variance across crypts as most crypts are likely to have just one tag.

That median variance initially increases in Fig. 3 is perhaps surprising. One might have expected that as σ increases from 0.5, the within‐crypt probability distribution would become increasingly less uniform and increasingly concentrated around one tag per crypt; this concentration would lower median variance (as was observed for σ = 0.99). As σ increases from 0.5, within‐crypt probability distribution does become less centred round a small set of values and this is consistent with the median variance across crypts increasing.

The method of calculating the lower moments of the distribution of the number of tags across a sample of crypts described here, is an underestimate of variance, as it was assumed that all differentiated cells have the same methylation pattern as the ancestral stem cell. Even with methylation error rates as low as considered here (2 × 10⁻⁵), there is a small chance of a methylation error occurring in a cell and the cell (or its descendent) being sampled. Therefore, the 97.5th percentile of the variance distribution may be higher than given in Table 1. This may make more of the model consistent with the data, that are currently inconsistent. For example, the 63‐year‐old patient with N = 4 and σ = 0.9, the observed variance is 2.3 and the 97.5th percentile is 2.03; the true 97.5th percentile of the variance for this model may be such that this model becomes consistent.

Yatabe et al. found evidence in favour of the stochastic model of stem cell turnover, but they assumed random strand segregation in their simulations (15). There is a long history of evidence for the immortal strand hypothesis (19), but it remains an area open to debate (20). Much of the controversy arises as a result of contradictory results in non‐stem cells (19). In this paper, it has been shown that the immortal model of stem cell turnover is consistent with empirical crypt methylation data if nonrandom strand segregation is incorporated into the model for colonic stem cell turnover; values of σ between 0.5 and 0.99 were considered. The higher value might represent the case where stem cells routinely pass on the template strand to daughter stem cells (during asymmetric division) but where the process does not have complete fidelity. However, according to calculations here, if stem cells do divide immortally, the error rate for this process would need to be relatively high as values of σ exceeding 0.99 yielded variances that were too small to be consistent with methylation data.

A defining feature of stem cells is their ability to produce both stem cells and differentiated daughter cells, but not necessarily at each cell division; asymmetric division is not a defining property of stem cells (24). There is evidence in many tissue‐specific stem cells to support the coexistence of both forms of cell proliferation, but the mechanisms and signals that determine stem cell proliferation are yet to be understood (24, 25). Following injury or cell death, a stem cell may go into apoptosis or senescence and it is difficult to see how asymmetric stem cell divisions alone could allow for their replacement. It therefore appears that there has to be the capacity for stem cell symmetric cell divisions, but the frequency at which these occur in the lifetime of a stem cell is not known. The mechanisms that regulate switching between the two states also remain unknown. If asymmetric division is the usual form of stem cell proliferation and symmetric division occurs only as a result of damage, then symmetric divisions may be very rare.

Because of the likelihood of at least some symmetric cell divisions over the lifetime of a stem cell, further research and modelling is needed to ascertain the effect of different levels of nonrandom strand segregation for other stem cell proliferation models to determine consistency with observed data. This would give some indication of the possible range of values that sigma could take under these models of stem cell proliferation. It may also be possible to estimate preferential segregation parameter in this case, using methylation data available and an Markov Chain Monte Carlo approach similar to that taken by Nicoles et al. (26) to infer stem cell numbers.

Appendix 1

It has been defined that 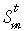to be the event that in generation t, strand m is the template strand in a stem cell.

If strand 1 is the template strand in the founder stem cell, then a descendent stem cell in generation t will have strand 1 as the template strand if, and only if, the stem cell offspring at each intervening cell division do not receive the parental template strand an even number of times. If

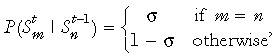it follows that

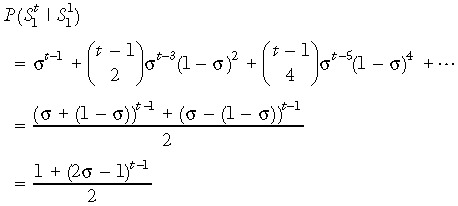Appendix 2

Initial definitions

• 1 N is the number of stem cells in a crypt;
• 2 M is the number of sampled epithelial cells;
• 3 Y is the random variable representing the number of unique methylation tags present in a sample of M epithelial cells;
• 4 G is the number of CpG sites in the genomic DNA sequence;
• 5 H is the set of all methylation tags for the genomic DNA sequence, such that H has cardinality2^G;
• 6 A^t(i) is the event that the template strand in the stem cell in generation t has methylation tag i;
• 7σ is the conditional probability that the template strand in the parent stem cell becomes the template strand in the daughter stem cell;
• 8 S is the event that the template strand in the parent stem cell becomes the template strand in the daughter stem cell (where P(S) = σ);
• 9 W(f) is the sum of P(A^t(i)) over those i contained in the set f(⊂H);
• 10 P_n(C) is the power set of all subsets of set C of size n;
• 11 R(i,j) is the conditional probability that in any given cell, the synthesized DNA strand has methylation pattern j given that the template DNA strand has methylation pattern i;
• 12 K_ab, where a,b = {0,1} the number of CpG sites for which the template strand has bit a and the synthesized strand has bit b (where bits 0 and 1 represent unmethylated and methylated CpG sites, respectively);
• 13µ is the probability that a CpG site synthesized from an unmethylated CpG site becomes methylated due to de novo methylation following DNA replication; and
• 14ρ is the probability that a CpG site synthesized from a methylated CpG site becomes methylated, due to maintenance methylation, following DNA replication.

It follows from the above definitions that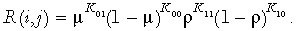

The model

Expression of P(Y = y) is required, the within‐crypt probability that M sampled cells contain exactly y unique methylation tags. This is done by conditioning on ancestral stem cells that the cells are descendents of. It is shown how to form the transition matrix for a Markov chain where the state space is the set of methylation tags of the stem cells. Finally, application of the inclusion/exclusion principle to the state space probabilities in a specific generation achieves the desired result.

Let D_i represent the number of sampled cells that are descendents of stem cell i (1 ≤ i ≤ N) . For 1 ≤ y ≤ min (N,2^G)

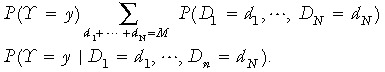(2)

Assume the crypt contains 2048 cells (10), the summation over d ₁, ..., d_N is subject to the further constraint d_i ≤ min(M, 2048/N); the number of cells sampled from the descendents of any stem cell must be less than both the number of cells sampled and the number of descendent cells that is being sampled from. The probability distribution for D ₁, D ₂, D ₃, D ₄ has the form

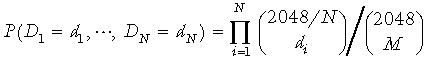(3)

The conditional probability in eqn (2), P(Y = y | D ₁= d ₁, ..., D_n = d_N), requires us to keep track of the tag probability distribution in descendent stem cells. We require P(A^{t +1}(j)) which can be obtained iteratively via

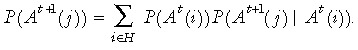(4)

Where the conditional part is given further by

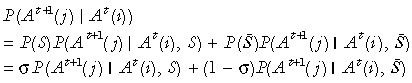P(A ^t+1(j) |A^t(i), S̄) =R(i, j) and P(A ^t+1(j) |A^t(i), S) = 1 if i=j and is zero otherwise.

• 1Therefore, eqn (4) simplifies to

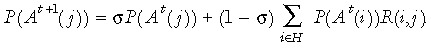(5)

Let X(t) represent a vector of length card (H), where X_j(t) represents the jth element. If we define X_j(t) =P(A^t(j)) so that X(t) represents the stem cell probabilities in generation t we wish to model, then eqn (5) can be written as:

(6)

Further define a matrix Q (of dimensions card (H) by card(H)) such that the elements of Q are given by Q_ji =R(i,j), then eqn (6) can be written in matrix notation:

X(t+ 1) =[σI+ (1 −σ)Q]X(t), (7)

where I is the (card(H) by card(H)) identity matrix. The matrix [σI + (1 – σ)Q] is therefore the transition matrix of the Markov chain describing the transition probabilities between methylation states of the stem cells. Because all cytosines in the stem cell template strand are initially unmethylated, the initial probability state vector is P(A ¹(j)) = 1 if j = 1 and is zero otherwise (where the first element of the state space (H) corresponds to the fully unmethylated state). Using this transition matrix and initial probability vector, we can calculate the state space probability vector for the methylation tags of a stem cell in generation t.

Using this probability vector for the methylation tags of a stem cell in generation t, we can determine P(Y =y | D₁ = d ₁, ..., D_n = d_N) in eqn (2) by applying the inclusion/exclusion principle to yield

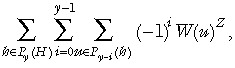(8)

where Z (Z ≤ N) is the number of stem cells with descendents that are sampled and W(u) represents the sum of probabilities P(A^t(i)) where the i are those corresponding to set u (subset of the methylation tag set H). We want the probability that the sampled cells will include exactly y methylation patterns among them. For any given set of methylation patterns of size y (first summation ensures we include all subsets of size y), we allow each sampled cell to take any of the y methylation patterns (explains the third summation). Because we are allowing each cell to select independently from the y methylation patterns, many of the unions of methylation patterns will not include all y tags. We consequently subtract all the ways of including exactly y – 1 patterns. Then find to have subtracted too many ways for the sampled cells to contain exactly y – 2 patterns so we add these back in. This process continues down to the case where all sampled cells have the same methylation pattern. This explains the second summation.

The exponent in eqn (8) is Z, rather than M because it is assumed that all cells descended from the same stem cell will have identical methylation patterns. This is valid only if we consider an X‐linked locus where only one allele is sequenced. Because the two chromosomes in a cell act independently, the effect of considering an autosomal locus would be to double Z in eqn (8).

To increase computational efficiency, the binary methylation patterns can be thought of as forming an n‐dimensional cube (otherwise known as a hypercube). The inclusion/exclusion computations can be simplified by considering certain symmetries of this hypercube. Such simplifications have been used previously in the context of identity by descent calculations (27, 28)). For the BGN locus consider, this simplification means considering 10 hypercube subsets rather than the 2⁹ vertices of the hypercube.