Abstract
This study examined the accuracy of different velocity-based methods in the prediction of bench press and squat one-repetition maximum (1RM) in female athletes. Seventeen trained females (age 17.8 ± 1.3 years) performed an incremental loading test to 1RM on bench press and squat with the mean velocity being recorded. The 1RM was estimated from the load–velocity relationship using the multiple- (8 loads) and two-point (2 loads) methods and group and individual minimum velocity thresholds (MVT). No significant effect of method, MVT or interaction was observed for the two exercises (p > 0.05). For bench press and squat, all prediction methods demonstrated very large to nearly perfect correlations with respect to the actual 1RM (r range = 0.76 to 0.97). The absolute error (range = 2.1 to 3.8 kg) for bench press demonstrated low errors that were independent of the method and MVT used. For squat, the favorable group MVT errors for the multiple- and two-point methods (absolute error = 7.8 and 9.7 kg, respectively) were greater than the individual MVT errors (absolute error = 4.9 and 6.3 kg, respectively). The 1RM can be accurately predicted from the load–velocity relationship in trained females, with the two-point method offering a quick and less fatiguing alternative to the multiple-point method.
Keywords: one-repetition maximum, velocity-based training, squat, bench press, GymAware, agreement
1. Introduction
Maximal strength refers to the maximum force or torque that can be exerted by the muscles [1]. Strength is highly important as it is used to prescribe an athlete’s training load [2] and can differentiate between levels of performance within a sport [3]. Moreover, in young athletes, strength is important to maximize athletic performance [4,5]. For example, Comfort and colleagues [4] established moderate to strong relationships between maximal strength and measures of sprint (r > −0.60) and jump (r > 0.76) performance. Thus, it is necessary for practitioners to assess and monitor an athlete’s strength. Maximal dynamic strength is frequently assessed via a one-repetition maximum (1RM) protocol, whereby the maximum load that can be lifted once is identified. However, direct determination of 1RM can be problematic as it is time-intensive, fatiguing and psychologically demanding [6,7]. Though repetitions-to-failure equations are alternatively used because they are time-efficient, they do not negate the fatiguing effects or psychological demand imposed when performing this type of test [6,7]. Fortunately, the recent popularisations of velocity-based devices have enhanced the ability to indirectly determine 1RM [7].
The inverse-linear relationship between movement velocity and load lifted can offer an alternative method to predict 1RM [6,7]. Typically, this relationship is modelled by assessing velocity over multiple submaximal loads (usually from 3 to 8 loads; i.e., the multiple-point method) [7]. Thereafter, 1RM is estimated as the load that is associated with the velocity at 1RM (i.e., the minimum velocity threshold; MVT). Whilst previous work has used an individualised MVT for each individual [8,9], the recent literature suggests that a group-based MVT can predict 1RM with acceptable precision in the bench press [10] and prone bench pull [11]. To our knowledge, only Jukic et al. [9] have compared the precision in the estimation of 1RM between individualised and group-based MVTs and revealed a comparable precision for both MVTs during the deadlift exercise. Like the Weakley et al. [7] commentary, the accuracy of individual versus group MVTs in the prediction of 1RM warrants investigation. Practically, the accurate estimation of 1RM would enhance training through the accurate prescription of the training load. This is even more important for female athletes due to the significant differences in the load–velocity profiles reported in previous studies between men and women [12,13,14].
As the relationship between movement velocity and load lifted is highly linear, it has been proposed that the relationship can be modelled using just two external loads (i.e., the two-point method) [6,15]. For example, Perez-Castilla et al. [6] noted that the multiple-point (i.e., 40, 55, 70 and 85% 1RM) and two-point (i.e., 40 and 85% 1RM) methods provided similar accuracy when predicting 1RM in two upper body pulling exercises. Indeed, a variety of literature confirms that the two-point method can predict 1RM across various different exercises with the same accuracy as the multiple-point method [6,9,15]. Importantly, the two-point method is less time-consuming and induces minimal fatigue when compared to the methods mentioned above (direct determination, repetitions to failure, load–velocity relationship modelled by multiple submaximal loads) [7].
Research on 1RM predictions from the load–velocity relationship in females is lacking. To date, only Perez-Castilla and colleagues [6] reported a comparable precision for men and women in the estimation of 1RM during the lat pulldown and seated cable row exercises. The lack of velocity-based training research with females and sports science in general is problematic for practitioners working with female athletes and likely reflects the patriarchal nature of sports medicine [16,17]. A study which determines the accuracy of 1RM predictions from the load–velocity relationship across resistance-training exercises will aid coaches when prescribing training loads in female athletes. This is particularly important as the slope of the load–velocity relationship is different in males and females [13,14]. Moreover, this would indicate that submaximal loads (i.e., % of 1RM) are associated with different velocities in females compared to males. Therefore, the aim of our study is to determine the accuracy of the load–velocity relationship when predicting the squat and bench press 1RM in trained females. The secondary aim is to determine if the load combination (multiple-point versus two-point methods) and the MVT selected (individualised versus group) affect the accuracy of the 1RM prediction. Given the dearth of comparable studies, we propose the null hypothesis for both of our aims: (1) that there will be no systematic differences between actual and predicted 1RM while their magnitudes would be highly correlated (that is, the accuracy will produce comparable values); and (2) the load combination and the MVT selected will not affect the 1RM prediction accuracy.
2. Materials and Methods
2.1. Participants
Seventeen resistance-trained females (age 17.8 ± 1.3 years, body mass 69.1 ± 9.6 kg) were recruited via convenience sampling. All participants belonged to the netball team within the sports academy of the host institution and performed bench press (1RM 38.6 ± 7.5 kg) and squat (1RM 86.5 ± 14.7 kg) as part of their training regime (minimum of 1-year systematic resistance training). Participants completed a pre-test health questionnaire and provided informed written consent (and parental consent for those under 18) for the study, which was approved by the host institution’s faculty ethics committee (ETHICS2019-14). The participants were instructed not to consume any ergogenic supplements (for example, caffeine) on the day of testing and to refrain from strenuous exercise in the 3 h before testing. The study adhered to the Declaration of Helsinki.
2.2. Experimental Design
The study comprised a randomised crossover design whereby participants attended the strength and conditioning gym on two occasions (one per exercise with 48 h between) during the competitive season. On each occasion (between 10.00 and 12.00 h), participants performed a standardised warm-up before completing an incremental loading procedure until 1RM was attained. The mean velocity (m/s−1) of each repetition performed at each load during the incremental loading procedures was recorded using a linear position transducer (GymAware, Kinetic Performance Technology, Canberra, Australia). Thereafter, four different velocity-based methods (2 load combinations × 2 MVTs) were used to predict 1RM. The data of eight loads (~40, 45, 55, 60, 70, 80, 85 and 90% 1RM for bench press and ~20, 30, 45, 55, 65, 75, 85 and 90% 1RM for squat; i.e., the multiple-point method) and only the two distant loads (~40 and 90% 1RM for bench press and 20 and 90% 1RM for squat; i.e., the two-point method) were used for the modelling of the individual load–velocity relationships by applying linear regression models. 1RM was estimated via linear regression equations using the individual load–velocity relationships as the load associated with a group and individual MVT. The group MVT values used to estimated 1RM for bench press and squat was 0.22 and 0.36 m/s−1, respectively. For the 1RM prediction from the individual MVTs, each participant’s MVT was used. These ranged from 0.15 to 0.32 and 0.24 to 0.47 m/s−1 for bench press and squat, respectively.
2.3. Incremental Loading Test
After performing a standardised warm-up, participants performed 1 set of 5 repetitions with a 15 kg free-weight barbell to determine their full range of motion. The incremental loading procedure has been described elsewhere [6]. In brief, participants started with a 15 kg barbell unless their perceived 1RM was > 100 kg, in which case the barbell was loaded to ~20% 1RM. The load was progressively increased in ~10% 1RM increments (~5 to 10 kg) until the mean velocity was < 0.60 m/s−1. Thereafter, the load was increased in smaller increments (~1 to 2.5 kg) until participants failed 1 repetition. 1RM was defined as the highest load (kg) that was lifted through a whole range of motion (as determined by the lead researcher). Any repetitions that were not performed with a full range of motion were excluded and repeated. Participants performed 2 repetitions when the mean velocity was > 0.60 m/s−1 and 1 repetition when the mean velocity was ≤ 0.60 m/s−1. Intra- and inter-set rest was 15 s and 5 min, respectively. The participants received verbal encouragement to improve the accuracy of the 1RM prediction [10]. This procedure was identical for bench press and squat exercise.
2.4. Description of Exercises
For the bench press exercise, participants held the barbell with a self-selected width and the pronated grip [18] and lowered it to their chest in a controlled manner and then, without bouncing the barbell, pushed it maximally until full elbow extension. For the squat exercise, with the barbell positioned across their shoulders, participants descended until their hips were below the knee joint and then ascended as rapidly as possible until their knees were at full extension. These exercises were standardised in line with the previous research [19,20,21].
2.5. Data Acquisition
GymAware was employed to measure mean velocity from time and displacement. GymAware adopts a variable sampling rate whereby movement is recorded and time-stamped when there is a change of 600 mm (0.0006 m) after which the data are filtered to 50 samples per second. Importantly, this method is deemed a valid and reliable tool in the assessment of mean velocity [21,22].
2.6. Statistical Analysis
The data were found to be normally distributed according to the Shapiro–Wilk test (p > 0.05). A two-factor repeated-measures analysis of variance (ANOVA) (MVT [group versus individual] × method [multiple versus two-point]) was applied on the absolute differences between the actual and predicted 1RM separately for each exercise. Furthermore, the validity of the 1RM prediction methods with respect to the actual 1RM was examined through Cohen’s d effect size (ES), the absolute and raw differences (kg) and the heteroscedasticity of the errors (r2; relationship of the raw differences between the actual and predicted 1RMs with their average values). Although not indicative of the agreement [21,23], Pearson’s correlation coefficients (r) were calculated to facilitate comparisons to the previous papers. Qualitative interpretations of the r coefficients were defined as follows: trivial (0.00–0.09), small (0.10–0.29), moderate (0.30–0.49), large (0.50–0.69), very large (0.70–0.89), nearly perfect (0.90–0.99), perfect (1.00) [24]. The magnitude of the ES was interpreted as follows: trivial (<0.20), small (0.20–0.59), moderate (0.60–1.19), large (1.20–2.00) and very large (>2.00) [24]. Heteroscedasticity of error was defined as r > 0.32 [25]. Alpha was set at 0.05. All the data were calculated using the SPSS software (version 26, IBM SPSS, INC., Chicago, IL, USA).
3. Results
3.1. Bench Press
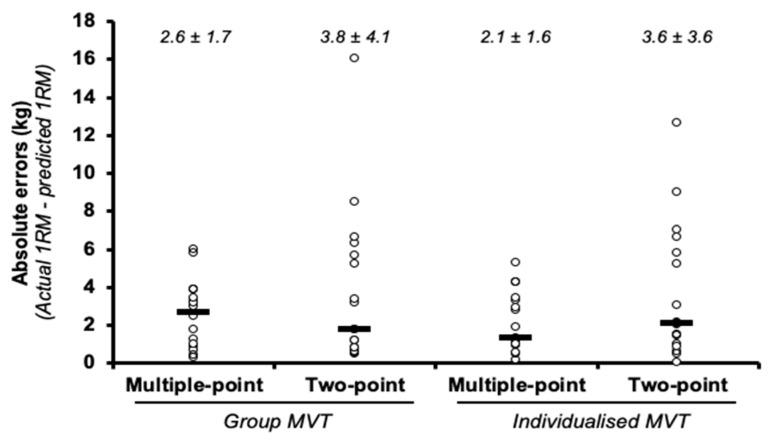
The ANOVA did not reveal a significant main effect for the MVT (F = 0.63, p = 0.438) or method (F = 4.3, p = 0.054). Furthermore, the MVT × method interaction did not reach statistical significance (F = 0.82, p = 0.380). The absolute errors ranged from 2.1 to 3.8 kg (Figure 1, with ESs that were trivial and small for the multiple- and two-point methods, respectively (Table 1). The correlations ranged from very large to nearly perfect (r range = 0.84 to 0.97), though higher 1RMs were associated with and increased overestimation (r range = 0.33 to 0.54).
Figure 1.
Comparison of the absolute differences (mean ± standard deviation) between the actual one-repetition maximum (1RM) and the 1RM estimated using the different prediction methods in the bench press exercise. Note: the black rectangle denotes the median value, while the circles represent individual data points.
Table 1.
Differences, associations and heteroscedasticity of the errors between the actual and predicted one-repetition maximums (1RM) during the bench press exercise.
| MVT | Method | Predicted 1RM (kg) | Raw Diff (kg) | ES | r(Pearson) | r(Heteroscedasticity) |
|---|---|---|---|---|---|---|
| Group | Multiple-point | 39.4 ± 8.6 | 0.8 ± 3.0 | 0.10 | 0.94 | 0.37 |
| Two-point | 41.3 ± 9.0 | 2.7 ± 4.9 | 0.32 | 0.84 | 0.33 | |
| Individualised | Multiple-point | 39.5 ± 8.8 | 0.9 ± 2.5 | 0.11 | 0.97 | 0.54 |
| Two-point | 41.3 ± 9.1 | 2.8 ± 4.3 | 0.33 | 0.89 | 0.39 |
Data are mean ± standard deviation. Raw diff, Raw differences; ES, Cohen’s d effect size ([Predicted 1RM − Actual 1RM]/SD both); rPeason, Pearson’s correlation coefficient; rheteroscedasticity, heteroscedasticity of the errors.
3.2. Squat
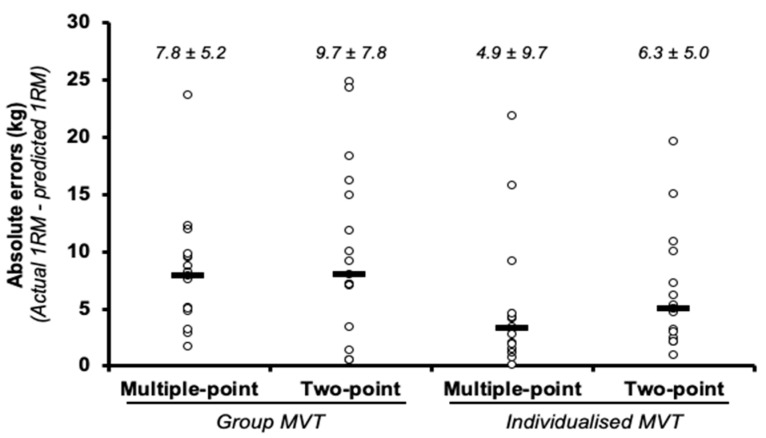
The ANOVA revealed no significant differences for MVT (F = 2.65, p = 0.123), method (F = 1.96, p = 0.180), or their interaction (F = 0.31, p = 0.585). The absolute differences ranged from 4.9 to 9.7 kg (Figure 2) with ESs that were trivial and small for the multiple- and two-point methods, respectively (Table 2). The correlations for the group methods were very large (r = 0.76 and 0.86 for multiple- and two-point methods, respectively) and nearly perfect for the individual methods (r = 0.95 and 0.93 for multiple- and two-point methods, respectively). Three of the four prediction methods demonstrated heteroscedasticity of the errors, with higher 1RMs associated with larger errors (i.e., a higher overestimation; r = 0.28 to 0.69).
Figure 2.
Comparison of the absolute differences (mean ± SD) between the actual 1 repetition maximum (1RM) and the 1RM estimated using the different prediction methods in the squat exercise. Note: the black rectangle denotes the median value, while the circles represent individual data points.
Table 2.
Differences, associations and heteroscedasticity of the errors between the actual and predicted one-repetition maximums (1RM) during the squat exercise.
| MVT | Method | Predicted 1RM (kg) | Raw Diff (kg) | ES | r(Pearson) | r(heteroscedasticity) |
|---|---|---|---|---|---|---|
| Group | Multiple-point | 88.6 ± 17.6 | 3.1 ± 9.1 | 0.19 | 0.86 | 0.37 |
| Two-point | 90.3 ± 17.8 | 4.7 ± 11.7 | 0.29 | 0.76 | 0.28 | |
| Individualised | Multiple-point | 88.3 ± 19.5 | 2.7 ± 7.1 | 0.16 | 0.95 | 0.69 |
| Two-point | 89.4 ± 18.1 | 3.8 ± 7.2 | 0.23 | 0.93 | 0.49 |
Data are mean ± standard deviation. Raw diff, Raw differences; ES, Cohen’s d effect size ([Predicted 1RM − Actual 1RM]/SD both); rPeason, Pearson’s correlation coefficient; rheteroscedasticity, heteroscedasticity of the errors.
4. Discussion
The aim of the study was to examine the accuracy of the load–velocity relationship when predicting 1RM in trained female athletes. We report here that velocity-based methods can be used to accurately predict bench press and squat 1RM in this population. Our second aim was to determine if the load combination (multiple-point versus two-point) and MVT (individual versus group) affect the accuracy of the prediction. We report that for bench press, both load combinations and MVTs can be used, though practically, a two-point method with a group MVT might be more time-efficient. For the squat exercise, although significant differences were not reached, irrespectively of the load combination, the individual MVT provided 1RM ~ 3 kg more precisely than the group MVT. Holistically, these findings suggest that the load–velocity relationship can be used to predict 1RM in trained female athletes, while there are no evident differences in the precision of different methods and MVTs.
Like previous reports conducted with males, our data demonstrated very large to nearly perfect correlations in the bench press between actual 1RM and predicted 1RMs irrespectively of the methods and MVTs [10,15,26,27,28]. However, measures of association are not indicative of agreement between prediction methods [21]; more important is the absolute agreement and random error between prediction methods. In this study, the small absolute differences and low random errors between actual 1RM and all predictions are in line with previous reports [10,15,26,28,29]. The absolute and random errors in this study, independent of the prediction method, were able to detect the ~ 6 and ~ 8 kg increases in bench press strength that occurred after 8 [30] and 7 [31] weeks of resistance training. For the younger (< 18-year-old) females in our sample, the absolute and random errors, which were similar across load combinations and MVT types, are likely able to detect moderate increases in strength (ES = 0.72) that occur in female youths [32]. It should be noted that all prediction methods for bench press demonstrated small heteroscedasticity, indicating that those with higher 1RMs are subject to greater error (higher overestimation). This is an important consideration, as 1RM is likely to increase with training age in these athletes. Nonetheless, bench press 1RM can be predicted from velocity-based methods in trained female athletes, though using the two-point method with group MVT may be more convenient for practitioners.
Squat demonstrated very large to nearly perfect correlations between direct 1RM and the prediction methods, similar to the previous works [8,33]. The absolute and random errors in this study show favourable agreement and are similar to the previous reports during the squatting exercise [34,35] but in contrast to two reports [8,33]. With the only exception of the two-point method using a group MVT, the remaining velocity-based methods displayed absolute errors lower than 10%. It is important to note that although significant differences were not reached the 1RM predicted using the individual MVTs demonstrated better agreement than the group MVT. The reason for this is unclear but would suggest that the group MVT (0.36 m/s−1), did not generally represent the MVT of all the individuals. Indeed, the heterogeneity in the MVTs amongst our sample (from 0.24 to 0.47 m/s−1) would support such a suggestion. This might be owing to the squat requiring a multi-jointed coordinated effort to produce the movement. However, the repeatability of the individualised MVT in female athletes is unknown and it is likely to have poor reliability as it has been shown for males [8,11,36]. Therefore, the individualised MVT recorded in one session may be inappropriate when 1RM is estimated in another session. Future studies should compare the precision in the estimation of 1RM between the group and individualised MVTs when the individualised MVT is obtained in a previous session, as it would be the case in real training scenarios (i.e., recording of the individual MVT in one session and use of this individual MVT for 1RM prediction through a training cycle). Regardless of the 1RM prediction method, the errors are all low enough to detect the changes that occur after resistance training in healthy (~ 15 kg [37]) and elite females (~ 12 kg [38]). Furthermore, for the younger participants in this study (i.e., those < 18 years), the errors in this study are likely able to detect moderate (ES = 0.72) improvements in strength that occur in female youths [32]. Like for the bench press exercise, the majority of the errors for squat were heteroscedastic. Therefore, practitioners should be mindful of the larger errors (higher overestimation) in stronger individuals. Collectively, these data suggest that velocity-based methods can be used to predict squat 1RM in trained female athletes. If coaches, however, require greater precision, then the use of individual MVTs is recommended, but it remains to be explored whether this advantage remains when the individual MVT is recorded in a previous session.
Readers should be mindful that we opted not to assess the menstrual cycle in this study. The reasons for this are two-fold. Firstly, the menstrual cycle does not appear to largely affect strength performance [39,40,41,42,43,44,45] or the accuracy in the prediction of 1RM from velocity-based methods [46]. Secondly, our sample was recruited from the sports academy and included U18 athletes. The assessment of the menstrual cycle in youths raises ethical concerns and is not commonplace in the youth literature. However, these potential limitations do provide implications for future research.
5. Conclusions
The bench press and squat 1RM can be accurately predicted from the load–velocity relationship in trained female athletes. These data reaffirm previous suggestions in males that 1RM can be predicted with similar accuracy with either the multiple- or the two-point method. From the practical point of view, it is more time-efficient and less fatiguing to use the two-point method. Concerning the type of the MVT used, although acknowledging a generally higher precision of the individual MVT, we failed to show significant differences in the absolute errors between the group and individualised MVTs. However, it is important that future studies elucidate whether the slight differences in favour of the individual MVT still remain when the individual MVT and the load–velocity relationship are obtained in different sessions. Readers should also be aware that low-cost phone applications (e.g., iLOAD, PowerLift), which can accurately measure velocity, are available to use if the most expensive equipment used in our study is not available.
Acknowledgments
We thank the participants for their time and effort.
Author Contributions
Conceptualization, E.J.G.C. and J.F.T.F.; methodology, E.J.G.C. & T.J.E.B.; formal analysis, E.J.G.C., A.F.D. and J.F.T.F.; writing—original draft preparation E.J.G.C. and J.F.T.F.; writing—review and editing, T.J.E.B., A.F.D., B.D., A.P.-C., A.G.-R. and J.A.; visualization, J.F.T.F., A.P.-C. and A.G.-R.; supervision, J.F.T.F. and B.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Knuttegen H.G., Komi P.V. Strength and Power in Sport. In: Komi P.V., editor. Strength and Power in Sport. Blackwell Publishing Company; Oxford, UK: 2003. pp. 3–11. [Google Scholar]
- 2.Scott B.R., Duthie G.M., Thornton H.R., Dascombe B.J. Training monitoring for resistance exercise: Theory and applications. Sport. Med. 2016;46:687–698. doi: 10.1007/s40279-015-0454-0. [DOI] [PubMed] [Google Scholar]
- 3.Fernandes J.F.T., Daniels M., Myler L., Twist C. Influence of playing standard on upper- and lower-body strength, power, and velocity characteristics of elite rugby league players. J. Funct. Morphol. Kinesiol. 2019;4:22. doi: 10.3390/jfmk4020022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Comfort P., Stewart A., Bloom L., Clarkson B. Relationship between strength sprint and jump performance in well-trained youth soccer players. J. Strength Cond. Res. 2014;28:173–177. doi: 10.1519/JSC.0b013e318291b8c7. [DOI] [PubMed] [Google Scholar]
- 5.Suchomel T.J., Nimphius S., Stone M.H. The importance of muscular strength in athletic performance. Sport. Med. 2016;46:1419–1449. doi: 10.1007/s40279-016-0486-0. [DOI] [PubMed] [Google Scholar]
- 6.Perez-Castilla A., Suzovic D., Domanovic A., Fernandes J.F.T., Garcia-Ramos A. Validity of different velocity-based methods and repetitions-to-failure equations for predicting the 1 repetition maximum during 2 upper-body pulling exercises. J. Strength Cond. Res. 2019:1–9. doi: 10.1519/JSC.0000000000003076. [DOI] [PubMed] [Google Scholar]
- 7.Weakley J., Mann B., Banyard H., Mclaren S., Scott T., Garcia-ramos A. Velocity-based training: From theory to application. Strength Cond. J. 2020:1–19. doi: 10.1519/SSC.0000000000000560. [DOI] [Google Scholar]
- 8.Banyard H.G., Nosaka K., Haff G.G. Reliability and validity of the load-velocity relationship to predict the 1RM back squat. J. Strength Cond. Res. 2017;31:1897–1904. doi: 10.1519/JSC.0000000000001657. [DOI] [PubMed] [Google Scholar]
- 9.Jukic I., García-Ramos A., Malecek J., Omcirk D., Tufano J.J. Validity of load–velocity relationship to predict 1 repetition maximum during deadlifts performed with and without lifting straps. J. Strength Cond. Res. 2020:1–9. doi: 10.1519/JSC.0000000000003596. [DOI] [PubMed] [Google Scholar]
- 10.Jiménez-Alonso A., García-Ramos A., Cepero M., Miras-Moreno S., Rojas F.J., Pérez-Castilla A. Velocity performance feedback during the free-weight bench press testing procedure: An effective strategy to increase the reliability and one repetition maximum accuracy prediction. J. Strength Cond. Res. 2020:1. doi: 10.1519/JSC.0000000000003609. [DOI] [PubMed] [Google Scholar]
- 11.García-Ramos A., Barboza-González P., Ulloa-Díaz D., Rodriguez-Perea A., Martinez-Garcia D., Guede-Rojas F., Hinojosa-Riveros H., Chirosa-Ríos L.J., Cuevas-Aburto J., Janicijevic D., et al. Reliability and validity of different methods of estimating the one-repetition maximum during the free-weight prone bench pull exercise. J. Sports Sci. 2019;37:2205–2212. doi: 10.1080/02640414.2019.1626071. [DOI] [PubMed] [Google Scholar]
- 12.Torrejón A., Balsalobre-Fernández C., Haff G.G., García-Ramos A. The load-velocity profile differs more between men and women than between individuals with different strength levels. Sport. Biomech. 2019;18:245–255. doi: 10.1080/14763141.2018.1433872. [DOI] [PubMed] [Google Scholar]
- 13.Balsalobre-Fernández C., García-Ramos A., Jiménez-Reyes P. Load–velocity profiling in the military press exercise: Effects of gender and training. Int. J. Sport. Sci. Coach. 2018;13:743–750. doi: 10.1177/1747954117738243. [DOI] [Google Scholar]
- 14.García-Ramos A., Suzovic D., Pérez-Castilla A. The load-velocity profiles of three upper-body pushing exercises in men and women. Sport. Biomech. 2019:1–3. doi: 10.1080/14763141.2019.1597155. [DOI] [PubMed] [Google Scholar]
- 15.García-Ramos A., Haff G.G., Pestaña-Melero F.L., Pérez-Castilla A., Rojas F.J., Balsalobre-Fernández C., Jaric S. Feasibility of the 2-point method for determining the 1-repetition maximum in the bench press exercise. Int. J. Sports Physiol. Perform. 2018;13:474–481. doi: 10.1123/ijspp.2017-0374. [DOI] [PubMed] [Google Scholar]
- 16.Costello J.T., Bieuzen F., Bleakley C.M. Where are all the female participants in Sports and Exercise Medicine research? Eur. J. Sport Sci. 2014;14:847–851. doi: 10.1080/17461391.2014.911354. [DOI] [PubMed] [Google Scholar]
- 17.O’Malley L.M., Greenwood S. Female coaches in strength and conditioning—Why so few? Strength Cond. J. 2018;40:40–48. doi: 10.1519/SSC.0000000000000401. [DOI] [Google Scholar]
- 18.Pérez-Castilla A., Jerez-Mayorga D., Martínez-García D., Rodríguez-Perea Á., Chirosa-Ríos L.J., García-Ramos A. Influence of grip width and anthropometric characteristics on the bench press load–velocity relationship. Int. J. Sports Physiol. Perform. 2020;1:1–9. doi: 10.1123/ijspp.2019-0840. [DOI] [PubMed] [Google Scholar]
- 19.Fernandes J.F.T., Lamb K.L., Twist C. The intra- and inter-day reproducibility of the FitroDyne as a measure of multi-jointed muscle function. Isokinet. Exerc. Sci. 2016;24:39–49. doi: 10.3233/IES-150599. [DOI] [Google Scholar]
- 20.Fernandes J.F.T., Lamb K.L., Twist C. A comparison of load-velocity and load-power relationships between well-trained young and middle-aged males during three popular resistance exercises. J. Strength Cond. Res. 2018;32:1440–1447. doi: 10.1519/JSC.0000000000001986. [DOI] [PubMed] [Google Scholar]
- 21.Fernandes J.F.T., Lamb K.L., Clark C.C.T., Moran J., Drury B., Garcia-Ramos A., Twist C. Comparison of the FitroDyne and GymAware rotary encoders for quantifying peak and mean velocity during traditional multijointed exercises. J. Strength Cond. Res. 2018;00:1–6. doi: 10.1519/JSC.0000000000002952. [DOI] [PubMed] [Google Scholar]
- 22.Dorrell H.F., Moore J.M., Smith M.F., Gee T.I. Validity and reliability of a linear positional transducer across commonly practised resistance training exercises. J. Sports Sci. 2019;37:67–73. doi: 10.1080/02640414.2018.1482588. [DOI] [PubMed] [Google Scholar]
- 23.McLaughlin P. Testing agreement between a new method and the gold standard-How do we test? J. Biomech. 2013;46:2757–2760. doi: 10.1016/j.jbiomech.2013.08.015. [DOI] [PubMed] [Google Scholar]
- 24.Hopkins W.G., Marshall S.W., Batterham A.M., Hanin J. Progressive statistics for studies in sports medicine and exercise science. Med. Sci. Sports Exerc. 2009;41:3–12. doi: 10.1249/MSS.0b013e31818cb278. [DOI] [PubMed] [Google Scholar]
- 25.Atkinson G., Nevill A.M. Statistical methods for assessing measurement error (reliability) in variables relevant to sports medicine. Sport. Med. 1998;26:217–238. doi: 10.2165/00007256-199826040-00002. [DOI] [PubMed] [Google Scholar]
- 26.Balsalobre-Fernández C., Marchante D., Muñoz-López M., Jiménez S.L. Validity and reliability of a novel iPhone app for the measurement of barbell velocity and 1RM on the bench-press exercise. J. Sports Sci. 2018;36:64–70. doi: 10.1080/02640414.2017.1280610. [DOI] [PubMed] [Google Scholar]
- 27.Pérez-Castilla A., Piepoli A., Garrido-Blanca G., Delgado-García G., Balsalobre-Fernández C., García-Ramos A. Precision of 7 commercially available devices for predicting bench-press 1-repetition maximum from the individual load–velocity relationship. Int. J. Sports Physiol. Perform. 2019;14:1442–1446. doi: 10.1123/ijspp.2018-0801. [DOI] [PubMed] [Google Scholar]
- 28.Pérez-Castilla A., Jerez-Mayorga D., Martínez-García D., Rodríguez-Perea Á., Chirosa-Ríos L.J., García-Ramos A. Comparison of the bench press one-repetition maximum obtained by different procedures: Direct assessment vs. lifts-to-failure equations vs. two-point method. Int. J. Sport. Sci. Coach. 2020;15:337–346. doi: 10.1177/1747954120911312. [DOI] [Google Scholar]
- 29.Pérez-Castilla A., Piepoli A., Delgado-García G., Garrido-Blanca G., García-Ramos A. Reliability and concurrent validity of seven commercially available devices for the assessment of movement velocity at different intensities during the bench press. J. Strength Cond. Res. 2019;33:1258–1265. doi: 10.1519/JSC.0000000000003118. [DOI] [PubMed] [Google Scholar]
- 30.Burnham T.R., Ruud J.D., McGowan R. Bench press training program with attached chains for female volleyball and basketball athletes. Percept. Mot. Skills. 2010;110:61–68. doi: 10.2466/pms.110.1.61-68. [DOI] [PubMed] [Google Scholar]
- 31.Nunes J.A., Crewther B.T., Viveiros L., de Rose D., Jr., Aoki M.S. Effects of resistance training periodization on performance and salivary immune-endocrine responses of elite female basketball players. J. Sports Med. Phys. Fit. 2016;2011:676–682. [PubMed] [Google Scholar]
- 32.Moran J., Sandercock G., Clark C.C.T., Fernandes J.F.T., Drury B. A meta-analysis of resistance training in female youth: Its effect on muscular strength, and shortcomings in the literature. Sport. Med. 2018;48:1661–1671. doi: 10.1007/s40279-018-0914-4. [DOI] [PubMed] [Google Scholar]
- 33.Hughes L.J., Banyard H.G., Dempsey A.R., Scott B.R. Using a load-velocity relationship to predict one repetition maximum in free-weight exercise: A comparison of the different methods. J. Strength Cond. Res. 2019;33:2409–2419. doi: 10.1519/JSC.0000000000002550. [DOI] [PubMed] [Google Scholar]
- 34.Loturco I., Pereira L.A., Cal Abad C.C., Gil S., Kitamura K., Kobal R., Nakamura F.Y. Using bar velocity to predict maximum dynamic strength in the half-squat exercise. Int. J. Sports Physiol. Perform. 2016;11:697–700. doi: 10.1123/ijspp.2015-0316. [DOI] [PubMed] [Google Scholar]
- 35.Bazuelo-Ruiz B., Padial P., García-Ramos A., Morales-Artacho A.J., Miranda M.T., Feriche B. Predicting maximal dynamic strength from the load-velocity relationship in squat exercise. J. Strength Cond. Res. 2015;29:1999–2005. doi: 10.1519/JSC.0000000000000821. [DOI] [PubMed] [Google Scholar]
- 36.Banyard H.G., Nosaka K., Vernon A.D., Gregory Haff G. The reliability of individualized load–velocity profiles. Int. J. Sports Physiol. Perform. 2018;13:763–769. doi: 10.1123/ijspp.2017-0610. [DOI] [PubMed] [Google Scholar]
- 37.Kell R.T. The influence of periodized resistance training on strength changes in men and women. J. Strength Cond. Res. 2011;25:735–744. doi: 10.1519/JSC.0b013e3181c69f22. [DOI] [PubMed] [Google Scholar]
- 38.Veliz R.R., Suarez-Arrones L., Requena B., Haff G.G., Feito J., de Villarreal S.E. Effects of in-competitive season power-oriented and heavy resistance lower-body train- ing on performance of elite female water polo players. J. Strength Cond. Res. 2015;29:458–465. doi: 10.1519/JSC.0000000000000643. [DOI] [PubMed] [Google Scholar]
- 39.Gür H. Concentric and eccentric isokinetic measurements in knee muscles during the menstrual cycle: A special reference to reciprocal moment ratios. Arch. Phys. Med. Rehabil. 1997;78:501–505. doi: 10.1016/S0003-9993(97)90164-7. [DOI] [PubMed] [Google Scholar]
- 40.McNulty K.L., Elliott-Sale K.J., Dolan E., Swinton P.A., Ansdell P., Goodall S., Thomas K., Hicks K.M. The effects of menstrual cycle phase on exercise performance in eumenorrheic women: A systematic review and meta-analysis. Sport. Med. 2020;50:1–5. doi: 10.1007/s40279-020-01319-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Fridén C., Hirschberg A.L., Saartok T. Muscle strength and endurance do not significantly vary across 3 phases of the menstrual cycle in moderately active premenopausal women. Clin. J. Sport Med. 2003;13:238–241. doi: 10.1097/00042752-200307000-00007. [DOI] [PubMed] [Google Scholar]
- 42.Lebrun C.M., McKenzie D., Lucia A., Diaz B., Hoyos J., Fernández C., Villa G., Bandrés F., Chicharro J.L., Giacomoni M., et al. Effects of menstrual cycle phase on athletic performance. Eur. J. Appl. Physiol. 2018;103:153–160. doi: 10.1249/00005768-199503000-00022. [DOI] [Google Scholar]
- 43.De Jonge X.J., Boot C.R., Thom J.M., Ruell P.A., Thompson M.W. The influence of menstrual cycle phase on skeletal muscle contractile characteristics in humans. J. Physiol. 2001;530:161–166. doi: 10.1111/j.1469-7793.2001.0161m.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Romero-Moraleda B., Del Coso J., Gutiérrez-Hellín J., Ruiz-Moreno C., Grgic J., Lara B. The influence of the menstrual cycle on muscle strength and power performance. J. Hum. Kinet. 2019;68:123–133. doi: 10.2478/hukin-2019-0061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Blagrove R.C., Bruinvels G., Pedlar C.R. Variations in strength-related measures during the menstrual cycle in eumenorrheic women: A systematic review and meta-analysis. J. Sci. Med. Sport. 2020:6–13. doi: 10.1016/j.jsams.2020.04.022. [DOI] [PubMed] [Google Scholar]
- 46.García-Pinillos F., Lago-Fuentes C., Bujalance-Moreno P., Pérez-Castilla A. Effect of the menstrual cycle when estimating 1 repetition maximum from the load-velocity relationship during the bench press exercise. J. Strenght Cond. Res. 2020;1:1–4. doi: 10.1519/JSC.0000000000003712. [DOI] [PubMed] [Google Scholar]