Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Oct 13;20(11):7980–7986. doi: 10.1021/acs.nanolett.0c02815

Folding a Single-Molecule Junction

Chuanli Wu †,‡, Demetris Bates †, Sara Sangtarash §, Nicoló Ferri †, Aidan Thomas †, Simon J Higgins †, Craig M Robertson †, Richard J Nichols †, Hatef Sadeghi §,*, Andrea Vezzoli †,∥,*
PMCID: PMC7662913  PMID: 33047599

Abstract

graphic file with name nl0c02815_0006.jpg

Stimuli-responsive molecular junctions, where the conductance can be altered by an external perturbation, are an important class of nanoelectronic devices. These have recently attracted interest as large effects can be introduced through exploitation of quantum phenomena. We show here that significant changes in conductance can be attained as a molecule is repeatedly compressed and relaxed, resulting in molecular folding along a flexible fragment and cycling between an anti and a syn conformation. Power spectral density analysis and DFT transport calculations show that through-space tunneling between two phenyl fragments is responsible for the conductance increase as the molecule is mechanically folded to the syn conformation. This phenomenon represents a novel class of mechanoresistive molecular devices, where the functional moiety is embedded in the conductive backbone and exploits intramolecular nonbonding interactions, in contrast to most studies where mechanoresistivity arises from changes in the molecule–electrode interface.

Keywords: single-molecule junctions, mechanoresistivity, conformational, switching, dionemolecular devices

Apart from fundamental studies focusing on archetypal saturated compounds such as α,ω-alkanedithiols1−3 and α,ω-alkanediamines,4−6 the majority of molecular wires employed to fabricate molecular junctions are rodlike, π-conjugated structures. They have found such a widespread use because their extensive conjugation results in high conductance, and the conformationally rigid π-system avoids complications which could arise, for instance, from gauche defects in saturated carbon chains.7,8 Controlled conformational flexibility, however, can be used to impart functionality. Franco et al. proposed a theoretical exploitation of flexible fragments in single-molecule junctions to develop force-sensitive single-molecule devices,9 based on π-stacking perylene units linked by a saturated propyl chain, that would “unstack” as the junction is stretched. Stacks of phenyl rings and other simple heteroaromatics are able to act as efficient conductors in molecular junctions,10,11 with charge transported through π–π interactions.12−18 In the device proposed by Franco et al., these effects are incorporated into a single molecule, where conductance is predicted to drop by orders of magnitude as the stacking configuration is mechanically unfolded and charge is forced to flow through the saturated propyl chain. Such a device would represent a new class of molecular electronic components responsive to mechanical stimuli, complementing the existing range that exploits changes in the electrode-molecule interface,19−26 stereoelectronic configuration switching,27,28 and stretching-dependent quantum interference effects12,29 as the molecular junction is compressed and relaxed.

Intrigued by these phenomena, we designed molecule 1 to have two phenyl rings spaced by a diketone chain. The molecule has a conformationally flexible bond between the two sp2-hybridized carbonyls (orange in Figure 1a). Although the ground state structure is a quasi-anti conformation, similar to benzil (an analogue of 1 without the thiomethyl termini),30 the central C—C bond in such compounds has a dihedral torsional barrier of only 15–45 kJ/mol (0.15–0.5 eV) for interconversion between the syn and anti conformations.31,32 We performed simple molecular mechanics calculations (MM2 Force Field) on 1 to obtain the ground state energy as a function of the (C=O)—(C=O) dihedral angle θ. We found that the energy profile has two minima with approximately 130° of difference between them (Figure 1) and shallow energy barriers. Our results suggest that a syn (θ < 90°) ⇌ anti (θ > 90°) conversion should be readily attained by compressing a metal–molecule–metal junction made with 1 and mechanically folding the molecule along the central C—C bond, like folding a piece of paper (Figure 1c). π–π interactions between the two phenyl rings in the syn conformer would then contribute significantly to charge transport (in a way akin to π-stacking), allowing us to detect the interconversion by measuring the junction conductance. This would represent a novel exploitation of mechanically triggered stereoelectronic effects to impart a binary (ON–OFF) conductance switching behavior, incorporating the advantages of π-stacking molecular junctions12−14 into a single-molecule device.

Figure 1.

Figure 1

Open in a new tab

Molecular Design. (a) Structure of compound 1 with the conformationally flexible bond highlighted in orange. (b) Energy vs O=C—C=O dihedral angle for compound 1 obtained by MM2 Force Field calculations. (c) Three-dimensional structures of 1 in the anti (dihedral of 155°) and syn (dihedral of 23°) conformations with S–S length shown.

We therefore synthesized 1 and used the scanning tunneling microscope–break junction technique (STM-BJ)1 to fabricate its molecular junctions and measure their conductance. In this method, Au point contacts having conductance G = G0 ≅ 77.48 μS are repeatedly fabricated and ruptured by driving an atomically sharp Au wire into and out of contact with a Au on mica substrate. When the process is performed in a solution of a suitable molecular wire, molecular junctions self-assemble in the freshly ruptured point contact, and charge transport can be determined as a function of electrode separation. The process is repeated thousands of times under DC bias voltage V, while recording the current I as a function of the electrode displacement z. Conductance is calculated as G = I/V and the obtained Gz traces are compiled into 1D histograms and 2D density maps yielding, respectively, the distribution of conductance values and the correlation of junction conductance and junction size.

We performed the process in a 1 mM mesitylene solution of 1, and the results can be observed in Figure 2. The conductance histogram (Figure 2b) shows two main contributions: a high-conductance (∼10–3G0) feature at smaller junction size (∼0.8 nm, accounting for the electrodes snapback19) and a low conductance feature (∼10–4.3 G0) at larger junction size (∼1.2 nm including snapback). The results therefore suggest the presence of two possible conformers of 1 in the junction that differ in conductance by more than 1 order of magnitude and in size by 0.4 nm. We then performed piezo-modulation experiments on the fabricated junctions. In these experiments, nanogaps able to accommodate the extended anti conformation (1.2 nm) are initially fabricated, and their size is then modulated by applying a square wave signal to the piezo voltage. The molecule is therefore allowed to assemble in the gap in its thermodynamically favored anti state, and it is then mechanically folded into the syn conformation by compressing the junction. More information on the piezo-modulation experiments can be found in our previous publications on the subject20,21 and details are provided in the SI. Under a modulation amplitude of 0.4 nm the junctions could be cycled reliably from the high-G to the low-G conformation with excellent repeatability and a conductance increase upon compression by a factor of ∼21 (Figure 2d, and more details in the SI).

Figure 2.

Figure 2

Open in a new tab

STM-BJ data for 1. (a) Example Gz traces for 1 under constant electrode displacement speed (20 nm/s). (b) Conductance histogram for 1 compiled with 7678 traces as shown in (a) with no data selection. (c) Conductance–electrode displacement density map of 1. (d) Density map of piezo-modulation experiments. After an abrupt 1.2 nm stretch that opens the nanogap, the junction size is compressed by 0.4 nm and then relaxed again for four times in 100 ms. The piezo signal is superimposed as a gray line for clarity. Histograms and 2D maps compiled with 100 bins/decade, 100 bins/nm, and 1000 bins/second. Experiments performed at 200 mV bias. White contours in (c) are a guide for the eye. Plots in (b,c) compiled from 7678 traces with no selection. Density map (d) obtained from 1767 traces, selected from a data set of 5036 traces using an automated algorithm, described in Section 2.2 of the SI.

We can rule out any contributions from variations in the molecule–electrode interface as a mechanism for the observed switching phenomena, as we have already demonstrated that thioanisole contacts do not change binding configuration upon junction compression.21 Similarly, we can discount an interpretation of our results based on the formation of shorter junctions through Au-carbonyl contacts, as no interactions between a (di)ketone and gold electrodes (e.g., in measurements of molecular wires containing fluorenones,33 anthraquinones,34 or diketopyrrolopyrroles35) have been reported. To verify that a syn ⇌ anti conformation change is responsible for the observed mechanoresistive effects, we performed power spectral density (PSD) analysis36 on the junctions in their relaxed and compressed state. PSD has been used in the literature to characterize through-space coupling in molecular junctions where charge transport does not follow the chemical bond organization but travels through eigenchannels opened by nonbonding interactions between the molecule and the electrodes,13,14 between pairs of π-stacking molecules,14,37 or between different fragments of the same molecule38 or biomolecule,39 through intramolecular interactions. When charge transport is purely through-bond, the noise power (the integral of the power spectral density) scales approximately with G, while the scaling increases when charge transport has a through-space character to approach the value found for pure through-space tunneling of G2. When noise power is normalized by the average conductance GAVG (noise power/GAVG), it is therefore generally found to be insensitive to the junction conductance for through-bond coupling. On the other hand, a strong correlation between noise power/GAVG and GAVG is observed when through-space coupling significantly contributes to charge transport.36 In order to estimate noise power/GAVG, we performed modulation experiments by fabricating junctions in their relaxed state, recording the current for 50 ms, then compressing them by 0.4 nm and recording the current for another 50 ms (Figure 3a). Slices of data (30 ms) in the relaxed and stretched state are then analyzed with a fast Fourier transform (FFT) algorithm to obtain the PSD, which is numerically integrated between 100 Hz and 1 kHz to yield the noise power in the region of interest. Normalization by the calculated average conductance of the junction yields noise power/GAVG which is plotted versus GAVG to examine their correlation. More information about the data collection and analysis process can be found in the SI.

Figure 3.

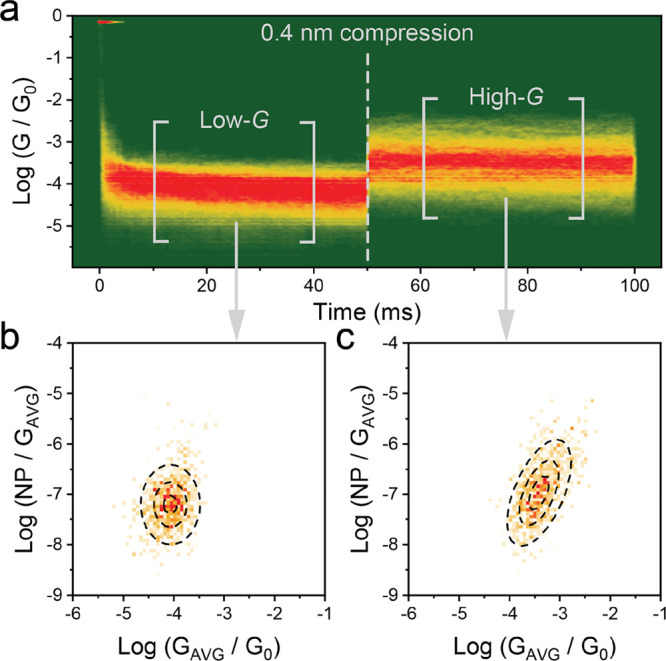
Figure 3

Open in a new tab

PSD analysis of 1. (a) Conductance versus time density map for a single compression cycle of 1. The portions between brackets were then cut off and analyzed with a FFT algorithm to calculate the noise power. (b) Normalized noise power versus GAVG heatmap for 1 in the relaxed, low-G state. (c) Normalized noise power versus GAVG heatmap for 1 in the compressed, high-G state The dashed lines in panels (b,c) are the 25, 50 and 75% height contours of a 2D Gaussian surface fitted to the experimental data. All experiments performed at 200 mV tip–substrate bias. Plots compiled from 8213 traces, using the data selection algorithms described in the SI.

Junctions in their relaxed, low-G state showed noise power insensitive to conductance, thus confirming a dominant through-bond mechanism of charge transport (Figure 3b). In the compressed, high-G state, however, noise power strongly correlates with the average conductance of the junction (Figure 3c), indicating that through-space tunneling phenomena are now contributing to the overall charge transport. This further reinforces our proposed interpretation of a mechanoresistive behavior arising from conformational change, where a nonbonding transport channel is opened upon folding the junction to the syn conformation. As a control experiment, we studied the functionalized (E)-stilbene 2 ((E)-1,2-bis(4-(methylthio)phenyl)ethene, see Figure 4a for structure and the SI for synthetic procedures), which is an analogue of 1 with a central, conformationally locked C=C bond. We found no evidence of mechanically-controlled conductance switching in the STM-BJ and piezo-modulation experiments (see Figure 4b; more details can be found in the SI), showing that (i) a conformationally flexible molecule is needed to attain the switching behavior and (ii) direct electrode–electrode tunneling does not contribute significantly to the overall charge transport with the piezo ramps used in this study. Furthermore, PSD analysis (see SI) indicates a purely through-bond charge transport mechanism (i.e., noise power/GAVG insensitive to GAVG) in both the relaxed and compressed state of junctions fabricated with the rigid 2. Our results may also provide a novel explanation for high-conductance features at short junction extensions, which have been seen in similar foldable molecules incorporating two phenyl rings such as MeS–C6H4–Q–Q–Q–C6H4–SMe (Q = CH2, SiMe2, GeMe2).40,41 It is worth noting that the prominence of the high conductance feature is significantly greater in our data compared to these systems, where it only appears as a weak peak in the histograms. We attribute this increased prominence to the sp2 hybridization of the diketone bridge of 1 (in contrast with the −Q–Q–Q– sp3 hybridization) that results in a preferential rotation around the (O=C)—(C=O) axis and a more efficient folding of the junction to the high-conductance state, which is also energetically favored by the relatively long C—C bond (1.54 Å in the solid-state crystal structure of 1). To provide further confirmation of the proposed mechanism, we also synthesized compound 3, that features only one phenyl ring and a carbonyl group (5-(methylthio)-1-(4-(methylthio)phenyl)pentan-1-one, see Figure 4a for structure and the SI for synthetic procedures). The absence of a phenyl ring means that no π–π interactions are present upon junction compression, and in fact only a small, three-fold mechanically controlled conductance switching was observed, demonstrating the need for two interacting π-systems to attain high conductance in the compressed state (Figure 4d shows a comparison of the three systems investigated). Furthermore, analysis of the conductance signal in the domain of frequency demonstrated that an intermediate through-bond/through-space mechanism of charge transport is operative for 3 in both the relaxed and compressed junction states, in contrast to the clear transition observed in 1 (see SI for further details on the control experiments).

Figure 4.

Figure 4

Open in a new tab

Control experiments. (a) Structures of compounds 2 and 3. (b) Density map of piezo-modulation experiments for 2. (c) Density map of piezo-modulation experiments for 3. (d) Comparison of line profile histograms obtained during modulation experiments (56 and 68 ms). Extended, low conductance junction in shaded, lighter color. Compressed, high-conductance junction in darker, solid color. The conductance boost upon compression is ∼21× for 1, ∼2× for 2, and ∼3× for 3. The same piezo ramp used for compound 1 and shown in Figure 2d was used to obtain the data in (b,c).

We then performed density functional theory (DFT) quantum transport calculations on the junction in the relaxed and extended states, by imposing constraints on the distance between the two metallic electrodes and letting the molecular portion of the junction relax to its energy minimum. DFT modeling predicts a total energy difference between the anti and the syn conformation of 0.38 eV and a dihedral torsional barrier of 0.42 eV (40.5 kJ/mol, in good agreement with the MM2 Force Field calculations; further details in the SI). Key here is that the conformation interconversion energy barrier is less than the binding energy between the molecule and the Au electrodes (0.54 eV), and we therefore expect the molecule to fold around the conformationally flexible C—C bond as the junction is compressed. Our calculations show that the molecule is therefore likely to adopt a syn conformation upon junction compression (Figure 5a). The Gollum code42 was then used to calculate the transmission coefficient T(E) for electrons of energy E passing from the source to the drain electrode of the junction, through molecule 1. The electrical conductance then was obtained using the Landauer formula, and we analyzed the whole behavior of T(E) within the HOMO–LUMO gap (see section 4 of the SI). Transport calculations on the two states (Figure 5b) show that the value of T(E) is indeed strongly dependent on molecular conformation. Our calculations show that T(E) is lower for the anti conformation compared to that of the syn conformation (calculated by constraining the junction size to ∼0.8 nm) for the whole energy range between the HOMO and the LUMO, in good qualitative agreement with the experiment. The best quantitative agreement is obtained for energies in the range showed in the gray-shaded region of Figure 5b, where T(E) increases by more than 1 order of magnitude in the compressed syn conformation.

Figure 5.

Figure 5

Open in a new tab

Theoretical calculations. (a) Structure of the junctions obtained by DFT and used for the transport calculations. (b) T(E) curves for compound 1 in the relaxed (anti) and compressed (syn) junction conformations, with and without through-space (π–π) couplings. The gray-shaded area represents the range of energy values where there is good agreement with the experimental data. (c) Schematic depiction of the junction structure used in the tight-binding calculations. (d) Tight-binding transmission function for 1 in the syn configuration, with ϵ0 = ϵ1 = 0, γ = −1, and α = −0.2.

The change of the (C=O)—(C=O) dihedral angle leads to a rotation of the two phenyl rings toward a face-to-face orientation. In addition, the force applied to the two halves of the molecule (when the electrode–electrode distance is reduced) moves them toward each other to form a new electronic coupling between the π-orbitals of the two phenyl rings (i.e., a stereoelectronic effect). This π–π interaction opens a new transport channel through the molecule that allows efficient short-range through-space tunneling, responsible for the observed boost in molecular conductance. To verify the proposed mechanism, we set the through-space couplings in the DFT Hamiltonian of the syn conformation (Hamiltonian matrix elements between orbitals of the two halves of the molecule) to zero, and recalculated T(E). We found that T(E) of the syn conformation with through-space couplings is significantly higher than that of the syn conformation without through-space couplings, and only in the former is there a satisfactory agreement with the experimental results where conductance increased by more than 1 order of magnitude upon junction compression (Figure 5b). This is further demonstrated by a single-orbital-per-atom tight-binding model (Figure 5c). Here, a scattering region (the molecule, black) is weakly coupled to two one-dimensional leads (gray). We then calculated T(E) in the absence and presence of through-space couplings β (dotted blue lines). We found that transmission through this simple model increases only when β ≠ 0, which is in agreement with our DFT calculations and the experimental results (Figure 5d).

In conclusion, we present here a novel way to impart mechanosensitivity to molecular junctions, by exploiting a flexible diketone moiety. We found a large increase in conductance upon compression of the junction, and power spectral density analysis combined with density functional theory calculations demonstrated that mechanosensitivity arises from an anti ⇌ syn conformation switch, as the molecule is folded along the flexible bond following junction compression. Intramolecular nonbonding interactions are increased in the folded syn state, allowing through-space charge tunneling that “shortcuts” a poorly conductive fragment of the molecule. The effect is completely decoupled from the metallic electrodes, and it arises from the formation of a new transport channel through π–π (stacking) interactions. The switching is reversible and robust, and fabricated junctions can be reliably cycled between high and low conductance states. Our results show the promise, beyond simple electronic decoupling,43 of deliberately introducing flexible fragments in otherwise rigid molecular wires and the fine degree of control on molecular conformation (and hence, charge transport properties) that can be attained in single-molecule junctions. Furthermore, they highlight the possibility of characterizing intramolecular charge transport phenomena using power spectral density analysis.

Methods

Chemicals

Compound 1 was synthesized by treating 2 equiv of 4-bromothioanisole with equimolar n-butyllithum, followed by transmetalation to copper (as LiBr adduct), and quenching with 1 equiv of oxalyl chloride, following the protocol for the preparation of α-diones developed by Babudri et al.44 Compound 2 was synthesized by Wittig olefination of 4-(methylthio)benzaldehyde with 4-(methylthio)benzyltriphenylphosphonium bromide, adapting a literature procedure.45 Compound 3 was synthesized by reaction of 4-(methylthio)benzoyl chloride with (4-methylthio)butyl)magnesium chloride. Detailed experimental procedure and characterization data can be found in the SI.

STM-BJ Measurements

Junctions were fabricated and characterized using the STM-BJ technique,1 using a modified Keysight 5500 STM. Further details on the equipment used, the data acquisition process, and its analysis are available in our previous publications on the subject20,21 and a summary is presented in the SI.

DFT and Transport Calculations

The optimized geometry with ground-state Hamiltonian and overlap matrix elements were obtained using DFT and the SIESTA46 code. These results were then combined with the Gollum42 implementation of the nonequilibrium Green’s function method47 to calculate the phase-coherent, elastic-scattering properties of the system, consisting of two gold electrodes and the molecule as the scattering region. Further details are available in the SI.

Acknowledgments

We thank Prof. Donald Bethell for useful discussion. C.W. acknowledges funding from the China Scholarship Council (Grant 201806860023). A.V. acknowledges funding from the Royal Society (University Research Fellowship URF\R1\191241) and the School of Physical Sciences of the University of Liverpool (start-up funds and Early Career Researchers grant). S.S. thanks the Leverhulme Trust for funding (Early Career Fellowship ECF-2018-375). H.S. thanks UKRI for funding (Future Leaders Fellowship MR/S015329/2). R.J.N., A.V., and S.J.H. are grateful for financial assistance from the EPSRC (Grants EP/M029522/1 and EP/M005046/1).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.0c02815.

  • Synthetic procedures and characterization; additional details on STM-BJ measurements; control experiments; additional details on DFT calculations (PDF)

Author Contributions

⊥ C.W., D.B., S.S. contributed equally to this work.

The authors declare no competing financial interest.

Notes

Raw single-molecule conductance data acquired for this study and the software used for its analysis are available free of charge on the Research Data Catalogue of the University of Liverpool at the address http://datacat.liverpool.ac.uk/id/eprint/1038 and at DOI: 10.17638/datacat.liverpool.ac.uk/1038

Supplementary Material

nl0c02815_si_001.pdf (3.3MB, pdf)

References

  1. Xu B.; Tao N. Measurement of Single-Molecule Resistance by Repeated Formation of Molecular Junctions. Science 2003, 301 (5637), 1221–1223. 10.1126/science.1087481. [DOI] [PubMed] [Google Scholar]
  2. Haiss W.; Nichols R. J.; van Zalinge H.; Higgins S. J.; Bethell D.; Schiffrin D. J. Measurement of Single Molecule Conductivity Using the Spontaneous Formation of Molecular Wires. Phys. Chem. Chem. Phys. 2004, 6, 4330–4337. 10.1039/b404929b. [DOI] [Google Scholar]
  3. Vezzoli A.; Brooke R. J.; Higgins S. J.; Schwarzacher W.; Nichols R. J. Single-Molecule Photocurrent at a Metal–Molecule–Semiconductor Junction. Nano Lett. 2017, 17 (11), 6702–6707. 10.1021/acs.nanolett.7b02762. [DOI] [PubMed] [Google Scholar]
  4. Venkataraman L.; Klare J. E.; Tam I. W.; Nuckolls C.; Hybertsen M. S.; Steigerwald M. L. Single-Molecule Circuits with Well-Defined Molecular Conductance. Nano Lett. 2006, 6 (3), 458–462. 10.1021/nl052373+. [DOI] [PubMed] [Google Scholar]
  5. Zhou J.; Chen G.; Xu B. Probing the Molecule-Electrode Interface of Single-Molecule Junctions by Controllable Mechanical Modulations. J. Phys. Chem. C 2010, 114 (18), 8587–8592. 10.1021/jp101257y. [DOI] [Google Scholar]
  6. Arroyo C. R.; Leary E.; Castellanos-Gómez A.; Rubio-Bollinger G.; González M. T.; Agraït N. Influence of Binding Groups on Molecular Junction Formation. J. Am. Chem. Soc. 2011, 133 (36), 14313–14319. 10.1021/ja201861k. [DOI] [PubMed] [Google Scholar]
  7. Li C.; Pobelov I.; Wandlowski T.; Bagrets A.; Arnold A.; Evers F. Charge Transport in Single Au | Alkanedithiol | Au Junctions: Coordination Geometries and Conformational Degrees of Freedom. J. Am. Chem. Soc. 2008, 130 (1), 318–326. 10.1021/ja0762386. [DOI] [PubMed] [Google Scholar]
  8. Haiss W.; van Zalinge H.; Bethell D.; Ulstrup J.; Schiffrin D. J.; Nichols R. J. Thermal Gating of the Single Molecule Conductance of Alkanedithiols. Faraday Discuss. 2006, 131, 253–264. 10.1039/B507520N. [DOI] [PubMed] [Google Scholar]
  9. Franco I.; George C. B.; Solomon G. C.; Schatz G. C.; Ratner M. A. Mechanically Activated Molecular Switch through Single-Molecule Pulling. J. Am. Chem. Soc. 2011, 133 (7), 2242–2249. 10.1021/ja1095396. [DOI] [PubMed] [Google Scholar]
  10. Schneebeli S. T.; Kamenetska M.; Cheng Z.; Skouta R.; Friesner R. A.; Venkataraman L.; Breslow R. Single-Molecule Conductance through Multiple π-π-Stacked Benzene Rings Determined with Direct Electrode-to-Benzene Ring Connections. J. Am. Chem. Soc. 2011, 133 (7), 2136–2139. 10.1021/ja111320n. [DOI] [PubMed] [Google Scholar]
  11. Bai M.; Liang J.; Xie L.; Sanvito S.; Mao B.; Hou S. Efficient Conducting Channels Formed by the π-π Stacking in Single [2,2]Paracyclophane Molecules. J. Chem. Phys. 2012, 136 (10), 104701. 10.1063/1.3692184. [DOI] [PubMed] [Google Scholar]
  12. Frisenda R.; Janssen V. A. E. C.; Grozema F. C.; van der Zant H. S. J.; Renaud N. Mechanically Controlled Quantum Interference in Individual π-Stacked Dimers. Nat. Chem. 2016, 8 (12), 1099–1104. 10.1038/nchem.2588. [DOI] [PubMed] [Google Scholar]
  13. Li X.; Wu Q.; Bai J.; Hou S.; Jiang W.; Tang C.; Song H.; Huang X.; Zheng J.; Yang Y.; et al. Structure-Independent Conductance of Thiophene-Based Single-Stacking Junctions. Angew. Chem., Int. Ed. 2020, 59 (8), 3280–3286. 10.1002/anie.201913344. [DOI] [PubMed] [Google Scholar]
  14. Fu T.; Smith S.; Camarasa-Gómez M.; Yu X.; Xue J.; Nuckolls C.; Evers F.; Venkataraman L.; Wei S. Enhanced Coupling Through π-Stacking in Imidazole-Based Molecular Junctions. Chem. Sci. 2019, 10 (43), 9998–10002. 10.1039/C9SC03760H. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Ghane T.; Nozaki D.; Dianat A.; Vladyka A.; Gutierrez R.; Chinta J. P.; Yitzchaik S.; Calame M.; Cuniberti G. Interplay between Mechanical and Electronic Degrees of Freedom in π-Stacked Molecular Junctions: From Single Molecules to Mesoscopic Nanoparticle Networks. J. Phys. Chem. C 2015, 119 (11), 6344–6355. 10.1021/jp512524z. [DOI] [Google Scholar]
  16. Wu S.; González M. T.; Huber R.; Grunder S.; Mayor M.; Schönenberger C.; Calame M. Molecular Junctions Based on Aromatic Coupling. Nat. Nanotechnol. 2008, 3 (9), 569–574. 10.1038/nnano.2008.237. [DOI] [PubMed] [Google Scholar]
  17. Martín S.; Grace I.; Bryce M. R.; Wang C.; Jitchati R.; Batsanov A. S.; Higgins S. J.; Lambert C. J.; Nichols R. J. Identifying Diversity in Nanoscale Electrical Break Junctions. J. Am. Chem. Soc. 2010, 132 (26), 9157–9164. 10.1021/ja103327f. [DOI] [PubMed] [Google Scholar]
  18. Chen L.; Wang Y.-H.; He B.; Nie H.; Hu R.; Huang F.; Qin A.; Zhou X.-S.; Zhao Z.; Tang B. Z. Multichannel Conductance of Folded Single-Molecule Wires Aided by Through-Space Conjugation. Angew. Chem., Int. Ed. 2015, 54 (14), 4231–4235. 10.1002/anie.201411909. [DOI] [PubMed] [Google Scholar]
  19. Quek S. Y.; Kamenetska M.; Steigerwald M. L.; Choi H. J.; Louie S. G.; Hybertsen M. S.; Neaton J. B.; Venkataraman L. Mechanically Controlled Binary Conductance Switching of a Single-Molecule Junction. Nat. Nanotechnol. 2009, 4 (4), 230–234. 10.1038/nnano.2009.10. [DOI] [PubMed] [Google Scholar]
  20. Ismael A. K.; Wang K.; Vezzoli A.; Al-Khaykanee M. K.; Gallagher H. E.; Grace I. M.; Lambert C. J.; Xu B.; Nichols R. J.; Higgins S. J. Side-Group-Mediated Mechanical Conductance Switching in Molecular Junctions. Angew. Chem., Int. Ed. 2017, 56 (48), 15378–15382. 10.1002/anie.201709419. [DOI] [PubMed] [Google Scholar]
  21. Ferri N.; Algethami N.; Vezzoli A.; Sangtarash S.; McLaughlin M.; Sadeghi H.; Lambert C. J.; Nichols R. J.; Higgins S. J. Hemilabile Ligands as Mechanosensitive Electrode Contacts for Molecular Electronics. Angew. Chem., Int. Ed. 2019, 58 (46), 16583–16589. 10.1002/anie.201906400. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Taniguchi M.; Tsutsui M.; Yokota K.; Kawai T. Mechanically-Controllable Single Molecule Switch Based on Configuration Specific Electrical Conductivity of Metal-Molecule-Metal Junctions. Chem. Sci. 2010, 1 (2), 247–253. 10.1039/c0sc00129e. [DOI] [Google Scholar]
  23. Kiguchi M.; Ohto T.; Fujii S.; Sugiyasu K.; Nakajima S.; Takeuchi M.; Nakamura H. Single Molecular Resistive Switch Obtained via Sliding Multiple Anchoring Points and Varying Effective Wire Length. J. Am. Chem. Soc. 2014, 136 (20), 7327–7332. 10.1021/ja413104g. [DOI] [PubMed] [Google Scholar]
  24. Meisner J. S.; Kamenetska M.; Krikorian M.; Steigerwald M. L.; Venkataraman L.; Nuckolls C. A Single-Molecule Potentiometer. Nano Lett. 2011, 11 (4), 1575–1579. 10.1021/nl104411f. [DOI] [PubMed] [Google Scholar]
  25. Bruot C.; Hihath J.; Tao N. Mechanically Controlled Molecular Orbital Alignment in Single Molecule Junctions. Nat. Nanotechnol. 2012, 7 (1), 35–40. 10.1038/nnano.2011.212. [DOI] [PubMed] [Google Scholar]
  26. Jia C.; Guo X. Molecule–Electrode Interfaces in Molecular Electronic Devices. Chem. Soc. Rev. 2013, 42 (13), 5642. 10.1039/c3cs35527f. [DOI] [PubMed] [Google Scholar]
  27. Su T. a.; Li H.; Steigerwald M. L.; Venkataraman L.; Nuckolls C. Stereoelectronic Switching in Single-Molecule Junctions. Nat. Chem. 2015, 7 (3), 215–220. 10.1038/nchem.2180. [DOI] [PubMed] [Google Scholar]
  28. Xin N.; Wang J.; Jia C.; Liu Z. Z. Z.; Zhang X.; Yu C.; Li M.; Wang S.; Gong Y.; Sun H.; et al. Stereoelectronic Effect-Induced Conductance Switching in Aromatic Chain Single-Molecule Junctions. Nano Lett. 2017, 17 (2), 856–861. 10.1021/acs.nanolett.6b04139. [DOI] [PubMed] [Google Scholar]
  29. Stefani D.; Weiland K. J.; Skripnik M.; Hsu C.; Perrin M. L.; Mayor M.; Pauly F.; van der Zant H. S. J. Large Conductance Variations in a Mechanosensitive Single-Molecule Junction. Nano Lett. 2018, 18 (9), 5981–5988. 10.1021/acs.nanolett.8b02810. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Brown C. J.; Sadanaga R. The Crystal Structure of Benzil. Acta Crystallogr. 1965, 18 (2), 158–164. 10.1107/S0365110X65000403. [DOI] [Google Scholar]
  31. Lopes S.; Gómez-Zavaglia A.; Lapinski L.; Chattopadhyay N.; Fausto R. Matrix-Isolation FTIR Spectroscopy of Benzil: Probing the Flexibility of the C-C Torsional Coordinate. J. Phys. Chem. A 2004, 108 (40), 8256–8263. 10.1021/jp047116s. [DOI] [Google Scholar]
  32. Pawelka Z.; Koll A.; Zeegers-Huyskens T. Solvent Effect on the Conformation of Benzil. J. Mol. Struct. 2001, 597 (1–3), 57–66. 10.1016/S0022-2860(01)00593-2. [DOI] [Google Scholar]
  33. Alanazy A.; Leary E.; Kobatake T.; Sangtarash S.; González M. T.; Jiang H.-W.; Bollinger G. R.; Agräit N.; Sadeghi H.; Grace I.; et al. Cross-Conjugation Increases the Conductance of Meta-Connected Fluorenones. Nanoscale 2019, 11 (29), 13720–13724. 10.1039/C9NR01235D. [DOI] [PubMed] [Google Scholar]
  34. Hong W.; Valkenier H.; Mészáros G.; Manrique D. Z.; Mishchenko A.; Putz A.; García P. M.; Lambert C. J.; Hummelen J. C.; Wandlowski T. An MCBJ Case Study: The Influence of π-Conjugation on the Single-Molecule Conductance at a Solid/Liquid Interface. Beilstein J. Nanotechnol. 2011, 2, 699–713. 10.3762/bjnano.2.76. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Zhang Y.-P.; Chen L.; Zhang Z.-Q.; Cao J.; Tang C.; Liu J.; Duan L.-L.; Huo Y.; Shao X.; Hong W.; et al. Distinguishing Diketopyrrolopyrrole Isomers in Single-Molecule Junctions via Reversible Stimuli-Responsive Quantum Interference. J. Am. Chem. Soc. 2018, 140 (21), 6531–6535. 10.1021/jacs.8b02825. [DOI] [PubMed] [Google Scholar]
  36. Adak O.; Rosenthal E.; Meisner J.; Andrade E. F.; Pasupathy A. N.; Nuckolls C.; Hybertsen M. S.; Venkataraman L. Flicker Noise as a Probe of Electronic Interaction at Metal–Single Molecule Interfaces. Nano Lett. 2015, 15 (6), 4143–4149. 10.1021/acs.nanolett.5b01270. [DOI] [PubMed] [Google Scholar]
  37. Magyarkuti A.; Adak O.; Halbritter A.; Venkataraman L. Electronic and Mechanical Characteristics of Stacked Dimer Molecular Junctions. Nanoscale 2018, 10 (7), 3362–3368. 10.1039/C7NR08354H. [DOI] [PubMed] [Google Scholar]
  38. Chen H.; Zheng H.; Hu C.; Cai K.; Jiao Y.; Zhang L.; Jiang F.; Roy I.; Qiu Y.; Shen D.; et al. Giant Conductance Enhancement of Intramolecular Circuits through Interchannel Gating. Matter 2020, 2 (2), 378–389. 10.1016/j.matt.2019.12.015. [DOI] [Google Scholar]
  39. Zhuang X.; Zhang A.; Qiu S.; Tang C.; Zhao S.; Li H.; Zhang Y.; Wang Y.; Wang B.; Fang B.; et al. Coenzyme Coupling Boosts Charge Transport through Single Bioactive Enzyme Junctions. iScience 2020, 23 (4), 101001. 10.1016/j.isci.2020.101001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Su T. A.; Li H.; Klausen R. S.; Widawsky J. R.; Batra A.; Steigerwald M. L.; Venkataraman L.; Nuckolls C. Tuning Conductance in π–σ–π Single-Molecule Wires. J. Am. Chem. Soc. 2016, 138 (24), 7791–7795. 10.1021/jacs.6b04394. [DOI] [PubMed] [Google Scholar]
  41. Klausen R. S.; Widawsky J. R.; Steigerwald M. L.; Venkataraman L.; Nuckolls C. Conductive Molecular Silicon. J. Am. Chem. Soc. 2012, 134 (10), 4541–4544. 10.1021/ja211677q. [DOI] [PubMed] [Google Scholar]
  42. Ferrer J.; Lambert C. J.; García-Suárez V. M.; Manrique D. Z.; Visontai D.; Oroszlany L.; Rodríguez-Ferradás R.; Grace I.; Bailey S. W. D.; Gillemot K.; et al. GOLLUM: A next-Generation Simulation Tool for Electron, Thermal and Spin Transport. New J. Phys. 2014, 16 (9), 093029. 10.1088/1367-2630/16/9/093029. [DOI] [Google Scholar]
  43. Jia C.; Migliore A.; Xin N.; Huang S.; Wang J.; Yang Q.; Wang S.; Chen H.; Wang D.; Feng B.; et al. Covalently Bonded Single-Molecule Junctions with Stable and Reversible Photoswitched Conductivity. Science 2016, 352 (6292), 1443–1445. 10.1126/science.aaf6298. [DOI] [PubMed] [Google Scholar]
  44. Babudri F.; Fiandanese V.; Marchese G.; Punzi A. A Direct Access to α-Diones from Oxalyl Chloride. Tetrahedron Lett. 1995, 36 (40), 7305–7308. 10.1016/0040-4039(95)01471-S. [DOI] [Google Scholar]
  45. Aradhya S. V.; Meisner J. S.; Krikorian M.; Ahn S.; Parameswaran R.; Steigerwald M. L.; Nuckolls C.; Venkataraman L. Dissecting Contact Mechanics from Quantum Interference in Single-Molecule Junctions of Stilbene Derivatives. Nano Lett. 2012, 12 (3), 1643–1647. 10.1021/nl2045815. [DOI] [PubMed] [Google Scholar]
  46. Soler J. M.; Artacho E.; Gale J. D.; García A.; Junquera J.; Ordejón P.; Sánchez-Portal D. The SIESTA Method for Ab Initio Order- N Materials Simulation. J. Phys.: Condens. Matter 2002, 14 (11), 2745–2779. 10.1088/0953-8984/14/11/302. [DOI] [Google Scholar]
  47. Sadeghi H. Theory of Electron, Phonon and Spin Transport in Nanoscale Quantum Devices. Nanotechnology 2018, 29 (37), 373001. 10.1088/1361-6528/aace21. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl0c02815_si_001.pdf (3.3MB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES