Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Sep 28;20(11):7860–7867. doi: 10.1021/acs.nanolett.0c02219

Field-Modulated Anomalous Hall Conductivity and Planar Hall Effect in Co3Sn2S2 Nanoflakes

Shuo-Ying Yang †, Jonathan Noky ‡, Jacob Gayles §,‡, Fasil Kidane Dejene †,∥, Yan Sun ‡, Mathias Dörr #, Yurii Skourski ∇, Claudia Felser ‡, Mazhar Nawaz Ali †, Enke Liu ‡,⊥,*, Stuart S P Parkin †,*
PMCID: PMC7662920  PMID: 32986438

Abstract

graphic file with name nl0c02219_0005.jpg

Time-reversal-symmetry-breaking Weyl semimetals (WSMs) have attracted great attention recently because of the interplay between intrinsic magnetism and topologically nontrivial electrons. Here, we present anomalous Hall and planar Hall effect studies on Co3Sn2S2 nanoflakes, a magnetic WSM hosting stacked Kagome lattice. The reduced thickness modifies the magnetic properties of the nanoflake, resulting in a 15-time larger coercive field compared with the bulk, and correspondingly modifies the transport properties. A 22% enhancement of the intrinsic anomalous Hall conductivity (AHC), as compared to bulk material, was observed. A magnetic field-modulated AHC, which may be related to the changing Weyl point separation with magnetic field, was also found. Furthermore, we showed that the PHE in a hard magnetic WSM is a complex interplay between ferromagnetism, orbital magnetoresistance, and chiral anomaly. Our findings pave the way for a further understanding of exotic transport features in the burgeoning field of magnetic topological phases.

Keywords: magnetic Weyl semimetal, anomalous Hall effect, planar Hall effect, Berry curvature

The theoretical prediction and experimental realization of Weyl semimetals (WSMs) in various forms have been of great interest in condensed matter physics in the recent past.1−9 WSMs are characterized by Fermi arcs at their surfaces and bulk Weyl fermions stemming from band splitting driven by spin–orbit coupling (SOC). The topological character of Weyl nodes results in a number of fascinating properties including an uncompensated Berry curvature, which corresponds to an intrinsic anomalous Hall effect (AHE).3,4,10,11 In addition, when an external electric field and magnetic field are applied parallel to each other, chiral charge pumping occurs between the two Weyl nodes, which have opposite chiralities, and manifests itself as a negative longitudinal magnetoresistance (NLMR)12−18 and a planar Hall effect (PHE).19−29

Recently, WSMs with intrinsic magnetism have attracted great attention.1−6 Compared with inversion-symmetry (IS)-breaking WSMs, time-reversal-symmetry (TRS)-breaking WSMs provide a playground where the interplay of intrinsic magnetism, Berry curvature, and topological character of Weyl nodes can give rise to rich physical phenomena, such as a Berry curvature-induced AHE and anomalous Nernst effect,3,4 a high-temperature quantum AHE in the 2D limit,30 as well as possible device applications connecting topological physics and thermoelectric devices.31,32 The close relationship between TRS-breaking and intrinsic magnetism makes it possible to manipulate the topological state via changes in the magnetic order.11,33−35

Since the realization of WSMs, most studies have centered around IS-breaking WSMs.36−42 The transport characteristics of TRS-breaking WSMs (like ferromagnetic WSMs), especially those in which the transport properties can be modified by changing magnetic properties, have been sparsely addressed. The prediction that the Kagome lattice compound, Co3Sn2S2, is a ferromagnetic TRS-breaking WSM was recently confirmed by direct observation of its Fermi arcs via ARPES and STM measurements.43,44 In this work, we present detailed magneto-transport measurements on 180 nm thick Co3Sn2S2 nanoflakes and discuss the intrinsic AHE, longitudinal magnetoresistance (LMR), and PHE in the context of ferromagnetic order with extremely large out-of-plane magnetic anisotropy (anisotropy field >5 T). In addition to a 22% enhancement of the intrinsic AHC compared with the bulk Co3Sn2S2 sample, the reduced thickness increases the coercive field by more than 15 times compared with the bulk, revealing an anomaly in the Hall resistivity which corresponds to a field modulated AHC that may be directly related to the Weyl node separation. In addition, we discuss the PHE in a Co3Sn2S2 nanoflake, which arises from a complex interaction of ferromagnetism, orbital magnetoresistance, and the chiral anomaly that has not been shown in other materials or previous analyses.45

Co3Sn2S2 crystallizes in a rhombohedral structure in which a quasi-2D Co3Sn layer is sandwiched between sulfur and tin atoms, as shown in Figure 1a. The magnetism originates from the cobalt atoms that sit on a Kagome lattice in the ab plane. Figure 1b shows a typical 180 nm thick nanoflake device used in this work in which the dashed lines outline the nanoflake before Ar ion etching. The current is applied along the a-axis. The temperature dependence of the longitudinal resistivity of a nanoflake at μ0H = 0 T displays a metallic behavior with a residual resistance ratio ρ(300 K)/ρ(2 K) of 14. Ferromagnetic ordering appears below the TC of 171 K, as indicated by the kink in Figure 1c. Figure 1d shows the transverse magnetoresistance (TMR) with μ0H applied perpendicular to the nanoflake at various temperatures. At temperatures above 100 K and below the TC, the TMR is negative, as typically seen in ferromagnets due to magnetic-field induced suppression of thermal spin fluctuations.46,47 At 2 K, the TMR reaches 139% at 14 T with no sign of saturation. The TMR also shows clear hysteresis with an extremely large perpendicular magnetic coercive field of ∼5 T at 2 K, which is 15 times larger than the coercive field measured in bulk Co3Sn2S2 (0.33 T at 2 K).3 We emphasize that the increase in the coercive field is not a result of differences in RRR between the samples. The RRR of the nanoflake of this study is in between the RRRs of the two bulk crystals reported in previous literature,3,45 but the Hc of the nanoflake is increased by an order of magnitude compared with the bulk samples (also see Supporting Information 7). Further magnetization measurements (Supporting Information) reveal that when the field is applied along the in-plane a-axis, the in-plane saturation field is as high as 24 T, implying it is extremely hard to align the moments in-plane.48 This reflects a very large coercive field as well as a large in-plane saturation field which are key to understanding the transport properties of the nanoflakes, as discussed below.

Figure 1.

Figure 1

Open in a new tab

Basic transport characterization of a Co3Sn2S2 nanoflake. (a) The crystal structure of Co3Sn2S2 in which an out-of-plane ferromagnetic Kagome lattice is formed with cobalt atoms. (b) An optical image of a typical device used in this work. The black dotted line shows the contour of the nanoflake before Ar ion etching. (c) The temperature dependence of longitudinal resistivity at a magnetic field of 0 and 14 T. The kink at 171 K corresponds to the TC. (d) Transverse magnetoresistance (TMR) measured at various temperatures with field applied out-of-plane perpendicular to the nanoflake, which changes from positive to negative with increasing temperature. (e,f) Zoom-in plot of the TMR at 30 and 2 K highlighted in the black dotted box in (d). The blue curves are the TMR measured when the field is swept from positive to negative and the orange curves are the TMR when the field is swept from negative to positive.

Figure 1e,f shows a magnified plot of the TMR as indicated by the black dotted box in Figure 1d. At temperatures higher than 30 K, the TMR increases when μ0H and effective out-of-plane magnetic moments Mz are antiparallel aligned, so that the TMR values drop at the coercive field. Interestingly, at temperatures below 20 K (see Figure 1f) the TMR decreases when μ0H and Mz are antiparallel aligned compared with when they are parallel aligned, therefore it jumps up at the coercive field. Such TMR behavior at 2 K is not typical for conventional ferromagnets and deserves some special attention. In a semimetal with strong out-of-plane ferromagnetic moments, there are three main contributions to TMR. The first one is the ordinary magnetoresistance (OMR) that is related to the carrier mobilities and scales with μB2. The second one is a spin-dependent magnetoresistance that results from spin orientation-dependent electron scattering; the overall resistance is relatively high when μ0H and Mz are antiparallel aligned because electron scattering is stronger in this configuration and weaker when μ0H and Mz are aligned. The third contribution originates from the strong out-of-plane moments which act as a fictitious magnetic field in addition to the external applied magnetic field and generates an extra OMR. When μ0H and Mz are antiparallel aligned, the effective out-of-plane moment Mz results in a reduced effective field and a smaller positive contribution to the OMR. The fact that the TMR at low and high temperatures shows different hysteresis behaviors is an indication of the competition between the last two mechanisms at different temperatures. At higher temperatures, scattering mechanisms dominate so that the TMR increases when μ0H and Mz are antiparallel. At low temperatures, contributions from scattering are smaller, making the effective OMR the dominant contribution.

The semimetallicity of the nanoflake devices is confirmed by the Hall effect measurements (Figure 2 as well as Supporting Information). Figure 2a shows the Hall resistivity at various temperatures at and below 30 K where the green line is the overall Hall response (ρxy), the dark blue line is the extracted two-carrier ordinary Hall resistivity (ρxyo), and the red line is the difference between the two (ρxy = ρxy – ρxyo). At low temperatures, ρxy displays a nonlinear behavior on top of a square-shaped hysteresis loop, indicating the coexistence of electron and hole carriers and a single hard magnetic phase, respectively. With increasing temperature, the carrier type gradually becomes hole-dominated (see Supporting Information).

Figure 2.

Figure 2

Open in a new tab

Field dependence of Hall resistivity and Hall conductivity measured at various temperatures. (a) The overall Hall resistivity ρxy (green line), two-carrier ordinary Hall resistivity ρxyo (dark blue line), and the difference between the two ρxy = ρxy – ρxyo (red). The yellow shadow shows the additional Hall resistivity component, which decreases with increasing temperature. (b) The overall Hall conductivity σxy (green line), two-carrier ordinary Hall conductivity σxy (dark blue), and the difference between the two (red). When the external field is antiparallel to Mz, the magnitude of the σxy* decreases with increasing field. (c) σxx dependence of σxy. σxyA is mostly independent of longitudinal σxx below 60 K, indicating its intrinsic origin.

Upon subtracting ρxyo, ρxy smoothly increases when μ0H and Mz are aligned antiparallel and shows a sharp antisymmetric peak at the coercive field. The Hall resistivity anomaly, highlighted by the yellow shading in Figure 2a, decreases with increasing temperature and disappears at about 50 K. This behavior cannot be explained by a typical ferromagnetic AHE, which is linearly dependent on magnetization (ρxyA = Rs4πMz): the Mz when μ0H and Mz are antiparallel will not exceed the maximum Mz achieved when the moments are fully saturated by the external magnetic field, meaning ρxy will not be maximized during the antiparallel alignment. The Hall resistivity anomaly resembles the topological Hall effect which has been seen in noncollinear magnetic systems due to a real space Berry phase49,50 arising from a spatially varying magnetic potential. However, given that numerous studies have shown the robust out-of-plane ferromagnetic ground state in Co3Sn2S2 at low temperatures,3,4,33,51 this is unlikely to be the origin of the Hall anomaly.

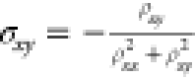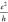Another possible reason for the Hall anomaly is a field-dependent AHE arising from a field-modulated splitting of Weyl points. To analyze this possibility, it is helpful to convert the Hall resistivity to Hall conductivity which is directly proportional to the magnitude of the uncompensated Berry curvature within the Brillouin zone. Figure 2b shows the overall Hall conductivity (Inline graphic), ordinary Hall conductivity (σxyo), and the difference between the two (σxy = σxy – σxyo) (green, dark blue, and red lines, respectively). In the antiparallel orientation, σxy continues to decrease when approaching the coercive field. A decreasing AHC could appear as a natural consequence of Weyl points moving toward each other in a magnetic WSM.7,10,11 If the ferromagnet undergoes a canting of the magnetic moments away from the easy axis resulting in a decreasing out-of-plane magnetization Mz, the reduction of spin splitting decreases the relative distance between the two Weyl points in k-space. As each plane between the two Weyl nodes can be seen as a 2D Chern insulator that has a chiral edge mode contributing a Hall conductance of Inline graphic, the intrinsic AHC becomes smaller when the Weyl points are closer together in k-space (Inline graphic where K is the distance between two Weyl points).11 Given the previously observed robust ferromagnetic ground state at low temperatures in Co3Sn2S2,3,4,33,52 we speculate that the field-modulated AHC due to changing Weyl point separation is likely to be the origin of the observed Hall anomaly and is easily resolved in the nanoflakes because of the increased coercive field compared with the bulk. Future studies on these nanoflakes such as neutron scattering, Lorentz transmission electron microscopy, or magnetic force microscopy to probe the magnetic sublattice and magnetization below Tc will help confirm the origin of the anomaly.

From the Hall measurements, the AHC (σxyA) at zero field is extracted at each measurement temperature (Supporting Information). Figure 2c shows the dependence of σxy on the longitudinal conductivity σxx. At temperatures below 60 K, σxyA appears mostly independent of temperature and σxx, a hallmark of an intrinsic AHE due to an uncompensated Berry curvature.53,54 Surprisingly, the magnitude of σxy of the nanoflakes reaches as high as 1379 Ω–1 cm–1 (see Supporting Information), approximately 22% higher than the σxyA of bulk Co3Sn2S2.3 Previous DFT calculations show that the magnitude of intrinsic AHC is highly sensitive to the local magnetic moment of Co: σxy (0.33 μB/Co) = 1310 Ω–1 cm–14 whereas σxyA (0.30 μbohr/Co) = 1110 ohm–1 cm–13). The origin of the AHC enhancement may be linked to a larger local moment in these nanoflakes and merits future thickness-dependent studies of the AHE and coercive field.

Having established that Co3Sn2S2 nanoflakes display an intrinsic AHE corresponding to the magnetically driven Weyl states, we now discuss the chiral anomaly in the nanoflakes through the PHE and LMR measurements, which have been predicted to reveal chiral charge transport in WSMs12,13,19,20 providing inherent current inhomogeneity is excluded. Figure 3c inset shows a typical schematic for the PHE measurements: μ0H rotates in the ab plane while the longitudinal and transverse voltages are measured simultaneously, which corresponds to the anisotropic magnetoresistance (AMR) and the change in planar Hall resistivity, respectively. After processing the data to get rid of the effect of misalignments (Supporting Information), the angular dependence of the AMR and PHE within the temperature and field ranges of this study can be well-described by

graphic file with name nl0c02219_m004.jpg
graphic file with name nl0c02219_m005.jpg 1
graphic file with name nl0c02219_m006.jpg 2

where ρ⊥ and ρ∥ are the longitudinal resistivity when μ0H is perpendicular or parallel to E, respectively, and Δρxy = ρ⊥ – ρ∥ describes the resistivity anisotropy. Figure 3a,b shows the angular dependence of the AMR ratio and the planar Hall resistivity measured at 2 K for μ0H varying from 1 to 9 T. The black dotted lines show fits of the AMR ratio and the PHE with eqs 1 and 2. At 2 K, the extracted Δρxy increases with increasing field, exhibiting a power-law dependence with an exponent of 1.81. Figure 3d,e shows the angular dependence of AMR and planar Hall resistivity at 9 T in temperatures from 2 to 100 K fitted with eqs 1 and 2. The extracted Δρxy increases with decreasing temperature and is observable at the highest temperature of 100 K.

Figure 3.

Figure 3

Open in a new tab

Anisotropic magnetoresistance and planar Hall effect. (a,b) AMR ratio and planar Hall resistivity measured at 2 K in magnetic fields from 1 T through 9 T. The black dotted lines show the fitting of the data with equations shown in the plot. (c) Field dependence of Δρxy obtained from fitting, which follows a power law with an exponent of 1.81. The inset shows schematics of the Hall bar device and the measurement configuration. The sample is rotated in the ab-plane while Vxx and VPHE are measured simultaneously. (d,e) AMR ratio and planar Hall resistivity measured at 9 T under temperatures ranging from 2 to 100 K. (f) Temperature dependence of Δρxy obtained from fitting in Figure 2e.

In a ferromagnetic WSM, there are three likely microscopic mechanisms to account for the observed PHE: (a) spin-dependent scattering in ferromagnets, which stems from the rotation of the magnetization with respect to the current direction that changes the band occupation and thus scattering rates,55−58 (b) anisotropic OMR, which arises from the anisotropy in Fermi pockets leading to ρ⊥ > ρ∥ > 0,18,28,29,59 and (c) the chiral anomaly effect, where chiral charge pumping results in an enhanced conductivity for certain alignments of the magnetic and electric fields giving rise to a PHE.19,20 Importantly, the band structures calculated along high symmetry lines including SOC with magnetization (M) aligned along [100], [010], and [001] directions (Figure 4a) show that Co3Sn2S2 is a WSM regardless of its M direction within the ferromagnetic state (i.e., M ∥ 110, M ∥ 010, or M ∥ 001). Thus, Co3Sn2S2 is unlike a typical nonmagnetic WSM which has anisotropic OMR and chiral anomaly contributions (i.e., Cd3As2 or WTe221,25) or a trivial semimetal which only has orbital contribution (i.e., Bi18,59). Only magnetic WSMs have all three possible origins, and their complex interactions and contributions to the PHE are now examined in detail.

Figure 4.

Figure 4

Open in a new tab

Band structure calculation, magnetoresistance with field applied in-plane parallel or perpendicular to the current direction at different temperatures. (a) Band structure calculation along high symmetry lines of Co3Sn2S2 with M aligned along [100], [010], and [001] directions including spin–orbit coupling. The red box highlights the gapped nodal line resulting in Weyl crossings which appear off high symmetry axes in all three cases. (b) Longitudinal magnetoresistance measured with μ0H parallel to E at various temperatures. (c) Transverse magnetoresistance measured with μ0H applied in-plane and perpendicular to E at various temperatures.

The PHE in ferromagnets depends on the current direction relative to the in-plane magnetization and can be described by58

graphic file with name nl0c02219_m007.jpg 3

in which k is a constant related to AMR arising from the ferromagnetism, M∥ is the in-plane projection of the magnetization M, α is the angle between M and the out-of-plane axis, and φ* is the angle between the applied electric field E and M∥ (Supporting Information). Because Co3Sn2S2 is a ferromagnet below 171 K, it could well be possible that ferromagnetism is the main origin of the observed PHE. However, we argue that the contribution from ferromagnetism is small, for the following reasons. First of all, the magnitude of PHE is directly related to M∥. The M of Co3Sn2S2 is 65.2 emu/cm3 and the in-plane saturation magnetic field μ0Hc is larger than 24 T (see Supporting Information). This is a significantly lower M and higher μ0Hc than conventional ferromagnetic systems in which a PHE has been observed (i.e., M (Py) ≈ 750 emu/cm3; μ0Hc (Py) ≈ 10 Oe). From eq 3, assuming a uniform canting of the moment, M∥ = 36.2 emu/cm3 at 2 K and 9 T, making the magnitude of Δρxy at least an order of magnitude smaller than a conventional ferromagnet-based PHE. In fact, right below TC where the magnetic moments preferentially align more in the plane of the flake than at lower temperatures, no PHE was observed. Second, the AMR ratio in Co3Sn2S2 is relatively large, that is, −25%, an order of magnitude larger than those in most conventional ferromagnetic metals and half-metallic ferromagnets for which the AMR is typically only a few percent (e.g., Fe = 0.3%; Ni = 2.2%; La0.7Sr0.3MnO3 = −0.15%60). Third, in many conventional ferromagnets, ρ⊥ is smaller than ρ∥ when the dominant s–d scattering process is spin-flip scattering,47,60,61 whereas we find that ρ⊥ is larger than ρ∥ for Co3Sn2S2. Lastly, if PHE of such a shape is due to ferromagnetism, it should track in temperature with magnetization and be observable immediately below the TC. We observe that the PHE in Co3Sn2S2 appears below 100 K, which is far below the ferromagnetic ordering temperature. Thus, we conclude that ferromagnetism is not the main contribution of the PHE in Co3Sn2S2.

However, the strong out-of-plane anisotropy makes it hard to fully disentangle the other two contributions. Figure 4b,c shows the LMR and TMR with μ0H applied in-plane, parallel, and perpendicular to E at various temperatures. Below 50 K, the LMR has a net weakly positive field dependence while above 50 K an NLMR can be seen. At 100 K, both LMR and TMR are negative and show hysteresis. In the case of a nonmagnetic isotropic IS-breaking WSM where only the chiral anomaly is present, ρ∥ is negative due to the chiral-anomaly induced NLMR, giving rise to a finite PHE. Previous studies have shown that this NLMR can be suppressed by a small angle between E and μ0H.16,62 In a TRS-breaking magnetic WSM with moments pointing strongly out-of-plane (i.e., a hard magnet like Co3Sn2S2), applying an in-plane field only cants the moments, leaving large out-of-plane components, shown by the red arrow in the inset to Figure 4b. These out-of-plane moments can act as a local out-of-plane field and generate a Lorentz force, thereby giving an additional positive contribution to ρ∥, resulting in a net ρ∥ with a weakly positive dependence on field, making the low-temperature NLMR absent in the Co3Sn2S2 nanoflakes of this study. At higher temperatures, it is easier to align the moments in-plane, thus the local out-of-plane field created by the Mz can vanish, making the chiral anomaly driven NLMR possible to observe. However, magnetic field-induced suppression of thermal spin fluctuations may also give rise to a NLMR at high temperatures, making the chiral anomaly and the ferromagnetic component of the NLMR hard to disentangle. To be able to observe the chiral anomaly through PHE or LMR measurements in WSMs, the OMR needs to be small.23 In previously measured bulk crystal PHE studies, the NLMR was not observed (likely due to a large OMR), but the OMR contribution to the PHE was ignored.45 For antiferromagnetic WSMs, it may be possible to probe the chiral anomaly driven PHE below the spin flop transition. For ferromagnetic WSMs, one needs to fully saturate the ferromagnetism and get rid of any out-of-plane moment to be able to unambiguously probe the chiral anomaly driven PHE.

In summary, we have carried out detailed magneto-transport measurements in Co3Sn2S2 nanoflakes to elucidate the origins of AHE and PHE in a magnetic WSM with strong out-of-plane anisotropy as large as 5 T. The reduced thickness increases the coercive field of the nanoflake by 15 times, affecting the transport properties; we observed a large intrinsic AHC that is 22% larger than bulk samples and a field-dependent Hall anomaly, the magnitude of which cannot be explained by classical magnetization strength driven AHE. It can, however, be related to the extent of the Weyl point separation in k-space, a direct manifestation of Weyl physics. Finally, we showed that the PHE and LMR in the Co3Sn2S2 nanoflake are a result of a complex interplay between contributions from ferromagnetism, orbital magnetoresistance, and the chiral anomaly. Our findings provide a direction for future understanding of exotic topological transport in Co3Sn2S2 as well as other TRS-breaking WSMs.

Material Growth and Device Fabrication

Co3Sn2S2 nanoflakes were grown using a chemical-vapor-transport (CVT) method on Al2O3 (0001) substrates. Surface morphology and thickness of selected flakes were measured using a Bruker Multimode 8 atomic force microscopy (AFM). The flake used in this work was 180 nm thick (Supporting Information). Selected flakes were fabricated into Hall bar geometry devices via standard e-beam lithography and Ar ion etching. Afterward, Ru/Au (10 nm/200 nm) electrodes were sputter deposited as contacts.

Magneto-Resistivity Measurements

The magneto-resistivity measurements were performed in a PPMS DynaCool (Quantum Design) with a magnetic field up to 14 T using the “DC Resistivity” option. The rotator insert (Quantum Design) was used to tilt the angle between the magnetic field and the current.

Density Functional Theory (DFT) Calculations

The ab initio DFT calculations were performed using the package VASP.

Acknowledgments

We thank Yuanfeng Xu and Kai Chang for useful discussions. This work was funded by the Deutsche Forschungsgemeinschaft SPP 1666. M.N.A acknowledges Alexander von Humboldt Foundation Sofia Kovalevskaja Award, the MINERVA ARCHES Award. E.L. thanks the National Natural Science Foundation of China (No. 11974394). We acknowledge HLD at HZDR, a member of the European Magnetic Field Laboratory (EMFL) for the high magnetic field measurements.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.0c02219.

  • Information about additional device used in this work, two-carrier model fitting on ordinary Hall effect, extraction of intrinsic AHE, additional data in temperature dependent Hall resistivity and Hall conductivity, misalignment in the planar Hall measurement, and saturation magnetization measurement; comparison between current work and previous studies on bulk and MBE-grown Co3Sn2S2 (PDF)

Author Contributions

S.Y.Y., E.L. C.F. and S.S.P.P. conceived the experiments. E.L. grew the nanoflake crystals. S.Y.Y. fabricated the device and performed the transport measurements. J.N., J.G. and Y.S. performed the DFT calculation. S.Y.Y., F.K.D., M.N.A analyzed the data. S.Y.Y., F.K.D., M.N.A and S.S.P.P. wrote the manuscript. C.F. and S.S.P.P. supervised the project.

The authors declare no competing financial interest.

Supplementary Material

nl0c02219_si_001.pdf (864.1KB, pdf)

References

  1. Hirschberger M.; et al. The chiral anomaly and thermopower of Weyl fermions in the half-Heusler GdPtBi. Nat. Mater. 2016, 15 (11), 1161–1165. 10.1038/nmat4684. [DOI] [PubMed] [Google Scholar]
  2. Kuroda K.; et al. Evidence for magnetic Weyl fermions in a correlated metal. Nat. Mater. 2017, 16 (11), 1090–1095. 10.1038/nmat4987. [DOI] [PubMed] [Google Scholar]
  3. Liu E.; et al. Giant anomalous Hall effect in a ferromagnetic Kagome-lattice semimetal. Nat. Phys. 2018, 14 (11), 1125–1131. 10.1038/s41567-018-0234-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Wang Q.; Xu Y.; Lou R.; Liu Z.; Li M.; Huang Y.; Shen D.; Weng H.; Wang S.; Lei H. Large intrinsic anomalous Hall effect in half-metallic ferromagnet Co3Sn2S2 with magnetic Weyl fermions. Nat. Commun. 2018, 9 (1), 3681. 10.1038/s41467-018-06088-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Sakai A.; et al. Giant anomalous Nernst effect and quantum-critical scaling in a ferromagnetic semimetal. Nat. Phys. 2018, 14 (11), 1119–1124. 10.1038/s41567-018-0225-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Ye L. D.; et al. Massive Dirac fermions in a ferromagnetic kagome metal. Nature 2018, 555 (7698), 638–642. 10.1038/nature25987. [DOI] [PubMed] [Google Scholar]
  7. Armitage N. P.; Mele E. J.; Vishwanath A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 2018, 90 (1), 015001. 10.1103/RevModPhys.90.015001. [DOI] [Google Scholar]
  8. Yan B.; Felser C. Topological materials: Weyl semimetals. Annu. Rev. Condens. Matter Phys. 2017, 8, 337–354. 10.1146/annurev-conmatphys-031016-025458. [DOI] [Google Scholar]
  9. Hasan M. Z.; et al. Discovery of Weyl fermion semimetals and topological Fermi arc states. Annu. Rev. Condens. Matter Phys. 2017, 8, 289–309. 10.1146/annurev-conmatphys-031016-025225. [DOI] [Google Scholar]
  10. Burkov A. A. Anomalous Hall effect in Weyl metals. Phys. Rev. Lett. 2014, 113 (18), 187202. 10.1103/PhysRevLett.113.187202. [DOI] [PubMed] [Google Scholar]
  11. Yang K. Y.; Lu Y. M.; Ran Y. Quantum Hall effects in a Weyl semimetal: Possible application in pyrochlore iridates. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 84 (7), 075129. 10.1103/PhysRevB.84.075129. [DOI] [Google Scholar]
  12. Burkov A. Negative longitudinal magnetoresistance in Dirac and Weyl metals. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 91 (24), 245157. 10.1103/PhysRevB.91.245157. [DOI] [Google Scholar]
  13. Son D.; Spivak B. Chiral anomaly and classical negative magnetoresistance of Weyl metals. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 88 (10), 104412. 10.1103/PhysRevB.88.104412. [DOI] [Google Scholar]
  14. Xiong J.; et al. Evidence for the chiral anomaly in the Dirac semimetal Na3 Bi. Science 2015, 350 (6259), 413–416. 10.1126/science.aac6089. [DOI] [PubMed] [Google Scholar]
  15. Huang X. C.; et al. Observation of the Chiral-Anomaly-Induced Negative Magnetoresistance in 3D Weyl Semimetal TaAs. Phys. Rev. X 2015, 5 (3), 031023. 10.1103/PhysRevX.5.031023. [DOI] [Google Scholar]
  16. Wang Y.; Liu E.; Liu H.; Pan Y.; Zhang L.; Zeng J.; Fu Y.; Wang M.; Xu K.; Huang Z.; Wang Z.; Lu H.-Z.; Xing D.; Wang B.; Wan X.; Miao F. Gate-tunable negative longitudinal magnetoresistance in the predicted type-II Weyl semimetal WTe2. Nat. Commun. 2016, 7, 13142. 10.1038/ncomms13142. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Zhang C.-L.; Xu S.-Y.; Belopolski I.; Yuan Z.; Lin Z.; Tong B.; Bian G.; Alidoust N.; Lee C.-C.; Huang S.-M.; Chang T.-R.; Chang G.; Hsu C.-H.; Jeng H.-T.; Neupane M.; Sanchez D. S.; Zheng H.; Wang J.; Lin H.; Zhang C.; Lu H.-Z.; Shen S.-Q.; Neupert T.; Zahid Hasan M.; Jia S. Signatures of the Adler-Bell-Jackiw chiral anomaly in a Weyl fermion semimetal. Nat. Commun. 2016, 7, 1–9. 10.1038/ncomms10735. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Liang S. H.; et al. Experimental Tests of the Chiral Anomaly Magnetoresistance in the Dirac-Weyl Semimetals Na3 Bi and GdPtBi. Phys. Rev. X 2018, 8 (3), 031002. 10.1103/PhysRevX.8.031002. [DOI] [Google Scholar]
  19. Nandy S.; et al. Chiral Anomaly as the Origin of the Planar Hall Effect in Weyl Semimetals. Phys. Rev. Lett. 2017, 119 (17), 176804. 10.1103/PhysRevLett.119.176804. [DOI] [PubMed] [Google Scholar]
  20. Burkov A. A. Giant planar Hall effect in topological metals. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96 (4), 041110. 10.1103/PhysRevB.96.041110. [DOI] [Google Scholar]
  21. Li H.; et al. Giant anisotropic magnetoresistance and planar Hall effect in the Dirac semimetal Cd3As2. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 97 (20), 201110. 10.1103/PhysRevB.97.201110. [DOI] [Google Scholar]
  22. Wu M.; et al. Probing the chiral anomaly by planar Hall effect in Dirac semimetal Cd3As2 nanoplates. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 98 (16), 161110. 10.1103/PhysRevB.98.161110. [DOI] [Google Scholar]
  23. Kumar N.; et al. Planar Hall effect in the Weyl semimetal GdPtBi. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 98 (4), 041103. 10.1103/PhysRevB.98.041103. [DOI] [Google Scholar]
  24. Li P.; et al. Giant Planar Hall Effect in the Dirac. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 98 (12), 121108. 10.1103/PhysRevB.98.121108. [DOI] [Google Scholar]
  25. Li P.; et al. Anisotropic planar Hall effect in the type-II topological Weyl semimetal WTe2. Phys. Rev. B: Condens. Matter Mater. Phys. 2019, 100 (20), 205128. 10.1103/PhysRevB.100.205128. [DOI] [Google Scholar]
  26. Li Z. G.; et al. Planar Hall effect in PtSe2. J. Appl. Phys. 2020, 127 (5), 054306. 10.1063/1.5133809. [DOI] [Google Scholar]
  27. Singha R.; et al. Planar Hall effect in the type-II Dirac semimetal VAl3. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 98 (8), 081103. 10.1103/PhysRevB.98.081103. [DOI] [Google Scholar]
  28. Liang D. D.; et al. Origin of planar Hall effect in type-II Weyl semimetal MoTe2. AIP Adv. 2019, 9 (5), 055015. 10.1063/1.5094231. [DOI] [Google Scholar]
  29. Liu Q. Q.; et al. Nontopological origin of the planar Hall effect in the type-II Dirac semimetal NiTe2. Phys. Rev. B: Condens. Matter Mater. Phys. 2019, 99 (15), 155119. 10.1103/PhysRevB.99.155119. [DOI] [Google Scholar]
  30. Muechler L.; et al. Emerging chiral edge states from the confinement of a magnetic Weyl semimetal in Co 3 Sn 2 S 2. Phys. Rev. B: Condens. Matter Mater. Phys. 2020, 101 (11), 115106. 10.1103/PhysRevB.101.115106. [DOI] [Google Scholar]
  31. Guin S. N.; et al. Zero-Field Nernst Effect in a Ferromagnetic Kagome-Lattice Weyl-Semimetal Co3Sn2S2. Adv. Mater. 2019, 31 (25), 1806622. 10.1002/adma.201806622. [DOI] [PubMed] [Google Scholar]
  32. Li G. W.; et al. Surface states in bulk single crystal of topological semimetal Co3Sn2S2 toward water oxidation. Sci. Adv. 2019, 5 (8), eaaw9867 10.1126/sciadv.aaw9867. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Guguchia Z.; Verezhak J. A. T.; Gawryluk D. J.; Tsirkin S. S.; Yin J.-X.; Belopolski I.; Zhou H.; Simutis G.; Zhang S.-S.; Cochran T. A.; Chang G.; Pomjakushina E.; Keller L.; Skrzeczkowska Z.; Wang Q.; Lei H. C.; Khasanov R.; Amato A.; Jia S.; Neupert T.; Luetkens H.; Hasan M. Z. Tunable anomalous Hall conductivity through volume-wise magnetic competition in a topological kagome magnet. Nat. Commun. 2020, 11 (1), 559. 10.1038/s41467-020-14325-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Lachman E.; Murphy R. A.; Maksimovic N.; Kealhofer R.; Haley S.; McDonald R. D.; Long J. R.; Analytis J. G. Exchange biased anomalous Hall effect driven by frustration in a magnetic kagome lattice. Nat. Commun. 2020, 11 (1), 1–8. 10.1038/s41467-020-14326-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Yang R.; et al. Magnetization-Induced Band Shift in Ferromagnetic Weyl Semimetal Co3Sn2S2. Phys. Rev. Lett. 2020, 124 (7), 077403. 10.1103/PhysRevLett.124.077403. [DOI] [PubMed] [Google Scholar]
  36. Lv B. Q.; et al. Experimental Discovery of Weyl Semimetal TaAs. Phys. Rev. X 2015, 5 (3), 031013. 10.1103/PhysRevX.5.031013. [DOI] [Google Scholar]
  37. Xu S. Y.; et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 2015, 349 (6248), 613–617. 10.1126/science.aaa9297. [DOI] [PubMed] [Google Scholar]
  38. Xu S.-Y.; et al. Experimental discovery of a topological Weyl semimetal state in TaP. Sci. Adv. 2015, 1 (10), e1501092 10.1126/sciadv.1501092. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Lv B. Q.; et al. Observation of Weyl nodes in TaAs. Nat. Phys. 2015, 11 (9), 724–727. 10.1038/nphys3426. [DOI] [Google Scholar]
  40. Deng K.; et al. Experimental observation of topological Fermi arcs in type-II Weyl semimetal MoTe 2. Nat. Phys. 2016, 12 (12), 1105–1110. 10.1038/nphys3871. [DOI] [Google Scholar]
  41. Huang L.; McCormick T. M.; Ochi M.; Zhao Z.; Suzuki M.-T.; Arita R.; Wu Y.; Mou D.; Cao H.; Yan J.; Trivedi N.; Kaminski A. Spectroscopic evidence for a type II Weyl semimetallic state in MoTe2. Nat. Mater. 2016, 15 (11), 1155–1160. 10.1038/nmat4685. [DOI] [PubMed] [Google Scholar]
  42. Ali M. N.; et al. Large, non-saturating magnetoresistance in WTe. Nature 2014, 514 (7521), 205. 10.1038/nature13763. [DOI] [PubMed] [Google Scholar]
  43. Liu D. F.; Liang A. J.; Liu E. K.; Xu Q. N.; Li Y. W.; Chen C.; Pei D.; Shi W. J.; Mo S. K.; Dudin P.; Kim T.; Cacho C.; Li G.; Sun Y.; Yang L. X.; Liu Z. K.; Parkin S. S. P.; Felser C.; Chen Y. L. Magnetic Weyl semimetal phase in a Kagome crystal. Science 2019, 365 (6459), 1282–1285. 10.1126/science.aav2873. [DOI] [PubMed] [Google Scholar]
  44. Morali N.; Batabyal R.; Nag P. K.; Liu E.; Xu Q.; Sun Y.; Yan B.; Felser C.; Avraham N.; Beidenkopf H. Fermi-arc diversity on surface terminations of the magnetic Weyl semimetal Co3Sn2S2. Science 2019, 365 (6459), 1286–1291. 10.1126/science.aav2334. [DOI] [PubMed] [Google Scholar]
  45. Shama; Gopal R.K.; Singh Y. Observation of planar Hall effect in the ferromagnetic Weyl semimetal Co3Sn2S2. J. Magn. Magn. Mater. 2020, 502, 166547. 10.1016/j.jmmm.2020.166547. [DOI] [Google Scholar]
  46. Yamada H.; Takada S. Negative Magnetoresistance of Ferromagnetic Metals Due to Spin Fluctuations. Prog. Theor. Phys. 1972, 48 (6a), 1828–1848. 10.1143/PTP.48.1828. [DOI] [Google Scholar]
  47. Smit J. Magnetoresistance of Ferromagnetic Metals and Alloys at Low Temperatures. Physica 1951, 17 (6), 612–627. 10.1016/0031-8914(51)90117-6. [DOI] [Google Scholar]
  48. Shen J.; et al. On the anisotropies of magnetization and electronic transport of magnetic Weyl semimetal Co3Sn2S2. Appl. Phys. Lett. 2019, 115 (21), 212403. 10.1063/1.5125722. [DOI] [Google Scholar]
  49. Neubauer A.; et al. Topological Hall Effect in the A Phase of MnSi. Phys. Rev. Lett. 2009, 102 (18), 186602. 10.1103/PhysRevLett.102.186602. [DOI] [PubMed] [Google Scholar]
  50. Kanazawa N.; et al. Large Topological Hall Effect in a Short-Period Helimagnet MnGe. Phys. Rev. Lett. 2011, 106 (15), 156603. 10.1103/PhysRevLett.106.156603. [DOI] [PubMed] [Google Scholar]
  51. Kassem M. A.; et al. Low-field anomalous magnetic phase in the kagome-lattice shandite Co3Sn2S2. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96 (1), 014429. 10.1103/PhysRevB.96.014429. [DOI] [Google Scholar]
  52. Kassem M. A.; Tabata Y.; Waki T.; Nakamura H. Low-field anomalous magnetic phase in the kagome-lattice shandite Co3Sn2S2. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96 (1), 014429. 10.1103/PhysRevB.96.014429. [DOI] [Google Scholar]
  53. Miyasato T.; et al. Crossover behavior of the anomalous Hall effect and anomalous nernst effect in itinerant ferromagnets. Phys. Rev. Lett. 2007, 99 (8), 086602. 10.1103/PhysRevLett.99.086602. [DOI] [PubMed] [Google Scholar]
  54. Onoda S.; Sugimoto N.; Nagaosa N. Intrinsic versus extrinsic anomalous Hall effect in ferromagnets. Phys. Rev. Lett. 2006, 97 (12), 126602. 10.1103/PhysRevLett.97.126602. [DOI] [PubMed] [Google Scholar]
  55. Yau K L; Chang J T H The planar Hall effect in thin foils of Ni-Fe alloy. J. Phys. F: Met. Phys. 1971, 1 (1), 38. 10.1088/0305-4608/1/1/307. [DOI] [Google Scholar]
  56. Tang H. X.; et al. Giant planar Hall effect in epitaxial (Ga,Mn)As devices. Phys. Rev. Lett. 2003, 90 (10), 107201. 10.1103/PhysRevLett.90.107201. [DOI] [PubMed] [Google Scholar]
  57. Seemann K. M.; et al. Origin of the Planar Hall Effect in Nanocrystalline Co60Fe20B20. Phys. Rev. Lett. 2011, 107 (8), 086603. 10.1103/PhysRevLett.107.086603. [DOI] [PubMed] [Google Scholar]
  58. Nazmul A. M.; et al. Planar Hall effect and uniaxial in-plane magnetic anisotropy in Mn delta-doped GaAs/p-AlGaAs heterostructures. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 77 (15), 155203. 10.1103/PhysRevB.77.155203. [DOI] [Google Scholar]
  59. Yang S.-Y.; Chang K.; Parkin S. S. Large planar Hall effect in bismuth thin films. Phys. Rev. Res. 2020, 2 (2), 022029. 10.1103/PhysRevResearch.2.022029. [DOI] [Google Scholar]
  60. Kokado S.; et al. Anisotropic Magnetoresistance Effects in Fe, Co, Ni, Fe4N, and Half-Metallic Ferromagnet: A Systematic Analysis. J. Phys. Soc. Jpn. 2012, 81 (2), 024705. 10.1143/JPSJ.81.024705. [DOI] [Google Scholar]
  61. Mcguire T. R.; Potter R. I. Anisotropic Magnetoresistance in Ferromagnetic 3d Alloys. IEEE Trans. Magn. 1975, 11 (4), 1018–1038. 10.1109/TMAG.1975.1058782. [DOI] [Google Scholar]
  62. dos Reis R D.; Ajeesh M O; Kumar N; Arnold F; Shekhar C; Naumann M; Schmidt M; Nicklas M; Hassinger E On the search for the chiral anomaly in Weyl semimetals: the negative longitudinal magnetoresistance. New J. Phys. 2016, 18 (8), 085006. 10.1088/1367-2630/18/8/085006. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl0c02219_si_001.pdf (864.1KB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES