The era of big data: Genome-scale modelling meets machine learning

Graphical abstract

Abstract

With omics data being generated at an unprecedented rate, genome-scale modelling has become pivotal in its organisation and analysis. However, machine learning methods have been gaining ground in cases where knowledge is insufficient to represent the mechanisms underlying such data or as a means for data curation prior to attempting mechanistic modelling. We discuss the latest advances in genome-scale modelling and the development of optimisation algorithms for network and error reduction, intracellular constraining and applications to strain design. We further review applications of supervised and unsupervised machine learning methods to omics datasets from microbial and mammalian cell systems and present efforts to harness the potential of both modelling approaches through hybrid modelling.

1. Introduction

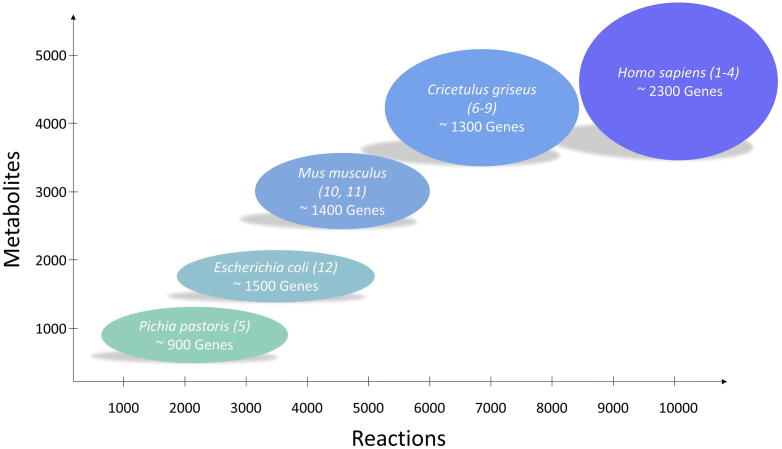
Genome-scale metabolic models (GeMs) are a database for all known information about an organism across multiple scales, including most of its known genes, the enzymes encoded by those genes and associated expression rules (gene-protein-reaction, GPR, rules), transport reactions and participating metabolites. There have been numerous GeMs published for a variety of organisms, most of which can be found in the BiGG database (http://bigg.ucsd.edu/). Relevant to the production of protein therapeutics are the human [1], [2], [3], [4], Pichia pastoris as described in Theron et al. [5], Chinese hamster ovary (CHO) cells [6], [7], [8], [9], murine cells [10], [11] and a plethora of GeMs for Escherichia coli [12], as summarised in Fig. 1.

Fig. 1.

Summary of genome-scale metabolic models for different organisms relevant to the production of recombinant proteins or valuable metabolic products.

Although GeMs provide valuable insight into biological networks, full integration of data across the genomic, transcriptomic, proteomic and metabolomic scales is yet to be effectively realised. Given the unprecedented rate of data generation, modelling efforts have evolved by, for example, developing hybrid kinetic/stoichiometric formulations to overcome the weaknesses of any individual approach whilst, at the same time, combining their strengths through alleviating the burden of parameter estimation [13], or including intracellular insight without loss of model tractability [14], [15]. The next logical step is the development of hybrid approaches that take advantage of known techniques that harness the information content of extensive datasets. Machine learning (ML) is the scientific study of algorithms applied to complex datasets for pattern recognition, classification, and prediction. The concept of automated learning was developed from the theory that machines learn without being pre-programmed on assignments of data patterns to classes. The iterative notion behind the learning theory relies on the independent adaptation of the ML model when presented to new data input. Such adaptation is based on the ability to recognise patterns in complex datasets to generate reliable, reproducible results from previous computations.

Herein, we review the latest advances in GeM development and application for process understanding and cell engineering and discuss efforts to hybridise FBA with dynamic kinetic models focusing on recombinant protein producing systems. These include CHO cells, which are the workhorse of industrial therapeutic glycoprotein production, but also microbial hosts such as Pichia pastoris and Escherichia coli. We then present the case for using ML to decipher the information carried in large omics datasets and review the main techniques for doing so, including supervised and unsupervised ML methods, as well as necessary data pre-treatment techniques prior to ML application. Given the limited number of studies on industrial protein production systems, we review the application of ML to omics more broadly, including microbial cell systems for metabolite or recombinant protein production as well as human disease models.

2. Advances in GeM development and application

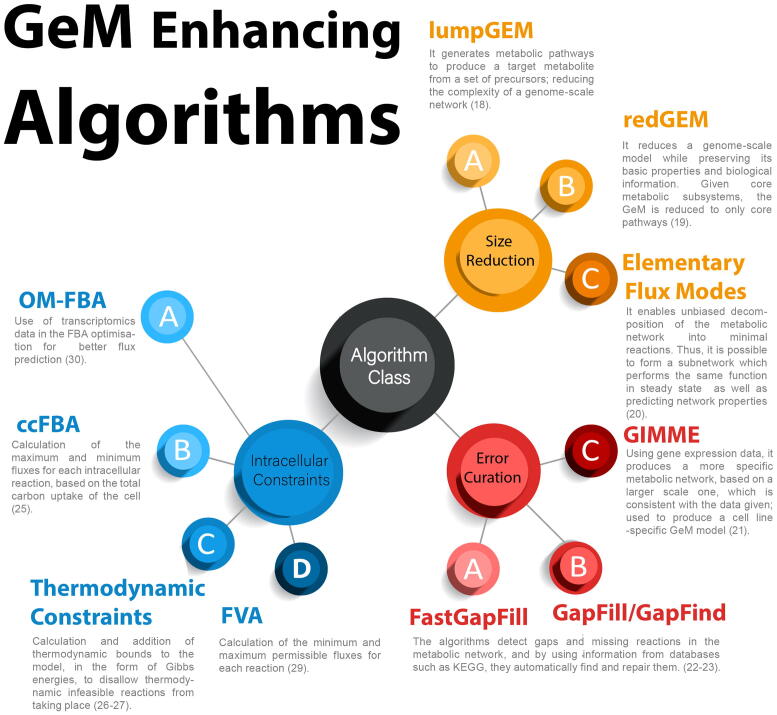
Research involving GeMs has largely focused on (a) the development of consensus models for commonly used organisms, (b) the advancement of computational algorithms and (c) the development of dynamic flux models. Recent key studies in these three areas are summarised in Fig. 2. Efforts to develop GeMs have yielded a new community-curated model of CHO cell metabolism developed by Hefzi et al. [6]. Their work includes cell line-specific models for CHO-S, CHO-K1 as well as the generic CHO GeM model, iCHO1766, which contains most of the known CHO genes, enzymes and metabolites. Calmels et al. have also developed a GeM specific to the DG-44 cell line [7]. The iCHO1766 GeM was recently expanded to include the secretory pathway in a study that paves the way for ascertaining the burden of individual recombinant protein molecules on metabolism and protein synthesis and secretion [16].

Fig. 2.

Algorithms used to improve the network and efficiency of genome-scale metabolic models.

A powerful tool for the analysis of GeMs and the calculation of fluxes is Flux Balance Analysis (FBA). FBA is an optimisation technique aiming to predict the flux distribution in a metabolic network. Cell metabolism can be represented by a stoichiometric matrix, S, whose columns represent the reactions, j, and rows the metabolites, i, of the metabolism. FBA assumes pseudo-steady state of the metabolite concentrations; so, if x represents the metabolite concentrations, $\frac{\mathit{Dx}}{\mathit{Dt}}=0$ thus $S\bullet v=0$, where v is a vector of the fluxes of the reactions. However, in any biological system the number of reactions is larger than the number of metabolites, so the number of degrees of freedom is greater than 1. Additionally, if we want to predict intracellular fluxes of a GeM using FBA we need to define the upper and lower bounds of fluxes [17].

Recent work on computational algorithms has focused on reducing model size [18], [19], [20] while keeping the core biological information intact as well as identifying missing links in the reaction network and filling them in with reactions from databases [21], [22], [23], such as the Kyoto Encyclopedia of Genes and Genomes or MetaCyC [24]. Lastly, considerable effort is being put into the development of computational techniques for the calculation of appropriate bounds for intracellular reactions [25], [26], [27], [28], [29], [30] and exchange reactions [31].

GeMs have found application in the optimisation-based design of genetic engineering strategies to alleviate the trade-off between cell growth and desired product formation. Key algorithms for this purpose [32], [33], [34], [35], [36], [37], [38], [39], [40] are summarised in Fig. 3. There are two distinct fields of optimisation techniques applied to metabolic models for this purpose: optimisation of the metabolic network or optimisation of the extracellular environment. The first is mainly composed of Mixed-Integer Linear Programming (MILP) algorithms, which identify reactions and therefore candidate genes for knockout, upregulation or downregulation. These algorithms have been applied to create engineered microbial strains as described in a recent review by Hendry et al. [41]. For example, Suástegui et al. applied the OptForce algorithm to increase shikimic acid production in Saccharomyces serevisiae [42], and Tan et al. were able to increase octanoic acid production in E. coli again with the use of OptForce [43]. Another example is the use of an E. coli GeM [44] to identify gene knock out strategies that improve glycan biosynthesis [45]. Saitua et al. employed a dynamic GeM of P. pastoris to predict system behaviour across batch and fed-batch cultivation under glucose-limited aerobic conditions, followed by the design of single knock-out genetic engineering strategies that can boost volumetric protein productivity [46]. The CHO GeM has also been used to identify burdensome host cell proteins for deletion to ease pressure on downstream processing [16], [47]. However, due to the size and complexity of mammalian cell GeMs, this kind of algorithms have not been widely applied to mammalian cell systems yet.

Fig. 3.

Algorithms used in strain design for the overproduction of metabolites.

The second category of optimisation applications is focused on improving the media formulation and/or feeding strategy of the culture. CHO cells have been the subject of numerous such studies due to their use for industrial antibody production. GeMs or smaller scale models have supported researchers to improve the design of culture media and feeds or develop more efficient CHO cell strains with the help of experimental data and FBA. The CHO-K1 GeM has been used to compare catabolism in the presence of different feeds and to optimise feed formulation using FBA [48]. Similarly, the CHO DG-44 GeM has been employed to predict cell phenotype when grown in different culture media and propose optimised formulations [7]. A reduced version of a CHO GeM was used by Xing et al. [49] to adjust the concentrations of certain amino acids in the culture media, by Junghans et al. [50] to propose changes to media and feed that could improve bioprocess efficiency and by Templeton et al. [51] to predict high producers based on intracellular flux distribution. The CHO GeM [6] has been used to study glucose and lactate metabolism using FBA coupled with dynamic equations to simulate the consumption and secretion rates of essential metabolites [52], and aid the design of new feeding strategies by analysing intracellular fluxes [53]. This approach has also been employed to model batch CHO cell culture conditions [54] and to study metabolic shifts as a result of switching from physiological temperature to mild hypothermic conditions [55].

Additionally, DFBA has been applied widely to microbial cell systems primarily for the prediction of biomass growth and production of metabolites. Topics of recent studies include the production of shikimic acid in E. coli [56], the prediction of growth rate and ethanol production in Saccharomyces cerevisiae [57] and the overproduction of secretory proteins in Streptomyces lividans [58]. In the context of recombinant protein production, Torres et al. applied a comprehensive GeM to chemostat cultures of P. pastoris conducted under different oxygenation levels to reveal high-order metabolic effects of different culture parameters on system performance [59]. An underpinning requirement for such applications is the availability of a high-fidelity GeM. To this end, a significant recent advancement was the refinement of P. pastoris GeM specifically for growth on non-glucose substrates such as glycerol and methanol, which are most relevant for recombinant protein production [60]. There are several methodologies for coupling FBA optimisation with kinetic equations to create a hybrid model as summarised in Table 1.

Table 1.

Techniques and algorithms used for steady-state and dynamic MFA and FBA.

Type	Advantages	Disadvantages	Description	Ref.
Static Optimisation approach	Simple implementation Suitable for GeM models  Fast	Provides a simple, not very detailed solution   Cannot predict metabolic shifts	Separates culture period into intervals of pseudo steady-state and performs an FBA optimisation for each of them	[131]
				[132]
Dynamic Optimisation Approach	Detailed representation of metabolism   Can describe metabolic shifts	Accurate parameter estimation in differential equations necessary    Need to avoid overfitting	Performs optimization over the whole period of interest with the use of differential equations to describe biomass and media concentrations	[132]
				[133]
				[54]
DMFA	Calculates intracellular fluxes	Requires extracellular metabolite concentrations thus, cannot be used in underdetermined systems	Uses a linear spline function to calculate intracellular fluxes	[55]
			Describes intracellular fluxes using linear changes of the fluxes though time	[134]
Multi-objective optimisation	Uses the duality theorem to achieve optimality	Numerical challenges arising from the DAE formulation	Uses logarithmic barrier functions on the constraints of the primal and dual problem. Converts them to a DAE with the dynamic balance equations for the substrates	[135]
	Deals with LP infeasibility that can be caused during time integration	Requires careful objective function setting to achieve realistic solution	DFBA using lexicographic optimisation to deal with the LP feasibility problem	[136]

3. Hybrid machine learning and constrained-based modelling approaches

Machine learning algorithms have found application in both the interpretation of high-dimensional metabolic data and the development of tools for the description of cellular metabolism. More specifically, unsupervised ML methods have been utilized for the identification of key metabolic parameters that accommodate model development, for the identification of sub-groups in the data and for the reduction of data complexity prior to downstream modelling applications. On the other hand, supervised algorithms have been used to both replace alternative approaches (kinetic and stoichiometric models) for metabolic modelling but also to synergistically work and improve the predictions of alternative models.

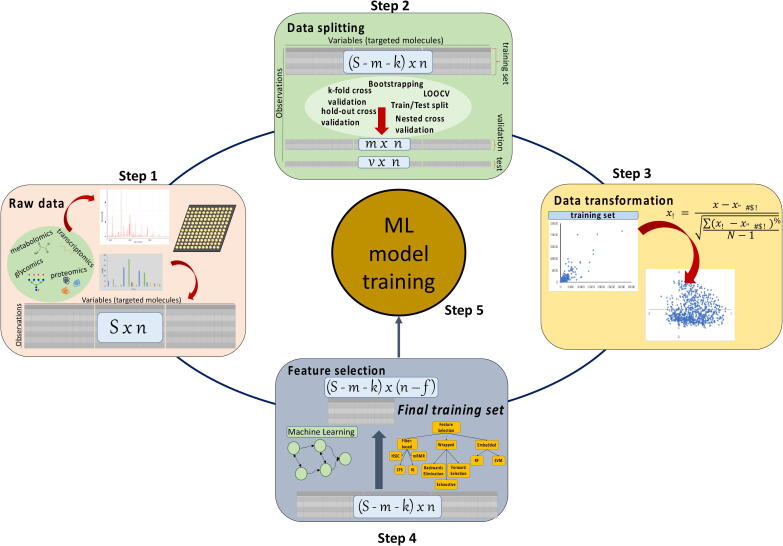
Prior to introducing the available dataset to the chosen ML configuration, data arising from different omics techniques requires pre-processing (Fig. 4) in order to increase model robustness and avoid overfitting. Typically, data pre-treatment is performed in three steps as described below. Whilst elaborating on data pre-treatment is not within the scope of this review, we invite interested readers to further explore the articles suggested herein.

Fig. 4.

Data pre-processing steps for improving the performance and ensuring the robustness of machine learning algorithms.

3.1. Data pre-treatment

3.1.1. Data splitting

As a first step, the dataset is sampled for the construction of (a) the training set, i.e. the data used for model training, (b) the validation set, the data used for tuning hyperparameters and (c) the test set, the set of data used to evaluate model’s predictive performance. Random sampling (RS) is typically applied for data splitting because it introduces low levels of bias and efficiently evaluates model generalization. RS methods can sample the same data point multiple times (RS with replacement) or only once (RS without replacement). Bootstrapping and cross validation (CV) are the most representative techniques of RS with and without replacement, respectively. Detailed comparisons of the data sampling methods can be found in Varoquaoux [61], Vabalas et al. [62], Kim [63], and Xu & Goodcare [64]. It is important to note that data splitting techniques such as CV, should not be used for the identification of optimum data splitting strategies but for the evaluation of model generalization. However, limitations arising from the underlying biological principles can introduce biases in the handling and splitting of the dataset, as the ML algorithms perform poorly when extrapolating. Thus, the user needs to ensure that the training set covers the space within which the validation and test sets lie. Hyperparameters are parameters of the ML algorithm that are set by the user in order to define the configuration of the model and remain constant during model training. The validation set is essential for tuning the hyperparameters (i.e. number of hidden layers and nodes) and should be separate to the training set. Grid or random search algorithms examine different combinations of hyperparameters to identify the top-performing set in an exhaustive or random manner, respectively. Whilst computationally intensive, nested or double cross validation, where the training set determined by the first CV is then further split to a new pair of training and validation sub-sets by a nested CV algorithm, is necessary in order to avoid overfitting of the estimated hyperparameters to the training set.

3.1.2. Data transformation (standardize/normalize)

Prior to any further data pre-processing, raw data are typically scaled in order to remove the bias towards the variables with the highest values. For example, large-scale discrepancies between the concentration of the targeted molecules are commonly observed in omics data and, if not appropriately scaled, the downstream ML algorithm will form strong dependencies to the most abundant targets. Whilst there is a plethora of available data transformation techniques that can be applied to omics data [65], [66] (Table 2), z-score normalization (also known as standardization or autoscaling) is the most widely used technique. Z-score normalization aims to equalize the variance of measured molecules by setting the mean of each variable equal to zero and the standard deviation equal to one. An excellent comparison between different transformation methods applied to metabolomics data prior to multivariate analysis is presented in van den Berg et al. [67]. Another pre-treatment step often applied in omics datasets and especially in single-cell RNA-seq data is the imputation for the estimation of missing points [68], [69], [70], [71], [72].

Table 2.

Summary of major data splitting, data transformation and feature selection techniques. Notation: $x_{\mathit{ij}}$ and ${\stackrel{}{x}}_{\mathit{ij}}$ are the raw and normalized values of variable $i$ in observation $j$, respectively. ${\stackrel{-}{x}}_i$ and ${\sigma }_i$ are the mean and standard deviation of variable $i$ in the available dataset, respectively. $x_{i,min}$ and $x_{i,max}$ are the minimum and maximum values of variable $i$ observed in the available dataset.

Class	Principle	Advantages	Disadvantages	Methods
Data splitting
Random Sampling (RS)	The training, validation and test sets are randomly chosen from the population	Minimal levels of bias introduced during sampling When iteratively repeated can be used for model generalization evaluation	Do not account for data distribution Model might perform poorly if requested to extrapolate Not appropriate for small sample sizes	Train/Test split k-fold cross-validation (CV) Hold-out cross-validation Nested cross-validation Leave-one-out-cross-validation (LOOCV) Bootstrapping
Data Transformation
z-score normalization	${\stackrel{}{x}}_{\mathit{ij}}=\frac{x_{\mathit{ij}}-{\stackrel{-}{x}}_i}{{\sigma }_i}$	Accounts for both the mean and the variability of the dataset	Assumes normal distribution Could lead to over-amplification of small differences Increases the impact of measurement error
Pareto scaling	${\stackrel{}{x}}_{\mathit{ij}}=\frac{x_{\mathit{ij}}-{\stackrel{-}{x}}_i}{\sqrt{{\sigma }_i}}$	Reduction of large values effect on model training	Reduction of large variance in the data
Range scaling	${\stackrel{}{x}}_{\mathit{ij}}=\frac{x_{\mathit{ij}}-{\stackrel{-}{x}}_i}{x_{i,max}-x_{i,min}}$	Transformed features are equally important	Outliers can undermine the correct interpretation of data variation
min-max normalization	${\stackrel{}{x}}_{\mathit{ij}}=\frac{x_{\mathit{ij}}-x_{i,min}}{x_{i,max}-x_{i,min}}$	Most applicable when the data does not follow a normal distribution	Sensitive to outliers Does not account for the data dispersion
Mean centering	${\stackrel{}{x}}_{\mathit{ij}}=x_{\mathit{ij}}-{\stackrel{-}{x}}_i$	Mean of all features is zero Can partially alleviate multicollinearity	Does not scale the data Usually applied in combination with other scaling methods
Log transformation	${\stackrel{}{x}}_{\mathit{ij}}={\log }_{10}({\stackrel{}{x}}_{\mathit{ij}})$	Can alleviate heteroskedasticity and impose normal distribution	Can be problematic when values reach transformation function boundaries
Feature Selection
Filter	Features are selected based on their performance in statistical algorithms	High efficiency Independent of the predictor	Do not interact with the predictor Results can be relatively poor	Correlation based Feature Selection (CFS) Information Gain (IG) minimum Redundancy-Maximum Relevance (mRMR) Hilbert Schmidt Independence Criterion Lasso (HSIC-Lasso)
Wrapped	Evaluation of feature subsets based on ML model performance. They are composed of a search and an evaluation algorithm	Results in feature subsets with good performance	Computationally expensive (greedy) as they require multiple model simulations Biased towards the examined model Exhaustive search and fast evaluation necessary Danger of overfitting Optimization of evaluation method may be necessary	Forward selection Backwards elimination Exhaustive search
Embedded	Feature selection is incorporated in model training	Non-contributing features are usually penalized Less computationally expensive than wrapped methods Robust to overfitting	Selection is biased towards the model in use	Least absolute shrinkage and selection operator (LASSO) Support Vector Machine (SVM) SVM-Recursive feature elimination (SVM-RFE) Random Forest (RF)

3.1.3. Feature selection

Implementation of ML algorithms usually requires the handling of large and high-dimensional datasets. Omics data typically include a vast number of measured variables (in the scale of thousands) that act as inputs for ML models, e.g. genes in RNA-seq or microarrays. Herein, the terms features and labels will be used to describe the inputs and outputs of ML models, respectively, following the convention used by the ML community. Feature selection is defined by the reduction of dataset dimensionality, meaning the selection of only a subset of features that maintain or even improve the accuracy of the model, as the importance of each feature towards labels prediction varies significantly [73]. Feature selection is a pre-processing step only performed on the training set to avoid information leaking from the test or validation sets to model training. Implementation of feature selection is necessary to avoid model overfitting and to ensure that the algorithm can correctly identify the dependencies and correlations between features and labels.

Feature selection methods pursue three possible objectives: (1) the identification and retention of the features that are (not necessarily linearly) strongly correlated with the labels and (2) the identification and exclusion of the features that are strongly correlated with each other and (3) the identification of feature combinations that improve model predictive capabilities. Feature selection, results in the designation of a subset of features that account for the maximum variance of the data or in a ranking list that reflects the importance of each feature toward labels variance [74]. Consequently, feature selection results in improved and faster model performance and deeper understanding of dependencies within the features and between the features and labels. Techniques for feature selection usually include unsupervised algorithms where the output is not known a priori. There are three popular classes of feature selection techniques: filter, wrapper and embedded methods [75], [76]. In filter methods, different statistical and ranking algorithms are applied to the available dataset to determine the highest scoring features [77], [78]. Wrapper methods include the development and training of several model configurations using different feature subsets [79]. Should the exclusion of the examined features not substantially decrease model performance, the features can be excluded from model construction [80], [81], [82], [83]. Finally, the ML models that include a dimensionality-reduction step and can be used simultaneously for feature selection and label prediction belong to the class of embedded algorithms. Ensembles that combine different modelling algorithms have also been proposed for feature selection [74]. More characteristics about these methods can be found in Table 2.

Although not typically included in any of the aforementioned feature selection classes, algorithms such as principal component analysis (PCA), hierarchical clustering, k-means clustering, k-nearest neighbours (k-NN) classification and autoencoders (unsupervised or self-supervised artificial neural networks) can contribute to dimensionality reduction. However, the dimensionality reduction techniques search for latent variables to explain the noise in data, whilst feature selection methods search within the available features of the input set. A further classification of dimensionality reduction to linear/non-linear methods and univariate/multivariate methods is also common. Unlike linear methods (i.e. least absolute shrinkage and selection operator – LASSO), algorithms that account for non-linear dependencies between the features and labels are more suitable when a non-linear predictor model is used [84]. Multivariate analysis involves the simultaneous evaluation of multiple variables for the better exploration of interdependencies between the examined variables.

3.2. Unsupervised machine learning applications

Omics data typically include thousands of measured variables. Unsupervised ML techniques have been widely used to process multidimensional datasets and expedite data analysis in biological and biomedical systems as summarised in Fig. 5. For example, autoencoders have been used as an initialization step in ML frameworks that classify breast cancer metabolomic data [13], while PCA of proteomic data has been utilized for the identification of metabolic engineering strategies for intensification of production in bacterial cultures [14]. Undoubtedly, PCA is the most widely used unsupervised tool for the interpretation of both experimental data and computational results. An overview of available methods and their application to cell systems is presented in Table 3.

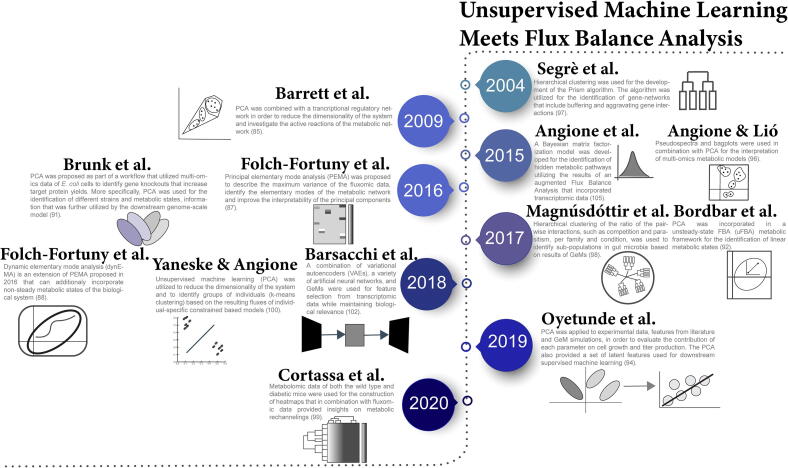
Fig. 5.

Timeline of unsupervised machine earning techniques and their application to constraint-based models.

Table 3.

Unsupervised machine learning methods used in combination with constraint-based models.

Unsupervised ML method	Description	Applications
PCA	Dimensionality reduction Data interpretability Data simplification Identification of variation sources	Dimensionality reduction of fluxomic data [85], [86] Can be applied to CBM results to identify central fluxes and pathways [85,86,95,96) Identification of metabolism active EMs [87], [88], [89], [90] Can be applied to experimental or simulation data to further inform downstream CBMs or ML algorithms [91], [92], [93], [94]
Clustering	Identification of sub-populations Clustering criteria, such as centroid- or distribution-based, vary depending on the chosen algorithm	Hierarchical clustering for the identification of populations and the development of population specific CBMs [98], [100] Gene network reconstruction [97] Heatmaps of metabolomics data for studying metabolic alterations [99] k-means clustering to group CBM results [100]
Autoencoders	Unsupervised artificial neural networks Dimensionality reduction	Variational autoencoders (VAEs) in combination with CBMs to identify biologically relevant features from microarray data [102] Autoencoders customized based on GeM models [104]
Bayesian factor model	Dimensionality reduction Identification of certain latent variables that account for data variation	Metabolic pathways analysis from gene expression data [105]
MCR-ALS	Dimensionality reduction Application of custom constraints	Pathways identification [106]

3.2.1. Applications of PCA

PCA is a dimensionality reduction method that searches for artificial latent components (principal components) that maximize data variance and are linear functions of the original variables. PCA has been applied to statistically explain the variability of metabolic fluxes and identify important metabolic pathways that are related to cellular behaviour. Barrett et al. [85] combined a transcriptional regulatory network with PCA to first identify the active reactions of a metabolic network in a defined medium and further reduce system dimensionality. A similar framework that applies PCA to fluxomic data for analysing cellular behaviour has been also presented by Gonzalez-Martinez et al. [86].

Whilst PCA is a powerful tool for dimensionality reduction and simplification of data visualization, the resulting principal components lack biologically relevant meaning. In order to overcome this limitation, principal elementary mode analysis (PEMA) has been proposed for the identification of important fluxes and metabolic pathways in E. coli cells [87]. Part of PEMA is the implementation of PCA on the elementary modes (EMs) of the metabolic model, leading to the formation of principal components that represent groups of EMs on the same metabolic pathway. Dynamic elementary mode analysis (dynEMA) has been proposed as an extension of PEMA for non-steady state fluxes [88]. In a similar manner, von Stosch et al. [89] proposed the principal EM (PEM) analysis as a computationally efficient framework for the evaluation of the EMs using a branch and bound technique that enables the reduction of EM combinations under examination. Bhadra et al. [90] proposed a hybrid of PCA and stoichiometric flux analysis, termed principal metabolic flux analysis (PMFA), that accounts for non-steady state scenarios and can be expanded to the Sparse-PMFA version of the method (components can have sparse loadings) in order to capture the variance of genome-scale gene data. PMFA successfully identified the active EMs of a P. pastoris metabolic network and was found to outperform both PEMA and PCA in predicting data variance.

Brunk et al. [91] applied PCA to time-course metabolomic data to uncover metabolic fingerprints of strains and distinct metabolic states, which the authors later utilized to further investigate strain variation using GeM. Similarly, Bordbar et al. [92] proposed a framework of unsteady-state FBA (uFBA) that incorporated PCA of time-course metabolomic data for the identification of linearized metabolic states that could be included in downstream metabolic model construction. PCA has also been used as a pre-processing dimensionality reduction step in genome-scale ML for the prediction of metabolite concentrations based on enzymatic expression levels [93]. In a study that combined bioprocess and simulated data from GeM, PCA was applied to evaluate the effect of various bioprocess parameters on cell growth and productivity [94]. The authors also extracted the 40 first principal components and used them as features for the downstream ML algorithm. Occhipinti et al. [95] applied PCA to FBA results to identify pathways that when appropriately manipulated lead to rhamnolipids (biosurfactant) overproduction in Pseudomonas aeruginosa. PCA, in combination with pseudospectra and bagplots, has also been applied for the interpretation of multi-omics metabolic models that incorporate gene expression, metabolism and codon usage [96].

3.2.2. Clustering

Clustering algorithms can be used for the identification of sub-populations and groups of either cells, genes or metabolic pathways. Segrè et al. [97] developed the Prism algorithm, an unsupervised hierarchical clustering method for the formation of gene networks where the resulting clusters interact with each other in a single way, trying to mimic the monochromatic buffering and aggravating interactions of genes. Hierarchical clustering has also been applied to identify sub-populations in gut microbia based on results from constraint-based GeMs [98]. Heatmaps of metabolomic data in combination with fluxomic data have been utilized for studying the rechannelling of metabolic fluxes under the supplementation of palmitate in hearts of diabetic mice [99]. Yaneske & Angione [100] developed personalised constraint-based metabolic models of breast cancer patients by modifying the acceptable boundaries of fluxes according to the relevant gene expression levels from transcriptomic data [101] in an effort to identify correlations between the fluxomic data and patient age. As a second step, the authors used unsupervised learning to identify the fluxes that explain most of the data variation, reduce dimensionality (PCA) and create patient groupings (k-means clustering).

3.2.3. Other unsupervised techniques

Barsacchi et al. [102] developed a deep learning framework that utilized variational autoencoders (VAEs) and GeMs in order to extract biologically relevant features from transcriptomic data, extending previous work on forming meaningful latent space from gene expression levels [103]. Autoencoders have also been used as part of DeepMetabolism, a deep learning framework that utilizes GeMs to customize the connections between the layers of the model [104], where genes are included in the input layer, proteins in the first hidden layer and the phenotype in the second hidden layer. Bayesian matrix factorization assuming Gaussian-Markov random field properties has been applied for the identification of latent pathways in fluxomic data harvested from augmented FBA modelling of transcriptomic data [105]. The Multivariate Curve Resolution – Alternating Least Squares (MCR-ALS) technique [106] has also been proposed for the decomposition of fluxomic data of a constraint-based model of P. pastoris [107].

3.3. Supervised ML applications

Supervised ML algorithms (summarised in Table 4) have largely focused on inferring the relationship between multi-omics layers such as the identification of essential genes from an array of features extracted from complex biological data [108]. Yet it has become clear that ML could also benefit from exploring different omics layers of information generated from white-box mechanistic models [109]. These include GeM and flux analyses, which represent biomolecular interactions involved in networks of biochemical reactions [17], thus contributing, in principle, albeit with added complexity, to a fuller description of topological features arising from gene expression [110]. An overview of key studies is presented in Fig. 6.

Table 4.

Supervised machine learning methods and examples of their application to bioinformatics.

Supervised ML method	Description	Strength	Weaknesses	Application examples
Linear Regression	Data Regression to its mean value Best Fit Line (Mean Pattern of the dataset) Gradient Descent Least Square Function Continuous Output Normality Assumption Linearity Assumption	Computationally inexpensive Weighed Sum Prediction Reduces complex dataset to a singular function Less prone to overfitting	Reduces larger complex dataset to a singular function Assumption of Linearity Relationship is seldom applicable Does not distinguish Outliers which might bias regression	Prediction and Evolutionary info analysis of protein structure [137] Prediction and evolutionary information analysis of protein solvent accessibility [138] Genetic Expression inference [139] Genotype Prediction based on Single Nucleotide Polymorphism [140] Prediction of protein secondary structure [141]
Logistic Regression	Extension of Linear Regression Logistic line fitting Probability modelling Non-linearity acceptance	Probability-based classification (rather than final classifications) Fast Training Extension to Multiclass Classifications Less prone to overfitting	Complex Multiplicative weighted function Complete Separation of classes Unrepresentative for classes that highly overlap	Cellular Phenotype classification based on gene expression profile [142] Gene Selection [143] Disease Classification from microarray data [144] Molecular Classification of Cancer [145]
Support Vector Machine	Hyperplane Data classification Classes separation on higher dimensionality Kernel Transformation	Easy implementation to well defined classified categories Effective in high dimensional spaces Non-linear input acceptance	Not suitable for overlapping classes Can be prone to overfitting when number of features exceeds the number of samples No probabilistic explanation for classification	Classification on Gene functional annotations from a combination of protein sequence and structure data [146] Cancer Classification from genetic expression [147] Protein subcellular classification prediction [148] Structural Classification of proteins [149]
Naïve- Bayers	Probabilistic Classification Probabilistic Bayer’s theorem Conditional Independence between variables Most used for classification	Reduced risk of overfitting on small datasets Probabilistic classification Fast training Computationally inexpensive Scales linearly	Does not incorporate feature interactions Performance sensitive to skewed data Requires assumption that variables are conditionally independent	MicroRNA target prediction [150] Prediction of Protein Interaction Sites [151] Prediction of Protein coupling specificity [152]
Decision Tree Classifier & Forest Tree	Classification or Regression modelling Parameter based Data splitting of variable with highest information gain Data entropy Information Gain Theory Gini Coefficient	Easy interpretation and analysis Valued on smaller datasets Multiclassification applicability White box model highlighting classification pattern Easily assembled	Tendency to overfit Lack of linear smoothness	Prediction of microorganism growth temperatures and enzyme catalytic optima [153] Protein Structure Prediction from enzymatic turnovers [129] Microbial Genome prediction [154] MS cancer data classification [155] Gene Selection for Cancer identification [156] Human protein function prediction [157] Prediction of Protein interaction [158]
k-NN	Classification and Regression modelling Clustering classification Instance-based learning, i.e. lazy learning Parameter selection on Kernel basis Higher dimensions for clustering	Simple to implement Learn non-linear boundary Robust to noise in input data	Inefficiency on training larger datasets Expensive computational cost K value evaluation based on mixed heuristics Unclear	Gene selection for sample classification based on gene expression data [159] Classification for Cancer diagnosis [160] Prediction of Metabolic pathways dynamics [161]

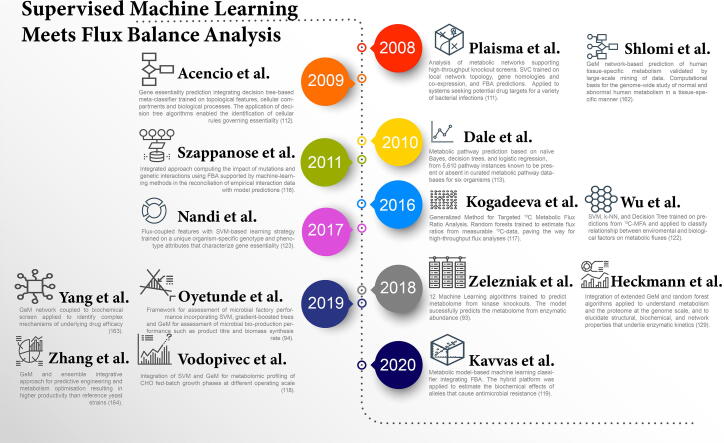
Fig. 6.

Timeline of efforts to integrate supervised machine learning with flux balance analysis. ([113], [117], [118], [119], [162], [163], [164].)

3.3.1. Gene essentiality analysis

Plaimas et al. [111] applied support vector machines (SVM) to an E. coli FBA network that incorporated both genomic and transcriptomic data to identify essential metabolic reactions and therefore essential enzymes. Acencio and Lemke [112] pushed the envelope further by training decision tree algorithms on several features including network topology, cellular compartments, and biological process information, such as cell cycle, metabolism, signal transduction, transcription, transport etc. Such a multi-faceted description not only aided the prediction of gene essentiality but also the identification of biological determinants of phenotypes. In addition, through the deconstruction of complex information by the application of decision tree classifiers, the study was able to identify cellular rules governing gene essentiality. In agreement with other studies [114], [115], the number of protein physical interactions, as the principal tree root node, was deemed the most important feature and therefore essential to algorithm performance.

Szappanos et al. [116] applied FBA to characterize gene interaction networks. In this case, a genetic algorithm was used to generate hypotheses that improved the prediction of gene interaction by reconciliating empirical interaction data with model predictions. Such a method is appealing, as it closes the gap between in silico and in vitro work. Nevertheless, and similar to previous studies [111], some of the predictions were compromised due to the inability of the FBA to capture the majority of experimentally determined genetic interactions, and the lack of regulation description at the gene expression and enzymatic reaction levels.

3.3.2. Integration with extracellular conditions

The integration of flux analysis and ML has also shown promising results in the context of analysing environmental impact on cell phenotype. Simple linear regression has been used to correctly predict E. coli growth from FBA data [120]. Zampieri et al. [121] applied supervised linear regression on gene expression profiling to estimate lactate production in CHO cells. The study successfully validated the hybrid modelling approach by comparing predicted lactate production with experimentally measured yields in a cross-validation setting. Other studies have investigated the extension of the hybrid approach to incorporate a wide description of factors ranging from the genome to the extracellular environment. For instance, Wu et al. [122] presented a web-based platform that applied an ensemble of ML techniques including SVM, k-nearest neighbours (k-NN), and decision tree, to literature data from nearly 100 ¹³C-FMA studies on heterotrophic bacteria. The approach enabled the prediction of fluxomes as a function of bacterial species, substrate type, growth rate, oxygen conditions, and cultivation methods.

In 2017, Nandi et al. [123] extended the hybrid methodology utilising SVM-based implementation for binary classification of E. coli genes based on gene sequencing and expression, network topology and flux-based features. By also accounting for environmental factors, the model was able to capture the minimal set of genes that are essential in any given environment. The model was trained on 4094 metabolic reaction–gene pairs, out of which 384 were essential, 3120 were non-essential, and for around 590 reaction–gene pairs there was no phenotype information available. In addition, the model predicted the essentiality of 317 genes previously unidentified by exhaustive genome-scale knockout experiments. Such work further highlights that the appropriate choice of features arising from the genome-phenotype configuration and their correct description improves the performance of supervised algorithms.

3.3.3. Incorporation of regulatory system features

The complexity of cellular phenotypes stems from global transcription events and their perturbation due to changes in the extracellular environment [124], [125], resulting changes in enzyme capacities as well as changes of enzyme activities through metabolite-enzyme interactions [126], but also metabolic enzyme regulation due to post-translational events such as enzyme phosphorylation [127]. Last but not least, a small subset of metabolic reactions can occur spontaneously or are mediated by small molecules [128]. This knowledge underlines how fundamentally intertwined the relationships between the different levels of omics information and data are. Recently, Zelezniak et al. [93] mapped these regulatory patterns through the combination of ML with metabolic control analysis enabling quantitative prediction of entire cell metabolomes. First, flux analysis highlighted the importance of largely overlooked mechanisms in metabolic regulation. Second, ML captured the inherently complex multifactorial relationships at protein level. As a result, the study successfully quantified the role of enzyme abundance changes in metabolic regulation. Interestingly, all kinase deletions triggered global enzymatic expression changes. In fact, the detected variation at proteomic level led to wide metabolic control shifts between different sets of enzymes. While in earlier studies supervised algorithms were trained on a limited scope of sometimes overlooked omics features, Zelezniak et al. demonstrated that the incorporation of additional omics information yields robust classifications.

Since the incorporation of proteomics has been proved essential, Heckmann et al. [129] applied such a hybrid approach to elucidate structural, biochemical and network properties that underline enzymatic kinetics. The study integrated an ensemble methodology, including random forest and neural network algorithms, to predict catalytic turnover in E. coli from enzymatic biochemistry, protein structure and FBA computations. In a similar fashion, Amin et al. [130] applied a decision tree algorithm on enzymatic promiscuity data to predict hundreds of reactions and metabolites that may exist in E. coli but may not have been accounted for in databases.

4. Summary and outlook

GeMs are indispensable for organising and analysing omics datasets for a variety of cell systems. The development of GeMs for industrially-relevant organisms routinely used for the production of high-value chemicals or recombinant protein therapeutics together with the advancement of optimisation algorithms is enabling the design of improved cell factories and production processes. This is achieved by detecting cellular and process bottlenecks and genetic engineering strategies for overcoming them, better understanding cellular physiology and identifying alternative pathways to desired phenotypes. Although generic models of model organisms are a more accurate representation of cellular mechanisms, there is also tremendous value in methodologies that support tailoring GeMs to specific cell lines as well as reducing their size to serve a specific application. This is evident by the fact that the scale and complexity of, for example, CHO cell GeMs has so far limited the application of optimisation algorithms commonly used for strain design in microbial systems like E. coli or P. pastoris. Apart from the associated computational challenges, the genetic engineering strategies returned by optimisation algorithms are also often too complex to implement experimentally. In this regard, the introduction of thermodynamic constraints can decrease the solution space. However, the lack of Gibbs free energy data for a large number of metabolic reactions has so far hampered the applicability of such model reduction algorithms to mammalian cell systems. An additional drawback is the fact that most algorithms are used to solve a steady state model whereas the actual process is inherently dynamic.

Biological knowledge does not, however, advance as quickly as the current data generation rate. Although mechanistic approaches such as stoichiometric models have long been used for understanding cell phenotype and data integration, they cannot yet capture the full information content of available omics datasets due to lack of underpinning understanding necessary for model formulation. This has led to the emergence of ML methodologies, which have found application in identifying features of gene essentiality for guiding cell engineering. Another promising development is the creation of hybrid ML/FBA formulations for dynamicising GeMs, while maintaining a lower parameter estimation burden compared to hybrid kinetic/FBA approaches. However, although studies have successfully investigated the incorporation of multiple features across omics layers, they seem to heavily rely on public domain information for data curation, which may involve error and bias. Another caveat is the danger of overfitting ML models, which can significantly limit applicability and robustness.

Without a doubt, the ever-increasing capacity for high-throughput experimentation and sample analysis renders hybrid ML/FBA modelling a promising tool for harnessing the information content of multi-omics datasets and GeMs. Within the bioprocessing industry, this could support cell line classification, and process screening, leading to accelerated host selection and process development, respectively. Despite the aforementioned limitations, the studies reviewed herein showcase the advantages of hybrid methodologies in terms of the systematic representation of feature-vector relationship and decision boundaries, when compared to individual modelling approaches, be they stochastic, deterministic or data-driven.

CRediT authorship contribution statement

Athanasios Antonakoudis: Methodology, Visualization, Writing - original draft. Rodrigo Barbosa: Methodology, Visualization, Writing - original draft. Pavlos Kotidis: Methodology, Visualization, Writing - original draft. Cleo Kontoravdi: Supervision, Writing - review & editing, Funding acquisition.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.