Compressed Sensing: From Research to Clinical Practice with Deep Neural Networks

Abstract

Compressed sensing (CS) reconstruction methods leverage sparse structure in underlying signals to recover high-resolution images from highly undersampled measurements. When applied to magnetic resonance imaging (MRI), CS has the potential to dramatically shorten MRI scan times, increase diagnostic value, and improve overall patient experience. However, CS has several shortcomings which limit its clinical translation such as: 1) artifacts arising from inaccurate sparse modelling assumptions, 2) extensive parameter tuning required for each clinical application, and 3) clinically infeasible reconstruction times. Recently, CS has been extended to incorporate deep neural networks as a way of learning complex image priors from historical exam data. Commonly referred to as unrolled neural networks, these techniques have proven to be a compelling and practical approach to address the challenges of sparse CS. In this tutorial, we will review the classical compressed sensing formulation and outline steps needed to transform this formulation into a deep learning-based reconstruction framework. Supplementary open source code in Python will be used to demonstrate this approach with open databases. Further, we will discuss considerations in applying unrolled neural networks in the clinical setting.

I. Introduction

Magnetic resonance imaging (MRI) enables non-invasive visualization of soft tissue anatomy, but is limited by long scan times and sensitivity to motion artifacts. Scan durations are directly related to the number of data samples measured; therefore, collecting fewer measurements enables faster imaging. However, sampling below the Nyquist rate will introduce aliasing artifacts which may obscure anatomy and reduce diagnostic confidence. In fully sampled imaging, trade-offs between resolution and signal-to-noise ratio (SNR) are necessary in order to achieve shorter scan times and reduce sensitivity to patient motion.

Over the past decades, constrained image reconstruction methods have been developed to enable rapid MRI techniques by leveraging prior information about the underlying signal to recover high-resolution images from relatively few measurements [1]. Compressed sensing (CS) is one such method that assumes the underlying signal to be sparse (or compressible) in some manually chosen transform domain [2]. With this assumption in mind, the signal can be iteratively recovered from highly undersampled data by solving a regularized inverse problem. Further undersampling rates are achieved by combining compressed sensing with parallel imaging [3]– [5], which leverages the localized sensitivity profiles of each receiver element in a coil array. The total scan time acceleration achieved by combined parallel imaging and compressed sensing (PICS) algorithms is powerful in enabling a broad range of clinical applications. For example, high-resolution volumetric imaging that would take minutes to acquire can now be achieved in a single breathhold [6]. This strategy minimizes the sensitivity of patient motion and increases the diagnostic quality of the resulting images.

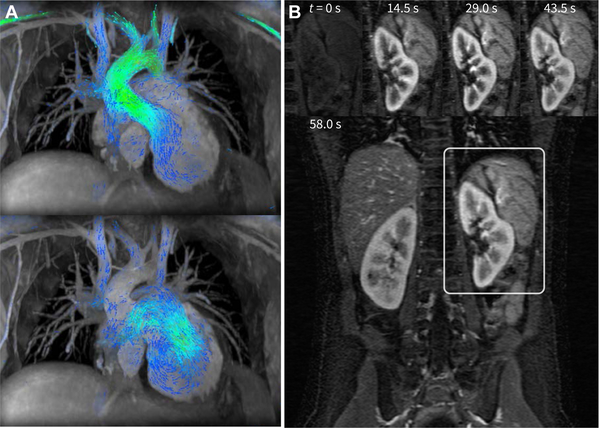
Over the past decade since compressed sensing was introduced to MRI, many developments have been made to extend this idea and bring it into clinical practice [7], [8]. One area with significant research and clinical activity is in multi-dimensional imaging. With more dimensions to exploit sparsity, the subsampling factor can be increased substantially (over 10 fold). As a result, multi-dimensional scans can be completed in clinically feasible scan times. For example, a volumetric time-resolved blood flow imaging sequence (4D flow) can be performed in a 5–10 min scan instead of an hour long scan needed to satisfy the Nyquist criterion [9]. This single 4D flow scan enables a comprehensive cardiac evaluation with flow quantification, functional assessment, and anatomical information. Instead of an hour long cardiac exam for congenital heart defect patients with complex cardiac anomalies, the exam can be completed in a simple-to-execute single 4D flow scan (Fig. 1A). Other examples of multi-dimensional compressed sensing include dynamic-contrast-enhanced imaging [10] (Fig. 1B), and “extra-dimensional” imaging with 4+ dimensions [11].

Fig. 1.

Example clinical applications of compressed sensing. In A, two cardiac phases of the cardiac-resolved volumetric velocity MRI (4D flow) are shown for the purpose of congenital heart defect evaluation. To enable a clinically feasible scan duration of 5–15 minutes while maintaining high spatial (0.9 × 0.9 × 1.6 mm³) and high temporal resolutions (22.0 ms), a subsampling factor of 15 was used [9]. In B, high spatial (1 × 1 × 2 mm³) with a 14.5-s temporal resolution was achieved for a dynamic contrast enhanced MRI using an acceleration factor of 6.5 [10]. High spatiotemporal resolutions are required for capturing the rapid hemodynamics of pediatric patients.

Additionally, rapid imaging has significant impact on the clinical workflow. Exam times can be significantly shortened to reduce patient burden and discomfort. For pediatric imaging, the shortened exam time enables the reduction of the depth and length of anesthesia [7]. For extremely short scan times (less than 15 minutes), anesthesia can entirely eliminated.

A. Remaining Challenges

Much success has been observed by applying compressed sensing to specific clinical applications such as for pediatric imaging [7] or for volumetric cardiac imaging [8]. However, the potential that compressed sensing brings is not fully realized in terms of maximal acceleration and breadth of applications. A number of challenges limit the use of compressed sensing for clinical practice.

In compressed sensing, the regularization function is typically designed to promote sparsity of the signal in a manually chosen transform domain, such as Wavelet or finite differences [2]. However, depending on the choice of transform, this assumption may not accurately model the underlying distribution of the data. For example, finite difference constraints (also known as total variation) can be used to dramatically reduce noise-like aliasing artifacts from the reconstructed images [12], but rely on the assumption that the image consists of piece-wise constant regions. For high undersampling rates, this can lead to unrealistic looking reconstructions with a cartoon-like appearance. More complex priors are highly desirable in order to sufficiently represent the complexity of the target data.

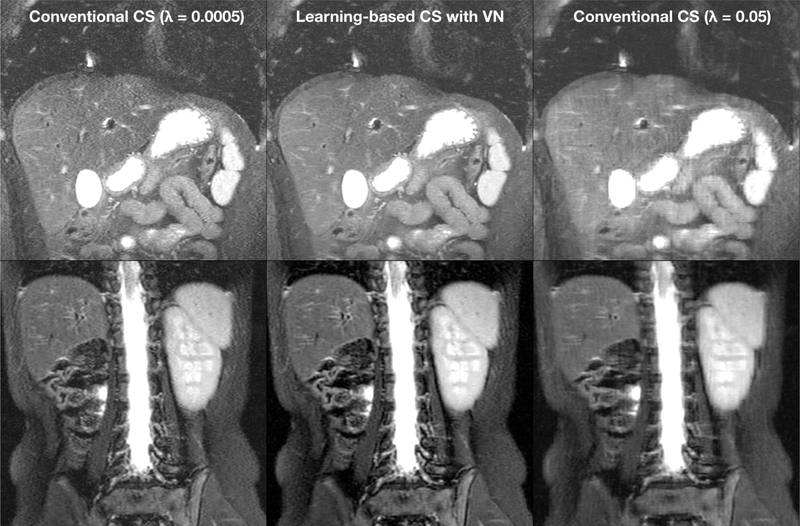
Second, compressed sensing is sensitive to tuning various optimization parameters. One example of these parameters is the regularization parameter, which determines the weight of the regularization term with respect to the data consistency term in the optimization’s objective. Increasing the regularization parameter will improve the perceived SNR of reconstructed images. However, while the perceived SNR improves, fine structures in the reconstructed images may be over-smoothed, or new image textures may be introduced, resulting in an artificial appearance of images. For high subsampling factors, the optimal value of the regularization parameter can vary among scans and patients making manual parameter tuning infeasible. The impact of the regularization parameter on the reconstruction performance is illustrated in Fig. 2.

Fig. 2.

Example results of compressed sensing (CS) and variational network (VN) reconstructions of 3.25X subsampled data acquired with a 32-channel torso coil [13], [14]. Conventional compressed sensing requires tuning of the regularization parameter λ. The optimal value of this parameter may vary with different scans. Compared to conventional CS using L1-ESPIRiT [5] (left and right columns), learning a VN (middle column) achieves proper regularization without the need of manual tuning the regularization parameter.

Lastly, compressed sensing usually has long reconstruction times due to use of iterative optimization algorithms. To achieve clinically acceptable image quality, the number of iterations may vary between 50 to over 100 depending on acquisition parameters [15]. For this reason, the number of iterations is set conservatively high to ensure convergence for various sets of acquisition parameters. Even with GPU acceleration, reconstruction times can vary from several minutes to over an hour depending on dataset size, dimensionality, and spatial encoding scheme. Long reconstruction times further lead to delays and queues in clinical workflows, as well as require expensive dedicated computational hardware.

B. Current Solutions

Much research has attempted to solve these challenges. The performance of compressed sensing is highly dependent on the regularization function and regularization parameters used. To reduce textural artifacts and bias, the regularization needs to be carefully chosen and hand-tuned for each application. Another class of constrained reconstruction methods which leverage low-rank structure in the underlying signal was concurrently developed with sparse CS [16]. In contrast to sparsity-based constraints which are enforced in a pre-selected transform domain, low-rank constraints are adaptive and depend on the subspace characteristics of each dataset. These methods are highly suitable for certain dynamic imaging applications, but can produce over-smoothed images when the underlying signals are not rank-deficient. Low-rank constraints have since been combined with sparsity-based constraints to achieve more expressive regularization functions [17]. However, these methods require extensive parameter tuning for each additional constraint.

Typically, the regularization parameter is fixed for all scans based on empirical tuning within a small number of datasets. This approach is shown to be effective for moderate subsampling rates across many patients in large clinical studies [7], [8]. Ideally, the regularization parameters should be chosen for each scan based on the system noise. However, many other factors such as patient motion contribute to measurement error. Previous works have shown that automatic parameter selection for each patient can improve image quality of compressed sensing reconstructions [18]. This comes at the cost of additional reconstruction time; as a result, automatic parameter selection is uncommon in practice.

In regards to reconstruction times, preconditioning techniques can reduce the number of iterations necessary for algorithmic convergence, but often require more computations per iteration [19]. Further acceleration in reconstruction time can be achieved by early truncation of the iterative reconstruction [20].

Most of these solutions require manual adjustment of the original compressed sensing problem to specific applications. This tuning and redesigning process requires extra time and effort, and constant attention as hardware and clinical protocols evolve. Previous solutions to automate some of this process involve additional memory and more complex computations.

C. Overview

To overcome the obstacles with compressed sensing, deep learning has recently become a compelling and practical approach [13], [14], [21]–[25]. The purpose of this tutorial is to review an existing framework for extending compressed sensing to a deep learning-based approach using unrolled neural networks. We also discuss a number of new challenges when using this framework including considerations for clinical deployment. We have released supplementary python code on GitHub¹ to demonstrate an example of this deep learning-based compressed sensing framework.

II. Unrolled Compressed Sensing

A. Background

The MRI reconstruction problem can be formulated as a minimization problem [2]. The optimization consists of solving the following equation:

$$\widehat{m}=\underset{m}{\arg \min }\frac{1}{2}\Vert Am-y{\Vert }_2^2+\text{λ}R(m)$$ (1)

where m is the reconstructed image set, A describes the imaging model, and y is the measured data in the k-space domain. The imaging model for MRI consists of signal modulation by coil sensitivity profile maps S, Fourier transform operation, and data subsampling. These sensitivity profile maps S are specific for each dataset y.

The goal of this optimization is to reconstruct an image set m that best matches the measured data y in the least squares sense. For highly subsampled datasets, this problem is ill posed — many solutions satisfy Eq. 1; thus, the regularization function R(m) and corresponding regularization parameter λ incorporate image priors to help constrain the problem. In CS, the regularization function is designed to promote transform sparsity in the optimal solution. Many optimization algorithms have been developed to solve the minimization problem in Eq. 1. For simplicity, we base our discussion on the proximal gradient method. We refer the reader to similar approaches based on other optimization algorithms [13], [21], [24].

To solve Eq. 1, we split the problem into two alternating steps that are repeated. For the k-th iteration, a gradient update is performed as

$$m^{(k+)}=m^{(k)}-2t{A}^H(A{m}^{(k)}-y),$$ (2)

where A^H is the transpose of the imaging model, and t is a scalar specifying the size of the gradient step. The current guess of image m is denoted here as m^(k+). Afterwards, the proximal problem with regularization function R is solved:

$$m^{(k+1)}={\mathbf{prox}}_{\lambda R}\left(m^{(k+)}\right)=\arg \underset{u}{\min }R(u)+\frac{1}{2t\text{λ}}{\Vert u-m^{(k+)}\Vert }_2^2,$$ (3)

where u is a helper variable that transforms the regularization into a convex problem that can be more readily solved. The updated guess of image m at the end of this k-th iteration is denoted as m^(k+1), and m^(k+1) is then used for the next iteration in Eq. 2. This proximal problem is a simple soft-thresholding step for specific regularization functions such as R(m) = ‖Ψm‖₁ where Ψ is a Wavelet transform [20].

B. Data-Driven Learning

To be able to develop fast and robust reconstruction algorithms for different MRI sequences and scans, a compelling alternative is to take a data-driven approach to learn the optimal regularization functions and parameters. Some approaches have attempted to directly learn a parameterized form of the regularization function using a field-of-experts model [13], [14]. This tutorial focuses on a different approach, which is to learn the proximal step in Eq. 3 and therefore implicitly learn both the regularization function and regularization parameter. In this setup, as described by Refs. [22], [23], [26], the proximal step is replaced with a deep neural network which is capable of learning a more natural regularization function than transform sparsity. With this in mind, the proximal update step in Eq. 3 can be re-written as:

$$m^{(k+1)}=E_{{\theta }_k}\left(m^{(k+)}\right).$$ (4)

where E_θk is the neural network and θ_k are the learned parameters.

The steps of Eqs. 2 and 4 can be unrolled with a fixed number of iterations [27] and be denoted as model G_θ (y, A) with inputs of measurements y and imaging model A. The training of such a model can then be performed using the following loss function:

$$\underset{\theta }{\min }\sum _i{\Vert G_{\theta }(y_i,A_i)-m_i\Vert }_2^2,$$ (5)

where m_i is the i-th ground truth example that is retrospectively subsampled by a sampling mask M in the k-space domain to generate y_i = M $A_i^H$ m_i. For deployment, new scans are acquired according to the sampling mask M, and the measured data y_i can be used to reconstruct images ${\hat{m}}_i$ as

$${\widehat{m}}_i=G_{\theta }(y_i,A_i),$$ (6)

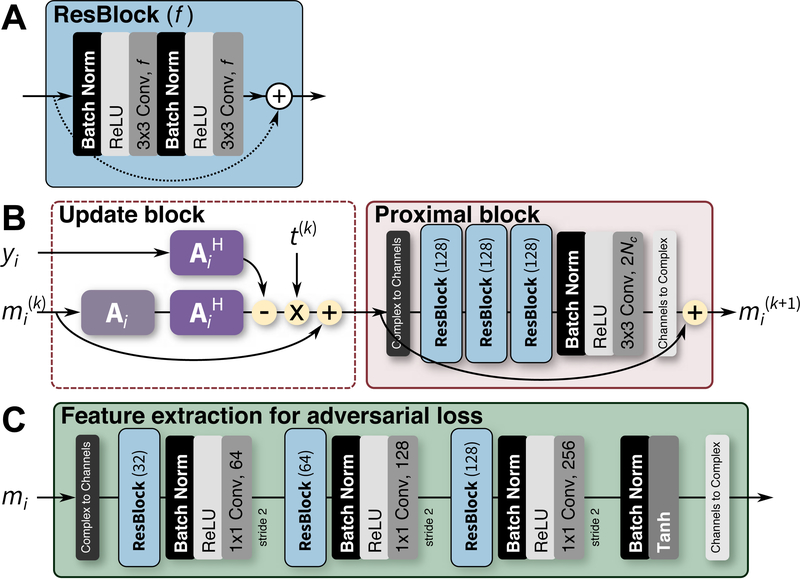
where A_i contains sensitivity profile maps S_i that can be estimated using algorithms like JSENSE [4] or ESPIRiT [5]. An example network is shown in Fig. 3AB.

Fig. 3.

Neural network architecture for MRI reconstruction. One residual block (ResBlock) [28] is illustrated in A with f feature maps. The ResBlock is used as a building block for the different networks. In B, one iteration of the reconstruction network is depicted where the i-th dataset is passed through the k-th iteration. Matrix A_i represents the imaging model, m_i represents the dataset in the image domain, and y_i represents the dataset in the k-space domain. The final output can be passed through the network in C to extract feature maps that can be compared to the feature maps extracted from the ground truth data using the same network. The tanh activation function in C is used to ensure that the values in the outputted feature maps are within ±1.

C. Neural Network Design for Unrolled MRI Reconstruction

Important considerations must be made when applying deep neural networks to MRI reconstruction. This includes handling of complex data [29], circular convolutions in image domain for Cartesian data [24], and incorporating the acquisition model [13].

Since the data measured during an MRI scan is complex, complex data is used for the MRI reconstruction process. As a result, the networks used for MRI reconstruction need to handle complex data types. Two approaches can be used to solve this issue. The first approach is to convert the complex data into two channels of data. This conversion can be performed as concatenating the magnitude of the data with the phase of the data in the channels dimension, or concatenating the real component with the imaginary component of the data in the channels dimension. The second approach is to build the neural network with operations that directly support and exploit structure in complex data. Several efforts have been made to enable complex operations in the convolutional layers (with complex back-propagation) and the activation functions [29]. For demonstration purposes, we construct the networks in Fig. 3BC with the first approach because of its simplicity.

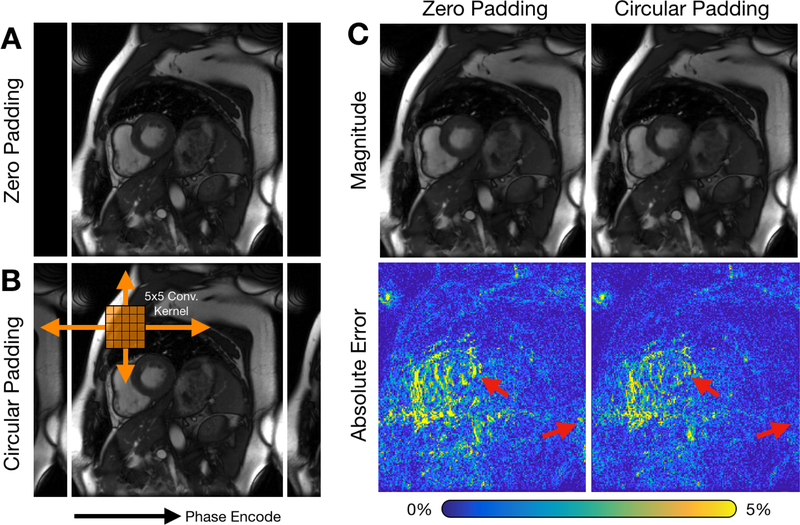
Another consideration in building neural networks for MRI reconstruction is handling the convolutional operation at the image edges. Assuming zeros beyond the image edges for image-domain convolutions is sufficient for most cases, especially when the imaging volume is surrounded by air and when no high-intensity signal exists near the edges of the field-of-view (FOV). However, when these conditions are not satisfied, this assumption may result in residual aliasing artifacts. These artifacts are usually observed when the imaging object is larger than the FOV. In Cartesian imaging, data are measured in the Fourier space and transformed using the fast Fourier transform algorithm (FFT) to the image domain; as a result, signals are circularly wrapped. Thus, circular convolutions should be performed when applying convolutions in the image domain. For this purpose, we first circularly pad the images before applying the convolutional layers (Fig. 4B). The padding width is set such that the “valid” portion of the output has the same image dimensions as the input. Note that for data acquired using non-Cartesian trajectories, such as radial or spiral, signal outside of the FOV will instead manifest as noise-like artifacts across the image. In these cases, circular padding should not be used.

Fig. 4.

Circular convolutional layer for MRI reconstruction. Current deep learning frameworks support zero-padding for convolutional layers (shown in A) to maintain the original dimensions. However, data are measured in the frequency space, and the FFT algorithm is used to convert this data into the image domain. Thus, for Cartesian imaging, circular convolutions should be performed. This circular convolution can be performed by first circularly padding the input data as shown in B and cropping the result to the original input dimension. For cardiac cine imaging, images can also be circular padded in time to take advantage of cyclical dynamics such as heart motion. Examples of 8X subsampled datasets reconstructed using a 3D unrolled neural network with and without circular spatiotemporal padding are shown in C. Images reconstructed with circular convolutions depict reduced error at image edges and heart tissue at end-systole (red arrows).

Leveraging a more accurate MRI acquisition model in the neural network will improve the reconstruction performance and simplify the network architecture. More specifically, data are measured using multi-channel coil receivers. The sensitivity profile maps of the different coil elements can be leveraged as a strong prior to help constrain the reconstruction problem. Further, by exploiting the (soft) SENSE model [5], the multi-channel complex data (y) are reduced to a single-channel complex image (m) before each convolutional network block denoted as the proximal block in Fig. 3B. As a further benefit, the learned network can be trained and applied to datasets with different numbers of coil channels, because the input to the learned convolutional network block only requires a single-channel complex image.

D. Training Data

Reconstructed image quality can vary depending on the quality, authenticity, and diversity of the training data used to train the network. Therefore, it is important to consider how training data is collected, pre-processed, and augmented.

Training data should be collected at the point in the imaging pipeline where the model will be deployed. For the purpose of image reconstruction of subsampled datasets, we would need to collect the raw measurement k-space data. Typically, raw imaging data are not readily available as only magnitude images are saved in DICOM format and stored in hospital imaging databases. Furthermore, these stored magnitude images are often processed with image filters which can bias network outputs. Additionally, accurate simulation of raw imaging data from DICOM images is difficult to perform if not impossible especially in simulating realistic phase information. To facilitate development, a number of different open data initiatives have been recently launched, including mridata.org [30] and fastMRI [31]. These resources provide an initial starting point for development, but more datasets of varying acquisition parameters, field strengths, and vendors are needed.

Data augmentation strategies should be used during training to prevent overfitting to the original training dataset. However, care must be taken when applying data augmentation transformations. For example, data interpolation is needed for random rotations which may degrade the quality of the input data. Other image domain operations may introduce unrealistic errors in the measurement k-space domain, such as aliasing in the k-space domain. Flipping and transposing the dataset will preserve the original data quality; thus, these operations can be included in the training.

Finally, data normalization strategies can help improve the training and the final performance of the learned model. For simplicity, the raw measurement data can be normalized according to the L2 norm of the central k-space signals. In our demonstration, we normalize the input data by the L2 norm of the central 5 × 5 region of k-space. Due to similarities to compressed sensing algorithms, training convergence and reconstruction accuracy may be improved by data pre-whitening and normalization by an estimate of the noise statistics among different coil array receivers. These noise statistics can be measured with a fast calibration scan during which data are measured with no RF excitation.

E. Loss Function

The performance of unrolled CS is highly dependent on the loss function used. The easiest loss functions to use for training are L1 and L2 losses. The L2 loss is described in Eq. 5 and can be converted to an L1 loss by using the L1 norm instead of the L2 norm.

L1 and L2 losses have been previously used to successfully train supervised reconstruction networks [13], [23]. Alternative loss functions that further capture the idea of structure or perception have also been studied in the literature. For example, a perceptual loss function can be constructed using a network pre-trained on natural images to extract “perceptual” features [32]. Though general, this feature extraction network should be trained for the specific problem domain and the specific task at hand. Generative adversarial networks (GANs) [33] can be used to model the properties of the ground truth images and to exploit that information for improving the reconstruction quality.

A feature extraction network D_ω (m), shown in Fig. 3C, is trained to extract the necessary features to compare the reconstruction output with the ground truth. The training loss function in Eq. 5 becomes:

$$\underset{\theta }{\min }\underset{\omega }{\max }\sum _i{\Vert D_{\omega }\left(G_{\theta }\left(y_i,A_i\right)\right)-D_{\omega }\left(m_i\right)\Vert }_2,$$ (7)

where parameters ω are optimized to maximize the difference between the reconstructed image G_θ (y_i, A_i) and the ground truth data m_i. At the same time, parameters θ are optimized to minimize the difference between the reconstruction and the ground truth data after passing both these images through network D_ω to extract feature maps. The optimization of Eq. 7 consists of alternating between the training of parameters ω with θ constant and the training of parameters θ with ω constant. We refer to this training approach as training with an “adversarial loss.”

This min-max loss function in Eq. 7 can be unstable and difficult to train. Two main components have been described by Ref. [33] to help stabilize the training. First, G_θ is pre-trained using either an L1 or L2 loss so that the parameters in this network are properly initialized. The network is then fine tuned with the adversarial network using a reduced training rate. Second, a pixel-wise cost function is added to Eq. 7:

$$\underset{\theta }{\min }\underset{\omega }{\max }\sum _i\mu {\Vert D_{\omega }\left(G_{\theta }\left(y_i,A_i\right)\right)-D_{\omega }\left(m_i\right)\Vert }_2^2+{\Vert G_{\theta }\left(y_i,A_i\right)-m_i\Vert }_2^2.$$ (8)

The images before passing through D_ω can be considered as additional feature maps to help stabilize the training process. The hyperparameter μ is used to weigh between the two components in the loss function, and must be heuristically tuned during the training phase.

III. Demonstration

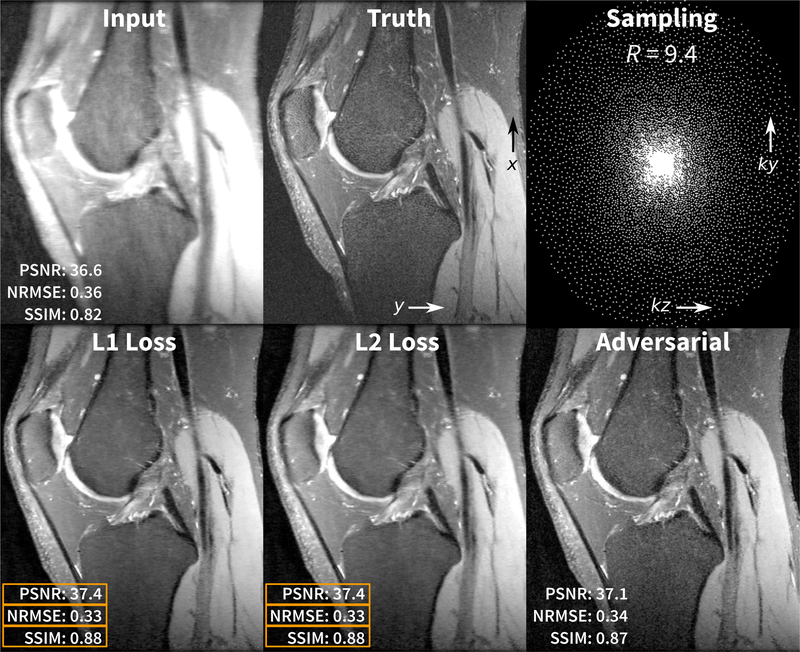
For demonstration of the unrolled CS reconstruction and for enabling reproducibilty of the results, we downloaded 20 fully sampled volumetric knee datasets that are freely available in the database of MRI raw data, mridata.org [30]. Each volume was collected with an 8-channel knee coil, proton density weighting, 320 slices in the readout direction in x, and each of these x-slices were treated as separate examples during training and validation. The datasets were divided by subject: 15 subjects for training (4800 x-slices), 2 subjects for validation (640 x-slices), and 3 subjects for testing. Sensitivity maps were estimated using JSENSE [4]. Poisson-disc sampling masks [2] were generated using an acceleration factor R of 9.4 with corner cutting (effective R of 12) and a fully-sampled calibration region of 20 × 20.

The networks in Fig. 3 were implemented in Python using the TensorFlow framework. Additional reconstruction components were performed using the SigPy Python package². The reconstruction network was built using 4 iterations; this setup allowed for relatively faster training for demonstration purposes. Performance can be improved by increasing the number of iterations. Training and experiments were performed on a single NVIDIA Titan Xp graphics card with 12GB of memory which supported a batch size of 2. The network was trained multiple times using different loss functions: an L1 loss for 20k steps and L2 loss for 20k steps. For adversarial loss, the network was first pre-trained using an L1 loss for 10k steps and then jointly trained with the adversarial loss and an L1 loss for 60k steps (10k steps were for the reconstruction network and 50k steps were for the adversarial feature extraction network). The data preparation, training, validation, and testing python scripts are available on GitHub. Example results are shown in Fig. 5.

Fig. 5.

Demonstration results of a volumetric knee dataset that is subsampled with an acceleration factor R of 9.4 with corner cutting (effective R or 12). In the bottom row, the volume was reconstructed slice by slice using three networks trained with different loss functions. The reconstruction using the network trained using the L1 and L2 losses yielded the best results in terms of PSNR, NRMSE, and SSIM. However, the reconstruction using the network trained with the adversarial loss yielded results with most realistic texture.

IV. Clinical Integration

A. Example Setup

Many of these algorithms are computationally intensive, but these algorithms can leverage off-the-shelf consumer hardware. The bulk of the computational burden is now in the network, and graphic processing units (GPUs) can be leveraged for this purpose. The compute system only needs the minimal central processing unit (CPU) and memory requirements to support the GPUs. Using an NVIDIA Titan Xp graphics card, one 320 × 256 slice took on average 0.1 seconds to reconstruct, 1.8 seconds for a batch of 16 slices, and a total of 36.0 seconds for the entire volume with 320 slices. These benchmarks include the time to transfer the data to and from the CPU to the GPU. The computational speed can be further improved using newer GPU hardware and/or more cards. Alternatively, inference on the reconstruction network can be performed on the CPU to be able to leverage more memory in a more cost effective manner, but this setup comes with slower inference speed.

B. Clinical Cases

Through initial developments, we have deployed a number of different models at our clinical site. Example results of unrolled compressed sensing with variational networks (VN) [13], [14] are shown in Fig. 2. Conventional compressed sensing using L1-ESPIRiT [5] achieved high noise when the regularization parameter was too low (0.0005, left column in Fig. 2), and high residual and blurring artifacts when the regularization parameter was too high (0.05, right column in Fig. 2). The optimal value of the regularization parameter may vary with different scans. Compared to conventional compressed sensing, learning a VN (middle column in Fig. 2) achieved proper regularization without the need to tune the regularization parameter.

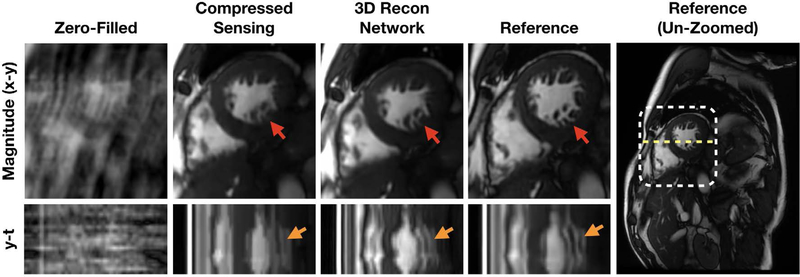
The best image prior for multi-dimensional imaging is more difficult to engineer, but these larger datasets benefits tremendously from subsampling due to long acquisition times. Thus, for multi-dimensional space, a compelling approach is to use data-driven learning. In Fig. 7, a reconstruction network consisting of 3D spatiotemporal convolutions was trained on 12 fully-sampled, breath-held, multi-slice cardiac cine datasets acquired with a balanced steady-state free precession (bSSFP) readout at multiple scan orientations. The reconstruction network enabled the acquisition of a cine slice in a single heartbeat and a full stack of cine slices in a single breathhold [34].

Fig. 7.

Clinical deployment of a 3D spatiotemporal convolutional reconstruction network for two-dimensional cardiac-resolved imaging. Above, a prospectively acquired short-axis dataset acquired with with 11.6 fold subsampling using a 32-channel cardiac coil was reconstructed using compressed sensing (L1-ESPIRiT) [5] and a trained 3D reconstruction network. These reconstructions were compared with the fully sampled reference images (acquired in a separate scan). The 3D network was able to reconstruct fine structures such as papillary muscles and trabeculae with less blurring than L1-ESPIRiT (red arrows). Furthermore, y-t profiles (plotted along yellow dotted line) show that the 3D network images depict more natural cardiac motion compared to L1-ESPIRiT with total variation, which introduced staircasing artifacts (orange arrows).

C. Evaluation

For development and prototyping, image metrics provide a straightforward method to evaluate performance. These metrics include peak signal-to-noise ratio (PSNR), normalized root-mean-square error (NRMSE), and structural similarity (SSIM). These metrics are described in the Appendix. However, what is more important in the clinical setting is the ability for clinicians to make an informed decision. Therefore, we recommend performing clinical studies.

For comparing methods, the evaluation of clinical studies can be performed with blinded grading of image quality by multiple radiologists. This evaluation can be based on set criteria including overall image quality, perceived signal-to-noise ratio, image contrast, image sharpness, residual artifacts, and confidence of diagnosis [14]. Scores from 1 to 5 or −2 to 2 are given for each clinical patient scan with a specific definition for each score for objectivity. An example of scoring for signal-to-noise ratio and image sharpness is described in Table I.

TABLE I.

Example scoring criteria to evaluate methods.

Score	Overall Image Quality	Signal-to-Noise Ratio	Sharpness
1	Nondiagnostic	All structures appear to be too noisy.	Some structures are not sharp on most images.
2	Limited	Most structures appear to be too noisy.	Most structures are sharp on some images.
3	Diagnostic	Few structures appear to be too noisy on most images.	Most structures are sharp on most images.
4	Good	Few structures appear to be too noisy on a few images.	All structures are sharp on most images.
5	Excellent	There is no noticeable noise on any of the images.	All structures are sharp on all images.

A total number of more than 20 consecutive scans are usually collected to achieve a comprehensive and statistically meaningful evaluation for an initial study. The difference between two reconstruction approaches can be statistically tested with Wilcoxon tests on the null hypothesis to show that there is no significant difference between two approaches. The Wilcoxon test is a non-parametric statistical test that evaluates the null hypothesis that the scores from the two different reconstructions are from the same distribution. Ideally, the new reconstruction algorithm should yield results that are from a different distribution compared to the original algorithm.

V. Discussion

This data-driven approach to accelerated imaging has the potential to eliminate many of the challenges associated with compressed sensing, including the need to design hand-crafted priors and to hand tune the regularization functions. In addition, the described framework inspired by iterative inference algorithms provides a principled approach for designing reconstruction networks [22]. However, the data-driven reconstruction framework faces new challenges, including data scarcity, generalizability, reliability, and meaningful metrics.

High quality training labels, or fully sampled datasets, are scarce especially in the clinical settings where patient motion impacts image quality and where lengthy fully-sampled acquisitions are impractical to perform if a faster solution exists. To address data scarcity, an important future direction pertains to designing compact network architectures that are effective with small training labels and are possibly trained in an unsupervised fashion. Early attempts are made in [26] where recurrent neural networks are leveraged for learning proximal operators using only a couple of residual blocks that performs well for small training sample sizes.

While neural networks do not need to be manually hand-tuned scan-to-scan like in conventional compressed sensing approaches, they may need to be re-trained or fine-tuned for each application to maximize performance. Knoll, et al. showed that reconstructed image quality is negatively impacted when a network is applied to data acquired with different SNR from that of the training data [35]. Since SNR can vary drastically across different applications, the network’s ability to generalize will depend on the heterogeneity of the noise statistics in the training data. To improve generalizability, the network can be re-trained or fine-tuned on heterogeneous data acquired with the SNR and acquisition parameter range of interest. However, this strategy requires sufficient training datasets for all different settings to be readily available.

Given the scarcity of training examples and the cost to collect these examples, another strategy is to design and train networks that are highly generalizable. This generalizability can be achieved with smaller networks as discussed before or by training with a larger image manifold such as using natural images. With this approach, a loss in performance may be observed since a larger than necessary manifold is learned [36]. In the worst case, the images reconstructed using this data-driven approach should not be worse than images reconstructed using a more conservative approach such as zero-filling or parallel imaging [3], [5].

Regarding generalizability, an important question concerns reconstruction performance for subjects with unseen abnormalities. Patient abnormalities can be quite heterogeneous, and these abnormalities are rare and unlikely to be included in the training dataset. If not designed carefully, generative networks have the possibility of removing or creating critical features that will result in misdiagnosis. The optimization-based network architecture utilizes data consistency, as exemplified by the gradient update step, for the image recovery problem. However, the inherent ambiguity of ill-posed problems does not guarantee faithful recovery. Therefore, a systematic study is required to analyze the recovery of images. Also, effective regularization techniques (possibly through adversarial training) are needed to avoid missing important diagnostic information. More efforts are needed to develop a holistic quality score capturing the uncertainty in the acquisition scheme and training data.

Developing a standard unbiased metric for medical images that assesses the authenticity of medical images is extremely important. Here, we discuss the use of different loss functions to train the network and common imaging metrics to evaluate the images. Additionally, we discuss an example of a possible clinical evaluation that can be performed to assess the algorithm in the clinical setting. However, the reconstruction task should ideally be optimized and evaluated for the end task which can consist of detection and quantification. With significant effort in automating image interpretation, this data-driven framework provides an opportunity to pursue the ability to train the reconstruction end-to-end for the ultimate goal of improving patient care.

In conclusion, deep learning has the potential to increase the accessibility and generalizability of rapid imaging through data subsampling. Previous challenges with compressed sensing can be approached with a data-driven framework to create a solution that is more readily translated to clinical practice.

Fig. 6.

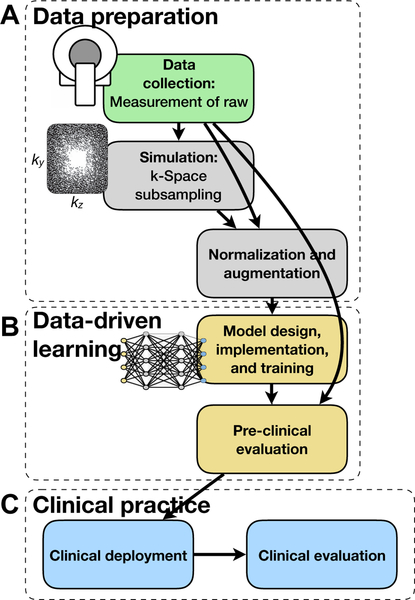
Example development cycle for the data-driven learning framework. In A, fully sampled raw k-space datasets are first collected and used to perform realistic simulation of subsampling. The reconstruction algorithm is then built, trained, and internally validated in B. Lastly, the reconstruction model is deployed and clinically evaluated in C.

Biography

Christopher Sandino (sandino@stanford.edu) is a Ph.D. candidate in electrical engineering at Stanford University. He is interested in applying deep learning methods to dynamic magnetic resonance imaging techniques to reduce scan time and image artifacts. Previously, he earned his bachelor’s degree in electrical engineering at University of Southern California.

Joseph Y. Cheng (jycheng@stanford.edu) received his B.S. and M.Eng degrees from the Department of Electrical Engineering & Computer Science at the Massachusetts Institute of Technology. He then received his Ph.D. degree from the Department of Electrical Engineering at Stanford University. He is currently a Senior Research Scientist in the Department of Radiology at Stanford University. His current research interests is in the development and application of deep learning to medical imaging.

Feiyu Chen (feiyuc@stanford.edu) received his Ph.D. in electrical engineering at Stanford University. He is interested in applying deep learning methods to magnetic resonance imaging. His other interests include designing new sampling schemes and developing new pulse sequences for magnetic resonance imaging. Previously, he earned his bachelor’s degree at Tsinghua University.

Morteza Mardani (morteza@stanford.edu) is a Research Scientist at the Stanford University, Departments of Electrical Engineering and Radiology. He received his Ph.D. in Electrical Engineering and Mathematics (minor) from the University of Minnesota, Twin cities, 2015. He was then a visiting scholar at the Electrical Engineering & Computer Science, UC Berkeley, Jan.–Jun. 2015, and then a Postdoctoral Fellow at Stanford University until Dec. 2017. His research interests lie in the area of machine learning and statistical signal processing for data science and artificial intelligence, where he is currently working on deep learning and generative adversarial neural networks for medical imaging. He is recipient of a Young Author Best Paper Award from IEEE Signal Processing Society (2017), and a Best Student Paper Award from IEEE Workshop on Signal Processing Advances in Wireless Communications (2012).

John M. Pauly (pauly@stanford.edu) received his Ph.D. in Electrical Engineering from Stanford University and is a Professor in the Department of Electrical Engineering at Stanford University. In 2012, he was awarded with the highly prestigious Gold Medal from the International Society of Magnetic Resonance in Medicine. He co-directs the Magnetic Resonance Systems Research Laboratory.

Shreyas S. Vasanawala (vasanawala@stanford.edu) is a Professor in the Department of Radiology at Stanford University. He received his bachelor’s degree in mathematics from Caltech, and then completed his M.D. medical training and Ph.D. at Stanford University. His research efforts are focused on developing fast and quantitative MRI methods. He serves as the Director of MRI at Stanford Hospital and Clinics and at Stanford Children’s. He also serves as the division chief of Body MRI.

Appendix

Appendix: Imaging Metrics

Imaging metrics are commonly used to evaluate results. This includes peak signal-to-noise ratio (PSNR) and normalized root-mean-square error (NRMSE). For these quantities, we use the following equations:

$$\mathrm{MSE}(x,x_r)=\frac{1}{NM}\sum _i^N\sum _j^M{|x[i,j]-x_r[i,j]|}^2,$$ (9)

$$\mathrm{PSNR}(x,x_r)=10{\log }_{10}(\max ({|x_r|}^2)/\text{MSE}),$$ (10)

$$\text{NRMSE}(x,x_r)=\sqrt{\text{MSE}}/\sqrt{\frac{1}{NM}\sum _i^N\sum _j^M{|x_r[i,j]|}^2},$$ (11)

where x denotes the test image, x[i, j] denotes the value of the test image at pixel (i, j), and x_r denotes the reference ground truth image.