Spatial inequalities of COVID-19 mortality rate in relation to socioeconomic and environmental factors across England

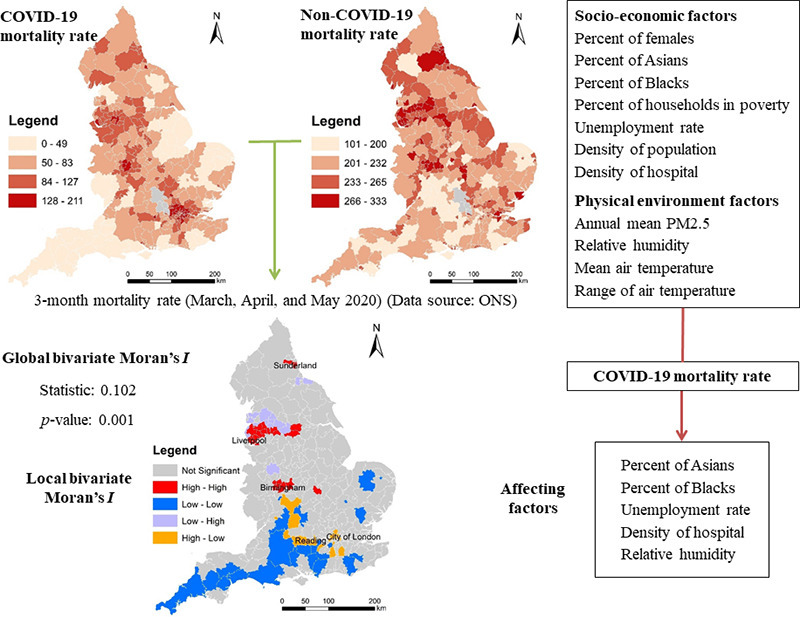
Abstract

In this study, we aimed to examine spatial inequalities of COVID-19 mortality rate in relation to spatial inequalities of socioeconomic and environmental factors across England. Specifically, we first explored spatial patterns of COVID-19 mortality rate in comparison to non-COVID-19 mortality rate. Subsequently, we established models to investigate contributions of socioeconomic and environmental factors to spatial variations of COVID-19 mortality rate across England (N = 317). Two newly developed specifications of spatial regression models were established successfully to estimate COVID-19 mortality rate (R² = 0.49 and R² = 0.793). The level of spatial inequalities of COVID-19 mortality is higher than that of non-COVID-19 mortality in England. Although global spatial association of COVID-19 mortality and non-COVID-19 mortality is positive, local spatial association of COVID-19 mortality and non-COVID-19 mortality is negative in some areas. Expectedly, hospital accessibility is negatively related to COVID-19 mortality rate. Percent of Asians, percent of Blacks, and unemployment rate are positively related to COVID-19 mortality rate. More importantly, relative humidity is negatively related to COVID-19 mortality rate. Moreover, among the spatial models estimated, the ‘random effects specification of eigenvector spatial filtering model’ outperforms the ‘matrix exponential spatial specification of spatial autoregressive model’.

Graphical abstract

1. Introduction

COVID-19 infection and mortality are gaining increasingly attentions from both policymakers and researchers. Owing to privacy protection individual-level COVID-19 data are not publicly available, aggregate COVID-19 data plays a key role in COVID-19 research. Recently, aggregate-level geocoded or georeferenced COVID-19 mortality data in some countries or regions have been released as well. Therefore, geovisualisation and spatiotemporal analysis of COVID-19 mortality rate are performable. As empirical evidence on the association of socioeconomic and environmental factors and a variety of health outcomes have been found, we could speculate that spatial variations of COVID-19 mortality rate might be associated with spatial variations of socioeconomic and environmental characteristics (e.g., Ji et al., 2020; Yao et al., 2020; Coker et al., 2020) and this speculation could be empirically validated by geographically aggregated COVID-19 death data.

In this study, we aimed to examine spatial inequalities of COVID-19 mortality rate in relation to spatial inequalities of socioeconomic and environmental factors. Specifically, we first explored spatial patterns of COVID-19 mortality rate in comparison to non-COVID-19 mortality rate. Subsequently, we modelled spatial variations of COVID-19 mortality rate from local-scale socioeconomic and environmental characteristics. Empirically, we used the England-wide COVID-19 mortality rate data aggregately collected from March to May of 2020. These 3 months are experiencing most fast-growing deaths duo to COVID-19 in England. England is chosen as the empirical study area because 1) England is one of the most serious countries in Europe according to either number of COVID-19 cases or number of COVID-19 deaths; 2) local-scale COVID-19 mortality data, socioeconomic data, and environmental data across England are publicly available.

This study can offer more evidence on the associations of COVID-19 mortality rate, socioeconomic and environmental factors. An understanding of spatial inequalities of COVID-19 mortality rate in relation to socioeconomic and environmental characteristics can inform policymakers to prioritise areas with a lower socioeconomic status or a lower environmental quality (e.g., air quality) in response to a second wave of COVID-19 or alike crises. Compared to the previous studies, this study is the first one taking account of both socioeconomic factors and environmental factors simultaneously in explaining spatial variations of COVID-19 mortality rate; and the first one focusing on spatial variations of COVID-19 mortality rate in relation to socioeconomic factors and environmental factors across England.

As the regression models are applied to geospatial data in this study, spatial regression models are highly recommended. Spatial autocorrelation is likely to exist in the residuals of non-spatial regression models (e.g., ordinary least squares models) applied to geospatial data. Presence of spatially autocorrelated residuals means individual observations are not completely independent, thereby violating the assumption of observation independence in regression models. In this case, we should replace nonspatial models with spatial regression models since spatial regression models, like spatial autoregressive models, are developed to reduce the adverse impact of auto-correlation in regression residuals. Therefore, in this study, we selected two typical spatial regression models: spatial autoregressive model and eigenvector spatial filtering model as the former is the most widely used one (e.g., Chi and Zhu, 2008; Lin, 2010) and the latter is likely to perform best (e.g., Chun, 2014; Helbich and Arsanjani, 2015). More specifically, the matrix exponential spatial specification model and fast random effects eigenvector spatial filtering model are selected to estimate models in this study. The ‘matrix exponential spatial specification’ is one of the best specifications in spatial autoregressive models (LeSage and Pace, 2009); whilst the ‘random effects specification’ is one of the new and effective specifications in eigenvector spatial filtering models (Murakami and Griffith, 2015). Compared with conventional specifications of spatial autoregressive models, the ‘matrix exponential spatial specification’ has advantages on computational efficiency and interpretation (e.g., generation of R ²) (LeSage and Pace, 2007), and the ‘random effects specification’ is likely to better explain the spatial variations with a higher value of R ² or a lower value of Akaike information criterion (Murakami and Griffith, 2015; Murakami and Griffith, 2019). Furthermore, we will compare the performance of the models estimated and determine which models are more appropriate.

This study can offer more evidence on the associations of COVID-19 mortality rate, socioeconomic and environmental factors. Particularly, this study empirically reveals that spatial variations of COVID-19 mortality rate are mainly attributable to spatial variations of socioeconomic and environmental characteristics across England. Healthcare resource allocation should prioritise some areas around Sunderland, Liverpool, and Birmingham since those areas are hotspots of COVID-19 mortality rate and non-COVID-19 mortality rate but have a lower level of access to hospital.

2. Literature review

Health inequalities exist among different socioeconomic groups since socioeconomic status (SES) reportedly influences health outcomes (e.g., Nobles et al., 2013; Präg et al., 2016; Kosidou et al., 2011). A number of studies had offered empirical evidence on the association of socioeconomic factors and human health, including physical health (e.g., Nobles et al., 2013; Präg et al., 2016) and mental health (e.g., Nobles et al., 2013; Präg et al., 2016; Kosidou et al., 2011). Adverse socioeconomic factors such as poverty, unemployment, and occupational risks are likely to cause negative health consequences. Socioeconomically disadvantaged people are likely to live a less healthy life, including lower access to healthcare, healthy food, or recreational facilities, a lower level of physical activity, a higher level of exposure to alcohol and/or tobacco, less knowledge of health maintenance, or a lower level of self-discipline. In general, people with a lower socioeconomic position are more likely to suffer from health problems than those with a higher socioeconomic position. Apart from socioeconomic factors, environmental factors are found to influence health outcomes (e.g., Hoek et al., 2013; Beelen et al., 2014; Wheeler et al., 2015; Lelieveld et al., 2015; Di et al., 2017). For instance, increased mortality due to different causes is reportedly associated with air pollution exposure (Hoek et al., 2013; Beelen et al., 2014; Lelieveld et al., 2015; Di et al., 2017), road traffic noise exposure (Halonen et al., 2015; Héritier et al., 2017), temperature (Gasparrini et al., 2015; Guo et al., 2014), and humidity (Barreca and Shimshack, 2012; Ou et al., 2014).

Some recent studies had performed interesting research using georeferenced COVID-19 case data though those data had been aggregated to a variety of geographic units (e.g., state/province, county/town/city, etc.) before being released. To search for COVID-19 incidence hotspots, some researchers detected spatiotemporal clusters of COVID-19 cases across United States (Hohl et al., 2020; Desjardins et al., 2020). To understand socioeconomic and environmental effects, some scholars modelled spatial variations of COVID-19 incidence rate from socioeconomic and environmental factors in China (e.g., Huang et al., 2020; Guliyev, 2020), United States (e.g., Mollalo et al., 2020), and Africa (e.g., Adekunle et al., 2020). Besides, some city-wide researches had been conducted as well (e.g., Cordes and Castro, 2020). Moreover, some scholars modelled the dynamic spread of COVID-19 through travel patterns of people (Zheng et al., 2020; Gatto et al., 2020; Velásquez and Lara, 2020; Danon et al., 2020; Pujari and Shekatkar, 2020).

Although not being discussed as much as COVID-19 infection or spread, COVID-19 mortality and its associations with socioeconomic and environmental characteristics have been discussed in a few studies. On the one hand, socio-economically advantaged communities are likely to have a higher risk of COVID-19 mortality. A recent study of primary COVID-19 data in England uncovers that Black, Asian and minority ethnic groups in England are at increased risk of death from COVID-19 (Aldridge et al., 2020). Similarly, another recent study reveals that substantial racial/ethnic disparities are observed in COVID-19 case fatality and mortality with Blacks/African Americans disproportionately affected across the United States (Holmes et al., 2020). In the United States, black people are being admitted to hospital and dying in disproportionate numbers from the covid-19 pandemic (Dyer, 2020). A systematic review of recent literature concludes that Black, Asian, and Minority Ethnic (BAME) individuals are at an increased risk of worse clinical outcomes from COVID-19 (Pan et al., 2020). Moreover, unemployment and poverty are reported to be an important factor in determining COVID-19 mortality rates in France (Goutte et al., 2020). More specifically, focusing on a densely populated region of France, Goutte et al. (2020) documented evidence that higher economic “precariousness indicators” such as unemployment and poverty rates, lack of formal education and housing are important factors in determining COVID-19 mortality rates. Besides, access to healthcare is likely to play a key role in affecting COVID-19 mortality rate. Spatial variations in healthcare resource availability and accessibility might partly explain spatial disparities variations in COVID-19 mortality rate across China (Ji et al., 2020). On the other hand, environmental characteristics (e.g., air quality, temperature range, and humidity) are likely to affect COVID-19 mortality. For instance, a recent study found positive associations between particulate matter pollution (PM_2.5 and PM₁₀) and COVID-19 case fatality rate (CFR) in Chinese cities (Yao et al., 2020). Another study on other Asian cities suggests that there exists a positive correlation between the level of air pollution of a region and the lethality related to COVID-19, indicating air pollution to be an elemental and concealed factor in aggravating the global burden of deaths related to COVID-19 (Gupta et al., 2020). Similarly, a positive association of ambient PM2.5 concentration on excess mortality related to the COVID-19 epidemic was found in Northern Italy (Coker et al., 2020). Effects of temperature variation and humidity on COVID-19 mortality rate were reported as well (Ma et al., 2020). More specifically, Ma et al. (2020) explored the effects of meteorological factors on COVID-19 mortality in Wuhan, and found that diurnal temperature range is positively associated with daily death counts of COVID-19 whilst absolute humidity is negatively associated with daily death counts of COVID-19.

3. Materials and methods

3.1. Research data

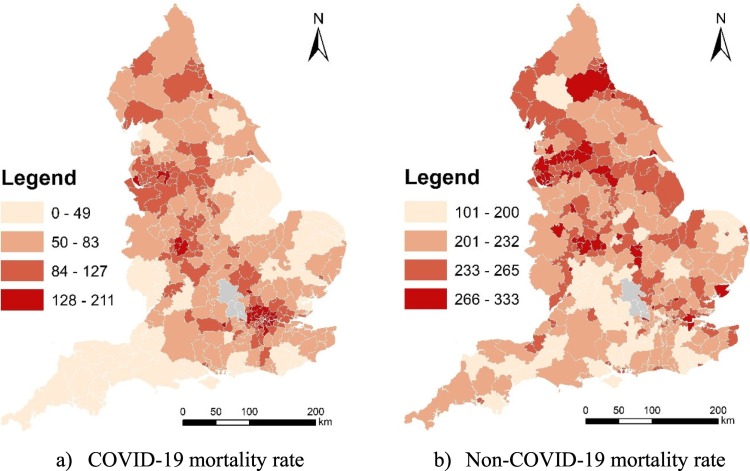
The mortality data is available for March, April and May in 2020 (https://www.ons.gov.uk/peoplepopulationandcommunity/birthsdeathsandmarriages/deaths/datasets/deathsinvolvingcovid19bylocalareaanddeprivation). The data offer the number of deaths and age-standardised rates by local authority districts (LADs) according to deaths occurring between March and May. Fig. 1 maps three-month COVID-19 mortality rate and non-COVID-19 mortality rate across England at the local authority district (LAD) level. Besides, there are 317 LADs constituting England. In Fig. 1, grey areas mean areas with no data.

Fig. 1.

3-month COVID-19 mortality rate and non-COVID-19 mortality rate across England at the local authority district (LAD) level (March, April, and May 2020).

(Data source: ONS)

Population by gender and LAD is available for 2019 (https://www.ons.gov.uk/peoplepopulationandcommunity/populationandmigration/populationestimates/datasets/populationestimatesforukenglandandwalesscotlandandnorthernireland), and population by ethnicity and LAD is available for 2017 (https://www.ons.gov.uk/peoplepopulationandcommunity/populationandmigration/populationestimates/adhocs/008781populationdenominatorsbybroadethnicgroupandforwhitebritishlocalauthoritiesinenglandandwales2011to2017). Unemployment rate by LAD is available for 2019 (https://www.ons.gov.uk/employmentandlabourmarket/peoplenotinwork/unemployment/datasets/modelledunemploymentforlocalandunitaryauthoritiesm01/current), and percent of households in poverty by LAD is available for 2014 (https://www.ons.gov.uk/peoplepopulationandcommunity/personalandhouseholdfinances/incomeandwealth/datasets/householdsinpovertyestimatesformiddlelayersuperoutputareasinenglandandwales). A household is thought to be in poverty if its income is below 60% of the median income before housing costs. Locations of hospitals are available from UK National Health Service (NHS) (https://www.nhs.uk/about-us/nhs-website-datasets/).

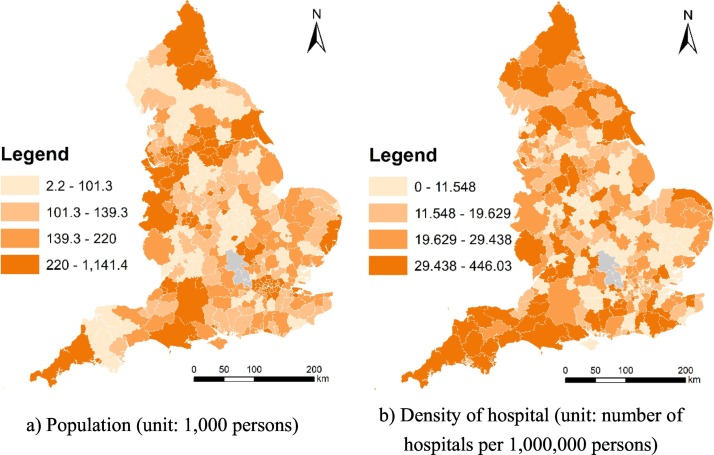
Since high-resolution PM_2.5 data and climatic data are not available for 2020, high-resolution PM_2.5 data and climatic data for 2019 were used. Specifically, Met Office offers 1 × 1 km gridded monthly relative humidity and air temperature (maximum and minimum) for 2019 (Met Office et al., 2020); whilst Defra offers 1 × 1 km gridded annual mean PM_2.5 data for 2019 (https://uk-air.defra.gov.uk/data/pcm-data). Air pollution maps at 1 × 1 km resolution are modelled each year under Defra's Modelling of Ambient Air Quality (MAAQ) contract. These maps are used to provide policy support for Defra and to fulfil the UK's reporting obligations to Europe. The models have been calibrated using monitoring data from the national network sites. Professional monitoring stations installed in monitoring sites are used to observe air quality, humidity, and temperature (see https://uk-air.defra.gov.uk/networks/network-info?view=aurn and https://www.metoffice.gov.uk/public/weather/observation/map). We used the average climatic measures of three months (i.e., March, April and May) in 2019 to represent the climatic measures (i.e., relative humidity and range of air temperature) used in this study. Although monthly high-resolution PM_2.5 is not available, population-weighted LAD-level annual mean PM_2.5 is available, and thereby is used to represent the annual mean PM_2.5 level used in this study. Technically, monthly relative humidity and monthly air temperature were aggregated from grids to LADs. Fig. 2 maps population and density of hospital across England at the local authority district (LAD) level in 2019. And, Fig. 3 maps annual mean PM2.5 across England at the local authority district (LAD) level in 2019.

Fig. 2.

Population and density of hospital across England at the local authority district (LAD) level in 2019.

(Data source: ONS and NHS)

Fig. 3.

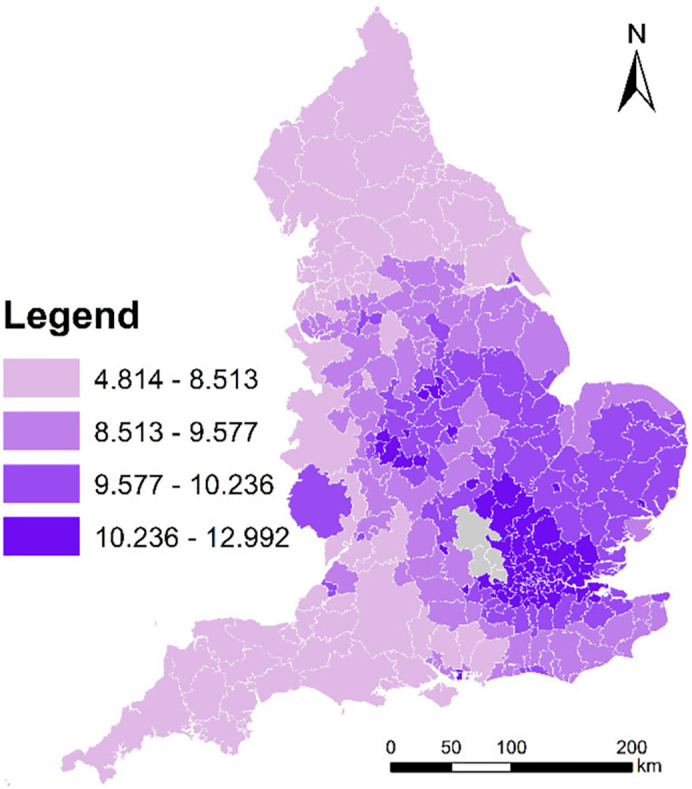
Annual mean PM_2.5 (unit: ug/m⁻³) across England at the local authority district (LAD) level in 2019.

(Data source: Defra)

3.2. Exploring spatial patterns of COVID-19 mortality rate

In this study, we first explored spatial patterns of COVID-19 mortality rate in comparison with non-COVID-19 mortality.

3.2.1. Assessing spatial inequalities of COVID-19 mortality and non-COVID-19 mortality

In this study, we assessed spatial inequalities of COVID-19 mortality rate and non-COVID-19 mortality rate by computing the Gini coefficient (the most commonly used measure of inequality).

3.2.2. Exploring spatial association of COVID-19 mortality and non-COVID-19 mortality

In this study, we explored spatial association of COVID-19 mortality rate and non-COVID-19 mortality rate by using bivariate Moran's I test. Specifically, bivariate Moran's I test includes global and local ones. The global one is also called “global indicators of spatial association (GISA)”, and the local one is also called “local indicators of spatial association (LISA)”. The global and local ones are used to quantify the global and local spatial association between two variables respectively. Specifically, a positive association (a positive Moran's I value) means high (low) values of one variable is surrounded by high (low) values of the other variable; whilst a negative association (a negative Moran's I value) means high (low) values of one variable is surrounded by low (high) values of the other variable.

3.3. Modelling spatial variations of COVID-19 mortality rate

3.3.1. Model variables

Table 1 lists the variables considered in this study. The response is three-month COVID-19 mortality rate (unit: deaths per 100,000 persons). The explanatory variables include socioeconomic characteristics (i.e., gender, ethnical, income, and employment characteristics), hospital accessibility, and physical environment characteristics (i.e., air pollution, humidity, and temperature measures). The range of air temperature equals the difference of maximum air temperature and minimum air temperature. Particularly, a population-based measure is used to quantify the level of hospital accessibility rather than an area-based one as the response is a population-based one as well. Table 1 also shows the statistical description for all the variables in this study.

Table 1.

Summary of variables and data sources in this study.

Variable	Full name	Mean	SD	Year	Source
CMR	3-month COVID-19 mortality rate (unit: deaths per 100,000 persons)	79.4	36.89	2020	ONS
P_F	Percent of females	50.65	0.83	2019	ONS
P_A	Percent of Asians	6.11	8.11	2017
P_B	Percent of Blacks	2.52	4.65	2017
P_HIP	Percent of households in poverty	15.84	3.36	2014
UE_R	Unemployment rate (%)	3.66	1.21	2019
D_P	Density of population (unit: 1000 persons per km2)	1.8	2.64	2019
D_H	Density of hospital (number of hospitals per 1000,000 persons)	23.33	27.96	2019	NHS
AM_PM	Annual mean PM2.5 (ug/m−3)	9.38	1.59	2019	Defra
R_H	3-month mean relative humidity (%)	76.28	1.9	2019	Met Office
R_AT	3-month mean range of air temperature (°C)	8.97	0.84	2019

There might be still potential bias because all the explanatory variables are measured in 2019 or earlier whilst the response (COVID-19 mortality rate) is measured in 2020. We made an assumption that spatial variations of socioeconomic and environment characteristics across a country should be consistent between continuous years. For instance, spatial variations of socioeconomic and environment characteristics across England in 2020 should be proportional to those in 2019; likewise, spatial variations of socioeconomic and environment characteristics in 2019 should be proportional to those in 2018 as well. Table 2 lists the correlations of LAD-level explanatory variables and their counterparts in the previous years (Note that P_HIP is not included due to the absence of data in other years). As Table 2 shows, high values of Pearson's correlation coefficients (R > 0.9) indicate that spatial variations of socioeconomic and environment characteristics in 2019 is highly proportional to those in 2018. Based on the assumption, spatial variations of socioeconomic and environment characteristics in 2020 is likely to be highly proportional to those in 2019 as well. Therefore, we can use spatial variations of socioeconomic and environment characteristics in 2019 or earlier to approximately represent spatial variations of them in 2020.

Table 2.

Correlations of LAD-level explanatory variables and their counterparts in the previous year or earlier (N = 317).

Pearson's correlation coefficient	P_F 2018	P_A 2016	P_B 2016	UE_R 2018	D_P 2018	AM_PM 2018	R_H 2018	R_AT 2018
P_F 2019	0.993
P_A 2017		0.999
P_B 2017			0.999
UE_R 2019				0.995
D_P 2019					0.999
AM_PM 2019						0.935
R_H 2019							0.9
R_AT 2019								0.933

3.3.2. Model selection and estimation

To select and estimate appropriate models, we will first estimate spatial regression models as well as non-spatial regression models, and subsequently check whether spatial regression models can reduce residual spatial autocorrelation in comparison with non-spatial regression models.

• Moran's I: Testing for spatial dependence:

To test whether there is significant spatial autocorrelation present in regression residuals, we will use the Moran's I testing method proposed by Moran (1950). Moran's I is widely used to measure the level of spatial autocorrelation between adjacent locations (Moran, 1950; Getis and Ord, 1992).

• Variable selection: the Lasso technique

Lasso (Tibshirani, 1996) performs automatic variable selection and is most likely the preferred method (Friedman et al., 2010; Engebretsen and Bohlin, 2019). In this study, we used Lasso to select explanatory variables and further estimate models to improve model estimation.

• Spatial regression models:

If significant spatial autocorrelation is found to exist in the residuals of non-spatial regression models estimated conventionally, we should consider spatial regression models. In this study, we will select two specifications from two types of spatial regression models (i.e., spatial autoregressive and eigenvector spatial filtering) since the former is the most widely used one and the latter is thought to be most high-performance one. Specifically, we will use the matrix exponential spatial specification (MESS) and random effects specification (RES) as specifications in the spatial autoregressive (SAR) models and in eigenvector spatial filtering (ESF) models respectively.

• Spatial autoregressive model (MESS-SAR):

Among different types of spatial regression models, spatial autoregressive model is the most popular one. A variety of spatial autoregressive (SAR) models have been proposed to remedy residual spatial autocorrelation. Specifically, we choose the matrix exponential spatial specification (MESS) as the specific SAR model in this study since the MESS model has analytical, computational, and interpretive advantages over other SAR models (LeSage and Pace, 2007). Additionally, the MESS-SAR model produces R ² values which are direct measures of the explanation capacity of the model; whilst conventional spatial regression models do not. The coefficients estimated in the MESS-SAR model are usually similar to those in OLS models, but residual spatial correlation is much lower (LeSage and Pace, 2007; LeSage and Pace, 2009). The MESS model can be described as follow (LeSage and Pace, 2007; LeSage and Pace, 2009):

“A spatial regression mode can be expressed as

$$\mathit{Sy}=\mathit{X\beta }+\mathrm{\varepsilon }$$ (1)

where the vector y contains n observations on the dependent variable, each associated with one region or point in space. The matrix X represents an n × k full column rank matrix of constants which correspond to observations on k independent variables for each region. The n-element vector ɛ is distributed as N (0, σ ² I _n). The k element vector β is a vector of corresponding parameters, and S denotes an n × n non-singular matrix of constants that may depend on an unknown real, scalar parameter.

The MESS specification replaces the conventional geometric decay of influence from higher-order neighbouring relationships implied by the spatial autoregressive process with an exponential pattern of decay in influence from higher-order neighbouring relationships. Specifically, the MESS model transforms S to model spatial dependence among the elements of the vector y:

$$\mathrm{S}={\mathrm{e}}^{\propto \mathrm{W}}=\sum _{\mathrm{i}=0}^{\infty }\frac{{\propto }^{\mathrm{i}}{\mathrm{W}}^{\mathrm{i}}}{\mathrm{i}!}$$ (2)

where W is an n × n non-negative matrix with zeros on the diagonal and α represents a scalar real parameter. W represents a spatial weight matrix, and W _ij > 0 indicates that observation j is a neighbour of observation i. The matrix exponential S, along with matrix W, imposes a decay of influence for higher-order neighbouring relationships.”

• Eigenvector spatial filtering model (RES-ESF):

Compared to spatial autoregressive models estimated based on parametric estimation methods (e.g., maximum likelihood estimation or Bayesian estimation), eigenvector spatial filtering is computer intensive since it is a nonparametric statistical method which is distribution free without sacrificing too much information in a sample (Tiefelsdorf and Griffith, 2007). Although eigenvector spatial filtering (ESF) models are computationally demanding, they are likely to outperform spatial autoregressive models in the applications of urban and regional studies, ecological studies, and so on (Murakami and Griffith, 2019). Furthermore, a random effects specification of ESF (RES-ESF) had been developed because of its usefulness for spatial dependence analysis considering spatial confounding (Murakami and Griffith, 2015). RES-ESF model is found to outperform conventional ESF model (Murakami and Griffith, 2015; Murakami and Griffith, 2019). Besides, the RES-ESF model can produce R ² values as well.

The eigenvector spatial filtering (ESF) is also called Moran's eigenvector-based spatial regression approach in regional science (Griffith, 2003), and ESF with a small number of eigenvectors (i.e., small L) can greatly reduce model misspecification errors and increases model accuracy (Murakami and Griffith, 2019). The ESF model is presented as follows (Chun et al., 2016):

“ESF utilizes the spectral decomposition of a transformed spatial weights matrix, C. The spectral decomposition of matrix MCM (where M = (I − 11 ^T)/n and 1 is a vector of ones) produces a set of n eigenvalues and their corresponding eigenvectors:

$$\mathbf{MCM}={\mathbf{E\Lambda E}}^{\mathbf{-}\mathbf{1}}={\mathbf{E\Lambda E}}^{\mathbf{T}}$$ (3)

where Λ is a diagonal matrix whose diagonal elements are the n eigenvalues λ = (λ₁, λ₂, …, λ _n) ordered from the largest value to the smallest value, and E = (e ₁, e ₂, …, e _n) represents the n corresponding eigenvectors. As an output of the spectral decomposition, the eigenvectors are mutually orthogonal and uncorrelated and (n − 1) have a zero mean, whilst one is proportional to the vector 1. Each of these eigenvectors represents a distinct nature and degree of spatial autocorrelation. ESF introduces a subset of the eigenvectors as control variables in a regression model specification in order to capture its spatial stochastic component.

In linear regression, an ESF model specification can be expressed as.

$$\mathbf{Y}=\mathbf{X\beta }+{\mathbf{E}}_k{\mathbf{\beta }}_{\mathrm{E}}+\mathbf{\epsilon }$$ (4)

where Y denotes the dependent variable, X denotes a matrix of independent variables, E _k denotes a selected set of k eigenvectors selected from the n eigenvectors E, (β, β _E) denote parameters, and ε denotes random noise that is distributed N(0, I σ ²). In this specification, E _k β _E captures the spatial stochastic component in the dependent variable Y. Hence, the regression model does not suffer from complications attributable to spatial autocorrelation, which is likely to be observed in its residuals if the spatial stochastic component is not explicitly addressed.

The identification of E _k can be achieved through a stepwise procedure. Specifically, eigenvectors that minimize the level of spatial autocorrelation at each step can be selected. Intuitively, although this minimizing residual spatial autocorrelation criterion adheres to the notion of isolating spatial autocorrelation, it becomes computationally demanding as n increases. That is, in order to evaluate whether the addition of an eigenvector reduces spatial autocorrelation in residuals, the expected value and variance of Moran's I for the residuals needs to be recalculated repeatedly, which involves the inversion of large matrices.

This identification procedure can be assisted further by excluding irrelevant eigenvectors. The stepwise procedure can be conducted from a noticeably smaller set (i.e., a candidate set) instead of the entire set of eigenvectors, E. A candidate set can be demarcated based upon several criteria. First, eigenvectors that do not explain much spatial variation can be excluded. Second, eigenvectors that represent negative spatial autocorrelation can be excluded when variable Y displays positive spatial autocorrelation, and vice versa. This exclusion procedure can be assisted by the eigenvalues λ, because λ _i is proportional to Moran's I value of a map that is a portrayal of E _i on the spatial tessellation from which C is created; Moran's I = λ _i n/1 ^T C1. Hence, a candidate set is often constructed with a threshold minimum Moran's I value of 0.25, which is related to approximately 5% of the variation in a response variable being attributable to spatial autocorrelation.”

3.3.3. Model validation

To further evaluate the model performance, the dataset was further split into training and test datasets. After being estimated based on the training dataset, and all the models were applied to the test dataset. Apart from the three types of regression models, a Bayesian model (i.e., the Bayesian linear regression model) and a popular machine learning model (i.e., the Random Forest regression model) were used to predict the test dataset for a broader comparison.

3.4. Implementation of analysis

In this study, the model selection, estimation, and validation were all implementable in R. Specifically, OLS model estimation, Moran's I testing, Lasso variable selection, MESS-SAR model estimation, and RES-ESF model estimation are supported by three R packages, named “stats”, “spdep”, “glmnet”, “spatialreg”, and “spmoran” respectively. And, prediction using Bayesian regression and Random Forest regression models were implemented via two R packages, named “bayesreg” and “randomForest” respectively. Besides, the bivariate Moran's I testing was implemented in GeoDa (http://geodacenter.github.io/index.html).

4. Results

In this section, spatial patterns of COVID-19 mortality rate are firstly explored, and lately, results of model selection and estimation are presented and discussed.

4.1. Spatial patterns of COVID-19 mortality rate

We first explored spatial patterns of COVID-19 mortality rate in comparison with non-COVID-19 mortality.

4.1.1. Spatial inequalities of COVID-19 mortality and non-COVID-19 mortality

The Gini coefficient for COVID-19 mortality rate and non-COVID-19 mortality rate across England is 0.257 and 0.079 respectively. COVID-19 mortality rate has a much higher (about 3 times of) Gini coefficient than non-COVID-19 mortality rate. This indicates that the level of spatial inequalities of COVID-19 mortality is higher than that of non-COVID-19 mortality in England.

4.1.2. Spatial association of COVID-19 mortality and non-COVID-19 mortality

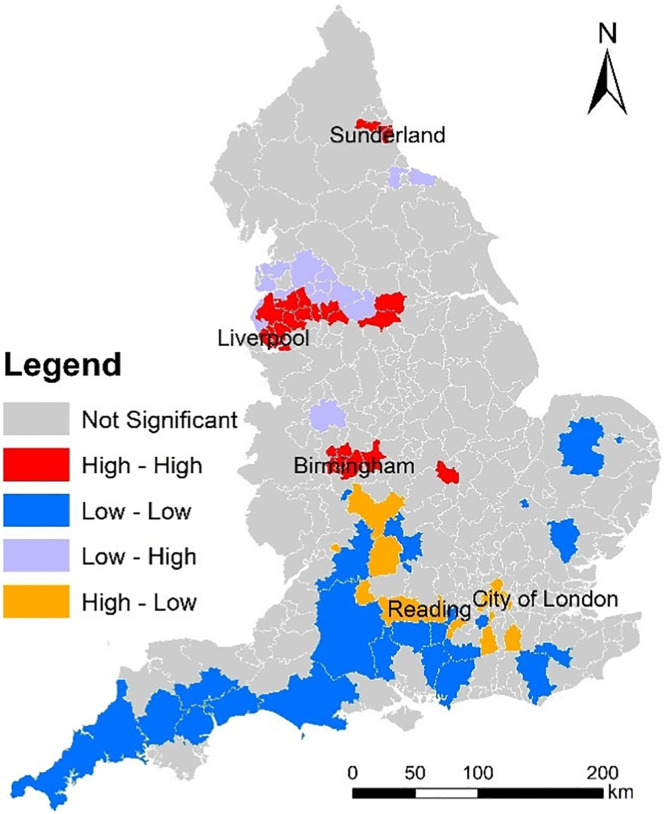
We performed the bivariate Moran's I tests of COVID-19 mortality rate and non-COVID-19 mortality rate. The global bivariate Moran's I value is 0.102 and the p-value is 0.001. The global spatial association of COVID-19 mortality rate and non-COVID-19 mortality rate is statistically significant and positive. The local bivariate Moran's I testing result is shown in Fig. 4 . Fig. 4 maps the clusters and outliers of COVID-19 mortality rate and non-COVID-19 mortality rate across England. In Fig. 4, all the clusters and outliers are statistically significant at the 0.05 level. Clusters and outliers indicate the existence of positive and negative local spatial association respectively. Specifically, ‘High - High’ and ‘Low - Low’ represent two types of clusters; whilst ‘Low - High’ and ‘High - Low’ represent two types of outliers. In Fig. 4, ‘High - High’ means an area (LAD) with a high value of ‘COVID-19 mortality rate’ is surrounded by areas (LADs) with a high value of ‘non-COVID-19 mortality rate’; ‘Low - Low’ means an area (LAD) with a low value of ‘COVID-19 mortality rate’ is surrounded by areas (LADs) with a low value of ‘non-COVID-19 mortality rate’; ‘Low - High’ means an area (LAD) with a low value of ‘COVID-19 mortality rate’ is surrounded by areas (LADs) with a high value of ‘non-COVID-19 mortality rate’; and ‘High - Low’ means an area (LAD) with a high value of ‘COVID-19 mortality rate’ is surrounded by areas (LADs) with a low value of ‘non-COVID-19 mortality rate’. For the COVID-19 prevention, areas deserving more attentions are ‘High - High’ and ‘High - Low’ areas. Specifically, ‘High - High’ areas are located around Sunderland, Liverpool, and Birmingham. ‘High - Low’ areas are located around London and Reading. Besides, ‘Low - Low’ areas are located in the southern England. Although global spatial association of COVID-19 mortality and non-COVID-19 mortality is positive, local spatial association of COVID-19 mortality and non-COVID-19 mortality is negative in some areas (e.g., ‘Low - High’ and ‘High - Low’ areas).

Fig. 4.

Clusters and outliers of COVID-19 mortality rate and non-COVID-19 mortality rate across England (March, April, and May 2020).

4.2. Model selection (spatial or non-spatial regression models)

4.2.1. Estimates of non-spatial regression model (OLS model)

First of all, non-spatial regression models (OLS models) were estimated based on 317 observations (317 LADs).

4.2.2. Estimates of spatial regression models (MESS and RES-ESF models)

Owing to the presence of significant spatial autocorrelation in the residuals of the OLS models estimated conventionally, we should select spatial models (e.g., MESS and RES-ESF models) instead of non-spatial models (OLS models). Likewise, spatial models were estimated based on 317 observations (317 LADs). Besides, in the estimation of ESF models, the eigenvectors were selected by a stepwise method (see Subsection 3.3.2). As aforementioned, threshold for the eigenvalues is set to 0.25 (see Subsection 2.3.2). As a result, 73 of 313 eigen-pairs were extracted.

Table 3 lists the estimation results for the non-spatial and spatial models estimated, including OLS, MESS-SAR, and RES-ESF models (N = 317). The RES-ESF model outperforms the OLS and MESS models owing to the highest R-squared value and the lowest Akaike information criterion (AIC) value (R ² = 0.797). Moreover, Moran's I test was used to test whether spatial autocorrelation is present in the residuals of regression models estimated. As Table 3 shows, statistically significant spatial autocorrelation is present in the OLS model but is not in the MESS-SAR and RES-ESF models. This indicates that the replacing non-spatial regression models (i.e., the OLS model) with spatial regression models (i.e., the MESS-SAR and RES-ESF models) can reduce the potential bias owing to residual spatial autocorrelation.

Table 3.

Estimation results for the non-spatial and spatial regression models (N = 317).

Coefficient	OLS	MESS-SAR	RE-ESF
Intercept	587.326***	248.922*	245.319.
P_F	2.448	1.002	2.809.
P_A	1.012***	0.782***	0.892***
P_B	2.758***	2.002***	2.58***
P_HIP	0.831.	0.504	0.602
UE_R	5.943***	5.378***	4.807***
D_P	−1.612	−0.612	0.321
D_H	−0.099.	−0.107*	−0.08*
AM_PM	−1.88	−1.984.	−1.598
R_H	−8.521***	−3.715**	−4.793***
R_AT	−0.795	1.512	3.852.
Adjusted R2	0.618	0.496	0.797
AIC	2858.418	2773.595	2776.084
Moran's I test for residuals	0.373***	0.032	−0.036

Note: ‘.’, ‘*’, ‘**’, and ‘***’ mean the p-values are below 0.1, 0.05, 0.01, and 0.001respectively.

Table 3 also shows the contributions of explanatory variables to spatial variations of COVID-19 mortality rate. We discussed the contributions of explanatory variables according to the estimation result of RE-ESF model (see Table 3). Expectedly, D_H (density of hospital) makes a statistically significant contribution, and it is negatively related to COVID-19 mortality rate. Therefore, areas with a low level of hospital accessibility are likely to suffer a high COVID-19 mortality rate. It is noted that some socioeconomic factors make statistically significant contributions to spatial variations of COVID-19 mortality rate (see Table 3). Specifically, P_A (percent of Asians), P_B (percent of Blacks), and UE_R (unemployment rate) are positively related to COVID-19 mortality rate. This indicates that areas with a high percent of Asians, a high percent of Blacks, or a high unemployment rate are likely to suffer a high COVID-19 mortality rate. More importantly, R_H (relative humidity) is statistically significantly and negatively related to COVID-19 mortality rate; whilst R_AT (range of air temperature) is not statistically significantly related to COVID-19 mortality rate.

4.2.3. Estimates of models after variable selection

Furthermore, to improve the model estimation, the Lasso technique is used to select the influential explanatory variables. The optimal selection of explanatory variables are: P_A, P_B, UE_R, D_H, and R_H. Table 4 lists the estimation results for the three models after the explanatory variable selection (N = 317). Expectedly, all the explanatory variables are statistically significantly associated with the response in the three models. The RES-ESF model consistently outperforms the OLS and MESS models owing to the highest R-squared value and the lowest Akaike information criterion (AIC) value (R ² = 0.793). Likewise, statistically significant spatial autocorrelation is present in the OLS model but is not in the MESS-SAR and RES-ESF models (see Table 4). Consistently, this indicates that the replacing non-spatial regression models with spatial regression models can reduce the bias owing to residual spatial autocorrelation. Moreover, Table 5 shows correlations of residuals and explanatory variables in the models estimated. In Table 5, all the Pearson's correlation coefficients are extremely lowly valued, indicating no significant endogeneity of regressors exists. Besides, variance inflation factor (VIF) was used to detect multicollinearity in all the models estimated. In all the models estimated, the VIF values for all the independent variables (predictors) are below 5, indicating no serious multicollinearity exists in all these models estimated. This means all the all the independent variables (predictors) are not highly correlated to each other. Table 4 also shows the coefficients of the RE-ESF model is closer to the OLS model than the MESS-SAR model.

Table 4.

Estimation results for the non-spatial and spatial regression models (N = 317).

Coefficient	OLS	MESS-SAR	RE-ESF
Intercept	506.644***	199.041**	390.149***
P_A	0.876***	0.708***	0.807***
P_B	2.155***	1.625***	2.522***
UE_R	6.756***	5.605***	4.971***
D_H	−0.124*	−0.129**	−0.122***
R_H	−6.029***	−2.366**	−4.423***
Adjusted R2	0.61	0.49	0.793
AIC	2859.7	2769.561	2784.813
Moran's I test for residuals	0.405***	0.046.	−0.028

Note: ‘.’, ‘*’, ‘**’, and ‘***’ mean the p-values are below 0.1, 0.05, 0.01, and 0.001respectively.

Table 5.

Correlations of residuals and explanatory variables in the models estimated.

Pearson's correlation coefficient	Residuals
	OLS	SAR-MESS	RE-ESF
P_A	−6.729 × 10−17	5.826 × 10−18	−2.270 × 10−13
P_B	−7.968 × 10−17	−3.181 × 10−17	−1.580 × 10−13
UE_R	−4.519 × 10−17	−7.588 × 10−17	−7.004 × 10−14
D_H	−5.759 × 10−17	−7.905 × 10−17	1.139 × 10−13
R_H	−9.482 × 10−16	−5.200 × 10−16	1.164 × 10−12

4.2.4. Validation of models estimated

In this study, the dataset used was further split into the training and test datasets. Specifically, 20% of the cases are randomly selected as the test cases; whilst the remaining cases are selected as the training cases. Apart from OLS, MESS-SAR and RE-ESF models, Random Forest (RF) and Bayesian linear (BL) regression models were estimated based on the training dataset, and subsequently they are applied to the test data for a broader comparison. In this study, the Normalized Mean Absolute Error (NMAE) was used to measure the difference of prediction and real values after adjusting for scales. NMAE is the average of mean error normalized over the average of all the actual values. Table 6 shows the NMAE values for the predictions of COVID-19 mortality rate by different models. The RE-ESF model achieves the highest prediction accuracies with the lowest NMAE value. The prediction results indicate the RE-ESF model consistently outperforms the OLS and SAR-MESS models.

Table 6.

Prediction accuracies of the regression models estimated.

Model	OLS	SAR-MESS	RE-ESF	BL	RF
NMAE	0.267, 808	0.368, 653	0.267, 177	0.267, 18	0.284, 087

4.3. Discussion

The RE-ESF model is likely to be the most proper model because 1) it outperforms the other two models in explaining spatial variations of COVID-19 mortality rate due to a higher R ²; 2) its coefficients are closer to the OLS model than the SAR-MESS model; 3) it substantially reduces the residual autocorrelation in comparison with the OLS model; and 4) it consistently outperforms the other models in predicting spatial variations of COVID-19 mortality rate due to a lower NMAE.

In the empirical study, some empirical findings were uncovered. Firstly, we uncovered that relative humidity is negatively related to COVID-19 mortality rate whilst PM_2.5 and air temperature measures are not significantly related. This finding is partly consistent with a previous study (e.g., Ma et al., 2020). In Wuhan, a positive association with COVID-19 daily death counts was observed for diurnal temperature range, but negative association for relative humidity (Ma et al., 2020). However, the negative association for relative humidity is consistent with our finding whilst the positive association for diurnal temperature range is not. More empirical studies are needed to examine the effects of temperature on COVID-19 daily death. Besides, a recent study found positive associations between particulate matter pollution (PM_2.5 and PM₁₀) and COVID-19 case fatality rate (CFR) in Chinese cities (Yao et al., 2020); whilst this study found no significant association between PM_2.5 and COVID-19 mortality rate. Secondly, we uncovered that percent of Asians and percent of Blacks is positively related to COVID-19 mortality rate. This is consistent with some previous findings on ethnical disparity in COVID-19 mortality (e.g., Aldridge et al., 2020; Holmes et al., 2020; Dyer, 2020; Pan et al., 2020). Thirdly, we uncovered that: unemployment rate is positively related to COVID-19 mortality rate; whilst density of hospital is negatively related to COVID-19 mortality rate. Consistent findings have been found to exist in France and China as discussed in the literature review section (Goutte et al., 2020; Ji et al., 2020). Particularly, combining Fig. 4, Fig. 2b, we examined whether the hotspots of COVID-19 mortality rate and non-COVID-19 mortality rate are the areas with a lower level of access to hospital. As Fig. 4 shows, high levels of COVID-19 mortality rate and high levels of non-COVID-19 mortality rate co-occur around Sunderland, Liverpool, and Birmingham. Those areas are likely to have a lower level of density of hospital as well (see Fig. 2b). Healthcare resource allocation should prioritise those areas around Sunderland, Liverpool, and Birmingham.

Furthermore, the model estimation results reveal that spatial variations of COVID-19 mortality rate across England is mainly attributable to spatial variations of socioeconomical and environmental factors. This suggests that the reduction of socioeconomic disadvantage could potentially contribute to decrease in COVID-19 mortality risk across England. Socioeconomically disadvantaged areas are more likely to suffer a high risk of COVID-19 mortality. Governments and policy makers should consider how to reduce spatial disparities in COVID-19 mortality risk through decreasing socioeconomically disadvantaged population. Extremely disadvantaged areas should be given priority in policy making. Furthermore, we compared the non-spatial regression models (OLS models) and the spatial regression models (MESS-SAR and RES-ESF models) estimated in this study. The R ² value of RES-ESF model estimated are higher than those of OLS and MESS-SAR models. Therefore, RES-ESF model is empirically found to outperform OLS and MESS-SAR models in this study. Applications of spatial regression models are likely to better model spatial variations of COVID-19 mortality rate across England. Moreover, RES-ESF model is highly recommended to be applied to a variety of applications in urban or regional studies.

In this study, PM_2.5 is not reported to be significantly associated with COVID-19 mortality whilst the significant association is reported in studies on some other regions (e.g., Yao et al., 2020; Gupta et al., 2020; Coker et al., 2020). One possible reason is: compared to the cities or areas in the previous studies (Yao et al., 2020; Gupta et al., 2020; Coker et al., 2020), England has a lower level of PM_2.5, thereby spatial variations of PM_2.5 between English LADs is likely to be smaller than those between the cities or areas in the previous studies. Additionally, we have taken account of other air pollutants (e.g., NO₂ and SO₂) as other potential environmental factors in more model estimations like Table 3, Table 4. Defra also offers 1 × 1 km gridded annual mean NO₂ and SO₂ data for 2019 (https://uk-air.defra.gov.uk/data/pcm-data). Like PM_2.5, NO₂ and SO₂ are not statistically significantly related to COVID-19 mortality rate after adjusting for the other socioeconomic and environmental factors.

5. Conclusion

In this study, we examined the spatial patterns of COVID-19 mortality rate in relation to socioeconomic and environmental factors across England. Two newly developed specifications of spatial regression models were established successfully to estimate COVID-19 mortality rate. The level of spatial inequalities of COVID-19 mortality is higher than that of non-COVID-19 mortality in England. Although global spatial association of COVID-19 mortality and non-COVID-19 mortality is positive, local spatial association of COVID-19 mortality and non-COVID-19 mortality is negative in some areas. The model estimated indicate that 1) relative humidity is negatively related to COVID-19 mortality rate; 2) hospital accessibility is negatively related to COVID-19 mortality rate; and 3) percent of Asians, percent of Blacks, and unemployment rate are positively related to COVID-19 mortality rate. Moreover, the RES-ESF model estimated outperforms the MESS-SAR model in modelling spatial variations of COVID-19 mortality rate across England.

However, there are some limitations in this study. Firstly, in this study, we take no account of behavioural factors, such as alcohol consumption and sugar drinks intake, due to the lack of data. Human health is found to be affected by behavioural factors (e.g., dietary patterns, diet quality, sugary drinks intake, fruits and vegetable intake, alcohol and tobacco consumption, sleep duration, sleep quality, etc.) (Richter et al., 2012; Patel et al., 2013). Secondly, as the poverty data used is for 2014, the time gap between poverty data and other data is relatively large. The existence of this time gap might have a potential influence on the model estimation in this study. Besides, the poverty data is available for 2014, whether the spatial variations of poverty are proportional to those in continuous years needs to be empirically validated. Thirdly, the data used reflect the registered deaths caused by COVID-19, but they might completely reflect the actual deaths caused by COVID-19. On the one hand, the presence of false positives is likely to over-estimate the number of deaths owing to COVID-19. On the other hand, some deaths caused by COVID-19 are likely to be recognised as non-COVID-19 deaths especially in the earlier stage of pandemic when testing capacity is low.

In the future, we will improve this study by addressing those limitations. Firstly, we will attempt to acquire data on behavioural characteristics from questionnaire-based surveys in collaboration with National Health Service (NHS) England. The acquired data will be used to measure behavioural factors. Secondly, the study needs to be repeated once some research data (e.g., poverty data) is updated in the future. The results would be compared with the those in this paper to discuss the influence of time gap in some data on the model estimation results.

Ethical approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Availability of supporting data

The datasets used and/or analyzed during the current study are available from the websites.

Funding

Not applicable.

CRediT authorship contribution statement

Yeran Sun: Conceptualization, Data curation, Formal analysis, Writing - review & editing. Xuke Hu: Conceptualization, Writing - review & editing. Jing Xie: Writing - review & editing.

Declaration of competing interest

The authors declare that they have no conflict of interest.

Editor: Jay Gan