Skip to main content
PMC home page
Clinical Infectious Diseases: An Official Publication of the Infectious Diseases Society of America logoLink to Clinical Infectious Diseases: An Official Publication of the Infectious Diseases Society of America
. 2020 Oct 29;73(1):e241–e245. doi: 10.1093/cid/ciaa1675

Dose-response Relation Deduced for Coronaviruses From Coronavirus Disease 2019, Severe Acute Respiratory Syndrome, and Middle East Respiratory Syndrome: Meta-analysis Results and its Application for Infection Risk Assessment of Aerosol Transmission

Xiaole Zhang 1,2, Jing Wang 1,2,✉
PMCID: PMC7665418  PMID: 33119733

Abstract

Background

A comprehensive understanding of the transmission routes of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) is of great importance to effectively control the spread of coronavirus disease 2019 (COVID-19). However, the fundamental dose-response relation is missing for evaluation of the infection risk.

Methods

We developed a simple framework to integrate the a priori dose-response relation for SARS-CoV-2 based on mice experiments, the recent data on infection risk from a meta-analysis, and respiratory virus shedding in exhaled breath to shed light on the dose-response relation for humans. The aerosol transmission infection risk was evaluated based on the dose-response model for a typical indoor environment.

Results

The developed dose-response relation is an exponential function with a constant k in the range of about 6.4 × 104 to 9.8 × 105 virus copies, which means that the infection risk caused by 1 virus copy in viral shedding is on the order of 10–6 to 10–5. The median infection risk via aerosol transmission with 1-hour exposure (10–6 to 10–4) was significantly lower than the risk caused by close contact (10–1) in a room with an area of 10 to 400 m2 with 1 infected individual in it and with a typical ventilation rate of 1 air change per hour.

Conclusions

The infection risk caused by aerosol transmission was significantly lower than the risk caused by close contact. It is still necessary to be cautious for the potential aerosol transmission risk in small rooms with prolonged exposure duration.

Keywords: dose-response relation, COVID-19, SARS-CoV-2, quantitative microbial risk assessment, infection risk

A dose-response relation of coronaviruses was developed. The infection risk caused by 1 virus copy in viral shedding is about 10–6 to 10–5. Aerosol transmission risk was significantly lower than the risk caused by close contact.

Control of the spread of coronavirus disease 2019 (COVID-19) is the urgent challenge throughout the world. A comprehensive understanding of the transmission routes of the causal pathogen, severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), is of great importance for effective control. Human-to-human transmission by close contact where large respiratory droplets play a significant role has been established as the main transmission route [1]. At the same time, transmission by microscopic respiratory particles (aerosol) is getting increasing attention.

A recent open letter from 239 scientists [2] appealed to the relevant communities and organizations to recognize the potential transmission of SARS-CoV-2 through aerosol. There is no distinct boundary between droplets and aerosol in nature, so it is natural to investigate the infection risk due to aerosol. A quantitative assessment of the infection risk through different transmission routes is essential to evaluate their relative importance and to prioritize control measures. However, the fundamental dose-response relation is still missing for any quantitative assessment.

In this study, we developed a simple framework to integrate the a priori dose-response relation for SARS-CoV-2 [3] based on mice experiments, the recent data on infection risk [4] from a systematic review and meta-analysis, and respiratory virus shedding in exhaled breath [5] in order to shed light on the dose-response relation for humans. We applied the developed dose-response relation to quantitatively evaluate the infection risk via aerosol transmission in a simple illustrative indoor scenario using quantitative microbial risk assessment (QMRA).

METHODS

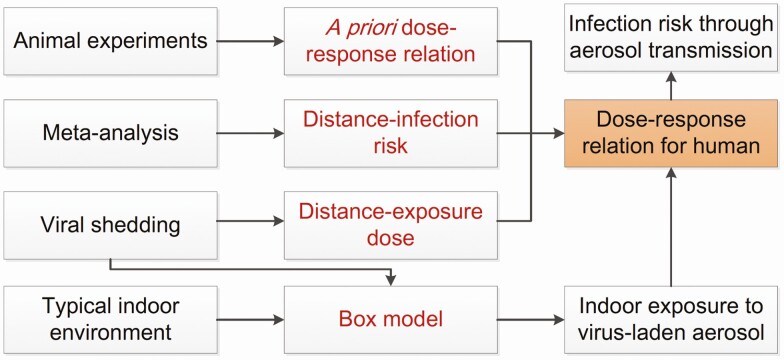
Figure 1 shows the schematic diagram of this study.

Figure 1.

Figure 1.

Open in a new tab

Schematic diagram for deducing the dose-response relation and quantitative microbial risk assessment for typical indoor environment.

A Priori Dose-Response Relation for SARS-CoV-2

Watanabe et al [3] found that the exponential model p = 1−exp(−d/k) could well depict the dose-response relation based on experiments that challenged mice with recombinant SARS-CoV-2 variants [6] and a murine coronavirus strain 1 [7], where p is the infection probability, d is the exposure dose, and k is the pathogen-dependent parameter. Based on Taylor’s formula, we could derive that p ~ d/k, applicable when the infection risk is relatively low, for example, below 15%, with the relative difference between p and d/k being smaller than 8%. We assume that the exponential model remains applicable for the dose-response relation for humans.

Distance-Infection Risk Relation From Meta-Analysis

A recent study reported by the World Health Organization COVID-19 Systematic Urgent Review Group Effort [4] indicated that the anticipated probability of viral infection is about 12.8% within 1 m and about 2.6% at greater distance. This was provided through a systematic review and meta-analysis on the beta-coronaviruses that causes severe acute respiratory syndrome, Middle East respiratory syndrome, and COVID-19. This important information provided us a unique opportunity to assess the dose-response relation of the viruses, if the exposure dose could be appropriately estimated.

Deducing the Exposure Dose

Recently, Leung et al [5] investigated the respiratory shedding of coronaviruses (NL63, OC43, HKU1, and 229E) in exhaled breath in real-life situations with breathing and coughing. The results showed that about 30% to 40% of the symptomatic individuals in the tests produced viral shedding (Evirus) in respiratory particles, with about 102 to 105 virus copies in samples of 30 minutes without wearing masks, with a geometric mean of about 104. Recent studies [8, 9] have shown that the respiratory viral loads were about 106 to 108 copies/mL. The viral shedding was estimated to be 102 to 104 copies per hour based on the particle number emission and size distribution for mouth breathing [10] following the method proposed by Zhang et al [11]. The results were in line with the measurements of the respiratory shedding of coronaviruses in exhaled breath.

An overall effective dilution rate is required to convert the viral shedding into the exposure dose at various distances. The overall effective dilution rate should be a combination of various factors, for example, the dilution when the exhaled air is mixed with the ambient air and the possibility for the exposed person to actually inhale the contaminated plume. A meta-analysis study [4] offered a plausible way to estimate this factor. It was shown that the probability of viral infection decreased by about a factor of 5 from within 1 m (12.8%) to greater distances (2.6%). According to the exponential model, the dose-response relation is nearly linear within the range of p <15% (k is a constant), which suggests that the viral dose should also be effectively diluted by about the same magnitude. Therefore, we used 5 as the effective dilution factor (fdilu) to estimate the exposure doses that correspond to the infection risks from the meta-analysis.

It was reported in the meta-analysis [4] that the duration of exposure varied from any duration to a minimum of 1 hour. Here, we used 1 hour as a representative duration (texpo), which was close to the total duration of close contact between a nurse/healthcare worker and a patient per day [12]. The deposition ratio (fdep) of the particles onto the mucus of the respiratory system was estimated based on the size distribution [10] of particles generated by breathing and coughing and the deposition model for bioaerosols [13]. The overall deposition ratio was about 90%. The exposure (virus copies) at a greater distance was estimated as d = Evirus/(fdilu) × texpo × fdep. Monte Carlo simulations were conducted to estimate the exposure dose. It was assumed that 40% of the infected individuals had positive viral shedding (Evirus), which followed log-normal distribution log10(Evirus)~Normal(4, 0.5). One million values of Evirus were generated for the simulation.

The infection risk from the meta-analysis [4] was the total risk through all the routes, for example, airborne viruses and contact transmission. The contribution from airborne virus-laden particles to the total exposure dose was uncertain. As a result, the dose-response relation was estimated based on 5 contribution levels (0.1, 0.25, 0.5, 0.75, and 1) of airborne virus-laden particles to the total exposure dose.

The Monte Carlo simulations for exposure dose were conducted using MATLAB codes. The parameter k in the dose-response relation was fitted by the nonlinear regression method in the Statistics and Machine Learning Toolbox in MATLAB R2019b based on the exposure dose levels and the infection risk.

Evaluation for Infection Risk Through Aerosol Transmission

Here, we used the developed dose-response relation, combined with a box model for the exposure estimation, to quantitatively evaluate the infection risk of SARS-CoV-2 through aerosol transmission and compared that with the risk due to close contact based on the QMRA methodology.

We considered a simple illustrative scenario of a room with 1 infected individual with positive viral shedding in that room. The room area varied from 10 to 400 m2 and the height was fixed at 3 m. The ventilation rate varied from 0.1 to 2 air changes per hour (ACH), with 1 ACH being the typical ventilation rate for offices [14]. Monte Carlo simulations were conducted to assess the risk for a representative exposure duration of 1 hour.

A box model [11] was used to estimate the virus concentration and deposition in the room. The box model assumed that the airborne virus-laden particles were well mixed and that the virus concentration was homogeneous in the room. The positions of the infected individual and other occupants of the room, their movements, and detailed ventilation pattern, which could vary strongly from one case to another, were not considered. The approach aims to quantify the typical risk level in representative scenarios and is widely adopted in epidemic modeling [15].

The key processes were integrated into the evaluation model, including the viral shedding, dispersion, deposition in air, biologic decay, and lung deposition. A recent study based on computational fluid dynamics [16] indicated that the aerosol mainly remained below 2 m for an indoor environment, so 2 m was used as the mixing height instead of the room height (3 m). Four key processes were considered in the model: viral shedding, biologic decay, ventilation, and deposition. In the Monte Carlo simulations, the viral shedding was a stochastic variable that followed the distribution log10(Evirus)~Normal(4, 0.5). The half-life period of the virus followed the triangular distribution with the lower limit, upper limit, and mode of log10(0.5), log10(100), and log10(10) based on the data reported in the literature [11]. The deposition velocities were estimated following the method proposed by Lai and Nazaroff [17] based on the size distribution [10] of particles generated by breathing and coughing. For the exposure estimation, the total respiratory volume was assumed to be 0.6 m3/h, and the deposition of particles in the respiratory system was estimated by a lung deposition model for bioaerosols [13]. In the dose-response model, it was assumed that k was a stochastic variable that followed the triangular distribution with lower limit, upper limit, and mode of 6.4 × 104, 9.8 × 105, and 1.6 × 105 copies.

RESULTS

Deduced Dose-Response Relation

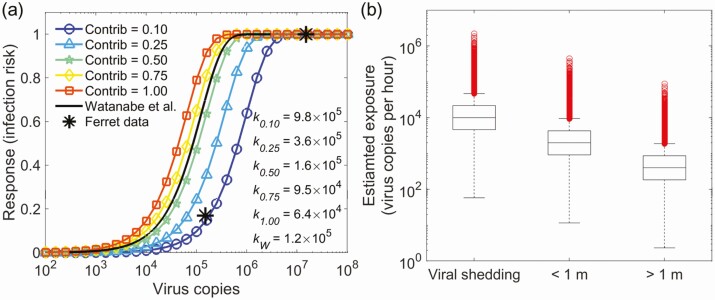
The final dose-response estimations for k are from 6.4 × 104 to 9.8 × 105 copies dependent on the contribution of the airborne virus-laden particles to the total dose, as shown in Figure 2. The results mean that the infection risk of 1 virus copy in viral shedding is on the order of 10−6 to 10−5. Watanabe et al used plaque-forming units (PFU) to quantify the dose. A previous study on SARS-CoV-2 [18] showed that about 300 viral genome copies were present per plaque-forming unit. Then, k in the Watanabe model [3] was about 1.2 × 105, close to our estimation with 50% contribution from airborne particles to the total dose. The results suggest that the experiments based on mice could provide reasonable insight for the human infection risk.

Figure 2.

Figure 2.

Open in a new tab

Results under the assumption of log-normal distribution of viral shedding log10(Evirus)~Normal(4, 0.5), with 40% positive viral shedding. A, The estimated dose-response relations based on different contribution levels (0.1, 0.25, 0.5, 0.75, and 1) of the airborne virus-laden particles to the total dose from both exposure to airborne viruses and contact transmission. The solid line is the dose-response relation for severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) based on mice experiments [3]. The stars are the dose-dependent response to infection with SARS-CoV-2 from the ferret model [19]. A conversion factor of 300 from plaque-forming units to virus copies was used based on a previous study on SARS-CoV-2 [18]. B, Viral shedding and exposure dose for 1 hour duration. Zero values are not shown in the figure.

A recent study [19] intranasally challenged ferrets with a range of titers of SARS-CoV-2 strain Victoria/1/2020 [20] (5 × 102, 5 × 104, and 5 × 106 PFU). It was shown that 5 × 104 and 5 × 106 PFU caused 100% infection; the dose of 500 PFU caused 1 infection among 6 ferrets (17%). Our dose-response curve with the k of 9.8 × 105 copies (airborne particle contribution level, 0.1) gave rise to similar infection risks of about 100%, 100%, and 15%, respectively, for the doses of 5 × 106, 5 × 104, and 5 × 102 PFU. The comparison with the ferret results is shown in Figure 2. The animal models are different from those for humans, and the conversion factor from plaque-forming units to virus copies is still uncertain. Nonetheless, the reasonable agreement is encouraging. Further studies are needed to evaluate and refine the developed dose-response relation.

As shown in Supplementary Figures 1–3, 2 fractions (40%, 100%) of the infected individuals for positive viral shedding and the 2 distributions log10(Evirus)~Normal(4, 0.5) and log10(Evirus)~Uniform(3, 5) were used to evaluate the sensitivities of the estimations to the chosen parameters. The variations of the dose-response curves among different settings were limited, demonstrating the stability of the estimations.

Infection Risk Assessment of Aerosol Transmission

The results indicate that the median infection risk to contract COVID-19 via the aerosol route is about 2.3 × 10–5 (95% confidence interval, 2.0 × 10–6 to 3.2 × 10–4) in a room with the area of 100 m2 with 1 ACH (Figure 3), which was more than 3 orders of magnitude lower than the risk due to close contact (about 12.8% within 1 m) based on the meta-analysis [4]. The infection risk due to close contact with an infected person is complicated and could be mainly attributed to the following 3 factors, as shown in Supplementary Figure 4: (1) respiratory droplets with a significant amount of liquid: produced by coughing, sneezing, singing, talking, or breathing; the droplets could be inhaled or deposited on mucous membranes; (2) aerosol (droplet nuclei after evaporation of the volatile part in small droplets): the exhaled plume is not fully diluted, and the aerosol concentration is high for close contact; (3) direct/indirect contact with the infected person: physical contact with the infected individual or the surfaces contaminated by the infected individual. It is extremely difficult to distinguish the contribution of each part. The meta-analysis indicated the overall close contact infection risk including all of the potential routes.

Figure 3.

Figure 3.

Open in a new tab

Influences of room size and ventilation on the infection risk via aerosol transmission. A, Infection risk via aerosol transmission in rooms of various sizes with ventilation rates of 1 air change per hour and 1 infected individual for 1 hour exposure. B, Infection risk via aerosol transmission in a 100-m2 room with different ventilation rates for 1 hour exposure.

It is suggested that the respiratory droplets might play an important role in transmission through close contact [1]. Measurements indicated that the viral shedding in respiratory droplets was comparable to the viral shedding in aerosols [5]. The exposure dose would be high if the respiratory droplets were inhaled or deposited on mucous membranes. A recent report from the Centers for Disease Control and Prevention (CDC) [21] also suggested respiratory droplets as a main route for transmission. The CDC report also suggested that spread from touching surfaces was not thought to be a common mode of transmission.

The risk via aerosol transmission might be used to approximate the infection probability for occupants of a room who had no close contact (close-distance interaction or indirect interaction through fomites) with an infected individual. Larger rooms can reduce the infection risk via aerosol transmission by enhancing the dilution of the airborne virus-laden particles. The decreasing rate of the risk was correlated with the area of the room, as shown in Figure 3A. The median risk decreased by about a factor of 4, from 2.3 × 10–5 to 5.1 × 10–6, when the room area increased in size from 100 m2 to 400 m2. The median risk increased to 2.4 × 10–4 in a room with the area of 10 m2. The ventilation rate had moderate effects on the infection risk due to the modulation of deposition. The median risk increased from 2.3 × 10–5 with 1 ACH to 5.2 × 10–5 with 0.1 ACH, as shown in Figure 3B.

DISCUSSION

The framework for the dose-response estimation was kept as simple as possible to avoid unnecessary uncertainties. The developed dose-response relation provides a tool to quantify the magnitude of the infection risk. The meta-analysis and evidence-based study provide a new opportunity to estimate the human dose-response relation. In the future, the uncertainties could be reduced by using new technology, for example, personal electronic devices, to record the distance, exposure duration, and environmental factors, which could greatly improve the quality of exposure dose estimation and thus the dose-response relation.

The developed dose-response relation could be used to quantify the magnitude of the infection risk via aerosol transmission. The uncertainties in the estimations were mainly due to the dose-response relation and the viral shedding. Despite the uncertainties, the assessment could still improve our understanding of the relative importance of different transmission routes. The median infection risk via aerosol transmission with 1 hour exposure (10–6 to 10–4) in the illustrative scenario was significantly lower than the risk caused by close contact (10–1).

Keeping an adequate distance is not enough to prevent the exposure to aerosol indoors. Wearing masks is helpful. The infection risk via aerosol transmission could increase for prolonged exposure durations, for example, at home and in the office. In addition, the expected number of infected cases could be considerable if there is a large number of exposed individuals, for example, in a nightclub. As a result, it is necessary to take precautions when there is the potential for aerosol transmission risk.

The ventilation rates are usually higher in healthcare facilities, which could reduce the infection risk. Increasing the ventilation to about 9 ACHs, which is normally used in healthcare facilities [14], made the risk about 3 times lower than the situation with 1 ACH [11]. However, the aerosol-generating procedures (AGPs) with patients are likely to generate higher viral shedding. Further information about viral shedding during AGPs is needed to better quantify the infection risk and protect clinicians.

Supplementary Data

Supplementary materials are available at Clinical Infectious Diseases online. Consisting of data provided by the authors to benefit the reader, the posted materials are not copyedited and are the sole responsibility of the authors, so questions or comments should be addressed to the corresponding author.

ciaa1675_suppl_Supplementary_Materials
Click here for additional data file. (791.5KB, docx)

Notes

Author contributions. J. W. conceived the study. J. W. and X. Z. designed the development procedures. X. Z. developed the calculation code. X. Z. and J. W. analyzed the results and wrote the article.

Potential conflicts of interest. All authors: No reported conflicts of interest. All authors have submitted the ICMJE Form for Disclosure of Potential Conflicts of Interest. Conflicts that the editors consider relevant to the content of the manuscript have been disclosed.

Materials and correspondence. The code for the calculation is available from J. W. (jing.wang@ifu.baug.ethz.ch) upon reasonable request.

References

  • 1. World Health Organization. Transmission of SARS-CoV-2: implications for infection prevention precautions (WHO Scientific Brief, July 9, 2020). WHO, 2020. Available at: https://www.who.int/publications/i/item/modes-of-transmission-of-virus-causing-covid-19-implications-for-ipc-precaution-recommendations. Accessed 7 November 2020.
  • 2. Morawska L, Milton DK. It is time to address airborne transmission of COVID-19. Clin Infect Dis 2020; 71:2311–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3. Watanabe T, Bartrand TA, Weir MH, Omura T, Haas CN. Development of a dose-response model for SARS coronavirus. Risk Anal 2010; 30:1129–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4. Chu DK, Akl EA, Duda S, et al. . Physical distancing, face masks, and eye protection to prevent person-to-person transmission of SARS-CoV-2 and COVID-19: a systematic review and meta-analysis. Lancet 2020; doi: 10.1016/s0140-6736(20)31142-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5. Leung NHL, Chu DKW, Shiu EYC, et al. . Author correction: Respiratory virus shedding in exhaled breath and efficacy of face masks. Nat Med 2020; 26:981. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6. Dediego ML, Pewe L, Alvarez E, Rejas MT, Perlman S, Enjuanes L. Pathogenicity of severe acute respiratory coronavirus deletion mutants in hACE-2 transgenic mice. Virology 2008; 376:379–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7. De Albuquerque N, Baig E, Ma X, et al. . Murine hepatitis virus strain 1 produces a clinically relevant model of severe acute respiratory syndrome in A/J mice. J Virol 2006; 80:10382–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8. Biguenet A, Bouiller K, Marty-Quinternet S, Brunel A-S, Chirouze C, Lepiller Q. SARS-CoV-2 respiratory viral loads and association with clinical and biological features. J Med Virol 2020; doi: 10.1002/jmv.26489 [DOI] [PubMed] [Google Scholar]
  • 9. van Kampen JJA, van de Vijver DAMC, Fraaij PLA, et al. . Shedding of infectious virus in hospitalized patients with coronavirus disease-2019 (COVID-19): duration and key determinants. medRxiv 2020; 2020.2006.2008.20125310, doi: 10.1101/2020.06.08.20125310 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10. Morawska L, Johnson GR, Ristovski ZD, et al. . Size distribution and sites of origin of droplets expelled from the human respiratory tract during expiratory activities. J Aerosol Sci 2009; 40:256–69. [Google Scholar]
  • 11. Zhang X, Ji Z, Yue Y, Liu H, Wang J. Infection risk assessment of COVID-19 through aerosol transmission: a case study of South China seafood market. Environ Sci Technol 2020; doi: 10.1021/acs.est.0c02895 [DOI] [PubMed] [Google Scholar]
  • 12. Adhikari U, Chabrelie A, Weir M, et al. . A case study evaluating the risk of infection from Middle Eastern respiratory syndrome coronavirus (MERS-CoV) in a hospital setting through bioaerosols. Risk Anal 2019; 39:2608–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13. Guha S, Hariharan P, Myers MR. Enhancement of ICRP’s lung deposition model for pathogenic bioaerosols. Aerosol Sci Technol 2014; 48:1226–35. [Google Scholar]
  • 14. Zaatari M, Nirlo E, Jareemit D, Crain N, Srebric J, Siegel J. Ventilation and indoor air quality in retail stores: a critical review (RP-1596). HVAC&R Res 2014; 20:276–94. [Google Scholar]
  • 15. Buonanno G, Stabile L, Morawska L. Estimation of airborne viral emission: Quanta emission rate of SARS-CoV-2 for infection risk assessment. Environ Int 2020; 141:105794. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16. Vuorinen V, Aarnio M, Alava M, et al. . Modelling aerosol transport and virus exposure with numerical simulations in relation to SARS-CoV-2 transmission by inhalation indoors. Saf Sci 2020; 130:104866. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17. Lai KAC, Nazaroff WW. Modeling indoor particle deposition from turbulent flow onto smooth surfaces. J Aerosol Sci 2000; 31:463–76. [Google Scholar]
  • 18. Sampath R, Hofstadler SA, Blyn LB, et al. . Rapid identification of emerging pathogens: coronavirus. Emerg Infect Dis 2005; 11:373–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19. Ryan KA, Bewley KR, Fotheringham SA, et al. . Dose-dependent response to infection with SARS-CoV-2 in the ferret model: evidence of protection to re-challenge. bioRxiv 2020; 2020.2005.2029.123810, doi: 10.1101/2020.05.29.123810 [DOI] [Google Scholar]
  • 20. Caly L, Druce J, Roberts J, et al. . Isolation and rapid sharing of the 2019 novel coronavirus (SARS-CoV-2) from the first patient diagnosed with COVID-19 in Australia. Med J Aust 2020; 212:459–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21. Centers for Disease Control and Prevention. How COVID-19 spreads. 2020. (updated 5 October 2020) Available at: https://www.cdc.gov/coronavirus/2019-ncov/prevent-getting-sick/how-covid-spreads.html. Accessed 7 November 2020.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ciaa1675_suppl_Supplementary_Materials
Click here for additional data file. (791.5KB, docx)

Articles from Clinical Infectious Diseases: An Official Publication of the Infectious Diseases Society of America are provided here courtesy of Oxford University Press

RESOURCES