Connecting pathological cellular mechanisms to large-scale seizure structures

Abstract

Epilepsy is a neurological disorder characterized by recurrent seizures, where abnormal electrical activity begins in a local brain area and propagates before terminating. In a recent study, Liou and colleagues used multiscale computational modeling to gain mechanistic insights into clinical seizure dynamics based on cellular-level biophysical properties.

Mechanistic understanding of epileptic seizures requires integration of the macroscale information provided by clinical electroencephalogram (EEG) with the cellular and synaptic properties of the underlying neuronal networks. Computational models that have previously been proposed for the study of seizure generation and spread fall into two broad categories. Phenomenological models such as the ‘Epileptor’ [1] utilize large-scale features of EEG to produce abstract depictions of transition states from normal to seizure state and back, but these models lack detailed analysis of the underlying physiological conditions. Models in the second category encompass changes in small-scale biophysical processes such as transmembrane chloride gradients [2] and intra- and extracellular potassium dynamics [3-4], but lack the wide field perspective to convey seizure dynamics as changes in multiple biophysical processes across many interconnected brain regions. This inability to resolve the micro- with the macroscale view has led to an overall disconnect in our comprehension of seizures [5].

To bridge this gap, Liou and colleagues [6] have recently proposed a biophysically inspired model of focal seizures that captures key aspects of seizure onset, propagation, evolution and termination, and which produces results consistent with EEG and multiunit array recordings in patients. Their model is instrumental in bridging how cellular and network interactions underlie the evolution of seizures.

To build their model, the authors first utilized a set of biophysically inspired parameters for generating a 2D neuronal framework. This framework contains excitatory model neurons that have two intrinsic leak and slow potassium conductances, as well as two synaptic excitatory and inhibitory conductances with static parameters based on previous experimentally recorded values. Within the framework, model neurons receive both local excitatory and inhibitory distance-dependent connections in addition to distance-independent inhibition. While this model does not spontaneously ‘seize’ and, therefore, is more a model of a healthy circuit in which parameters controlling the development of seizures can be tuned, one can trigger a ‘seizure’ in the model externally by delivering a transient excitatory input. Liou and colleagues showed that the resulting ictal wave in their model replicates what has been observed from patient recordings, namely, the development of a slow-outward wave that advances and recruits more neurons to expand the seizure space, and a fast-inward reverberation that causes repetitive bursting in the inner core.

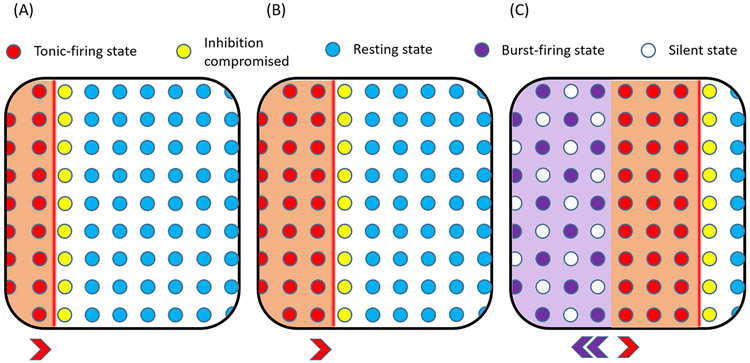
Propagation of the ictal wave in their model is based on two hypothesized changes taking place: i) usage-dependent exhaustion of inhibition, and ii) upregulation of adaptation intrinsic currents, which are represented by intracellular chloride accumulation and slow afterhyperpolarization (sAHP) conductance activation, respectively. The authors utilized a 1D version of their model to gain further insight into these physiological mechanisms responsible for ictal wave propagation (Figure 1). In their model, strong feedforward GABAergic inhibition from the ictal core results in intracellular chloride accumulation ahead of the ictal wavefront. This accumulation results in the breakdown of GABA_A receptor-mediated inhibition, leading neurons to transition from a resting to a tonic-firing state as they become part of the ictal wavefront. This state of excessive neuronal firing leads to activation of the sAHP conductance, which triggers a hyperpolarizing potassium current to curb neuronal excitability. As a result, the tonically firing neurons in the wavefront progress to a repetitive bursting state interspersed with periods of silence to form the periodic inward traveling waves.

Figure 1. Components of the ictal wavefront as modeled by Liou et al. [6].

A) Accumulation of intracellular chloride ahead of the slow ictal wavefront compromises inhibition. B) Inhibition is overcome, and neurons transition from a resting to a tonic firing state as they join the ictal wavefront. C) Tonic firing subsequently activates the slow afterhyperpolarization (sAHP) intrinsic cellular conductance, leading to a hyperpolarizing potassium current to curb neuronal excitability. The tonically firing neurons transition into periods of repetitive burst firing alternating with periods of silence, constituting periodic fast inward traveling waves.

As the ictal wavefront progresses in the model, it repeatedly encounters increasingly more inhibition, which has been recruited as the seizing area expands. This leads to slowing of the wavefront and, at the point where the propagation speed is no longer sufficient for the neurons to escape from sAHP-induced suppression of activity, the wavefront is extinguished. Seizure termination follows, characterized by clinicallyobserved trends in decreased peak firing rate, increased interburst intervals, decreased inward traveling wave speed, and increasing burst width.

The authors showed that their model can replicate critical features of seizures as seen from clinical recordings. For instance, model simulations show that different seizure-onset patterns, as seen in patients, can develop just by varying the distribution of recurrent inhibitory projections. In addition, the model was able to recapitulate the slower propagation of outward traveling waves compared to inward traveling ones, a phenomenon that has been observed in patient recordings. By incorporating spike-timing dependent plasticity, the authors further showed the emergence of seizure foci, while introducing noise into their model led to the development of persistent seizure activity as seen during status epilepticus.

While the model by Liou and colleagues is able to incorporate neurophysiological components to generate large-scale seizure dynamics similar to what is seen in human focal seizures, there are several future steps that can be taken to enable further testing of hypotheses regarding seizure dynamics. Similar to painting using only primary colors, this model is constrained by the limited number of parameters it incorporates, and their static set points. To fully capture the rich dynamics of a seizure while also enabling the manipulation of other components of interest, such as specific receptors or signaling molecules, requires the incorporation of more biophysically relevant parameters. This will enable testing, for instance, whether ‘knocking out’ specific molecular components that have been found experimentally to lead to the development of seizures can generate in the model seizures on its own, without the external input needed for seizure generation in the current version of the model. In addition, while this model can replicate key features of seizure dynamics without incorporating detailed interneuron characteristics, to be able to test hypotheses regarding the targeting of different interneuron populations for control of seizure spread would require their inclusion in the model.

Another area that could benefit from further exploration relates to the basic assumptions of the model, some of which may not hold true for all types of seizure. For example, as the authors point out, while intracellular chloride accumulation is a possible mechanism for usage-dependent exhaustion of inhibition, other mechanisms have been proposed that could also have a role. Indeed, the authors show that they were able to generate similar seizure dynamics using just a generalized inhibition exhaustion process. The model developed by Liou and colleages offers a useful basis for future studies along these lines. Altogether, the model represents a significant advance in linking pathological cellular mechanisms to large-scale seizure dynamics and has revealed general principles underlying seizure development and progression.