Single-Arm Trials with External Comparators and Confounder Misclassification: How Adjustment Can Fail

Abstract

Background:

“Single-arm trials” with external comparators that contrast outcomes in those on experimental therapy to real-world patients have been used to evaluate efficacy and safety of experimental drugs in rare and severe diseases. Regulatory agencies are considering expanding the role these studies can play; guidance thus far has explicitly considered outcome misclassification with little discussion of misclassification of confounding variables.

Objectives:

This work uses causal diagrams to illustrate how adjustment for a misclassified confounder can result in estimates farther from the truth than ignoring it completely. This theory is augmented with quantitative examples using plausible values for misclassification of smoking in real-world pharmaceutical claims data. A tool is also provided for calculating bias of adjusted estimates with specific input parameters.

Results:

When confounder misclassification is similar in both data sources, adjustment generally brings estimates closer to the truth. When it is not, adjustment can generate estimates that are considerably farther from the truth than the crude. While all non-randomized studies are subject to this potential bias, single-arm studies are particularly vulnerable due to perfect alignment of confounder measurement and treatment group. This is most problematic when the prevalence of the confounder does not differ between data sources and misclassification does, but can occur even with strong confounder-data source associations.

Discussion:

Researchers should consider differential confounder misclassification when designing protocols for these types of studies. Subsample validation of confounders, followed by imputation or other bias correction methods, may be a key tool for combining trial and real-world data going forward.

INTRODUCTION

Researchers are always searching for ways to leverage data to maximize efficiency. The historic gold standard for regulatory approval of new treatments has been the randomized controlled trial, but these experiments are costly in terms of both time and resources. Recently, regulators and stakeholders in healthcare research have expressed interest in using real-world data (RWD) to supplement these randomized experiments; the 21^st Century Cures Act has prompted particular discussion on the topic in the United States.^1–3

One potential use of RWD is the creation of external contemporary or historical untreated comparator (or control) cohorts with a disease of interest to stand-in for the placebo arm after early testing of a new treatment has been conducted in those with the disease.^4,5 This approach is particularly useful when new therapies appear so much better than standard care during early testing that it is difficult to ethically justify patients not receiving the treatment, when the pool of patients with the disease is too small to allow for sufficient outcomes in an internal untreated group, or when the disease is so fatal that benefits are almost certain to outweigh the risks to the individual.

As the treatment group is no longer randomized, these studies rely on methods and assumptions from non-experimental (or observational) research to estimate valid treatment effects. In particular, these methods assume that individuals in the two treatment arms are “exchangeable conditional on measured covariates.”⁶ Traditionally, outcome rates have been compared with expected rates from historical “controls” in such settings, often with limited to no attempt to adjust for differences in the two groups of patients.^7–9 More recently, the availability of routinely collected health data (e.g. insurance claims, electronic health records [EHR]) increasingly allows patients receiving investigational treatments to be compared with contemporary cohorts of patients that did not receive the treatment of interest. Access to individual-level data for the comparators has also enabled the use of propensity score-based methods or outcome modeling that do not rely on the assumption that historical rates of the outcome apply directly to the target population. One major single-arm trial compared those in a phase II test of blinatumomab with an external comparator drawn from EHR data and closely replicated the results of the subsequent randomized controlled trial mandated by FDA.^10,11

If external comparators are to be used more frequently alongside early studies, it is vital to investigate the methodologic challenges that may be particularly problematic in single-arm trials with external comparators such as differential confounder misclassification across treatment groups.^12,13 These studies are particularly vulnerable to this bias due to the perfect alignment between the differing methods of confounder measurement and the treatment groups. Specifically, prospectively enrolled individuals in the experimental arm are likely to have had more detailed, complete and accurate confounder assessment than those in an external comparator group. This work adds to existing literature on bias induced by misclassification of confounding variables by investigating the special case of external and/or historical ‘control’ groups. We use causal diagrams and simple quantitative examples to explore when and how adjustment for mismeasured confounders can remove, limit, or even add bias to estimates of treatment effect in the context of single-arm trials with external comparators.

METHODS

Worst case:

Suppose researchers are interested in evaluating a novel drug, Xylobegron, that laboratory tests suggest will markedly improve survival in patients diagnosed with a rare but deadly disease of the respiratory tract. While conducting the phase II trial of the drug in patients with the disease, the investigators noticed improved survival compared to expected outcomes based on existing literature. While waiting for the results of a large-scale randomized controlled trial, the FDA and the researchers decide to conduct a single-arm trial and use historical RWD to construct a comparator arm and potentially begin marketing the drug if those findings are favorable. Knowing that smoking has a strong negative association with survival after diagnosis with this rare disease (multiplying mortality risk by a factor of 5), and believing that smokers are less likely to enroll in the trial because of correlations between smoking, socioeconomic status, and inability to reach study centers, they pre-specify that the primary analysis will match each trial patient to two patients from the RWD with similar smoking status to control for the potential confounding.¹

When they combine the trial and RWD, they discover that most variables like age and sex appear similar between the phase II trial patients and the patients in the RWD. The exception is smoking, as they expected. Only 3.8% of the patients in the RWD smoke, while 20.85% of the trial participants do. The crude risk ratio for all-cause mortality with the new drug in the total cohort is 1.00 (95% C.I. 0.87, 1.28), while the risk ratio for all-cause mortality in the matched cohort is 0.80 (95% C.I. 0.68, 0.93), with a corresponding p value of 0.005. They report the matched estimate as the truth, stating that the difference between these two estimates was the result of confounding by smoking status and they have identified a statistically significant benefit for Xylobegron.

Unfortunately, the crude estimate was the correct one; the weighted estimate is considerably biased away from the null. Why is this the case? How can adjustment for a variable result in more biased estimates?

The problem is that there was never any difference in smoking rates between the two groups (20% of each group were smokers); the observed difference in smoking rates was entirely the result of the fact that smoking was measured by interviews with near-perfect sensitivity of 0.99 in the trial but via a claims-based algorithm with sensitivity of 0.15 in the RWD.

Explaining how these biases come about can be difficult outside of a dedicated mathematical framework. Causal diagrams, specifically directed acyclic graphs,^14,15 have been previously used to clarify problems of outcome and exposure misclassification.^16–18 Here, we apply them in the context of a study with an external comparator arm and potentially differential confounder misclassification.

Causal diagrams:

This situation can be encoded in the directed acyclic graphs in Figure 1: X represents Xylobegron; Y mortality; C “true” smoking; and C_measured the recorded value of smoking in the trial or RWD. In these graphs, an arrow drawn from one variable to another means that a change in the first variable would change the second. For example, altering someone’s smoking status (C) will result in a change in their mortality (Y); there is thus an arrow from C to Y in all three diagrams in Figure 1. When estimating the effect of X on Y, we generally want to adjust for variables that are causes of the two of them to close non-causal, or “backdoor,” paths that result in biased estimates.

Figure 1:

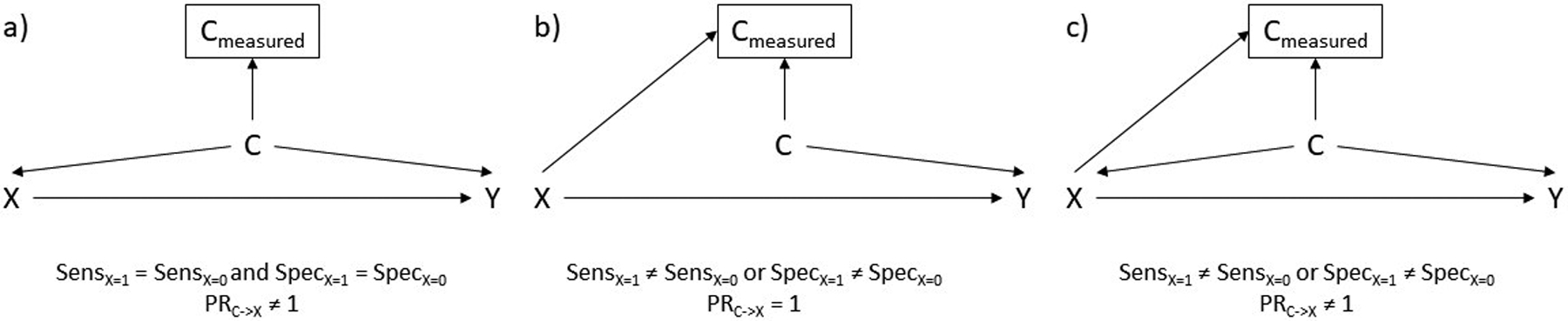
Potential directed acyclic graphs for the relationship between Xylobegron use (X), a confounder requiring measurement like smoking (C), and an outcome like mortality (Y). An arrow from one variable into another means that intervening on the first variable would result in a change in the second. A box around a variable means that we are adjusting for it. Sens_X=1 refers to sensitivity in the trial, while Sens_X=0 refers to sensitivity in the RWD. Similarly, Spec_X=1 refers to specificity in the trial while Spec_X=0 refers to specificity in the RWD. PR_C->X refers to the association between C and X.

Figure 1a represents the case where sensitivity and specificity of the in-person evaluation and the RWD review are identical and there is confounding by smoking status (i.e. there is a causal effect of smoking status on both trial enrollment and the outcome). Figure 1b represents the scenario where sensitivity or specificity differ between the trial and RWD but there is no confounding by smoking status (as was the case for Xylobegron); there is an arrow from X to C_measured because swapping someone from the trial to the RWD or vice versa could result in a change in their measured value of smoking. Figure 1c, the most plausible scenario, allows for differing sensitivity and specificity and confounding by smoking status. In all three diagrams the effect of X on Y is unbiased if investigators could match, weight by, or otherwise adjust for C (though it is unnecessary in Figure 1b). Unfortunately, they only have access to C_measured. What are the potential consequences for adjusting for C_measured, rather than C itself in each case?

In Figure 1a, adjusting for C_measured will reduce confounding bias by C provided that the confounder affects the outcome in the same direction in those with and without X (which is likely).^13,19 The amount of confounding that remains depends on the measurement error (i.e. sensitivity and specificity) of C_measured as well as the overall prevalence of C.

In Figure 1b and Figure 1c, however, they cannot expect results to be less biased. In Figure 1b, where there is no direct association between C and X, adjusting for C_measured opens a path between X and Y through C because C_measured is a consequence of both C and X (variables like C_measured are often referred to as colliders because an arrow from X and an arrow from C “collide” at C_measured).²⁰ This creates bias when the crude would have been unbiased. In Figure 1c, the combination of 1a and 1b, adjusting for C_measured partially controls for the confounding by C but opens up colliding path through C_measured. In examples with large differences in sensitivity or specificity between the trial and RWD, this can result in estimates that adjust for C_measured being more biased than the crude estimate. Unfortunately, this is the limit of what graphs can tell us.

Additional scenarios:

We can, however, turn to quantitative examples of Figure 1c. It is possible to encode this situation in an Excel spreadsheet given binary X, C, and Y (Supplemental Digital Content 1). While spreadsheets exist that allow researchers to correct for measurement error using observed data,²¹ this spreadsheet instead uses potential confounder prevalence, associations between the confounder, enrollment (or treatment), and the outcome, and differences in sensitivity and specificity to generate expected results.

Based upon input parameters, this spreadsheet calculates crude estimates of the effect of X on Y as well as estimates based on several different strategies for adjusting for C_measured, including various propensity-score based weighting methods (one method, standardized morbidity ratio (SMR) weighting, is asymptotically equivalent to propensity score matching) and restricting to those with a specific value of C_measured. Though each of these methods estimates a different treatment effect,²² if is no treatment effect heterogeneity all of them will be identical.²³ While we included a sample size field in the spreadsheet for those interested in examining how many individuals would be expected to be misclassified in the trial and RWD, the fields are calculated based upon expected proportions (allowing for fractions of people).

Table 1 lists the parameters involved in four distinct scenarios that include differential confounder misclassification. To ensure the treatment effect estimate was noticeably confounded, the association between the confounder and the outcome was set to a high constant risk ratio of 5.0. In scenario 1 and 2, we based our values for smoking measurement sensitivity (0.15 in claims data, 0.875 in trial data) on literature discussing the sensitivity of claims-based algorithms^24,25 and a meta-analysis of self-reported smoking.²⁶ Assuming specificity would be near-perfect in both settings, we used specificities of 0.99. In scenario 1, smoking was positively associated with enrollment (20% chance of enrollment for nonsmokers, 60% for smokers), while in scenario 2 it was negatively associated with enrollment (60% chance of enrollment for nonsmokers, 20% for smokers).

Table 1:

Key parameter values in four illustrative quantitative scenarios.

Scenario	Overall C prevalence	C->X association	Sensitivity	Specificity
Scenario 1: Plausible values, C increases P(X)	Rare (0.10)	PR = 3.00	Trial = 0.875 RWD = 0.15	Trial = 0.99 RWD = 0.99
Scenario 2: Plausible values, C reduces P(X)	Rare (0.10)	PR = 0.33	Trial = 0.875 RWD = 0.15	Trial = 0.99 RWD = 0.99
Scenario 3: Extreme example (lower RWD specificity)	Rare (0.10)	PR = 3.00	Trial = 0.99 RWD = 0.99	Trial = 0.99 RWD = 0.60
Scenario 4: Extreme example (lower RWD sensitivity)	Common (0.80)	PR = 0.33	Trial = 0.99 RWD = 0.60	Trial = 0.99 RWD = 0.99
Scenario 5: Blinatumomab-based example	Uncommon (0.27)	PR = 0.46	Trial = 0.99 RWD = 0.50	Trial = 0.99 RWD = 0.99

PR = prevalence ratio.

We then created two scenarios specifically designed to showcase where the adjusted estimate might be more biased than the crude one. In scenario 3, we examined the possibility of a “rare” (10% prevalence) confounder with lower specificity (0.60) in the RWD than the trial, creating a large number of false positives. In scenario 4, we considered a common (80% prevalence) confounder with lower sensitivity (0.60) in the RWD than the trial, creating a large number of false negatives.

Finally, we created scenario 5 based on the published results of the blinatumomab study¹⁰ whose findings were subsequently replicated by a randomized trial.¹¹ We treated second leukemic relapse without a graft as the confounder and six-month all-cause mortality as the outcome and then derived confounder-outcome and confounder-exposure associations from their stratified results. We then considered what their results might have been had they been using a RWD source with poorer sensitivity (0.50) to detect past treatment and cancer history, like commercial claims.

RESULTS

Table 2 lists the estimated risk ratios for the effect of X on Y (true risk ratio=1.0) in the crude and after adjustment. The crude risk ratio is confounded in all scenarios, albeit in different directions from the truth. In scenario 1, where smokers had triple the chance of trial enrollment than non-smokers, SMR weighted and non-smoker restricted estimates were closer to the truth, i.e. less biased, than the crude, while smoker-restricted estimates were more biased. When the confounder-enrollment association was reversed in scenario 2, risk ratios were generally as biased after adjustment as they were in the crude except when restricting to smokers.

Table 2:

Calculated RRs in the crude and after various methods of adjustment in four illustrative scenarios.

	Crude	SMR weighted	Strata CM=1	Strata CM=0
Scenario 1 RR (truth = 1.00)	1.65	1.29	1.73	0.98
Scenario 2 RR (truth = 1.00)	0.66	0.66	1.00	0.62
Scenario 3 RR (truth = 1.00)	1.65	1.78	3.29	1.01
Scenario 4 RR (truth = 1.00)	0.72	0.72	1.00	0.26
Scenario 5 RR (truth: varies)a	0.69	0.69	0.74	0.68

RR=risk ratio. SMR=standardized morbidity ratio.

^aBecause Scenario 5 used real confounder-outcome associations from the blinotumomab trial, the risk ratio was not constant across levels of C. It was 0.71 for the SMR-weighted population, 0.71 for those without C, and 0.75 for those with C.

In scenario 3, all estimates were more biased than the crude except for the one restricting to non-smokers, with restricting to smokers inducing the most bias. In scenario 4, adjustment resulted to similarly biased estimates to the crude, restricting to smokers removed all bias, and restricting to non-smokers resulted in extremely biased estimates. In scenario 5, results were only slightly biased regardless of adjustment for C, likely because the overall confounder-outcome association was small.

Somewhat counterintuitively, despite the high specificity for smoking (0.99) in both the trial and RWD restricting to smokers was not a good method for confounding control in scenario 1. Because of the low prevalence of smoking and very poor sensitivity in the RWD, patients in the RWD classified as smokers were more likely to be non-smokers (55%) than smokers (45%), leading to considerable confounding in the “measured smoker” stratum; so much, in fact, that the estimate in those patients is more biased than the crude. Had specificity been perfect (1.00), then those in the “measured smoker” stratum would have all been smokers and all confounding by smoking would have been removed when restricting to that population.

Figure 2 helps illustrate the importance of the direction of the confounder-enrollment association. This figure uses the sensitivity and specificity parameters from Scenarios 1 and 2 and fixes the probability of trial enrollment for those with C=0 at 0.50. We then varied the probability of trial enrollment for those with C=1 from 0.001 to 0.999 at 0.001 intervals to show the impacts of varying the magnitude and direction of the confounder-enrollment association on the crude (solid line) and SMR-weighted (dashed line) risk ratios.

Figure 2:

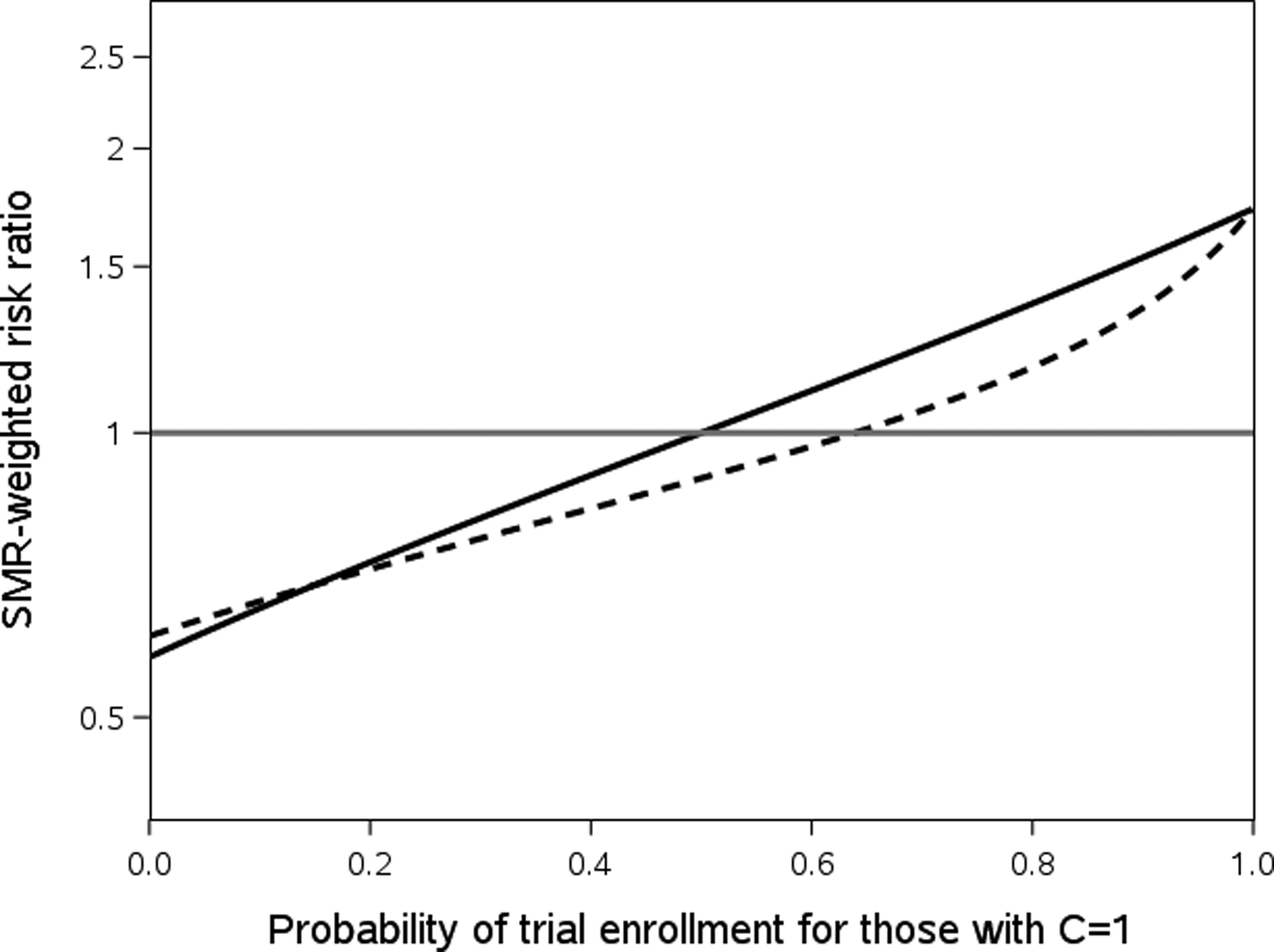
Crude risk ratios (solid black line) and SMR-weighted risk ratios (dashed black line) observed with Scenario 1 sensitivity and specificity when varying the probability of trial enrollment for those with C=1 while the probability of trial enrollment for those with C=0 is held fixed at 0.50. In all cases the true value is 1.00, the gray reference line.

When the association between the confounder and trial enrollment is strong and positive (the right side of the chart), the collider bias induced from the difference in sensitivity pushes the risk ratio downwards and closer to the null. Once the association between the confounder and trial enrollment is null or negative (the left side of the chart), controlling for the measured confounder still typically pushes the estimate downward, but it is now farther from the null than the crude.

DISCUSSION

Adding external comparator cohorts to single-arm trials represents a major potential application of RWD for researchers. When conducting such studies, perfect exposure and outcome classification are not enough; the fact that these non-randomized analyses must deal with the potential for confounding means they have to worry about confounders and how well confounders are measured in both cohorts as well. Unless investigators take steps to resolve differential confounder misclassification, controlling for variables that appear to be confounders can increase rather than decrease bias in estimates.

Whether this is the case depends on the overall prevalence of the confounder, the magnitude and direction of the association between the confounder and the data source, and the specific breakdown of specificity and sensitivity for the confounder in the trial and RWD. The association between the confounder and the outcome impacts the amount of bias, but not whether it increases or decreases after controlling for the measured confounder. It’s also important to note that if researcher identify a perfect comparator arm (i.e. one with no association between data source and confounders, like Figure 1b), then any differences observed in the prevalence of confounders are due to differential measurement error, and adjusting for them will only add bias to the estimates. Researchers should be especially wary of these problems when dealing with variables known to be poorly captured in RWD (e.g. body mass index or obesity,²⁷ smoking,²⁴ race and ethnicity,²⁸ and alcohol consumption), especially when they are unlikely to be associated with whether an individual participates in the experimental arm.

There are some ways to ameliorate these concerns.²⁹ Subsample validation of the RWD arm as well as linking trial data directly to a source of RWD for imputation can help ensure confounder measurement is no longer differential.^30–33 This allows investigators to be more comfortable assuming that their adjustment sets do not increase bias based on fewer and more plausible assumptions; unfortunately, it does not guarantee results closer to the truth than adjusting for the misclassified confounder. Sensitivity analyses for measurement error akin to those used in traditional non-experimental studies or more sophisticated tools like multiple bias modeling can also shed light on the robustness of results to these types of biases.^21,34,35 Additionally, there are situations where restricting to one strata of the confounder is a reliable technique for removing some or most of the bias from differential measurement error; while this is useful given perfect specificity (or perfect sensitivity), even narrow departures from perfection can result in sizeable remaining confounding within strata as we see in Scenario 1 and 2.

This work is by no means comprehensive. Additional analyses on the interplay of multiple confounders with correlated differential measurement error and how this bias could interact with treatment and outcome misclassification are vital. We hope that some future single-arm trials using RWD controls will build on this work by validating both outcomes and confounder measurement and allow a greater understanding of misclassification’s impact on real studies. Continuous confounders are another important area of investigation, particularly when random variation across data sources is also differential. The interplay of these misclassified covariates with other, better measured confounders is also a key area for further investigation. Finally, many single-arm studies use external comparator cohorts as benchmarks for survival outcomes like median time to progression or for log-rank tests, with or without adjustment for confounding. While differential confounder misclassification can be problematic regardless of the outcome in question, further investigation of the specific impacts on time-to-event or continuous outcomes would be valuable.

Conclusion

Conducting single-arm trials that integrate trial data with the kind of data used in non-experimental studies allows researchers to answer new and interesting questions but can create biases that are less common in the context of studies limiting themselves to one data source. Investigators need to think carefully about whether observed differences in covariates between the trial and RWD arms of these single-arm studies are real or an artifact of differential measurement error when deciding whether they want to use techniques to adjust for confounding.