Power and Sample Size Calculations for Genetic Association Studies in the Presence of Genetic Model Mis-Specification

Abstract

Introduction:

When analyzing data from large-scale genetic association studies, such as targeted or genome-wide resequencing studies, it is common to assume a single genetic model, such as dominant or additive, for all tests of association between a given genetic variant and the phenotype. However, for many variants, the chosen model will result in poor model fit and may lack statistical power due to model mis-specification.

Objective:

We develop power and sample size calculations for tests of gene and gene by environment interaction, allowing for mis-specification of the true mode of genetic susceptibility.

Methods:

The power calculations are based on a likelihood ratio test framework and are implemented in an open-source R package (“genpwr”).

Results:

We use these methods to develop an analysis plan for a resequencing study in idiopathic pulmonary fibrosis and show that using a 2-degree of freedom test can increase power to detect recessive genetic effects while maintaining power to detect dominant and additive effects.

Conclusions:

Understanding the impact of model mis-specification can aid in study design and developing analysis plans that maximize power to detect a range of true underlying genetic effects. In particular, these calculations help identify when a multiple degree of freedom test or other robust test of association may be advantageous.

Introduction

Genetic association studies remain an important study design for testing hypotheses related to the relationship between DNA polymorphism and biological or clinical traits. Many of these studies are now more focused than a genome-wide study as the results of genome-wide studies are used to design follow-up investigations of the impact of identified genetic risk variants. For example, some studies examine the association between disease-risk variants and the clinical features related to that disease, such as FEV1 in studies of COPD [1–3]. Other study designs use re-sequencing of a small portion of the genome identified in a larger study to further understand how many and which variants are contributing to an association signal identified by relatively sparse genotyping [4–7]. As such, there remains a need to estimate power and/or sample size in the design of genetic association studies.

Several tools for power and sample size calculations for genetic association studies are available [8–14], although many are specialized for specific study designs. For example, GWAPower performs power and sample size calculations for quantitative traits, assuming 1-degree of freedom tests (additive, dominant or recessive genetic effects) and allows users to specify effect sizes in terms of heritability [8]. CaTS was developed specifically to aid in the design 2-stage genetic association studies with a discrete phenotype and allows for multiplicative, recessive, additive and dominant genetic effects [14]. QUANTO is a power calculation tool for both discrete and quantitative phenotypes and for testing gene by environment interactions. QUANTO allows for additive, dominant or recessive genetic effects [9, 10]. ESSPRESSO is a flexible simulation-based approach to power and sample size calculations for both quantitative and discrete phenotypes and gene by environment interactions, while accounting for genotyping errors and phenotype mis-classification [15, 16]. Additive and binary genetic effects are allowed. GPC was originally developed for power calculations for variance component tests for quantitative traits, although other tests are also available[12].

While these tools are all helpful aids for study design, most assume that the model being tested represents the true underlying biological model, which is not known in practice. For example, many studies choose to assume an additive model for testing purposes, based on convenience and/or because it has been shown to be more robust to model misspecification than either a dominant or recessive model [17]. Previous simulation studies have demonstrated the loss of power that can occur when the statistical model is mis-specified (e.g. using an additive model when the true genetic model of susceptibility is recessive)[17–19]. Several robust test statistics have been proposed to address the issue of model mis-specification in the analysis of genetic association studies [20–29]. Popular approaches involve taking the maximum of test statistics assuming several plausible genetic models. For example, the MAX3 or So-Sham test statistic [18] takes a maximum of test statistics assuming additive, recessive and dominant models, with p-values appropriately adjusted to account for these multiple comparisons. While these robust tests have lower power than a correctly specified model, they perform well for additive, dominant and recessive tests and have higher power than an incorrect model [30, 31]. Another simple approach is to use a 2-degree of freedom test, sometimes referred to as a genotypic test, which does not impose any assumptions about the underlying genetic model. Simulation studies have shown that 2-degree of freedom tests are slightly less powerful than the robust tests described above for truly additive, dominant and recessive genetic effects; however, they are more powerful for other arbitrary genetic effects that do not follow these models, as is the case in overdominance. In addition, 2-degree of freedom tests were found to have the best efficiency robustness when arbitrary genetic effects were considered in addition to the standard genetic models, and have been recommended as a viable alternative to robust test statistics for genome wide scans [30–32].

When designing a genetic association study, it is important that the power calculations match the statistical analysis plan as closely as possible, as data analysis choices can influence statistical power [33]. However, most power and sample size calculation tools do not allow for model mis-specification or for the use of robust test statistics or 2-degree of freedom tests [19]. We know that using an incorrect model, a robust test statistic or a 2-degree of freedom test will result in lower power than a correctly specified model. Assuming that a single model is correct for all variants when performing sample size calculations may lead to an underpowered study. Understanding how model misspecification influences power and sample size calculations is essential to appropriately power genetic association studies and to develop robust analysis plans. Given the wide range of potential study parameters, including sample size, type of outcome, and expected strength of the associations, no one model is most powerful or appropriate for all studies.

To address this need, we have developed a power and sample size calculation tool, GENPWR, that allows calculation of power and sample size under model misspecification. Importantly, we include power calculations for a 2-degree of freedom test. As simulation studies have shown that these tests are slightly less powerful than robust test statistics for the most common genetic models, these calculations can serve as conservative estimates or lower bounds of power (or upper bounds on required sample size) for studies that plan to use robust test statistics in their analyses. GENPWR allows for both discrete and continuous phenotypes, as well as gene by environment interactions.

Materials and Methods

Notation and Models for Genetic Association

In this paper, we extend power and sample size calculations proposed by Gauderman (2002) to account for genetic model misspecification. For consistency, we follow Gauderman’s notation where possible [10]. Let Y be the phenotype of interest, either a binary disease trait or a continuous, normally distributed phenotype. If Y is a binary disease trait, define p_d as the prevalence of disease in the study population. If Y is a continuous, normally distributed measurement, let σ_Y be the standard deviation of the measurement in the study population.

Let G be the genotype at a candidate locus with risk allele A and alternative allele a and let q_A represent the risk allele frequency (RAF). Assuming Hardy-Weinberg equilibrium, the distribution of the genotypes is $P\left(g=AA\mid q_A\right)=q_A^2,P\left(g=aA\mid q_A\right)=2q_A\left(1-q_A\right)\text{ and }P\left(g=aa\mid q_A\right)={\left(1-q_A\right)}^2$. In order to perform statistical testing using a linear or logistic regression model, we must choose a genetic model and code the three possible genotypes into a genetic covariate or covariates, X (Table 1). However, the model that we assume for the pattern of inheritance may be incorrect, which can impact power to detect associations between phenotype and genotype. To allow greater flexibility, we might use two covariates to represent genotype, with X₁ as an indicator of genotype aA and X₂ as an indicator of gentoype AA. We refer to this as “genotypic” or “2 degree of freedom” (2df) coding.

Table 1:

Coding of Genetic Covariates for Inclusion in Regression Models

Model	Genotype	X1	X2
Dominant	aa	0	-
	aA	1	-
	AA	1	-
Additive	aa	0	-
	aA	1	-
	AA	2	-
Recessive	aa	0	-
	aA	0	-
	AA	1	-
2df	aa	0	0
	aA	1	0
	AA	0	1

For categorical Y, we consider the logistic regression model:

$$P(Y=1\mid X)=\frac{e^{{\beta }_0+X{\beta }_g}}{1+e^{{\beta }_0+X{\beta }_g}}$$

where $\frac{e^{{\beta }_0}}{1+e^{{\beta }_0}}$ is the probability of disease when X = 0 (or when X₁ = 0 and X₂= 0 for 2df coding) and $O{R}_g=e^{{\beta }_g}$ is the genetic odds ratio comparing X = 1 to X = 0 for dominant, recessive and additive coding. For 2df coding, β_g = (β_g1,_g2), with $e^{{\beta }_{g1}}$ representing the odds ratio comparing genotype aA to aa and $e^{{\beta }_{g2}}$ comparing AA to aa. For continuous Y, we use a linear regression model:

$$f(Y\mid X)={\beta }_0+X{\beta }_g+\epsilon$$

where β₀ is the baseline mean of Y, β_g is the genetic effect, and ε is a normally distributed error term with mean 0 and standard deviation σ_∈. Again, for 2df coding, β_g = (β_g1,_g2), with β_g1 representing the difference in means between aA and aa and β_g2 the difference between AA and aa. To perform power and sample size calculations, the parameters in the above models need to be specified. For the logistic regression model, OR_g and p_d are sufficient to define all model parameters, as β₀ can be calculated from these two quantities. For the linear model, β_g and σ_Y must be specified; from this, σ_∈ can be determined.

True vs. Test Models

As mentioned in Section 2.1, the coding of the genotype covariates for inclusion in the statistical model relies on assumptions about the pattern of inheritance for genetic susceptibility, which may or may not hold for any given candidate gene. For example, we may use dominant coding in our statistical model when in reality the effect of the risk allele on the outcome is additive. Define X* as the true or correct coding of genetic susceptibility for a gene, and X^M as the coding in the model used to perform statistical testing. Define ${\beta }^{*}={\left({\beta }_0^{*},{\beta }_g^{*}\right)}^{\prime }$ as the true values of β₀ and β_g when genotype is correctly included in the model as X* and ${\beta }^M={\left({\beta }_0^M,{\beta }_g^M\right)}^{\prime }$ as the values of β₀ and β_g when genotype is included in the model as X^M. Similarly, let ${\sigma }_{ϵ}^{*}$ be the value of σ_∈ when genotype is coded as X* and ${\sigma }_{ϵ}^M$ be the value when genotype is coded as X^M.

Calculation of Power and Sample Size

Following Gauderman (2002), we base our power and sample size calculations on likelihood ratio tests. The likelihood ratio test statistic is Λ = 2(L¹ − L⁰), where L¹ is the log likelihood of the full model and L⁰ is the log likelihood of the reduced model, where β_g is constrained to its null value of 0. Under the null hypothesis, $\Lambda ~{\chi }_{\text{p}}^2$, where p is the difference in the number of parameters between the full and reduced models; for additive, dominant, and recessive tests p = 1, while for the 2df test p=2. Under the alternative hypothesis, Λ follows a non-central chi-square distribution with the non-centrality parameter equal to Λ [34].

For a single observation, the log likelihood for the logistic regression model is:

$$\text{log}\left[L^1\left({\beta }^M\right)\right]=Y\text{log}\left(\frac{{\text{e}}^{{\beta }_0^M+X^M{\beta }_g^M}}{1+{\text{e}}^{{\beta }_0^M+X^M{\beta }_g^M}}\right)+(1-\text{Y})\text{log}\left(\frac{1}{1+{\text{e}}^{{\beta }_0^M+X^M{\beta }_g^M}}\right)$$

For the linear regression model, the log likelihood is:

$$\text{log}\left[L^1\left({\beta }^M\right)\right]=-0.5\text{log}\left(2\pi {\sigma }_{ϵ}^{2\text{M}}\right)-\frac{{\left(\text{Y}-{\beta }_0^{\text{M}}-{\mathrm{X}}^{\text{M}}{\beta }_{\mathrm{g}}^{\text{M}}\right)}^2}{2{\sigma }_{ϵ}^{2\text{M}}}$$

The likelihoods depend on the value of Y. Therefore, we calculate the expected log likelihood, given the true parameter values, β*, X*, q_A, p_d and ${\sigma }_{ϵ}^{*}$. This differs from the method proposed by Gauderman et al [10], since we allow the coding of the genetic covariate to differ between the true pattern of genetic susceptibility and the coding used in statistical tests of association. In other words, we allow for X^M ≠ X* and β^M ≠ β*.

For the logistic regression model the expected log likelihood is:

$$\begin{gathered} E\left(\text{log}\left[L\left({\beta }^M\right)\right]\right)=\sum _{G}P\left(g\mid q_A\right)\left[E(Y\mid G=g)\text{log}\left(\frac{e^{{\eta }_g^M}}{1+e^{{\eta }_g^M}}\right)+E(1-Y\mid G=g)\text{log}\left(\frac{1}{1+e^{{\eta }_g^M}}\right)\right] \\ =\sum _{G}P\left(g\mid q_A\right)\left[\frac{e^{{\eta }_g^{*}}}{1+e^{{\eta }_g^{*}}}\text{log}\left(\frac{e^{{\eta }_g^M}}{1+e^{{\eta }_g^M}}\right)+\frac{1}{1+e^{{\eta }_g^{*}}}\text{log}\left(\frac{1}{1+e^{{\eta }_g^M}}\right)\right] \end{gathered}$$

where ${\eta }_g^{*}={\beta }_0^{*}+X_g^{*}{\beta }_g^{*}$ and ${\eta }_g^M={\beta }_0^M+X_g^M{\beta }_g^M$ under the alternative hypothesis and ${\eta }_g^M={\beta }_0^M$ under the null hypothesis. $X_g^{*}$ is the value of X* for genotype g and $X_g^M$ is the value of X^M for genotype g. For the linear regression model:

$$\begin{gathered} E\left(\text{log}\left[L\left({\beta }^M\right)\right]\right)=\sum _{G}P\left(g\mid q_A\right)\left\{-0.5\text{log}\left(2\pi {\sigma }_{ϵ}^{2M}\right)-E\left[\frac{{\left(Y-{\eta }_g^M\right)}^2}{2{\sigma }_{ϵ}^{2M}}\right]\right\} \\ =\sum _{G}P\left(g\mid q_A\right)\left\{-0.5\text{log}\left(2\pi {\sigma }_{ϵ}^{2M}\right)-\frac{{\sigma }_{ϵ}^{2*}+{\left({\eta }_g^{*}\right)}^2-2{\eta }_g^{*}{\eta }_g^M+{\left({\eta }_g^M\right)}^2}{2{\sigma }_{ϵ}^{2M}}\right\} \end{gathered}$$

Power and/or sample size can be calculated using these expected likelihoods as described by Gauderman et al [10].

Extensions for Tests of Gene × Environment Interactions

The above framework can easily be extended to tests of gene × environment interaction. Let E be an exposure or environmental factor, which can be either categorical or continuous. For continuous E, we assume E is normally distributed with standard deviation σ_e. For categorical E, we define p_e as the probability of exposure in the study population. We assume independence of the exposure and genotype in the population.

Again, we consider two basic models to describe the association of genotype, environment and the outcome, a logistic regression for categorical Y and a linear regression for continuous Y. For the logistic regression model:

$$P(Y=1\mid X,E)=\frac{e^{{\beta }_0+X}{\beta }_g+E{\beta }_e+XE{\beta }_{ge}}{1+e^{{\beta }_0+X{\beta }_g+E{\beta }_e+XE{\beta }_{ge}}}$$

where $\frac{e^{{\beta }_0}}{1+e^{{\beta }_0}}$ is the probability of disease when X = E = 0, $O{R}_g=e^{{\beta }_g}$ is the genetic odds ratio when E = 0, $O{R}_e=e^{{\beta }_e}$ is the odds ratio for the environment when G = 0, and $O{R}_{ge}=e^{{\beta }_{ge}}$ is the interaction odds ratio. For the linear regression model:

$$f(Y\mid X)={\beta }_0+X{\beta }_g+E{\beta }_e+XE{\beta }_{ge}+\epsilon$$

where β₀ is the baseline mean of Y, β_g is the genetic effect, β_e is the environment effect, β_ge is the interaction effect, and ε is a normally distributed error term with mean 0 and standard deviation σ_∈. To perform power and sample size calculations for the logistic regression model, OR_g, OR_e, OR_ge, p_d, and either p_e or σ_e are sufficient to define all model parameters, as β₀ can be calculated from these quantities. For the linear model, β_g, β_e, β_ge, σ_Y, and either p_e or σ_e must be specified; from this, σ_∈ can be determined.

For a categorical environmental factor, the expected log likelihood for the logistic regression model is:

$$E\left(\text{log}\left[L\left({\beta }^M\right)\right]\right)=\sum _E\sum _{G}P\left(X_e\mid p_e\right)P\left(g\mid q_A\right)\left[\frac{e^{{\eta }_{ge}^{*}}}{1+e^{{\eta }_{ge}^x}}\text{log}\left(\frac{e^{{\eta }_{ge}^M}}{1+e^{{\eta }_{ge}^M}}\right)+\frac{1}{1+e^{{\eta }_{ge}^{*}}}\text{log}\left(\frac{1}{1+e^{{\eta }_{ge}^M}}\right)\right]$$

where ${\eta }_{ge}^{*}={\beta }_0^{*}+X_g^{*}{\beta }_g^{*}+X_e{\beta }_e^{*}+X_g^{*}{X}_e{\beta }_{ge}^{*}$, ${\eta }_{ge}^M={\beta }_0^M+X_g^M{\beta }_g^M+X_e{\beta }_e^M+X_g^M{X}_e{\beta }_{ge}^M$ under the alternative hypothesis and ${\eta }_{ge}^M={\beta }_0^M+X_g^M{\beta }_g^M+X_e{\beta }_e^M$ under the null hypothesis. For the linear regression model:

$$E\left(\text{log}\left[L\left({\beta }^M\right)\right]\right)=\sum _E\sum _{G}P\left(X_e\mid p_e\right)P\left(g\mid q_A\right)\{-0.5\text{log}\left(2\pi {\sigma }_{ϵ}^{2M}\right)-\frac{{\sigma }_{ϵ}^{2*}+{\left({\eta }_{ge}^{*}\right)}^2-2{\eta }_{ge}^{*}{\eta }_{ge}^M+{\left({\eta }_{ge}^M\right)}^2}{2{\sigma }_{ϵ}^{2M}}\}$$

For a continuous environment variable, the summations over E can be replaced with an integral:

$$E\left(\text{log}\left[L\left({\beta }^M\right)\right]\right)=\frac{1}{\sqrt{(}2\pi {\sigma }_e^2)}\int e^{\frac{X_e^2}{2{\sigma }_e^2}}\left[\sum _{G}P\left(g\mid q_A\right)E\left(\text{log}\left[L\left({\beta }^M\right)\right]\mid G=g,E=X_e\right)\right]d{X}_e$$

Power and sample size can be computed as described in Gauderman to test for ${\beta }_{ge}^M=0$, using the expected log likelihoods $E\left(\text{log}\left[L\left({\beta }_0^M,{\beta }_g^M,{\beta }_e^M,{\beta }_{ge}^M\right)\right]\right)$ and $E\left(\text{log}\left[L\left({\beta }_0^M,{\beta }_g^M,{\beta }_e^M\right)\right]\right)$ for the alternative and null hypotheses, respectively.

Comparison of Power Across Study Designs

In Figures 1 and 2, we depict how power to detect an odds ratio of 1.5 in a case control GWA study changes as a result of differing sample size, significance level, RAF and proportion of cases in the study population. In Figures 3 and 4 we focus on variants with relatively low RAF’s ranging from 0.005 to 0.05. As expected, higher sample sizes and less stringent significance thresholds result in increased power for both RAF > 0.05 and < 0.05. In Figures 2 and 4 we see that a balanced study design, with a 1:1 ratio of cases and controls results in the higher power than study designs with either 25% cases or 75% cases for both RAF > 0.05 and < 0.05.

Fig. 1.

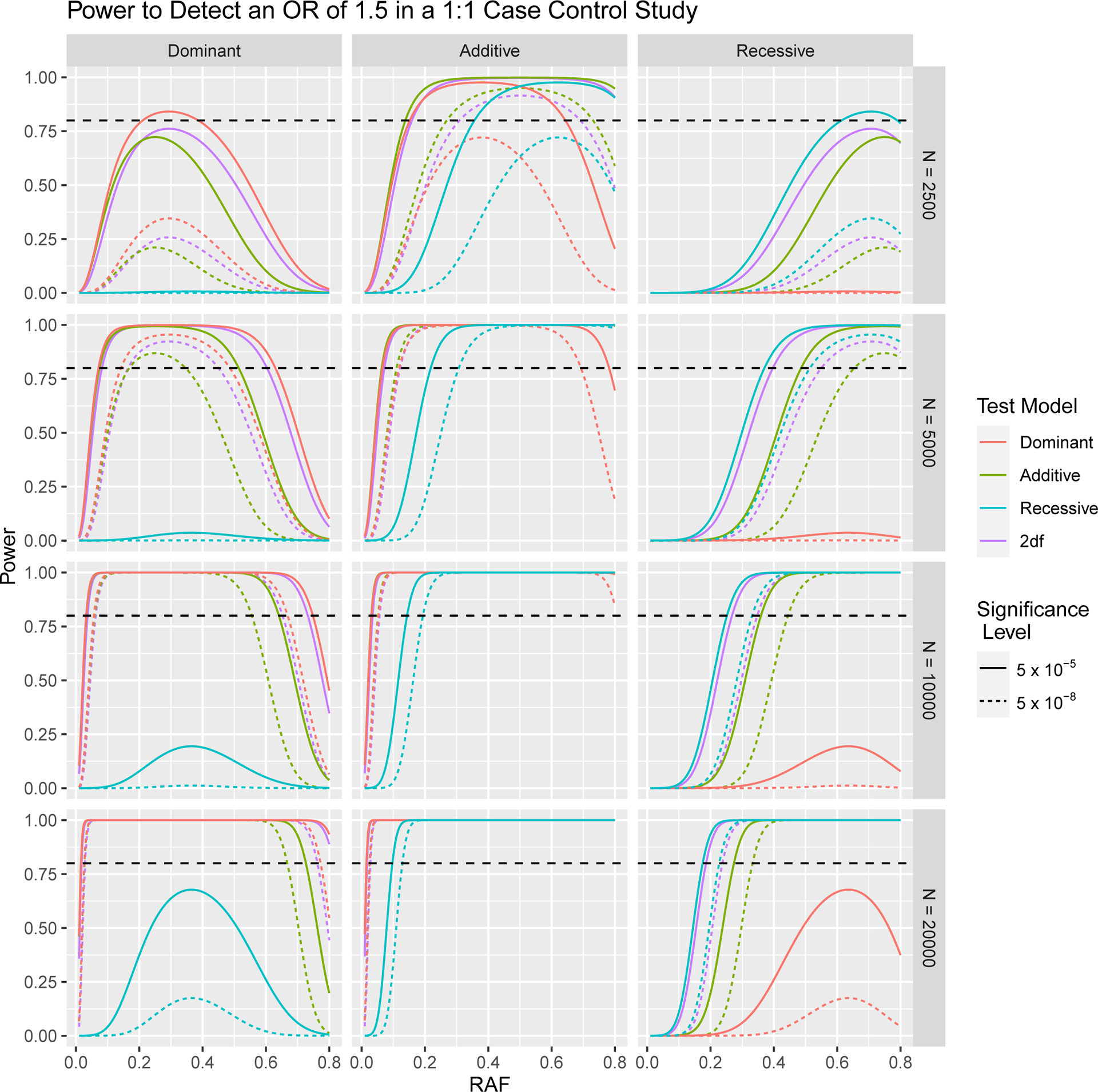
Power to Detect an Odds Ratio of 1.5 in 1:1 Case Control Study with a Total of N Subjects, at 5 × 10⁻⁵ and 5 × 10⁻⁸ Significance Levels. The horizontal dashed line indicates 80% power.

Fig. 2.

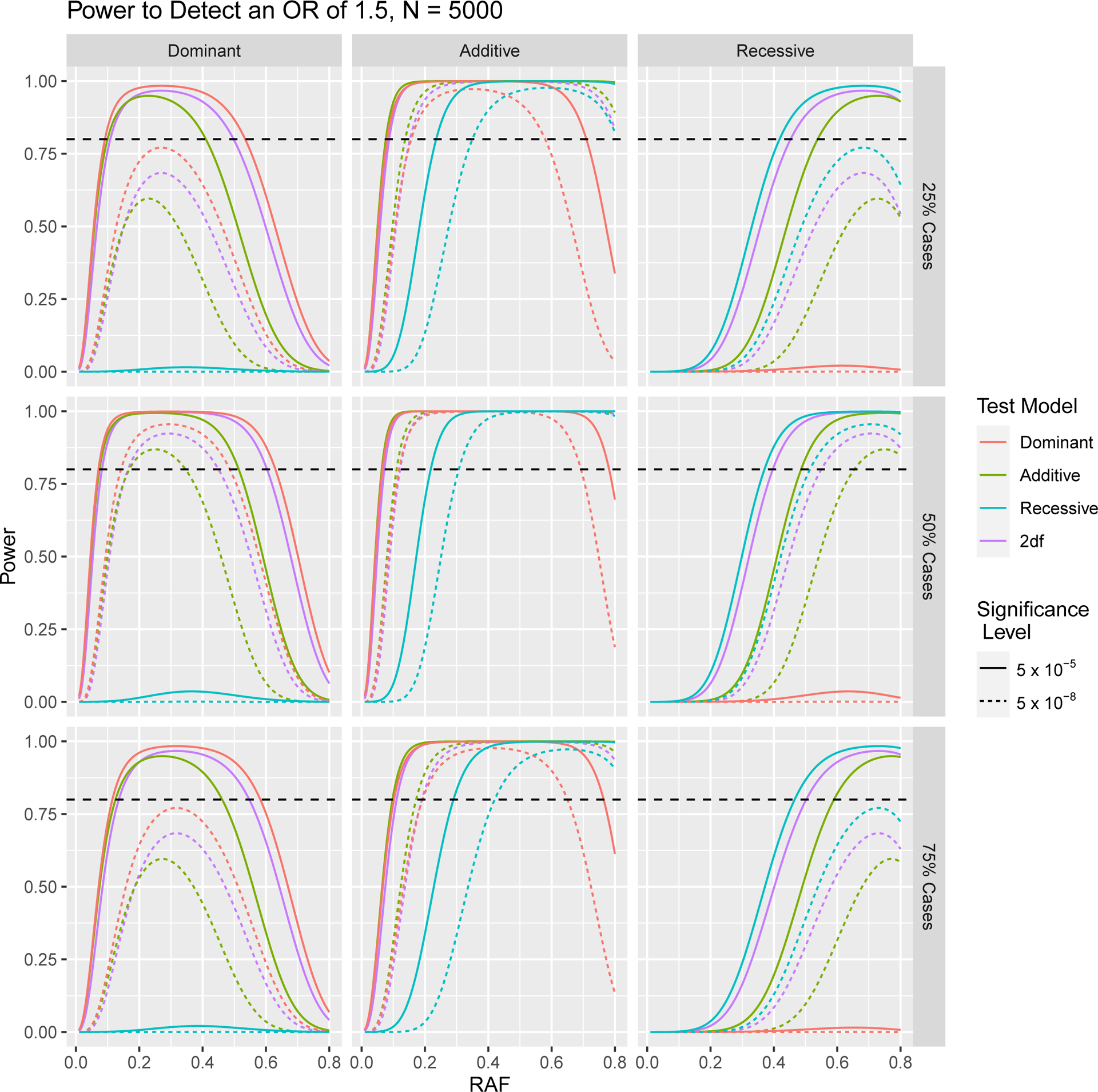
Power to Detect an Odds Ratio of 1.5 in Case Control Study with a Total of 5,000 Subjects for Different Ratios of Cases to Controls, at 5 × 10⁻⁵ and 5 × 10⁻⁸ Significance Levels. The horizontal dashed line indicates 80% power.

Fig. 3.

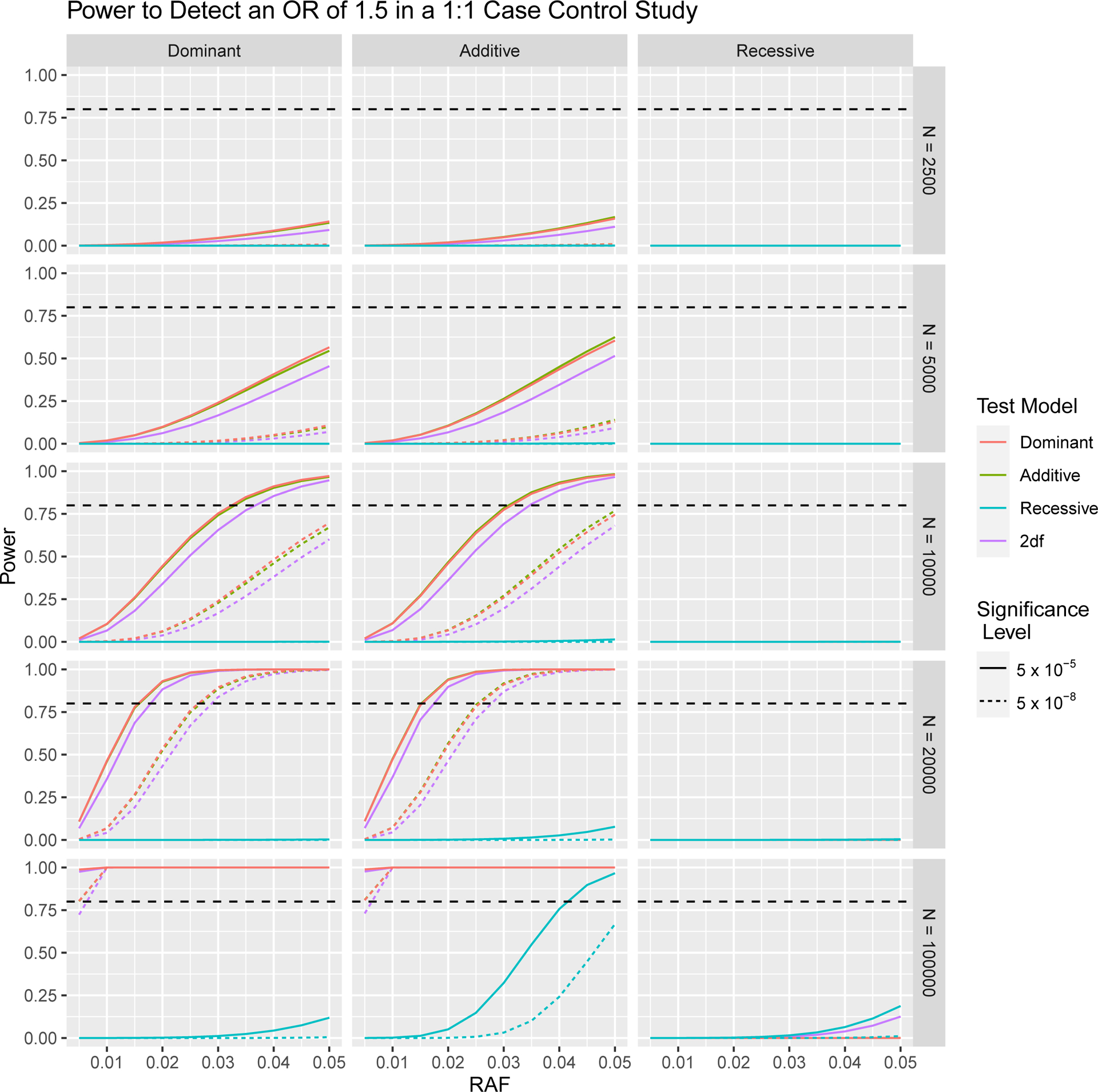
Power to Detect an Odds Ratio of 1.5 in 1:1 Case Control Study with a Total of N Subjects, at 5 × 10⁻⁵ and 5 × 10⁻⁸ Significance Levels at Low RAFs. The horizontal dashed line indicates 80% power.

Fig. 4.

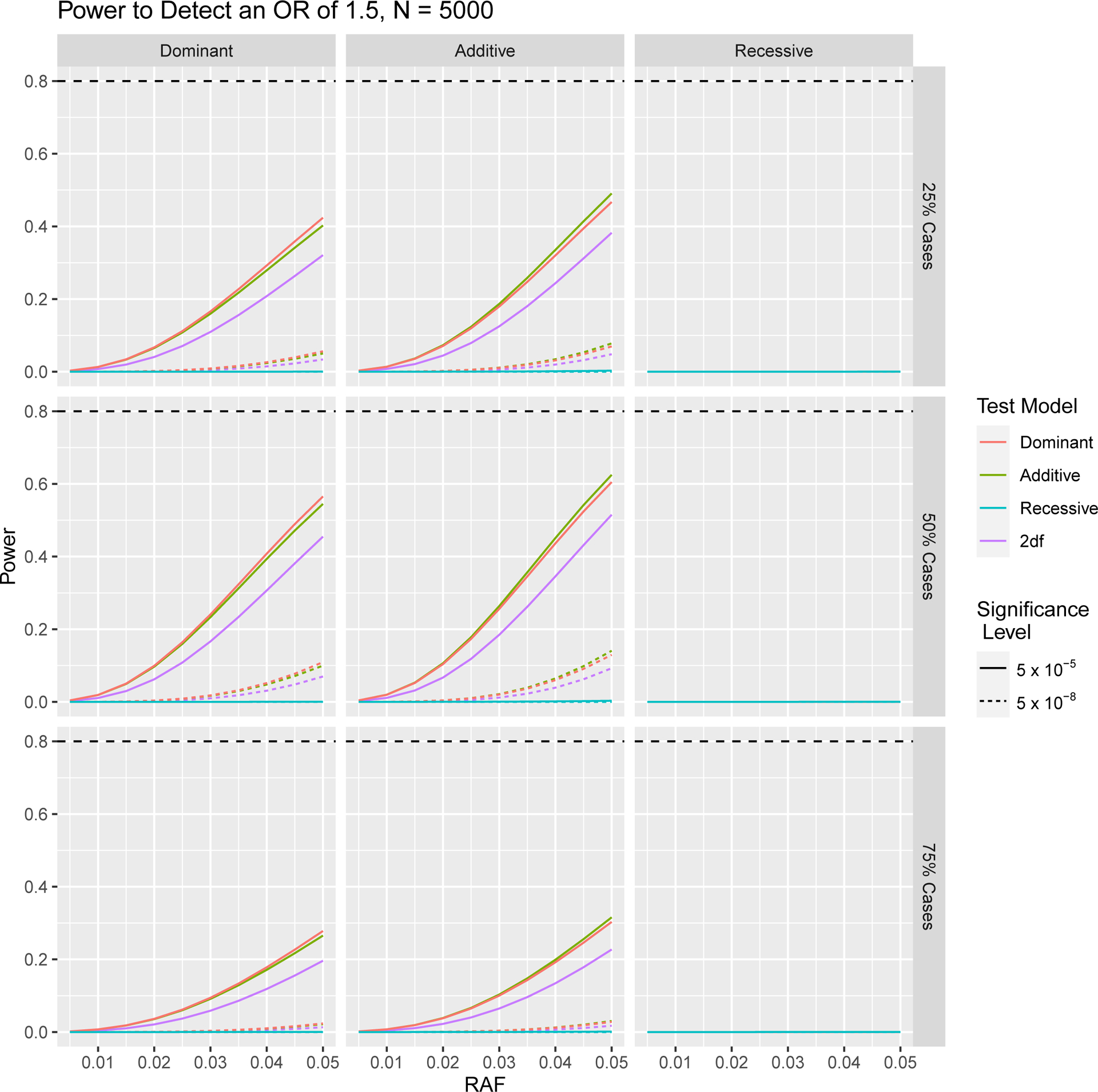
Power to Detect an Odds Ratio of 1.5 in Case Control Study with a Total of 5,000 Subjects for Different Ratios of Cases to Controls, at 5 × 10⁻⁵ and 5 × 10⁻⁸ Significance Levels at Low RAFs. The horizontal dashed line indicates 80% power.

As expected, the correctly specified model always has the highest power to detect an OR of 1.5 across the range of RAFs; however, in practice, the correct model is unknown. The relative performance of incorrectly specified models and the 2df model depends on the RAF, the sample size, the significance level and the odds ratio to detect. For variants that act in a dominant manner, the additive model has higher power than the 2df model for lower RAF, but lower power for higher RAF. A similar pattern is seen when using 2df and dominant coding to test truly additive genetic effects. The exact RAF at which the power curves for the 2df test and the mis-specified additive or dominant test cross depends on the sample size, significance threshold, ratio of cases to controls and OR to detect. With increasing sample size, the RAF beyond which 2df tests have higher power decreases. For example, assuming a 5 × 10⁻⁸ significance level and a 1:1 case control design, with a total sample size of 5,000, the 2df test has higher power to detect an additive genetic effect than the dominant test for all RAF greater than 14.5%, while with 20,000 subjects, the 2df test has higher power for all RAF greater than 8.5%. This RAF also decreases with less stringent significance thresholds and larger detectable OR’s.

For truly recessive effects, the 2df test has higher power than either the additive or dominant models, particularly at lower RAF. Notably, for low RAF there is very low power to detect recessive effects, even when using a correctly specified model, as the probability of observing a subject homozygous for the risk allele becomes extremely low. For example, with a RAF of 0.01 and sample size of 5,000, we would expect < 1 subject homozygous for the risk allele. In the absence of subjects with the aa genotype, the additive, dominant and genotypic tests become equivalent. We see that power for these tests becomes increasingly similar as RAF declines, regardless of the true genetic effect.

Example Modeling Strategies for GWA Study with N = 5,000

We illustrate how these results could be used to develop analysis plans for a 1:1 case control GWA study design with total sample size of 5,000, assuming a 5 × 10⁻⁸ level is used to determine statistical significance. With a sample size of 5,000, additive odds ratios of 1.5 can be detected with 80% power with either the dominant, additive or 2df models for RAF ≥≈ 12% (12%, 11.5%, and 12.5%, respectively, Table 2). For truly additive effects, the 2df test has higher power than the dominant test for all RAF greater than 14.5%.

Table 2:

Smallest Risk Allele Frequency (RAF) with at Least 80% Power to Detect an Odds Ratio of 1.5 for a 1:1 Case Control Study with a Total of N Subjects, at 5 × 10⁻⁸ Significance Level

		True Mode of Genetic Susceptibility
N	Model Coding	Dominant	Additive	Recessive
5,000	Dominant	0.145	0.120	-
	Additive	0.170	0.115	0.655
	Recessive	-	0.310	0.515
	2df	0.165	0.125	0.550
20,000	Dominant	0.030	0.030	-
	Additive	0.030	0.030	0.335
	Recessive	-	0.130	0.230
	2df	0.030	0.030	0.240

For variants that act in a dominant manner, using the correctly specified dominant model coding results in greater than 80% power to detect an OR of 1.5 for all RAF ≥ 14.5%, while for additive and 2df coding, greater than 80% power is achieved for RAF ≥ 17% and 16.5% respectively (Table 2). For truly dominant effects, the 2df test has higher power than the additive test for all RAF greater than 15.5%.

For recessive variants, no testing model has power greater than 80% to detect an OR of 1.5 for RAF < 50%. However, moderate size recessive OR’s can be detected at a RAF of 30% using a 2df or recessive model (Table 3. Given these power curves, we would recommend using the 2df test or another robust test of association for all variants with RAF greater than 15.5%, as this model has higher power than an incorrectly specified dominant or additive model. For variants with RAF below 15.5%, we would suggest using either the additive or dominant test, since there is little power to detect recessive odds ratios and these tests have higher power than the 2df test to test for additive or dominant effects in this RAF range (Figure 1, second row). However, it should be noted that power drops below 50% for all tests for RAF < 8%; we would suggest considering alternative testing strategies, such as a grouped variant testing method for these low RAFs.

Table 3:

Detectable Odds Ratios for a 1:1 Case Control Study with a Total of N Subjects, at 80% Power and 5 × 10⁻⁸ Significance Level

			True Mode of Genetic Susceptibility
N	qA	Model Coding	Dominant	Additive	Recessive
			Detectable OR
5,000	0.1	Dominant	1.58	1.55	>100
		Additive	1.60	1.53	>100
		Recessive	15.10	3.59	10.39
		2DF	1.61	1.56	12.53
	0.3	Dominant	1.43	1.36	27.85
		Additive	1.48	1.32	2.63
		Recessive	3.26	1.51	1.88
		2DF	1.45	1.33	1.94
20,000	0.1	Dominant	1.26	1.24	>100
		Additive	1.26	1.23	>100
		Recessive	3.12	1.68	2.56
		2DF	1.27	1.25	2.68
	0.3	Dominant	1.19	1.16	2.95
		Additive	1.22	1.15	1.59
		Recessive	1.79	1.23	1.37
		2DF	1.20	1.15	1.39

Application to a Re-Sequencing Study of Idiopathic Pulmonary Fibrosis

We use these methods to develop an analysis plan for a study of gene by environment interaction. Idiopathic pulmonary fibrosis (IPF) is a progressive fibrotic lung disease with a median survival of 3 years [35]. Studies of both familial and sporadic disease have identified rare mutations in telomerase (TERT, TERC, RTEL1, and PARN) and surfactant protein (SFTPC and SFTPA2) genes [36–39] and common variants in 12 genetic loci [40–43]. The strongest known risk factor for both familial and sporadic IPF is a polymorphism in the distal promoter region of MUC5B gene, rs35705950. The risk variant is common (10% frequency) among individuals of European ancestry and acts in an additive fashion, with each additional risk allele resulting in approximately a 5 times increase in the odds of IPF. In comparison, other polymorphisms associated with IPF have odds ratios ranging from approximately 1.25 to 1.5 [44].

In addition to these genetic polymorphisms, other potential risk factors for the development of IPF have been identified, including environmental and occupational exposures, tobacco smoking, and comorbidities such as gastroesophageal reflux disease. Meta-analyses have found that odds of IPF are 1.58 times higher in ever-smokers compared to never smokers (95% CI 1.27–1.97) [45]. The prevalence of ever-smoking in IPF cases has been reported at 72% vs. 63% in age, sex and geographically matched controls [46] and there may be a dose response relationship, with those with longer smoking histories having increased odds of disease [47].

An important question is whether the effect of smoking on the odds of IPF is modified by genetic risk factors. For example, genetic variants that lead to over-expression of the MUC5B mucin may impair mucociliary function [48]. This may in turn cause excess retention of inhaled substances, such as cigarette smoke, and could increase the potential for inhaled substances to damage the lungs. We develop an analysis plan to test for gene by smoking interactions in a cohort of 3,624 cases with IPF and 4,442 controls. Subjects in the cohort have previously had targeted, deep sequencing in regions with GWAS signals associated with IPF. Our analysis decisions are informed by considering power to detect a gene by smoking interaction odds ratio of 1.5, 1.75 and 2, assuming a 5 × 10⁻⁵ significance level, chosen based on the number of variants available for analysis. We perform power calculations assuming genetic odds ratios of 1.25, 1.5, and 5, based on the range of effects seen in previous studies of IPF and assume a 1.6 odds ratio for ever-smoking and an ever-smoking prevalence of 67%.

Power curves to detect gene by smoking interaction odds ratios of 1.5, 1.75 and 2 are presented in Figures 5, 6, and 7. First we note that results for OR_g of 1.25 and 1.5 are very similar to one another and that these results largely follow the same patterns as the tests for genetic association seen in Section 3, with the correct test being the most powerful. For OR_g of 1.25 and 1.5, we again see that for dominant (additive) variants, a mis-specified additive (dominant) test is more powerful than the 2df test only for lower RAF. For recessive variants, the 2df test is more powerful than additive or dominant tests.

Fig. 5.

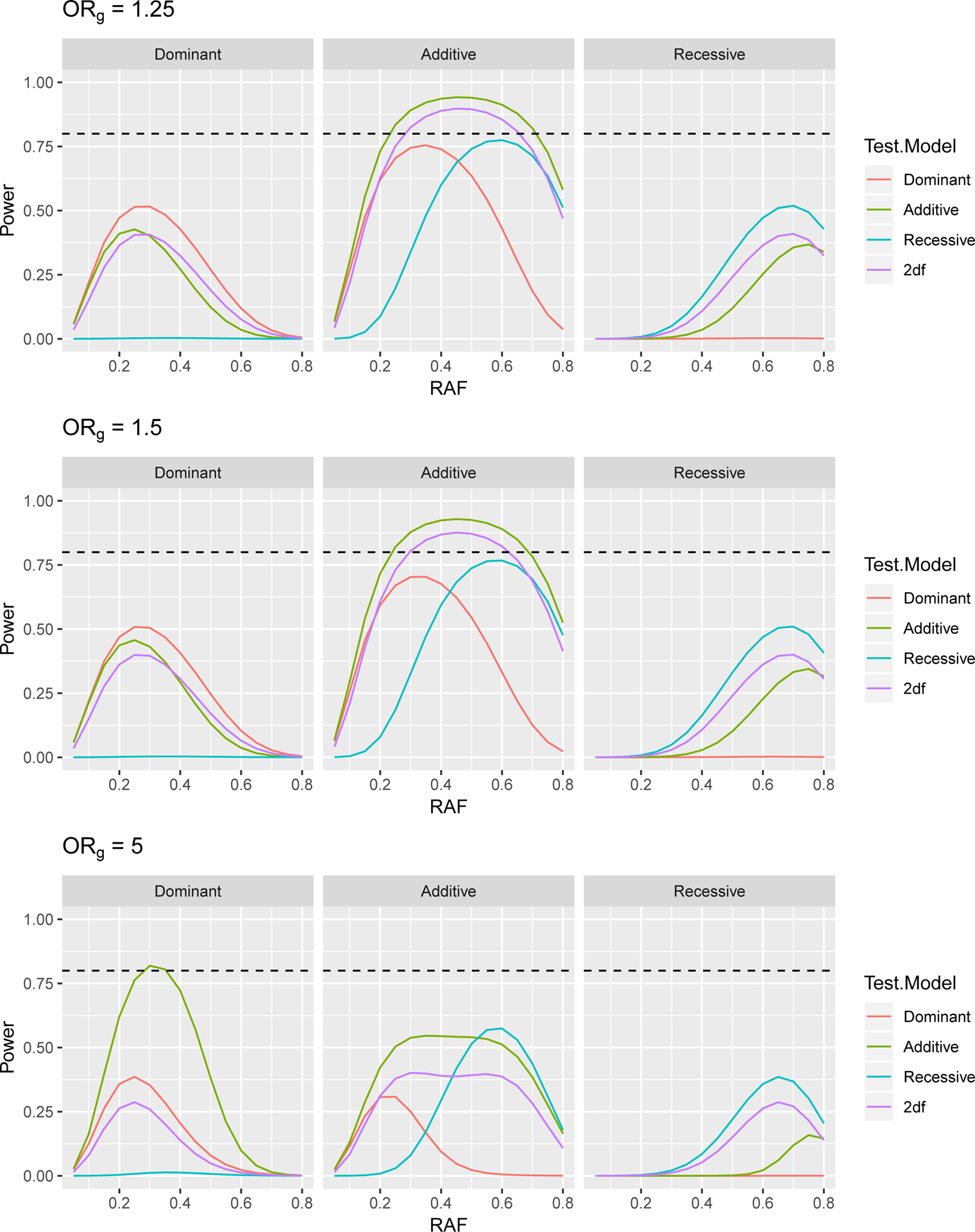
Power to Detect a Gene × Environment (G × E) Odds Ratio of 1.5 in a Case Control Study with 3,624 Cases and 4,442 Controls, at 5 × 10⁻⁵ Significance Level, Assuming a Genetics Odds Ratio of OR_g when E=0. The dashed line indicates 80% power.

Fig. 6.

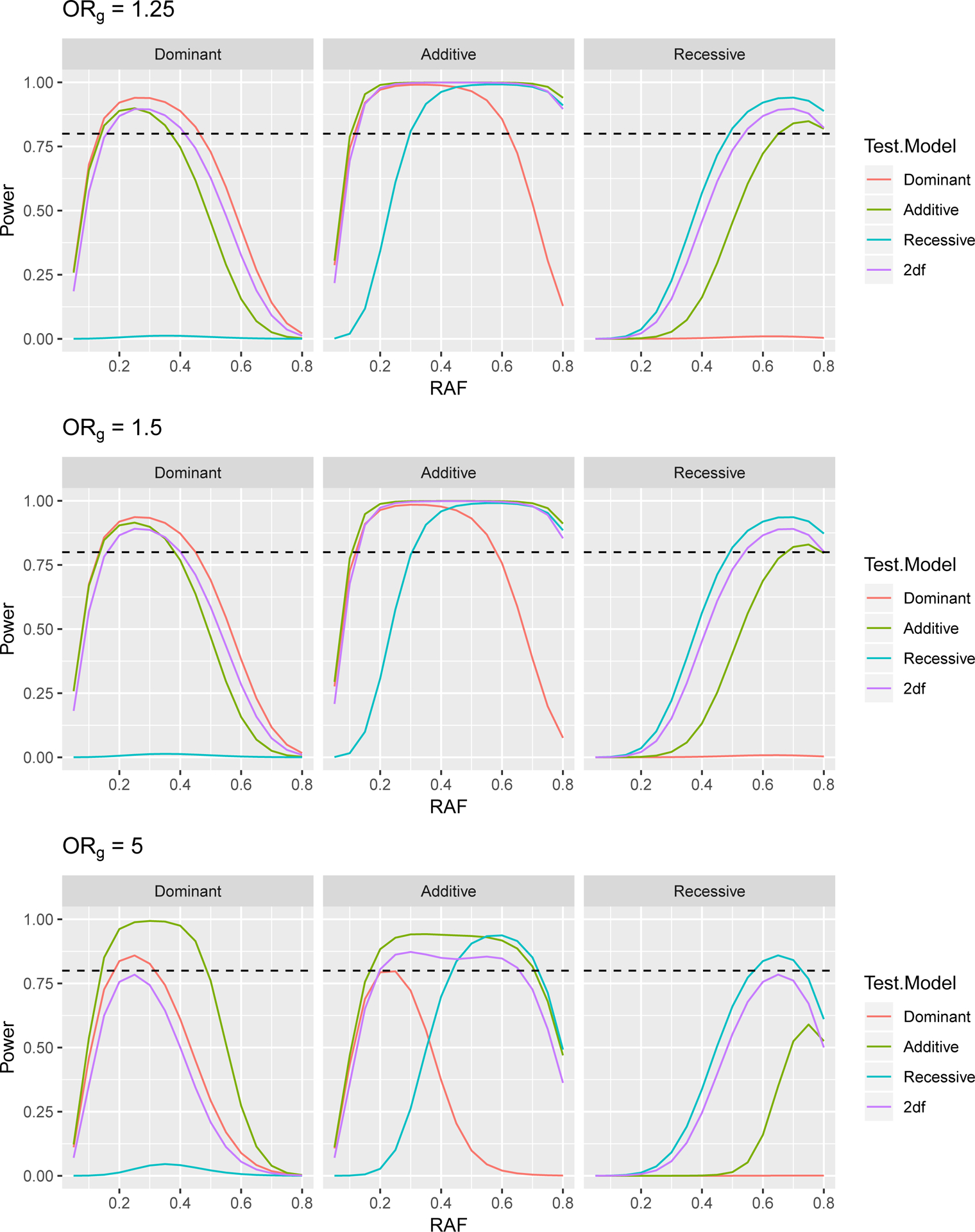
Power to Detect a Gene × Environment (G × E) Odds Ratio of 1.75 in a Case Control Study with 3,624 Cases and 4,442 Controls, at 5 × 10⁻⁵ Significance Level, Assuming a Genetics Odds Ratio of OR_g when E=0. The dashed line indicates 80% power.

Fig. 7.

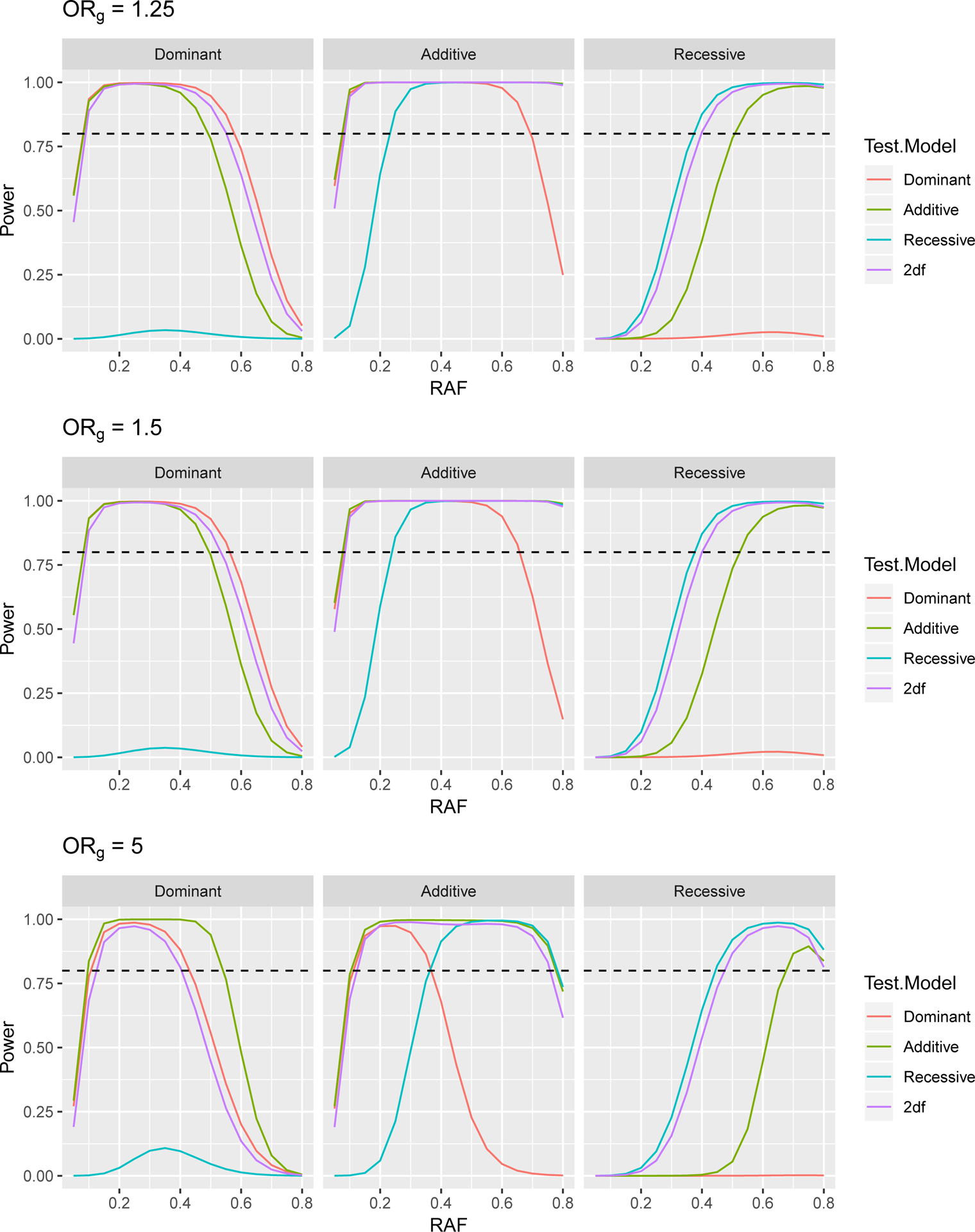
Power to Detect a Gene × Environment (G × E) Odds Ratio of 2 in a Case Control Study with 3,624 Cases and 4,442 Controls, at 5 × 10⁻⁵ Significance Level, Assuming a Genetics Odds Ratio of OR_g when E=0. The dashed line indicates 80% power.

In the case of OR_g of 5, we see that the power for most tests is reduced compared to when OR_g is smaller. This may be due to the extreme odds ratio resulting in few subjects in certain disease status and genotype combinations. For example, with such a large odds ratio, we would expect few controls to be homozygous for the risk allele. While results for additive and recessive tests follow the same patterns as described above, for dominant variants, the additive test somewhat unexpectedly has the highest power. While the expected log likelihood for the correctly specified dominant model is higher than that of the mis-specified additive model, the difference in expected log likelihoods between the null and full models is larger for the additive model. This larger change indicates a bigger improvement in model fit when the gene by smoking interaction term is included in the additive model, resulting in higher power.

As we believe that the majority of variants will have odds ratios much less than 5, we focus on the results for genetic OR’s of 1.25 and 1.5. In addition, we see that there is limited power to detect interaction odds ratios of 1.5, and therefore focus on OR_ge of 1.75 and 2. For dominant variants, the 2df model has higher power to detect the GxE effect than the additive model for all RAF > 0.26 when OR_g= 1.25 and for RAF > 0.335 when OR_g= 1.5. However, the power for the 2df model and the incorrectly specified additive model remain relatively similar even at RAF of 0.2. For additive variants, the 2df model has higher power to detect the GxE effect than the dominant model for all RAF > 0.16 when OR_g= 1.25 and for RAF > 0.155 when OR_g= 1.5. Since compared to the additive and dominant models, the 2df model has substantially increased power to detect interactions for recessive variants, we plan to test all variants with RAF > 0.2 with the 2df model and all variants with RAF ≤ 0.2 with the additive model.

Discussion/Conclusion

We have described and implemented a power and sample size approach that allows misspecification of the statistical model used for testing compared to the true underlying biological model. The ability to assess the impact of model misspecification on power is important when considering the trade-offs between analysis approaches in terms of type I error, power, and simplicity of implementation. We have shown that our approach is helpful for making both study design and analysis approach decisions based on the specifics of the goals and parameters of the study of interest.

Using these power calculation tools, we show when using a 2df test or another robust test of association is advantageous compared to mis-specified additive or dominant models. 2df tests have higher power to detect recessive genetic effects across the range of RAF. For additive and dominant effects, 2df tests have higher power than an incorrectly specified additive or dominant model for higher RAF and lower power for low RAF. The RAF where these power curves cross depends on several factors, including the sample size, the ratio of cases to controls, the OR to detect, and the significance level. In general, as sample size, significance level and OR to detect increase, the RAF at which a 2df test becomes more powerful decreases. While it is clear that a 2df or robust tests of association should be used at higher RAF due to higher power than other mis-specified tests for additive, dominant and recessive variants, an additive or dominant test may be preferable at lower RAF where there is little power to detect recessive effects and mis-specified additive (or dominant) models have higher power than 2df tests for truly dominant (or additive) genetic effects. Notably, as RAF decreases, the power of additive and dominant tests become more similar since the probability of observing a subject homozygous for the risk allele becomes smaller.

We also illustrate how to utilize these calculations to develop analysis plans for testing gene by environment interactions in a study of idiopathic pulmonary fibrosis. For moderate genetic odds ratios, the results for power to detect a gene by smoking interaction largely followed the same patterns as the power for tests of single variants. However, when considering genes with high odds ratios, such as MUC5B, some results were unexpected. Power to detect a gene by environment interaction in the presence of a large genetic odds ratio was reduced compared to more moderate genetic odds ratios, likely because the larger odds ratio resulted in fewer subjects in some disease status and genotype combinations. With this larger genetic odds ratio, we also found that for dominant variants, the mis-specified additive test had the highest power to detect a gene by environment interaction, due to a bigger improvement in model fit when the gene by smoking interaction term is included in the additive model. This illustrates the importance of considering the full range of possible parameter values when performing power and sample size calculations, particularly for gene by environment interactions.

The calculations we have described are implemented in the genpwr R package, which is available on the Comprehensive R Archive Network (CRAN). This software performs power and sample size calculations assuming either dichotomous or continuous outcomes, while also allowing for optional dichotomous or continuous environmental exposures and can provide information for tests of both main and interaction effects. In the R package, the user specifies one or more “true” models, such as additive, dominant, and/or recessive, which represent the biological relationships between genotype and the outcome, as well as one or more “test” models (additive, dominant, recessive and/or 2df), which indicate how the genetic effect will be coded for statistical testing. The genpwr package can calculate sample size, power, or detectable effect size, given that the other two of these variables are specified by the user. In addition, the user must also specify a range of minor allele frequencies and type 1 error rate. For binary outcomes, either the disease prevalence in the study population or the number of controls per case must be specified. For continuous outcomes, the standard deviation of the outcome in the study population is required. For calculations involving a gene by environment interaction, depending on the type of exposure measurement, either the prevalence or the standard deviation of the exposure in the study population must be specified.