Abstract
Nanoparticle (NP)-based imaging and drug delivery systems for systemic (e.g., intravenous) therapeutic and diagnostic applications are inherently a complex integration of biology and engineering. A broad range of length and time scales are essential to hydrodynamic and microscopic molecular interactions mediating NP (drug nanocarriers, imaging agents) motion in blood flow, cell binding/uptake, and tissue accumulation. A computational model of time-dependent tissue delivery, providing in silico prediction of organ-specific accumulation of NPs, can be leveraged in NP design and clinical applications. In this article, we provide the current state-of-the-art and future outlook for the development of predictive models for NP transport, targeting, and distribution through the integration of new computational schemes rooted in statistical mechanics and transport. The resulting multiscale model will comprehensively incorporate: (i) hydrodynamic interactions in the vascular scales relevant to NP margination; (ii) physical and mechanical forces defining cellular and tissue architecture and epitope accessibility mediating NP adhesion; and (iii) subcellular and paracellular interactions including molecular-level targeting impacting NP uptake.
Keywords: Targeted drug delivery, multiscale modeling, nanoparticle membrane interactions, nanoparticle cell adhesion, nanoparticle hydrodynamics
Graphical abstract
Caption: The objective is to develop easily computable and physiologically predictive mechanism-based multiscale pharmacodynamic models for targeted drug delivery.
Introduction
Clinical medicine has entered an era of burgeoning nanotechnology through the use of drug-carrying nanoparticles (NPs) [1, 2]. Nanoparticle (NP)-based imaging and drug delivery systems for systemic (e.g., intravenous) therapeutic and diagnostic applications are inherently complex blends of biology and engineering. NPs have enormous potential to enhance imaging or drug delivery in diagnosing and treating diseases [3–5] in humans while minimizing potential toxicity [6, 7]. Some NPs (e.g., Feraheme, Doxil), are already dramatically changing clinical care by introducing new, or improving upon current, therapies and diagnostic methods, and will do more so in the future [8]. NPs have seemingly limitless possibilities for serving as tissue targeting devices, but their tremendous potential is also a significant impediment to their bench to bedside translation. Empirical determination of optimum characteristics to employ for a particular application is extremely costly [9]. Our inadequate understanding of parameters affecting NP delivery impedes NP optimization for treating human disease.
Multiscale Modeling of NP Transport and Binding
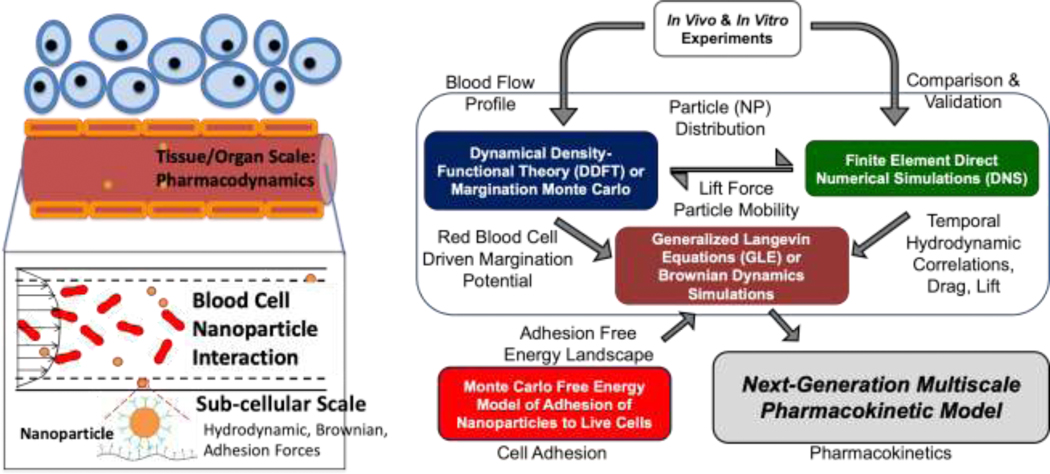
Using quantitative physiologically relevant inputs to develop and validate a computational model for in silico prediction of time-dependent organ-specific NP accumulation to indicate how NP characteristics impact tissue delivery will minimize the future need for empirical in vivo experimentation. Assessing NP delivery efficacy through computational approaches is already informing mechanisms of NP-cell interactions and the effects of many design factors such as size, chemical composition, and surface charge influencing their tissue delivery. In traditional design, the relevant estimates are typically generated using compartmental analyses or pharmacokinetic (PK) models [10–12]; however, such models do not fully include mechanistic interactions of NPs with the vasculature. Hydrodynamic and microscopic molecular interactions mediating NP (drug nanocarriers, imaging agents) motion in blood flow, cell binding/uptake and biodistribution in different tissues involve a broad range of length and time scales warranting a multiscale modeling approach [9]. A predictive mechanism-based nanoparticle targeting model (see Fig. 1) integrates physiology, subcellular, and molecular levels and is customizable to different NP materials, chemistries, shapes, sizes, and other features. Moreover, the multiscale model should be transferable across NP architecture, chemistry, size, shape, and other factors. Recently, such models have been developed in order to provide a predictive landscape of NP hydrodynamics and margination in the vasculature, NP-cell adhesion, and ultimately NP tissue uptake. The predictive power of these methods are valuable to clinicians, academicians or researchers in the industry for applications in clinical healthcare, research, or NP development. Recent progress in modeling focused on hydrodynamics, cellular adhesion, and molecular recognition, and the multiscale integration of the three components (Fig. 1) are discussed below.
Figure 1:
(left) Schematic of the multiscale pharmacokinetic model showing the different length scales and resolutions of the transport problem in targeted drug delivery. (right) A flowchart for an algorithmic implementation of the multiscale model consisting of the “Hydrodynamics” component, the “Cellular Adhesion” component, and the “Pharmacokinetics” component. The arrows represent the flow of information between the suite of models and the flow of information for experimental validation.
Hydrodynamic Factors
In the multiscale framework, the macroscale is focused on vascular hydrodynamics and NP margination. The transport of NPs and their approach to the endothelium in the presence of blood flow through a process called margination is mediated by the hydrodynamic (i.e., fluid-flow-mediated) interactions of the nanoparticles with the red blood cells and the vessel walls [13–21]. To develop the hydrodynamics elements of the modeling, the physiological and NP characterization parameters of interest include blood vessels diameter and length distributions, blood viscosity, cell-free layer (CFL) characteristics, flow rates or velocity distributions and physiology specific vasculature traits (such as tumor versus normal), all of which collectively dictate the NP margination from the core to the periphery of the blood vessels. Blood flow in microvascular networks have been modeled using the apparent viscosity dependence on hematocrit, vessel diameter, and reduced hematocrit in daughter vessels, and based on experimental data on tube diameter and length [22, 23]. Previous works have developed an Immersed Finite Element Method (IFEM) [24] and Lattice Boltzmann (LB) numerical method based on the Immersed Boundary Method (IBM) for the simulation of biological and particulate systems. These numerical methods have been used to model the deposition of platelets on injured vessel walls [24], 3D aggregation of red blood cells, and blood flow in a capillary [24]. In these applications, the complex deformation, motion, and binding of cells of arbitrary shapes are modeled. The transport and deposition of nanoparticles under shear and blood flow have also been investigated by coupling fluid dynamics with adhesion kinetics [24–31].
NPLive Cell Adhesion
Endothelial cells lining the luminal surface of blood vessels are the critical target and barrier for vascular therapeutic delivery. NPs (10–200 nm) coated with antibodies (Abs) or affinity peptides that bind specifically to endothelial surface receptors provide targeted delivery of therapeutic cargoes to these cells. Endothelial targeting consists of several phases, including circulation in the bloodstream, anchoring on the endothelial surface, and, in some cases, intracellular uptake and trafficking of the internalized materials [5]. In addition to dynamic parameters of the vasculature, including the blood hydrodynamics, physiological factors such as surface density, accessibility, cell membrane mobility, and clustering of target determinants modulate NP biodistribution, particularly when targeting strategies are involved. Furthermore, controlled parameters of the design of therapeutic or diagnostic NPs such as affinity, surface density, and epitope specificity of targeting Abs, carrier size, shape, and flexibility also modulate endothelial targeting and resultant subcellular distribution [4, 5, 9].
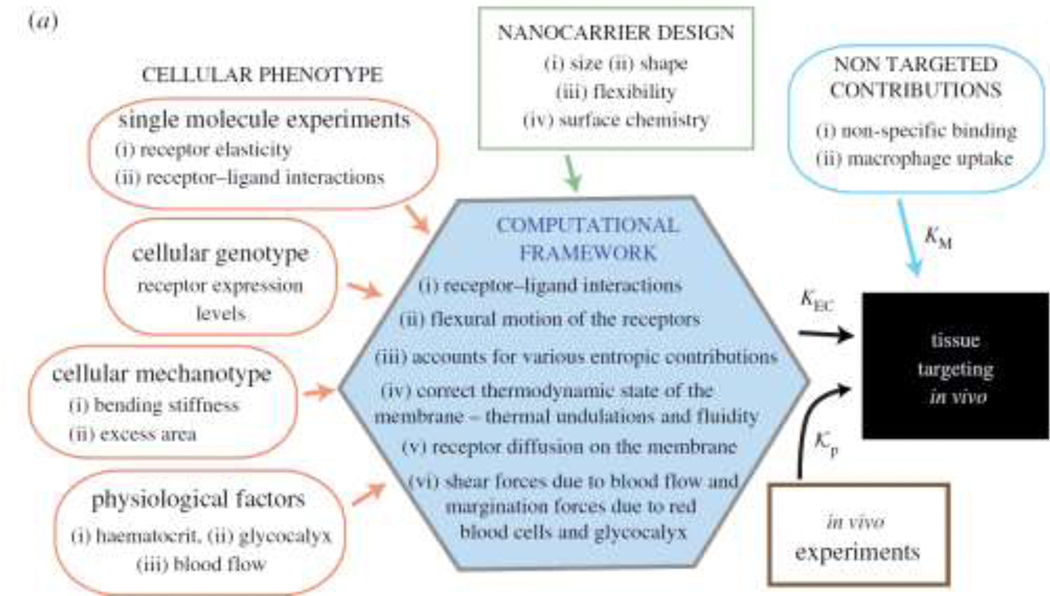
Computational models [32–40], have been developed to delineate the roles played by targeting ligand density, target protein expression, mechanical factors of the target cell membrane as well as the glycocalyx in determining the avidity of functionalized NCs to live cells. These models can be described using a common integrative framework (Fig. 2): the input to the models can be broadly classified into three categories that represent (i) cellular phenotype, (ii) NC design parameters and (iii) non-targeted contributions (Kp) which denotes the partitioning coefficient measured in experiments. Flow chart of a computational framework to compute the association constants (KEC and KM) for NCs binding to live endothelial cells and macrophages is provided in Fig. 2. Computational techniques for computing live cell adhesion are based upon the framework of equilibrium statistical mechanics; the best models combine continuum field models for cell membranes with coarse-grained molecular-scale models for the NC, Abs, and target receptors. Fig. 2 highlights the major components of the proposed computational approach, which can be broadly classified as: (i) a set of input parameters for the coarse-grained and continuum models that define entirely the protein expression and mechanical properties of the target cell membrane, the biochemical interactions of the receptor-ligand bond, the flexural rigidity of the target receptors, and experimentally controllable quantities such as the geometry and the surface chemistry of the functionalized NC; (ii) a computational engine to accurately compute the association constant Ka, for a specified mechano-chemical microenvironment and (iii) a framework that accounts for the targeted contributions due to NC binding to other cells such as a macrophage. The expression for Ka is adopted and generalized based on studies from molecular simulations of drug binding, which have formulated techniques to compute the absolute free energy of binding [32, 41]. The main output of the model is the calculation of the free energy landscape for carrier binding to the cells, which is quantified through enhanced sampling methods [42, 43]. The primary learnings from the computational studies have been the compensation of different entropy, and the enthalpy terms are dependent on NP flexibility, membrane tension, receptor density, and receptor-ligand interaction strength [32, 33, 37–40, 44, 45].
Figure 2:
(a) Depiction of the live cell adhesion NP tissue targeting highlighting the parameter mapping (inputs and outputs). A Monte Carlo framework constitutes the live cell adhesion suite.
Molecular Scale Factors in NP Membrane Interactions
There are several aspects of the multiscale problem (Fig. 1) that deserve molecular-level treatment and characterization. Engineering antibodies and studying receptor-ligand interactions using molecular modeling already has a rich literature in computational chemistry. Engineering the structural and mechanical features associated with the receptor-ligand interactions that have already been identified as critical variables through sensitivity analyses, such as flexural rigidity [34], catch-bond behavior [46], can be vastly improved and influenced through advances in molecular simulations and multiscale methods [47–49]. Recently it was hypothesized that while targeting adhesion molecules with antibodies represent strong binding (SB) interactions, the surface protein epitopes such as Fc receptors and even albumin will represent intermediate binding (IB) and weak binding (WB) on the surface of the NP [33]. Moreover, targeting flow adapted healthy endothelial cells versus leaky endothelial cells can be different because the later presents a less stiff membrane due to lack of flow adaptation and improper glycocalyx; here, parameter variations involving cytoskeletal pinning and excess membrane area can be considered. The effect of opsonization was considered by tuning the ratios of SB:IB:WB on the NP.
Conclusion and Future Outlook
An integrative mechanism-based model for tissue biodistribution and prediction of NP tissue targeting can be obtained via a unified multiscale model combining the different modules in Fig. 1. The resultant multiscale model will power exploration of a myriad of tunable physical options for NP design for clinical tissue targeting. We envision an integrative multiscale framework to combine the different scales using formalisms discussed above. The models will need to be tightly and iteratively coupled with in vitro, cellular, as well as in vivo experimentation to validate, to predict, and to guide the design of targeted nanoparticles in translational applications of targeted nanomedicine.
One promising area of future development in design is to combine the bivalent and bispecific Abs, along with the multivalency of engaging SB, IB, and WB receptors [50]. The nature of interactions of these bivalent bispecific interactions on an immobilized NP surface, on a flexible polymeric NP or liposome, or engaging receptors on a fluid membrane. On the membrane interface, several molecular-scale considerations can impact and revolutionize the NP cell interactions: (1) membrane curvature aids and influences the NP cell adhesion [44, 51]; (2) the mechanisms through which curvature inducing proteins generate curvature and influence NP binding and subsequent internalization are hugely important [52]; (3) the clustering of receptors on the membrane interface can be mediated through formation of lipid domains often involving phosphoinositide proteins [53]; (4) lipid, and in particular, phosphoinositide nanocluster formation, has a significant influence on actin nucleation and subsequent NP internalization [54–56]; (5) the nature of the molecular assembly and curvature at the membrane interface is not only influenced by cell mechanics and the mechanics of the tissue microenvironment, but also impacts the internalization of rigid, semi-rigid, and flexible NPs differently [51].
While the previous models, including those described above, have been successful in evaluating the effects of Ab density and NP targeting to different cell types, accurate representations of specific and non-specific contributions require a more detailed description of the tissue morphology and the physiological conditions. First, in the modeling of live cell adhesion, will need to extend the analysis to include the effects of NP surface functionalization (such as PEGylation) [57], targeting of multiple receptors using bivalent and bispecific antibodies [58, 59], and NP opsonization (by surface deposition of albumin and Fc receptors on NPs to consider the architecture and chemistry of the NP). These factors will need to be considered in addition to physiological factors such as glycocalyx [35, 36, 60], cell membrane compliance and deformation [32], and vascular margination. Second, cell microenvironment effects need to be considered, such as: (a) the effect of the cytoskeleton and cytoskeletal heterogeneity; (b) the effect of cortical tension and cell-cell adhesion is considered through frame tension [61, 62]. These variables lead to significant heterogeneity in the adhesion surface by inducing/inciting morphological features. The topographical heterogeneity induced by the effects described under couples with biochemical heterogeneity because of lipids and proteins sort in the membrane phase in a curvature-dependent fashion [52, 63, 64]. These features can be included by following the methods recently described [52, 64].
New multiscale bridging algorithms warrant future development in order to realize the coupling of hydrodynamic and adhesion models and their objective validation against experimentation. One avenue could be to develop functionals incorporating relevant physicochemical and hydrodynamic interactions. An example is through the use of dynamical density functional theory, which utilizes a functional approach to treat the far-field many-body hydrodynamics [57, 65], near-field hydrodynamics [66–71], and multivalent adhesion of NPs to soft membranes can be combined into one coherent framework in order to either obtain the spatial distribution of NP [44, 45]; another example is through the use of stochastic dynamics using generalized Langevin equation methods [70, 71] to capture the temporal dynamics of NP [70–72]. A second avenue to realize the multiscale integration is to use a loosely coupled framework where a small number of parameters are passed between the different scales, and the integration is achieved through high-performance computing workflow management software such as TAVERNA [73], MUSCLE [74], or the VPH hypermodel framework [75]. As a computational scientist, one is also encouraged and optimistic about machine-learning [76, 77] enabled multiscale methods to improve accuracy, speed-up performance, and utilize the emerging high-performance computing architectures.
Highlights.
Computational methods for modeling hydrodynamic factors in nanoparticle membrane interactions in targeted drug delivery
Computational frameworks for predicting lice cell adhesion of nanoparticles
Molecular-level considerations in nanoparticle cell membrane interactions
Outlook for multiscale model integration for developing the next-generation mechanism-based pharmacokinetic models
Acknowledgments
We acknowledge valuable discussions from members of the Eckmann, Radhakrishnan, and Janmey laboratories. This work was supported in part by the National Institutes of Health grants EB016027, CA227550, GM111942, and GM136259.
Funding
No funding was received for this work.
Footnotes
Intellectual Property
We confirm that we have given due consideration to the protection of intellectual property associated with this work and that there are no impediments to publication, including the timing of publication, with respect to intellectual property. In so doing we confirm that we have followed the regulations of our institutions concerning intellectual property.
Research Ethics
We further confirm that any aspect of the work covered in this manuscript that has involved human patients has been conducted with the ethical approval of all relevant bodies and that such approvals are acknowledged within the manuscript
Conflict of Interest
No onflict of interest exists
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.D’aquino R, T.H., Vas CR, Nanobiotechnology: fulfilling the promise of nanomedicine. Chemical Engineering Progress, 2006. 102(2): p. 35–37.•Various advantages provided by nanobiotechnology to biomedical and pharmaceutical sciences are discussed. Nanobiotechnology make use of nanomaterials, offering improved performance benefits for medical-device coatings, diagnostic contrast agents, analytical components in nanoscale biodetection devices, and advanced drug-delivery systems.
- 2.Blanco E, Shen H, and Ferrari M, Principles of nanoparticle design for overcoming biological barriers to drug delivery. Nature Biotechnology, 2015. 33: p. 941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Peer D, et al. , Nanocarriers as an emerging platform for cancer therapy. Nature Nanotechnology, 2007. 2(12): p. 751–760. [DOI] [PubMed] [Google Scholar]
- 4.Swaminathan TN, et al. , Dynamic factors controlling carrier anchoring on vascular cells. IUBMB Life, 2011. 63(8): p. 640–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Muzykantov VR, Radhakrishnan R, and Eckmann DM, Dynamic factors controlling targeting nanocarriers to vascular endothelium. sssCurr Drug Metab, 2012. 13(1): p. 70–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kabanov AV, Batrakova EV, and Alakhov VY, Pluronic (R) block copolymers as novel polymer therapeutics for drug and gene delivery. Journal of Controlled Release, 2002. 82(2–3): p. 189–212. [DOI] [PubMed] [Google Scholar]
- 7.Klibanov AL, Ligand-carrying gas-filled microbubbles: Ultrasound contrast agents for targeted molecular imaging. Bioconjugate Chemistry, 2005. 16(1): p. 9–17. [DOI] [PubMed] [Google Scholar]
- 8.Anselmo AC and Mitragotri S, Nanoparticles in the clinic. Bioengineering & Translational Medicine, 2016. 1(1): p. 10–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ayyaswamy PS, et al. , Nanocarrier Hydrodynamics and Binding in Targeted Drug Delivery: Challenges in Numerical Modeling and Experimental Validation. J Nanotechnol Eng Med, 2013. 4(1): p. 101011–1010115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jones HM, Mayawala K, and Poulin P, Dose selection based on physiologically based pharmacokinetic (PBPK) approaches. AAPS J, 2013. 15(2): p. 377–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lin Z, et al. , Development and application of a multiroute physiologically based pharmacokinetic model for oxytetracycline in dogs and humans. J Pharm Sci, 2015. 104(1): p. 233–43. [DOI] [PubMed] [Google Scholar]
- 12.Lin Z, Monteiro-Riviere NA, and Riviere JE, Pharmacokinetics of metallic nanoparticles. Wiley Interdiscip Rev Nanomed Nanobiotechnol, 2015. 7(2): p. 189–217. [DOI] [PubMed] [Google Scholar]
- 13.Vahidkhah K. and Bagchi P, Microparticle shape effects on margination, near-wall dynamics and adhesion in a three-dimensional simulation of red blood cell suspension. Soft Matter, 2015. 11(11): p. 2097–2109. [DOI] [PubMed] [Google Scholar]
- 14.Thompson AJ, Mastria EM, and Eniola-Adefeso O, The margination propensity of ellipsoidal micro/nanoparticles to the endothelium in human blood flow. Biomaterials, 2013. 34(23): p. 5863–5871. [DOI] [PubMed] [Google Scholar]
- 15.Namdee K, et al. , Margination propensity of vascular-targeted spheres from blood flow in a microfluidic model of human microvessels. Langmuir, 2013. 29(8): p. 2530–2535. [DOI] [PubMed] [Google Scholar]
- 16.Thompson AJ and Eniola-Adefeso O, Dense nanoparticles exhibit enhanced vascular wall targeting over neutrally buoyant nanoparticles in human blood flow. Acta Biomaterialia, 2015. 21: p. 99–108. [DOI] [PubMed] [Google Scholar]
- 17.Gekle S, Strongly accelerated margination of active particles in blood flow. Biophysical Journal, 2016. 110(2): p. 514–520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.D’Apolito R, et al. , Red blood cells affect the margination of microparticles in synthetic microcapillaries and intravital microcirculation as a function of their size and shape. Journal of Controlled Release, 2015. 217: p. 263–272. [DOI] [PubMed] [Google Scholar]
- 19.Müller K, Fedosov DA, and Gompper G, Margination of micro- and nano-particles in blood flow and its effect on drug delivery. Scientific Reports, 2014. 4: p. 4871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Champion JA and Mitragotri S, Role of target geometry in phagocytosis. Proc Natl Acad Sci U S A, 2006. 103(13): p. 4930–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Huang RB, et al. , Dynamic and cellular interactions of nanoparticles in vascular-targeted drug delivery (review). Mol Membr Biol, 2010. 27(4–6): p. 190–205. [DOI] [PubMed] [Google Scholar]
- 22.Pries AR, et al. , Blood flow in microvascular networks. Experiments and simulation. Circulation Research, 1990. 67(4): p. 826–834. [DOI] [PubMed] [Google Scholar]
- 23.Fedosov DA, et al. , Computational biorheology of human blood flow in health and disease. Ann Biomed Eng, 2014. 42(2): p. 368–87.• The article presents an overview of a general computational framework based on dissipative particle dynamics (DPD) which has broad applicability in cell biophysics with implications for diagnostics, therapeutics and drug efficacy assessments for a wide variety of human diseases.
- 24.Liu YL and Liu WK, Rheology of red blood cell aggregation by computer simulation. Journal of Computational Physics, 2006. 220(1): p. 139–154. [Google Scholar]
- 25.Tan J, Thomas A, and Liu Y, Influence of red blood cells on nanoparticle targeted delivery in microcirculation. Soft Matter, 2012. 8(6): p. 1934–1946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Shah S, et al. , Modeling particle shape-dependent dynamics in nanomedicine. Journal of Nanoscience and Nanotechnology, 2011. 11(2): p. 919–928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Liu Y, et al. , The shape of things to come: importance of design in nanotechnology for drug delivery. TherDeliv, 2012. 3(2): p. 181–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Tan J, et al. , The influence of size, shape and vessel geometry on nanoparticle distribution. Microfluid Nanofluidics, 2013. 14(1–2): p. 77–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tan J, et al. , Characterization of nanoparticle dispersion in red blood cell suspension by the Lattice Boltzmann-Immersed Boundary Method. Nanomaterials (Basel), 2016. 6(2): p. 30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Fedosov DA, Caswell B, and Karniadakis GE, A multiscale red blood cell model with accurate mechanics, rheology, and dynamics. Biophys J, 2010. 98(10): p. 2215–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tan J, et al. , Coupled Particulate and Continuum Model for Nanoparticle Targeted Delivery. Comput Struct, 2013. 122(0): p. 128–134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ramakrishnan N, et al. , Biophysically inspired model for functionalized nanocarrier adhesion to cell surface: roles of protein expression and mechanical factors. R Soc Open Sci, 2016. 3(6): p. 160260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.McKenzie M, et al. , Multivalent Binding of a Ligand-Coated Particle: Role of Shape, Size, and Ligand Heterogeneity. Biophysical Journal, 2018. 114(8): p. 1830–1846.•The study presents a multiscale modeling framework to study the effect of shape, size, and ligand composition on the efficacy of binding of a ligand-coated particle to a substrate functionalized with the target receptors.
- 34.Liu J, et al. , Multiscale Modeling of Functionalized Nanocarriers in Targeted Drug Delivery. Current Nanoscience, 2011. 7: p. 727–735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Liu J, et al. , Multivalent binding of nanocarrier to endothelial cells under shear flow. Biophys J, 2011. 101(2): p. 319–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Liu J, et al. , Computational model for nanocarrier binding to endothelium validated using in vivo, in vitro, and atomic force microscopy experiments. Proc Nat Acad Sci, 2010. 107(38): p. 16530–16535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Dubacheva GV, et al. , Multivalent Recognition at Fluid Surfaces: The Interplay of Receptor Clustering and Superselectivity. J Am Chem Soc, 2019. 141(6): p. 2577–2588.• The authors present a novel experimental model system and an analytical model that allows us to compare systematically the effects of multivalent interactions on fluid and immobile surfaces. Multivalent binding platform will greatly facilitate the rational design of nanoprobes for the superselective targeting of cells.
- 38.Tito NB, Angioletti-Uberti S, and Frenkel D, Communication: Simple approach for calculating the binding free energy of a multivalent particle. J Chem Phys, 2016. 144(16): p. 161101. [DOI] [PubMed] [Google Scholar]
- 39.Tito NB and Frenkel D, Optimizing the Selectivity of Surface-Adsorbing Multivalent Polymers. Macromolecules, 2014. 47(21): p. 7496–7509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Albertazzi L, et al. , Spatiotemporal control and superselectivity in supramolecular polymers using multivalency. Proc Natl Acad Sci U S A, 2013. 110(30): p. 12203–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Woo HJ and Roux B, Calculation of absolute protein-ligand binding free energy from computer simulations. Proceedings of the National Academy of Sciences of the United States of America, 2005. 102(19): p. 6825–6830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Frenkel D. and Smit B, Understanding molecular simulation: from algorithms to applications. 2002, San Diego: Academic Press. [Google Scholar]
- 43.Bonati L, Zhang Y-Y, and Parrinello M, Neural networks-based variationally enhanced sampling. Proceedings of the National Academy of Sciences, 2019. 116(36): p. 17641.•This article bridges the fields of enhanced sampling and machine learning and enables leveraging of the rapidly growing advances in. deep learning. Specifically, the authors show that by combining a variational approach with deep learning, new sampling approaches can be devised to extend the scope of such simulations.
- 44.Farokhirad S, et al. , Stiffness can mediate balance between hydrodynamic forces and avidity to impact the targeting of flexible polymeric nanoparticles in flow. Nanoscale, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Farokhirad S, et al. , Nanofluid Dynamics of Flexible Polymeric Nanoparticles Under Wall Confinement. Journal of Heat Transfer, 2019. 141(5): p. 052401–052401-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Vogel V, et al. , Structural insights into the mechanical regulation of molecular recognition sites. Trends Biotechnol, 2001. 19(10): p. 416–23. [DOI] [PubMed] [Google Scholar]
- 47.Voth GA, New and notable: key new insights into membrane targeting by proteins. Biophys J, 2013. 104(3): p. 517–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Saunders MG and Voth GA, Coarse-graining of multiprotein assemblies. Curr Opin Struct Biol, 2012. 22(2): p. 144–50. [DOI] [PubMed] [Google Scholar]
- 49.Bradley R. and Radhakrishnan R, Coarse-Grained Models for Protein-Cell Membrane Interactions. Polymers, 2013. 5(3): p. 890–936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Spiess C, Zhai Q, and Carter PJ, Alternative molecular formats and therapeutic applications for bispecific antibodies. Molecular Immunology, 2015. 67(2, Part A): p. 95–106. [DOI] [PubMed] [Google Scholar]
- 51.Farokhirad S, Bradley RP, and Radhakrishnan R, Thermodynamic analysis of multivalent binding of functionalized nanoparticles to membrane surface reveals the importance of membrane entropy and nanoparticle entropy in adhesion of flexible nanoparticles. Soft Matter, 2019. 15(45): p. 9271–9286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Ramakrishnan N, et al. , Biophysics of membrane curvature remodeling at molecular and mesoscopic lengthscales. J Phys Condens Matter, 2018. 30(27): p. 273001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Slochower DR, et al. , Counterion-mediated pattern formation in membranes containing anionic lipids. Adv Colloid Interface Sci, 2014. 208: p. 177–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Kapus A. and Janmey P, Plasma membrane--cortical cytoskeleton interactions: a cell biology approach with biophysical considerations. Compr Physiol, 2013. 3(3): p. 1231–81. [DOI] [PubMed] [Google Scholar]
- 55.Bucki R, et al. , Lateral distribution of phosphatidylinositol 4,5-bisphosphate in membranes regulates formin- and ARP2/3-mediated actin nucleation. Journal of Biological Chemistry, 2019. 294(12): p. 4704–4722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Janmey PA, Bucki R, and Radhakrishnan R, Regulation of actin assembly by PI(4,5)P2 and other inositol phospholipids: An update on possible mechanisms. Biochemical and Biophysical Research Communications, 2018. 506(2): p. 307–314.•The article summarizes the physiological and physiochemical implications of lipid heterogeneity in mammalian cell membranes and the roles of phosphoinositides in membrane protein recruitment and actin assembly, two factors that are crucial for NP-membrane interactions.
- 57.Sarkar A, et al. , Hydrodynamic interactions of deformable polymeric nanocarriers and the effect of crosslinking. Soft Matter, 2015. 11(29): p. 5955–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Zern BJ, et al. , Reduction of nanoparticle avidity enhances the selectivity of vascular targeting and PET detection of pulmonary inflammation. ACS Nano, 2013. 7(3): p. 2461–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Brenner JS, et al. , Mechanisms that determine nanocarrier targeting to healthy versus inflamed lung regions. Nanomedicine: Nanotechnology, Biology and Medicine, 2017. 13(4): p. 1495–1506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Agrawal NJ and Radhakrishnan R, The Role of Glycocalyx in Nanocarrier-Cell Adhesion Investigated Using a Thermodynamic Model and Monte Carlo Simulations. J Phys Chem C Nanomater Interfaces, 2007. 111(43): p. 15848–15856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Ramakrishnan N, et al. , Excess area dependent scaling behavior of nano-sized membrane tethers. Phys Biol, 2018. 15(2): p. 026002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Kandy SK and Radhakrishnan R, Emergent membrane morphologies in relaxed and tense membranes in presence of reversible adhesive pinning interactions. Physical Biology, 2019. 16(6): p. 066011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Bradley RP and Radhakrishnan R, Curvature-undulation coupling as a basis for curvature sensing and generation in bilayer membranes. Proc Natl Acad Sci U S A, 2016. 113(35): p. E5117–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Ramakrishnan N, Sunil Kumar PB, and Radhakrishnan R, Mesoscale computational studies of membrane bilayer remodeling by curvature-inducing proteins. Physics Reports, 2014. 543(1): p. 1–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Yu H-Y, et al. , Microstructure of Flow-Driven Suspension of Hardspheres in Cylindrical Confinement: A Dynamical Density Functional Theory and Monte Carlo Study. Langmuir, 2017. 33(42): p. 11332–11344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Jabeen Z, et al. , Rheology of colloidal suspensions in confined flow: Treatment of hydrodynamic interactions in particle-based simulations inspired by dynamical density functional theory. Physical Review E, 2018. 98(4): p. 042602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Ramakrishnan N, et al. , Motion of a nano-ellipsoid in a cylindrical vessel flow: Brownian and hydrodynamic interactions. Journal of Fluid Mechanics, 2017. 821: p. 117–152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Uma B, et al. , Nanoparticle Brownian motion and hydrodynamic interactions in the presence of flow fields. Phys Fluids (1994), 2011. 23(7): p. 73602–7360215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Vitoshkin H, et al. , Nanoparticle stochastic motion in the inertial regime and hydrodynamic interactions close to a cylindrical wall. Phys Rev Fluids, 2016. 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Yu H-Y, et al. , Composite generalized Langevin equation for Brownian motion in different hydrodynamic and adhesion regimes. Physical Review E, 2015. 91(5): p. 052303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Hsiu-Yu Yu DME, Portovovo S. Ayyaswamy, Ravi Radhakrishnan, Effect of wall-mediated hydrodynamic fluctuations on the kinetics of a Brownian nanoparticle. Proceedings of the Royal Society of London. Series A, 2016. 472: p. 20160397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Ravi Radhakrishnan H-YY, David M. Eckmann, Portovovo S. Ayyaswamy, Computational Models for Nanoscale Fluid Dynamics and Transport Inspired by Nonequilibrium Thermodynamics. J Heat Transfer, 2017. 39: p. 033001.•The article discusses several techniques that are founded on the basis of combining computational fluid dynamics methods with the theory of nonequilibrium statistical mechanics in order to simultaneously conserve thermal equipartition and to show correct hydrodynamic correlations. These include the fluctuating hydrodynamics method, the generalized Langevin method, the hybrid method, and the deterministic method. Through the examples discussed, the article demonstrates a top-down multiscale progression of temporal dynamics from the colloidal scales to the molecular scales, and the associated fluctuations, hydrodynamic correlations.
- 73.Wolstencroft K, et al. , The Taverna workflow suite: designing and executing workflows of Web Services on the desktop, web or in the cloud. Nucleic Acids Res, 2013. 41(Web Server issue): p. W557–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Borgdorff J, et al. , Distributed multiscale computing with MUSCLE 2, the Multiscale Coupling Library and Environment. Journal of Computational Science, 2014. 5(5): p. 719–731. [Google Scholar]
- 75.Tartarini D, et al. The VPH Hypermodelling framework for cancer multiscale models in the clinical practice. in Proceedings of the 2014 6th International Advanced Research Workshop on In Silico Oncology and Cancer Investigation - The CHIC Project Workshop (IARWISOCI). 2014. [Google Scholar]
- 76.Alom ZM, et al. , A State-of-the-Art Survey on Deep Learning Theory and Architectures. Electronics, 2019. 8(3).•This article presents a survey on the advances in Deep Learning (DL), starting with the Deep Neural Network (DNN). It covers Convolutional Neural Network (CNN), Recurrent Neural Network (RNN), including Long Short-Term Memory (LSTM) and Gated Recurrent Units (GRU), Auto-Encoder (AE), Deep Belief Network (DBN), Generative Adversarial Network (GAN), and Deep Reinforcement Learning (DRL).
- 77.Bastanlar Y. and Ozuysal M, Introduction to machine learning. Methods Mol Biol, 2014. 1107: p. 105–28. [DOI] [PubMed] [Google Scholar]