Multimodal Cross-registration and Quantification of Metric Distortions in Marmoset Whole Brain Histology using Diffeomorphic Mappings

Abstract

Whole brain neuroanatomy using tera-voxel light-microscopic data sets is of much current interest. A fundamental problem in this field is the mapping of individual brain datasets to a reference space. Previous work has not rigorously quantified in-vivo to ex-vivo distortions in brain geometry from tissue processing. Further, existing approaches focus on registering uni-modal volumetric data; however, given the increasing interest in the marmoset model for neuroscience research and the importance of addressing individual brain architecture variations, new algorithms are necessary to cross-register multimodal datasets including MRIs and multiple histological series. Here we present a computational approach for same-subject multimodal MRI-guided reconstruction of a series of consecutive histological sections, jointly with diffeomorphic mapping to a reference atlas. We quantify the scale change during different stages of brain histological processing using the Jacobian determinant of the diffeomorphic transformations involved. By mapping the final image stacks to the ex-vivo post-fixation MRI, we show that a) tape-transfer assisted histological sections can be re-assembled accurately into 3D volumes with a local scale change of 2.0±0.4% per axis dimension; in contrast, b) tissue perfusion/fixation as assessed by mapping the in-vivo MRIs to the ex-vivo post fixation MRIs shows a larger median absolute scale change of 6.9 ± 2.1% per axis dimension. This is the first systematic quantification of local metric distortions associated with whole-brain histological processing, and we expect that the results will generalize to other species. These local scale changes will be important for computing local properties to create reference brain maps.

Graphical Abstract:

In this paper, we present methods for guided volume reconstruction of serial section animal brain histology with an evaluation of registration accuracy. Using methods derived from diffeomorphometry, we quantify the 3D distortion caused by two steps in the histology tissue processing pipeline: 1) reassembly of tape-transfer assisted histology sections and 2) tissue perfusion and fixation.

1. Introduction

The common marmoset (Callithrix jacchus, RRID:NCBITaxon 9483) is an increasingly important model species for both scientific and preclinical neuroscience research. As compared with other non-human primates, the marmoset brain has unique advantages for brain mapping including a compact brain size, a lissencephalic cortex, and the availability of transgenic lines (Sasaki et al., 2009), (Kishi, Sato, Sasaki, & Okano, 2014). However, mapping the complete neural circuitry of the marmoset brain is a time consuming and complex process that requires a coordinated effort involving multidisciplinary scientific knowledge and collaboration. One important task in any circuit mapping project is to map the whole-brain neuroanatomical data to a reference atlas. This is more challenging for primate species such as the marmoset when compared with commonly used animal models such as the mouse, due to higher individual variability in brain geometry and the increased complexity of the brain architecture of the primate brain. To address these issues it is necessary to obtain multimodal data sets showing different kinds of contrast, including in-vivo and ex-vivo magnetic resonance imaging (MRI) volumes in combination with whole-brain light-microscopic images of a series of histologically labelled sections, cf. Nissl stains, myelin stains and the use of fluorescent probes.

In this paper, we focus on the computational problem mapping of serially-sectioned whole-brain image datasets of different modalities and scales into the same coordinate space. In particular, we describe the registration procedure on a specific experimental methodology for obtaining brain-wide connectivity information using neurohistological preparations, where thinly sliced brain sections are systematically subjected to different histological procedures in order to obtain a broad spectrum of information about cytoarchitectonic structure. The sections were obtained using a high-throughput neurohistological pipeline that has been previously described (Lin et al., 2019), along with in-vivo and ex-vivo MRI volumes. Our results demonstrate that the local metric distortions of the brain after histological preparations are relatively small with the exception of the perfusion-fixation step. Our results provide a systematic characterization of the metric distortions associated with the perfusion-fixation step, which can be generalized to the brains of other species as well. Although much of the presented data is produced by histology, we include as a subset methods for 3D image data generated by techniques (eg MRI) that do not require section-registration. The analysis of in-vivo to ex-vivo MRI mappings described in this paper do not require the section registration step.

Prior work on artifacts associated with reassembling 2D sections

Light-microscopic histological image section reconstruction guided by reference imagery has been previously explored by several groups. The problem of accumulated long range distortions in unguided reconstruction was studied by Malandain (Malandain, Bardinet, Nelissen, & Vandu el, 2004) and one of the earlier proposed guided-reconstruction solution was Block-matching i.e. using block-face photographs during histology to align sections (Dauguet et al., 2007). Feature extraction and manually defined landmarks have also been applied to guide reconstruction (Streicher, Weninger, & Muller, 1997). More recent methods have used same-subject MRI to guide reconstruction of human (Adler et al., 2014) and mouse (Yang, Richards, Kurniawan, Petrou, & Reutens, 2012) brain structures. None of these studies however provide the metric quantification reported in this paper. We believe our methods constitute a significant advance that will be of particular importance for quantitative studies, in particular for large volume brains such as that of non-human primates and humans.

Prior work on diffeomorphic methods for registering brain volumes

Diffeomorphic mapping of brain volumes has been a central focus in the field of Computational Anatomy (U. Grenander & Miller, 1998; Dupuis, Grenander, & Miller, 1998; M. Miller & Younes, 2001; Toga & Thompson, 2001; M. I. Miller, Trouvé, & Younes, 2002; Thompson & Toga, 2002; M. Miller, 2004; Beg, Helm, McVeigh, Miller, & Winslow, 2004; Joshi, Davis, Jomier, & Gerig, 2004; Ashburner & Friston, 2007; M. Grenander & Miller, 2007; Durrleman, Pennec, Trouvé, Thompson, & Ayache, 2008; Ashburner, 2009; Younes, Arrate, & Miller, 2009; Younes, 2010; Pennec, 2011; Adams, Stephan, Brown, Frith, & Friston, 2013). Mapping methods initially followed the small deformation and elasticity methods of Bajcsy and others (Bajcsy, Lieberson, & Reivich, 1983; Bajcsy & Kovačič, 1989; Amit, Grenander, & Piccioni, 1991; Gee, Reivich, & Bajcsy, 1993; M. I. Miller, Christensen, Amit, & Grenander, 1993; Richard D. Rabbitt, 1995). Subsequently Christensen et al (G. Christensen, Miller, & Rabbit, 1995) introduced large deformation flows for topology preservation in dense volume matching (G. E. Christensen, Joshi, & Miller, 1997). Since these early inceptions many methods have been developed based on both landmark and triangulated surface based spline deformations (F. L. Bookstein, 1989, 1991; F. Bookstein, 1996) as well as large deformation methods (Joshi & Miller, 2000; Camion & Younes, 2001; Glaunes, Trouvé, & Younes, 2004; Vaillant & Glaunès, 2005; Glaunès, Qiu, Miller, & Younes, 2008). For dense images (i.e. 3D voxelized image volumes) with multiple modalities and tensor fields such as Diffusion track imaging (DTI), these methods were further developed and form the basis of the multiple contrast, multi-scale algorithmic framework that is well-described in the literature, but note that much of this work has focussed on MRI volumes as opposed to the LM based teravoxel volumes of interest to the present study (B. Avants & Gee, 2004; Beg, Miller, Trouvé, & Younes, 2005; Beg & Khan, 2007; Vercauteren, Pennec, Perchant, & Ayache, 2008; B. B. Avants, Epstein, Grossman, & Gee, 2008; Ceritoglu et al., 2009, 2010; Risser et al., 2011; Sommer, Nielsen, Lauze, & Pennec, 2011; D. Tward et al., n.d.; Du, Younes, & Qiu, 2011; Vadakkumpadan, Arevalo, Ceritoglu, Miller, & Trayanova, 2012; Tang, Mori, & Miller, 2012; Du, Goh, & Qiu, 2012; Du et al., 2014; Risser, Vialard, Baluwala, & Schnabel, 2013; D. Tward, Ma, Miller, & Younes, 2013; Khan, Wang, & Beg, 2013).

Prior work on histology-associated deformations

Deformation of brain tissue caused by histological procedures is well known and has been reported in the previous literature. The chemical composition of the fixation solution and duration of exposure have been previously shown to cause significant tissue shrinkage (Mouritzen, 1979; L, 1971; Quester & Schroder, 1997). More recently, histological distortions have been quantified with imaging techniques like MRI or computed tomography using variables such as total brain volume and the distance between hand-selected landmarks, in comparisons before and after mouse brain histology (Wehrl et al., 2015). Others have assessed dense local deformative effects of extraction and fixation by examining the strain resulting from a non-rigid displacement field (Schulz et al., 2011). Comparison of the total tissue area of imaged histological sections with block-face images can quantify the global in-plane shrinkage caused by sectioning, and neuronal density in the cutting axis has been used to quantify the non-uniformity of shrinkage in that direction (Carlo & Stevens, 2011).

Contributions of this work

Here, we propose an automated computational pipeline for same-subject MRI reference guided reconstruction of multi-modal histological image stacks of the marmoset brain followed by registration to a labeled atlas. We build upon our recent work incorporating Sobolev priors to solve the histological stacking problem of Nissl stacks onto high resolution atlases at the light microscope scale (Lee, Tward, Mitra, & Miller, 2018). However, this previous work only employed a standard reference atlas, and did not have access to same-brain MRIs. In the present paper, our reconstruction process is informed by the ex-vivo MRI of the brain prior to histology as well as an image intensity smoothness prior. To perform robust atlas-mapping, we have used a variant of the multi-channel large deformation diffeomorphic metric mapping (LDDMM, RRID:SCR 009590) algorithm which applies voxel-level weights to the image similarity metric to account for contrast changes, as well as damage or noise in histological sections.

We apply our new methodology to a dataset of marmoset brains obtained as part of the RIKEN Brain/MINDS project and demonstrate solutions to the multi-modal stack reconstruction problem as well as robust atlas mapping results across four modalities. Importantly, we are able to quantify the 3D tissue distortion caused by two major parts of the histology procedure – the “sectioning” process (cryoprotection, freezing, sectioning) captured by the ex-vivo MRI to histology mapping and “preparatory” process (injection, incubation, perfusion, fixation) captured by the in-vivo MRI to ex-vivo MRI mapping. The former histological process causes only a ~2% scale change (median absolute local scale change), whereas the perfusion-fixation step causes a much larger scale change of ~7%. This is an important contribution that extends our previous work demonstrating the Cramer-Rao bounds on estimating the first fundamental form given by the Jacobian determinant (D. Tward, Mitra, & Miller, 2019).

2. Materials and Methods

2.1. Data

The marmoset brain dataset used in this paper was prepared using a high throughput histological and image processing pipeline, described in (Lin et al., 2019). Briefly, each individual marmoset brain dataset consists of high resolution (9.4T) MRI scans (both in-vivo and ex-vivo post perfusion/extraction/fixation preparations) and high resolution images of a series of brain sections that have undergone histological processing to stain for Nissl substance, Myelin, Fluoroscent neuronal tracers and the expression of Cholera toxin B (CTB). The in-vivo MRI was acquired from the marmosets prior to any experiments at a resolution of 0.269 mm * 0.269mm * 0.539 mm per voxel. The ex-vivo MRI was acquired after the injection of tracers, the incubation period, perfusion, and fixation at a resolution of 0.1 mm *0.1 mm * 0.2mm per voxel. The histological sections were imaged after sucrose cryoprotection, freezing, and cryo-sectioning. For simplicity, we refer to the procedures that occur between the in-vivo and ex-vivo MRI acquisitions as the “preparatory processes” and the procedures that occur between ex-vivo MRI acquisition and histology as the “sectioning process”. The histological image data was originally acquired at 0.46 μm in-plane resolution with 20 μm section thickness (alternating through four stains resulting in 80 μm gap between sections of a single modality, resulting in a ~174x factor of anisotropy between XY and Z directions) and was downsampled to 80 μm in-plane resolution for computational purposes. We additionally use the Brain/MINDS marmoset brain atlas (Digital Brain Atlas of the Common Marmoset, RRID:SCR 005069) (Woodward et al., 2018) which includes a nissl-stained 3D volume as part of our processing pipeline.

In following sections, we describe two image registration algorithms (see Methods section 2.2) applied towards mapping the multimodal datasets of the marmoset brain (n=15) (Lin et al., 2019) between the in-vivo MRI, ex-vivo MRI, and post-sectioning states within a single animal, as well as to a common population atlas. Firstly, we generated informed estimates of reconstructed stacks of Nissl-stained sections by simultaneously calculating a diffeomorphism φ (a nonlinear smooth, 1-to-1, invertible mapping) from any given reference brain to the target coordinates and the unknown rigid jitter motions associated to each section (Model 2 in 2.2). Where available for a particular animal, ex-vivo MRI was substituted as the reference brain and is then matched to the histology stack using a low-dimensional linear rigid-scale/affine motion φ (6 or 12 degrees of freedom) of the MRI volume coupled to the rigid motions of the individual sections. Gradient descent based algorithms were then implemented as described in (Lee et al., 2018). A variant of the large deformation diffeomorphic metric mapping (LDDMM) algorithm (Beg et al., 2005) that accounts for missing structures or damaged sections was also employed to compute maps between the Nissl based reference atlases and the reconstructed Nissl stained brain data (Lee et al., 2018). For cross-modal registration of histological sections, we use a mutual-information based cross-modality matching function (S. Kutten et al., 2016;D. J. Tward et al., 2020). The full computational approach from multiple histological series to cross-modal registration and atlas-mapping followed by 3D reconstruction of tracer tracts is illustrated in Fig 1.

Figure 1: Computational workflow.

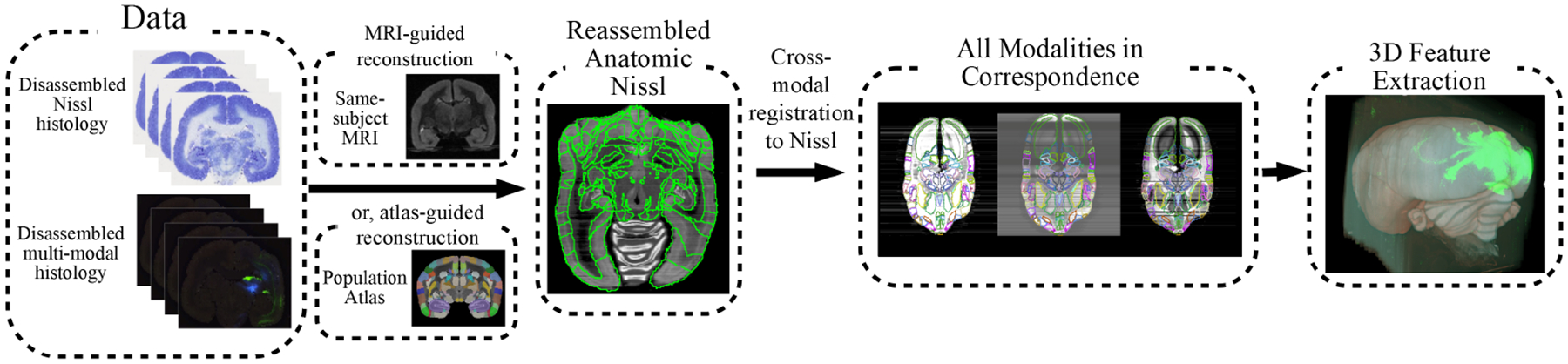
Reconstruction pipeline workflow from multi-modality histological image sections to segmented data and connectivity analysis. The proposed workflow starts with disassembled multi-modal histology and reconstructs 3D Nissl-stained volumes using either MRI or atlas guidance. Cross-modal reconstructions are then achieved by registration to the corresponding Nissl reconstruction. Segmentations are obtained as a side product of atlas registration. In the final step, connectivity-related features are extracted from the 3D volumes in a common coordinate space.

2.2. Models used in the pipeline: Volume to Volume model and Tape-transfer histology sectioning model

The algorithmic framework proposed in this paper is based on the random orbit model (M. Grenander & Miller, 2007). In this paper, we explicitly examine two statistical models defined as follows:

$$\text{Model}1:\text{Volume}-\text{Volume }J\left(x,y,z\right)=I\circ {\phi }^{-1}\left(x,y,z\right)+\mathit{\text{noise}}\left(x,y,z\right)$$ Model 1: Volume-Volume

Model 1 expresses cross-sectional (across subjects) anatomical variations by modeling this variation as a three-dimensional deformation field between two brain volumes. Here, this nonlinear three-dimensional deformation φ is restricted to the group of diffeomorphisms – smoothly varying, 1-to-1, and invertible mappings. Under the assumption that anatomical structures and their variations are smooth and continuous, the diffeomorphism model is well suited for the quantitative study of anatomy as it always provides correspondences between coordinate spaces and guarantees preservation of the underlying topology in the image. Model 1 assumes that the measured image J is a coherent volumetric image of a whole brain that is only distorted by additive imaging noise, and I is some exemplar or atlas image deformed by φ. This is classically known as the ” random orbit model” in which observed objects are generatively treated as deformations of some exemplar or atlas. Model 1 is therefore suited for describing the variation between two coherent 3D volumes or structures where the only noise introduced is imaging noise. Comparison of two MRI volumes is an examples of such a problem.

$$\text{Model}2:\text{Stack}-\text{Volume }J\left(R_i\left(x,y\right),z_i\right)=I\circ {\phi }^{-1}\left(x,y,z_i\right)+\mathit{\text{noise}}\left(x,y,z_i\right)$$ Model 2: Stack-Volume

On the other hand, Model 2 includes an additional transformation parameter on top of a 3D diffeomorphism, introduced by modeling the jitter caused by the histological processing steps; for morphometry purposes, the jitter is treated as some nuisance parameter to be estimated alongside the variation φ. Model 2 does not assume that the two images to be compared are coherent, well-formed 3D volumes, but instead assumes one images to be a ”jittery” stack of serial sections prior to reconstruction. Because we use a tape-transfer sectioning technique which largely preserves the tissue structure, we model the additional transformation required to reconstruct the serial-sectioned stack as a rigid motion on each 2D section, adding three degrees of freedom R_i for each z-section i. Hence, Model 2 is an extension to Model 1 for the case where the observed imaged J is a jittery histological stack and I is some exemplar (for instance a population atlas image or a pre-sectioning MRI of the structure observed in J).

Estimates of the reconstructed stack J^R = J(R_i(x, y), z_i), i = 1, … , n are generated by simultaneously calculating the transform φ from the atlas to the target coordinates and the unknown rigid jitter motions R_i, i = 1, … , n forming the iteratively reconstructed stack J^R. When I is a population atlas image from a different subject, φ is a diffeomorphism. Given a labeled atlas like the Brain/MINDs atlas, the registration of I to J^R by diffeomorphism φ allows the projection of region labels directly onto the reconstructed histology stack. When I is a same-subject reference image like an MRI volume, φ can be constrained to a rigid or affine transformation and labeled regions can be obtained by an additional atlas to stack diffeomorphism. In the following sections, we will use Model 2 to perform reconstruction and segmentation of histology stack J, guided by MRI or population atlas I. We will use Model 1 to study the deformative effects of the histological sectioning and tissue processing by a quantitative comparison of 3D volumes.

2.3. Distances for Variational Methods

The variational methods described above require building distances between the mean fields in Models 1 and 2 and the histology stacks. In general, we perform guided histology reconstruction as described in Model 2 above using the nissl-stained histology sections due to their anatomical clarity. The guiding image, I, is then the nissl Brain/MINDS atlas or a pre-sectioning MRI of the same subject brain. In the first case, as matching is performed within modalities, we define a similarity metric based on squared error of intensities. In the second case, cross-modal matching is driven by a mutual information similarity metric. The transformations for the additional stains/modalities (myelin, CTB, fluoro) are driven by the cross-modal metric.

To build correspondences between the histological stack 2D sections J^R(·, z_i) and sections of the Nissl atlas or cross-modality MRI image I(·, z_i) we define a similarity metric based on either squared-error (same modality) or mutual information (cross modality) as described by Kutten et al (S. Kutten et al., 2016).

Squared-error within modality

Define the error function between images d : (I, J) → R⁺ a positive squared-error function between images can be defined as the square of the Euclidean distance;

$$d\left(I,J\right)=\frac{1}{2}{\Vert J(\cdot )-I(\cdot )\Vert }_2^2=\frac{1}{2}\sum _{x,y,z}{\left|I\left(x,y,z\right)-J\left(x,y,z\right)\right|}^2.$$

Mutual information

Across modalities, p_I,J is the empirical estimate of the joint histogram density and p_I, p_J are the corresponding marginals. The mutual information d(I, J) is given by

$$d\left(I,J\right)=-\sum _{\eta }\sum _{\psi }{p}_{I,J}\left(\eta ,\psi \right)\text{log }\left(\frac{p_{I,J}\left(\eta ,\psi \right)}{p_I\left(\eta \right)p_J\left(\psi \right)}\right).$$ (1)

Decreasing the degrees of freedom for rigid motions

Following (Lee et al., 2018) for the stacking reconstructions J^R(·, z_i) = J(R_i(x, y), z_i), i = 1, … , n we introduce a Sobolev penalty imposing a prior on the smoothness under the assumption anatomical structures are smooth and arising from a smooth Sobolev space H^k equipped with norm:

$${\Vert J\Vert }_{H^k}^2=\sum _k\sum _{x,y,z}{\left|{\partial }_{h}J\left(x,y,z\right)\right|}^2,$$ (2)

with ∂_h denoting a total of h-derivatives in the three x, y, z coordinates. This is a natural assumption that ensures the resulting integrity of the reconstructed stack.

2.4. Diffeomorphic atlas-mapping

Having defined the metrics of similarity between histology and exemplar as well as metrics of integrity within the histology stack, we now describe the computation of the transforms: diffeomorphism φ and restacking parameters R_i. We choose to model 3D transformations as diffeomorphisms due to their suitability for computational anatomy, and in order to generate diffeomorphic maps between atlas φ : I → J we use the LDDMM algorithm (Beg et al., 2005) to generate flows ${\dot{\phi }}_t=v_t\circ {\phi }_t$, with φ = φ₁. The shortest flows that minimize the distance are calculated by defining an energy and calculating the variational minimizers of the flows:

$${\int }_0^1{\Vert v_t\Vert }_V^{2}dt+d\left(I\circ {\phi }_1^{-1},J^R\right).$$ (3)

For the L2 error we employ a multi-channel version of the LDDMM algorithm (Ceritoglu et al., 2009), defining multiple distances ${\Vert C_n\left(I_n\circ {\phi }_1^{-1}-J_n^R\right)\Vert }_2^2$ associated to different masks. Here, C_n is a matrix of the same size and dimension as I and J^R taking on values from 0 to 1, where 1 represents full confidence in the subject data, 0 represents no confidence in the subject data (i.e. histological sections that are known to be excluded), and values in between indicate varying noise levels (i.e. partially damaged histological sections). This cost mask is multiplied element-wise with the similarity metric.

In the algorithmic framework, based on the random orbit model (M. Grenander & Miller, 2007), we explicitly model both the cross-sectional anatomic variations via smooth deformations of templates, as well as the random jitter introduced by the histological sectioning process. The biological anatomic variations are modeled as a smooth change of coordinates via diffeomorphisms of some set of exemplars or templates, so that I = I_temp ∘ φ for some φ ∈ Diff the diffeomorphism group, with 3D images $I\left(x,y,z\right),\left(x,y,z\right)\in {\mathbb{S}}^3$. Measurement noise was modeled as a spatial white noise, through the usage of an L₂ norm between the data and the template, or different data sets. The technical variations from the histology pipeline were modeled using rigid motions of a series of 2D sections with z-axis section coordinates z_i, i = 1, … , n. The random jittering of planar sectioning is represented as a series of rigid planar transformations R(x, y) = (x cos θ + y sin θ + t^x,−x sin θ + y cos θ + t^y) with three degrees of freedom for each plane. The restacking parameters were constrained to rigid transforms due to the well-preserved nature of the tissue in-plane as a result of using tape-transfer sectioning. The limitation of this constraint is that this parameterization may not handle severe in-plane distortions or tissue damage, hence our inclusion of the term C_n above which allows us to censor damaged sections and reduce their weight in the overall deformation. A natural extension of this parameterization without changing the underlying optimization scheme could be to model a 2D rigid motion and a 2D diffeomorphism for each histology section.

2.5. Diffeomorphometry of Histological Procedures

The use of the diffeomorphic random orbit model (of Model 1) allows the quantitative analysis of deformative effects at each stage of the histology process (the preparatory and the sectioning processes). Using Model 1, we compute transformations between the in-vivo MRI and ex-vivo MRI, and between ex-vivo MRI and the histology stack produced by guided reconstruction, thus separating the deformative effects of the preparatory process from the sectioning process. In order to quantify the non-linear distortion between these coordinate spaces, we examine the first fundamental form of the mapping computed by the above method determines how vectors are transformed under mapping between coordinate systems (Atlas vs MRI vs histological image coordinates) and is specified by the Jacobian matrix (∂_Xφ).

$${\partial }_X\phi \left(x,y,z\right)=\left(\begin{array}{ccc}\frac{\partial {\phi }_1\left(x,y,z\right)}{\partial x}& \frac{\partial {\phi }_2\left(x,y,z\right)}{\partial x}& \frac{\partial {\phi }_3\left(x,y,z\right)}{\partial x}\\ \frac{\partial {\phi }_1\left(x,y,z\right)}{\partial y}& \frac{\partial {\phi }_2\left(x,y,z\right)}{\partial y}& \frac{\partial {\phi }_3\left(x,y,z\right)}{\partial y}\\ \frac{\partial {\phi }_1\left(x,y,z\right)}{\partial z}& \frac{\partial {\phi }_2\left(x,y,z\right)}{\partial z}& \frac{\partial {\phi }_3\left(x,y,z\right)}{\partial z}\end{array}\right).$$ (4)

The determinant |det ∂_Xφ| and its logarithm are fundamental measures of coordinate change and in the comparative study of the in-vivo and ex-vivo MRI and histology, directly measures the amount of metric distortion within the same animal, and the change in measure across coordinate systems of different animals. Naturally, the mapping between each coordinate space (in-vivo, ex-vivo, histology) may contain a rigid 3D component which we exclude from our morphometric measurement. The non-rigid component of the 3D distortion caused by the histology processing is isolated by performing affine registrations between each coordinate space (in-vivo MRI, ex-vivo MRI, and histology) as a pre-processing step to diffeomorphic registration. The scale change assocated with the determinant of the affine transform matrix is included in the reported percent scale change.

3. Results

3.1. Reconstruction and Atlas Mapping

Brain region parcellations were generated by the proposed joint optimization of an LDDMM-based atlas mapping procedure with stack reconstruction of a Nissl-stained histological volume of Section 2.2. The histological restacking was guided by a same-subject ex-vivo MRI scan where available. These informed variational solutions were optimized for each of fifteen brains in the Brain/MINDS dataset and we observed accurate estimates of the reconstructed stacks consistent with simulations previously reported in (Lee et al., 2018). Segmentations were projected from the registered Brain/MINDS atlas as an auxiliary output of the reconstruction workflow and sample segmentation and process detection results are depicted in Fig 2 for an individual marmoset brain. Segmentation of the fluorescence, myelin, and CTB images was achieved using the same reconstruction framework that was applied to the original Nissl stack, by using the corrected Nissl stack as an exact shape prior with only rigid in-plane cross-registration connecting the two series and using the cross-modality similarity metrics of Section 2.3. Fig 2 shows examples of fluorescent image stacks being reconstructed by transferring the segmentation computed on the Nissl stack. The top two rows of Fig 2 show the computed transforms applied to the full resolution fluorescence image stack. Major connections and fiber tracts originating from the fluoroscent tracer injections (Red: TRE3-tdTomato anterograde; Green:TRE3-Clover anterograde; Blue: Fast Blue retrograde) can be identified from the color-coded stains in 3D. The bottom row of Fig 2 shows 3D reconstructions of the tracings.

Figure 2: Sample Nissl-stained and fluorescent data displayed with segmented and reconstructed tracer detections.

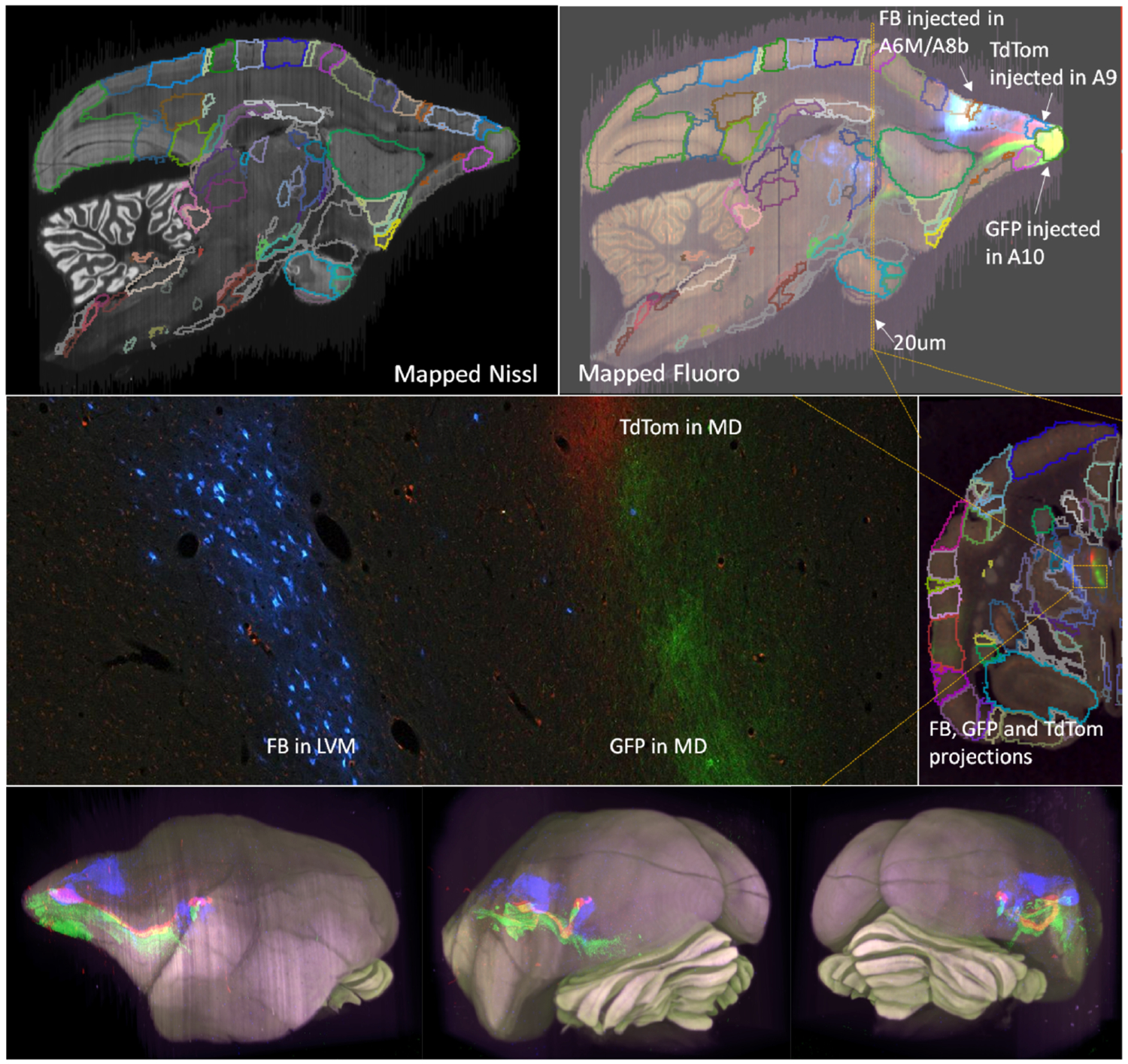
Top two rows: Nissl and fluorescent reconstructed segmented volumes. NB: the sections are originally cut in the coronal section; a sagittal virtual cut of the 3D reconstructed brain is shown. The upsampled reconstruction transforms are applied to the full resolution fluorescent tracer images where tract tracing can be performed. Here, the three injected tracers are labeled in the high resolution image (bottom left). Bottom row: 3D visualization of the Nissl stack reconstruction overlayed with the red, green, and blue tagged tracer paths detected from the registered fluorescence volumes.

3.2. Quantification of Metric Distortions

We examine the first fundamental form, or determinant of the metric tensor, of the diffeomorphic mapping as described in Eq (4) (see Methods section 2.5). We do this to quantify the distortion caused by the histological process. Several preparatory processes occur in between the in-vivo MRI acquisition and the ex-vivo MRI acquisition – we interpret the Jacobian determinant of the mapping between these coordinates spaces as the combined deformative effect of tracer injection, extraction, perfusion, and tissue fixation. We report the “percent scale change factor” which is computed as $|\text{det }{\partial }_X\phi {|}^{\frac{1}{3}}$, the cube root of the Jacobian determinant, and which represents the per-axis local scale change. Similarly, the freezing and sectioning processes occur between the ex-vivo MRI acquisition and the histological imaging. Under our informed histological reconstruction model of Section 2.2 we can interpret the scale change between these two coordinate spaces as the combined deformative effect of freezing/sectioning.

We illustrate the quantitative properties of the Jacobian matrix as a first-order description of the map. Four sample measurements (two of the sectioning process, A and B, and two of the preparatory process, C and D) from the dataset are shown in Fig 3. These demonstrate that there is minimal metric scale change away from the identity map for the ex-vivo MRI to sectioned histology maps. However, the measured metric scale was much higher for the in-vivo pre-preparatory MRI to ex-vivo post-preparatory MRI maps. Panels A and B show the percentage metric change away from the identity of the cube-root of the Jacobian between ex-vivo MRI and the Nissl reconstructed brains. Shown as a heat-map superimposed over the gray level images is the cubed root of the Jacobian determinant for the central sagittal section of each subject for each of two brains for mapping ex-vivo to histology stack section. As depicted by the color bar, the maximum value of blue represents 20 percent expansion in a dimension, with the red implying contraction. Panels C and D show similar analyses for two brains corresponding to ex-vivo to in-vivo MRI maps, indicating several areas of significant contraction and expansion. Overall, we report the mean across 15 subjects of the median absolute percent scale change as 1.97 ± 0.38 % for the sectioning process (ex-vivo MRI to reconstructed histology mapping) and 6.90 ± 2.08 % for the fixation process (ex-vivo MRI to in-vivo MRI mapping).

Figure 3: Local scale factor change in two ex-vivo to histology mappings and two in-vivo to ex-vivo mappings.

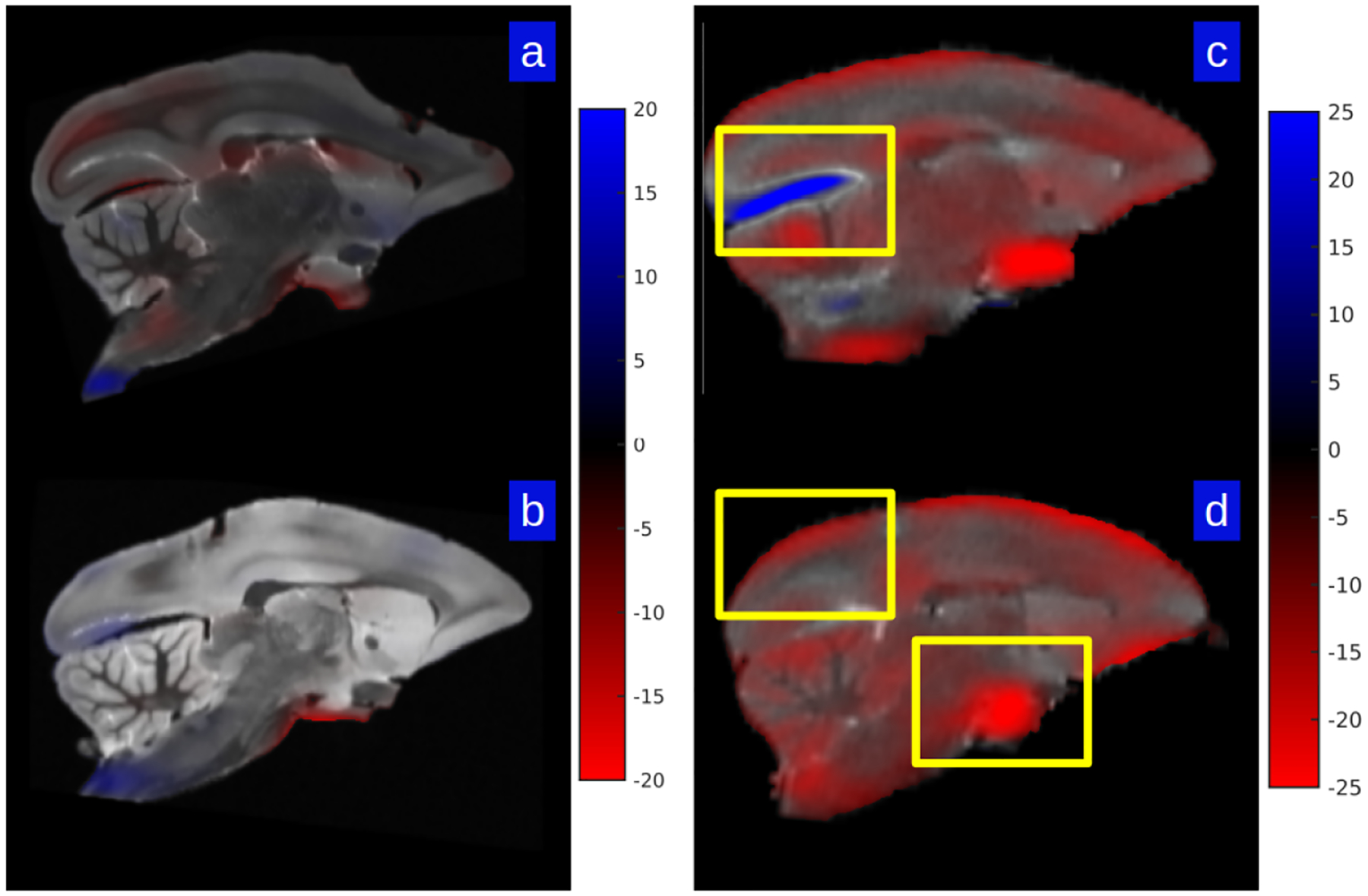
Shown is the percent scale change away from the identity of the mapping as measured by the cube-root of Jacobian determinant; blue depicts shrinkage, red expansion. Panels A and B show two examples of ex-vivo MRI mapped to Nissl histological stack; panels C and D show the same for the ex-vivo to in-vivo MRI. Yellow boxes depict intense scale changes which are depicted via grid deformation shown in Fig 5.

Shown in Fig 4 are histograms of the percent scale change factor between the ex-vivo to Nissl histological stack (A & B) and the ex-vivo to in-vivo spaces (C & D) for the same brains shown in Fig 3.

Figure 4: Histograms of local percent scale factor change in two ex-vivo to histology mappings and two in-vivo to ex-vivo mappings.

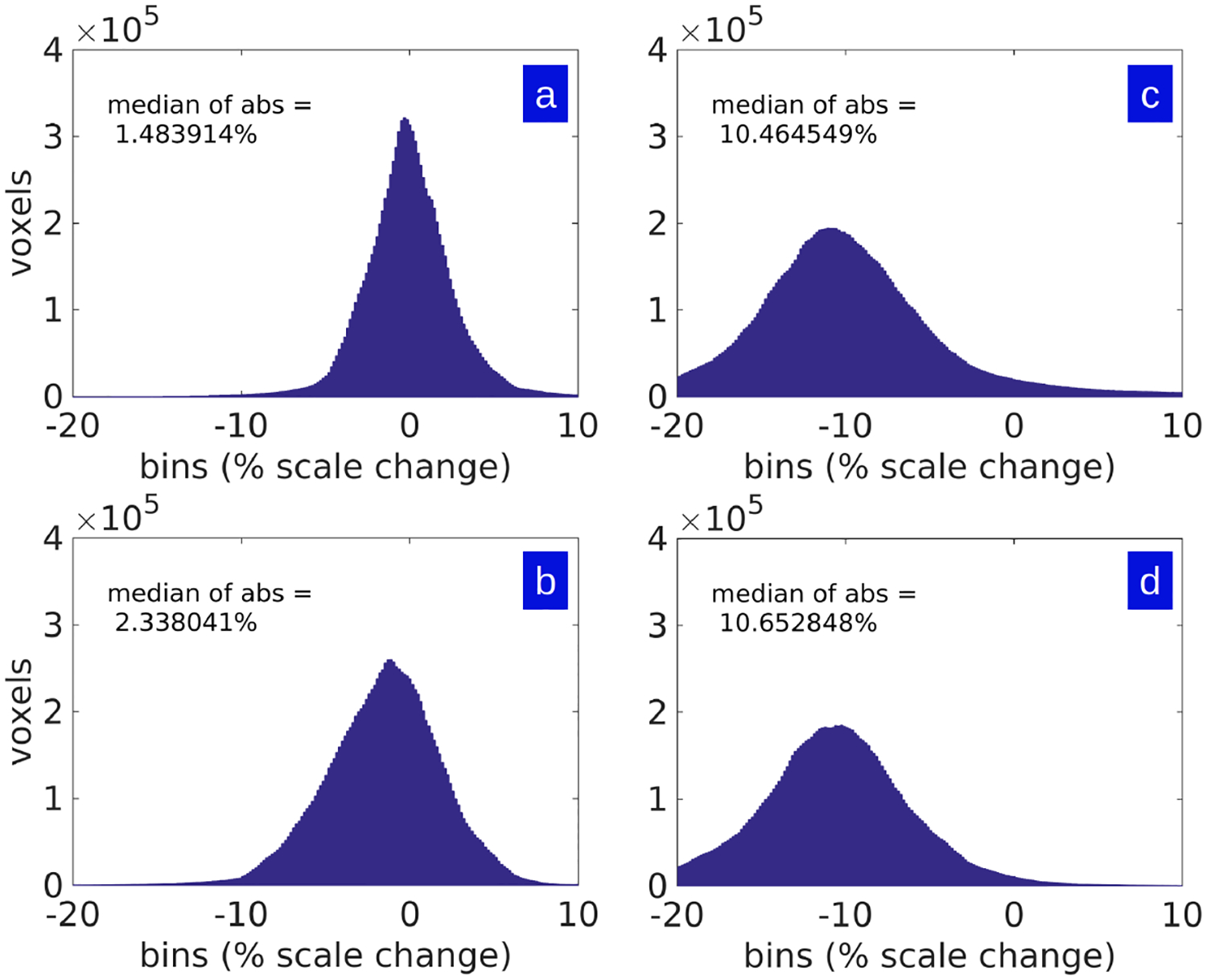
Shown are histograms of the percent scale in single axis dimension as measured by cube-root of Jacobian determinant of maps shown in Fig 3. Panels A and B show the ex-vivo MRI mapped to Nissl histological stack; Panels C and D show the ex-vivo MRI to in-vivo MRI histograms.

As seen in Fig 3 and Fig 4, the change in measures between the ex-vivo post-preparatory and in-vivo MR-measured coordinate systems are large and mostly contractive in each dimension as measured by the cubed-root of Jacobian determinant. In comparison, the corresponding metric change due to the sectioning process are small, and are almost symmetric around zero (so that both shrinkage and expansion occurs in roughly equal proportions). The histograms of Fig 4 demonstrate that the range of the ex-vivo post-preparatory to in-vivo MR maps are nearly three times in terms of median absolute scale change. Fig 5 shows that scale change can be as much as 20–25 percent in a single axis dimension as measured by the cubed-root of Jacobian determinant. Shown are sample in-plane deformations for magnified brain regions from Fig 3. Notice that the intense blue indicates 25 percent expansion, and intense red indicates 25 percent contraction along a single axis dimension.

Figure 5: Metric scale change associated with subvolume sections between in-vivo and ex-vivo MRIs.

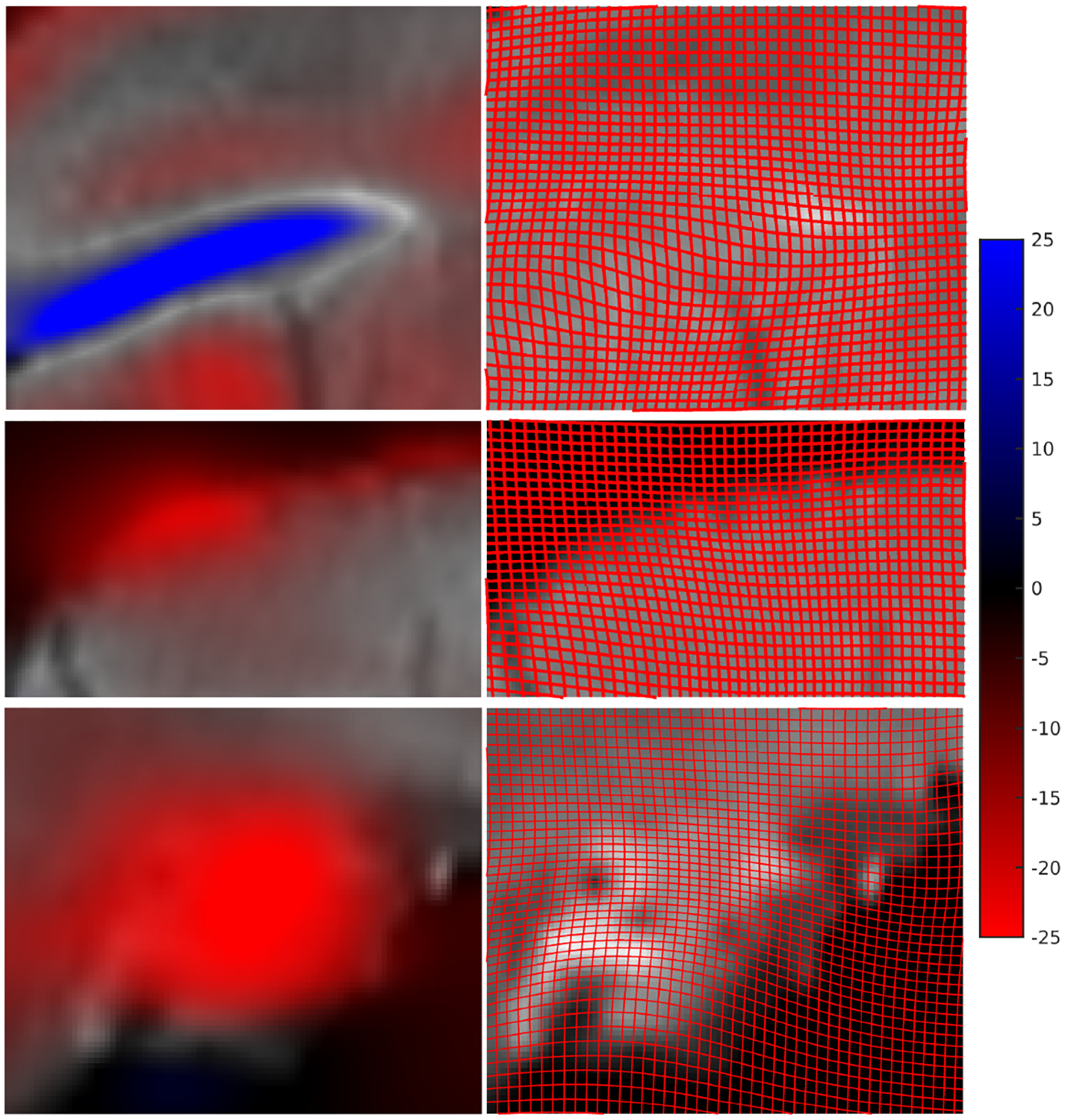
Maximum blue indicates 25 percent expansion, maximum red indicates 25 percent contraction as measured by the cubed-root of Jacobian determinant. Right column shows the how a uniform square grid on the in-vivo brain deforms when mapping to the ex-vivo brain. This helps visualize the scale factor change from identity. Both grid expansion (top row blue) and grid contraction (bottom row red) is seen.

A closer examination of the brain-wide distribution of changes in tissue volume due to the preparatory process between the in-vivo and the ex-vivo MR images is shown in Fig 6. The heat map of the percent scale change factor of one mapping from in-vivo to ex-vivo MRI is shown in sagittal and transverse sections of the same brain, with maximal red depicting 8 percent shrinkage along a single scale dimension. Delineation of cortical and sub-cortical structures (lines in Fig 6) from the atlas mapping shows that the distortions are not uniformly distributed across the cortex. Thus, in future work quantifying cell or process densities, it would be important to take into account these local scale changes, rather than relying on an overall scale factor which may or may not reflect what is going on at a specific location in the brain. Note the importance of acquiring an in-vivo and an ex-vivo MRI scan, without which this analysis is not possible.

Figure 6: Metric scale change of in-vivo to ex-vivo mapping in atlas coordinates.

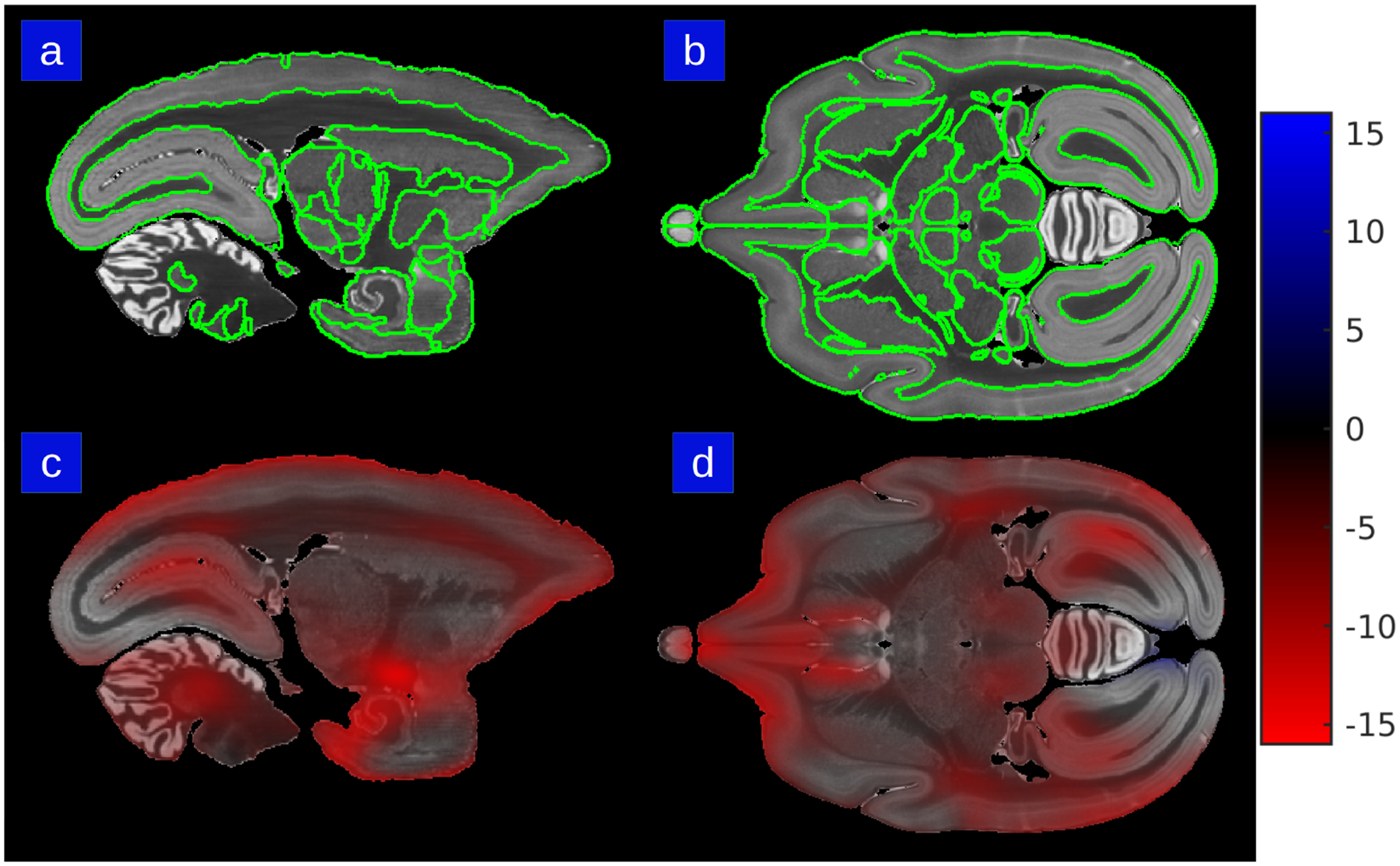
Percent scale factor heat map is superimposed on olfactory bulb, cortical areas, septum, thalamus, epithalamus, pretectum, brainstem, hypothalamus, cerebellum, cranial nerve, entorhinal cortex. Panels A & B show section outlines of structures in the Paxinos/Hashikawa atlas in sagittal and transverse views. Panels C & D show the metric scale change for the same sections. The color bar depicts maximum red of percent scale contraction in a single axis dimension.

The ex-vivo to histology coordinate mapping captures the deformative effects of the “sectioning” process. This mapping enables not only the histological reconstruction but also the segmentation of brain regions which allows the quantitative measurements of scale factor change. In an analysis of the dataset of 15 brains, the cerebral cortical areas, thalamus, brainstem and the cranial nerves showed a local scale change of < 1% per axis as measured by the percent scale change factor. The hippocampus, basal ganglia, pretectum and cerebellum showed a local change of 2–3% and the hypothalamus showed a local change of 4% per axis. The in-vivo to ex-vivo coordinate mapping encompassing the extraction, perfusion, and fixation procedures shows much higher levels of distortions when averaged across the dataset. The cerebral cortical areas, thalamus, brain stem and the cranial nerves show a significantly larger absolute scale change of 5–6% per axis. For the hippocampus, basal ganglia, pretectum, cerebellum, the difference was 6–8% for the in-vivo to ex-vivo maps. The hypothalamus showed a large change of 10% per axis.

3.3. Evaluation of Reconstruction Accuracy

The constraint of anatomical smoothness within a brain volume is critical to producing accurate reconstructions, particularly in cases with missing data or tissue damage (for instance, the cross-modality registration presented here in the case where the Nissl stack is damaged or has missing sections). As part of our registration and reconstruction model described in Methods section 2.2, we previously introduced a smoothness prior in the form of a Sobolev derivative norm to provide robustness and control the dimension during the diffeomorphic mapping and restacking solution. The Sobolev prior couples adjacent sections and results in continuity of the reconstruction. It is particularly noticeable in the registration of multiple subject modalities to one another where sections are missing or damaged. The importance of this prior is visible in panels A-C of Fig 7.

Figure 7: Reconstruction examples depicting the effect of the smoothness prior.

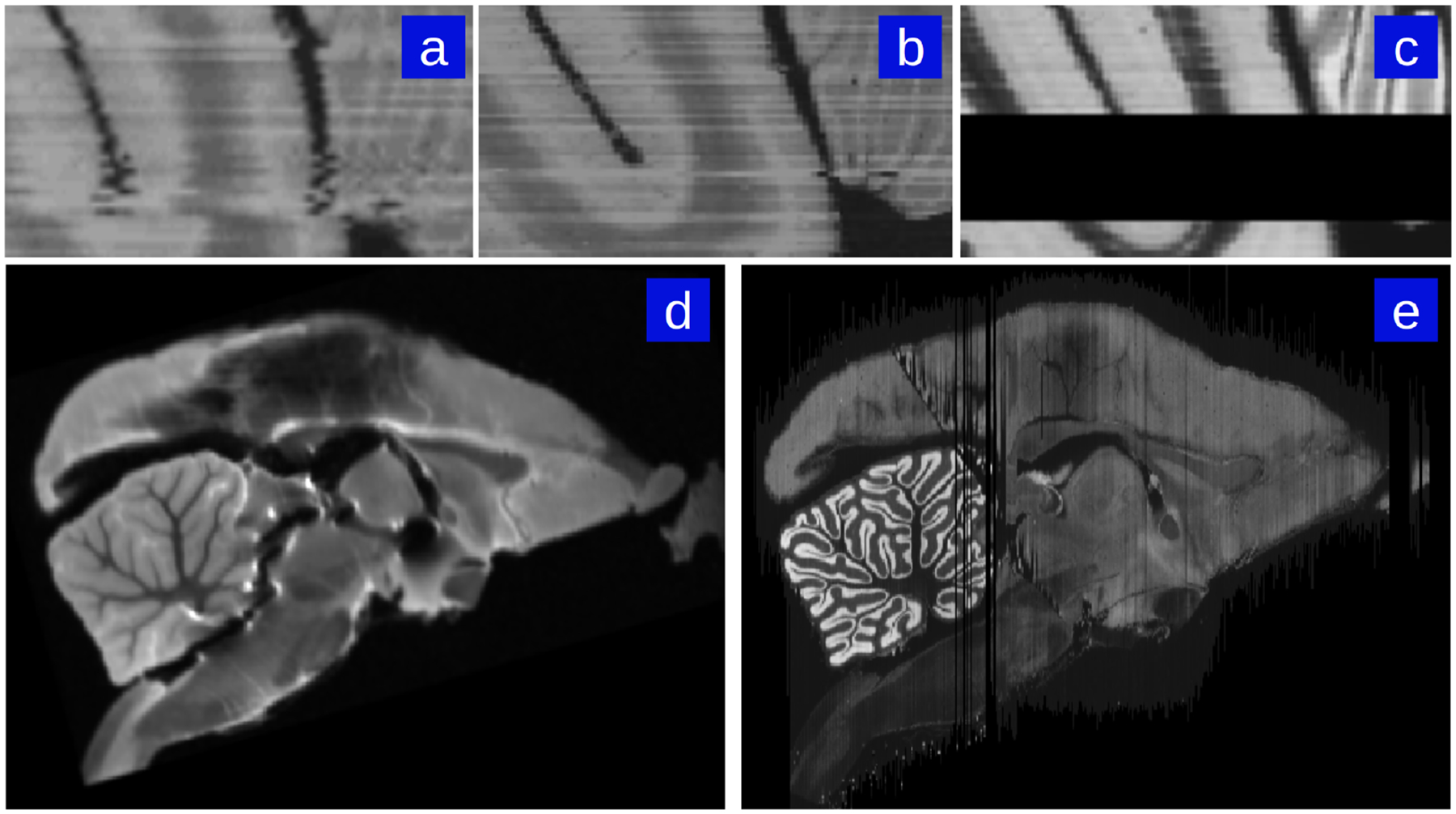
When the Nissl stack (c) has missing or noisy sections, reconstruction to the next-best Nissl section contains small distortion accumulations (a). Inclusion of a smoothness constraint corrects this error (b). Additionally, highly damaged Nissl stacks can still be reconstructed despite major differences between damaged Nissl sections to corresponding MRI sections. For instance, ex-vivo MRI of a particular subject marmoset brain prior to sectioning (d) and successful Nissl reconstruction of the same marmoset brain despite major damage caused by sectioning process (e).

The effect of the image intensity smoothness prior also manifests during Nissl-to-MRI stack reconstruction when there is significant damage to the Nissl brain. An example of our framework’s ability to achieve accurate reconstruction when there is significant tissue damage (such as cutting and folding in particular sections) to the sections is shown in panels D and E of Fig 7.

Our pipeline also allows for the correction of curvature artifacts associated with the histological restacking unguided by same-subject MRIs. Fig 8 shows examples of the curvature artifacts associated with 2D-3D reconstructions unguided by a reference brain (Malandain et al., 2004). These figures demonstrate that the MRI guided registration pipeline solves the curvature issue. An example of this problem is shown in Fig 8. The left 2 columns show the unguided stacking alignment which results in a large curvature artifact (highlighted within the yellow bounding box). The third and fourth columns show the guided restacking using our current pipeline. The yellow bounding boxes depict the areas with highest curvature bias effects. The curvature of the coordinate grid depicted in Figure 8 is encoded by the 2D component of the 3 × 3 Jacobian matrix of the transformation. Notice the curvature of the grid is more extreme for the unguided reconstruction which has no MRI to guide it globally. The Malandain curvature artifact is present in the warping of the grids in the uncorrected restacking case due to the higher metric cost of φ required to map an atlas onto the accumulated distortions of an unguided reconstruction.

Figure 8: Histology restacking examples from Brain/MINDS dataset.

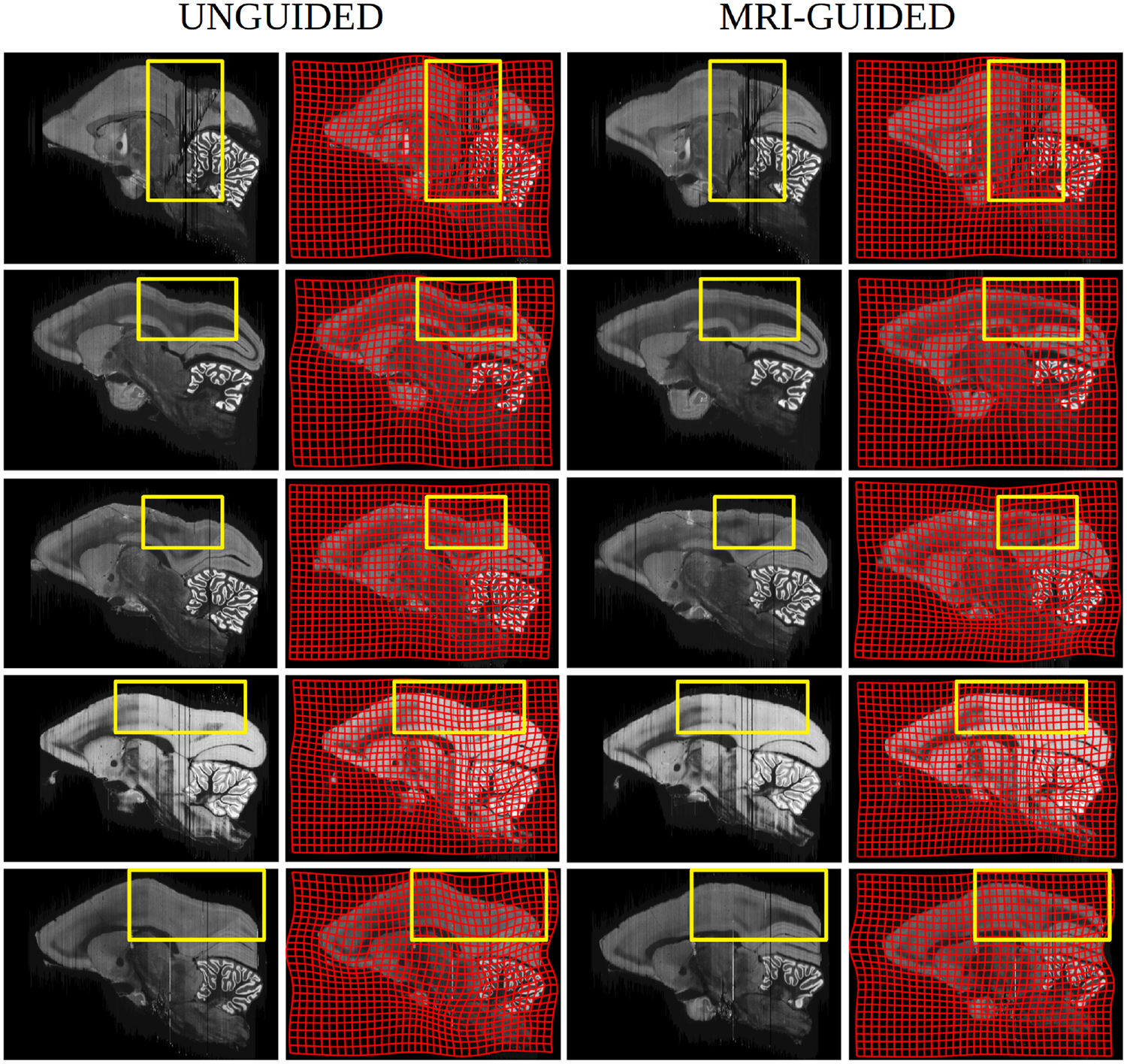
Columns 1 and 2 depict sections exhibiting Malandain curvature artifact (notice cortical bend) associated to the unguided alignment with column 2 showing deformation of the underlying coordinate associated to the atlas-to-target warping; columns 3 and 4 show the Nissl histological stackings which are guided via the template based deformation. Regions of large artifact compared to none are highlighted via yellow boxes.

The proposed method was also evaluated on a new simulated dataset (1000 examples) where sections of the Brain/MINDS atlas were randomly rotated and translated. The simulations demonstrated virtually unbiased estimates of the reconstructed stack with <1 voxel and <1 degree standard deviations and root mean squared error for both the translation and rotational aspects of the rigid motion at two levels of Gaussian white noise (standard deviation of 0 and 0.5 times the mean voxel intensity of brain tissue in the phantom image). Included in Fig 8 are clear illustrations of the use of the MRI atlas for dealing with the Malandain curvature artifact.

3.4. Evaluation of Registration Accuracy

The 3D-to-3D volume mapping of Model 1 (Section 2.2) is applied twice in the above quantification of metric distortions and an additional time in the computational pipeline: 1) the in-vivo MRI to ex-vivo MRI mapping which describes the preparatory processes, 2) the ex-vivo MRI to nissl reconstruction mapping which describes the sectioning processes, and 3) the Brain/MINDS atlas to nissl reconstruction mapping which brings the brains into a common coordinate space. Although the performance of LDDMM is well described in the literature, we additionally evaluate the accuracy of our cross-modal 3D-to-3D registration model by identifying eight landmarks in the marmoset brain (see Table 1 for summary of landmarks and description of their identification), six of which are drawn from the Brain/MINDS study (Woodward et al., 2018): center of the anterior commissure, mid-sagittal anterior corpus callossum, mid-sagittal posterior corpus callossum, left and right anterior dorsal lateral geniculate nucleus. We identify two additional landmarks of our own, the meeting of the left and right lateral sulcus with the cortical surface at the anterior-most point. These eight landmarks are manually identified across all in-vivo MRI, ex-vivo MRI, and nissl reconstructions in our distortion quantification dataset, and an analysis of mean landmark transfer accuracy across all 15 subjects is performed on the three mappings. We report an average transfer accuracy across all eight landmarks of 0.2602 mm for the atlas to nissl reconstruction mapping, 0.2319 mm for the ex-vivo MRI to nissl reconstruction mapping, and 0.3487 mm for the in-vivo MRI to ex-vivo MRI mapping. Both mappings used to quantify tissue distortions have landmark transfer error of 1–2 voxels for all landmarks, which we consider to be within the error range expected for human landmark identification and transform interpolation. Sample image overlaps resulting from registration warps are displayed in Figure 9.

Table 1:

Summary of landmarks selected for registration accuracy evaluation alongside mean landmark transfer accuracy across 15 subjects.

Landmark	Location Description	Transfer Accuracy: In-vivo to Ex-vivo (mm)	Transfer Accuracy: Ex-vivo to Nissl (mm)	Transfer Accuracy: Atlas to Nissl (mm)
Dorsal lateral geniculate nucleus (left)	Posterior-most point of left dorsal lateral geniculate nucleus in coronal view	0.2432	0.1615	0.1789
Dorsal lateral geniculate nucleus (right)	Posterior-most point of right dorsal lateral geniculate nucleus in coronal view	0.2411	0.1372	0.2106
Anterior commissure	Mid-sagittal anterior-most point of the anterior commissure	0.3632	0.1302	0.1866
Corpus callossum, anterior	Anterior-most point of the corpus callossum in mid-sagittal plane	0.4326	0.2859	0.1625
Corpus callossum, posterior	Posterior-most point of the corpus callossum in mid-sagittal plane	0.2875	0.3486	0.2648
Lateral sulcus (left)	Posterior-most intersection of left lateral sulcus with cortical surface	0.4939	0.3290	0.4156
Lateral sulcus (right)	Posterior-most intersection of right lateral sulcus with cortical surface	0.5201	0.3578	0.4887
Fastidium of fourth ventricle	Mid-sagittal point of the fastigium of the fourth ventricle	0.2083	0.1053	0.1742

Figure 9: Image overlap after volume to volume registration.

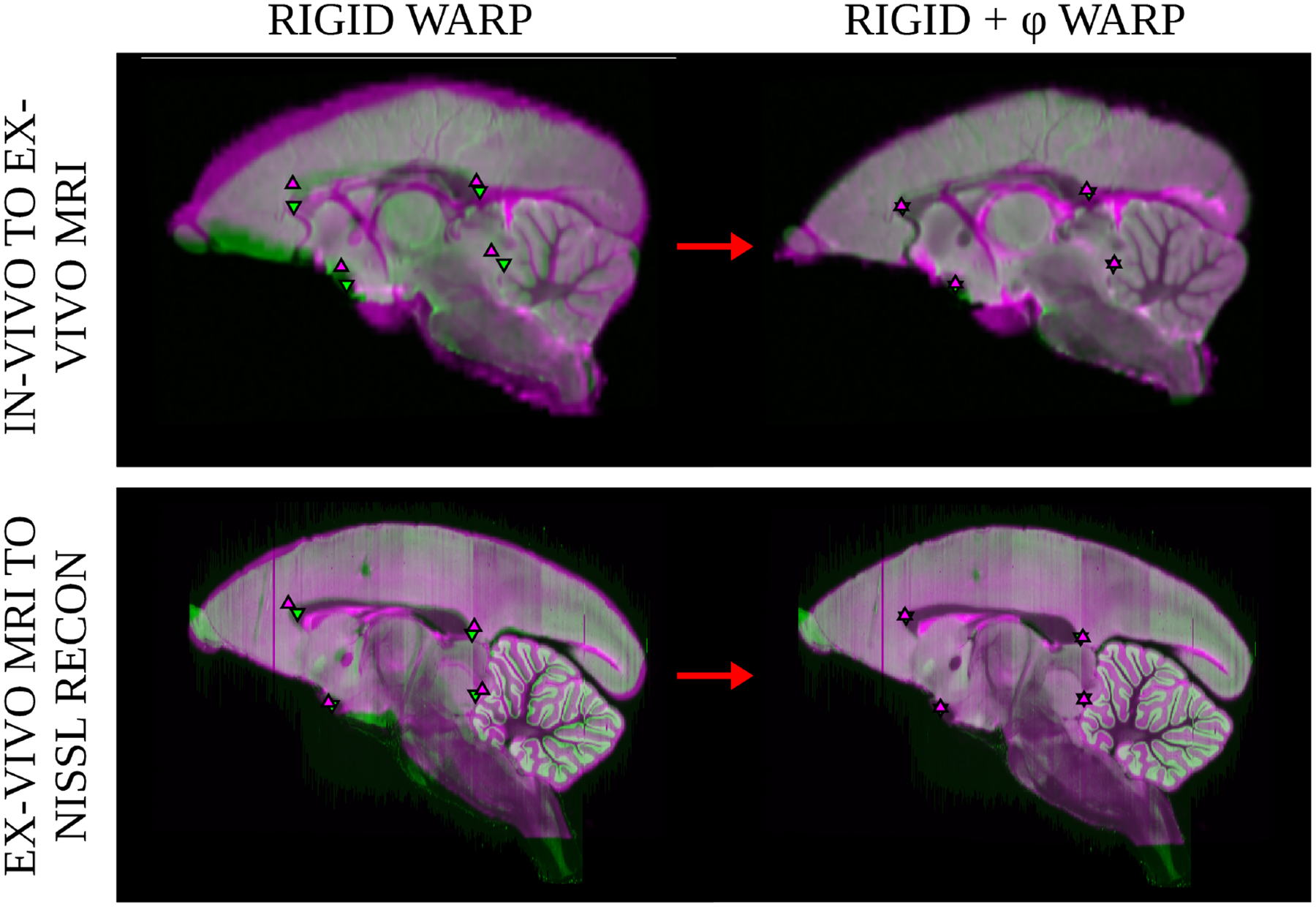
Registration accuracy was measured to validate quantitative distortion measurements. The top row shows overlap of a subjectφs in-vivo MRI (magenta) mapped to the ex-vivo MRI (green) and the bottom row shows overlap of a subjectφs ex-vivo MRI (magenta) mapped to the nissl reconstruction (green). Landmarks located near the mid-sagittal plane from the landmark transfer analysis are overlayed on each image: posterior and anterior corpus callossum, anterior commissure, and the fastidium of the fourth ventricle.

4. Discussion

In this paper, we have shown the application of an LDDMM based registration pipeline to a multimodal dataset of marmoset brains. The methodology described in this paper is a significant advance over the unbiased re-stacking and integration to a reference atlas for a similar histological pipeline for the mouse brain, which did not include same-subject MRI volumes (Lee et al., 2018).

Our results (Fig 3) reveal that the general deformation effect caused by the histological process is shrinkage in certain areas of the brain, and also expansion in other regions. The shrinkage is not surprising as it is generally well-known that some tissue shrinkage is caused by the histology procedures (Mouritzen, 1979). Examination of the mean image (Fig 6) shows that shrinkage is not uniform throughout the brain but is generally located in the central and inferior regions of the brain, and near the ventricles. However, we note that some areas of the brain also showed expansions as depicted in the almost symmetric histogram of scale changes. More importantly, the methodology provides a quantitative measure for every brain voxel of the associated scale factor.

The diffeomorphic maps were generated for the population of 15 brains. The cubed-root of the determinant of the Jacobian was averaged across the empirical sample and the percent difference away from the identity was calculated for all of the structures within the template. The average metric scale was computed for select brain areas such as the olfactory bulb, cortical areas, septum, thalamus, epithalamus, pretectum, brainstem, hypothalamus, cerebellum, cranial nerves, entorhinal cortex. Our 3D volume reassembled maps from the tape transfer assisted histological sections matched very closely with the ex-vivo MRI maps. When the reassembled volumes from sections using the tape transfer technique (Pinksly et al., 2015) were compared with the ex-vivo post perfusion MRI, the effciency of the technique in preserving the tissue becomes evident.

In contrast, quantification of the impact of the preparatory processes which was achieved by mapping the in-vivo MRIs to the ex-vivo MRIs, confirms the large, uni-directional shrinkage of brain tissue that has been reported in the literature. Again, we believe that this is the first time there is a detailed quantification of these changes brain-wide. We show that this shrinkage is not uniform across the brain and different brain areas show quite different levels of change.

As first described by Malandain in the context of brain histology (Malandain et al., 2004), correct reconstruction of a sectioned object without prior knowledge of the object’s shape is diffcult and easily prone to error. Here, we presented models to inform our histological reconstruction algorithm with the best available shape prior – either an MRI of the brain prior to sectioning or an atlas volume of the same species and modality. In the case of the reconstructions on the Brain/MINDS dataset, we showed results of the former model. For datasets that do not include same-subject reference imagery, the availability of whole brain 3D marmoset atlases, e.g. Paxinos (Paxinos, Watson, Petrides, Rosa, & Tokuno, 2012) or Brain/MINDS (Woodward et al., 2018), allow us to accurately reconstruct both the local and global restacking properties that are also free from the (Malandain et al., 2004) curvature artifacts. Our simulation results show that same-subject reference guided reconstruction was able to recover the re-sectioning parameters with high accuracy, which not only provides value in improved visualization but also improves registration and segmentation accuracy.

When the shape prior is a same subject reference volume, the guided reconstruction acts as an improved initialization for nonlinear image registration, placing the voxels of the subject volume closer to their corresponding voxels in the atlas volume. As with any gradient-based optimization framework, LDDMM benefits from improved initialization as this reduces the likelihood of falling into a local minimum in the objective function. As shown in Fig 8 the sample maps generated by registration of the Brain/MINDS atlas to an unguided reconstruction versus a guided reconstruction reveals an increased curvature of the underlying coordinate grid warp associated with the atlas mapping in the unguided case, indicating a displacement field with higher magnitudes and less homogeneity.

The addition of the smoothness prior via the Sobolev norm is valuable for providing robustness in the presence of noise or missing data or when the shape prior is not an exact reference volume. The driving intuition behind the smoothness prior is that in addition to the subject brain taking the shape of the reference volume, its image should be continuous and smooth. The effect of this prior is particularly noticeable in the registration of multiple subject modalities to one another where sections are missing or damaged. This is visible in the top row of Fig 7.

In conclusion, we have measured the local scale changes associated with the two major steps of histological processing for brain perfusion and sectioning reassembly. We measured the metric scale change using the fundamental form of the diffeomorphic mappings involved. We found that freezing and tape-transfer assisted histological sectioning produces minimallocal scale changes of ~2 ± 0.4% per axis dimension. The preparatory step as assessed by mapping in-vivo MRI to ex-vivo MRI shows a much larger scale change of ~ 6–8 % per axis dimension. To the best of our knowledge, this is the first systematic quantification of the local metric distortions associated with whole-brain processing.