Standardizing Discrete-Time Hazard Ratios With a Disease Risk Score

Abstract

The disease risk score (DRS) is a summary score that is a function of a potentially large set of covariates. The DRS can be used to control for confounding by the covariates that went into estimation of the DRS and obtain a standardized estimate of an exposure’s effect on disease. However, to date, literature on the DRS has not addressed analyses that focus on estimation of survival or hazard functions, which are common in epidemiologic analyses of cohort data. Here, we propose a method for standardization of hazard ratios using the DRS in longitudinal analyses of the association between a binary exposure and an outcome. This approach to handling a potentially large set of covariates through a model-based approach to standardization may provide a useful tool for cohort analyses of hazard ratios and may be particularly well-suited to settings where an exposure propensity score is difficult to model. Simulations are used in this paper to illustrate the approach, and an empirical example is provided.

Abbreviations

DRS

disease risk score

EPS

exposure propensity score

IPE

inverse probability of exposure

SMR

standardized mortality ratio

Suppose that an investigator wants to estimate the association between an exposure variable and a binary outcome variable while using standardization to control for confounding. One approach to achieving standardization in a regression model framework is to use a balancing score, such as the exposure propensity score (EPS) or the disease risk score (DRS), to reduce a potentially large vector of covariates to a single scalar summary variable (1–5). For risk ratios or prevalence ratios, recent work has demonstrated that this can be done using inverse probability of exposure (IPE) weights or DRS-based methods (3, 5–7). For hazard ratios, previous work has demonstrated how IPE weights can be used to obtain a standardized estimate in a proportional hazards model framework (8–10). However, an approach to the use of the DRS for analyses of hazard ratios has not been proposed.

We propose an approach for estimating the effect of a binary point exposure on the hazard of an outcome in a regression model framework that leverages the DRS for covariate control. The DRS may be preferable to the EPS for multivariable standardization if the exposure is extremely rare (11, 12), relatively novel (i.e., newly emerging), or difficult to model (13).

METHODS

Consider a study in which deaths have been ascertained without loss to follow-up for a closed cohort. Let X_i denote a binary point exposure of primary interest and Z_i denote baseline covariates (such as age at study entry, race, and sex), noting that i indexes cohort members and we use subscript i to denote the values of variables for cohort member i.

Suppose the cohort information is recorded in discrete time, meaning that continuous time has been divided into a sequence of contiguous time periods of equal duration (e.g., person-years). Define study entry as time 0 and administrative censoring at the end of the study, τ. Denote by T_i person i’s failure time (possibly occurring after τ, in which case the person was observed through the end of study), and let d_i denote an indicator of failure during the study period (d = 1) or censoring (d = 0). Denote the time of last observation for person i, T_i^*, equal to T_i or τ, whichever occurs first. Here we focus on analysis in a cohort mortality study, but we note that the proposed methods readily extend to analysis of incident first events and also could apply to repeated independent events.

A person-oriented data structure for a cohort mortality study may include 1 row of data per person in the cohort (Figure 1A), which records i, X_i,  Z_i, τ, T_i, and d_i. Alternatively, a person-period data structure includes multiple rows of data per person in the cohort (Figure 1B). Let j index discrete time from study entry (j = 0) and let subscript j denote the values of variables in time period j. Note that, throughout, X_i and Z_i denote baseline covariates that do not change over time j. Denote by Y_ij a binary time-varying indicator of the outcome status associated with person i in period j that takes a value of 0 except at time T_i, when Y_ij is assigned the value of the binary indicator of failure status for person i, d_i. In addition, for each record in the data structure, we define a time-varying variable, q_ij, that equals 1 for periods j ≤ T_i^* and 0 for periods T_i^*< j ≤ τ.

Figure 1.

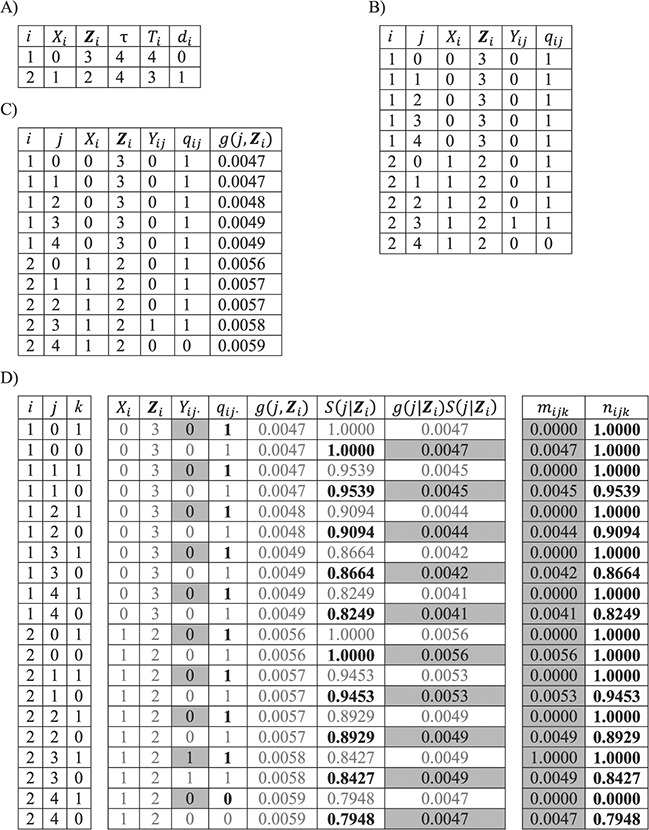
Possible data structures for 2 people in a cohort study. A) A person-level data structure; B), a person-period data structure; C) a person-period data structure with a disease risk score appended; D) an expanded data structure with 2 records per person-period. In these data structures, i indexes cohort members, X_i is a binary point exposure of primary interest, Z_i denotes baseline covariates, 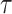is the administrative end of the study, T_i is person i’s failure time, d_i denotes a binary indicator of failure during the study period (d = 1) or censoring (d = 0), j indexes discrete time, Y_ij is a binary indicator of case status for person i in period j, q_ij is a binary indicator of whether person i was “at risk” in period j, 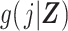is the disease risk score, k is an index for 2 rows of information for each person-period (where k = 1 corresponds to the information for estimation of the numerator of the ratio of standardized discrete-time hazards and k = 0 corresponds to the information for estimation of the denominator of the ratio), S(j, Z) is the survival function, m_ijk is the outcome variable in the proposed regression model for obtaining a standardized estimate of the discrete-time hazard ratio (gray fill illustrates which values inform calculation of m_ijk), and n_ijk is used to define an offset in the proposed regression model for obtaining a standardized estimate of the discrete-time hazard ratio (boldface text illustrates which values inform calculation of n_ijk).

For the purposes of defining the estimand of interest, let h(j|Z,X) denote the discrete-time hazard function, and let 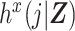denote the potential discrete-time hazard function for the intervention setting X = x. Suppose that i = 1 to p represent the exposed (X = 1) cohort members (i.e., the cohort has been sorted by X). We define a ratio of standardized potential discrete-time hazards contrasting X = 1 with X = 0, where the target population is the exposed (X = 1), as

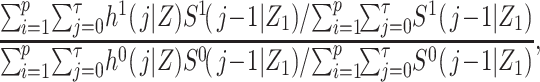(1)

where 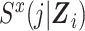denotes the probability of surviving through time j; that is,

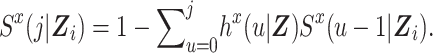We define 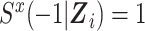, and we assume that the discrete-time hazard in any time interval j is suitably small for this approximation. Note that the quantities in the numerator and denominator of this standardized ratio measure have the form of expected numbers of events divided by expected times in the study, and consequently these quantities could be termed rates.

Disease risk score

Using just the records for at-risk person-periods observed among the unexposed (q_ij = 1 and X_i = 0), we can estimate the discrete-time hazard of the outcome in the absence of exposure, which we refer to as the DRS.

Since Y_ij is bounded by 0 and 1, the DRS can be modeled as having a logistic dependence on a set of predictors by fitting a pooled logistic model of the form

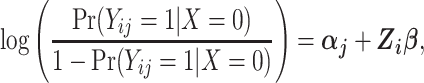where the vector of parameters, α_j, describes the baseline hazard function and β is a vector of parameters associated with covariates Z. Estimation of a vector of j parameters associated with discrete time intervals of the baseline logit hazard function, α_j, may be inefficient; and often a smooth function of time, j, might be specified using, for example, splines or polynomial bases. Also note that product terms for interaction between the time scale and covariates can of course be included in the model, if appropriate. Using the estimated coefficients from the fitted model, the DRS (Figure 1C) may be calculated for all members of the cohort, i, and all periods, j, as .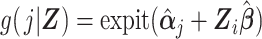

Estimating standardized ratios

Estimation of the ratio of standardized discrete-time hazards in equation 1 may be done using the DRS. We proceed by assuming 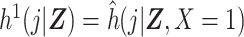, under consistency, and 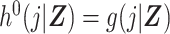, under the additional assumptions of correct model specification and conditional exchangeability.

Suppose that we expand the person-period data set to include 2 rows for each person-period: The first corresponds to the information needed for estimation of the numerator of the standardized ratio, and the second corresponds to information needed for estimation of the denominator of the standardized ratio (Figure 1D). Let 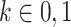index these 2 rows of information for each person-period. The expanded data set includes rows indexed by person i, period j, and stratum k.

In this expanded data set, k = 1 corresponds to the information needed for estimation of the numerator of the ratio (Table 1). When k = 1, m_ijk = 1 and n_ijk = 1 correspond to a binary indicator of case status for person i in period j, Y_ij, and an indicator of whether person i was “at risk” in period j, q_ij, respectively.

Table 1.

Definitions of the Outcome Variable (m_ijk) and the Antilog of an Offset (n_ijk) in a Proposed Regression Model Fitted to an Expanded Data Structure to Obtain a Standardized Estimate of the Discrete-Time Hazard Ratio

k a	k = 1	k = 0
mijk	Yij b	c , d
nijk	qij e

^a Index for 2 rows of information for each person-period. k = 1 corresponds to the information for estimation of the numerator of the ratio of standardized discrete-time hazards, and k = 0 corresponds to the information for estimation of the denominator of the ratio.

^b  Y_ij is a binary indicator of case status for person i in period j.

^c  g(j,Z) is the disease risk score.

^d  S(j,Z) is the survival function.

^e  q_ij is a binary indicator of whether person i was “at risk” in period j.

In the expanded data set, k = 0 corresponds to the information needed for estimation of the denominator of the ratio (Table 1). When k = 0, m_ijk = 0 and n_ijk = 0 correspond to 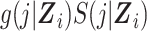and 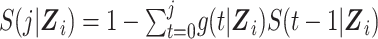, respectively, where S(j,Z) is the survival function and we define .

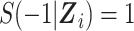Using just the records with X = 1, a regression model fitted to the expanded data structure may take the form

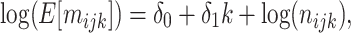where the antilog of estimated parameter 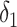estimates the standardized ratio comparing the observed discrete-time hazard at X = 1 with the expected discrete-time hazard among persons with X = 1 had their exposure been set to X = 0. When n_ijk = 0, a small constant is added to allow calculation of log(n_ijk). Estimation of robust confidence intervals is recommended given the 2-stage regression (first estimation of the DRS and second fitting the marginal structural model) (14). In the Web Appendix (available at https://academic.oup.com/aje), we provide illustrative SAS code (SAS Institute, Inc., Cary, North Carolina) for obtaining discrete-time hazard ratios with both robust confidence intervals and bootstrapped confidence intervals.

Simulation example

We use simulated data under a cohort study design to demonstrate the implementation of the proposed approach and as confirmatory of the mathematical results (rather than as a comprehensive analysis of finite sample properties). Data were simulated for 1,000 cohort studies with 10,000 members in each cohort. In each simulation, at baseline we generated 10 covariates, denoted Z₁–Z₁₀. Among these, Z₁–Z₄ were confounders associated with both exposure and outcome, Z₅–Z₇ were exposure predictors, and Z₈–Z₁₀ were outcome predictors. Z₁, Z₃, Z₅, Z₆, Z₈, and Z₉ were random binary variables, and the others were continuous variables assigned as the absolute value of standard normal random variables with mean 0 and variance 1. The relationships between variables follow the structure described by Lee et al. (15), with correlations induced between several of the variables (Figure 1). We generated a random binary exposure, X, with an exposure prevalence of approximately 10%; we encoded dependence of X on covariates by specifying that X took a value of 1 with probability 1/{1 + exp[−(−0.1 – 1 × Z₁ – 0.5 × Z₂ – 0.5 × Z₃ – 0.5 × Z₄ – 0.5 × Z₅ – 0.5 × Z₆ – 0.5 × Z₇)]}.

Each person entered the study at t = 0 and was followed until t = 20. Each person-year, we generated a random binary outcome Y in which we encoded dependence of the outcome on X, covariates, and time in the study. Two simulation scenarios were examined. In the first simulation scenario, there was homogeneity of stratum-specific ratios, such that Y took a value of 1 with probability exp(−3 + 0.1 × log(t) + 1 ×X − 0.5 × Z₁ – 0.1 × Z₂ – 0.5 × Z₃ – 0.1 × Z₄ – 0.5 ×Z₈ – 0.5 × Z₉ – 0.1 × Z₁₀). In the second simulation scenario, there was heterogeneity of stratum-specific ratios, such that Y took a value of 1 with probability exp(−3 + 0.1 × log(t) + 1 × X – 0.5 × Z₁ – 0.1 × Z₂ – 0.5 × Z₃ – 0.1 × Z₄ – 0.5 × Z₈ – 0.5 × Z₉ – 0.1 × Z₁₀ + 1 × X × Z₁).

First, we estimated the crude discrete-time hazard ratio by fitting a regression model for Y as a function of X, and we estimated a covariate-adjusted hazard ratio by fitting a regression model for Y as a function of X, log(t), and Z₁–Z₁₀, including each covariate as a main effect in the regression model (and not including any product terms for interaction between covariates or between covariates and the exposure of interest, X).

Next, we estimated the DRS by fitting a regression model to predict Y as a function of log(t) and Z₁–Z₁₀ among the unexposed (X = 0), including each covariate as a main effect in the regression model (and not including any product terms for interaction between covariates). We used the method described in this paper (and the SAS code shown in the Web Appendix) to obtain a standardized estimate of the discrete-time hazard ratio, and we used the robust variance estimator.

We also estimated a standardized ratio using an IPE-weighted marginal structural log binomial model, with robust variance (16). We fitted a logistic model to each simulated cohort at baseline to predict X as a function of Z₁, Z_2, …, Z₁₀, including each covariate as a main effect in the regression model (and not including any product terms for interaction between covariates). The predicted probability of exposure from the fitted model is the EPS. We constructed standardized mortality ratio (SMR) weights to estimate the standardized ratio where the target population is the exposed group (2, 17); exposed cohort members are given a weight of 1, while unexposed cohort members are given weights that are defined as the ratio of the estimated propensity score to 1 minus the estimated propensity score. We also constructed stabilized IPE weights to estimate the ratio for scenarios where the target population is the total study population; exposed cohort members are given a weight defined as the ratio of the marginal probability of exposure to the estimated propensity score, while unexposed cohort members are given a weight defined as the ratio of 1 minus the marginal probability of exposure to 1 minus the estimated propensity score. In each analysis, we summarized results from 1,000 simulated cohorts by computing the mean log discrete-time hazard ratio (log hazard ratio), the estimated standard deviation of the 1,000 log hazard ratios, and the average estimated robust standard error of the log hazard ratio. Simulations were conducted over the 1,000 cohorts, and the mean values of the exposure group-specific log hazard ratios and associated 95% confidence intervals were calculated.

Empirical example

We used the method described in this paper to estimate a standardized ratio, and also estimated a standardized ratio using an IPE-weighted marginal structural log binomial model, in empirical data from Kalbfleisch and Prentice (18) that were derived from the Veteran’s Administration Lung Cancer Trial, a study in which there was imbalance in covariates across treatment arms. The data concerned a cohort of 137 male patients with advanced, inoperable lung cancer who were given either standard therapy or experimental chemotherapy. The exposure of primary interest was a binary variable coded “1” for treatment by the test chemotherapy or “0” for standard therapy, and the outcome of interest was vital status (1 = deceased, 0 = censored), with survival time recorded in days; in the current analysis, we assumed administrative censoring at 999 days. Covariates included histological type of the tumor (coded 1 for squamous cell carcinoma, 2 for small cell carcinoma, 3 for adenocarcinoma, or 4 for large cell carcinoma), age at study entry (in years), Karnofsky performance score for overall patient status at study entry (range, 0–100), time between diagnosis and start of the study (in months), and a binary indicator for whether the patient had received prior therapy. We derived standardized estimates of the discrete-time hazard ratio for scenarios where the target population was the exposed group and used the robust variance estimator.

RESULTS

Simulations

In the first simulation scenario, there was homogeneity of stratum-specific ratios. The crude estimate differed from the value specified under the simulation setup (Table 2). The covariate-adjusted estimate was equivalent to the specified value.

Table 2.

Estimated Difference in the Mean Log Discrete-Time Hazard Ratio, Empirical Standard Error, and Average Estimated Standard Error for 1,000 Cohorts With 1,000 Observations

Simulation Setup	Simulation Result
	Log HR	ESE	ASE a
Simulation scenario 1 (homogeneity)
Crude	1.13	0.05	0.05
Adjusted in multivariable outcome model	1.00	0.05	0.05
EPS-weighted (ATE)	0.93	0.06	0.06
EPS-weighted (ATT)	0.93	0.05	0.05
DRS-based (equation 1; ATT)	0.93	0.05	0.04
Simulation scenario 2 (heterogeneity)
Crude	1.38	0.04	0.04
Adjusted in multivariable outcome model	1.28	0.05	0.05
EPS-weighted (ATE)	1.38	0.05	0.06
EPS-weighted (ATT)	1.18	0.05	0.05
DRS-based (equation 1; ATT)	1.18	0.05	0.04

Abbreviations: ASE, average standard error; ATE, average treatment effect in the total population; ATT, average treatment effect in the treated; DRS, disease risk score; EPS, exposure propensity score; ESE, empirical standard error; HR, hazard ratio.

^a For crude and multivariable-adjusted estimates, ASE is the average standard error estimated across 1,000 simulated cohorts. For DRS- and EPS-based estimates, ASE is the average robust standard error.

The hazard ratio is not a collapsible measure of association, meaning that the standardized marginal estimate of the hazard ratio need not equal the covariate-adjusted hazard ratio estimate, even in the absence of confounding (19, 20). Consistent with that fact, the DRS-based estimate does not equal the covariate-adjusted estimate. However, the DRS-based method yielded an estimate of association that was equivalent to the estimates obtained from marginal structural log-binomial models using IPE weights and SMR weights (Table 2). Note that when there is homogeneity of the effect measure across levels of covariates, the choice of target population does not affect estimates of the standardized ratios, and the IPE- and SMR-weighted estimates will be equivalent.

In the second simulation scenario, there was heterogeneity of stratum-specific ratios (Table 2). Again, the DRS-based method yielded an estimate of association that was equivalent to the estimates obtained from marginal structural log-binomial models using SMR weights. Given heterogeneity of the discrete-time hazard ratio across levels of covariates, the choice of target population does matter, and the IPE-weighted estimate of the ratio (which targets the total population) differs from the estimate obtained using SMR-type weights (which, like the proposed DRS-based method, targets the exposure effect among the exposed).

Empirical example

The empirical cohort included 137 patients, of whom 68 (49.6%) received chemotherapy and 128 (93.4%) were deceased by the end of follow-up. Chemotherapy-treated patients were more likely to have squamous cell carcinoma (57% vs. 43%) or adenocarcinoma (67% vs. 33%) than standard therapy patients. Chemotherapy-treated patients were slightly older than standard-therapy patients (mean age = 59 years vs. 57 years). Chemotherapy-treated patients were similar to standard therapy patients with respect to Karnofsky performance score, time between diagnosis and the start of the study, and proportion of patients who had received another type of therapy before the current one.

Fitting the proposed DRS-based model yielded a standardized discrete-time hazard ratio estimate of 0.85 (95% confidence interval: 0.60, 1.18). Fitting a marginal structural model with SMR weights yielded a standardized hazard ratio estimate of 0.86 (95% confidence interval: 0.55, 1.33) when the target population was the exposed cohort. Similarly to the simulations, the proposed DRS-based model yielded an estimated discrete-time hazard ratio that was very similar to the SMR-weighted estimate obtained using marginal structural models with weights derived using the EPS.

DISCUSSION

This paper has focused on implementation of regression models using a DRS to obtain estimates of standardized discrete-time hazard ratios. The proposed DRS-based model may be appealing in study settings where the EPS is difficult to model well. In simulations and in our empirical example, it was feasible to estimate both the DRS and the EPS; however, in practice there are settings in which one approach or the other may be preferable or most feasible. Use of the DRS may be attractive, for example, if the exposure of interest is newly emerging or extremely rare, because under such conditions it may be difficult to reliably model the EPS. When exposure does not occur in some strata of covariates, the EPS may be difficult or impossible to estimate. For example, in a study of the safety or effectiveness of a newly introduced therapy, the DRS may be appealing, relative to the EPS, if there are historical data with which to model the DRS before introduction of the new therapy. Similar settings arise in occupational and environmental studies, where a novel environmental contaminant or a change in industrial process occurs, if there are historical data with which to model the DRS prior to that change. Our proposed approach focuses on estimation of the exposure effect among the exposed, and therefore it pertains only to strata of covariates where there were exposed cohort members. The proposed approach leverages a DRS model fitted using the data for the unexposed cohort members to estimate the potential outcomes expected among the exposed had they been unexposed.

An issue that has received attention in the literature on the DRS is what group to use to fit the model for estimation of the DRS (13). We note that in the proposed approach we split the data, estimating the DRS only in the records for the unexposed and estimating the standardized discrete-time hazard ratio only using records for the exposed. The problem of “overfitting” to the unexposed by estimating the DRS in the same sample as that used for the calculated predictions may be minimized in this way; however, further work on this topic is warranted. We note that the DRS, 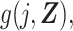could be estimated in a well-chosen out-of-sample group, and estimation of the discrete-time hazard ratio would proceed in the same fashion as when the DRS is estimated in an unexposed in-sample group.

One challenge to using a DRS-based method is the difficulty of assessing whether the model for estimation of the DRS is appropriately specified. Wyss et al. (21) have suggested a “dry-run” analysis in which the referent group is partitioned into pseudo-exposed and pseudo-unexposed groups so that differences in the observed covariates resemble differences between the actual exposed and unexposed populations but the adjusted (pseudo-)exposure–outcome association is expected to be null. Under their proposed approach, a DRS model is evaluated by its ability to retrieve an unconfounded null estimate after adjustment in this “dry-run” analysis. Such an approach could also be applied in the setting considered in the current paper, where the target of estimation is the standardized discrete-time hazard ratio.

In this paper we focused on analyses of a single outcome of interest, setting aside the issue of competing risks. We note that this approach can be extended to analyses of cause-specific mortality in which we model 2 (or more) competing risks for mortality. As in standard estimates of the cause-specific hazard ratio, common risk factors should be controlled for in the analytical approach (e.g., via regression adjustment or weighting), and such approaches may be necessary with DRS-based estimates of the discrete-time hazard ratio as well.

Classical approaches to standardization of rates commence with categorization of covariates and cross-classification of person-time and events into these categories. The alternative approach considered here commences with a balancing score, which we refer to as the DRS. Using a regression model, this approach can allow us to reduce a potentially large vector of covariates to a single scalar summary variable; the approach accommodates continuous covariates as well as ordinal or nominal categorical variables, and rather than complete saturation of the model, as implemented classically by the cross-classification of information by levels of all covariates, simpler models for the DRS may be fitted if appropriate.

Hansen (6) laid out a basis for understanding the DRS as a method for inducing prognostic balance in observed data for studies of response to treatment. Here we have extended the use of the DRS to induce prognostic balance in time-to-event analyses, by which, in the absence of right-censoring, we are referring to a setting where the potential time to the event of interest under the control treatment is independent of covariates, Z_i, conditional on the DRS. In our setting of estimation of a ratio of standardized discrete-time hazards, where the target population is the exposed, this is achieved by taking the DRS as an estimate of 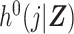and using this quantity to generate potential times to event among the exposed had they been unexposed. Prognostic balance hinges upon our estimated DRS function 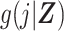being sufficient to serve this purpose. Further work, formally demonstrating the properties of prognostic balance in the setting of discrete-time hazards, is beyond the scope of the current paper but would make a useful contribution to the literature on the DRS. Other investigators have described related approaches to using a DRS in the context of proportional hazards regression, implemented through matching, stratification, or covariate adjustment (e.g., entering the score by means of indicator terms for categories) (22, 23). In this paper we describe an approach to estimation of a ratio of standardized discrete-time hazard ratios that avoids coarsening (as might occur when matching, stratifying, or adjusting for categories defined by the DRS) or the need to specify a parametric form when including the DRS as a continuous explanatory variable in a regression model.

The approach described here focuses on a setting where Z_i denotes baseline covariates. We have not addressed the setting of time-varying covariates, and notably have not addressed settings of time-varying covariates affected by prior exposure. Extension of the DRS to these more analytically complex settings is beyond the scope of the current paper but is an important direction for future work.

We have focused on a setting involving a contrast defined by a binary point exposure of primary interest. In recent work, we have discussed conditions and approaches to analysis of standardized risk ratios using the DRS when the exposure variable has more than 2 levels (24). Extension of the present approach to a contrast involving more than 2 categories may be considered in future work involving estimation of standardized discrete-time hazard ratios when the exposure variable has more than 2 levels.

The proposed approach yields a standardized discrete-time hazard ratio that may be useful for summarization of research findings. This standardized ratio corresponds to an estimate of a causal contrast, the exposure effect among the exposed. This has the appeal of conveying an estimate that pertains to a well-defined target population, and it is a useful summary measure of potential interest in a range of settings. In a study of the safety or effectiveness of a therapy, the treatment effect among the treated is often what is desired; similarly, in occupational settings, a manager or regulator considering a policy or intervention designed to reduce exposure to an agent often desires an estimate of the exposure’s effect among the exposed. In such settings, a marginal estimate of the exposure’s effect, in the form of the proposed standardized ratio, is one potentially appealing quantitative summary. As illustrated in the Web Appendix, calculation of the proposed DRS-based standardized discrete-time hazard ratio is readily performed.