Abstract
Purpose
A major challenge for accurate quantitative SPECT imaging of some radionuclides is the inadequacy of simple energy window based scatter estimation methods, widely available on clinic systems. A deep learning approach for SPECT/CT scatter estimation is investigated as an alternative to computationally expensive Monte Carlo (MC) methods for challenging SPECT radionuclides, such as 90Y.
Methods
A deep convolutional neural network (DCNN) was trained to separately estimate each scatter projection from the measured 90Y bremsstrahlung SPECT emission projection and CT attenuation projection that form the network inputs. The 13 layer deep architecture consisted of separate paths for the emission and attenuation projection that are concatenated before the final convolution steps. The training label consisted of MC-generated ‘true’ scatter projections in phantoms (MC is needed only for training) with the mean square difference relative to the model output serving as the loss function. The test data set included a simulated sphere phantom with a lung insert, measurements of a liver phantom and patients after 90Y radioembolization. OS-EM SPECT reconstruction without scatter correction (NO-SC), with the true scatter (TRUE-SC) (available for simulated data only), with the DCNN estimated scatter (DCNN-SC), and with a previously developed MC scatter model (MC-SC) were compared, including with 90Y PET when available.
Results
The contrast recovery (CR) vs. noise and lung insert residual error vs. noise curves for images reconstructed with DCNN-SC and MC-SC estimates were similar. At the same noise level of 10% (across multiple realizations) the average sphere CR was 24%, 52%, 55% and 67% for NO-SC, MC-SC, DCNN-SC and TRUE-SC, respectively. For the liver phantom, the average CR for liver inserts were 32%, 73% and 65% for NO-SC, MC-SC and DCNN-SC, respectively while the corresponding values for average contrast-to-noise ratio (visibility index) in low-concentration extra hepatic inserts were 2, 19 and 61, respectively. In patients, there was high concordance between lesion-to-liver uptake ratios for SPECT reconstruction with DCNN-SC (Median 4.8, range 0.02 −13.8) compared with MC-SC (Median 4.0, range 0.13 – 12.1; CCC = 0.98) and with 90Y PET (Median 4.9, range 0.02 – 11.2; CCC = 0.96) while the concordance with NO-SC was poor (Median 2.8, range 0.3 – 7.2; CCC = 0.59). The trained DCNN took ~ 40 seconds (using a single i5 processor on a desktop computer) to generate the scatter estimates for all 128 views in a patient scan, compared to ~ 80 min for the MC scatter model using 12 processors.
Conclusions
For diverse 90Y test data that included patient studies, we demonstrated comparable performance between images reconstructed with deep learning and MC based scatter estimates using metrics relevant for dosimetry and for safety This approach, that can be generalized to other radionuclides by changing the training data, is well suited for real-time clinical use because of the high speed, orders of magnitude faster than MC, while maintaining high accuracy.
Keywords: Scatter correction, deep learning, SPECT/CT, 90Y, Monte Carlo methods, convolutional neural network (CNN), radioembolization
Introduction
Accurate scatter estimation is essential for improving quantitative SPECT for dosimetry applications as well as to improve visibility of low-uptake regions that is important for safety in some applications. It is generally accepted that the Monte Carlo (MC) method that fully models the physics of photon transport in the patient and camera provides the most accurate scatter estimation. However, MC simulation is very time consuming because one must track many photon histories to generate low-noise estimates. Hence, simpler but less accurate energy window based scatter approximation methods are commonly used in the clinic. Although high quantitative accuracy with practical methods such as the triple-energy window scatter estimation has been demonstrated for Tc-99m SPECT [1], performance is less well-established for more complex radionuclides with multiple high intensity gamma-rays, large downscatter components and cross-talk. Furthermore, energy window based methods are generally not suited for bremsstrahlung photons because the energy spectrum is continuous. MC scatter modeling has demonstrated enhanced 90Y bremsstrahlung SPECT/CT imaging [2,3], but only in a clinical research setting where its high computational cost/complexity is acceptable.
Machine learning methods in medical imaging, including deep learning, have rapidly advanced in the past 5 years [4,5] with next generation tools in CT reconstruction recently receiving FDA clearance. Recently, there has been an increase in studies reporting on using machine learning methods to enhance nuclear medicine imaging [6–9]. In PET, promising initial results have been presented using convolutional neural networks (CNNs) for image denoising, image reconstruction and compensation for attenuation and scatter [10–15]. Due to the challenges of deriving attenuation coefficient maps from MR, the focus in deep learning based attenuation correction has been for PET/MR applications, mostly using CNNs trained to generate pseudo-CT images from the MR images [9]. For PET scatter correction, two studies report initial results using CNNs trained to generate scatter profiles from input PET emission and attenuation data. Berker et al [11] used the popular U-Net structure [16], trained with single-scatter simulation, to generate single-scatter profiles. In brain imaging, high accuracy was demonstrated relative to the conventional model based single scatter simulation, but performance was poor for the bed position with the high uptake bladder extending outside the axial field-of-view, questioning the adequacy of using single scatter simulation for training. Qian et al [12] used a deep learning approach to estimate both single and multiple scatter as an alternative to Monte Carlo based total scatter estimation. Initial results limited to testing of PET scatter profiles in phantom studies were promising but the need for further evaluation was emphasized.
The few studies reporting on deep learning to enhance gamma camera planar imaging and SPECT, thus far, have been limited to post-reconstruction image denoising [17, 18]. For Tc-99m MAA SPECT, recently, a U-net structure was used to enhance FBP reconstruction in image space [17]. For whole body 99mTc-hydroxydiphosphonate bone scans, a CNN, trained with sets of Monte Carlo generated noisy and noiseless images, demonstrated denoising with little or no resolution loss [18]. For SPECT attenuation correction, a recent study reports on a deep CNN to directly estimate the attenuation map from emission images without using CT-information [19]. For SPECT scatter estimation/correction, although artificial neural networks trained on (energy) spectral analysis were proposed over two decades ago [20–22], to our knowledge, there have been no studies that exploit the recent advances in deep learning.
The aim of this study was to investigate a deep learning based SPECT scatter estimation that overcomes the accuracy-computational efficiency trade-off associated with MC scatter modeling. We incorporate the scatter projections estimated by the trained deep CNN (DCNN) into the forward model of the traditional model-based iterative reconstruction. While our proposed method is applicable to SPECT scatter correction in general, we implement and evaluate it here for the challenging case of scatter estimation in 90Y SPECT/CT that relies on bremsstrahlung photons due to the lack of gamma-ray emissions. The continuous 90Y bremsstrahlung energy spectrum extends up to 2.3 MeV, and there is substantial downscatter into the acquisition window that is typically set in the range 100 – 250 keV. In phantom measurements and simulations, we compare images reconstructed with the proposed DCNN scatter estimate with those reconstructed with our previous MC scatter model [3] as well as with the true scatter, in the case of simulated data. Application in 90Y microsphere radioembolization (RE) patient imaging is also demonstrated and compared with 90Y PET, generally considered as superior to 90Y SPECT for quantitative imaging.
Materials and Methods
Overview
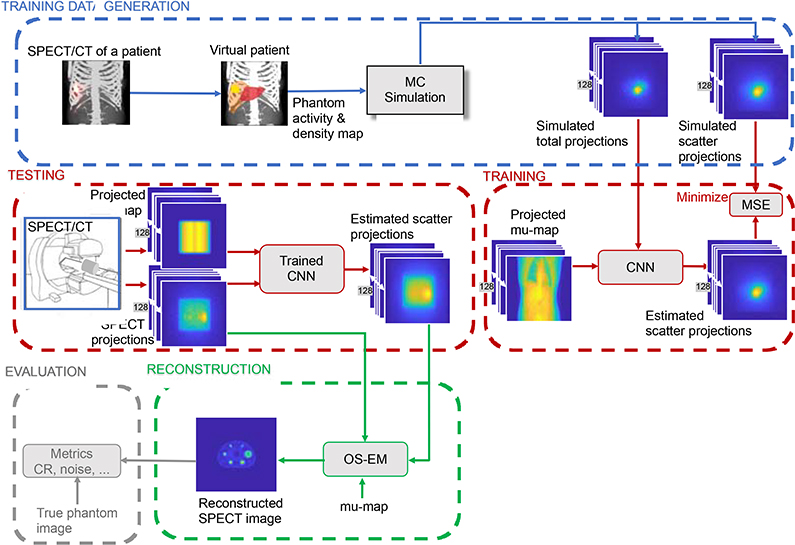
Fig. 1 shows the entire workflow that includes generation of phantom projection data for training, the training process and the evaluation of reconstructed test images. The DCNN is trained to estimate each scatter projection from the corresponding measured total (primary + scatter) SPECT projection view and the projected (to SPECT projection space) CT-based linear attenuation coefficient map (mu-map). The training process involves minimizing the mean square error (MSE) between the DCNN output and the “ground truth” for the (phantom) training data set, which is the true scatter we generate by high-count Monte Carlo simulation. MC simulation is needed only once, for a given SPECT system, to generate training data, since the network learns to reproduce the MC-based scatter output given only the acquired projections as input. For testing with independent data, the estimated scatter from the trained DCNN is used as an additive term in the OS-EM forward projection reconstruction model. We use qualitative/quantitative metrics to evaluate the reconstructed test images.
Fig. 1.
Overview of the scatter correction workflow showing the data generation, training and testing of the trained DCNN.
Network
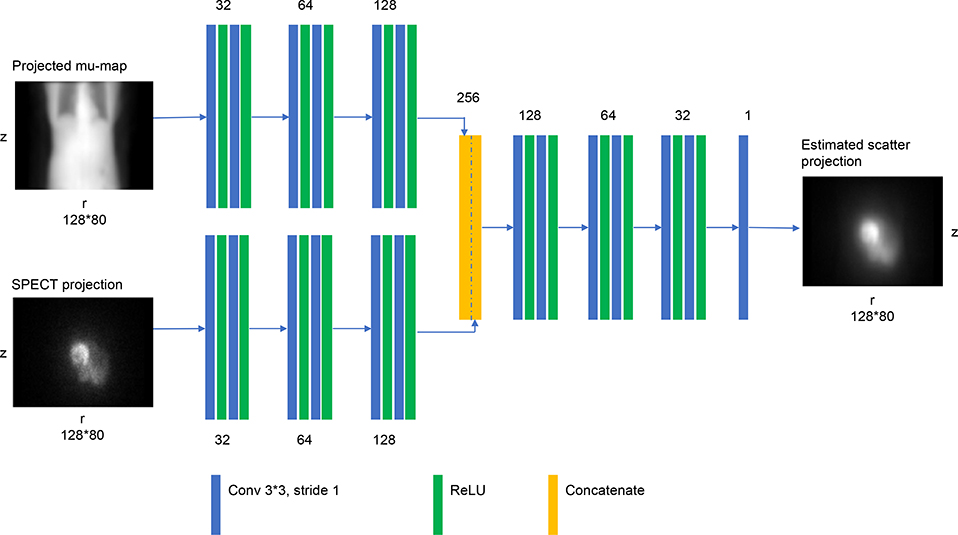
Very deep convolutional networks such as VGG [23] and ResNet [24] have been successfully used recently for large-scale image recognition. We mimic these architectures, but with modifications relevant for the current task of estimating 2D scatter projections (Fig. 2): the pooling layer and the fully connected layer are not used because the desired scatter projections and the input projections are of the same size and the training data set is limited. The depth of our network is determined to balance the trade-off between over-fitting and size of receptive field. Following the designs of [23,24], the size of the convolution filters is set to a typical value (3 × 3). The spatial dimensions are maintained by using zero-padding after 3 × 3 convolution with a stride of 1. After evaluating different choices for the number of filters for the convolutional layers, the final design used 32, 64, 128 with the number set to first increase and then decrease as in popular encoder-decoder designs such as U-net [16]. Except for the last convolutional layer, a rectified linear unit (ReLU) is added after each convolutional layer as the nonlinear function. The filter size, together with the depth of the network is designed to work well enough on training dataset, while maintaining a reasonable training speed.
Fig. 2.
DCNN architecture. Number near each block refers to the number of filters for each layer. Each projection view is processed independently.
The input to the network is the scaled SPECT projection measurements and the projected attenuation map. Scaling is used because the total counts in the emission projections vary largely between MC simulation used for training and the patient measurements. We included the attenuation projection as an additional input because scatter within a patient depends both on the activity distribution and the attenuation map. There are 128 projection views (of matrix size 128 × 80) per patient study and each view is processed separately. First, there are 2 separate paths for the attenuation coefficient projection and SPECT emission projection respectively, each consisting of 3 separate convolutional layers (Fig 2). Then, the outputs of these two paths are concatenated and finally, the concatenated projection passes through 3 convolutional layers to produce the scatter projection. The total number of convolutional layers for each (emission and attenuation projection) path is 13 and the number of trainable parameters is about 0.5 million. We train the DCNN to minimize the pixel-wise mean square error (MSE) between model output (estimated scatter) and the ground truth (‘true’ scatter from Monte Carlo phantom simulations) (Fig. 1). The MSE is optimized by backpropagation using Adam optimizer method [25] using 100 epochs, with the initial learning rate of 0.0001. Our network is implemented in Python using Tensorflow [26] deep learning library and trained on NVIDIA GPU (8GB GTX 1080).
Training and validation data
Using measurement data for training the DCNN is infeasible because the camera records all events within the acquisition window and it is impossible to separate the scatter only events to be used as ground truth training label. Thus, we generated training/validation data using the SIMIND MC code [27] by coupling digital phantoms with the SPECT/CT camera model. Parameters used for 90Y patient imaging in our clinic (Siemens Intevo with HE collimators, a 5/8” crystal, a 105 – 195 keV acquisition window, 128 views, 128 × 80 matrix, 4.8 × 4.8 mm pixel size) were modeled. Approximately 1 billion MC histories per projection were used to generate the training data with low statistical noise. The SIMIND model includes full photon transport in the object and camera, including collimator septal penetration and scatter effects in the object, collimator, the NaI(Tl) crystal and a backscatter layer. For 90Y, because SIMIND does not include electron transport, we used a pre-calculated spectrum of bremsstrahlung photons to sample the photon emission energy. The bremsstrahlung spectrum included the contribution from external bremsstrahlung (EB) photons that are produced as beta particles traverse tissue and internal bremsstrahlung (IB), which arises during the beta decay process itself. IB photons are sampled at the decay location while EB photons are sampled using a distance histogram that accounts for the distance between the beta decay location and bremsstrahlung generation site. We previously validated SIMIND for 90Y SPECT using this model [28]. Training and validation sets used SIMIND-generated SPECT projections corresponding to the following anthropomorphic and non-anthropomorphic digital phantoms:
Virtual patient phantoms for training/validation
To emulate highly clinically relevant scatter conditions, 8 digital representations (virtual patients) were generated from 90Y SPECT/CT images of patients who underwent RE at our clinic (see upper branch of Fig. 1). To generate the activity map, masks of the radiologist-segmented lesions, the treated non-tumoral liver lobe and the entire non-tumoral liver were combined after scaling the voxel values in the masks to reflect the lesion-to-liver uptake ratios in the patient’s SPECT image. The density map was generated from the patient CT using a calibration curve that was experimentally determined using a Tissue Characterization Phantom [Gammex, Inc.]. The virtual patient matrix size was 512 × 512 × 196 with voxel size of 0.98 × 0.98 × 2 mm3. The SIMIND generated total projections were each scaled to the same count-level as the corresponding actual SPECT patient projection images before addition of Poisson noise (For the 8 patients selected, administered 90Y activities ranged from 0.7 to 5.6 GBq and total projection counts ranged from 3 to 20 million). These digitized ‘patient’ phantoms cover a range of noise levels, liver and lesion volumes, and lesion-to-liver uptake ratios typical for 90Y RE. Thus, a wide range of scatter conditions that is clinically relevant were represented. Six (6 × 128 projections) of the virtual patients were used for training and 2 (2 × 128 projections) for validation. The validation data is used to monitor the network performance during the training process to avoid overfitting.
XCAT phantom for training
Eighty slices of the 3D XCAT [29] phantom ranging from lung to liver were generated. The voxel activity values for lesion: liver: lung: rest-of-body were set to 100: 20: 1: 0 to be representative of patients following Y-90 RE. Activity and density maps were 128 × 128 × 80 with voxel size of 4.8 × 4.8 × 4.8 mm3. The SIMIND generated projections were scaled to 10 million counts before the addition of Poison noise.
Sphere phantom for training
An elliptical shaped phantom with six 90Y filled spheres and a single non-radioactive water filled sphere at the center was generated. The sphere-to-background ratio was set to 6:1. The 90Y sphere volumes were 2, 4, 8, 16, 29 and 113 mL, the non-radioactive sphere volume was 95 mL and the total phantom volume was 10,000 mL. The density of the phantom was assumed to be that of water. The SIMIND generated projections were scaled to a count-level of 3 million counts before the addition of Poisson noise.
Test data for evaluating trained DCNN
For testing the performance of the trained DCNN, we used data from 90Y phantom measurements as well as a phantom simulation using SIMIND. The SPECT/CT acquisition system/parameters were same as those used for training. The phantoms were selected to represent a relevant range of non-uniform activity distributions and heterogeneous tissue densities, both of which impact scatter.
Simulation of a sphere phantom with a lung insert
This phantom is a digital representation of the NEMA 2012 PET phantom [30], but with the sphere volumes expanded in size to be more relevant to SPECT spatial resolution capabilities. The modified sphere volumes were 2.7, 4, 7, 16, 33, and 50 mL. All other dimensions were identical to that of the NEMA phantom. The sphere-to-background activity concentration ratio was set to 8:1. The simulated projections were scaled to 90 million total counts before addition of Poisson noise (count level set to ~10 times higher than in a typical patient because the phantom background volume was ~10 times higher than the typical liver volumes). Five noise realizations of the projection data were generated to evaluate noise.
Measurement with liver phantom
The torso phantom (Data Spectrum) consists of a liver compartment filled with water, lung compartments filled with Styrofoam beads and water (to mimic lung tissue density) and a spine insert mimicking bone density. The liver (1200 mL) was modified to include 3 lesion inserts (insert 1 = 29 mL ovoid, insert 2 = 16 mL sphere, insert 3 = 8 mL sphere). In addition, to mimic inadvertent extra-hepatic deposition of microspheres, two inserts (insert 1 = 11 mL ovoid, insert 2 = 14 mL sphere) were positioned in the non-radioactive background outside the liver. The total 90Y activity in the phantom at time of imaging was 2.0 GBq. The lesion-to-liver background activity concertation ratio was 5:1 and the lung shunt was 5%. The activity concentrations in the liver inserts were 6.4–7.8 MBq/mL and liver minus inserts was 1.3 MBq/mL, which are clinically relevant conditions for 90Y RE. The two extrahepatic inserts were filled with very low activity concentrations (insert 1 = 11 mL ovoid with 0.6 MBq/mL; insert 2 = 14 mL sphere with 0.09 MBq/mL). A second non-radioactive water filled cylindrical phantom was placed adjacent to the liver during imaging to mimic scatter in abdomen/pelvis in patients. The acquisition time on the Intevo SPECT/CT was 30 min as in our patient scans, hence the count-level (9 million counts) was in the range observed in typical patient studies.
Measurement with 3D printed non-uniform activity sphere
A sphere with concentric fillable shells of volume 8 mL, 58 mL and 143 mL, was positioned off axis in a water-filled phantom. The 3 ‘layers’ of the sphere were filled with 90Y according to the following ratios core: inner layer:outer layer 0.0 : 0.7 : 2.1 MBq/mL to represent a lesion with a necrotic core and enhancing rim. The acquisition time on the SPECT/CT system was 90 minutes and the total projection counts were 6 million. For comparison, a 90 min 90Y time-of-flight PET/CT acquisition was also performed on a Siemens Biograph mCT system.
SPECT reconstruction with scatter estimate
Test data, including the patient data, were reconstructed using an in-house developed OS-EM algorithm with the scatter estimate included as an additive term in the following statistical model:
| (1) |
where denotes the number of counts measured in the ith detector pixel, denotes elements of the system matrix A that models effects of depth-dependent attenuation and collimator/detector blur for a photon leaving the jth voxel towards the ith detector pixel, denotes the estimated scatter component for the ith detector pixel and denotes the vector of unknown 90Y activity voxel values. The current implementation used the same CNN-generated scatter estimate in all iterations, without updating. OS-EM reconstruction according to above equation was performed 1) without SC (NO-SC) using clinic software (Siemens Flash 3D) 2) with our previously reported [3] MC scatter model (MC-SC) 3) with the scatter estimate from the trained DCNN (DCNN-SC) 4) with the true scatter estimate from SIMIND (TRUE-SC), which was available only in the case of the simulated test data set. All reconstructions included CT-based attenuation correction, 3D collimator-detector response compensation and no post-filtering. MC-SC used two updates of the SIMIND generated scatter estimate based on our prior findings on convergence [3].
Metrics used to evaluate reconstructed phantom images
Contrast recovery (CR) for each 90Y sphere in the NEMA-like phantom simulation and hepatic inserts in the liver phantom measurement is calculated as:
| (2) |
where is the mean counts in the target VOI, is the mean background counts, is the true activity concentration in the target, and is the true activity concentration in the background. The background VOI was defined as the total phantom (or liver) minus the inserts, eroded by 1 cm in all directions.
The visibility or detectability of the hepatic and extra-hepatic inserts of the liver phantom is assessed by the contrast-to-noise ratio calculated as:
| (3) |
where is the standard deviation of voxel counts in the background region.
The residual count error in the lung insert in the NEMA-lime phantom is calculated as:
| (4) |
Where is the mean counts in the lung insert and is the mean counts in the background of the phantom for the reconstruction with the true scatter.
The normalized root mean square is calculated as:
| (5) |
Where is the total number of voxels, is the reference (true) image, is the estimated image, subscript indicates the th voxel of the object.
From the multiple realizations of the NEMA-like phantom simulations the image ensemble noise across realizations is calculated as:
| (6) |
Where is the total number of realizations, indicates the th realization and is the total number of voxels in the uniform background region.
Patient studies
90Y SPECT/CT data from 6 patients with HCC or metastatic liver cancer treated with glass microspheres (Theraspheres, 1 to 3.9 GBq) were selected to demonstrate clinical application. This test data set were distinct from the cases used for generating the virtual patients for training. These patients were selected to represent a range of clinically relevant count levels and scatter conditions. 90Y PET/CT images were also available for these patients, for comparison. The acquisition time for Y-90 SPECT/CT and PET/CT were both ~ 30 min and were performed within a couple of hours of the RE procedure. PET/CT data were reconstructed with 1 iteration (21 subsets) of Siemens OS-EM including time-of-flight information, PSF modeling, standard corrections for scatter, attenuation and randoms and a 5 mm Gaussian post-filter, which are typical parameters used in our clinic.
Patient SPECT emission projections and CT-based mu-map (available from the vendor software) projected to SPECT space were input to the trained DCNN to generate the corresponding scatter estimates that were used in the in-house OS-EM reconstruction (15 iterations, 8 subsets). In addition to visual assessment of image quality and comparison of profiles, we also compare the lesion-to-non-tumoral liver activity concentration ratios for the different SPECT/CT reconstructions and the 90Y PET/CT. Lesions > 2 mL were defined manually on baseline diagnostic quality CT or MRI by a radiologist and applied to co-registered 90Y SPECT/CT and PET/CT. The liver was segmented using semi-automatic atlas based software. The non-tumoral liver was defined as the entire liver minus lesion VOIs.
Results
Network training, validation and speed
Supplemental Fig. 1(a) shows the convergence of the MSE (MSE vs. epochs) for training and validation. The decrease in loss as a result of the network learning is evident. Supplemental Fig. 1(b) compares the profiles across DCNN estimated and SIMIND (true) scatter projections for a typical projection in the training set.
It took about 8 hours to train this DCNN on a 2.3 GHz Intel Core i5 CPU and approximately 30 minutes to train on a GTX 1080 8GB GPU. Once trained, the DCNN takes about 40 seconds on the i5 CPU to estimate all 128 scatter projection views of 128 × 80 matrix size. The time to generate one update of the corresponding SIMIND MC scatter estimate with 50 million histories per projection is ~ 40 min using twelve i5 processors (this number of histories was found to be sufficient for low noise scatter estimation, in our prior study [3]). We used two MC scatter updates in the current study; hence the total simulation time was 80 min on 12 processors (or 16 hours on a single i5).
Testing in phantoms
Sphere phantom with lung insert simulation
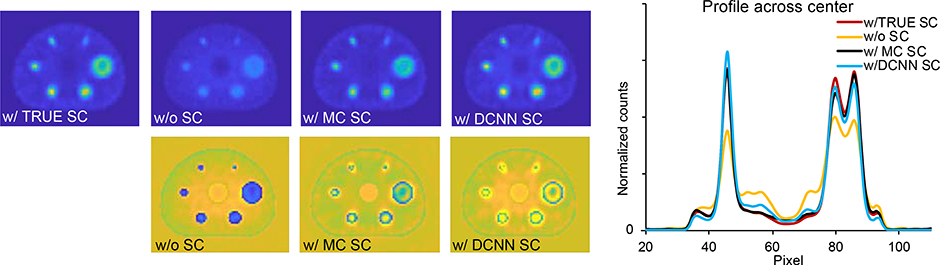
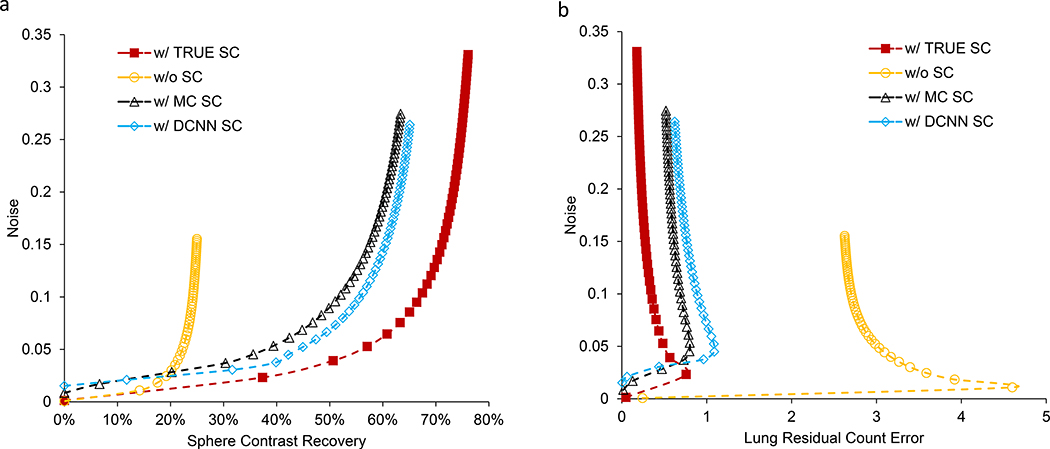
The center slice of the reconstructed images with the different scatter estimates and the corresponding NRMSE images are compared in Fig. 3. The NRMSE for the sphere regions was 0.66, 0.52, 0.45 and 0.45 for the reconstruction with NO-SC, with MC-SC, with DCNN-SC and TRUE-SC, respectively. The corresponding NRMSE for the total image was 0.50, 0.42, 0.41 and 0.36, respectively. The image ensemble noise versus CR (averaged over the 6 spheres) and the noise versus RE in the lung insert are plotted in Fig. 4(a) and (b) for iterations 1 to 50 (8 subsets). Considering trade-off between CR and noise evident in these plots, we selected 15 iterations (8 subsets) for the results presented in the rest of the paper. At this number of updates the noise, CR and RE were 0.07, 23% and 2.8 for NO-SC, 0.11, 54% and 0.66 for MC-SC, 0.11, 57% and 0.86 for DCNN-SC and 0.15, 71% and 0.28 for TRUE-SC.
Fig. 3.
Axis slices of the different reconstructions of the test phantom simulation (top row) and profiles across the center. Images have been normalized by the sum counts. The NRMSE images relative to the true phantom are shown in the bottom row.
Fig. 4.
Test results from the multiple realizations of the phantom of Fig. 3. (a) Noise vs. contrast recovery averaged over 6 spheres (b) Noise vs. residual count error for the lung insert. The data points represent OS-EM iteration number.
Liver phantom measurement
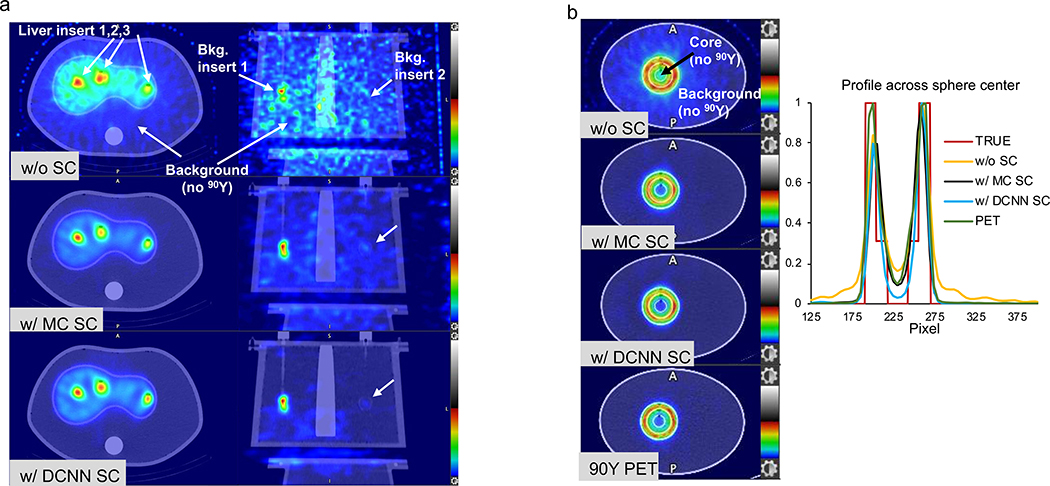
Two axial slices with the different reconstructions are compared in Fig. 5(a). The 0.09 MBq/ML extra-hepatic insert is not visible on the NO-SC image, but is faintly visible on the DCNN-SC image. Table 1 compares the CR and CNRs for the different reconstructions.
Fig. 5.
Measured 90Y phantom images. (a) Axiel and coronal SPECT/CT slices of the liver phantom for the different reconstructions. (b) Center slice and profiles of the non-uniform sphere for the different SPECT/CT reconstructions compared with 90Y PET. SPECT images without scatter correction show high counts in the regions without 90Y and demonstrate the improvement in contrast with MC and DCNN scatter estimation. Images have been normalized to the maximum counts in the slice.
Table 1:
CR and CNR for inserts in the liver phantom measurement of Fig. 5(a)
| Contrast recovery (%) | CNR (visibility index) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Liver insert 1 | Liver insert 2 | Liver insert 3 | Liver insert 1 | Liver insert 2 | Liver insert 3 | Bkg. insert 1 | Bkg. insert 2 | ||
| w/o SC | 41 | 31 | 23 | 9.7 | 8.3 | 4.9 | 3.6 | −0.2 | |
| w/ MC SC | 92 | 60 | 67 | 20.3 | 15.2 | 13.3 | 35.8 | 1.2 | |
| w/ DCNN SC | 75 | 56 | 65 | 15.5 | 13.1 | 11.9 | 119.2 | 3.9 | |
3D printed sphere measurement
Fig. 5 (b) compares center slice and profiles of the different SPECT reconstructions with 90Y PET.
Application in patients
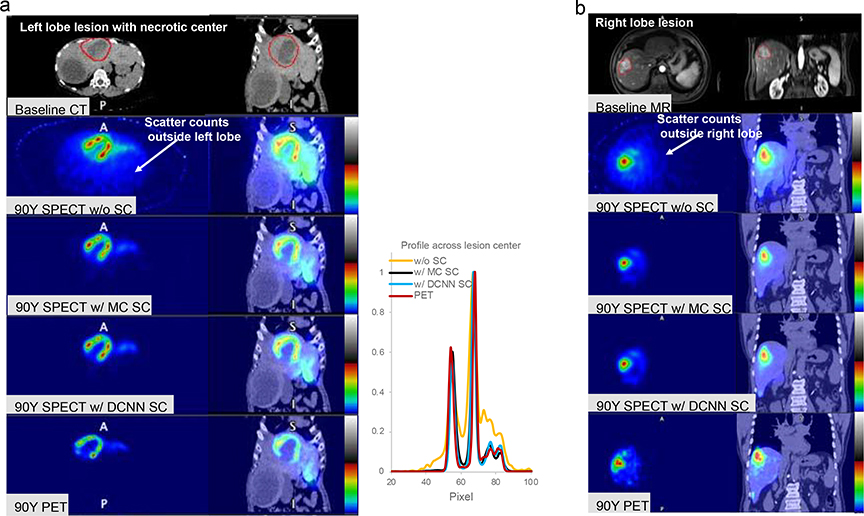
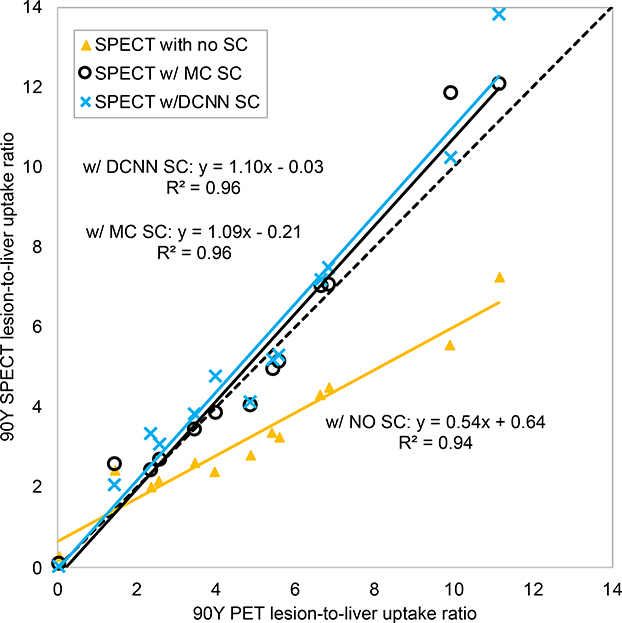
Fig. 6 compares images corresponding to the different 90Y SPECT/CT reconstructions and 90Y PET/CT for two example patients,. A total of 13 lesions > 2 mL were segmented in the 6 patients. Lesion volumes ranged from 4 mL to 818 mL. Fig. 7 shows lesion-to-non-tumoral liver uptake ratios for 90Y SPECT/CT vs. 90Y PECT/CT for the different SPECT reconstructions (supplemental Table 1 lists the individual values). There was high concordance between uptake ratios for SPECT reconstruction with DCNN (Median 4.9, range 0.02 −11.2) compared with MC-SC (Median 4.0, range 0.13 – 12.1; CCC = 0.98) as well as with 90Y PET (Median 4.9, range 0.02 – 11.2; CCC = 0.96) while the concordance with NO-SC was poor (Median 2.8, range 0.3 – 7.2; CCC = 0.59).
Fig. 6.
Comparison of SPECT/CT and PET/CT images following Y-90 radioembolization (a) Patient with large 818 mL lesion with a necrotic center and enhacing rim treated with 3.9 GBq to the left-lobe (b) Patient with a 6 mL lesion treated with 2.9 GBq to the right lobe.
Fig. 7.
Patient lesion-to-non-tumoral liver uptake ratios from the different Y90 SPECT/CT reconstructions plotted vs. the corresponding ratios from 90Y PET/CT. The dashed line indicates the identity line. Full results for the 13 lesions in 6 patients are given in Supplemental Table 1.
Discussion
With test data that covered a range of noise-levels and scatter conditions pertinent to 90Y RE, we demonstrated that a trained DCNN can be used for the challenging task of estimating scatter in 90Y bremsstrahlung SPECT/CT with accuracy similar to MC based estimation, but at a fraction of the time. Although generating the training data by MC simulation with full radiation transport physics and the training process itself is computationally expensive, these steps are only performed once. Furthermore, the ability to use simulated data as training labels in the scatter estimation application circumvents the difficulties associated with obtaining sufficient real patient data sets for training that has been a challenge in some other applications of deep learning such as lesion segmentation. In the current study, the trained DCNN generated patient scatter projections for all 128 views in < 1 minute using a single processor on a desktop computer, which is about 3 orders of magnitude faster than our previous method of estimating bremsstrahlung scatter by MC [3].
Although CNN based fast scatter estimation of the current study is applicable to SPECT/CT imaging in general, it has the most value for bremsstrahlung SPECT or SPECT with radionuclides that have multiple gamma-ray emissions where accurate scatter estimation by empirical window-based methods is challenging. Furthermore, DCNN based scatter estimation may be particularly well suited for the RE application because the source is almost exclusively limited to the liver, hence patient-to-patient variation in scatter conditions may be less than in some other applications. Thus, fewer training data sets may suffice compared to applications with radiotracers that distribute throughout the body.
In testing with the phantom simulation, the reconstruction with DCNN-SC performed similarly to MC-SC, both visually and in terms of sphere contrast – noise trade-off and lung insert residual error – noise tradeoff (Fig. 4). For example, at a noise level of 10% across multiple realizations, the average sphere CR was 24%, 52%, 55% and 67% for NO-SC, MC-SC, DCNN-SC and TRUE-SC, respectively. In Fig. 4, even when the true scatter estimate is used the CR is < 100% and the RE is > 0, because of resolution effects. In the phantom measurements, the improvement in contrast with both MC and DCNN scatter estimation is clearly visible (Fig. 5) and evident from the CR and CNR values of Table 1. Improving CR is clinically relevant for dosimetry applications and improving CNR (visibility index) is important because of the safety concerns associated with inadvertent microsphere deposition (typically of very low concentration) outside the liver. Going from reconstruction without SC to with DCNN SC the CNR increased from 4 to 119 for the 0.6 MBq/mL extra-hepatic insert. The extra-hepatic insert with ultra-low 90Y concentration of 0.09 MBq/mL is not visible on the reconstruction w/o SC where CNR is −0.2, but is faintly visible on the reconstruction w/ DCNN SC where CNR is 4. This is consistent with the Rose criteria [31] that states that for an object to be detectable the CNR must exceed 3 – 5, although this applies to idealized conditions of an approximately circular shaped object and a relatively uniform background. In the measurement with the challenging scatter conditions of a sphere with a small non-radioactive central core region surrounded by 2 rings of 90Y, the impact of the scatter correction is clearly visible in the core region (Fig. 5b). The visual image quality and profiles of DCNN-SC approached that of 90Y TOF PET/CT. This geometry was chosen to represent scatter conditions encountered in lesions with a necrotic core and enhancing rim as in Fig 6 (a), for example.
The patient test cases included a diverse range of scatter conditions corresponding to a range of lesion sizes (4 – 818 mL), administered activity (1 – 3.9 GBq), left vs. right lobe treatment and lesions with necrotic cores and enhancing cores (Fig. 6). Although the true distribution is unknown, in our comparison of the lesion-to-non-tumoral liver uptake ratio, a quantity pertinent to dosimetry applications, results for DCNN-SC showed high concordance with both MC-SC (CCC=0.98) and with 90Y PET (CCC= 0.96). Some of the difference in uptake ratios compared with PET could be due to mis-registration effects and differences in partial volume effects for the two modalities. While 90Y PET/CT is generally considered as superior to bremsstrahlung SPECT for quantitative imaging, 90Y SPECT has higher sensitivity. Improving 90Y SPECT/CT is also important from a pragmatic standpoint because of the wider availability and the fact that, typically, only SPECT imaging of 90Y is reimbursed by insurance.
In our test data set, DCNN-SC was compared with our previous iterative approach for generating MC scatter updates for 90Y SPECT. Here, an initial image reconstructed without scatter correction provides the emission activity distribution for generating the SIMIND scatter estimate, which is used in the subsequent reconstructions. Two such MC updates were used in the current work, based on prior findings on convergence. The alternative fully MC based projector that has been proposed by Elschot et al [2] for 90Y SPECT is even more computationally complex and was not investigated in the current study. However, CR and RE values reported in their study are comparable to results reported here, although direct comparison is difficult due to difference in reconstruction parameters and phantom geometries.
Our network for projection space scatter estimation borrows concepts from widely used architectures for pattern recognition and image segmentation [16, 23,24]. Despite using only modest amounts of training data (8 phantoms x 128 projections), the network provided highly promising results as determined by multiple metrics applied to reconstructed images. In the future, further optimization of the network can be investigated, for example by including down sampling layers that might exploit the spatial smoothness of scatter. For FDG-PET brain imaging Yang et al. [13] proposed a joint correction of attenuation and scatter with a DCNN trained to directly map uncorrected images to attenuation and scatter corrected images in image space. We expect that the approach of combining deep learning based scatter projections with an imaging physics-based iterative reconstruction framework, as in the current study, will have more generalizability than methods that use DCNNs for post-reconstruction enhancement. However, this conjecture can be tested only by direct comparison of our approach with post-reconstruction approaches. Despite the fact that scatter is a depth-dependent process, our 2D projection-by-projection scatter estimation performed well in the current application. To potentially further improve accuracy/generalizability, we plan to investigate an iterative process starting with the current 2D projection space DCNN for an initial scatter estimate for the initial reconstruction followed by refinement with a 3D DCNN for subsequent scatter estimation. Advantages of the current 2D approach compared with fully 3D training are reduced requirements on GPU memory and potentially on the number of training data sets. For 3D DCNNs, methods to reduce requirements on training data such as data augmentation, patch-based learning and transfer learning can be explored. Future studies will include generalization to other SPECT radionuclides and different anatomical regions than evaluated here, potentially by changing just the training data.
Conclusion
We constructed a DCNN to find the mapping from measured SPECT emission and CT attenuation projections and the estimated scatter events. The performance of the proposed method, evaluated with reconstructed images, was comparable to our previous MC-based scatter estimation for 90Y SPECT/CT, but took a fraction of the time in a test-data set that had varied noise-levels and scatter conditions relevant to RE. In patient studies, there was high concordance between lesion-to-non tumoral liver uptake ratios for reconstructions with DCNN-SC compared with MC-SC and with 90Y PET/CT. The DCNN scatter estimation holds much promise for real time clinical use because of the short processing time (< 1 minute on a desktop computer for 128 projections) while maintaining high accuracy even under challenging scatter conditions encountered in bremsstrahlung SPECT.
Data Availability
Python code for the DCNN of Fig. 2 and phantom training and test data are available at: https://github.com/haoweix/spect-scatter-deep-learning
Select 90Y SPECT/CT patient test data sets (anonymized) are available at the University of Michigan Library Deep Blue repository: https://doi.org/10.7302/v07v-z854
Supplementary Material
Acknowledgments
We would like to thank Phantech, Madison, Wisconsin for providing us the 3-D printed phantom insert.
Funding This work was supported by grant R01 EB022075 awarded by the National Institute of Biomedical Imaging and Bioengineering (NIBIB), United States Department of Health and Human Services.
Footnotes
Compliance with ethical standards
Conflict of interest The authors declare that they have no conflict of interest.
Ethical approval All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards.
Informed consent Informed consent was obtained from all individual participants included in the study according to University of Michigan Institutional Review Board (IRB) criteria.
References
- 1.Zeintl J, Vija AH, Yahil A, Hornegger J, Kuwert T. Quantitative accuracy of clinical 99mTc SPECT/CT using ordered-subset expectation maximization with 3-dimensional resolution recovery, attenuation, and scatter correction. J Nucl Med. 2010;51:921–928. [DOI] [PubMed] [Google Scholar]
- 2.Elschot M, Lam MG, van den Bosch MA, Viergever MA, de Jong HW. Quantitative Monte Carlo based 90Y SPECT reconstruction. J Nucl Med. 2013;54:1557–1563. [DOI] [PubMed] [Google Scholar]
- 3.Dewaraja YK., et al. Improved quantitative 90Y bremsstrahlung SPECT/CT reconstruction with Monte Carlo scatter modeling. Med Phys. 2017;44:6364–6376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Greenspan BH, van Ginneken B, Summers RM. Guest editorial – deep learning in medical imaging: overview and future promise of an exciting new techniques. IEEE Trans Med Imag. 2016;35:1153–1159. [Google Scholar]
- 5.Ravishankar S, Ye JC, Fessler JA. Image reconstruction: from sparsity to data-adaptive methods and machine learning. Proceedings of the IEEE. 2020;108:86–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Veit-Haibach P, Buvat I, Herrmann K. EJNMMI supplement: bringing AI and radiomics to nuclear medicine. Eur J Nucl Med Mol Imaging. 2019;46:2627–2629. [DOI] [PubMed] [Google Scholar]
- 7.Uribe CF, Mathotaarachchi S, Gaudet V, Smith KC, Rosa-Neto P, Bénard F, Black SE, Zukotynski K. Machine Learning in Nuclear Medicine: Part 1-Introduction. J Nucl Med. 2019;60:451–458. [DOI] [PubMed] [Google Scholar]
- 8.Zaharchuk G Next generation research applications for hybrid PET/MR and PET/CT imaging using deep learning. Eur J Nucl Med Mol Imaging. 2019;46:2700–2707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gong K, Berg E, Cherry SR, Qi J. Machine Learning in PET: From Photon Detection to Quantitative Image Reconstruction. Proceedings of the IEEE, 2020;108:51–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Xu J, Gong E, Pauly J, Zaharchuk G. 200x low-dose PET reconstruction using deep learning, arXiv preprint arXiv:1712.04119, 2017. [Google Scholar]
- 11.Berker Y, Joscha M, and M. Kachelries M, Deep scatter estimation in PET: Fast scatter correction using a convolutional neural network. Proc IEEE Nucl Sci Symp Med Imag Conf. 2018, pp. 1–25. [Google Scholar]
- 12.Qian H, Rui X, Ahn S, Deep learning models for PET scatter estimations. Proc IEEE Nucl Sci Symp Med Imag Conf. 2017, pp. 1–5. [Google Scholar]
- 13.Yang J, Park D, Gullberg GT, Seo Y. Joint correction of attenuation and scatter in image space using deep convolutional neural networks for dedicated brain (18)F-FDG PET. Phys Med Biol. 2019;64:075019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Häggström I, Schmidtlein CR, Campanella G, Fuchs TJ. DeepPET: A deep encoder-decoder network for directly solving the PET image reconstruction inverse problem. Med Image Anal. 2019;54:253–262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cui J, Gong K, Guo N,et al. PET image denoising using unsupervised deep learning. Eur J Nucl Med Mol Imaging. 2019;46:2780–2789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ronneberger O, Fischer P, Brox T. U-Net: Convolutional Networks for Biomedical Image Segmentation. 2015. https://arxiv.org/abs/1505.04597
- 17.Dietze MMA, Branderhorst W, Kunnen B, Viergever MA, de Jong HWAM. Accelerated SPECT image reconstruction with FBP and an image enhancement convolutional neural network. EJNMMI Phys. 2019;6:14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Minarik D, Enqvist O, Trägårdh E. Denoising of Scintillation Camera Images using a Deep Convolutional Neural Network: A Monte Carlo Simulation Approach. J Nucl Med. 2020;61:298–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Shi L, Onofrey JA, Liu H et al. Deep learning-based attenuation map generation for myocardial perfusion SPECT. Eur J Nucl Med Mol Imaging. 2020. 10.1007/s00259-020-04746-6 [DOI] [PubMed] [Google Scholar]
- 20.Bai J, Hashimoto J, Ogawa K, et al. Scatter correction based on an artificial neural network for 99mTc and 123I dual-isotope SPECT in myocardial and brain imaging. Ann Nucl Med. 2007;21:25–32 [DOI] [PubMed] [Google Scholar]
- 21.Ogawa K, Nishizaki N. Accurate scatter compensation using neural networks in radionuclide imaging. IEEE Trans Nucl Sci 1993; 40:1020–1025. [Google Scholar]
- 22.El Fakhri G, Moore SC, Maksud P, Aurengo A, Kijewski MF. Absolute activity quantitation in simultaneous 123I/99mTc brain SPECT. J Nucl Med. 2001;42:300–8. [PubMed] [Google Scholar]
- 23.Simonyan K, Zisserman A, 2014. Very deep convolutional networks for large-scale image recognition, 1409.1556, pp. 1–14. doi: 10.1016/j.infsof.2008.09.005 https://arxiv.org/abs/1409.1556v6 [DOI] [Google Scholar]
- 24.He K, Zhang X, Ren S and Sun J, “Deep Residual Learning for Image Recognition,” 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, 2016, pp. 770–778. or arXiv:1512.03385v1 [Google Scholar]
- 25.Kingma DP and Ba J, Adam: A method for stochastic optimization, 2017. https://arxiv.org/abs/1412.6980
- 26.Abadi M, Agarwal A, Barham P. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. https://arxiv.org/abs/1603.04467 [Google Scholar]
- 27.Ljungberg M The SIMIND Monte Carlo program In: Ljungberg M, Strand SE, King MA, eds. Monte Carlo Calculation in Nuclear Medi- cine: Application in Diagnostic Imaging, 2nd edn. Florida: Taylor & Francis; 2012. [Google Scholar]
- 28.Dewaraja YK, Fleming R, Simpson P, Ljungberg M, Wilderman S. Impact of internal bremsstrahlung on Y-90 SPECT Imaging. J Nucl Med. 2018; 59 supplement 1, 577 [Google Scholar]
- 29.Segars W, Sturgeon G, Mendonca S, Grimes J, Tsui BM, 4D XCAT phantom for multimodality imaging research. Med Phys.2010; 37:4902–4915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.NEMA 2012 PET phantom Digital Reference Object. Developed at the University of Washington supported by the Quantitative Imaging Biomarker Alliance. http://depts.washington.edu/petctdro/DROsuv_main.html [Google Scholar]
- 31.Rose A: Vision: Human and Electronic. New York, 1973, Plenum Press, pp 1–27. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Python code for the DCNN of Fig. 2 and phantom training and test data are available at: https://github.com/haoweix/spect-scatter-deep-learning
Select 90Y SPECT/CT patient test data sets (anonymized) are available at the University of Michigan Library Deep Blue repository: https://doi.org/10.7302/v07v-z854