Abstract
Different analytic techniques operate optimally with different types of data. As the use of EHR-based analytics expands to newer tasks, data will have to be transformed into different representations, so the tasks can be optimally solved. We classified representations into broad categories based on their characteristics, and proposed a new knowledge-driven representation for clinical data mining as well as trajectory mining, called Severity Encoding Variables (SEVs). Additionally, we studied which characteristics make representations most suitable for particular clinical analytics tasks including trajectory mining. Our evaluation shows that, for regression, most data representations performed similarly, with SEV achieving a slight (albeit statistically significant) advantage. For patients at high risk of diabetes, it outperformed the competing representation by (relative) 20%. For association mining, SEV achieved the highest performance. Its ability to constrain the search space of patterns through clinical knowledge was key to its success.
Keywords: Data Science, Electronic Health Records, Data Mining
Introduction
The widespread adoption of electronic health records (EHRs)[1] enables new kinds of analytics such as explicitly modeling population heterogeneity or identifying benefit groups for an intervention[2,3]. It is well understood that different analytics tasks and techniques operate optimally on different types of data[4]. For example, association pattern mining requires binary or categorical data[5] and most regression models assume that the predictor variables have an additive effect[6]. Data, as it exists in the EHR, is not ideal for many analytics tasks.
A data representation is a transformation of data into a format amenable to a particular analytic technique. Data transformations are not new, e.g., log or rank transformations of non-normally distributed variables[7] have been a mainstay for decades. The recent success of deep learning in some applications[8] has put data representation into the spotlight and is, at least in part, attributed to the underlying data representation. In this work, we propose a data representation, which is specific to the clinical domain and represents data at a high level and enriches it with clinical knowledge.
Specifically, SEV augments the original data with a set of ordered or partially ordered binary variables, combining information about patients’ state from multiple perspectives: therapies, diagnoses, and whether or not the laboratory results or vital signs are normal and/or achieve a typical therapeutic target. These variables are (at least partially) ordered: the variable ‘patient is under control with first-line oral therapy’, represents a lower severity than the variable ‘patient is not under control despite last-line therapy’. These variables are highly interpretable, as they follow clinical reasoning and incorporate clinical knowledge.
To make the discussion concrete, we carry out our study in the context of type 2 diabetes (T2D). Diabetes is a common disease with severe complications[9], affecting 29.1 million Americans. T2D can be prevented or delayed through lifestyle modifications and/or pharmacological treatment[10], hence identifying patients at high risk is of high importance. From a technical perspective, T2D is an ideal evaluation platform, as it exhibits common challenges: T2D is heterogeneous; risk factors are correlated and not necessarily additive; and the time frame between the risk factors and the onset of diabetes can be as long as 20 years, which makes missing data inevitable[2,11].
We encode diabetes risk factors, hyperlipidemia, hypertension, and obesity as SEVs (a set of SEVs for each disease) and perform two clinical tasks related to type-II diabetes. The first task is to predict the onset of diabetes using a Cox model and the second one is to model population heterogeneity in terms of the risk of T2D incidence using association pattern mining. We will compare SEV to five other data presentations, including the original data. The main objective is to study the characteristics of the data representations.
Related Works
Data representations transform the data into a new data set. For a dimensionality-expanding representation, the new data has more features than the original data, while for a dimensionality-reducing representations, it has fewer. The key concern in dimensionality reduction is information loss. Representations can also be outcome-specific or outcome-independent. Outcome-specific data representations are specific to a particular study end point (outcome) and can potentially limit the information loss that is relevant to the outcome, while outcome-independent representations do not consider an outcome.
Outcome-specific Representation
A severity score (SS)[12] quantifies disease burden with respect to some outcome of interest. For example, the Framingham diabetes score[13] associates disease burden, defined by a handful of risk factors, with the risk of developing diabetes (an outcome). Severity score is a dimensionality-reducing representation, as it summarizes numerous original risk factors into a single number, which is proportional to the burden conferred by those risk factors on some outcome.
Outcome-independent Representations
Outcome-independent representations transform the original data into a new set of features, typically with a different dimensionality. Many currently existing representations, such as principal component analysis (PCA)[14] and nonnegative matrix factorization (NMF) [15] have the specific aim of reducing the problem dimensionality. PCA is a statistical procedure that transforms a set of features into a new (ordered) set of orthogonal features (called principal components) in a manner such that each subsequent component explains maximal amount of residual variance, and NMF factorizes the original matrix into two matrices having only non-negative values, in a way that each subsequent component captures maximal amount of the residual information. Dimensionality reduction is achieved by using only the first few components.
Deep neural networks (DNNs)[8] are computational models that are inspired by neural networks in animal brains and have recently achieved considerable success. Much of this success is attributed to the data representation of these techniques, which is known as de-noising autoencoders (DAE). DAEs consist of successive layers of transformations, where the outcome of each layer is the input to the next. Each layer is thought to extract features that are higher-level than those of the previous layer. The criterion for the goodness of the transformation is the reconstruction error, which is a measure of how well an autoencoder can reconstruct the original data from its output.
Severity Encoding Variables
Severity Encoding Variables (SEV) is our proposed outcome-independent representation. The purpose of SEV is to summarize the numerous facets of a disease into a single hierarchical variable. Nodes at the same level in the hierarchy are fully or partially ordered.
The construction of the hierarchy replicates the clinical reasoning steps of determining the severity of a certain disease. Reasoning involves a sequence of questions: (i) are lab results and vital signs present and normal, (ii) has an intervention been initiated, and if it has, how aggressive is it (first-line treatment, combination therapy, etc.), and (iii) has a diagnosis been recorded. Accordingly, the first split (at the root) produces three nodes: patient with missing, normal, and abnormal lab results. Next, we reason about medications. Each of the three nodes can be split indicating whether treatment has been initiated and how aggressive those treatments are. The final question splits the nodes based on the presence of diagnoses.
Figure 1 illustrates the SEV for hyperlipidemia. At the root of the hierarchy, we ask whether lab results (LDL, HDL and TG) are normal (if they are not missing) and which (if any) are abnormal. At the next level, we reason using medications. For example, does a patient under control use medications? If medications are used, are they first-line medications (statins in case of HL), other drugs, or combinations of drugs? On the last level, we reason using diagnoses. Naturally, diagnoses are most helpful if no other indication of disease exists.
Figure 1:
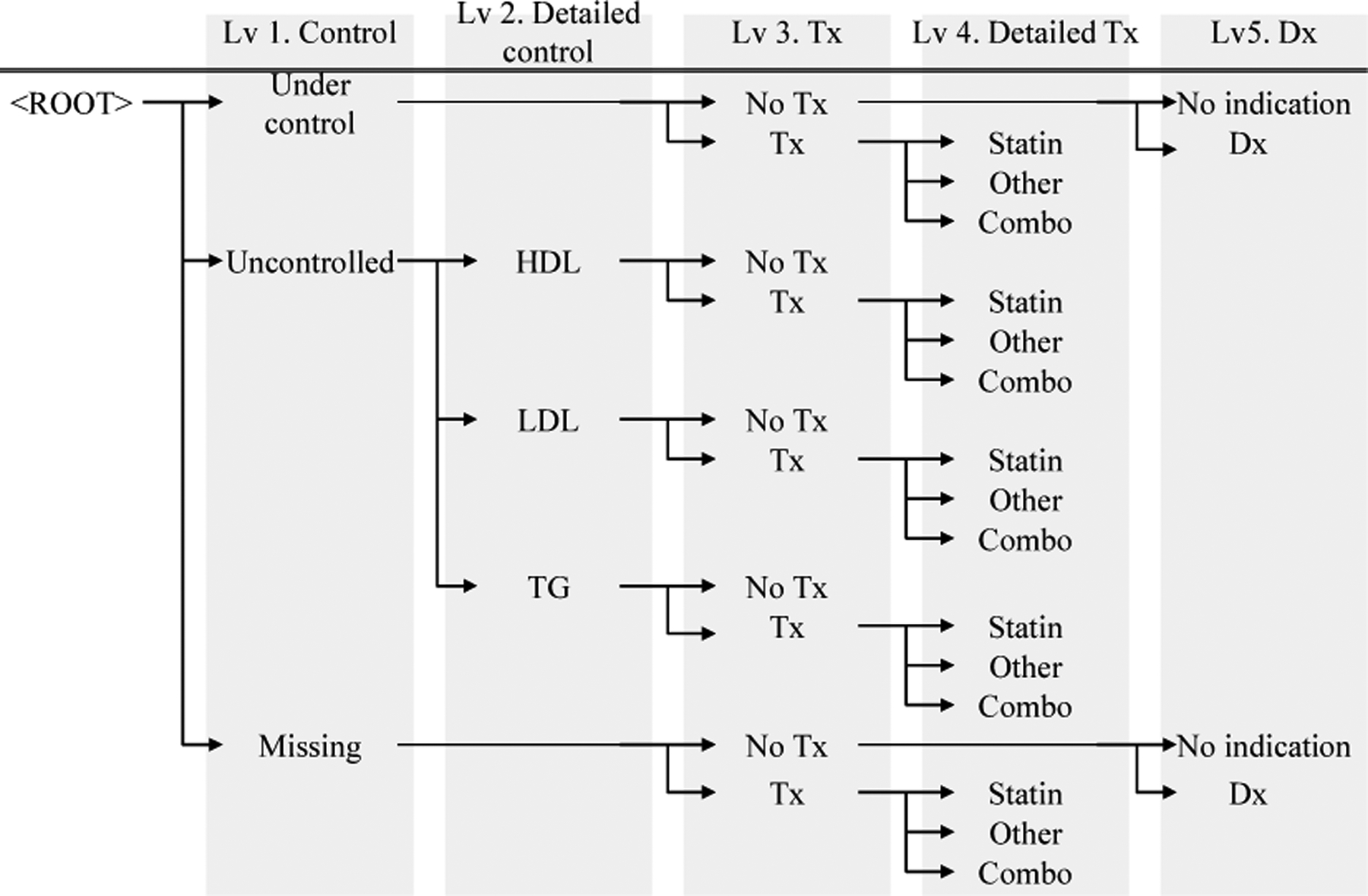
Sample Severity Encoding Variable Hierarchy for Hyperlipidemia. Abbreviations used: Treatment (Tx), Diagnosis (Dx), High-density lipoprotein (HDL), Low-density lipoprotein (LDL), Triglycerides (TG).
For analysis, the hierarchy can be cut at any level and the nodes at that level are taken as binary variables. For example, cutting the hierarchy at the top-most level results in a set of three binary variables: ‘patient is under control’, ‘patient is not under control’, and ‘laboratory results are missing’. These variables are partially ordered: being under control could (but does not have to) indicate lower severity than not being under control, but ‘lab results are missing’ is not comparable to the other two in terms of severity. Cutting the hierarchy at the (say) third level yields 10 leaves and incorporates information about medication use. One of these leaves would be ‘patient has abnormal LDL despite medication’. By changing the level at which the hierarchy is cut, we can increase the number of leaves (and information content).
SEV is a framework for representing diseases as hierarchies induced by a sequence of clinical decisions; it is not a set algorithm for modeling all diseases. Recall that SEV is outcome independent; once a SEV is constructed, it can be used for multiple study end-points. The diseases that we build SEVs for are predictors of the outcome and the construction of the SEV can (and possibly should) depend on the disease that we build the SEV for. Depending on the disease in question, a different ordering of the same clinical questions could yield a more clinically meaningful hierarchy, and other diseases may incorporate altogether different questions (for example, stage and grade of cancer). We have not observed substantial changes in predictive performance in terms of the ordering of the questions.
Materials and Methods
Data, Cohort Construction and Study Design
Mayo Clinic, located in Rochester, MN, provides primary care to a large population. Resources available at Mayo Clinic are described elsewhere[16]. After IRB approval, a cohort of 75,317 patients aged 18 or older on 01/01/2005 with research consent was constructed. The cohort was followed from the baseline of 01/01/2005 until the end of 2015. To determine patients’ baseline status, we retrospectively collected diagnoses of obesity, hyperlipidemia, hypertension, and prediabetes; laboratory test results for lipid panels and fasting plasma glucose (FPG); vital signs (blood pressure, and body mass index [BMI]); demographic information (age, gender); and medications for hypertension and hyperlipidemia. From the cohort, we excluded patients with preexisting diabetes at or before baseline (11,897 patients) and suspicion of diabetes (3 patients with fasting plasma glucose > 125 ml/dL and 2 patients taking anti-diabetic drugs), resulting in a final cohort of 63,415 patients.
Comparative Representation
Severity Scores (SS):
A severity score is computed for each diabetes risk factor (obesity, hypertension, hyperlipidemia, pre-diabetes) quantifying the risk factor’s contribution to diabetes. While all features could be combined into a single severity score (analogously to the Framingham score), we compute a severity score for each risk factor, combining only the features that are related to the specific risk factor. Modeling the risk factors separately allows us to retain the relationships among them.
For each risk factor, the corresponding SS is the linear prediction from a Cox model, whose independent variables are the data elements that describe the risk factor in question and the dependent variable is diabetes outcome. Missing blood pressure measurements were imputed using mean imputation and a bias-correcting indicator variable signaling whether imputation was performed for each patient was added.
Principal Component Analysis (PCA):
In this study, logistic principal component analysis (PCA)[14] is applied to the risk factors, resulting in a single set of principal components. We kept the first 9 principal components because additional components are unable to explain significant amounts of variation. PCA is thus a dimensionality-reducing, outcome-independent representation.
Deep autoencoder (DAE):
For this study, we used two configurations, tuned via cross-validation. Both used the hyperbolic tangent activation function, had two hidden layers with 20 nodes on the first layer and had 9 and 34 nodes on the second layer, respectively. The first configuration (DAE-9) has the lowest reconstruction error among configurations that reduce the dimensionality of the problem, while the 34-node configuration (DAE-34) has the lowest reconstruction error among all configurations. DAE-9 is a dimensionality-reducing representation, while DAE-34 is a dimensionality-expanding representation.
Severity Encoding Variables (SEV):
A severity encoding was constructed for each of the four risk factors of diabetes independently. The hierarchy was cut at the leaf level, making it dimensionality-expanding (there are more nodes in the hierarchy than original features).
The Two Tasks
Regression Analysis:
The objective is to measure the impact of the data representations on the predictive performance of estimating patients’ 8-year risk of T2D. Risk factors (lab results, vital signs, diagnoses (ICD-9 billing code rolled up into categories), and prescriptions rolled up into NDF-RT pharmaceutical subclasses) are determined at baseline. We use this information transforming into the five new representations. The sixth representation is RAW, the original (untransformed) data. Six Cox proportional hazard models are constructed using age, gender and each of the six data representations as independent variables. Backwards elimination is applied.
Association Pattern Analysis:
The central concept in association pattern mining is an item, which is a binary variable such as ‘presence of hyperlipidemia diagnosis’ or ‘LDL ≥ 130 mg/dL’. Items are combined into conjunctive sets, called itemsets (e.g. ‘LDL ≥ 130 mg/dL AND diagnosis of hyperlipidemia’). The association of an itemset with the outcome is measured through confidence, which is the fraction of patients presenting with the outcome among patients who present with all conditions in the itemset (fraction of patients who developed diabetes among those with LDL ≥ 130 mg/dL and diagnosis of hyperlipidemia in our example). Association pattern mining systematically enumerates all itemsets and computes their confidence. In the Classification Based on the Association (CBA) framework[17], the risk of diabetes for a patient is the confidence of the highest-confidence rule that applies to that patient.
Continuous variables (age, severity scores, scores from PCA and DAE) are categorized into deciles (with backwards elimination discarding superfluous categories) and laboratory results and vital signs are dichotomized using the American Diabetes Association[18] cutoffs. Of interest are the number of patterns and their predictive performance. A data representation that can achieve higher predictive performance with a lower number of rules is preferable.
Results
Regression Analysis
Figure 2 (a) shows the concordance of the various data representations as box plots. The top, middle, and bottom line in each box correspond to the upper quartile, median, and the lower quartiles of the concordances estimated from the 1,000 bootstrap replications, respectively. The representations are ordered left to right by the number of features they produce.
Figure 2:
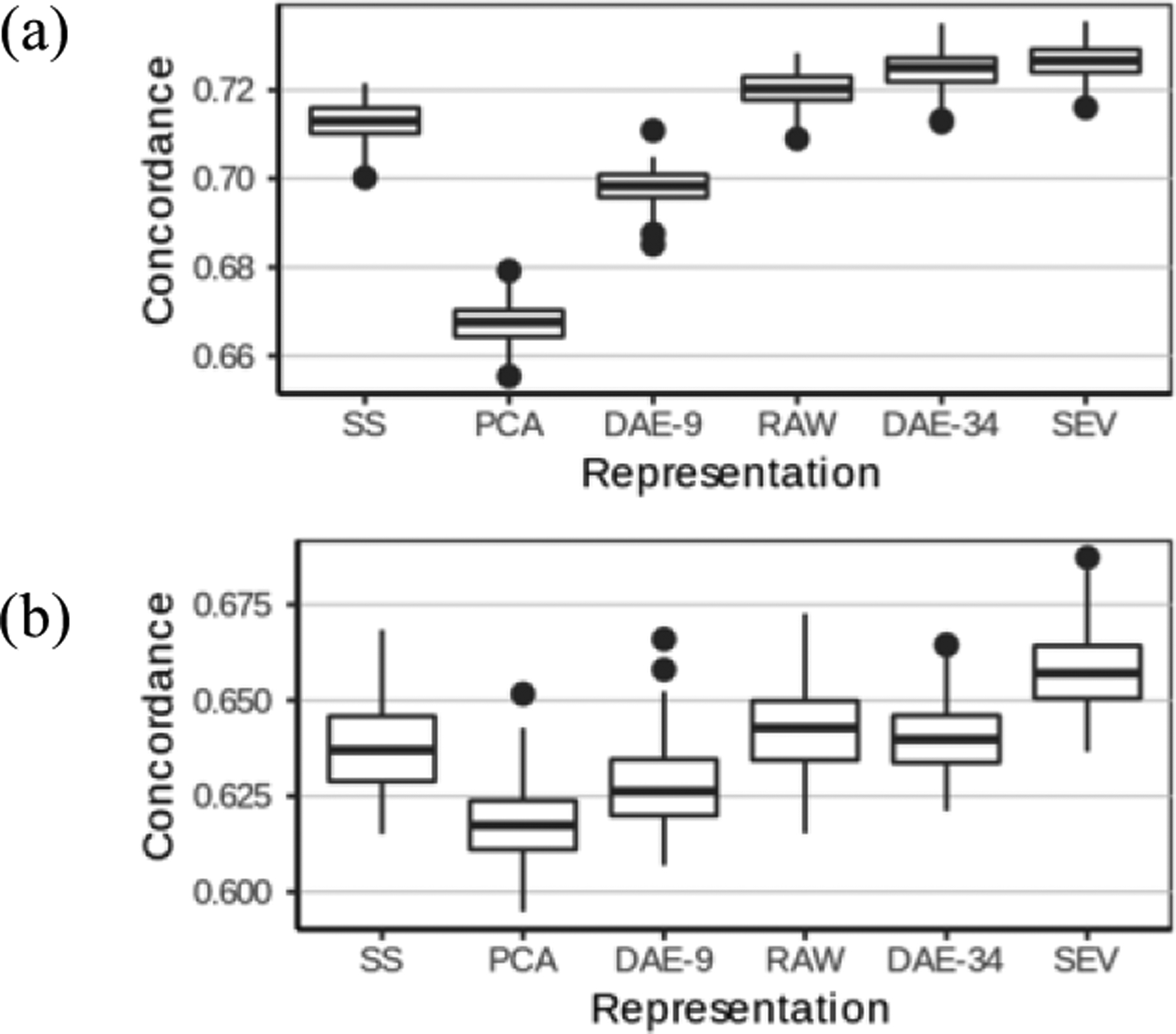
(a) Performance comparison of data representations for the regression task. (b) Comparison of concordance on subpopulation with Framingham score ≥ 20.
While all performance differences are statistically significant, some are not substantial. Our population consists of relatively healthy patients, hence all methods achieved high discrimination. A more clinically meaningful question is to accurately estimate diabetes in risk patients who are at relatively high risk and may actually benefit from an intervention. To this end, we consider patients with Framingham score of at least 20 and in Figure 2 (b), we present the predictive performance of the Cox model on the 6 data representations on these 2,493 patients.
Association Analysis
Association rule mining can discover an exponentially large number of patterns, many of which can be coincidental. The parameter that controls the number of patterns is Minimum Support in Cases (minsupC), the number of cases (patients who developed diabetes) to whom the pattern applies. Figure 3 displays the concordance and number of patterns discovered as a function of minsupC.
Figure 3:
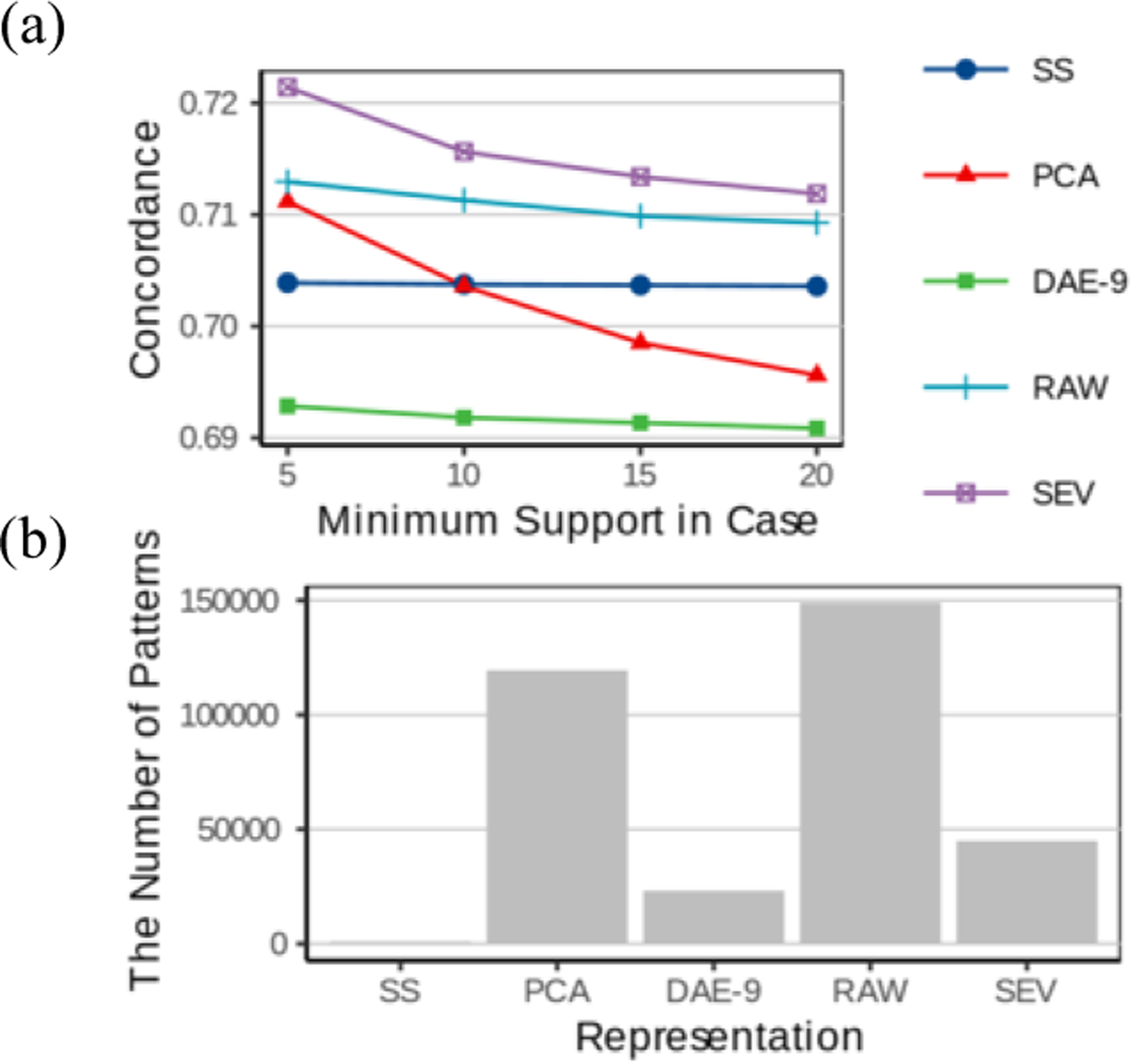
(a) Comparison of the predictive performance of the association patterns discovered using the various data representations as a function of the minimum support in cases (minsupC) (b) The number of association patterns discovered using the various data representations. (minsupC=5)
Discussion
As the paradigm for clinical studies continues to shift toward precision medicine, the range of tasks that clinical data analysis is used for will broaden. Since these newer tasks may operate optimally with different data representations, understanding existing and developing new data representations will become increasingly important. In this manuscript, we proposed a new data representation, Severity Encoding Variables, which represents diseases at a high level and is enriched with clinical knowledge. We compared SEV to five other existing data representations using two clinical tasks.
Assessing the Risk of Incident Diabetes through Regression
The key concern in regression is information loss. The two dimensionality expanding methods, SEV and DAE-34, achieved the highest performance, as they can extract more information (e.g. SEV encodes some interactions and Deep Autoencoders can encode non-linearities). While the performance difference between these two methods in the entire population was minimal (although statistically significant), when we focused on the subpopulation with very high Framingham score (20 or higher), the performance gap widened substantially and SEV outperformed DAE by 20%. Given their high risk of developing diabetes, this is precisely the group of patients for which we need to estimate the risk accurately so that we can effectively target preventive measures to the patients most in need.
Mechanistically, SEV’s performance advantage stems primarily from interactions. It can distinguish between patients who have similar lab results at baseline but are in very different states of severity: e.g. patients who are not yet pharmaceutically treated are very different from those who are already undergoing combination therapy at baseline. Despite having similar (abnormal) lab results, the latter patients are at a disproportionately higher risk and interaction among the various facets of the disease are required to model this correctly. Second, SEV can handle missing data without imputation, identifying that the presence of the diagnosis code is more important in patients who have no available lab results than in patients where the lab results already suggest the presence of the disease.
While interactions among various facets of a disease partly explain how SEV achieves high performance, selecting the right interactions is important. Some classification methods, such as decision trees or association rules, are capable of automatically discovering interactions, however, as our experiment with association rules demonstrates, finding the right combination of interactions is non-trivial.
Dimensionality-reducing data representations did not perform well. Dimensionality reduction can reduce noise and can also lead to information loss. Given that our problem is “tall”, the number of patients far exceeds the number of variables, dimensionality reduction led to information loss. Among the dimensionality-reducing methods, SS takes the diabetes outcome into account, and hence managed to preserve most of the outcome-related information, achieving a reasonable performance with the smallest number of features. PCA and DAE-9 are outcome-independent, and have suffered greater outcome-related information loss than SS despite having more features.
Modeling Patient Population Heterogeneity through Association Pattern Mining
On this task, SEV performed substantially (and statistically significantly) better than others. The association mining algorithm itself performs dimensionality expansion by forming combinations of the features the data representation provides. To find high-risk patients, we typically focus on patterns that occur in small patient groups, which can yield less reliable risk estimates and higher predisposition to overfitting (finding patterns that happen to randomly coincide with diabetes). Different data representations offer different mechanisms to reduce overfitting. The severity scores reduce the number of items an itemset can have. For example, for SS, there are only 5 axes (demographics, obesity, hypertension, hyperlipidemia and prediabetes), each of which is categorized into multiple bins. Since a patient cannot fall into two different bins along the same axis, the maximal number of conditions in a pattern is 5, which seriously limits the number of patterns. Some patterns have as many as 11 conditions in the RAW representation.
SEV, the data representation that achieved the highest performance on association pattern mining, applies a different mechanism. SEV uses the same dichotomization as RAW, but SEV combined these dichotomized variables into predefined “sub-patterns”. For instance, the SEV item ‘lipids under control’ is a combination of three RAW items: LDL is normal AND HDL is normal AND TG is normal. These higher-level items constrain the space of possible patterns (based on clinical knowledge) and thus reduce the tendency for overfitting.
Generalizability
We tested the data representations with a regression model and association pattern mining to highlight certain characteristics of the SEV representation. We believe that these results generalize to other classification methods, as well. First, the SEV representation offers a high-level clinical description of the diseases enhancing clinical interpretability of the models. Second, SEV can improve predictive performance by automatically handling missing lab results and by incorporating clinically meaningful high-order interactions. Third, as we have mentioned earlier, some methods have the ability to discover interactions, and discovering high-order interaction is non-trivial. Currently, there are no classification methods that can do all three well.
Limitations
Unlike the data-driven representations, the construction of the SEV requires clinical expertise. Most of the effort is spent on classifying diagnoses into categories and determining pharmaceutical subclasses for drugs. This effort is not specific to SEVs; even the RAW representation had access to these higher-level categorizations. The effort that is specific to SEV is determining whether lab results and vital signs are normal and whether a drug is first-line or last-line medication. This information is often readily available from practice guidelines, such as the American Diabetes Association guidelines for diabetes. The effort to include this information is small, but non-negligible. However, SEV is outcome-independent, thus once a hierarchy for a risk factor or disease is defined, it can be used for numerous outcomes without the need to change it.
Conclusions
For both regression and association pattern mining, SEV provides the highest performance, substantially higher than the other data representations in a high-risk subpopulation, where accurate risk assessment is particularly important to appropriately target preventive measures. Besides having the highest performance, SEV produces clinically interpretable models and can also handle missing values.
Table 1.
Categorization of the Data Representations.
| Outcome-Specific | Outcome Independent | ||
|---|---|---|---|
| Data-Driven | Knowledge-Driven | ||
| Dimensionality-Reducing | SS | PCA DAE-9 |
SEV |
| Dimensionality-Expanding | DAE-34 | SEV | |
Acknowledgements
This work was supported by NIH award LM011972, NSF awards IIS 1602394 and IIS 1602198. The views expressed in this paper are those of the authors and do not necessarily reflect the views of the funding agencies.
References
- [1].Jensen PB, Jensen LJ, and Brunak S, Mining electronic health records: towards better research applications and clinical care, Nature Reviews Genetics 13 (2012), 395. [DOI] [PubMed] [Google Scholar]
- [2].Oh W, Kim E, Castro MR, Caraballo PJ, Kumar V, Steinbach MS, and Simon GJ, Type 2 Diabetes Mellitus Trajectories and Associated Risks, Big data 4 (2016), 25–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Kim E, Oh W, Pieczkiewicz DS, Castro MR, Caraballo PJ, and Simon GJ, Divisive hierarchical clustering towards identifying clinically significant pre-diabetes subpopulations, in: AMIA Annual Symposium Proceedings, American Medical Informatics Association, 2014, p. 1815. [PMC free article] [PubMed] [Google Scholar]
- [4].Bengio Y, Courville A, and Vincent P, Representation learning: a review and new perspectives, IEEE Transactions on Pattern Analysis and Machine Intelligence 35 (2013), 1798–1828. [DOI] [PubMed] [Google Scholar]
- [5].Agrawal R, Imieliński T, and Swami A, Mining association rules between sets of items in large databases, in: Acm Sigmod Record, ACM, 1993, pp. 207–216. [Google Scholar]
- [6].Tolles J and Meurer WJ, Logistic regression: relating patient characteristics to outcomes, JAMA 316 (2016), 533–534. [DOI] [PubMed] [Google Scholar]
- [7].Moore DS, McCabe GP, and Craig BA, Introduction to the Practice of Statistics, 6th ed., Freeman WH, (2007). [Google Scholar]
- [8].Shickel B, Tighe PJ, Bihorac A, and Rashidi P, Deep EHR: a survey of recent advances in deep learning techniques for electronic health record (EHR) analysis, IEEE Journal of Biomedical and Health Informatics 22 (2017), 1589–1604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Centers for Disease Control and Prevention, National Diabetes Statistics Report, 2017, Atlanta, GA, 2017. [Google Scholar]
- [10].Diabetes Prevention Program Research Group, Reduction in the incidence of type 2 diabetes with lifestyle intervention or metformin, New England journal of medicine 346 (2002), 393–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Hulsegge G, Spijkerman A, Van Der Schouw Y, Bakker SJ, Gansevoort R, Smit H, and Verschuren W, Trajectories of metabolic risk factors and biochemical markers prior to the onset of type 2 diabetes: the population-based longitudinal Doetinchem study, Nutrition & Diabetes 7 (2017), e270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Pelz JO, Stojadinovic A, Nissan A, Hohenberger W, and Esquivel J, Evaluation of a peritoneal surface disease severity score in patients with colon cancer with peritoneal carcinomatosis, Journal of Surgical Oncology 99 (2009), 9–15. [DOI] [PubMed] [Google Scholar]
- [13].Wilson PW, Meigs JB, Sullivan L, Fox CS, Nathan DM, and D’Agostino RB, Prediction of incident diabetes mellitus in middle-aged adults: the Framingham Offspring Study, Archives of internal medicine 167 (2007), 1068–1074. [DOI] [PubMed] [Google Scholar]
- [14].Landgraf AJ and Lee Y, Dimensionality reduction for binary data through the projection of natural parameters, arXiv preprint arXiv:1510.06112 (2015). [Google Scholar]
- [15].Ho JC, Ghosh J, Steinhubl SR, Stewart WF, Denny JC, Malin BA, and Sun J, Limestone: High-throughput candidate phenotype generation via tensor factorization, Journal of Biomedical Informatics 52 (2014), 199–211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].St Sauver JL, Grossardt BR, Yawn BP, Melton LJ III, Pankratz JJ, Brue SM, and Rocca WA, Data resource profile: the Rochester Epidemiology Project (REP) medical records-linkage system, International Journal of Epidemiology 41 (2012), 1614–1624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Liu B, Hsu W, and Ma Y, Integrating classification and association rule mining, in: Proceedings of the Fourth International Conference on Knowledge Discovery and Data Mining, 1998, pp. 24–25. [Google Scholar]
- [18].American Diabetes Association, 2. Classification and diagnosis of diabetes: standards of medical care in diabetes—2018, Diabetes care 41 (2018), S13–S27. [DOI] [PubMed] [Google Scholar]


