Abstract
All-atom molecular dynamics simulations with stratified alchemical free energy calculations were used to predict the octanol-water partition coefficient log Pow of eleven small molecules as part of the SAMPL6 log P blind prediction challenge using four different force field parametrizations: standard OPLS-AA with transferable charges, OPLS-AA with non-transferable CM1A charges, AMBER/GAFF, and CHARMM/CGenFF. Octanol parameters for OPLS-AA, GAFF and CHARMM were validated by comparing the density as a function of temperature to experimental values. The partition coefficients were calculated from the solvation free energy for the compounds in water and pure (“dry”) octanol or “wet” octanol with 27 mol % water dissolved. Absolute solvation free energies were computed by thermodynamic integration (TI) and the Multistate Bennett Acceptance Ratio (MBAR) with uncorrelated samples from data generated by an established protocol using 5-ns windowed alchemical free energy perturbation (FEP) calculations with the Gromacs molecular dynamics package. Equilibration of sets of FEP simulations was quantified by a new measure of convergence based on the analysis of forward and time-reversed trajectories. The accuracy of the log Pow predictions was assessed by descriptive statistical measures such as the root mean square error (RMSE) of the data set compared to the experimental values. Discarding the first 1 ns of each 5-ns window as an equilibration phase had a large effect on the GAFF data, where it improved the RMSE by up to 0.8 log units, while the effect for other data sets was smaller or marginally worsened the agreement. Overall, CGenFF gave the best prediction with RMSE 1.2 log units, although for only eight molecules because the current CGenFF workflow for Gromacs does not generate files for certain halogen-containing compounds. Over all eleven compounds, GAFF gave an RMSE of 1.5. The effect of using a mixed water/octanol solvent slightly decreased the accuracy for CGenFF and GAFF and slightly increased it for OPLS-AA. The GAFF and OPLS-AA results displayed a systematic error where molecules were too hydrophobic whereas CGenFF appeared to be more balanced, at least on this small data set.
Keywords: molecular dynamics, solvation free energy, OPLS-AA force field, AMBER force field, CHARMM force field, ligand parametrization, free energy perturbation, octanol-water partition coefficient
1. Introduction
One key consideration in the design of small-molecule drugs is to enable these molecules to efficiently reach their site of action, which typically requires the crossing of the lipid bilayer of the cell membrane such as in the epithelial lining of the gut or the blood-brain barrier. Although in some cases active transport processes are co-opted for drug transport [1], passive diffusion across the cell membrane remains the primary route for drug absorption [2]. The ability of a molecule to partition into the water or the lipid phase can be assessed by its water-octanol partition coefficient Pow (or its decadic logarithm log Pow, often just written as “logP”) where octanol is taken as a simple approximation to the lipid membrane. A log Pow < 0 indicates a hydrophilic molecule, log Pow ≈ 0 indicates equal distribution in water and octanol phase, and log Pow > 0 indicates lipophilicity. The log Pow value is one of the quantities in the “rule of five” guidelines to assess drug permeability [3], where log Pow > 5 is indicative of poor drug solubility and permeability (in conjunction with more than 5 hydrogen-bond donors/2×5 acceptors, and a molecular weight greater than 500).
Partition coefficients are physico-chemical quantities that are, in principle, straightforward to calculate with physics-based simulation approaches from the solvation free energies of the solute in the two solvents (ΔGw in water and ΔGo in octanol)
| (1) |
where R = 8.31446261815×10−3 kJ·mol−1 · K−1 is the universal Gas constant (i.e., Boltzmann’s constant for 1 mol), T is the temperature, and e Euler’s number. Calculation of partition coefficients requires (1) accurate representation of the interactions between solvent and solute, (2) proper representation of the solute structure (tautomers) and (3) correct sampling of the thermodynamic equilibrium. Therefore, they make for good benchmark systems to assess the current state of the art in predictive free energy calculations, as evidenced by the 2016 SAMPL5 challenge on cyclohexane partition coefficients [4] and the 2019 SAMPL6 challenge on the water-octanol partition coefficients. The chemical structures of compounds included in the SAMPL6-logP data set are shown in Figure 1. The logP values of the compounds were measured by the organizers and had not been previously published [5]; participants submitted blind predictions for evaluation against the experimental values.
Fig. 1:
Chemical structures of the SAMPL6-logP data set with the selected microstates.
For the SAMPL6 challenge we used the same approach as for previous solvationfree energy based challenges [6–8], namely classical molecular dynamics (MD) with explicit solvent. We evaluated three widely used force fields, OPLS-AA, AMBER/GAFF, and CHARMM/CGenFF. For all three force fields reasonably user-friendly parametrization tools exist and we wondered what performance a user could expect from just using these tools. Additionally, we also used the same in-house approach to generate OPLS-AA topologies that we had employed in previous challenges [6–8].
2. Methods
Our computational approach to calculating solvation free energies with classical MD and our mdpow Python package (https://github.com/Becksteinlab/mdpow/) is similar to our previous SAMPL contributions [6–8]. Nevertheless, we will describe the details for completeness together with improvements that resulted from lessons that we learned during this challenge. Previously, we only evaluated OPLS-AA parametrizations but for this challenge we also evaluated additional force fields (AMBER and CHARMM) with the same protocol.
2.1. Force field parameters
Molecules included in the SAMPL6-log P data set (Figure 1) were parameterized with different force fields, as detailed below. Three-dimensional coordinates for molecules included in this study were obtained from our participation [9] in the SAMPL6 pKa prediction challenge [10], the gas-phase geometry optimization being performed with Gaussian09 version D.01 [11] at the B3LYP/6-311+G(d,p) level.
The OPLS-AA [12–18] parameters for these compounds were generated either with transferable charges using our in house mol2ff algorithm (O. Beckstein and B. I. Iorga, unpublished), based on the Cactvs Chemoinformatics Toolkit (http://www.xemistry.com/), or with CM1A charges (scaled with a factor of 1.14 for neutral molecules) using the LigParGen web server [19] (http://zarbi.chem.yale.edu/ligpargen/)
The parameters of SAMPL6-logP compounds for the CHARMM/CGenFF force field [20] were obtained from the CGenFF server (https://cgenff.umaryland.edu/) using the CGenFF program version 2.2.0 and CGenFF 4.0 [21, 22] with mol2 files as inputs. The resulting CHARMM files were converted to Gromacs files with the Python script cgenff_charmm2gmx.py (downloaded from http://mackerell.umaryland.edu/download.php?filename=CHARMM_ff_params_files/cgenff_charmm2gmx.py, copyright notice from 2014). This version of the conversion script cannot correctly process recent CGenFF parameters for lone pairs to represent compounds with certain halogen substituents [23]. Because compounds SM04, SM12 and SM16 contained halogens with lone pairs, we were not able to obtain CGenFF parameters in the Gromacs format and could not include them in the CGenFF results. Although it is possible to manually fix topologies and represent the lone pairs with Gromacs virtual site constructs, we decided against doing so as the average user would likely not be able to perform such topology hacking; furthermore, such functionality should be automated and tested in the conversion script and not performed on a case-by-case basis in order to aid reproducibility and applicability to large data sets.
The AMBER/GAFF [24] parameters for the SAMPL6-logP data set were generated with AM1-BCC charges using AmberTools15 (http://ambermd.org) with version 1.4 of GAFF and ACPYPE [25].
The OPLS-AA hydration free energies simulations were performed using the TIP4P water model [26] and those using CHARMM36 [27] and AMBER99sb [28] force fields were carried out using the TIP3P water model [29], which are the water models used for the development of the corresponding force fields, respectively. For simulations with octanol, we generated parameters for this solvent molecule for OPLS-AA with mol2ff, for GAFF with AmberTools17, and for CGenFF with the CGenFF server, and tested them with simulations of bulk octanol, as described in Results (Section 3.1).
In addition to the pure octanol solvent, we decided to use a water-octanol mixture for solvation free energy calculations, as the experimental octanol-water partition coefficients were measured in a way that the water and octanol phases might not be pure water and octanol. The solubility of octanol in water is very low [30–32] so we only considered pure water phases. On the other hand, the equilibrium solubility of water in octanol at room temperature (298 K) is about 5 mass % [30–32]. Hence we also prepared a mixed solvent water-octanol (“wet” octanol) box with a mole fraction of water in octanol of 27 mol % and performed octanol solvation free energy calculations with either the pure octanol solvent (dry) or the wet octanol.
2.2. Solvation free energy and partition coefficient calculation
Solvation free energies were calculated as described previously [33] via stratified all-atom alchemical free energy perturbation (FEP) MD simulations. All simulations were performed with the mdpow Python package (https://github.com/Becksteinlab/mdpow/, 0.7.0 development version) with Gromacs 2018.2 [34] as its MD engine. Autocorrelation analysis, thermodynamic integration (TI), and the multistate Bennett acceptance ratio (MBAR) [35] were performed with the alchemlyb Python package (https://github.com/alchemistry/alchemlyb), release 0.3.0 [36].
A periodic cubic simulation cell was employed with at least 1.5 nm between the solute and the box surfaces. The simulations were run as Langevin dynamics (integration time step 2 fs) for temperature control, with the friction coefficient for each particle computed as mass/0.1 ps [37]. All simulation were run in the NPT ensemble, and the average pressure was maintained near the target value 1 bar with an isotropic pressure Parinello-Rahman barostat [38] with relaxation time constant τp = 1 ps and compressibility κT = 4.6×10−5 bar−1 for both water and octanol. Lennard-Jones interactions were calculated up to a cutoff of 1 nm without force-switching for OPLS-AA and AMBER simulations and a cutoff of 1.2 nm with a force-switching cutoff of 1.0 nm for CHARMM simulations, and a dispersion correction was applied to energy and pressure to account for van der Waals interactions beyond the cutoff in a mean field manner [39] for OPLS-AA and AMBER. Coulomb interactions were evaluated with the SPME method [40] with an initial short range cutoff of 1 nm, 0.12 nm Fourier grid spacing, sixth order spline interpolation, and a relative tolerance of 10−6. Each simulation was run on six CPU cores and a single GPU and Gromacs was allowed to tune the Coulomb short range cut-off to optimize performance. All bonds containing hydrogen atoms were constrained with the P-LINCS algorithm [41] using a twelfth order expansion with a single iteration.
Solvated systems were energy minimized and relaxed with a NPT MD simulation with a time step of 0.1 fs and duration of 5 ps. An initial NPT equilibrium simulation at constant temperature and pressure (T = 300 K, P = 1 bar) was carried out for 15 ns. The last frame of the equilibrium simulation served as the starting configuration for the windowed FEP calculations. The FEP calculations were also carried out in the NPT ensemble. Coulomb interactions (partial charges) were linearly switched off over five windows (coupling parameter λCoul ∈ {0, 0.25, 0.5, 0.75, 1}) for water simulations, and seven windows (coupling parameter λCoul ∈ {0, 0.125, 0.25, 0.375, 0.5, 0.75, 1}) for dry octanol or wet octanol simulations, while the van der Waals (Lennard-Jones) interactions were maintained (i.e. λvdW = 0); sixteen windows were used to switch off the Lennard-Jones term for the uncharged solute (λCoul = 1 and λvdW ∈ {0, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1}). Each window was simulated for 5 ns. The van der Waals calculations used soft core potentials with the values suggested by Mobley and colleagues [37] (α = 0.5, power 1, and σ = 0.3 nm). The calculations made use of the “couple-intramol = no” feature in Gromacs [34, 42, 43], which maintains intramolecular interactions while decoupling all intermolecular ones.
Autocorrelation analysis was applied to the simulation data to obtain uncorrelated samples of the derivative of the Hamiltonian with respect to the coupling parameter λ, , and energy differences ΔUi,j [44, 45]. For a time series of N samples, the autocorrelation function of the observable A at a given time frame i was defined as
| (2) |
The integrated autocorrelation time τac and statistical inefficiency g were given by
| (3) |
| (4) |
Once the statistical inefficiency was found, every gth sample of the original data set was selected to build up a set of uncorrelated samples. In practice, we used as the observable A. Solvation free energies and statistical errors for the discharging and decoupling process were originally calculated with thermodynamic integration
| (5) |
where the derivative of the Hamiltonian with respect to the coupling parameter λ, , was saved for every time step. In the mdpow implementation of TI, Eq. 5 was integrated numerically with the composite Simpson’s rule [46] from SciPy (http://www.scipy.org) [47]. The error on ΔG was calculated by propagating the errors of the individual FEP windows through Simpson’s rule as described previously [6]. The TI implementation of alchemlyb uses the trapezoid rule and provides appropriate error estimates for uncorrelated data points. The alchemlyb library provides the Multistate Bennett Acceptance Ratio (MBAR) estimator [35], which also requires uncorrelated data for uncertainty estimates. We compared all three estimators and found that they generally agreed with each other. The final results shown in this paper were calculated with uncorrelated samples and the MBAR estimator [35].
The total solvation free energy (transfer from gas phase to aqueous phase at the 1M/1M Ben-Naim standard state)
| (6) |
was calculated as the sum of the Coulomb and van der Waals contributions, with the minus sign originating from the convention in Gromacs that λ = 0 corresponds to the fully coupled (solvated) state while λ = 1 describes a fully decoupled (gas-phase) solute.
In principle the partition coefficient contains contributions from multiple tautomers with significant populations. To simplify the calculations, we only picked a single tautomer, typically with the lowest quantum mechanical ground state energy [9] and neutral overall charge, and calculated the octanol-water partition coefficients log Pow, Eq. 1, for one fixed state of the compound via the solvation free energies (Eq. 6).
2.3. Error analysis
As described previously [8], the error ε on log Pow was calculated by error propagation from the errors of the individual free energies in Eq. 1 as
| (7) |
The difference between experimental and computed octanol-water coefficients (“signed error”) for each of the N compounds, labeled with its identification code α=SM02,SM04, …, was calculated as
| (8a) |
| (8b) |
with the uncertainty εΔ of Δ determined as the standard error from propagating the experimental and simulation errors (Eq. 7) through Eq. 8a. The root mean square error (RMSE) was determined from the individual errors Δ as
| (9) |
the absolute unsigned error (AUE) as
| (10) |
and the signed mean error (ME, also called the “mean signed error”, MSE) as
| (11) |
The standard errors of the RMSE, AUE, and ME were estimated via error propagation of the individual uncertainties Eq. 8b through Eqs. 9–11 as
| (12a) |
| (12b) |
Eq. 12a followed the derivation of the root mean square error of prediction in Ref. [48] but remains more conservative by omitting a correction factor of .
2.4. Data sharing
Data related to this work are shared in the GitHub repository Becksteinlab/SAMPL6_logP_data that is archived on Zenodo at DOI 10.5281/zenodo.3549988. Input files for Gromacs 2018 and results in CSV format for the SAMPL6 submissions and the improved protocol discussed in Results are included.
3. Results and Discussion
3.1. Validation of octanol parameters
Octanol was parameterized (1) using mol2ff and the standard OPLS-AA parameters [13] distributed with the Gromacs package, (2) using AmberTools, ACPYPE [25] and GAFF [24] and (3) using the CGenFF server [21, 22] for CHARMM/CGenFF [20]. The parametrization was validated by (1) computing the density as a function of temperature, (2) calculation of the chemical potential, (3) calculation of the hydration free energy, and (4) calculation of the octanol-water partition coefficient and comparison to experimental values.
The bulk density of octanol was calculated from simulations in a 5.6 nm-length cubic box of dry octanol (512 octanol molecules) or wet octanol (374 octanol molecules and 138 water molecules) of 100 ns length at five temperatures from 273 K to 373 K and P = 1 bar (Figure 2 and Supplementary Table S1). The experimental data for dry 1-octanol were retrieved from REAXYS (https://www.reaxys.com, accessed on 10 September 2019). The simulations of dry and wet octanol with CGenFF, GAFF, and OPLS-AA parameters gave similar results, with the exception of the wet octanol simulation with OPLS-AA parameters at 273 K, as discussed below. The simulated density slightly underestimated the experimental density between −1% at low temperatures and −5.7% near the boiling point of water. The wet octanol density was always higher than the dry octanol density.
Fig. 2:
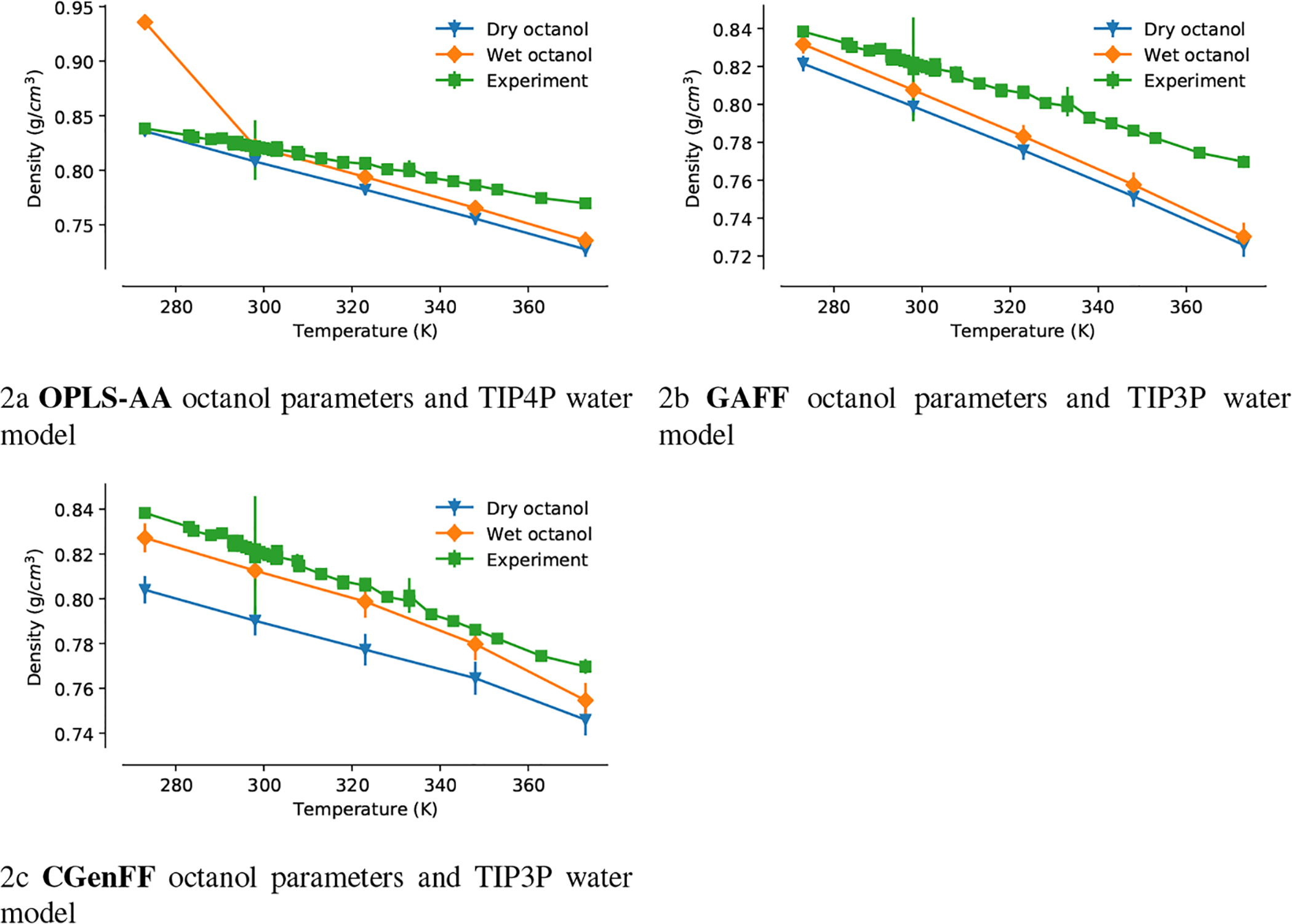
Dependence of the density of dry and wet octanol on the temperature. Green squares are experimental data; blue triangles were computed from 100-ns MD simulations with dry octanol; orange diamonds were computed from 100-ns MD simulations with wet octanol
The OPLS-AA wet octanol system underwent a phase transition to a dense solid phase during the simulation at 273 K (Figure 2a). The experimental melting temperature of pure octanol is 258.5 K and although water-octanol mixtures will have a different melting temperature, the behavior that we observed here is likely unphysical because similar behavior was recently reported and considered a consequence of exaggerated attractive interactions between the alkane chains of the alcohols in standard OPLS-AA [49]. Because we observed no phase transition in simulations at temperatures around our simulation temperature (300 K) we used the standard OPLS-AA parameters of octanol for the OPLS-AA calculations in this work.
The chemical potential of octanol μoctanol is the transfer free energy of a octanol molecule from vacuum to the pure octanol solvent, . We calculated for all octanol parameters with the FEP protocol described above (Table 1). The hydration free energy of octanol was calculated in a similar way and the octanol-water partition coefficient was calculated using Eq. 1. The computed chemical potential values were −7.63 ± 0.16 kcal/mol for GAFF, −8.59 ± 0.16 kcal/mol for OPLS-AA, and −8.98 ± 0.19 kcal/mol for CGenFF, which match the experimental value −8.13 kcal/mol fairly well. The calculated hydration free energy values of −3.26 ± 0.05 kcal/mol for OPLS-AA and −3.82 ± 0.05 for CGenFF agree fairly well (< 1 kcal/mol error) with the experimental value −4.09 ± 0.60 kcal/mol, while the GAFF value −2.62 ± 0.05 kcal/mol was 1.47 kcal/mol higher than the experimental value. The calculated octanol-water partition coefficients for all three octanol models ranged from 3.6 to 3.9 log-units, about 1 log-unit higher than the experimental value 2.92 ± 0.09 kcal/mol.
Table 1:
Hydration free energies, chemical potentials and octanol-water partition coefficients for all octanol parameters were calculated and compared with experimental values.
| Parametrization | ΔGw (kcal/mol) | Δa | μb (kcal/mol) | Δa | log Pow | Δa |
|---|---|---|---|---|---|---|
| GAFF | −2.62(5) | 1.47(60) | −7.63(16) | 0.50(16) | 3.65(12) | 0.73(15) |
| OPLS-AA | −3.26(5) | 0.83(60) | −8.59(16) | −0.46(16) | 3.89(13) | 0.97(16) |
| CGenFF | −3.82(5) | 0.27(60) | −8.98(19) | −0.85(19) | 3.76(15) | 0.84(17) |
| Expc | −4.09(60) | −8.13 | 2.92(9) |
The difference Δ (Eq. 8a) between experimental and computed hydration free energies, chemical potentials and octanol-water partition coefficients is shown for each octanol parametrization. The standard error of the mean in the last significant digits is given in parentheses (Eq. 8b).
The chemical potential of octanol μ is the transfer free energy of an octanol molecule from vacuum to the pure octanol solvent ΔGo.
Experimental log Powvalues were retrieved from REAXYS (https://www.reaxys.com). Multiple values were averaged and errors were taken as the standard deviation of the mean. The experimental octanol chemical potential μ (no reported uncertainty) and hydration free energy ΔGw were retrieved from the Minnesota Solvation Database (https://comp.chem.umn.edu/mnsol/); the latter agrees with the value from the FreeSolv database (DOI 10.5281/zenodo.1161245).
For GAFF and CGenFF, the parametrization reproduced the density of octanol satisfactorily. For OPLS-AA, we would not recommend using the parameters at lower temperatures but they appear satisfactory at room and higher temperatures. The free energies of solvation matched experimental data reasonably well, with GAFF showing a trend towards undersolvating octanol in both water (like all three force fields) and also in octanol itself. For all three force field parametrizations, the log Pow is about 1 unit too high, a trend that also became apparent for the SAMPL6 compounds for the OPLS-AA and GAFF force fields, as discussed below.
3.2. Improvements to the FEP protocol
We started with our standard FEP protocol [6–8], with calculations in the NPT ensemble for water, dry octanol, and wet octanol (27 mol % water in octanol) solutions. All log Pow values were computed from the solvation free energies according to Eq. 1. After submission and release of the experimental values, we made two changes to our protocol, which are discussed in more detail below: We switched our estimators to use our new alchemlyb library [36] and we added an equilibration phase to the FEP windows by discarding the first nanosecond during preprocessing (also made easy by the preprocessing module in alchemlyb).
3.2.1. Estimator comparison
The log Pow results submitted to the SAMPL6-logP challenge as entries cp8kv, 623c0 (OPLS-AA (mol2ff) dry/wet), eufcy, mwuua (OPLS-AA (LigParGen) dry/wet), sqosi, 6nmtt (GAFF dry/wet), and 3oqhx (CGenFF dry) (Supplementary Tables S4–S7 in the Supplementary Information) were calculated with the mdpow-TI estimator, which uses all data but decorrelates the data for the error estimation [6]. We have been developing the alchemlyb library [36] as a reference FEP analysis library to be used as a drop-in replacement for in-house code. We took the analysis of the SAMPL6 data as an opportunity to switch mdpow to using alchemlyb and in particular, to use alchemlyb’s MBAR estimator. We first established that mdpow-TI (Simpson’s rule) and alchemlyb-TI (trapezoid rule) gave similar results when applied to all data, with typical root mean square differences (RMSD) close to 0 (range 0.10–0.15; see Supplementary Figure S1). Furthermore, alchemlyb-MBAR also gave similar log Pow-values as the two TI estimates (RMSDs 0.04–0.21). The estimated uncertainties from alchemlyb were, however, much smaller than the ones from mdpow because the raw data were highly correlated. To estimate the uncertainties free of bias, uncorrelated data were generated by applying the autocorrelation analysis to simulations for all λ windows, according to Eqs. 2–4; the resulting alchemlyb uncertainties were comparable to the ones obtained with the mdpow-TI estimator.
This preliminary analysis established that we could safely replace the mdpow-TI estimator with the alchemlyb ones. Given that alchemlyb-TI and MBAR gave similar answers (RMSDs 0.04–0.10) we focused on results with the MBAR estimator which, at least in principle, makes better use of the available data [35].
3.2.2. The importance of equilibration
In our simulation protocol we used all data from each FEP window because in previous SAMPL challenges with water and cyclohexane we were concerned with sufficient sampling and had no indication that windows might require appreciable equilibration time. However, David Mobley’s group shared with us their AMBER/GAFF results, which were more accurate than our AMBER/GAFF results (their RMSE 1.6 compared to our 2.4, Table 2) even though the force field and overall protocol seemed similar [50]. The root mean square difference (RMSD) between the two data sets for dry octanol was 2.3 (our sqosi vs REF07 from Ref. [50]) with a similar RMSD of 2.4 for wet octanol (6nmtt vs REF02) as shown in Figure S5 in the Supplementary Information. (Işık et al [50] discussed a comparison between the different simulations in more detail and concluded that octanol equilibration period, assignment of charges to carboxylic acids, and also tautomer selection all contributed to different results.)
Table 2.
RMSE, AUE and ME when all data in each λ window (0–5 ns) was used and when the first nanosecond was discarded as equilibration (1–5 ns)
| Parameter | Oct | All (0–5 ns) | Equilibrated (1–5 ns) | Entrya | ||||
|---|---|---|---|---|---|---|---|---|
| RMSE | AUE | ME | RMSE | AUE | ME | |||
| OPLS-AA | Dry | 2.83(5) | 2.68(5) | 2.68(5) | 2.79(5) | 2.61(5) | 2.61(5) | cp8kv |
| OPLS-AA | Wet | 2.62(5) | 2.50(4) | 2.50(4) | 2.72(5) | 2.61(5) | 2.61(5) | 623c0 |
| LigParGen | Dry | 1.90(6) | 1.79(6) | 1.66(6) | 1.71(6) | 1.57(6) | 1.57(6) | eufcy |
| LigParGen | Wet | 1.80(6) | 1.68(6) | 1.68(6) | 1.62(6) | 1.51(6) | 1.51(6) | mwuua |
| GAFF | Dry | 2.36(8) | 2.13(7) | 2.13(7) | 1.52(7) | 1.28(7) | 1.28(7) | sqosi |
| GAFF | Wet | 2.26(7) | 2.07(7) | 2.07(7) | 1.71(8) | 1.48(7) | 1.48(7) | 6nmtt |
| CGenFF | Dry | 1.08(6) | 0.90(6) | 0.24(6) | 1.17(5) | 0.91(6) | −0.32(6) | 3oqhx |
| CGenFF | Wet | 1.48(5) | 1.21(5) | 0.16(5) | 1.42(5) | 1.05(5) | −0.10(5) | —b |
The corresponding submission entry codes for the raw data used to calculate the results. Entries in this table were processed with alchemlyb-MBAR and are not the results that were submitted to SAMPL6; instead see Tables S4–S7 in the Supplementary Information for the submitted results, which were processed with mdpow-TI (Simpson’s rule).
Results with CGenFF in wet octanol had not been submitted to SAMPL6 but were computed for this work to enable a complete comparison.
One major difference between the protocols appeared to be that the Mobley group followed their own best practices and eliminated any non-equilibrated region of the trajectories [44], which was particularly important for the octanol simulations [50]. We therefore discarded the first 1 ns of all trajectories as equilibration and re-computed all free energies and log Pow from the data at 1–5 ns in each FEP window. Comparing the RMSE for using all data (0–5 ns) with the equilibrated (1–5 ns) values showed that leaving out the first nanosecond lead to a large improvement for the GAFF results, which decreased by 0.84 log units to 1.53 for dry octanol and by 0.55 units to 1.71 for wet octanol (Table 2). The improvement for OPLS-AA (LigParGen) was modest (decreased by 0.19 and 0.18), about within uncertainties for OPLS-AA (mol2ff) and CGenFF, where it marginally worsened the RMSE by 0.09.
Because of the large improvement in the RMSE for the GAFF simulations we sought to assess equilibration behavior. As an example we investigated SM14 for which omitting the equilibration improved agreement with experiment by about 1.5 log units. Time-reversed convergence plots [44, 51] were used to determine the non-equilibrated region in each λ window. We calculated the time-forward average and time-reversed average of by
| (13) |
| (14) |
For a simulation with a time length of T, the convergence time tc was defined as the smallest time t for which both the forward and the reverse average were within ε = 1 kJ/mol of the value computed over all T,
| (15) |
For example, Figure 3a shows an example where the forward and reverse averages rapidly approach the ε band around the final average, which is indicative of rapid equilibration. On the other hand, Figure 3b shows an example that is poorly equilibrated because forward and reverse averages only come close near the very end of the simulation time.
Fig. 3:
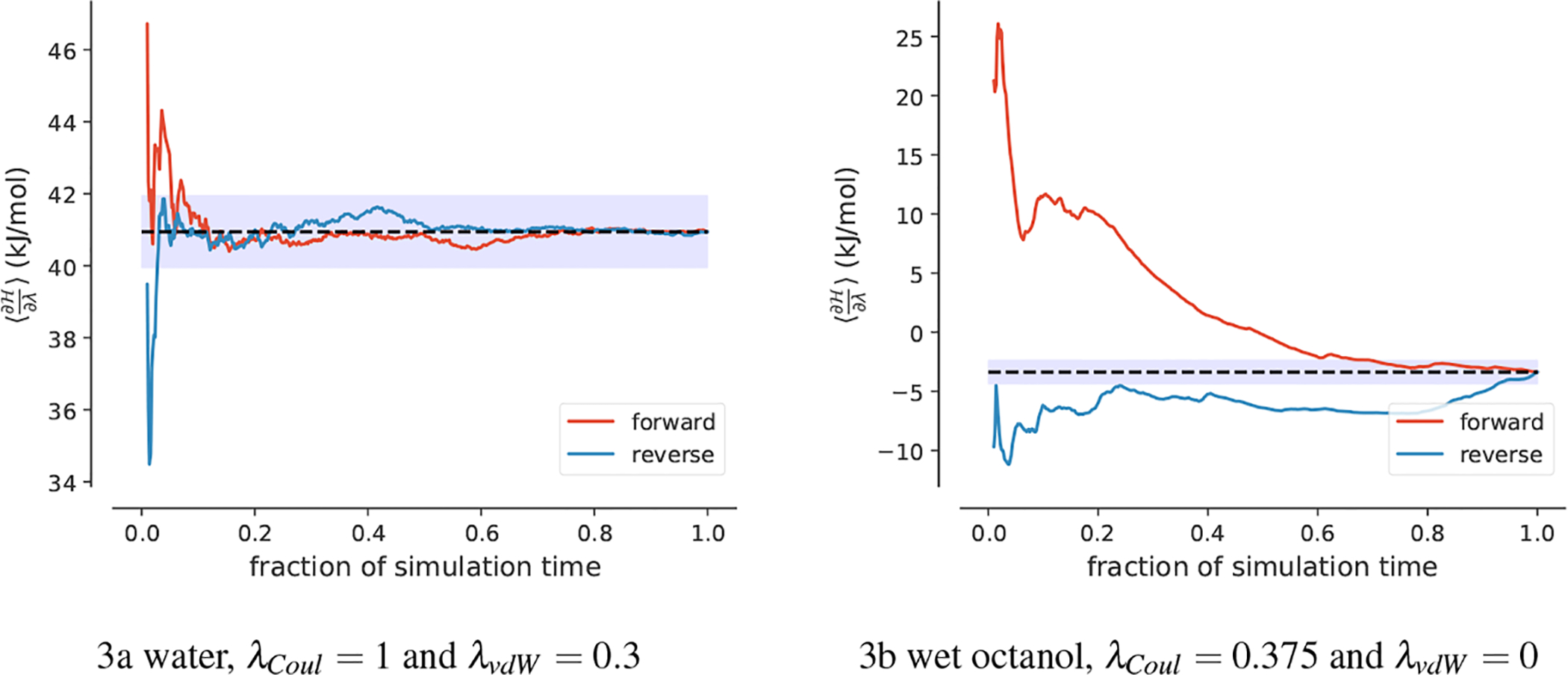
time-reversed and time-forward convergence plots for SM14. The calculated convergence time fraction Rc was 0.05, indicating a well equilibrated window. b The calculated Rc was 0.89, indicating that this window was not well equilibrated.
To make the time point of convergence easily comparable, we defined the convergence time fraction Rc as
| (16) |
Rc denotes the fraction of the simulation time from which on the system appears to be equilibrated, with Rc = 0 indicating the system is well equilibrated at the beginning, and Rc = 1 that the whole trajectory is not equilibrated.
Using Rc as a measure of convergence, we analyzed the complete set of λ windows for SM14 by computing Rc(λ) for each window and then plotting a cumulative probability distribution function of these values, which measures what fraction of windows has at least the given Rc. For a perfectly equilibrated FEP calculation, resembles a unit step function neara Rc = 0 because all windows have Rc(λ) ≈ 0. For a poorly equilibrated calculation, rises steeply near Rc = 1.
The cumulative distributions of the convergence time fractions of all Coulomb and VDW windows from the whole data (all data, 0–5 ns) for SM14 and GAFF showed that the water simulations equilibrated much faster than the dry and the wet octanol simulations (Figure 4). This behavior was particularly apparent for the Coulomb part of the calculation. The data discarding the first 1 ns (reduced data, 1–5 ns) showed the same trends, with water simulations reaching equilibrium after about 20% of the simulation time (Figure 4). Discarding the first 1 ns as equilibration improved the equilibration behavior of the Coulomb part of the octanol simulations as shown by the “1–5 ns” graph (solid line) emerging above the “0–5 ns” graph in Figure 4. Despite this improvement, overall convergence of the octanol simulation windows remained poor.
Fig. 4:
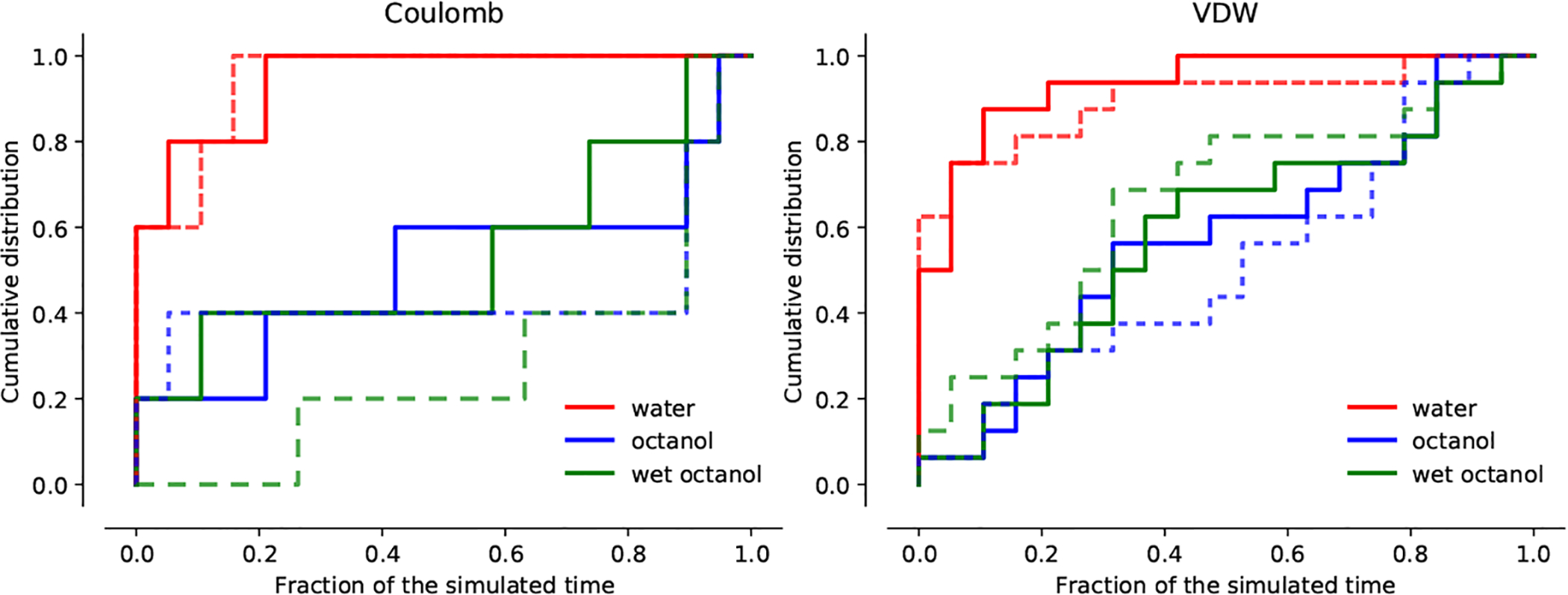
Cumulative distribution functions of the convergence time fraction Rc for Coulomb and VDW λ windows from all data (0–5 ns) (dashed lines) and data with the first 1 ns discarded as equilibration (1–5 ns) (solid lines) for SM14 (GAFF).
Instead of using visual comparison of graphs, we sought to define a quantitative quality measure for the convergence of a whole set of λ windows in the form of a single number. The area Ac under the cumulative distribution ,
| (17) |
turned out to be a suitable quantity with a simple interpretation. Ac is a number between 0 and 1 because it is based on a cumulative probability function (monotonically increasing from 0 to 1) that is integrated over the range 0 to 1. Ac can be interpreted as the ratio of the equilibrated simulation time to the whole simulation time for a set of simulations. Ac = 1 means that all simulation time frames in all windows can be considered equilibrated (with the meaning of Eq. 15), while Ac = 0 indicates that nothing is equilibrated.
For example, the equilibration ratios Ac of all Coulomb and VDW windows from both all data and reduced data for SM14 (Table 3) showed that over 90% of the sampled time of water simulations was equilibrated. One the other hand, the dry and the wet octanol simulations only had Ac ranging from 0.27 to 0.66, again indicating poorly equilibrated octanol simulations.
Table 3:
Equilibration ratio Ac of all data (0–5 ns) and reduced data (1–5 ns) for SM14 (GAFF), separated by FEP Coulomb and VDW windows.
| Water | Diy Octanol | Wet Octanol | ||||
|---|---|---|---|---|---|---|
| Coulomb | VDW | Coulomb | VDW | Coulomb | VDW | |
| 0–5 ns | 0.95 | 0.90 | 0.44 | 0.51 | 0.27 | 0.66 |
| 1–5 ns | 0.95 | 0.93 | 0.51 | 0.57 | 0.54 | 0.58 |
Although dry octanol and wet octanol results indicated a lack of equilibration in both data sets for SM14, discarding the first nanosecond improved the convergence behavior of the Coulomb part. Specifically, Ac for the Coulomb windows in dry octanol improved from 0.44 to 0.51 and from 0.27 to 0.54 for wet octanol (Table 3). For the wet octanol VDW simulations, discarding data slightly worsened equilibration as seen in the equilibration ratio decrease from 0.66 to 0.68. Nevertheless, for all other windows, discarding the initial part of the windows improved Ac (Table 3).
To test whether Ac could describe the equilibration of the simulations, we ran longer FEP simulations for SM14 (GAFF) using a protocol with one initial 100 ns NPT equilibrium simulation and 50 ns production simulations for each window. As expected, the ten-fold longer simulation time improved convergence in all cases, with the largest increase in Ac for the wet octanol Coulomb windows from 0.27 to 0.69 (Figure S4 and Table S3 in the Supplementary Information).
The picture across the whole data set of GAFF simulations was not as striking as for SM14 although discarding the first nanosecond also improved Ac for the octanol simulations from 0.44 to 0.46 (dry) and 0.40 to 0.47 (wet), as shown in Table S2 and Figure S3 in the Supplementary Information. For almost all force fields, the reduced data showed better equilibration ratios than the 0–5 ns data, with the occasional small decrease by up to 0.02. The OPLS-AA (LigParGen) simulations were the only ones with exceptional behavior in that the reduced simulations had a markedly decreased water Coulomb Ac from 0.85 to 0.76 but a substantially increased octanol Coulomb Ac from 0.27 to 0.49 (dry) and 0.35 to 0.42 (wet).
These data suggested an overall improvement in convergence due to discarding an initial equilibration phase in each λ-window, so we decided to take equilibration into account, in line with FEP best practices [44]. For simplicity, we applied the 1 ns equilibration time to all data sets; in the future, this could certainly be optimized for individual data sets, using, for instance Ac (Eq. 17). (We also attempted to use the equilibrium detection algorithm [45] as implemented in alchemlyb’s preprocessing.subsampling.equilibrium_detection() function but did not manage to obtain consistent and robust results for the equilibration period.)
3.3. Predicted partition coefficients
For all eleven molecules (Figure 1), absolute solvation free energy calculations were carried out using topologies generated with standard OPLS-AA atom types with fixed charges (referred to as OPLS-AA (mol2ff) or simply OPLS-AA), OPLS-AA with variable 1.14*CM1A charges (OPLS-AA (LigParGen) or just LigParGen), and AMBER/GAFF (GAFF). CHARMM/CGenFF (CGenFF) topologies for eight of the eleven molecules were used to calculate solvation free energies; three halogen-containing molecules were omitted as explained in Methods (Section 2.1). We included the CGenFF results for the eight compounds because when we calculated the RMSE for the other three force fields for the same eight compounds as for CGenFF (Supplementary Table S8), the difference compared to calculating it over all eleven values (Table 2) was small.
As the effect of equilibration was sizable and the preliminary analysis in terms of Ac (Eq. 17) indicated systematic improvements, we decided to treat the first 1 ns as equilibration for all data sets. Thus, the following detailed results for log Pow differ from the submitted results in that (1) a 1 ns equilibration time was discarded for each FEP window and (2) the free energies were calculated with the MBAR estimator.
The predictions were compared to the experimental values, with a summary for all eight data sets shown in Table 2. In addition to RMSE, AUE, and ME, the Pearson correlation coefficient and the Kendall rank correlation coefficients were calculated, although the sample size might not be big enough to adequately capture the statistics. In the following we discuss in more detail the individual data sets, sorted by force field parametrization.
3.3.1. OPLS-AA (mol2ff)
OPLS-AA with transferable charges did not perform well. The RMSE was 2.05 for dry octanol and 2.72 ± 0.05 for wet octanol (Table 4). The correlation between experimental and computed values in Figure 5 showed none of the compounds were within one log unit, most were off by two to three units, with SM08 off by five units. The Pearson correlation coefficients r for the dry and the wet calculations were 0.41 and 0.49 (with r = 1 indicating perfect correlation, 0 no correlation, and −1 perfect anticorrelation), summarizing the moderate success in quantitatively predicting log Pow. The Kendall rank correlation coefficient τ was computed to evaluate the ability to rank-order the data; a value of τ = 1 indicates that the simulations predict the same ranking of compounds by log Pow as the experimental data whereas if the rankings were completely reversed τ would obtain the value −1 and if the simulations produced random results, a value close to 0 would be expected. The dry octanol data yielded τ = 0.60, better than the value of 0.38 for the wet octanol predictions. The dry octanol simulations were moderately successful at rank-ordering compounds, while the wet octanol ones did not perform well.
Table 4:
Computed (log Pow) and experimental octanol-water partition coefficients with error estimate for the OPLS-AA (mol2ff) results processed with alchemlyb-MBAR. The same raw data processed with mdpow-TI (Simpson’s rule) were submitted as entries cp8kv (Protocol Dry) and 623c0 (Protocol Wet), see Table S4 in the Supplementary Information
| id | Exp. | Dry Octanol | Wet Octanol | ||
|---|---|---|---|---|---|
| log Pow | Δa | log Pow | Δa | ||
| SM02 | 4.09(3) | 5.46(21) | 1.37(21) | 5.93(16) | 1.84(16) |
| SM04 | 3.98(3) | 6.12(13) | 2.14(13) | 7.31(14) | 3.33(14) |
| SM07 | 3.21(4) | 5.34(14) | 2.13(14) | 4.97(13) | 1.76(13) |
| SM08 | 3.1(3) | 8.54(20) | 5.44(20) | 7.18(20) | 4.08(20) |
| SM09 | 3.03(7) | 5.4(16) | 2.37(17) | 4.82(20) | 1.79(21) |
| SM11 | 2.1(4) | 4.99(15) | 2.89(15) | 5.06(13) | 2.96(13) |
| SM12 | 3.83(3) | 6.35(17) | 2.52(17) | 5.77(21) | 1.94(21) |
| SM13 | 2.92(4) | 5.24(18) | 2.32(18) | 5.11(18) | 2.19(18) |
| SM14 | 1.95(3) | 4.53(12) | 2.58(12) | 4.99(12) | 3.04(12) |
| SM15 | 3.07(3) | 5.73(14) | 2.66(14) | 5.3(15) | 2.23(15) |
| SM16 | 2.62(1) | 4.93(23) | 2.31(23) | 6.18(19) | 3.56(19) |
| RMS Error (RMSE)b | 2.79(5) | 2.72(5) | |||
| Absolute Unsigned Error (AUE) | 2.61(5) | 2.61(5) | |||
| Mean Error (ME) | 2.61(5) | 2.61(5) | |||
Fig. 5:
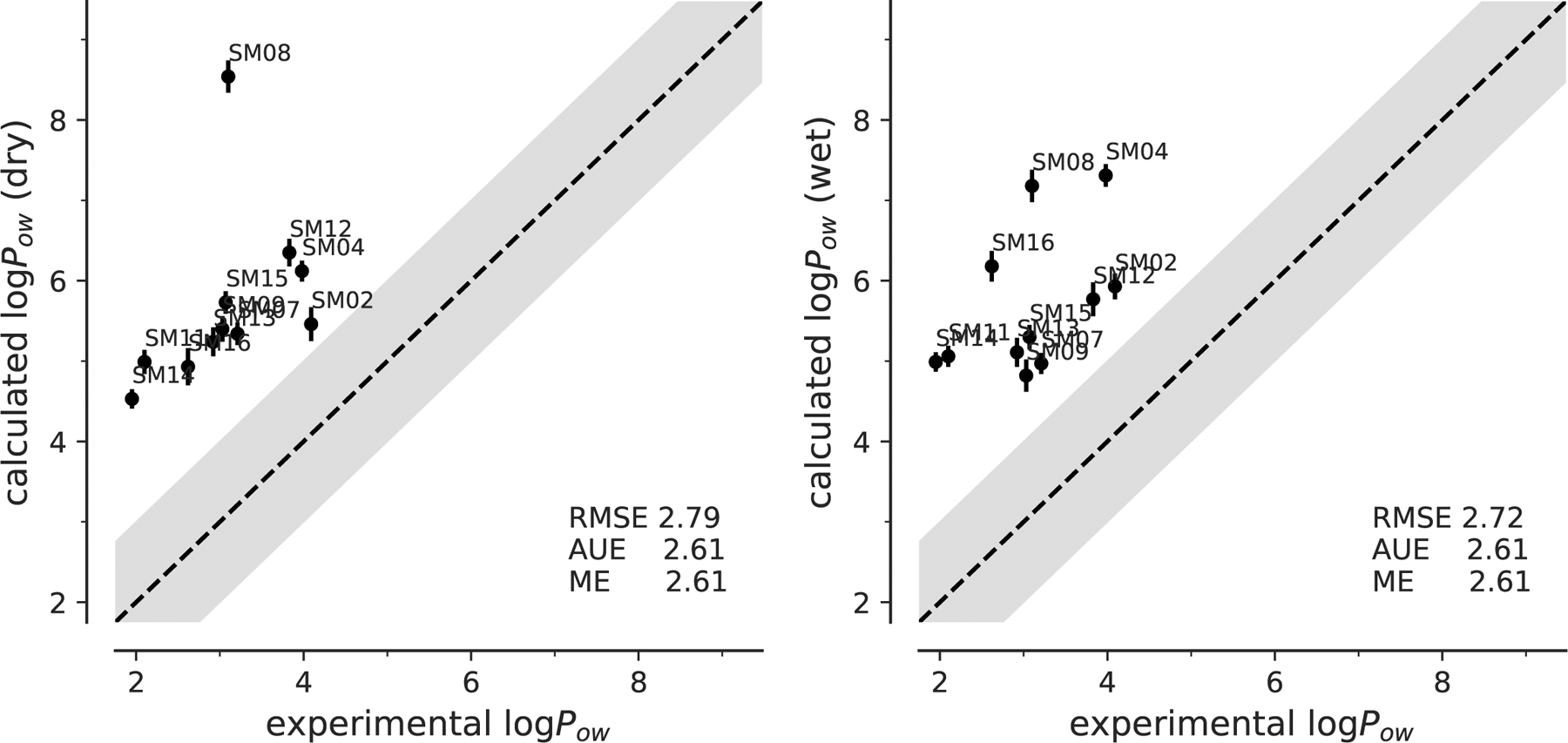
Correlation between experimental and computed octanol-water coefficients log Pow for simulations performed with dry or wet octanol with OPLS-AA (mol2ff) parameters. The gray band indicates ±1 log-units from ideal correlation, shown by the dashed line. The root mean square error (RMSE), the absolute unsigned error (AUE), and the (signed) mean error (ME) are indicated. Error bars represent the error in the experiments or the error on the mean, derived from the simulations.
The AUE (2.61) was the same as the absolute value of ME for both the dry and wet octanol, which corresponds to the visual inspection of the correlation plot (Figure 5) that all the prediction were larger than the experimental values. If we corrected our results by shifting the values by the ME, then the shifted dry octanol data would have had an RMSE of 0.97 instead of 2.79; the shifted wet octanol data would have had an RMSE of 0.78 instead of 2.72, which would have constituted a dramatic improvement.
Overall, these results suggested a systematic error in OPLS-AA calculations that overestimated the log Pow. As in our previous work on cyclohexane distribution coefficients [8] (and unpublished data) we suspect that the primary problem lies with the hydration free energy calculations, which are too positive, i.e., the molecules are under-solvated in water.
3.3.2. OPLS-AA (LigParGen)
OPLS-AA with non-transferable charges performed somewhat better than OPLS-AA with transferable charges, although the same tendencies remained: The RMSE was 1.71 ± 0.07 for the dry octanol and 1.62 ± 0.07 for wet octanol (Table 5). An improvement of about 0.2 log units in RMSE was obtained by removing the equilibrium part. While a few compounds such as SM14 and SM15 were within one log unit, most were off by 1 to 2.5 units in Figure 6. The Pearson correlation coefficients r for the dry and the wet calculations were 0.78 and 0.60, summarizing the moderate success in quantitatively predicting log Pow. The dry octanol data yielded the Kendall rank correlation coefficient τ = 0.64, slightly better than the value of 0.56 for the wet octanol predictions. Both the dry and wet octanol simulations were moderately successful at rank-ordering compounds.
Table 5:
Computed (log Pow) and experimental octanol-water partition coefficients with error estimate for the OPLS-AA (LigParGen) results processed with alchemlyb-MBAR. The same raw data processed with mdpow-TI (Simpson’s rule) were submitted as entries eufcy (Protocol Dry) and mwuua (Protocol Wet), see Table S5 in the Supplementary Information
| id | Exp. | Dry Octanol | Wet Octanol | ||
|---|---|---|---|---|---|
| log Pow | Δ | log Pow | Δ | ||
| SM02 | 4.09(3) | 5.47(28) | 1.38(28) | 6.0(30) | 1.91(30) |
| SM04 | 3.98(3) | 5.77(23) | 1.79(23) | 5.01(17) | 1.03(17) |
| SM07 | 3.21(4) | 5.14(20) | 1.93(20) | 4.43(18) | 1.22(18) |
| SM08 | 3.1(3) | 5.15(20) | 2.05(20) | 5.45(22) | 2.35(22) |
| SM09 | 3.03(7) | 4.36(24) | 1.33(25) | 4.64(30) | 1.61(30) |
| SM11 | 2.1(4) | 4.62(20) | 2.52(20) | 4.31(18) | 2.21(18) |
| SM12 | 3.83(3) | 5.72(17) | 1.89(17) | 4.47(22) | 0.64(22) |
| SM13 | 2.92(4) | 5.13(27) | 2.21(27) | 3.67(22) | 0.75(22) |
| SM14 | 1.95(3) | 1.94(18) | −0.01(18) | 4.09(17) | 2.14(17) |
| SM15 | 3.07(3) | 3.85(14) | 0.78(14) | 4.03(18) | 0.96(18) |
| SM16 | 2.62(1) | 4.03(22) | 1.41(22) | 4.36(18) | 1.74(18) |
| RMS Error (RMSE) | 1.71(7) | 1.62(7) | |||
| Absolute Unsigned Error (AUE) | 1.57(7) | 1.51(7) | |||
| Mean Error (ME) | 1.57(7) | 1.51(7) | |||
Fig. 6:
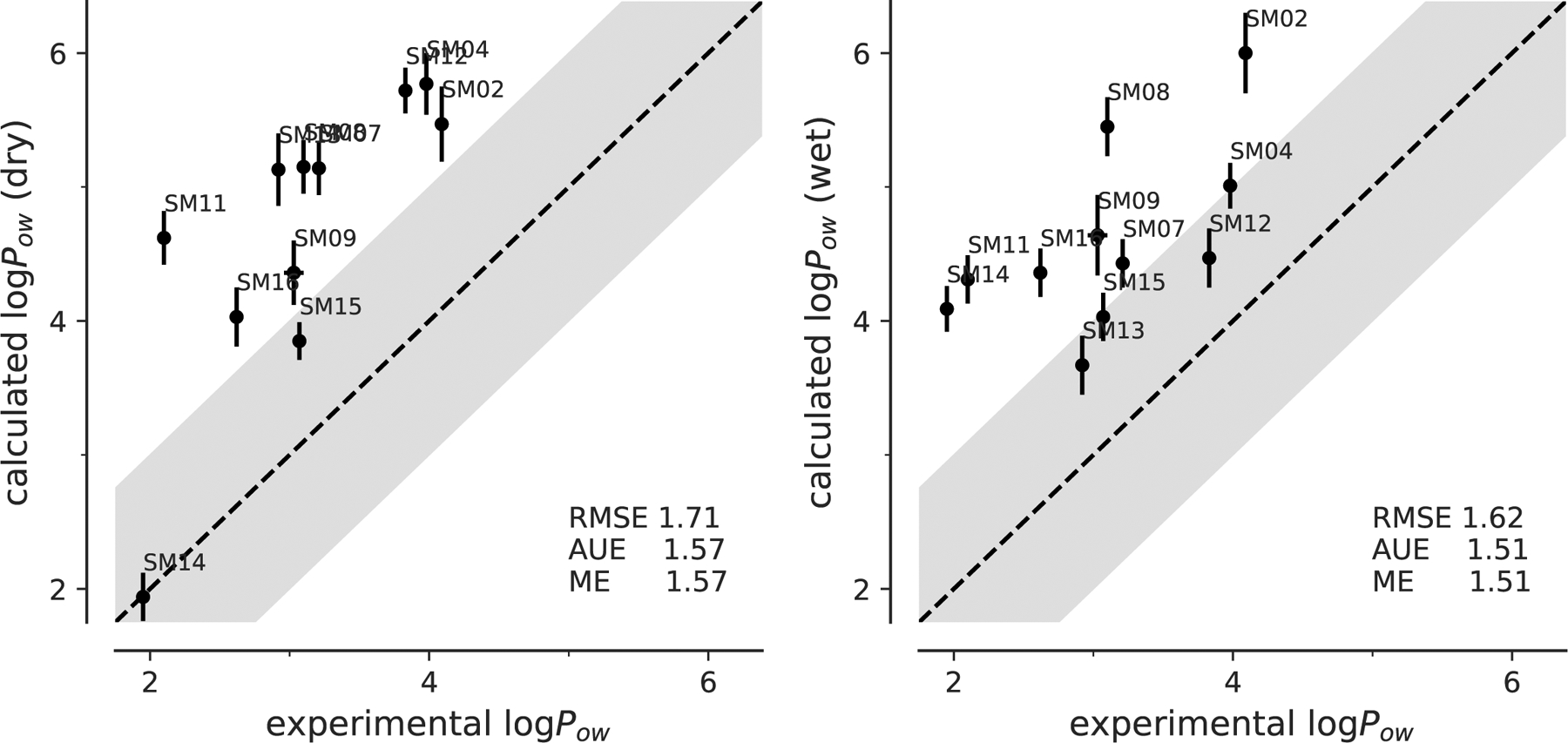
Correlation between experimental and computed octanol-water coefficients log Pow for simulations performed with dry or wet octanol with OPLS-AA (LigParGen) parameters.
Similar to the OPLS-AA (mol2ff) results, the AUE (1.57 for dry and 1.51 for wet) was the same as the absolute value of ME for both the dry and wet octanol, which again indicated a systematical shift in the calculated results. Shifting the values by the ME would have improved the dry octanol RMSE to 0.68 instead of 1.71 and wet octanol RMSE to 0.59 instead of 1.61, which would have been a 1-log-unit improvement.
Compared to OPLS-AA with transferable charges, OPLS-AA with non-transferable CM1A charges produced a better prediction but still suffered from a large systematic error, likely related to hydration. It appears that sacrificing the transferability of the original OPLS-AA atom types can buy moderately higher accuracy at the cost of having to parameterize the charges for every single molecule.
3.3.3. GAFF
As mentioned before, the GAFF parametrization benefited most from implementing the equilibration preprocessing, which turned the poor initial GAFF accuracy into a reasonably good one, by lowering the RMSE by 0.84 units. The RMSE was 10.08 for the dry octanol and 1.71 ± 0.08 for wet octanol (0.55 lower) (Table 6). In Figure 7, several compounds like SM11, SM14 and SM15 were within one log unit, most of the other compounds were off by 1 to 2 units, with SM13 as far as 3.6 units. The Pearson correlation coefficients r for the dry and the wet calculations were 0.80 and 0.71, showing a better ability to quantitatively predict log Pow. The Kendall rank correlation coefficient for the dry octanol simulations was 0.53, slightly worse than the wet octanol predictions with τ = 0.59. Both the dry and wet octanol simulations were moderately successful at rank-ordering compounds.
Table 6:
Computed (log Pow) and experimental octanol-water partition coefficients with error estimate for the GAFF results processed with alchemlyb-MBAR. The same raw data processed with mdpow-TI (Simpson’s rule) were submitted as entries sqosi (Protocol Dry) and 6nmtt (Protocol Wet), see Table S6 in the Supplementary Information
| id | Exp. | Dry Octanol | Wet Octanol | ||
|---|---|---|---|---|---|
| log Pow | Δ | log Pow | Δ | ||
| SM02 | 4.09(3) | 5.54(20) | 1.45(20) | 5.75(19) | 1.66(19) |
| SM04 | 3.98(3) | 6.03(22) | 2.05(22) | 5.66(18) | 1.68(18) |
| SM07 | 3.21(4) | 4.37(27) | 1.16(27) | 4.55(23) | 1.34(23) |
| SM08 | 3.1(3) | 5.41(28) | 2.31(29) | 4.55(21) | 1.45(21) |
| SM09 | 3.03(7) | 3.79(24) | 0.76(25) | 4.74(24) | 1.71(25) |
| SM11 | 2.1(4) | 2.15(25) | 0.05(25) | 2.99(28) | 0.89(28) |
| SM12 | 3.83(3) | 5.0(19) | 1.17(19) | 5.24(23) | 1.41(23) |
| SM13 | 2.92(4) | 5.5(21) | 2.58(21) | 6.6(31) | 3.68(31) |
| SM14 | 1.95(3) | 2.32(21) | 0.37(21) | 2.62(26) | 0.67(26) |
| SM15 | 3.07(3) | 3.27(18) | 0.20(18) | 3.13(23) | 0.06(23) |
| SM16 | 2.62(1) | 4.56(31) | 1.94(31) | 4.3(36) | 1.68(36) |
| RMS Error (RMSE) | 1.52(8) | 1.71(8) | |||
| Absolute Unsigned Error (AUE) | 1.28(7) | 1.48(8) | |||
| Mean Error (ME) | 1.28(7) | 1.48(8) | |||
Fig. 7:
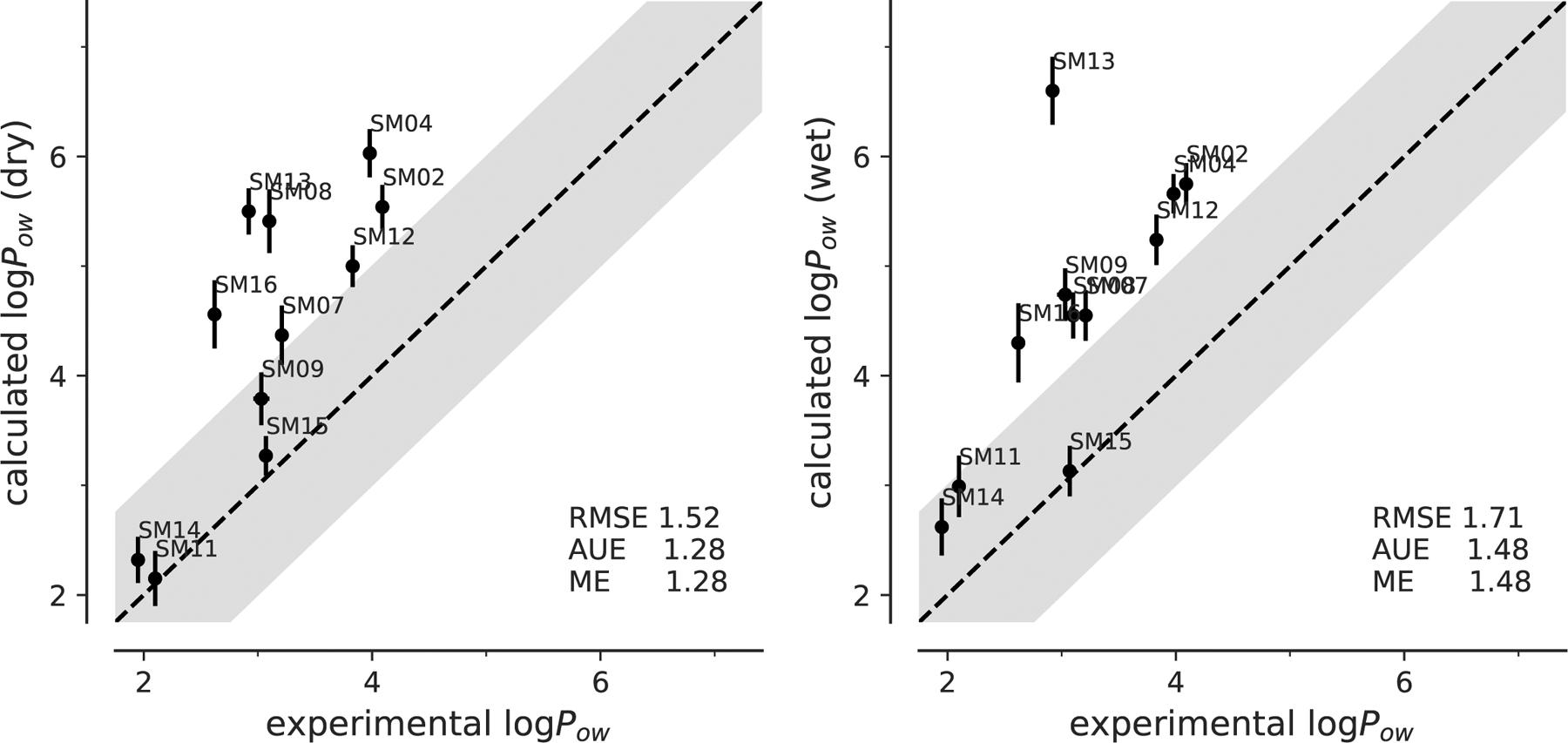
Correlation between experimental and computed octanol-water coefficients log Pow for simulations performed with dry or wet octanol with GAFF parameters.
Similar to both OPLS-AA results, the AUE (1.28 for dry and 1.48 for wet) was the same as the absolute value of ME for both the dry and wet octanol, which also indicated a systematical error in the calculated results. After subtracting the ME from the results, the dry octanol data would have had an RMSE of 0.83 instead of 1.52; the wet octanol data would have had an RMSE of 0.86 instead of 1.71, resulting in a 0.8-log-unit improvement.
Our calculations showed a systematic error in our GAFF calculations but it is not clear that it has the same basis as the one for OPLS-AA. For OPLS-AA we can draw on other data for the hypothesis that water-solute interactions might be at the core of the problem. For GAFF we do not have the same data available but future analysis of our data in the context of other SAMPL6-logP submissions might indicate problematic areas. Nevertheless, the overall performance of GAFF, especially after equilibration, was reasonably good.
3.3.4. CGenFF
The compounds SM04, SM12 and SM16 contained halogens with lone pairs and could therefore not be processed with the cgenff_charmm2gmx.py script so that we were not able to obtain Gromacs CGenFF parameters (see Section 2.1). Hence we excluded these three compounds and only report results for the remaining eight compounds.
The CGenFF results were qualitatively different from the OPLS-AA and AMBER/GAFF results in almost all aspects: The RMSE was 1.17 ± 0.06 for the dry octanol and 1.42 ± 0.06 for wet octanol (Table 7), and removing the equilibration period showed no improvement. This behavior could indicate that the CGenFF simulations equilibrated faster or that the set-up protocol prepared them in a state closer resembling equilibrium. Either way, one of our lessons of this study is that careful analysis of convergence should be carried out regardless of the force field. In Figure 8, about half of the compounds were within one log unit, with the others off by 1 to 2.5 units. The Pearson correlation coefficients r for the dry and the wet calculations were 0.27 and 0.16. The dry octanol data yielded a Kendall rank correlation coefficient τ = 0.29, and the value for the wet octanol predictions was 0.07. These coefficients indicated a poor ability rank-ordering the data although eight samples might not be enough to obtain reasonable results from these correlation analysis tools. Different from previous results, no systematic shift in the CGenFF results was observed from the AUE (0.91 for dry and 1.05 for wet) and the absolute value of ME (−0.32 for dry and −0.10 for wet).
Table 7:
Computed (log Pow) and experimental octanol-water partition coefficients with error estimate for the CGenFF results processed with alchemlyb-MBAR. The same raw data processed with mdpow-TI (Simpson’s rule) were submitted as entry 3oqhx for Protocol Dry (protocol Wet was not submitted), see Table S7 in the Supplementary Information
| id | Exp. | Dry Octanol | Wet Octanol | ||
|---|---|---|---|---|---|
| log Pow | Δ | log Pow | Δ | ||
| SM02 | 4.09(3) | 2.74(20) | −1.35(20) | 3.39(19) | −0.70(19) |
| SM07 | 3.21(4) | 1.37(15) | −1.84(15) | 0.88(18) | −2.33(18) |
| SM08 | 3.1(3) | 5.19(21) | 2.09(21) | 5.69(19) | 2.59(19) |
| SM09 | 3.03(7) | 3.32(16) | 0.29(17) | 3.09(20) | 0.06(21) |
| SM11 | 2.1(4) | 1.95(20) | −0.15(20) | 3.14(17) | 1.04(17) |
| SM13 | 2.92(4) | 2.24(21) | −0.68(21) | 3.0(19) | 0.08(19) |
| SM14 | 1.95(3) | 1.9(23) | −0.05(23) | 1.92(21) | −0.03(21) |
| SM15 | 3.07(3) | 2.22(21) | −0.85(21) | 1.52(17) | −1.55(17) |
| RMS Error (RMSE) | 1.17(6) | 1.42(6) | |||
| Absolute Unsigned Error (AUE) | 0.91(6) | 1.05(6) | |||
| Mean Error (ME) | −0.32(6) | −0.10(6) | |||
Fig. 8:
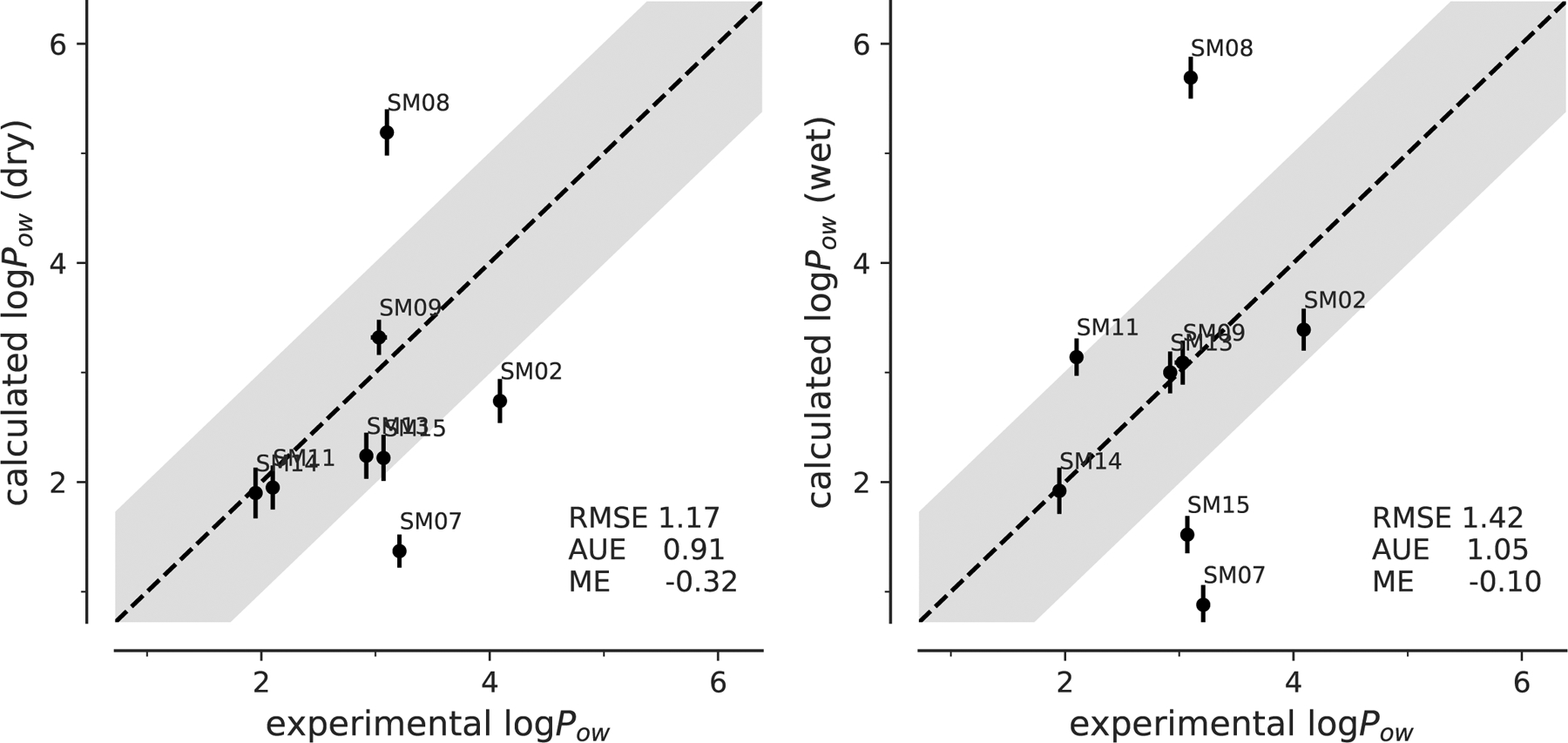
Correlation between experimental and computed octanol-water coefficients log Pow for simulations performed with dry or wet octanol with CGenFF parameters.
In terms of RMSE, the CGenFF parametrization produced the best result. This remained true when the RMSEs for the other three parametrizations were also only calculated for the eight compounds for which CGenFF data were available (Supplementary Table S8). However, eight data points might not be enough to properly assess the true accuracy, as indicated by the poor Pearson and Kendall coefficients.
It is encouraging that CGenFF did not exhibit an obvious systematic shift, which suggested that the observed shift for OPLS-AA and GAFF was not an inherent problem in our FEP protocol but was more closely tied to the specific force field implementation (including the water model). The use of different water models in simulations with OPLS-AA (TIP4P) on the one hand, and GAFF or CGenFF (TIP3P) on the other, could contribute to the differences that we observed in our predictions. As noted previously [52, 53], TIP3P has a lower dielectric constant than TIP4P and this could give rise to lower hydration free energies compared to TIP4P. More generally, the OPLS-AA and AMBER/GAFF (and to some degree CHARMM/CGenFF) force fields are known to be underpolarized [54, 55], which also leads to systematically too positive hydration free energies for small molecules [55].
3.4. Effect of tautomers
For SM08 we originally chose and submitted micro010 (SM08_10), based on the assumption that the aromaticity of the pyridine ring with the potential hydrogen bond of the hydroxyl with the carboxylate would make it the most stable one. However, contrary to our chemical intuition, the ground state energies from quantum chemical optimization calculations with the CPCM continuous water model [9] showed that micro011 (Figure 9) seemed to be the most stable (about 6 kcal/mol lower than micro010). In the same conditions, the zwitterionic micro008 (Figure 9) was about 3.5 kcal/mol more stable than micro010. We therefore also computed the octanol-water coefficients for micro008 (SM08_08) and micro011 (SM08_11) (Figure 9). The results in Table 8 indicated that the micro011 gave closer predictions to the experimental values for both dry and wet octanol with the four parametrization methods with a 0.2 to 1 log unit improvement in the RMSE, while were unable to reproduce the experimental values with micro008.
Fig. 9:
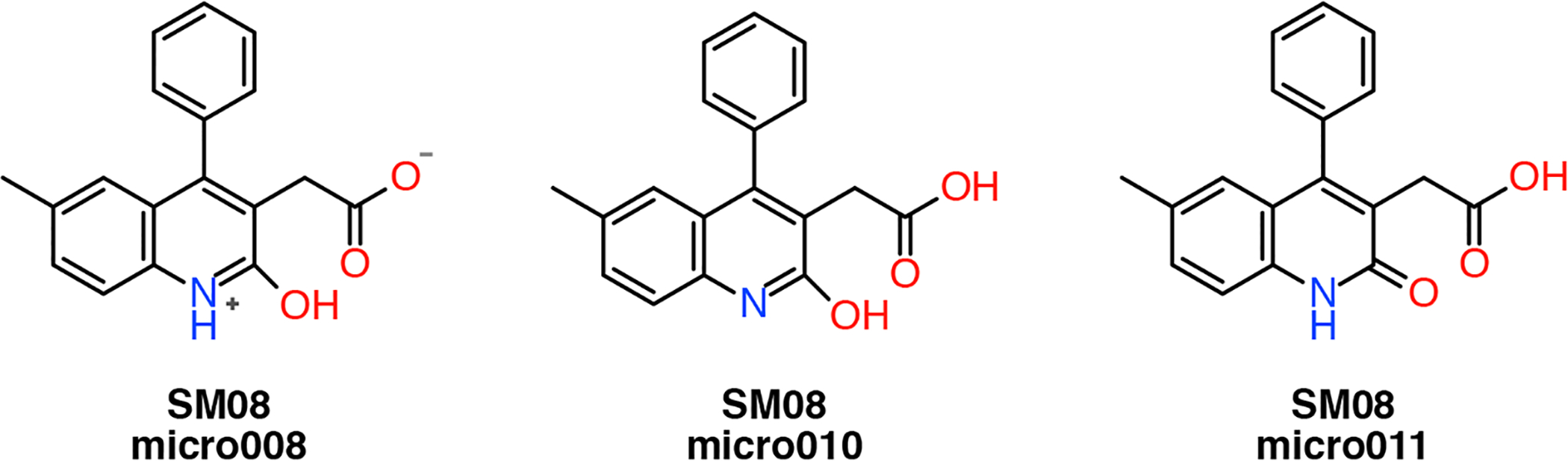
Chemical structures of the three microstates of compound SM08 evaluated in this study.
Table 8:
Computed (log Pow) and experimental octanol-water partition coefficients with error estimate for the three microstates of compound SM08.
| id | Exp. | Dry Octanol | Wet Octanol | Parametrization | ||
|---|---|---|---|---|---|---|
| log Pow | Δ | log Pow | Δ | |||
| SM08_08 | 3.1(3) | −1.8(83) | −4.90(83) | 1.0(56) | −2.10(56) | OPLS-AA |
| SM08_08 | 3.1(3) | 1.05(39) | −2.05(39) | 3.2(43) | 0.10(43) | LigParGen |
| SM08_08 | 3.1(3) | 4.31(44) | 1.21(44) | 4.64(32) | 1.54(32) | GAFF |
| SM08_08 | 3.1(3) | −0.78(85) | −3.88(85) | 1.6(43) | −1.50(43) | CGenFF |
| SM08_10 | 3.1(3) | 8.54(20) | 5.44(20) | 7.18(20) | 4.08(20) | OPLS-AA |
| SM08_10 | 3.1(3) | 5.15(20) | 2.05(20) | 5.45(22) | 2.35(22) | LigParGen |
| SM08_10 | 3.1(3) | 5.41(28) | 2.31(29) | 4.55(21) | 1.45(21) | GAFF |
| SM08_10 | 3.1(3) | 5.19(21) | 2.09(21) | 5.69(19) | 2.59(19) | CGenFF |
| SM08_11 | 3.1(3) | 6.58(21) | 3.48(21) | 6.55(23) | 3.45(23) | OPLS-AA |
| SM08_11 | 3.1(3) | 4.03(24) | 0.93(24) | 4.48(28) | 1.38(29) | LigParGen |
| SM08_11 | 3.1(3) | 3.53(39) | 0.43(39) | 5.01(17) | 1.91(17) | GAFF |
| SM08_11 | 3.1(3) | 4.11(33) | 1.01(33) | 5.59(21) | 2.49(21) | CGenFF |
These tautomer calculations indicated that the choice of tautomer could have a large effect on calculated log Pow values. However, from this single example it was not clear that the quantum chemical calculations in implicit solvent provided the correct free energy differences between tautomers that would allow one to calculate the proper statistical mechanical average over all tautomer free energies [9]. Clearly, more work is needed to establish a consistent protocol that takes all important tautomers into consideration.
4. Conclusions
We used explicit solvent all-atom MD simulations using four different force field parametrizations (standard OPLS-AA with transferable charges, OPLS-AA with non-transferable CM1A charges, AMBER/GAFF, and CHARMM/CGenFF) to predict water-octanol partition coefficients for the eleven compounds included in the SAMPL6-logP challenge. Force field parameters of the octanol solvent in OPLS-AA, GAFF and CHARMM were validated by comparing computed against experimental values, namely the density as a function of temperature, the hydration free energy, the chemical potential, and the octanol-water partition coefficient. The partition coefficients for the SAMPL6 logP compounds were calculated from the solvation free energy of compounds in water and pure (dry) octanol or wet octanol with 27 mol % water dissolved. We used 5-ns windowed alchemical free energy perturbation calculations to compute absolute solvation free energies with thermodynamic integration (TI) and the multistate Bennett acceptance ratio (MBAR) (from the alchemlyb library) with uncorrelated samples from the MD simulations.
An important lesson was that an initial equilibration period can have a negative effect on the accuracy and we introduced a new quantity, the equilibration ratio Ac, to assess equilibration of sets of alchemical λ windows. Discarding the first 1 ns of each 5-ns window as an equilibration phase improved the RMSE of the GAFF log Pow predictions by up to 0.8 log units. The improved accuracy was due to improved convergence in the Coulomb FEP windows with the octanol solvent. Equilibration (and sampling) of the octanol simulations appeared to be more demanding than the water simulations.
Overall, CGenFF gave the best prediction with RMSE 1.2 log units although only for a partial data set of eight compounds and with relatively low Pearson correlation coefficient. When considering all eleven compounds, GAFF gave a respectable RMSE of 1.5. The GAFF and OPLS-AA results displayed a systematic error where molecules were too hydrophobic whereas CGenFF appeared to be more balanced, at least on this small data set. For OPLS-AA this error is possibly related to undersolvation; for GAFF its origin remains speculative although both force fields are known to be underpolarized. Sufficient sampling appears to be especially important for the octanol simulations whereas the force field accuracy appears the remaining challenge for the hydration simulations. Thus, log P calculations represent a well-balanced challenge for moving the field of molecular simulations forward.
Supplementary Material
Acknowledgements
The authors would like to thank David L. Mobley and Teresa Danielle Bergazin for useful discussions and sharing unpublished data.
Research reported in this publication was supported by the National Institute Of General Medical Sciences of the National Institutes of Health under Awards Number R01GM118772 and R01GM125081. BII was supported in part by grants ANR-10-LABX-33 (LabEx LERMIT) and ANR-14-JAMR-0002-03 (JPIAMR) from the French National Research Agency (ANR), and by a grant DIM MAL-INF from the Région Ile-de-France.
Footnotes
Publisher's Disclaimer: This Author Accepted Manuscript is a PDF file of an unedited peer-reviewed manuscript that has been accepted for publication but has not been copyedited or corrected. The official version of record that is published in the journal is kept up to date and so may therefore differ from this version.
Contributor Information
Shujie Fan, Department of Physics, Arizona State University, P.O. Box 871504, Tempe, AZ 85287-1504, USA.
Bogdan I. Iorga, Institut de Chimie des Substances Naturelles, CNRS UPR 2301, Université Paris-Saclay, Labex LERMIT, 1 Avenue de la Terrasse, 91198 Gif-sur-Yvette, France
Oliver Beckstein, Department of Physics and Center for Biological Physics, Arizona State University, P.O. Box 871504, Tempe, AZ 85287-1504, USA.
References
- 1.Kramer W (2011) Transporters, Trojan horses and therapeutics: suitability of bile acid and peptide transporters for drug delivery. Biol Chem 392(1–2):77–94, DOI 10.1515/BC.2011.017 [DOI] [PubMed] [Google Scholar]
- 2.Leeson PD, Springthorpe B (2007) The influence of drug-like concepts on decision-making in medicinal chemistry. Nat Rev Drug Discov 6(11):881–90, DOI 10.1038/nrd2445 [DOI] [PubMed] [Google Scholar]
- 3.Lipinski CA, Lombardo F, Dominy BW, Feeney PJ (1997) Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings. Advanced Drug Delivery Reviews 23(1):3–25.1, DOI 10.1016/S0169-409X(96)00423-1 [DOI] [PubMed] [Google Scholar]
- 4.Bannan CC, Burley KH, Chiu M, Shirts MR, Gilson MK, Mobley DL (2016) Blind prediction of cyclohexane–water distribution coefficients from the SAMPL5 challenge. Journal of Computer-Aided Molecular Design 30(11):927–944, DOI 10.1007/s10822-016-9954-8, URL 10.1007/s10822-016-9954-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Işık M, Levorse D, Mobley DL, Rhodes T, Chodera JD (2020) Octanol-water partition coefficient measurements for the SAMPL6 blind prediction challenge. J Comput Aided Mol Des. 34(4): 405–420, DOI 10.1007/s10822-019-00271-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Beckstein O, Iorga BI (2012) Prediction of hydration free energies for aliphatic and aromatic chloro derivatives using molecular dynamics simulations with the OPLS-AA force field. J Comput Aided Mol Des 26(5):635–645, DOI 10.1007/s10822-011-9527-9 [DOI] [PubMed] [Google Scholar]
- 7.Beckstein O, Fourrier A, Iorga BI (2014) Prediction of hydration free energies for the SAMPL4 diverse set of compounds using molecular dynamics simulations with the OPLS-AA force field. J Comput Aided Mol Des 28(3):265–276, DOI 10.1007/s10822-014-9727-1 [DOI] [PubMed] [Google Scholar]
- 8.Kenney IM, Beckstein O, Iorga BI (2016) Prediction of cyclohexane-water distribution coefficients for the SAMPL5 data set using molecular dynamics simulations with the OPLS-AA force field. J Comput Aided Mol Des 30(11):1045–1058, DOI 10.1007/s10822-016-9949-5 [DOI] [PubMed] [Google Scholar]
- 9.Selwa E, Kenney IM, Beckstein O, Iorga BI (2018) SAMPL6: calculation of macroscopic pKa values from ab initio quantum mechanical free energies. Journal of Computer-Aided Molecular Design 32(10):1203–1216, DOI 10.1007/s10822-018-0138-6, URL http://link.springer.com/10.1007/s10822-018-0138-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.IŞlk M, Levorse D, Rustenburg AS, Ndukwe IE, Wang H, Wang X, Reibarkh M,Martin GE, Makarov AA, Mobley DL, Rhodes T, Chodera JD (2018) pKa measurements for the SAMPL6 prediction challenge for a set of kinase inhibitor-like fragments. J Comput Aided Mol Des 32(10):1117–1138, DOI 10.1007/s10822018-0168-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, Nakatsuji H, Caricato M, Li X, Hratchian HP, Izmaylov AF, Bloino J, Zheng G, Sonnenberg JL, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Vreven T, Montgomery JA Jr, Peralta JE, Ogliaro F, Bearpark M, Heyd JJ, Brothers E, Kudin KN, Staroverov VN, Kobayashi R, Normand J, Raghavachari K, Rendell A, Burant JC, Iyengar SS, Tomasi J, Cossi M, Rega N, Millam JM, Klene M, Knox JE, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Martin RL, Morokuma K, Zakrzewski VG, Voth GA, Salvador P, Dannenberg JJ, Dapprich S, Daniels AD, Farkas O, Foresman JB, Ortiz JV, Cioslowski J, Fox DJ (2009) Gaussian 09 Revision D.01. Gaussian Inc. Wallingford CT [Google Scholar]
- 12.Kaminski G, Duffy E, Matsui T, Jorgensen W (1994) Free energies of hydration and pure liquid properties of hydrocarbons from the OPLS all-atom model. J Phys Chem 98(49):13,077–13,082, DOI 10.1021/j100100a043 [DOI] [Google Scholar]
- 13.Jorgensen WL, Maxwell DS, Tirado-Rives J (1996) Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J Am Chem Soc 118(45):11,225–11,236, DOI 10.1021/ja9621760 [DOI] [Google Scholar]
- 14.Damm W, Frontera A, Tirado-Rives J, Jorgensen W (1997) OPLS all-atom force field for carbohydrates. J Comput Chem 18(16):1955–1970, DOI [DOI] [Google Scholar]
- 15.Jorgensen WL, McDonald NA (1998) Development of an all-atom force field for heterocycles. Properties of liquid pyridine and diazenes. J Mol Struct THEOCHEM 424(1–2):145–155, DOI 10.1016/S0166-1280(97)00237-6 [DOI] [Google Scholar]
- 16.McDonald NA, Jorgensen WL (1998) Development of an all-atom force field for heterocycles. Properties of liquid pyrrole, furan, diazoles, and oxazoles. J Phys Chem B 102(41):8049–8059, DOI 10.1021/jp981200o [DOI] [Google Scholar]
- 17.Rizzo RC, Jorgensen WL (1999) OPLS all-atom model for amines: Resolution of the amine hydration problem. J Am Chem Soc 121(20):4827–4836, DOI 10.1021/ja984106u [DOI] [Google Scholar]
- 18.Kaminski GA, Friesner RA, Tirado-Rives J, Jorgensen WL (2001) Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J Phys Chem B 105(28):6474–6487, DOI 10.1021/jp003919d [DOI] [Google Scholar]
- 19.Dodda LS, Cabeza de Vaca I, Tirado-Rives J, Jorgensen WL (2017) LigParGen web server: an automatic OPLS-AA parameter generator for organic ligands. Nucleic Acids Res 45(W1):W331–W336, DOI 10.1093/nar/gkx312 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Vanommeslaeghe K, Hatcher E, Acharya C, Kundu S, Zhong S, Shim J, Darian E, Guvench O, Lopes P, Vorobyov I, Mackerell AD Jr (2010) CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J Comput Chem 31(4):671–90, DOI 10.1002/jcc.21367 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Vanommeslaeghe K, Raman EP, MacKerell AD (2012) Automation of the CHARMM General Force Field (CGenFF) II: Assignment of bonded parameters and partial atomic charges. Journal of Chemical Information and Modeling 52(12):3155–3168, DOI 10.1021/ci3003649, URL http://pubs.acs.org/doi/abs/10.1021/ci3003649, http://pubs.acs.org/doi/pdf/10.1021/ci3003649 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Vanommeslaeghe K, MacKerell AD (2012) Automation of the CHARMM General Force Field (CGenFF) I: bond perception and atom typing. Journal of Chemical Information and Modeling 52(12):3144–3154, DOI 10.1021/ci300363c, URL http://pubs.acs.org/doi/abs/10.1021/ci300363c, http://pubs.acs.org/doi/pdf/10.1021/ci300363c [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Soteras Gutiérrez I, Lin FY, Vanommeslaeghe K, Lemkul JA, Armacost KA, Brooks CL, MacKerell AD (2016) Parametrization of Halogen Bonds in the CHARMM General Force Field: Improved treatment of ligand-protein interactions. Bioorganic & medicinal chemistry 24(20):4812–4825, DOI 10.1016/j.bmc.2016.06.034, URL https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5053860/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wang J, Wolf RM, Caldwell JW, Kollman PA, Case DA (2004) Development and testing of a general AMBER force field. J Comput Chem 25(9):1157–74, DOI 10.1002/jcc.20035 [DOI] [PubMed] [Google Scholar]
- 25.Sousa da Silva AW, Vranken WF (2012) ACPYPE - AnteChamber Python Parser interfacE. BMC Res Notes 5:367, DOI 10.1186/1756-0500-5-367 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML (1983) Comparison of simple potential functions for simulating liquid water. J Chem Phys 79(2):926–935, DOI 10.1063/1.445869 [DOI] [Google Scholar]
- 27.Huang J, MacKerell AD Jr (2013) CHARMM36 all-atom additive proteinforce field: validation based on comparison to NMR data. J Comput Chem 34(25):2135–45, DOI 10.1002/jcc.23354 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Maier JA, Martinez C, Kasavajhala K, Wickstrom L, Hauser KE, Simmerling C (2015) ff14SB: Improving the accuracy of protein side chain and backbone parameters from ff99SB. J Chem Theory Comput 11(8):3696–713, DOI 10.1021/acs.jctc.5b00255 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Price DJ, Brooks CL 3rd (2004) A modified TIP3P water potential for simulation with Ewald summation. J Chem Phys 121(20):10,096–103, DOI 10.1063/1.1808117 [DOI] [PubMed] [Google Scholar]
- 30.Šegatin N, Klofutar C (2004) Thermodynamics of the Solubility of Water in 1-Hexanol, 1-Octanol, 1-Decanol, and Cyclohexanol. Monatshefte für Chemie / Chemical Monthly 135(3):241–248, DOI 10.1007/s00706-003-0053-x, URL 10.1007/s00706-003-0053-x [DOI] [Google Scholar]
- 31.Lang BE (2012) Solubility of Water in Octan-1-ol from (275 to 369) K. Journal ofChemical & Engineering Data 57(8):2221–2226, DOI 10.1021/je3001427, URL 10.1021/je3001427 [DOI] [Google Scholar]
- 32.Cumming H, Rücker C (2017) Octanol–Water Partition Coefficient Measurementby a Simple 1H NMR Method. ACS Omega 2(9):6244–6249, DOI 10.1021/acsomega.7b01102, URL 10.1021/acsomega.7b01102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kenney IM, Beckstein O, Iorga BI (2016) Prediction of cyclohexane-water distribution coefficients for the SAMPL5 data set using molecular dynamics simulations with the OPLS-AA force field. Journal of Computer-Aided Molecular Design 30(11):1045–1058, DOI 10.1007/s10822-016-9949-5, URL http://link.springer.com/10.1007/s10822-016-9949-5 [DOI] [PubMed] [Google Scholar]
- 34.Abraham MJ, Murtola T, Schulz R, Páll S, Smith JC, Hess B, Lindahl E (2015) GROMACS: High performance molecular simulations through multilevel parallelism from laptops to supercomputers. SoftwareX 1–2:19–25, DOI 10.1016/j.softx.2015.06.001 [DOI] [Google Scholar]
- 35.Shirts MR, Chodera JD (2008) Statistically optimal analysis of samples from multiple equilibrium states. J Chem Phys 129(12):124,105, DOI 10.1063/1.2978177, URL https://aip.scitation.org/doi/10.1063/1.2978177 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Dotson D, Beckstein O, Wille D, Kenney I, shuail, trje3733, Lee H, Lim V, brycestx, Barhaghi MS (2019) alchemistry/alchemlyb: 0.3.0. Software, DOI 10.5281/zenodo.3361016, URL 10.5281/zenodo.3361016 [DOI] [Google Scholar]
- 37.Mobley DL, Dumont E, Chodera JD, Dill KA (2007) Comparison of charge models for fixed-charge force fields: Small-molecule hydration free energies in explicit solvent. J Phys Chem B 111(9):2242–2254, DOI 10.1021/jp0667442 [DOI] [PubMed] [Google Scholar]
- 38.Parrinello M, Rahman A (1981) Polymorphic transitions in single crystals: A new molecular dynamics method. J Appl Phys 52(12):7182–7190, DOI 10.1063/1.328693, URL http://link.aip.org/link/?JAP/52/7182/1 [DOI] [Google Scholar]
- 39.Shirts MR, Pitera JW, Swope WC, Pande VS (2003) Extremely precise free energy calculations of amino acid side chain analogs: Comparison of common molecular mechanics force fields for proteins. J Chem Phys 119(11):5740–5761, DOI 10.1063/1.1587119 [DOI] [Google Scholar]
- 40.Essman U, Perela L, Berkowitz ML, Darden T, Lee H, Pedersen LG (1995) A smooth particle mesh Ewald method. J Chem Phys 103:8577–8592, DOI 10.1063/1.470117 [DOI] [Google Scholar]
- 41.Hess B (2008) P-LINCS: A parallel linear constraint solver for molecular simulation. J Chem Theory Comput 4(1):116–122, DOI 10.1021/ct700200b [DOI] [PubMed] [Google Scholar]
- 42.Hess B, Kutzner C, van der Spoel D, Lindahl E (2008) GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J Chem Theory Comput 4(3):435–447, DOI 10.1021/ct700301q [DOI] [PubMed] [Google Scholar]
- 43.Páll S, Abraham MJ, Kutzner C, Hess B, Lindahl E (2015) Tackling exascale software challenges in molecular dynamics simulations with GROMACS In: Markidis S, Laure E (eds) Solving Software Challenges for Exascale: International Conference on Exascale Applications and Software, EASC 2014, Stockholm, Sweden, April 2–3, 2014, Revised Selected Papers, Lecture Notes in Computer Science, vol 8759, Springer International Publishing, Switzerland, pp 3–27, DOI 10.1007/978-3-319-15976-8_1 [DOI] [Google Scholar]
- 44.Klimovich PV, Shirts MR, Mobley DL (2015) Guidelines for the analysis of free energy calculations. J Comput Aided Mol Des 29(5):397–411, DOI 10.1007/s10822-015-9840-9, URL http://link.springer.com/10.1007/s10822-015-9840-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Chodera JD (2016) A simple method for automated equilibration detection in molecular simulations. J Chem Theory Comput 12(4):1799–1805, DOI 10.1021/acs.jctc.5b00784, URL https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4945107/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Jorge M, Garrido N, Queimada A, Economou I, Macedo E (2010) Effect of the integration method on the accuracy and computational efficiency of free energy calculations using thermodynamic integration. J Chem Theory Comput 6(4):1018–1027, DOI 10.1021/ct900661c20467461 [DOI] [Google Scholar]
- 47.Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, Burovski E, Peterson P, Weckesser W, Bright J, van der Walt SJ, Brett M, Wilson J, Millman KJ, Mayorov N, Nelson ARJ, Jones E, Kern R, Larson E, Carey CJ, Polat I, Feng Y, Moore EW, VanderPlas J, Laxalde D, Perktold J, Cimrman R, Henriksen I, Quintero EA, Harris CR, Archibald AM, Ribeiro AH, Pedregosa F, van Mulbregt P, and SciPy Contributors (2020) “SciPy 1.0: fundamental algorithms for scientific computing in Python,” Nature Methods 17(3): 261–272, DOI 10.1038/s41592-019-0686-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Faber NKM (1999) Estimating the uncertainty in estimates of root mean square error of prediction: application to determining the size of an adequate test set in multivariate calibration. Chemometrics and Intelligent Laboratory Systems 49(1):79–89, DOI 10.1016/S0169-7439(99)00027-1 [DOI] [Google Scholar]
- 49.Zangi R (2018) Refinement of the OPLSAA Force-Field for Liquid Alcohols. ACS Omega 3(12):18,089–18,099, DOI 10.1021/acsomega.8b03132, URL 10.1021/acsomega.8b03132 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Işık M, Bergazin TD, Fox T, Rizzi A, Chodera JD, Mobley DL (2020) Assessing the accuracy of octanol-water partition coefficient predictions in the SAMPL6 Part II log P challenge. J Comput Aided Mol Des 34(4): 335–370, DOI 10.1007/s10822-020-00295-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Yang W, Bitetti-Putzer R, Karplus M (2004) Free energy simulations: Use of reverse cumulative averaging to determine the equilibrated region and the time required for convergence. J Chem Phys 120(6):2618–2628, DOI 10.1063/1.1638996, URL https://aip.scitation.org/doi/abs/10.1063/1.1638996 [DOI] [PubMed] [Google Scholar]
- 52.Paranahewage SS, Gierhart CS, Fennell CJ (2016) Predicting water-to-cyclohexane partitioning of the SAMPL5 molecules using dielectric balancing of force fields. Journal of Computer-Aided Molecular Design 30(11):1059–1065, DOI 10.1007/s10822-016-9950-z, URL 10.1007/s10822-016-9950-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Brini E, Fennell CJ, Fernandez-Serra M, Hribar-Lee B, Lukšič M, Dill KA (2017) How water’s properties are encoded in its molecular structure and energies. Chemical Reviews 117(19):12,385–12,414, DOI 10.1021/acs.chemrev.7b00259, URL 10.1021/acs.chemrev.7b00259 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Swope WC, Horn HW, Rice JE (2010) Accounting for polarization cost when using fixed charge force fields. II. Method and application for computing effect of polarization cost on free energy of hydration. The Journal of Physical Chemistry B 114(26):8631–8645, DOI 10.1021/jp911701h [DOI] [PubMed] [Google Scholar]
- 55.Lundborg M, Lindahl E (2015) Automatic gromacs topology generation and comparisons of force fields for solvation free energy calculations. J Phys Chem B 119(3):810–23, DOI 10.1021/jp505332p [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


