Acidity and nucleophilic reactivity of glutathione persulfide

Abstract

Persulfides (RSSH/RSS⁻) participate in sulfur trafficking and metabolic processes, and are proposed to mediate the signaling effects of hydrogen sulfide (H₂S). Despite their growing relevance, their chemical properties are poorly understood. Herein, we studied experimentally and computationally the formation, acidity, and nucleophilicity of glutathione persulfide (GSSH/GSS⁻), the derivative of the abundant cellular thiol glutathione (GSH). We characterized the kinetics and equilibrium of GSSH formation from glutathione disulfide and H₂S. A pK_a of 5.45 for GSSH was determined, which is 3.49 units below that of GSH. The reactions of GSSH with the physiologically relevant electrophiles peroxynitrite and hydrogen peroxide, and with the probe monobromobimane, were studied and compared with those of thiols. These reactions occurred through S_N2 mechanisms. At neutral pH, GSSH reacted faster than GSH because of increased availability of the anion and, depending on the electrophile, increased reactivity. In addition, GSS⁻ presented higher nucleophilicity with respect to a thiolate with similar basicity. This can be interpreted in terms of the so-called α effect, i.e. the increased reactivity of a nucleophile when the atom adjacent to the nucleophilic atom has high electron density. The magnitude of the α effect correlated with the Brønsted nucleophilic factor, β_nuc, for the reactions with thiolates and with the ability of the leaving group. Our study constitutes the first determination of the pK_a of a biological persulfide and the first examination of the α effect in sulfur nucleophiles, and sheds light on the chemical basis of the biological properties of persulfides.

Persulfides (RSSH/RSS⁻)⁷ can be formed in biological systems through several pathways, some of which are dependent on hydrogen sulfide (H₂S/HS⁻)⁸. Beyond its toxicity, H₂S exerts physiological effects with potential health benefits in mammals. Persulfides have been proposed to transduce these effects; the modification of critical protein thiols (RSH/RS⁻) to persulfides would unleash downstream effects of H₂S (1). In addition, persulfides are intermediates in the biosynthesis of iron-sulfur clusters and other cofactors (2). They also constitute intermediates in the mitochondrial oxidation of H₂S (1).

Persulfides can be formed in vivo via reactions of H₂S with oxidized thiol derivatives, i.e. disulfides (RSSR′) or sulfenic acids (RSOH) (3), via reactions of thiolates with oxidized sulfur derivatives, e.g. polysulfides (HS_nS⁻, n ≥ 1) (4), and via free radical–mediated processes (5). Note that H₂S and thiols do not react directly with each other. H₂S-independent pathways for persulfide synthesis also exist, in which the sulfur is donated by thiols or disulfides (6–9). Moreover, there are enzymes capable of producing, transferring, and reacting with persulfides. Sulfide quinone oxidoreductase (SQOR) catalyzes the oxidation of H₂S to glutathione persulfide (GSSH), the persulfide derivative of the very abundant cellular thiol glutathione (GSH), and reduces ubiquinone (10–12). GSSH is the substrate of persulfide dioxygenase (also called ETHE1) (10, 13), an enzyme that oxidizes GSSH to sulfite (SO₃²⁻) at the expense of O₂ and whose inborn errors are associated with severe clinical conditions (14). Rhodanese can catalyze the reversible reaction between GSSH and sulfite to form GSH and thiosulfate (10, 12, 15). These processes suggest that GSSH plays key roles in vivo; indeed, concentrations of ∼35 pmol/mg protein (∼7 μm) in mouse liver tissue have been recently reported (16). Despite the growing interest in persulfides, their chemical characteristics are poorly understood.

Hydropersulfides (RSSH) ionize in water to form deprotonated persulfides (RSS⁻). Compared with thiols, a higher acidity is expected for persulfides (1). In fact, the pK_a of 2-[(3-aminopropyl)amino]ethane persulfide was estimated to be 6.2 ± 0.1, which is lower than the pK_a of 7.6 ± 0.1 determined for the corresponding thiol (17). The pK_a of cumyl persulfide was proposed to be 7 (18), whereas the pK_a of cumyl thiol is likely to be higher than 10 according to the values for similar thiols (19). The pK_a of cysteine persulfide was computationally estimated to be ∼4 units lower than that of the cysteine thiol (3).

In contrast to thiols, which possess only nucleophilic character, persulfides also have electrophilic character when protonated. The electrophilicity can be ascribed to both sulfur atoms. If the outer sulfur is attacked by a thiolate, the sulfur is transferred and a new persulfide is formed, constituting a transpersulfidation reaction. If the inner sulfur is attacked, H₂S is released and a mixed disulfide is formed.

Persulfides have been proposed to be stronger nucleophiles than thiolates. Enhanced reactivities were observed for arylpersulfides compared with arylthiolates toward alkyl halides in organic solvent (20). Enhanced reactivities were also observed for the persulfides formed in albumin and in the Mycobacterium tuberculosis peroxiredoxin AhpE toward 4,4′-dithiodipyridine compared with the corresponding protein thiols (3, 21). In addition, under certain conditions, GSSH reacted with H₂O₂ whereas GSH did not (7), and persulfide reactions with one-electron oxidants were faster than those of thiols (18, 22). The high nucleophilicity of persulfides can be understood in terms of the so-called α effect (3, 20, 23, 24). The α effect was first defined as the enhancement of nucleophilicity when the atom adjacent to a nucleophile bears a lone pair of electrons (25). This definition is ambiguous because the α nucleophile can be compared either with a structural analog (e.g. HOO⁻ and HO⁻, NH₂-NH₂ and NH₃, and RSS⁻ and RS⁻) or with a nucleophile of equal basicity, in the context that for several reactions nucleophilicity correlates with Brønsted basicity. Given that the α nucleophile is not always more reactive than the structural analog (26), the α effect is more accurately defined as the positive deviation from the corresponding Brønsted plot (log k versus nucleophile pK_a) (27, 28). For this definition to be valid, the α and reference nucleophiles should react by similar mechanisms (29).

Because of their dual nucleophilic and electrophilic character, persulfides decay in aqueous solution, making their preparation and quantification challenging. Many methods for persulfide determination are either indirect, slow, or unspecific (1). The direct detection by MS is inconvenient because of their instability. Thus, derivatization with different alkylating agents, e.g. iodoacetamide, N-ethylmaleimide, or monobromobimane (mBrB) (7, 23, 30, 31), has become a common practice in which the rate of the alkylation step is crucial (30).

The reaction between glutathione disulfide (GSSG) and H₂S forms GSSH and GSH in a reversible process (3, 23, 32). This reaction is often used to prepare GSSH in vitro (13, 23, 31), and sometimes the concentration of the formed GSSH is estimated from that of the produced GSH or from the initial reactants, assuming stoichiometric relations. Nevertheless, because of the reactivity of persulfides, subsequent reactions are likely to happen and affect the yield, calling for a better characterization of the mixtures.

Considering that persulfides are involved in biosynthesis and catabolism, and that they play roles in cellular signaling, it is important to better understand their chemical properties. Herein, we studied the formation, acidity, and nucleophilicity of GSSH. A method to quantify GSSH was adapted and subsequently employed to characterize the reaction between GSSG and H₂S, providing kinetic and equilibrium constants. The pK_a of GSSH was determined, representing the first pK_a report for a persulfide formed in biological systems. The nucleophilicity of GSSH toward mBrB, peroxynitrite (ONOOH/ONOO⁻)⁹, and H₂O₂ was investigated. These electrophiles were chosen because there is information available for their reactions with thiols, enabling comparison. In addition, mBrB facilitates monitoring of the reactions by fluorescence, whereas peroxynitrite and H₂O₂ are biologically relevant oxidants. To understand the molecular basis of the differential reactivity, we performed hybrid quantum-classical (quantum mechanics/molecular mechanics, QM/MM) calculations for the model pair methanethiolate/methanepersulfide anion (MeS⁻/MeSS⁻) toward the same electrophiles. Our results provide the first quantitative study of the nucleophilicity of a persulfide and its comparison with thiols. This constitutes, to our knowledge, the first examination of the α effect in sulfur nucleophiles.

Results and discussion

Quantification of GSSH

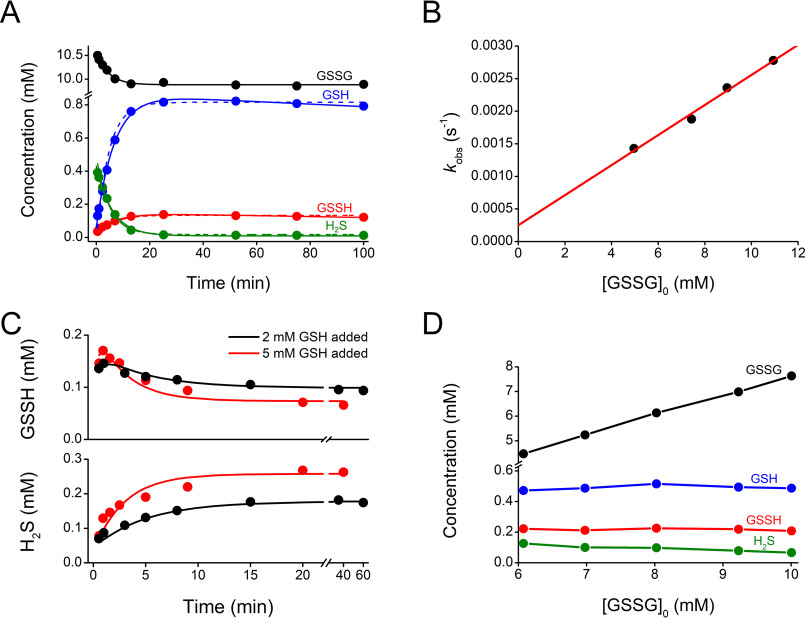
A reversed-phase HPLC method based on mBrB derivatization (7, 33–35) was adapted to quantify GSSH in a mixture of species. GSSG and H₂S reacted to form GSH and GSSH, and excess mBrB was added to label H₂S, GSH, and GSSH as the derivatized species B-S-B, GS-B, and GSS-B, respectively (Fig. 1A). A peak with a retention time of 7.7 min was ascribed to GSS-B because it disappeared in the presence of the reductant tris(2-carboxyethyl)phosphine (TCEP), and when more mBrB was added, GS-B and B-S-B increased. The peaks corresponding to GSSG, GS-B, and B-S-B were assigned using standards (retention times of 5.8, 7.3, and 9.8 min, respectively) (Fig. 1B). The identities of the four species were confirmed by electrospray ionization MS and MS/MS; the results for GS-B and GSS-B were consistent with a mass increase of 32 Da for the latter (Fig. 1C). Calibration curves at 260 nm for GSSG and at 396 nm for GS-B and B-S-B were performed. Considering that GSS-B and GS-B have the same absorptivity at 396 nm because of the bimane moiety, the calibration curve for GS-B was used to quantify GSS-B.

Figure 1.

Derivatization with mBrB and characterization of chromatographic peaks. A, reactions of GSH, GSSH, and H₂S with mBrB to form GS-B, GSS-B, and B-S-B, respectively. B, representative HPLC runs of 1) mBrB (2 mm), 2) GS-B (0.2 mm), 3) GSSG (1 mm), 4) B-S-B (0.2 mm), 5) mixture of GSSG and H₂S (3 mm each, 20 min) diluted 15-fold and incubated with mBrB (2 mm), 6) reduction of 5 with TCEP (4.5 mm), and 7) addition of mBrB (6.9 mm) to 6. Reactions were done in phosphate buffer (0.1 m, pH 7.4, 25 °C). All chromatograms were recorded at 396 nm, except 3 (GSSG) at 260 nm. C, mass spectra and fragmentation patterns of the fractions eluting at 7.3 (GS-B, m/z 498.2) and 7.7 min (GSS-B, m/z 530.1). The product ions of GS-B are ascribable to neutral loss of NH₃ and HCOOH (435.1), minus glycine (360.1), or minus a sulfur-bimane derivative (211.0), loss of glutamate (369.1), and formation of the sulfur-bimane derivative (223.0 and 225.0). The fragmentation pattern of GSS-B showed peaks analogous to GS-B plus 32 (sulfur atom), assigned to the loss of NH₃ and HCOOH (467.1), minus glycine (392.0), or minus the sulfur-bimane derivative (243.0), loss of glutamate (401.1), and the formation of the sulfur-bimane derivative (223.0). The peak at m/z 339.1 could correspond to the protonated homolysis product GSS^•. Fragments of m/z 192 were assigned to the bimane protonated radical as previously observed (7, 30, 36).

To measure accurate concentrations, the derivatization step must be faster than the interconversion of species (30). Because reaction rates are the products of rate constants and concentrations, it can be calculated that labeling was ≥100-fold faster than interconversion in our conditions (3, 30, 35–38). Indeed, the detected concentrations of GSH and GSSH were independent of the amount of mBrB applied (Fig. S1). Furthermore, GSS-B was relatively stable and its decay within 100 min was minor (Fig. S2). In summary, under the conditions employed herein, the concentration of the derivatives represent those present in the original mixtures.

Kinetics and thermodynamics of the reaction of GSSG with H₂S

Given the feasibility of quantifying GSSG, GSH, GSSH, and H₂S, we first studied the kinetics of the reaction of GSSG and H₂S (Reaction 1).

$$\text{GSSG}+{\text{H}}_{\text{2}}\text{S}\hspace{0.17em}\begin{array}{c}{k}_{\text{1}}\\ \text{⇌}\\ k_{\text{-1}}\end{array}\hspace{0.17em}\text{GSH}+\text{GSSH}\hspace{0.17em}$$

Reaction 1

GSSG (5–11 mm) was incubated with H₂S (0.5 mm), and the reactions were stopped at different times by dilution and derivatization with mBrB. Time courses were obtained, and a second-order forward rate constant (k_1,pH) of 0.23 ± 0.02 m⁻¹ s⁻¹ (pH 7.46, 24 °C) was determined from H₂S decay (Fig. 2, A and B). This is in agreement with the reported value of 0.16 ± 0.01 M⁻¹ s⁻¹ (pH 7.4, 25 °C) previously determined by the methylene blue method (3).

Figure 2.

Kinetics and thermodynamics of the reaction of GSSG and H₂S to give GSH and GSSH. A, time courses of the reaction between GSSG (11 mm) and H₂S (0.5 mm) in phosphate buffer (0.1 m, pH 7.4, 25 ± 1 °C). Solid lines represent the fitted single exponential or exponential plus linear functions. The rate constants of a model consisting of Reactions 1 and 2 were estimated with COPASI using four independent experiments, obtaining k_1,pH = 0.33 ± 0.01, k_−1,pH = 0.51 ± 0.08, k_2,pH = 1.6 ± 0.3, and k_−2,pH = 9 ± 2 M⁻¹ s⁻¹. Dashed lines represent simulated time courses for a representative experiment. B, exponential rate constants (k_obs) of H₂S decay versus initial GSSG. The k_1,pH obtained from the fit of four independent experiments was 0.23 ± 0.02 m⁻¹ s⁻¹ (pH 7.46 $\text{±}$ 0.01, 24 °C). C, mixtures of GSSG (5 mm) and H₂S (0.5 mm), preincubated for 1 h in the mentioned buffer, were exposed to 2–12.5 mm GSH, and the reactions were followed by derivatization and HPLC (pH 7.28 $\text{±}$ 0.05, 25 °C). Using eight independent experiments, COPASI simulations in which k_1,pH was fixed to 0.23 m⁻¹ s⁻¹, and initial concentrations of GSSG, GSSH, and H₂S were 3.7 mm, 90 µm, and 50 µm, respectively, according to HPLC quantification, yielded k_−1,pH = 1.11 ± 0.06, k_2,pH = 2.3 ± 0.5, k_−2,pH = 3.1 ± 0.4 m⁻¹ s⁻¹, and [GSSSG]₀ = 0.27 ± 0.01 mm. Solid lines represent simulated time courses for two representative experiments. D, equilibrium concentrations. GSSG (6–10 mm) and H₂S (0.5 mm) were incubated in the mentioned buffer under shaking. After 2 h, 4 mm mBrB was added and the GSSH-containing mixtures were analyzed by HPLC. The apparent equilibrium constant of Reaction 1 obtained from six independent determinations was 0.194 ± 0.005 (mean ± S.D., pH 7.4, 25 °C.).

The final concentration of GSSH was always lower than that of GSH. Furthermore, the final concentration of GSSH was lower than the initial concentration of H₂S (the limiting reagent) whereas that of GSH was higher (Fig. 2A). Considering that GSSG was in excess, it is proposed that GSSH and GSSG reacted in a second relatively fast reaction to form glutathione trisulfide (GSSSG) and GSH (Reaction 2).

$$\text{GSSH}+\text{GSSG}\hspace{0.17em}\begin{array}{c}{k}_{\text{2}}\\ \text{⇌}\\ k_{-2}\end{array}\hspace{0.17em}\text{GSH}+\text{GSSSG}$$

Reaction 2

Accordingly, MS analysis of a mixture of excess GSSG and H₂S derivatized with iodoacetamide presented a peak with a m/z of 645.1, consistent with GSSSG (not shown). This is in agreement with previous reports where the corresponding trisulfides were observed (30, 39). The low sensitivity at 260 nm might have precluded the chromatographic detection of GSSSG. In addition, GSSSG was unlikely to co-elute with the characterized species, because it was not detected in the mass spectra of the chromatogram peaks but appeared in the mass spectrum of the whole mixture.

Rate constants were estimated with the software COPASI (40) using a model consisting of Reactions 1 and 2 and four independent sets of time courses of GSSH, GSH, and H₂S. Values of k_1,pH = 0.33 ± 0.01, k_−1,pH = 0.51 ± 0.08, k_2,pH = 1.6 ± 0.3, and k_−2,pH = 9 ± 2 m⁻¹ s⁻¹ were obtained (Fig. 2A). The value of k_1,pH was consistent with that obtained from H₂S decay (0.23 m⁻¹ s⁻¹, Fig. 2B).

Regarding the physiological relevance of the reaction between GSSG and H₂S, and considering the relatively low rate constant (0.23 m⁻¹ s⁻¹) and concentration of GSSG in vivo (<5 μm in cytosol of yeast (41, 42)), it can be concluded that GSSG is unlikely to constitute a major consumer of H₂S compared with preferential targets. Among the preferential targets of H₂S, SQOR deserves special mention because, in addition to reacting very fast with H₂S (k_cat/K_m,H2S = 1.1 × 10⁷ m⁻¹ s⁻¹, pH 7.4), it can form GSSH as product (11, 12).

To obtain a better estimate of the kinetics of the reverse Reaction 1, GSH (2–12.5 mm) was added to a mixture of GSSG and H₂S (pH 7.28, 25 °C) that had been preincubated for 1 h. At consecutive times, aliquots were analyzed. GSSH time courses showed a fast increase followed by a slower decrease, whereas H₂S increased (Fig. 2C). This is consistent with Reactions 1 and 2, whereby GSSH is rapidly formed by GSH and GSSSG (reverse Reaction 2) and consumed by GSH forming H₂S and GSSG in a slower process (reverse Reaction 1). Because both reactions are reversible, GSSH was not completely consumed. Eight independent time courses of GSSH and H₂S were analyzed with COPASI (40) according to a model consisting of Reactions 1 and 2, yielding k_−1,pH = 1.11 ± 0.06, k_2,pH = 2.3 ± 0.5, k_−2,pH = 3.1 ± 0.4 m⁻¹ s⁻¹, and an initial concentration of GSSSG of 0.27 ± 0.01 mm (Fig. 2C). This experimental design allows a more robust estimation of k_−1,pH than that of Fig. 2A. The estimated concentration of GSSSG was consistent with mass balance considerations that initial H₂S equals the sum of H₂S, GSSH, and GSSSG in equilibrium and with previous observations under conditions of excess GSSG that the concentration of GSSSG is ∼1/2 GSH in equilibrium (30). In our case, the concentrations of GSSH inferred from these relationships matched by 93 ± 8% (n = 6) those measured by HPLC. Of note, our kinetic analysis contemplated only two reactions. Whereas this simplification is reasonable when excess GSSG is used, other minor processes may probably occur, e.g. reaction of GSS⁻ with GSSSG or GSSH.

Reactions with thiolates constitute one of the main decay pathways for persulfides in vivo (16, 43, 44). To our knowledge, the value of k_−1,pH (1.11 m⁻¹ s⁻¹) is the first report for the rate constant of a reaction between a low molecular weight (LMW) persulfide and a LMW thiolate at physiological pH. While there is an estimation for cysteine persulfide and cysteine of 0.09 ± 0.01 m⁻¹ s⁻¹ (45), it corresponds to pH 10, a condition in which the carboxylate and amine of cysteine are deprotonated, likely affecting the kinetics of reaction (46).

We also analyzed the composition of the GSSH-containing mixtures once the concentrations remained stationary. GSSG (6–10 mm) and H₂S (0.5 mm) were incubated for 2 h, the reactions were stopped, and the species were quantified (Fig. 2D). A concentration quotient of 0.194 ± 0.005 (pH 7.4, 25 °C, 0.1 m phosphate buffer) was obtained for Reaction 1. Assuming that irreversible processes such as H₂S release, elemental sulfur precipitation, or oxidation by oxygen are insignificant in this timescale, this quotient reflects the apparent equilibrium constant (K_eq1,pH) of Reaction 1 at pH 7.4. The value is consistent with k_1,pH being lower than k_−1,pH and with the apparent equilibrium constant calculated from kinetic experiments (k_1,pH/k_−1,pH = 0.21).

From the apparent K_eq1,pH of 0.194, the ΔG°′ of Reaction 1 can be calculated to be +1.0 kcal/mol (pH 7.4, 25 °C). This agrees with a value of +1.4 kcal/mol estimated from thermochemical calculations for a generic RSSR reacting with HS⁻ to form RSS⁻ and RSH (the predominant species at neutral pH) (47) and supports that the Gibbs energy change is close to zero at physiological pH.

Our results underscore the existence of reverse and consecutive reactions and, together with the fact that persulfides disproportionate, indicate that GSSH cannot be purified in aqueous solutions; instead, it will be stationarily present in a mixture of species. This assertion is supported by several unsuccessful attempts to purify GSSH (not shown). Our results also lead to a note of caution for situations in which the concentration of persulfides is estimated from the thiol formed or from the initial concentration of reactants, because the quantities formed are not stoichiometric.

Acidity of GSSH and kinetics of the reaction with mBrB

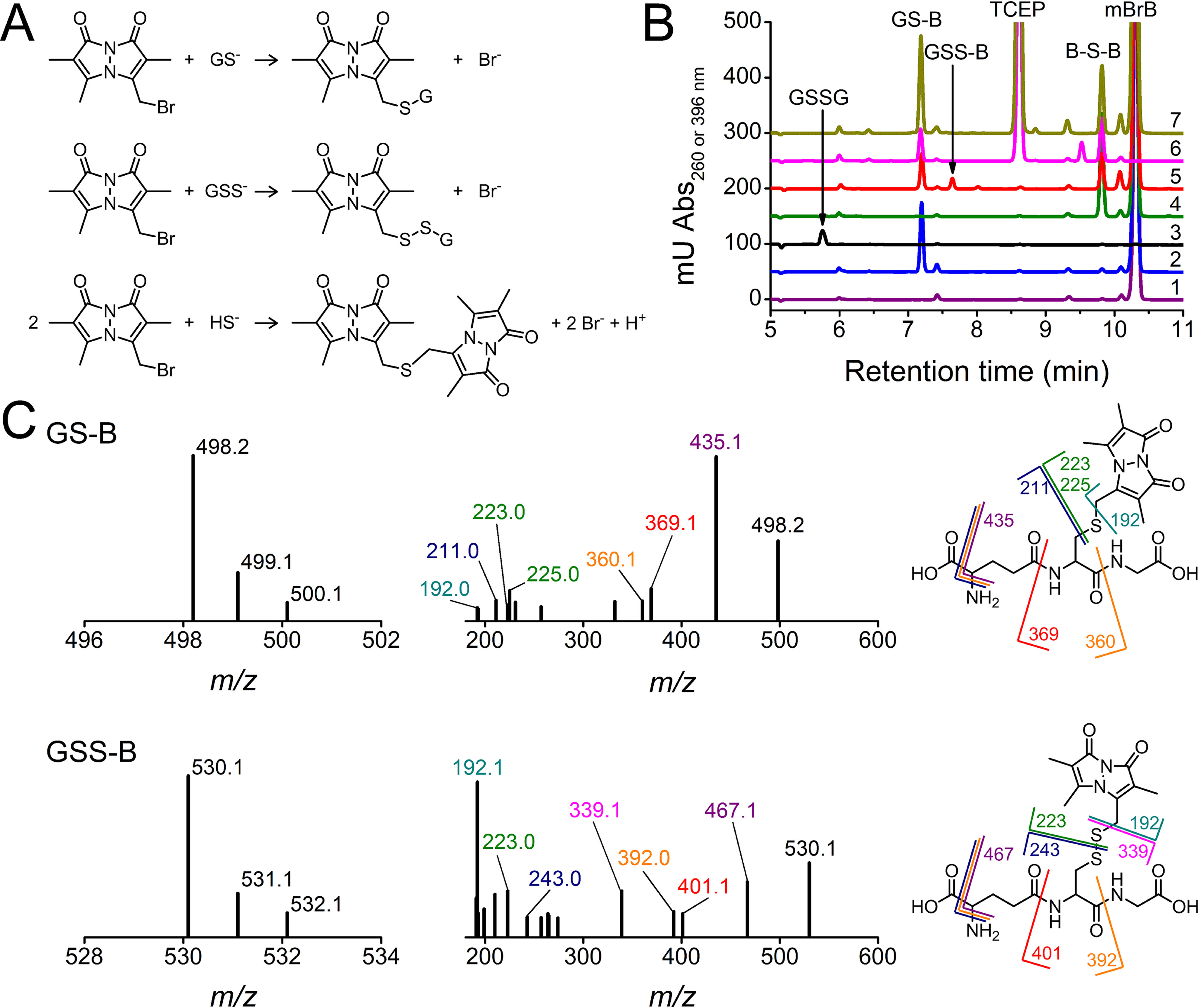
After the GSSH-containing mixture had been characterized, the pK_a of GSSH was measured by the pH dependence of the reaction with mBrB, exploiting that mBrB does not accept or release protons within the pH range studied and that the reactions can be followed by product fluorescence. As previously performed for GSH, an initial rate study was performed (37, 48) by reacting low concentrations of a GSSH-containing mixture and mBrB at different pHs at 25 °C. The initial slopes of the fluorescence variations increased with pH according to a one-pK_a function, yielding a pK_a of 5.50 ± 0.08 (Fig. 3A). The contributions of GSH and H₂S to the fluorescence change were calculated from the known rate constants, initial concentrations, and pK_a values, and found to be negligible (e.g. 0.015 and 0.007%, respectively, of the contribution of GSSH at pH 6) (30, 35–38).

Figure 3.

pH dependence of the reaction of GSSH with mBrB. A, a mixture containing GSSH (∼0.75 µm) reacted with mBrB (1 µm) in acetic/MES/tris buffer (pHs 4.16–6.86, 25 °C). Linear functions fitted to initial fluorescence increases (λ_ex = 396 nm, λ_em = 472 nm) yielded slopes (inset) that had a sigmoid dependence with pH. The data pooled from two independent experiments gave a pK_a of 5.50 ± 0.08 (parameter ± error of the fit). The points shown are quadruplicates of one representative experiment. No interference from the buffer was detected. B, representative stopped-flow fluorescence kinetic traces (λ_ex = 396 nm, emission cutoff 435 nm) of the reaction of 118 µm mBrB with a mixture containing ∼1.6 µm GSSH, ∼6.3 µm GSH, and ∼1 µm H₂S (final concentrations) in phosphate buffer (0.1 m, pH 7.40, 25 °C, 0.1 mm dtpa) (red) and with controls of 6.3 µm GSH (blue) or buffer alone (black). C, GSSH-containing mixtures (∼2 µm GSSH) reacted with 18–81 µm mBrB in acetic/MES/Tris buffer (pHs 4.19–7.41, 25 °C). Representative stopped-flow fluorescence time courses with 40 µm mBrB. Exponential plus linear or double exponential plus linear functions were fitted to kinetic traces during 10 half-lives. At the more acidic pHs, an additional fast phase was noted; the origin is unclear but its amplitude was less than 15% of the sum of the amplitudes and was not studied further. D, k_obs attributed to the reaction of GSSH against mBrB concentration. The circles represent the mean ± S.D. of repetitions of a representative experiment. Error bars are usually smaller than symbols. The slopes of the fits represent the second-order rate constants. At the more alkaline pHs, a small negative y-intercept was observed, probably because of reactant impurities or to a fast reaction with a species present in low concentration. E, second-order rate constants versus pH. A one-pK_a function fitted the data pooled from two independent experiments (black squares and blue circles), giving a pK_a of 5.45 ± 0.03 and a maximum (pH-independent) second-order rate constant of (9.0 ± 0.2) × 10³ m⁻¹ s⁻¹ (parameters ± errors of the fit). A small but systematic decrease in the k_pH at pH > 6.5 was observed, and its cause is unknown.

Furthermore, we studied the pH dependence of the second-order rate constant (k_pH) by reacting GSSH-containing mixtures with excess mBrB. The fluorescence increases were biphasic and exponential plus linear functions were fitted. The fast exponential phase was attributed to the reaction of mBrB with GSSH, whereas the slow linear phase was attributed to the reaction with GSH and, secondarily, with H₂S, based on controls and on the rate constants for GSH and H₂S (Fig. 3B) (30, 35–38). Moreover, the amplitude was consistent with independent HPLC determinations of GSS-B, assuming similar fluorescence quantum yield as GS-B. Possibilities such as reaction of mBrB with GSS_nS⁻ or HS_nS⁻ (n ≥ 1) cannot be discarded for the fast exponential phase. However, given that our mixtures had excess GSSG, the concentration of these species, if formed, is likely to be low. The k_obs attributed to GSSH increased linearly with mBrB concentration. The k_pH had a sigmoid dependence with pH, resulting in a pK_a of 5.45 ± 0.03 and a pH-independent rate constant (k_ind) for the reaction of GSS⁻ with mBrB of (9.0 ± 0.2) × 10³ m⁻¹ s⁻¹ (Fig. 3, C–E). The k_ind represents the rate constant that would be measured if all the persulfide were ionized and shows that, with mBrB, the persulfide anion reacts 44 times faster than the thiolate of glutathione (208 m⁻¹ s⁻¹) (37). At pH 7.4, GSSH reacted with an apparent rate constant of (7.02 ± 0.04) × 10³ m⁻¹ s⁻¹, 1200 times faster than that with GSH (Table 1). Importantly, similar pK_a values were obtained from both the initial rate and integral methods.

Table 1.

Rate constants for the reactions of GSSH with electrophiles and comparison with those of thiols

	$k_{\text{pH}}^{\text{GSSH}}$ (m−1 s−1)	$k_{\text{ind}}^{\text{GSSH}}$ (m−1 s−1)	$\frac{k_{\text{pH}}^{\mathrm{GSSH}}}{k_{\text{pH}}^{\text{GSH}a}}$	$\frac{k_{\text{ind}}^{\text{GSSH}}}{k_{\text{ind}}^{\text{GSH}a}}$	$\frac{k_{\text{ind}}^{\text{GSSH}}}{k_{\text{ind}}^{\text{RSH}{\text{p}K}_a\text{5.45}}}$	βnuc for the reaction with LMW thiolates
mBrB	(7.02 ± 0.04) × 103b	(9.0 ± 0.2) × 103	1200b	44	1670	0.52 ± 0.08
Peroxynitrite	(1.25 ± 0.03) × 105c	(4.7 ± 0.1) × 105	97c	1.8	50	0.42 ± 0.06d
H2O2	7.5 ± 0.6e	7.7 ± 0.6	22e	0.24	3.2	0.27 ± 0.06

^aReported rate constants for the reactions of GSH with mBrB (37), peroxynitrite (54, 56), and H₂O₂ (37).

^bRate constants at pH 7.40, 25 °C.

^cRate constants at pH 7.23, 37 °C.

^dβ_nuc calculated in this paper (see legend to Fig. 6).

^eRate constants at pH 7.02, 25 °C.

To sum up, the pK_a of GSSH was 5.45 ± 0.03, 3.49 units below that of GSH (8.94) (37). This means that at pH 7.4, the availability of the deprotonated species is 2.8% for GSH but 99% for GSSH.

We then performed a computational analysis of the acidity of persulfides and thiols by electronic structure calculations with the aim of understanding the molecular basis of the difference. The ionization equilibrium of an acid XH can be dissected in several steps: XH and H₂O desolvation, homolytic X-H bond cleavage, X^• electron affinity and hydrogen ionization, H₂O proton affinity, and X⁻ and H₃O⁺ solvation. The energetics of each step can be separately computed at different levels of theory. Then, the standard Gibbs energy change for the global process ($\Delta G_a^{°}$) can be calculated as the sum of the individual steps, and the contribution of each step to the global process can be discerned. Gibbs energy calculations were performed with the simplified models methanepersulfide (MeSSH) or methanethiol (MeSH) to avoid the optimization of zwitterionic structures in vacuum. Although the electronic structure method and basis sets used affected the computed values, general trends were maintained (Table S1).

The thermodynamic relation between the Gibbs energy change and the acidity constant is given by Equation 1, where R is the ideal gas constant and T is the temperature.

$${\Delta G}_a^{°}=\text{2.303}\hspace{0.17em}\text{RT}\hspace{0.17em}\text{p}{K}_a$$ (Eq. 1)

A difference in pK_a between thiol and persulfide (ΔpK_a) of 7.2 was calculated using Equation 1 and Gibbs energy changes obtained for the global ionization process with the electronic structure coupled cluster singles and doubles method (CCSD) employing the 6-31 G(d′) basis set. However, small errors (∼1 kcal/mol) in the computed Gibbs energies would affect the estimated pK_a values. The main difference in the energetics of the individual steps between thiol and persulfide was found in the homolytic S-H bond cleavage, which was ∼20% lower for MeSSH than for MeSH (Table S1). This is consistent with S-H bond dissociation energies reported for alkyl thiols and persulfides, which differed by 24% (49), and with IR spectra, which showed shifted S-H stretching frequencies (50–52). The acidity of MeSSH was also estimated in the context of the proton-exchange method previously used to estimate the pK_a of cysteine persulfide (3, 53), yielding a ΔpK_a of 1.7 with CCSD/6-31 G(d′). Considering the pK_a of MeSH, 10.33 (19), a pK_a of 8.6 would be predicted for MeSSH.

Overall, our calculations follow the same trend as the experimental data and suggest that the factor that contributes the most to the lower pK_a of persulfides with respect to thiols is the weaker S-H bond in the persulfide compared with the thiol.

After determining the pK_a of GSSH, we analyzed the pH dependence of the apparent rate and equilibrium constants of Reaction 1 (Table S2 and Fig. S3). At pH 7.4, k_1,pH is similar to k_1,ind because most H₂S is ionized (pK_{a H2S}, 6.98) (38). In contrast, only a fraction of k_−1,ind (∼3600 m⁻¹ s⁻¹) is evidenced at pH 7.4 (1.11 m⁻¹ s⁻¹); k_−1,pH decreases by deprotonation of GSSH (pK_{a GSSH}, 5.45) and protonation of GS⁻ (pK_{a GSH}, 8.94) (37). Thus, at pH 7.4, the apparent equilibrium constant K_{eq1,pH 7.4} is 0.194, whereas K_eq1,ind is 8.3 × 10⁻⁵. This value of K_eq1,ind corresponds to an endergonic ΔG° of +5.6 kcal/mol. The change in the apparent equilibrium constant at pH 7.4 translates into a difference of −4.6 kcal/mol. In other words, at pH 7.4, deprotonation of GSSH and protonation of GS⁻ drive Reaction 1 to the right.

The fact that k_−1,ind is higher than k_1,ind, is consistent with GS⁻ being a better nucleophile than HS⁻ and GS⁻ being a poorer leaving group than HS⁻ (3), because H₂S has a lower pK_a than GSH. Furthermore, the unfavorable thermodynamics can be rationalized by better solvation of HS⁻ than GS⁻ and higher bond dissociation energy for the S-S bond in GSSG than GSSH (47, 49).

Kinetics of the reactions of GSSH with physiological electrophiles

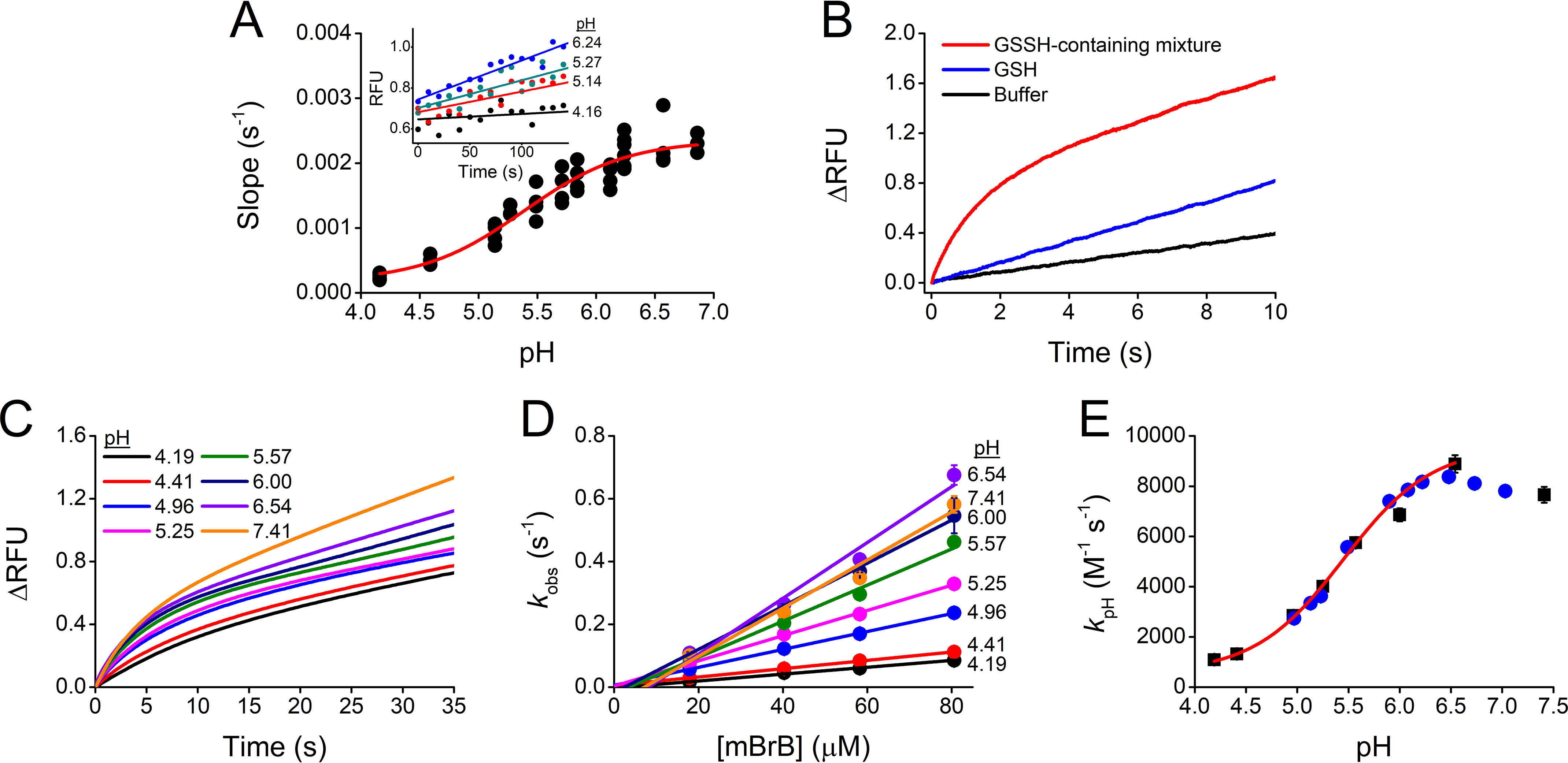
The kinetics of the reactions of GSSH with peroxynitrite and H₂O₂ were studied using a pseudo-first-order excess of GSSH and the other components of the mixture. GSSH-containing mixtures were reacted with peroxynitrite (pH 7.23, 37 °C) and followed by the decrease in absorbance (Fig. 4A). The temperature was chosen to facilitate comparison with data reported for thiols (54). The k_obs obtained from peroxynitrite exponential decay correlated linearly with GSSH concentration (Fig. 4B). Precisely, the slope represents the sum of the contributions of the reactions of peroxynitrite with GSSH, GSH, and H₂S. The contributions of GSH and H₂S were calculated and subtracted from the global decay considering the rate constants at the working pH (1.29 × 10³ m⁻¹ s⁻¹ for GSH (54), 7.93 × 10³ m⁻¹ s⁻¹ for H₂S (38, 55, 56)) and the concentrations, which were measured separately. Thus, a k_{pH 7.23} of (1.25 ± 0.03) × 10⁵ m⁻¹ s⁻¹ was determined for the reaction of peroxynitrite and GSSH, 97 times higher than GSH under the same conditions. Given the pK_as of GSSH (5.45) and ONOOH (6.8) (56), k_ind was calculated to be (4.7 ± 0.1) × 10⁵ m⁻¹ s⁻¹ with Equation 2. This value is 1.8 times higher than for GS⁻ (54, 56) (Table 1).

$$k_{\text{pH}}=k_{\text{ind}}\left(\frac{K_a^{\text{RSSH}}}{K_a^{\text{RSSH}}+\left[{\text{H}}^{+}\right]}\right)\left(\frac{\left[{\text{H}}^{+}\right]}{K_a^{\text{ONOOH}}+\left[{\text{H}}^{+}\right]}\right)$$ (Eq. 2)

Figure 4.

Kinetics of the reactions between GSSH and peroxynitrite or H₂O₂. A, reaction with peroxynitrite. Mixtures containing GSSH (137–191 µm), GSH (5.11 times GSSH), and H₂S (0.57 times GSSH) were mixed with 26 µm peroxynitrite (final concentrations) in phosphate buffer (0.1 m, pH 7.23, 37 °C, 0.1 mm dtpa) in a stopped-flow spectrophotometer. Normalized absorbance versus time. Representative time courses of peroxynitrite decay at 302 nm in the absence (black) or presence of 137 (red), 159 (blue), and 177 µm GSSH (green). Exponential plus linear functions were fitted to the time courses. Kinetic traces presented an increase in absorbance after seven half-lives, probably because of secondary reactions of H₂S (not shown) (55). B, k_obs versus GSSH concentration. The k_obs represents the sum of the contributions of the different decay processes, k_obs = k_{pH GSSH} [GSSH] + k_{pH GSH} [GSH] + ${\text{k}}_{\text{pH}\hspace{0.17em}{\text{H}}_{\text{2}}\text{S}}$ [H₂S] + k_{pH peroxynitrite decay}. The slope of (1.36 ± 0.03) × 10⁵ m⁻¹ s⁻¹ (parameter ± error of the fit) is k_{pH GSSH} + 5.11 k_{pH GSH} + 0.57 ${\text{k}}_{\text{pH}\hspace{0.17em}{\text{H}}_{\text{2}}\text{S}}$. Then, the k_{pH 7.23 GSSH} was (1.25 ± 0.03) × 10⁵ M⁻¹ s⁻¹. The rate constant without GSSH-containing mixture was 1.13 ± 0.04 s⁻¹ (mean ± S.D.), consistent with peroxynitrite spontaneous decay (99). The experiment shown is representative of four independent experiments. C. reaction with H₂O₂. Decay of 50 µm H₂O₂ in the presence of a mixture containing 0.71 mm GSSH, 2.0 mm GSH, and 0.37 mm H₂S (red), 2.0 mm GSH (blue), or 0.37 mm H₂S (green) in the same buffer (pH 7.02, 25 °C). Aliquots were diluted 100-fold and mixed with peroxiredoxin Prx5v (2–4 µm). The reactions were followed by the intrinsic fluorescence (λ_ex = 280 nm, λ_em = 340 nm) of Prx5v in phosphate buffer (50 mm, pH 7.4, 25 °C, 0.1 mm dtpa) in a plate reader. The exhibited time courses are representative experiments. The mean ± S.D. of three independent determinations yielded a k_obs of (6.2 ± 0.4) × 10⁻³ s⁻¹ for H₂O₂ decay in the presence of the mixture, whereas the k_obs corresponding to GSH or H₂S controls were one or two orders of magnitude lower, respectively. Controls of Prx5v and GSH in the absence and presence of H₂O₂ showed no interference with the intrinsic fluorescence of the enzyme (not shown). The k_{pH 7.02} for the reaction of H₂O₂ and GSSH was 7.5 ± 0.6 m⁻¹ s⁻¹ (see main text).

The measurements of the kinetics of the reaction with H₂O₂ proved to be challenging, and the best results were obtained when peroxiredoxin 5 was used as a probe for H₂O₂. The fluorescence of peroxiredoxin 5 (Prx5) increases as it is oxidized by H₂O₂ (37, 57). Actually, a variant named Prx5v was used. This variant behaves similarly to WT with respect to the reaction with H₂O₂ but the formation of the disulfide from the sulfenic acid and the resolving cysteine is faster, minimizing parallel reactions of the sulfenic acid and improving the performance of the probe (Fig. S4). A GSSH-containing mixture was incubated with H₂O₂. Aliquots were taken at increasing times, diluted, and mixed with Prx5v. The intrinsic fluorescence of the enzyme, which is proportional to H₂O₂ (Fig. S5), was measured. From the k_obs of the decay of H₂O₂ in the presence of the mixture (Fig. 4C), after subtracting the contributions of GSH and H₂S to H₂O₂ decay (37, 38, 58), the k_{pH 7.02} for the reaction of H₂O₂ and GSSH was determined to be 7.5 ± 0.6 m⁻¹ s⁻¹ (pH 7.02, 25 °C) (Fig. 4C). This value is 22 times higher than that of GSH under the same conditions. The k_ind of the reaction of GSS⁻ and H₂O₂ was calculated with Equation 3 considering that H₂O₂ does not ionize, because it has a pK_a of 11.62 (59). A value of 7.7 ± 0.6 m⁻¹ s⁻¹ was obtained, which is 4 times lower than the corresponding reaction of GS⁻ (37) (Table 1).

$$k_{\text{pH}}=k_{\text{ind}}\left(\frac{K_a^{\text{RSSH}}}{K_a^{\text{RSSH}}+\left[{\text{H}}^{+}\right]}\right)$$ (Eq. 3)

Computational insight into the reactions of persulfides and thiols with electrophiles

To provide a complementary microscopic insight into the reactivity of persulfide anions and thiolates, we studied computationally the reactions of the simplified models, MeS⁻ and MeSS⁻, with mBrB, ONOOH, and H₂O₂. We employed a multi-scale QM/MM approach that allows to treat explicitly the solvent molecules while keeping the quantum nature needed for modeling the reactive species. This realistic representation of a chemical reaction in aqueous solution at room temperature enabled an accurate comparison between the simulations and the experimental data.

Inspection of the Gibbs energy profiles revealed that the transition states for both MeS⁻ and MeSS⁻ were reached early. The geometries were almost identical (Fig. 5, A–C). The linear arrangement of the nucleophilic sulfur, the electrophilic center, and the closest atom of the leaving group suggests typical bimolecular nucleophilic substitutions (S_N2), as shown previously for thiolates (60, 61). A post-transition state proton transfer occurred in the case of H₂O₂ (37, 60, 62). The products were MeS-B/MeSS-B + Br⁻, MeSOH/MeSSOH + NO₂⁻, and MeSO⁻/MeSSO⁻ + H₂O, for the reactions with mBrB, ONOOH and H₂O₂, respectively. The reactions were strongly exergonic (Fig. 5, D–F).

Figure 5.

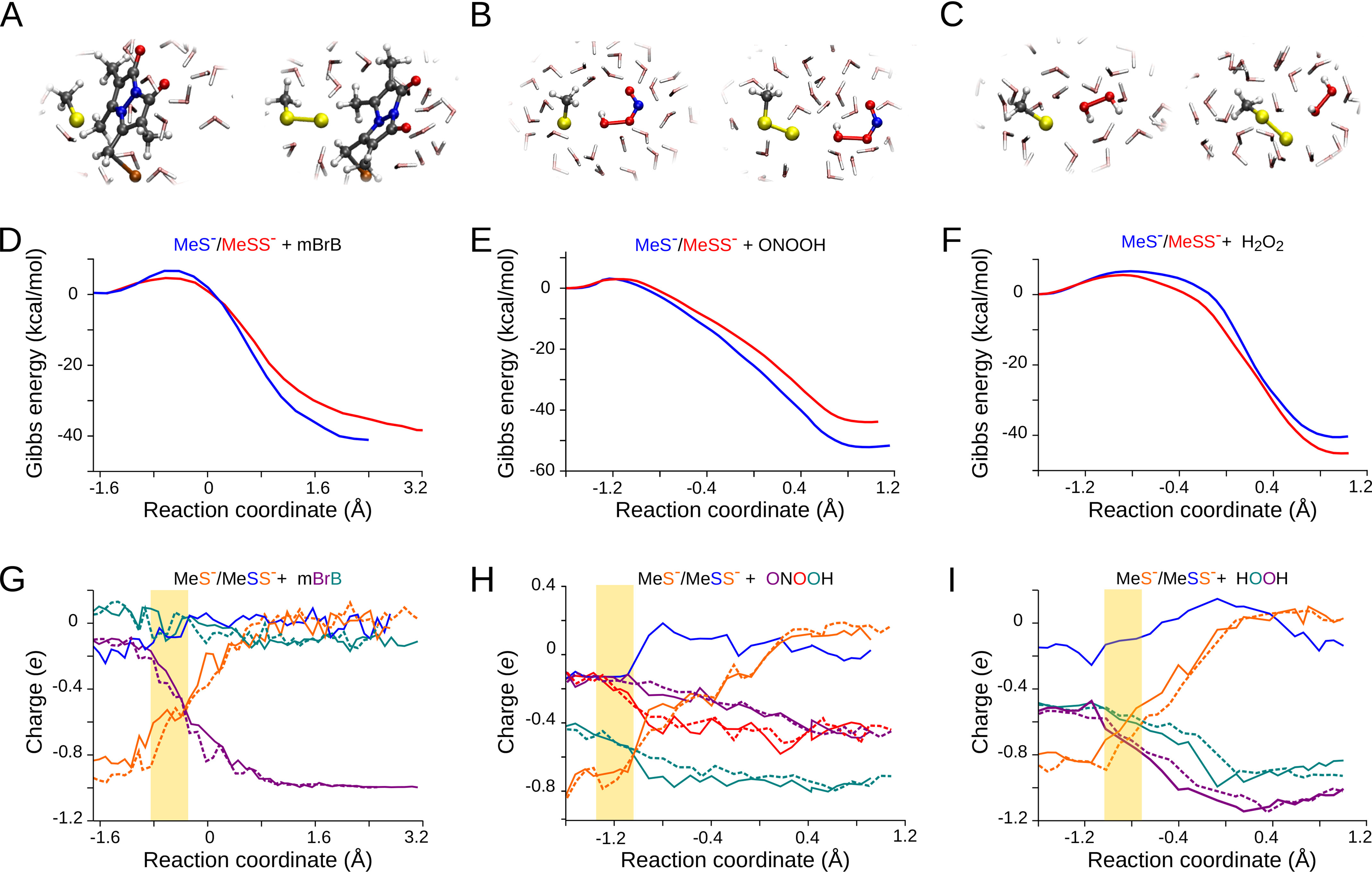
Transition states, Gibbs energy profiles, and evolution of charges. Reactions of MeS⁻ or MeSS⁻ with mBrB (panels A, D, and G), ONOOH (panels B, E, and H), and H₂O₂ (panels C, F, and I) were studied by umbrella sampling in a QM/MM scheme. A–C, representative snapshots of the transition states of the thiolate (left) and persulfide anion (right). D–F, Gibbs energy profiles for MeS⁻ (blue lines) or MeSS⁻ (red lines). G–I, average Mulliken populations as a function of reaction coordinate for MeS⁻ (dashed lines) or MeSS⁻ (solid lines) reactions. Charges of atoms that exhibited significant variations are shown in the corresponding colors. The regions corresponding to the transition states are indicated with a yellow box.

The simulated activation Gibbs energies (ΔG^‡, obtained from the maxima of the Gibbs energy profiles) for the reactions of MeS⁻/MeSS⁻ were compared with those calculated for GS⁻/GSS⁻ from the experimental pH-independent rate constants k_ind according to the Transition State Theory (63) (Table S3). The rate constant k relates to ΔG^‡ through Equation 4, where R is the ideal gas constant, T is the temperature, $k_B$ and h are the Boltzmann and Plank constants, C° is 1 m, and τ is the transmission coefficient, assumed in this case to have a value of one.

$$k\approx \frac{\tau k_{\text{B}}\text{T}}{h{\text{C}}^{\mathrm{o}}}{\text{e}}^{-\Delta G^{‡}/\text{RT}}$$ (Eq. 4)

The expected trends were observed for the Gibbs activation energies of the reactions with both thiolate and persulfide anion: ΔG^‡_H2O2 > ΔG^‡_mBrB > ΔG^‡_ONOOH (Table S3). When comparing MeS⁻ to MeSS⁻, the differences in simulated ΔG^‡ were ΔΔG^‡ = 2.1 ± 0.9 for mBrB, 0.2 ± 0.8 for ONOOH, and 1.0 ± 0.8 kcal/mol for H₂O₂. These values are consistent with those determined from the experimental k_ind of 2.2, 0.5, and −0.8 kcal/mol, respectively (Table S3), although close to the reliability limit of the computational methodology. In fact, the ΔΔG^‡ of GS⁻/GSS⁻ toward H₂O₂ was computationally estimated as 0.0 ± 0.5 kcal/mol (not shown). We evaluated the influence of the level of theory by performing calculations using an implicit solvent model with a variety of electronic structure schemes. The density functional theory (DFT) approach using the Perdew-Burke-Ernzerhof (PBE) functional employed in the QM/MM simulations, and more accurate electronic structure methods, showed similar differences when comparing the ΔG^‡ of MeS⁻ and MeSS⁻ (Table S4).

We then evaluated the influence of the electronic structure of the species on the observed trends by monitoring Mulliken populations of selected atoms as a measure of charge distribution along the reactions. At the reactant complex, in the reactions with mBrB, the net −1 e charge was localized in MeS⁻ or MeSS⁻, whereas with ONOOH and H₂O₂, the charge in MeS⁻ or MeSS⁻ was approximately −0.85 to −0.90 e (Fig. 5, G–I). In every case, MeS⁻ exhibited the charge almost completely in its single sulfur atom whereas in MeSS⁻ the charge was partitioned between both sulfur atoms. The largest redistributions of charges were observed around the transition states. The atoms constituting the leaving groups acquired a more negative charge, whereas the sulfur atoms became more positive. At the transition state, the atoms integrating MeS⁻ or MeSS⁻ summed up a charge of approximately −0.59, −0.73, and −0.69 e (mean values for MeS⁻ and MeSS⁻) in the reactions with mBrB, ONOOH, and H₂O₂, respectively (Table S5). The percent charge transferred from the reactant complex to the transition state had the same trend as ΔΔG^‡, mBrB > H₂O₂ > ONOOH (Table S3 and Table S5). Remarkably, the percent charge transferred was higher for MeSS⁻ than MeS⁻ for the three electrophiles. In the case of mBrB, both the experimentally determined increase in nucleophilicity of GSS⁻ versus GS⁻ and the computed charge transferred in the transition state were the highest.

Finally, to monitor potential solvent effects, we computed radial correlation functions centered on the nucleophilic atoms. In the absence of an electrophile, the nucleophilic sulfur atoms of both MeS⁻ and MeSS⁻ yielded the typical solvation patterns of diffuse anions (Fig. S6), consistent with previous work (60, 64). Their solvation structures became looser along the reaction as a consequence of the significant charge redistribution. The same effect was observed, to a lower extent, for the inner sulfur atom of MeSS⁻ (not shown). No significant differences were found between MeS⁻ and MeSS⁻ reactions with respect to the evolution of solvation patterns.

Overall, the relatively good correlation between the experimental and simulated data validates the use of MeS⁻/MeSS⁻ as simplified models. Our results suggest that the reactions occur through similar S_N2 mechanisms and that differences in reactivity are mainly due to electronic structure differences and not to solvent effects.

α effect in persulfides

Brønsted plots correlate the nucleophilic capability with the basicity for a certain family of compounds according to Equation 5 (log of k_ind versus pK_a of the nucleophile), where β_nuc, typically between 0 and 1, is the Brønsted nucleophilic factor and C is a constant.

$$\text{log}\hspace{0.17em}{k}_{\text{ind}}={\beta }_{\text{nuc}}\hspace{0.17em}\text{p}{K}_a+\text{C}$$ (Eq. 5)

Nucleophiles with high electron density in the atom adjacent to the nucleophilic atom show positive deviations from these plots and exhibit higher reactivity than expected according to their basicity (65). This deviation is known as the α effect.

Using our newly determined rate constants, the pK_a of GSSH, and published data for LMW thiols (37, 54, 56, 66), we constructed Brønsted plots (Fig. 6). Notably, the k_ind of GSS⁻ appeared above the trend reported for LMW thiolates with mBrB, ONOOH, and H₂O₂. The nucleophilicity of GSS⁻ was enhanced compared with that predicted for a thiolate with similar basicity by 1670-fold for mBrB, 50-fold for ONOOH, and 3.2-fold for H₂O₂ (Table 1).

Figure 6.

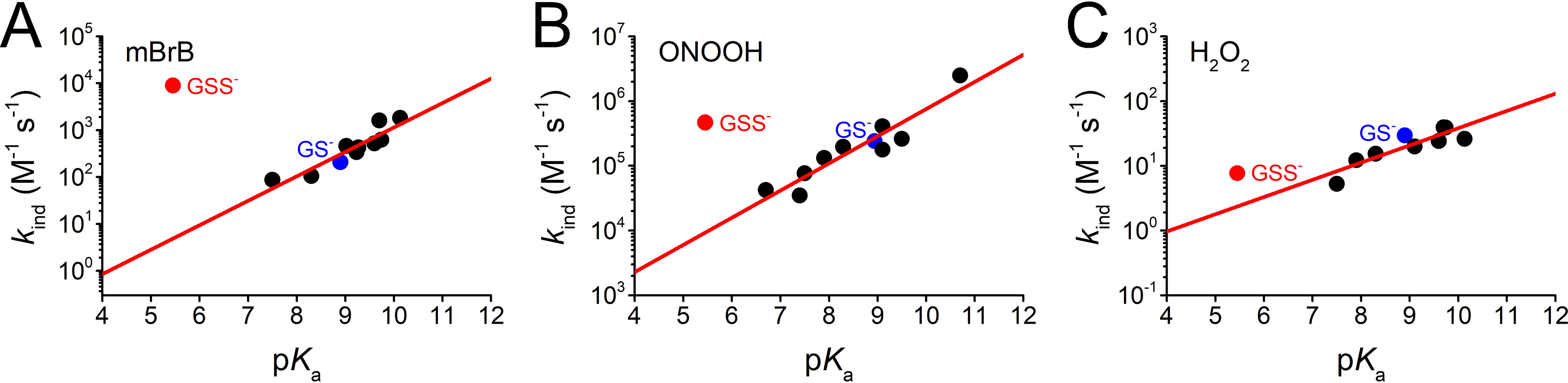
Comparison of the reactivity of GSS⁻ and thiolates with mBrB, ONOOH, and H₂O₂. Brønsted plots depicting the reported pH-independent rate constants (in logarithmic scale) versus thiol pK_a for the reactions of several LMW thiolates (black circles, GS⁻ in blue) with A, mBrB at 25 °C (β_nuc = 0.52 ± 0.08) (37); B, ONOOH at 37 °C (plot updated from (66) considering more recent pK_a estimations (37, 56); the fit yielded β_nuc = 0.42 ± 0.06 and C = 1.7 ± 0.5); and C, H₂O₂ at 25 °C (β_nuc = 0.27 ± 0.06) (37). The red circles show the pH-independent rate constants for GSS⁻ versus GSSH pK_a, reported herein.

The trend in the magnitude of the α effect (mBrB > ONOOH > H₂O₂) correlated with the $\beta$_nuc for the reactions of thiolates, which are 0.52 for mBrB, 0.42 for ONOOH, and 0.27 for H₂O₂ (37, 54, 66) (Table 1). These correlations have been previously observed for other nucleophile families (28, 67, 68) and are now observed for these sulfur nucleophiles. In addition, although comparisons between electrophiles of different types (i.e. centered in carbon or in oxygen) should be carried out with caution, a correlation was also observed between the α effect and the ability of the leaving group, which is related with the acidity of the conjugated acid (HBr > HNO₂ > H₂O, pK_as of −8.8, 3.35, and 14, respectively (69–71)). Note that in the reactions with H₂O₂ the proton transfer takes place after the transition state; thus, OH⁻ is the leaving group (37, 60, 62).

In summary, we evidenced the enhanced nucleophilicity of the biologically relevant persulfide GSS⁻ toward three electrophiles compared with the expected nucleophilicity of a thiolate of equal basicity. To our knowledge, our study represents the first examination of the α effect in sulfur nucleophiles.

Biological implications

The high acidity of GSSH (pK_a 5.45, 3.49 units below GSH), if extrapolated to other persulfide/thiol pairs, means that in biological systems the persulfides will be ionized whereas the thiols will be mainly protonated. The appearance of a negative charge could alter the functional properties of the original thiol. The situation may be different in particular proteins where the local environment may change the pK_a values.

The enhanced nucleophilic reactivity of GSSH compared with GSH at physiological pH is the result of two aspects, the higher availability of the ionized species due to its lower pK_a and, depending on the electrophile, the increased nucleophilicity of GSS⁻. This is relevant for enzymatic (i.e. with persulfide dioxygenase) and nonenzymatic reactions (i.e. with one- and two-electron oxidants and other electrophiles) in which GSSH acts as a nucleophile. Extrapolation to other persulfide/thiol pairs would indicate an enhancement in reactivity of one to three orders of magnitude (Table 1), which could vary depending on the specific molecular environment, the pH, and the electrophilic partner. The relatively high nucleophilic reactivity of persulfides could contribute to the proposed protective effects of persulfidation. Oxidation of persulfides can lead to products (i.e. RSSO₂H and RSSO₃H) that can be reduced by cellular reductants systems, whereas analogous oxidation of thiols yields irreversible oxidation products (i.e. RSO₂H and RSO₃H) (4, 16, 24, 44).

Importantly, the biological properties of persulfides can also be attributed to their electrophilicity, as in transpersulfidation reactions, which is a property absent in thiols. It is likely that both the enhanced nucleophilicity and the electrophilicity contribute to the persulfide-mediated downstream effects of H₂S.

Our analysis of persulfide pK_a and nucleophilicity has implications for the reaction catalyzed by the mitochondrial enzyme SQOR. It has been proposed that this enzyme contains a trisulfide (RSSSR) instead of a disulfide (RSSR) in its two active site cysteines (72). Reaction of H₂S with RSSSR instead of RSSR to form two persulfides could imply an acceleration of ∼two orders of magnitude, because persulfide is a better leaving group than thiol because of its lower pK_a (3). In the following step of the reaction, which involves the attack of the enzyme-formed persulfide or thiolate on the electrophilic FAD cofactor, an acceleration of one to three orders of magnitude would be expected for the persulfide. These estimations are based on considerations for LMW species; as is typical with enzymes, specific protein effects could lead to further acceleration factors. In fact, recent computational estimations suggest a rate increase of ∼10⁵-fold for the first step if the active site of SQOR is in the trisulfide instead of the disulfide state (73).

Conclusions

This study reveals several aspects about the formation, acidity, and nucleophilicity of GSSH, summarized as follows. 1) A reversed-phase HPLC method based on mBrB derivatization can be used for quantification of GSSH in mixtures. 2) Excess GSSG and H₂S generate GSSH, GSH, and GSSSG through at least two reversible reactions, Reaction 1 (GSSG + H₂S) and Reaction 2 (GSSG + GSSH). At physiological pH and 25 ± 1 °C, the rate constants are k_1,pH = 0.23 ± 0.02, k_−1,pH = 1.11 ± 0.06, k_2,pH = 1.6-2.3, and k_−2,pH = 3.1-9 M⁻¹ s⁻¹. 3) The apparent equilibrium constant K_eq1,pH is 0.194 ± 0.005 (pH 7.4, 25 ± 1 °C). 4) The reaction of GSSG with HS⁻ to form GSSH and GS⁻ is endergonic but is driven by −4.6 kcal/mol through deprotonation of GSSH and protonation of GS⁻ at physiological pH. 5) In mixtures of GSSG and H₂S, the formation of GSSH is not stoichiometric with respect to GSH nor to the initial concentration of H₂S because the products undergo subsequent reactions. 6) The pK_a of GSSH is 5.45 ± 0.03, 3.49 units below the pK_a of GSH. This is, to our knowledge, the first report of the pK_a of a biological persulfide. 7) The higher acidity of persulfides compared with thiols is due mainly to the weaker S-H bond. 8) At physiological pH, GSSH reacts 1200, 97, and 22 times more rapidly than GSH with the electrophiles mBrB, peroxynitrite, and H₂O₂, respectively. This can be explained by the increased availability of the ionized species and, depending on the electrophile, by the increased nucleophilicity. 9) The reactions of GSSH occur through S_N2 mechanisms similar to those of thiols. 10) The differences in reactivity are related to the electronic structures of the species rather than to solvent effects. 11) The α effect is evidenced by the positive deviation in Brønsted plots. 12) The increased reactivity of GSS⁻ compared with a thiolate of similar basicity is 1670-fold with mBrB, 50-fold with ONOOH, and 3.2-fold with H₂O₂. 13) The magnitude of the α effect varies with the electrophile. It correlates with the ${\beta }_{\mathrm{nuc}}$ for the reactions with thiolates and with the ability of the leaving groups. An examination of the α effect in sulfur nucleophiles is unprecedented to our knowledge. Overall, our study contributes to the understanding of the basic chemical properties of persulfides, which affects their roles in biosynthesis, catabolism, and H₂S signaling.

Experimental procedures

Reagents and solutions

Solutions of GSSG (AppliChem) were prepared in sodium phosphate buffer (0.1 m, pH 7.4). When specified, the buffer also contained 0.1 mm diethylenetriamine pentaacetic acid (dtpa, ACROS). Depending on the desired final pH, 1.5–2 equivalents of NaOH were added. GSH (ACROS) was dissolved in the mentioned buffer. Crystals of Na₂S·9H₂O (Carlo Erba), stored under argon in a desiccator, were washed with distilled water, dissolved in ultrapure water, and used within a few hours. Solutions containing H₂S were prepared in sealed vials with minimum headspace and manipulated with gas-tight Hamilton syringes. Concentrated stocks of mBrB (Sigma-Aldrich) (50 mm) were prepared in acetonitrile; dilutions (<120 μm) were freshly prepared in ultrapure water or buffer and quantified by absorbance at 396 nm (ε₃₉₆ = 5300 m⁻¹ cm⁻¹) (74). Solutions of TCEP (Sigma-Aldrich) were prepared in distilled water. Solutions of H₂O₂ (BAKER) were prepared in ultrapure water and quantified by absorbance at 240 nm (ε₂₄₀ = 39.4 m⁻¹ cm⁻¹) (75, 76). Peroxynitrite stocks were prepared as previously and quantified by absorbance at 302 nm (ε₃₀₂ = 1700 m⁻¹ cm⁻¹) (56, 77, 78); dilutions (26 μm) were freshly prepared in 2 mm NaOH.

Reversed-phase HPLC

Reversed-phase chromatography was performed using a 1260 Infinity HPLC (Agilent) with a diode array UV-visible absorbance detector and a C18 Ascentis column (100 × 4.6 mm, 3 μm, Sigma-Aldrich). Samples derivatized with mBrB were diluted 2-fold in 0.1% (v/v) TFA (Fluka) prior to injection and eluted with a gradient of 0.1% (v/v) TFA:acetonitrile (100:0 from 0 to 2 min, 60:40 from 8 to 10 min, 5:95 from 12 to 14 min) at a flow rate of 0.8 ml/min. Chromatograms were recorded at 260 and 396 nm.

MS

Fractions collected from the HPLC underwent two cycles of evaporation in a vacuum concentrator to remove the TFA and redissolved in ultrapure water. The aqueous fractions were then diluted in 0.1% (v/v) formic acid and analyzed by direct infusion into a hybrid triple-quadrupole/linear ion trap mass spectrometer (QTRAP4500, AB Sciex). Mass spectrometer parameters were optimized for best signal quality according to the corresponding analyte and method. For molecular ion identification, Q1 mode was employed in positive mode, electrospray voltage and declustering potential were set to 5.5 kV and 70 V, respectively, and the scan speed was set to 1000 Da/s. Fragmentation experiments were performed in the Product Ion mode with a collision energy ramp from 20 to 50 V. Data were acquired with Analyst 1.6.2 software and analyzed with PeakView 2.2 (AB Sciex).

Kinetics and equilibrium studies followed by HPLC

To study the reaction between GSSG and H₂S, 5–11 mm GSSG and 0.5 mm H₂S were incubated for increasing time periods in sodium phosphate buffer (0.1 m, pH 7.4, 25 ± 1 °C). In another set of experiments, 5 mm GSSG and 0.5 mm H₂S were preincubated for 1 h in the mentioned buffer; then, 2–12.5 mm GSH was added, leaving minimum headspace in the vial. At the end of the experiments, the final pHs of the reaction mixtures were measured. In both sets of experiments, aliquots were taken at different incubation times and the reactions were stopped by 2.5- to 9.5-fold dilution in 4 or 10 mm mBrB, final concentrations, in sodium phosphate buffer (80–95 mm, pH 7.4). The derivatized samples were then analyzed by HPLC. For GSSG, the chromatograms at 260 nm were used, whereas for the other species, the chromatograms at 396 nm corresponding to the bimane derivatives were used. The concentrations of GSSG, GSH, GSSH, and H₂S were determined by measurement of the area under the peaks and comparison with calibration curves of known standards. Considering that the bimane derivatives of GSSH and GSH have the same absorptivity because of the bimane moieties, the calibration curve for GSH was used to quantify GSSH. OriginPro 8.6 was used to analyze data. COPASI (40), a software application for the simulation and analysis of biochemical networks, was used to simulate time courses and fit kinetic parameters. Parameters in COPASI were estimated with the Levenberg-Marquardt algorithm.

To characterize the apparent equilibrium constant, K_eq1,pH, 6–10 mm GSSG and 0.5 mm H₂S were incubated in sodium phosphate buffer (0.1 m, pH 7.4, 25 °C), under shaking, in glass insert tubes inside sealed vials with almost no headspace. After 2 h, 4 mm mBrB was added and the samples were analyzed by HPLC.

Determination of the pK_a of GSSH

The pK_a of GSSH was determined by the pH dependence of the reaction with mBrB using both an initial rate approach, as previously described for thiols, and an integral method under pseudo-first-order conditions with mBrB in excess (48). A three-component, constant ionic strength (I = 0.15 m) buffer was used in the pH range of 4.16–7.41 (79). The buffer (1×) contained 15 mm acetic acid (Dorwil, Argentina), 15 mm MES (Applichem), 30 mm Tris (Applichem), 120 mm NaCl (Applichem), 0.1 mm dtpa, and variable amounts of HCl or NaOH to adjust the pH.

In the initial rate approach, stock solutions of mBrB and mixtures of 10 mm GSSG and 2 mm H₂S, which had been incubated for 1 h in sodium phosphate buffer (0.1 m, pH 7.4) to form GSSH, were freshly diluted in ultrapure water immediately before use. The initial rates of the reaction between 1 μm mBrB and mixtures that contained ∼0.75 μm GSSH (final concentrations) were measured in a Varioskan Flash plate reader (Thermo Fisher Scientific) at 25 °C. In a 384-well black plate, 11 or 12 reactions at different pHs were prepared in quadruplicate. Each well contained 20 μl of the three-component buffer 5× and 50 μl of the diluted GSSH-containing mixture. The reactions were started by the injection of 30 μl of mBrB using the automatic dispenser of the plate reader. Fluorescence (λ_ex = 396 nm, λ_em = 472 nm) was measured during 5–13 min and linear functions were fitted to the readings. The obtained slope, which is proportional to the initial rate, was determined for each pH. To evaluate buffer interference, controls without the GSSH-containing mixture were performed. The pHs of the solutions were measured immediately after the reactions. An aliquot of the GSSH-containing mixture was derivatized with 9 mm mBrB for HPLC analysis.

In pseudo-first-order experiments, rapid kinetics were studied in the presence of excess mBrB in a stopped-flow spectrofluorimeter (Applied Photophysics SX20). To prepare GSSH-containing mixtures, 10 mm GSSG and 2 mm H₂S were preincubated for at least 1 h in sodium phosphate buffer (0.1 m, pH 7.4, 0.1 mm dtpa) and then diluted in ultrapure water immediately before use. The diluted GSSH-containing mixtures (∼2 μm GSSH) were reacted with 18–81 μm mBrB, final concentrations, prepared in the three-component buffer 2× at different pHs at 25 °C. The fluorescence (λ_ex = 396 nm, emission cutoff 435 nm) of the product was recorded during 18–500 s. The final pHs were measured. At pH 7.40, experiments were also performed in sodium phosphate buffer (0.1 m, 0.1 mm dtpa) and included controls with 118 μm mBrB and 6.3 μm GSH or buffer alone. The data were analyzed with OriginPro 8.6 or Pro-Data SX20 software (Applied Photophysics).

Kinetics of the reaction of GSSH with peroxynitrite

The kinetics of the reaction was studied under pseudo-first-order conditions with excess GSSH. The decay of peroxynitrite was followed by the decrease in absorbance at 302 nm in the stopped-flow. To prepare GSSH, 10 mm GSSG and 2 mm H₂S were preincubated for 1.5 h in sodium phosphate buffer (0.2 m, pH 7.4, 0.2 mm dtpa) at 25 °C. The GSSH-containing mixtures were diluted up to 1.4-fold in the mentioned buffer (137–191 μm) minimizing headspace and were reacted with freshly prepared solutions of 26 μm peroxynitrite, final concentrations, at 37 °C. The pH was measured at the end of each reaction. The peroxynitrite-dependent change in absorbance at 302 nm was recorded for 1 s. Controls of the spontaneous decay of peroxynitrite in buffer alone were performed under the same conditions. In parallel, aliquots of the GSSH-containing mixtures were separated for HPLC quantification of GSSH, GSH, and H₂S. Data were analyzed with the software OriginPro 8.6.

Kinetics of the reaction of GSSH with H₂O₂

The decay of H₂O₂ was monitored using Prx5 as a sensor of H₂O₂ because the intrinsic fluorescence of this enzyme increases with oxidation (37, 57)_. The Prx5 variant (Prx5v) that was used contained an N-terminal 6×His-Tag and extra residues in the C-terminal end. The molecular mass of this protein was verified by SDS-PAGE and MALDI-TOF MS. The sequence was verified by trypsin digestion and MALDI-TOF MS and MS/MS analysis of the tryptic peptides (4800 MALDI-TOF/TOF, AB Sciex). The fast reaction with H₂O₂ was characterized (Fig. S4). Prx5v reacted with H₂O₂ with a similar rate constant to WT ((2.9 ± 0.7) × 10⁵ m⁻¹ s⁻¹, pH 7.1, 25 °C). Nevertheless, the formation of the disulfide from the sulfenic acid and the resolving cysteine was faster than in WT (127 ± 2 s⁻¹, pH 7.1, 25 °C, for Prx5v versus 14.7 s⁻¹, pH 7.4, 25 °C (57) or 21 s⁻¹, pH 6.9, 25 °C (37), for WT). This minimizes parallel reactions of the sulfenic acid and improves probe performance.

To prepare GSSH-containing mixtures, 10 mm GSSG was preincubated with 2 mm H₂S in sodium phosphate buffer (0.1 m, pH 7.4, 0.1 mm dtpa). After 1.5 h, 50 μm H₂O₂ was added. Aliquots of 2 μl were taken at increasing incubation times and mixed with 198 μl of reduced Prx5v (2–4 μm) in sodium phosphate buffer (50 mm, pH 7.4, 0.1 mm dtpa). Fluorescence (λ_ex = 280, λ_em = 340 nm) was immediately measured in a Varioskan Flash plate reader at 25 °C. Then, the pH of the reaction mixtures was measured. Calibration curves of H₂O₂ were simultaneously done in each experiment using the same dilution of reduced Prx5v (Fig. S5). Prior to the reaction with H₂O₂, an aliquot of the GSSH-containing mixture was analyzed by HPLC for quantification of GSSH, GSH, and H₂S. Controls with the concentrations of GSH or H₂S equivalent to those present in the GSSH-containing mixtures were performed under the same conditions. Data were analyzed using the software OriginPro 8.6.

The decay of H₂O₂ in the presence of excess GSSH was studied by two additional methods that yielded rate constants within the same order of magnitude as Prx5v (not shown), namely the formation of oxygen in the presence of catalase in an oxymeter and the fluorescence produced by Amplex UltraRed oxidation by H₂O₂ in the presence of horseradish peroxidase. Methods based on Amplex Red and xylenol orange essays had interference from species present in the mixtures.

Computational methods

MeSH/MeS⁻ and MeSSH/MeSS⁻ were used as models of thiol and persulfide, respectively. Electronic structure calculations were performed with Gaussian09 (80) whereas QM/MM molecular dynamics (MD) simulations were performed using LIO (https://github.com/MALBECC/LIO), a software developed by the Group of Molecular Modeling in the Universidad de Buenos Aires, compiled with Amber14 (81, 82). Dynamics visualizations and molecular drawings were performed with VMD 1.9.1 (83).

Computational comparison of the acidity of persulfides and thiols

All structures were optimized using DFT-based methodology. Computations were performed at the generalized gradient approximation level, using the PBE combination of exchange and correlation functional with a double-zeta plus polarization (dzvp) Gaussian basis set (84, 85). Frequency calculations were performed in each case and Gibbs energy changes were estimated by means of standard statistical mechanics formalism. The polarizable continuum solvent model was employed with the default parameters of aqueous solvation (86). Additionally, electronic structure calculations were performed employing the Møller-Plesset perturbation theory (at the MP2 level) with dzvp basis, and the ωB97x-D and M062X methods combined with a 6-31 G(d') basis set, which have been reported to yield good accuracy for thermochemistry and kinetic applications where noncovalent interactions are significant (87–89). Finally, we repeated the simulations with a more accurate CCSD methodology, also employing a 6-31 G(d') basis set.

Initial survey of the system in vacuum and implicit solvent

Structures of reactant complexes, transition states, and product complexes were optimized in vacuo and using polarizable continuum solvent model with aqueous solvation default parameters (86) at the DFT level. Computations were performed at the generalized gradient approximation level, using the PBE combination of exchange and correlation functional, with a dzvp Gaussian basis set (84, 85). Frequency calculations were performed in each case to ensure that the obtained structures for reactant complexes and product complexes corresponded to minima in the potential energy surface. Transition-state structures were confirmed by exploring the intrinsic reaction coordinate (90). Gibbs energies were estimated by means of standard statistical mechanics formalism, as implemented in the Gaussian09 suite. Single-point calculations on the PBE/dzvp optimized structures were calculated employing Møller-Plesset perturbation theory (at the MP2 level) with dzvp basis to evaluate activation barrier underestimations inherent to pure DFT functionals. We also employed the ωB97X-D and M062X methods combined with a 6-31 G(d') basis set, which have been reported to yield good accuracy for thermochemistry and kinetics applications where noncovalent interactions are significant (88, 89).

Multi-scale QM/MM MD: preparation of the initial system

Reactants were described by QM at the DFT PBE/dzvp level of theory and solvated with explicit classical (MM) water molecules described with the TIP3P model (91) in a truncated 25-Å octahedral box. Initial structures for the reactants were those previously optimized in Gaussian09 at the same level of theory. Periodic boundary conditions were used. The Lennard-Jones parameters (ε and σ) for the QM subsystem atoms were those of the general AMBER force field, i.e. 0.3200, 0.2500, 0.2104, 0.1700, 0.1094, and 0.0157 kcal/mol, and 2.220, 2.000, 1.7210, 1.8240, 1.9080, and 1.4870 Å, for Br, S, O, N, C, and H atoms, respectively (92). The system was relaxed optimizing first only the atoms integrating the QM subsystem, maintaining the MM subsystem fixed, and then optimizing both the QM and MM subsystems. Next, the MM subsystem was heated from 0 to 300 K during 0.1 ns of MM MD with the Berendsen thermostat (93), followed by a 1-ps-long QM/MM MD employing an uncoupled Berendsen thermostat, to ensure a reliable thermalization of the full system and to control the local kinetic energy of the relatively small QM subsystem.

Multi-scale QM/MM MD: Calculation of Gibbs energy profiles

Gibbs energy profiles were obtained with the umbrella sampling method (94, 95). The reaction coordinate was defined as the difference in the distance between the nucleophilic sulfur atom and the electrophilic center (the carbon atom bound to bromine in mBrB and the H-bonded oxygen in ONOOH and H₂O₂) and the distance between the electrophilic center and the closest atom of the leaving group.

Initial structures for the umbrella sampling calculations were extracted from a 25-ps-long steered QM/MM MD using a force constant of 200 kcal/mol/Ų. Windows were centered at different reaction coordinate reference values, spaced by 0.1 Šin most cases. Then, a quadratic bias potential function also centered in the reference values was added to the reaction coordinate, and the windows were carefully relaxed following a protocol that combined classical MD and QM/MM optimizations to improve solvation sampling at an affordable computational cost (96). A 5-ps-long QM/MM MD simulation was generated of each window with the uncoupled Berendsen thermostat, and then another 5-ps QM/MM MD simulation was performed employing the stochastic Langevin thermostat to ensure a canonical distribution (97). Finally, Gibbs energy profiles were computed employing the Langevin MD data and the umbrella integration method (98).

Data availability

The data that support the findings of this study are contained within this article and in the supporting information. Raw data are available upon request (mmoller@fcien.edu.uy, dario@qi.fcen.uba.ar, beatriz.alvarez@fcien.edu.uy).