The niobium and tantalum concentration in the mantle constrains the composition of Earth’s primordial magma ocean

Significance

Silicate Earth is widely considered identical to chondrites in its refractory lithophile element ratios. However, its subchondritic Nb/Ta signature deviates from the chondritic paradigm. To resolve this Nb deficit, its sequestration in Earth’s core under very reducing core-forming conditions has been proposed based on low-pressure data. Here, we show that under conditions relevant to core formation Nb is siderophile at high pressures under all redox conditions, corroborating Nb inventory in Earth’s core. Further core formation modeling shows that Earth’s core could have formed under moderately reducing or oxidizing conditions, whereas highly reducing conditions mismatch the geochemical observables; although Earth may have sampled a variety of reservoirs, it is problematic to accrete primarily from materials as reduced as enstatite chondrites.

Abstract

The bulk silicate Earth (BSE), and all its sampleable reservoirs, have a subchondritic niobium-to-tantalum ratio (Nb/Ta). Because both elements are refractory, and Nb/Ta is fairly constant across chondrite groups, this can only be explained by a preferential sequestration of Nb relative to Ta in a hidden (unsampled) reservoir. Experiments have shown that Nb becomes more siderophile than Ta under very reducing conditions, leading the way for the accepted hypothesis that Earth’s core could have stripped sufficient amounts of Nb during its formation to account for the subchondritic signature of the BSE. Consequently, this suggestion has been used as an argument that Earth accreted and differentiated, for most of its history, under very reducing conditions. Here, we present a series of metal–silicate partitioning experiments of Nb and Ta in a laser-heated diamond anvil cell, at pressure and temperature conditions directly comparable to those of core formation; we find that Nb is more siderophile than Ta under any conditions relevant to a deep magma ocean, confirming that BSE’s missing Nb is in the core. However, multistage core formation modeling only allows for moderately reducing or oxidizing accretionary conditions, ruling out the need for very reducing conditions, which lead to an overdepletion of Nb from the mantle (and a low Nb/Ta ratio) that is incompatible with geochemical observations. Earth’s primordial magma ocean cannot have contained less than 2% or more than 18% FeO since the onset of core formation.

Niobium and tantalum are among those “geochemical twins” (e.g., Zr and Hf, Mo and W) located vertically adjacent to each other in the periodic table that share similar chemical properties during planetary differentiation. As both refractory and lithophile elements, Nb and Ta may be assumed to have condensed into planetary bodies in chondritic ratio (1) yet solely remained in the silicate portion of planets after core–mantle (metal–silicate) differentiation. However, in contrast to other trace element ratios (e.g., Zr/Hf and Ce/Pb), which indicate the complementarity between Earth’s mantle and (continental or oceanic) crust with respect to chondritic meteorites, Nb/Ta ratios in all major reservoirs of silicate Earth (the crust, depleted mid-ocean ridge basalt mantle, and ocean island basalts) are invariably subchondritic (<19.9) (2). This apparent deficit of Nb relative to Ta in the bulk silicate Earth (BSE), known as the “Nb paradox,” has been attributed to 1) a hitherto unsampled reservoir with a superchondritic Nb/Ta ratio in the lowermost mantle formed by an ancient subducted crust as early as the Hadean (3–5) and/or 2) the sequestration of Nb into the core during core–mantle differentiation (6–8).

The metal–silicate partitioning behavior of Nb, a lithophile element, was first found to mimic that of V, a slightly siderophile element, at elevated pressures (25 GPa) (6).This invariably leads to an increase in Nb solubility in metal relative to Ta in a deep magma ocean and has been proposed as a reason for the subchondritic Nb/Ta ratio observed in the BSE. This requires, however, just as in the case of V, the magma ocean to start and remain very reducing (very low FeO concentration) for an extended period during core segregation. Reducing conditions were considered as the only pathway to an increase in the siderophility of V and Nb. Indeed, all experiments to date (performed in piston-cylinder or multianvil press up to ∼25 GPa) show that oxygen fugacity is the dominant parameter (that superimposes pressure [P], temperature [T], and composition) to incorporate Nb in the metal during core–mantle equilibration (7, 8), despite the dependence of partitioning on pressure and temperature (9–12). Further experiments, along with multistage core formation models confirmed that in order to match the Nb abundance and the Nb/Ta in the mantle by core formation alone, a highly reducing magma ocean (very low FeO concentration) was required, with a silicate liquid containing significantly less than 1 wt % FeO (7, 13, 14). The natural consequence of those findings was that the behavior of V and Nb (and to a lesser extent Cr and Ta) during core formation requires Earth to have accreted and remained very reduced for a significant amount of time.

The initiation of metal–silicate partitioning experiments in the laser-heated diamond anvil cell (LHDAC) extended the P and T conditions of metal–silicate experiments to those directly relevant (43 to 75 GPa and 3,000 to 4,400 K) to core formation on Earth (15). One of the new outcomes of this class of experiments was the significant increase in oxygen concentration in the metal at those conditions (16, 17) and its effect on the metal–silicate partitioning of trace elements. Other elements present in the metal (Si, S, and C) also affect metal–silicate partitioning, but their influences have been modeled and constrained extensively in the metallurgy literature (room pressure) and by large-volume (piston-cylinder and multianvil press) experiments at elevated pressure. Oxygen, on the other hand, requires extreme conditions of P–T to dissolve in the metal in sufficiently large amounts, and hence the effect of oxygen on trace-element metal–silicate partitioning was only recently quantified. The magnitude of those interactions with oxygen can be so dramatic in the final stages of core formation (highest P and T conditions) that the partitioning of siderophile (17, 18) and even nominally lithophile elements (19–22) is strongly affected. The magnitude of those effects is beyond merely quantitative and brings qualitative changes. Ref. 18 found that Cr and V become exceedingly siderophile at extreme P and T conditions, an effect largely due to the oxygen content of the metal. This provides a new pathway toward the sequestration of those elements in the core. To the traditional method of increasing their siderophility by partitioning under reducing conditions comes a new mechanism accomplishing the same by increasing the oxygen content of the core. Intriguingly, high oxygen contents in the core are indicative of rather oxidizing conditions, quite opposite to the classical pathway. Based on those two elements, ref. 18 relaxed the need for highly reducing conditions during prolonged periods of core formation on the basis of V and Cr partitioning.

The question now is whether the same holds for Nb and Ta, which are the remaining elements requiring such extremely reducing conditions during accretion and core formation, that is, whether increasing oxygen content of core-forming metal enhances the siderophile character of those two elements in a way that is compatible with the geochemical records (absolute concentrations and Nb/Ta in the mantle). We performed a series of metal–silicate partitioning experiments up to 94 GPa and 4,500 K in LHDACs and observed that both Nb and Ta also become more siderophile by interacting with oxygen dissolved in the liquid metal. Thermodynamic modeling of the global partitioning dataset (previous experiments augmented by our data) allowed us to unravel exceedingly large interaction parameters of Nb and Ta with oxygen in liquid iron, even larger than the ones found for Cr or V, and on the order of those found for U. Incorporating these into a multistage core formation model shows interestingly that highly reducing conditions, such as those posited in the literature fail to reproduce both the abundance of Nb and the Nb/Ta ratio in Earth’s mantle (both are too low). Highly oxidizing conditions can satisfy the abundance of Nb but not the Nb/Ta ratio, which becomes too high. Only starting magma ocean compositions between 2 and 18 mol % FeO can satisfy the observables.

Results

Five superliquidus experiments were performed at various P–T conditions (SI Appendix, Table S1) in LHDACs. The starting metal, an Fe–Ni–V–Cr alloy, was synthesized in a 150-ton end-loaded piston cylinder press (Materials and Methods), whereas the starting silicates were glasses synthesized in a gas-mixing aerodynamic levitation laser furnace; starting compositions (analyzed by electron microprobe) are given in SI Appendix, Table S2. Similar to previous superliquidus metal–silicate partitioning experiments performed in DACs (16, 17, 19, 20, 23), quench texture was found in all of our experiments. As shown by a backscattered scanning electron microscopy (SEM) image in Fig. 1, the typical morphology that the sample inherited from quenching is a spherical metallic blob (bright sphere) embedded in a molten silicate (gray area), which is separated by a layer of untransformed solid glass from the diamond anvils. The unique texture was formed by the rapid exsolutions of Si–O-rich and Fe–Ni-rich phases (<200 nm) in the metal and silicate during quenching, respectively. Large window (raster-scanned electron beam) analysis shows chemical homogeneity in both phases over the entire recovered sample. The chemical composition measured by electron probe microanalyzer (EPMA) is reported in SI Appendix, Table S3.

Fig. 1.

Backscattered electron field emission SEM image of a focused ion beam section recovered from a superliquidus metal–silicate equilibration at 47 GPa and 4,100 K in the LHDAC. The quench morphology consists of a metallic blob (bright sphere) embedded in the silicate melt.

The partitioning of Nb and Ta between metal and silicate occurs via an exchange reaction:

$$\begin{array}{c}{\text{MO}}_{\frac{n}{2}}+\frac{n}{2}\text{Fe}=\frac{n}{2}\text{FeO}+\text{M}\end{array},$$ [1]

where n is the valence of the cation M (Nb and Ta are both 5+) in the silicate melt. The metal–silicate partition coefficient of element M is D_M = x_M/x_MOn/2, where x the molar fraction. The exchange coefficient, K_D(M) = D_M/D_Fe^n/2, is a more suitable parameter to handle thermodynamically, because it conveniently removes the explicit dependence of partitioning on oxygen fugacity expressed by D_Fe, but more importantly because it is closely linked to the essential thermodynamic quantity governing reaction 1, the equilibrium constant K(M). The equilibrium constant K(M) of reaction 1 can be explicitly rewritten in terms of exchange coefficient (K_D) and activity coefficients (γ) in the silicate and metallic phases and expressed as a function of P, T, and silicate melt composition by

$$\begin{array}{c}logK\left(M\right)=log{K}_D\left(M\right)+log\frac{{\gamma }_M^{metal}}{{\left({\gamma }_{Fe}^{metal}\right)}^{\frac{n}{2}}}+log\frac{{\left({\gamma }_{FeO}^{silicate}\right)}^{\frac{n}{2}}}{{\gamma }_{M{O}_{\frac{n}{2}}}^{silicate}}=a+\frac{b}{T}+\frac{c·P}{T}+d\cdot \left(\frac{nbo}{t}-2.7\right)\end{array},$$ [2]

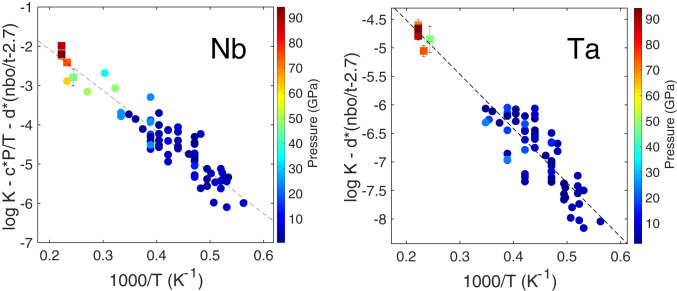
where a is the entropy, b the enthalpy, and c the volume change of reaction 1. Following previous studies of the valence of Nb and Ta in silicate melts (7, 11, 12, 24), we fixed the valence of Nb and Ta to pentavalent (5+; SI Appendix). The activity coefficient ratio in silicate (third term in Eq. 2) for high-valence cations may vary largely and is hard to be evaluated due to the unavailability of relevant data. To account for the compositional effect of silicate melt on partitioning of highly charged cations, we introduced an empirical parameter nbo/t (25), the molar ratio of nonbridging oxygens (nbo) per tetrahedrally coordinated cations (t), which is an empirical proxy valid at low pressures where silicon is tetrahedrally coordinated. The nbo/t expresses the degree of polymerization of a silicate melt and was corrected to a value of 2.7 corresponding to the nbo/t of a pyrolitic melt (the correction was not used in all LHDAC data above 25 GPa; details are given in SI Appendix). Since the activity coefficients in the metal can be significantly influenced by light components (e.g., Si, O, S, and C) dissolved in liquid iron (26–29), we followed the interaction parameter approach (SI Appendix) to calculate the activity coefficients γ_Fe and γ_i (30). The calculated equilibrium constant K using the interaction parameter model was fitted to the thermodynamic model described in Eq. 2, using multivariate least-squares linear regression (reported in Table 1). Previously published metal–silicate partitioning experiments with samples containing Nb (6, 7, 9, 11, 12, 16, 18, 31) or Ta (6, 7, 9–12) are compiled in Dataset S1; these data are plotted in Fig. 2, along with our data. It is noticeable that the present work fills in the gap of partitioning data for both Nb and Ta at the conditions of core formation (15).

Table 1.

Thermodynamic parameters of the metal–silicate partitioning of Nb and Ta

Element (i)	a	b, K	c, K/GPa	d	${\epsilon }_i^O$	${\epsilon }_i^{Si}$	${\epsilon }_i^C$	${\epsilon }_i^S$	${\epsilon }_i^i$	lnγi0	N	R2
Nb	0	−10,314 (108)	−67 (7)	−0.39 (4)	−34.9	−6.1	−5.2	0	−0.7	−1.61	74	0.852
Ta	−2.71 (26)	−9,270 (607)	0	−0.18 (5)	−60.6	−8.7	−10.5	0	79.7	−3.22	72	0.906
O						−5			−1
Si									12.4

Parameters of Eq. 2 for Nb and Ta partitioning: a, b, and c represent the entropy, enthalpy, and volume change of reaction 1; values in parentheses are SEs (1σ) obtained from the least-squares regressions. ${\epsilon }_i^j$ is the interaction parameter of element j on element i and γ_i⁰ the activity coefficient of solute i at infinite dilution in liquid iron; interaction parameters in boldface are calculated from this study and other values are taken from metallurgy data (41). Interaction parameters and activity coefficients are reported at 1,873 K (details are given in SI Appendix). N is the number of data used in each thermodynamic modeling and R² the coefficient of determination of the fitted model.

Fig. 2.

Equilibrium constants (log K) for Nb and Ta as a function of reciprocal temperature (1,000/T). The dashed lines correspond to least-squares linear regressions to the data, and error bars (only for the data from this study, shown where larger than symbols) were propagated from the analytical uncertainties in SI Appendix, Table S3. Pressure is reported in symbol color. Experimental data for Nb are taken from refs. 6, 7, 9, 11, 12, 16, 18, and 31 (circles) and this study (squares). Ta data are taken from refs. 6, 7, and 9–12 (circles) and this study (squares). As shown in the y-axis legend, we are plotting equilibrium constants adjusted to zero pressure and pyrolitic silicate melt compositions, in order to compare things that are comparable.

P–T Dependence.

The expanded P–T conditions obtained in LHDAC experiments allow for better constraints on the thermodynamic conditions during core–mantle (metal–silicate) differentiation. As shown in Table 1, the pressure effect (parameter c) on the partitioning of Nb is found to be negative, that is, Nb becomes less siderophile with increasing pressure, which is consistent with previous low-pressure results (9–12) but to a lesser magnitude, while for the partitioning of Ta the influence of pressure is statistically negligible, as evidenced by the P value of 0.8 (return to the null hypothesis) when incorporating the pressure term in the multivariate regression.

For both Nb and Ta, temperature increases their affinity for metallic phase (b is negative). The dependence of log K on temperature for Nb and Ta agrees with piston-cylinder and multianvil data (9–12) but is in contrast to ref. 7, who found negligible pressure and temperature effect. Because log K has a multivariate dependency on P, T, and nbo/t, and in order to compare things that are comparable, we corrected the dataset to zero pressure and pyrolitic silicate composition (nbo/t = 2.7) and plotted log K as a function of reciprocal temperature in Fig. 2. Plotting partitioning as a function of temperature is the classical way of presenting the data, but for the sake of completeness we also reported the same analysis as a function of nbo/t (by correcting to zero pressure and temperature; SI Appendix, Fig. S2) and as a function of P (by correction to zero temperature and pyrolitic composition with nbo/t = 2.7; SI Appendix, Fig. S3).

Metal Composition Dependence.

While the starting metal contained neither oxygen nor any lithophile elements (SI Appendix, Table S2), oxygen, magnesium, and aluminum were observed along with siderophile elements in the recovered metal (SI Appendix, Table S3). The increasing solubility of these elements, especially oxygen, is intrinsically a temperature effect (16, 19). Light elements (e.g., C, S, Si, and O) dissolved in the liquid iron are known to deviate the iron alloys from an ideal solution regarding metal–silicate partitioning. Using the activity model described in SI Appendix, we have modeled the effect of metal composition by fitting the interaction parameters, a constant that describes the interactions among solutes. In Table 1, the fitted absolute values of interaction parameter ${\epsilon }_i^O$ for Nb and Ta are much larger than those of ${\epsilon }_i^{Si}$, ${\epsilon }_i^S$, and ${\epsilon }_i^C$, which means that oxygen dissolved in liquid iron has more pronounced influence on the partitioning of Nb and Ta than silicon, sulfur, or carbon does. As a result of their interactions with oxygen, Nb and Ta become more siderophile, though to different extents (the interaction parameter ${\epsilon }_{Ta}^O$ is almost twice that of ${\epsilon }_{Nb}^O$).

Implication for Core Formation Modeling.

The thermodynamic models of Nb and Ta metal–silicate partitioning used in recent models were derived from experiments performed at low to moderate pressures (<25 GPa), significantly lower than the putative conditions of core formation on Earth (40 to 75 GPa). As previously indicated, those thermodynamic models only allow a single pathway for Nb incorporation in the core, that of highly reducing initial conditions that were sustained for an extended period of time, to explain the subchondritic Nb/Ta ratio in the mantle. This has given new impetus for core formation occurring under very reducing conditions (7, 14). Here, our all-encompassing thermodynamic model (based on the previous data augmented by the high-pressure data obtained by LHDAC experiments) offers a second pathway for accomplishing the same requirement—that of oxygen incorporation in the metal.

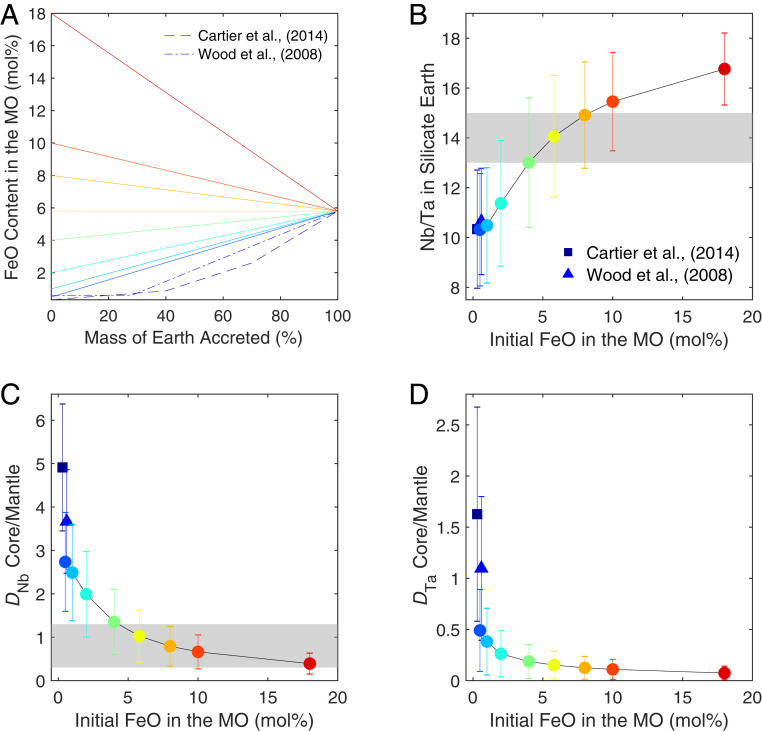
We ran a campaign of multistage core formation models (15) using the thermodynamic parameters in Table 1. We started with different initial FeO concentrations in the magma ocean (ranging from 1 to 18 mol %) and allowed them to evolve linearly throughout accretion to reach the present-day value of 6 mol % at the end of accretion. Accordingly, the fO₂ is a free parameter in our models; however, the more reducing conditions follow closely the evolution of fO₂ proposed by ref. 14. We also tested two models proposed by refs. 7 and 10, where the initial FeO content is extremely low and the evolution of magma ocean FeO is sublinear (Fig. 3A). For each one of those magma ocean compositional models, we ran 136 multistage core formation models where the final depth of the magma ocean varied from 0 to 135 GPa (with 1-GPa increments); because we also tracked Ni and Co metal–silicate partitioning at the same time, we discriminated a range of pressures providing “valid” models, that is, those where their abundances matched the terrestrial mantle values.

Fig. 3.

(A) The evolution of FeO content in the magma ocean (MO) during Earth’s accretion. The color is coded according to redox states of the MO, with warmer colors corresponding to more oxidizing conditions. (B) Nb/Ta ratio in the BSE, and core–mantle partition coefficients of Nb (C) and Ta (D) at the end of Earth’s accretion, as a function of initial FeO content in the magma ocean. Each point in B–D corresponds to an output of the multistage core formation model with a linear evolution of fO₂ in A, except for the squares and triangles that follow the fO₂ paths proposed by refs. 7 and 10, dashed and dashed-dotted lines in A, respectively. The uncertainties are the intervals of y in the pressure range (40 to 70 GPa) of the MO allowed by the observables of Ni and Co partitioning (SI Appendix). The horizontal bars correspond to the targets, that is, present-day bulk D between core and mantle or subchondritic Nb/Ta ratio in the BSE. The observed subchondritic Nb/Ta ratio and Nb abundance in the BSE are matched with the initial FeO concentration from 2 to 18%.

For each compositional model, we therefore obtained a range of Nb and Ta concentrations in the mantle (corresponding to each model’s valid range of final magma ocean pressures; SI Appendix, Fig. S4), which are reported in Fig. 3. The bulk core–mantle partition coefficient of Nb and Ta, as well as the Nb/Ta ratio in the BSE by the time Earth’s core was formed, were plotted (Fig. 3) as a function of initial FeO content in the magma ocean. It is clear from this that Nb and Ta are more siderophile as the starting conditions are reducing (low FeO), evidenced by the high Ds in Fig. 3 C and D. On the other hand, the Nb/Ta ratio in the magma ocean rises with increasing initial FeO (Fig. 3B). Very reducing conditions prevailing for a long time (7, 10) end up with too high a D_Nb, or too low an Nb concentration in the mantle and a Nb/Ta ratio that is too subchondritic, lower than the overserved value. On the other end of the compositional range, a very oxidized magma ocean (18 mol % initial FeO) could match the mantle abundance of Nb but ends up with a subchondritic Nb/Ta ratio in the mantle which is too high compared to the observed value. The only magma ocean compositional models that satisfy both constraints, the Nb abundance in the mantle and its Nb/Ta ratio, are those where the initial FeO concentration is between 2 and 18 mol %. Interestingly, this range is in impeccable agreement with core formation models where the Si isotopic composition of the mantle was used as a constraint (32). We therefore conclude that neither extremely reducing nor highly oxidizing conditions can account for Earth’s subchondritic Nb/Ta signature and Nb inventory. The magma ocean may still have started more reduced or more oxidized than the present-day mantle (and evolved toward it), but any extremes have to be ruled out.

In order to quantify the extent of oxygen interaction on the outcome of core formation models, we ran the same series of models, setting the oxygen interaction parameters to 0. Doing this, the sole difference is that the effect oxygen dissolved in the core stops acting on Nb and Ta partitioning. The results are plotted in SI Appendix, Fig. S5, following the same rationale of Fig. 3. We observed a less protracted solution space, biased toward reducing conditions. The affinity for liquid iron decreases for both Nb and Ta, though to different degrees, which propels their ratio upward and shifts the solution to more reducing conditions. It highlights that oxidizing conditions, with their associated oxygen enrichment of the cores, increase the siderophile behavior of both Nb and Ta, which allows for a much larger range of magma ocean compositions to match the relevant geochemical observables. This gracefully explains why previous core formation scenarios found solutions only through initially reduced conditions (7, 10, 14, 31), and why the actual solution space is broader now and encompasses a wider range of redox conditions going all of the way into “oxidizing” models.

The other alternatives for the Nb depletion in the BSE include 1) volatile loss of Nb during incomplete accretion and 2) a “hidden” reservoir with superchondritic Nb/Ta ratio in the lower mantle. The first assumption is not supported by the calculated condensation temperatures for Nb and Ta (33). As there is no direct evidence for a large-scale superchondritic Nb/Ta reservoir in Earth (3–5), heat flux data seem to argue against an early-formed hidden layer enriched in incompatible elements (34). Our data and the models it reveals show that the niobium deficit in Earth’s mantle and its subchondritic Nb/Ta ratio can be explained by core formation alone. This can take place in an initial magma ocean with composition bracketing that of enstatite and carbonaceous/ordinary chondrites, that is, moderately reducing or oxidizing conditions, without the ad hoc hidden reservoir. It does exclude, however, the most extreme conditions that have been deemed most plausible until now.

Materials and Methods

Starting Materials.

The silicate starting materials were synthesized using levitation method according to a pyrolitic composition (35) without FeO. The metallic starting materials were either commercial reagent Fe-rich metal balls (91% Fe + 9% Si) or trace-element-bearing iron–nickel alloy synthesized in a piston-cylinder apparatus at Institut de Physique du Globe de Paris (IPGP) (details for sample synthesis can be found in SI Appendix). Starting materials were analyzed by an EPMA at Camparis to confirm the chemical homogeneity (SI Appendix, Table S2). The silicate glasses were polished down to ∼20 μm thick and subsequently machined into small disks suitable for DAC loading. Synthesized metal was recovered and finely ground to serve as starting metal for DAC experiments. In order to test their lithophility, that is, the direction of the partitioning, all of the interested metals (Nb and Ta) were added in the starting silicates (SI Appendix, Table S2).

LHDAC Experiments.

Symmetric DACs were used to generate high pressure. Diamond anvils with flat culet diameters of 200 μm or 300 μm were used. Re gaskets were preindented to 40 to 50 μm thick with a gasket hole of ∼100 μm or 150 μm in diameter to serve as a sample chamber. The silicate glasses were double-polished to 18 to 23 μm and cut into disks adapted to the diameter (10 μm smaller) of the sample chamber (gasket hole), using a picosecond laser micromachining instrument. The disks were loaded directly on both diamond culets, and a single chunk of metal was loaded in the center of one of the disks; once closed, the sample consists of a silicate capsule with the metal sitting in its middle (both radially and axially). The silicate disks also served as thermal and chemical insulator during laser heating.

Sample assembly was compressed to target pressures and subsequently heated from both sides using a fiber laser (λ = 1,070 nm, 200 W) with a focused beam size of ∼20 μm in diameter. Typical heating lasted up to several minutes, with temperature ramping at first and then held at maximal (target) temperature for at least 60 s before instantaneous (a few 10s of microseconds) quench. Time series experiments under similar extreme conditions have demonstrated the achievement of equilibrium in a few seconds (9, 36). To make sure the pyrolite fully melted, all runs were conducted well above the liquidus of pyrolite (e.g., 4,500 K at 94 GPa) (37, 38). Temperature was measured every second (simultaneously from both sides) by fitting the visible portion of the black-body radiation (500 to 750 nm) of the hot spot with an uncertainty around ±250 K (39). Pressure was determined by diamond Raman spectroscopy of the anvils before heating (40) and corrected for thermal pressure following ΔP = 2.7 MPa/K (16, 37, 38). Samples were recovered from the laser-heated areas (Fig. 1) using a focused ion beam instrument (Zeiss Auriga 40 at IPGP) and analyzed by an EPMA (Cameca SX-five) at Camparis. Details of sample recovery and chemical analysis are described in SI Appendix.

Data Availability.

All study data are included in the paper, SI Appendix, and Datasets S1 and S2.