A symmetry-derived mechanism for atomic resolution imaging

Significance

An “image” is a representation of an object, providing information about its form and structure. In many imaging systems, image contrast arises when the object alters the energy, phase, and/or amplitude of the probing radiation. Here, we introduce an image contrast that arises when the object alters the symmetry of the probing radiation. We demonstrate this in scanning transmission electron microscopy, visualizing changes in object symmetry at the picometer scale. These atomic-resolution symmetry images provide information that can be important in understanding any material where symmetry plays a significant role, including symmetry-breaking events, such as point and planar structural defects, strain, and local electric and magnetic fields.

Abstract

We introduce an image-contrast mechanism for scanning transmission electron microscopy (STEM) that derives from the local symmetry within the specimen. For a given position of the electron probe on the specimen, the image intensity is determined by the degree of similarity between the exit electron-intensity distribution and a chosen symmetry operation applied to that distribution. The contrast mechanism detects both light and heavy atomic columns and is robust with respect to specimen thickness, electron-probe energy, and defocus. Atomic columns appear as sharp peaks that can be significantly narrower than for STEM images using conventional disk and annular detectors. This fundamentally different contrast mechanism complements conventional imaging modes and can be acquired simultaneously with them, expanding the power of STEM for materials characterization.

In scanning transmission electron microscopy (STEM), images can be generated by scanning an electron beam across the object and, at each position of the electron beam, detecting the scattered electron-intensity distribution after transmission through the specimen. The most common STEM imaging modes integrate the scattered intensity in the diffraction plane across a particular angular range, using either disk or annular detector geometries, to generate phase-contrast bright field (BF) and adsorptive-contrast high-angle annular dark-field (HAADF) images, respectively (or a mix of phase and adsorptive contrast, in the case of annular bright field [ABF]). Recently, the advent of fast read-out, high-dynamic-range detectors (1–6) has enabled the full angular distribution of scattered intensity to be recorded at each beam position. This represents a revolution in STEM, providing access to a vast and rich palate of additional specimen information (7). Fast detectors have already been applied, for example, to improve STEM spatial resolution using ptychography (8–12) to map electric (13, 14) and magnetic fields (4, 15–18), strain (11, 18–21), polarization domains (22), and octahedral tilts (23), representing just the beginning of this powerful new era in STEM.

Here, we propose an image-contrast mechanism for atomic-resolution STEM based on a measurement of the degree of symmetry in the scattered intensity distribution at each point of a scan: Symmetry STEM (S-STEM). By virtue of the strong electron–specimen interaction and resultant dynamical scattering, the symmetry of the illuminated specimen volume is encoded in the symmetry of the scattered intensity distribution, independent of the specimen thickness and accelerating voltage (24–27). In this paper, the scattered intensity distribution is in the form of a convergent beam electron diffraction (CBED) pattern (Fig. 1A), the most common case for STEM (28), but the approach can be applied, in principle, to any form of scattered intensity distribution in any optical plane and also to other scanning-microscopy techniques.

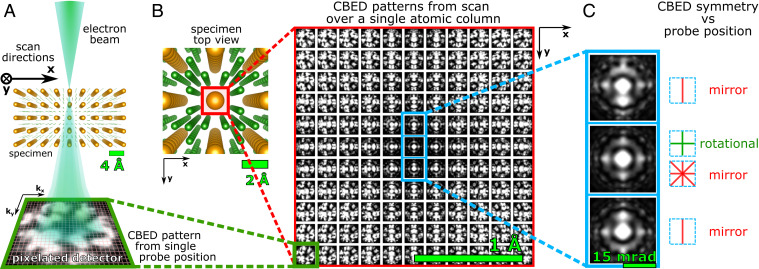
Fig. 1.

Schematic of a S-STEM experiment. (A) An atomic-scale electron probe scans the specimen. A convergent beam-electron diffraction pattern is imaged in the far field by a fast pixelated detector (green box) for each point of the scan. (B) Grid of simulated CBED patterns resulting from a scan across a Ce atomic column (red box) in a CeB₆ crystal. Each CBED pattern is arranged according to the position of the electron probe in real space; scan step size is 20 pm. (C) CBED patterns for the probe on the center of the Ce column (Middle) and shifted 20 pm either side of the center (but still on the atomic column) (Top and Bottom), showing the rapid change in pattern symmetry (4mm to m).

The “degree” of symmetry in a pattern can be analyzed by a comparison of the scattered intensity distribution with itself after an applied symmetry operation (29). For a given two-dimensional (2D) pattern $\mathbf{A}$, the symmetry intensity $I$ is given by:

$$I=max\left[\mathbf{A}*\underset{\mathit{operation}}{\overset{\mathit{symmetry}}{\hspace{0.17em}}}\left(\mathbf{A}\right)\right],$$ [1]

where $*$ is a normalized cross-correlation and the symmetry operation can be chosen (for example, a rotation or a mirror). If $\mathbf{A}$ is invariant under the symmetry operation, then the intensity will be maximum, $I=1$, and $I<1$ if the symmetry is not matched. Analogous algorithms have been applied to visualize biological macromolecules (30, 31) and in measurements of local polarization domains (32, 33). Here, our goal is different, namely, to deliver an image-contrast mechanism that derives from spatial variations in symmetry, measured at picometer intervals.

In the case of S-STEM, the intensity will be calculated from each CBED pattern at each point of a 2D scan, $\left(x,y\right)$, which can be plotted as an image $\mathbf{I}=I_{x,y}$. Each CBED pattern resolves the electron distribution in reciprocal space at a particular point, $\left(x,y\right)$, of a scan $\mathbf{A}={\mathbf{A}}_{x,y}\left(k_x,k_y\right)$, denoting one point in a so called four-dimensional (4D) STEM dataset (34). Data processing was based on methodology introduced in refs. 15, 35, and 36 and implemented in graphics processing unit (GPU)-accelerated ArrayFire library (37). The application of Eq. 1 to a 4D-STEM dataset generates an entirely different image-contrast mechanism, neither phase-contrast nor adsorption-contrast, which provides access to new specimen information at the atomic level.

Results

Calculations.

The sensitivity to local symmetry that underpins the S-STEM contrast mechanism is illustrated with a STEM simulation on a test case, CeB₆. CeB₆ has both small (B–B: 1.2 Å) and large (Ce–Ce : 4.1 Å) column spacings and comprises light (B = 5) and heavy (Ce = 58) atoms, which are challenging to image simultaneously in BF or ADF STEM. Fig. 1B shows an array of simulated CBED patterns corresponding to a 0.67-Å full-width at half-maximum (FWHM) probe scanning across the Ce column in $⟨100⟩$-oriented CeB₆. Each simulated CBED pattern is arranged according to the corresponding real-space position, $\left(x,y\right)$, of the probe, with the Ce column position centered at the center of the array. The GPU-accelerated parallel implementation of the multislice simulations were performed by using the Prismatic software package (38–40) using parameters described in STEM Simulations. The arranged CBED patterns give a clear sense of how the symmetry changes as the probe is scanned across the Ce atomic column in 0.2-Å steps (Fig. 1C). For example, there is an immediate shift from fourfold and multiple mirrors (4mm) to a single-mirror symmetry (m) as the probe center moves from the absolute center of the atomic column to just 20 pm off-center (but is, nevertheless, still located on the atomic column). This highlights the acute sensitivity to local specimen symmetry that is delivered by dynamical scattering (25–27, 41) and forms the basis of image contrast in S-STEM. (Calculations illustrating this further are given in SI Appendix, section 2, Fig. S1 A and B.)

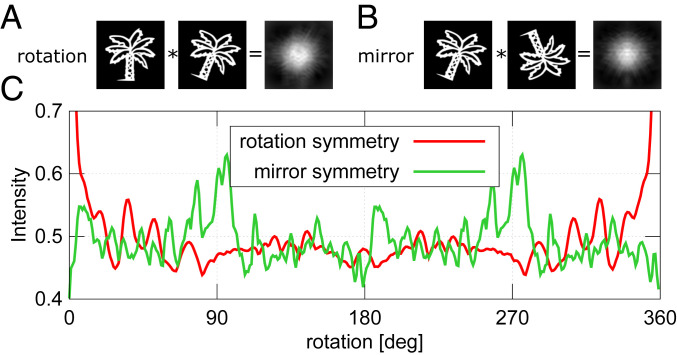
Eq. 1 provides an extremely efficient method for distilling the local symmetry information present in the pattern. This is illustrated generically in Fig. 2 for an intensity distribution, ${\mathbf{A}}_{\mathbf{p}}$, in the form of a palm tree. Two classes of symmetry are tested, a rotation and mirror symmetry. These symmetry operations can be tested for an arbitrary angle on this arbitrary pattern, ${\mathbf{A}}_{\mathbf{p}}$ (e.g., Fig. 2A shows a $20°$ rotation correlation and Fig. 2B a horizontal mirror at $20°$ rotation correlation for the palm-tree pattern). The cross-correlation is calculated for $0°$ to $360°$ (Fig. 2C). It can be seen that even if the pattern does not possess a perfect symmetry element, there still exist local maxima in the analysis. For the palm-tree pattern, this signal arises when the leaves are overlapping after application of a given symmetry operation. It should be noted that only $0°$ to $180°$ angles need to be calculated because only the relative rotation matters. $1°$ clockwise and $1°$ anticlockwise rotations have the same maximum of cross-correlation (ignoring interpolation errors). For additional notes about this symmetry analysis, please see SI Appendix.

Fig. 2.

Example of symmetry search for a palm-tree pattern. A and B show cross-correlation patterns for rotation and mirror symmetry, respectively. The pattern was rotated by $20°$. Mirror symmetry was tested along the vertical axis of the pattern after the rotation. (C) Maximum cross-correlation plot for $0°$ to $360°$ rotation. $I$ is only shown for the range containing maximum variations.

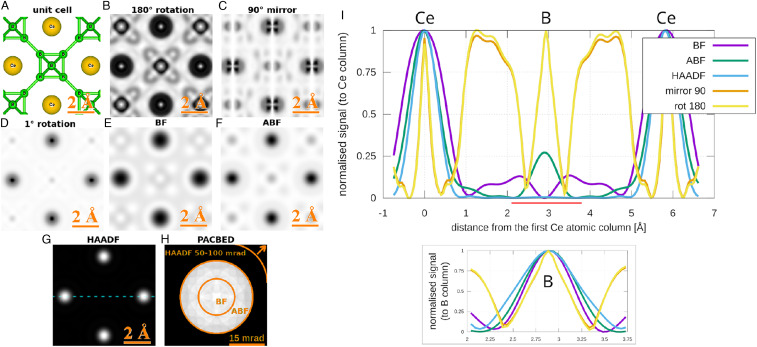
To demonstrate S-STEM, the symmetry analysis of Eq. 1 will now be applied to the simulated scanning CBED dataset (Fig. 1) across a field of view slightly larger than a CeB₆ unit cell (Fig. 3A), again using the parameters described in STEM Simulations. S-STEM images corresponding to $180°$ rotation, $90°$ mirror, and $1°$ rotation were generated (Fig. 3 B–D, respectively). For comparison, standard STEM BF, ABF, and HAADF images were also reconstructed (Fig. 3 E–G, respectively) by integrating across the angular ranges indicated in (Fig. 3H) for each probe position.

Fig. 3.

(A) Schematic of CeB₆ unit cell in $⟨100⟩$ orientation. (B–D) Reconstructions of S-STEM images for different applied-symmetry operations. E–G show reconstructions of conventional STEM images with integration areas shown on the position-averaged diffraction pattern in H. (I) Comparison of the corresponding Ce–B–Ce image peaks for S-STEM (B and C) and conventional images (E–G) (line in G shows where the profiles were taken). The line profiles were normalized and inverted to demonstrate the Ce peak widths in the main part of I, and the same is provided for the B peak in the smaller graph. (The smaller graph for B was taken from the area defined by the red line.)

As anticipated, the S-STEM images exhibited atomic-scale contrast, revealing local maxima wherever some degree of the applied symmetry element is present, reaching a maximum value near one when there is an identity, such as on the Ce column at $180°$ rotation and $90°$ mirror. $180°$ rotation symmetry shows exceptionally intense and sharp contrast for Ce and small local maxima at all B positions, and also it highlights the $180°$ symmetry with a broad maxima halfway between Ce atomic columns along $⟨100⟩$ (Fig. 3B). The $90°$ mirror symmetry shows bright contrast where mirror planes within the lattice match the symmetry (Fig. 3C). An interesting contrast arises when a small rotation symmetry of $1°$ is measured (Fig. 3D), giving extra sensitivity to the rate of change of the local symmetry. Strong “intensity” appears where the CBED pattern is rotationally symmetric or it varies slowly with angle $\left(k_x,k_y\right)$—namely, at the position of asymmetric B-atom sites, with weak intensity at the Ce sites, where the pattern varies rapidly.

Importantly, local maxima at atomic sites in the S-STEM images are exceptionally sharp with low-intensity “moats” around them. This is particularly the case for the peaks at Ce columns with a FWHM of $\sim$0.25 Å (Fig. 3I), which are significantly narrower than the peaks in the corresponding conventional BF, ABF, and HAADF STEM images (using a diffraction-limited probe with FWHM 0.8 Å [Fig. 3I]). Local maxima due to the presence of a symmetry element, but in the absence of an atomic column, do not show the “moat” because the rate of change of specimen symmetry is more slowly varying than in the presence of an atomic column. This enables atom sites to be distinguished from atom-free symmetry sites. This distinction can be further checked when S-STEM images derived from different symmetry elements are compared.

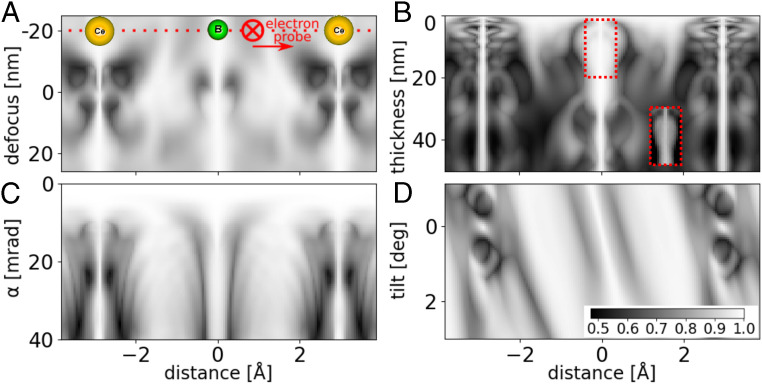
We examined further the imaging properties of S-STEM by calculating a line scan over Ce–B–Ce atomic columns in $⟨100⟩$ CeB₆ for different defocus and probe size and sample thickness and tilt (Fig. 4) and electron energy (SI Appendix, section 2, Fig. S1 A and B). The symmetry element was chosen to be a $180°$ rotation, and the base parameters were as specified in STEM Simulations and kept constant unless otherwise noted. (Analogous calculations for a thicker specimen of 20 nm for defocus and tilt are shown in SI Appendix, section 3, Fig. S2A.) For comparison, we have also calculated the corresponding BF, ABF, and ADF STEM line scans (SI Appendix, section 4, Fig. S3).

Fig. 4.

S-STEM intensity for a scan across Ce–B–Ce atoms along $⟨100⟩$. (A) Intensity versus defocus (varied between $-25\hspace{0.17em}\text{nm}$ and 27 nm with the sample located at 0 to 2.8 nm). Convergence semiangle is 15 mrad. (B) Intensity versus thickness (varied 0.4 to 50 nm; 1 to 200 unit cells). Convergence semiangle is 15 mrad. (Locally enhanced contrast from a red box is in B, Inset). (C) Intensity versus convergence semiangle for 2.8-nm-thick sample. (D) Intensity versus tilt for 2.8-nm-thick sample and 15-mrad convergence semiangle.

Dependence on thickness, defocus, and energy.

As S-STEM probes local symmetry within the sample, the contrast does not change in the vicinity of the center of atomic sites due to the change of defocus (Fig. 4A and SI Appendix, Fig. S2A) nor thickness (Fig. 4B) nor energy (SI Appendix, Fig. S2B). This is a consequence of the fact that, while the scattered intensity distribution can vary rapidly with thickness, accelerating voltage, and defocus, its’ symmetry remains invariant. This is a great advantage over standard methods, for which the sign and magnitude of the signal can change. For all thicknesses, the intensity peaks at atomic sites are an almost constant, extremely narrow width ($\sim$0.25 Å), with some local variations in the vicinity of the B octahedra likely due to scattering onto nearby high-symmetry sites. Nevertheless, even in the presence of this “cross-talk,” the narrow peak persists (Fig. 4 B, Inset).

Resolution and probe size.

S-STEM is an example of a “two-step” imaging system (as defined by Gureyev, Paganin, and colleagues in refs. 42 and 43) with resolution a consequence of both the experimental system and the virtual postprocessing (SI Appendix, section 5). The sharpness of an intensity maxima and consequent ability to resolve two features in S-STEM depends on the ability of the probe to detect a symmetry change. In other words, it depends on the probe size relative to the rate of change with position of the symmetry of the local specimen potential. The resolution of S-STEM images is therefore only a function of the direct electron-optical imaging system in so far as this system defines a probe size [which is set by the collective effect of the spatial coherence function, probe-forming aberrations and aperture size (44)].

In the aberration-free, spatially coherent calculations, the convergence semiangle defines the probe size and was varied from 0.5 to 40 mrad (Fig. 4C). The signal is constant and identity at $<4$ mrad ($<2.4$ Å probe FWHM) because the probe is greater than the unit cell in this perfect crystal, so no change in symmetry can be detected. Put another way, the CBED patterns have nonoverlapping CBED disks and, hence, do not change with position.

From the calculations, it can be seen that when the convergence semiangle ($>4$ mrad) generates a probe FWHM ($<2.4$ Å) comparable to the atomic radius ($\sim$2.35 Å van der Waals), we start to resolve clearly the two Ce columns. With higher convergence ($\sim$7 mrad), the probe FWHM ($\sim$1.7 Å) approaches two-thirds of the atomic radius, and the image peaks sharpen significantly to $\sim$0.4 Å FWHM (Fig. 4C, compared with $\sim$1.3 Å FWHM for the corresponding image peaks in BF-, ABF-, and ADF-STEM images in SI Appendix, section 4, Fig. S3 B–D). This trend continues to $\sim$22 mrad, where the probe FWHM is 0.44 Å, less than a quarter of the atomic radius. Here, the image peak width is $<$0.2 Å, which is half of the diffraction-limited probe size set by this convergence angle and a fifth of the image peak width for conventional BF-, ABF-, and ADF-STEM modes (SI Appendix, section 4, Fig. S3 B and C). The sharpness of the peak reduces for convergence angles larger than $\sim$25 mrad, possibly due to scattering onto nearby atomic sites promoted by the larger transverse momentum of the incident probe.

Dependence on tilt.

Tilt of a sample is a crucial parameter to study, as it changes the excitation errors and, hence, the symmetry of the scattering matrix and resulting CBED pattern. The sample was tilted from the $⟨100⟩$ zone axis by $-1°$ to $3°$ in the plane of the line scan (Fig. 4D and SI Appendix, Fig. S2B). When the sample is tilted more than $\sim 0.05°$, the sharp symmetry peak located at the Ce atomic column position starts to disappear; meanwhile, an adjacent broader and less intense maximum develops, which is displaced relative to the position of the initial maxima and the top of the tilted Ce column. The B peak broadens and is displaced in the same way as Ce, but persists (likely due to the B octahedra acting effectively as a single scatterer). In some crystalline specimens, this sensitivity to tilt could be helpful for the precise alignment of the crystal along a zone axis, without the problem of significant defocus change with tilt (Fig. 4A).

We also considered the possible influence of noise, phonon scattering, and aberrations on S-STEM contrast and found that, in most cases, it was not significant (SI Appendix, sections 6, 7, and 8, respectively).

Experiment.

Finally, we compared the S-STEM analysis of simulated data with experimental data from CeB₆ (Fig. 5). The scanned CBED data were collected at 300 kV on an early generation double-spherical aberration-corrected FEI ${\mathrm{T}\mathrm{i}\mathrm{t}\mathrm{a}\mathrm{n}}^3$ 80-300 field emission gun TEM (FEGTEM) equipped with a pixelated electron microscope pixel array detector (EMPAD) (4). Aberrations were largely corrected within the convergence semiangle of 15 mrad. Conventional BF and ABF STEM images were reconstructed (Fig. 5 A and B, respectively) to compare with the S-STEM signals with the same symmetry operations as applied in Figs. 3 and 5. (The HAADF signal was not collected here because the large angular field of view required would constrain the symmetry measurement from the central disk area.) The $1°$ and $180°$ rotation images (Fig. 5 D and E, respectively), show contrast closely related to the theoretical calculations (Fig. 3). In particular, the $180°$ rotation image shows extremely sharp peaks surrounded by dark “moats,” corresponding to the symmetry maxima when the probe is positioned at the absolute center of the Ce atomic column and the break of symmetry as soon as the beam shifts slightly from the center, but remains on the column, as seen in the calculations (Fig. 3F). We can also see the symmetric position of the central B-atomic column; however, the asymmetric sites of other B-atomic positions are not as clear, most likely due to imperfect instrument and specimen stability and a lack of local $180°$ rotation symmetry in the position. The $1°$ rotation image shows very strong signal-to-noise at the Ce columns and also shows some residual specimen tilt effects. A nonaveraged and averaged (from five unit cells) unit-cell image is compared with the calculated image in Fig. 5F.

Fig. 5.

Experimental S-STEM imaging. A 128 × 128 probe positions dataset collected on FEI ${\mathrm{T}\mathrm{i}\mathrm{t}\mathrm{a}\mathrm{n}}^3$ 80-300 FEGTEM equipped with a pixelated EMPAD detector (4). The probe convergence semiangle was 15 mrad. (A) Reconstruction of BF signal from 0 to 7.5 mrad. (B) ABF signal reconstructed from annulus 7.5 to 15 mrad. (C) Averaged diffraction pattern for the whole sample. (D) $1°$ rotation S-STEM image. (E) $180°$ rotation S-STEM image. (F) Comparison of simulation and averaged (Upper Right) and nonaveraged (Lower Left) experiment for S-STEM for $180°$ rotation.

Discussion

In S-STEM, the symmetry of the local specimen potential defines the mathematical symmetry of the dynamical N-dimensional scattering matrix (25–27), and this, in turn, defines the symmetry of the scattered intensity distribution (CBED pattern), which is extracted by using Eq. 1, providing an intrinsically different image-contrast mechanism.

For perfect crystals, a reduction in symmetry can be detected as soon as an atomic-scale probe shifts a few picometers from the center of an atomic column. Our calculations show that this can generate extremely sharp image peaks at atomic-column positions (Fig. 3I) that have smaller FWHM than the corresponding peaks/troughs in conventional diffraction-limited BF-, ABF-, and ADF-STEM images derived from the same 4D-STEM dataset (Fig. 4I and SI Appendix, section 4, Fig. S3). That said, we emphasize that S-STEM will only detect atoms (or any other feature) if the probe size is sufficiently small relative to the atom (or feature) to detect the local change in symmetry it induces.

For unknown structures, the presence of a mirror or any point-symmetry element can be detected through the automated application of the S-STEM algorithm (Eq. 1) for any rotation angle, as illustrated in Fig. 2 and Movies S1 and S2. In principle, if the crystal structure is unknown, S-STEM can provide a spatial map of each and every point-symmetry element within the unit cell, for a given crystal orientation, and this can provide boundary conditions that could help to constrain a structure-determination algorithm. Conversely, in a known structure, S-STEM provides a mechanism to image where a given point-symmetry element is broken within a unit cell due to a local defect (such as a vacancy). This can enable defects to be highlighted.

In experimental data, the practical limit is the stability of the instrument and specimen, collectively, “scan noise.” The proof-of-concept examples in Fig. 5 were taken on a decade-old instrument. The ongoing improvements in instrument stability and detector speeds bode well for the further development of this technique.

The remarkable robustness of S-STEM images to thickness, accelerating voltage, and defocus is because the mathematical symmetry of the scattering matrix, and, hence, the CBED pattern symmetry does not depend on these quantities. The acute sensitivity to tilt is because it does. The latter provides an opportunity for an automated, high-precision tilt alignment (45).

The potential of S-STEM to obtain atomic-resolution images of light and heavy atoms from thick and thin crystals across a wide selection of accelerating voltages opens up a range of applications in material science that are otherwise challenging to image, including thick and beam-sensitive specimens. In particular, S-STEM has potential for development as a low-dose imaging method. It makes use of the whole scattered signal, rather than isolating some part of it. In addition, a quantitative measure of the scattered intensity is not required. As long as sufficient electrons are detected to discern the symmetry element, contrast can be obtained. When combined with the increased flexibility in the choice of accelerating voltage noted above, S-STEM may provide an option for the imaging of beam-sensitive materials. The ability to image defects due to the change in symmetry they induce also opens opportunities, including the imaging of dopant atoms and dislocations. The method could also be applied to the imaging of atomic magnetic fields in electromagnetic circular dichroism (46). Furthermore, S-STEM is likely to be sensitive to atomic displacements which induce a local change in symmetry, such as can occur with strain or octahedral tilts.

Methods

STEM Imaging.

Imaging of a tripod-polished CeB₆ specimen (47) was performed using a double-spherical-aberration-corrected ${\mathrm{T}\mathrm{i}\mathrm{t}\mathrm{a}\mathrm{n}}^3$ 80-300 FEGTEM equipped with an EMPAD (4) and operating at 300-kV electron energy with a 15-mrad probe convergence semiangle. The dataset was 4D-STEM data of 128 × 128 probe positions with the size 1 GB.

Data Availability.

A custom-made C++ code using GPU accelerated library ArrayFire (37) was used to analyze symmetry in 2D diffraction-pattern images. A maximum value of a normalized cross(phase)-correlation for a specific symmetry operation was plotted for each point of a scan. S-STEM code is partially based on the PixelatedDPC code used for Lorentz microscopy and introduced in refs. 15, 35, and 36. S-STEM is available from GitHub, https://github.com/matkraj/SymmetrySTEM (48). The presented data from the paper is included in the repository in ref. 48. The raw experimental data is available upon request from the authors.

STEM Simulations.

The Prismatic software package (38, 39) was used to simulate 4D-STEM datasets. The parameters were as follows: CeB₆ sample was 41.3 nm (Fig. 1) or 2.8 nm (Figs. 3 and 4) thick, in $⟨100⟩$ orientation; convergence semiangle was 15 mrad; acceleration voltage was 300 kV; slice thickness was 1 Å; the beam was focused on the top surface; and no aberrations were used. The size of a single dataset was 2.5 GB and included 124 × 124 probe positions.