Two-step crystallization and solid–solid transitions in binary colloidal mixtures

Significance

Crystallization—the spontaneous formation of an ordered solid from a disordered fluid—has fascinated humankind for centuries. Contrary to longstanding theories, which predict that crystals form by a single nucleation event, recent experiments have shown that crystallization can traverse multiple intermediate states. In this paper, we observe a two-step crystallization pathway, in which a metastable crystal forms first and later transforms into another crystal with a different crystallographic symmetry. This transformation is diffusionless: The particles undergo coherent, local rearrangements. Using complementary computer simulations, we show that the two-step crystallization pathway is driven by competing thermodynamic forces and, thus, could be common to many physical systems.

Abstract

Crystallization is fundamental to materials science and is central to a variety of applications, ranging from the fabrication of silicon wafers for microelectronics to the determination of protein structures. The basic picture is that a crystal nucleates from a homogeneous fluid by a spontaneous fluctuation that kicks the system over a single free-energy barrier. However, it is becoming apparent that nucleation is often more complicated than this simple picture and, instead, can proceed via multiple transformations of metastable structures along the pathway to the thermodynamic minimum. In this article, we observe, characterize, and model crystallization pathways using DNA-coated colloids. We use optical microscopy to investigate the crystallization of a binary colloidal mixture with single-particle resolution. We observe classical one-step pathways and nonclassical two-step pathways that proceed via a solid–solid transformation of a crystal intermediate. We also use enhanced sampling to compute the free-energy landscapes corresponding to our experiments and show that both one- and two-step pathways are driven by thermodynamics alone. Specifically, the two-step solid–solid transition is governed by a competition between two different crystal phases with free energies that depend on the crystal size. These results extend our understanding of available pathways to crystallization, by showing that size-dependent thermodynamic forces can produce pathways with multiple crystal phases that interconvert without free-energy barriers and could provide approaches to controlling the self-assembly of materials made from colloids.

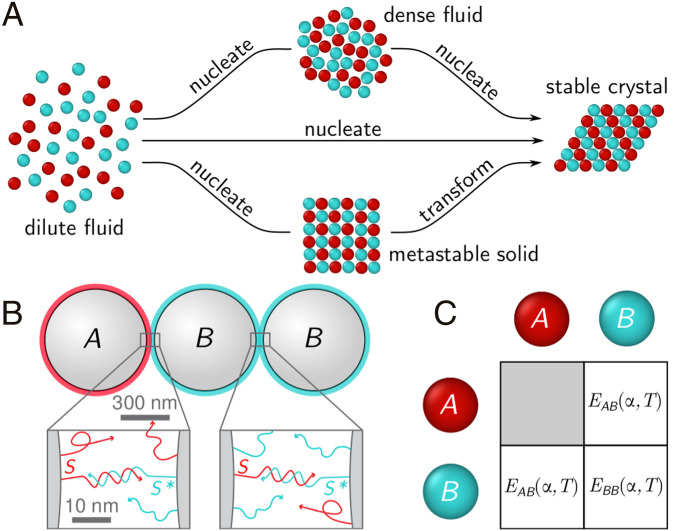
The spontaneous nucleation and growth of crystals from supersaturated fluids is common across a variety of material platforms, including metallic alloys (1), oppositely charged ions (2), proteins (3), and colloidal suspensions (4). Whereas classical theories predict that nucleation is governed by a single free-energy barrier (5, 6), recent studies report multistep transitions, in which the system traverses multiple phases along the pathway to the final crystal structure (7–12). Many of these observations can be understood by combining classical nucleation theory, which describes the nucleation barrier, with Ostwald’s step rule (13, 14), which predicts that nucleation will proceed via subsequent child phases having free energies closest to their parents. For instance, two-step crystallization pathways observed in single-component suspensions of colloids (11, 12) and proteins (8, 15, 16) proceed via a metastable liquid intermediate that nucleates first, owing to its low surface energy (Fig. 1A). Recent studies of crystallization in attractive binary colloidal mixtures (17, 18) suggest the possibility of an alternative multistep pathway: that two-step crystallization could proceed via a crystal intermediate that nucleates directly from a gas and then transforms into the final crystal structure by a diffusionless transformation (Fig. 1A). Such a diffusionless transformation does not follow classical predictions; thus, identifying its underlying mechanisms would advance our fundamental understanding of crystallization and enable engineering more efficient crystallization processes. However, our theoretical understanding of this class of pathways is limited, and such pathways have yet to be observed directly in experiment.

Fig. 1.

(A) A supersaturated fluid may crystallize via different types of one-step or two-step pathways. (B) Schematic of a binary mixture of DNA-coated colloids: Particle $\mathit{\text{A}}$ is coated in sequence $\mathit{\text{S}}$ (red, dark), and particle $\mathit{\text{B}}$ is coated in the mixture of sequence $\mathit{\text{S}}$ and sequence $\mathit{\text{S*}}$ (cyan, bright). The mixing ratio $\alpha$ is the fraction of $\mathit{\text{S}}$ on particle $\mathit{\text{B}}$. (C) The resulting pair interactions are summarized in a symmetric matrix. $E_{ij}$ is the depth of pair-potential minimum between particles $i$ and $j$. $E_{\mathit{\text{AA}}}$ is always zero; $E_{\mathit{\text{AB}}}$ and $E_{\mathit{\text{BB}}}$ depend on the mixing ratio $\alpha$ and temperature $T$.

In this article, we combine computer simulations and optical microscopy to investigate the physics underlying one- and two-step crystallization pathways in a two-dimensional (2D) binary mixture of DNA-coated colloids. We observe a rich diversity of crystal phases with different symmetries and compositional orders upon changing the matrix of pairwise interactions between the particle species. We also characterize both one-step and two-step crystallization pathways, as well as a solid–solid phase transition. Using biased sampling techniques, we show that the two-step crystallization pathway results from a competition between the free-energy landscapes of two crystal phases that depend on crystal size. The free energy of each crystal phase alone is a quadratic function of its characteristic radius, which agrees with predictions of classical nucleation theory. But the observed two-step transition is not described by classical nucleation theory alone, since the crystal structure, as well as the bulk and surface free energies, change along the crystallization pathway. Moreover, the two-step crystallization pathway that we find is also qualitatively different from previous observations in two important aspects: First, the metastable crystal nucleates directly from a dilute gas and is thus not influenced by gas–liquid critical phenomena (12, 15, 16); and, second, the crystal-to-crystal transition follows a diffusionless pathway rather than diffusive nucleation from a metastable liquid (10, 12). Taken together, these differences highlight that two-step crystallization can proceed along new types of pathways that have yet to be explored.

Results and Discussion

Experimental and Computational Approaches.

Our experimental system consists of a binary mixture of DNA-coated colloids confined to two dimensions, whose interactions are tuned by varying the amounts of two complementary sequences of single-stranded DNA: $\mathit{\text{S}}$ and $\mathit{\text{S*}}$. We grafted particle $\mathit{\text{A}}$ with sequence $\mathit{\text{S}}$ and particle $\mathit{\text{B}}$ with a mixture of sequence $\mathit{\text{S}}$ and its complement $\mathit{\text{S*}}$ (Fig. 1B). We define the mixing ratio $\alpha$ as the fraction of sequence $\mathit{\text{S}}$ on particle $\mathit{\text{B}}$. Both $\mathit{\text{S}}$ and $\mathit{\text{S*}}$ consist of a 58-nucleotide-long spacer and a seven-nucleotide “sticky end.” We used click chemistry to graft the DNA to 619-nm-diameter polystyrene particles (19) and confined the colloidal suspension to a 2D chamber by squeezing the suspension between two plasma-cleaned glass coverslips. The volume fraction of the colloidal suspension was roughly 1.0%, and the stoichiometry of $\mathit{\text{A}}$ to $\mathit{\text{B}}$ was roughly 1:1.

The resulting mixture has three pairwise interactions that are tuned by varying the mixing ratio $\alpha$ and the temperature $T$. The interactions due to DNA hybridization are described by an effective pair potential with a short-range attraction (20). We define the binding strength $E_{ij}$ as the depth of the potential well between particle type $i$ and type $j$ (with $i$ and $j$ being either $\mathit{\text{A}}$ or $\mathit{\text{B}}$). Fig. 1C shows the binding strengths between different combinations of binary species. $E_{\mathit{\text{AA}}}$ is zero because particle $\mathit{\text{A}}$ cannot bind to particle $\mathit{\text{A}}$, while $E_{\mathit{\text{AB}}}$ and $E_{\mathit{\text{BB}}}$ are functions of $\alpha$ and $T$. At fixed $T$, $E_{\mathit{\text{AB}}}$ decreases and $E_{\mathit{\text{BB}}}$ increases as $\alpha$ goes from 0 to 0.5. As temperature is lowered, both interactions become stronger. Therefore, crystallization can be induced in situ by cooling the suspension.

We simulated crystallization using grand canonical Monte Carlo (GCMC) simulations. We used an experimentally validated pair potential (20), whose range is approximately 5% of the particle diameter, to match our experimental system. Initially, particles were randomly dispersed with area fraction equal to 0.5%, which corresponds to the number density in the ideal gas reservoir. The chemical potentials of $\mathit{\text{A}}$ and $\mathit{\text{B}}$ in the reservoir were equal. We simulated assembly using displacive moves, insertion/deletion moves, and particle-species flipping moves (21). We attempted insertion/deletion moves and particle-species flips with an average frequency of 1 per 1,000 displacive moves. Complete details about the experiments and simulations are given in SI Appendix.

Crystallization Experiments.

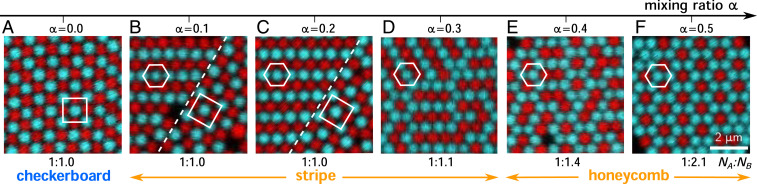
Our experiments yielded a variety of crystals with different crystallographic symmetries, compositional orders, and stoichiometries at different mixing ratios. Fig. 2 shows representative fluorescence micrographs of 2D crystals formed at mixing ratios between $\alpha =$ 0.0 and 0.5. At $\alpha =0.0$, all crystals had square symmetry and checkerboard compositional order, with alternating particle species along each row and column. At $\alpha =0.1$, we observed a hexagonal lattice with a stripe compositional order, in which the same types of particles are aligned in rows. The stripe phase coexisted with the checkerboard phase for $\alpha$ = 0.1 to 0.3, and the fraction of checkerboard crystals decreased from roughly 70% to 30% to $<10\%$ with increasing $\alpha$. At $\alpha$ = 0.4, the stripe pattern vanished, leaving small clusters of $\mathit{\text{A}}$ particles surrounded by $\mathit{\text{B}}$ particles. Finally, at $\alpha$ = 0.5, we observed a new hexagonal crystal with honeycomb compositional order, characterized by a periodic pattern of $\mathit{\text{A}}$ particles surrounded by six $\mathit{\text{B}}$ particles. Upon increasing $\alpha$, the stoichiometry of $\mathit{\text{A}}$ to $\mathit{\text{B}}$ decreased monotonically from 1:1 to roughly 1:2, even though the initial stoichiometry of all samples was 1:1 (Fig. 2). For each lattice type, we measured the pair-correlation function (SI Appendix, Fig. S3). The center-to-center distance between nearest neighbors was roughly 640 nm for all three lattices, which is consistent with our interaction potential (20).

Fig. 2.

Experimental fluorescence micrographs of 2D crystal lattices self-assembled at different mixing ratios $\alpha$. $N_{\mathit{\text{A}}}:N_{\mathit{\text{B}}}$ is the measured stoichiometry between $\mathit{\text{A}}$ and $\mathit{\text{B}}$, which decreases going from left to right (A–F). Dashed lines show grain boundaries between stripe and checkerboard lattices. Squares and hexagons are visual guides to the crystal symmetries. $A$ particles are red (dark); $B$ particles are cyan (bright).

If crystallization were governed by equilibrium thermodynamics, as is often the case for DNA-coated colloids (22), our observations suggest that entropy plays a key role in determining the final crystal structures. First, consider the case with $E_{\mathit{\text{BB}}}=0$. At low temperatures, the binding free energies of the checkerboard and stripe crystals should be the same because they both have two $\mathit{\text{A}}$–$\mathit{\text{B}}$ contacts per particle on average. Yet, all crystals at $\alpha =0$ have a checkerboard structure, suggesting that the checkerboard lattice has a lower free energy and, thus, a higher entropy than the stripe phase. This hypothesis is consistent with recent calculations of the vibrational-mode spectrum of 2D checkerboard crystals (23), which show that the checkerboard lattice has a large number of “floppy modes,” as compared to the stripe lattice. Our experimental observations that the checkerboard crystals are floppy, whereas the stripe crystals are rigid (SI Appendix, Fig. S4), also agree with this hypothesis. Moreover, the checkerboard lattice should also have higher configurational entropy because it is less densely packed. For example, we find that the checkerboard lattice has a packing fraction of 0.76, whereas the stripe lattice has a packing fraction of roughly 0.84 (see SI Appendix for details). Thus, a particle in the checkerboard lattice has more free area than a particle in the stripe lattice.

Next, consider the cases with nonzero-like attraction ($E_{\mathit{\text{BB}}}>0$). Following the mean-field estimate above, the total binding free energy should increase going from the honeycomb ($-2E_{\mathit{\text{AB}}}-E_{\mathit{\text{BB}}}$ per particle) to the stripe ($-2E_{\mathit{\text{AB}}}-\frac{1}{2}{E}_{\mathit{\text{BB}}}$ per particle) to the checkerboard phase ($-2E_{\mathit{\text{AB}}}$ per particle). Again, our experiments disagree with this prediction. At $\alpha$ = 0.1 to 0.3, the checkerboard and stripe phases coexist, suggesting that they have similar free energies. Furthermore, the stripe phase forms first upon increasing $\alpha$, not the honeycomb phase. We hypothesize that mixing entropy stabilizes the stripe phase relative to the honeycomb phase. In particular, there is a lower mixing entropy cost to form the stripe lattice, since its 1:1 stoichiometry matches the global stoichiometry, whereas the honeycomb lattice has a 2:1 stoichiometry. This mixing entropy difference could stabilize the stripe lattice for weak binding free energies, while above a threshold value of $E_{\mathit{\text{BB}}}$, the binding free energy will dominate, making the honeycomb lattice more favorable.

Alternative hypotheses to the thermodynamic ones rely on kinetically controlled mechanisms. For one, the system may be kinetically arrested—i.e., the free-energy minimum crystal phase cannot form within an experimentally accessible timescale. Alternatively, according to a recent study (24), hydrodynamic correlations between colloidal particles can cause anisotropic mobility along different pathways between crystal phases, thus biasing formation of certain phases over others with similar free energies. These mechanisms could influence the crystal types that we observed in our experiments. For example, consider that the honeycomb phase is thermodynamically favorable, but kinetically less accessible than the stripe phase, due to hydrodynamic interactions. Once the stripe crystal forms, a large free-energy barrier could prevent interconversion into the honeycomb crystal within experimental timescales.

Equilibrium States from Monte Carlo Simulations.

To test the two classes of hypotheses—thermodynamic versus kinetic control—we simulated crystallization under different sets of binding affinities using GCMC simulations. We performed each simulation for at least 2 $\times$10¹⁰ displacive trial moves to ensure convergence to an equilibrium distribution. To monitor the progress and morphology of the crystals that self-assemble, we defined an order parameter

$$\mathrm{\Phi }=\frac{2}{\pi }{\tan }^{-1}\left(\frac{{\mathrm{\Psi }}_6}{{\mathrm{\Psi }}_4}\right),$$ [1]

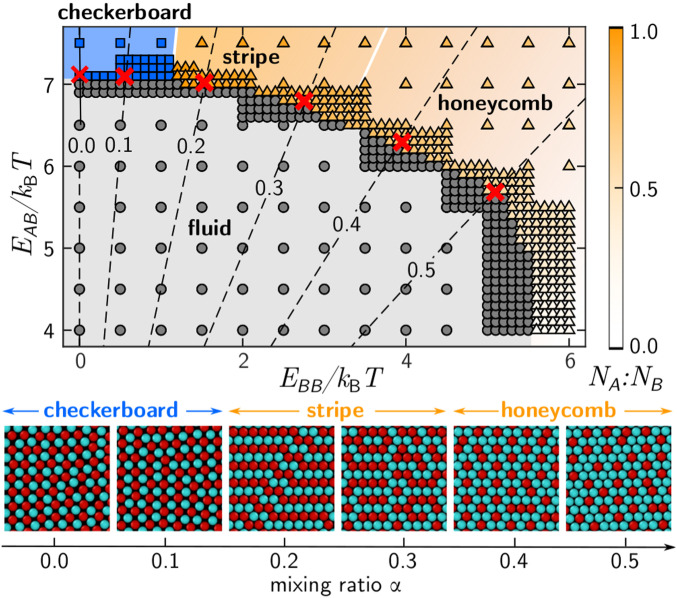
where ${\mathrm{\Psi }}_m$ is a global bond-orientation order parameter (12), which measures the m-fold global symmetry of a crystal. ${\mathrm{\Psi }}_4=1$ for fourfold symmetry, and ${\mathrm{\Psi }}_6=1$ for sixfold symmetry. Thus, $\mathrm{\Phi }$ distinguishes different lattice structures on the basis of their symmetry: Crystals with $\mathrm{\Phi }\gtrsim 0.9$ have hexagonal lattice structure, while crystals with $\mathrm{\Phi }\lesssim 0.5$ have square lattice structure. We tracked $\mathrm{\Phi }$ of the largest crystalline domain in the simulation box to monitor equilibration. A crystalline domain is defined as a set of continuously connected particles with consistent local order and bond orientation. We determined the phase diagram within the $E_{\mathit{\text{AB}}}$–$E_{\mathit{\text{BB}}}$ space from the simulation end states (Fig. 3). Complete details of the analysis are provided in SI Appendix.

Fig. 3.

Simulated phase diagram as a function of “like” and “unlike” pair interactions. Each point corresponds to one simulation: Circles show the fluid phase; squares show the crystal phases with square symmetry; and triangles show the crystal phases with hexagonal symmetry. Hexagonal phases are classified by using stoichiometry $N_{\mathit{\text{A}}}:N_{\mathit{\text{B}}}$ (color map). Stripe composition: $N_{\mathit{\text{A}}}:N_{\mathit{\text{B}}}$ = 1:1; and honeycomb composition: $N_{\mathit{\text{A}}}:N_{\mathit{\text{B}}}\hspace{0.17em}\approx$ 1:2. White lines show boundaries between checkerboard, stripe, and honeycomb compositions. Black dashed lines show model predictions of binding strengths as a function of temperature for different mixing ratios $\alpha$. Red crosses correspond to the approximate conditions used in experiments. Snapshots show simulated crystal phases corresponding to red crosses.

Our Monte Carlo (MC) simulations produce a comparable diversity of 2D crystal structures, as observed in experiments. When both $E_{\mathit{\text{AB}}}$ and $E_{\mathit{\text{BB}}}$ are weak, we find an isotropic low-density fluid phase. For weak $E_{\mathit{\text{BB}}}$ and strong $E_{\mathit{\text{AB}}}$, particles form a square lattice with checkerboard order. Increasing $E_{\mathit{\text{BB}}}$ above $1.2\hspace{0.17em}{k}_{\text{B}}T$ yields a variety of crystals with hexagonal symmetry, but varying compositional order, characterized by the stoichiometry of $N_{\mathit{\text{A}}}:N_{\mathit{\text{B}}}$ (Fig. 3, color map). Going from the upper left to lower right of the hexagonal region of the phase diagram, the compositional order changes from stripe to honeycomb to a demixed composition, in which the crystal is largely composed of $\mathit{\text{B}}$ particles, and the majority of $\mathit{\text{A}}$ particles remain in the fluid phase. This sequence of phases is accompanied by a change in the relative stoichiometry from one to zero. These results are consistent with previous computational studies (25, 26).

The equilibrium states from our computer simulations match our experimental observations. We estimated the experimental values of $E_{\mathit{\text{AB}}}$ and $E_{\mathit{\text{BB}}}$ as functions of temperature and mixing ratio $\alpha$ using a mean-field model (20). The dashed lines in Fig. 3 show contours of constant $\alpha$. Because we performed experiments at temperatures for which interactions are weak and dynamic, we inferred that our experiments occurred near the fluid–crystal phase boundary (red crosses in Fig. 3). As $\alpha$ increases, we see that the red crosses scan from the upper left to lower right, yielding a sequence from checkerboard to stripe to honeycomb, identical to the sequence observed in our experiments (Fig. 2). Since hydrodynamics are not included in the simulations, the match between simulation and experiment supports the hypothesis that thermodynamics, and not hydrodynamics, determines the crystals that form. However, some mysteries remain. Our simulations do not show coexistence between checkerboard and stripe phases: The system forms checkerboard crystals at low $\alpha$ and stripe crystals at slightly higher values of $\alpha$, but never both phases simultaneously. Is the coexistence of phases that we observe in experiment just a snapshot of an intermediate along the crystallization pathway? We answer this question and others by following the full pathways in both experiments and simulations.

Crystallization Pathways.

We used bright-field microscopy, MC simulations, and umbrella sampling to study the crystallization pathways. We characterized the transitions of individual crystals by quantifying two progress coordinates: the total number of particles in the crystal $N_c$ and the orientation order parameter $\mathrm{\Phi }$ (Eq. 1).

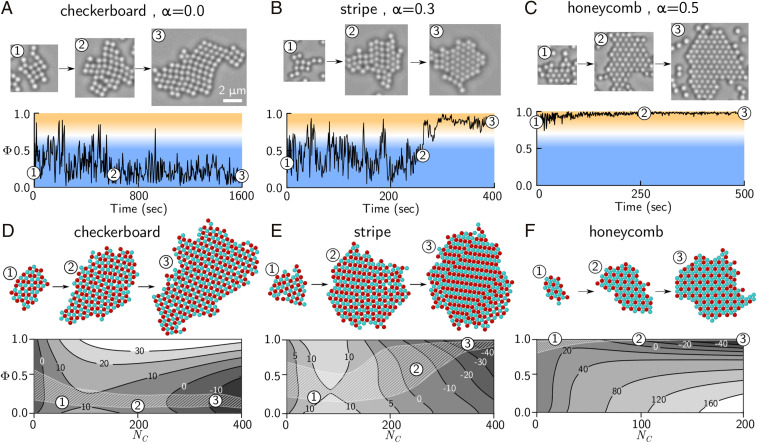
Interestingly, we observed both one-step and two-step crystallization pathways in experiments at different mixing ratios $\alpha$. Fig. 4 A–C shows micrographs and the corresponding order parameter $\mathrm{\Phi }$ for single crystals as a function of time for three values of $\alpha$: 0, 0.3, and 0.5. At $\alpha$ = 0, a square lattice forms first and then grows, retaining its square symmetry throughout (Fig. 4A). In contrast, at $\alpha$ = 0.3, a square crystal nucleates first, but then switches back and forth between a square lattice and a hexagonal lattice as it grows (Fig. 4B). Indeed, we observed coexistence of both hexagonal and square domains in the same crystal. Eventually, the crystal becomes completely and stably hexagonal at the largest sizes. At $\alpha$ = 0.5, the pathway returns to one-step behavior: A hexagonal crystal forms first and remains hexagonal during growth (Fig. 4C). Comparing these three experiments, $\alpha =0$ and $\alpha =0.5$ form in a single step, whereas crystals at $\alpha =0.3$ form via a two-step pathway, in which a square lattice nucleates and then transforms to a hexagonal lattice during growth.

Fig. 4.

Experimental and simulated crystallization pathways for different crystal phases. (A–C) Experimental trajectories of the order parameter $\mathrm{\Phi }$ as a function of time, for mixing ratios $\alpha =0$ (A), $\alpha =0.3$ (B), and $\alpha =0.5$ (C). Snapshots show data of the same crystal at different time points. Blue regions correspond to square symmetry, while orange regions correspond to hexagonal symmetry. (D–F) Free-energy landscapes with respect to the crystal size $N_c$ and order parameter $\mathrm{\Phi }$. The white shaded region in each plot encloses 68% of the pathways from 200 independent, unbiased MC simulations. Images show snapshots from unbiased simulations at different crystal sizes $N_c$. The contours show the free energy in $k_{\text{B}}T$. Results correspond to different interaction matrices: $E_{\mathit{\text{AA}}}=E_{\mathit{\text{BB}}}=0,E_{\mathit{\text{AB}}}=7.0\hspace{0.17em}{k}_{\text{B}}T$ (D), $E_{\mathit{\text{AA}}}=0,E_{\mathit{\text{BB}}}=1.6\hspace{0.17em}{k}_{\text{B}}T,E_{\mathit{\text{AB}}}=7.0\hspace{0.17em}{k}_{\text{B}}T$ (E), and $E_{\mathit{\text{AA}}}=0,E_{\mathit{\text{BB}}}=3.5\hspace{0.17em}{k}_{\text{B}}T,E_{\mathit{\text{AB}}}=6.3\hspace{0.17em}{k}_{\text{B}}T$ (F).

These observations demonstrate that colloidal crystallization, even in simple binary mixtures, is more complex than classical pictures would suggest. While the one-step transitions that we observe could be consistent with classical nucleation theory, the two-step crystallization pathways are not. There, the crystal structure changes as the crystal grows, switching from square to hexagonal, which is inconsistent with the capillary approximation made in classical nucleation theory (27). This transformation could be driven by different processes. One possibility is a competition between two crystal phases with similar free energies, but different dependencies on the crystal size: The square lattice is favorable at small sizes, and the hexagonal lattice is favorable at large sizes. Another possibility is that the two-step transition is driven by kinetics. Recent studies suggest that hydrodynamic coupling (24), heterogeneity in the binding free energies (28), or even the details of single-molecule kinetics (29) could influence the available kinetic pathways for crystallization.

To investigate the mechanisms underlying crystallization, we computed the free-energy landscapes (21, 30) as a function of $N_c$ and $\mathrm{\Phi }$ for the three crystals that we observed: checkerboard, stripe, and honeycomb. Although $\mathrm{\Phi }$ only monitors the crystal symmetry and does not explicitly depend on compositional order, we confirmed that biasing on the symmetry alone drives the system to the intended crystal structures (SI Appendix, Fig. S7). To determine how closely the system dynamics follows the underlying free-energy landscape, we also performed unbiased simulations starting from the saddle points separating local minima in the free-energy landscape and followed their trajectories within the $N_c$–$\mathrm{\Phi }$ phase space (see SI Appendix for details).

Our calculations show that the checkerboard, stripe, and honeycomb crystals are governed by qualitatively different free-energy landscapes. All three landscapes have a free-energy barrier between minima at small and large sizes, as expected, but the favored minima at small and large sizes can have different symmetries (Fig. 4 D–F). The checkerboard crystal has free-energy minima with $\mathrm{\Phi }<0.5$, corresponding to square symmetry (Fig. 4D). The honeycomb crystal also exhibits minima at small and large sizes with the same symmetry, but these are located near $\mathrm{\Phi }\approx 1$, corresponding to hexagonal symmetry (Fig. 4F). In contrast, the stripe-crystal free-energy landscape has minima with symmetries that depend on size: $\mathrm{\Phi }<0.5$ for the minimum at small sizes and $\mathrm{\Phi }\approx 1$ for the minimum at large sizes (Fig. 4E).

Comparing unbiased trajectories with our free-energy calculations shows that the system follows free-energy gradients. Fig. 4 D–F shows the distribution of pathways explored by our unbiased MC simulations. The corresponding snapshots show the crystal symmetry and compositional order at different sizes, reproducing the experimentally observed sequence of phases.

Taken together, the free-energy calculations and unbiased simulations show that the crystallization pathways are governed by the underlying thermodynamic landscape. At their respective parameter sets, the checkerboard and honeycomb crystals are thermodynamically favorable for all crystal sizes and, thus, form by one-step crystallization. However, for the stripe crystal, the checkerboard phase is favorable at small sizes, and the stripe phase is favorable at large sizes, leading to the two-step crystallization pathway. We conclude that the coexistence between checkerboard and stripe phases that we observe in experiment at $\alpha$ = 0.1 to 0.2 reflects an incomplete transition, probably because the transition size is large, and most crystals are unable to grow to such large sizes within the experimental time scale. Above all, we observed the same one- and two-step mechanisms for the same crystals in experiments and simulations. Therefore, we conclude that other factors, such as hydrodynamics or single-molecule binding kinetics, which are absent from our simulations, do not significantly contribute to controlling the pathways. Finally, preliminary molecular-dynamics simulations also show a checkerboard-to-stripe transition, demonstrating that the two-step transition is not an artifact of our MC approach and hinting at an interesting diffusionless mechanism driven by coherent sliding of parallel rows of atoms (31, 32) (see SI Appendix for details).

Interpretation of One-Step and Two-Step Pathways.

To understand the roles of entropy and binding free energy in our free-energy landscapes, we analyze our computational results within the framework of classical nucleation theory. We write the free-energy difference between the crystal and fluid phases as

$$\mathrm{\Delta }G=\mathrm{\Delta }g{N}_c+\sigma N_{\mathrm{surface}}=\stackrel{\sim }{g}{N}_c+\stackrel{\sim }{\sigma }\sqrt{N_c},$$ [2]

where $\mathrm{\Delta }g$ and $\sigma$ are, respectively, the per-particle bulk free-energy difference and surface free energy. In general, both $\mathrm{\Delta }g$ and $\sigma$ depend on the binding free energies, as well as the entropy of the crystal itself. $N_{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}}\sim \sqrt{N_c}$ is the number of particles at the crystal surface. Assuming the crystals are circular, $\stackrel{\sim }{g}$ and $\stackrel{\sim }{\sigma }$ are the effective bulk free-energy density and surface free-energy density, which account for differences in the bulk and surface densities of the crystal structures. We determined $\stackrel{\sim }{g}$ and $\stackrel{\sim }{\sigma }$ of the competing square and hexagonal lattices within the three free-energy landscapes in Fig. 4 by integrating the Boltzmann weights over $\mathrm{\Phi }$ at each crystal size and fitting the result to Eq. 2 (Fig. 5 and SI Appendix, Table S1). We took $\mathrm{\Phi }<0.5$ and $\mathrm{\Phi }>0.9$ to be the square and hexagonal lattices, respectively. Complete details are in SI Appendix.

Fig. 5.

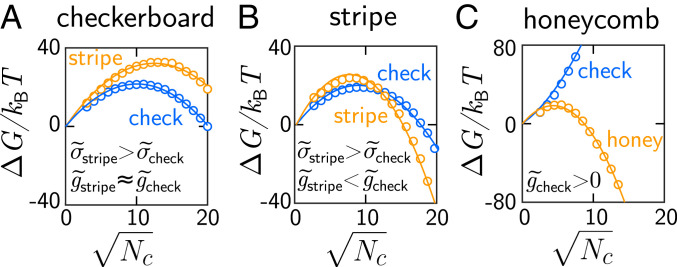
Gibbs free energy $G$ versus crystal size $N_c$ for the free-energy landscapes in Fig. 4. Blue circles and lines correspond to checkerboard crystals; orange circles and lines correspond to stripe (A and B) or honeycomb (C) crystals. Free energies are calculated by integrating the Boltzmann weights in Fig. 4 D–F over $\mathrm{\Phi }$ at fixed $N_C$. Lines are quadratic fits of Eq. 2. $\stackrel{\sim }{\sigma }$ is the effective surface free-energy density and $\stackrel{\sim }{g}$ is the effective bulk free-energy density. Subscripts indicate the corresponding lattice structure. The binding free energies are $E_{\mathit{\text{AA}}}=E_{\mathit{\text{BB}}}=0,E_{\mathit{\text{AB}}}=7.0\hspace{0.17em}{k}_{\text{B}}T$ (A), $E_{\mathit{\text{AA}}}=0,E_{\mathit{\text{BB}}}=1.6\hspace{0.17em}{k}_{\text{B}}T,E_{\mathit{\text{AB}}}=7.0\hspace{0.17em}{k}_{\text{B}}T$ (B), and $E_{\mathit{\text{AA}}}=0,E_{\mathit{\text{BB}}}=3.5\hspace{0.17em}{k}_{\text{B}}T,E_{\mathit{\text{AB}}}=6.3\hspace{0.17em}{k}_{\text{B}}T$ (C).

The balance of surface and bulk free energies makes different lattice symmetries thermodynamically favored for different binding free energies and crystal sizes. For the conditions at which the checkerboard crystal forms (Fig. 5A), $\stackrel{\sim }{g}$ is roughly the same for the checkerboard and stripe lattices, but $\stackrel{\sim }{\sigma }$ is lower for the checkerboard lattice, thus causing the checkerboard lattice to be favorable. We highlight that the low surface free energy of the checkerboard phase is consistent with our experimental observation that checkerboard crystals have very irregular surfaces (Fig. 4A and SI Appendix, Fig. S1A). For the conditions at which the honeycomb phase forms (Fig. 5C), $\stackrel{\sim }{g}$ is positive for the checkerboard lattice and negative for the honeycomb lattice, causing the honeycomb lattice to be favored. Again, the formation of the stripe phase is the exception to the rule (Fig. 5B): $\stackrel{\sim }{g}$ is lower for the stripe lattice, but $\stackrel{\sim }{\sigma }$ is lower for the checkerboard lattice. Consequently, the checkerboard crystal dominates at small sizes, and the stripe crystal dominates at large sizes, as observed.

Simple bond-counting estimates of the surface free-energy densities highlight the importance of entropy in determining the crystallization pathways. We estimated $\stackrel{\sim }{\sigma }$ by adding up the binding free energies per unit length of all bonds that are broken when a perfect crystal is split along a given crystallographic axis (see SI Appendix for details). For each lattice type, we considered only the crystallographic axis with the lowest surface free-energy density. Interestingly, while our estimates were all comparable to the values that we find from fitting the free-energy landscapes, the bond-counting estimates were systematically larger (SI Appendix, Table S2). We hypothesize that this systematic deviation is again due to entropy, which would act to lower $\stackrel{\sim }{\sigma }$. We also notice that our estimates of ${\stackrel{\sim }{\sigma }}_{\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{c}\mathrm{k}}$ are greater than our estimates of ${\stackrel{\sim }{\sigma }}_{\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{p}\mathrm{e}}$ in the cases shown in Fig. 5 A and B. This observation is contrary to the results that we obtained by fitting the free-energy landscapes, presumably due to the fact that the entropic contribution to the surface free energy of the checkerboard lattice is larger than the contribution to the stripe lattice. Therefore, while bond-counting estimates are useful for approximating the magnitude of surface free energies in binary colloidal crystals, care is required to draw conclusions from their precise values.

In conclusion, our detailed free-energy calculations identify a generic mechanism by which free energy controlled crystallization can exhibit two-step pathways, even when both phases have crystalline order: One phase has a lower effective bulk free energy, but higher effective surface free energy, than a competing phase. If both effective bulk and surface free energies are lower for the same phase, free-energy control will lead to one-step transitions. We point out that while this generic two-step mechanism is consistent with Ostwald’s original statement of his step rule—that the child phase with a free energy closest to the parent phase will nucleate first (13)—it need not be consistent with a later formulation of the step rule due to Stranski and Totomanow (33), which is commonly used today. Their formulation of the step rule states that the phase that nucleates first is the one with the lowest free-energy barrier to formation. Although the specific case that we show in Fig. 5B satisfies this formulation as well, we hypothesize that there are combinations of binding free energies, and thus bulk and surface free-energy densities, that satisfy our inequality relationship, but that give rise to a two-step transition, in which the phase that forms first has a higher free-energy barrier than the subsequent phase. Therefore, the transition would happen below the nucleation barrier of the metastable crystal phase. We note that this type of pathway would be difficult to infer from bulk measurements. But one of the powerful features of our approach is that, because we are able to follow individual assemblies, we could observe such a transition, as demonstrated in SI Appendix, Fig. S8.

Conclusions

We show that the crystallization pathways of a 2D binary mixture are determined by their underlying free-energy landscapes. We observe a variety of crystal phases, as well as both one-step and two-step crystallization pathways. In the one-step pathways, a single crystal lattice has the lowest free energy, regardless of its size. In the two-step pathway, one crystal lattice, which has a lower free energy at small sizes—but not necessarily a lower free-energy barrier to crystallization—forms first and then transforms to another lattice with a lower free energy at large sizes. This two-step mechanism cannot be completely explained by classical nucleation theory alone, since the bulk and surface free-energy densities are different before and after the transition, and, thus, depend on the crystal size. We stress that while our experimental observations come from a highly specific experimental system—micrometer-scale particles interacting by hybridization of scores of complementary DNA molecules—our coarse-grained simulations are quite general. Our simulations consist of a collection of small particles interacting via a short-range interaction potential. Importantly, these coarse-grained simulations capture almost all of phase behaviors and dynamic transitions that we find in our experiments. Thus, the same physical principles could govern crystallization pathways in other systems with short-range specific interactions, such as proteins.

We highlight that the crystallization pathways and the resulting crystal phases are governed by a balance between entropy and the binding free energy. For example, mean-field estimates of the stabilities of various crystal phases based solely on binding free energies disagree with our experimental observations, suggesting that entropy strongly influences crystal structures. This observation is significant since configurational entropy, vibrational entropy, and mixing entropy of the lattice are neglected in models commonly used to predict or rationalize the structures of DNA-coated colloidal crystals, such as the complementary-contact model (22). Future experiments will explore other stoichiometries to further investigate the role of entropy in dictating the pathways and relative stability of the various crystal phases. Furthermore, we have shown that both the bulk and surface free-energy densities sculpt the underlying free-energy landscape. Thus, bulk and surface entropy differences between various crystal types are important in determining crystallization pathways. Together, these observations suggest that entropy is a key driving force in soft-matter systems (34).

Our findings offer insights into strategies for engineering crystallization pathways. Rather than forming a desired crystal in a single step, traversing a series of intermediates may facilitate the assembly of the final structure. Many efforts have sought multistep crystallization pathways as a route to forming unique crystals or reconfigurable structures (16, 35–38). Our results identify additional considerations for designing such transitions. First, to avoid kinetic traps, the intermediate states must be kinetically accessible, as in our diffusionless transformation between checkerboard and stripe crystals. Fortunately, there are many other reported diffusionless transformations (39, 40). For example, some iron-based alloys can transform from face-centered-cubic to body-centered-cubic structures upon cooling (40). Second, the states along the pathway need to have comparable free energies, as well as bulk and surface free energies that can be prescribed. Constructing systems with fully prescribed free energies is a grand challenge in self-assembly and is usually empirical at present. There is no generic approach to determine the interparticle interactions required to produce a given structure. This challenge provides a unique opportunity to integrate tools, like machine learning, to help solve the inverse design problem (41, 42) and construct new pathways to crystallization.

Materials and Methods

Particle Preparation.

We synthesized DNA-grafted colloidal particles following a modified version of the method described in ref. 19. The method comprised three steps: 1) We attached azide groups to the ends of polystyrene-poly(ethylene oxide) diblock copolymers; 2) we physically grafted azide-modified diblock copolymers to the surface of polystyrene colloids; and 3) we conjugated dibenzocyclooctyne-modified DNA to the ends of the grafted block copolymers by strain-promoted click chemistry. The DNA sequences that we used were: $\mathit{\text{S}}$ 5′-(T)₅₁-GA GTT GCG GTA GAC-3′ and $\mathit{\text{S*}}$ 5′-(T)₅₁-AA TGC CTG TCT ACC-3′. The full synthesis protocol is described in SI Appendix.

Crystallization Experiments.

We squeezed particles between two plasma-cleaned glass coverslips to create a 2D suspension and observed crystallization using an optical microscope. We controlled the sample temperature in situ using a thermoelectric cooler driven by a proportional–integral–derivative controller. To crystallize the sample, we quenched an initial gas phase to a temperature slightly above the melting temperature, defined as the temperature at which 50% of the particles are unbound, and held the sample at that temperature for roughly 1 h. We acquired bright-field digital videos of crystallization using a Nikon Eclipse Ti2 and CoolSNAP HQ2 charge-coupled device camera. After crystallization, we used a Leica SP8 to acquire confocal fluorescence images of the crystalline domains (see SI Appendix for details).

GCMC Simulations.

We used an in-house code written in C++ to perform GCMC simulations. We used periodic boundary conditions with a box size of 53.3 $\times$ 53.3 particle diameters. The pair potential that we employed was obtained from experimental measurements (20). The width of the potential was rescaled to roughly 5% of the particle diameter to match our experimental system. We initialized the system with an area fraction of 0.5%, which corresponded to the density of the particle reservoir. We made displacive moves, insertion/deletion moves, and particle species flipping moves, and determined whether or not to accept these moves using the Metropolis criterion. To facilitate equilibration, we made particle species flipping trials, in which the species of a random particle was flipped.

Data Availability.

Data are available upon request from the corresponding author.