Reconfigurable multifunctional ferrofluid droplet robots

Significance

This work proposes reconfigurable multifunctional ferrofluid droplets as soft robots to overcome the limitation of existing magnetically actuated miniature soft robots based on elastomers, i.e., they cannot navigate inside very clustered and constrained spaces and reconfigure their shapes in situ for diverse tasks, due to limited deformability and predesigned shapes. We propose a fundamental mechanism of controlling reconfigurable large deformation (e.g., splitting) and coordinated motions of multiple ferrofluid droplets by programming external magnetic fields spatiotemporally. We employ this mechanism to achieve multiple functionalities, including on-demand liquid-cargo delivery, morphing for efficient and versatile manipulation of delicate objects, and programmable fluidic-mixing function, potentially enabling unprecedented functionalities in lab/organ-on-a-chip, fluidics, bioengineering, and medical device applications, beyond magnetically actuated elastomer-based soft robots.

Abstract

Magnetically actuated miniature soft robots are capable of programmable deformations for multimodal locomotion and manipulation functions, potentially enabling direct access to currently unreachable or difficult-to-access regions inside the human body for minimally invasive medical operations. However, magnetic miniature soft robots are so far mostly based on elastomers, where their limited deformability prevents them from navigating inside clustered and very constrained environments, such as squeezing through narrow crevices much smaller than the robot size. Moreover, their functionalities are currently restricted by their predesigned shapes, which is challenging to be reconfigured in situ in enclosed spaces. Here, we report a method to actuate and control ferrofluid droplets as shape-programmable magnetic miniature soft robots, which can navigate in two dimensions through narrow channels much smaller than their sizes thanks to their liquid properties. By controlling the external magnetic fields spatiotemporally, these droplet robots can also be reconfigured to exhibit multiple functionalities, including on-demand splitting and merging for delivering liquid cargos and morphing into different shapes for efficient and versatile manipulation of delicate objects. In addition, a single-droplet robot can be controlled to split into multiple subdroplets and complete cooperative tasks, such as working as a programmable fluidic-mixing device for addressable and sequential mixing of different liquids. Due to their extreme deformability, in situ reconfigurability and cooperative behavior, the proposed ferrofluid droplet robots could open up a wide range of unprecedented functionalities for lab/organ-on-a-chip, fluidics, bioengineering, and medical device applications.

Compared with miniature untethered robots actuated by light (1, 2), chemical (3), and other stimuli (4), magnetically actuated ones could be fast and precise, as well as access optically nontransparent and deep enclosed small spaces, such as inside microfluidic channels, biochips, and the human body, making them appealing for fluidics (5), lab/organ-on-a-chip (6), and biomedical applications (7, 8). For example, magnetically actuated microrobots have been shown to manipulate hydrogel blocks with embedded cells for building tissue scaffolds (6). Recently, magnetically actuated soft millirobots made of elastomer and hard magnetic microparticle composites (9–11) have demonstrated programmable deformations for bioinspired soft-bodied robotic locomotion (12–15) and manipulation functions (14, 16, 17). Such untethered soft robots could directly access currently unreachable and difficult-to-reach regions inside the human body toward minimally invasive medical diagnostic or therapeutic operations. However, their limited deformability prevents them from navigating inside very clustered, narrow, and constrained spaces, such as squeezing through narrow crevices much smaller than the robot size, and their functionalities are currently restricted by their predesigned shapes, which is challenging to be reconfigured in situ in enclosed spaces (18).

In contrast, magnetically actuated droplets, such as ferrofluids (19), are much softer and gentler (20). Due to their liquid properties, they could potentially negotiate through narrow and constrained spaces better than elastomer-based soft robots, as well as maintain biocompatibility and avoid damaging the surrounding biological tissues during biomedical operations (21, 22). Fundamental studies have provided striking insights into the physics of ferrofluid droplets at the micro and macro scales (23–25). Recent works have also demonstrated utilizing these magnetic droplets for engineering applications (26–30). For example, magnetically actuated droplets have been controlled to navigate on various terrains by forming self-assembled structures and disassemble into multiple smaller droplets to pass through a narrow gap (26), while the functionality of such collective droplets is simple and their ability to complete cooperative tasks is also restricted by the lack of addressability of individual droplets. In addition, other magnetically actuated droplet robots have also been proposed with promising proof-of-concept functionalities, such as transporting liquid samples and mixing chemicals in lab-on-a-chip applications (28, 29). Yu et al. (28) have proposed to employ ferrofluids as droplet robots for automated sample collection and transportation by controlling the magnetic field produced by a millimeter-scale permanent magnet on top of an electromagnet array. Li et al. (29) have developed magnetically actuated droplets by controlling two steel beads to manipulate a water or oil droplet, which has been utilized for sequential chemical reaction and simulated calculi removal. Despite recent advances in this field, existing magnetically actuated droplets can only have limited deformability, such as only simple elongation under a uniform magnetic field. Meanwhile, although parallel motions of multiple droplets have been reported (19), cooperative functions among groups of droplets are challenging to achieve due to the lack of coordination control, while such cooperation could potentially enable more complex functionalities compared with single-body droplet robots. Therefore, it is still challenging to achieve the full potential of magnetically actuated droplets in critical engineering applications, restricted by their simple deformation and isolated motions.

To tackle this challenge, we report reconfigurable multifunctional ferrofluid droplet robots (FDRs) with programmable morphology and cooperative behaviors by programming external magnetic fields spatiotemporally. We first report the fundamental mechanism to control the complex shape-morphing behaviors and two-dimensional (2D) motions of ferrofluid droplets on solid substrates and in confined spaces, which allows producing much larger deformations (e.g., splitting) of these droplets compared with existing magnetic soft elastomeric robots, and on-demand complex shape-morphing ability compared with existing droplet robots. Then, we demonstrate that these droplet robots could have reconfigurable multiple functionalities, such as splitting and merging for cargo delivery, navigating through narrow channels much smaller than their sizes, and reconfiguring into different shapes for versatile and efficient 2D manipulation of delicate objects. Furthermore, the controllable splitting ability allows a single droplet to disassemble into multiple subdroplets, which can then coordinate their motions and complete cooperative tasks, such as working as a programmable fluidic-mixing device for addressable and sequential mixing of liquid chemicals. Therefore, our proposed reconfigurable multifunctional FDRs could open up a wide range of opportunities to enable diverse unprecedented functionalities that are essential for advanced lab/organ-on-a-chip and biomedical applications.

Results

Concept of Multifunctional FDRs.

A typical ferrofluid consists of ${\text{Fe}}_3{\text{O}}_4$ nanoparticles in diameters of ∼10 nm (SI Appendix, Fig. S1), carrier fluids (oil-based organic solvent or water), and surfactants. The carrier fluids allow ferrofluids to maintain liquid properties. The surfactants produce the van der Waals force to prevent aggregation of nanoparticles upon being magnetized by applying an external magnetic field, which makes ferrofluids stable for a relatively long time. Ferrofluid droplets form when oil-based (or water-based) ferrofluids are mixed with water-based (or oil-based) solutions, due to the immiscibility and surface tension. Particularly, oil-based ferrofluid droplets are promising for lab-on-a-chip (28) and bioengineering (21, 22) applications, because water-based fluids widely exist in microfluidic channels and the human body, including blood and other biological fluids (20).

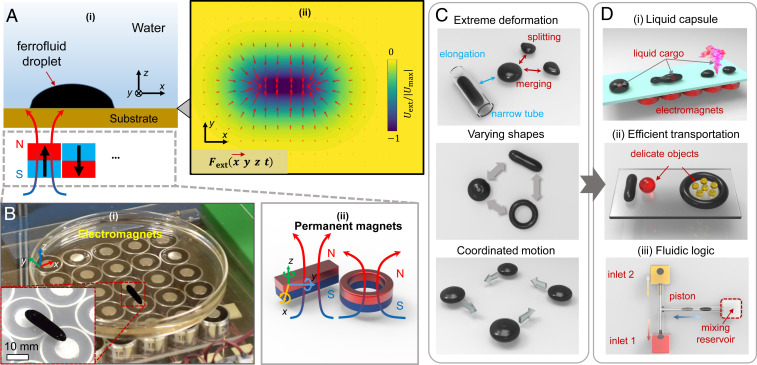
Here, our method to realize multifunctional FDRs is by spatiotemporally programming the external magnetic fields and, therefore, the magnetic potential energy distribution (Fig. 1A), where the functionalities mainly emerge from the programmable shapes and coordinated motions. Without external magnetic fields and gravity, a ferrofluid droplet tends to be spherical due to the confinement of surface tension on the boundary layer. Although a uniform magnetic field would elongate the droplet shape slightly (25), a distributed static magnetic field $\mathit{H}\left(\mathit{r}\right)$ could induce complex shape deformation by exerting a distributed magnetic volume force ${\mathit{F}}_{\text{m}}\left(\mathit{r}\right)=-\nabla \mathit{U}\left(\mathit{r}\right)=-{\mu }_0\nabla \left(\mathit{M}\cdot \mathit{H}\left(\mathit{r}\right)\right)$ (see SI Appendix, Fig. S2 for the schematics), where $\mathit{r}$ is the Eulerian coordinate of a sampled point in the global coordinate. Here, ${\mu }_0=4\pi \cdot {10}^{-7}H/m$ denotes the magnetic permeability of vacuum, and $\mathit{H}\left(\mathit{r}\right)$ is a summation of both the externally applied and internally produced magnetic fields ${\mathit{H}}_{\text{ext}}$ and ${\mathit{H}}_{\text{ferro}}\left(\mathit{M}\right).$ The magnetization of ferrofluids is given by $\mathit{M}=\chi \left({\mathit{H}}_{\text{ext}}+{\mathit{H}}_{\text{ferro}}\left(\mathit{M}\right)\right)$ due to the paramagnetic property, where $\mathit{\chi }$ is the volume susceptibility of the ferrofluid (31). When smartly programming ${\mathit{H}}_{\text{ext}}$ $({\mathit{B}}_{\text{ext}}$ is equivalently used in later sections) by using either electromagnets (30) or permanent magnets (29) as illustrated in Fig. 1B, unique capabilities in terms of both morphology and mobility can be realized, such as splitting and merging behaviors, elongating to navigate through confined spaces, morphing into complex shapes, and coordinating group motions (Fig. 1C). These capabilities further enable multiple functionalities demonstrated by three showcases, including delivering liquid cargo in phantom vascular structures and a challenging maze as a liquid capsule, efficiently transporting and sorting delicate objects by reconfiguring shapes and cooperatively pumping and mixing chemicals in fluidic channels after being disassembled into multiple subdroplets (Fig. 1D).

Fig. 1.

Concept of reconfigurable multifunctional FDRs. (A) System concept and overview. (A, i) Schematics of controlling the 2D shape and motion of an FDR by programming the external magnetic field ${\mathit{B}}_{\text{ext}}$ spatiotemporally. (A, ii) Example distributed external magnetic potential energy $U_{\text{ext}}\left(x,y,z,t\right)$ (color maps) and force ${\mathit{F}}_{\text{ext}}\left(x,y,z,t\right)$ (red arrows). (B) Example experimental setup for generating spatiotemporally distributed external magnetic fields by either a 2D electromagnet array (B, i) or a permanent magnet (or array) (B, ii). The external magnetic fields can be programmed spatiotemporally by controlling the currents of electromagnets or the rigid-body translational and rotational motions of permanent magnets. (C) Illustration of the unique capabilities of an FDR. The FDR can realize extreme large deformation, such as elongation in a narrow tubular structure much smaller than its size, and split into two smaller droplets or remerge on demand. The shape of the FDR can be reconfigured for specific tasks. After disassembling into multiple smaller FDRs, their 2D motions can be controlled in a coordinated manner for cooperative tasks. (D) Illustration of the demonstrated multiple functionalities of FDRs enabled by their complex large deformation and coordinated motion. (D, i) Active liquid-cargo delivery in confined spaces. (D, ii) Efficient manipulation of delicate objects by reconfiguring shapes. (D, iii) Programmable fluidic mixing by coordinating the motions of multiple FDRs as pistons and valves.

Mechanism and Characterization of Controlling Complex Shapes of FDRs.

FDRs have both passive deformation, where their shapes can adapt to the boundaries of the environment due to liquid properties, and active deformation, where their shapes can be controlled on demand by programming external magnetic fields. Here, we produce external magnetic fields by using an electromagnet array (see SI Appendix, Fig. S3 for the electromagnet system) or permanent magnets in various shapes. In Fig. 2 and Movie S1, we study the active deformation behaviors of FDRs, including their controllable splitting and merging subject to a time-varying ${\mathit{B}}_{\text{ext}}\text{,}$ and deforming into complex shapes under a patterned static ${\mathit{B}}_{\text{ext}}\text{.}$

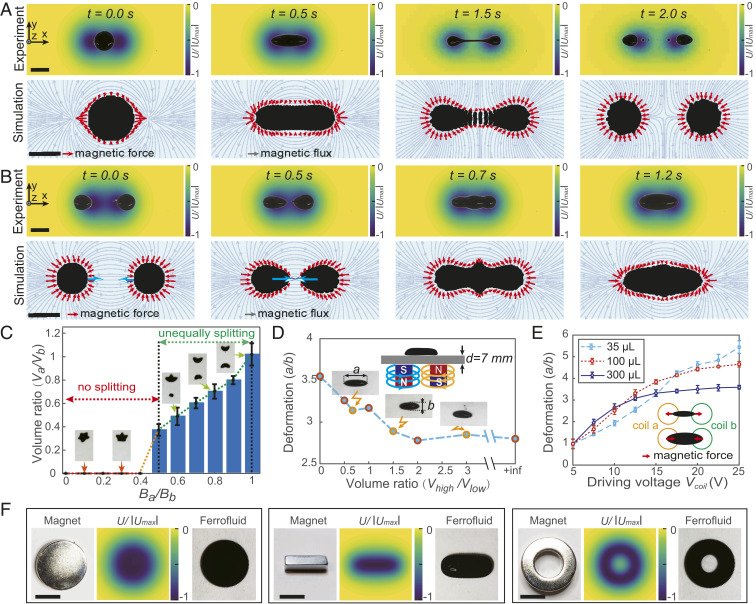
Fig. 2.

Control mechanism and characterization of extreme and complex deformations of FDRs. (A) Experimental and simulated time frames of the controllable splitting behavior of an FDR. (B) Experimental and simulated time frames of the controllable merging behavior of an FDR. In A and B, the top row has the experimental video snapshots overlapped on the simulated magnetic potential-energy distributions. (C) The volume ratio $\left(V_a/V_b\right)$ of two split droplets as a function of the relative magnetic field strength $\left(B_a/B_b\right)$ produced by two coils under the droplets. (D) The deformation of an FDR as a function of the mixing-volume ratio $V_{\text{high}}/V_{\text{low}}$ of two types of ferrofluids (dynamic viscosities: ${\eta }_{\text{high}}=80\hspace{0.17em}\text{mPa}\cdot \text{s;}$ ${\eta }_{\text{low}}=8\hspace{0.17em}\text{mPa}\cdot \text{s}$). The deformation here is defined as the relative length ratio $\left(a/b\right)$ between the long axis and short axis of the FDR. (E) The deformation of an FDR as a function of different driving voltages (or equivalently magnetic-field strengths). (F) Programming complex shapes of an FDR using distributed ${\mathit{B}}_{\text{ext}}$ produced by ferromagnets in disk-, cube-, and ring-shapes. The color maps represent the normalized $U_{\text{ext}}$ on the actuation plane at 5 mm above the ferromagnets. In all experiments except that in D, only the ferrofluids with dynamic viscosities of 8 mPa·s (EMG 901; Ferrotec Corporation) were used here. (Scale bars, 10 mm.)

In Fig. 2A, we first investigate the splitting behavior of an FDR in both experiments and simulations. The splitting behavior of an FDR on a substrate surface is realized by applying electric currents in the same direction in two coils located under the substrate. The splitting force on the FDR is the spatial gradient of the induced magnetic potential energy $U_{\text{ext}},$ as shown in the top row of Fig. 2A. To illustrate the splitting process of an FDR, we simulate its shape transformation under a magnetic force distribution using a simplified 2D model (SI Appendix, Supplementary Text, section 2), as shown in the bottom row of Fig. 2A. The simulation results show that the magnetic forces applied on an FDR point to the two regions with the minimum $U_{\text{ext}}.$ Therefore, while being confined by surface tension, the FDR is elongated due to the opposite attractive magnetic forces applied on its left and right parts and ends up being split into two subdroplets. Similarly, Fig. 2B shows the merging behavior of two FDRs, realized by generating magnetic fields in opposite directions in two nearby coils. In contrast to splitting, only one magnetic potential energy minimum exists in this case, so that the magnetic forces all point toward the center of the magnetic potential energy well. Two FDRs are driven by such magnetic forces to move toward each other, collide, merge, and stabilize the shape jointly by the magnetic force and surface tension. In addition to the external magnetic forces, the magnetic forces between two droplets also help the merging and splitting process of the FDRs, as illustrated in SI Appendix, Fig. S4. In the splitting process, we observe the potential formation of small droplets if the splitting process is relatively fast. This is because a slender ferrofluid channel is connected between two subdroplets before they are completely separated, and upon a rapid splitting, the channel breaks, resulting in small droplets that cannot be pulled away effectively due to weak magnetic pulling forces (23). These small droplets can be easily collected back by the subdroplets by moving the magnetic potential well close, such as utilizing the control signal in the merging behavior.

More importantly, in the splitting behavior, we can control the volume ratio $V_a/V_b$ of the resulting two sub-FDRs by adjusting the relative strength $B_a/B_b$ (measured at d = 7 mm above the coil, with $B_b$ fixed) of the magnetic fields generated by each coil, as shown in Fig. 2C. When $B_a/B_b$ is less than 0.4, the attraction force by Coil a on the FDR is not strong enough to overcome surface tension to induce any splitting (the “no-splitting” phase). Therefore, the FDR is attracted toward Coil b. However, when $B_a/B_b\ge 0.4$, the volume ratio $V_a/V_b$ increases linearly as $B_a/B_b$ increases (the “unequally splitting” phase), which enables an FDR to split into small droplets with various splitting volume ratios. This mechanism could allow an FDR to split into multiple subdroplets in different sizes on demand, which is useful for creating a team of FDRs for cooperative tasks or controlling microreactions in chemical engineering applications (29).

Subject to a given actuating magnetic field, the deformation of an FDR depends on the confinement effect caused by the surface tension force, which is a function of the droplet local curvature and the surface tension coefficient on the droplet interface (SI Appendix, Supplementary Text section 2). In Fig. 2 D and E, we further study the effect of the viscosity and volume of an FDR on its shape deformability. The deformability is defined by the length ratio $\left(a/b\right)$ of the long and short axes of the deformed FDR when subject to a static magnetic field by specifying a driving voltage (15 V) of the actuation coils (see SI Appendix, Fig. S5 for the mapping between the magnetic fields and driving voltage). Here, FDRs in different viscosities can be obtained by mixing two types of ferrofluids in different viscosities according to specific volume ratios, while keeping the total volume constant (∼200 μL). Fig. 2D shows that FDRs with a higher viscosity have weaker deformability but better stability due to a smaller Bond number, which is defined by $B_o={\left(L/{\lambda }_c\right)}^2,$ where $L$ is the characteristic length and ${\lambda }_c$ is the capillary length (32). Besides, the deformability of an FDR is also dependent on its volume. Fig. 2E shows the deformation of FDRs in three different volumes (50, 100, and 300 µL; dynamic viscosity: 8 mPa·s) when varying the actuating magnetic-field strength. For the FDR of 300 µL, a plateau appears when the applied voltage exceeds 15 V. This is because when the FDR is relatively large, its further elongation is restricted by the size of the coils, as illustrated in Fig. 2E. On the other hand, when the size of the droplet keeps decreasing, the surface tension force becomes more dominant over volume-based external magnetic forces. The deformability of an FDR in our experimental setup is more significantly affected by the surface tension coefficient when the droplet volume is below 62 μL, compared with an FDR in a larger volume, as shown in SI Appendix, Fig. S6. In our experiments, the volumes of FDRs are empirically kept less than 250 µL to allow the maximal deformation with the minimal volume of the droplet in water-based fluidic environments.

We also investigated the deformation and motion of an FDR when it is submerged in liquids of different dynamic viscosities. In general, the inertia effect helps in the splitting and merging behavior of an FDR, which is in accordance with the finding in (23). As shown in SI Appendix, Fig. S7, when the dynamic viscosity of the surrounding fluid ${\eta }_e$ is less than 35 mPa·s and the Reynolds number (Re) larger than 1, the inertia effect allows the splitting and merging behaviors of FDRs under a relatively small minimum driving voltage (∼8 to 15 V). When ${\eta }_e$ keeps increasing to be more than 105 mPa·s and Re is much smaller than 1, the inertia effect diminishes in the splitting and merging behaviors of FDRs, as the minimum driving voltage to induce the splitting and merging behaviors remains constant (∼16 V).

In addition, the viscosity of the surrounding fluidic environment does not affect the deformation of an FDR at a quasi-static state (SI Appendix, Fig. S8A), while it mainly limits the dynamic performance of an FDR. The larger shear stress from the surrounding fluid does slow down the process when an FDR deforms (SI Appendix, Fig. S8B) and reduces the step-out frequency when an FDR moves (SI Appendix, Fig. S8C). However, it should be noted that an FDR can still achieve movement, shape deformation, as well as splitting and merging behaviors, even in an extremely viscous fluidic environment (∼1,000 times viscous than water).

Lastly, we demonstrate that various complex shapes of FDRs can be realized by programming ${\mathit{B}}_{\text{ext}}$ spatiotemporally using permanent magnets with special shapes as templates (Movie S1). Fig. 2F shows that an FDR exhibits a similar morphology to the shape of a magnetic potential energy well, as the magnetic nanoparticles inside the FDR always tend to move to the location with the lowest $U_{\text{ext}},$ similar to ref. 33. This allows an FDR that can vary its morphology on demand for diverse manipulation tasks. Compared with electromagnets, permanent magnets allow more complex shapes of FDRs but are less flexible for controlling the magnetic-field strength and reconfiguring their patterns. In this work, we employ a combination of electromagnets and permanents to control FDRs depending on the demonstrated specific function.

Mechanism and Characterization of Controlled Motions of FDRs.

We can also control the movement of an FDR by programming ${\mathit{B}}_{\text{ext}}$ spatiotemporally. Fig. 3 and Movie S2 present the fundamental mechanism of controlling the motion of an FDR. By controlling the applied currents in the electromagnet array or the rigid-body rotational and translational motion of a permanent magnet, the magnetic potential energy well can be shifted across the workspace, enabling the navigation ability of an FDR. For actuation by electromagnets, unlike recent works where only independent electromagnets (“single-coil” mode) are used to actuate ferrofluid droplets each time (28, 30), here, we simultaneously control two neighboring electromagnets (“double-coil” mode) to allow an FDR achieving both body elongation and navigation in narrow spaces.

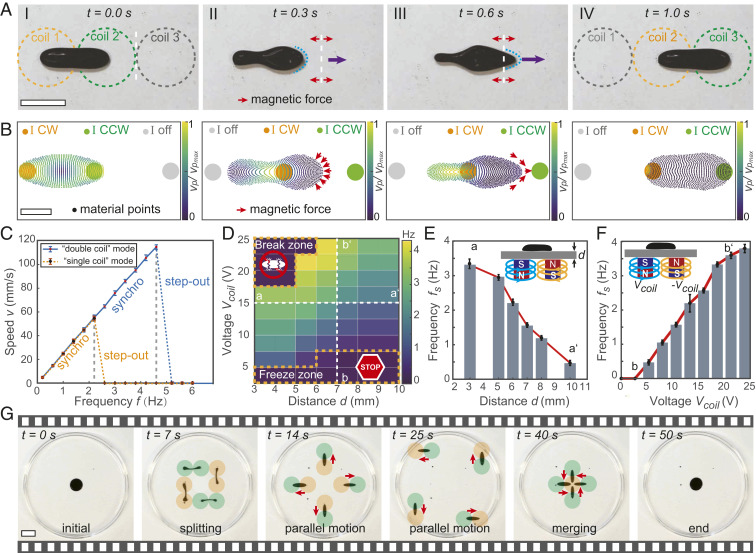
Fig. 3.

Actuation mechanism and characterization of the single-body and coordinated motions of FDRs. (A) Snapshots of the dynamic motion of an FDR actuated in the double-coil mode. The white dashed lines indicate the boundary line of neighboring coils. The red arrows near the white dashed lines indicate the magnetic pulling forces change their directions. The purple arrows and blue dots mark the motion and shape of the FDR, respectively. (Scale bar, 20 mm.) (B) Simulated velocity $V_p$ of an FDR under the spatiotemporal magnetic pulling forces. The applied current $I$ in each coil is marked as clockwise (CW), counterclockwise (CCW), or “off.” (Scale bar, 10 mm.) (C) Speed of an FDR as a function of the actuation frequency $f$ in the double-coil (blue lines) and single-coil (yellow lines) modes. Error bars represent the SD for $n\hspace{0.17em}=\hspace{0.17em}3$ measurements. (D) The step-out frequency $f_s$ of an FDR in the double-coil mode as a function of the applied voltages in the electromagnet array (equivalent to $\left|{\mathit{B}}_{\text{ext}}\right|)$ and the actuation distance $d$ from the electromagnet array to the actuation plane in water. In the “freeze zone,” FDRs cannot move. In the “break zone,” FDRs split. (E) The step-out frequency for an FDR as a function of $d$ along the line aa′ in D. (F) The step-out frequency for an FDR as a function of the applied voltage along the line bb′ in D. (G) Sequential snapshots of the splitting, coordinated navigation, and merging behaviors of FDRs. Red arrows indicate the moving directions of FDRs. The yellow and green dots denote coils with currents in the CW and CCW directions, respectively. (Scale bar, 20 mm.) In all experiments, only the ferrofluids with a dynamic viscosity of 8 mPa·s (EMG 901; Ferrotec Corporation) were used.

To illustrate the motion-control mechanism of an FDR, we systematically investigate the mobility of an FDR using both numerical simulations and quantitative experiments. As shown in Fig. 3 A and B, the motion process of an FDR can be classified into four phases. In the “initialization” phase, the FDR is stretched into a strip shape by the magnetic forces from Coil 1 and Coil 2. In the “accumulation” phase, nonzero opposite currents are applied in Coil 2 and Coil 3, while a zero current in Coil 1, so that the FDR moves toward Coil 2 due to the resulting magnetic pulling force. Once the FDR crosses the boundary line of two coils (marked with white dashed lines), the magnetic pulling force from Coil 2 is slowing down its forward motion, as indicated by its rounded head (marked with blue dots). However, such a pulling force is compensated by the attractive force from Coil 3, allowing the FDR to elongate toward Coil 3 together with the squeezing magnetic forces in other directions. In the “extension” phase, as the FDR further elongates and moves forward, it moves rapidly toward Coil 3 with a sharp head (marked with blue dots), as the magnetic pulling force from Coil 3 becomes dominant in its moving direction. Finally, in the “stabilization” phase, the FDR stabilizes its shape at a position between Coil 2 and Coil 3 due to the competition of magnetic forces, interparticle van der Waals forces, surface tension, gravity, and other forces. The above analysis explains that the double-coil mode not only makes full use of attractive forces induced by two coils but also allows significant body deformation of the FDR. The elongation along the navigation direction makes it easier for the FDR to move between neighboring coils and also significantly reduces the fluid drag due to the streamline shape of its body.

In Fig. 3 C–F, we show that compared with the single-coil mode, the double-coil actuation mode allows better motion performance of FDRs. In Fig. 3C, we first use the step-out frequency $f_s$ to quantify the speed of the FDR (volume: ∼195 µL), which defines the maximum frequency that the FDR can keep pace with, when shifting the magnetic potential energy well at a frequency $f.$ This implies that when $f>f_s,$ the speed of an FDR decreases to zero quickly due to the “step-out” effect (34). In the double-coil mode, we have $f_s\hspace{0.17em}=\hspace{0.17em}4.6\hspace{0.17em}\text{Hz}$, and the maximum speed $v_{\text{max}}=\hspace{0.17em}11.5\hspace{0.17em}\mathrm{cm}\hspace{0.17em}{\mathrm{s}}^{-1},$ which is twice of that in the single-coil mode $(v_{\text{max}}=5.5\hspace{0.17em}\mathrm{cm}\hspace{0.17em}{\mathrm{s}}^{-1}$, $f_s=2.2\hspace{0.17em}\mathrm{Hz)}\mathrm{.}$ To find the actuation parameters to achieve the most efficient motion of an FDR, we characterize its motion performance in the double-coil mode, when varying the actuation voltage $V_{\text{coil}}$ (proportional to the magnetic flux density $B_{\text{ext}})$ and the actuation distance $d$ from the coils to the FDR. Fig. 3D shows that $f_s$ as a function of $V_{\text{coil}}$ and $d$ can be classified into three regions: the break zone, the freeze zone, and the feasible zone. In the break zone, where B is relatively large and $d$ is relatively small, the FDR is unstable, forming spikes and being split into smaller droplets. In the freeze zone, where $V_{\text{coil}}$ is relatively small and $d$ is relatively large, the external magnetic force is so weak that the FDR cannot overcome the surface friction from the substrate to move. However, in the feasible zone, where $V_{\text{coil}}$ and $d$ have moderate values, $f_s$ is nearly proportional to $V_{\text{coil}}$ (Fig. 3E) and inversely proportional to $d$ (Fig. 3F). Therefore, in order to produce efficient motions, $V_{\text{coil}}$ and $d$ should be selected properly to maintain an FDR in the feasible zone. Compared with the single-coil mode (SI Appendix, Fig. S9), the double-coil mode allows a larger proportion of the feasible zone, proving again its advantage in actuating FDRs.

Lastly, by utilizing these discussed motion-control strategies, single and multiple droplets can be controlled to navigate in programmable trajectories by controlling the distributed magnetic fields produced by an electromagnet array or permanent magnets. Fig. 3G shows that the FDR first follows a spiral trajectory and then splits into four subdroplets. Next, the smaller droplets move along programmable trajectories independently. Finally, all the subdroplets gather at the initial position and merge into a large droplet again. The ability of splitting into multiple droplets on demand and coordinately working together could enable completing complex tasks more efficiently than a single FDR.

Mechanism and Characterization of an FDR Navigating in Confined and Narrow Spaces.

A major advantage of an FDR is that it can squeeze through narrow spaces and enter enclosed areas with minimal damage to the surrounding environments that previous soft robots with a comparable overall size cannot reach. As an FDR has both passive and active deformability, it can easily adapt to the confined environmental spaces while maintaining exceptional mobility, especially in narrow tubular structures (Movie S3). To understand the mobility of an FDR in confined spaces, in Fig. 4 A–C, we systematically investigate the minimum diameter $D_{\text{min}}$ of the tubes that an FDR can pass through, when varying the dynamic viscosity $\eta$ and volume of ferrofluids as well as the strength $B$ and actuation distance $d$ of external magnetic fields in both the double-coil and single-coil modes.

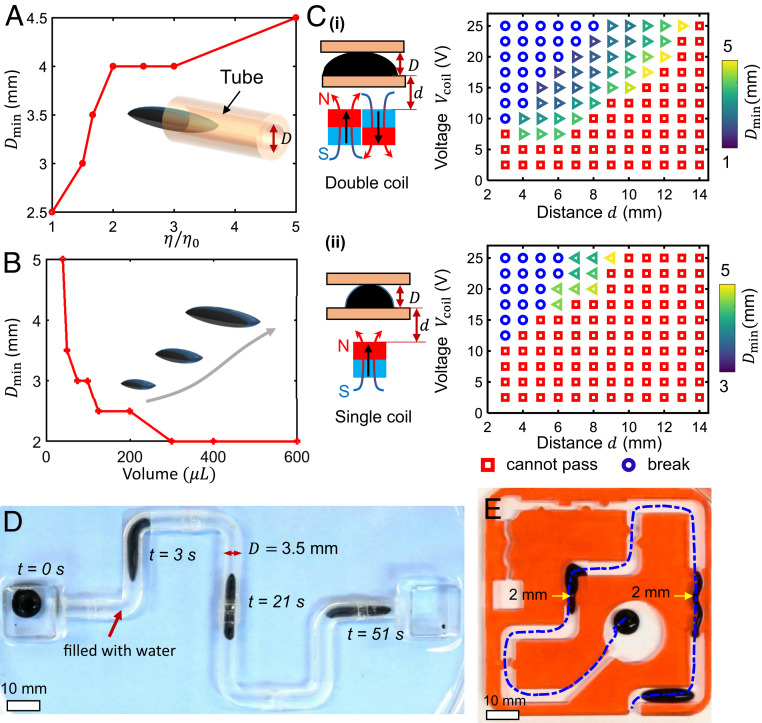
Fig. 4.

Characterization and demonstration of the navigation ability of an FDR in confined 2D environments. (A) The minimum diameter of narrow tubes to pass through by an FDR as a function of its dynamic viscosity. The x axis represents the normalized ferrofluid dynamic viscosity $\left({\eta }_0=8\hspace{0.17em}\text{mPa}\cdot \text{s}\right),$ when mixing two types of ferrofluids in different dynamic viscosities $\left({\eta }_{\text{high}}=80\hspace{0.17em}\text{mPa}\cdot \text{s};\hspace{0.17em}{\eta }_{\text{low}}=8\hspace{0.17em}\text{mPa}\cdot \text{s}\right).$ (B) The minimum diameter of narrow tubes to pass through by an FDR when varying its volume. (C) Comparison of the minimum diameters of narrow tubes to pass through by an FDR, when varying the applied voltages of electromagnetic coils and the actuation distance for the double-coil (C, i) and single-coil (C, ii) modes. (D) Overlapped sequential snapshots of a video, when an FDR is actuated in the double-coil mode to navigate through a narrow tube with meandering structures. The tube with an inner diameter $D\hspace{0.17em}=3.5\hspace{0.17em}\mathrm{mm}$ is filled with water. (E) Overlapped sequential snapshots of a video, when an FDR is actuated in the double-coil mode to navigate through a maze with specially designed narrow features. In B–E, ferrofluids with a dynamic viscosity of 8 mPa·s (EMG 901; Ferrotec Corporation) were used.

First, the material properties of an FDR, such as its dynamic viscosity and volume, significantly affect its navigation ability in narrow tubes. Fig. 4A shows a positive correlation between $\eta$ and $D_{\text{min}},$ while keeping $B$ and $d$ (in a double-coil mode) as well as the droplet volume identical. This is because an FDR with a smaller $\eta$ both can be actively deformed more by the external magnetic fields and has better passive deformability in narrow tubes than an FDR with a relatively large $\eta .$ Fig. 4B shows that the volume of an FDR also influences the navigation ability of a droplet in narrow tubes. An interesting phenomenon, in terms of the droplet volume, is that a smaller droplet is not necessarily able to pass through a narrow tube. This is because a small droplet cannot experience enough magnetic pulling force to overcome the surface friction, due to its relatively long distance from neighboring coils. On the other hand, when the droplet volume keeps increasing, $D_{\text{min}}$ is mainly limited by the droplet viscosity rather than its size.

In addition to the material properties, the strength and actuation mode of external magnetic fields also affect the minimum diameter of the tubes to pass through. Fig. 4C shows the minimum diameter of the tube to pass through when both varying the actuation distance $d$ and the applied voltage of electromagnet coils $V_{\text{coil}}.$ For each experiment, two actuation modes (double-coil and single-coil modes) are used, where $D_{\text{min}}$ is measured and compared. According to the experimental results, the droplet mobility in tubes can be realized only with moderate magnetic-field strengths and actuation distances to avoid either breaking of the droplet into parts or failing to pass through narrow tubes. Compared with the single-coil mode, the double-coil mode yields a larger workable parameter space to allow the droplet passing through narrow tubes with a smaller $D_{\text{min}}$ (1 mm for the double-coil mode; 3 mm for the single-coil mode). As shown in Movie S3, under the same conditions, the FDR can be actuated by the external magnetic field in the double-coil mode to pass a narrow channel, while failing to pass through the same channel in the single-coil mode.

Finally, we show that an FDR with properly designed parameters can confine to environment boundaries while still being able to move freely. In Fig. 4D, we demonstrate that an FDR (volume: 250 µL; dynamic viscosity: 8 mPa·s) can navigate freely through a tube (inner diameter $D=3.5\hspace{0.17em}\mathrm{mm}$) filled with water. The droplet is actuated by an electromagnet array in the double-coil mode. During the navigation, the droplet can elongate its shape along the moving direction in the tube. The passive and active deformability allow it to negotiate over meandering tube structures easily. In Fig. 4E, we show that an FDR can even navigate in a complex maze (filled with water) with various narrow crevices (minimum gap: 2 mm) and multiple branches, demonstrating its adaptive mobility in challenging confined spaces.

Efficient and Versatile Manipulation of Delicate Objects by Shape-Programmable FDRs.

With the abilities mentioned above, here, we demonstrate three unique functionalities of FDRs, enabled by their programmable shape-morphing behaviors as well as single-body and coordinated mobility in confined spaces. In Fig. 5 and Movie S4, we demonstrate the function of efficient and versatile manipulation of delicate objects in confined environments, by reconfiguring the shape of an FDR and controlling its self-breaking and self-recovering behaviors. The ability of wirelessly manipulating delicate objects could have broad applications in bioengineering, such as wirelessly and dexterously manipulating delicate biological cells or samples (35, 36).

Fig. 5.

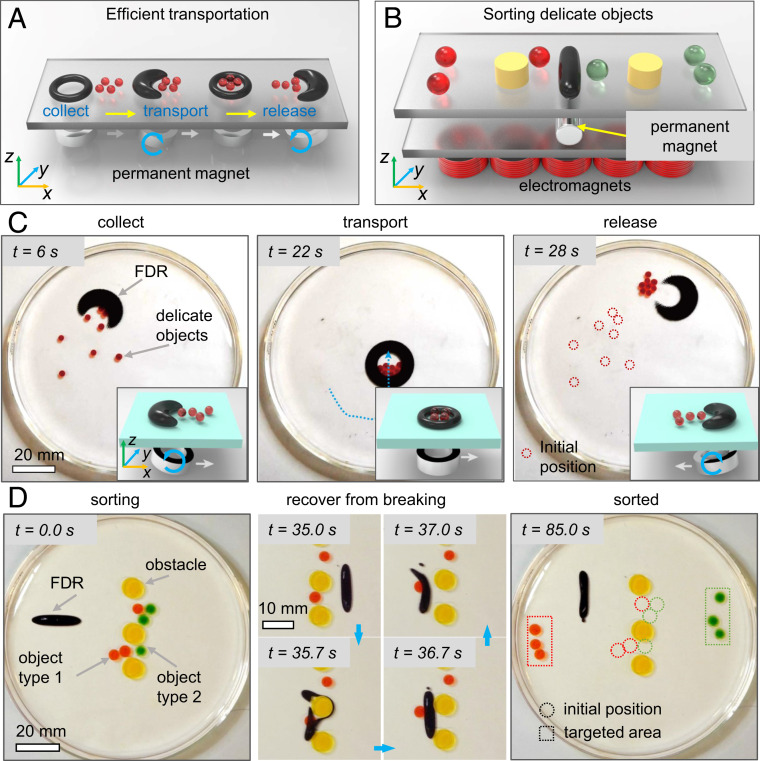
Shape-programmable FDRs demonstrating efficient and versatile manipulations of delicate objects. (A) Schematics of a ring-shaped FDR transporting multiple delicate objects (hydrogel balls) in a glass Petri dish filled with water. The ring-shaped FDR is produced by a ring-shaped NdFeB magnet (outer diameter: 20 mm; inner diameter: 15 mm; N45; Supermagnet.de). The “collect,” “transport,” and “release” motions are further induced by controlling the rotational and translational motion of the NdFeB magnet. (B) Schematics of an ellipsoidal FDR sorting delicate objects in a clustered environment in a glass Petri dish filled with water. The ellipsoidal FDR is produced by a cylindrical NdFeB magnet (dimensions: $\varphi 10\hspace{0.17em}\mathrm{mm}\times 25\hspace{0.17em}\mathrm{mm}$; N45; Supermagnet.de), which is further actuated and controlled by an electromagnet array. (C) Sequential video snapshots of the manipulation process by the ring-shaped FDR. The FDR collects, transports, and then releases multiple hydrogel balls (diameter: 2 mm). The motions of the external NdFeB magnet are shown in Insets. The white arrows and the blue arrows indicate translational and rotational motion directions of the magnet, respectively. (D) Sequential video snapshots of the sorting process of delicate objects by the ellipsoidal FDR. Two types of hydrogel balls (diameter: 4 mm) are coded as red and green. The ellipsoidal FDR can move freely sorting delicate objects and recover from breaking due to its fluid properties. In all experiments, the ferrofluids with $\eta =80\hspace{0.17em}\mathrm{mPa}\cdot \mathrm{s}$ (MFR-DP1; Supermagnet.de) were used.

Fig. 5A illustrates that by programming a ring-shaped $U_{\text{ext}},$ an FDR could be programmed into a ring-shape, which could trap, transport, and release multiple delicate objects efficiently. As shown in Fig. 5C, the magnetic field is produced by an external ring-shaped permanent magnet (NdFeB) (outer diameter: 20 mm; inner diameter: 15 mm; N45; Supermagnet.de), where its translation and rotation can be controlled manually or via a robotic manipulator. The FDR can move freely, and its body shape can be switched between a ring-shape and “C”-shape by adjusting the position and orientation of the permanent magnet. For example, when the ring magnet is parallel to the plane where the droplet is located, the droplet appears as a ring-shape. When the magnet is inclined, the droplet appears as a C-shape. The C-shape of an FDR allows “open” to collect multiple objects. The ring-shape allows “close” to trap and transport multiple objects simultaneously and efficiently.

Furthermore, an ellipse-shaped FDR (deformation: $a/b>5)$ could push delicate objects and sort them into two groups in a clustered environment, as illustrated in Fig. 5B. The long ellipse-shape of the FDR is controlled by a long cylinder-shaped permanent magnet (NdFeB) (dimension: $\varphi 10\hspace{0.17em}\mathrm{mm}\times 25\hspace{0.17em}\mathrm{mm}$; N45; Supermagnet.de). The translational and rotational motion of the permanent magnet is further actuated and controlled by the electromagnet array. Here, the ellipse-shaped FDR allows robustly pushing single or multiple objects. Another unique capability of the FDR is that it can break itself when the force applied on an obstacle or manipulated object exceeds a threshold, as shown in Fig. 5D. This allows the FDR to be safe to the manipulated objects, as well as to be able to negotiate over obstacles and recover quickly from breaking to continue the manipulation task. The threshold of the pushing force when the FDR starts breaking can be adjusted by varying the mixing-volume ratio of the two types of ferrofluids. Our experimental results show that the more viscous an FDR is, the larger velocity (equivalently the exerted pushing force) the hydrogel ball can get (SI Appendix, Fig. S10). Analysis of experimental data shows that the maximum pushing force on a hydrogel ball is from 57 to 88 μN before an FDR breaks (SI Appendix, Supplementary Text, section 3), which can be tuned on demand according to a specific task, making it appealing for manipulating various delicate objects.

Liquid Capsule for On-Demand Liquid-Cargo Delivery in Narrow Tubes.

Minimally invasive drug delivery is a challenging task in biomedical applications (37). Existing works on wirelessly actuated magnetic soft-capsule endoscopes (38, 39) have demonstrated targeted drug delivery in phantom models of the human gastrointestinal tract. Magnetic nanoparticles with drug coatings have also been shown to deliver drugs by thermal triggering using induction heating (37). However, the triggering mechanism is complex, and the amount of carried drugs is relatively small. In Fig. 6 and Movie S5, we demonstrate that an FDR can work as a liquid capsule for liquid-cargo delivery in confined spaces, using simple yet efficient cargo-transportation and -releasing mechanisms. The liquid capsule is much gentler and has better shape adaptability to surrounding environments to allow navigating through challenging narrow spaces such as bile ducts (40), which are difficult to reach for existing wireless endoscopic capsules (38, 39) and catheters (41). Therefore, our demonstration may provide unprecedented opportunities for minimally invasive targeted drug delivery in biomedicine in the future.

Fig. 6.

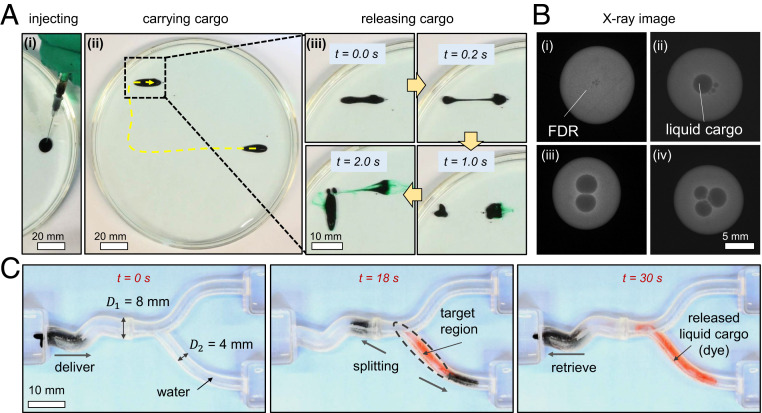
Liquid capsule demonstrating on-demand liquid-cargo delivery in narrow tubes. (A) Video snapshots of the experimental procedures of loading, transporting and releasing liquid cargos. (A, i) The water-based liquid cargo (water-based food dye, ∼12 μL) is loaded on an FDR (∼195 μL) using a syringe injector. (A, ii) The FDR moves freely while carrying the liquid cargo without breaking. Yellow dashed lines: the trajectory of the FDR. (A, iii) The liquid cargo is released on demand using the splitting mechanism by controlling external magnetic fields. (B) X-ray images of an FDR with and without liquid cargos inside. The X-ray images show an FDR without liquid cargos (B, i), with one liquid droplet (B, ii), two liquid droplets (B, iii), and multiple liquid droplets inside (B, iv). (C) Sequential video snapshots demonstrating on-demand “drug delivery” in a vascular phantom model with narrow branches. The FDR carrying liquid cargos navigates through the phantom with varying inner diameters (4 to 8 mm), delivers liquid cargos (food dye) at a target location on a branch by splitting, and is retrieved after the task. In all experiments, the ferrofluids used were obtained by mixing ferrofluids with dynamic viscosities of 80 mPa·s (MFR-DP1; Supermagnet.de) and 8 mPa·s (EMG 901; Ferrotec Corporation) according to a volume ratio of 1:1.

Fig. 6A shows a typical process of loading, transporting, and splitting of a liquid capsule in an open area. The water-based liquid cargo (∼12 µL) is injected into the oil-based ferrofluid droplet (∼195 µL) using a syringe injector. The liquid capsule is then controlled by an electromagnet array to navigate while carrying the cargo. Here, the ferrofluid droplet is prepared by mixing two types of ferrofluids with different viscosities $({\eta }_{\text{low}}=8\hspace{0.17em}\mathrm{mPa}\cdot \mathrm{s}$; ${\eta }_{\text{high}}=80\hspace{0.17em}\mathrm{mPa}\cdot \mathrm{s}$) according to a volume ratio of about one to one for both stability and deformability. Besides, the FDR can keep single or multiple water-based cargos stably inside itself, as shown in the X-ray images in Fig. 6B, where the surface tension between the oil and water prevents the water-based cargo from leaking. After being transported to the targeted location, the cargoes can be released sequentially by splitting the FDR, as shown in SI Appendix, Fig. S11.

With the decent deformability and adaptive mobility in confined spaces, the liquid capsule can still maneuver freely while carrying liquid cargo in water-based liquids even inside a tubal structure with meandering shapes. In Fig. 6C, we first demonstrate liquid-cargo delivery by an FDR in a vascular phantom. The softness of the FDR could cause minimal damage to the surrounding boundary walls. The liquid capsule could navigate through narrow tubes with a minimum diameter of 4 mm in a 3D-printed phantom model. It should be noted that the stability of the liquid droplet during the transportation is maintained by applying a relatively low driving voltage (15 V), in contrast to the relatively high voltage (20 V) while releasing the cargo at the target location. This is because compared with a lower driving voltage, a higher driving voltage indicates a larger magnetic force, rendering the droplet as more stretched in the double-coil mode, resulting in a thinner and easy-to-break boundary interface layer between the ferrofluid and the liquid cargo. In SI Appendix, Fig. S12, we show that this control mechanism even enables a liquid capsule to navigate through more complex environments without breaking, such as a maze, which has complex structures with a minimum gap of 2.5 mm.

Multiple FDRs Enabling Programmable Fluidic Mixing by Coordinated Motions.

Programmable fluidic logics (42–44) in lab-on-a-chip applications are promising for realizing addressable and sequential reactions in fluidic channels. Here, in Fig. 7 and Movie S6, we demonstrate that multiple FDRs could allow programmable fluidic mixing by coordinating their motions in fluidic channels. Compared with existing programmable mixing devices (44–46), our programmable fluidic-mixing device is simple, wireless, and reconfigurable, and could cause minimal damage and contaminants to the fluids due to the gentleness and insolubility of FDRs in water-based fluids.

Fig. 7.

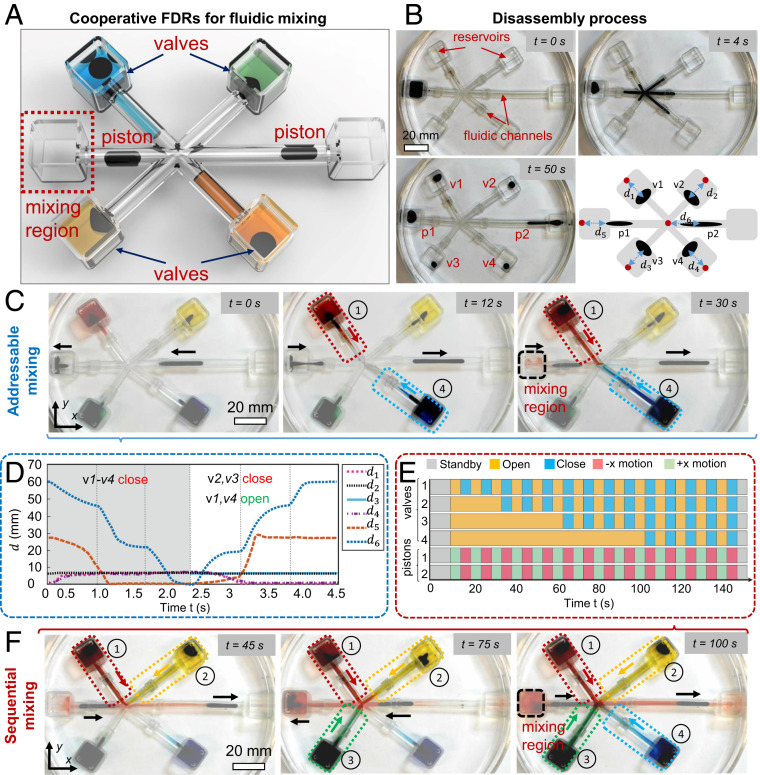
Multiple FDRs demonstrating programmable fluidic mixing by coordinated independent motion control. (A) Concept of the programmable fluidic-mixing device. The motion of each FDR can be controlled independently to work either as a piston or valve. The selected liquids in an arbitrary reservoir can be pumped into the “mixing zone” by controlling the “open” or “closed” states of the corresponding valve. (B) A single FDR is injected into a fluidic channel with a specific topology and then disassemble into multiple FDRs. States of the device are characterized by the relative displacement $d_i\left(i=1,\dots ,6\right)$ from the ith FDR to its reference point. The valve is open or closed when the FDR is far away from or close to the reference point, respectively. The dye is pumped into or away from the main channel when the FDR as a piston is far away from or close to the reference point, respectively. (C) Sequential video snapshots of selectively mixing the red and blue dyes. The selected channels are marked with dashed rectangles. (D) The sequential relative displacements $d_i$ of all FDRs in C within a full pumping period. (E) Sequential states of the valves and pistons in the demonstration of sequentially mixing dyes in four channels according to a specified order (“1-2-3-4”). (F) Video snapshots of sequentially mixing dyes in four channels corresponding to the sequential system states shown in E. In all experiments, ferrofluids with a dynamic viscosity of 8 mPa·s were used. The average volume flow rate of the flow into the mixing region is about 23.6 µL·s⁻¹ in C and F.

As illustrated in Fig. 7A, the independent motions as well as the adaptive confinement of these droplets in tubes allow them to work as pistons or valves simultaneously for fluidic-mixing functions. Fig. 7B shows that the process of a single FDR being controlled to split into multiple FDRs, forming a fluidic-mixing device. First, a ferrofluid droplet with a relatively low viscosity (dynamic viscosity: 8 mPa·s) is injected into a fluidic channel. Then, it is controlled to split into multiple smaller droplets. Finally, each droplet performs a sequence of preprogrammed motions and cooperates to complete a mixing task controlled by the electromagnet array. The controlled spatiotemporal motion of each droplet can be quantified by predefining six reference points. For example, a valve is closed or open, if a droplet is moving away from or close to the reference point in the lateral branches, respectively. For the pistons, the dye is either injected into or drawn back out of the pump, when the droplet is moving away from or close to the reference in the main branch, respectively.

To illustrate the utility of the fluidic-mixing device, we demonstrate proof-of-concept functions of addressable and sequentially mixing various “chemicals” (simulated using dyes) in the same device. As shown in Fig. 7C, two selected dyes in reservoir 1 and 4 are pumped into the main channel with an average volume flow rate of ∼23.6 µL·s⁻¹ when two pistons are moving in the +x direction, by keeping only valve 1 and valve 4 open and all other valves closed. The time-varying displacements of all droplets within a cycle are also shown in Fig. 7D to quantitatively describe the state of each FDR in the device (see SI Appendix, Fig. S13 for the control signals of the electromagnets). Similarly, as all channels are addressable, the device can also realize sequential mixing of various chemicals. By controlling the open and close states of the valves, as well as the forward and backward motions of the pistons (Fig. 7E), we can sequentially mix multiple dyes one by one according to an arbitrary given order, as shown in Fig. 7F. The sequential-mixing function may allow programmable reactions of chemicals by controlling the coordinated states of these valves and pistons. The unique advantage of the demonstrated fluidic-mixing device is that an FDR could be split into multiple sub-FDRs on demand and then coordinate their motions for a specific task, allowing more flexible and reconfigurable fluidic functions in situ compared with conventional mixing devices (46). Moreover, the FDR could be safe when interacting with (e.g., pumping) biological fluids (e.g., blood) in the future (20), allowing minimal shear stress on the cells.

Discussion

We have reported reconfigurable multifunctional FDRs by programming external magnetic fields spatiotemporally. Our method allows producing much larger deformation (e.g., splitting) in these droplet robots compared with existing magnetically actuated elastomer-based soft robots and enables on-demand complex shape-morphing behaviors compared with existing droplet robots. Multiple functionalities of these droplet robots have been demonstrated, including splitting and merging for liquid-cargo delivery, navigating through narrow channels much smaller than their sizes, and reconfiguring into different shapes for efficient and versatile manipulation of delicate objects. Moreover, cooperative functions have also been realized by coordinating the group motions after a single droplet being split into multiple droplets. We have demonstrated a fluidic-mixing device for mixing chemicals selectively or sequentially in a programmable manner.

The realization of multiple functionalities in FDRs relies on the fundamental understanding of the controllable complex dynamics of ferrofluid droplets. We systematically investigated the dynamic behavior of FDRs to understand how the dynamic behaviors of ferrofluid droplets can be controlled by programming spatiotemporal magnetic fields. These investigations involve the shape-morphing behaviors of FDRs, e.g., splitting and merging, the mobility of FDRs in confined spaces, and the interaction of FDRs with manipulated objects. The experimental observation and analysis, such as the role of the inertia effect in the splitting and merging behaviors of FDRs and the “self-breaking” and “self-recovering” mechanisms when an FDR interacts with objects, could provide insights into droplet physics and are essential for creating multiple functionalities in FDRs.

The widely applicable working environments and biocompatibility of FDRs also make them promising for critical bioengineering applications. We show that FDRs can also work in biological fluids, such as phosphate-buffered saline and normal saline (SI Appendix, Fig. S14 and Movie S2). In addition, the complex deformation of the developed FDRs might potentially be utilized for versatile spatiotemporal stimulation and local measurement of the mechanical properties of biological tissues in bioengineering applications, such as investigating the spatially varying tissue mechanics of embryonic tissues, as demonstrated in refs. 21 and 22. Although such an application is beyond the scope of this work, it is possible to use FDRs for these bioengineering applications in the future, which could allow more complex spatiotemporal stimulation compared with previous works, by controlling the complex large deformation of single or multiple FDRs. Therefore, the proposed FDRs could open up wide opportunities to enable diverse unprecedented functionalities that are promising for critical lab/organ-on-a-chip, fluidics, bioengineering, and biomedical applications in the future.

Materials and Methods

Magnetic-Actuation Systems.

The spatiotemporally varying external magnetic fields in the experiments were produced by either a 2D electromagnet array or various permanent magnets with specific shapes. Our primary magnetic-actuation system was a 5 × 5 electromagnet array composed of 25 solenoids $(\varphi 25\times 30\hspace{0.17em}\mathrm{mm;}$ ITS-MS-3025-24VDC; Conrad.de), as shown in Fig. 1 (see the description of the system components in SI Appendix, Fig. S3). The current in each solenoid was controlled to follow preprogrammed waveforms or teleoperated using a joystick for more flexible control. The electromagnet array could generate a distributed magnetic field across an area of 125 × 125 mm² at a specific actuation plane. For each solenoid, the maximum magnetic-field strength was about 6.7 mT at an actuation distance of 10 mm. The distance from the electromagnet to the actuation plane could also be adjusted in the experiments to vary the magnetic-field strength while keeping the applied voltage identical (see SI Appendix, Fig. S5 for characterization data). The actuation distance from the top surface of the electromagnet array to the substrate was about 10 mm, which might not be enough for some specific future applications. The actuation distance could be further increased in multiple ways, such as by using stronger electromagnets with a cooling system or using a combination of both an electromagnet array and permanent magnets (27), which will be explored in the future. In addition, we used NdFeB permanent magnets (N45; Supermagnet.de) in various shapes for controlling the complex shapes of ferrofluid droplets. Compared with an electromagnet array, a permanent magnet (or array) can provide a stronger magnetic field due to a high-power density and produce a more complex magnetic-field distribution, while the reconfigurability is limited.

Preparation and Characterization of Ferrofluid Droplets.

Two types of ferrofluids with dynamic viscosities of 8 mPa·s (EMG 901; Ferrotec Corporation) and 80 mPa·s (MFR-DP1; Supermagnet.de) were used in the experiments. The properties of the ferrofluids are summarized in SI Appendix, Table S1. SI Appendix, Fig. S1 shows the transmission electron microscope image of the iron oxide nanoparticles in ferrofluids (MFR-DP1; Supermagnet.de) and the magnetization hysteresis curve. To create the ferrofluid droplets in the experiments, two types of ferrofluids were first mixed according to different volume ratios (or used separately). The ferrofluids were then transferred by a pipette into a container filled with water and other water-based liquids. More details of the tubular phantom structures and mazes, the manipulated objects, as well as the characterization, modeling, and analysis are provided in SI Appendix.

Data Availability.

All study data are included in the article and supporting information.