Ensemble Forecast and Parameter Inference of Childhood Diarrhea in Chobe District, Botswana

Abstract

Diarrheal disease is the second largest cause of mortality in children younger than 5, yet our ability to anticipate and prepare for outbreaks remains limited. Here, we develop and test an epidemiological forecast model for childhood diarrheal disease in Chobe District, Botswana. Our prediction system uses a compartmental susceptible-infected-recovered-susceptible (SIRS) model coupled with Bayesian data assimilation to infer relevant epidemiological parameter values and generate retrospective forecasts. Our model inferred two system parameters and accurately simulated weekly observed diarrhea cases from 2007–2017. Accurate retrospective forecasts for diarrhea outbreaks were generated up to six weeks before the predicted peak of the outbreak, and accuracy increased over the progression of the outbreak. Many forecasts generated by our model system were more accurate than predictions made using only historical data trends. Accurate real-time forecasts have the potential to increase local preparedness for coming outbreaks through improved resource allocation and healthcare worker distribution.

Introduction

Diarrhea is the second leading cause of death in children under 5 years of age worldwide; it kills more children than HIV/AIDS, measles, and malaria combined (World Health Organization, 2015). Rates of under-5 diarrhea in Africa are particularly high, with an estimated incidence of 3.3 episodes of diarrheal disease per child each year, and 11% of under-5 mortality caused by diarrhea (Fischer Walker et al., 2013; Walker et al., 2012).

Botswana is a politically stable, middle-income country in southern Africa whose government has invested in free healthcare and piped water for its citizens. However, the country still experiences seasonal outbreaks of diarrhea that result in under-5 morbidity and case fatality rates as high as 30% and 20%, respectively (Statistics Botswana and Ministry of Health, 2009). Annual outbreaks occur during the pronounced wet and dry seasons (Alexander et al., 2013, 2012), and attack rates are highest for children younger than one year (Kaltenthaler et al., 1996; Mach et al., 2009). Further, rates of diarrhea incidence vary considerably from year-to-year. For instance, in 2006 Botswana experienced a diarrhea outbreak that resulted in a four-fold increase in the number of cases of diarrhea among young children, and 25% more diarrheal deaths than in the previous two years (Mach et al., 2009).

Hospitals and clinics in Botswana have limited resources and are understaffed. Hence, few resources are available to prospectively investigate outbreak dynamics (Alexander and Blackburn, 2013). During the 2006 outbreak, the Botswana Ministry of Health announced the occurrence of the outbreak a month after it began and had no projections of the outbreak trajectory, leaving hospitals and clinics unprepared for its magnitude. Real-time forecasts of the outbreak timing, scale, and progression might have prevented diarrhea cases and deaths had such predictions been available and well-integrated into public health and clinical response.

Diarrhea is a syndrome that can be caused by a variety of viruses, bacteria, and parasites. To date, the etiology of childhood diarrhea in Botswana is not well characterized. Several studies have investigated pathogen specific diarrhea, but they rely on small convenience samples. One study found that 20% and 3.5% of children with diarrhea tested positive for Shigella and Salmonella, respectively (Urio et al., 2001), whereas other analyses estimated the prevalence of Shigella to be 4% (Rowe et al., 2010), and the prevalence of Salmonella to be 38% (Creek et al., 2010). Rotavirus prevalence estimates range from 6% to 78% (Basu et al., 2003; Creek et al., 2010; Welch et al., 2013), and prevalence estimates for Cryptosporidium range from 2% to 60% (Alexander et al., 2012; Creek et al., 2010; Goldfarb et al., 2014; Rowe et al., 2010).

Here we develop and test an epidemiological forecasting model for childhood diarrhea in Botswana. Due to the inconsistencies in diarrhea etiology estimation, we use a compartmental model to represent the dynamics of diarrhea as a syndrome. While compartmental models are traditionally used to characterize the propagation of a single pathogen, they have been previously used to accurately forecast influenza-like-illness syndrome (Shaman and Karspeck, 2012; Biggerstaff et al., 2016). However, parameter estimations derived from model simulations of syndromic data cannot be interpreted in a traditional manner as they represent the transmission dynamics of multiple pathogens. Here we focus on two syndromic parameters: 1) the basic reproduction number R₀ and 2) the typical period between infections δ. Traditionally, R₀ represents the number of secondary infections resulting from one infected individual in a completely susceptible population, but in our analysis it describes the force of transmission for one or more pathogens (Diekmann and Heesterbeek, 2000). Similarly, δ traditionally represents the rate of waning immunity to a pathogen but here we use it to estimate the time between diarrhea infections. Because these parameters represent the dynamics of multiple pathogens, we allow their flexible adjustment over time in order to capture seasonal and annual variations in multi-pathogen transmission.

Our compartmental model is coupled with Bayesian inference, or data assimilation, methods that adjust the model state variables and parameters to optimal values using time series observations of diarrhea incidence. This process enables ensemble forecasting of future conditions with the optimized model. In effect, the data assimilation ‘trains’ the model to represent current outbreak dynamics and thus facilitates better forecasting of future conditions, including prediction of outbreak peak timing and attack rate. Similar model-inference and inference frameworks have been successfully used to estimate critical epidemiological parameters and generate real time forecasts for human influenza (Dukic et al. 2012; Ong et al. 2010; Shaman et al. 2013a), Ebola (Shaman et al., 2014), West Nile virus (DeFelice et al., 2017) and Dengue (van Panhuis et al., 2014), but notably have not been applied to diarrheal disease.

Here, we present the diarrhea model-inference system, syndromic parameter estimates, and retrospective seasonal forecasts generated for Chobe District, Botswana during 2007–2017. Our results have implications for outbreak preparedness in low resource environments where diarrheal disease continues to present a critical public health threat.

Methods

Study site

Botswana is a semi-arid, landlocked country in southern Africa. The country has a subtropical climate with annual wet (November-March) and dry (April-October) seasons. Intra- and inter-annual precipitation variability are high, resulting in frequent droughts and flooding (Tsheko, 2003). This study focuses on the Chobe District, located in northeastern Botswana. Most of the population obtains piped water through direct reticulation or public taps (Alexander et al., 2013). While health services are provided by the Government of Botswana at a nominal charge, the district only contains one primary hospital, three clinics, and 12 health posts (Alexander et al., 2013) to serve about 25,000 people (Central Statistics Office of Botswana, 2011). Kasane Primary Hospital, the largest healthcare provider in the district, has just 29 beds (Statistics Botswana and Ministry of Health, 2009). Furthermore, there is very limited staffing within district hospitals, clinics, and health posts (Alexander et al., 2013).

Weekly diarrhea observations

Weekly under-5 diarrhea case reports were obtained for 10 health facilities (the Kasane primary hospital and 9 health posts) in Chobe District from the Botswana Integrated Disease Surveillance and Response Program (IDSR, 2007–2017), which collates weekly numbers of children under five presenting to district health facilities with diarrhea. A diarrhea case was defined as the occurrence of at least three loose stools in a 24-hour period within the four days preceding the healthcare facility visit. Case data represent summary clinical diagnoses of attending physicians or nurses in Government medical facilities in the District.

Correcting for missing under-5 diarrhea data.

In the IDSR record, missing data exist for each of the ten reporting clinics and hospitals. Weeks with no reports (i.e., all 10 health facilities not reporting) were not included in the analysis (13 of 551 weeks). For remaining weeks (i.e., data from 1–10 health facilities), we used the total number of cases reported in a given week and divided this by the number of health facilities reporting that week. This provides a weekly estimate of total under-5 diarrhea cases per health facility reporting, but does not account for differences in average patient volume between reporting locations.

Smoothing under-5 diarrhea observations.

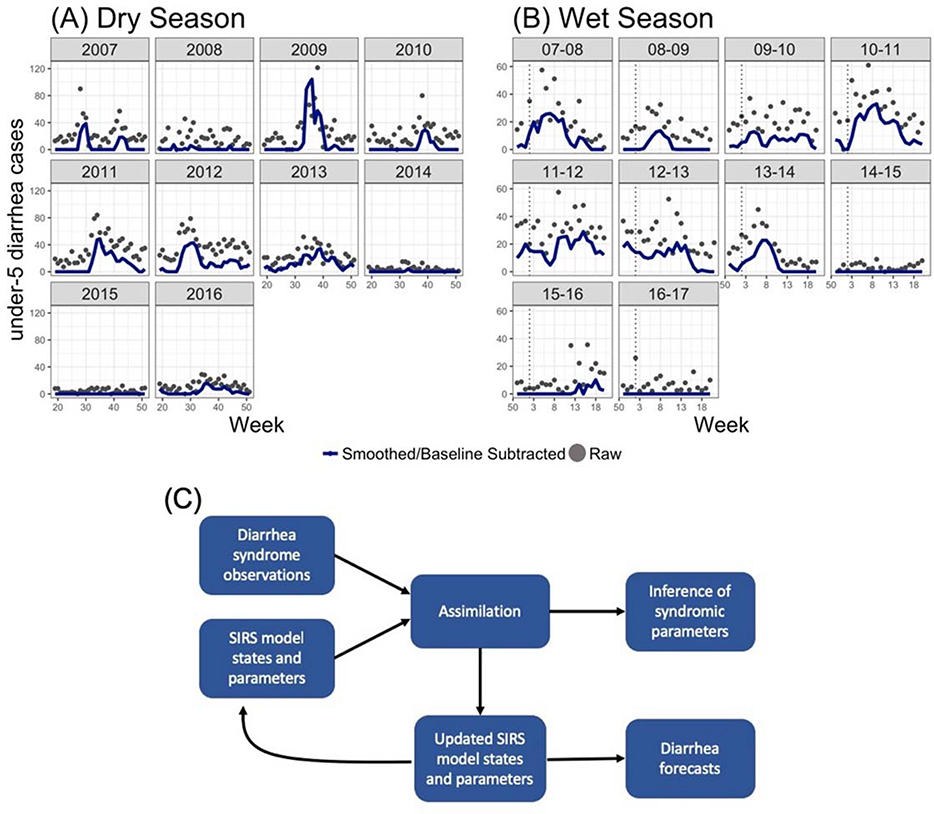
To decrease the level of noise in the diarrhea observations, we generated a three week moving average of the observations (using the current and two previous observations). In addition, to isolate the outbreak signal we subtracted a baseline signal from all outbreaks. In the dry season, we subtracted 25 cases from 2007–2012, and 10 cases from 2013–2016. The baseline lowered in 2013 following the introduction of a rotavirus vaccine in July 2012 (Enane et al., 2016). In the wet season, we subtracted 15 cases in all yearly outbreaks. Rotavirus is specific to the dry season, so no changes were made to the wet season baseline after 2012. These baseline levels were chosen based on visually inspecting the diarrhea outbreak data. We varied them as sensitivity tests and found similar results irrespective of the baseline chosen. Raw under-5 diarrhea counts and smoothed counts with baselines subtracted are shown in Figure 1.

Figure 1.

Data smoothing and model system structure. (A) Weekly cases of under-5 diarrhea (after correction for missing data) in the dry seasons (weeks 20–51) in 2007–2016 are shown as grey points. Blue lines show under-5 diarrhea data after smoothing and subtraction of a baseline (see text for more details). (B) as for (A) but in the wet seasons (weeks 50–20) from 2007–2008 to 2016–2017. (C) Diagram of the model-system structure and outcomes. We use an SIRS model structure and weekly syndromic observations of under-5 diarrhea. The data assimilation system combines syndromic observations with SIRS model states and parameters to (1) infer syndromic epidemiological parameters, and (2) generate updated SIRS model states and parameters. The updated SIRS model states and parameters are then used to either (1) propagate the SIRS model forward one week, after which the assimilation process is repeated, or (2) generate forecasts by propagating the SIRS model forward until the end of the season.

Model-inference system

We developed and evaluated a model-inference system for forecasting under-5 diarrhea in Chobe District. Broadly, we used the Ensemble Adjusted Kalman Filter (EAKF)(Anderson, 2001) in conjunction with observations of under-5 diarrhea rates to iteratively update estimates of the state variables and parameters of an SIRS model. Similar assimilation, or filtering, methods have previously been used for system optimization and forecasting of diseases such as human influenza (Dukic et al., 2012; Ong et al., 2010; Shaman et al., 2013b; Shaman and Karspeck, 2012), Ebola (Shaman et al., 2014), West Nile virus (DeFelice et al., 2017) and Dengue (van Panhuis et al., 2014). This system uses real-time observations to iteratively update the dynamic model state variables and parameters to better match the ongoing outbreak dynamics (Figure 1C). This inference of critical epidemiological parameters and the model states enables generation of more accurate ensemble forecasts of future diarrheal incidence.

There are three main components of this system: 1) a dynamic state-space model describing the propagation of diarrhea through the local population; 2) scaled observations of under-5 diarrhea (described above); and 3) a data assimilation, or Bayesian inference, method. The form and function of each system component is further described below.

Dynamic state-space model for diarrhea transmission.

Under-5 diarrhea dynamics were simulated using a compartmental susceptible-infected-recovered-susceptible (SIRS) mathematical model. The movement of the population between each disease stage is determined by parameters defining transition rates between compartments. The model has the form:

$$\frac{dS}{dt}=–\frac{\beta SI}{N}+\delta R$$

$$\frac{dI}{dt}=\frac{\beta SI}{N}–\gamma I$$

$$R=N–S–I$$

where S is the number of susceptible people in the population, I is the number of infected people, β is the rate of transmission, γ is the rate of recovery, δ is the rate of waning immunity, and N is the population size, which is held constant at 25,000. Simulations consisted of a 300-member ensemble integrated using the data assimilation methods described below. For each ensemble member, initial values for the parameters and state variables were randomly selected from prescribed ranges using Latin Hypercube sampling. Prescribed ranges were determined based on preliminary model fitting and estimates of duration of infection, incubation period, and waning immunity from the Center for Disease Control and Prevention (Table S1).

Observations of under-5 diarrhea.

To use the diarrhea observations to train the EAKF model-inference system, we mapped the observations to weekly incidence and assigned an error structure to the observations. Specifically, weekly under-5 observed case counts of diarrhea were assimilated into a pseudo model state variable representing the number of new infections each week. To accomplish this, we defined a scaling factor, α, that maps diarrhea observations to new weekly diarrhea cases across the population. Given Bayes’ rule:

$$\begin{gathered} p(diarrhea)=\frac{p(m)*p(diarrhea|m)}{p(m|diarrhea)} \\ =\alpha *p(m)*p(diarrhea|m) \end{gathered}$$

Here, $p(diarrhea)$ represents the probability of new under-5 diarrhea infections, $p\left(m\right)$ represents the probability a child seeks medical care for any reason, $p(m|diarrhea)$ is the probability a child seeks medical care given he or she has diarrhea, and $p(diarrhea|m)$ is the probability a child has diarrhea given he or she seeks medical care. Our under-5 diarrhea observations are weekly diarrhea case reports from all health facilities in Chobe District, which can be represented as $p(m)*p(diarrhea|m)$. We define the scaling factor α as $1/p(m|diarrhea)$, which allows us to estimate $p(diarrhea)$, or the diarrhea incidence across the entire population. This parameter is then used to adjust a pseudo state variable in the SIRS model representing the weekly number of new diarrhea cases. We tried many different values for α, and ultimately chose α =60 in the wet season and α =40 in the dry season, which produced diarrhea forecasts with the lowest root mean square error (RMSE) between predicted and observed diarrhea cases.

Observational error variance (OEV) is another input for the EAKF data assimilation algorithm, and represents the error associated with the observations. Here we use the OEV structure presented by Shaman et al. (2012), where OEV for observations at week k is represented as:

$${OEV}_k=\left[\frac{1\times {10}^5+\frac{{\left({\mathrm{\Sigma }}_{j=k–3}^{k–1}\frac{{diarrhea}_j}{3}\right)}^2}{5}}{10}\right]$$ (4)

The OEV increases in this structure in proportion to the sum of the prior three weeks of observations. We tested different OEV levels by changing the denominator to 1,10, and 100. Calibration analyses (described below) showed that the model was best calibrated when the denominator was set to 10.

Ensemble Adjusted Kalman Filter (EAKF).

The EAKF uses the scaled under-5 diarrhea observations to iteratively update estimates of the SIRS model state variables and parameters. First, 300 ensemble members were initialized using randomly selected parameters and state variables. These ensemble members were then parallelly integrated forward in time, using the SIRS compartmental model equations, until the first diarrhea observation of the season. The model integration was then halted and the estimates of the observed and unobserved states (S, I, R) and parameters (beta, gamma, delta) at this time point were deemed the prior and treated as state variables in the EAKF procedure. The EAKF then updated the prior estimates using the under-5 diarrhea observation and OEV for that time point, generating a posterior distribution of observed and unobserved parameters and state variables. The updated SIRS model was then integrated forward to the next observation, and the assimilation process was repeated. This iterative updating ‘trained’ the model to not only better estimate observed conditions but also infer the unobserved state variables and epidemiologically significant parameters. That is, by training the model to replicate observations as thus far observed, the ensemble of simulations converged to variable and parameter estimates that better matched the evolving dynamics of the current outbreak. Integration of the optimized ensemble of simulations into the future without further updating was then used to generate forecasts.

Syndromic parameter inference

Results from synthetic testing, in which the model-inference systems is applied to known, model-generated outbreaks, indicated that our model system can accurately infer important outbreak parameter values, including δ (the rate of waning immunity) and the basic reproduction number R₀, which is defined as β/γ (see supplement for details, Figure S1). Our model is representing diarrhea as a syndrome instead of a pathogen specific disease, so R₀ can be thought of as the force of transmission for one or more pathogens and δ could describe the typical period between individual infections rather than waning immunity. The SIRS-EAKF system was fit to under-5 diarrhea observations for each year in the wet and the dry season 10 times (to account for stochasticity during model initialization). Mean posterior estimates of δ and R₀ were extracted at the peak of each seasonal outbreak for 2007–2016.

Retrospective forecasts and model calibration

We produced retrospective weekly forecasts for the wet and dry seasons of 2007–2016. Each week, following EAKF updating of the ensemble of simulations, forecasts were generated using the most recent posterior estimates by simply integrating the SIRS model through time until the end of the season without further updating. This process was repeated every week, and each successive forecast assimilated one additional week of data. In the dry season, forecasts began at week 18 and were made consecutively until week 52. Wet season forecasts began at week 50 and continued to week 20. Diarrheal cases did not rise above the subtracted baseline during the 2014–2015 wet season or the 2008, 2014, and 2015 dry seasons, so no forecasts were generated for these seasons.

Forecast accuracy was determined by comparing the mean ensemble trajectories with observed under-5 diarrhea cases. Specifically, we focused on three epidemiologically important parameters: peak timing, peak intensity, and overall attack rate. Peak timing is defined as the week with the highest incidence of diarrhea cases, peak intensity is the total number of cases at the peak, and the attack rate is the total number of cases during the outbreak. Forecasts were deemed accurate if they (1) peaked within ±1 week of the observed peak, (2) projected peak intensity within ±25% of the observed peak intensity, and (3) projected a total attack rate within ±25% of the observed attack rate. Forecast accuracy was compared based on predicted lead week, i.e. how many weeks before or after the predicted peak the forecast was generated.

Forecasts generated by the SIRS-EAKF model were compared to forecasts based only on historical data. Historical predictions for a season were made using the median of observed peak timing, peak intensity, and attack rate from all other years in the dataset. In other words, the median observation across all years except year_t was taken to be the prediction for year_t. Accuracy was evaluated as for the SIRS-EAKF forecasts.

Lastly, we evaluated the calibration of the SIRS-EAKF forecasts. The assimilation approach is based on the assumption that both the model and observations represent the true state of the population with error. While we validate our forecasts using observations, we also need to verify that the model is not overfit to the data. To assess this, we calculated the percentage of observations falling within the forecast ensemble spread. For example, a 95% ensemble prediction interval for diarrhea incidence should include diarrhea observations 95% of the time, across all years and seasons.

Results

Retrospective simulations and syndromic parameter inference

The SIRS-EAKF model system was able to simulate under-5 diarrhea outbreak dynamics across all years in the wet and dry seasons (Figures S2 and S3). The average RMSE and correlation between the observations and simulations across all wet season outbreaks was 0.79 and 0.99, respectively. Similarly, average RMSE and correlation across dry season outbreaks were 1.33 and 0.99, respectively.

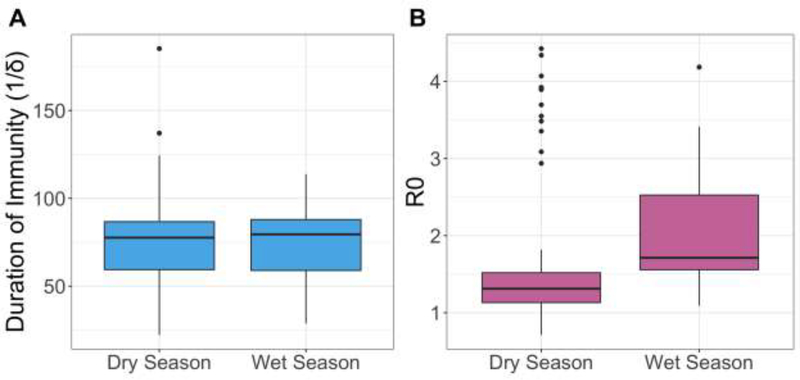
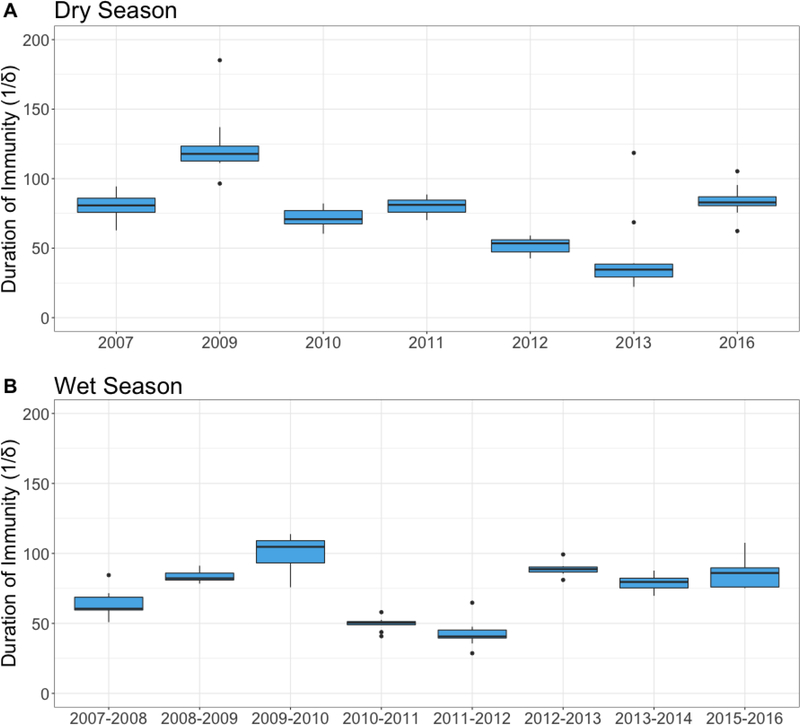
Estimates of the duration of immunity (1/δ) were very similar between the wet season (mean=74.1 days) and the dry season (mean=76.4 days) (Figure 2). However, there was a range of duration of immunity (1/δ) estimates across years in both seasons (Figure 3). In the dry season, mean duration of immunity estimates ranged from 22.2 in 2013 to 185.2 days in 2009. The range of mean duration of immunity estimates in the wet season was slightly smaller; the lowest estimate was 28.6 days in 2011–2012 and the highest was 113.8 days in 2009–2010.

Figure 2.

Parameter estimates across seasons. Estimates in both the wet season and dry season are shown in (A) for duration of immunity (1/δ) and (B) for the basic reproduction number R₀. The boxplots show variation in estimates from 10 simulations run each year.

Figure 3.

Estimates of the duration of immunity (1/δ) in days across years and seasons. Estimates for duration of immunity (1/δ) are shown for the dry season (A) and wet season (B) across years. Here we are modeling diarrheal disease as a syndrome caused by multiple pathogens, so 1/δ can be interpreted as the typical period between infections rather than waning immunity. Boxplots show variability in estimates across the 10 simulations run each year.

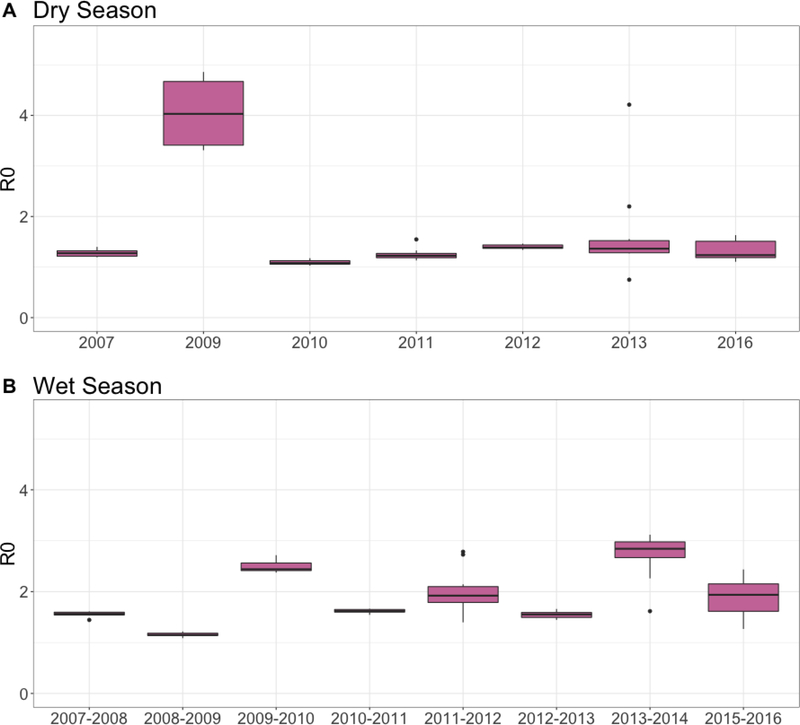
The mean estimated basic reproduction number R₀ was higher in the wet season (1.94) than the dry season (1.67) (Figure 2). Similar to the δ estimates, R₀ estimates ranged across years. Dry season estimates mostly ranged from 1.5–2 except for estimates from 2009, which ranged from 2.5–4.5 (Figure 4). In the wet season, R₀ estimates remained between 1.5 and 2.5 across all years.

Figure 4.

Estimates of the basic reproduction number (R₀) across years and seasons. Estimates for R₀ are shown for (A) the dry season and (B) wet season across years. Here we are modeling diarrheal disease as a syndrome caused by multiple pathogens, so R₀ describes the force of transmission for one or more pathogens that may vary through time. Boxplots show variability in estimates across the 10 simulations run each year.

Retrospective forecasts

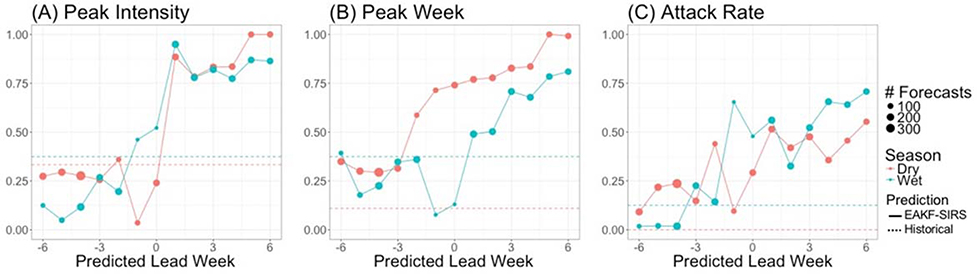
Figure 5 shows retrospective forecast accuracies across seasons for peak week timing, peak intensity, and overall attack rate. Accuracy metrics are shown based on the predicted lead week (i.e. the number of weeks before or after the predicted peak week the forecasts were generated) and compared with predictions derived from historical distributions.Predictions for peak intensity reached very high accuracy for both the wet (98%) and dry (84%) seasons when they were initiated one week after the predicted peak week. Historical peak intensity accuracies were similar for the wet season (38%) and dry season (33%). Accuracy of dry season forecasts did not markedly exceed historical accuracy until one week after the peak, whereas wet season forecast accuracy exceeded historical accuracy beginning one week before the predicted peak.

Figure 5.

Improvements in forecast accuracy achieved over predictions made based on historical distributions. Forecast accuracy is shown for three metrics: (A) peak intensity (proportion of forecasts accurate within 25% of observed peak intensity), (B) peak week timing (proportion of forecasts accurate within ±1 week), and (C) attack rate (proportion accurate within 25% of observed attack rate). Dry season accuracies are shown in red and wet season accuracies are shown in blue. Historical accuracy is represented by dashed lines, while SIRS-EAKF forecast accuracy are solid lines. The x-axis represents the timing of the forecast in relation to the predicted peak week; negative values represent forecasts made before the predicted peak. The size of the points represents the number of forecasts produced at each predicted lead week.

Dry season peak week timing forecast accuracy exceeded historical accuracy at all lead weeks, and reached over 50% accuracy two weeks before the predicted peak. Historical prediction accuracy for peak week was higher in the wet season, indicating greater regularity in the timing of these outbreaks; retrospective forecasts during the wet season only improved on historical accuracy when initiated after the predicted peak.

Lastly, retrospective forecasts poorly predicted overall attack rate within ±25% of the observed attack rates. Dry season forecasts never exceeded 50% accuracy, and wet season predictions never exceeded 75% accuracy. However, our model-inference system predictions outperformed historical predictions beginning six and three weeks before the predicted peak for the dry and wet seasons, respectively.

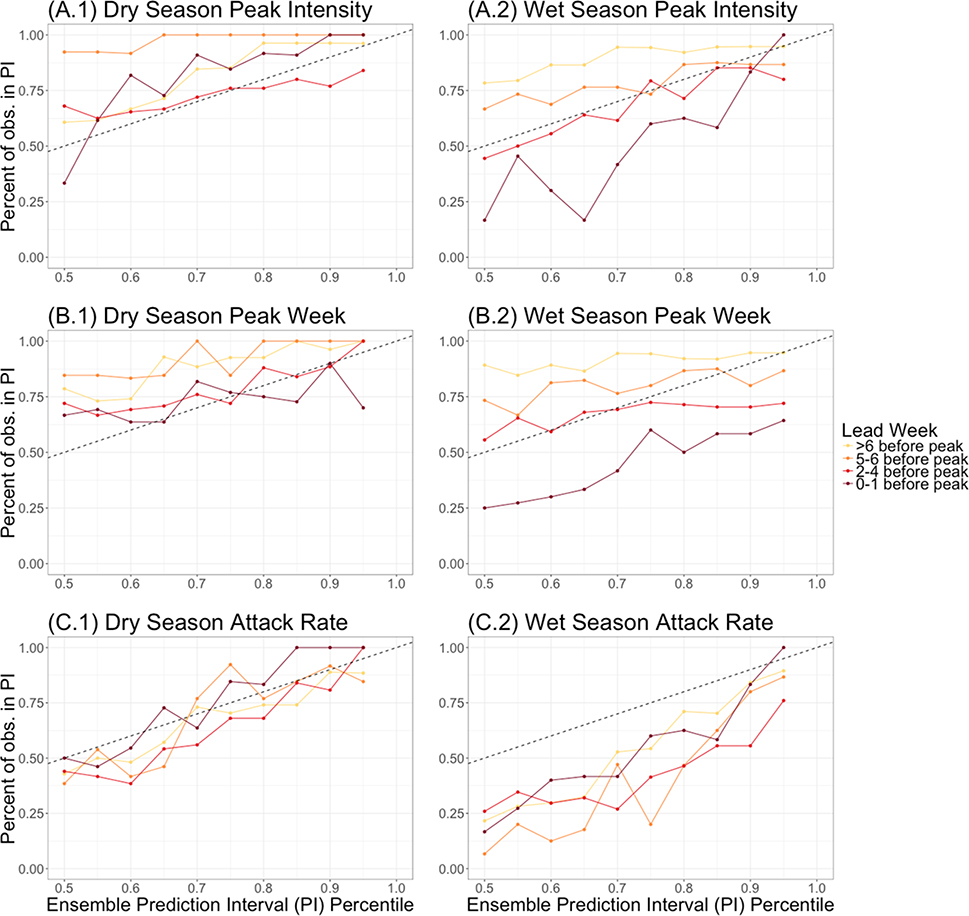
Calibration

Forecasts were generally well calibrated but were better calibrated in the dry season than the wet season (Figure 6). Forecasts of attack rate made prior to the predicted peak were well calibrated in the dry season, but underdispersed in the wet season. Model prediction intervals for dry season peak week timing and peak intensity were well calibrated when made 0–4 weeks before the predicted peak, but slightly overdispersed when made more than 4 weeks in advance. In contrast, wet season forecasts made 2–6 weeks before the predicted peak were well calibrated, but forecasts made 0–1 weeks before the peak were underdispersed and those made 6 or more weeks before the peak were overdispersed.

Figure 6.

Calibration across seasons and accuracy metrics. Calibration of forecasts generated before the predicted peak are shown by the solid colored lines. The x-axis represents the ensemble prediction interval (PI) percentiles of the forecasts and the y-axis represents the percent of observations that fall within those prediction intervals. The dashed line represents a 1:1 line of an ideally calibrated forecast model. Calibration is shown for (A) peak intensity, (B) peak week timing, and (C) overall attack rate.

Discussion

In this paper we estimated epidemiologically important syndromic parameters for under-5 diarrhea outbreaks in Botswana and demonstrated that a compartmental model coupled with data assimilation can be used to generate accurate forecasts of diarrheal disease. Compartmental epidemiological models are commonly used to model the propagation of a single pathogen through a population, but here we employ this model form to simulate a syndrome. Similar applications of compartmental models have been used for influenza-like illness, which represents multiple, non-specified respiratory pathogens that vary from year-to-year (Shaman and Karspeck, 2012, Biggerstaff et al., 2016).

Utilizing a compartmental model to represent a syndrome implies that parameter estimates must be interpreted carefully. In an SIRS model representing the dynamics of one pathogen, R₀ represents the number of secondary infections resulting from one infected individual in a completely susceptible population, and δ represents the rate of waning immunity to that pathogen (Diekmann and Heesterbeek, 2000). Here, R₀ describes the force of transmission for one or more pathogens that vary through time and δ describes the typical period between infections rather than waning immunity, per se. Our findings showed that R₀ estimates were higher on average in the wet season (1.94) than the dry season (1.67) but varied largely across years. These R₀ estimates generally fall within established R₀ ranges for specific diarrhea-causing pathogens (Table 1). Our average estimates for δ were similar between seasons, but also differed greatly among years.

Table 1.

R₀ estimates for diarrhea-causing pathogens

	R0	Reference
E.coli 0157:H7	~1	(Woolhouse, 2002)
Shigellosis	1.02–2.3	(Joh et al., 2013)
Giardia	1.08	(Waters et al., 2016)
Rotavirus	1.2–25	(de Blasio et al., 2010; Pitzer et al., 2012, 2011, 2009)

These differences in estimated R₀ and δ among years and seasons support the notion that the dominant diarrhea causing pathogens vary over time; however, we cannot infer which particular pathogens are prevalent in a given season or year. Further, the limited number of systematic etiologic studies in Botswana prevents determination of the pathogens responsible for diarrhea outbreaks across seasons and years; however, there is an expectance that dry and wet season pathogens differ. For instance, studies have shown that rotavirus prevalence in Botswanan children is highest during the dry season (June-October).

The model-inference system developed here was also able to accurately simulate and predict under-5 diarrhea outbreaks. Forecasts of under-5 diarrhea with higher accuracy than historical predictions (i.e., predictions based on historical distributions) were generated up to six weeks before the predicted peak of the outbreak, and accuracy increased over the progression of the outbreak. Most notably, forecast accuracies for dry season peak week timing and total attack rate, as well as wet season total attack rate, were higher than historical prediction accuracies prior to the predicted peak. In addition, forecasts generated after the predicted peak for all metrics and seasons were more accurate than historical predictions. Forecasts after the peak remain important for affirming that cases will not rise higher in the future and for quantifying overall attack rates.

Such accurate predictions of under-5 diarrhea outbreaks, if generated in real time, could help officials anticipate, respond to, and mitigate childhood diarrhea outbreaks. The majority of diarrhea-related deaths and cases of extreme dehydration can be prevented with a cheap and simple mixture of clean water, sugar, and salt called oral rehydration salts (ORS) (Desforges et al., 1990). Predictions of peak timing and peak intensity at several week lead times could help inform vaccine distribution, hospital and clinic staffing, and the management of healthcare supplies (e.g. ORS) and beds in anticipation of patient surges. Public health warnings and intervention recommendations are being distributed in Botswana by the Government through different media including SMS messages to owners of cell phones. This forecast system could inform the timing of public health messaging for at risk populations. Predictions may also increase household health behaviors. For example, parents may focus more effort on securing safer sources of water that might be purchased, filtered or boiled; increasing hand washing; and making sure their children avoid close contact with other children while sick. Predictions could also influence health-seeking behaviors. Heightened awareness of the impending peak of diarrheal disease cases may sensitize parents to the threat and encourage greater communication and response to diarrheal disease in the household.

While these forecast models have potential to improve children’s health, the real-time surveillance data they require are rarely available. Here, we have demonstrated forecast accuracy using retrospective data. To generate operational, real-time forecasts, under-5 diarrhea incidence would need to be surveilled and made available to modelers quickly and regularly. The Botswana Integrated Disease Surveillance and Response Program (IDSR) was developed to provide healthcare professionals with information about ongoing disease outbreaks in Botswana. This data is not, however, available to the public. Even if data were accessible, long lag times between patient presentation and public release of data greatly reduce the utility of predictive models such as the one we present here. Hence, researchers, healthcare providers, and public health workers in Botswana and around the world must promote and support the collection of high quality real time diarrhea surveillance that can be accessed quickly and used to inform public health responses.