“Stay nearby or get checked”: A Covid-19 control strategy

Abstract

This paper repurposes the classic insight from network theory that long-distance connections drive disease propagation into a strategy for controlling a second wave of Covid-19. We simulate a scenario in which a lockdown is first imposed on a population and then partly lifted while long-range transmission is kept at a minimum. Simulated spreading patterns resemble contemporary distributions of Covid- 19 across EU member states, German and Italian regions, and through New York City, providing some model validation. Results suggest that our proposed strategy may significantly reduce peak infection. We also find that post-lockdown flare-ups remain local longer, aiding geographical containment. These results suggest a tailored policy in which individuals who frequently travel to places where they interact with many people are offered greater protection, tracked more closely, and are regularly tested. This policy can be communicated to the general public as a simple and reasonable principle: Stay nearby or get checked.

1. Introduction

Many countries facing the spread of Covid-19 are currently exiting a lockdown regime in which person-to-person contact was severely restricted. The constraints placed on social and economic interaction have had high cost. Public supportfor nation-wide restraints on freedom of movement has waned. This raises the question: what alternative control strategies may be possible that are less taxing?

Here we explore the leverage gained from differentiating between short-distance and long-distance ties in post-lockdown policy. The idea is that the blockage of transmission through long-distance ties increases the effective diameter of a network, which is inversely related to the speed of propagation (Kretzschmar & Wallinga, 2009; Wallinga et al., 1999). In practice, such geographic differentiation may be achieved through location tracking technologies and prioritization of non-local travel and transport in policy restrictions, enforcement and medical testing. The relative sparsity of long-range ties may make tight control feasible through a focus of resources on a small number of key individuals or interactions.

Results show that reductions in transmission through long-range ties slow down Covid- 19 to a much greater extent than reductions in short-range ties. Selective scrutiny of long-distance ties has two added benefits: Post-lockdown flare-ups of Covid-19 are local, allowing geographically focused interventions that are of limited economic damage and logistically more feasible. And social toll is diminished, as the intimacy of human relations and need for face-to-face contact are known to decrease sharply with geographical distance (Park, 1924; Zipf, 1949; Granovetter, 1983; Marsden & Campbell, 1984; LatanéJames et al., 1995; Groh et al., 2013; Kaltenbrunner et al., 2012).

Our paper is organized as follows. In section 2 we describe our proposed strategy. In section 3 we describe our mathematical model and validate it against the data. In section 4 we present the results of model simulations. Section 5 summarizes our findings and recommendations.

2. Related work

Social network models of disease spreading have been around for decades. What sets our work apart is an analysis of the epidemiological leverage of government policies that differentiate long-distance from short-distance ties in social networks.

2.1. Social network models of infectious disease spread

Many epidemiological studies assume random mixing of individuals within demographic subgroups (e.g. by age) (Manzo & van der Rijt, 2020; Prem et al., 2020). However, most contact occurs between people who live very close to one another (Butts & Carley, 2002; Ferguson et al., 2006). We draw on the well-known small-world model of Watts and Strogatz (Watts & Strogatz, 1998) to capture the fundamental difference in viral risk between close-range and long-range ties: Close-range ties connect infected individuals with others who are already infected or are about to regardless. Long-range ties expose faraway contacts who would otherwise not be at risk and who may in turn infect others who are otherwise safe. The small-world approach to the study of epidemiological dynamics is not new. Network analysis was introduced into mainstream epidemiology at the turn of the century to explicitly incorporate the contact structure among individuals. It is well known that diffusion processes on networks depend on the corresponding connectivity patterns (Kleinberg, 2007, chap. 24). Research has shown that subtle features of the network structure have a major impact on the transmission of an epidemic (Sun and Gao, 2007, 2018) and that social networks can be modelled through random modifications of regular networks, such as lattice networks (Watts & Strogatz, 1998; Kleinberg, 2000). This subtle difference consists of a small portion of random ties to distant localities on the lattice, producing a dramatic reduction in a network’s diameter. The epidemiological dynamics on such networks has been examined for a range of models in (Keeling & Eames, 2005; Moore & Newman, 2000; Newman, 2002), which all show that the speed of the spread is inversely proportional to the diameter. As social networks have a small diameter (the well known six degrees of freedom), epidemics are hard to contain in time within confined regions of a population.

Since all social network show similar epidemiological dynamics,1 we choose to model the covid19 epidemic on a small-world graph, which is a very well understood model. A small-world SEIR model was used in (Younsi, Ahmed, Hamdadou, & Omar, 2015) to model an influenza outbreak in the city of Oran (Algeria). In a study closest to ours, Small and Tse investigate disease spread in a small-world network with separate infection probabilities for short-distance and long-distance ties (Small & Tse, 2005). Using a SEIR model of the SARS epidemic dynamics they find that exponential growth in infection occurs upon onset of several non-local infections. They conclude that key to capturing the empirically observed transmission dynamics is differentiating local from non-local transmission probabilities. We build on this observation to explore the leverage that the targeting of Covid-19 post-lockdown policies at reductions of non-local transmission may provide to global, national, or regional policy makers.

2.2. Interventions

In epidemiological models effects of both general and targeted interventions on disease spread have been studied (Halloran, Ferguson, & Stephen, 2008). General interventions such as social distancing and school closures aim to bring down overall infection probabilities or those within and between demographic subgroups (Prem et al., 2020). Targeted interventions seek to identify high-risk individuals: Antiviral treatment and household isolation of identified cases, prophylaxis and quarantine of household members. We propose a different kind of targeting that is not aimed at specific nodes but at high-impact edges of a network.

A challenge faced by contemporary policy makers is when and how to ease interventions. How can a second wave be minimized while at the same time preventing enormous economic costs? It is well known that when a lockdown is lifted, a virus tends to reappear (Ferguson, Laydon, & Nedjati-Gilani, 2020) and this has indeed happened in many countries. How can a second wave be contained while at the same time preventing enormous economic costs? Therefore it is of paramount importance to find ways to regain some form of normal life (alleviating lockdown) while at the same time preventing the virus from going viral again. The main idea proposed here is that restricting certain high-risk interactions within the social network may be a better strategy than to restrict those of an entire population. ‘Long-distance’ ties represent interaction between individuals that are dis-tant to each other in a network. Typically this means they are also physically distant, i.e. think of a truck driver that delivers goods to a company on the other side of the country or individuals traveling by plane that encounter each other at airports and in airplanes where social distancing is difficult or next to impossible. Small-world models suggest that long-distance ties greatly accelerate the speed of transmission. Long-range ties stemming from infected individuals allow disease to start spreading in distant other localities and much more often lead to not-yet-infected individuals and regions. At a global level, long ties predominantly involve international highways and airline transportation. Topological properties of airline transportation networks can explain patterns in viral disease spread worldwide (Colizza et al., 2007; Ferguson et al., 2006). At a national level, long ties pertain to mobility through major roads and trains between cities and at a regional level to commuting and local delivery services.

3. Model

3.1. Small world SEIR model

We model the spread of the disease by a small world network, in which each node of the network is either Susceptible, Exposed, Infectious, or Recovered (an SEIR model (Martcheva, 2015; Younsi, Ahmed, Hamdadou, & Omar, 2015)). In this model, nodes are individuals and we extrapolate our results to large communities (countries, continents). Initially, a node is in state S. If it is infected, it moves through states E, I, and R. While in state I, a node may infect each of its neighbors with a probability r per time step (fixed at one day in our simulations). The duration of state E is the incubation period, and the duration of state I is the infection period, both of which are lognormally distributed (Ottino-Loffler, Scott, & Strogatz, 2017). The probability r is our single calibration parameter and all other parameters are fixed according to values that have been reported in the literature. In our simulations, the incubation period has a mean of 5 days and the infection time has a mean of 6.5 days, both periods have a standard deviation of 3 days. This is comparable to values reported in (Kucharski, Russell, Diamond, & Liu, 2020; Li et al., 2020a, 2020b; Prem et al., 2020). Each simulation is started by infecting a single random node (patient zero).

The network in our model is the familiar Watts-Strogatz small world network, which distinguishes between short and long ties. For purposes of illustration a small example network with N = 100, k = 20, and p = 0.05 is shown in Fig. 1. It allows us to focus on a policy in which individuals that travel and interact with many people need to be regularly tested (checked). We call this policy: stay nearby or get checked.

Fig. 1.

An example of a Watts-Strogatz small-world graph with N = 100, k = 20 and p = 0.05.

The network is described by two parameters k, p, where k is the number of ties per node, which is equal for all nodes, and p is the fraction of randomly selected long ties. In the simulations we fix N = 10000, k = 20, and p = 0.1, which is in the standard range (Neuman & Mizruchi, 2010) and has been used to model an influenza outbreak in the Oran region of Algeria (Younsi, Ahmed, Hamdadou, & Omar, 2015). Results are robust to reasonable changes in these parameters.

3.2. Model calibration

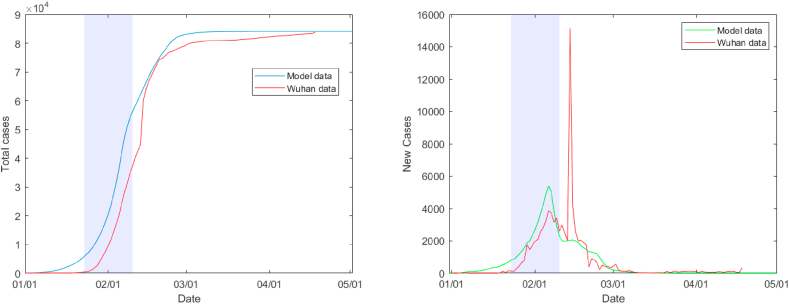
We calibrated our model against the number of infections in Wuhan (source: Johns Hopkins), which went into an initial lockdown from January 23, followed by a heavy lockdown from February 10 (Li et al., 2020b). A substantial number of infections remains undetected and our simulations are based on the estimate that only ten percent of the infected cases are officially confirmed (Li et al., 2020c). After an exposed individual becomes infectious, it may take several days to develop symptoms, and from development of symptoms it takes an average of 5 days to diagnosis (Li et al., 2020b), after which the patient quarantines and no longer spreads the disease. We therefore set the duration of the infectious state to 10 days in our model. We calibrated our model parameter r with values 0.055 in the period before lockdown, 0.0065 for the initial lockdown and 0.0012 for the severe lockdown. By using these values, we were able to reproduce the total number of officially confirmed cases, as demonstrated in Fig. 2 below .

Fig. 2.

Total number of officially confirmed cases (left) and daily number of new cases in the Hubei area. The shaded part represents the initial lockdown, between Jan 23 and Feb 10. The spike in new cases on Feb 12 was due to an inclusion of previously uncounted clinically diagnosed patients. The model data are an average of 200 Monte Carlo simulations.

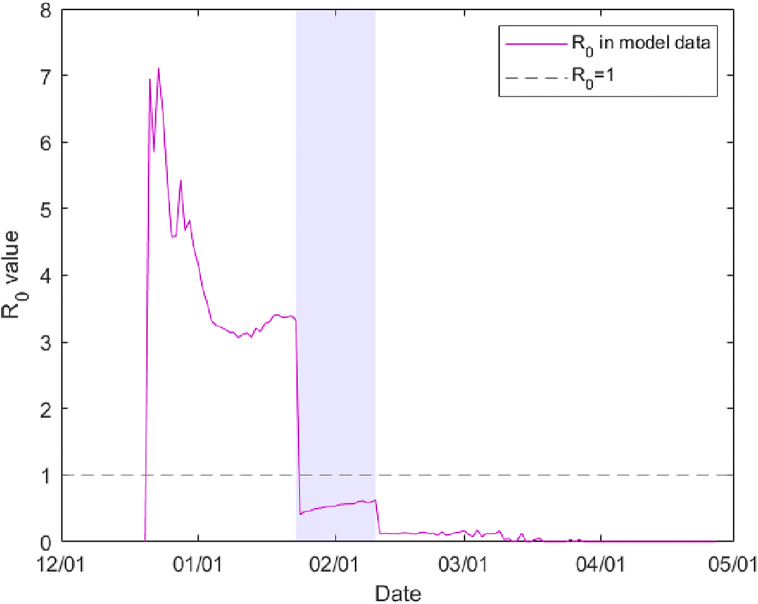
The reproduction number R0 at the onset of the epidemic is equal to r k t in our model. This value is high at the onset, but reduces already before the initial lockdown due to the clustered structure of the network. We find an average R0 = 3.9 pre-lockdown, R0 = 0.54 during the initial lockdown and 0.12 during the severe lockdown (see Fig. 3). These numbers agree with the statistical analysis in (Li et al., 2020b).

Fig. 3.

The computed reproduction number R0 during the simulation reduces from an initial 7.15 (from r = 0.055, k = 20, t = 6.5) but drops even before the lockdown of January 23. Its average is 0.54 during the initial lockdown (shaded area) and reduces even further during the severe lockdown.

We fixed r = 0.055 for all simulations of the spread of the disease before lockdown. We calibrated r after lockdown against the data of several European countries: Italy, Austria, Sweden, Germany (see Fig. 4, Fig. 5, Fig. 6). Italy announced its lockdown relatively late. We used r = 0.01 after lockdown. We find R0 = 4.0 pre-lockdown, which is marginally higher than the 3.8 found in (Li et al., 2020b), and R0 = 0.84 post-lockdown.

Fig. 4.

Daily number of officially confirmed new cases in Italy (left) with r = 0.01 after lockdown. Our simulation starts with a single infected node on January 31 and we set the initial date of the lockdown at March 9, when the government announced nationwide regulations. We plotted one standard deviation difference in dark green, and a 98 percent confidence interval in light green around the model data to illustrate the accuracy of our model. We find an average reproduction number R0 = 4.0 (right) before lockdown and R0 = 0.84 after lockdown.

Fig. 5.

Daily number of officially confirmed new cases in Austria (left) with r = 0.0055 after lockdown. Our simulation starts with a single infected node on February 22 and a lockdown at March 15. We find an average reproduction number R0 = 4.2 (right) before lockdown and R0 = 0.55 after lockdown. Austria implemented a relatively severe lockdown. We found that a parameter value of r = 0.0055 post-lockdown reproduces the number of confirmed cases.

Fig. 6.

A comparison of the daily number of officially confirmed new cases in ten EU countries during March and April 2020. The numbers are averaged over six days. In the right hand figure, this data is adjusted so that the peak of the number of cases occur after 50 days. This is compared to the 99% confidence band of a model computation with r = 0.055 pre-lockdown and r = 0.0075 during lockdown. Not all countries fit in the confidence band because their waves plateaued, while our model shows a sharp peak. The increase and decrease of the wave in our model does match the data.

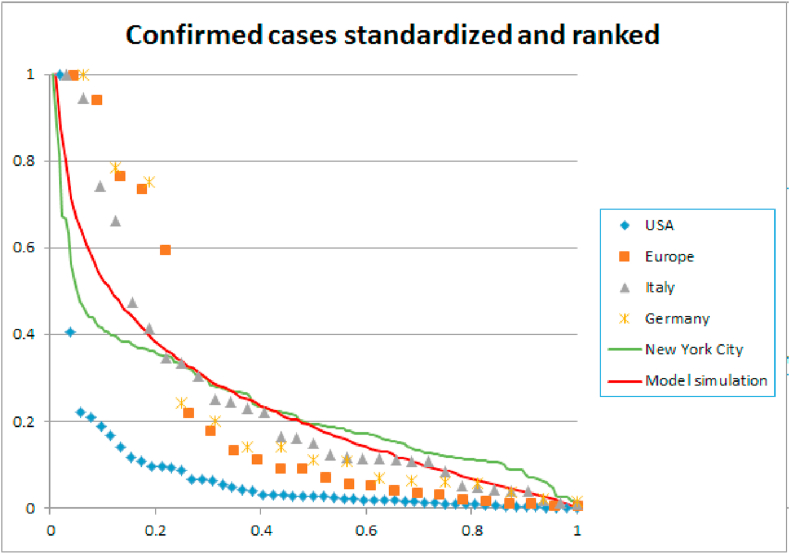
To verify if the spread of the virus in our network model matches the observed spread of the disease, we compare our model to data on different scales: countries (American states, European countries), regions (in Italy and Germany), and cities (New York City zip codes). We order the data from largest to smallest and normalize by dividing by the largest number of cases. We find that the spread of the disease in our network model is comparable to the data, as illustrated in Fig. 7. We summarize our calibration of the model in a table:1.

Fig. 7.

Number of confirmed cases on three different scales: USA and Europe – Regione and Bundeslander – NYC zip codes. The data is ranked from largest to smallest and normalized. On each scale, the spread of the disease displays a similar exponential decay. The figure also shows the spatial distribution of Covid-19 spread in our model after 60 days, 25 days into lockdown. To this end we arbitrarily divided the ring lattice of N = 10,000 nodes into 100 regions of 100 nodes each. The spatial distribution in our network is comparable to the data of Europe, Germany, Italy, and New York City. The spread of the disease in the USA is more concentrated, with an exceptional number of cases in New York and New Jersey.

Table. 1.

Model parameter r compared to the lockdown measures in various countries.

r	Intepretation
0.001	Complete lockdown as in Wuhan after February 10th, 2020. Fully controlled society.
0.005	Severe lockdown as in Austria in March 2020. Strong restrictions on travel, shopping, gatherings.
0.01	Moderate regulations and social distancing. As in many EU countries after March 15, 2020.
0.02	Requested social distancing, but no regulations.
0.055	Pre-lockdown situation. No social distancing.

3.3. Model validation

We calibrated our model against the initial outbreaks in China and the subsequent out-breaks in Europe at the beginning of 2020. In the European Union, the outbreak was followed by a lockdown which was more or less imposed simultaneously and uniformly by all member states in March, and was eased cautiously about three months later by first opening internal borders mid June and then some external borders on 1 July. The response of the USA to the disease was more checkered. After an initial lockdown, which as in the EU began in March, some states eased their regulations at the end of April, and others did this one month later. This was followed by more tightened regulations at the end of July.

We validated our model against the number of infections in the EU and the USA using the calibrated parameters. For our simulation of the number of infections in the EU, we varied r uniformly. It was set at 0.01 during lockdown, and 0.015 post-lockdown. For the USA we used a more varied approach. The lockdown was shorter and was followed by a post-lockdown parameter of 0.02 for a major part of the network and 0.015 for a minor part of the network. This was followed by a reduction to 0.01 fifty days later. The results in Fig. 8 show that our small word SEIR model is able to reproduce the transmission of the disease quite well.

Fig. 8.

Number of infections per 1 million of the population (source:Johns Hopkins). Europe versus USA. Our model parameters were r = 0.01 during a lockdown of hundred days in the EU and sixty days in the USA. For the post-lockdown period we used r = 0.015 for the EU and r = 0.02 for 85 percent of the USA and r = 0.015 for the remaining 15 percent. The post-lockdown in the USA lasted for fifty days in our model computations, after which we reduced the parameter to r = 0.01 for the entire network. To match the number of infections in our model with the real world data, we assumed that currently only 5 percent of positive cases is detected.

4. Impact of a stay-nearby-or-get-checked policy

4.1. Peak reduction

As countries get out of lockdown, restrictions are lifted, and the basic reproduction num-ber will increase, possibly inducing a second wave. Our proposed policy is to control the long ties to flatten the second wave. To simulate this policy, we use the parameters of the calibrated model. During an initial lockdown of 75 days, spreading risk is reduced to r = 0.0075. After lockdown, the parameter is increased to r = 0.02 (requested social distancing, but no regulations), but some fraction of edges is checked, preventing propa-gation along those edges. Fig. 8 contrasts a scenario in which random edges are checked (panel A) with one in which only long edges are checked (panel B). Results show that targeting long edges is efficient. Without intervention a second wave occurs with a peak several times higher than the first. By targeting long ties, checking 7.5% of ties is sufficient to bring the second peak below the first peak, thereby also delaying its occurrence. If instead random ties are chosen the second wave peak remains well above the first.

In Fig. 9 we contrast three post-lockdown strategies for controlling a second wave. Here we use r_short to denote transmission probabilities on all short ties and r_long transmission probabilities on long ties. The first strategy is to not differentiate long ties from short ties (panel A). Results show that at r_long = r_short = 0.02 (requested social distancing without further regulations) the second wave peaks much higher than the first, and that further regulation is needed to control it (see Fig. 11) (see Fig. 10).

Fig. 9.

Peak reduction with baseline r = 0.02 and some edges checked.

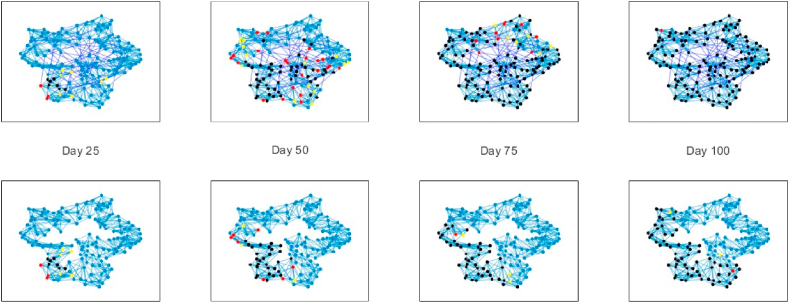
Fig. 11.

Effect of shutting down long-range transmission. From left to right graphs show disease propagation at 25 day intervals in a small-world network with N = 150, k = 10 and p = 0.1. All graphs have r_short = 0.055. The top graphs have r_long = 0.055, while the bottom graphs have r_long = 0. Node color indicates SEIR states, blue = susceptible, yellow = exposed, red = infectious, black = resistant.

Fig. 10.

Three policy approaches to opening up a lockdown of 75 days, with varying post-lockdown levels of r: (a) policy does not differentiate long and short ties, (b) policy targets long ties while all other restrictions are lifted, and (c) policy targets long ties while social distancing is encouraged.

The second strategy is to open up society back to what it was before the pandemic (r_short = 0.055), with no social distancing, and then target the 10% of long ties for checking. Panel B shows various levels of effectiveness in intervening on long ties, varying r_long. Panel B shows that this strategy only works if disease propagation in long ties can be fully prevented. In panel C, society is opened back up but social distancing is requested at an r = 0.02. Now, imperfect checking of long ties r_long = 0.005 can also accomplish a reduction of the second peak below the first.

4.2. Spatial concentration

Post-lockdown flare-ups are more easily controlled with geographically focused efforts when they remain local longer. Economic and social costs of control measures are then also lower. We study the spatial concentration of Covid-19 outbreaks by measuring the number of components of the subgraph of infected nodes and short edges. Fig. 9 compares the spread of the virus for the scenario where r_long = r_short = 0.055 with the alternative scenario where long-range transmission is maximally repressed, r_long = 0. The latter scenario is characterized by a smaller number of components during the second wave. The spread of the virus with r_long = 0 is contained in one region.

5. Discussion and policy

In this paper we have through model simulation explored spatially differentiating policies in which interventions target nonlocal spread of Covid-19. Our results show that reductions of long-distance transmission are highly efficient for curbing the spread of Covid-19. The close monitoring and checking of long-distance ties allows overall policy to be more permissible and still control a second wave. Because flare-ups remain local longer, inter-ventions can be of limited geographical scope and thus less costly and invasive.

What policies could constrain long-range transmission? Medical testing and mobility-tracking apps may be targeted specifically at transport, travel, and delivery. Perhaps medical testing and/or mobility tracking should be encouraged or required for flight, use of highways, trains, regional bus lines and for individuals with jobs in the transport and delivery sector. Self-isolation after exposure of such individuals may perhaps be more stringently enforced. What helps is that long-range ties are relatively sparse, so resources may be focused on a limited number of individuals or activities. That said, our results show that effects are particularly strong when transmission through long-range ties is not just reduced but largely eliminated. This concords with studies showing that international traffic constraints are particularly effective when severe (Ferguson et al., 2006). The logistical, technological and ethical challenges of geographic targeting in location tracking, testing, and police enforcement require further interdisciplinary study.

Finally, we point out that we studied the effect of our proposed policy by a mathematical model, which necessarily leaves out potentially relevant real world details. po In the real world, the pandemic will cease if a sufficient percentage of the population reaches immunity (either through contracting the disease or through immunization). In our model, immunity is only reached if everybody has contracted the disease. The size of our network is in the order of 10 thousand nodes, while the actual scale of the societies that we model is 10–100 million people. Our model is too coarse to model the passing of the epidemic, but it does reproduce its early and middle stage, when government policy can be most effective. The small-world network that we use in our computations is a simple approximation ofactual societal networks. It only has two scales (short and long) while real social networks have more scales, and can even be scale-free. There is a reason to expect that our proposed policy of ‘getting checked’ will be even more effective in the real world than in our model. The small world network lacks highly connected nodes (superspreaders) that contact surveys reveal exist [Manzo & Van de Rijt, 2020]. Such hubs could be efficiently targeted, neutralizing a large fraction of dangerous edges through restrictions on a small number of individuals.

Handling editor: Dr. J Wu